数据结构与算法分析课后题答案
罗文劼《数据结构与算法》第4版-第1章课后习题参考答案

第1章绪论1.选择题(1)C (2)B (3)C (4)D (5)B2.判断题(1)√(2)Ⅹ(3)Ⅹ(4)Ⅹ(5)√3.简答题(1)根据数据元素之间的不同逻辑关系,通常将其划分为哪几类结构?【解答】常见的四种逻辑结构有:①集合结构:数据元素间的关系是“属于同一个集合”。
②线性结构:数据元素之间存在着一对一的关系。
③树型结构:数据元素之间存在着一对多的关系。
④图型结构:数据元素之间存在着多对多的关系。
(2)请描述线性结构中数据元素与数据元素之间的关系特点?【解答】线性结构的特点是数据元素之间是一种线性关系,数据元素“一个接一个的排列”。
在线性结构中,有且仅有一个元素被称为“第一个”,除第一个元素之外其他元素均有唯一一个“前驱”;有且仅有一个元素被称为“最后一个”,除最后一个元素之外其他元素均有唯一一个“后继”。
(3)请描述树形结构中数据元素与数据元素之间的关系特点?【解答】树形存储结构,就是数据元素与元素之间存在着一对多关系的数据结构。
在树形存储结构中,树的根节点没有前驱结点,其余的每个节点有且只有一个前驱结点,除叶子结点没有后续节点外,其他节点的后续节点可以有一个或者多个。
(4)常用的存储结构有哪几种,各自的特点是什么?【解答】常见的四种存储结构有:①顺序存储:把逻辑上相邻的元素存储在物理位置相邻的存储单元中。
顺序存储结构是一种最基本的存储表示方法,通常借助于程序设计语言中的数组来实现。
②链接存储:对逻辑上相邻的元素不要求不要求物理位置相邻的存储单元,元素间的逻辑关系通过附设的指针域来表示。
③索引存储:通过建立索引表存储结点信息的方法,其中索引表一般存储结点关键字和一个地点信息,可通过该地址找到结点其它信息。
④散列存储:根据结点的关键字直接计算出该结点的存储地址的方法。
(5)简述算法和程序的区别。
【解答】一个算法若用程序设计语言来描述,则它就是一个程序。
算法的含义与程序十分相似,但又有区别。
一个程序不一定满足有穷性。
Mark Allen Weiss 数据结构与算法分析 课后习题答案9

This flow is not unique. For instance, two units of the flow that goes from G to D to A to E could go by G to H to E.
-47-
9.12 Let T be the tree with root r , and children r 1, r 2, ..., rk , which are the roots of T 1, T 2, ..., Tk , which have maximum incoming flow of c 1, c 2, ..., ck , respectively. By the problem statement, we may take the maximum incoming flow of r to be infinity. The recursive function FindMaxFlow( T, IncomingCap ) finds the value of the maximum flow in T (finding the actual flow is a matter of bookkeeping); the flow is guaranteed not to exceed IncomingCap . If T is a leaf, then FindMaxFlow returns IncomingCap since we have assumed a sink of infinite capacity. Otherwise, a standard postorder traversal can be used to compute the maximum flow in linear time. _ ______________________________________________________________________________ FlowType FindMaxFlow( Tree T, FlowType IncomingCap ) { FlowType ChildFlow, TotalFlow; if( IsLeaf( T ) ) return IncomingCap; else { TotalFlow = 0; for( each subtree Ti of T ) { ChildFlow = FindMaxFlow( Ti , min( IncomingCap, ci ) ); TotalFlow += ChildFlow; IncomingCap -= ChildFlow; } return TotalFlow; } } _ ______________________________________________________________________________ 9.13 (a) Assume that the graph is connected and undirected. If it is not connected, then apply the algorithm to the connected components. Initially, mark all vertices as unknown. Pick any vertex v , color it red, and perform a depth-first search. When a node is first encountered, color it blue if the DFS has just come from a red node, and red otherwise. If at any point, the depth-first search encounters an edge between two identical colors, then the graph is not bipartite; otherwise, it is. A breadth-first search (that is, using a queue) also works. This problem, which is essentially two-coloring a graph, is clearly solvable in linear time. This contrasts with three-coloring, which is NP-complete. (b) Construct an undirected graph with a vertex for each instructor, a vertex for each course, and an edge between (v ,w ) if instructor v is qualified to teach course w . Such a graph is bipartite; a matching of M edges means that M courses can be covered simultaneously. (c) Give each edge in the bipartite graph a weight of 1, and direct the edge from the instructor to the course. Add a vertex s with edges of weight 1 from s to all instructor vertices. Add a vertex t with edges of weight 1 from all course vertices to t . The maximum flow is equal to the maximum matching.
数据结构与算法分析习题与参考答案
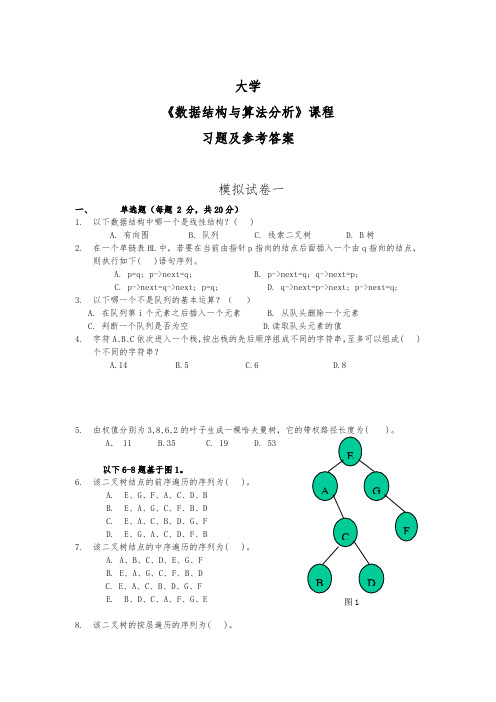
大学《数据结构与算法分析》课程习题及参考答案模拟试卷一一、单选题(每题 2 分,共20分)1.以下数据结构中哪一个是线性结构?( )A. 有向图B. 队列C. 线索二叉树D. B树2.在一个单链表HL中,若要在当前由指针p指向的结点后面插入一个由q指向的结点,则执行如下( )语句序列。
A. p=q; p->next=q;B. p->next=q; q->next=p;C. p->next=q->next; p=q;D. q->next=p->next; p->next=q;3.以下哪一个不是队列的基本运算?()A. 在队列第i个元素之后插入一个元素B. 从队头删除一个元素C. 判断一个队列是否为空D.读取队头元素的值4.字符A、B、C依次进入一个栈,按出栈的先后顺序组成不同的字符串,至多可以组成( )个不同的字符串?A.14B.5C.6D.85.由权值分别为3,8,6,2的叶子生成一棵哈夫曼树,它的带权路径长度为( )。
以下6-8题基于图1。
6.该二叉树结点的前序遍历的序列为( )。
A.E、G、F、A、C、D、BB.E、A、G、C、F、B、DC.E、A、C、B、D、G、FD.E、G、A、C、D、F、B7.该二叉树结点的中序遍历的序列为( )。
A. A、B、C、D、E、G、FB. E、A、G、C、F、B、DC. E、A、C、B、D、G、FE.B、D、C、A、F、G、E8.该二叉树的按层遍历的序列为( )。
A.E、G、F、A、C、D、B B. E、A、C、B、D、G、FC. E、A、G、C、F、B、DD. E、G、A、C、D、F、B9.下面关于图的存储的叙述中正确的是( )。
A.用邻接表法存储图,占用的存储空间大小只与图中边数有关,而与结点个数无关B.用邻接表法存储图,占用的存储空间大小与图中边数和结点个数都有关C. 用邻接矩阵法存储图,占用的存储空间大小与图中结点个数和边数都有关D.用邻接矩阵法存储图,占用的存储空间大小只与图中边数有关,而与结点个数无关10.设有关键码序列(q,g,m,z,a,n,p,x,h),下面哪一个序列是从上述序列出发建堆的结果?( )A. a,g,h,m,n,p,q,x,zB. a,g,m,h,q,n,p,x,zC. g,m,q,a,n,p,x,h,zD. h,g,m,p,a,n,q,x,z二、填空题(每空1分,共26分)1.数据的物理结构被分为_________、________、__________和___________四种。
Mark Allen Weiss 数据结构与算法分析 课后习题答案8

8.1 We assume that unions operated on the roots of the trees containing the arguments. Also, in case of ties, the second tree is made a child of the first. Arbitrary union and union by height give the same answer (shown as the first tree) for this problem. Union by size gives the second tree. 1 2 6 4 5 7 3 10 11 12 8 2 8.4 In both cases, have nodes 16 and 17 point directly to the root. Claim: A tree of height H has at least 2H nodes. The proof is by induction. A tree of height 0 clearly has at least 1 node, and a tree of height 1 clearly has at least 2. Let T be the tree of height H with fewest nodes. Thus at the time of T ’s last union, it must have been a tree of height H −1, since otherwise T would have been smaller at that time than it is now and still would have been of height H , which is impossible by assumption of T ’s minimality. Since T ’s height was updated, it must have been as a result of a union with another tree of height H −1. By the induction hypothesis, we know that at the time of the union, T had at least 2H −1 nodes, as did the tree attached to it, for a total of 2H nodes, proving the claim. Thus an N -node tree has depth at most log N . All answers are O (M ) because in all cases α(M , N ) = 1. Assuming that the graph has only nine vertices, then the union/find tree that is formed is shown here. The edge (4,6) does not result in a union because at the time it is examined, 4 and 6 are already in the same component. The connected components are {1,2,3,4,6} and 4 5 7 10 11 12 13 14 15 16 17
Mark Allen Weiss 数据结构与算法分析 课后习题答案11

Chapter11:Amortized Analysis11.1When the number of trees after the insertions is more than the number before.11.2Although each insertion takes roughly log N ,and each DeleteMin takes2log N actualtime,our accounting system is charging these particular operations as2for the insertion and3log N −2for the DeleteMin. The total time is still the same;this is an accounting gimmick.If the number of insertions and DeleteMins are roughly equivalent,then it really is just a gimmick and not very meaningful;the bound has more significance if,for instance,there are N insertions and O (N / log N )DeleteMins (in which case,the total time is linear).11.3Insert the sequence N ,N +1,N −1,N +2,N −2,N +3,...,1,2N into an initiallyempty skew heap.The right path has N nodes,so any operation could takeΩ(N )time. 11.5We implement DecreaseKey(X,H)as follows:If lowering the value of X creates a heaporder violation,then cut X from its parent,which creates a new skew heap H 1with the new value of X as a root,and also makes the old skew heap H smaller.This operation might also increase the potential of H ,but only by at most log N .We now merge H andH 1.The total amortized time of the Merge is O (log N ),so the total time of theDecreaseKey operation is O (log N ).11.8For the zig −zig case,the actual cost is2,and the potential change isR f ( X )+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )− R i ( G ).This gives an amortized time bound ofAT zig −zig =2+ R f ( X )+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )− R i ( G )Since R f ( X )= R i ( G ),this reduces to=2+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )Also,R f ( X )> R f ( P )and R i ( X )< R i ( P ),soAT zig −zig <2+ R f ( X )+ R f ( G )−2R i ( X )Since S i ( X )+ S f ( G )< S f ( X ),it follows that R i ( X )+ R f ( G )<2R f ( X )−2.ThusAT zig −zig <3R f ( X )−3R i ( X )11.9(a)Choose W (i )=1/ N for each item.Then for any access of node X ,R f ( X )=0,andR i ( X )≥−log N ,so the amortized access for each item is at most3log N +1,and the net potential drop over the sequence is at most N log N ,giving a bound of O (M log N + M + N log N ),as claimed.(b)Assign a weight of q i /M to items i .Then R f ( X )=0,R i ( X )≥log(q i /M ),so theamortized cost of accessing item i is at most3log(M /q i )+1,and the theorem follows immediately.11.10(a)To merge two splay trees T 1and T 2,we access each node in the smaller tree andinsert it into the larger tree.Each time a node is accessed,it joins a tree that is at leasttwice as large;thus a node can be inserted log N times.This tells us that in any sequence of N −1merges,there are at most N log N inserts,giving a time bound of O (N log2N ).This presumes that we keep track of the tree sizes.Philosophically,this is ugly since it defeats the purpose of self-adjustment.(b)Port and Moffet[6]suggest the following algorithm:If T 2is the smaller tree,insert itsroot into T 1.Then recursively merge the left subtrees of T 1and T 2,and recursively merge their right subtrees.This algorithm is not analyzed;a variant in which the median of T 2is splayed to the rootfirst is with a claim of O (N log N )for the sequence of merges.11.11The potential function is c times the number of insertions since the last rehashing step,where c is a constant.For an insertion that doesn’t require rehashing,the actual time is 1,and the potential increases by c ,for a cost of1+ c .If an insertion causes a table to be rehashed from size S to2S ,then the actual cost is 1+ dS ,where dS represents the cost of initializing the new table and copying the old table back.A table that is rehashed when it reaches size S was last rehashed at size S / 2, so S / 2insertions had taken place prior to the rehash,and the initial potential was cS / 2.The new potential is0,so the potential change is−cS / 2,giving an amortized bound of(d − c / 2)S +1.We choose c =2d ,and obtain an O (1)amortized bound in both cases.11.12We show that the amortized number of node splits is1per insertion.The potential func-tion is the number of three-child nodes in T .If the actual number of nodes splits for an insertion is s ,then the change in the potential function is at most1− s ,because each split converts a three-child node to two two-child nodes,but the parent of the last node split gains a third child(unless it is the root).Thus an insertion costs1node split,amor-tized.An N node tree has N units of potential that might be converted to actual time,so the total cost is O (M + N ).(If we start from an initially empty tree,then the bound is O (M ).)11.13(a)This problem is similar to Exercise3.22.Thefirst four operations are easy to imple-ment by placing two stacks,S L and S R ,next to each other(with bottoms touching).We can implement thefifth operation by using two more stacks,M L and M R (which hold minimums).If both S L and S R never empty,then the operations can be implemented as follows:Push(X,D):push X onto S L ;if X is smaller than or equal to the top of M L ,push X onto M L as well.Inject(X,D):same operation as Push ,except use S R and M R .Pop(D):pop S L ;if the popped item is equal to the top of M L ,then pop M L as well.Eject(D):same operation as Pop ,except use S R and M R .FindMin(D):return the minimum of the top of M L and M R .These operations don’t work if either S L or S R is empty.If a Pop or E j ect is attempted on an empty stack,then we clear M L and M R .We then redistribute the elements so that half are in S L and the rest in S R ,and adjust M L and M R to reflect what the state would be.We can then perform the Pop or E j ect in the normal fashion.Fig. 11.1shows a transfor-mation.Define the potential function to be the absolute value of the number of elements in S L minus the number of elements in S R .Any operation that doesn’t empty S L or S R can3,1,4,6,5,9,2,61,2,63,1,4,65,9,2,6 1,4,65,2S L S R M L RL S RM L M R Fig.11.1.increase the potential by only1;since the actual time for these operations is constant,so is the amortized time.To complete the proof,we show that the cost of a reorganization is O (1)amortized time. Without loss of generality,if S R is empty,then the actual cost of the reorganization is | S L | units.The potential before the reorganization is | S L | ;afterward,it is at most1. Thus the potential change is1− | S L | ,and the amortized bound follows.。
《数据结构与算法分析》(C++第二版)【美】Clifford A.Shaffer著 课后习题答案 二

《数据结构与算法分析》(C++第二版)【美】Clifford A.Shaffer著课后习题答案二5Binary Trees5.1 Consider a non-full binary tree. By definition, this tree must have some internalnode X with only one non-empty child. If we modify the tree to removeX, replacing it with its child, the modified tree will have a higher fraction ofnon-empty nodes since one non-empty node and one empty node have been removed.5.2 Use as the base case the tree of one leaf node. The number of degree-2 nodesis 0, and the number of leaves is 1. Thus, the theorem holds.For the induction hypothesis, assume the theorem is true for any tree withn − 1 nodes.For the induction step, consider a tree T with n nodes. Remove from the treeany leaf node, and call the resulting tree T. By the induction hypothesis, Thas one more leaf node than it has nodes of degree 2.Now, restore the leaf node that was removed to form T. There are twopossible cases.(1) If this leaf node is the only child of its parent in T, then the number ofnodes of degree 2 has not changed, nor has the number of leaf nodes. Thus,the theorem holds.(2) If this leaf node is the child of a node in T with degree 2, then that nodehas degree 1 in T. Thus, by restoring the leaf node we are adding one newleaf node and one new node of degree 2. Thus, the theorem holds.By mathematical induction, the theorem is correct.32335.3 Base Case: For the tree of one leaf node, I = 0, E = 0, n = 0, so thetheorem holds.Induction Hypothesis: The theorem holds for the full binary tree containingn internal nodes.Induction Step: Take an arbitrary tree (call it T) of n internal nodes. Selectsome internal node x from T that has two leaves, and remove those twoleaves. Call the resulting tree T’. Tree T’ is full and has n−1 internal nodes,so by the Induction Hypothesis E = I + 2(n − 1).Call the depth of node x as d. Restore the two children of x, each at leveld+1. We have nowadded d to I since x is now once again an internal node.We have now added 2(d + 1) − d = d + 2 to E since we added the two leafnodes, but lost the contribution of x to E. Thus, if before the addition we had E = I + 2(n − 1) (by the induction hypothesis), then after the addition we have E + d = I + d + 2 + 2(n − 1) or E = I + 2n which is correct. Thus,by the principle of mathematical induction, the theorem is correct.5.4 (a) template <class Elem>void inorder(BinNode<Elem>* subroot) {if (subroot == NULL) return; // Empty, do nothingpreorder(subroot->left());visit(subroot); // Perform desired actionpreorder(subroot->right());}(b) template <class Elem>void postorder(BinNode<Elem>* subroot) {if (subroot == NULL) return; // Empty, do nothingpreorder(subroot->left());preorder(subroot->right());visit(subroot); // Perform desired action}5.5 The key is to search both subtrees, as necessary.template <class Key, class Elem, class KEComp>bool search(BinNode<Elem>* subroot, Key K);if (subroot == NULL) return false;if (subroot->value() == K) return true;if (search(subroot->right())) return true;return search(subroot->left());}34 Chap. 5 Binary Trees5.6 The key is to use a queue to store subtrees to be processed.template <class Elem>void level(BinNode<Elem>* subroot) {AQueue<BinNode<Elem>*> Q;Q.enqueue(subroot);while(!Q.isEmpty()) {BinNode<Elem>* temp;Q.dequeue(temp);if(temp != NULL) {Print(temp);Q.enqueue(temp->left());Q.enqueue(temp->right());}}}5.7 template <class Elem>int height(BinNode<Elem>* subroot) {if (subroot == NULL) return 0; // Empty subtreereturn 1 + max(height(subroot->left()),height(subroot->right()));}5.8 template <class Elem>int count(BinNode<Elem>* subroot) {if (subroot == NULL) return 0; // Empty subtreeif (subroot->isLeaf()) return 1; // A leafreturn 1 + count(subroot->left()) +count(subroot->right());}5.9 (a) Since every node stores 4 bytes of data and 12 bytes of pointers, the overhead fraction is 12/16 = 75%.(b) Since every node stores 16 bytes of data and 8 bytes of pointers, the overhead fraction is 8/24 ≈ 33%.(c) Leaf nodes store 8 bytes of data and 4 bytes of pointers; internal nodesstore 8 bytes of data and 12 bytes of pointers. Since the nodes havedifferent sizes, the total space needed for internal nodes is not the sameas for leaf nodes. Students must be careful to do the calculation correctly,taking the weighting into account. The correct formula looks asfollows, given that there are x internal nodes and x leaf nodes.4x + 12x12x + 20x= 16/32 = 50%.(d) Leaf nodes store 4 bytes of data; internal nodes store 4 bytes of pointers. The formula looks as follows, given that there are x internal nodes and35x leaf nodes:4x4x + 4x= 4/8 = 50%.5.10 If equal valued nodes were allowed to appear in either subtree, then during a search for all nodes of a given value, whenever we encounter a node of that value the search would be required to search in both directions.5.11 This tree is identical to the tree of Figure 5.20(a), except that a node with value 5 will be added as the right child of the node with value 2.5.12 This tree is identical to the tree of Figure 5.20(b), except that the value 24 replaces the value 7, and the leaf node that originally contained 24 is removed from the tree.5.13 template <class Key, class Elem, class KEComp>int smallcount(BinNode<Elem>* root, Key K);if (root == NULL) return 0;if (KEComp.gt(root->value(), K))return smallcount(root->leftchild(), K);elsereturn smallcount(root->leftchild(), K) +smallcount(root->rightchild(), K) + 1;5.14 template <class Key, class Elem, class KEComp>void printRange(BinNode<Elem>* root, int low,int high) {if (root == NULL) return;if (KEComp.lt(high, root->val()) // all to leftprintRange(root->left(), low, high);else if (KEComp.gt(low, root->val())) // all to rightprintRange(root->right(), low, high);else { // Must process both childrenprintRange(root->left(), low, high);PRINT(root->value());printRange(root->right(), low, high);}}5.15 The minimum number of elements is contained in the heap with a single node at depth h − 1, for a total of 2h−1 nodes.The maximum number of elements is contained in the heap that has completely filled up level h − 1, for a total of 2h − 1 nodes.5.16 The largest element could be at any leaf node.5.17 The corresponding array will be in the following order (equivalent to level order for the heap):12 9 10 5 4 1 8 7 3 236 Chap. 5 Binary Trees5.18 (a) The array will take on the following order:6 5 3 4 2 1The value 7 will be at the end of the array.(b) The array will take on the following order:7 4 6 3 2 1The value 5 will be at the end of the array.5.19 // Min-heap classtemplate <class Elem, class Comp> class minheap {private:Elem* Heap; // Pointer to the heap arrayint size; // Maximum size of the heapint n; // # of elements now in the heapvoid siftdown(int); // Put element in correct placepublic:minheap(Elem* h, int num, int max) // Constructor{ Heap = h; n = num; size = max; buildHeap(); }int heapsize() const // Return current size{ return n; }bool isLeaf(int pos) const // TRUE if pos a leaf{ return (pos >= n/2) && (pos < n); }int leftchild(int pos) const{ return 2*pos + 1; } // Return leftchild posint rightchild(int pos) const{ return 2*pos + 2; } // Return rightchild posint parent(int pos) const // Return parent position { return (pos-1)/2; }bool insert(const Elem&); // Insert value into heap bool removemin(Elem&); // Remove maximum value bool remove(int, Elem&); // Remove from given pos void buildHeap() // Heapify contents{ for (int i=n/2-1; i>=0; i--) siftdown(i); }};template <class Elem, class Comp>void minheap<Elem, Comp>::siftdown(int pos) { while (!isLeaf(pos)) { // Stop if pos is a leafint j = leftchild(pos); int rc = rightchild(pos);if ((rc < n) && Comp::gt(Heap[j], Heap[rc]))j = rc; // Set j to lesser child’s valueif (!Comp::gt(Heap[pos], Heap[j])) return; // Done37swap(Heap, pos, j);pos = j; // Move down}}template <class Elem, class Comp>bool minheap<Elem, Comp>::insert(const Elem& val) { if (n >= size) return false; // Heap is fullint curr = n++;Heap[curr] = val; // Start at end of heap// Now sift up until curr’s parent < currwhile ((curr!=0) &&(Comp::lt(Heap[curr], Heap[parent(curr)]))) {swap(Heap, curr, parent(curr));curr = parent(curr);}return true;}template <class Elem, class Comp>bool minheap<Elem, Comp>::removemin(Elem& it) { if (n == 0) return false; // Heap is emptyswap(Heap, 0, --n); // Swap max with last valueif (n != 0) siftdown(0); // Siftdown new root valit = Heap[n]; // Return deleted valuereturn true;}38 Chap. 5 Binary Trees// Remove value at specified positiontemplate <class Elem, class Comp>bool minheap<Elem, Comp>::remove(int pos, Elem& it) {if ((pos < 0) || (pos >= n)) return false; // Bad posswap(Heap, pos, --n); // Swap with last valuewhile ((pos != 0) &&(Comp::lt(Heap[pos], Heap[parent(pos)])))swap(Heap, pos, parent(pos)); // Push up if largesiftdown(pos); // Push down if small keyit = Heap[n];return true;}5.20 Note that this summation is similar to Equation 2.5. To solve the summation requires the shifting technique from Chapter 14, so this problem may be too advanced for many students at this time. Note that 2f(n) − f(n) = f(n),but also that:2f(n) − f(n) = n(24+48+616+ ··· +2(log n − 1)n) −n(14+28+316+ ··· +log n − 1n)logn−1i=112i− log n − 1n)= n(1 − 1n− log n − 1n)= n − log n.5.21 Here are the final codes, rather than a picture.l 00h 010i 011e 1000f 1001j 101d 11000a 1100100b 1100101c 110011g 1101k 11139The average code length is 3.234455.22 The set of sixteen characters with equal weight will create a Huffman coding tree that is complete with 16 leaf nodes all at depth 4. Thus, the average code length will be 4 bits. This is identical to the fixed length code. Thus, in this situation, the Huffman coding tree saves no space (and costs no space).5.23 (a) By the prefix property, there can be no character with codes 0, 00, or 001x where “x” stands for any binary string.(b) There must be at least one code with each form 1x, 01x, 000x where“x” could be any binary string (including the empty string).5.24 (a) Q and Z are at level 5, so any string of length n containing only Q’s and Z’s requires 5n bits.(b) O and E are at level 2, so any string of length n containing only O’s and E’s requires 2n bits.(c) The weighted average is5 ∗ 5 + 10 ∗ 4 + 35 ∗ 3 + 50 ∗ 2100bits per character5.25 This is a straightforward modification.// Build a Huffman tree from minheap h1template <class Elem>HuffTree<Elem>*buildHuff(minheap<HuffTree<Elem>*,HHCompare<Elem> >* hl) {HuffTree<Elem> *temp1, *temp2, *temp3;while(h1->heapsize() > 1) { // While at least 2 itemshl->removemin(temp1); // Pull first two treeshl->removemin(temp2); // off the heaptemp3 = new HuffTree<Elem>(temp1, temp2);hl->insert(temp3); // Put the new tree back on listdelete temp1; // Must delete the remnantsdelete temp2; // of the trees we created}return temp3;}6General Trees6.1 The following algorithm is linear on the size of the two trees. // Return TRUE iff t1 and t2 are roots of identical// general treestemplate <class Elem>bool Compare(GTNode<Elem>* t1, GTNode<Elem>* t2) { GTNode<Elem> *c1, *c2;if (((t1 == NULL) && (t2 != NULL)) ||((t2 == NULL) && (t1 != NULL)))return false;if ((t1 == NULL) && (t2 == NULL)) return true;if (t1->val() != t2->val()) return false;c1 = t1->leftmost_child();c2 = t2->leftmost_child();while(!((c1 == NULL) && (c2 == NULL))) {if (!Compare(c1, c2)) return false;if (c1 != NULL) c1 = c1->right_sibling();if (c2 != NULL) c2 = c2->right_sibling();}}6.2 The following algorithm is Θ(n2).// Return true iff t1 and t2 are roots of identical// binary treestemplate <class Elem>bool Compare2(BinNode<Elem>* t1, BinNode<Elem* t2) { BinNode<Elem> *c1, *c2;if (((t1 == NULL) && (t2 != NULL)) ||((t2 == NULL) && (t1 != NULL)))return false;if ((t1 == NULL) && (t2 == NULL)) return true;4041if (t1->val() != t2->val()) return false;if (Compare2(t1->leftchild(), t2->leftchild())if (Compare2(t1->rightchild(), t2->rightchild())return true;if (Compare2(t1->leftchild(), t2->rightchild())if (Compare2(t1->rightchild(), t2->leftchild))return true;return false;}6.3 template <class Elem> // Print, postorder traversalvoid postprint(GTNode<Elem>* subroot) {for (GTNode<Elem>* temp = subroot->leftmost_child();temp != NULL; temp = temp->right_sibling())postprint(temp);if (subroot->isLeaf()) cout << "Leaf: ";else cout << "Internal: ";cout << subroot->value() << "\n";}6.4 template <class Elem> // Count the number of nodesint gencount(GTNode<Elem>* subroot) {if (subroot == NULL) return 0int count = 1;GTNode<Elem>* temp = rt->leftmost_child();while (temp != NULL) {count += gencount(temp);temp = temp->right_sibling();}return count;}6.5 The Weighted Union Rule requires that when two parent-pointer trees are merged, the smaller one’s root becomes a child of the larger one’s root. Thus, we need to keep track of the number of nodes in a tree. To do so, modify the node array to store an integer value with each node. Initially, each node isin its own tree, so the weights for each node begin as 1. Whenever we wishto merge two trees, check the weights of the roots to determine which has more nodes. Then, add to the weight of the final root the weight of the new subtree.6.60 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15-1 0 0 0 0 0 0 6 0 0 0 9 0 0 12 06.7 The resulting tree should have the following structure:42 Chap. 6 General TreesNode 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Parent 4 4 4 4 -1 4 4 0 0 4 9 9 9 12 9 -16.8 For eight nodes labeled 0 through 7, use the following series of equivalences: (0, 1) (2, 3) (4, 5) (6, 7) (4 6) (0, 2) (4 0)This requires checking fourteen parent pointers (two for each equivalence),but none are actually followed since these are all roots. It is possible todouble the number of parent pointers checked by choosing direct children ofroots in each case.6.9 For the “lists of Children” representation, every node stores a data value and a pointer to its list of children. Further, every child (every node except the root)has a record associated with it containing an index and a pointer. Indicatingthe size of the data value as D, the size of a pointer as P and the size of anindex as I, the overhead fraction is3P + ID + 3P + I.For the “Left Child/Right Sibling” representation, every node stores three pointers and a data value, for an overhead fraction of3PD + 3P.The first linked representation of Section 6.3.3 stores with each node a datavalue and a size field (denoted by S). Each child (every node except the root)also has a pointer pointing to it. The overhead fraction is thusS + PD + S + Pmaking it quite efficient.The second linked representation of Section 6.3.3 stores with each node adata value and a pointer to the list of children. Each child (every node exceptthe root) has two additional pointers associated with it to indicate its placeon the parent’s linked list. Thus, the overhead fraction is3PD + 3P.6.10 template <class Elem>BinNode<Elem>* convert(GTNode<Elem>* genroot) {if (genroot == NULL) return NULL;43GTNode<Elem>* gtemp = genroot->leftmost_child();btemp = new BinNode(genroot->val(), convert(gtemp),convert(genroot->right_sibling()));}6.11 • Parent(r) = (r − 1)/k if 0 < r < n.• Ith child(r) = kr + I if kr +I < n.• Left sibling(r) = r − 1 if r mod k = 1 0 < r < n.• Right sibling(r) = r + 1 if r mod k = 0 and r + 1 < n.6.12 (a) The overhead fraction is4(k + 1)4 + 4(k + 1).(b) The overhead fraction is4k16 + 4k.(c) The overhead fraction is4(k + 2)16 + 4(k + 2).(d) The overhead fraction is2k2k + 4.6.13 Base Case: The number of leaves in a non-empty tree of 0 internal nodes is (K − 1)0 + 1 = 1. Thus, the theorem is correct in the base case.Induction Hypothesis: Assume that the theorem is correct for any full Karytree containing n internal nodes.Induction Step: Add K children to an arbitrary leaf node of the tree withn internal nodes. This new tree now has 1 more internal node, and K − 1more leaf nodes, so theorem still holds. Thus, the theorem is correct, by the principle of Mathematical Induction.6.14 (a) CA/BG///FEDD///H/I//(b) CA/BG/FED/H/I6.15 X|P-----| | |C Q R---| |V M44 Chap. 6 General Trees6.16 (a) // Use a helper function with a pass-by-reference// variable to indicate current position in the// node list.template <class Elem>BinNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>BinNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’/’) {curr++;return NULL;}BinNode<Elem>* temp = new BinNode(inlist[curr++], NULL, NULL);temp->left = converthelp(inlist, curr);temp->right = converthelp(inlist, curr);return temp;}(b) // Use a helper function with a pass-by-reference // variable to indicate current position in the// node list.template <class Elem>BinNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>BinNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’/’) {curr++;return NULL;}BinNode<Elem>* temp =new BinNode<Elem>(inlist[curr++], NULL, NULL);if (inlist[curr] == ’\’’) return temp;45curr++ // Eat the internal node mark.temp->left = converthelp(inlist, curr);temp->right = converthelp(inlist, curr);return temp;}(c) // Use a helper function with a pass-by-reference// variable to indicate current position in the// node list.template <class Elem>GTNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>GTNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’)’) {curr++;return NULL;}GTNode<Elem>* temp =new GTNode<Elem>(inlist[curr++]);if (curr == ’)’) {temp->insert_first(NULL);return temp;}temp->insert_first(converthelp(inlist, curr));while (curr != ’)’)temp->insert_next(converthelp(inlist, curr));curr++;return temp;}6.17 The Huffman tree is a full binary tree. To decode, we do not need to know the weights of nodes, only the letter values stored in the leaf nodes. Thus, we can use a coding much like that of Equation 6.2, storing only a bit mark for internal nodes, and a bit mark and letter value for leaf nodes.7Internal Sorting7.1 Base Case: For the list of one element, the double loop is not executed and the list is not processed. Thus, the list of one element remains unaltered and is sorted.Induction Hypothesis: Assume that the list of n elements is sorted correctlyby Insertion Sort.Induction Step: The list of n + 1 elements is processed by first sorting thetop n elements. By the induction hypothesis, this is done correctly. The final pass of the outer for loop will process the last element (call it X). This isdone by the inner for loop, which moves X up the list until a value smallerthan that of X is encountered. At this point, X has been properly insertedinto the sorted list, leaving the entire collection of n + 1 elements correctly sorted. Thus, by the principle of Mathematical Induction, the theorem is correct.7.2 void StackSort(AStack<int>& IN) {AStack<int> Temp1, Temp2;while (!IN.isEmpty()) // Transfer to another stackTemp1.push(IN.pop());IN.push(Temp1.pop()); // Put back one elementwhile (!Temp1.isEmpty()) { // Process rest of elemswhile (IN.top() > Temp1.top()) // Find elem’s placeTemp2.push(IN.pop());IN.push(Temp1.pop()); // Put the element inwhile (!Temp2.isEmpty()) // Put the rest backIN.push(Temp2.pop());}}46477.3 The revised algorithm will work correctly, and its asymptotic complexity will remain Θ(n2). However, it will do about twice as many comparisons, since it will compare adjacent elements within the portion of the list already knownto be sorted. These additional comparisons are unproductive.7.4 While binary search will find the proper place to locate the next element, it will still be necessary to move the intervening elements down one position in the array. This requires the same number of operations as a sequential search. However, it does reduce the number of element/element comparisons, and may be somewhat faster by a constant factor since shifting several elements may be more efficient than an equal number of swap operations.7.5 (a) template <class Elem, class Comp>void selsort(Elem A[], int n) { // Selection Sortfor (int i=0; i<n-1; i++) { // Select i’th recordint lowindex = i; // Remember its indexfor (int j=n-1; j>i; j--) // Find least valueif (Comp::lt(A[j], A[lowindex]))lowindex = j; // Put it in placeif (i != lowindex) // Add check for exerciseswap(A, i, lowindex);}}(b) There is unlikely to be much improvement; more likely the algorithmwill slow down. This is because the time spent checking (n times) isunlikely to save enough swaps to make up.(c) Try it and see!7.6 • Insertion Sort is stable. A swap is done only if the lower element’svalue is LESS.• Bubble Sort is stable. A swap is done only if the lower element’s valueis LESS.• Selection Sort is NOT stable. The new low value is set only if it isactually less than the previous one, but the direction of the search isfrom the bottom of the array. The algorithm will be stable if “less than”in the check becomes “less than or equal to” for selecting the low key position.• Shell Sort is NOT stable. The sublist sorts are done independently, andit is quite possible to swap an element in one sublist ahead of its equalvalue in another sublist. Once they are in the same sublist, they willretain this (incorrect) relationship.• Quick-sort is NOT stable. After selecting the pivot, it is swapped withthe last element. This action can easily put equal records out of place.48 Chap. 7 Internal Sorting• Conceptually (in particular, the linked list version) Mergesort is stable.The array implementations are NOT stable, since, given that the sublistsare stable, the merge operation will pick the element from the lower listbefore the upper list if they are equal. This is easily modified to replace“less than” with “less than or equal to.”• Heapsort is NOT stable. Elements in separate sides of the heap are processed independently, and could easily become out of relative order.• Binsort is stable. Equal values that come later are appended to the list.• Radix Sort is stable. While the processing is from bottom to top, thebins are also filled from bottom to top, preserving relative order.7.7 In the worst case, the stack can store n records. This can be cut to log n in the worst case by putting the larger partition on FIRST, followed by the smaller. Thus, the smaller will be processed first, cutting the size of the next stacked partition by at least half.7.8 Here is how I derived a permutation that will give the desired (worst-case) behavior:a b c 0 d e f g First, put 0 in pivot index (0+7/2),assign labels to the other positionsa b c g d e f 0 First swap0 b c g d e f a End of first partition pass0 b c g 1 e f a Set d = 1, it is in pivot index (1+7/2)0 b c g a e f 1 First swap0 1 c g a e f b End of partition pass0 1 c g 2 e f b Set a = 2, it is in pivot index (2+7/2)0 1 c g b e f 2 First swap0 1 2 g b e f c End of partition pass0 1 2 g b 3 f c Set e = 3, it is in pivot index (3+7/2)0 1 2 g b c f 3 First swap0 1 2 3 b c f g End of partition pass0 1 2 3 b 4 f g Set c = 4, it is in pivot index (4+7/2)0 1 2 3 b g f 4 First swap0 1 2 3 4 g f b End of partition pass0 1 2 3 4 g 5 b Set f = 5, it is in pivot index (5+7/2)0 1 2 3 4 g b 5 First swap0 1 2 3 4 5 b g End of partition pass0 1 2 3 4 5 6 g Set b = 6, it is in pivot index (6+7/2)0 1 2 3 4 5 g 6 First swap0 1 2 3 4 5 6 g End of parition pass0 1 2 3 4 5 6 7 Set g = 7.Plugging the variable assignments into the original permutation yields:492 6 4 0 13 5 77.9 (a) Each call to qsort costs Θ(i log i). Thus, the total cost isni=1i log i = Θ(n2 log n).(b) Each call to qsort costs Θ(n log n) for length(L) = n, so the totalcost is Θ(n2 log n).7.10 All that we need to do is redefine the comparison test to use strcmp. The quicksort algorithm itself need not change. This is the advantage of paramerizing the comparator.7.11 For n = 1000, n2 = 1, 000, 000, n1.5 = 1000 ∗√1000 ≈ 32, 000, andn log n ≈ 10, 000. So, the constant factor for Shellsort can be anything less than about 32 times that of Insertion Sort for Shellsort to be faster. The constant factor for Shellsort can be anything less than about 100 times thatof Insertion Sort for Quicksort to be faster.7.12 (a) The worst case occurs when all of the sublists are of size 1, except for one list of size i − k + 1. If this happens on each call to SPLITk, thenthe total cost of the algorithm will be Θ(n2).(b) In the average case, the lists are split into k sublists of roughly equal length. Thus, the total cost is Θ(n logk n).7.13 (This question comes from Rawlins.) Assume that all nuts and all bolts havea partner. We use two arrays N[1..n] and B[1..n] to represent nuts and bolts. Algorithm 1Using merge-sort to solve this problem.First, split the input into n/2 sub-lists such that each sub-list contains twonuts and two bolts. Then sort each sub-lists. We could well come up with apair of nuts that are both smaller than either of a pair of bolts. In that case,all you can know is something like:N1, N2。
《数据结构与算法》习题与答案

《数据结构与算法》习题与答案(解答仅供参考)一、名词解释:1. 数据结构:数据结构是计算机存储、组织数据的方式,它不仅包括数据的逻辑结构(如线性结构、树形结构、图状结构等),还包括物理结构(如顺序存储、链式存储等)。
它是算法设计与分析的基础,对程序的效率和功能实现有直接影响。
2. 栈:栈是一种特殊的线性表,其操作遵循“后进先出”(Last In First Out, LIFO)原则。
在栈中,允许进行的操作主要有两种:压栈(Push),将元素添加到栈顶;弹栈(Pop),将栈顶元素移除。
3. 队列:队列是一种先进先出(First In First Out, FIFO)的数据结构,允许在其一端插入元素(称为入队),而在另一端删除元素(称为出队)。
常见的实现方式有顺序队列和循环队列。
4. 二叉排序树(又称二叉查找树):二叉排序树是一种二叉树,其每个节点的左子树中的所有节点的值都小于该节点的值,而右子树中的所有节点的值都大于该节点的值。
这种特性使得能在O(log n)的时间复杂度内完成搜索、插入和删除操作。
5. 图:图是一种非线性数据结构,由顶点(Vertex)和边(Edge)组成,用于表示对象之间的多种关系。
根据边是否有方向,可分为有向图和无向图;根据是否存在环路,又可分为有环图和无环图。
二、填空题:1. 在一个长度为n的顺序表中,插入一个新元素平均需要移动______个元素。
答案:(n/2)2. 哈希表利用______函数来确定元素的存储位置,通过解决哈希冲突以达到快速查找的目的。
答案:哈希(Hash)3. ______是最小生成树的一种算法,采用贪心策略,每次都选择当前未加入生成树且连接两个未连通集合的最小权重边。
答案:Prim算法4. 在深度优先搜索(DFS)过程中,使用______数据结构来记录已经被访问过的顶点,防止重复访问。
答案:栈或标记数组5. 快速排序算法在最坏情况下的时间复杂度为______。
Mark Allen Weiss 数据结构与算法分析 课后习题答案1

Σ Fi =
sum on the right is Fk +2 − 2 + Fk +1 = Fk +3 − 2, where the latter equality follows from the definition of the Fibonacci numbers. This proves the claim for N = k + 1, and hence for all N. (b) As in the text, the proof is by induction. Observe that φ + 1 = φ2. This implies that φ−1 + φ−2 = 1. For N = 1 and N = 2, the statement is true. Assume the claim is true for N = 1, 2, ..., k . Fk +1 = Fk + Fk −1 by the definition and we can use the inductive hypothesis on the right-hand side, obtaining Fk +1 < φk + φk −1 < φ−1φk +1 + φ−2φk +1 Fk +1 < (φ−1 + φ−2)φk +1 < φk +1 and proving the theorem. (c) See any of the advanced math references at the end of the chapter. The derivation involves the use of generating functions. 1.10 (a) (2i −1) = 2 Σ i − Σ 1 = N (N +1) − N = N 2. Σ i =1 i =1 i =1
数据结构与算法分析java课后答案

数据结构与算法分析java课后答案【篇一:java程序设计各章习题及其答案】>1、 java程序是由什么组成的?一个程序中必须有public类吗?java源文件的命名规则是怎样的?答:一个java源程序是由若干个类组成。
一个java程序不一定需要有public类:如果源文件中有多个类时,则只能有一个类是public类;如果源文件中只有一个类,则不将该类写成public也将默认它为主类。
源文件命名时要求源文件主名应与主类(即用public修饰的类)的类名相同,扩展名为.java。
如果没有定义public类,则可以任何一个类名为主文件名,当然这是不主张的,因为它将无法进行被继承使用。
另外,对applet小应用程序来说,其主类必须为public,否则虽然在一些编译编译平台下可以通过(在bluej下无法通过)但运行时无法显示结果。
2、怎样区分应用程序和小应用程序?应用程序的主类和小应用程序的主类必须用public修饰吗?答:java application是完整的程序,需要独立的解释器来解释运行;而java applet则是嵌在html编写的web页面中的非独立运行程序,由web浏览器内部包含的java解释器来解释运行。
在源程序代码中两者的主要区别是:任何一个java application应用程序必须有且只有一个main方法,它是整个程序的入口方法;任何一个applet小应用程序要求程序中有且必须有一个类是系统类applet的子类,即该类头部分以extends applet结尾。
应用程序的主类当源文件中只有一个类时不必用public修饰,但当有多于一个类时则主类必须用public修饰。
小应用程序的主类在任何时候都需要用public来修饰。
3、开发与运行java程序需要经过哪些主要步骤和过程?答:主要有三个步骤(1)、用文字编辑器notepad(或在jcreator,gel, bulej,eclipse, jbuilder等)编写源文件;(2)、使用java编译器(如javac.exe)将.java源文件编译成字节码文件.class;(3)、运行java程序:对应用程序应通过java解释器(如java.exe)来运行,而对小应用程序应通过支持java标准的浏览器(如microsoft explorer)来解释运行。
数据结构与算法分析课后习题答案

数据结构与算法分析课后习题答案【篇一:《数据结构与算法》课后习题答案】>2.3.2 判断题2.顺序存储的线性表可以按序号随机存取。
(√)4.线性表中的元素可以是各种各样的,但同一线性表中的数据元素具有相同的特性,因此属于同一数据对象。
(√)6.在线性表的链式存储结构中,逻辑上相邻的元素在物理位置上不一定相邻。
(√)8.在线性表的顺序存储结构中,插入和删除时移动元素的个数与该元素的位置有关。
(√)9.线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。
(√)2.3.3 算法设计题1.设线性表存放在向量a[arrsize]的前elenum个分量中,且递增有序。
试写一算法,将x 插入到线性表的适当位置上,以保持线性表的有序性,并且分析算法的时间复杂度。
【提示】直接用题目中所给定的数据结构(顺序存储的思想是用物理上的相邻表示逻辑上的相邻,不一定将向量和表示线性表长度的变量封装成一个结构体),因为是顺序存储,分配的存储空间是固定大小的,所以首先确定是否还有存储空间,若有,则根据原线性表中元素的有序性,来确定插入元素的插入位置,后面的元素为它让出位置,(也可以从高下标端开始一边比较,一边移位)然后插入x ,最后修改表示表长的变量。
int insert (datatype a[],int *elenum,datatype x) /*设elenum为表的最大下标*/ {if (*elenum==arrsize-1) return 0; /*表已满,无法插入*/else {i=*elenum;while (i=0 a[i]x)/*边找位置边移动*/{a[i+1]=a[i];i--;}a[i+1]=x;/*找到的位置是插入位的下一位*/ (*elenum)++;return 1;/*插入成功*/}}时间复杂度为o(n)。
2.已知一顺序表a,其元素值非递减有序排列,编写一个算法删除顺序表中多余的值相同的元素。
数据结构与算法邓丹君课后题答案

数据结构与算法邓丹君课后题答案1.数据的运算描述是定义在数据的逻辑结构上的。
[判断题] *对(正确答案)错2.数据运算的实现是基于数据的逻辑结构的。
[判断题] *对错(正确答案)3.一个数据结构中,如果数据元素值发生改变,则它的逻辑结构也随之改变。
[判断题] *对错(正确答案)4.非线性结构中,每个元素最多只有一个前趋元素。
[判断题] *对错(正确答案)5.线性表中所有元素的数据类型必须相同。
[判断题] *对(正确答案)错6.线性表中的结点按前趋,后继关系可以排成一个线性序列。
[判断题] *对(正确答案)错7.线性表中每个元素都有一个前趋元素和一个后继元素。
[判断题] *对错(正确答案)8.线性表的长度是线性表占用的存储空间的大小。
[判断题] *对错(正确答案)9.线性表的逻辑顺序总与其物理顺序一致。
[判断题] *对错(正确答案)10.线性表的顺序存储结构优于链式存储结构。
[判断题] *对错(正确答案)11.顺序表具有随机存取特性,而链表不具有随机存取特性。
[判断题] *对(正确答案)错12.栈的定义不涉及数据的逻辑结构。
[判断题] *错(正确答案)13.栈和队列都是线性表,只是在插入和删除时受到了一些限制。
[判断题] *对(正确答案)错14.栈和队列都是限制存取端的线性表。
[判断题] *对(正确答案)错15.队列时一种对进队、出队操作的次序做了限制的线性表。
[判断题] *对错(正确答案)16.队列时一种对进队、出队操作的次数做了限制的线性表。
[判断题] *对错(正确答案)17.n个元素进队的顺序和出队的顺序总是一致的。
[判断题] *对(正确答案)错18.n个元素通过一个队列,其出队序列时唯一的。
[判断题] *对(正确答案)19.串是由有限个字符构成的序列。
() [判断题] *对(正确答案)错20.串中每个元素只能是字母。
[判断题] *对错(正确答案)21.一个串的长度至少为1. [判断题] *对错(正确答案)22.空串是只含有空格的串。
Mark Allen Weiss 数据结构与算法分析 课后习题答案2

Chapter 2:Algorithm Analysis2.12/N ,37,√ N ,N ,N log log N ,N log N ,N log (N 2),N log 2N ,N 1.5,N 2,N 2log N ,N 3,2N / 2,2N .N log N and N log (N 2)grow at the same rate.2.2(a)True.(b)False.A counterexample is T 1(N ) = 2N ,T 2(N ) = N ,and f (N ) = N .(c)False.A counterexample is T 1(N ) = N 2,T 2(N ) = N ,and f (N ) = N 2.(d)False.The same counterexample as in part (c)applies.2.3We claim that N log N is the slower growing function.To see this,suppose otherwise.Then,N ε/ √ log N would grow slower than log N .Taking logs of both sides,we find that,under this assumption,ε/ √ log N log N grows slower than log log N .But the first expres-sion simplifies to ε√ logN .If L = log N ,then we are claiming that ε√ L grows slower than log L ,or equivalently,that ε2L grows slower than log 2 L .But we know that log 2 L = ο (L ),so the original assumption is false,proving the claim.2.4Clearly,log k 1N = ο(log k 2N )if k 1 < k 2,so we need to worry only about positive integers.The claim is clearly true for k = 0and k = 1.Suppose it is true for k < i .Then,by L’Hospital’s rule,N →∞lim N log i N ______ = N →∞lim i N log i −1N _______The second limit is zero by the inductive hypothesis,proving the claim.2.5Let f (N ) = 1when N is even,and N when N is odd.Likewise,let g (N ) = 1when N is odd,and N when N is even.Then the ratio f (N ) / g (N )oscillates between 0and ∞.2.6For all these programs,the following analysis will agree with a simulation:(I)The running time is O (N ).(II)The running time is O (N 2).(III)The running time is O (N 3).(IV)The running time is O (N 2).(V) j can be as large as i 2,which could be as large as N 2.k can be as large as j ,which is N 2.The running time is thus proportional to N .N 2.N 2,which is O (N 5).(VI)The if statement is executed at most N 3times,by previous arguments,but it is true only O (N 2)times (because it is true exactly i times for each i ).Thus the innermost loop is only executed O (N 2)times.Each time through,it takes O ( j 2) = O (N 2)time,for a total of O (N 4).This is an example where multiplying loop sizes can occasionally give an overesti-mate.2.7(a)It should be clear that all algorithms generate only legal permutations.The first two algorithms have tests to guarantee no duplicates;the third algorithm works by shuffling an array that initially has no duplicates,so none can occur.It is also clear that the first two algorithms are completely random,and that each permutation is equally likely.The third algorithm,due to R.Floyd,is not as obvious;the correctness can be proved by induction.SeeJ.Bentley,"Programming Pearls,"Communications of the ACM 30(1987),754-757.Note that if the second line of algorithm 3is replaced with the statementSwap(A[i],A[RandInt(0,N-1)]);then not all permutations are equally likely.To see this,notice that for N = 3,there are 27equally likely ways of performing the three swaps,depending on the three random integers.Since there are only 6permutations,and 6does not evenly divide27,each permutation cannot possibly be equally represented.(b)For the first algorithm,the time to decide if a random number to be placed in A [i ]has not been used earlier is O (i ).The expected number of random numbers that need to be tried is N / (N − i ).This is obtained as follows:i of the N numbers would be duplicates.Thus the probability of success is (N − i ) / N .Thus the expected number of independent trials is N / (N − i ).The time bound is thusi =0ΣN −1N −i Ni ____ < i =0ΣN −1N −i N 2____ < N 2i =0ΣN −1N −i 1____ < N 2j =1ΣN j 1__ = O (N 2log N )The second algorithm saves a factor of i for each random number,and thus reduces the time bound to O (N log N )on average.The third algorithm is clearly linear.(c,d)The running times should agree with the preceding analysis if the machine has enough memory.If not,the third algorithm will not seem linear because of a drastic increase for large N .(e)The worst-case running time of algorithms I and II cannot be bounded because there is always a finite probability that the program will not terminate by some given time T .The algorithm does,however,terminate with probability 1.The worst-case running time of the third algorithm is linear -its running time does not depend on the sequence of random numbers.2.8Algorithm 1would take about 5days for N = 10,000,14.2years for N = 100,000and 140centuries for N = 1,000,000.Algorithm 2would take about 3hours for N = 100,000and about 2weeks for N = 1,000,000.Algorithm 3would use 1⁄12minutes for N = 1,000,000.These calculations assume a machine with enough memory to hold the array.Algorithm 4solves a problem of size 1,000,000in 3seconds.2.9(a)O (N 2).(b)O (N log N ).2.10(c)The algorithm is linear.2.11Use a variation of binary search to get an O (log N )solution (assuming the array is preread).2.13(a)Test to see if N is an odd number (or 2)and is not divisible by 3,5,7,...,√N .(b)O (√ N ),assuming that all divisions count for one unit of time.(c)B = O (log N ).(d)O (2B / 2).(e)If a 20-bit number can be tested in time T ,then a 40-bit number would require about T 2time.(f)B is the better measure because it more accurately represents the size of the input.2.14The running time is proportional to N times the sum of the reciprocals of the primes lessthan N .This is O (N log log N ).See Knuth,Volume2,page394.2.15Compute X 2,X 4,X 8,X 10,X 20,X 40,X 60,and X 62.2.16Maintain an array PowersOfX that can befilled in a for loop.The array will contain X ,X 2,X 4,up to X 2 log N .The binary representation of N (which can be obtained by testing even or odd and then dividing by2,until all bits are examined)can be used to multiply the appropriate entries of the array.2.17For N =0or N =1,the number of multiplies is zero.If b (N )is the number of ones in thebinary representation of N ,then if N >1,the number of multiplies used islog N + b (N )−12.18(a)A .(b)B .(c)The information given is not sufficient to determine an answer.We have only worst-case bounds.(d)Yes.2.19(a)Recursion is unnecessary if there are two or fewer elements.(b)One way to do this is to note that if thefirst N −1elements have a majority,then the lastelement cannot change this.Otherwise,the last element could be a majority.Thus if N is odd,ignore the last element.Run the algorithm as before.If no majority element emerges, then return the N th element as a candidate.(c)The running time is O (N ),and satisfies T (N )= T (N / 2)+ O (N ).(d)One copy of the original needs to be saved.After this,the B array,and indeed the recur-sion can be avoided by placing each B i in the A array.The difference is that the original recursive strategy implies that O (log N )arrays are used;this guarantees only two copies. 2.20Otherwise,we could perform operations in parallel by cleverly encoding several integersinto one.For instance,if A=001,B=101,C=111,D=100,we could add A and B at the same time as C and D by adding00A00C+00B00D.We could extend this to add N pairs of numbers at once in unit cost.2.22No.If Low =1,High =2,then Mid =1,and the recursive call does not make progress. 2.24No.As in Exercise2.22,no progress is made.。
数据结构与算法分析课后习题答案

数据结构与算法分析课后习题答案第一章:基本概念一、题目:什么是数据结构与算法?数据结构是指数据在计算机中存储和组织的方式,如栈、队列、链表、树等;而算法是一系列解决问题的清晰规范的指令步骤。
数据结构和算法是计算机科学的核心内容。
二、题目:数据结构的分类有哪些?数据结构可以分为以下几类:1. 线性结构:包括线性表、栈、队列等,数据元素之间存在一对一的关系。
2. 树形结构:包括二叉树、AVL树、B树等,数据元素之间存在一对多的关系。
3. 图形结构:包括有向图、无向图等,数据元素之间存在多对多的关系。
4. 文件结构:包括顺序文件、索引文件等,是硬件和软件相结合的数据组织形式。
第二章:算法分析一、题目:什么是时间复杂度?时间复杂度是描述算法执行时间与问题规模之间的增长关系,通常用大O记法表示。
例如,O(n)表示算法的执行时间与问题规模n成正比,O(n^2)表示算法的执行时间与问题规模n的平方成正比。
二、题目:主定理是什么?主定理(Master Theorem)是用于估计分治算法时间复杂度的定理。
它的公式为:T(n) = a * T(n/b) + f(n)其中,a是子问题的个数,n/b是每个子问题的规模,f(n)表示将一个问题分解成子问题和合并子问题的所需时间。
根据主定理的不同情况,可以得到算法的时间复杂度的上界。
第三章:基本数据结构一、题目:什么是数组?数组是一种线性数据结构,它由一系列具有相同数据类型的元素组成,通过索引访问。
数组具有随机访问、连续存储等特点,但插入和删除元素的效率较低。
二、题目:栈和队列有什么区别?栈和队列都是线性数据结构,栈的特点是“先进后出”,即最后压入栈的元素最先弹出;而队列的特点是“先进先出”,即最先入队列的元素最先出队列。
第四章:高级数据结构一、题目:什么是二叉树?二叉树是一种特殊的树形结构,每个节点最多有两个子节点。
二叉树具有左子树、右子树的区分,常见的有完全二叉树、平衡二叉树等。
Mark Allen Weiss 数据结构与算法分析 课后习题答案3Mark Allen Weiss 数据结构与算法分析 课后习题答案3

List Intersect( List L1, List L2 ) {
List Result; Position L1Pos, L2Pos, ResultPos;
L1Pos = First( L1 ); L2Pos = First( L2 ); Result = MakeEmpty( NULL ); ResultPos = First( Result ); while( L1Pos != NULL && L2Pos != NULL ) {
(b) The bound can be improved by multiplying one term by the entire other polynomial, and then using the equivalent of the procedure in Exercise 3.2 to insert the entire sequence. Then each sequence takes O (MN ), but there are only M of them, giving a time bound of O (M 2N ).
if( L1Pos->Element < L2Pos->Element ) L1Pos = Next( L1Pos, L1 );
else if( L1Pos->Element > L2Pos->Element ) L2Pos = Next( L2Pos, L2 );
else {
Insert( L1Pos->Element, Result, ResultPos ); L1 = Next( L1Pos, L1 ); L2 = Next( L2Pos, L2 ); ResultPos = Next( ResultPos, Result ); } } return Result; } _______________________________________________________________________________
数据结构与算法分析java课后答案

数据结构和算法分析java课后答案【篇一:java程序设计各章习题及其答案】>1、 java程序是由什么组成的?一个程序中必须有public类吗?java源文件的命名规则是怎样的?答:一个java源程序是由若干个类组成。
一个java程序不一定需要有public类:如果源文件中有多个类时,则只能有一个类是public类;如果源文件中只有一个类,则不将该类写成public也将默认它为主类。
源文件命名时要求源文件主名应和主类(即用public修饰的类)的类名相同,扩展名为.java。
如果没有定义public类,则可以任何一个类名为主文件名,当然这是不主张的,因为它将无法进行被继承使用。
另外,对applet小使用程序来说,其主类必须为public,否则虽然在一些编译编译平台下可以通过(在bluej下无法通过)但运行时无法显示结果。
2、怎样区分使用程序和小使用程序?使用程序的主类和小使用程序的主类必须用public修饰吗?答:java application是完整的程序,需要独立的解释器来解释运行;而java applet则是嵌在html编写的web页面中的非独立运行程序,由web浏览器内部包含的java解释器来解释运行。
在源程序代码中两者的主要区别是:任何一个java application使用程序必须有且只有一个main方法,它是整个程序的入口方法;任何一个applet小使用程序要求程序中有且必须有一个类是系统类applet的子类,即该类头部分以extends applet结尾。
使用程序的主类当源文件中只有一个类时不必用public修饰,但当有多于一个类时则主类必须用public修饰。
小使用程序的主类在任何时候都需要用public来修饰。
3、开发和运行java程序需要经过哪些主要步骤和过程?答:主要有三个步骤(1)、用文字编辑器notepad(或在jcreator,gel, bulej,eclipse, jbuilder等)编写源文件;(2)、使用java编译器(如javac.exe)将.java源文件编译成字节码文件.class;(3)、运行java程序:对使用程序应通过java解释器(如java.exe)来运行,而对小使用程序应通过支持java标准的浏览器(如microsoft explorer)来解释运行。
Mark Allen Weiss 数据结构与算法分析 课后习题答案12

Chapter12:Advanced Data Structuresand Implementation12.3Incorporate an additionalfield for each node that indicates the size of its subtree.Thesefields are easy to update during a splay.This is difficult to do in a skip list.12.6If there are B black nodes on the path from the root to all leaves,it is easy to show byinduction that there are at most2B leaves.Consequently,the number of black nodes on a path is at most log N .Since there can’t be two consecutive red nodes,the height is bounded by2log N .12.7Color nonroot nodes red if their height is even and their parents height is odd,and blackotherwise.Not all red black trees are AVL trees(since the deepest red black tree is deeper than the deepest AVL tree).12.19See H.N.Gabow,J.L.Bentley,and R.E.Tarjan,"Scaling and Related Techniques forComputational Geometry,"Proceedings of the Sixteenth Annual ACM Symposium on Theory of Computing(1984),135-143,or C.Levcopoulos and O.Petersson,"Heapsort Adapted for Presorted Files,"Journal of Algorithms14(1993),395-413.12.29Pointers are unnecessary;we can store everything in an array.This is discussed in refer-ence[12].The bounds become O (k log N )for insertion,O (k 2log N )for deletion of a minimum,O (k 2N )for creation(an improvement over the bound in[12]).12.35Consider the pairing heap with1as the root and children2,3,...N .A DeleteMinremoves1,and the resulting pairing heap is2as the root with children3,4,...N ;the cost of this operation is N units.A subsequent DeleteMin sequence of2,3,4,...will take total timeΩ(N 2).-66-。
《数据结构与算法分析:C语言描述_原书第二版》CH2算法分析_课后习题_部分解答

《数据结构与算法分析:C语⾔描述_原书第⼆版》CH2算法分析_课后习题_部分解答对于⼀个初学者来说,作者的Solutions Manual把太多的细节留给了读者,这⾥尽⾃⼰的努⼒给出部分习题的详解:不当之处,欢迎指正。
1、按增长率排列下列函数:N,√2,N1.5,N2,NlogN, NloglogN,N log2N,Nlog(N2),2/N,2N,2N/2,37,N2logN,N3。
指出哪些函数以相同的增长率增长。
答:排列如下2/N < 37 < √2 < N < NloglogN < NlogN < Nlog(N2) < Nlog2N < N1.5 < N2 < N2logN < N3 < 2N/2 < 2N。
其中,NlogN 与 Nlog(N2) 的增长率相同,均为O(NlogN)。
补充说明:a) 其中 Nlog2N 与 N1.5, N3与 2N/2⼤⼩关系的判定,可以连续使⽤洛必达法则(N->∞时,两个函数⽐值的极限,等于它们分别求导后⽐值的极限)。
当然,更简单的是两边直接求平⽅。
b) 同时注意⼀个常⽤法则:对任意常数k,log k N = O(N)。
这表明对数增长得⾮常缓慢。
习题3中我们会证明它的⼀个更严格的形式。
2、函数NlogN 与 N1+ε/√logN (ε>0) 哪个增长得更快? 分析:我们⾸先考虑的可能是利⽤洛必达法则,但是对于第⼆个函数其上下两部分皆含有变量,难以求导(当然也不是不⾏,就是⿇烦些,如果你愿意设y = N1+ε/√logN,然后对两边取对数的话)。
这⾥我们将利⽤反证法: 要证NlogN < N1+ε/√logN,即证 logN < Nε/√logN。
既然⽤反证法,那么我们假设 Nε/√logN < logN。
两边取对数有ε/√logN logN < loglogN。
数据结构与算法_桂林电子科技大学中国大学mooc课后章节答案期末考试题库2023年

数据结构与算法_桂林电子科技大学中国大学mooc课后章节答案期末考试题库2023年1.算法分析的两个主要方面是()答案:空间复杂性和时间复杂性2.线性表若采用链式存储结构时,要求内存中可用存储单元的地址()答案:连续或不连续都可以3.一个栈的入栈序列a,b,c,d,e,则栈的不可能的输出序列是()答案:dceab4.判定一个循环队列QU(最多元素为m)为满队列的条件是()答案:QU—>front= =(QU—>rear+1)%m5.已知某二叉树的后序遍历序列是dabec,中序遍历序列是debac,它的先序遍历序列是()答案:cedba6.以数据集{4,5,6,7,10,12,18}为结点权值所构造的Huffman树,其带权路径长度之和是()答案:1657.对于顺序存储的有序表(5,12,20,26,37,42,46,50,64),若采用折半查找,则查找元素26的比较次数为()答案:48.假设在构建散列表时,采用线性探测解决冲突。
若连续插入的n个关键字都是同义词,则查找其中最后插入的关键字时,所需进行的比较次数为( )答案:n9.采用排序算法对n个元素进行排序,其排序趟数肯定为n-1趟的排序方法是()答案:直接选择和直接插入10.对关键码序列28,16,32,12,60,2,5,72 快速排序,从小到大一次划分结果为()答案:(5,16,2,12)28(60,32,72)11.设有5000个待排序的记录关键字,如果需要用最快的方法选出其中最小的10个记录关键字,则用下列()方法可以达到此目的答案:堆排序12.下面的二叉排序树中,是平衡二叉排序数的个数()答案:413.对下图采用迪杰斯特拉算法求a到其他各个顶点的最短路径,得到的第一条最短路径的目标顶点是b,第二条最短路径的目标顶点是c,后续的其余各最短路径的目标顶点依次是()答案:f, d, e14.下图中的二叉树进行了()线索化。
答案:中序15.二叉树转换为森林后,得到的树有()棵答案:416.已知模式串p=‘ababacdd',其对应的next[]数组如下,请问?的地方应该是()答案:217.链表不具备的特点是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 6:Priority Queues (Heaps)6.1Yes.When an element is inserted,we compare it to the current minimum and change the minimum if the new element is smaller.DeleteMin operations are expensive in this scheme.6.21326754151412910111381321264815149751113106.3The result of three DeleteMins, startingwith both of the heaps in Exercise 6.2,is as fol-lows:4651371081514129114651271081514913116.46.5 These are simple modifications to the code presented in the text and meant as programming exercises.6.6225.To see this,start with i =1and position at the root.Follow the path toward the last node,doubling i when taking a left child,and doubling i and adding one when taking a right child.-29-w ww .k h d a w .c o m课后答案网6.7(a)We show that H (N ),which is the sum of the heights of nodes in a complete binary treeof N nodes,is N − b (N ),where b (N )is the number of ones in the binary representation of N .Observe that for N = 0and N = 1,the claim is true.Assume that it is true for values of k up to and including N −1.Suppose the left and right subtrees have L and R nodes,respectively.Since the root has height log N ,we haveH (N ) = log N + H (L ) + H (R )= log N + L − b (L ) + R − b (R )= N − 1 + ( log N − b (L ) − b (R ))The second line follows from the inductive hypothesis,and the third follows because L + R = N − 1.Now the last node in the tree is in either the left subtree or the right sub-tree.If it is in the left subtree,then the right subtree is a perfect tree,and b (R ) = log N − 1.Further,the binary representation of N and L are identical,with the exception that the leading 10in N becomes 1in L .(For instance,if N =37=100101,L =10101.)It is clear that the second digit of N must be zero if the last node is in the left sub-tree.Thus in this case,b (L ) = b (N ),andH (N ) = N − b (N )If the last node is in the right subtree,then b (L ) = log N .The binary representation of R is identical to N ,except that the leading 1is not present.(For instance,if N =27=101011,L =01011.)Thus b (R ) = b (N ) − 1,and again H (N ) = N − b (N )(b)Run a single-elimination tournament among eight elements.This requires seven com-parisons and generates ordering information indicated by the binomial tree shown here.abc de f g hThe eighth comparison is between b and c .If c is less than b ,then b is made a child of c .Otherwise,both c and d are made children of b .(c)A recursive strategy is used.Assume that N = 2k .A binomial tree is built for the N elements as in part (b).The largest subtree of the root is then recursively converted into abinary heap of 2k −1elements.The last element in the heap (which is the only one on an extra level)is then inserted into the binomial queue consisting of the remaining binomial trees,thus forming another binomial tree of 2k −1elements.At that point,the root has a sub-tree that is a heap of 2k −1 − 1elements and another subtree that is a binomial tree of 2k −1elements.Recursively convert that subtree into a heap;now the whole structure is a binary heap.The running time for N = 2k satisfies T (N ) = 2T (N / 2) + log N .The base case is T (8) = 8.-30-w w w .k h d a w .c o m 课后答案网6.8Let D 1,D 2,...,D k be random variables representing the depth of the smallest,second smal-lest,and k th smallest elements,respectively.We are interested in calculating E (D k ).In what follows,we assume that the heap size N is one less than a power of two (that is,the bottom level is completely filled)but sufficiently large so that terms bounded by O (1 / N )are negligible.Without loss of generality,we may assume that the k th smallest element is in the left subheap of the root.Let p j ,k be the probability that this element is the j th smal-lest element in the subheap.Lemma:For k >1,E (D k ) = j =1Σk −1p j ,k (E (D j ) + 1).Proof:An element that is at depth d in the left subheap is at depth d + 1in the entire subheap.Since E (D j + 1) = E (D j ) + 1,the theoremfollows.Since by assumption,the bottom level of the heap is full,each of second,third,...,k −1th smallest elements are in the left subheap with probability of 0.5.(Technically,the probabil-ity should be ⁄12 − 1/(N −1)of being in the right subheap and ⁄12 + 1/(N −1)of being in the left,since we have already placed the k th smallest in the right.Recall that we have assumed that terms of size O (1/N )can be ignored.)Thusp j ,k = p k −j ,k = 2k −21____( j −1k −2)Theorem:E (D k ) ≤ log k .Proof:The proof is by induction.The theorem clearly holds for k = 1and k = 2.We then show that it holds for arbitrary k > 2on the assumption that it holds for all smaller k .Now,by the inductive hypothesis,for any 1 ≤ j ≤ k −1,E (D j ) + E (D k −j ) ≤ log j + log k − j Since f (x ) = log x is convex for x > 0,log j + log k − j ≤ 2log (k / 2)ThusE (D j ) + E (D k −j ) ≤ log (k / 2) + log (k / 2)Furthermore,since pj ,k = p k −j ,k ,p j ,k E (D j ) + p k −j ,k E (D k −j ) ≤p j ,k log (k / 2) + p k −j ,k log (k / 2)From the lemma,E (D k ) =j =1Σk −1p j ,k (E (D j ) + 1)= 1 + j =1Σk −1p j ,k E (D j )ThusE (D k ) ≤ 1 +j =1Σk −1p j ,k log (k / 2)-31-w w w .k h d a w.c o m 课后答案网≤ 1 + log (k / 2)j =1Σk −1p j ,k ≤ 1 + log (k / 2)≤ log kcompleting theproof.It can also be shown that asymptotically,E (D k ) ∼∼log (k −1) − 0.273548.6.9(a)Perform a preorder traversal of the heap.(b)Works for leftist and skew heaps.The running time is O (Kd )for d -heaps.6.11Simulations show that the linear time algorithm is the faster,not only on worst-case inputs,but also on random data.6.12(a)If the heap is organized as a (min)heap,then starting at the hole at the root,find a pathdown to a leaf by taking the minimum child.The requires roughly log N comparisons.To find the correct place where to move the hole,perform a binary search on the log N ele-ments.This takes O (log log N )comparisons.(b)Find a path of minimum children,stopping after log N − log log N levels.At this point,it is easy to determine if the hole should be placed above or below the stopping point.If it goes below,then continue finding the path,but perform the binary search on only the last log log N elements on the path,for a total of log N + log log log N comparisons.Other-wise,perform a binary search on the first log N − log log N elements.The binary search takes at most log log N comparisons,and the path finding took only log N − log log N ,so the total in this case is log N .So the worst case is the first case.(c)The bound can be improved to log N + log *N + O (1),where log *N is the inverse Ack-erman function (see Chapter 8).This bound can be found in reference [16].6.13The parent is at position (i + d − 2)/d .The children are in positions (i − 1)d + 2,...,id + 1.6.14(a)O ((M + dN )log d N ).(b)O ((M + N )log N ).(c)O (M+ N 2).(d)d = max (2, M / N ).(See the related discussion at the end of Section 11.4.)-32-w w w.k h d a w .c o m课后答案网6.16311891041585211162121118176.171237654891011121314156.18This theorem is true,and the proof is very much along the same lines as Exercise 4.17.6.19If elements are inserted in decreasing order,a leftist heap consisting of a chain of left chil-dren is formed.This is the best because the right path length is minimized.6.20(a)If a DecreaseKey is performed on a node that is very deep (very left),the time to per-colate up would be prohibitive.Thus the obvious solution doesn’t work.However,we can still do the operation efficiently by a combination of Delete and Insert .To Delete an arbi-trary node x in the heap,replace x by the Merge of its left and right subheaps.This might create an imbalance for nodes on the path from x ’s parent to the root that would need to be fixed by a child swap.However,it is easy to show that at most log N nodes can be affected,preserving the time bound.This is discussed in Chapter 11.6.21Lazy deletion in leftist heaps is discussed in the paper by Cheriton and Tarjan [9].The gen-eral idea is that if the root is marked deleted,then a preorder traversal of the heap is formed,and the frontier of marked nodes is removed,leaving a collection of heaps.These can be merged two at a time by placing all the heaps on a queue,removing two,merging them,and placing the result at the end of the queue,terminating when only one heap remains.6.22(a)The standard way to do this is to divide the work into passes.A new pass begins whenthe first element reappears in a heap that is dequeued.The first pass takes roughly-33-w ww .k h d a w .com 课后答案网2* 1* (N / 2)time units because there are N / 2merges of trees with one node each on the right path.The next pass takes 2* 2* (N / 4)time units because of the roughly N / 4merges of trees with no more than two nodes on the right path.The third pass takes 2* 3* (N / 8)time units,and so on.The sum converges to 4N .(b)It generates heaps that are more leftist.6.23311891041585211162121118176.241327564151113914101286.25This claim is also true,and the proof is similar in spirit to Exercise 4.17or 6.18.6.26Yes.All the single operation estimates in Exercise 6.22become amortized instead ofworst-case,but by the definition of amortized analysis,the sum of these estimates is a worst-case bound for the sequence.6.27Clearly the claim is true for k = 1.Suppose it is true for all values i = 1,2,...,k .A B k +1tree is formed by attaching a B k tree to the root of a B k tree.Thus by induction,it containsa B 0through B k −1tree,as well as the newly attached B k tree,proving the claim.6.28Proof is by induction.Clearly the claim is true for k = 1.Assume true for all values i = 1,2,...,k .A B k +1tree is formed by attaching a B k tree to the original B k tree.The original-34-w w w .k h d a w.c o m 课后答案网thus had ( d k )nodes at depth d .The attached tree had ( d −1k )nodes at depth d −1,which are now at depth d .Adding these two terms and using a well-known formula estab-lishes the theorem.6.29413152318246551122124651426161822955116.30This is established in Chapter 11.6.31The algorithm is to do nothing special −merely Insert them.This is proved in Chapter 11.6.35Don’t keep the key values in the heap,but keep only the difference between the value of thekey in a node and the value of the key in its parent.6.36O (N + k log N )is a better bound than O (N log k ).The first bound is O (N )ifk = O (N / log N ).The second bound is more than this as soon as k grows faster than a constant.For the other values Ω(N / log N ) = k = ο(N ),the first bound is better.When k = Θ(N ),the bounds are identical.-35-w w w.k h d a w.c o m 课后答案网。
