河南中考23题典型例题讲解
2021-2022学年河南省中考物理经典试题附解析

2021-2022学年河南省中考物理经典试题学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、单选题1.下列说法中,哪些是正确的.............................................................................................. ()A.物体受力,运动状态一定改变B.物体不受力,运动状态一定不改变C.物体运动状态不变,说明它不动D.物体运动过程中速度大小不变,则它受到的力是平衡力2.一场大雪过后,人们会感到外面万籁俱寂。
究其原因,你认为正确的是()A.可能是大雪后,行驶的车辆减少,没有噪声B.可能是大雪蓬松且多孔,对噪声有吸收作用C.可能是大雪后,大地银装素裹,噪声被反射D.可能是大雪后气温较低,噪声传播速度变慢3.如图所示四种现象中,由于光的反射而形成的()4.100℃的水蒸气变成100℃的水,水蒸气的温度将()A.上升 B.下降 C.保持不变 D.先下降后上升.5.戴眼镜的乘客乘坐冷气很强的出租汽车一阵后下车,有时会发觉眼镜镜片模糊。
此现象是由于车外空气中的水蒸气遇到冰冷的镜片发生............................................................. ()A.液化B.凝华C.熔化D.凝固6.用绸子摩擦过的玻璃棒接触验电器的金属球,发现金属箔张开,金属箔张开的原因是()A.质子从玻璃棒转移到金属箔上B.质子从金属箔转移到玻璃棒上C.电子从玻璃棒转移到金属箔上D.电子从金属箔转移到玻璃棒上.7.用蓄电池给用电器供电,放电时的电流为5A,可持续放电150s,若放电时的电流为2A,则放电时间为()A.150s B.300s C.375s D.425s8.下列关于声现象的说法中,正确的是()A.在噪声较大的环境中工作时,人们常佩带耳罩,属于在声源处减弱噪声B.用一根棉线和两个纸杯可以制成“土电话”,说明固体能够传声C.我们无法听到蝴蝶飞过的声音,是因为它发出声音的响度太小D.我们能区分出小提琴和二胡的声音,是因为它们发出声音的音调不同.9.如图所示,ab是闭合电路的一部分导体,与灵敏电流计相连。
中考数学专题复习 专题23 平行四边形(教师版含解析)

中考专题23 平行四边形问题1.平行四边形定义有两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD”表示,读作“平行四边形ABCD”。
2.平行四边形的性质(1)平行四边形的对边平行且相等;(2)平行四边形的对角相等;(3)平行四边形的对角线互相平分。
3.平行四边形的判定(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)对角线互相平分的四边形是平行四边形;(5)两组对角分别相等的四边形是平行四边形。
4.平行四边形的面积:S平行四边形=底边长×高=ah【经典例题1】(2020年•温州)如图,在△ABC中,∠A=40°,AB=AC,点D在AC边上,以CB,CD为边作▱BCDE,则∠E的度数为( )A.40°B.50°C.60°D.70°【标准答案】D【分析】根据等腰三角形的性质可求∠C,再根据平行四边形的性质可求∠E.【答案剖析】∵在△ABC中,∠A=40°,AB=AC,∴∠C=(180°﹣40°)÷2=70°,∵四边形BCDE是平行四边形,∴∠E=70°.【知识点练习】(2019•山东临沂)如图,在平行四边形ABCD中,M、N是BD上两点,BM=DN,连接AM、MC、CN、NA,添加一个条件,使四边形AMCN是矩形,这个条件是( )A.OM=AC B.MB=MO C.BD⊥AC D.∠AMB=∠CND【标准答案】A【答案剖析】由平行四边形的性质可知:OA=OC,OB=OD,再证明OM=ON即可证明四边形AMCN是平行四边形.证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD∵对角线BD上的两点M、N满足BM=DN,∴OB﹣BM=OD﹣DN,即OM=ON,∴四边形AMCN是平行四边形,∵OM=AC,∴MN=AC,∴四边形AMCN是矩形.【经典例题2】(2020年•凉山州)如图,▱ABCD的对角线AC、BD相交于点O,OE∥AB交AD于点E,若OA=1,△AOE的周长等于5,则▱ABCD的周长等于16 .【标准答案】16.【答案剖析】由平行四边形的性质得AB=CD,AD=BC,OB=OD,证OE是△ABD的中位线,则AB=2OE,AD=2AE,求出AE+OE=4,则AB+AD=2AE+2OE=8,即可得出标准答案.∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,OB=OD,∵OE∥AB,∴OE是△ABD的中位线,∴AB=2OE,AD=2AE,∵△AOE的周长等于5,∴OA+AE+OE=5,∴AE+OE=5﹣OA=5﹣1=4,∴AB+AD=2AE+2OE=8,∴▱ABCD的周长=2×(AB+AD)=2×8=16;【知识点练习】(2019•湖北武汉)如图所示,在▱ABCD中,E.F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为.【标准答案】21°.【答案剖析】设∠ADE=x,∵AE=EF,∠ADF=90°,∴∠DAE=∠ADE=x,DE=AF=AE=EF,∵AE=EF=CD,∴DE=CD,∴∠DCE=∠DEC=2x,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠DAE=∠BCA=x,∴∠DCE=∠BCD﹣∠BCA=63°﹣x,∴2x=63°﹣x,解得:x=21°,即∠ADE=21°。
题型:河南近几年中学考试数学第23题(新颖)

近几年中考数学第23题23.(11分)(2016)如图1,直线y=-43x+n交x轴于点A,交y轴于点C(0,4)抛物线y=23x2+bx+c经过点A,交y轴于点B(0,-2).点P为抛物线上的一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB.(1)求抛物线的解析式.(2)当△BDP为等腰直角三角形时,求线段PD的长.(3)如图2,将△BDP绕点B逆时针旋转,得到△BD/P/,且∠PBP/=∠OAC,当点P的对应点P/落在坐标轴上时,请直接写出P点的坐标.解:(1)由y=-43x+n过点C(0,4),得n=4,则y=-43x+4当y=0时,得-43x+4=0,解得:x=3,∴点A坐标是(3,0)…………………………………………………1分∵y=23x2+bx+c经过点A(3,0), B(0,-2)图1备用图∴22033b+c32c⎧=⨯+⎪⎨⎪-=⎩,解得:4b3c2⎧=-⎪⎨⎪=-⎩∴抛物线的解析式是23x2-43x-2……………………………………………3分(2)∵点P的横坐标为m,∴P(m,23m2-43m-2),D(m,-2)…………4分若△BDP为等腰直角三角形时,则PD=BD;①当点P在直线BD上方时,PD=23m2-43m-2+2=23m2-43m,(ⅰ)若P在y轴左侧,则m<0,BD=-m;∴23m2-43m=-m,解得:m=12或m=0(舍去)…………………………………5分(ⅱ)若P在y轴右侧,则m>0,BD=m;∴23m2-43m=m,解得:m=72或m=0(舍去)…………………………………6分②当点P在直线BD下方时,PD=-2-(23m2-43m-2) =-23m2+43m,则m>0,BD=m;∴-23m2+43m=m,解得:m=12或m=0(舍去)……………………………7分综上:m=72或m=12。
即当△BDP为等腰直角三角形时, PD的长为72或12。
2014河南数学中招23题

米斯林
(五)
★
2014年压轴题
23题解析
23. (11分)如图,抛物线y=-x2+bx+c与x轴交于A(- 1,0),B(5,0)两点,直线y=- x+3与y轴交于点C,与x轴交 于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x 轴于点F,交直线CD于点E.设点P的横坐标为m。 • (1)求抛物线的解析式; • (2)若PE =5EF,求m的值; • (3)若点E/是点E关于直线PC的对称点、是否存在点P, 使点 E 落在y轴上?若存在,请直接写出相应的点P的坐 标;若不存在,请说明理由。
理由如下: ∵点 E'和 E 关于直线PC对称, ∴∠1=∠2 又∵PE∥y轴 ∴∠3=∠2 ∴∠1=∠3 ∴ CE=PE 过点E作EM ⊥y轴于点M ∴∠CME=∠COD=90° ∵∠ECM=∠DCO ∴ △CME∽△COD
'
ቤተ መጻሕፍቲ ባይዱ
∴
ME CE OD CD
• 由直线y= -
m +3 得,C(03), D(4,0)
∵PE=5EF
∴ -m
2
19 + 4 m+2
2
= 5(
4
“上纵—下纵”,数形结合思想
即 m - m-17 =0 1 69 m 解得,m
3
1 69 综上所述,m的值为2 或 2
2
1 69 (舍去) 2
• • 2 • 0 1 • 4 • 年 2 • 3 • 题 3 • / • 5 • •
y P
C
A
E O F D
B X
2014年23题解析1/5
y 解: P 2 (1)∵抛物线y =-x +bx +c与x 轴交于A (-1,0) , B (5,0)两点,
2020年河南省中考数学试题(含答案解析)

2020年河南省中考数学试卷(共23题,满分120分)一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.2的相反数是()A.﹣2B.C.D.22.如图摆放的几何体中,主视图与左视图有可能不同的是()A.B.C.D.3.要调查下列问题,适合采用全面调查(普查)的是()A.中央电视台《开学第一课》的收视率B.某城市居民6月份人均网上购物的次数C.即将发射的气象卫星的零部件质量D.某品牌新能源汽车的最大续航里程4.如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为()A.100°B.110°C.120°D.130°5.电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B.某视频文件的大小约为1GB,1GB等于()A.230B B.830B C.8×1010B D.2×1030B6.若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y的图象上,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y3>y1C.y1>y3>y2D.y3>y2>y17.定义运算:m☆n=mn2﹣mn﹣1.例如:4☆2=4×22﹣4×2﹣1=7.则方程1☆x =0的根的情况为()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.只有一个实数根8.国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x,则可列方程为()A.500(1+2x)=7500B.5000×2(1+x)=7500C.5000(1+x)2=7500D.5000+5000(1+x)+5000(1+x)2=75009.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为()A.(,2)B.(2,2)C.(,2)D.(4,2)10.如图,在△ABC中,AB=BC,∠BAC=30°,分别以点A,C为圆心,AC 的长为半径作弧,两弧交于点D,连接DA,DC,则四边形ABCD的面积为()A.6B.9C.6D.3二、填空题(每小题3分,共15分)11.请写出一个大于1且小于2的无理数.12.已知关于x的不等式组其中a,b在数轴上的对应点如图所示,则这个不等式组的解集为.13.如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是.14.如图,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为.15.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为.三、解答题(本大题共8个小题,满分75分)16.(8分)先化简,再求值:(1),其中a1.17.(9分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:[收集数据]从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如下:甲:501 497 498 502 513 489 506 490 505 486 502 503 498 497 491 500 505 502 504 505乙:505 499 502 491 487 506 493 505 499 498 502 503 501 490 501 502 511 499 499 501[整理数据]整理以上数据,得到每袋质量x(g)的频数分布表.质量频数机器485≤x<490490≤x<495495≤x<500500≤x<505505≤x<510510≤x<515甲224741乙135731 [分析数据]根据以上数据,得到以下统计量.统计量机器平均数中位数方差不合格率甲499.7501.542.01b乙499.7a31.8110%根据以上信息,回答下列问题:(1)表格中的a=,b=;(2)综合上表中的统计量,判断工厂应迭购哪一台分装机,并说明理由.18.(9分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, 1.41);(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.19.(9分)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;(2)求打折前的每次健身费用和k2的值;(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.20.(9分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具﹣﹣三分角器.图1是它的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,.求证:.21.(10分)如图,抛物线y=﹣x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,且OA=OB,点G为抛物线的顶点.(1)求抛物线的解析式及点G的坐标;(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的纵坐标y Q的取值范围.22.(10分)小亮在学习中遇到这样一个问题:如图,点D是上一动点,线段BC=8cm,点A是线段BC的中点,过点C 作CF∥BD,交DA的延长线于点F.当△DCF为等腰三角形时,求线段BD的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:(1)根据点D在上的不同位置,画出相应的图形,测量线段BD,CD,FD的长度,得到下表的几组对应值.BD/cm0 1.0 2.0 3.0 4.0 5.0 6.07.08.0 CD/cm8.07.77.2 6.6 5.9a 3.9 2.40 FD/cm8.07.4 6.9 6.5 6.1 6.0 6.2 6.78.0操作中发现:①“当点D为的中点时,BD=5.0cm”.则上表中a的值是;②“线段CF的长度无需测量即可得到”.请简要说明理由.(2)将线段BD的长度作为自变量x,CD和FD的长度都是x的函数,分别记为y CD和y FD,并在平面直角坐标系xOy中画出了函数y FD的图象,如图所示.请在同一坐标系中画出函数y CD的图象;(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF为等腰三角形时,线段BD长度的近似值(结果保留一位小数).23.(11分)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当α=60°时,△DEB′的形状为,连接BD,可求出的值为;(2)当0°<α<360°且α≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出的值.2020年河南省中考数学试卷答案解析一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.1.2的相反数是()A.﹣2B.C.D.2【解答】解:2的相反数是﹣2.故选:A.2.如图摆放的几何体中,主视图与左视图有可能不同的是()A.B.C.D.【解答】解:A、主视图和左视图是长方形,一定相同,故本选项不合题意题意;B、主视图和左视图都是等腰三角形,一定相同,故选项不符合题意;C、主视图和左视图都是圆,一定相同,故选项不符合题意;D、主视图是长方形,左视图是正方形,故本选项符合题意;故选:D.3.要调查下列问题,适合采用全面调查(普查)的是()A.中央电视台《开学第一课》的收视率B.某城市居民6月份人均网上购物的次数C.即将发射的气象卫星的零部件质量D.某品牌新能源汽车的最大续航里程【解答】解:A、调查中央电视台《开学第一课》的收视率,适合抽查,故本选项不合题意;B、调查某城市居民6月份人均网上购物的次数,适合抽查,故本选项不合题意;C、调查即将发射的气象卫星的零部件质量,适合采用全面调查(普查),故本选项符合题意;D、调查某品牌新能源汽车的最大续航里程,适合抽查,故本选项不合题意.故选:C.4.如图,l1∥l2,l3∥l4,若∠1=70°,则∠2的度数为()A.100°B.110°C.120°D.130°【解答】解:∵l1∥l2,∠1=70°,∴∠3=∠1=70°,∵l3∥l4,∴∠2=180°﹣∠3=180°﹣70°=110°,故选:B.5.电子文件的大小常用B,KB,MB,GB等作为单位,其中1GB=210MB,1MB=210KB,1KB=210B.某视频文件的大小约为1GB,1GB等于()A.230B B.830B C.8×1010B D.2×1030B 【解答】解:由题意得:210×210×210B=210+10+10=230B,故选:A.6.若点A(﹣1,y1),B(2,y2),C(3,y3)在反比例函数y的图象上,则y1,y2,y3的大小关系是()A.y1>y2>y3B.y2>y3>y1C.y1>y3>y2D.y3>y2>y1【解答】解:∵点A(﹣1,y1)、B(2,y2)、C(3,y3)在反比例函数y 的图象上,∴y16,y23,y32,又∵﹣3<﹣2<6,∴y1>y3>y2.故选:C.7.定义运算:m☆n=mn2﹣mn﹣1.例如:4☆2=4×22﹣4×2﹣1=7.则方程1☆x =0的根的情况为()A.有两个不相等的实数根B.有两个相等的实数根C.无实数根D.只有一个实数根【解答】解:由题意可知:1☆x=x2﹣x﹣1=0,∴△=1﹣4×1×(﹣1)=5>0,故选:A.8.国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x,则可列方程为()A.500(1+2x)=7500B.5000×2(1+x)=7500C.5000(1+x)2=7500D.5000+5000(1+x)+5000(1+x)2=7500【解答】解:设我国2017年至2019年快递业务收入的年平均增长率为x,由题意得:5000(1+x)2=7500,故选:C.9.如图,在△ABC中,∠ACB=90°,边BC在x轴上,顶点A,B的坐标分别为(﹣2,6)和(7,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为()A.(,2)B.(2,2)C.(,2)D.(4,2)【解答】解:如图,设正方形D′C′O′E′是正方形OCDE沿x轴向右平移后的正方形,∵顶点A,B的坐标分别为(﹣2,6)和(7,0),∴AC=6,OC=2,OB=7,∴BC=9,∵四边形OCDE是正方形,∴DE=OC=OE=2,∴O′E′=O′C′=2,∵E′O′⊥BC,∴∠BO′E′=∠BCA=90°,∴E′O′∥AC,∴△BO′E′∽△BCA,∴,∴,∴BO′=3,∴OC′=7﹣2﹣3=2,∴当点E落在AB边上时,点D的坐标为(2,2),故选:B.10.如图,在△ABC中,AB=BC,∠BAC=30°,分别以点A,C为圆心,AC 的长为半径作弧,两弧交于点D,连接DA,DC,则四边形ABCD的面积为()A.6B.9C.6D.3【解答】解:连接BD交AC于O,∵AD=CD,AB=BC,∴BD垂直平分AC,∴BD⊥AC,AO=CO,∵AB=BC,∴∠ACB=∠BAC=30°,∵AC=AD=CD,∴△ACD是等边三角形,∴∠DAC=∠DCA=60°,∴∠BAD=∠BCD=90°,∠ADB=∠CDB=30°,∵AB=BC,∴AD=CD AB=3,∴四边形ABCD的面积=23,故选:D.二、填空题(每小题3分,共15分)11.请写出一个大于1且小于2的无理数.【解答】解:大于1且小于2的无理数是,答案不唯一.故答案为:.12.已知关于x的不等式组其中a,b在数轴上的对应点如图所示,则这个不等式组的解集为x>a.【解答】解:∵b<0<a,∴关于x的不等式组的解集为:x>a,故答案为:x>a.13.如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是.【解答】解:自由转动转盘两次,指针所指区域所有可能出现的情况如下:共有16种可能出现的结果,其中两次颜色相同的有4种,∴P(两次颜色相同),故答案为:.14.如图,在边长为2的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为1.【解答】解:设DF,CE交于O,∵四边形ABCD是正方形,∴∠B=∠DCF=90°,BC=CD=AB,∵点E,F分别是边AB,BC的中点,∴BE=CF,∴△CBE≌△DCF(SAS),∴CE=DF,∠BCE=∠CDF,∵∠CDF+∠CFD=90°,∴∠BCE+∠CFD=90°,∴∠COF=90°,∴DF⊥CE,∴CE=DF,∵点G,H分别是EC,FD的中点,∴CG=FH,∵∠DCF=90°,CO⊥DF,∴CF2=OF•DF,∴OF,∴OH,OD,∵OC2=OF•OD,∴OC,∴OG=CG﹣OC,∴HG1,故答案为:1.15.如图,在扇形BOC中,∠BOC=60°,OD平分∠BOC交于点D,点E为半径OB上一动点.若OB=2,则阴影部分周长的最小值为.【解答】解:如图,作点D关于OB的对称点D′,连接D′C交OB于点E′,连接E′D、OD′,此时E′C+E′C最小,即:E′C+E′C=CD′,由题意得,∠COD=∠DOB=∠BOD′=30°,∴∠COD′=90°,∴CD′2,的长l,∴阴影部分周长的最小值为2.故答案为:.三、解答题(本大题共8个小题,满分75分)16.(8分)先化简,再求值:(1),其中a1.【解答】解:=a﹣1,把a1代入a﹣11﹣1.17.(9分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500g,与之相差大于10g为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:[收集数据]从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g)如下:甲:501 497 498 502 513 489 506 490 505 486 502 503 498 497 491 500 505 502 504 505乙:505 499 502 491 487 506 493 505 499 498502 503 501 490 501 502 511 499 499 501[整理数据]整理以上数据,得到每袋质量x(g)的频数分布表.质量频数机器485≤x<490490≤x<495495≤x<500500≤x<505505≤x<510510≤x<515甲224741乙135731 [分析数据]根据以上数据,得到以下统计量.统计量机器平均数中位数方差不合格率甲499.7501.542.01b乙499.7a31.8110%根据以上信息,回答下列问题:(1)表格中的a=501,b=15%;(2)综合上表中的统计量,判断工厂应迭购哪一台分装机,并说明理由.【解答】解:(1)将乙的成绩从小到大排列后,处在中间位置的两个数都是501,因此中位数是501,b=3➗20=15%,故答案为:501,15%;(2)选择乙机器,理由:乙的不合格率较小,18.(9分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m.(1)求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40, 1.41);(2)“景点简介”显示,观星台的高度为12.6m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.【解答】解:(1)过A作AD⊥PM于D,延长BC交AD于E,则四边形BMNC,四边形BMDE是矩形,∴BC=MN=16m,DE=CN=BM=1.6m,∵∠AED=90°,∠ACE=45°,∴△ACE是等腰直角三角形,∴CE=AE,设AE=CE=x,∴BE=16+x,∵∠ABE=22°,∴tan22°0.40,∴x≈10.7(m),∴AD=10.7+1.6=12.3(m),答:观星台最高点A距离地面的高度约为12.3m;(2)∵“景点简介”显示,观星台的高度为12.6m,∴本次测量结果的误差为12.6﹣12.3=0.3m,减小误差的合理化建议为:为了减小误差可以通过多次测量取平均值的方法.19.(9分)暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下.方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.设某学生暑期健身x(次),按照方案一所需费用为y1(元),且y1=k1x+b;按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;(2)求打折前的每次健身费用和k2的值;(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.【解答】解:(1)∵y1=k1x+b过点(0,30),(10,180),∴,解得,k1=15表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元,b=30表示的实际意义是:购买一张学生暑期专享卡的费用为30元;(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),则k2=25×0.8=20;(3)选择方案一所需费用更少.理由如下:由题意可知,y1=15x+30,y2=20x.当健身8次时,选择方案一所需费用:y1=15×8+30=150(元),选择方案二所需费用:y2=20×8=160(元),∵150<160,∴选择方案一所需费用更少.20.(9分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具﹣﹣三分角器.图1是它的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB与AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,AB =OB,EN切半圆O于F.求证:EB,EO就把∠MEN三等分.【解答】解:已知:如图2,点A,B,O,C在同一直线上,EB⊥AC,垂足为点B,AB=OB,EN切半圆O于F.求证:EB,EO就把∠MEN三等分,证明:∵EB⊥AC,∴∠ABE=∠OBE=90°,∵AB=OB,BE=BE,∴△ABE≌△OBE(SAS),∴∠1=∠2,∵BE⊥OB,∴BE是⊙E的切线,∵EN切半圆O于F,∴∠2=∠3,∴∠1=∠2=∠3,∴EB,EO就把∠MEN三等分.故答案为:AB=OB,EN切半圆O于F;EB,EO就把∠MEN三等分.21.(10分)如图,抛物线y=﹣x2+2x+c与x轴正半轴,y轴正半轴分别交于点A,B,且OA=OB,点G为抛物线的顶点.(1)求抛物线的解析式及点G的坐标;(2)点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q为抛物线上点M,N之间(含点M,N)的一个动点,求点Q的纵坐标y Q的取值范围.【解答】解:(1)∵抛物线y=﹣x2+2x+c与y轴正半轴分别交于点B,∴点B(0,c),∵OA=OB=c,∴点A(c,0),∴0=﹣c2+2c+c,∴c=3或0(舍去),∴抛物线解析式为:y=﹣x2+2x+3,∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点G为(1,4);(2)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴对称轴为直线x=1,∵点M,N为抛物线上两点(点M在点N的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,∴点M的横坐标为﹣2或4,点N的横坐标为6,∴点M坐标为(﹣2,﹣5)或(4,﹣5),点N坐标(6,﹣21),∵点Q为抛物线上点M,N之间(含点M,N)的一个动点,∴﹣21≤y Q≤4或﹣21≤y Q≤﹣5.22.(10分)小亮在学习中遇到这样一个问题:如图,点D是上一动点,线段BC=8cm,点A是线段BC的中点,过点C 作CF∥BD,交DA的延长线于点F.当△DCF为等腰三角形时,求线段BD的长度.小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:(1)根据点D 在上的不同位置,画出相应的图形,测量线段BD,CD,FD的长度,得到下表的几组对应值.0 1.0 2.0 3.0 4.0 5.0 6.07.08.0BD/cmC8.07.77.2 6.6 5.9a 3.9 2.40 D/cm8.07.4 6.9 6.5 6.1 6.0 6.2 6.78.0FD/cm操作中发现:①“当点D 为的中点时,BD=5.0cm”.则上表中a的值是5;②“线段CF的长度无需测量即可得到”.请简要说明理由.(2)将线段BD的长度作为自变量x,CD和FD的长度都是x的函数,分别记为y CD和y FD,并在平面直角坐标系xOy中画出了函数y FD的图象,如图所示.请在同一坐标系中画出函数y CD的图象;(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF为等腰三角形时,线段BD长度的近似值(结果保留一位小数).【解答】解:(1)∵点D为的中点,∴,∴BD=CD=a=5cm,故答案为:5;(2)∵点A是线段BC的中点,∴AB=AC,∵CF∥BD,∴∠F=∠BDA,又∵∠BAD=∠CAF,∴△BAD≌△CAF(AAS),∴BD=CF,∴线段CF的长度无需测量即可得到;(3)由题意可得:(4)由题意画出函数y CF的图象;由图象可得:BD=3.8cm或5cm或6.2cm时,△DCF为等腰三角形.23.(11分)将正方形ABCD的边AB绕点A逆时针旋转至AB′,记旋转角为α,连接BB′,过点D作DE垂直于直线BB′,垂足为点E,连接DB′,CE.(1)如图1,当α=60°时,△DEB′的形状为等腰直角三角形,连接BD,可求出的值为;(2)当0°<α<360°且α≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B′,E,C,D为顶点的四边形是平行四边形时,请直接写出的值.【解答】解:(1)∵AB绕点A逆时针旋转至AB′,∴AB=AB',∠BAB'=60°,∴△ABB'是等边三角形,∴∠BB'A=60°,∴∠DAB'=∠BAD﹣∠BAB'=90°﹣60°=30°,∵AB'=AB=AD,∴∠AB'D=∠ADB',∴∠AB'D75°,∴∠DB'E=180°﹣60°﹣75°=45°,∵DE⊥B'E,∴∠B'DE=90°﹣45°=45°,∴△DEB'是等腰直角三角形.∵四边形ABCD是正方形,∴∠BDC=45°,∴,同理,∴,∵∠BDB'+∠B'DC=45°,∠EDC+∠B'DC=45°,∴BDB'=∠EDC,∴△BDB'∽△CDE,∴.故答案为:等腰直角三角形,.(2)①两结论仍然成立.证明:连接BD,∵AB=AB',∠BAB'=α,∴∠AB'B=90°,∵∠B'AD=α﹣90°,AD=AB',∴∠AB'D=135°,∴∠EB'D=∠AB'D﹣∠AB'B=135°45°,∵DE⊥BB',∴∠EDB'=∠EB'D=45°,∴△DEB'是等腰直角三角形,∴,∵四边形ABCD是正方形,∴,∠BDC=45°,∴,∵∠EDB'=∠BDC,∴∠EDB'+∠EDB=∠BDC+∠EDB,即∠B'DB=∠EDC,∴△B'DB∽△EDC,∴.②3或1.若CD为平行四边形的对角线,点B'在以A为圆心,AB为半径的圆上,取CD的中点.连接BO交⊙A于点B',过点D作DE⊥BB'交BB'的延长线于点E,由(1)可知△B'ED是等腰直角三角形,∴B'D B'E,由(2)①可知△BDB'∽△CDE,且BB'CE.∴1111=3.若CD为平行四边形的一边,如图3,点E与点A重合,∴1.综合以上可得3或1.。
【河南中考面对面】中考数学总复习 题型6 第23题函数动态变化问题课件

性质求解.
解:∵设点P的横坐标为t, 17 5 2 ∴点M坐标为(t,- t + t+1), 4 4 设直线AB的解析式为y=kx+b, 将A(0,1),B(3, 5 )代入, 2 b= 1 得 5 3 k +b = , 1 2 k= 解得 2 b= 1, 1 ∴直线AB的解析式为y= x+1, 2 ∵点P在直线AB上,点P的横坐标为t,
∴AD2=[5-(-3)]2=64, 5 121 2 2 2 2 BD =4 =16,AE =[ -(-3)] = , 2 4 EM2=m2, 25 BF2=(5- 5 )2= ,MF2=(4-m)2, 4 2 ∴在Rt△ABD中,AB2=AD2+BD2=80, 121 在Rt△AEM中,AM2=AE2+EM2=m2+ , 25 4 2 2 2 在Rt△BFM中,BM =BF +MF = +(4-m)2. 4 要使△ABM是以AB为直角边的直角三角形,
∴线段PQ等于抛物线与直线的纵坐标之差,
1 3 1 2 x +56x+4)-( x+ ) 2 2 6 5 1 2 1 =- x + x+ 2 6 3 1 8 2 =- (x-1) + . 6 3 由此可见,当点P的横坐标为1(-3≤x≤5)时, 8 线段PQ有最大值 . 3
即y=(-
(3)【思路分析】借助两点之间的线段长
【方法指导】三角形周长与四边形判定结
合的函数动态问题可从以下几个方面思考:
河南省中考数学第23题压轴题(2010-2020)
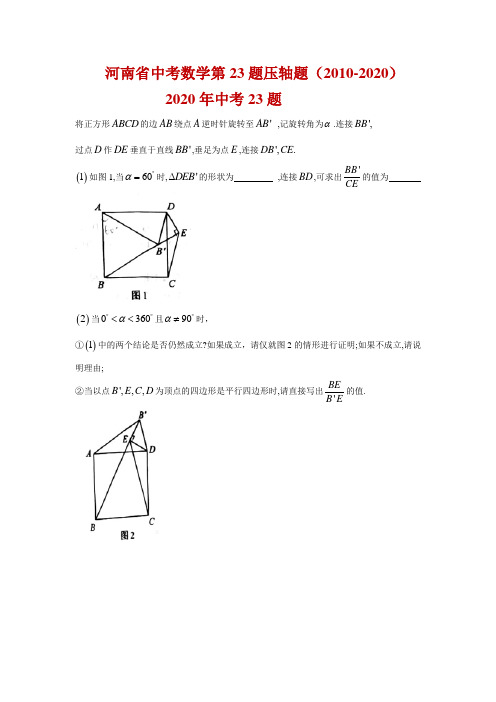
河南省中考数学第23题压轴题(2010-2020)2020年中考23题将正方形ABCD 的边AB 绕点A 逆时针旋转至'AB ,记旋转角为α.连接',BB 过点D 作DE 垂直于直线'BB ,垂足为点E ,连接',.DB CE()1如图1,当60α︒=时,'DEB ∆的形状为 ,连接BD ,可求出'BB CE的值为()2当0360α︒︒<<且90α︒≠时,①()1中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点',,,B E C D 为顶点的四边形是平行四边形时,请直接写出'BEB E的值.2019年中考23题如图,抛物线212y ax x c =++交x 轴于A ,B 两点,交y 轴于点C .直线122y x =--经过点A ,C . (1)求抛物线的解析式.()()()()22141241202162,00,42,00,42212-+=∴⎪⎩⎪⎨⎧-==∴⎩⎨⎧-==--↓→----→--=x x y c a c c a C A C A x y 抛物线(2)点P 是抛物线上一动点,过点P 作x 轴的垂线,交直线AC 于点M ,设点P 的横坐标为m .①当△PCM 是直角三角形时,求点P 的坐标;21P AC C C P y C P PC M y PM 的垂线交抛物线于点作处的作图方法是:过点点轴的平行线交抛物线于作处的作图方法是:过点处都可能是直角处不可能是直角轴,∥直角三角形的存在性:∴()()()10,62222141222212,22214122,0221222P x y x x y x y x y P x x C CP CP AC ∴⎪⎩⎪⎨⎧-=-+=-=--=--∴-+=--②作点B 关于点C 的对称点B′,则平面内存在直线l ,使点M ,B ,B′到该直线的距离都相等.当点P 在y 轴右侧的抛物线上,且与点B 不重合时,请直接写出直线l :y =kx +b 的解析式.(k ,b 可用含m 的式子表示)的中位线所在的直线这一问就是求△M BB 12018年中考23题如图,抛物线y =ax 2+6x +c 交x 轴于A ,B 两点,交y 轴于点C .直线y =x -5经过点B ,C .(1)求抛物线的解析式. ()()()()565,00,55,00,552-+-=→--→-=x x y C B C B x y 抛物线 (2)过点A 的直线交直线BC 于点M .①(两定两动)当AM ⊥BC 时,过抛物线上一动点P (不与点B ,C 重合),作直线AM 的平行线交直线BC 于点Q ,若以点A ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标;32118,P P AP PBC AP A BC P A BC AM AMPQ PQAM 个单位,就得到直线向下平移将交抛物线于点∥作过点直线的距离相等到∥∴⊥=∴ ()⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛+,2415,2415,4321P P P②连接AC ,当直线AM 与直线BC 的夹角等于∠ACB 的2倍时,请直接写出点M 的坐标.()()⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-====-+=+===67,623,617,6136223,6213621323222522212122221212M M CM CM m m m AM DM AD BC BD AD2017年中考23题如图,直线23y x c =-+与x 轴交于点A (3,0),与y 轴交于点B ,抛物线243y x bx c =-++经过点A ,B .(1)求点B 的坐标和抛物线的解析式;()()()2310342,00,32,02322++-=→→+-=→x x y B A B x y A 抛物线(2)M (m ,0)为x 轴上一动点,过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P ,N .①点M 在线段OA 上运动,若以B ,P ,N 为顶点的三角形与△APM 相似,求点M 的坐标;⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛∴⊥2,25,,811,,2211N N AB B B N N x B N N B P AB BP y x PN 的垂线交抛物线于点作处直角:过点点轴的平行线交抛物线于作处直角:过点处有直角处不能有直角上,在直线轴轴,即平行于M,N,P 三点的横坐标一样②点M 在x 轴上自由运动,若三个点M ,P ,N 中恰有一点是其它两点所连线段的中点(三点重合除外),则称M ,P ,N 三点为“共谐点”.请直接写出使得M ,P ,N 三点成为“共谐点”的m 的值.()()()()023223103432310342232:2232223103410,231034,232,2222=+-+++-⎪⎭⎫⎝⎛++-=+-⎪⎭⎫ ⎝⎛+-=++-⎪⎭⎫⎝⎛++-⎪⎭⎫⎝⎛+-m m m M m m m N m m m P m M m m m N m m P 是中点:是中点是中点:2016年中考23题如图1,直线43y x n =-+交x 轴于点A ,交y 轴于点C (0,4).抛物线223y x bx c=++经过点A ,交y 轴于点B (0,-2).点P 为抛物线上一个动点,过点P 作x 轴的垂线PD ,过点B 作BD ⊥PD 于点D ,连接PB ,设点P 的横坐标为m .(1)求抛物线的解析式;234322--=x x y (2)当△BDP 为等腰直角三角形时,求线段PD 的长;()()1271,27343234323432,2,2,023432,2222或或==∴=∴-=-=-∴=-==--⎪⎭⎫⎝⎛--PD BD m m m m m m m PDBD m m PD m BD m D B m m m P(2)如图2,将△BDP 绕点B 逆时针旋转,得到△BD ′P ′,且旋转角∠PBP ′=∠OAC ,当点P 的对应点P ′落在坐标轴上时,请直接写出点P 的坐标.()()mm PD m BD m D B m m m P 3432,2,2,023432,22-==--⎪⎭⎫⎝⎛-- 52543432532211==+⎪⎭⎫ ⎝⎛-==+m m m m OB I D HD ()()mm PD m BD m D B m m m P 3432,2,2,023432,22-==--⎪⎭⎫⎝⎛-- 8255334325422==⎪⎭⎫ ⎝⎛-=m m m m BIH P()()mm PD m BD m D B m m m P 3432,2,2,023432,22-=-=--⎪⎭⎫⎝⎛-- ()525434325325453223333-==--⎪⎭⎫ ⎝⎛-=-=-m m m m ID D P HI HD图2DD'P'CO y ABxP2015年中考23题如图,边长为8的正方形OABC 的两边在坐标轴上,以点C 为顶点的抛物线经过点A ,点P 是抛物线上点A ,C 间的一个动点(含端点),过点P 作PF ⊥BC 于点F .点D ,E 的坐标分别为(0,6),(-4,0),连接PD ,PE ,DE .(1)请直接写出抛物线的解析式.8812+-=x y(2)小明探究点P 的位置发现:当点P 与点A 或点C 重合时,PD 与PF的差为定值.进而猜想:对于任意一点P ,PD 与PF 的差为定值.请你判断该猜想是否正确,并说明理由.()猜想正确22812812816881,881,0,818,881,2222222222222=-∴+=∴⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛-+=+=-+-==⎪⎭⎫ ⎝⎛+-=⎪⎭⎫⎝⎛+-PF PD m PD m m m DH PH PD m DH m PH m H m PF m F m m P(3)小明进一步探究得出结论:若将“使△PDE 的面积为整数”的点P 记作“好点”,则存在多个“好点”,且使△PDE 的周长最小的点P 也是一个“好点”.请直接写出所有“好点”的个数,并求出△PDE 的周长最小时“好点”的坐标.()081364143412142238122381623,881,62322222≤≤-++-=+--=⨯⨯⎪⎭⎫⎝⎛+--=+--=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+-+=m m m m m m S m m PM m m M m m P x y PED DE △个点中周长最小的点在这时,有两个点但是面积是个面积整数共有,到面积从11121013,12,11,910,8,7,6,5,41342014年中考23题如图,抛物线2y x bx c =-++与x 轴交于A (-1,0),B (5,0)两点,直线334y x =-+与y 轴交于点C ,与x 轴交于点D .点P 是x 轴上方的抛物线上一动点,过点P作PF ⊥x 轴于点F ,交直线CD 于点E .设点P 的横坐标为m .(1)求抛物线的解析式;542++-=x x y (2)若PE =5EF ,求m 的值;()()2691,2343524193432419510,,343,54,222+=∴+-=++-+-=++-=-⎪⎭⎫⎝⎛+-++-m m m m m EF m m PE m m F m m E m m m P ()()269134352419204213205234434352419222+=∴⎪⎭⎫⎝⎛+--=++-==--=+-⎪⎭⎫ ⎝⎛+-=++-m m m m m m m m m m m m(3)若点E'是点E 关于直线PC 的对称点,是否存在点P ,使点E'落在y 轴上?若存在,请直接写出相应的点P 的坐标;若不存在,请说明理由.P 点在y 轴和直线CD 的角平分线上()4,21433524194335343,,3,0241922-=∴=++-∴=⎪⎭⎫⎝⎛+-++-==m m m m mCE m m E C m m PE CE PE()()()()5,113,3112,1135432323215,414324411舍掉,超过了知:互相垂直根据邻补角的角平分线)知由(+--∴⎩⎨⎧++-=+-=+-=+=P P x x y x y x y x y P CP CP CP2013年中考23题如图,抛物线y =-x 2+bx +c 与直线221+=x y 交于C ,D 两点,其中点C 在y 轴上,点D 的坐标为)273(,.点P 是y 轴右侧的抛物线上一动点,过点P 作PE ⊥x轴于点E ,交CD 于点F .(1)求抛物线的解析式.()25.32,02++-=x x y C(2)(两定两动)若点P 的横坐标为m ,当m 为何值时,以O ,C ,P ,F 为顶点的四边形是平行四边形?请说明理由.()()2173,2,1232325.0,25.3,222-=∴=+-∴=+-=+++-m m m CO PF OC m m PF m m F m m m P ∥(3)若存在点P ,使∠PCF =45°,请直接写出....相应的点P 的坐标.由此可知P应该有两个点212532525221111=∴=+-∴=∴==∴==∴m m m m m F P m CF FG CG G P FG G P FG P CFH ∵∽△△()⎪⎭⎫ ⎝⎛∴=∴⎪⎪⎩⎪⎪⎨⎧++-=+-=+-=+=⎪⎭⎫⎝⎛1813,6236232272312312327,211221221P x x x y x y x y x y P CP CP CP 得到互相垂直由于邻补角的角平分线得到知由2012年中考23题如图,在平面直角坐标系中,直线112y x =+与抛物线23y ax bx =+-交于A ,B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上一动点(不与点A ,B 重合),过点P 做x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D .(1)求a ,b 及sin ACP ∠的值;()()()()3212121,213,40,23,40,21212--=-==→--→+=x x y b a B A B A x y 抛物线55252sin sin 51,2)1,0==∠=∠=∴==AEO ACP AE EO AO E E y AB 为(,则点轴交于点与设直线(2)设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;PC PD PC PD AE AO EAO DPC AE EO AO 55255252cos cos 51,2=∴====∠=∠=∴== 5594121552,12121421552421121,,32121,222=⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛-⨯-=⎪⎭⎫⎝⎛++-=∴++-=⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛--为最大时,当PD m m m PD m m PC m m C m m m P②(铅锤法求面积)连接PB ,线段PC 把△PDB 分成两个三角形,是否存在合适的m 的值,使这两个三角形的面积之比为9:10?若存在,直接写出m 的值;若不存在,说明理由.以PC 为底,面积之比,也就是底之比,⎪⎭⎫⎝⎛++-==⎪⎭⎫ ⎝⎛++-∴∠==∠-===4215251421552sin sin 491010922m m DF m m DF EAO PD DF DPC mBG BG DF BG DF 或 932,2591052109525244215242152491010922==+=+∴+=-⎪⎭⎫ ⎝⎛++-=⎪⎭⎫ ⎝⎛++-=-===m m m m m m m BG DF m m DF mBG BG DF BG DF 或或2011年中考23题如图,在平面直角坐标系中,直线3342y x =-与抛物线214y x bx c =-++交于A ,B 两点,点A 在x 轴上,点B 的横坐标为-8.(1)求该抛物线的解析式.2543412+--=x x y(2)点P 是直线AB 上方的抛物线上一动点(不与点A ,B 重合),过点P 作x 轴的垂线,垂足为C ,交直线AB 于点D ,作PE ⊥AB 于点E . ①设△PDE 的周长为l ,点P 的横坐标为x ,求l 关于x 的函数关系式,并求出l 的最大值;⎪⎭⎫ ⎝⎛+--==+--=⎪⎭⎫⎝⎛-⎪⎭⎫ ⎝⎛+--42341512512423412343,254341,222x x PD l x x PD x x D x x x P 15341223-最大为最大时,当l l x -=⎪⎭⎫ ⎝⎛--= ②连接PA ,以PA 为边作图示一侧的正方形APFG .随着点P 的运动,正方形的大小、位置也随之改变.当顶点F 或G 恰好落在y 轴上时,直接写出对应的点P 的坐标.双垂直全等的横纵坐标一样即P PMPC =22的纵坐标是即P OA PC ==⎪⎪⎭⎫⎝⎛+-+-⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛+-2897,2897,2,2173,2,2173P2010年中考23题在平面直角坐标系中,已知抛物线经过A (-4,0)B (0,-4)C (2,0)(1)求抛物线的解析式4212-+=x x y(2)(面积的铅锤法)若点M 为第三象限内抛物线上一个动点,点M 的横坐标为m ,△AMB 的面积为S ,求S 关于m 的函数关系式,并求出S 的最大值()()42124-42142212214,4421,2222时面积最大,最大为当△-=--=--=⨯⨯⎪⎭⎫⎝⎛--=+=----=⎪⎭⎫ ⎝⎛-+m mm m m S mm MD m m D x y m m m M ABM B A(3)(两定两动,考虑OB 是边和对角线)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P,Q,B,O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标()4,522,52244221,421,422---+-==-+=-⎪⎭⎫ ⎝⎛-+==m m m PQ m m Q m m m P PQ OB PQ OB 时∥当()()()4442104,0,0,0,421,22=∴⎪⎩⎪⎨⎧-=--+=+∴--⎪⎭⎫ ⎝⎛-+n n m m n m B O n n Q m m m P OB 是对角线时当。
河南省2018年中考数学总复习课件解答题突破 专题12二次函数综合题(中考23题)

解:(1)对于直线 y=-x-3,当 x=0 时,y=-3; 当 y=0 时,x=-3,∴A(-3,0),C(0,-3).
9-3b+c=0, b=2, 代入抛物线解析式可得 解得 c=-3, c=-3.
∴抛物线的解析式为 y=x2+2x-3.
(2)如答图 1,设点 N 的横坐标为 t,则点 N 的坐标为(t, t2+2t-3),点 M 的坐标为(t,-t-3). ∵N 在 AC 下方,∴MN=-t-3-(t2+2t-3)=-t2-3t
3 3 ∴y=5x-5.
x =-12, 3 3 2 y= x- , 5 x1=1, 5 5 与抛物线联立可得 解得 或 51 y1=0 2 y2=-25. y=x +2x-3,
12 51 ∴点 E 坐标为- 5 ,-25.
例 如图1①,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于 点C,顶点为D.直线y=-x-3经过点A,C.
(1)求抛物线的解析式; (2)在AC下方的抛物线上有一点N,过点N作直线l∥y轴,交AC与点 M,当点N坐标为多少时,线段MN的长度最大?最大是多少? (3)在抛物线上是否存在一点E,使BE平分△ABC的面积,若存在,求 出点E的坐标;若不存在,说明理由;
(4)作垂直于 x 轴的直线 x=-1,交直线 AC 于点 M,交抛物线于点 Q, 点 E 为坐标轴内一点,以 A,M,Q,E 为顶点作平行四边形,求第四个顶 点 E 的坐标; (5)点 P 是抛物线上 x 轴下方一个动点,作 PH⊥x 轴于 H,是否存在点 P,使得△PAH 与△OBC 相似?若存在,求出点 P 的坐标;若不存在,说 明理由.
(4)如答图 3,由题知,x=-1 是抛物线的对称轴. ∴Q(-1,-4). 由(2)知,直线 AC 的解析式为 y=-x-3. ∴M(-1,-2). ①若 AQ 为对角线,则 AQ 中点坐标为(-2,-2), 且此点为 ME 中点. ∴E(-3,-2);
2024届河南省洛阳市第23中学中考物理模拟精编试卷含解析

2024届河南省洛阳市第23中学中考物理模拟精编试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、单选题(本大题共10小题,共30分)1.如图所示,加热-40o C的冰,下列说法正确的是()A.BC段表示当前物体的状态仍是固体B.冰的融化过程温度不变,说明熔化不需要吸热C.水的沸腾过程温度不变,说明它的内能不变D.由图可判断,加热时间相同时冰升温比水快,说明冰的比热容比水小2.下列数据,最接近实际情况的是A.教室课桌的高度约80cmB.人步行的平均速度约为100m/sC.现在教室的温度40℃D.一个苹果的质量约为500g3.在下列实例中,用做功的方式来改变物体内能的是( )A.热水倒入茶杯,茶杯的温度升高B.将冰冻食物放在水中解冻,水变凉C.刚煮熟的鸡蛋放在冷水中,鸡蛋的温度降低D.寒冷的冬天,双手互搓,手的温度升高4.如图所示,闭合开关S,灯泡L1、L2都能正常发光,两只电表都有示数,工作一段时间后,灯泡L1突然熄灭,L2仍然正常发光,两只电表均无示数,则故障可能是( )A.电压表短路B.电流表断路C.L1断路D.L1短路5.下列说法正确的是A.在同一水平桌面上做加速运动的物体,受到的滑动摩擦力会越来越大B.自行车的坐垫很宽是为了增大压强,使人更舒服一些C.甲、乙两队拔河比赛甲队获胜,但甲队对乙队的拉力等于乙队对甲队的拉力D.汽车紧急刹车时,车上的人会向前倾倒,说明汽车有惯性6.在标准大气压下,根据下表所提供的资料数据,下列说法正确的是A.-190℃氧为液态B.可选用锡锅熔化铜块C.酒精温度计可以测量100℃的沸水温度D.水银温度计可以在-50℃下工作7.测量电流时,需要将电流表串联在电路中,通常,电流表的电阻比待测电路的电阻小得多,因此对测量值的影响可以忽略不计.下列研究方法与此相同的是A.在探究平面镜成像特点实验中,用两个相同的棋子探究像与物的大小关系B.根据被压物体形变大小反映压力作用效果C.在探究二力平衡条件的实验中,选用轻质卡片D.在研究光的传播现象时,引入光线8.学校运动会上进行百米赛跑,当甲同学超越乙同学时,下列判断正确的是A.甲同学相对于乙同学是向后运动的B.乙同学相对于地面是向后运动的C.裁判员看甲乙两同学都是向前运动的D.观众看甲同学是向前运动的,看乙同学是向后运动的9.下列有关声音的说法正确的是A.声音在15℃的真空和空气中的传播速度都为340m/sB.考场附近禁止鸣笛是为了阻断噪声传播C.“暮鼓晨钟”里的钟声和鼓声是人们依据振动频率来分辨的D.震耳的鼓声是由鼓面振动产生的10.下图所示,在家庭电路中,电路的连接和操作正确的是A.B.C.D.二、多选题(本大题共3小题,共12分)11.关于运动和力,下列说法正确的是A.加速下落的排球所受合力可能为零B.做匀速直线运动的汽车所受合力一定为零C.踢出去的足球由于具有惯性,还能在水平草地上继续运动一段距离D.静止在水平地面上的课桌,它对地面的压力与地面对它的支持力是一对平衡力12.用相同的电加热器分别对质量相等A和B两种液体加热(不计热量损失),如图是A和B的温度随加热时间变化的图象,下列说法正确的是()A.A的比热容与B的比热容之比为2:1B.A的比热容与B的比热容之比为2:3C.加热相同的时间,B吸收的热量比A吸收的热量多D.A和B升高相同的温度,A吸收的热量较多13.如图所示,电源电压保持不变,小灯泡L1、L2分别标有“6V 3W”和“6V 6W”的字样,滑动变阻器R的阻值变化范围为0~12Ω,当S1、S2、S3都闭合,滑动变阻器的滑片滑到a端时,两灯都正常发光.不考虑温度对灯泡电阻的影响,则()A.电源电压为6VB.两灯都正常发光时电流表的示数为1.5AC.整个电路的最小功率2.25WD.整个电路的最大功率9W三、填空题(本大题共5小题,共10分)14.刚装修完的房子,打开房门就会闻到刺鼻的气味,这是_____运动的结果.为了减少新房子有害气体对人体造成的危害,根据温度越高,______越快,可以采取在高温季节来临前装修完并搁置一段时间、加强通风等措施.15.阅读短文,并回答问题.第四代电光源﹣﹣﹣﹣﹣LED光源如图甲是时下较为流行的LED手电筒和LED吸顶灯,它的主要部分是高亮度白色发光二极管,这种发光二极管主要由硅、砷等半导体材料制成,具有光效高、耗电少,寿命长、易控制、免维护、安全环保等优点,是继白炽灯、卤素灯和节能荧光灯后新兴的第四代电光源,是极具发展前途的新光源.LED的发光原理与白炽灯先发热后发光的原理截然不同,是直接把电能转换成光能的器件,因而其发光效率较高,是新一代固体冷光源,将逐步取代传统光源.图乙是LED的元件实物及符号.由于二极管具有单向导电性,使用时必须将它的正极与电源正极相连,二极管才能处于导通状态,否则处于截止状态.利用图丙所示电路可以研究发光二极管的工作特性:把一个额定电压为3V的LED接入电源电压恒为4.5V的电路,闭合开关S,LED即处于导通状态,调节变阻器滑片,改变LED两端的电压和电路中电流,记录多组电压、电流数据,可以得到电压表与电流表示数关系,如丁所示.(1)LED灯主要由_____(导体/半导体/超导体)材料制成;它之所以节能,被称为冷光源,是因为电热转换损耗的能量较白炽灯_____(高/低);(2)在图丙中,闭合S,调节滑动变阻器,使LED正常发光;断开S,改变电源的正负极后再闭合S,LED_____(能/不能)发光;此时两电表的示数为_____A.4.5V 20mA B.3V 20mA C.4.5V 0mA D.3V 0mA(3)某个家庭原来全部用白炽灯来照明,平均每月照明用电50kW•h,现全部改用LED灯.相同情况下可节能约70%.已知每消耗l度电相当于排入1.1kg的二氧化碳,则改用LED灯后,这个家庭平均每月能减排二氧化碳约_____kg.16..小明一家外出旅游,出门时电能表示数为,回来时为,这期间消耗了______度电。
专题 23 化学计算-2020年中考真题化学分专题训练(第02期)(教师版含解析)

专题 23 化学计算1.(2020黑龙江哈尔滨)实验室欲测定一包黄铜样品中锌的质量分数(假设样品中只含铜和锌),取50g 黄铜样品粉末于烧杯中,先加入100g 稀硫酸,充分反应后得固液混合物149.8g ,再继续加入200g 相同浓度的稀硫酸,充分反应后过滤,得滤液312.6g ,则黄铜样品中锌的质量分数为( ) A .39% B .74%C .61%D .26%【答案】D【解析】设锌的质量为x ,参与反应稀硫酸的质量为y ,生成硫酸锌的质量为z2442Zn +H SO =ZnSO +H 6598161zxy↑由题意可知滤液中质量的增加是生成的硫酸盐的质量大于反应消耗的硫酸质量,即溶液质量差为312.6g-200g-100g=12.6g ,即z-=312.6g-200g-100g=12.6g y ,则65=161-9812.6g x,x=13g ,98=161-9812.6g y ,y =19.6g ,161z =161-9812.6g ,z=32.2g ,锌的质量分数为13g100%=26%50g⨯,故选D 。
2.(2020河南省卷)已知镁和铝的相对原子质量之比为8:9,若镁和铝分别与足量盐酸反应,生成氢气的质量相等,则参加反应的镁和铝的质量比为( ) A .3:2 B .4:3C .1:1D .1:2【答案】B【解析】镁与稀盐酸反应:22Mg+2HCl=MgCl +H ↑,铝与稀盐酸反应:322Al+6HCl=2AlCl +3H ↑,根据化学方程式可知,一份镁产生一份氢气,23份铝产生一份氢气,得Mg~H 2,23Al~H 2,假设氢气质量均为2g ,则Mg 需要24g ,Al 需要18g ,则镁和铝的比例为24g:18g=4:3。
故选B 。
3.(2020江苏扬州)一定质量的CH 4可与常见物质M 反应,同时放出少量热量;将所得产物Cu 2O 与O 2反应又生成M ,同时放出较多热量。
其反应原理如下图所示。
河南23题二次函数培优课件

(1)求抛物线的解析式; (2)如图②,当点F恰好在抛物线上时,求线段OD的长; (3)在(2)的条件下: ①连接DF,求tan∠FDE的值; ②试探究在直线l上,是否存在点G,使∠EDG = 45°,若存在,请 直接写出点G 的坐标;若不存在,请说明理由.
类型二
面积问题
2
1.(2015攀枝花)如图,已知抛物线 y = + x bx + c与x轴 交于A(-1,0),B(3,0)两点,与 y轴交于点C,抛物线的对 称轴与抛物线交于点 P,与直线 BC相交于点M,连接PB. (1)求该抛物线的解析式; (2)在(1)中位于第一象限内的抛物线上是否存在点D, 使得△BCD的面积最大?若存在,求出点D的坐标及△BCD 面积的最大值;若不存在,请说明理由; (3)在(1)中的抛物线上 是否存在点Q,使得△QMB 与△PMB的面积相等?若存 在,求出点Q的坐标;若不 存在,请说明理由.
数关系问题. 解题技巧一般是过特殊点作x轴或y轴的垂线,将所
求面积进行分割,从而将面积问题转化为线段问题,建立未知 量和已知变量之间的联系,通过二次函数的增减性得到相应的
最值.
【方法指导】 特殊图形的判定问题,常与点的存在 性问题相结合,解决此类问题的关键是要熟练掌握特殊 图形的判定方法及性质,如:对边平行且相等的四边形 是平行四边形,等边三角形的三边相等. 解决此类问题 最常用的方法是假设法,一般先假设存在满足题意的点, 根据特殊图形的性质画出草图,确定点的位置,然后根 据题中已知条件和特殊图形的性质及判定方法建立动点 与已知点的关系,最后列方程求解. 在画草图时,要做 到不重不漏地画出所有可能的情况,以免在求解过程中 遗漏答案, 对所求出的结果要进行检验,看是否符合题 意,如果不符合题意,应舍去.
河南中招数学22、23题总结

18.(2008)(9分)复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,已知在△ABC 中,AB =AC ,P 是△ABC 内部任意一点,将AP 绕A 顺时针旋转至AQ ,使∠QAP =∠BAC ,连接 BQ 、CP ,则BQ =CP .”小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ ≌△ACP ,从而证得BQ =CP 之后,将点P 移到等腰三角形ABC 之外,原题中的条件不变,发现“BQ =CP ”仍然成立,请你就图②给出证明.23.(2008)(12分)如图,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0). (1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S . ① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由; ③在运动过程中,当△MON 为直角三角形时,求t 的值.21.(2009) (10分)如图,在Rt △ABC 中,∠ACB =90°, ∠B =60°,BC =2.点0是AC 的中点,过点0的直线L 从与AC 重合的位置开始,绕点0作逆时针旋转,交AB 边于点D .过点C 作C E ∥A B 交直线l 于点E ,设直线L 的旋转角为α.(1)①当α=________度时,四边形EDBC 是等腰梯形,此时AD 的长为_________; ②当α=________度时,四边形EDBC 是直角梯形,此时AD 的长为_________; (2)当α=90°时,判断四边形EDBC 是否为菱形,并说明理由.图①QPCBAAQBPC图②23.(2009)(11分)如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y =ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交A C 于点E ①过点E 作EF ⊥AD 于点F ,交抛物线于点G .当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值.22.(2010)(10分) (1)操作发现如图,矩形ABCD 中,E 是AD 的中点,将△AB E 沿BE 折叠后得到△GBE ,且点G 在矩行ABCD 内部.小明将BG 延长交DC 于点F ,认为GF =DF ,你同意吗?说明理由.(2)问题解决保持(1)中的条件不变,若DC =2DF ,求ABAD的值; (3)类比探求保持(1)中条件不变,若DC =nDF ,求AB AD的值.GABCD EG23.(2010)(11分)在平面直角坐标系中,已知抛物线经过A )0,4(-,B )4,0(-,C )0,2(三点. (1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S .求S 关于m 的函数关系式,并求出S 的最大值.(3)若点P 是抛物线上的动点,点Q 是直线x y -=上的动点,判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.22. (2011)(10分)如图,在Rt △ABC 中,∠B =90°,BC =53,∠C =30°.点D 从点C 出发沿CA 方向以每秒2个单位长的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D 、E 运动的时间是t 秒(t >0).过点D 作DF ⊥BC 于点F ,连接DE 、EF .(1)求证:AE =DF ;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由. (3)当t 为何值时,△DEF 为直角三角形?请说明理由.第22题图 23.(2011)(11分)如图,在平面直角坐标系中,直线3342y x =-与抛物线214y x bx c =-++交于A 、B 两点,点A 在x 轴上,点B 的横坐标为-8.求:(1)求该抛物线的解析式;(2)点P 是直线AB 上方..的抛物线上一动点(不与点A 、B 重合),过点P 作x 轴的垂线,垂足为C ,交直线AB 于点D ,作PE ⊥AB 于点E .①设△PDE 的周长为l ,点P 的横坐标为x ,求l 关于x 的函数关系式,并求出l 的最大值;MC BA Oxy②连接PA ,以PA 为边作图示一侧的正方形APFG .随着点P 的运动,正方形的大小、位置也随之改变.当顶点F 或G 恰好落在y 轴上时,直接写出对应的点P 的坐标.22.(2012)(10分)类比转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整。
2020年河南省信阳市淮滨一中中考化学模拟试卷(23)(含答案解析)

2020年河南省信阳市淮滨一中中考化学模拟试卷(23)一、单选题(本大题共14小题,共14.0分)1.有关物质的组成、构成与性质关系的说法正确的是()A. 水和过氧化氢组成元素相同,故它们的化学性质相同B. 稀硫酸和盐酸溶液中都含有大量氢离子,故它们具有一些共同的化学性质C. 构成金刚石和石墨的原子相同但排列方式不同,故它们的化学性质不同D. 氢氧化铜和氢氧化钠都含有氢氧根离子,故它们都能使无色酚酞试液变红色2.下列实验操作、现象与结论对应关系正确的是()A. AB. BC. CD. D3.下列除去杂质的方法中,正确的是()A. AB. BC. CD. D4.自来水厂要对自然界中的水进行净化处理,通常需要经过沉降、过滤、吸附、消毒几个过程,以下关于这些过程的说法错误的是()A. 为使水中的悬浮杂质沉降,可在水中加入适量的明矾B. 通过过滤的方法可以将不溶于水的固体杂质与水分离开来C. 吸附过程中常常利用活性炭来除去一些可溶性杂质和异味D. 自来水厂常用氯气消毒,此过程发生的变化是物理变化5.常温下,将5g硝酸钾投入盛有45g水的烧杯中,用玻璃棒搅拌至无固体剩余.下列与此溶液相关的说法中不正确的是()A. 该溶液中溶质是硝酸钾,溶剂是水,溶液的质量为50 gB. 该溶液的溶质质量分数为10%C. 从该溶液中取出10 g,所取溶液的溶质质量分数为2%D. 取出10 g后的剩余溶液中溶质的质量为4 g6.善于梳理化学知识,能使你头脑更加聪明。
以下归纳完全正确的一项是()A.对化学资源的认识B.对化学元素的认识①工厂产生的废水应净化后再利用②合成橡胶、碳纤维都属于合成材料③可燃冰是未来能源,是可再生能源①人体中含量最多的金属元素是钙②目前使用最多的金属是铁③稀土资源是不可再生的重要战略资源,应合理利用与保护C.化学中常见的“三”D.化学与人体健康①煤、石油、氢气--三大化石燃料②CO2、SO2、NO2--三种污染性气体③原子、中子、电子--构成物质的三种粒子①可燃性气体泄漏--先打开排气扇②缺铁会引起贫血症③甲醛水溶液浸泡过的海产品不能食用A. AB. BC. CD. D7.某分子模型如图所示,有关说法中正确的是()A. 该物质是有机高分子B. 一个分子中含有19种元素C. 该物质是氧化物,化学式为C8H8O3D. 该物质中氧的质量分数约为31.6%8.因为含磷洗衣粉会对水体污染而被禁止使用,其中有一种成分:Na5P X O10(已知P的化合价为+5价),则X的值为()A. 1B. 2C. 3D. 49.煤燃烧生成的气体中能形成酸雨的是()①一氧化碳;②二氧化碳;③二氧化硫;④二氧化氮.A. ①②B. ①③C. ③④D. ②④10.下列说法中不正确的是()A. 喝了汽水以后,常常会打嗝,说明此时气体的溶解度变大了B. 在生煤火炉时,可点燃木柴来引燃煤,是为了使温度达到煤的着火点C. 合金被广泛的使用,是因为合金比组成它们的纯金属具有更多优良性能D. 做饭时,若燃气灶的火焰呈现黄色,锅底出现黑色,则需要调大灶具的进风口11.下列物质属于纯净物的是()A. 生铁B. 液氧C. 果汁D. 空气12.下列实验设计不能达到实验目的是()序号A B C D实验设计实验目的证明石墨具有导电性证明蜡烛中含有氢元素验满氧气证明CO2密度大于空气A. AB. BC. CD. D13.下列有关微粒的说法正确的是()A. 所有气体都由分子直接构成B. 二氧化锰(MnO2)中含有氧分子(O2)C. 氯化钠晶体是由大量氯化钠分子聚集而成D. 原子可以结合成分子,分子也能分解成原子14.下列符号表示2个氢分子的是()A. H2B. 2H2C. 2HD. 2H+二、填空题(本大题共8小题,共19.0分)15.小明将一种暗紫色固体A放在试管中加热生成了B和C以及D,常温下过氧化氢溶液遇到C时分解放出D,其中C在反应前后的质量和化学性质都没有改变,他又将细铁丝放在盛有D的集气瓶中点燃,发现能剧烈燃烧,火星四射,生成黑色固体E.(1)按要求回答以下问题;①C在过氧化氢溶液分解中起______作用;②物质D、E的名称:D______;E______(2)用符号表达式表示有关的化学反应.①______;②______;③______.(3)为使铁丝在氧气中持续燃烧,他把光亮的细铁丝盘成螺旋状,待______时,缓慢插入集气瓶中.为防止集气瓶炸裂,应事先在集气瓶中放少量______.16.空气中含量最多的气体是______,标出硝酸钠中各元素的化合价______.17.工业的发展离不开金属的应用。
河南省2024年历史中考热点备考重难专题:中考第23、24、25题全面解读(课前练习)

河南省2024年历史中考热点备考重难专题:中考第23、24、25题全面解读第23题1.(7分)中华人民共和国成立以来,社会主义建设成就斐然。
阅读材料,回答问题。
材料一在纺织工业部统一部署和河南省委的双重领导下,1953年初各路大军陆续开往郑州,在十分艰苦的条件下,开始了一场纺织基地建设的大会战。
正是高涨的社会主义建设的热情,建设者们才战胜了恶劣的环境条件、生活条件,突破了一项项建设短板,“又好又快”的完成了郑州纺织工业基地的建设。
——摘编自张林鹏《“一五”计划时期郑州纺织工业发展研究》材料二1988年中国对外开放的部分数据——摘编自张岂之主编《中国历史新编:中华人民共和国史》(1)根据材料一指出郑州纺织工业基地的建设人物“又好又快”完成的原因。
(2分)(2)根据材料二,归纳1988年中国对外开放的特点,并分析其原因。
(4分)(3)综合上述材料和所学知识,归纳中国特色社会主义建设给我们带来怎样的经验教训?(1分)2.(7分)阅读下列材料,回答问题。
材料一 1980—1988年我国粮食产量的变化示意图材料二改革开放以来我国城镇居民主要食物消费变化表(单位:kg/人年)时间原粮蔬菜动物性食品(肉、禽、蛋、奶、水产品类)1978年215.8 141.5 15.51984年180 165 411990年170 142 421996年125 110 51.52002年98 117.5 60——据国家统计局数据整理20世纪90年代中后期以来,随着商品经济发展、对外开放扩大以及统一市场形成,食物产品南来北往、内外交流,全国各地食物的花色品种空前地丰富多彩。
生活水平的提高,营养优质和多样化食品成为人们追逐的对象。
肉食、禽蛋、水产品都有较多的增长,享受性食物比重开始上升,人们由单纯追求数量转向更多地注重质量,食物消费质量提高。
——摘编自李哲敏《中国城乡居民食物消费及营养发展研究》(1)根据材料一,指出我国1980—1988年粮食产量发生了怎样的变化,并概括发生变化的主要原因。
