必修4__三角函数图像性质(总复习)
高二数学三角函数的图像与性质

必修4 第一章
三角函数
第二课时
三角函数的图象和性质
学习目标
理解正弦、余弦、正切函数的图 象画法及性质的运用,理解三角函 数的周期性;知道y=Asin(ωx+φ) 的图象及其实际意义;理解三角函 数模型的简单应用并关注其实践应 用.
【问题4】三角函数的性质分析
1 5730 p 2
y min
1 = 4
y max
3 = 4
【问题5】三角函数图象的变换与应用
例3 已知函数y=Asin(ωx+φ) (A>O,ω>0,|φ|<π)的最小正周期 2p 5 p 是 3 ,且图象数的解析式; (2)说明这个函数的图象是由函数y= sinx的图象经过怎样的变换而得到的.
3p 9p aÎ ( , ) 4 8
p p x = 对称,试推断是否存在 x 0 Î [0, ] 6 2 5
使 f (x 0 ) =
p 例6 已知函数 f (x ) = sin(2wx - ) + 1 6 的最小正周期为π,其图象关于直线
3
,说明你的理由.
不存在
; 微信红包群
wpf71xsz
原本如群星璀璨的蓝色眼睛不太友好的瞪了韩哲轩一眼,“还有,别叫我小黑!”“知道了!百蝶要是有你一半的忠诚就好了……”韩哲轩 突然问道,“小……我是说……茉莉,你有木有跳槽的兴趣啊?包吃包住,定期……”“没有。”茉莉快步走开了。“唉~这也太忠心了点 吧?”韩哲轩摇了摇头,很不甘心的感觉。(古风一言)伤弦笙,怜旧盟,碎语遥寄烟花冷。第030章 歌伎柳茗“看来慕容凌娢是真的忘记百 蝶之前和她见过了。”韩哲轩见茉莉停下了脚步,狡诈的一笑,继续说道,“你不准备告诉她吗?”“不了,主人没让我那么做。”茉莉原 本如群星璀璨的蓝色眼睛不太友好的瞪了韩哲轩一眼,“还有,别叫我小黑!”“知道了!百蝶要是有你一半的忠诚就好了……”韩哲轩突 然问道,“茉莉,你有木有跳槽的兴趣啊?包吃包住,定期……”“没有。”茉莉快步走开了。“唉~这也太忠心了点吧?”韩哲轩摇了摇 头,很不甘心的感觉。……慕容凌娢推开了清荷间的门,首先传来的就是一阵噼里啪啦摔碎东西的声音。慕容凌娢刚想探头往里面仔细看, 却听到一声暴怒的吼声。“你……我让你进来了吗?”“对不起,我重新来……”慕容凌娢说着毫不犹豫的推出去关上了门。自己都在佩服 自己的机智。“呼~”站在门外喘了一口气,整理了一下表情,慕容凌娢又带着她那标准的笑容敲了敲门。门被一个怀抱琵琶的女子打开了, 等慕容凌娢进门后,她就出去了。好奇怪啊……客人还在这里,怎么说走就走,不怕被百蝶惩罚吗?慕容凌娢朝她的背影望了望,那女子几 乎是夺门而出跑走的,那样子就好像在逃脱一个极其危险的地方。再向屋内看去,慕容凌娢立刻傻眼了,说好的这不是青楼,只卖艺卖酒, 不买身啊!怎么会有这么多花枝招展的姑娘衣着暴露的坐在一旁陪酒。虽然手里都拿着乐器,像是普通的陪酒,可是……场面这么香 艳, 很容易失控啊。太容易让人想歪了。慕容凌娢咽了口吐沫,把酒壶放下,刚想溜之大吉,却被人一把拽住了。“哟,怎么叫这么一个小丫头 来送酒啊,一点意思都没有……”拉住慕容凌娢是一个四五十岁的大叔,满嘴的酒气,让慕容凌娢恶心的想吐,最可恶的是他的手居然还还 想在慕容凌娢身上乱摸。看到这个举动,慕容凌娢立刻恼怒了。摸什么摸?我就不信你能摸到什么……“猥琐大叔”这个词用在你身上实在 是太贴切不过了。慕容凌娢用力挣扎了几下,居然没能挣脱,反而被他拽的更紧了。她向那群歌伎投去求助的目光,根本没有反应。她们都 装作没看见的样子,俯首低眉等待差遣。“你这小东西居然这么不老实……还敢反抗,知道爷是谁吗?”猥琐大叔粗暴的把慕容凌娢撒开了, 慕容凌娢跪在一旁低头不语。来到古代,保命的最
高考数学必修4总复习《三角函数:三角函数的图像与性质》

∴y=sin2x+52π为偶函数.
答案:B
4. (教材改编题)函数 f(x)=tanx+π4的单调递增区间为(
)
A. kπ-2π,kπ+π2(k∈Z)
B. (kπ,(k+1)π)(k∈Z)
C. kπ-34π,kπ+4π(k∈Z)
D. kπ-π4,kπ+34π(k∈Z)
(2)求满足 f(x)=0 的 x 的取值;
(3)求函数 f(x)的单调递减区间.
解 (1) 2sin2x-3π>0⇒
sin2x-π3>0⇒2kπ<2x-π3<2kπ+π,
k
∈
Z
⇒
kπ
+
π 6
<x<kπ
+
2 3
π
,
k
∈
Z.
故
函
数
的
定
义
域
为
kπ+π6,kπ+23π,k∈Z.
(2)∵f(x)=0,∴sin 2x-3π =
第五节 三角函数的图像与性质
1. 理解正弦函数、余弦函数、正切函数的图像和性质,会用 “五点法”画正弦函数、余弦函数的简图. 2. 了解周期函数与最小正周期的意义.
1. 周期函数
(1)周期函数的定义
对于函数f(x),如果存在一个非零常数T,使得当x取定义域内的每一个值
时,都有 f(x+T)=f(x,) 那么函数f(x)就叫做周期函数. 非零常数T 叫做这个函数
2 2
⇒2x-
π 3
=2kπ+
π 4
或2kπ+
3 4
π,k∈Z⇒x=kπ+
7 24
π或x=kπ+
13 24
π,k∈Z,故x的取值是
x|x=kπ+274π或x=kπ+1234π,k∈Z. (3)令2kπ+π2≤2x-π3<2kπ+π,k∈Z⇒2kπ+56π≤2x<2kπ+43π,
数学必修4——三角函数的图像与性质

数学必修4——三⾓函数的图像与性质数学必修4——三⾓函数的图像与性质⼀. 教学内容:三⾓函数的图像与性质⼆. 教学⽬标:了解正弦函数、余弦函数、正切函数的图像和性质,会⽤“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图,理解A、ω、φ的物理意义。
三. 知识要点:1. 正弦函数、余弦函数、正切函数的图像2. 三⾓函数的单调区间:的递增区间是,递减区间是;的递增区间是,递减区间是的递增区间是,3. 函数最⼤值是,最⼩值是,周期是,频率是,相位是,初相是;其图象的对称轴是直线,凡是该图象与直线的交点都是该图象的对称中⼼。
4. 由y=sinx的图象变换出y=sin(ωx+)的图象⼀般有两个途径,只有区别开这两个途径,才能灵活地进⾏图象变换。
利⽤图象的变换作图象时,提倡先平移后伸缩,但先伸缩后平移也经常出现.⽆论哪种变形,请切记每⼀个变换总是对字母x⽽⾔,即图象变换要看“变量”起多⼤变化,⽽不是“⾓变化”多少。
途径⼀:先平移变换再周期变换(伸缩变换)先将y=sinx的图象向左(>0)或向右(<0=平移||个单位,再将图象上各点的横坐标变为原来的倍(ω>0),便得到y=sin(ωx+)的图象。
途径⼆:先周期变换(伸缩变换)再平移变换。
先将y=sinx的图象上各点的横坐标变为原来的倍(ω>0),再沿x轴向左(>0)或向右(<0,平移个单位,便得到y=sin(ωx+)的图象。
5. 对称轴与对称中⼼:的对称轴为,对称中⼼为;的对称轴为,对称中⼼为;对于和来说,对称中⼼与零点相联系,对称轴与最值点相联系。
6. 五点法作y=Asin(ωx+)的简图:五点法是设X=ωx+,由X取0、、π、、2π来求相应的x值及对应的y值,再描点作图。
【典型例题】例1. 把函数y=cos(x+)的图象向左平移个单位,所得的函数为偶函数,则的最⼩值是()A. B. C. D.解:先写出向左平移4个单位后的解析式,再利⽤偶函数的性质求解。
数学(浙江专用)总复习教师用书:第四章 三角函数、解三角形 第讲 三角函数的图象与性质

第3讲三角函数的图象与性质最新考纲 1.能画出y=sin x,y=cos x,y=tan x的图象,了解三角函数的周期性;2。
理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴的交点等),理解正切函数在区间错误!内的单调性。
知识梳理1。
用五点法作正弦函数和余弦函数的简图(1)正弦函数y=sin x,x∈[0,2π]的图象中,五个关键点是:(0,0),错误!,(π,0),错误!,(2π,0).(2)余弦函数y=cos x,x∈[0,2π]的图象中,五个关键点是:(0,1),错误!,(π,-1),错误!,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k∈Z)函数y=sin x y=cos x y=tan x图象定义域R R{x错误!错误!值域[-1,1][-1,1]R周期性2π2ππ奇偶性奇函数偶函数奇函数1。
判断正误(在括号内打“√”或“×")(1)由sin错误!=sin 错误!知,错误!是正弦函数y=sin x(x∈R)的一个周期。
( )(2)余弦函数y=cos x的对称轴是y轴.()(3)正切函数y=tan x在定义域内是增函数.( )(4)已知y=k sin x+1,x∈R,则y的最大值为k+1。
( )(5)y=sin|x|是偶函数。
()解析(1)函数y=sin x的周期是2kπ(k∈Z).(2)余弦函数y=cos x的对称轴有无穷多条,y轴只是其中的一条.(3)正切函数y=tan x在每一个区间错误!(k∈Z)上都是增函数,但在定义域内不是单调函数,故不是增函数。
(4)当k〉0时,y max=k+1;当k<0时,y max=-k+1.答案(1)×(2)×(3)×(4)×(5)√2。
(2015·四川卷)下列函数中,最小正周期为π的奇函数是( )A。
y=sin错误!B。
y=cos错误!C.y=sin 2x+cos 2xD.y=sin x+cos x解析y=sin错误!=cos 2x是最小正周期为π的偶函数;y=cos错误!=-sin 2x是最小正周期为π的奇函数;y=sin 2x+cos 2x=2sin错误!是最小正周期为π的非奇非偶函数;y=sin x+cos x=错误!sin错误!是最小正周期为2π的非奇非偶函数.答案B3。
北师大版 高考数学总复习 三角函数-余弦函数的图像与性质 名师点悟+易错盘点

时 作
要
业
点
导
学
第18页
第一章 §6 6.1、2
北师大版 ·数学 ·必修4
自 主
(1)求函数 f(x)= 2cos x- 2的定义域;
预
习
(2) 已 知 x ∈ -π3,23π , 则 y = cos x 的 值 域 为 课
时
要 __________________;
作 业
点 导
(3)求函数 y=3cos2x-4cos x+1 的最大值和最小值.
自 主
点?
预
习
提示:余弦曲线的对称中心是余弦曲线与 x 轴的交点,即
要
kπ+π2,0,余弦曲线的对称轴一定过余弦曲线的最高点或最低
课 时 作 业
点
导 学
点,方程为 x=kπ,k∈Z,此时余弦值取得最大或最小.
第10页
第一章 §6 6.1、2
自 主 预 习 要 点 导 学
第11页
北师大版 ·数学 ·必修4
课 时 作
要
点 导
所以当 x=0 时,y=cos x 取得最大值 1.
业
学
当 x=23π时,y=cos x 取得最小值-12.
所以值域为-12,1.
第22页
第一章 §6 6.1、2
北师大版 ·数学 ·必修4
(3)令 t=cos x,则-1≤t≤1,问题转化为求函数 y=3t2-4t
自 主
+1(-1≤t≤1)的最大值和最小值.
作 业
32π,0,(2π,1).
第6页
第一章 §6 6.1、2
北师大版 ·数学 ·必修4
问题探究 1:余弦函数的图像还有什么画法?
自 主
人教版数学必修四三角函数复习讲义

第一讲 任意角与三角函数诱导公式1. 知识要点角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。
按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。
射线的起始位置称为始边,终止位置称为终边。
象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。
如果角的终边在坐标轴上,就认为这个角不属于任何象限。
终边相同的角的表示:α终边与θ终边相同(α的终边在θ终边所在射线上)⇔2()k k αθπ=+∈Z 。
注意:相等的角的终边一定相同,终边相同的角不一定相等.α终边在x 轴上的角可表示为:,k k Z απ=∈; α终边在y 轴上的角可表示为:,2k k Z παπ=+∈;α终边在坐标轴上的角可表示为:,2k k Z πα=∈. 角度与弧度的互换关系:360°=2π 180°=π 1°=0.01745 1=57.30°=57°18′注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.α与2α的终边关系:任意角的三角函数的定义:设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点),它与原点的距离是0r =>,那么sin ,cos y xr rαα==, ()tan ,0y x x α=≠,cot x y α=(0)y ≠,sec rxα=()0x ≠,()csc 0r y y α=≠。
三角函数值只与角的大小有关,而与终边上点P 的位置无关。
三角函数线的特征:正弦线MP“站在x 轴上(起点在x 轴上)”、余弦线OM“躺在x 轴上(起点是原点)”、正切线AT“站在点(1,0)A 处(起点是A )”同角三角函数的基本关系式:1. 平方关系:222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= 2. 倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1, 3. 商数关系:sin cos tan ,cot cos sin αααααα==注意:1.角α的任意性。
高中数学必修4三角函数的图像与性质
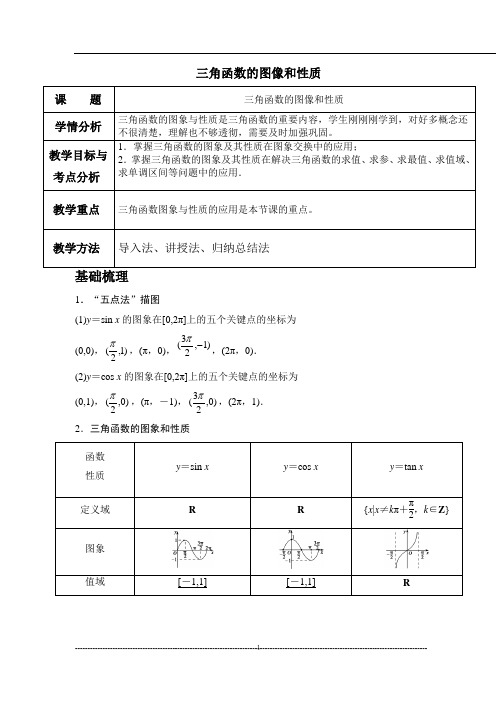
三角函数的图像和性质课 题 三角函数的图像和性质学情分析三角函数的图象与性质是三角函数的重要内容,学生刚刚刚学到,对好多概念还 不很清楚,理解也不够透彻,需要及时加强巩固。
教学目标与 考点分析 1.掌握三角函数的图象及其性质在图象交换中的应用;2.掌握三角函数的图象及其性质在解决三角函数的求值、求参、求最值、求值域、求单调区间等问题中的应用.教学重点 三角函数图象与性质的应用是本节课的重点。
教学方法导入法、讲授法、归纳总结法1.“五点法”描图(1)y =sin x 的图象在[0,2π]上的五个关键点的坐标为(0,0),)1,2(π,(π,0),)1,23(-π,(2π,0).(2)y =cos x 的图象在[0,2π]上的五个关键点的坐标为(0,1),)0,2(π,(π,-1),)0,23(π,(2π,1).2.三角函数的图象和性质 函数 性质 y =sin x y =cos x y =tan x定义域R R{x |x ≠k π+π2,k ∈Z }图象值域[-1,1][-1,1]R(1)周期性函数y=A sin(ωx+φ)和y=A cos(ωx+φ)的最小正周期为2π|ω|,y=tan(ωx+φ)的最小正周期为π|ω|.(2)奇偶性三角函数中奇函数一般可化为y=A sin ωx或y=A tan ωx,而偶函数一般可化为y=A cos ωx+b的形式.三种方法求三角函数值域(最值)的方法:(1)利用sin x、cos x的有界性;(2)形式复杂的函数应化为y=A sin(ωx+φ)+k的形式逐步分析ωx+φ的范围,根据正弦函数单调性写出函数的值域;(3)换元法:把sin x或cos x看作一个整体,可化为求函数在区间上的值域(最值)问题.双基自测1.函数)3cos(π+=x y ,x ∈R ( ).A .是奇函数B .是偶函数C .既不是奇函数也不是偶函数D .既是奇函数又是偶函数2.函数)4tan(x y -=π的定义域为( ). A .},4|{Z k k x x ∈-≠ππ B .},42|{Z k k x x ∈-≠ππ C .},4|{Z k k x x ∈+≠ππD .},42|{Z k k x x ∈+≠ππ3.)4sin(π-=x y 的图象的一个对称中心是( ).A .(-π,0)B .)0,43(π-C .)0,23(πD .)0,2(π4.函数f (x )=cos )62(π+x 的最小正周期为________.考向一 三角函数的周期【例1】►求下列函数的周期:(1))23sin(x y ππ-=;(2))63tan(π-=x y考向二 三角函数的定义域与值域(1)求三角函数的定义域实际上是解简单的三角不等式,常借助三角函数线或三角函数图象来求解.(2)求解三角函数的值域(最值)常见到以下几种类型的题目:①形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值);②形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值).【例2】►(1)求函数y =lg sin 2x +9-x 2的定义域. (2)求函数y =cos 2x +sin x )4|(|π≤x 的最大值与最小值.【训练2】 (1)求函数y =sin x -cos x 的定义域;(2))1cos 2lg(sin )4tan(--=x xx y π的定义域(3)已知)(x f 的定义域为]1,0[,求)(cos x f 的定义域.考向三 三角函数的单调性求形如y =A sin(ωx +φ)+k 的单调区间时,只需把ωx +φ看作一个整体代入y =sin x 的相应单调区间内即可,若ω为负则要先把ω化为正数. 【例3】►求下列函数的单调递增区间.(1))23cos(x y -=π,(2))324sin(21x y -=π,(3))33tan(π-=x y .【训练3】 函数f (x )=sin )32(π+-x 的单调减区间为______.考向四 三角函数的对称性正、余弦函数的图象既是中心对称图形,又是轴对称图形.正切函数的图象只是中心对称图形,应熟记它们的对称轴和对称中心,并注意数形结合思想的应用. 【例4】►(1)函数y =cos )32(π+x 图象的对称轴方程可能是( ).A .x =-π6B .x =-π12C .x =π6D .x =π12(2)若0<α<π2,)42sin()(απ++=x x g 是偶函数,则α的值为________.【训练4】 (1)函数y =2sin(3x +φ))2|(|πϕ<的一条对称轴为x =π12,则φ=________.(2)函数y =cos(3x +φ)的图象关于原点成中心对称图形.则φ=________.难点突破——利用三角函数的性质求解参数问题含有参数的三角函数问题,一般属于逆向型思维问题,难度相对较大一些.正确利用三角函数的性质解答此类问题,是以熟练掌握三角函数的各条性质为前提的,解答时通常将方程的思想与待定系数法相结合.【示例】► 已知函数f (x )=sin )3(πω+x (ω>0)的单调递增区间为]12,125[ππππ+-k k (k ∈Z ),单调递减区间为]127,12[ππππ++k k (k ∈Z ),则ω的值为________.练一练:1、已知函数)33sin()(π+=x x f(1)判断函数的奇偶性;(2)判断函数的对称性.2、设函数)0)(2sin()(<<-+=ϕπϕx x f 的图象的一条对称轴是直线8π=x ,则=ϕ______.课后练习:三角函数的图象与性质·练习题一、选择题(1)下列各命题中正确的是 [ ](2)下列四个命题中,正确的是 [ ]A.函数y=ctgx在整个定义域内是减函数B.y=sinx和y=cosx在第二象限都是增函数C.函数y=cos(-x)的单调递减区间是(2kπ-π,2kπ)(k∈Z)(3)下列命题中,不正确的是 [ ]D.函数y=sin|x|是周期函数(4)下列函数中,非奇非偶的函数是 [ ](5)给出下列命题:①函数y=-1-4sinx-sin2x的最大值是2②函数f(x)=a+bcosx(a∈R且b∈R-)的最大值是a-b以上命题中正确命题的个数是 [ ]A.1B.2C.3D.4[ ] A.sinα<cosα<tgαB.cosα>tgα>sinαC.sinα>tgα>cosαD.tgα>sinα>cosα(7)设x为第二象限角,则必有 [ ][ ]二、填空题(9)函数y=sinx+sin|x|的值域是______.的值是______.(11)设函数f(x)=arctgx的图象沿x轴正方向平移2个单位,所得到的图象为C,又设图象C1与C关于原点对称,那么C1所对应的函数是______.(12)给出下列命题:①存在实数α,使sinαcosα=1⑤若α,β是第一象限角,α>β则tgα>tgβ其中正确命题的序号是______.三、解答题(14)已知函数y=cos2x+asinx-a2+2a+5有最大值2,试求实数a的值.答案与提示一、(1)B (2)D (3)D (4)B (5)D (6)D (7)A (8)D提示(2)y=ctgx在(kπ,kπ+π)(k∈Z)内是单调递减函数.y=cos(-x)=cosx在[2kπ-π,2kπ](k∈Z)上是增函数,而在[2kπ,2kπ+π]上是减函数.(3)可画出y=sin |x|图象验证它不是周期函数或利用定义证之.(5)①=-y(sinx+2)2+3 sinx=-1时,y max=2②当cosx=-1时,f(x)max=a-b∴cosα<sinα<tgα二、(9)[-2,2] (10)2或3 (11)y=arctg(x+2) (12)③④提示(11)C:y=arctg(x-2),C1:-y=arctg(-x-2),∴y=arctg(x+2)由390°>45°,但tg390°=tg30°<tg45°,故⑤不正确.综上,③④正确.三、。
人教版高中数学必修四1.4三角函数的图象与性质1.4.2二含答案

1.4.2 正弦函数、余弦函数的性质(二) 课时目标 1.掌握y =sin x ,y =cos x 的最大值与最小值,并会求简单三角函数的值域或最值.2.掌握y =sin x ,y =cos x 的单调性,并能用单调性比较大小.3.会求函数y =A sin(ωx +φ)及y =A cos(ωx +φ)的单调区间.正弦函数、余弦函数的性质: 函数 y =sin xy =cos x 图象定义域______ ______ 值域______ ______ 奇偶性______ ______ 周期性最小正周期:______ 最小正周期:______ 单调性在__________________________________ 上单调递增;在__________________________________________________上单调递减 在__________________________________________上单调递增;在______________________________上单调递减 最值 在________________________时,y max =1;在________________________________________时,y min =-1在______________时,y max =1;在__________________________时,y min =-1 一、选择题1.若y =sin x 是减函数,y =cos x 是增函数,那么角x 在( )A .第一象限B .第二象限C .第三象限D .第四象限 2.若α,β都是第一象限的角,且α<β,那么( )A .sin α>sin βB .sin β>sin αC .sin α≥sin βD .sin α与sin β的大小不定3.函数y =sin 2x +sin x -1的值域为( )A.[]-1,1B.⎣⎡⎦⎤-54,-1 C.⎣⎡⎦⎤-54,1 D.⎣⎡⎦⎤-1,54 4.函数y =|sin x |的一个单调增区间是( )A.⎝⎛⎭⎫-π4,π4B.⎝⎛⎭⎫π4,3π4 C.⎝⎛⎭⎫π,3π2 D.⎝⎛⎭⎫3π2,2π 5.下列关系式中正确的是( )A .sin 11°<cos 10°<sin 168°B .sin 168°<sin 11°<cos 10°C .sin 11°<sin 168°<cos 10°D .sin 168°<cos 10°<sin 11°6.下列函数中,周期为π,且在⎣⎡⎦⎤π4,π2上为减函数的是( )A .y =sin(2x +π2)B .y =cos(2x +π2) C .y =sin(x +π2) D .y =cos(x +π2) 题 号 1 2 3 4 5 6 答 案二、填空题7.函数y =sin(π+x ),x ∈⎣⎡⎦⎤-π2,π的单调增区间是____________. 8.函数y =2sin(2x +π3)(-π6≤x ≤π6)的值域是________. 9.sin 1,sin 2,sin 3按从小到大排列的顺序为__________________.10.设|x |≤π4,函数f (x )=cos 2x +sin x 的最小值是______. 三、解答题11.求下列函数的单调增区间.(1)y =1-sin x 2; (2)y =log 12(cos 2x ).12.已知函数f (x )=2a sin ⎝⎛⎭⎫2x -π3+b 的定义域为⎣⎡⎦⎤0,π2,最大值为1,最小值为-5,求a 和b 的值.能力提升13.已知sin α>sin β,α∈⎝⎛⎭⎫-π2,0,β∈⎝⎛⎭⎫π,32π,则( ) A .α+β>π B .α+β<πC .α-β≥-32πD .α-β≤-32π 14.已知函数f (x )=2sin ωx (ω>0)在区间⎣⎡⎦⎤-π3,π4上的最小值是-2,则ω的最小值等于( ) A.23 B.32C .2D .31.求函数y =A sin(ωx +φ)(A >0,ω>0)单调区间的方法是:把ωx +φ看成一个整体,由2k π-π2≤ωx +φ≤2k π+π2(k ∈Z )解出x 的范围,所得区间即为增区间,由2k π+π2≤ωx +φ≤2k π+32π (k ∈Z )解出x 的范围,所得区间即为减区间.若ω<0,先利用诱导公式把ω转化为正数后,再利用上述整体思想求出相应的单调区间.2.比较三角函数值的大小,先利用诱导公式把问题转化为同一单调区间上的同名三角函数值的大小比较,再利用单调性作出判断.3.求三角函数值域或最值的常用求法将y 表示成以sin x (或cos x )为元的一次或二次等复合函数再利用换元或配方、或利用函数的单调性等来确定y 的范围.1.4.2 正弦函数、余弦函数的性质(二)答案知识梳理 R R [-1,1] [-1,1] 奇函数 偶函数 2π 2π [-π2+2k π,π2+2k π](k ∈Z ) [π2+2k π,3π2+2k π] (k ∈Z ) [-π+2k π,2k π] (k ∈Z ) [2k π,π+2k π] (k ∈Z ) x =π2+2k π (k ∈Z ) x =-π2+2k π (k ∈Z ) x =2k π (k ∈Z ) x =π+2k π (k ∈Z ) 作业设计1.C 2.D3.C [y =sin 2x +sin x -1=(sin x +12)2-54当sin x =-12时,y min =-54; 当sin x =1时,y max =1.]4.C [由y =|sin x |图象易得函数单调递增区间⎣⎡⎦⎤k π,k π+π2,k ∈Z ,当k =1时,得⎝⎛⎭⎫π,32π为y =|sin x |的单调递增区间.]5.C [∵sin 168°=sin (180°-12°)=sin 12°,cos 10°=sin (90°-10°)=sin 80°由三角函数线得sin 11°<sin 12°<sin 80°,即sin 11°<sin 168°<cos 10°.]6.A [因为函数周期为π,所以排除C 、D.又因为y =cos(2x +π2)=-sin 2x 在⎣⎡⎦⎤π4,π2上为增函数,故B 不符合.故选A.]7.⎣⎡⎦⎤π2,π8.[0,2]解析 ∵-π6≤x ≤π6,∴0≤2x +π3≤2π3. ∴0≤sin(2x +π3)≤1,∴y ∈[0,2] 9.b <c <a解析 ∵1<π2<2<3<π, sin(π-2)=sin 2,sin(π-3)=sin 3.y =sin x 在⎝⎛⎭⎫0,π2上递增,且0<π-3<1<π-2<π2, ∴sin(π-3)<sin 1<sin(π-2),即sin 3<sin 1<sin 2.∵b <c <a . 10.1-22解析 f (x )=cos 2x +sin x =1-sin 2x +sin x=-(sin x -12)2+54∵|x |≤π4,∴-22≤sin x ≤22. ∴当sin x =-22时,f (x )min =1-22. 11.解 (1)由2k π+π2≤x 2≤2k π+32π,k ∈Z , 得4k π+π≤x ≤4k π+3π,k ∈Z .∴y =1-sin x 2的增区间为[4k π+π,4k π+3π] (k ∈Z ). (2)由题意得cos 2x >0且y =cos 2x 递减.∴x 只须满足:2k π<2x <2k π+π2,k ∈Z . ∴k π<x <k π+π4,k ∈Z . ∴y =log 12(cos 2x )的增区间为⎝⎛⎭⎫k π,k π+π4,k ∈Z . 12.解 ∵0≤x ≤π2,∴-π3≤2x -x 3≤23π, ∴-32≤sin ⎝⎛⎭⎫2x -π3≤1,易知a ≠0. 当a >0时,f (x )max =2a +b =1,f (x )min =-3a +b =-5.由⎩⎨⎧ 2a +b =1-3a +b =-5,解得⎩⎨⎧a =12-63b =-23+123. 当a <0时,f (x )max =-3a +b =1,f (x )min =2a +b =-5. 由⎩⎨⎧ -3a +b =12a +b =-5,解得⎩⎨⎧a =-12+63b =19-123. 13.A [∵β∈⎝⎛⎭⎫π,32π, ∴π-β∈⎝⎛⎭⎫-π2,0,且sin(π-β)=sin β. ∵y =sin x 在x ∈⎝⎛⎭⎫-π2,0上单调递增,∴sin α>sin β⇔sin α>sin(π-β)⇔α>π-β⇔α+β>π.]14.B [要使函数f (x )=2sin ωx (ω>0)在区间[-π3,π4]上的最小值是-2,则应有T 4≤π3或34T ≤π4,即2π4ω≤π3或6πω≤π,解得ω≥32或ω≥6. ∴ω的最小值为32,故选B.]附赠材料答题六注意 :规范答题不丢分提高考分的另一个有效方法是减少或避免不规范答题等非智力因素造成的失分,具体来说考场答题要注意以下六点:第一,考前做好准备工作。
(完整版)人教高中数学必修四第一章三角函数知识点归纳

三角函数一、随意角、弧度制及随意角的三角函数1.随意角(1)角的观点的推行①按旋转方向不一样分为正角、负角、零角.正角 : 按逆时针方向旋转形成的角随意角 负角: 按顺时针方向旋转形成的角零角 : 不作任何旋转形成的角②按终边地点不一样分为象限角和轴线角.角 的极点与原点重合,角的始边与 x 轴的非负半轴重合,终边落在第几象限,则称 为第几象限角.第一象限角的会合为 k 360ok 360o 90o , k第二象限角的会合为 k 360o 90o k 360o 180o , k第三象限角的会合为 k 360o 180o k 360o 270o , k第四象限角的会合为k 360o 270ok 360o360o , k终边在 x 轴上的角的会合为 k 180o , k终边在 y 轴上的角的会合为 k 180o 90o , k终边在座标轴上的角的会合为k 90o ,k(2)终边与角 α同样的角可写成 α+ k ·360 °(k ∈ Z).终边与角 同样的角的会合为k 360o, k(3)弧度制① 1 弧度的角:把长度等于半径长的弧所对的圆心角叫做1 弧度的角.②弧度与角度的换算: 360°= 2π弧度; 180°= π弧度.③ 半径为 r 的圆的圆心角所对弧的长为 l ,则角的弧度数的绝对值是lr④ 若扇形的圆心角为 为弧度制 ,半径为 r ,弧长为 l ,周长为 C ,面积为 S ,则 lr,C2r l ,S1 lr 1 r2 . 222 .随意角的三角函数定义设 α是一个随意角,角 α的终边上随意一点P(x , y),它与原点的距离为 r rx 2 y 2 ,那么角 α的正弦、余弦、rrx(三角函数值在各象限的符号规律归纳为:一全正、二正弦、三正切分别是: sin α= y , cos α= x , tan α= y.正切、四余弦)3.特别角的三角函数值角度030456090120135150180270360函数角 a 的弧度0π /6π/4π /3π /22π /33π /45π/6π3π /22πsina01/2√ 2/2√ 3/21√ 3/2√ 2/21/20-10 cosa1√ 3/2√ 2/21/20-1/2-√ 2/2-√ 3/2-101 tana0√ 3/31√ 3-√ 3-1-√ 3/300二、同角三角函数的基本关系与引诱公式A.基础梳理1.同角三角函数的基本关系(1)平方关系: sin2α+ cos2α= 1;(在利用同角三角函数的平方关系时,若开方,要特别注意判断符号)sin α(2)商数关系:=tanα.(3)倒数关系:tan cot 1cos α2.引诱公式公式一: sin( α+ 2kπ)=sin α, cos(α+ 2kπ)=cos_α,tan(2k )tan此中 k∈Z .公式二: sin( π+α)=- sin_α, cos( π+α)=- cos_α, tan( π+α)= tan α.公式三: sin( π-α)= sin α, cos( π-α)=- cos_α,tan tan.公式四: sin( -α)=- sin_α, cos(-α)= cos_α,tan tan .ππ公式五: sin -α= cos_α, cos-α= sin α.22ππ公式六: sin 2+α= cos_α, cos2+α=- sin_α.π口诀:奇变偶不变,符号看象限.此中的奇、偶是指π引诱公式可归纳为 k· ±α的各三角函数值的化简公式.的奇数22倍和偶数倍,变与不变是指函数名称的变化.假如奇数倍,则函数名称要变( 正弦变余弦,余弦变正弦 ) ;假如偶数倍,则函数名称不变,符号看象限是指:把πα当作锐角时,依据 k· ±α在哪个象限判断原三角函数值的符号,最后作为结....2...果符号.B. 方法与重点一个口诀1、引诱公式的记忆口诀为:奇变偶不变,符号看象限.2、四种方法在求值与化简时,常用方法有:sin α(1)弦切互化法:主要利用公式tan α=化成正、余弦.cos α(2)和积变换法:利用 (sin θ±cos θ)2=1 ±2sin θcos θ的关系进行变形、转变.( sin cos、sin cos、sin cos三个式子知一可求二)(3)巧用 “1”的变换: 1= sin 2θ+ cos 2θ= sinπ=tan 42(4)齐次式化切法:已知 tank ,则 a sinbcos a tan b ak bm sinn cos m tan n mk n三、三角函数的图像与性质学习目标:1 会求三角函数的定义域、值域2 会求三角函数的周期 :定义法,公式法,图像法(如y sin x 与 y cosx 的周期是)。
(完整版)高中必修四三角函数知识点总结

§04。
三角函数 知识要点1. ①与α(0°≤α<360°)终边相同的角的集合(角α与角β的终边重合):{}Z k k ∈+⨯=,360|αββ②终边在x 轴上的角的集合: {}Z k k ∈⨯=,180|ββ ③终边在y 轴上的角的集合:{}Z k k ∈+⨯=,90180|ββ ④终边在坐标轴上的角的集合:{}Z k k ∈⨯=,90| ββ ⑤终边在y =x 轴上的角的集合:{}Z k k ∈+⨯=,45180| ββ⑥终边在x y -=轴上的角的集合:{}Z k k ∈-⨯=,45180| ββ⑦若角α与角β的终边关于x 轴对称,则角α与角β的关系:βα-=k 360 ⑧若角α与角β的终边关于y 轴对称,则角α与角β的关系:βα-+= 180360k ⑨若角α与角β的终边在一条直线上,则角α与角β的关系:βα+=k 180⑩角α与角β的终边互相垂直,则角α与角β的关系: 90360±+=βαk2. 角度与弧度的互换关系:360°=2π 180°=π 1°=0。
01745 1=57。
30°=57°18′ 注意:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零.、弧度与角度互换公式: 1rad =π180°≈57。
30°=57°18ˊ. 1°=180π≈0。
01745(rad )3、弧长公式:rl ⋅=||α。
扇形面积公式:211||22s lr r α==⋅扇形4、三角函数:设α是一个任意角,在α的终边上任取(异于原点的)一点P (x,y)P与原点的距离为r,则 ry =αsin ; rx =αcos ; =αtan yx=αcot ; xr =αsec ;。
yr=αcsc 。
5、三角函数在各象限的符号:(一全二正弦,三切四余弦)正切、余切余弦、正割正弦、余割6、三角函数线正弦线:MP ; 余弦线:OM; 正切线: AT.SIN \COS 三角函数值大小关系图1、2、3、4表示第一、二、三、四象限一半所在区域16. 几个重要结论:8、同角三角函数的基本关系式:αααtan cos sin = αααcot sin cos = 1cot tan =⋅αα 1sin csc =α⋅α 1cos sec =α⋅α1cos sin 22=+αα 1tan sec 22=-αα 1cot csc 22=-αα9、诱导公式:2k παα±把的三角函数化为的三角函数,概括为: “奇变偶不变,符号看象限"公式组二 公式组三(完整版)高中必修四三角函数知识点总结x x k x x k x x k x x k cot )2cot(tan )2tan(cos )2cos(sin )2sin(=+=+=+=+ππππ x x x x xx x x cot )cot(tan )tan(cos )cos(sin )sin(-=--=-=--=- 公式组四 公式组五 公式组六xx x x x x xx cot )cot(tan )tan(cos )cos(sin )sin(=+=+-=+-=+ππππ xx x x x x xx cot )2cot(tan )2tan(cos )2cos(sin )2sin(-=--=-=--=-ππππ xx x x xx xx cot )cot(tan )tan(cos )cos(sin )sin(-=--=--=-=-ππππ(二)角与角之间的互换公式组一 公式组二 βαβαβαsin sin cos cos )cos(-=+ αααcos sin 22sin =βαβαβαsin sin cos cos )cos(+=- ααααα2222sin 211cos 2sin cos 2cos -=-=-= βαβαβαsin cos cos sin )sin(+=+ ααα2tan 1tan 22tan -=βαβαβαsin cos cos sin )sin(-=- 2cos 12sinαα-±= βαβαβαtan tan 1tan tan )tan(-+=+ 2cos 12cos αα+±=βαβαβαtan tan 1tan tan )tan(+-=- 公式组三 公式组四 公式组五2tan 12tan2sin 2ααα+= 2tan 12tan 1cos 22ααα+-= 2tan 12tan2tan 2ααα-=42675cos 15sin -== ,42615cos 75sin +== ,3275cot 15tan -== ,3215cot 75tan +== 。
(优秀经典)1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象课件新人教A版必修4

3.正弦曲线、余弦曲线 (1)定义:正弦函数y=sinx,x∈R和余弦函数y=cosx,x∈R的图象分别叫 做_正__弦_____曲线和余__弦______曲线. (2)图象:如图所示.
[解析] (1)列表
x
0
π 2
π
3 2π
2π
sinx
0
1
0
-1
0
sinx-1
-1
0
-1
-2
-1
描点,连线,如图
(2)列表:
x
0
π 2
π
3 2π
2π
cosx
1
0
-1
0
1
2+cosx
3
2
1
2
3
描点连线,如图
『规律总结』 用“五点法”画函数 y=Asinx+b(A≠0)或 y=Acosx+b(A≠0)
[解析] (1)首先用五点法作出函数y=cosx,x∈[0,2π]的图象,再作出y= cosx关于x轴对称的图象,最后将图象向上平移1个单位.如图(1)所示.
(2)首先用五点法作出函数y=sinx,x∈[0,4π]的图象,再将x轴下方的部分 对称到x轴的上方.如图(2)所示.
『规律总结』 函数的图象变换除了平移变换外,还有对称变换.如本 例.一般地,函数f(x)的图象与f(-x)的图象关于y轴对称;-f(x)的图象与f(x)的 图象关于x轴对称;-f(-x)的图象与f(x)的图象关于原点对称;f(|x|)的图象关于 y轴对称.
高中数学必修4三角函数的图像与性质
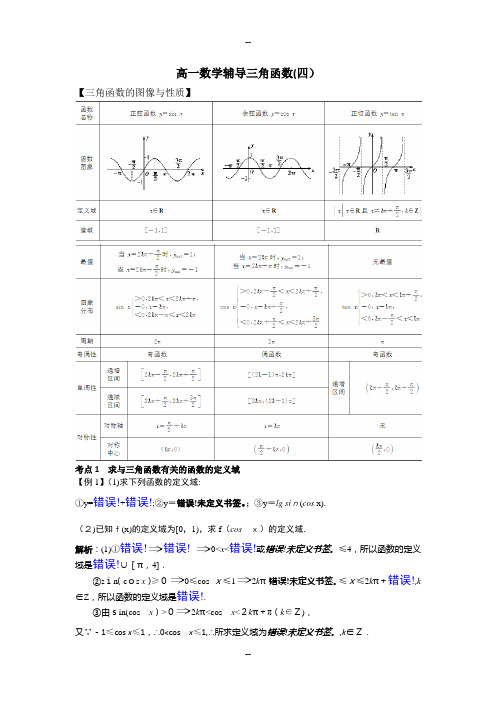
高一数学辅导三角函数(四)【三角函数的图像与性质】考点1 求与三角函数有关的函数的定义域【例1】(1)求下列函数的定义域:①y=错误!+错误!;②y=错误!未定义书签。
;③y=lg sin(cos x).(2)已知f(x)的定义域为[0,1),求f(cosx)的定义域.解析:(1)①错误!错误!0<x<错误!或错误!未定义书签。
≤4,所以函数的定义域是错误!∪[π,4].②sin(cos x)≥00≤cos x≤12kπ-错误!未定义书签。
≤x≤2kπ+错误!,k ∈Z,所以函数的定义域是错误!.③由sin(cos x)>02kπ<cos x<2kπ+π(k∈Z),又∵-1≤cos x≤1,∴0<cos x≤1,∴所求定义域为错误!未定义书签。
,k∈Z.(2)0≤co s x<12k π-\f (π,2)≤x≤2k π+π2,且x ≠2k π(k ∈Z),∴所求函数的定义域为错误!未定义书签。
∪(2k π,2kπ+\f(π,2)],k ∈Z. 考点2 求三角函数的单调区间【例2】 求下列函数的单调区间:(1)y=错误!sin 错误!未定义书签。
; (2)y=-错误!未定义书签。
.解析:(1)∵y=\f (1,2)sin 错误!未定义书签。
=-错误!未定义书签。
s in错误!未定义书签。
,且函数y =sin x 的单调递增区间是错误!未定义书签。
,单调递减区间是错误!(k ∈Z).∴由2k π-π2≤错误!未定义书签。
-π4≤2k π+错误!3kπ-错误!≤x≤3k π+错误!(k ∈Z ),由2k π+π2≤错误!未定义书签。
-错误!≤2k π+错误!未定义书签。
3k π+错误!未定义书签。
≤x≤3k π+错误!(错误!Z),即函数的单调递减区间为[3k π-错误!未定义书签。
,3k π+\f (9π,8)](k ∈Z),单调递增区间为[3k π+错误!,3k π+错误!]错误!(2)作出函数y =-错误!未定义书签。
高中数学必修4三角函数的图像与性质

高中数学必修4三角函数的图像与性质高一数学辅导三角函数(四)【三角函数的图像与性质】考点1 求与三角函数有关的函数的定义域【例1】(1)求下列函数的定义域:①y=2+log1x+tan x;②y=2sin(cos x);③y=lg sin(cos x).(2)已知f(x)的定义域为[0,1),求f(cos x)的定义域.解析:(1)①⎩⎪⎨⎪⎧2+log 12x ≥0,tan x ≥0,x >0⎩⎪⎨⎪⎧0<x ≤4,k π≤x <k π+π2,k ∈Z , 0<x <π2或π≤x ≤4,所以函数的定义域是⎝⎛⎭⎪⎪⎫0,π2∪[π,4].②sin(cos x )≥00≤cos x ≤12k π-π2≤x≤2k π+π2,k ∈Z ,所以函数的定义域是⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪⎪2k π-π2≤x ≤2k π+π2,k ∈Z . ③由sin(cos x )>02k π<cos x <2k π+π(k ∈Z),又∵-1≤cos x ≤1,∴0<cos x ≤1,∴所求定义域为⎝⎛⎭⎪⎫2k π-π2,2k π+π2,k ∈Z.(2)0≤cos x <12k π-π2≤x ≤2k π+π2,且x ≠2k π(k ∈Z),∴所求函数的定义域为⎣⎢⎢⎡⎭⎪⎪⎫2k π-π2,2k π∪(2k π,2k π+π2],k ∈Z.考点2 求三角函数的单调区间 【例2】 求下列函数的单调区间:(1)y =12sin ⎝ ⎛⎭⎪⎫π4-2x 3; (2)y =-⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫x +π4.解析:(1)∵y =12sin ⎝ ⎛⎭⎪⎪⎫π4-2x 3=-12sin ⎝ ⎛⎭⎪⎪⎫2x 3-π4,且函数y =sin x 的单调递增区间是⎣⎢⎢⎡⎦⎥⎥⎤2k π-π2,2k π+π2,单调递减区间是⎣⎢⎢⎡⎦⎥⎥⎤2k π+π2,2k π+3π2(k ∈Z). ∴由2k π-π2≤2x 3-π4≤2k π+π23k π-3π8≤x ≤3k π+9π8(k ∈Z),由2k π+π2≤2x 3-π4≤2k π+3π23k π+9π8≤x ≤3k π+21π8(k ∈Z),即函数的单调递减区间为[3k π-3π8,3k π+9π8](k ∈Z),单调递增区间为[3k π+9π8,3k π+21π8](k ∈Z ). (2)作出函数y =-⎪⎪⎪⎪⎪⎪⎪⎪sin ⎝⎛⎭⎪⎪⎫x +π4的简图(如图所示),由图象得函数的单调递增区间为⎣⎢⎢⎡⎦⎥⎥⎤k π+π4,k π+3π4(k ∈Z),单调递减区间为⎣⎢⎢⎡⎦⎥⎥⎤k π-π4,k π+π4(k ∈Z).考点3 求三角函数的最小正周期、最值(值域) 【例3】(1)求下列函数的值域。
高中数学必修4三角函数常考题型正切函数性质与图像

【知识梳理】1.正切函数的性质函y=tanx 数定πxx≠kπ+,k∈Z 义域2函y=tan x 数值域(-∞,+∞)周期T=π奇偶性奇函数在每个开区间kπ-π,kπ+π(k∈Z)上都是增22单调性函数2.正切函数的图像正切函数的图像:正切函数的图像叫做正切曲线.正切函数的图像特征:正切曲线是被相互平行的直线x=π+kπ,k∈Z所隔开的无穷多支曲线组成的.2【常考题型】题型一、正切函数的定义域、值域问题【例1】求以下函数的定义域和值域:(1)y=tan x+πy=3-tanx.4;(2)ππ[解](1)由x+4≠kπ+2(k∈Z)得,πx≠kπ+,k∈Z,4ππ所以函数y=tan x +4的定义域为xx≠kπ+4,k∈Z,其值域为(-∞,+∞).(2)由3-tan x≥0得,tan x≤3.结合y=tan x的图像可知,在ππ-2,2上,ππ满足tan x≤3的角x应满足-2<x≤3,所以函数y=3-tan x的定义域为xkπ-π<x≤kπ+π,k∈Z,其值域为[0,+∞).23【类题通法】求正切函数定义域的方法及求值域的注意点求与正切函数有关的函数的定义域时,除了求函数定义域的一般要求外,还要保证正切函π数y=tan x有意义,即x≠2+kπ,k∈Z.而对于构建的三角不等式,常利用三角函数的图像求解.解形如tan x>a的不等式的步骤:【对点训练】1求函数y=1+tan x的定义域.解:要使函数有意义,那么有1+tanx≠0,ππ∴tan x≠-1,∴x≠kπ-4且x≠kπ+2,k∈Z.1因此,函数y=1+tan x的定义域为ππ.xx≠kπ-且x≠kπ+,k∈Z42题型二、正切函数的单调性及应用【例2】(1)求函数y=tan 1πx-的单调区间;2413π12π(2)比较tan-4与tan-5的大小.[解](1)由k π-π<1-π<π+π(k∈Z)得,22x4k2π3π2kπ-2<x<2kπ+2,k∈Z,1ππ3π所以函数y=tan2x-4的单调递增区间是2kπ-2,2kπ+2(k∈Z).13π-4π+3π3ππ12π(2)由于tan-4=tan4=tan4=-tan4,tan-5=-2π2πtan2π+5=-tan5,π2ππ又0<4<5<2,而y=tan x在0,π上单调递增,2π2ππ2π所以tan4<tan5,-tan4>-tan5,13π12π即tan-4>tan-5.【类题通法】1.求函数y =tan(+)(,,φ都是常数)的单调区间的方法AωxφAω(1)假设ω>0,由于y=tan x在每一个单调区间上都是增函数,故可用“整体代换〞的思想,ππ令kπ-2<ωx+φ<kπ+2,求得x的范围即可.(2)假设ω<0,可利用诱导公式先把y=tan(+)转化为y=tan[-(--)]=-AωxφAωxφtan(--),即把x 的系数化为正值,再利用“整体代换〞的思想,求得x的范围即可.Aωxφ2.运用正切函数单调性比较大小的方法运用函数的周期性或诱导公式将角化到同一单调区间内.运用单调性比较大小关系.【对点训练】1.比较tan1,tan2,tan3的大小.解:因为tan2=tan(2-π),tan3=tan(3-π).ππ又因为2<2<π,所以-2<2-π<0.因为π<3<π,所以-π<3-π<0.22ππ显然-2<2-π<3-π<1<2,ππ又y=tan x在-2,2内是增函数,所以tan(2-π)<tan(3-π)<tan1,即tan2<tan3<tan1.2.求函数y=3tan π-24x的单调区间.ππ解:y=3tan4-2x=-3tan2x-4,由-ππ<2-πππ得,+<+422πk3πk-+π<<+π(∈Z),82x82k所以y=3tan π-24x的单调递减区间为πk3πk-+π,8+π(k∈Z).822题型三、与正切函数有关的周期性、奇偶性问题π【例3】(1)求f(x)=tan2x+3的周期;判断y=sin x+tan x的奇偶性.[解](1)∵tan2x+π+π=tan2x+π,33即tan2π+π=tan2x+π,x+33 2ππf(x)=tan2x+3的周期是2.π,k∈Z,关于原点对称,(2)定义域为xx≠kπ+2∵f(-x)=sin(-x)+tan(-x)=-sin x-tan x=-f(x),∴它是奇函数.【类题通法】与正切函数有关的函数的周期性、奇偶性问题的解决策略π一般地,函数y=A tan(ωx+φ)的最小正周期为T=|ω|,常常利用此公式来求周期.(2)判断函数的奇偶性要先求函数的定义域,判断其是否关于原点对称.假设不对称,那么该函数无奇偶性,假设对称,再判断f(-x)与f(x)的关系.【对点训练】关于x的函数f(x)=tan(x+φ)有以下几种说法:π①对任意的φ,f(x)都是非奇非偶函数;②f(x)的图像关于2-φ,0对称;③f(x)的图像关于(π-φ,0)对称;④f(x)是以π为最小正周期的周期函数.其中不正确的说法的序号是________.解析:①假设取φ=kπ(k∈Z),那么f(x)=tan x,此时,f(x)为奇函数,所以①错;观察正切函数y=tan x的图像,可知y=tan x关于kπ,0(k∈Z)对称,令x+φ=kπ得x=kπ-222φ,分别令k=1,2知②、③正确,④显然正确.答案:①【练习反响】1.函数y=tan x πx≠kπ+,k∈Z的单调性为() 2A.在整个定义域上为增函数B.在整个定义域上为减函数C.在每一个开区间ππ-+kπ,+kπ(k∈Z)上为增函数22D.在每一个开区间π+2kπ,π-+2kπ(k∈Z)上为增函数22解析:选C由正切函数的图像可知选项C正确.2.函数y=tan(cos x)的值域是()C.[-tan1,tan1]D.以上均不对解析:选C ∵-1≤cos x ≤1,且函数 y =tan x 在[-1,1]上为增函数,∴ tan(-1)≤tanx ≤tan1.即-tan 1≤tan x ≤tan1.x 3.函数y =5tan -的最小正周期是________.2解析:=π=2π.T1-2答案:2π4.函数 y =3tan( π+ x ),- π < ≤ π4 的值域为________.x 6y =3tan(π+x )= 3tan x ,因为正切函数在 -π π解析:函数2,上是增函数,所以-2 3<y ≤ 3,所以值域为 (-3,3].1答案:(-3, 3]2π15.求函数y =tan 2x -6的定义域、周期及单调区间.2 ππ解:由2x -6≠2+k π,k ∈Z ,4π得x ≠+2k π,k ∈Z ,31 π所以函数y =tan2x -6的定义域为4π xx ≠3+2k π,k ∈Z.πT =1=2π,所以函数y =tan1x -π26的周期为2π.2π1ππ由-+k π<x -22<+k π,k ∈Z ,得622π 4π13+2k π<x <3+2k π,k ∈Z.2π所以函数y =tan2x -6的单调递增区间为-2π+2kπ,4π+2kπ(k∈Z).33。
第2讲 三角函数的诱导公式和三角函数的图像与性质(必修4)

三角函数的诱导公式和三角函数的图像与性质一、知识温故:诱导公式◆ 终边相同的角的三角函数值相等()()()zk , t an 2t an z k , 2zk , 2∈=+∈=+∈=+απααπααπαk Cos k Cos Sin k Sin轴对称关于与角角x αα-()()()ααααααt a n t a n -=-=--=-C o s C o s S i n S i n♦ 轴对称关于与角角y ααπ-()()()ααπααπααπt a n t a n -=--=-=-C o s C o s S i n S i n⌧ 关于原点对称与角角ααπ+()()()ααπααπααπt a n t a n =+-=+-=+C o sC o s S i n S i n⍓对称关于与角角x y =-ααπ2ααπααπααπcot 2t an 22=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-Sin Cos Cos Sin ααπααπααπc o t2t a n 22-=⎪⎭⎫ ⎝⎛+-=⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛+S i nC o s C o s S i n 注:上述的诱导公式记忆口诀:“奇变偶不变,符号看象限”周期问题◆()()()()()()ωπωϕωωπωϕωωπωϕωωπωϕωωπωϕωωπωϕω2T , 0b , 0 , 0A , b 2T , 0 b , 0 , 0A , b T , 0 , 0A , T , 0 , 0A , 2T , 0 , 0A , 2T , 0 , 0A , =≠>>++==≠>>++==>>+==>>+==>>+==>>+=x ACos y x ASin y x ACos y x ASin y x ACos y x ASin y()()()()ωπωϕωωπωϕωωπωϕωωπωϕω=>>+==>>+==>>+==>>+=T , 0 , 0A , cot T , 0 , 0A , tan T, 0 , 0A , cot T , 0 , 0A , tan x A y x A y x A y x A y三角函数的图像及性质(i )正弦函数、余弦函数的图像1. 函数sin ,cos y x y x ==的图像2. 函数sin ,cos y x y x ==的性质 正弦函数余弦函数 定义域 定义域 值域 值域 周期性 周期性 奇偶性 奇偶性 单调性单调性最大(小)值最大(小)值 对称性对称性3. 周期函数的定义:一般地,对于函数()f x ,如果存在一个非零数T ,使得当x 取定义域内的每一个值时,都有()()f x T f x +=,那么函数()f x 就叫做周期函数,非零常数T 叫做这个函数的周期。
第13讲 必修4第一章三角函数的图像与性质(教师版)

11.α是第一象限角,tan α=34,则sin α=()A.45 B.35C.-45D.-35解析:选B tan α=sin αcos α=34,sin2α+cos2α=1,且α是第一象限角,所以sin α=35.2.(2013·安徽名校模拟)已知tan x=2,则sin2x+1=()A.0 B.95 C.43 D.53解析:选B sin2x+1=2sin2x+cos2xsin2x+cos2x=2tan2x+1tan2x+1=95.3.(2013·西安模拟)已知2tan α·sin α=3,-π2<α<0,则sin α=()A.32B.-32 C.12D.-12解析:选B由2tan α·sin α=3得,2sin2αcos α=3,即2cos2α+3cos α-2=0,又-π2<α<0,解得cos α=12(cos α=-2舍去),故sin α=-3 2.4.若cos α+2sin α=-5,则tan α=()A.12B.2 C.-12D.-2解析:选B∵cos α+2sin α=-5,结合sin2α+cos2α=1得(5sin α+2)2=0,∵sin α=-255,cos α=-55,∵tan α=2.5.化简sin ⎝ ⎛⎭⎪⎫π2+α·cos ⎝ ⎛⎭⎪⎫π2-αcos π+α+sin π-α·cos ⎝ ⎛⎭⎪⎫π2+αsin π+α=________.解析:原式=cos α·sin α-cos α+sin α-sin α-sin α=-sin α+sin α=0.答案:01.(教材改编)函数y =12sin x ,x ∵[-π,π]的单调性是( )A .在[-π,0]上是增函数,在[0,π]上是减函数B .在⎣⎡⎦⎤-π2,π2上是增函数,在⎣⎡⎦⎤-π,-π2和⎣⎡⎦⎤π2,π上都是减函数 C .在[0,π]上是增函数,在[-π,0]上是减函数D .在⎣⎡⎦⎤π2,π和⎣⎡⎦⎤-π,-π2上是增函数,在⎣⎡⎦⎤-π2,π2上是减函数 答案 B2.函数y =tan 2x 的定义域是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π+π4,k ∵Z B.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π8,k ∵Z C.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π+π8,k ∵Z D.⎩⎨⎧⎭⎬⎫x ⎪⎪ x ≠k π2+π4,k ∵Z 答案 D解析 由2x ≠k π+π2,k ∵Z ,得x ≠k π2+π4,k ∵Z ,∵y =tan 2x 的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠k π2+π4,k ∵Z . 3.若函数f (x )=sin ωx (ω>0)在区间[0,π3]上单调递增,在区间[π3,π2]上单调递减,则ω等于( )A.23B.32 C .2 D .3 答案 B解析 ∵f (x )=sin ωx (ω>0)过原点,∵当0≤ωx ≤π2,即0≤x ≤π2ω时,y =sin ωx 是增函数; 当π2≤ωx ≤3π2,即π2ω≤x ≤3π2ω时, y =sin ωx 是减函数.由f (x )=sin ωx (ω>0)在⎣⎡⎦⎤0,π3上单调递增,在⎣⎡⎦⎤π3,π2上单调递减知,π2ω=π3,∵ω=32. 4.(2015·安徽)已知函数f (x )=A sin(ωx +φ)(A ,ω,φ均为正的常数)的最小正周期为π,当x =2π3时,函数f (x )取得最小值,则下列结论正确的是( ) A .f (2)<f (-2)<f (0) B .f (0)<f (2)<f (-2)C .f (-2)<f (0)<f (2)D .f (2)<f (0)<f (-2) 答案 A解析 由于f (x )的最小正周期为π, ∵ω=2,即f (x )=A sin(2x +φ),又当x =2π3时,2x +φ=4π3+φ=2k π-π2(k ∵Z ),∵φ=2k π-11π6(k ∵Z ),又φ>0,∵φmin =π6,故f (x )=A sin(2x +π6).于是f (0)=A sin π6,f (2)=A sin ⎝⎛⎭⎫4+π6=A sin ⎣⎡⎦⎤π-⎝⎛⎭⎫4+π6=A sin ⎝⎛⎭⎫5π6-4, f (-2)=A sin ⎝⎛⎭⎫-4+π6=A sin ⎝⎛⎭⎫13π6-4=A sin ⎣⎡⎦⎤π-⎝⎛⎭⎫13π6-4=A sin ⎝⎛⎭⎫4-7π6. 又∵-π2<5π6-4<4-7π6<π6<π2,又f (x )在⎝⎛⎭⎫-π2,π2上单调递增, ∵f (2)<f (-2)<f (0),故选A.5.函数y =3-2cos ⎝⎛⎭⎫x +π4的最大值为________,此时x =________. 答案 5 3π4+2k π(k ∵Z )解析 函数y =3-2cos ⎝⎛⎭⎫x +π4的最大值为3+2=5, 此时x +π4=π+2k π(k ∵Z ),即x =3π4+2k π(k ∵Z ).1.用五点法作正弦函数和余弦函数的简图跟踪练习1 (1)函数y =lg(sin x )+cos x -12的定义域为__________________________.(2)函数y =sin x -cos x +sin x cos x 的值域为______________________________________.答案 (1)⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3+2k π,k ∵Z(2)⎣⎡⎦⎤-12-2,1 解析 (1)要使函数有意义必须有⎩⎪⎨⎪⎧sin x >0,cos x -12≥0, 即⎩⎪⎨⎪⎧ sin x >0,cos x ≥12,解得⎩⎪⎨⎪⎧2k π<x <π+2k πk ∵Z ,-π3+2k π≤x ≤π3+2k πk ∵Z , ∵2k π<x ≤π3+2k π(k ∵Z ),∵函数的定义域为⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3+2k π,k ∵Z .(2)设t =sin x -cos x ,则t 2=sin 2x +cos 2x -2sin x cos x ,sin x cos x =1-t 22,且-2≤t ≤ 2.∵y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-2时,y min =-12- 2.∵函数的值域为⎣⎡⎦⎤-12-2,1.题型二 三角函数的单调性例2 (1)函数f (x )=tan ⎝⎛⎭⎫2x -π3的单调递增区间是( ) A.⎣⎡⎦⎤k π2-π12,k π2+5π12(k ∵Z ) B.⎝⎛⎭⎫k π2-π12,k π2+5π12(k ∵Z ) C.⎝⎛⎭⎫k π+π6,k π+2π3(k ∵Z ) D.⎣⎡⎦⎤k π-π12,k π+5π12(k ∵Z ) (2)已知ω>0,函数f (x )=sin ⎝⎛⎭⎫ωx +π4在⎝⎛⎭⎫π2,π上单调递减,则ω的取值范围是________. 答案 (1)B (2)⎣⎡⎦⎤12,54解析 (1)由k π-π2<2x -π3<k π+π2(k ∵Z )得,踪练习3 (1)已知函数f (x )=2sin(ωx +φ),对于任意x 都有f ⎝⎛⎭⎫π6+x =f ⎝⎛⎭⎫π6-x ,则f ⎝⎛⎭⎫π6的值为________. (2)已知函数f (x )=sin x +a cos x 的图象关于直线x =5π3对称,则实数a 的值为( )A .- 3B .-33 C. 2 D.22答案 (1)2或-2 (2)B解析 (1)∵f ⎝⎛⎭⎫π6+x =f ⎝⎛⎭⎫π6-x ,∵x =π6是函数f (x )=2sin(ωx +φ)的一条对称轴.∵f ⎝⎛⎭⎫π6=±2.(2)由x =5π3是f (x )图象的对称轴,可得f (0)=f ⎝⎛⎭⎫10π3, 解得a =-33.1、 (2014陕西,2,5分,∵∵∵)函数f(x)=cos 的最小正周期是( )A. B.π C.2π D.4π 思路点拨 根据公式T=计算.[答案] B [解析] T===π.故选B.2、(2013江苏,1,5分,∵∵∵)函数y=3sin的最小正周期为________.[答案]π[解析]由题意知ω=2,所以T==π.3、(2015山东烟台模拟,∵∵∵)求下列函数的最小正周期:(1)y=sin;(2)y=|sin x|.思路点拨(1)利用公式求最小正周期;(2)可利用图象法求最小正周期.[答案]答案见解析[解析](1)y=sin,其中ω=2,∵T==π.(2)函数y=|sin x|的图象如下图所示,可知其最小正周期为π.4、(2015四川,5,5分,∵∵∵)下列函数中,最小正周期为π的奇函数是()A.y=sinB.y=cosC.y=sin 2x+cos 2xD.y=sin x+cos x思路点拨利用函数的奇偶性逐项验证.[答案]B[解析]A中,y=cos 2x,最小正周期为π,为偶函数,不符合题意;B中,y=-sin 2x,最小正周期为π,且为奇函数,符合.C,D为非奇非偶的函数.5、(2014陕西西安模拟,∵∵∵)下列函数中是奇函数的是()A.y=-|sin x|B.y=sin(-|x|)C.y=sin |x|D.y=x·sin |x|思路点拨利用f(-x)=-f(x)进行判断.[答案]D[解析]四个函数的定义域都是R,设f(x)=x·sin|x|,则f(-x)=(-x)·sin|-x|=-x·sin|x|=-f(x),∵y=x·sin|x|是奇函数,故选D.6、(2014广东,5,5分,∵∵∵)下列函数为奇函数的是()A.y=2x-B.y=x3sin xC.y=2cos x+1D.y=x2+2x思路点拨根据奇函数的定义判断.[答案]A[解析]由函数奇偶性的定义知,B、C中的函数为偶函数,D中的函数为非奇非偶函数,只有A中的函数为奇函数,故选A.7、(2012天津,6,5分,∵∵∵)下列函数中,既是偶函数,又在区间(1,2)内是增函数的为()A.y=cos 2x,x∵RB.y=log2|x|,x∵R且x≠0C.y=,x∵RD.y=x3+1,x∵R思路点拨根据选项中各个函数的性质判断,有一定的综合性.[答案]B[解析]函数y=cos 2x在区间上单调递减,在区间上单调递增,不合题意,排除A;函数y=是奇函数,排除C;y=x3+1是非奇非偶函数,排除D;y=log2|x|=是偶函数,且在(0,+∞)上是增函数,故选B.8、(2012大纲全国,3,5分,∵∵∵)若函数f(x)=sin (φ∵[0,2π])是偶函数,则φ=()A. B. C. D.思路点拨根据特例来求解.[答案]C[解析]∵f(x)是偶函数,∵=+kπ(k∵Z).∵φ=π+3kπ(k∵Z),又φ∵[0,2π],∵φ=π.9、(2014安徽,14,5分,∵∵∵)若函数f(x)(x∵R)是周期为4的奇函数,且在[0,2]上的解析式为f(x)=则f+f=________.思路点拨根据函数的周期性将待求函数值的自变量值转化到分段函数中的定义域范围内,结合奇函数性质求解.[答案][解析]∵f(x)是以4为周期的奇函数,∵f=f=f,f=f=f.∵当0≤x≤1时, f(x)=x(1-x),∵f=×=.∵当1<x≤2时, f(x)=sin(πx),∵f=sin=-.又∵f(x)是奇函数,∵f=-f=-,f=-f=.∵f+f=-+=.10、(2012课标全国,9,5分,∵∵∵)已知ω>0,函数f(x)=sin在单调递减,则ω的取值范围是()A. B. C. D.(0,2]思路点拨利用正弦函数的单调性及单调区间求解.[答案]A[解析]由<x<π得+<ωx+<ωπ+,又y=sin α在(k∵Z)上递减,∵解得由ω>0知+2k>0,∵k>-.若要不等式组有解,则+4k≤+2k,解得k≤,又k∵Z,∵k=0,∵≤ω≤,故选A.11、(2011安徽,9,5分,∵∵∵)已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤对x∵R恒成立,且f>f(π),则f(x)的单调递增区间是()A. (k∵Z)B. (k∵Z)C. (k∵Z)D. (k∵Z)思路点拨恒成立问题可转化为最值问题,然后根据单调区间等知识求解.[答案]C[解析]∵f(x)≤恒成立,∵=1.∵+φ=+kπ,k∵Z.∵φ=+kπ,k∵Z.又∵f>f(π),即sin(π+φ)>sin(2π+φ),∵-sin φ>sin φ,∵2sin φ<0,∵sin φ<0.∵当k=1时,φ=+π=,满足sin φ<0,∵f(x)=sin=-sin.∵要求f(x)的单调递增区间,只需2kπ+≤2x+≤2kπ+,k∵Z,即kπ+≤x≤kπ+,k∵Z.∵f(x)的单调递增区间是(k∵Z).12、(2015上海长宁区一模,∵∵∵)设ω>0,若函数f(x)=2sin ωx在上单调递增,则ω的取值范围是________.思路点拨∵ω>0,先求出f(x)=2sin ωx的单调递增区间,而是其中的一个子集,由集合关系,求出ω的取值范围.[答案][解析]三角函数f(x)=2sin ωx的图象如图.由图知f(x)在上是单调增函数,结合题意得解得0<ω≤.13、(2014福建,7,5分,∵∵∵)已知函数f(x)=则下列结论正确的是()A.f(x)是偶函数B.f(x)是增函数C.f(x)是周期函数D.f(x)的值域为[-1,+∞)思路点拨分段函数问题可以考察各段函数的性质,或结合图象判断.[答案]D[解析]作出f(x)的图象如图所示,可排除A,B,C,故D正确.14、(2014课标∵,6,5分,∵∵∵)如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示成x的函数f(x),则y=f(x)在[0,π]上的图象大致为()思路点拨列出函数y=f(x)的表达式后判断函数的图象,或取x的几个特殊值来验证.[答案]C[解析]由题图可知:当x=时,OP∵OA,此时f(x)=0,排除A、D;当x∵时,OM=cos x,设点M到直线OP 的距离为d,则=sin x,即d=OMsin x=sin xcos x,∵f(x)=sin xcos x=sin 2x≤,排除B,故选C.15、(2013江西改编,∵∵∵)设f(x)=2sin,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.思路点拨对已知条件“对任意实数x都有|f(x)|≤a”的理解是解答关键,把此条件转化为函数f(x)的最大值问题.[答案] [2,+∞) [解析] ∵≤1,∵≤2,即对任意实数x,有|f(x)|≤2,要使|f(x)|≤a 恒成立,只要a 不小于|f(x)|的最大值即可,∵a≥2.[方法与技巧]1.讨论三角函数性质,应先把函数式化成y =A sin(ωx +φ)(ω>0)的形式.2.函数y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为2π|ω|,y =tan(ωx +φ)的最小正周期为π|ω|.3.对于函数的性质(定义域、值域、单调性、对称性、最值等)可以通过换元的方法令t =ωx +φ,将其转化为研究y =sin t 的性质.4.对于已知函数的单调区间的某一部分确定参数ω的范围的问题:首先,明确已知的单调区间应为函数的单调区间的子集;其次,要确定已知函数的单调区间,从而利用它们之间的关系可求解. [失误与防范]1.闭区间上最值或值域问题,首先要在定义域基础上分析单调性,含参数的最值问题,要讨论参数对最值的影响.2.要注意求函数y =A sin(ωx +φ)的单调区间时ω的符号,若ω<0,那么一定先借助诱导公式将ω化为正数.3.三角函数的最值可能不在自变量区间的端点处取得,直接将两个端点处的函数值作为最值是错误的.A 组 专项基础训练 (时间:35分钟)1.对于函数f (x )=sin ⎝⎛⎭⎫πx +π2,下列说法正确的是( ) A .f (x )的周期为π,且在[0,1]上单调递增B .f (x )的周期为2,且在[0,1]上单调递减C .f (x )的周期为π,且在[-1,0]上单调递增D .f (x )的周期为2,且在[-1,0]上单调递减 答案 B解析 因为f (x )=sin ⎝⎛⎭⎫πx +π2=cos πx ,则周期T =2,在[0,1]上单调递减,故选B. 2.函数y =2sin ⎝⎛⎭⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为( ) A .2- 3B .0C .-1D .-1-3 答案 A解析 利用三角函数的性质先求出函数的最值.∵0≤x ≤9,∵-π3≤π6x -π3≤7π6,∵sin ⎝⎛⎭⎫π6x -π3∵⎣⎡⎦⎤-32,1.由2k π-π2≤2x +π4≤2k π+π2,k ∵Z ,解得k π-3π8≤x ≤k π+π8,k ∵Z .当k =0时,-3π8≤x ≤π8,故选C.12.已知函数f (x )=2sin ωx (ω>0)在区间⎣⎡⎦⎤-π3,π4上的最小值是-2,则ω的最小值等于( ) A.23 B.32 C .2 D .3答案 B解析 ∵ω>0,-π3≤x ≤π4,∵-ωπ3≤ωx ≤ωπ4.由已知条件知-ωπ3≤-π2,∵ω≥32.13.(2014·北京)设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________. 答案 π解析 ∵f (x )在⎣⎡⎦⎤π6,π2上具有单调性, ∵T 2≥π2-π6, ∵T ≥2π3.∵f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3,∵f (x )的一条对称轴为x =π2+2π32=7π12.又∵f ⎝⎛⎭⎫π2=-f ⎝⎛⎭⎫π6, ∵f (x )的一个对称中心的横坐标为π2+π62=π3.∵14T =7π12-π3=π4,∵T =π. 14.已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π2),y =f (x )的部分图象如图,则f (π24)=________. 答案 3解析 由题中图象可知,此正切函数的半周期等于3π8-π8=π4,即最小正周期为π2,所以ω=2.∵g (x )的单调减区间为⎝⎛⎭⎫k π+π6,k π+π3,k ∵Z .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图象的两相邻对称轴间的距离为 2 (1)求f ( )的值;
8
(2008山东卷17)
(2)将函数y f ( x)的图象向右平移 个单位后,再将得到的图象上 6 各点的横坐标伸长到原来的4倍(纵坐标不变),得到函数y g ( x)的 图象, 求g ( x)的单调递减区间. 解 : (1) f ( x) 3sin( x ) cos( x )
解:函数可化为:y = - sin 2 x , 3
范例解析
(1) 例2 求y sin( 2 x)的单调递减区间. 3
由题意可得2k - 2 x 2k , k z. 2 3 2 5 k - x k , k z. 12 12
题型一:求三角函数的值域和最值
3
(1)求函数y sin x 3 cos x, x 的值域. 2 答案:y 2sin( x ) ,值域为1 . ,2
(2)求函数y cos x sin x, x
2
2
1 2 5 答案:y 1 sin x sin x (sin x ) , 2 4
)
y
2
0
2
x
题型二:三角函数的单调性
变式引申
变式练习:函数f(x)=2sinx在[ , ]上是增函数 34
4 在此区间上最大值为 3,则的值为_____ 3
y
0
x
走进高考,身临其境 题型三:三角函数的奇偶性 例4 已知函数f (x) 3sin(x ) cos(x )(0 , 0)为偶函数,且函数
x 2k
2
2
y , k z 时, min 1 x 2k , k z 时, min 1 y
无最值 奇函数
对称中心: (
奇偶性
对称中心:
奇函数
(k ,0)(k z )
2 ,k Z
偶函数
对称中心:(k
2
, 0)(k z )
对称性
对称轴:x k 对称轴: x k , k Z
2[
3 1 sin( x ) cos( x )] 2sin( x ) 2 2 6
f ( x)为偶函数.
对x R, f ( x) f ( x)恒成立.
sin( x ) f ( x)恒成立.
走进高考,身临其境 题型三:三角函数的奇偶性 例4 已知函数f (x) 3sin(x ) cos(x )(0 , 0)为偶函数,且函数
图象的两相邻对称轴间的距离为 2 (1)求f ( )的值;
函数的单调递减区间为 5 k - ,k (k z). 12 12
题型二:三角函数的单调性
范例解析
例2 (2)比较tan1,tan2,tan3的大小.
解: tan2=tan 2- , tan 3 tan 3 y tan x在 , 上是增函数, 2 2 且-
1.考纲要求:
理解正弦函数、余弦函数在区间0,2 的性质 (如单调性、最大值和最小值与轴的交点等). 理解正切函数在区间 , 的单调性. 2 2 了解三角函数的周期性.
2.教学重点:
三角函数性质的应用
函数
1
y sin x
y
1
y cos x
y
y tan x
6 cos( ) 0 0, 且x R. 6 又 0 , f ( x) 2sin( x ) 2 cos x 6 2 2 2 又由题意得 2 , 2, f ( x) 2cos 2 x. f ( ) 2 cos 2 8 4 2 整理得 sin x cos( ) 0.
k , 0)( k z ) 2
无对称轴
题型一:求三角函数的值域和最值
范例解析
例1 求y=sin2 x+2sinxcosx+3cos2 x 的值域 . 解:y 1 2cos2 x 2sinxcosx 1 (1 cos2x) sin2x 2 cos2x sin2x 2 2sin(2x ) 4 x ) 1. x R 1 sin(2 4 函数的值域为 2 2, 2 2 .
8
(2008山东卷17)
(2)将函数y f ( x)的图象向右平移 个单位后,再将得到的图象上 6 各点的横坐标伸长到原来的4倍(纵坐标不变),得到函数y g ( x)的 图象, 求g ( x)的单调递减区间. 解 : (2)
让 我 们 一 起 思 考
题型二:三角函数的单调性
变式练习: 2.(2007江苏)函数f(x)=sinx- 3 cos x x [ ,0]的单调增区间是______.
2
<2- 3 1
2
.
tan 2- tan 3 tan1 即 tan 2 tan 3 tan1.
2
0
2
3 2
x
范例解析
例3 已知y=sinx在( , )内是减函数,则(
22 (A)0 1 (B)-1 0 (C) 1 (D) 1
我 行 我 能 我 要 成 功 我 能 成 功
练习:
1 sin x 已知f ( x) log 1 . 2 1 sin x
(1)求f(x)的定义域和值域
(2)判断它的奇偶性、周期性; (3)判断f(x)的单调性.
1 2 5 值域为 ,. 4 2
4
的值域.
注:最终化为一个角的三角函数式或其复合式.
互动探究
(1)求y=7-4sinxcosx+4cos2 x 4cos4 x的最值
.
(2)求y sin x cos x sin x cos x的值域 .
题型二:三角函数的单调性
8
3 1 2[ sin( x ) cos( x )] 2sin( x ) 2 2 6
f ( x)为偶函数.
sin( x ) sin( x ), 6 6 即 sin x cos( ) cos x sin( ) sin x cos( ) cos x sin( ). 6 6 6 6
例4
已知函数f ( x) 3sin(x ) cos(x )(0 , 0)为偶函数,且函数 (1)求f ( )的值; 图象的两相邻对称轴间的距离为 2
解 : (1) f ( x) 3 sin( x ) cos( x )
y
2
图象
1
0
2
x
1
0
2
x
3 2
2
0
3 2
x
单调性
最值
3 [ 2k, 2k ](k z ) 上递减 [ 2k, 2 2k ](k z) 上递增 2 2 ( k , k )(k z ) 上递增 2 [ 2k, 2k ](k z ) 上递增 [2k , 2k ](k z)上递减 2 2 2 x 2k , k z时,ymax 1 x 2k , k z 时, max 1 y
