拉格朗日插值c语言表述
拉格朗日插值法编程

拉格朗日插值法编程一、引言拉格朗日插值法是一种常见的数值插值方法,用于根据已知的离散数据点,估计出函数的近似值。
在许多领域中,这种方法被广泛应用,如数学建模、图像处理、信号处理等。
本文将详细介绍拉格朗日插值法的原理,并给出相应的编程实现。
二、拉格朗日插值法原理拉格朗日插值法的原理基于拉格朗日函数,通过已知的离散数据点来逼近函数的值。
设已知n+1个数据点{(x0, y0), (x1, y1), … , (xn, yn)},其中xi为自变量的值,yi为因变量的值。
要通过这些数据点来逼近函数f(x)。
拉格朗日插值多项式的表达式如下:L(x) = Σ(yi * Li(x)) 其中Li(x)为拉格朗日基函数,定义为:Li(x) = Π((x - xj) / (xi - xj)), j≠iLi(x)的含义是在第i个数据点处,Li(x)取值为1,在其他数据点处,Li(x)取值为0。
通过将已知的n+1个数据点代入拉格朗日插值多项式,并求和,就可以得到一个对函数f(x)的近似。
三、拉格朗日插值法的实现步骤1.输入已知的离散数据点,包括自变量的值(xi)和因变量的值(yi)。
2.计算每个数据点处的拉格朗日基函数Li(x)。
3.将已知的n+1个数据点代入拉格朗日插值多项式,并求和,得到近似函数L(x)。
4.输入待求点的自变量值x,将其代入近似函数L(x),得到近似值f(x)。
四、示例代码实现下面是用Python实现拉格朗日插值法的示例代码:# Step 1: 输入已知的离散数据点x = [2, 4, 6, 8]y = [5, 3, 9, 1]# Step 2: 计算每个数据点处的拉格朗日基函数Li(x)def lagrange_basis(i, xi, x):basis = 1for j, xj in enumerate(xi):if j != i:basis *= (x - xj) / (xi[i] - xj)return basis# Step 3: 计算近似函数L(x)def lagrange_interpolation(xi, yi, x):L = 0for i, xi in enumerate(xi):L += yi[i] * lagrange_basis(i, xi, x)return L# Step 4: 输入待求点的自变量值x,得到近似值f(x)x_test = 5y_test = lagrange_interpolation(x, y, x_test)print("f({}) ≈ {}".format(x_test, y_test))五、优缺点分析拉格朗日插值法的优点是简单易懂、计算方便,并且可以通过增加数据点的数量来提高近似的精确度。
拉格朗日插值牛顿插值C语言实验报告

实验报告:数学与统计学系信息与计算科学专业实验报告一、题目1、上机作业题程序12、上机作业题程序2二、算法1、Lagrange 插值//输入被插值点的数目POINT;int main(){int n;inti,j;POINT points[MAX_N+1];double diff[MAX_N+1];doublex,tmp=0,lagrange=0,tx,ty;printf("\nInput n value:");scanf("%d",&n);if(n>MAX_N){printf("The input n is larger thenMAX_N,please redefine the MAX_N.\n");return 1;}if(n<=0){printf("Please input a number between 1 and %d\n",MAX_N);return 1;}//输入被插值点printf("Now input the (x_i,y_i),i=0,...,%d:\n",n);for(i=0;i<=n;i++)scanf("%lf%lf",&points[i].x,&points[i].y);printf("Now input the x value:"); //输入计算Lagrange插值多项式的x值scanf("%lf",&x);for(i=0;i<=n;i++){diff[i]=0;tx=1;ty=1;for(j=0;j<=n;j++){if(i!=j){tx=tx*(x-points[j].x);ty=ty*(points[i].x-points[j].x);}}diff[i]=tx/ty;}for(i=0;i<=n;i++){tmp=points[i].y*diff[i];printf("%f",tmp);lagrange+=tmp;}printf("lagrange(%f)=%f\n",x,lagrange);return 0;}2、Newton 插值//输入被插值点的数目POINT;int main(){ int n;inti,j;POINT points[MAX_N+1];double diff[MAX_N+1];doublex,tmp,newton=0;printf("\nInput n value: ");scanf("%d",&n);if (n>MAX_N){printf("The input n is larger thenMAX_N,please redefine the MAX_N.\n");return 1;}if(n<=0){printf("Please input a number between 1 and %d\n",MAX_N);// getch(); return 1;}//输入被插值点printf("Now input the (x_i,y_i),i=0,...,%d:\n",n);for (i=0;i<=n;i++)scanf("%lf%lf",&points[i].x,&points[i].y);printf("Now input the x value: ");//输入计算Newton插值多项式的x值scanf("%lf",&x);for (i=0;i<=n;i++)diff[i]=points[i].y;for (i=0;i<n;i++){for (j=n;j>i;j--){diff[j]=(diff[j]-diff[j-1])/(points[j].x-points[j-1-i].x);}//计算f(x_0,…,x_n)的差商}tmp=1;newton=diff[0];for(i=0;i<n;i++){tmp=tmp*(x-points[i].x);newton=newton+tmp*diff[i+1];}printf("newton(%f)=%f\n",x,newton);return 0;}三、C程序1、Lagrange 插值#include <stdio.h>#define MAX_N 20typedefstructtagPOINT{double x;double y;}POINT;int main(){int n;inti,j;POINT points[MAX_N+1];double diff[MAX_N+1];doublex,tmp=0,lagrange=0,tx,ty;printf("\nInput n value:");scanf("%d",&n);if(n>MAX_N){printf("The input n is larger thenMAX_N,please redefine the MAX_N.\n");return 1;}if(n<=0){printf("Please input a number between 1 and %d\n",MAX_N); return 1;}printf("Now input the (x_i,y_i),i=0,...,%d:\n",n);for(i=0;i<=n;i++)scanf("%lf%lf",&points[i].x,&points[i].y);printf("Now input the x value:");scanf("%lf",&x);for(i=0;i<=n;i++){diff[i]=0;tx=1;ty=1;for(j=0;j<=n;j++){if(i!=j){tx=tx*(x-points[j].x);ty=ty*(points[i].x-points[j].x);}}diff[i]=tx/ty;}for(i=0;i<=n;i++){tmp=points[i].y*diff[i];printf("%f",tmp);lagrange+=tmp;}printf("lagrange(%f)=%f\n",x,lagrange);return 0;}2、Newton 插值#include <stdio.h>#define MAX_N 20typedefstructtagPOINT{ double x;double y;} POINT;int main(){ int n;inti,j;POINT points[MAX_N+1];double diff[MAX_N+1];doublex,tmp,newton=0;printf("\nInput n value: ");scanf("%d",&n);if (n>MAX_N){printf("The input n is larger thenMAX_N,please redefine the MAX_N.\n");return 1;}if (n<=0){printf("Please input a number between 1 and %d.\n",MAX_N);return 1;}//输入被插值点(x_i,y_i)printf("Now input the (x_i,y_i),i=0,...,%d:\n",n);for (i=0;i<=n;i++)scanf("%lf%lf",&points[i].x,&points[i].y);printf("Now input the x value: ");scanf("%lf",&x);for (i=0;i<=n;i++)diff[i]=points[i].y;for (i=0;i<n;i++){for (j=n;j>i;j--){diff[j]=(diff[j]-diff[j-1])/(points[j].x-points[j-1-i].x);}}tmp=1;newton=diff[0];for(i=0;i<n;i++){tmp=tmp*(x-points[i].x);newton=newton+tmp*diff[i+1];}printf("newton(%f)=%f\n",x,newton);return 0;}四、运行结果1、Lagrange 插值1910年Larange插值计算得到的人口数:1965年Larange插值计算得到的人口数:2002年Larange插值计算得到的人口数:从插值计算得出的结果1910年的人口数是31872000人,1965年的人口数约为193081511人,2002年的人口数约为26138748,而1910年的实际人口数为91772000人,1960年的实际人口数为179323000人,1970年的人口数为203212000人,所以拉格朗日插值计算得出的结果只有1965年的人口数与实际值相差较近,而1910年和2002年的计算结果都与实际值相差较大,所以插值计算得到的数据准确性并不高。
数值分析所有代码

实验一:拉格朗日插值多项式命名(源程序.cpp及工作区.dsw):lagrange问题:4//Lagrange.cpp#include <stdio.h>#include <conio.h>#define N 4int checkvalid(double x[], int n);void printLag (double x[], double y[], double varx, int n);double Lagrange(double x[], double y[], double varx, int n);void main (){double x[N+1] = {0.4, 0.55, 0.8, 0.9, 1};double y[N+1] = {0.41075, 0.57815, 0.88811, 1.02652, 1.17520};double varx = 0.5;if (checkvalid(x, N) == 1){printf("\n\n插值结果: P(%f)=%f\n", varx, Lagrange(x, y, varx, N));}else{printf("结点必须互异");}getch();}int checkvalid (double x[], int n){int i,j;for (i = 0; i < n; i++){for (j = i + 1; j < n+1; j++){if (x[i] == x[j])//若出现两个相同的结点,返回-1{return -1;}}}return 1;}double Lagrange (double x[], double y[], double varx, int n) {double fenmu;double fenzi;double result = 0;int i,j;printf("Ln(x) =\n");for (i = 0; i < n+1; i++){fenmu = 1;for (j = 0; j < n+1; j++){if (i != j){fenmu = fenmu * (x[i] - x[j]);}}printf("\t%f", y[i] / fenmu);fenzi = 1;for (j = 0; j < n+1; j++){if (i != j){printf("*(x-%f)", x[j]);fenzi = fenzi * (varx - x[j]);}}if (i != n){printf("+\n");}result += y[i] / fenmu * fenzi;}return result;}运行及结果显示:实验二:牛顿插值多项式命名(源程序.cpp及工作区.dsw):newton_cz问题:4//newton_cz.cpp#include<stdio.h>#include<iostream.h>#include<conio.h>#define N 4int checkvaild(double x[],int n){int i,j;for(i=0;i<n+1;i++){for(j=i+1;j<n+1;j++)if(x[i]==x[j])return -1;}return 1;}void chashang(double x[],double y[],double f[][N+1]){int i,j,t=0;for(i=0;i<N+1;i++){f[i][0]=y[i];//f[0][0]=y[0],f[1][0]=y[1];f[2][0]=y[2];f[3][0]=y[3];f[4][0]=y[4] }for(j=1;j<N+1;j++)// 阶数j{for(i=0;i<N-j+1;i++) //差商个数if[i][j]=(f[i+1][j-1]-f[i][j-1])/(x[t+i+1]-x[i]);//一阶为f[0][1]~f[3][1];二阶为f[0][2]~f[2][2]//三阶为f[0][3]~f[1][3];四阶为f[0][4]t++;}}double compvalue(double t[][N+1],double x[],double varx){int i,j,r=0;double sum=t[0][0],m[N+1]={sum,1,1,1,1};printf("i\tXi\t F(Xi)\t 1阶\t 2阶\t\t3阶\t 4阶\n");printf("--------------------------------------------------------------------------------");for(i=0;i<N+1;i++){r=i;printf("x%d\t%f ",i,x[i]);for(j=0;j<=i;j++){printf("%f ",t[r][j]);r--;}printf("\n");}printf("--------------------------------------------------------------------------------");/**/ printf("N(x) =\n");printf(" %f\n",t[0][0]);for(i=1;i<N+1;i++){for(j=0;j<i;j++)m[i]=m[i]*(varx-x[j]);m[i]=t[0][i]*m[i];sum=sum+m[i];}for(i=1;i<N+1;i++){ printf(" +%f*",t[0][i]);for(j=0;j<i;j++)printf("(x-%f)",x[j]);printf("\n");}return sum;}void main(){double varx,f[N+1][N+1];double x[N+1]={0.4,0.55,0.8,0.9,1};double y[N+1]={0.41075,0.57815,0.88811,1.02652,1.17520};checkvaild(x,N);chashang(x,y,f);varx=0.5;if(checkvaild(x,N)==1){chashang(x,y,f);printf("\n\n牛顿插值结果: P(%f)=%f\n",varx,compvalue(f,x,varx));}elseprintf("输入的插值节点的x值必须互异!");getch();} 运行及结果显示:实验三:自适应梯形公式命名(源程序.cpp 及工作区.dsw ):autotrap ][n T问题:计算⎰+=10214dx x π的近似值,使得误差(EPS )不超过610- //autotrap.cpp #include<stdio.h> #include<conio.h> #include<math.h> #define EPS 1e-6 double f(double x) { return 4/(1+x*x); } double AutoTrap(double(*f)(double),double a,double b,double eps) { double t2,t1,sum=0.0; int i,k; t1=(b-a)*(f(a)+f(b))/2; printf("T(%4d)=%f\n",1,t1); for(k=1;k<11;k++) { for(i=1;i<=pow(2,k-1);i++) sum+=f(a+(2*i-1)*(b-a)/pow(2,k)); t2=t1/2+(b-a)*sum/pow(2,k); printf("T(%4d)=%f\n",(int)pow(2,k),t2); if(fabs(t2-t1)<EPS) break; else t1=t2; sum=0.0; } return sum; } void main(){ double s;s=AutoTrap(f,0.0,1.0,EPS);getch();} 运行及结果显示:实验四:龙贝格算法命名(源程序.cpp 及工作区.dsw ):romberg问题:求⎰+=10214dx x π的近似值,要求误差不超过610-//romberg.cpp #include <stdio.h> #include <conio.h> #include <math.h> #define N 20 #define EPS 1e-6 double f(double x){return 4/(1+x*x);} double Romberg(double a,double b,double (*f)(double),double eps) { double T[N][N],p,h;int k=1,i,j,m=0;T[0][0]=(b-a)/2*(f(a)+f(b));do{p=0;h=(b-a)/pow(2,k-1);for(i=1;i<=pow(2,k-1);i++)p=p+f(a+(2*i-1)*h/2);T[0][k]=T[0][k-1]/2+p*h/2;for(i=1;i<=k;i++){j=k-i;T[i][j]=(pow(4,i)*T[i-1][j+1]-T[i-1][j])/(pow(4,i)-1); }k++; p=fabs(T[k-1][0]-T[k-2][0]);}while(p>=EPS);k--; while(m<=k){for(i=0;i<=m;i++) printf("T(%d,%d)=%f ",i,m-i,T[i][m-i]);m++;printf("\n");}return T[k][0]; } void main() {printf("\n\n 积分结果 = %f",Romberg(0,1,f,EPS)); getch(); } 运行及结果显示:实验五:牛顿切线法问题:求方程01)(3=--=x x x f 在5.1=x ,6.0=x 附近的根(精度31021-⨯=) //newton_qxf.cpp#include <math.h>#include<conio.h>#include <stdio.h>#define MaxK 1000#define EPS 0.5e-3double f(double x){return x*x*x-x-1;}double f1(double x){return 3*x*x-1;}int newton(double (*f)(double), double (*f1)(double), double &x0, double eps) {double xk, xk1;int count = 0;printf("k\txk\n");printf("-----------------------\n");xk = x0;printf("%d\t%f\n", count, xk);do{if((*f1)(xk)==0)return 2;xk1 = xk - (*f)(xk) / (*f1)(xk);if (fabs(xk - xk1) < eps){count++;xk = xk1;printf("%d\t%f\n", count, xk);x0 = xk1;return 1;}count++;xk = xk1;printf("%d\t%f\n", count, xk);}while(count < MaxK);return 0;}void main(){for(int i=0;i<2;i++){double x=0.6;if(i==1)x=1.5;printf("x0初值为%f:\n",x);if (newton(f, f1, x, EPS) == 1){printf("-----------------------\n");printf("the root is x=%f\n\n\n", x);}else{printf("the method is fail!");}}getch();}实验六:牛顿下山法命名(源程序.cpp 及工作区.dsw ):newton_downhill 问题:求方程01)(3=--=x x x f 在5.1=x ,6.0=x 附近的根(精度31021-⨯=) //newton_downhill.cpp #include <stdio.h> #include <conio.h> #include <math.h> #include <stdlib.h> #define Et 1e-3//下山因子下界 #define E1 1e-3//根的误差限 #define E2 1e-3//残量精度 double f(double x) { return x * x * x - x - 1; } double f1(double x) { return 3 * x * x - 1; } void errormess(int b){char *mess;switch(b){case -1:mess = "f(x)的导数为0!";break;case -2:mess = "下山因子已越界,下山处理失败";break;default:mess = "其他类型错误!";}printf("the method has faild! because %s", mess);}int Newton(double (*f)(double), double (*f1)(double), double &x0) {int k = 0;double t;double xk, xk1;double fxk, fxk_temp;printf("k t xk f(xk)\n");printf("----------------------------------------------------------\n");printf("%-20d", k);xk = x0;printf("%-15f", x0);fxk = (*f)(xk);printf("%-20f", fxk);printf("\n");for (k = 1; ; k++){t = 1;while(1){printf("%-10d", k);printf("%-10f", t);if((*f1)(xk) != 0){xk1 = xk - t * (*f)(xk) / (*f1)(xk);}else{return -1;}printf("%-15f", xk1);fxk_temp = (*f)(xk1);printf("%-20f", fxk_temp);if(fabs(fxk_temp) >fabs(fxk)){t = t / 2;printf("\n");if (t < Et){return -2;}}else{printf("下山成功\n");break;}}if (fabs(xk-xk1)<E1){x0 = xk1;return 1; } xk = xk1; } }void main() {int b;double x0; x0 = 0.6;b = Newton(f, f1, x0); if (b == 1) printf("\nthe root x=%f\n", x0); else errormess(b); getch(); }运行及结果显示:实验七:埃特金加速算法命名(源程序.cpp 及工作区.dsw ):aitken问题:求方程01)(3=--=x x x f 在5.1=x ,6.0=x 附近的根(精度31021-⨯=) //aitken.cpp#include <math.h> #include <stdio.h> #include <conio.h> #define MaxK 100 #define EPS 0.5e-3double g(double x) {return x * x * x - 1; }int aitken (double (*g)(double), double &x, double eps) {int k;double xk = x, yk, zk, xk1;printf("k xk yk zk xk+1\n");printf("-------------------------------------------------------------------\n"); for (k = 0;k<MaxK; k++) { yk = (*g)(xk); zk = (*g)(yk);xk1 = xk - (yk - xk) * (yk - xk) / (zk - 2 * yk + xk); printf("%-10d%-15f%-15f%-15f%-15f\n", k, xk, yk, zk, xk1); if (fabs(yk-xk)<=eps) { x = xk1; return k + 1; } xk = xk1; }return -1; }void main () {double x = 1.5; int k;k = aitken(g, x, EPS); if (k == -1) printf("迭代次数越界!\n"); else printf("\n 经k=%d 次迭代,所得方程根为:x=%f\n", k, x); getch(); }运行及结果显示:实验八:正割法问题:求方程01)(3=--=x x x f 在5.1=x 附近的根(精度0.5e-8) //ZhengGe.cpp #include <math.h> #include <stdio.h> #include <conio.h>#define MaxK 1000 #define EPS 0.5e-8double f(double x) {return x*x*x-x-1;}int ZhengGe(double (*f)(double), double x0, double &x1, double eps) {printf("k xk f(xk)\n");printf("---------------------------------------------\n");int k;double xk0, xk, xk1;xk0 = x0;printf("%-10d%-15f%-15f\n", 0, x0, (*f)(x0));xk = x1;for (k=1;k<MaxK;k++){if((*f)(xk)-(*f)(xk0)==0)return -1;xk1 = xk - (*f)(xk) / ( (*f)(xk) - (*f)(xk0) ) * (xk - xk0);printf("%-10d%-15f%-15f\n", k, xk, (*f)(xk));if (fabs(xk1 - xk)<=eps){printf("%-10d%-15f%-15f\n\n", k + 1, xk1, (*f)(xk1));printf("---------------------------------------------\n\n");x1 = xk1;return 1;}xk0 = xk;xk = xk1;}return -2;}void main (){double x0 = 1, x1 = 2;if (ZhengGe(f, x0, x1, EPS) == 1){printf("the root is x = %f\n", x1);}else{printf("the method is fail!");}getch();}实验九:高斯列选主元算法命名(源程序.cpp 及工作区.dsw ):colpivot问题:求解方程组并计算系数矩阵行列式值 ⎪⎩⎪⎨⎧=-+=+-=-+2240532321321321x x x x x x x x x//colpivot.cpp#include <math.h> #include <stdio.h> #include <conio.h> #define N 3static double aa[N][N]={{1,2,-1},{1,-1,5},{4,1,-2}}; static double bb[N+1]={3,0,2};void main() {int i,j;double a[N+1][N+1],b[N+1],x[N+1],det;double gaussl(double a[][N+1],double b[],double x[]); for(i=1;i<=N;i++) { for(j=1;j<=N;j++) a[i][j]=aa[i-1][j-1]; b[i]=bb[i-1]; }det=gaussl(a,b,x); if(det!=0) { printf("\n 方程组的解为:"); for(i=1;i<=N;i++) printf(" x[%d]=%f",i,x[i]); printf("\n\n 系数矩阵的行列式值=%f",det); }else printf("\n\n 系数矩阵奇异阵,高斯方法失败 !:"); getch(); }double gaussl(double a[][N+1],double b[],double x[])//a传入增广矩阵(有效元素为a[1,1]...a[n,n+1]),x负责传入迭代初值并返回解向量//(有效值为x[1]...x[n]);返回值:系数矩阵行列式值detA{double det=1.0,F,m,temp;int i,j,k,r;void disp(double a[][N+1],double b[]);printf("消元前增广矩阵:\n");disp(a,b);for(k=1;k<N;k++){temp=a[k][k];r=k;for(i=k+1;i<=N;i++){if(fabs(temp)<fabs(a[i][k])){temp=a[i][k];r=i;}//按列选主元,即确定ik}if(a[r][k]==0)return 0;//如果aik,k=0,则A为奇异矩阵,停止计算if(r!=k){for(j=k;j<=N;j++){a[k][j]+=a[r][j];a[r][j]=a[k][j]-a[r][j];a[k][j]-=a[r][j];}b[k]+=b[r];b[r]=b[k]-b[r];b[k]-=b[r];det=-det;//如果ik!=k,则交换[A,b]第ik行与第k行元素printf("交换第%d, %d行:\n",k,r);disp(a,b);}for(i=k+1;i<=N;i++){m=a[i][k]/a[k][k];for(j=1;j<=k;j++)a[i][j]=0.0;for(j=k+1;j<=N;j++)a[i][j]-=m*a[k][j];b[i]-=m*b[k];}printf("第%d次消元:\n",k);disp(a,b);det*=a[k][k];} //大FOR循环结束x[N]=b[N]/a[N][N];for(i=N-1;i>0;i--){F=0.0;for(j=i+1;j<=N;j++)F+=a[i][j]*x[j];x[i]=(b[i]-F)/a[i][i];}det*=a[N][N];return det;}void disp(double a[][N+1],double b[])//显示选主元及消元运算中间增广矩阵结果 {int i,j;for(i=1;i<=N;i++) {for(j=1;j<=N;j++)printf("%10f\t",a[i][j]); printf("%10f\n",b[i]); } }运行及结果显示:实验十:高斯全主元消去算法 命名(源程序.cpp 及工作区.dsw ):fullpivot问题:利用全主元消去法求解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----9555.04525.015.0201.0321x x x //fullpivot.cpp#include <math.h> #include <stdio.h> #include <conio.h> #define N 3 double x[N+1];static double aa[N][N]={{0.01,2,-0.5},{-1,-0.5,2},{5,-4,0.5}}; static double bb[N]={-5,5,9};void main(){int i,j;double a[N+1][N+1],b[N+1],x[N+1],det;int t[N+1];//引入列交换保存x向量的各分量的位置顺序double gaussl(double a[][N+1],double b[],double x[],int t[]);for(i=1;i<=N;i++){for(j=1;j<=N;j++) a[i][j]=aa[i-1][j-1];b[i]=bb[i-1];}for(i=1;i<=N;i++)t[i]=i;det=gaussl(a,b,x,t);if(det!=0){ printf("\n方程组的解为:");for(i=N;i>=1;i--){printf(" x[%d]=%f",t[i],x[i]);if(i>1)printf(" -->");}printf("\n\n系数矩阵的行列式值=%f",det);}else printf("\n\n系数矩阵奇异阵,高斯方法失败!:");getch();}double gaussl(double a[][N+1],double b[],double x[],int t[])//a传入增广矩阵(有效元素为a[1,1]...a[n,n+1]),x负责传入迭代初值并返回解向量//(有效值为x[1]...x[n]);返回值:系数矩阵行列式值detA{double det=1.0,F,m,temp;int i,j,k,r,s;void disp(double a[][N+1],double b[],int x[]);// printf("消元前增广矩阵:\n");//disp(a,b,t);for(k=1;k<N;k++){temp=a[k][k];r=k;s=k;for(i=k;i<=N;i++)for(j=k;j<=N;j++)if(fabs(temp)<fabs(a[i][j])){temp=a[i][j];r=i;s=j;}//选主元,选取ik,jkif(a[r][s]==0)return 0;if(r!=k){for(j=k;j<=N;j++){a[k][j]+=a[r][j];a[r][j]=a[k][j]-a[r][j];a[k][j]-=a[r][j];}b[k]+=b[r];b[r]=b[k]-b[r];b[k]-=b[r];det=-det;printf("交换第%d, %d行:\n",k,r);disp(a,b,t);}if(s!=k){for(i=0;i<=N;i++){a[i][k]+=a[i][s];a[i][s]=a[i][k]-a[i][s];a[i][k]-=a[i][s];}t[k]+=t[s];t[s]=t[k]=t[s];t[k]-=t[s];det=-det;printf("交换第%d, %d列:\n",k,s);disp(a,b,t);}for(i=k+1;i<=N;i++){m=a[i][k]/a[k][k];for(j=1;j<=k;j++)a[i][j]=0.0;for(j=k+1;j<=N;j++)a[i][j]-=m*a[k][j];b[i]-=m*b[k];} //消元计算printf("第%d次消元:\n",k);disp(a,b,t);det*=a[k][k];} //大FOR循环结束x[N]=b[N]/a[N][N];for(i=N-1;i>0;i--){F=0.0;for(j=i+1;j<=N;j++)F+=a[i][j]*x[j];x[i]=(b[i]-F)/a[i][i];}//回代计算det*=a[N][N];return det;}void disp(double a[][N+1],double b[],int x[])//显示选主元及消元运算中间增广矩阵结果{int i,j;for(i=1;i<=N;i++){for(j=1;j<=N;j++)printf("%f\t",a[i][j]);printf("| x%d = %f\n",x[i],b[i]);}}运行及结果显示:实验十一:LU 分解算法命名(源程序.cpp 及工作区.dsw ):LU问题:利用LU 法求解方程组 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡472111312613321x x x //LU.cpp#include<math.h> #include<stdio.h> #include<conio.h> #define N 3static aa[N][N]={{3,1,6},{2,1,3},{1,1,1}}; static bb[N]={2,7,4};void main() {int i,j;double a[N+1][N+1],b[N+1];void solve(double a[][N+1],double b[N+1]); int LU(double a[][N+1]); for(i=1;i<=N;i++) { for(j=1;j<=N;j++) a[i][j]=aa[i-1][j-1]; b[i]=bb[i-1]; }if(LU(a)==1){printf("矩阵L如下\n");for(i=1;i<=N;i++){for(j=1;j<=i;j++)if(i==j)printf("%12d ",1);else printf("%12f",a[i][j]);printf("\n");}printf("\n矩阵U如下\n");for(i=1;i<=N;i++){for(j=1;j<=N;j++)if(i<=j)printf("%12f",a[i][j]);else printf("%12s","");printf("\n");}solve(a,b);for(i=1;i<=N;i++)printf("x[%d]=%f ",i,b[i]);printf("\n");}else printf("\nthe LU method failed!\n");getch();}int LU(double a[][N+1])//对N阶矩A阵进行LU分解,结果L、U存放在A的相应位置{int i,j,k,s;double m,n;for(i=2;i<=N;i++)a[i][1]/=a[1][1];for(k=2;k<=N;k++){for(j=k;j<=N;j++){m=0;for(s=1;s<k;s++)m+=a[k][s]*a[s][j];a[k][j]-=m;}if(a[k][k]==0){printf("a[%d][%d]=%d ",k,k,0);return -1;//存在元素akk为0}for(i=k+1;i<=N;i++){n=0;for(s=1;s<k;s++)n+=a[i][s]*a[s][k];a[i][k]=(a[i][k]-n)/a[k][k];}}return 1;//正常结束}void solve(double a[][N+1],double b[N+1])//利用分解的LU求x//回代求解,L和U元素均在A矩阵相应位置;b存放常数列,返回时存放方程组的解{double y[N+1],F;int i,j;y[1]=b[1];for(i=2;i<=N;i++){F=0.0;for(j=1;j<i;j++)F+=a[i][j]*y[j];y[i]=b[i]-F;}b[N]=y[N]/a[N][N];for(i=N-1;i>0;i--){F=0.0;for(j=N;j>i;j--)F+=a[i][j]*b[j];b[i]=(y[i]-F)/a[i][i];}}运行及结果显示:实验十二:Guass-Sediel 算法命名(源程序.cpp 及工作区.dsw ):GS问题:利用G -S 法求解方程组 ⎪⎩⎪⎨⎧=+--=-+-=--2.453.82102.7210321321321x x x x x x x x x (精度为41021-⨯)//Guass_sediel.cpp#include "iostream.h"#include "math.h"#include "stdio.h"#include<conio.h>#define N 3 //方程的阶数#define MaxK 100 //最大迭代次数#define EPS 0.5e-4 //精度控制static double aa[N][N]={{10,-1,-2},{-1,10,-2},{-1,-1,5}};static double bb[N]={7.2,8.3,4.2};void main(){int i,j;double x[N+1];double a[N+1][N+1],b[N+1];int GaussSeidel(double a[][N+1],double b[],double x[]);for(i=1;i<=N;i++){for(j=1;j<=N;j++)a[i][j]=aa[i-1][j-1];b[i]=bb[i-1];x[i]=0;}if(GaussSeidel(a,b,x)==1){printf("the roots is:");for(i=1;i<=N;i++)printf(" x[%d]=%f ",i,x[i]);printf("\n");}else printf("\nthe G-S method failed!\n");getch();}int GaussSeidel(double a[][N+1],double b[],double x[])//a传入系数矩阵(有效元素为a[1,1]...a[n,n]),b为方程组右边常数列,x传入迭代初值并返回解向量//x**(k+#x)=Gx**(k)+f{int k=1,i,j;double m,max,t[N+1];while(true){printf("k=%d:",k);max=0.0;for(i=1;i<=N;i++){if(a[i][i]==0)return -1;//存在元素akk为0m=0.0;t[i]=x[i];for(j=1;j<=N;j++)if(j!=i)m+=a[i][j]*x[j];x[i]=(b[i]-m)/a[i][i];if(max<fabs(x[i]-t[i]))max=fabs(x[i]-t[i]);printf(" x[%d]=%f ",i,x[i]);}printf("\n");if(max<EPS)return 1;//正常结束elsek++;if(k>MaxK)return -2;//迭代次数越界}}运行及结果显示:实验十三:SOR 算法命名(源程序.cpp 及工作区.dsw ):sor问题:利用SOR 法求解方程组⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----111141111411114111144321x x x x (精度为51021-⨯) //SOR.cpp#include "math.h"#include "stdio.h"#include "conio.h"#define N 4#define MaxK 1000#define EPS 0.5e-5static double aa[N][N]={{-4,1,1,1},{1,-4,1,1},{1,1,-4,1},{1,1,1,-4}}; static double bb[N]={1,1,1,1};void main(){int i,j;double x[N+1];double a[N+1][N+1],b[N+1];int Sor(double a[][N+1],double b[],double w,double x[]);for(i=1;i<=N;i++){for(j=1;j<=N;j++)a[i][j]=aa[i-1][j-1];b[i]=bb[i-1];x[i]=0;}if(Sor(a,b,1.3,x)==1){printf("the roots is:");for(i=1;i<=N;i++)printf(" x[%d]=%f ",i,x[i]);printf("\n");}else printf("\nthe G-S method failed!\n");getch();}int Sor(double a[][N+1],double b[],double w,double x[]) {int i,j,k;double loft,comb;for(k=0;k<=N;k++)x[k]=0;for(i=1;i<=MaxK && fabs(comb)>EPS;i++){printf("k=%d:\t",i);comb=0;for(k=1;k<=N;k++){loft=b[k];for(j=1;j<N+1;j++)loft-=a[k][j]*x[j];if(a[k][k]==0)return -1;else loft=w*loft/a[k][k];x[k]=x[k]+loft;printf("x[%d]=%10f \t",k,x[k]);if(fabs(loft)>comb)comb=fabs(loft);}printf("\n");}if(i>MaxK)return -2;elsereturn 1;}运行结果(w=1)=。
拉格朗日插值c++代码

#include
using namespace std;
#define L 2
int main()
{
int C,i,k;
double x;
double y=0.0;
double t=1.0;
cout<<"请输入已知有多少个点对"<<endl;< p="">
cin>>C;
double (*p)[L]=new double[C][L];
cout<<"输入各个点对的值"<<endl;< p="">
for(i=0;i<c;i++)< p="">
for(k=0;k<l;k++)< p="">
cin>>p[i][k];
cout<<"输入你要估算的x的值";
cin>>x;
for(k=0;k<c;k++)< p="">
{ቤተ መጻሕፍቲ ባይዱ
for(i=0;i<c;i++)< p="">
{
if(i==k) continue ;
t=(x-p[i][0])/(p[k][0]-p[i][0])*t;
}
y=y+t*p[k][1];
t=1;
}
cout<<"当x="<<x<<" delete[]="" p="" p;<="" 时,估计的结果为:"<<y<
拉格朗日和牛顿插值法的C 方法实现(数值分析上机实验)

数值分析上机实验实验一一.上机题目:已知: 4 =2,9 =3,16 =4分别用二次Lagrange和Newton插值法求7 的近似值。
二.解题方法:1.lagrange方法:设x0=4,y0=2,x1=9,y1=3,x2=16,y2=4代入方程:(x1-X)(x2-X)/(x1-x0)(x2-x0)*y0+(x0-X)(x2-X)/(x0-x1)(x2-x1)*y1+(x1-X)(x0-X)/(x1-x2)(x0-x2)*y2令X=7代入方程得 Y=2.628572.Newton方法:设x0=4,y0=2,x1=9,y1=3,x2=16,y2=4建表4 29 3 0.216 4 0.14286 -0.00476f(x)=f(x0)+f[x0,x1](X-x0)+f[x0,x1,x2](X-x0)(X-x1)(X-x2)令X=7代入方程得Y=2.62857三.算法公式步骤:grange方法:通过公式写出算法并得出最后的值Y:for(b=0;b<m;b++)//完成公式f(Xn)外层嵌套循环f[b]=i//{double l=1;//保证每次跳出内层循环将L置1 不会将第一项的值带入下一项//for(a=0;a<m;a++)//完成公式f(Xn)内层嵌套循环f[a]=j//{if(a!=b)//完成定义i=1,i!=j//l=(f[a]-F)/(f[a]-f[b])*l;//完成(j-m)/(j-i)//la=l*g[b];//完成公式的F(X0)=f(X0)*Y0并累乘输出结果// }Y=la+Y;//累加x0y0+x1y1+...得最后结果//}2.Newton方法:先建表,通过二维数组的思想建表for(l=2;l<m+2;l++)//外层循环控制y阶数//{for(k=1;k<m+1;k++)//内层循环控制x个数//{a[k][l]=(a[k][l-1]-a[k-1][l-1])/(a[k][0]-a[k-l+1][0]);//完成f(x0,x1,...,xn)并存表//}}填表。
数值分析-代码

注:凡“in.open("C:\\Users\\Administrator\\Desktop\\data-拉格朗日插值.txt")”等里面的路径自己合理修改。
1-1.拉格朗日插值(用一系列已知点求近似函数,并估计未知点的函数值)#include<fstream.h>#include<stdlib.h>int n; //插值节点个数double *X,*Y;//插值节点数组double x;//估计点void read(){double temp;ifstream in;in.open("C:\\Users\\Administrator\\Desktop\\data-拉格朗日插值.txt");if(!in){cout<<"can not open the file !"<<endl;exit(0);}in>>n;X=new double[n];Y=new double[n];for(int i=0;i<n;i++){in>>temp;X[i]=temp;cout<<temp<<" ";in>>temp;Y[i]=temp;cout<<temp<<"\n";}in>>temp;x=temp;cout<<"x="<<temp<<endl;in.close();}void main(){double t,y=0;read();for(int k=0;k<n;k++){t=1;for(int i=0;i<n;i++)if(k!=i)t=(x-X[i])/(X[k]-X[i])*t;y=y+t*Y[k];}cout<<"y="<<y<<endl;}1-2.埃特金逐步插值法(同上)#include<fstream.h>#include<stdlib.h>double *X,*Y; //插值节点(x,y)double x; //带估点int n; //N个插值点,插n-1次。
用C语言实现拉格朗日插值

用C语言实现拉格朗日插值拉格朗日插值是一种在给定有限个数据点的函数值的情况下,用一个多项式函数逼近这些数据点,从而在数据点之间进行插值和外推的方法。
这个多项式函数称为拉格朗日插值多项式。
拉格朗日插值多项式的形式如下:P(x) = Σ L(x) * yi其中,i的取值范围是从0到n,n为给定的数据点的数量。
L(x)代表拉格朗日基函数,可以表示为:L(x) = Π (x - xj) / (xi - xj), 其中i ≠ j接下来,我们将用C语言实现拉格朗日插值。
首先,我们定义一个结构体来存储数据点的x和y坐标:```ctypedef structdouble x;double y;} DataPoint;```然后,我们定义一个函数来计算拉格朗日基函数的值:```cdouble lagrange_basis(double x, DataPoint* data_points, int data_count, int index)double result = 1.0;for (int i = 0; i < data_count; i++)if (i != index)result *= (x - data_points[i].x) / (data_points[index].x - data_points[i].x);}}return result;```接下来,我们定义一个函数来计算拉格朗日插值多项式的值:```cdouble lagrange_interpolation(double x, DataPoint*data_points, int data_count)double result = 0.0;for (int i = 0; i < data_count; i++)result += data_points[i].y * lagrange_basis(x, data_points, data_count, i);}return result;```最后,我们可以在主函数中使用这些函数来进行插值。
拉格朗日插值法c语言

实验报告实验课程名称数值计算方法实验项目名称 Lagrange插值公式年级专业学生姓名学号理学院实验时间:201 年月日学生实验室守则一、按教学安排准时到实验室上实验课,不得迟到、早退和旷课。
二、进入实验室必须遵守实验室的各项规章制度,保持室内安静、整洁,不准在室内打闹、喧哗、吸烟、吃食物、随地吐痰、乱扔杂物,不准做与实验内容无关的事,非实验用品一律不准带进实验室。
三、实验前必须做好预习(或按要求写好预习报告),未做预习者不准参加实验。
四、实验必须服从教师的安排和指导,认真按规程操作,未经教师允许不得擅自动用仪器设备,特别是与本实验无关的仪器设备和设施,如擅自动用或违反操作规程造成损坏,应按规定赔偿,严重者给予纪律处分。
五、实验中要节约水、电、气及其它消耗材料。
六、细心观察、如实记录实验现象和结果,不得抄袭或随意更改原始记录和数据,不得擅离操作岗位和干扰他人实验。
七、使用易燃、易爆、腐蚀性、有毒有害物品或接触带电设备进行实验,应特别注意规范操作,注意防护;若发生意外,要保持冷静,并及时向指导教师和管理人员报告,不得自行处理。
仪器设备发生故障和损坏,应立即停止实验,并主动向指导教师报告,不得自行拆卸查看和拼装。
八、实验完毕,应清理好实验仪器设备并放回原位,清扫好实验现场,经指导教师检查认可并将实验记录交指导教师检查签字后方可离去。
九、无故不参加实验者,应写出检查,提出申请并缴纳相应的实验费及材料消耗费,经批准后,方可补做。
十、自选实验,应事先预约,拟订出实验方案,经实验室主任同意后,在指导教师或实验技术人员的指导下进行。
十一、实验室内一切物品未经允许严禁带出室外,确需带出,必须经过批准并办理手续。
学生所在学院:专业:班级:韩非子名言名句大全,韩非子寓言故事,不需要的朋友可以下载后编辑删除!!1、千里之堤,毁于蚁穴。
——《韩非子·喻老》2、华而不实,虚而无用。
——《韩非子·难言》3、欲速则不达。
拉格朗日插值和牛顿插值多项式的C程序算法毕业论文

本科生毕业论文题目: 拉格朗日插值和牛顿插值多项式的C程序算法原创性声明本人郑重声明: 所提交的学位论文是本人在导师指导下, 独立进行研究取得的成果. 除文中已经注明引用的内容外, 论文中不含其他人已经发表或撰写过的研究成果, 也不包含为获得**大学或其他教育机构的学位证书而使用过的材料. 对本文的研究做出重要贡献的个人和集体, 均已在文中以明确方式标明. 本人承担本声明的相应责任.学位论文作者签名: 日期指导教师签名: 日期目录拉格朗日插值多项式的C程序算法 (1)1引言 (1)1.1插值问题的提出 (1)1.2插值法 (2)1.3插值法思想 (2)2拉格朗日插值法 (3)2.1拉格朗日插值法的由来 (3)2.2n次插值基函数 (4)2.3拉格朗日插值多项式 (4)3牛顿插值法 (5)3.1均差: (5)3.2牛顿插值多项式: (6)4C程序设计 (7)4.1算法设计: (7)4.2程序源码编写 (8)5程序检测 (12)5.1对拉格朗日插值的检测 (12)5.2对牛顿插值的检测 (13)总结 (15)参考文献 (16)致谢 (17)摘要本论文着重研究了用C语言编写程序计算拉格朗日插值和牛顿插值的方法。
在前人已有的研究成果的基础上,首先介绍了拉格朗日插值和牛顿插值的思想和方法,通过添加可以循环计算功能和输入非法数值时的纠错功能,改进了已有文献的方法,对其进行了推广,使之更加的合理和完美,并且通过实际的例子进行了具体的验证。
最后,总结了一下本论文的主要研究成果和应用前景。
关键词:拉格朗日插值,牛顿插值,C算法,精确解AbstractThis article discuss the method to calculate Lagrange interpolation and Newton interpolation with C program. Base on the results of predecessors' research, firstly, this article introduces the thoughts and methods of Lagrange interpolation and Newton interpolation. Improving the old method by adding functions which can repeatedly computing interpolation and correct illegal data. Then spreading it and making it more reasonable and perfect, checking it with some examples. Finally, summing up the main results of this article and application prospect.Key words:Lagrange interpolation; Newton interpolation ; C program;拉格朗日插值多项式的C 程序算法1引言插值法是一种古老的数学研究方法,他的产生来自与社会的生产实践活动。
拉格朗日插值--C语言实现

1.源程序
#include "stdlib.h"
#include "stdio.h"
#include "conio.h"
#include "string.h"
#include "graphics.h"
#include "math.h"
typedef struct
{
float x;
float y;
{
int i;
int Max_y;
Max_y = 0.0;
for(i=0;i<n;++i)
if(Max_y<fabs(Table[i].y))
Max_y=fabs(Table[i].y);
return(Max_y);
}
void DrawCoordinate(int X1,int Y1,int X2,int Y2,float x1,float y1,float x2,float y2)
{
char String[20];
setcolor(color);
gcvt(RealNumber,Length,String);
outtextxy(x,y,String);
}
void ShowTable(POINT Table[],int n)
{
int i;
char String_x[20],String_y[20];
line1(0,20,639,20,7);
line(30,0,30,40);
outtextxy1(10,8,"x",14);
outtextxy1(10,28,"y",14);
拉格朗日插值法C语言

机械CAD/CAM技术读书报告姓名:***学号:*********班级:机械1401专业:机械设计制造及其自动化学院:机械工程学院指导老师:***日期:2017年6月3日摘要插值法是函数逼近的一种重要方法,.数学上来说,拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数.Lagrange插值是n次多项式插值,其成功地用构造插值基函数的方法,解决了求n次多项式插值函数问题.Lagrange插值的基本思想是将待求的n次多项式插值函数改写成另一种表示方式,再利用插值条件确定其中的待定函数,从而求出插值多项式.拉格朗日插值法是一种很实用的插值方法,可以应用在渔业资源评估中、化学中、工程中、工业中、机械设计与制造领域,以及计算机方面.通过C语言的编写,将拉格朗日算法在计算机中实现,求得相应的解.进一步体现拉格朗日插值法在解决问题时的实际意义关键词插值基函数插值多项式 Lagrange插值;算法一、读书报告的目的进一步熟悉拉格朗日插值法。
掌握编程语言字符处理程序的设计和调试技术。
二、拉格朗日插值多项式:三、.程序流程(1)输入已知点的个数;(2)分别输入每个点的X、Y的值(3)通过程序自动显示插值点的拉格朗日函数(4)输入具体所要插入点的值(5)求得所需插值点的函数值拉格朗日插值流程图四、程序设计思路为了实现拉格朗日插值函数的运算和函数方程的显示,我设立了一个main主函数和getpoints和insert两个辅助函数。
在main主函数中我首先建立了两个数组X[]和Y[],分别用来记录所输入的点的X和Y坐标值,通过getpoints函数来从窗口读入参数并传递给main函数。
接下来为了显示拉格朗日函数我设立了两个for循环,第一个for循环是为了显示拉格朗日函数多项式的其中某一项,也就是通过连乘的方式实现,第二个for循环是把上一个循环得出的每一个多项式进行连加。
其中的if语句是由于拉格朗日插值函数中i≠j 所规定的。
拉格朗日插值法(c++)

拉格朗⽇插值法(c++)已给sin0.32=0.314567,sin0.34=0.333487,sin0.36=0.352274,计算sin0.3367的值#include <iostream>#include<iomanip>#include <cmath>using namespace std;int main(){double numerator_cofficient; //⽤来记录插值分⼦的乘积结果double denominator_coefficient; //⽤来记录插值分母乘积的结果double input_x; //需要输⼊的x的值double x[3]={0.32,0.34,0.36}; //已知x的值double y[3]={0.314567,0.333487,0.352274}; //已知y的值double result=0; //⽤来记录插值结果cout<<"通过拟合得到的拉格朗⽇多项式为:"<<endl;for (int i=0;i<3;i++){denominator_coefficient=1;cout<<y[i]<<"*";for (int j=0;j<3;j++){if (i==j)continue;cout<<"("<<"x-"<<x[j]<<")";}cout<<"/";for (int j=0;j<3;j++){if (i==j)continue;denominator_coefficient*=(x[i]-x[j]);}cout<<denominator_coefficient<<"*"<<"("<<"x-"<<x[i]<<")";if (i<3){cout<<"+";}}cout<<endl;cout<<"请输⼊需要插值的x:";cin>>input_x;for (int i=0;i<3;i++){numerator_cofficient=1;denominator_coefficient=1;for (int j=0;j<3;j++){if (i==j)continue;numerator_cofficient*=(input_x-x[j]);}for (int j=0;j<3;j++){if (i==j)continue;denominator_coefficient*=(x[i]-x[j]);}result+=(y[i]*numerator_cofficient/denominator_coefficient);}cout<<"插值结果为:"<<setiosflags(ios::fixed)<<setprecision(10)<<result<<endl;cout<<"函数的真实值:"<<sin(0.3367)<<endl;cout<<"计算误差为:"<<100*(abs(result-sin(0.3367))/sin(0.3367))<<"%"<<endl; return 0;}。
线性插值、抛物插值、拉格朗日、牛顿插值代码

计算机数值计算方法及程序设计P63函数值为//拉格朗日插值P63#include <stdio.h>float czl(int n,float x1,float *px,float *py);int main(){float x1,y1;int n;float *p1,*p2;float x[10]={1,2,3,4,5,6,7};float y[10]={1,1.414214,1.732051,2,2.236068,2.449490,2.645751};printf("Input numbers:x1 n=\n");scanf("%f%d",&x1,&n);p1=x;p2=y;y1=czl(n,x1,p1,p2);printf("y1=%f\n",y1);getch();return 0;}float czl(int n,float x1,float *px,float *py){int i,j;float x[10],y[10],t,y1;y1=0.0;for(i=0;i<n;i++,px++,py++){x[i]=*px;y[i]=*py;}for(i=0;i<n;i++){t=1.0;for(j=0;j<n;j++)if(i!=j)t=t*(x1-x[j])/(x[i]-x[j]);y1=y1+t*y[i];}return(y1);}//输入为//2.5 4//输出为//y=1.582274//线性插值P58#include <stdio.h>float cz(float x0,float x1,float y0,float y1,float x); int main(void){float x0,x1,y0,y1,x,y;printf("Input numbers:x0,x1,y0,y1,x=?\n");scanf("%f%f%f%f%f",&x0,&x1,&y0,&y1,&x);y=cz(x0,x1,y0,y1,x);printf("y=%f\n",y);}float cz(float x0,float x1,float y0,float y1,float x) {float l0,l1,y;l0=(x-x1)/(x0-x1);l1=(x-x0)/(x1-x0);y=l0*y0+l1*y1;return (y);}/*输入:1 5 1 2.6.68 2.5输出y=1.463526 *////抛物插值P60#include<stdio.h>float cz(float x0,float x1,float x2,float y0,float y1,float y2,float x); float cz(float x0,float x1,float x2,float y0,float y1,float y2,float x) {float l0,l1,l2,y;l0=(x-x1)*(x-x2)/((x0-x1)*(x0-x2));l1=(x-x0)*(x-x2)/((x1-x0)*(x1-x2));l2=(x-x0)*(x-x1)/((x2-x0)*(x2-x1));y=l0*y0+l1*y1+l2*y2;return(y);}int main(void){float x0,x1,x2,y0,y1,y2,x,y;printf("Input numbers:x0 x1 x2 y0 y1 y2 x=?\n");freopen("in.txt","r",stdin);freopen("out.txt","w",stdout);scanf("%f%f%f%f%f%f%f",&x0,&x1,&x2,&y0,&y1,&y2,&x);y=cz(x0,x1,x2,y0,y1,y2,x);printf("y=%f\n",y);getch();getch();return 0;}/*输入:1 3 5 1 1.732051 2.236068 2.5输出y=1.570416 *///牛顿插值P83#include<stdio.h>#include<math.h>#define N 6float sub(float a[],float b[],float x,float e); main(){float u[N]={100,121,122,169,196,225}; float v[N]={10,11,12,13,14,15};float x,y,e,*p1,*p2;printf("Input number x e= ");scanf("%f%e",&x,&e);p1=u;p2=v;y=sub(p1,p2,x,e);printf("y=%f\n",y);getch();getch();}float sub(float *pp1,float *pp2,float x,float e) {float a[N],b[N],t[N],y,y1,c;int i,k;for(i=0;i<N;i++,pp1++) {a[i]=*pp1;printf("%12.6",a[i]);}printf("\n");for(i=0;i<N;i++,*pp2++) {b[i]=*pp2;printf("%12.6f",b[i]);}printf("\n");y1=b[0];y=0;c=1.0;for(k=1;k<N;k++) {for(i=k;i<N;i++){t[i]=(b[i]-b[i-1])/(a[i]-a[i-k]);}c=c*(x-a[k-1]);y1=y1+c*t[k];if(fabs(y-y1)<e) y=y1;for(i=k;i<N;i++){b[i]=t[i];}}return(y);}。
拉格朗日插值与牛顿插值
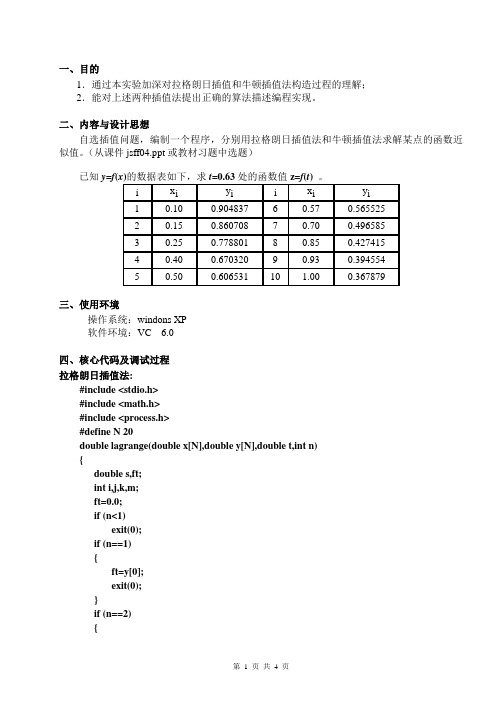
一、目的1.通过本实验加深对拉格朗日插值和牛顿插值法构造过程的理解;2.能对上述两种插值法提出正确的算法描述编程实现。
二、内容与设计思想自选插值问题,编制一个程序,分别用拉格朗日插值法和牛顿插值法求解某点的函数近似值。
(从课件jsff04.ppt或教材习题中选题)已知y=f(三、使用环境操作系统:windons XP软件环境:VC 6.0四、核心代码及调试过程拉格朗日插值法:#include <stdio.h>#include <math.h>#include <process.h>#define N 20double lagrange(double x[N],double y[N],double t,int n){double s,ft;int i,j,k,m;ft=0.0;if (n<1)exit(0);if (n==1){ft=y[0];exit(0);}if (n==2){ft=(t-x[1])*y[0]/(x[0]-x[1])+(t-x[0])*y[1]/(x[1]-x[0]);exit(0);}i=0;while ((x[i]<t) && (i<n))i++;k=i-4;if (k<0)k=0;m=i+3;if (m>n-1)m=n-1;for (i=k;i<=m;i++){s=1.0;for (j=k;j<=m;j++)if (j!=i)s=s*(t-x[j])/(x[i]-x[j]);ft=ft+s*y[i];}return (ft);}void main(){double x[N]={0.10,0.15,0.25,0.40,0.50,0.57,0.70,0.85,0.93,1.00};doubley[N]={0.904837,0.860708,0.77801,0.670320,0.6065310,0.565525,0.496585,0.427418,0.394554,0.3 67879};double t=0.63,ft;ft=lagrange(x,y,t,10);printf("f(0.63)=%lf\n",ft);}运行结果:牛顿插值法:#include <stdio.h>void main(){double x[]={0.10,0.15,0.25,0.40,0.50,0.57,0.70,0.85,0.93,1.00};doubley[]={0.904837,0.860708,0.77801,0.670320,0.6065310,0.565525,0.496585,0.427418,0.394554,0.367 879};double c[10][10];double b[10];double t=0.63,ft;int n,i,j,k;for (i=0;i<10;i++)c[i][0]=y[i];for (i=1;i<10;i++)for (j=1;j<=i;j++)c[i][j]=(c[i][j-1]-c[i-1][j-1])/(x[i]-x[i-j]);b[9]=c[9][9];for (k=9;k>=1;k--)b[k-1]=c[k-1][k-1]+b[k]*(t-x[k-1]);ft=b[0];printf("f(t=0.63)=%lf\n",ft);}运行结果:总结1.通过本实验加深了对拉格朗日插值和牛顿插值法构造过程的理解。
c++拉格朗日插值法

c++拉格朗日插值法
C++程序实现Lagrange插值公式
Lagrange插值公式,是属于数值分析方面的内容。
此处我想用C++语言程序来实现n各插值节点插值公式的求解,并求出在某一个插值节点对应的函数值。
对于Lagrange插值算法的基本思想,在这里我只想略提两点,一个是拉格朗日插值公式,一个是拉格朗日插值基函数的求解。
因为这两者才是算法需要解决的最根本的问题。
(1)采用插值多项式来近似的逼近拉格朗日差值多项式。
(2)上面的插值多项式中的L(x)即为拉格朗日插值多项式的插值基函数的通项。
该版本可根据输入的插值点自动选取其周围的8个点进行7次插值运算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L=Lagrange(x,y,xx,n);
printf("\n插值点结果L=%f\n",L);
printf("=============================================\n");
1.通过指针分配空间求Lagrange插值;
#include"stdio.h"
#include"conio.h"
#include"malloc.h"
#define N 100
float Lagrange(float *x,float *y,float xx,int n)
{ int i,j;
scanf("%f",&x[i]);
}
for(i=0;i<n;i++)
{
printf("y[%d]=",i);
scanf("%f",&y[i]);
}
L=Lagrange(x,y,xx,n);
printf("插值点结果L=%f\n",L);
scanf("%f",&xx);
for(i=0;i<n;i++)
{
printf("x[%d]=",i);
scanf("%f",&x[i]);
}
for(i=0;i<n;i++)
{
printf("y[%d]=",i);
}
2.通过函数调用数组求Lagrange插值;
#include"stdio.h"
#include"conio.h"
#include"malloc.h"
#define N 100
float Lagrange(float x[N],float y[N],float xx,int n)
{ int i,j;
float *a,yy=0.0;
a=(float *)malloc(sizeof(float));
for(i=0;i<n;i++)
a[i]=y[i];
for(j=0;j<n;j++)
{ for(i=0;i<j;i++)
a[j]*=(xx-x[i])/(x[j]-x[i]);
scanf("%f",&y[i]);
}
printf("===========================================\n");
for(i=0;i<n;i++)
printf("x[%d]=%f\t\n",i,x[i]);
for(i=0;i<n;i++)
}
L+=y[j];
}
return L; } 源自int main() { int n,i;
float x[N],y[N],xx,L;
printf("请输入插值结点个数n:\n");
scanf("%d",&n);
printf("请输入插值点xx:\n");
float L=0;
for(j=0;j<n;j++)
{ for(i=0;i<j;i++)
y[j]*=(xx-x[i])/(x[j]-x[i]);
for(i=j+1;i<n;i++)
y[j]*=(xx-x[i])/(x[j]-x[i]);
for(i=j+1;i<n;i++)
a[j]*=(xx-x[i])/(x[j]-x[i]);
yy+=a[j];
}
return yy;
}
int main()
{ int n,i;
float x[N],y[N],xx,L;
printf("请输入插值结点个数n:\n");
scanf("%d",&n);
printf("请输入插值点xx:\n");
scanf("%f",&xx);
for(i=0;i<n;i++)
{
printf("x[%d]=",i);
