Smith
smith裂解法的名词解释

smith裂解法的名词解释Smith裂解法,即Smith pyrolysis method,是一种石油化工领域常用的裂解工艺,旨在通过高温、缺氧条件下将重质石油馏分裂解为较轻质的石油产品和石油化工原料,如汽油、柴油、液化石油气等。
该方法以其高效、灵活的特点,在石油行业中得到广泛应用。
首先,我们需要了解裂解的含义。
裂解是指在一定的温度、压力和反应条件下,将长链烃化合物分解为短链烃化合物的过程。
石油中的长链烃化合物在裂解过程中被打破,转化为较轻质的石油产品和原料。
Smith裂解法与其他裂解方法相比,其关键在于是通过高温和缺氧条件下进行的。
Smith裂解法的基本过程是将重质石油馏分(也称作馏分)送入裂解器,通过加热到高温(通常为500°C至650°C)并控制缺氧造气(通常为氮气或干燥的空气),使馏分中的长链烃化合物分解为较轻的烃化合物。
在这个过程中,不同的长链烃化合物会以不同的速度裂解,从而得到不同碳数的烃化合物。
裂解产物主要包括气态产品(如液化石油气、石脑油等)和液态产品(如汽油、柴油等)。
其中,气态产品在裂解过程中会通过裂解气分离装置分离出来,而液态产品则在裂解过程中保持液态状态,并进一步经过精馏、加工等环节得到成品油(如汽油和柴油)。
Smith裂解法的具体实施操作非常复杂,需要考虑多种参数和因素。
首先是温度的控制,裂解温度可以影响裂解效果和产物分布。
过高的温度可能导致烷烃和芳烃的裂解产物过多,而过低的温度则可能导致不充分的裂解。
其次是不同种类的重质馏分的裂解反应速度和产物分布也有所不同。
另外,缺氧造气的选择和控制也是影响裂解效果的重要因素之一。
Smith裂解法的应用非常广泛,可以用于重油、焦油和催化裂化高温阻点渣等各种石油馏分的裂解。
它在石油化工生产中具有重要地位,不仅可以提高石油产品的产率,还可以改善产品质量,增加石油加工的灵活性。
此外,Smith裂解法也可以与催化裂化等工艺相结合,进一步提高石油产品的产率和质量。
Smith 圆图—原理与分析

Smith 圆图—原理与分析
Smith 圆图是一种用于分析电路中的匹配网络的工具。
它由美国电气工程师Phillip H. Smith于1950年提出,并被广泛应用于射频电路设计和天线设计领域。
Smith 圆图的原理基于复阻抗的概念。
在Smith 圆图中,电路中的每个点都可
以表示为一个复阻抗,即由实部和虚部组成的复数。
这样,整个电路可以表示为一个复阻抗的集合。
Smith 圆图将复阻抗表示为一个圆形图形,其中圆心表示纯电阻,圆的边界表
示纯电抗。
圆的半径表示电阻的大小,而圆的位置表示电抗的大小和相位。
通过在Smith 圆图上绘制电路中的复阻抗,可以直观地分析电路的匹配情况。
当电路的复阻抗位于Smith 圆图的边界上时,表示电路是纯电抗的,即无功。
当电路的复阻抗位于Smith 圆图的圆心时,表示电路是纯电阻的,即有功。
通过分析Smith 圆图上的复阻抗,可以确定电路的匹配情况。
匹配是指电路中
的负载阻抗与发射源或传输线的特性阻抗相匹配。
在Smith 圆图中,当负载阻抗与特性阻抗相匹配时,负载阻抗位于Smith 圆图的边界上,此时电路的反射系数为零,表示无反射。
Smith 圆图还可以用于计算电路中的反射系数、驻波比、传输线的特性阻抗等
参数。
通过在Smith 圆图上测量复阻抗的位置,可以直接读取这些参数的数值。
总之,Smith 圆图是一种简单直观的工具,可以帮助工程师分析电路中的匹配
情况,并优化电路设计。
它在射频电路设计和天线设计中具有重要的应用价值。
常用的好听的美国人的名字

美国人最常用的50个姓名史密斯(Smith)、约翰逊(Johnson)、威廉姆斯(Williams)、琼斯(Jones)、布朗(Brown)……这些姓氏均入围美国2000年人口普查的前100个姓氏。
下面把最常见的“百家姓”逐一列出,包括每一个姓氏的起源和含义。
耐人寻味的是,美国人口调查局1990年编写这份姓氏报告以来,其中的两个西班牙姓氏——加西亚(Garcia)和罗德里格斯(Rodriguez)——如今已跃进前10名。
1.史密斯(Smith)统计人数:2376206这一姓氏源自一种职业,是从事金属加工业的男士的姓氏(smith本身有铁匠或锻工之意)。
金属加工是最初几个对专业能力有特定要求的职业之一,任何中国都需要这种手艺,这个姓氏随之“闻名天下”。
2.约翰逊(Johnson)统计人数:1857160约翰逊这个名字源自英国的一对父子,父亲的名字叫“约翰(John)”,儿子的名字是“约翰的儿子(Johnson)”含义是“上帝的馈赠”。
3.威廉姆斯(Williams)统计人数:1534042一般认为,威廉姆斯这个名字也源自一对父子,父亲的名字叫“威廉(William)”,儿子的名字是“威廉的儿子(Williams)”。
不过也有其他说法。
4.布朗(Brown)统计人数:1380145这是一个具有描述性的词,意为“褐色头发的”或“棕色皮肤的”。
5.琼斯(Jones)统计人数:1362755这也是一个源自父亲名字的姓氏,“约翰(John)的儿子”,意为“上帝的恩宠”。
6.米勒(Miller)统计人数:1127803对这个姓氏的起源,最普遍的看法是:它是从事谷物碾磨工作人们的专有姓氏。
7.戴维斯(Davis)统计人数:1072335一个源自父亲名字的姓氏,“大卫(David)的儿子”,含义是“心爱的人”。
8.加西亚(Garcia)统计人数:858289这个流行的西班牙姓氏有很多种起源说法,最普遍的一种是“加西亚(Garcia)的子孙后代,加西亚(Garcia)本是西班牙对男人的一种称呼”。
smith圆图的原理和应用

Smith圆图的原理和应用1. 前言Smith圆图是一种用于分析和解决电路中匹配问题的有效工具。
它由英国电气工程师Philip H. Smith于1939年创造,被广泛应用于射频电路、微波电路和天线设计等领域。
本文将介绍Smith圆图的基本原理和其在电路设计中的应用。
2. Smith圆图的基本原理2.1 反射系数和阻抗的关系Smith圆图是基于反射系数和阻抗之间的关系来进行分析的。
在电路中,反射系数表示反射波与入射波之间的关系,它是一个复数,可以用幅值和相位角来表示。
而阻抗则表示电路的负载特性,是一个实数。
Smith圆图将反射系数和阻抗之间的关系以一种直观而又简洁的方式进行了可视化。
2.2 Smith圆图的表示方式Smith圆图以单位圆为基础,将纯虚轴表示为电阻为无穷大的点,将实轴表示为电抗为零的点。
反射系数的值可以通过在Smith圆图上找到相应的点来表示。
例如,反射系数为0时,点位于单位圆的中心,反射系数为1时,点位于单位圆的边缘。
3. Smith圆图的应用3.1 反射系数的测量Smith圆图可以用于测量电路中的反射系数。
通过将电路与信号源和负载连接,可以使用向电路中注入信号的方式来测量反射系数。
通过测量反射系数的幅值和相位角,并将其在Smith圆图上进行标记,可以得到电路的匹配情况。
3.2 阻抗匹配Smith圆图可以帮助我们进行阻抗匹配,即调整电路的参数,以使得电路的输入和输出阻抗相匹配。
在Smith圆图上,我们可以通过移动点的位置来调整电路的参数,直至反射系数最小化。
通过在Smith圆图上定位匹配的点,可以快速找到合适的参数设置。
3.3 确定失配的原因Smith圆图可以帮助我们确定电路中失配的原因。
当电路的反射系数不为零时,可以使用Smith圆图来定位反射点,并判断失配的原因。
例如,如果反射系数位于实轴上,则说明电路存在电抗失配;如果反射系数位于圆心,则说明电路存在电阻失配。
3.4 天线设计Smith圆图在天线设计中也有广泛的应用。
史密斯是姓还是名

史密斯是姓还是名
smith是姓,意思是史密斯。
例如:William Smith史密斯威廉。
英语中,smith的原意是用金属材料制造东西的人,如:blacksmith(铁匠),goldsmith(金匠),coppersmith(铜匠),tinsmith(锡匠)。
历史上有很长一段时期smith一直是个重要的职业,现在在英国人的姓氏中仍被使用。
smith主要用作名词、及物动词、不及物动词,作名词时译为“铁匠;锻工;制作者”,作及物动词时译为“锻制”,作不及物动词时译为“锻打金属;当锻工”。
例句:
1、Smith Senior。
年长的那位史密斯。
2、Smith Wore Glasses And His Front Teeth Stuck Out。
史密斯戴眼镜,门牙前突。
3、Master John Smith Is Seven Years Old。
约翰·史密斯少爷七岁了。
4、General Smith Is In Command Of The Army。
史密斯将军统率陆军。
5、The Very Reverend Jane Smith。
受人尊敬的简·史密斯。
Smith预估器

0 引言时滞现象常产生于化工、轻化、冶金、计算机网络通讯和交通等系统中[1,2]。
就控制系统而言,时滞是指作用于系统上的输入信号或控制信号与在它们的作用下系统所产生的输出信号之间存在的时间上的延迟,当时滞较大时,将会使系统中的被调量不能及时反映控制信号的作用;另外,当被控对象受到干扰而使被调量改变时,控制器产生的控制作用不能及时有效地抑制干扰的影响,从而导致较大的超调量和较长的调节时间,甚至产生不稳定。
因此,大时滞系统一直受到人们关注,成为目前过程控制研究领域的一个重要课题。
过程控制中,通常用过程纯滞后时间常数和系统时间常数之比来衡量过程时滞。
当τ/T≤0.3时,称为一般时滞过程,过程比较容易控制,常规PID控制就能收到良好的控制效果;当τ/T>0.3时,称为大时滞过程,需要采取特殊的高级控制方法,其控制难度随τ/T的比值增加而增加。
本文分析了在过程控制中广泛采用的大时滞过程控制算法——Smith预估补偿法,即Smith预估器,并重点讲述了其改进算法——双自由度Smith预估器,最后进行了仿真。
仿真结果表明该改进算法是可行的。
1 传统Smith预估器传统Smith预估器实质上是一种模型补偿控1.1 Smith预估控制基本思路Smith预估控制是瑞典科学家Smith于1957年提出的一种解决时滞系统控制问题的预估控制方法,其控制基本思路是预先估计出过程在基本扰动下的动态特性,然后由预估器进行补偿控制,使被延迟了的被调量提前反映到调节器,并使之动作,以此来减小超调量与加速调节过程[3]。
1.2 Smith预估控制补偿算法引入补偿环节Gk(s)后的闭环系统方框图如图1所示。
其中,Gc(s )e-τσ表示实际过程,Gk(s)表示系统一般PID调节器。
由图1可知系统闭环传递函数为引入补偿环节Gk (s)后,希望系统闭环传递函数的分母不再含e-τσ项,即要求1+Gc(s )Gk(s )+Gc(s )Gk(s )e-τσ=1+Gc(s)Gp(s) (2)即Gk(s)=(1-e-τσ)Gp(s) (3)将式(3)代入图1便可得到图2所示的传统连续Smith预估器方框图。
smith控制原理

smith控制原理
Smith控制原理,又称为比例-积分-微分(PID)控制器,是一种广泛应用于自动控制系统的控制算法。
它基于反馈控制的概念,通过连续监测系统的输出并与目标值进行比较,计算出一个控制量来调整系统的操作,使其尽可能接近目标值。
Smith控制原理的核心是PID控制器,其中包含了三个主要的控制参数:比例、积分和微分。
比例控制参数用于调整控制器输出与目标值之间的差异,积分控制参数用于校正系统的累积误差,而微分控制参数则用于修正系统的动态响应。
在Smith控制原理中,比例控制参数根据当前误差的大小和方向来调整控制器的输出。
具体来说,如果系统的输出比目标值偏低,那么比例控制参数将增加控制器输出,以使系统趋向于目标值。
相反,如果系统的输出比目标值偏高,比例控制参数将减小控制器输出,以使系统逼近目标值。
积分控制参数用于处理系统的累积误差,并在一段时间内进行补偿。
如果系统存在较大的累积误差,积分控制参数将逐渐增加控制器的输出。
这使得系统可以更快地达到目标值,并且在达到目标值后保持最小的稳态误差。
微分控制参数用于校正系统的动态响应。
它通过监测误差的变化率来预测系统的趋势,并相应地调整控制器的输出。
通过引入微分控制参数,可以减小系统的超调量和快速响应的振荡,提高系统的稳定性和控制精度。
综上所述,Smith控制原理通过比例、积分和微分三个控制参数,以及反馈控制的概念,实现了对系统的精确控制。
它广泛应用于工业自动化、机械控制、飞行器导航等领域,在提高系统的性能和稳定性方面发挥了重要作用。
smith标准型

smith标准型Smith标准型是一种常见的工业标准型号,广泛应用于机械设备、汽车零部件、航空航天等领域。
它具有一定的特点和优势,可以满足不同行业的需求。
下面将对Smith标准型进行详细介绍。
首先,Smith标准型具有高精度和稳定性。
它采用先进的加工工艺和材料,能够保证产品的精度和稳定性,满足高要求的工程应用。
无论是在高速运转还是在恶劣环境下,Smith标准型都能够保持良好的性能,确保设备的正常运行。
其次,Smith标准型具有良好的耐磨性和耐腐蚀性。
在工业生产中,设备往往需要长时间运转,因此耐磨性和耐腐蚀性是至关重要的。
Smith标准型采用优质材料制造,经过特殊处理,能够有效抵抗磨损和腐蚀,延长使用寿命,降低维护成本。
此外,Smith标准型还具有良好的可靠性和安全性。
在工业生产中,设备的可靠性和安全性是最重要的考量因素之一。
Smith标准型经过严格的质量控制和测试,确保产品符合相关标准和规定,能够可靠地运行,保障生产安全。
另外,Smith标准型还具有良好的通用性和标准化。
由于Smith 标准型符合国际标准,具有通用性,可以广泛应用于不同的设备和系统中。
同时,标准化的设计和制造,使得Smith标准型能够与其他设备和零部件完美匹配,方便安装和维护。
总的来说,Smith标准型具有高精度、稳定性、耐磨性、耐腐蚀性、可靠性、安全性、通用性和标准化等优点,适用于各种工业领域的需求。
它的出现,为工业生产提供了更多的选择,推动了工业的发展。
综上所述,Smith标准型是一种具有广泛应用前景和良好市场前景的产品,具有重要的意义和价值。
相信随着科技的不断进步和工业的不断发展,Smith标准型将会发挥越来越重要的作用,为人们的生活和生产带来更多的便利和效益。
smith标准型

smith标准型Smith标准型。
Smith标准型是一种管理学中常见的管理模式,它主要是以管理者的名字Smith命名的。
Smith标准型管理模式主要是指在企业管理中,通过制定一系列的标准和规范,来规范企业内部的各项管理活动,从而提高企业的管理效率和管理水平。
Smith标准型管理模式的提出,对企业的管理理念和管理方式产生了深远的影响,成为了企业管理中的一个重要的理论体系。
Smith标准型管理模式的核心理念是建立标准化的管理体系,通过明确的标准和规范,来规范企业内部的各项管理活动。
在Smith标准型管理模式中,管理者需要对企业的各项管理活动进行全面的规划和设计,制定出一系列的管理标准和规范,然后通过培训和教育,将这些标准和规范传达给企业内部的员工,确保员工能够全面地理解和执行这些标准和规范。
Smith标准型管理模式的实施,能够有效地提高企业的管理效率和管理水平。
首先,通过建立标准化的管理体系,能够使企业的各项管理活动更加有序和规范,避免了管理中的混乱和混乱现象的出现,提高了企业的管理效率。
其次,通过明确的管理标准和规范,能够提高员工的工作质量和工作效率,从而提高了企业的整体管理水平。
在实施Smith标准型管理模式的过程中,管理者需要注意以下几点。
首先,要注重标准和规范的科学性和合理性,不能盲目地制定一些不切实际的标准和规范,否则会影响到企业的正常运转。
其次,要注重员工的培训和教育,确保员工能够全面地理解和执行这些标准和规范,避免出现执行不到位的情况。
最后,要注重标准和规范的动态调整,要根据企业的实际情况,不断地对标准和规范进行修订和完善,以适应企业的发展和变化。
总的来说,Smith标准型管理模式是一种重要的管理模式,它通过建立标准化的管理体系,提高了企业的管理效率和管理水平。
在实施Smith标准型管理模式的过程中,管理者需要注重标准和规范的科学性和合理性,注重员工的培训和教育,以及注重标准和规范的动态调整。
求smith标准型

求smith标准型Smith标准型是指一种用于矩阵的行化简形式,它的特点是主元全为1,且每个主元所在的列在它之前的列中全为0。
求Smith标准型是一种重要的矩阵运算,它在代数几何、模运算、密码学等领域都有着重要的应用。
本文将介绍求Smith标准型的基本方法和步骤。
首先,我们需要了解什么是Smith标准型。
对于一个矩阵A,求它的Smith标准型就是将A通过一系列的行变换和列变换,化为一个对角矩阵D,使得D的对角线上的元素满足d1|d2|...|dn-1|dn,其中di|di+1表示di整除di+1,且di是唯一的。
这样的对角矩阵D就是A的Smith标准型。
接下来,我们来介绍求Smith标准型的基本方法。
首先,我们需要对矩阵A进行初等行变换,将A化为行阶梯形矩阵。
然后,再对行阶梯形矩阵进行初等列变换,将其化为对角形矩阵。
最后,对对角形矩阵进行初等行变换,使得其满足Smith标准型的定义。
需要注意的是,初等行变换和初等列变换是可逆的,因此对A的操作不会改变A的行列式。
在实际操作中,我们可以采用高斯消元法来进行初等行变换,将矩阵A化为行阶梯形矩阵。
然后,再利用初等列变换将行阶梯形矩阵化为对角形矩阵。
最后,再利用初等行变换将对角形矩阵化为Smith标准型。
需要注意的是,求Smith标准型的过程中可能会涉及到整数的因子分解和最大公因子的计算。
因此,在实际操作中,我们需要借助计算机软件来进行求解,以提高求解的效率和准确性。
在密码学中,Smith标准型的应用也是非常广泛的。
例如,在RSA公钥密码算法中,我们需要对大整数进行因子分解,而求Smith标准型的方法可以帮助我们快速地进行因子分解,从而加快RSA算法的加密和解密速度。
总之,求Smith标准型是一种重要的矩阵运算,它在代数几何、模运算、密码学等领域都有着重要的应用。
通过本文的介绍,相信读者对求Smith标准型有了更深入的了解,希望本文能够对读者有所帮助。
smith翻译

smith翻译
最近,“Smith翻译”成为了一则热门话题。
那么,“Smith翻译”究竟是什么呢?
“Smith翻译”,也被称为“Smith术”,是一种新出现的「神经机器翻译」(Neural Machine Translation)方法,它是由美国著名认知科学家和机器学习研究者John Smith提出的。
Smith术的基本思想是使用神经网络来将英文语言转换成另一种语言,例如汉语、俄语等。
Smith术采用一种称为“双向神经网络”(bi-directional neural network)的技术来实现翻译,这种技术能够识别句子的语义,从而更准确的将原语言翻译成目标语言。
它的工作原理是:首先,神经网络模型将原语言句子分析出其语义结构;然后,这些语义结构将被转换成另一种语言的语义结构;最后,将语义结构转换为目标语言句子。
Smith术已经取得了显著的成功,特别是当将英文转换成汉语时,它的翻译结果一般会比现有翻译工具,如Google Translate更准确、更流利。
因此,Smith术已经被众多翻译和认知研究人员所欢迎,它已经成为当今最流行的翻译技术之一。
另外,Smith术还可以被应用于其他领域,例如机器人、自然语言处理、智能聊天机器人和自然语言搜索引擎。
此外,它还可以帮助我们更好的理解人类语言,这样就可以更好的分析文字信息,提高技术的精度和准确性。
总的来说,Smith翻译是一种令人兴奋的技术,它不仅可以提高翻译水平,而且还可以应用于其他各种科技领域,给人类带来许多便利。
Smith数的判断

Smith数的判断题⽬描述:smith数是指满⾜下列条件的可分解的整数:其所有位数上的数字和等于其全部素数因⼦的数字之和。
例如,9975是smith数,9975=3*5*5*7*19,即9975的数字和=因⼦的数字总和=30.补充说明⼀下:根据smith数的定义,素数不是smith数。
输⼊多组数据,判断输⼊的数是否为smith数,如果是输出Yes,否则输出No解题思路:设输⼊的数为n(1)⾸先求出n的各个位之和,这个很简单,不再赘述(2)求输⼊数的质数因⼦(既能整除n,⼜是质数),这⾥需要注意的⼀点就是质因⼦的重复问题,思路详见在代码。
(3)求出质因⼦的各位数之和。
(注意!质因⼦也是求各位之和哦!)(4)判断各位数之和和质因⼦各位数之和是否相等。
#include<iostream>#include<algorithm>using namespace std;/*判断⼀个数是否为素数*/bool isPrime(int n) {if (n <= 3) {return n > 1;}// 求平⽅根,注意sqrt()的参数为 double 类型,这⾥要强制转换m的类型int k = (int)sqrt((double)n);int i;for (i = 2; i <= k; i++) {if (n % i == 0) {return false;}}// 如果完成所有循环,那么m为素数return true;}/*求个位数之和*/int sumgewei(int num) {int sumg = 0;//各位之和while (num) {sumg += num % 10;//计算每⼀位的和num = num / 10;}return sumg;}int main() {int n;while (scanf_s("%d", &n)) {if (isPrime(n)) {//素数不是smith数printf("No");}else {int sumg = sumgewei(n);//各位之和nint sump = 0;//质因⼦之和for (int i = 2; i <= n;) {if ((n%i == 0) && isPrime(i)) {sump += sumgewei(i);n = n / i;}else {// 因为要对找出以⼀个质因⼦后得到的除数在找质因⼦,⽽且还是要从i = 2开始// i++;放在这⾥既解决了上述问题,也对上述除数提供了循环i++;}}if (sumg == sump) { printf("Yes");}else {printf("No");}}}system("pause"); return0;}。
矩阵smith标准型

矩阵smith标准型
矩阵smith标准型是线性代数中一个重要的概念,它可以帮助我们更好地理解矩阵的结构和性质。
在本文中,我们将介绍矩阵smith标准型的定义、性质和计算方法。
首先,让我们来看一下矩阵smith标准型的定义。
对于一个n阶矩阵A,存在两个可逆矩阵P和Q,使得P^-1AQ=D,其中D是一个对角矩阵,其对角线上的元素称为A的不变因子。
如果D的对角线上的元素都是1,那么称A为可约矩阵;否则称A为Smith标准形式的矩阵。
接下来,我们来讨论一下矩阵smith标准型的性质。
首先,矩阵smith标准型是唯一的,也就是说,对于一个给定的矩阵A,其smith标准型是唯一确定的。
其次,矩阵smith标准型的对角线上的元素是A的不变因子,它们描述了矩阵A的结构和性质。
最后,矩阵smith标准型可以帮助我们求解线性方程组和矩阵的相似变换问题,具有重要的应用价值。
最后,我们来介绍一下计算矩阵smith标准型的方法。
首先,我们需要对矩阵A进行初等行变换和初等列变换,将其化为初等因子型。
然后,我们再对初等因子型的矩阵进行初等行变换和初等列变换,最终得到矩阵A的smith标准型。
需要注意的是,计算矩阵smith标准型的过程可能比较复杂,需要一定的数学功底和计算技巧。
总之,矩阵smith标准型是线性代数中一个重要的概念,它可以帮助我们更好地理解矩阵的结构和性质,具有重要的理论和应用价值。
希望本文的介绍能够对你有所帮助,谢谢阅读!。
改良Smith评分

改良Smith评分
背景
Smith评分是一种用于评估患者创伤严重程度的指标,通常用于评估颅脑损伤。
然而,传统的Smith评分在某些方面存在一些局限性,包括不够准确和易于出错等问题。
因此,我们对___评分进行了改良,旨在提高其准确性和可靠性。
改良方法
我们提出了以下几个改良措施来优化Smith评分:
1.细化评估指标:对于每个评估指标,我们增加了更多具体的细分项,以便更全面地评估患者的临床情况。
例如,在意识状态评估中,我们除了常规的清醒、嗜睡和昏迷之外,还增加了更具体的意识水平描述,如亚醒、呓语等。
2.赋予权重:我们对不同的评估指标赋予了不同的权重,以反映其在创伤严重程度评估中的重要性。
例如,颅内压评估在Smith 评分中具有较高权重,因为它反映了患者的脑损伤情况。
3.提供更详细的操作指南:我们为每个评估项目提供了更详细的操作指南,确保评估的一致性和准确性。
同时,我们还提供了一份改良Smith评分表格,以便医护人员记录和计算评分。
实施与效果
我们在某医院进行了改良Smith评分的试行实施,并与传统的Smith评分进行了比较。
初步结果显示,改良Smith评分在准确性和可靠性方面表现出明显的改善。
医护人员对新的评分指标和操作指南也给予了积极的反馈。
总结
通过改良Smith评分,我们旨在提高创伤严重程度评估的准确性和可靠性。
我们将继续完善评估指标和操作指南,并进行更广泛
的实施和评估。
希望这一改良措施能在患者治疗和护理中发挥积极的作用。
Smith预估
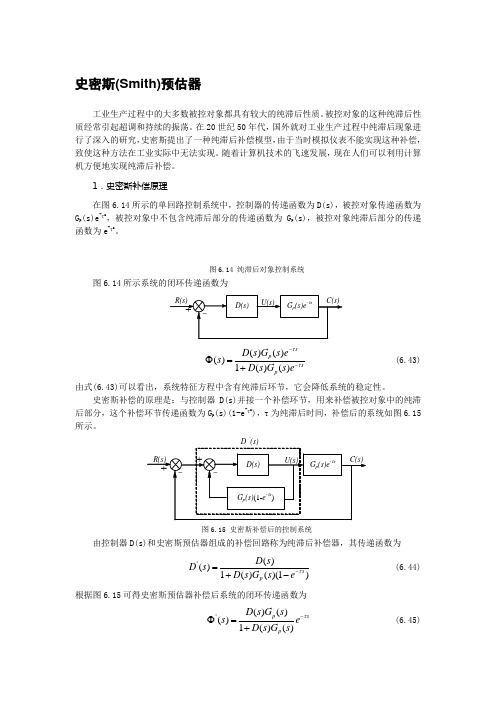
史密斯(Smith)预估器工业生产过程中的大多数被控对象都具有较大的纯滞后性质。
被控对象的这种纯滞后性质经常引起超调和持续的振荡。
在20世纪50年代,国外就对工业生产过程中纯滞后现象进行了深入的研究,史密斯提出了一种纯滞后补偿模型,由于当时模拟仪表不能实现这种补偿,致使这种方法在工业实际中无法实现。
随着计算机技术的飞速发展,现在人们可以利用计算机方便地实现纯滞后补偿。
1.史密斯补偿原理在图6.14所示的单回路控制系统中,控制器的传递函数为D(s),被控对象传递函数为G p (s)e -τs ,被控对象中不包含纯滞后部分的传递函数为G p (s),被控对象纯滞后部分的传递函数为e -τs 。
图6.14 纯滞后对象控制系统图6.14所示系统的闭环传递函数为()()()1()()sp s p D s G s e s D s G s e ττ--Φ=+ (6.43)由式(6.43)可以看出,系统特征方程中含有纯滞后环节,它会降低系统的稳定性。
史密斯补偿的原理是:与控制器D(s)并接一个补偿环节,用来补偿被控对象中的纯滞后部分,这个补偿环节传递函数为G p (s)(1-e -τs ),τ为纯滞后时间,补偿后的系统如图6.15所示。
‘图6.15 史密斯补偿后的控制系统由控制器D(s)和史密斯预估器组成的补偿回路称为纯滞后补偿器,其传递函数为'()()1()()(1)s p D s D s D s G s e τ-=+- (6.44) 根据图6.15可得史密斯预估器补偿后系统的闭环传递函数为 '()()()1()()p s p D s G s s e D s G s τ-Φ=+ (6.45)由式(6.45)可以看出,经过补偿后,纯滞后环节在闭环回路外,这样就消除了纯滞后环节对系统稳定性的影响。
拉氏变换的位移定理说明e -τs仅仅将控制作用在时间座标上推移了一个时间τ,而控制系统的过渡过程及其它性能指标都与对象特性为G p (s)时完全相同。
smith标准型技巧

smith标准型技巧Smith标准型技巧。
Smith标准型技巧是一种常用的技术标准,它可以帮助我们更好地完成工作。
在日常工作中,我们经常会遇到各种各样的问题,而掌握Smith标准型技巧可以帮助我们更好地解决这些问题,提高工作效率。
下面,我们将介绍一些Smith标准型技巧的应用方法,希望能对大家有所帮助。
首先,Smith标准型技巧的第一项应用是在问题分析中。
在面对问题时,我们需要对问题进行全面的分析,找出问题的根源。
使用Smith标准型技巧,我们可以通过系统性的方法,对问题进行分解,找出每个部分的关键因素,从而更好地理解问题的本质。
这样一来,我们就能够更有针对性地制定解决方案,提高解决问题的效率。
其次,Smith标准型技巧在团队合作中也有着重要的作用。
在团队合作中,经常会出现沟通不畅、目标不明确等问题。
而使用Smith标准型技巧,我们可以帮助团队成员更好地理解问题,明确目标,分工合作,从而提高团队的整体效率。
通过对问题进行系统性的分析和解决方案的制定,团队成员可以更好地协作,达成共识,完成工作任务。
此外,Smith标准型技巧在决策制定中也有着重要的作用。
在面对复杂的决策问题时,我们需要全面地考虑各种因素,做出明智的决策。
使用Smith标准型技巧,我们可以对决策问题进行系统性的分析,找出各种因素之间的关系,从而更好地制定决策方案。
通过对问题的全面分析,我们可以更好地预测各种可能的结果,避免决策失误,提高决策的准确性和效率。
最后,Smith标准型技巧在问题解决中也有着重要的作用。
在面对各种问题时,我们需要有条不紊地解决问题,而使用Smith标准型技巧,我们可以通过系统性的方法,找出问题的解决方案。
通过对问题进行全面的分析和系统性的解决方案制定,我们可以更好地解决问题,提高工作效率,为团队的发展做出贡献。
总的来说,Smith标准型技巧是一种非常实用的技术标准,它可以帮助我们更好地解决问题,提高工作效率。
smith标准型定义

smith标准型定义Smith标准型定义。
Smith标准型是指在工程设计和制造中广泛使用的一种标准化产品型号。
它是以工程师J. Smith的名字命名的,因为他首先提出并推广了这种标准化产品型号的概念。
Smith标准型的定义是指在特定领域内,经过一定的标准化设计和制造流程,生产出来的具有一定规格和性能的产品。
这种标准型产品不仅可以提高生产效率,降低成本,还可以保证产品的质量和可靠性,因此在工程设计和制造中得到了广泛的应用。
Smith标准型的特点之一是统一的规格和尺寸。
在设计和制造过程中,Smith标准型产品的尺寸和规格是经过严格的标准化和统一的。
这样一来,不同厂家生产的Smith标准型产品之间可以互相替换使用,从而降低了生产成本,提高了生产效率。
另外,由于规格和尺寸的统一,也方便了产品的维护和维修,增强了产品的可维护性。
另一个特点是稳定的性能和质量。
Smith标准型产品经过严格的设计和制造流程,保证了产品的稳定性能和优良质量。
这种稳定的性能和质量使得Smith标准型产品在各种工程设计和制造中得到了广泛的应用,例如在机械设备、电子电气、航空航天等领域。
此外,Smith标准型产品还具有通用性和可靠性。
由于其规格和性能的统一标准化,Smith标准型产品可以在不同的工程设计和制造中通用,从而降低了产品的研发和生产成本。
同时,经过严格的设计和制造流程,Smith标准型产品具有很高的可靠性,能够满足各种复杂的工程需求。
总的来说,Smith标准型产品在工程设计和制造中具有重要的意义。
它不仅可以提高生产效率,降低成本,还可以保证产品的质量和可靠性。
因此,我们应该进一步推广和应用Smith标准型产品,以促进工程设计和制造的发展,推动工业化进程。
smith降解法的名词解释

smith降解法的名词解释Smith降解法,又称为手性降解法,是一种用于合成手性有机物的方法。
该方法是由1977年诺贝尔化学奖得主W. Eugene Smith首次提出的,主要用于合成手性镜像体物质。
手性化合物是指分子在空间中存在两个非对称中心,因而存在左旋和右旋两种镜像体。
在自然界中,两种镜像体的化学和生物活性可能截然不同,因此合成对映体具有极高的重要性。
Smith降解法的基本原理是利用酶或微生物将目标化合物分解为反应底物,并通过化学反应将底物转化为手性产品。
这种方法的优点在于不依赖于对映选择性很高的手性合成试剂,而是通过生物催化体系实现了对映选择性的控制。
在Smith降解法中,酶是起到关键作用的生物催化剂。
酶是一类具有高效催化和高专一性的蛋白质,可以识别和转化特定的底物。
酶通过与底物相互作用,将其酶解为较简单的代谢物。
在降解过程中,酶会选择性地结合底物的特定对映体,以实现手性选择。
一种典型的Smith降解法的实施方法是通过合成手性底物,并将其与适合催化底物降解的酶结合。
在催化的作用下,底物被分解并生成手性产物。
酶底物转化的过程中,通过合成底物的对映体比例、合成底物和酶之间的交互作用等方式,可以实现对映选择性的控制。
Smith降解法在合成手性有机物中具有广泛的应用。
它不仅可以用于解决手性合成中的难题,还可以用于合成天然产物和药物中的手性中间体。
通过利用Smith 降解法,可以合成出具有高手性纯度的手性产品,从而提高药物的活性和减少副作用。
然而,Smith降解法也存在一定的局限性。
酶是一种比较复杂的生物催化剂,其活性和稳定性受到多种因素的影响,如温度、pH值、底物浓度等。
此外,酶底物转化的速率和底物的结构有很大的关联性,复杂结构的底物往往需要更复杂的酶体系来催化。
综上所述,Smith降解法是一种有效的合成手性有机物的方法。
通过利用生物催化体系,可以实现对映选择性的控制,合成出具有高手性纯度的产物。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
duc d. The wor n rncpl d c e ki g p i i e an omposton oft e s t r n a dwa e wer ve ii h ofwa e a d h r r e gi n.The pr c ia es i g a tc lt tn o r ton s ws t t t i ys e ha h a t r dv nc d d sgn,hi on r lng a c a y,go na c pe a i ho ha h s s t m s c ar c e s ofa a e e i gh c t oli c ur c od dy mi r s nsbiiy,go d r la lt n h r pr pe te . e po i lt o e ibiiy a d ot e o r is
D l V 现 场 总 线 设 备 , 们 分 析 D l V 提 供 的各 种 et a 我 et a 功 能模 块 , 设 多种 实 验课 程 。 中就 有 S t 开 其 mi h预估 器
模 块 。 们 打算 用 S t 我 mi h预 估 器控 制 电加 热炉 , 由于 电
加 热 炉 用 三 根 电热 丝 加 热 , 率 比较 大 , 炉 又 比较 功 锅 小 , 本没 有 滞后 。因此 , S t 估 器输 出模 块 前 基 在 mi h预
加 一 个滞 后模 块 , 这样 可 以任 意控 制 系统滞 后 时 间 , 满
足使用 S t mi h预估 器 条件 。
图 1 电加热炉的温度控制系统硬件结构
1 电加 热 炉 温 度 控 制 系 统 的 硬 件 结 构
电加 热炉 温 度控 制 系统 的硬 件 由 图 1所示 各 部分
维普资讯
第 2 l卷 第 5期
20 0 2年 1 月 0
实 验
室 研
究
与
探
索
Vo . l No. 1 2 5 OC .2 0 t 0 2
LA BO RA T OR Y RESEA R CH ND A EXPL0R A T 1 N 0
HUB连 接构 成 以太 网 。控 制 器下 挂 接模 拟输 入 、 出 输
模块 和 H1 链 路 活动 调 度器 ) ( 。H1 过 网络双 绞线 和 通 现场 总 线 的 阀门 、 液位 变 送器 进行 通 信 。 电加 热 炉 实际 温 度 可通 过热 电阻 P l 0测 量 得到 。 De a 上 除 了 tO 而 hV 标 准 的 4 2 mA 输 入 模 块 外 , 安装 热 电阻 输 入 模 ~ 0 未
S t mi h预 估 器 在 F F控 制 系统 中 的应 用
程 建 石 , 张 凤 登
( 海 理工 大 学 光 电学 院 , 海 2 0 9 ) 上 上 0 0 3
摘 要 : 绍 使 用 现 场 总 线 实 现 的 S t 介 mi h预 估 器 控 制 系统 ; 出 了 该 系统 的 实现 原 理 及 软 硬 件 组 成 , 给 经
实验 室 实 际/ - ' , 系统 具有 设计 先 进 , 制精 度 高 、 态响 应好 、 gg a 试 该 il - 控 动 可靠 性 高等特 点 。
关 键 词 : mi S t h预 估 器 ;电 加 热 炉 ;现 场 总 线 ;温 控
中 图分 类号 : 3 18 TP 9 .
文献 标 识码 : B
控 制是 克 服过 程 纯 滞后 影 响 的一 种有 效 方法 。根据 电
加 热 炉 的结 构 和 一 般 热 力 学 原 理 , 得 到 以下 电 加 热 可
炉 的被 控对 象 的传递 函数 , 其近 似 表示 为 :
Gk s ( )一 e ~ 一 Go s e~ () () 1
』 s T 1
文 章 编 号 :0 67 6 ( 0 2 0 — 0 10 1 0 — 1 7 2 0 ) 50 6 — 2
Ap iaton OfSm ih Pr pl c i t edi t n FF Con r l g Sy t c ori tol n s em i
CH EN G an s , ZH AN G n de g Ji — hi Fe g— n
块 , 此 , 电 阻 信 号还 需 经 温 度 变 送 单 元 处 理 , 而 因 热 从 得 到 与输 入模 块 相 适应 的输 入 信号 。输 出模 块输 出的
组成 。组 态 站 ( r fsin l l s 和 控 制 器 通 过 主 副 P oe s a P u ) o
2 S t mi h预 估 控 制 实 验 原 理
具 有 大 纯 滞 后 工 艺 过 程 的 自动 控 制 , 过 程 控 制 是
中最感 棘 手 的 问题 之一 。 理论 与 实践 证 明 ,mi S t h预估
Ke y wor ds:s ih pr d c or;e e t i atng o n;f m t e it lc rc he i ve oun ton fe d da i i l bus;t m pe a ur ontol e r t ec r
为 了 充 分 利 用 F S R— OS MoUNT 的 I HE R E
( Sha gha n v. S i n e a c ol gy,Sha gha 0 9 n iU i c e c nd Te hn o n i2 00 3,Chi a) n
Ab ta t Th e p a u e c sr c : e t m er t r ontoli y t m l c rc h a i g o n ba e r lng s s e ofan e e t i e tn ve s d on Sm ih pr dit a n r t e c or w s i t o—
