专题四、戴维南定理与诺顿定理
戴维南定理、诺顿定理

戴维南定理、诺顿定理戴维南定理和诺顿定理是电路分析中常用的两个重要定理。
它们分别用于简化复杂电路的计算和分析,为工程师提供了便利。
本文将依次介绍戴维南定理和诺顿定理的原理和应用。
一、戴维南定理戴维南定理是一种将电路中的电源和负载分离计算的方法。
它通过将电源和负载分别替换为等效电源和等效电阻,简化了电路的计算过程。
根据戴维南定理,我们可以将电源替换为一个等效电压源,其电压等于原电源的电压,内阻等于原电源的内阻。
同样地,我们可以将负载替换为一个等效电阻,其阻值等于原负载的阻值。
通过这样的替换,原本复杂的电路被简化为一个等效电压源和一个等效电阻的串联电路。
这样的简化使得电路的计算更加便捷,尤其适用于大规模复杂电路的分析。
二、诺顿定理诺顿定理是一种将电路中的电源和负载分离计算的方法。
它通过将电源和负载分别替换为等效电流源和等效电阻,简化了电路的计算过程。
根据诺顿定理,我们可以将电源替换为一个等效电流源,其电流等于原电源的电流,内阻等于原电源的内阻。
同样地,我们可以将负载替换为一个等效电阻,其阻值等于原负载的阻值。
通过这样的替换,原本复杂的电路被简化为一个等效电流源和一个等效电阻的并联电路。
这样的简化使得电路的计算更加便捷,尤其适用于大规模复杂电路的分析。
三、戴维南定理和诺顿定理的应用戴维南定理和诺顿定理在电路分析中有着广泛的应用。
它们可以用于计算电路中的电流、电压、功率等参数,帮助工程师进行电路设计和故障排查。
通过戴维南定理,我们可以将复杂的电路转化为等效电路,从而简化计算。
例如,在求解电路中某个分支的电流时,我们可以将其他分支看作一个等效电阻,这样就可以利用欧姆定律直接计算电流。
而诺顿定理则更适用于电流的计算。
通过将电路中的电源和负载分离,我们可以更方便地计算负载电流。
例如,在计算电路中某个负载的电流时,我们可以将电源看作一个等效电流源,利用欧姆定律计算电流。
戴维南定理和诺顿定理为电路分析提供了重要的工具和方法。
分别用戴维宁定理和诺顿定理

分别用戴维宁定理和诺顿定理一、戴维宁定理戴维宁定理是数学家约翰·戴维宁(John Davidihing)重要的成就,它有助于证明局部可导的函数的极限是全局可导的。
这一定理具有重要的理论意义,因为它丰富了函数极限的概念,并为微分几何和复分析提供了重要的技术工具。
戴维宁定理的具体内容是:设f(x)是连续在[a, b]上的函数,并且存在以(a, b)为间隔的非负实数n,使得在[a, b]上部分可导函数(存在区间[c, d]上 n-1次可导,则[a,b]上也存在n-1次可导)那么f(x)在[a, b]上可以进行n次连续可导,并且在[a, b]上有n次导数存在。
戴维宁定理可以简单阐述如下:如果函数在某个区间中可导,那么它在整个区间中也是可导的。
即当函数f(x)在区间[a, b]上有 n-1次可导,则它在[a, b]上也存在n次可导,并且在[a, b]上的n次导数存在。
二、诺顿定理诺顿定理是数学家约翰·诺顿(John Nortonon)在1915年提出的一个定理,它宣告函数在极限中变得越来越平滑。
该定理表明,当一个函数可以在某一区间内满足n次可连续可导的条件后,它将会在整个区间都满足这些条件。
将进一步阐明,诺顿定理的条件非常简单。
它指出,除非函数f(x)在[a,b]上存在以下两个条件:(1)f(x)是n次可连续导数(2)且f(a)、f《b)不同,则函数f(x)在[a,b]上存在n+1次可连续导数。
从这里可以看出,诺顿定理是一种进一步完善的定理,其它定理都表明函数变得复杂,而该定理却表明函数变得越来越平滑或者更准确地说,变得更理想。
总之,戴维宁定理和诺顿定理都是函数理论中极其重要的两个定理,它们对于广义函数和微积分中函数极限的理解有着深远的影响。
戴维南定理和诺顿定理

电压源的电压等于该含源二端网络在端钮处的开路电
压uOC;其串联电阻等于该含源二端网络中所有独立源
置零时,由端钮看进去的等效电阻Req。此即为戴维南
定理。
N
a +
_uOC
N0
b
a
Req
b
a戴 维
RS=Req 南
+
等
_uS=uOC
效 电
b路
一、定理
对于任意一个线性含源二端网络N,就其两个端
钮a、b而言,都可以用一条最简单的有源支路对外部
UO*C 0.2V
b、求等效电阻Re*q。
1A 1Ω
0.8Ω c a
2Ω
2Ω
R*eq +
1Ω
0.2V
_
b d
Re*q
32 32
0.8
2
解
1、先求左边部分电路 1Ω
的戴维南等效电路。 a、求开路电压Uo*c。 1Ω
UO*C 0.2V
b、求等效电阻Re*q。
32 Req* 3 2 0.8 2
进行等效:
用一条实际电流源支路对外部进行等效,其 中电流源的电流等于该含源二端网络在端钮处的短路
电流iSC;其串联电阻等于该含源二端网络中所有独立 源置零时,由端钮看进去的等效电阻Req。此即为诺顿
定理。
N
a
iSC N0
a
Req
b
iS=iSC
a
RS=Req
诺 顿 等 效
b
b电
路
二、步骤
1、断开待求支路,求开路电压uOC。
1V 6
解
第一步:求开路电压Uoc。
方法:叠加定理
1、电压源单独作用,
电路定理——戴维南,诺顿,等效

电路定理——戴维南,诺顿,等效
1.戴维南定理
戴维南定理是一种简化线性电路分析的方法,它的出发点是利用电压和电流之间的关系,把原来的电路转化为一个等效的电压源和电阻的串联电路,从而简化了电路的分析。
戴维南定理的基本思想是:在一个电路中,任何两个端点之间都可以看成是一个电压源和一个内部电阻的串联,其等效电路的电压源等于这两个端点之间的电压,内部电阻等于这两个端点看到的电阻。
式子表示为:
Vth=Voc
Rth = Voc/Isc
其中,Vth为等效电路的电压源,Rth为等效电路的内部电阻,Voc为开路电压,Isc 为短路电流。
2.诺顿定理
In = Isc
3.等效电路
等效电路是指具有相同电学特性的两个电路,它们在电性能上是等价的,可以相互替代。
在分析和设计电路时,我们可以将一个复杂的电路转化为一个简单的等效电路来替代原电路,从而使分析和设计电路变得更容易。
等效电路的基本特点是:
1)等效电路与原电路在端口参数方面具有相同的电学特性。
等效电路的应用主要有以下两个方面:
1)简化电路分析。
将一个复杂的电路转化为等效电路来代替原电路,从而使电路的分析变得更简单和方便。
2)设计和优化电路。
根据等效电路的特性和性能,我们可以对电路进行优化和设计,从而实现电路的更好性能和更高效的运行。
本文简要介绍了戴维南定理、诺顿定理和等效电路的概念和基本原理。
希望读者可以通过学习这些电路定理,更好地掌握电路分析和设计的技能。
戴维南定理与诺顿定理

戴维南定理与诺顿定理
六、实验报告要求:
1、根据测量数据,在同一坐标系中绘制等效
前后的U-I曲线;
2、将理论值与实验测量数据相比较,分析(fēnxī)
产生误差的原因;
3、实验小结。
共十六页
内容(nèiróng)总结
戴维南定理与诺顿定理。戴维南定理与诺顿定理。戴维南定理与诺顿定 理。1、通过验证戴维南定理与诺顿定理,加深对等效概念的理解。2、学 习测量有源二端网络的开路电压和等效内阻的方法。将原网络端口a、b之 间用导线短接,流过导线的电流就是短路电流Isc。戴维南定理和诺顿定理 是一对互为对偶形式的定理。Uoc = Isc ×Ro。1、利用戴维南定理和诺顿定 理分别计算(jìsuàn)该网络的开路电压U’oc、等效电阻R’o和短路电流I’sc
源Is=10mA,接入实验电路,测量该网络(wǎngluò)的
开路电压Uoc、等效内阻Ro和短路电流Isc,分别 填入表2.3.3中。(注:本实验中开路电压Uoc 、等效内阻Ro 的测量均采用直接测量法。)
Uoc(V)
Isc(mA)
R0(Ω)
Uoc/Isc (Ω)
实测值
共十六页
戴维南定理与诺顿定理
2、诺顿定理:
任何(rènhé)一个线性有源二端网络,对外电路来说,总 可以用一个理想电流源和电导并联的有源支路代替,
其中理想电流(diànliú)源的电流(diànliú)值等于原
网络端口的短路电流Isc,电导等于原网络中所有独 立电源为零时的等效电导。
诺顿等效
共十六页
戴维南定理与诺顿定理
戴维南定理和诺顿定理是一对 互为对偶(duì ǒu)形式的定理。对同一 个电路而言,其开路电压Uoc、短 路电流Isc和等效内阻Ro满足下式:
戴维宁定理和诺顿定理

戴维宁定理和诺顿定理戴维南定理(Thevenin’s theorem):含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。
电压源的电压等于单口网络在负载开路时的电压uoc;电阻R0是单口网络内全部独立电源为零值时所得单口网络N0的等效电阻。
戴维南定理(又译为戴维宁定理)又称等效电压源定律,是由法国科学家L·C·戴维南于1883年提出的一个电学定理。
由于早在1853年,亥姆霍兹也提出过本定理,所以又称亥姆霍兹-戴维南...对于含独立源,线性电阻和线性受控源的单口网络(二端网络),都可以用一个电压源与电阻相串联的单口网络(二端网络)来等效,这个电压源的电压,就是此单口网络(二端网络)的开路电压,这个串联电阻就是从此单口网络(二端网络)两端看进去,当网络内部所有独立源均置零以后的等效电阻。
uoc 称为开路电压。
Ro称为戴维南等效电阻。
在电子电路中,当单口网络视为电源时,常称此电阻为输出电阻,常用Ro表示;当单口网络视为负载时,则称之为输入电阻,并常用Ri表示。
电压源uoc 和电阻Ro的串联单口网络,常称为戴维南等效电路。
当单口网络的端口电压和电流采用关联参考方向时,其端口电压电流关系方程可表为:U=R0i+uoc。
戴维南定理和诺顿定理是最常用的电路简化方法。
由于戴维南定理和诺顿定理都是将有源二端网络等效为电源支路,所以统称为等效电源定理或等效发电机定理。
诺顿定理(Norton’s theorem):含独立源的线性电阻单口网络N,就端口特性而言,可以等效为一个电流源和电阻的并联。
电流源的电流等于单口网络从外部短路时的端口电流isc;电阻R0是单口网络内全部独立源为零值时所得网络N0的等效电阻。
诺顿定理与戴维南定理互为对偶的定理。
定理指出,一个含有独立电源线性二端网络N, 就其外部状态而言,可以用一个独立电流源isc 和一个松弛二端网络N0的并联组合来等效。
戴维南定理和诺顿定理

戴维南定理和诺顿定理引言在电路理论中,戴维南定理和诺顿定理都是非常重要的理论。
戴维南定理和诺顿定理是解决电路中相互独立的两个部分联通时的问题,最早于19世纪初被提出。
本文将介绍这两个定理的定义、证明以及应用。
戴维南定理定义戴维南定理是指任何由电阻、电源和电线组成的电路网络,在一对电端子之间的电势差等于这一对电端子在电路网络中所取的任何一条通路的电阻乘以沿此通路的电流的代数和。
证明设电路网络中有一对电端子,其电压为V,电流为I,连接这一对电端子的任意通路电阻为R。
则戴维南定理可以写成如下的方程:V = IR戴维南定理可以很容易地从欧姆定律推导出来。
因为电势差等于电流和电阻的乘积:V = IR应用戴维南定理可以应用于解决电路中的任何问题。
例如,可以使用戴维南定理计算两个点之间的电位差;可以使用戴维南定理计算电路中的总电阻,以及计算电阻的并联和串联等。
诺顿定理定义诺顿定理是指任何由电阻、电流源和电线组成的电路网络,在任意两个电端子之间的电流等于这一对电端子所取的任意一条通路的电流源的代数和和这一对电端子所取的任意一条通路的电阻的倒数之和。
证明设电路网络中有一对电端子,其电流为I,连接这一对电端子的任意通路电阻为R,通路电流源为Is。
则诺顿定理可以写成如下方程式:I = I_s - IR将其化简可得:I_s = IR + I诺顿定理的本质和戴维南定理相同,只是引入了电流源。
应用诺顿定理和戴维南定理可以互相转换。
诺顿定理通常用于求解对称网络中的电路,因为对于这类电路,电压源和电流源的作用是相同的。
戴维南定理和诺顿定理是电路理论中非常基础的两个定理。
熟练掌握这两个定理可以在解决电路问题中起到重要的作用,可以大大简化计算难度。
同时,掌握这两个定理还可以帮助我们更深入地理解电路中电势、电流以及电阻等基本概念。
戴维南定理和诺顿定理

01
பைடு நூலகம்
戴维南定理
任何有源线性二端网络,总可以用一个电压源和一个电阻串联来表示。
电压源的电压等于网络的开路电压,电阻等于网络内部所有独立源为零
时的等效电阻。
02
诺顿定理
任何有源线性二端网络,总可以用一个电流源和一个电阻并联来表示。
电流源的电流等于网络的短路电流,电阻等于网络内部所有独立源为零
时的等效电阻。
交叉学科研究
随着电子工程与其他学科的交叉融合,戴维南定理和诺顿定理可以与其他学科的理论和方法相结合,开 展交叉学科的研究和应用。
THANKS
戴维南定理与诺顿定理在电路分析中的应用选择
选择应用戴维南定理或诺顿定理取决于具体电路的特性和需求。如果需要计算一端口网络的开路电压 或短路电流,则应用戴维南定理;如果需要计算一端口网络的等效电阻或等效电流,则应用诺顿定理 。
在实际应用中,可以根据一端口网络的性质和电路分析的目的选择合适的定理。例如,对于一个无源 一端口网络,如果需要计算其等效电阻,则可以选择应用诺顿定理;对于一个有源一端口网络,如果 需要计算其开路电压或短路电流,则可以选择应用戴维南定理。
诺顿定理
任何一个有源线性二端网络,对其外部电路来说,都可以用一个等效的理想电流 源和电阻并联的电源模型来代替。其中,理想电流源的电流等于有源线性二端网 络的短路电流,电阻等于该网络的开路电压与电流源电流的比值。
戴维南定理和诺顿定理的重要性
简化电路分析
通过应用戴维南定理和诺顿定理,可以将复杂的有源电路简化为简单的电源模型,从而简化电路 分析过程。
电子设备设计
在电子设备设计中,可以利用戴维南定理来计算电路的性能 参数,如电压放大倍数、输入电阻等。
戴维南定理和诺顿定理

戴维南定理和诺顿定理1.戴维南定理一个线性含源一端口网络,对外电路来说,可以用一个电压源和电阻串联的电路等效替换。
电压源电压等于该一端口网络的开路电压uoc;电阻等于一端口网络内部所有独立源置零后的等效电阻Req 。
线性含源网络11′1′1戴维南等效电路u oc+–u oc+–R eq2.诺顿定理一个线性含源一端口网络,对外电路来说,可以用一个电流源和电阻并联的电路等效替换。
电流源电流等于该一端口网络的短路电流isc;电阻等于一端口网络内部所有独立源置零后的等效电阻Req 。
线性含源网络11′诺顿等效电路i scR eq1′1i sc3.定理证明R eq u oc +–线性含源网络支路支路i u +–i线性含源网络u (1)+–线性含源网络)2()1(u u +=oc u =i R eq −=iu (2)+–线性无源网络i R u eq oc −==+R eq iR u eq oc −=u +–i–u +i有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)线性无源网络4.定理应用线性含源网络支路支路线性含源网络u oc :将代求支路断开后的一端口的开路电压。
R eq :将一端口内部独立电源全部置零后所得无源一端口的等效电阻。
u oc +–R eqR eq u oc+–戴维南定理的应用线性无源网络R eq 的计算方法(1)一端口内部不含受控源,电阻串联、并联和Y-∆等效法。
(2)一端口内部含有受控源,电压比电流法:加电压求电流或加电流求电压。
(3)开路电压-短路电流法。
iuR =eq i sc i sc u oc +–scoc eq i u R =eqocR u =线性含源网络R eq u oc+–ii u +–线性无源网络线性含源网络支路支路线性含源网络i sc :将代求支路断开后的一端口的短路电流。
R eq :将一端口内部独立电源全部置零后所得无源一端口的等效电阻。
R eq诺顿定理的应用i scR eq 诺顿等效电路可由戴维南等效电路经电源等效变换得到i scu oc+–sc oceq i u R =惠斯通电桥x eq oc R R u I +=+–u s R 2R 4R 1R 3I R x +–u s 11′R 2R 4R 1R 3R eq u oc+–11′R x I 求戴维南等效电路)(211433s oc -R R R R R R u u ++=4422R R R R R R R R R +++=3311eq 断开R x 支路42423131s 424313sc R R R R R R R R u R R R R R R i ++++−+=)(i sc R 411′R 2R 1R 3。
戴维宁定理和诺顿定理

戴维宁定理和诺顿定理
1 戴维宁定理
戴维宁定理是数学家汤姆森·戴维宁(Thomas Davidet Alain Davie)提出的一个有关不可划分系统的重要概念,是系统理论的基础定理之一。
他的定理强调的是当系统的每个部分处于完整和可更改的状态时,它们将把整个系统从不可再划分进行分割,从而使系统被认为是不可再分割的。
它用来区分一般形式和不可分割形式之间的关系,它的定理是:当一个系统的每一部分是完整的(可更改的)时,它们将把整个系统从不可再划分状态分割出来;但是,如果系统的任意一部分是不可更改的,它将被认为是不可分割的。
戴维宁定理也可用于更改现有系统,可以帮助把它们划分为更加可控制的组件,这有助于在系统推出时获得最佳性能或改善系统稳定性。
2 诺顿定理
诺顿定理是英国数学家约翰·诺顿(John von Neumann)提出的另一个重要定理,在他的重要著作《决策理论》中有精彩的讨论。
他的定理认为,当一个系统的每个部分是完整的,可以控制的,协调的时,它们将使该系统从可再划分变得不可再划分。
诺顿定理也强调了
系统是由可控制的,可调整的组件构成的,而且每个组件可以协调运作以最小化系统的总能耗,同时可以更加有效地运行系统。
诺顿定理也可以帮助系统的设计者更加有效地运用系统的资源,可以更有效地快速解决难题。
它也可以帮助改善和协调系统的性能,同时明确的表示出系统的控制计划。
总之,戴维宁定理和诺顿定理都是系统理论建筑中重要的概念,旨在帮助系统设计者更加有效地理解和利用系统资源,以改善系统性能,可以有效地帮助快速解决系统问题,也可以为系统构建带来一定的帮助。
(整理)戴维南定理和诺顿定理
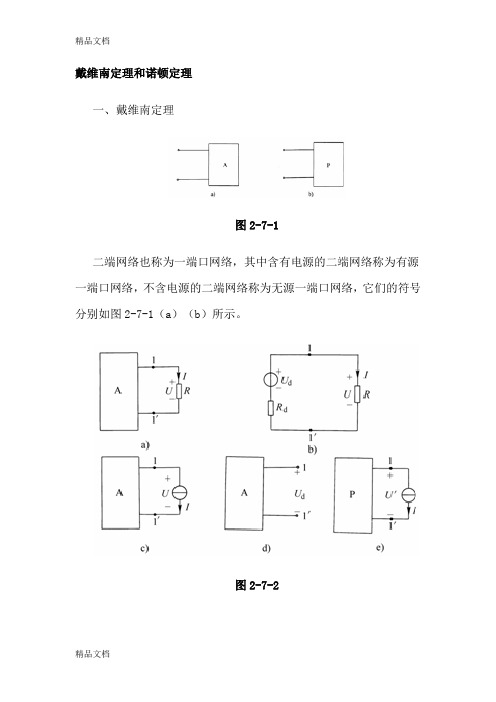
戴维南定理和诺顿定理一、戴维南定理图2-7-1二端网络也称为一端口网络,其中含有电源的二端网络称为有源一端口网络,不含电源的二端网络称为无源一端口网络,它们的符号分别如图2-7-1(a)(b)所示。
图2-7-2任一线性有源一端口网络(如图2-7-2(a)所示)对其余部分而言,可以等效为一个电压源和电阻相串联的电路(如图2-7-2(b)所示),其中的大小等于该有源一端口网络的开路电压,电压源的正极与开路端高电位点对应;等于令该有源一端口网络内所有独立源为零(即电压源短接、电流源开路)后所构成的无源一端口网络的等效电阻。
这就是戴维南定理,也称为等效电源定理;与串联的电路称为戴维南等效电路。
要计算一个线性有源一端口网络的戴维南等效电路,其步骤和方法为:1、计算:利有电路分析方法,计算相应端口的开路电压;2、计算:当线性有源一端口网络A中不含受控源时,令A内所有独立电源为零后得到的无源一端口网络P则为纯电阻网络,利用无源一端口网络的等效变换就可求出端口等效电阻;当线性一端口网络A中含有受控源时,令A内所有独立电源为零后得到的一端口网络P 中仍含有受控源,这时,可采用加压法和开路短路法求。
图2-7-3例2-7-1 利用戴维南定理求图2-7-4(a)所示电路中的电流I 为多少?图2-7-4 例2-7-1附图解:将A、B左边部分电路看作有源一端口网络,用戴维南等效电路替代后如图2-10-4(b)所示。
(1)求:将A、B端口开路,得到图2-10-4(c)所示电路。
由米尔曼公式得:(2)求等效电阻:令A、B以左的三个独立源为零,得到图2-10-4(d)所示电路,则A、B端口的等效电阻为:(3)从图2-10-4(b)中求I:图2-10-5 例2-7-2附图例2-7-2 在图2-7-5(a)所示电路中,已知,,求A、B端口的戴维南等效电路。
解:(1)求:图2-10-5(a)中A、B端口处于开路状态,列写KVL方程:(2)求等效电阻:下面分别用两种方法求解。
戴维南定理及诺顿定理
3
断开待求支 路,求开路 电压U0 ;
求等效电阻 R0 ;
画出戴维南 等效电路, 求出待求量。
1、诺顿定理的描述
任何一个线性的、含源的二端网络对于外部电路而言, 都可以等效为一个电流源模型。 理想电流源电流 Is :为二端网络输出端的短路电流; 内阻R0 :等于该有源二端网络中所有电源移去后得到 的无源网络ab两端之间的等效电阻。
R4
B
U 0 I 2R2 I 4 R4 R2 R4 E E R1 R2 R3 R4 30 20 10 10 20 30 30 20 2 43; C E
Step2 求 等 效 电 阻
_
R2 D
R 00 U
R R33 B
R4
R0
R0 R1 // R2 R3 // R4 20 // 30 30 // 20 24()
(1)当R0=∞的时候,没有戴维南等效电路
(2)当R0=0的时候,没有诺顿等效电路
含授控源电路
3 I I 3
4I
4I
解
10V 10V
U
UO 2
4A 4A
I=4A
UO 4I 3I 10 14V
I 3 I 3 4I
4I
10V
R 0
U
2
I
I5 R5
C
R3 B R4
D
R0
R3
R4
已知: R1=20 , R2=30 R3=30 , R4=20 E=10V
R0 R1 // R2 R3 // R4 24
等效电路
I5 A 10 B
R1
+ _
R2
简述戴维宁定理和诺顿定理的内容

简述戴维宁定理和诺顿定理的内容
1 戴维宁定理
戴维宁定理,又称交叉定理,是线性代数中非常有用的一个定理,它说明了两个给定的矩阵A,B之间存在着如下关系:
$$A \cdot B = B \cdot A$$
该定理表明,乘积AB与乘积BA具有相同的值,也就是说,乘积
AB等于乘积BA,它的意义在于可以方便的推导,便于矩阵的秩的计算。
2 诺顿定理
诺顿定理也称诺比特定理,是一个描述矩阵交换秩的定理。
该定
理告诉我们,如果我们在定义矩阵时不能交换行和列,那么把这种矩
阵看做是确定的;而如果我们可以任意交换行和列,那么这种秩就等
于1。
具体地说,一个n阶矩阵若秩等于一,表示当你任意地把它的行和列互换时,它仍然能够变换成有序行向量或列向量,秩越大,表示
你矩阵在你把行和列任意交换也不能得到一个有序的行向量或者列向量.
总而言之,戴维宁定理可以让我们更好的计算矩阵的乘积,而诺
顿定理则让我们更好的理解矩阵的秩。
这两个定理都在现代线性代数
中占有重要的位置。
[电路分析]戴维南定理和诺顿定理
![[电路分析]戴维南定理和诺顿定理](https://img.taocdn.com/s3/m/299191adfc4ffe473268aba9.png)
戴维南定理和诺顿定理一、戴维南定理出发点:对于一个复杂的含有独立源的电路,如果只要计算某条支路上的电压和电流,那么就可以把电路分解成两个部分,把该条支路作为一个部分,把电路的其余部分作为另一个部分,并用一个含源二端网络 Ns 来表示。
试图找到一个简化的等效电路去替换 Ns ,则该支路上的电压和电流的计算就会简单得多。
1 、戴维南定理图 4.3-1 ( a )中, Ns 是含源二端网络,欲计算电阻 R 的端电压 u 和端电流 i 。
根据替代定理,可以用一个电流为 i 的理想电流源去替代外电路,如图 4.3-1 ( b )所示,替代之后,电路中其他支路上的电压和电流则保持不变。
用叠加定理计算 a 、 b 端钮的电压 u 。
当含源二端网络 Ns 中的独立源单独作用时,外部的电流源 i 应视为开路,这时的电路如图 4.3-1 ( c )所示。
显然,这时的端钮电压就是含源二端网络 Ns 的开路电压。
当外部的电流源 i 单独作用时,把含源二端网络 Ns 中的所有独立源都视为 0 ,这时Ns 中只剩下线性电阻和线性受控源等元件,没有独立源,成为一个无源二端网络,用 N 表示,其电路如图 4.3-1 ( d )所示。
显然,无源二端网络 N 可以等效为一个电阻,这个电阻称为含源二端网络 Ns 的等效内阻用 Ro 表示。
这时电阻的端电压为。
根据叠加定理,得图 4.3-1 ( a )电路中电阻的端电压为戴维南定理(Thevenin's theorem ):对于一个线性的含源二端网络,对外电路而言,它可以用一个理想电压源和一个内阻相串联的支路来等效,这条支路称为戴维南等效支路,又称戴维南模型。
其中,等效电压源的电压为该含源二端网络的开路电压,等效内阻为该含源二端网络中所有独立源都取 0 时的等效电阻。
2 、戴维南模型参数的计算1 、电压的计算先画出含源二端网络 Ns 开路时的电路,然后再计算开路电压。
2 、等效内阻的计算( 1 )如果无源二端网络 N 中没有受控源,可以用电阻网络的等效方法,如电阻的串、并联方法等。
电路中的戴维南定理和诺顿定理

电路中的戴维南定理和诺顿定理在电路中,戴维南定理(Kirchhoff's current law)和诺顿定理(Norton's theorem)这两个定理扮演着重要的角色。
它们是电路分析中的基础理论,能够帮助我们理解和解决各种复杂的电路问题。
首先,我们来看一下戴维南定理。
戴维南定理是由德国物理学家叶夫根·戴维南于19世纪提出的。
该定理表明,在一个节点(连接两个或多个电路元件的交叉点)中,流入该节点的电流之和必须等于流出该节点的电流之和。
从宏观的角度来看,该定理可以解释为电荷守恒定律的特例。
换句话说,电流永远不会在电路中“丢失”,它们必须在节点处平衡。
举例来说,如果我们考虑一个简单的电路,其中有两个电流源和几个电阻。
按照戴维南定理,我们可以在节点处设置一个方程,将流入节点的电流与流出节点的电流相等。
这样,我们就可以通过解这些方程,来计算出电路中各个部分的电流和电压值。
另一方面,诺顿定理是由美国电气工程师佩尔·诺顿在19世纪初提出的。
诺顿定理在某种程度上与戴维南定理有些相似,但它主要用于简化电路的分析。
根据诺顿定理,任何电路都可以用一个电流源和一个等效电阻来代替,这个等效电阻被称为诺顿电阻。
这样,原本复杂的电路可以被简化成一个等效电路。
诺顿定理的一个重要应用是求解电路中的最大功率传输问题。
根据该定理,当电阻负载和源电压固定时,最大功率传输发生在负载电阻等于诺顿电阻的情况下。
这个最大功率可以通过诺顿电流的平方乘以负载电阻得到。
因此,诺顿定理帮助我们确定如何选择负载电阻,以使电路达到最大的功率传输效果。
戴维南定理和诺顿定理在实际电路设计和分析中有着广泛的应用。
无论是在电子设备中,还是在电力系统中,这两个定理都能为我们提供重要的指导。
它们不仅能够帮助我们理解电路中的电流分布和电势差,还能够解决各种电路故障和优化电路性能的问题。
总结起来,戴维南定理和诺顿定理是电路分析中的基础定理,能够帮助我们理解和解决电路中的各种问题。
[电路分析]戴维南定理和诺顿定理
![[电路分析]戴维南定理和诺顿定理](https://img.taocdn.com/s3/m/299191adfc4ffe473268aba9.png)
戴维南定理和诺顿定理一、戴维南定理出发点:对于一个复杂的含有独立源的电路,如果只要计算某条支路上的电压和电流,那么就可以把电路分解成两个部分,把该条支路作为一个部分,把电路的其余部分作为另一个部分,并用一个含源二端网络 Ns 来表示。
试图找到一个简化的等效电路去替换 Ns ,则该支路上的电压和电流的计算就会简单得多。
1 、戴维南定理图 4.3-1 ( a )中, Ns 是含源二端网络,欲计算电阻 R 的端电压 u 和端电流 i 。
根据替代定理,可以用一个电流为 i 的理想电流源去替代外电路,如图 4.3-1 ( b )所示,替代之后,电路中其他支路上的电压和电流则保持不变。
用叠加定理计算 a 、 b 端钮的电压 u 。
当含源二端网络 Ns 中的独立源单独作用时,外部的电流源 i 应视为开路,这时的电路如图 4.3-1 ( c )所示。
显然,这时的端钮电压就是含源二端网络 Ns 的开路电压。
当外部的电流源 i 单独作用时,把含源二端网络 Ns 中的所有独立源都视为 0 ,这时Ns 中只剩下线性电阻和线性受控源等元件,没有独立源,成为一个无源二端网络,用 N 表示,其电路如图 4.3-1 ( d )所示。
显然,无源二端网络 N 可以等效为一个电阻,这个电阻称为含源二端网络 Ns 的等效内阻用 Ro 表示。
这时电阻的端电压为。
根据叠加定理,得图 4.3-1 ( a )电路中电阻的端电压为戴维南定理(Thevenin's theorem ):对于一个线性的含源二端网络,对外电路而言,它可以用一个理想电压源和一个内阻相串联的支路来等效,这条支路称为戴维南等效支路,又称戴维南模型。
其中,等效电压源的电压为该含源二端网络的开路电压,等效内阻为该含源二端网络中所有独立源都取 0 时的等效电阻。
2 、戴维南模型参数的计算1 、电压的计算先画出含源二端网络 Ns 开路时的电路,然后再计算开路电压。
2 、等效内阻的计算( 1 )如果无源二端网络 N 中没有受控源,可以用电阻网络的等效方法,如电阻的串、并联方法等。
戴维南定理、诺顿定理

戴维南定理、诺顿定理戴维南定理和诺顿定理是电路理论中的两个重要定理,它们在电路分析和设计中有着广泛的应用。
本文将分别介绍这两个定理的概念和应用,并探讨它们在电路领域中的重要性。
一、戴维南定理戴维南定理,也称为戴维南-诺顿定理,是电路理论中的基本定理之一。
它是由英国科学家戴维南和诺顿在19世纪末提出的,用于简化复杂电路的分析。
该定理表明,任何一个线性电路都可以用一个电压源和一个串联的电阻模型等效代替。
戴维南定理的核心思想是将电路分为两部分:被测电路和测量电路。
被测电路是指需要分析的电路,而测量电路是指用于测量电路参数的电路。
根据戴维南定理,可以将被测电路的复杂结构简化为一个等效的电压源和串联电阻。
通过戴维南定理,我们可以方便地计算电路中的电流和电压。
例如,在分析直流电路时,可以通过测量电压源的电压和串联电阻的电流,来确定整个电路的特性。
这样,我们可以将复杂的电路问题转化为简单的电路问题,从而更容易解决。
二、诺顿定理诺顿定理,也称为诺顿-戴维南定理,是电路理论中的另一个重要定理。
它与戴维南定理相似,也是用于简化电路分析的工具。
诺顿定理表明,任何一个线性电路都可以用一个电流源和一个并联的电导模型等效代替。
诺顿定理的思想与戴维南定理相似,同样将电路分为被测电路和测量电路。
不同的是,诺顿定理通过一个电流源和并联电导来简化被测电路。
这样,我们可以通过测量电流源的电流和并联电导的电压,来确定整个电路的特性。
诺顿定理的应用同样广泛。
在分析交流电路时,诺顿定理可以帮助我们简化电路结构,从而更方便地计算电流和功率。
通过将复杂的电路分解为简单的电路,我们可以更加精确地预测电路的性能,并进行相应的设计和调整。
三、戴维南定理与诺顿定理的关系戴维南定理和诺顿定理虽然在表述上有所不同,但实质上是等效的。
它们都可以将复杂的电路简化为一个等效的电源和电阻或电流源和电导。
两者的转换关系可以通过一些简单的数学运算实现。
具体而言,戴维南定理可以通过将电流源的电流与串联电阻的阻值相除,得到等效的电压源和串联电阻。
戴维南定理与诺顿定理

戴维南定理与诺顿定理导言:在电路理论中,戴维南定理(Kirchhoff's Current Law)和诺顿定理(Norton's Theorem)是两个非常重要的基本定理。
它们为我们分析和解决电路问题提供了有力的工具。
本文将从理论原理、应用范围以及实际案例等方面介绍戴维南定理与诺顿定理,帮助读者更好地理解和应用这两个定理。
一、戴维南定理1.1 原理戴维南定理,又称作电流守恒定律,是由德国物理学家叶史瓦·戴维南于1845年提出的。
该定理表明,在任何一个电路中,进入某节点的电流之和等于离开该节点的电流之和。
简而言之,电流在节点处守恒。
1.2 应用戴维南定理为我们分析电路提供了一个重要的基本原则。
在实际应用中,我们可以通过应用戴维南定理来简化电路,从而更方便地求解电路中的各种参数。
通过将复杂的电路分解为多个简单的节点,我们可以利用戴维南定理将电路简化为一系列串、并联的电阻,从而求解电流和电压的分布情况。
1.3 例子为了更好地理解戴维南定理的应用,我们来看一个简单的例子。
假设有一个由三个电阻串联而成的电路,电阻分别为R1、R2和R3,电流为I。
根据戴维南定理,我们可以得到以下等式:I = I1 = I2 = I3其中,I1、I2和I3分别表示通过R1、R2和R3的电流。
通过这个等式,我们可以得到I与三个电阻的关系,从而求解电路中的各个参数。
二、诺顿定理2.1 原理诺顿定理是由美国工程师爱德华·诺顿于1926年提出的。
该定理表明,在任何一个电路中,可以通过一个等效的电流源和一个等效的电阻来代替电路中的复杂部分。
这个等效的电流源称为诺顿电流源,等效的电阻称为诺顿电阻。
2.2 应用诺顿定理为我们分析电路提供了一种简化的方法。
通过将电路中的复杂部分转化为一个等效的电流源和电阻,我们可以更方便地计算电路的各种参数。
诺顿定理在电路分析和设计中有着广泛的应用,特别是在大规模集成电路设计和复杂电路的分析中,诺顿定理可以帮助工程师简化电路结构,提高设计的效率。
专题四、戴维南定理与诺顿定理
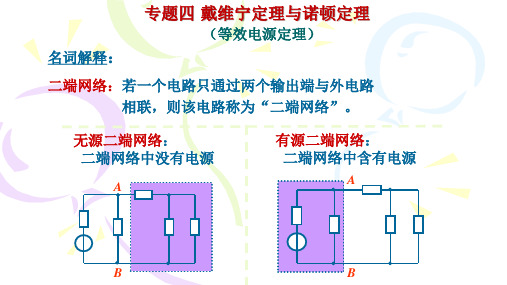
1A
E Uoc 9 V
R 0 57 Ω
R0 57 +
E _ 9V
33
U
第四步:求解未知电压U
R0 57 +
E _ 9V
33 U
U 9 33 3.3 V 57 33
例 4:图示电路中,已知:US1=US2=1V,IS1=1A,IS2=2A, R1=R2=1。用戴维宁定理求A,B两点间的等效电压源。
I =2.83A
U0
3 9 63
3V
R0 6
+ Uoc 9V
–
a +
3 U0 -
b
计算含受控源电路的等效电阻是用外加电源法还是开 路、短路法,要具体问题具体分析,以计算简便为好。
(二) 诺顿定理 概念: 有源二端网络用电流源模型等效。
有源
A
A
二端 网络
=
R0
B
Is
B
等效电阻 R0 仍为相应除源二端网络的等效电阻 等效电流源 Is 为有源二端网络输出端的短路电流
源和内阻 R0 串联的电源来等效代替。
有源 二端 网络
aI
+
U –
RL
b 等效电源
R0 +
E_
aI
+
U
RL
–
b
注意:“等效”是指对端口外等效
即用等效电源替代原来的二端网络后,待求支路(上图是RL) 的电压、电流不变。
有源 A
二端网络
R
B
等效电压源的电动势
(E)等于有源二端
网络的开路电压Uoc;
有源
.
R1
+ US 2
-
R2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、戴维宁定理
+ + E1 E2 – – R3 I1 R1 I2 R2
b 解:3. 画出等效电路求电流I3
a
a I3 R0 + E _ b R3 I3
E 30 I3 2A R0 R3 2 13
例2 R1
I5
R2 R5
等效电路
R3
+ E _
R4
R1
+ _
R2
I5 R5
E
有源 二端 网络
A
B
=
R0 Is B
等效电阻 R0 仍为相应除源二端网络的等效电阻
等效电流源 Is 为有源二端网络输出端的短路电流
例: R1
I5
R2 R5
R4 R1 +
等效电路
R3 +
E _
R3
_ E
R2
I5
R5
R4
已知:R1=20 、 R2=30 R3=30 、 R4=20 E=10V 求:当 R5=10 时,I5=?
戴维宁定理的应用
(1) 开路电压Uoc 的计算 戴维宁等效电路中电压源电压等于将外电路断开时的开路电压Uoc,电 压源方向与所求开路电压方向有关。计算Uoc的方法视电路形式选择前面学过的 任意方法,使易于计算。 (2)等效电阻的计算 等效电阻为将一端口网络内部独立电源全部置零(电压源短路,电流源 开路)后,所得无源二端网络的输入电阻。常用下列方法计算:
D R4 Is
VD 0 R1 20
VC 10 V R2 30
C
VA V B 5 V
VC VA I1 0.25A R1 VA VD I2 0.167A R2
I s I 1 I 2 0 . 083 A
R1 + _
R2
I5 R5
等效电路
E
R3
R3
-
R4
.
B
. .
-
I + - US1 R5
.B
R6 R4
US2
-
为使I=0,必取U0=US1。即:
U0 = R5 R4 U S2 U S2 = U S1 R1 R2 R5 R1 R3 R4
解得:R1=6
戴维南定理解题步骤归纳
(1)将待求支路与原有源二端网络分离,对断开的两个端钮分别标以 记号(如A、B);
R4
0.083A
I5 R0 24
A 10
R5
Is
B
第三步:求解未知电流 I5。
I5
0.083A
R0 24 R5
A 10 B
Is
R0 I5 Is 0.059A R0 R5
例1
求电流I 。 a I 4 sc I b + 10
(2) 求等效电阻Req
2
–
I1
I2
–
a Req
10 2
R3
已知:R1=20 、 R2=30 R3=30 、 R4=20 E=10V
求:当 R5=10 时,I5=?
R4
有源二端 网络
(1)求有源二端网络的开端电压Uoc
(2)求对应无源网络的等效电阻 R0(电 压源短路,电流源开路)
A R1 C R3 B + E R4 _ R2 Uoc R1
步骤: 有源网络 无源网络 外加电压 U 求电流 I
a
R0
a I
R0
+ Us –
+ U – b
Is
U R0 I
b
3 开路电压,短路电流法。
有源 网络
U0c
有源 网络
Is
求 开端电压 Uoc 与 短路电流 Is
等效 内 阻
R0
U oc
Is
2 3
方法更有一般性。
对含有受控源的电路必须采用加压求流法或者是开短路法
24V
+
b
12V
Req =10//2=1.67
(3) 诺顿等效电路: 应用分 流公式 I
解
(1) 求短路电流Isc
I1 =12/2=6A I2=(24+12)/10=3.6A
a 4 b
-9.6A
1.67
Isc=-I1-I2=- 3.6-6=-9.6A
I =2.83A
A
R2 D
D
C R3
B
R0
R4
Uoc UAD UDB R2 R4 E E R1 R 2 R3 R 4 2V
R 0 R1//R 2 R 3//R 4
=20 30 +30 =24
20
画出等效电路
I5
R1
+ _ R2 I5 R5 R4 R0 E + _ R5
E
R3
E2V R 0 24 Ω
有源二 端网络
第一步:求输入电阻R0。
A
R1 + E R3
_
R2
I5 R5
R1 C
R2 D
R0
R4
R3 B
R4
已知: R1=20 , R2=30 R3=30 , R4=20 E=10V
R0 R1 // R2 R3 // R4 24
第二步:求短路电流 Is A
R1
C R3 + _
(2)应用所学过的各种电路求解方法,对有源二端网络求解其开路电 压UOC; (3)把有源二端网络进行除源处理(恒压源短路、恒流源开路),对 无源二端网络求其入端电阻RAB;
(4)让开路电压等于等效电源的US,入端电阻等于等效电源的内阻R0, 则戴维南等效电路求出。此时再将断开的待求支路接上,最后根据欧 姆定律或分压、分流关系求出电路的待求响应。
A、B
R2 R1//R3 R2//R4 + E D
D
R4
E
B 有源二端网络
R5
C Is
VA=VB Is =0 ?
已知: R1=20 、 R2=30 R3=30 、 R4=20 E=10V
VD 0
VC 10 V
VA VB 5 V
I1 A
R1 + R3 B
I2
_ E
R2
5
R0
R 0 50 4//4 5 57
D
4 + 8V _ E 50
C
+
A
10V RL
5 33
第三步:画出等效电路
U
4
B
1A
E Uoc 9 V
R 0 57 Ω
R0 E
57 + _ 9V
33
U
第四步:求解未知电压U
R0 E
57 + _ 9V
33
U
D 4 + 8V _ E 50 4 5 B C _ + 10V A
Uoc
1A
Uoc U AC UCD U DE U EB 10 0 4 5 9V
D
C_ 50
+
A Uoc
第二步:
求输入电阻 R0。
4 + 8V _ E
10V 5 B 1A
4
50
4
4
1 当网络内部不含有受控源时可采用电阻串并联和△-Y 互换的方法计
算等效电阻;
A R1 C R3 R2 D B A R5 R3 R4 R0
对应 无源 网络
R0
R0 R1 // R2 R3 // R4
R1 C
R2 D R4 R0
不能用简单 串/并联 方法 求解, 怎么办?
B
2 外加电源法(加压求流或加流求压)。
(3)画出等效电路,求未知电流I5
I5
R0 E +
_ R5
R5 10 时
2 I5 R 0 R 5 24 10 0.059 A E
E = Uoc = 2V R0=24
Байду номын сангаас3
D
4 + 8V _ E 50 4
C _
+
10V
A
RL
5 33 B 1A
U
求:U=?
第一步:求开端电压Uoc。
例
求U0 。
6 – 6I + a I + 3 b a U0 –
– 6I + a I
6
+ 9V 3
+
9V – 3
+
3 Uoc –
–
b
解
(1) 求开路电压Uoc
Uoc=6I+3I
+
U0
I=9/9=1A Uoc=9V
(2) 求等效电阻R0 方法1:加压求流
R0 Uoc + –
3 b
-
6 3
换为较简单的含源支路(电压源与电阻串联或电流源与电阻并联支路), 使分析
和计算简化。戴维宁定理和诺顿定理正是给出了等效含源支路的计算方法。 4 6 Rx a I b 10V 6 4 计算Rx分别为1.2、 5.2时的I I
a
Rx
+
–
R0 + E – b
无源 二端 网络
a
a R b + _E a
9 U 33 3.3 V 57 33
例 4:图示电路中,已知:US1=US2=1V,IS1=1A,IS2=2A, R1=R2=1。用戴维宁定理求A,B两点间的等效电压源。
.
-
U S1 + R1
A
B
.
R2 IS2
IS1
.
