奥林匹克训练题库·数值代入法
中国数学奥林匹克赛前培训练习4

中国数学奥林匹克赛前培训练习41. 设n 是大于1的整数,记,1,,1,0,2sin 2cos -=+=n k n k i n k k ππξ 试求下式的最简表示:∏-≤<≤-112.)(n k j k j ξξ2. 证明:如果+=∈=∑Z n k a ni k i ,,11, 则nk ni k k in i i n n a a )(1111+≥+∏∑=-= 3. 如果正整数n 的所有正因数(包括本身)之和为2n ,则称n 为完全数。
如6的正因数之和1 + 2 + 3 + 6 = 2×6,故6为完全数。
证明:不存在形如p a q b r c 的完全数,其中a , b , c 为正整数,p , q , r 为奇质数。
4.设f (x )是整系数多项式,并且f (x )=1有整数根,约定将所有满足上述条件的f 的组成的集合记为F 。
对于任意给定的整数k > 1,求最小的整数m (k ) > 1,要求能保证存在f ∈F ,使得f (x ) = m (k )恰有k 个不相同的整数根。
5.一次体育比赛共设有()2 2n n ≥个项目,每个选手恰好报名参加其中的两个项目,而任两个人都至多有一个相同的项目,假定对于每个{}1,2,,1k n ∈-,不超过k 人报名的项目少于k 个.证明:存在2n 个选手,使得每个项目都恰好有其中的两人参加.1、 设n 是大于1的整数,记w k = cos2k πn + i sin 2k πn,k = 0, 1, 2, …, n -1,试求下式的最简表示:∏1≤j < k ≤n -1(w j -w k )2 。
解:设f (x ) = ∏h = 1n -1(x -εh ) = x n -1 + x n -2 + … + x + 1,则 ∏h = 1n -1(1-εh ) = 1 + 1 + … + 1 + 1 (n 个1) = n∏h = 1n -1(εj -εj + h ) = ∏h = 1n -1εj (1-εh ) =n εj n -1,∏1≤j ≠k ≤n -1(εj -εk ) =n n -1(π ε j )n -1∏j = 1n -1 ( ε j -1)= n n -1(-1)n -1(-1)n -1n= n n -2 故∏1≤j < k ≤n -1(εj -εk )2= (-1)(n -1)(n -2)2·∏1≤j ≠k ≤n -1(εj -εk) = (-1)(n -1)(n -2)2·n n -2。
奥林匹克数学训练题集 pdf

1.已知一张桌子的价钱是一把椅子的10倍,又知一张桌子比一把椅子多288元,一张桌子和一把椅子各多少元?2. 3箱苹果重45千克。
一箱梨比一箱苹果多5千克,3箱梨重多少千克?3. 甲乙二人从两地同时相对而行,经过4小时,在距离中点4千米处相遇。
甲比乙速度快,甲每小时比乙快多少千米?4. 李军和张强付同样多的钱买了同一种铅笔,李军要了13支,张强要了7支,李军又给张强0.6元钱。
每支铅笔多少钱?5.甲乙两辆客车上午8时同时从两个车站出发,相向而行,经过一段时间,两车同时到达一条河的两岸。
由于河上的桥正在维修,车辆禁止通行,两车需交换乘客,然后按原路返回各自出发的车站,到站时已是下午2点。
甲车每小时行40千米,乙车每小时行45千米,两地相距多少千米?(交换乘客的时间略去不计)6. 学校组织两个课外兴趣小组去郊外活动。
第一小组每小时走4.5千米,第二小组每小时行3.5千米。
两组同时出发1小时后,第一小组停下来参观一个果园,用了1小时,再去追第二小组。
多长时间能追上第二小组?7. 有甲乙两个仓库,每个仓库平均储存粮食32.5吨。
甲仓的存粮吨数比乙仓的4倍少5吨,甲、乙两仓各储存粮食多少吨?8. 甲、乙两队共同修一条长400米的公路,甲队从东往西修4天,乙队从西往东修5天,正好修完,甲队比乙队每天多修10米。
甲、乙两队每天共修多少米?9. 学校买来6张桌子和5把椅子共付455元,已知每张桌子比每把椅子贵30元,桌子和椅子的单价各是多少元?10. 一列火车和一列慢车,同时分别从甲乙两地相对开出。
快车每小时行75千米,慢车每小时行65千米,相遇时快车比慢车多行了40千米,甲乙两地相距多少千米?11. 某玻璃厂托运玻璃250箱,合同规定每箱运费20元,如果损坏一箱,不但不付运费还要赔偿100元。
运后结算时,共付运费4400元。
托运中损坏了多少箱玻璃?12. 五年级一中队和二中队要到距学校20千米的地方去春游。
第一中队步行每小时行4千米,第二中队骑自行车,每小时行12千米。
奥林匹克数的技巧中篇

奥林匹克数学的技巧(中篇)2-7-8配配的形式是多的,有数字的凑整配或共配,有分析式的称配或整体配,有子集与其集的配,也有会集象与原象的配。
凡此各样,都体了数学和美的追求与力量,小高斯乞降(1+2+ ⋯ +99+100 )首了配,IMO 16 3也用到了配。
502例 2-143求n 0305n [] 之。
502解作配理n 0[ 305n ]503251n 1([ 305n ][ 305(503n) ])251 304 503304 251 76304 503503n 1503例 2-144乞降a n C n12C n2⋯kC n k⋯ nC n n解一由 C n k C n n k把 a n倒排,有 a n0C n01C n12C n2⋯ kC n k⋯nC n n a n nC n n(n 1)C n n 1⋯ (n k )C n n k⋯ 0C n n相加2a n n(C n0C n1⋯ C n n ) n? 2n得a n n ?2n 1解二会集S1,2, ⋯, n,注意到k⋯kC n A , k1,2,, nA S , A k有 a nA SA了求得A SA把每一A S ,它与集 A 配,共有2n1,且每中均有 A A n于是 a nA SA n n ⋯ n n ? 2n 1两种解法形式上有不一样,但本上是完整一的,有一个解法例2-149。
例 2-145x1, x2 ,⋯, x n是定的数,明存在数x 使得x x1x x2⋯x x n n1 2里的y表示 y 的小数部分。
明有y y1,y Z知 y y10,y Z下边利用一配式的。
f i x i x1x1x2x i x nnC n 2n(n 1)f i( x ix jx j x i )1 i 11 i j n1 i j n2 据抽屉原理①知,必存在k(1 k n) ,使 f1 C2 n 1kn n2取 xx k ,由上式得x x 1x x 2⋯x n1x n22-7-9 特别化特别化表现了以退求进的思想:从一般退到特别,从复杂退到简单,从抽象退到详尽,从整体退到部分,从较强的结论退到较弱的结论,从高维退到低维,退到保持特色的最简单状况、退到最小独立完整系的状况,先解决特别性,再归纳、联想、发现一般性。
数学奥林匹克高中训练题(20)及答案

数学奥林匹克高中训练题(20)第一试一、选择题(本题满分 36分,每小题6分)x — a1.(训练题25)已知函数y 的反函数的图象关于点(-1,3)成中心对称图形,则实数 a 等于x-a -1(A ).(A ) 2 (B )3(C )-2(D )-4,5 I222.(训练题25)我们把离心率等于黄金比 丄二的椭圆称之为“优美椭圆”.设二•爲=1(a > b >2a 2b 20)为优美椭圆,F, A 分别是它的左焦点和右端点,B 是它的短轴的一个端点,贝y ■ ABF 等于(C ).复数一定是(C ).Z 26.(训练题25)在集合M 二{1,2,3,)11,10}的所有子集中,有这样一族不同的子集,不是空集,那么这族子集最多有(B ). (A ) 210 个(B ) 29 个(C )102 个(D ) 92 个(A) 60o(B)75°(C)90o(D)120°3.(训练题25)已知 ABC 三边的长分别是a,b,c , 复数Z i ,Z 2满足 Z i =a, Z 2 =b,乙+ z 2 = c ,那么(A )是实数(B)是虚数(C)不是实数(D) 不是纯虚数4.(训练题25)函数 f (X)二 1(-厂卩:21 c2 c 2CE 的最大值是(D ). (A) 20(B)10(C)-10(D)-205 .(训练题 25)以O 为球心,4为半径的球与三条相互平行的直线分别切于A,B,C 三点.已知S.BOC = 4 ,S ABC 16,则• ABC 等于(B).Ji(A)—12(B)5■: 7■:12(C)12(D)11- 12它们两两的交集都二、填空题(本题满分54分,每小题9分)1.(训练题25)在直角坐标系中,一直角三角形的两条直角边分别平行于两坐标轴,且两直角边上的中3线所在直线方程分别是 v =3x • 1和v = mx • 2,则实数m 的值是3或124x2 •(训练题25)设f (x ) J (a .0,a ") , [m]表示不超过实数m 的最大整数,则函数1+a x1 1[f (x ) ] [f (-x )]的值域是 ___________ {-1,0} ________ •2 2 ------------------------------3 •(训练题25)设a, b,c 是直角三角形的三条边长,c 为斜边长,那么使不等式a 2 (bc ) b 2 (c a ) c 2 (a • b ) _ kabc 对所有直角三角形都成立的 k 的最大值是2 3 r 2•4.(训练题25)如图,正三棱柱 ABC -ABG 的各条棱长都是1,截面BCD 1 在棱AA 上的交点为D ,设这个截面与底面ABC 和三个侧面ABB 1A 1,BCC 1B 1,CAAC 1所成的二面角依次为:「,:七,〉,若 c o :s^ c o 2s-c 3o S,则截面的面积等于 —3乜 _______________85.(训练题25)已知f (x )是定义域在实数集的函数,且f (X • 2)[1 - f (X )] =1 • f (x )•若f (1) =2,,3 , 则 f (1949)的值是 ___________ p 3 - 2 .6.(训练题25)设x 1是方程.3sin x 「3cosx = 2a 「1的最大负根,x 2是方程2cos 2x 「2sin 2x = a 的最小正根,那么,使不等式为Ex?成立的实数a 的取值范围是 ________ - -43^a^~或 a= 2 __________.2第二试一、 (训练题25)(本题满分25分)某眼镜车间接到一任务,需要加工 6000个A 型零件和2000个B 型 零件,这个车间有 214名工人,他们每一个人加工 5个A 型零件的时间可加工 3个B 型零件•将这些 人分成两组同时工作,每组加工同一型号的零件,为了在最短的时间完成,应怎样分组? 77二、 (训练题25)(本题满分25分)已知一个四边形的各边长都是整数, 并且任意一边的长都能整除其余三边之和.求证:这个四边形必有两边相等.B 1B(训练题25)(本题满分35 分)实数数列a1, a2, |a3, ,a M足a P 帕弋钏帕996—為97=1997若数列{0}满足:b k = ai+:+川%(k =1,2川1997).求bf —b2 + b2 —…+0 996-匕997的最大可能值.四、(训练题25)(本题满分35分)给定两个七棱锥,它们有公共的底面A,A2A3A4A5A6A7,顶点R,P2在底面的两侧•现将下述线段中的每一条染红,蓝两色之一:R,P2,底面上的所有的对角线和所有的侧棱.求证:图中心存在一个同色三角形.。
数学奥林匹克高中训练题(27)及答案.doc

数学奥林匹克高中训练题(27)第一试一、选择题(本题满分36分,每小题6分)1.(训练题57)若()f x 是R 上的减函数,且()f x 图像经过点(0,3)A 和点(3,1)B -,则不等式(1)12f x +-<的解集为(D).(A)(,3)-∞ (B)(,2)-∞ (C)(0,3) (D) (1,2)- 2.(训练题57)若函数2()sin 2(2)cos 2f x a x a x =+-的图像关于直线8x π=-对称,则a 的值等于(C).或 (B)1或1- (C)1或2- (D)1-或23.(训练题57)设椭圆的方程为221,(0,1)3x y A +=-为短轴的一个端点,,M N 为椭圆上相异两点,若总存在以MN 为底边的等腰AMN ∆,则直线MN 的斜率k 的取值范围是(C).(A)(1,0]- (B)[0,1] (C)(1,1)- (D)[1,1]-4.(训练题57)()f x 是定义在R 上的函数,且对任意的x 满足(1)()f x f x +=-.已知当(2,3]x ∈时,()f x x =.那么,当(2,0]x ∈-时,()f x 的表达式为(C).(A)()4f x x =+ (B)4,(2,1]()2,(1,0]x x f x x x +∈--⎧=⎨-+∈-⎩(C)4,(2,1]()3,(1,0]x x f x x x +∈--⎧=⎨--∈-⎩ (D)1,(2,1]()3,(1,0]x x f x x x --∈--⎧=⎨--∈-⎩5.(训练题57)已知1111ABCD A B C D -是边长为1的正方体,P 为线段1AB 上的动点,Q 为底面ABCD 上动点.则1PC PQ +的最小值为(A).(A)12+(C)2 (D)122+ 6.(训练题57)已知在数列{}n a 中,11,n a S =为前n 项的和,且满足2(1,2,)n n S n a n ==.则n a 的表达式为(D).(A)1(2)2n n ≥+ (B)1(3)(1)n n n ≥- (C)1(4)2(1)n n ≥+ (D)2(1)n n + 二、填空题(本题满分54分,每小题9分) 1.(训练题57)在ABC ∆中,AD BC ⊥于D ,且13AD BC =.则AC ABAB AC+2.(训练题57)已知函数1a xy x a -=--的反函数图像关于点(1,4)-成中心对称.则实数a 的值 3.3.(训练题57)集合11{|(1)},{|}22A x a xB x x =>+=-<,当A B ⊆时,a 的取值范4.(训练题57)已知线段//AD 平面α,且到平面α的距离等于8,点B 是平面α内的一动点,且满足10AB =.若21AD =,则点D 与B 距离的最小值为 17 .5.(训练题57)已知多项式21x x --整除多项式541ax bx ++.则实数a = 3 ,b5-. 6.(训练题57)设[2002]S =++++,其中的最大整数。
六年级奥林匹克数学基础教程 20 数值代入法

小学数学奥数基础教程数值代入法有一些看起来缺少条件的题目,按常规解法似乎无法求解,但是仔细分析发现,题中只涉及几个存在着倍数或比例关系的数量,而题目中缺少的条件,对于答案并无影响,这时就可以采用“数值代入法”,即对于题目中“缺少”的条件,假设一个数代入进去(当然假设的这个数应尽量方便计算),然后求出解答。
例1足球赛门票15元一张,降价后观众增加一倍,收入增加五分之一。
问:一张门票降价多少元?分析与解:初看似乎缺少观众人数这个条件,实际上观众人数与答案无关。
因为降价前后观众人数存在倍数关系,收入也存在比例关系,所以可以使用数值代入法。
我们随意假设观众人数,为了方便,假设原来只有一个观众。
,则降价后每张票价为9元,每张票降价15-9=6(元)。
例2 某幼儿园中班的小朋友平均身高115厘米,其中男孩人数比女孩人分析与解:题中没有男、女孩的人数,我们可以假设女孩有5人,则男孩有6人。
这时总身高为:115×(5+6)=1265(厘米)。
例3 甲、乙分别由A,B两地同时出发,甲、乙两人步行的速度比是7∶5。
如果相向而行,那么0.5时后相遇;如果按从A到B的方向同向而行,那么甲追上乙需要多少小时?分析与解:设甲、乙的速度分别为7千米/时和5千米/时,则A,B两地相距(7+5)×0.5=6(千米)。
同向而行,甲追上乙需要65÷(7—5)=3(时)。
需要说明的是,A,B两地的距离并不一定是6千米,6千米是根据假设甲、乙的速度分别为7千米/时和5千米/时而计算出来的。
假设不同的速度,会得出不同的距离,因为假设的速度与计算出的距离成正比,所求的时间是“距离÷速度差”,所以不影响结论的正确性。
例4五年级三个班的人数相等,一班的男生人数与二班女生人数相等,三几?分析:由“三个班人数相等,一班男生数与二班女生数相等”知,一班女生数等于二班男生数,因此一、二班男生人数的和以及一、二班女生人数的和给三班的男生人数设一个具体数值,那么就可依次求出全部男生人数以及一、二班男生人数的和(即每班人数),问题就迎刃而解了。
数学奥林匹克高中训练题(01)及答案.doc

数学奥林匹克高中训练题(01)第一试一、选择题(本题满分30分,每小题6分) 1.(训练题06)设211)(xx x f +=,对任意自然数n ,定义))(()(11x f f x f n n =+,则)(1993x f 的解析式为(C).(A)211993xx + (B)21993xx + (D)2199311993xx +2.(训练题06)若1532>==zy x ,则z y x 5,3,2从小到大的顺序是(A).(A)z x y 523<< (B)y x z 325<< (C)z y x 532<< (D)x y y 235<< 3.(训练题06)自然数q p n m ,,,满足等式2222q p n m +=+,则q p n m +++(B).(A)是质数 (B)是合数 (C)可能是质数,也可能是合数 (D)既不是质数,也不是合数 4.(训练题06)一圆台的上底半径为cm 1,下底半径为cm 2,母线AB 为cm 4,现有一蚂蚁从下底面圆周的A 点,绕圆台侧面(即要求与圆台的每条母线均相交)向上底面圆周的B 点爬行的最短路线是 (A).(A)3234π+(B)3434π+ (C)3232π+ (D)3432π+ 5.(训练题06)若复数z 的共轭复数是z ,且1=z 又)1,0(),0,1(-=-=B A 为定点,则函数))(1()(i z z x f -+=取最大值时在复平面上以B A Z ,,三点为顶点的图形是(C).(A)等边三角形 (B)直角三角形 (C)等腰直角三角形 (D)等腰三角形6.(训练题06)若ABC ∆是钝角三角形,则)arccos(sin)arccos(sin )arccos(sin C B A ++的值域是(C).(A)(0,]2π(B)}2{π (C)3(,)22ππ (D)3(0,)2π二、填空题(本题满分30分,每小题5分)1.(训练题06)满足不等式log log x x yy xy ≥的点),(y x 的集合是{(,)|1}{(,)|01}x y x y x x y x y x >><<<且且.2.(训练题06)一个圆锥和一个圆柱,下底面在同一平面上,它们有公共的内切球,记圆锥的体积为1V ,圆柱的体积为2V ,且21kV V =,则k 的最小值是43.3.(训练题06)一个三位自然数321a a a 称为凹数,如果同时有2321,a a a a >>(例如849,525,104都是凹数而200,684,123都不是凹数),则所有的凹数的个数是 285 .4.(训练题06)如图,已知椭圆221,,,2x y DA AB CB AB +=⊥⊥2,23==CB DA ,动点P 在AB 上移动,则PCD ∆是45.(训练题06)四次方程038420234=++-kx x x 的四个根当中的两个的积是24,则k 的值是 140 . 6.(训练题06)四个正数之和为4,平方和为8,则这四个数中最大的那个数的最大值是 1+ 三、(训练题06)(本题满分20分)n a a a a 321,,是互不相等的自然数,证明:+++++)(7737271n a a a a ≥++++)(5535251n a a a a 333321232()n a a a a ++++.四、(训练题06)(本题满分20分)设M P ,分别在正方形ABCD 的边CD BC ,上,PM 与以AB 为半径的圆相切,线段PA 与MA 分别交对角线BD 于N Q ,,证明:五边形PQNMC 内接于圆.五、(训练题06)(本题满分20分)100个火柴盒,标号为1至100.我们可以问其中任15个盒子总共含有的火柴为奇数或偶数,至少要问几才能确定1号盒子里的火柴数的奇偶性. (3个问题)第二试一、(训练题06)(本题满分35分)右图中CDE BCD ABC ∆∆∆,,都是正三角形,线段FG ∥BA ,连EF DG ,相交于O ,连CO 并延长与AB 的延长线相交于P ,证明:D二、(训练题06)(本题满分35分)假定10321,,a a a a 和10321,,b b b b 都是由不相等的复数所组成的序列,已知对10,,2,1 =i 均有1210()()()100i i i a b a b a b +⋅+⋅⋅+=.证明:对任何10,,2,1 =j ,乘积1210()()()j j j b a b a b a +++都等于同一常数,并求出此常数.三、(训练题06)(本题满分35分)证明任意28个介于104和208之间(包括104和208)的不同的正整数,其中必有两个数不互素(即此二数的最大公约数大于1).。
奥林匹克训练题库_数值代入法

■说明:北师大东莞石竹附属学校2008—2009学年度第二学期初中毕业班第一次模拟考试卷时间:120分钟感;遥望大海, ;仰望蓝天,懂得品味这些快乐的人,自然会得到快乐的青睐。
万世c ogsmg (),悲欢岁月,满分120分痛苦难免,可是,懂得寻找快乐的人,快乐的旋律总会在他的心头回响。
要相信,仰起1 .全卷共4页。
满分120分,考试用时2. 答卷前,考生必须将自己的姓名、年级、 的指定位置上;3. 答题可用黑色或蓝色字迹的钢笔或签字笔按各题要求写在答卷上,不能用铅笔和红色字 迹的笔;若要修改, 不准使用涂改液。
120分钟。
班级、考场、座次按要求填在答卷密封线左边把要修改的答案划上横线,在旁边有空位的地方写上修改后的答案。
一、基础(28分) (10 分) 0 :1.根据课文默写古诗文。
'(1)几处早莺争暖树, '(2)求之不得, __________________ 。
:(3)杜牧的《泊秦淮》中表现诗人对国事危迫,朝廷上下却依然醉生梦死的深重忧虑 ;的诗句: * (4)分) ,(5) 头,就有蓝天!3. 根据拼音写出文段括号处应填入的词语。
(2分) b ol Cn ( ) c mgsog ()4.联系上下文,仿照划波浪线的句子在横线处补充恰当的词句。
(2分)遥望大海, _____________________________________________ ; 仰望蓝天, _____________________________________________ 。
5.使用下面词语,另写一段连贯的话,至少用上其中两个。
(3分)广袤无垠 沁人心脾 感人肺腑 青睐 回响 品味答:。
(白居易《钱塘湖春行》)(1分) ,辗转反侧。
(《关雎》)(1分) _________ 。
(2 分) 。
朔气传金柝,寒光照铁衣。
(《木兰诗》) 把孟浩然《过故人庄》默写完整。
(4分) 故人具鸡黍,邀我至田家。
六年级奥赛 第29讲 数值代入法和枚举法

第29讲数值代入法和枚举法
1、从自然数1~100中,每次取出2个不同的自然数相加,使其和大于100,共有多少种不同的取法?
2、把六个字母A、A、E、E、F、F排成一行,使相同的字母不相邻,并且自左至右前三个字母各不相同,这样的排法有几种?
3、由数字1、2、3、
4、6、7,共可组成多少个没有重复数字的四位数?
4、从3、
5、7、13、17、19这六个数中,每次取两个数组成真分数,这样的真分数有多少个?
5、黑板上有5和7两个数,现在规定:将黑板上任意两个数相加的和写在黑板上。
问:经过若干次操作后,黑板上能否出现23 ?
6、将3个相同的小球放入A、B、C三个盒子中,共有多少种不同的放法?
7、书架上有6本不同的画报和10本不同的故事书,请你每次从书架上取出一本画报和一本故事书,共有多少种不同的取法?
8、如图,从上往下,沿线读出“我们爱好学数学”,一共有多少种不同的读法?
9、4枚硬币都是国徽一面朝上放着,每次同时将其中3枚硬币翻面,至少要翻
几次才能把所有的硬币都翻成另一面?
10、有一列数,第一个数是1949,第二个数是2011,从第三个数起,每个数是
它前面两个数的平均数的整数部分。
问:这列数的第100个数是多少?
答案:
1、99+97+95+93+……+1=2500(种)
2、8×3=24(种)
3、6×5×4×3=360(个)
4、1+2+3+4+5=15(个)
5、不能。
因为5a+7b≠23
6、10种
7、6×10=60(种)8、20种
9、至少4次
(1)(2) (3)
(4)
10、1989。
数学奥林匹克高中训练题(19)及答案

数学奥林匹克高中训练题(19)第一试、选择题(本题满分 36分,每小题6分) 1.(训练题 24)对于每一对实数x,y ,函数f 满足方程f (x • y)「f (x)「f (y) -T xy ,且fl 仁•那么,f(n) =n(n =1)的整数n 的个数共有(B)个. (B)1 (C)2 (D) (A)0 2 .(训练题24)有六个座位连成一排,三人就座,恰有两个空位相邻的排法种数为 (A)72 (B)96 (C) 48 (D) 3 .(训练题24)在一次体育比赛中,红白两队各有 5名队员参加,比赛记分办法是: 几名就为本队得几分,且每个队员的得分均不同,得分少的队获胜,则可能获胜的分数是 3 (A).以上都不对队员在比赛中获第(C).27 (A)29 (B)28 4.(训练题24)现有下面四个命题: ① 底面是正多边形,其余各面都是等腰三角形的棱锥是正棱锥. ② 底面是正三角形,相临两侧面所成二面角都相等的三棱锥是正三棱锥. ③ 有两个面互相平行,其余四个面都是全等的等腰梯形的六面体是正四棱台. ④ 有两个面互相平行,其余各个面是平行四边形的多面体是棱柱. 其中,正确的命题的个数是 (A) 3 (B) (D). 2 (C) (C) (D) (D) 13 5.(训练题24)设f : N > N , 且对所有正整数 有 f(n 1) f(n), f( f( rj) 3n .f (1997)的值为(C). (A)1997 (B)1268 (C)3804 (D)5991-训练题24唱爲:;胯豐 的解(x, y)共有(B)组. (A)4 二、填空题 (B)2 (C)1 (D) (本题满分 54分,每小题9分) 1.(训练题 24)数列{a n }的前 14 项是 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, 33,34, 35, 38,….按此规律,则2.(训练题24)函数f (x)二(長- ~^)( J x T + r 1——)丄的值域是v xJ x —1 x(0,1)3.(训练题24)方程x^1 x ; /I 2 x.二 1 远的解是—2 ■ 36 714.(训练题24)若方程x2(^2i)x 3m -i =0(m R)有一实根、一虚根,则此虚根是2i—25 .(训练题24)平面上有四点A, B, C, D,其中代B为定点,且AB = J3,C, D为动点,且AD DC =|BCT ,记S咎BD=T为也BCD的面积.贝U S2+T2的取值范围是2、「3 -3 2 2 7S2T2:4 811 1 16.(训练题24)使不等式——- - a-1995—对一切自然数n都成立的最小自然数n+1 n+2 2n+1 3a 是1997 ______ .第二试2 2一、(训练题24)(本题满分25分)已知F1, F2是椭圆笃=1(a b 0)的左、右焦点,c为半焦距,a b弦AB过焦点F2•求■ F1AB的面积的最大值.n、(训练题24)(本题满分25分)若X j・0,二人=1, x, x-i, n,求证:三、(训练题24)(本题满分35分)已知ABC是等腰三角形,AB=AC,CD是腰AB上的高线,CD1的中点为M,AE _ BM于E, AF _CE于F •求证:AF _丄AB .3四、(训练题24)(本题满分35分)46个国家派代表队参加一次国际竞赛,比赛共4个题,结果统计如下:做对第一题的选手235人,做对第一、二的选手59人,做对第一、三的选手29人,做对第一、四的选手15人,全做对的3人•存在这样的选手,他做对了前三题,但没有做对第四题•求证:存在一个国家,这个国家派的选手中至少有4个人,他们只做对了第一题.。
数学奥林匹克高中训练题134

数学奥林匹克高中训练题(134)第一试一、填空题(每小题8分,共64分) 1.以正十二边形的顶点作为三角形的顶点,可构成锐角三角形和钝角三角形共计__________个.2.设多项式()f x 满足()2213(1)101132f x f x x x ++-=++.则()f x =__________. 3.30!末尾最后一个不为零的数字为__________.4.F 是椭圆2211612x y +=的右焦点,P 是椭圆上的动点.对于定点(22A PA PF =-+,的最小值是__________.5.设44sin cos 1(0)a b a b a bθθ+=>+、.则8833sin cos a bθθ+=__________.6.四面体ABCD 中,有一条棱长为3,其余的五条棱长都为2.则其外接球的半径为__________.7.若在任何n 个连续的正整数中,必存在一数,其各位数字之和是7的倍数,则最小的n =__________.8.正实数集合X 满足:x X ∈当且仅当{}2x x +为整数(其中,{}x 表示x 的小数部分).将X 中各数按严格递增顺序排列,则前100项之和是__________. 二、解答题(共56分) 9.(16分)给定一个四面体,若存在一个侧面(其所在平面为α),使得在将其余三个侧面分别绕其位于平面仅上的边向体外方向旋转至平面α上时,四个侧面在平面α共同组成的图形恰好是一个三角形,则称该四面体是一个“平展四面体”.若有一个平展四面体,它的一个侧面的三边长为a b c 、、,试确定a b c 、、的关系,并求该四面体的体积(用a b c 、、表示). 10.(20分)P 是椭圆22221(0)x y a b a b+=>>上的任意一定点,以P 为圆心作一个圆,与椭圆的长轴AB 交于点M N 、,设P M P N 、分别交椭圆于点E F 、.证明:直线EF 的斜率为定值.11.(20分)给定两个数列,满足{}01113n a a a ==,∶,21164()n n n a a n a ++-+=∈N ;{}01n b b =∶,19)n n b b n +=∈N .证明:对任意的n ∈N ,n n a b +可表为两个正整数的平方和.加试一、(40分)如图1,四边形ABCD 内接于圆,E 是弧 CD 上的任意一点,点D 关于边BC CA AB 、、的对称点分别为123D D D 、、,联结1ED 、2ED 、3ED 分别交BC CA AB 、、所在直线于点1E 、2E 、3E .证明:图1D 1D 2D 3E 3E 1ABC DE E 2(1)1D 、2D 、3D 三点共线; (2)1E 、2E 、3E 三点共线. 二、(40分)证明:满足不等式122001012200x x x +++>--- 的实数x 的集合E 可以表为一些互不相交的开区间之并,试求出这些区间长度的总和. 三、(50分)一个正整数若不含大于1的平方因子,则称此数是“单纯的”.试确定在1,2,⋯,2 010中,共有多少个数是单纯的?四、(50分)对于集合{1222}n M n = ,,,,()n +∈N ,若存在两个数列 1212()()n n A a a a B b b b == ,,,,,,,满足(i ){}|12k k a b k n Mn == ,,,,, (ii )(12)k k a b k k n -== ,,,, 则称n M 为一个“友谊集”,称()A B ,为n M 的一种“友谊排列”.如(310796)A =,,,,和(28451)B =,,,,便是集合5M 的一种友谊排列,记为 31079 6 28451⎡⎤⎢⎥⎣⎦,,,,,,,,. (1)证明:若n M 为一个友谊集,则存在偶数种友谊排列;(2)确定集合4M 及5M 的全体友谊排列.参考答案第一试一、1.160.圆周12个点,可得三角形312C 220=个;12等分圆的弦中有直径6条,每条直径对应10个直角三角形,故得60个直角三角形. 因此,锐角三角形和钝角三角形有 220-60=160(个). 2.2235x x ++.注意到(1)f x +与(1)f x -的次数相同,而右边为二次的,故设2()f x ax bx c =++. 代入题设等式并比较两边系数得 235a b c ===,,. 因此, 2()235f x x x =++. 3.8. 注意到2614742230!2357111317192329=⨯⨯⨯⨯⨯⨯⨯⨯⨯.则1914422730!23711131719232910=⨯⨯⨯⨯⨯⨯⨯⨯ 1914422237137939(mod10)≡⨯⨯⨯⨯⨯⨯⨯⨯.因为43、47模10均余1,且42n 模10余6,所以, 3730!28(mod10)10≡≡. 4.10.易知,椭圆的离心率为12,右准线l 的方程为8x =,点A 到l 的距离为10. 设点P 到l 的投影为H .则 12PF PH=. 故210PA PF PA PH +=+≥. 当点P 在线段AH 上时,取此最小值.5.31()a b +.记2sin x θ=.则题设等式变为22(1)1x x a b a b-+=+.解得1a bx x a b a b=-=++,. 故88443333sin cos (1)x x a b a b θθ-+=+ 4311()()()a b a b a b =+=++. 6. 如图2,设3BC =,2AB AC AD BD CD =====,图2AB CDEFH OE F 、分别是BC AD 、的中点.则点D 在面ABC 上的射影H 是ABC △的外心,且外接球球心O 在DH 上.因ABC DBC △△≌,所以,AE DE =. 于是,EF 为AD 的中垂线.因此,球心O 是DH 与EF 的交点,且是等腰EAD △的垂心. 记球半径为r .由DOF EAF △△∽,得AE DFr EF⋅=. 而222372124AE DF AF ⎛⎫=-=== ⎪⎝⎭,,22234EF AE AF =-=,所以,r =. 7.13.首先指出,12个连续正整数(如994,995,⋯,1 005),其中任一数的各位数字之和都不是7的倍数,因此,13n ≥.其次说明,任何连续13个正整数中,必有一个数,其各位数字之和是7的倍数. 对每个非负整数a ,设其各位数字之和为()f a ,称集合 {}10101109a A a a a =++ ,,,为一个“基本段”,其对应的f 值依次为()()1()9f a f a f a ++ ,,,.故a A 中任意连续7个数中必有一个,值为7的倍数.于是,13个连续正整数,要么属于两个基本段,要么属于三个基本段. 上述两种情况中,均有连续的7个数,属于同一个基本段,其中必有一个的,值是7的倍数.因此,所求的最小值为13. 8.2 475+显然,每个正整数x 皆属于X ,将其按严格递增顺序依次记为12a a ,,…. 下面考虑X 中不是正整数的元素,将其按严格递增顺序依次记为12b b ,,…. 因{}x x 2+为整数当且仅当{}{}2x x +为整数,且{}01x <<,所以,{}{}21x x +=.解得{}x =.从而,1(12)k k b k a k k =-+== ,,,且X 的前100项自小到大排列是: 11225050b a b a b a ,,,,,,.故501001()2475k k k S b a ==+=+∑二、9.如图3,若四面体PDEF 为平展四面体,且沿DEF △所在平面展平后的三角形为ABC △,则DE 、EF FD 、为ABC △的中位线.ABC △被其三条中位线所划分成的四个全等三角形构成四面体的四个侧面,从而,四面体中共顶点的三个面角恰等于ABC △的三个内角.故ABC △为锐角三角形,且三边长为222a b c 、、.DEFP图3不妨设PD EF a ==, PE DF b PF DE c ====,. 则由ABC △为锐角三角形知222222222b c a c a b a b c +>+>+>,,.下面计算四面体PDEF 的体积V . 设DEF △的外接圆半径为R , FDE DEF EFD αβγ∠=∠=∠=,,. 则PDE β∠=,PDF γ∠=.设二面角P DE F --的平面角为ϕ.则cos cos cos cos sin sin γαβϕαβ-⋅=⋅.故sin ϕ=注意到4DEF PDE abcS S R==△△, 且2sin 2sin a R b R αβ==,,则 2sin 3DEF PDE S S V DEϕ⋅=△△13==10.如图4,作O :222x y a +=,分别过点P E F 、、作x 轴的垂线,图4垂足为H 、L 、T ,交O 于点C 、D 、G 、Q .设椭圆上的各点坐标为 (cos sin )E a b αα,, (cos sin )F a b ββ,, (cos sin )P a b θθ-,,则(cos sin )D a a θθ-,, (cos sin )(cos sin )G a a Q a a ααββ,,,. 注意到 sin sin sin sin NT TF b a TQNH HP b a HD ββθθ====--. 所以,D N Q 、、三点共线. 同理,D M G 、、三点共线. 因为HM HN =,所以, MDH NDH ∠=∠.则C 为劣弧 GQ的中点,即2αβθ+=.故(sin sin )(cos cos )EF b k a αβαβ-=-=-cot cot 2b b a aαβθ+=-. 又因P 为定点,所以,θ为定值. 故斜率EF k 为定值. 11.对于数列{}n a 有 013113233a a a ===,,.由2222112n n n n n n n n a a a a a a a a ++++++++= 221212(64)n n n n a a a a ++++++=221212(64)n n n n a a a a ++++++=211313122n n n n n n n n a a a a a a a a ++++++++++==,于是,对任意的n ∈N , 2021112331813n n n a a a a a a +++++===. 所以,2118n n n a a a ++=-. ①对于数列{}n b ,由条件知数列严格递增.将19n n b b +-221118640n n n n b b b b ++-++=.②在式②中用1n +代替n 得22212118640n n n n b b b b ++++-++=. ③由式②、③知,2n n b b +、是关于t 的方程 221118640n n t b t b ++-++=的两个相异根,于是,由根与系数关系得 2118n n n b b b +++=,即210118113n n n b b b b b ++=-==,,. ④ 由式①、④知,{}{}n n a b 、为同一个数列,因此, 2()n n n a b a n +=∈N .又据式①知,数列{}n a 的各项为正整数,且 22022122232210113232338134 1813455.a a a a ==+==+==+==+,,,构作辅助数列{}{}n n x y 、,其中, 0112024(2)n n n x x x x x n --===+,,≥; ⑤ 0112134(2)n n n y y y y y n --===+,,≥. ⑥显然,当1n ≥时,n n x y 、皆为正整数,且 n n y x >.下面证明:对任意的n ∈N ,22()()0n n n f n a x y =-+=.⑦对n 用数学归纳法. 当3n ≤时已验证.设当n k <时,式⑦成立. 当n k =时,由于 ()(2)f k f k +-2222222()()k k k k k k a x y a x y ---=-++-+222212218()()k k k k k a x y x y ---=-+-+222222111118()()(4)(4)k k k k k k k k x y x y x x y y ----=+-+----222211112(44)k k k k k k k k x x x x y y y y ----=+-++-2211112()k k k k k k x x x y y y +-+-=-+-,则(1)(3)f k f k -+-2221212()k k k k k k x x x y y y ----=-+-222211112(44)k k k k k k k k x x x x y y y y ----=--+--()(2)f k f k =---.而据归纳假设有(1)(2)(3)0f k f k f k -=-=-=. 因此,()0f k =.故由归纳法,对一切n ∈N ,式⑦成立. 由式⑦得2222()n n n n n a b a x y +==+22()()n n n n y x y x =-++,其中,n n n n y x y x -+、为正整数.加 试一、(1)设123DD DD DD 、、分别与BC CA AB 、、交于点123F F F 、、. 由西姆松定理知123F F F 、、三点共线.而12121313D D F F D D F F ,∥∥,则123D D D 、、三点共线. (2)由于A B C D 、、、四点共圆,则 2122DAD DAC DBE ∠=∠=∠ 1DBD =∠,DAE DBE ∠=∠.相减得21EAD EBD ∠=∠. 故1212EBD EAD S BE BD BE BDS AE AD AE AD ⋅⋅==⋅⋅△△. 同理,31EAD ECD S AD AES CD CE⋅=⋅,△△23ECD EBD S CD CES BD BE⋅=⋅△△.由于点123E E E 、、分别在ABC △的三边BC CA AB 、、所在直线上,且 312312AE BE CE E B E C E A⋅⋅312312EAD EBD ECD EBD ECD EAD S S S S S S =⋅⋅△△△△△ 312123EAD EBD ECD ECD EAD EBD S S S S S S =⋅⋅△△△△△△ 1AD AE BE BD CD CECD CE AE AD BD BE⋅⋅⋅=⋅⋅=⋅⋅⋅,故由梅涅劳斯逆定理得123E E E 、、三点共线. 二、考虑函数()122001012200f x x x x =+++---- . 当1x <时,()0f x <,故在区间(1)-∞,内,不存在使()0f x >的实数x . 对于集合{12200} ,,,中的任一个k ,当0x k →-时,()f x →-∞,而当0x k →+时,()f x →+∞,且当x →+∞时,10x →-,所以,方程()0f x =在区间 (1,2),(2,3),…,(199,200),(200,+∞)内各有一个解. 依次记这200个解为12200x x x ,,,. 构作多项式()(1)(2)(200)()P x x x x f x =--- .由于()P x 是一个200次多项式,故方程()0P x =至多有200个互异根.显然,每个使()0f x =的i x 都是()0P x =的根.因此,12200x x x ,,,是()0P x =的全部根. 这表明,每个k x 是其所在区间(1)k k +,(12199)k = ,,,及(200)+∞,中的唯一根. 从而,不等式()0f x >的解集是 12200(1)(2)(200)E x x x = ,,,.故所有区间长度的总和为11200(1)(2)(200)S x x x =-+-++- 12200()(12200)x x x =+++-+++=2001102010i i x =-⨯∑.①注意到20020011()()10i i i P x x i x i==⎡⎤⎛⎫=-- ⎪⎢⎥-⎝⎭⎣⎦∑∏,如将()P x 展开,其最高次项系数为-10.所以,()P x 中的199x 的系数是()20011011120 100k k =+=⨯∑.从而,200111 2 010i i x ==⨯∑.由式①得200110 2 010 2 010i i S x ==-⨯=∑.三、注意到2 010<245.于是,若集合{12 2 010}M = ,,,中的某数n 不单纯,则必含有质数集 {235711131719232931374143}N =,,,,,,,,,,,,, 中的一个或多个平方因子.以下记22220102010()()s p s p q p p q ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,等等. 则()()()25023223580s s s ===,,,()()()74111161311s s s ===,,,()()()176195233s s s ===,,,()()29312s s ==,()()()3741431s s s ===. 利用a a n m mn ⎡⎤⎡⎤⎢⎥⎢⎥⎡⎤⎣⎦⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦,得 (23)55(25)20(27)10s s s ===,,,,,,(211)4(213)2(217)1s s s ===,,,,,,(219)15(223)0(35)8s s ===,,,,,,(37)4(311)(313)1s s s ===,,,,,(317)0(57)1(511)0s s s ===,,,,,;(235)2(237)1s s ==,,,,,,(2311)(357)0s s ==,,,,.故所求为2010()()()p N p q N p q r N s p s p q s p q r ∈∈∈-+-∑∑∑、、、,,,=2 010(5022238041161165322111)-+++++++++++++ ()()55201042118411121+++++++++++-+2 0108941083 1 221=-+-=.四、(1)由题设对Mn 的任意一种友谊排列()A B ,,作()A B ,的对偶排列()A B ,,其中, 1212()()n n A a a a B b b b == ,,,,,,,2121(12)i i i i a n b b n a i n =+-=+-= ,,,,. 显然,()A B ,也是M 的一种友谊排列,且若12A A ≠,则12A A ≠. 再证A A ≠. 事实上,假若A A ≠,则由22222123a a n b n a ==+-=+-,得2223a n =+,矛盾. 从而,n M 的所有友谊排列可分成若干个对偶排列组,每组两个.因此,n M 的友谊排列有偶数种.(2)设4M 的友谊排列为12341234a a a a b b b b ⎡⎤⎢⎥⎣⎦,,,,,,. 则4411()10k k k k a b k ==-==∑∑.又4811()36k k k k a b k ==+==∑∑,以上两式相减得123413b b b b +++=. ①显然,1B ∈而8A ∈.于是,由式①得1234{}B b b b b =,,,只有三种情况: {1237}{1246}{1345}B =,,,,,,,,,,,.(i ){1237}B =,,,. 则{4568}A =,,,. 由于14i i a b ≤-≤,于是,A 中的元素8只能与B 中的元素7搭配. 而A 中的元素6只能与B 中的元素2或3搭配,因此,只有两种排列128465854672317312T T ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,,,,,,,,,,,. (ii ){1246}B =,,,. 则{3578}A =,,,.于是,A 中的元素7、8只能与B 中的元素4或6搭配,也只有两种排列343875735826416124T T ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,,,,,,,,,,,. (iii ){1345}B =,,,. 则{2678}A =,,,. 于是,A 中的元素2只能与B 中的元素1搭配,8只能与4或5搭配,只有两种排列562768268715341453T T ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,,,,,,,,,,,. 因此,4M 共有6种友谊排列.同理,5M 共有10种友谊排列:124109579541073861283162T T ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,,,,,,,,,,,,,,,′′, 341074681048769512392531T T ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,,,,,,,,,,,,,,,′′, 569376103107968142528451T T ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,,,,,,,,,,,,,,,′′, 782610982968101475317345T T ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,,,,,,,,,,,,,,,′′, 9108351093810597126426714T T ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,,,,,,,,,,,,,,,,,′′. (陶平生江西科技师范学院数学与计算机科学系.330013)。
奥林匹克数学题型数值分析基础

奥林匹克数学题型数值分析基础奥林匹克数学题型:数值分析基础数值分析是数学的一个分支,用于解决数值计算问题,以及分析数值解的误差和收敛性。
在奥林匹克数学竞赛中,数值分析是一个重要的题型。
本文将介绍奥林匹克数学竞赛中涉及的数值分析基础知识和解题技巧。
一、整数运算在奥林匹克数学竞赛中,整数运算是最基础的计算题型之一。
它要求选手能够熟练进行整数的加减乘除运算,计算结果可以是整数、分数、小数等形式。
同时,选手还需要注意运算过程中的进位、借位、除法的余数等细节问题。
二、多项式插值多项式插值是数值分析中常用的一种方法,用于通过已知数据点的函数值,构造出一个经过这些数据点的多项式函数。
在奥林匹克数学竞赛中,常出现需要通过已知数据点的函数值,找出满足某些条件的多项式函数的问题。
这就需要选手掌握多项式插值的理论知识和计算方法。
三、数值积分数值积分是计算曲线或者曲面下的面积、体积等物理量的一种方法。
在奥林匹克数学竞赛中,常常出现需要计算某个曲线或者曲面下的面积、体积的问题。
选手需要熟悉数值积分的基本原理和计算方法,例如用矩形法、梯形法、辛普森法等近似计算积分的方法。
四、线性方程组的数值解法线性方程组是数值分析中经常出现的问题之一,解线性方程组可以通过直接法和迭代法两种方法。
在奥林匹克数学竞赛中,选手往往需要运用适当的数值解法,求解给定的线性方程组。
对于规模较大的线性方程组,迭代法是一种常用的解法,例如雅可比迭代法、高斯-赛德尔迭代法等。
五、数值微分与数值微分方程数值微分是数值分析中重要的内容之一,它研究如何用差商来近似计算函数的导数。
在奥林匹克数学竞赛中,常常出现需要求解数值微分或数值微分方程的问题。
选手需要了解数值微分的基本概念和计算方法,例如用差分法、前进差分、后退差分等方法进行数值微分的近似计算。
结论:奥林匹克数学竞赛中的数值分析基础题型涵盖了整数运算、多项式插值、数值积分、线性方程组的数值解法、数值微分与数值微分方程等多个方面。
奥林匹克训练题库·数值代入法

数值代入法26 有甲、乙、丙三个数,已知甲数是乙数的 3倍,乙数是丙数的2倍,那么甲数是乙、丙两数之和的几倍?27 甲、乙二人同时出发从A地到B地,甲骑自行车,乙前一半路程骑摩托车,后一半路程步行。
已知骑自行车的速度是步行的2倍,是骑摩托车上(含80分),他们的平均分数是90分。
求低于80分的人的平均分。
分数线高4分,而没达到优秀的学生的平均分比优秀的分数线低11分,所有学生的平均分是 87分。
问:优秀的分数线是多少分?31 有一堆苹果平均分给甲、乙两班的每个人,每人得6个苹果。
若只分给甲班,则每人得10个苹果。
如果只分给乙班,那么每人得几个苹果?,那么这时A桶中的水是B桶中水的几分之几?33 一次考试共有5道试题。
做对第1,2, 3,4,5题的分别占参加考试人数的81%,91%,85%,79%,74%,如果做对三道或三道以上为及格,那么这次考试的及格率至少是多少?34 甲、乙两人步行的速度之比是9∶7,若甲、乙分别由A,B两地沿同一公路同向而行,则甲追上乙需4时,若相向而行,则多长时间相遇?35 一艘轮船往返于A,B两地,去时顺流每时行36千米,返回时逆流每时行 24千米,往返一次共用 15时。
A,B两地相距多少千米?36 在一个梯形内有两个面积分别是6和8的三角形(右图),梯形下底的长是上底长的2倍。
求阴影部分的面积。
37 李彦以每分行 100米的速度从家步行到学校去,到校门口发现书包忘带了,他立刻借了一辆自行车,以每分行300米的速度回家,拿了书包又返回学校。
如果借自行车及拿书包的时间忽略不计,那么李彦从第一次离家到第二次到校期间的平均速度是多少?38 商店购进甲、乙两种不同的糖,所用费用之比为2∶1,已知甲种糖每千克6元,乙种糖每千克2元。
如果把这两种糖混在一起成为什锦糖,那么这种什锦糖每千克的成本是多少元?。
数学奥林匹克高中训练题_200

4.
JT
.
注 意 到
由 /( 幻 在 区 间
,
上单调
知 U /
)
,
年第 2 0 1 6
2期
43
叫 卜 的 最小正 周 期 r
-
ff
f.
均 在 一 个与 平 面 脚 平 行 的 平 面 《 上 .
f 0 / 7
拉卜 作 因 为
_
所以
,
,
)
设 平 面 a 与 〇// 有 交 点 c 且 c// =
7
y ^
=
1
,
+ ;
1
?
此 对任 意 的 + { 因
y ,
,
斤Z
r=
+,
,
.
2
n = kx^
\
由
g
^
+ ^
2
1
=l
l
w= b
-
X
b .
k
\ y B = j2
从 而 W r
,
2
5
t x
=
^^
=
^ y
,
4
2 ^ = .
2
8.
3
k
+ ^-
2
y.
U K ^ 令 \
x = 8
.
2
/
/5
;
+ 4 s i n 0
"
7
-
-
由 于 函 数 在
区间
(
〇 ,
2
]
上单调 递减
,
在
一 ̄
^
f .
单 区 间 2 + 〇〇 上 调 递 增 故
最新小学奥林匹克数学 数阵练习(2)

数阵练习
1.将2~8分别填入下图的7个○内,使每条线段上的三个○内数的和相等。
2.将1~9填入下图的○中,使横、竖行五个数相加的和都等于26。
3.将1~11十一个数分别填入下图○里,使每条线上3个○内的数的和相等。
4.如下图,四个小三角形的顶点处有六个圆圈。
如果在这些圆圈中分别填上六个质数,它们的和是20,而且每个小三角形三个顶点上的数的和相等。
问这个六个质数的积是多少?
5.将九个不同的自然数填入下面方格中,使每行、每列、每条对角线上三个数的积都相等。
6.将1~9九个自然数分别填入下图的九个小三角形中,使靠近大三角形每条边上五个数的和
相等,并且尽可能大,这五个数之和最大是多少?
7.在空格中填入不同的数,使每一横行、竖行、斜行的三个数的和等于18。
8.将5、6、7、9、10、11六个数分别填在下面图的小圆圈里,使每个大圆的三个数及每条
直线上的三个数加起来分别等于24。
9.将1~7七个自然数分贝填入图中圆圈里,使每条线上三个数的和相等。
10.将1~8八个数分别填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四
格以及对角线四格内四个数的和都是18。
11.将1~8八个数分别填入下图的○内,使每边上的三个数的和相等。
12.将2~9八个数分别填入下图○内,使外圆四个数的和,内圆四个数的和以及横行、竖行
上四个数的和都等于22。
13.将1~9九个数分别填入下图○内,使外三角形边上○内数字和等于里面三角形边上○内数字的和。
数学奥林匹克高中训练题(06)及答案.doc
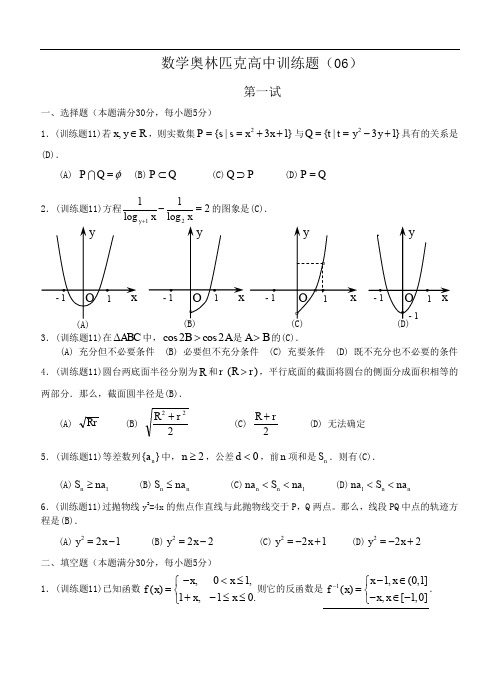
数学奥林匹克高中训练题(06)第一试一、选择题(本题满分30分,每小题5分)1.(训练题11)若,x y R ∈,则实数集2{|31}P s s x x ==++与2{|31}Q t t y y ==-+具有的关系是(D).(A) PQ φ= (B)P Q ⊂ (C)Q P ⊃ (D)P Q =2.(训练题11)方程112log log y x x+-=的图象是(C).3.(训练题11)在ABC ∆中,cos2cos2B A >是A B >的(C).(A) 充分但不必要条件 (B) 必要但不充分条件 (C) 充要条件 (D) 既不充分也不必要的条件4.(训练题11)圆台两底面半径分别为R 和r ()R r >,平行底面的截面将圆台的侧面分成面积相等的两部分.那么,截面圆半径是(B).(A) Rr (B) 222r R + (C) 2r R + (D) 无法确定5.(训练题11)等差数列{}n a 中,2n ≥,公差0d <,前n 项和是n S .则有(C).(A)1n S na ≥ (B)n n S na ≤ (C)1n n na S na << (D)1n n na S na << 6.(训练题11)过抛物线y 2=4x 的焦点作直线与此抛物线交于P ,Q 两点。
那么,线段PQ 中点的轨迹方程是(B).(A)221y x =- (B)222y x =- (C)221y x =-+ (D)222y x =-+二、填空题(本题满分30分,每小题5分)1.(训练题11)已知函数, 01,()1, 10.x x f x x x -<≤⎧=⎨+-≤≤⎩则它的反函数是11,(0,1](),[1,0]x x f x x x --∈⎧=⎨-∈-⎩.2.(训练题11)已知复数z 的模1z =且,111z z +=,则z=1(1)2±. 3.(训练题11)某市电话号码从六位升至七位,这一改可增加761010-个拨号. 4.(训练题11)1arctan arctan1x x x -++的值是 3144ππ-或 . 5.(训练题11)平面α内有圆ABC (如图)AB 是直径,SA α⊥,C 是AB 上一点.若::1:2:2AC AB SA =,则二面角C SB A --的平面角的余弦值是5.6.(训练题11)ABC ∆顶点在以x 轴为对称轴,原点为焦点的抛物线上,已知(6,8)A -,且ABC ∆的重心在原点,则过B ,C 两点的直线方程为480x y +-=. 三、(训练题11)(本题满分20分) 如图,四棱锥S ABCD -的顶点在底面的射影恰是底面对角线的交点O ,已知棱锥S ABCD -的高恒为3,22,(,,)S ADO S BCO V m V n m n R m n +--==∈≠.问当四棱锥S ABCD -取得最小体积时,底面ABCD 是怎样的四边形?四、(训练题11) (本题满分20分) 抛物线22(0)y px p =>的焦点是F .问:是否存在内接等腰直角三角形,该三角形的一条直角边过F 点?如果存在,存在几个?如果不存在,说明理由五、(训练题11)(本题满分20分)数列{}n a 的首项0a ≠,该数列是公比为a -的等比数列.记lg n n n b a a =,1nn i i S b ==∑.(1) 证明: 当1a ≠-时,对一切n N ∈,都有12lg [1(1)(1)](1)n nn a a S n na a a +=+-+++. (2) 当01a <<时,是否存在自燃数m ,使得对任何自然数n ,都有n m b b ≤.第二试一、(训练题11)(本题满分35分)H 为ABC ∆的垂心,,,D E F 分别是,,BC CA AB 中点,一个以H为SCBAO D圆心的H 交直线,,EF FD DE 于121212,,,,,A A B B C C .求证:121212AA AA BB BB CC CC =====.二、(训练题11)(本题满分35分)若n 是素数,证明存在0,1,2,,1n -的一个排列12(,,,)n a a a ,使得11212312,,,,n a a a a a a a a a 被n 除的余数各不相同.三、(训练题11)(本题满分35分)某组学生进行一次考试,共有3道选择题,每题有四个选择支.已知这组学生中任何两人的答案都至多有一题相同,而且只要再加一人,则无论该人答案如何,上述性质都不再成立.问这组学生最少有多少人?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值代入法
26 有甲、乙、丙三个数,已知甲数是乙数的 3倍,乙数是丙数的2倍,那么甲数是乙、丙两数之和的几倍?
27 甲、乙二人同时出发从A地到B地,甲骑自行车,乙前一半路程骑摩托车,后一半路程步行。
已知骑自行车的速度是步行的2倍,是骑摩托车
上
(含80分),他们的平均分数是90分。
求低于80分的人的平均分。
分数线高4分,而没达到优秀的学生的平均分比优秀的分数线低11分,所有学生的平均分是 87分。
问:优秀的分数线是多少分?
31 有一堆苹果平均分给甲、乙两班的每个人,每人得6个苹果。
若只分给甲班,则每人得10个苹果。
如果只分给乙班,那么每人得几个苹果?
,那么
这时A桶中的水是B桶中水的几分之几?
33 一次考试共有5道试题。
做对第1,2, 3,4,5题的分别占参加考试人数的81%,91%,85%,79%,74%,如果做对三道或三道以上为及格,那么这次考试的及格率至少是多少?
34 甲、乙两人步行的速度之比是9∶7,若甲、乙分别由A,B两地沿同一公路同向而行,则甲追上乙需4时,若相向而行,则多长时间相遇?
35 一艘轮船往返于A,B两地,去时顺流每时行36千米,返回时逆流每时行 24千米,往返一次共用 15时。
A,B两地相距多少千米?
36 在一个梯形内有两个面积分别是6和8的三角形(右图),梯形下底的长是上底长的2倍。
求阴影部分的面积。
37 李彦以每分行 100米的速度从家步行到学校去,到校门口发现书包忘带了,他立刻借了一辆自行车,以每分行300米的速度回家,拿了书包又返回学校。
如果借自行车及拿书包的时间忽略不计,那么李彦从第一次离家到第二次到校期间的平均速度是多少?
38 商店购进甲、乙两种不同的糖,所用费用之比为2∶1,已知甲种糖每千克6元,乙种糖每千克2元。
如果把这两种糖混在一起成为什锦糖,那么这种什锦糖每千克的成本是多少元?。
