ILU预处理Newton—Krylov方法的潮流计算
牛顿拉夫逊法计算潮流步骤

牛顿拉夫逊法计算潮流步骤牛顿拉夫逊法(Newton-Raphson Method)是一种常用于计算潮流的数值求解方法。
它是基于潮流计算的功率流方程的非线性特性而设计的,通过迭代求解来逼近潮流计算的稳态解。
下面将介绍牛顿拉夫逊法计算潮流的基本步骤。
首先,我们需要明确潮流计算的目标,即确定电力系统中各节点的电压相角和幅值。
这些节点是电力系统中的发电机、负荷和交流输电线路的连接点。
通过潮流计算,我们可以得到各节点的电压相角和幅值,从而分析系统的功率分布、电压稳定性等运行特性。
接下来,我们需要建立电力系统的潮流计算模型。
这个模型中,我们需要考虑发电机的注入功率、负荷的吸收功率、线路的传输损耗等因素。
通过利用功率流方程,我们可以将这些因素表示为电压、功率和导纳之间的方程。
然后,我们需要进行初始化操作。
在进行牛顿拉夫逊法迭代计算之前,我们需要对电力系统的各节点进行初始电压值的设定。
这些初始值可以根据经验或者历史数据来得到,但需要满足物理约束条件,如一致性、电压幅值在合理范围内等。
接下来,我们进入迭代计算的过程。
首先,我们需要对系统的节点进行编号,然后选择某一节点作为基准节点,其他节点相对于基准节点的电压相角进行计算。
然后,我们根据节点注入功率和导纳矩阵的关系,得到节点注入电流。
接着,我们根据节点注入电流和电压相角的关系,计算各节点的电压相角和幅值的改变量。
在计算改变量后,我们需要对节点电压进行更新。
更新后,我们判断系统是否达到收敛条件。
如果满足收敛条件,则停止迭代,得到最终的潮流计算结果;如果不满足收敛条件,则继续进行下一轮迭代计算。
最后,我们对潮流计算结果进行分析和验证。
通过比较计算得到的结果和实际运行数据进行对比,我们可以评估潮流计算的准确性。
同时,我们还可以通过故障分析、电压稳定性评估等手段对电力系统进行优化和改进。
总而言之,牛顿拉夫逊法是一种常用的求解潮流计算问题的方法。
它通过迭代求解潮流计算的功率流方程,逼近潮流计算的稳态解。
牛顿拉夫逊法计算潮流步骤

牛顿拉夫逊法计算潮流步骤牛顿拉夫逊法(Newton-Raphson method)是一种用于求解非线性方程组的迭代方法,它可以用来计算电力系统潮流的解。
潮流计算是电力系统规划和运行中的重要任务,它的目标是求解电力系统中各节点的电压幅值和相角,以及线路的功率流向等参数,用于分析电力系统的稳定性和安全性,以及进行电力系统规划和调度。
下面是使用牛顿拉夫逊法计算潮流的一般步骤:步骤1:初始化首先,需要对电力系统的各个节点(包括发电机节点和负荷节点)的电压幅值和相角进行初始化,一般可以使用其中一种估计值或者历史数据作为初始值。
步骤2:建立潮流方程根据电力系统的潮流计算模型,可以建立节点电压幅值和相角的平衡方程,一般采用节点注入功率和节点电压的关系来表示。
潮流方程一般是一个非线性方程组,包含了各个节点之间的复杂关系。
步骤3:线性化方程组将潮流方程组进行线性化处理,一般采用泰勒展开的方法,将非线性方程组变为线性方程组。
线性化的过程需要计算雅可比矩阵,即方程组中的系数矩阵。
步骤4:求解线性方程组利用线性方程组的求解方法,比如高斯消元法或LU分解法等,求解线性方程组,得到电压幅值和相角的修正量。
步骤5:更新节点电压根据线性方程组的解,更新各个节点的电压幅值和相角,得到新的节点电压。
步骤6:检查收敛性判断节点电压的修正量是否小于设定的收敛阈值,如果满足收敛条件,则停止迭代;否则,返回步骤3,循环进行线性化方程组和线性方程组的求解。
步骤7:输出结果当潮流计算收敛时,输出最终的节点电压幅值和相角,以及线路的功率流向等参数。
牛顿拉夫逊法是一种高效、快速且收敛性良好的方法,广泛应用于电力系统潮流计算。
在实际应用中,可能会遇到多次迭代或者收敛性不好的情况,此时可以采用退火技术或其他优化算法进行改进。
此外,牛顿拉夫逊法的计算也可以并行化,利用多核处理器或者分布式计算集群来加速计算过程。
总之,牛顿拉夫逊法是一种重要的潮流计算方法,通过迭代计算逼近非线性方程组的解,可以得到电力系统中各节点的电压幅值和相角,用于分析电力系统的稳定性和安全性。
几种Krylov迭代法在潮流计算中的对比

接求 解大规模稀疏 线性方程 组 , 常结合 ቤተ መጻሕፍቲ ባይዱy v rl 迭代法 o
来 使 用 。 常 用 的 Kyo rl v迭 代 法 有 : 轭 梯 度 法 共 ( G)31广 义极 小 残 余 算 法 ( MR S L7、 i G C L 、 4 G E )51 B・ — - C
Co mpa io fS v r lKr l v I e a ie M e h d n Po r Fl w lu a i n rs n o e e a yo t r tv t o s i we o Ca c l to
Z NG Jn h i U Da HE i — u .L ( c ol f no u t nS i c n eh o g , i e nvr t , i e 6 0 5 C ia S h o fn a o ce e ad T c nl y X a n U i s y X a n3 10 , hn ) oI i n o m ei m
郑锦辉 , 陆 达
( 门大 学信 息科 学与 技 术 学 院 , 建 厦 门 3 10 ) 厦 福 60 5
摘要 : 在潮流计算时, 大部分时间都 用在求解 大规模 稀疏 线性 方程组 A 绝 x=b 。众 多文献 中运用的迭代 法并不统一 , 上
它们 只 注 重预 处理 方法 的 改 进 。本 文 就针 对几 种 流 行 的 Kyo 迭 代 法进 行详 细介 绍 , 结 特性 , 利 用 实验 来 分析 它 们 rl v 总 并
Ke od :G;G E ; C Q yw r sC MR S B G; MR
0 引 言
一
.
有不 少学者在 潮流计 算 时使 用 迭 代 法来 求 解 大规 模
牛顿-拉夫逊法潮流计算程序与讲解

(四)小阻抗支路
(五)R/X值过大
• 线路电阻大于电抗,导致一些网络电抗远 大于电阻的潮流算法失效 • 在PQ分解法中,为了将不断变化的H、L矩 阵用常数矩阵来代替,认为互导纳中 |Gij|<|Bij|,因此当线路电阻大于电抗时,可能 会造成不收敛。
结束
谢谢
牛顿-拉夫逊法潮流计算程序与 讲解
组员:刘澍 邢越 薛伦 孙韬备
线路参数文件
节点功率文件
• 程序设计部分
• 主要讲N_L法
计算潮流
潮流不收敛的原因
• • • • 初值偏离终值过大 系统有功不平衡 系统无功不平衡 小阻抗支路的存在
(一)初值偏离终值过大
• 实际系统中,受稳定性要求的限制,各个 节点间的相位差不能很大,故各节点的相 位初值一般给定为0; • 正常运行情况下,各母线的电压都在额定 电压附近,因此电压有效值得初值都给定 为1
(二)系统有功不平衡
• • • • plot (yg,kkkk,'.') axis([0,10,-2,2]) xlabel('注入功率') ylabel('收敛性')
(二)系统有功不平衡
(三)系统无功不平衡
• wugong=0; • for m=1:200 • wugong=wugong+1; • wg(m)=wugong; • for t=1:mn • if b(t,2)==1 • b(t,4)=wugong; • break • end • …… • …… • end
(一)初值偏离终值过大
• • • • • • • • • • canchu=0; for m=1:200 canshu=canshu+0.02;%参数从0增大 cs(m)=canshu; for i=1:4 if b(i,2)==1%改变PQ节点给定的电压初值 b(i,5)=canshu; end end ……
牛顿拉夫逊法潮流计算

牛顿拉夫逊法潮流计算
油田自出井管网的潮流模拟分析是油田开发运行中的重要工作,是保
证油田系统安全运行的基础性工作。
牛顿-拉夫逊法是一种经典的油田自
出井管网的潮流模拟计算方法。
本文介绍了牛顿-拉夫逊法的概念,原理,特点,以及利用牛顿-拉夫逊法求解油田自出井管网潮流问题的基本方法
和步骤。
一、牛顿-拉夫逊方法的概念
牛顿-拉夫逊法也叫牛顿-拉夫逊潮流计算法,它是一种迭代法,用于
求解牛顿-拉夫逊方程,即求解由牛顿-拉夫逊节点组成的网络中流动矢量
的幅值和相位角。
牛顿-拉夫逊方程是以节点电压和电流矢量以及节点内
的电阻和电感量建立的方程组,是油田自出井管网潮流模拟计算的基础方
程组。
牛顿-拉夫逊方程是一组非线性方程,其解依赖节点网络结构,因
此实施计算时需要迭代求解,因此被称为牛顿-拉夫逊迭代法或牛顿-拉夫
逊方法。
二、牛顿-拉夫逊方法原理
牛顿-拉夫逊方法是一种迭代法,它采用迭代新旧节点电压矢量的比
例来求解油田自出井管网潮流模拟问题,算法充分利用了网络的放大、收敛、稳定特性,每一次迭代,都可以有效地拿到更新的节点电压矢量。
牛顿拉夫逊法潮流计算

牛顿拉夫逊法潮流计算牛顿-拉夫逊法(Newton-Raphson method)是一种用于求解非线性方程的数值方法。
它通过迭代逼近根的方式,将非线性方程转化为一系列的线性方程来求解。
在电力系统中,潮流计算用于确定电力网中节点的电压幅值和相角。
潮流计算是电力系统分析的重要基础,可以用于计算电力系统的潮流分布、功率损耗、节点电压稳定度等参数,为电力系统的规划、运行和控制提供参考依据。
牛顿-拉夫逊法是一种常用的潮流计算方法,它的基本思想是通过不断迭代来逼近电网的潮流分布,直到满足一定的收敛条件。
下面将对牛顿-拉夫逊法的具体步骤进行详细介绍。
首先,我们需要建立电力网络的节点潮流方程,即功率方程。
对于每一个节点i,其节点功率方程可以表示为:Pi - Vi * (sum(Gij * cos(θi - θj)) - sum(Bij * sin(θi -θj))) = 0Qi - Vi * (sum(Gij * sin(θi - θj)) + sum(Bij * cos(θi -θj))) = 0其中,Pi和Qi分别为节点i的有功功率和无功功率,Vi和θi分别为节点i的电压幅值和相角,Gij和Bij分别为节点i和节点j之间的导纳和电纳。
接下来,我们需要对每个节点的电压幅值和相角进行初始化。
一般情况下,可以将电压幅值设置为1,相角设置为0。
然后,我们可以开始进行迭代计算。
在每一轮迭代中,我们需要计算每个节点的雅可比矩阵和功率残差,然后更新电压幅值和相角。
雅可比矩阵可以通过对节点功率方程进行求导得到,具体如下:dPi/dVi = -sum(Vj * (Gij * sin(θi - θj) + Bij * cos(θi - θj)))dPi/dθi = sum(Vj * (Gij * Vi * cos(θi - θj) - Bij * Vi * sin(θi - θj)))dQi/dVi = sum(Vj * (Gij * cos(θi - θj) - Bij * sin(θi - θj)))dQi/dθi = sum(Vj * (Gij * Vi * sin(θi - θj) + Bij * Vi * cos(θi - θj)))功率残差可以通过将节点功率方程代入得到,如下:RPi = Pi - Vi * (sum(Gij * cos(θi - θj)) - sum(Bij *sin(θi - θj)))RQi = Qi - Vi * (sum(Gij * sin(θi - θj)) + sum(Bij *cos(θi - θj)))最后,我们可以使用牛顿-拉夫逊法的迭代公式来更新电压幅值和相角,具体如下:Vi(new) = Vi(old) + ΔViθi(new) = θi(old) + Δθi其中,ΔVi和Δθi分别为通过求解线性方程组得到的电压幅值和相角的增量。
牛顿拉夫逊法计算潮流计算

例题
PG1 P1 PL1 0.5 1 0.5
QG1 Q1 QL1 0.02363 0.5 0.52363
3
3
QG2 Q2 f2 (G2 je j B2 j f j ) e2 (G2 j f j B2 je j ) 0.05708
2 3
0
e3 0
f3 0
例题
0 20 0 10
J (0) 2 0 0 10
0
0
0 20
0
0
2
0
第五步:求修正量
UP222(0(0) ) UP322(30(0) )
J
(0)
fe22((00)) fe33((00))
2)计算各节点运算功率:
S (0) i
S Li
U
(
0)
2 i
yi
0
配电网前推回推潮流计算的步骤
3)从网络末端开始,逐步前推,由节点电
U (0) i
压 ,求全网各支路功率分布。
前推过程为:
P (1) ij
Pj(0)
P (1) jk
Pij(1)
kC j
Q(1) ij
Q(0) j
j 1
j 1
1 (10 0.66693410 0.0166934) 0.5
3
3
Q1 f1 (G1 je j B1 j f j ) e1 (G1 j f j B1 je j )
j 1
j 1
1 (20 10 0.99777610 0.999861) 0.02363
牛顿拉夫逊潮流计算
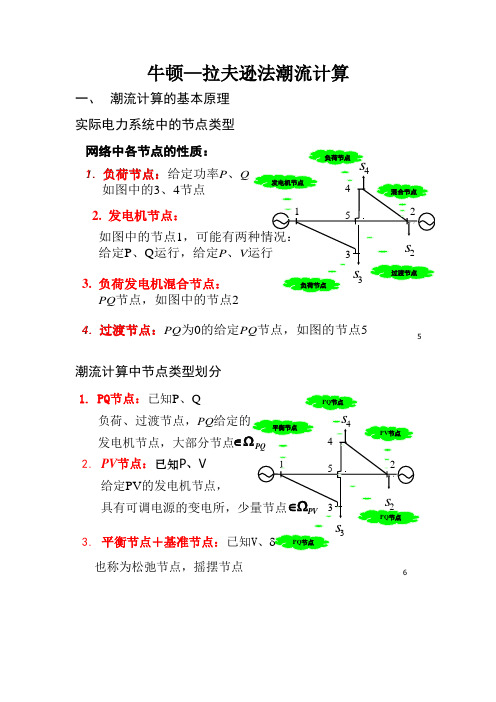
牛顿—拉夫逊法潮流计算一、 潮流计算的基本原理实际电力系统中的节点类型5二、实际电力系统中的节点类型123452s 3s 4s 过渡节点:PQ 为0的给定PQ 节点,如图的节点5网络中各节点的性质:负荷节点:给定功率P 、Q 如图中的3、4节点如图中的节点1,可能有两种情况:给定P 、Q 运行,给定P 、V 运行3. 负荷发电机混合节点:PQ 节点,如图中的节点2发电机节点负荷节点负荷节点混合节点过渡节点1. 负荷节点:2. 发电机节点:4.潮流计算中节点类型划分6三、潮流计算中节点类型的划分也称为松弛节点,摇摆节点123452s 3s 4s 平衡节点PQ 节点PQ 节点PV 节点PQ 节点PQ∈Ω1. PQ 节点:已知P 、Q负荷、过渡节点,PQ 给定的发电机节点,大部分节点PV ∈Ω给定PV 的发电机节点,具有可调电源的变电所,少量节点2.PV 节点:已知P 、V3. 平衡节点+基准节点:已知V 、δ采用极坐标,节点电压表示为()cos sin i i i i i i V V V j δδδ=∠=+节点功率将写成⎪⎪⎭⎪⎪⎬⎫-=+=∑∑==n j ij ij ij ij j i i nj ij ij ij ij j i i B G V V Q B G V V P 11)cos sin ()sin cos (δδδδ (1) 式中,ij i j δδδ=-,是i 、j 两节点电压的相角差。
方程式把节点功率表示为节点电压的幅值和相角的函数。
在有n 个节点的系统中,假定第1~m 号节点为P Q 节点,第1~1m n +-号节点为PV 节点,第n 号节点为平衡节点。
n V 和n δ是给定的,PV 节点的电压幅值11~m n V V +-也是给定的。
因此,只剩下1n -个节点的电压相角121,,,n δδδ- 和m 个节点的电压幅值12,,,m V V V 是未知量。
实际上,对于每一个P Q 节点或每一个PV 节点都可以列写一个有功功率不平衡量方程式()1(cos sin )01,2,,1ni is i is i j ij ij ij ij j P P P P V V G B i n δδ=∆=-=-+==-∑ (2)而对于每一个P Q 节点还可以再列写一个无功功率不平衡量方程式()1(sin cos )01,2,,ni is i is i j ij ij ij ij j Q Q Q Q V V G B i m δδ=∆=-=--==∑ (3)式(2)和式(3)一共包含了1n m -+个方程式,正好同未知量的数目相等,而比直角坐标形式的方程少了1n m -+个。
牛顿拉斐逊法潮流计算

牛顿拉斐逊法潮流计算牛顿拉夫逊法(Newton-Raphson method)是一种数值计算方法,用于解非线性方程。
其原理是通过迭代来逼近方程的根。
在电力系统中,牛顿拉夫逊法常用于求解潮流计算问题。
潮流计算是电力系统调度运行和规划的基础工作,其目的是确定电力系统各节点的电压幅值和相角,以及各支线上的功率和无功功率。
通过潮流计算可以有效地评估电力系统的稳定性和运行状态,并为电力系统的调度和规划提供参考依据。
牛顿拉夫逊法的核心思想是通过接近方程的根来求解非线性方程。
其基本步骤如下:1.初始化:选取一个初始点作为方程的近似解,通常选择电力系统的平衡状态作为初值。
2.构造雅可比矩阵:根据潮流方程的特点,建立牛顿拉夫逊法的雅可比矩阵。
雅可比矩阵描述了非线性方程的导数关系,用于迭代计算过程中的线性化。
3.迭代计算:利用雅可比矩阵和当前解向量,构建迭代格式,并计算得到新的解向量。
迭代格式中,包括牛顿方程和拉夫逊方程。
牛顿方程用于计算不平衡功率的校正量,而拉夫逊方程用于计算不平衡电压的校正量。
4.收敛判断:判断迭代计算得到的新解是否满足收敛条件。
通常使用误差向量的范数作为判断依据。
如果误差向量的范数小于预先设定的阈值,即可认为迭代已经收敛。
5.循环迭代:如果迭代计算得到的新解不满足收敛条件,继续进行迭代计算,直到达到收敛条件为止。
牛顿拉夫逊法的优点是收敛速度较快,尤其适用于求解非线性方程的问题。
然而,该方法也存在一些缺点。
首先,牛顿拉夫逊法需要提供一个合适的初始点,如果初始点选择不当,可能会导致迭代过程发散。
其次,构造雅可比矩阵和计算迭代格式的过程较为复杂,需要一定的数学基础和计算能力。
在电力系统潮流计算中,牛顿拉夫逊法广泛应用于求解节点电压和支路功率的平衡方程。
通过牛顿拉夫逊法,可以准确地计算出系统各节点的电压幅值和相角,指导电网的调度运营和规划工作。
总之,牛顿拉夫逊法是一种重要的数值计算方法,特别适用于求解非线性方程。
牛顿拉夫逊法潮流计算

摘要本文,首先简单介绍了基于在MALAB中行潮流计算的原理、意义,然后用具体的实例,简单介绍了如何利用MALAB去进行电力系统中的潮流计算。
众所周知,电力系统潮流计算是研究电力系统稳态运行情况的一种计算,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态:各线的电压、各元件中流过的功率、系统的功率损耗等等。
在电力系统规划的设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性、可靠性和经济性。
此外,在进行电力系统静态及暂态稳定计算时,要利用潮流计算的结果作为其计算的基础;一些故障分析以及优化计算也需要有相应的潮流计算作配合;潮流计算往往成为上述计算程序的一个重要组成部分。
以上这些,主要是在系统规划设计及运行方式安排中的应用,属于离线计算范畴。
牛顿-拉夫逊法在电力系统潮流计算的常用算法之一,它收敛性好,迭代次数少。
本文介绍了电力系统潮流计算机辅助分析的基本知识及潮流计算牛顿-拉夫逊法,最后介绍了利用MTALAB程序运行的结果。
关键词:电力系统潮流计算,牛顿-拉夫逊法,MATLABABSTRACTThis article first introduces the flow calculation based on the principle of MALAB Bank of China, meaning, and then use specific examples,a brief introduction, how to use MALAB to the flow calculation in power systems.As we all know, is the study of power flow calculation of power system steady-state operation of a calculation, which according to the given operating conditions and system wiring the entire power system to determine the operational status of each part: the bus voltage flowing through the components power, system power loss and so on. In power system planning power system design and operation mode of the current study, are required to quantitatively calculated using the trend analysis and comparison of the program or run mode power supply reasonable, reliability and economy. In addition, during the power system static and transient stability calculation, the results of calculation to take advantage of the trend as its basis of calculation; number of fault analysis and optimization also requires a corresponding flow calculation for cooperation; power flow calculation program often become the an important part. These, mainly in the way of system design and operation arrangements in the application areas are off-line calculation.Newton - Raphson power flow calculation in power system is one commonly used method, it is good convergence of the iteration number of small, introduce the trend of computer-aided power system analysis of the basic knowledge and power flow Newton - Raphson method, introduced by the last matlab run results.Keywords:power system flow calculation, Newton – Raphson method, matlab目录1 绪论 (1)1.1 课题背景 (1)1.2 电力系统潮流计算的意义 (2)1.3 电力系统潮流计算的发展 (2)1.4 潮流计算的发展趋势 (4)2 潮流计算的数学模型 (5)2.1 电力线路的数学模型及其应用 (5)2.2 等值双绕组变压器模型及其应用 (6)2.3 电力网络的数学模型 (8)2.4 节点导纳矩阵 (9)2.4.1 节点导纳矩阵的形成 (9)2.4.2 节点导纳矩阵的修改 (10)2.5 潮流计算节点的类型 (11)2.6 节点功率方程 (12)7 潮流计算的约束条件 (13)2·3 牛顿-拉夫逊法潮流计算基本原理 (14)3.1 牛顿-拉夫逊法的基本原理 (14)3.2 牛顿-拉夫逊法潮流计算的修正方程 (17)3.3 潮流计算的基本特点 (20)3.4 节点功率方程 (21)4牛顿-拉夫逊法分解潮流程序 (22)41 牛顿-拉夫逊法分解潮流程序原理总框图 (22)·4.2 形成节点导纳矩阵程序框图及代码 (23)4.21 形成节点导纳矩阵程序框图 (23)。
潮流计算的基本算法及使用方法

(i,j=1,2,…,n-1)
(2-5)
(i,j=1,2,…,m)
(2-6)
(2-7)
(2-8)
将式(2-7)和式(2-8)分别代入式(2-2)和(2-3),便得到:
用和分别左乘以上两式便得简化了的修正方程式,可展开写成:
(2-9) (2-10) 式(2-9)和式(2-10)就是快速分解法潮流计算的修正方程式, 其中系数矩阵都是由节点导纳矩阵的虚部构成,只是阶次不同,矩阵为 阶,不含平衡节点对应的行和列,矩阵为阶,不含平衡节点和节点对应 的行和列。 (2-11) (2-12) 修正方程式(2-9)和(2-10)与功率误差方程式(2-11)和(2 -12)构成了快速分解法迭代的基本计算公式。 2.3 快速分解法的特点 快速分解法与牛顿法潮流计算的主要差别表现在它们的修正方程 上。快速分解法通过对电力系统具体特点的分析,对牛顿法修正方程式 的雅克比矩阵进行了有效的简化和改进,得到式(2-9)、式(2- 10)所示的修正方程式。这两组方程式和牛顿法的修正方程相比主要有 三个特点: a)快速分解法的修正方程式用两个阶线性方程组代替了一个阶线方 程组。 b)快速分解法的修正方程式中系数矩阵的所有元素在迭代过程中维 持常数不变。 c)快速分解法的修正方程式中系数矩阵是对称矩阵。 这些特点在提高计算速度和减少内存方面的作用是很明显的:首 先,因为修正方程式的系数矩阵是导纳矩阵的虚部,因此在迭代过程中 不必像牛顿法那样每次都要重新计算雅克比矩阵,这样不仅减少了运算 量,而且也大大简化了程序;其次,由于系数矩阵在迭代过程中维持不 变,因此在求解修正方程式时,不必每次都对系数矩阵进行消去运算, 只需要在进入迭代过程以前,将系数矩阵用三角分解形成因子表,然后 反复利用因子表对不同的常数项或进行消去和回代运算,就可以迅速求 得修正量,从而显著提高了迭代速度;第三,由于对称矩阵三角分解
(完整word版)牛顿拉夫逊法潮流计算

摘要本文,首先简单介绍了基于在MALAB中行潮流计算的原理、意义,然后用具体的实例,简单介绍了如何利用MALAB去进行电力系统中的潮流计算。
众所周知,电力系统潮流计算是研究电力系统稳态运行情况的一种计算,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态:各线的电压、各元件中流过的功率、系统的功率损耗等等。
在电力系统规划的设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性、可靠性和经济性。
此外,在进行电力系统静态及暂态稳定计算时,要利用潮流计算的结果作为其计算的基础;一些故障分析以及优化计算也需要有相应的潮流计算作配合;潮流计算往往成为上述计算程序的一个重要组成部分。
以上这些,主要是在系统规划设计及运行方式安排中的应用,属于离线计算范畴。
牛顿-拉夫逊法在电力系统潮流计算的常用算法之一,它收敛性好,迭代次数少.本文介绍了电力系统潮流计算机辅助分析的基本知识及潮流计算牛顿-拉夫逊法,最后介绍了利用MTALAB程序运行的结果。
关键词:电力系统潮流计算,牛顿-拉夫逊法,MATLABABSTRACTThis article first introduces the flow calculation based on the principle of MALAB Bank of China,meaning, and then use specific examples,a brief introduction, how to use MALAB to the flow calculation in power systems。
As we all know, is the study of power flow calculation of power system steady-state operation of a calculation,which according to the given operating conditions and system wiring the entire power system to determine the operational status of each part:the bus voltage flowing through the components power, system power loss and so on. In power system planning power system design and operation mode of the current study, are required to quantitatively calculated using the trend analysis and comparison of the program or run mode power supply reasonable, reliability and economy.In addition, during the power system static and transient stability calculation, the results of calculation to take advantage of the trend as its basis of calculation;number of fault analysis and optimization also requires a corresponding flow calculation for cooperation;power flow calculation program often become the an important part. These,mainly in the way of system design and operation arrangements in the application areas are off—line calculation。
ILU 预处理Newton-Krylov方法的潮流计算

ILU 预处理Newton-Krylov方法的潮流计算廖小兵;王文超;李奔【期刊名称】《计算技术与自动化》【年(卷),期】2015(000)004【摘要】Due to the high-dimensional and sparse characteristics of correction equations in power systems,the preconditioned Krylov subspace methods were applied to solve the correction equations,thus forming the Newton-Krylov power flow calculation methods.With the ILU preconditioner,this paper compared the computational efficiency of three kinds of the most commonly used Newton-Krylov methods for solving power flow equations.Through power flow calculation ofIEEE30,IEEE118,IEEE300 and 3 Poland large-scale power systems,the results show that the three Newton-Krylov methods are effective methods for power flow calculation,which have good convergence property and computational efficiency.%由于电力系统修正方程组具有高维、稀疏的特点,本文提出将预处理 Krylov 子空间方法应用于潮流修正方程组的求解,形成预处理Newton-Krylov 的潮流计算方法。
基于Neumann级数预处理的Newton-GMRES潮流计算方法

Email: wangwb0802@, lxbctgu@
Abstract: This paper presents a new preconditioning technique, which is used to improve the convergence performance of Newton-GMRES power flow computation. By using of four basic types of matrix splitting algorithms and the matrix inversion technique based on Neumann series, a new kind of preconditioner based on Neumann series is derived. This kind of preconditioning technique used for power flow computation of Newton-GMRES method can significantly improve the convergence performance and the efficiency of power flow computation. Finally, Power flow computation results of IEEE 118-bus system verify the effectiveness of the proposed method. Keywords: Matrix splitting; Neumann series; Preconditioning; Newton-GMRES; Convergence performance
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ILU预处理Newton—Krylov方法的潮流计算作者:廖小兵王文超李奔来源:《计算技术与自动化》2015年第04期摘要:由于电力系统修正方程组具有高维、稀疏的特点,本文提出将预处理Krylov子空间方法应用于潮流修正方程组的求解,形成预处理NewtonKrylov的潮流计算方法。
结合ILU 预处理方法,比较了最常用的3类NewtonKrylov方法求解潮流方程的计算效果。
通过对IEEE30、IEEE118、IEEE300 和3个Poland大规模电力系统进行潮流计算,结果表明:3类NewtonKrylov方法是电力系统潮流计算的有效方法,呈现出良好的收敛特性和计算效率。
关键词:潮流计算;修正方程组;ILU预处理;NewtonKrylov方法中图分类号:TM744 文献标识码:A1引言潮流计算是电力系统分析中最古老的经典课题之一。
传统的电力系统潮流计算通常以牛顿法为主[1]。
牛顿法是求解非线性代数方程组的有效方法之一,它将非线性方程组的求解转化为线性代数方程组的求解,但由于每次迭代后都需更新雅可比矩阵的元素,导致每次都需求解高维的线性代数方程组。
传统的直接法,如Gauss消去法,LU分解等,计算量和存储量较大,且固有的前推回代过程难以并行[2-3]。
迄今为止,越来越多的国内外研究人员在电力系统潮流计算中采用NewtonKrylov方法求解潮流方程[4-8]。
NewtonKrylov方法是在不精确牛顿法的基础上,结合Krylov子空间迭代法,形成的一类新的求解非线性方程组的数值方法。
这类方法结合了Newton方法的良好收敛特性,以及Krylov子空间方法的存储量少、计算量小、易于并行等优点[9],非常适合并行求解大规模的非线性方程组问题[10]。
文献[4]首次将Krylov子空间法中的GMRES方法应用于潮流计算中。
文献[5]将此类迭代法与不精确牛顿法相结合(NewtonGMRES),同时采用不同的预处理方法,对两个大规模电力系统进行了对比分析计算。
结果表明:结合适当的预处理的NewtonGMRES方法比NewtonLU方法约快2倍。
迄今为止,在潮流计算中应用最广泛的NewtonKrylov方法是NewtonGMRES方法。
结合预处理技术的NewtonGMRES方法具有良好的收敛特性和数值稳定性,已成为大规模电力系统潮流计算首选方法之一。
目前,关于其它NewtonKrylov方法[11]在潮流计算中的应用还缺乏相关的报道,以及它们在潮流计算中计算效率的比较。
因此,本文结合ILU预处理技术,将3种最常用的NewtonKrylov方法应用于潮流计算,并比较了它们的收敛性和计算效率。
3预处理NewtonKrylov方法的潮流计算Krylov子空间方法是求解大型稀疏线性代数方程组的一类有效方法,其收敛速度依赖于其系数矩阵特征值的分布。
通过选取适当的矩阵M使M-1A尽可能接近单位阵,来改善系数矩阵特征值分布的方法称为预处理技术,。
通常的做法是令M在某种意义下接近A并且M-1的计算易于实现或选取接近于A-1的M-1并且M-1容易求取。
迄今为止,潮流计算常用的预处理方法主要包括直接抽取矩阵的对角线元素作为预条件子、ILU分解(incomplete LU factorization)、不完全 Cholesky 分解、Jacobi 预条件子等。
文献[10]对这几种预处理方法,采用不同规模的电力系统进行了潮流计算,结果表明:结果表明:基于ILU分解的预处理方法比其它预处理方法具有更少的迭代次数和浮点运算次数。
NewtonKrylov潮流计算方法的本质是一种双层迭代法。
在求解过程中,均含内、外两类迭代过程:一般将牛顿法迭代过程称为外迭代;将稀疏线性代数方程组的迭代求解过程称为内迭代,即Krylov子空间迭代。
严格来说,NewtonKrylov潮流计算方法并不是一种新方法。
但由于结合了预处理技术,而预处理方法的选择极具灵活性,所以是一种极具潜力的计算方法。
4算例仿真和分析本文所有仿真分析均基于MATLAB平台,设计实现了3种NewtonKrylov(NG法,NB 法,NC法)潮流计算程序,并以此详细比较3种NewtonKrylov方法求解潮流方程的效率。
外迭代的收敛容差为1e-6(基准功率100MVA),内迭代的收敛容差为1e-2。
图1是基于ILU 预处理NewtonKrylov方法潮流计算流程图。
图1基于ILU预处理NewtonKrylov方法潮流计算流程图所采用的算例模型包括 IEEE标准测试系统 IEEE30、IEEE118和IEEE300,以及3个Poland互联大规模电力系统模型,测试时间取平均值。
表1给出了6个算例系统的网络规模和雅可比矩阵的条件数。
从表1可以看出随着电力系统规模的扩大,其初次形成的雅可比矩阵J 的条件数往往是很大的(cond(J)>1e+3),接近极限运行状态。
表2是基于ILU预处理NewtonKrylov方法进行潮流计算的结果。
从表2可以看出,3种NewtonKrylov方法的收敛性都非常强健;在同样收敛精度的情况下,NB法和NC法在收敛速度上比NG法快,大约减少一半的迭代次数;但NB法和NC法包含了两次正交化的过程,计算量大约是NG法的两倍,因此,从整体上来说求解效率并没有明显提高。
再结合表3可知,当电力系统规模较小时,NB法和NC法都比NG法节省计算时间;随着电力系统规模的增大(上千节点时),NG法的计算时间较NB法和NC法减少。
需要说明一下,对于IEEE30系统而言,ILU预处理的精度太高,将迭代法变成了直接法,相当于ILU预处理和内迭代中两次分解雅克比矩阵,使得IEEE30系统的计算时间比IEEE118系统还要多。
5结论及讨论3类NewtonKrylov方法是计算电力系统潮流的有效方法,具有良好的收敛特性和计算效率。
在同样的收敛精度下,基于ILU预处理的NG法和NC法的内迭代次数较NG法明显减少,但NG法和NC法的计算量大约是NG法的两倍,因此,在计算时间上并没有明显提高。
总体上说,3类算法各有优缺点,要根据电力系统的规模,选择合适的算法。
NewtonKrylov潮流计算方法成功的核心在于预处理矩阵的选取,本文采用最常用的ILU预处理方法,其它预处理方法对3类NewtonKrylov的方法计算效率的影响,及如何针对不同规模的电力系统,选取合适的预处理方法,都缺乏相关的结论。
预处理方法和NewtonKrylov 的方法怎样协调配合计算不同规模的电力系统潮流,都有待进一步研究和验证。
参考文献[1]张伯明,陈寿孙. 高等电力网络分析[M]. 北京:清华大学出版社, 2007[2]刘凯,陈红坤,向铁元,等. 以对称反对称分裂预条件处理GMRES(m)的不精确牛顿法潮流计算[J]. 电网技术, 2009, 33(19): 123-126.[3]胡博,谢开贵,曹侃. 基于Beowulf集群的大规模电力系统牛顿法潮流求解的并行GMRES方法[J]. 电工技术学报, 2011, 26(4): 145-152.[4]SEMLYEN A. Fundamental concepts of a Krylov subspace power flow methodology[J]. IEEE Trans on Power Systems, 1996, 11(3): 1528-1537.[5]FLUECK A J,CHIANG H D. Solving the nonlinear power flow equations with an inexact Newton method using GMRES [J]. IEEE Trans on Power Systems, 1998, 13(2): 269-273.[6]ALVES A B,ASADA E N, MONTICELLI A. Critical evaluation of direct and iterative methods for solving AX=b systems in power flow calculations and contingency analysis[J]. IEEE Trans on Power Systems, 1999, 14(2): 702-708.[7]蔡大用,陈玉荣. 用不完全 LU分解预处理的不精确潮流计算方法[J]. 电力系统自动化, 2002, 22(25): 11-14.[8]刘洋,周家启,谢开贵,等. 预条件处理CG法大规模电力系统潮流计算[J]. 中国电机工程学报, 2006, 26(7): 89-94.[9]蔡大用,白峰杉. 现代科学计算[M]. 北京:科学出版社, 2000.[10]胡博,周家启,刘洋,等. 基于预条件处理 GMRES的不精确牛顿法潮流计算[J].电工技术, 2007, 22(2): 98-104.[11]梁恒,白峰杉. 对称不定问题的不精确Newton法[J]. 计算数学, 2002, 24(3):319-326.[12]SAAD Y,SCHULTZ M H. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM Journal on Scientific and Statistical Computing,1986, 7(3): 856-869.[13]SAAD Y. Iterative methods for sparse linear systems[M]. Second Edition. U.S: Society for Industrial and Applied Mathematics, 2003.[14]LANCZOS C. Solution of systems of linear equations by minimized iteration[J]. Res. Nat. Bur. Stand, 1952, 49: 33-53.。
