电磁场总复习
电磁场与电磁波总复习

一、 填空题(10)——已写入的答案——力佐提供1.如果两个不等于零的矢量的点积等于零,则此两个矢量必然相互 垂直 。
2.如果两个不等于零的矢量的叉积等于零,则此两个矢量必然相互 平行 。
3.矢量z y x e e e A ˆˆˆ++=的大小为 3 。
4.矢量场)(r A穿过闭合曲面S 的通量的表达式为:()sA r d s ∙⎰⎰ 。
5.磁感应强度沿任一曲面S 的积分称为穿过曲面S 的 磁能量 。
6.从场角度来讲,电流是电流密度矢量场的 通量 。
7.矢量场)(r A在闭合曲线C 上环量的表达式为:C()d r A r ∙⎰ 。
8.如果一个矢量场的旋度等于零,则称此矢量场为 无旋场 。
9.如果一个矢量场的散度等于零,则称此矢量场为 无散场 。
10.静电场是无旋场,故电场强度沿任一条闭合路径的积分等于0 。
11.恒定磁场是无散场,故磁感应强度沿任一闭合曲面的积分等于 0 。
12.一个标量场的性质,完全可以由它的 梯度 来表征。
13. 亥姆霍兹定理告诉我们,研究任何一个矢量场应该从矢量的 散度与旋度 两个角度去研究。
14.从矢量场的整体而言,无散场的 旋度 不能处处为零。
15.从矢量场的整体而言,无旋场的 散度 不能处处为零。
16.由相对于观察者静止的,且其电量不随时间变化的电荷所产生的电场称为 静电场 。
17.由恒定电流所产生的磁场称为 恒磁场 。
18.在均匀各向同性线性媒质中,设媒质的导磁率为μ,则磁感应强度B和磁场H满足的方程为: =B H μ .19. 在均匀各向同性线性媒质中,设媒质的介电常数为ε,则电位移矢量D 和电场E满足的方程为: =D E ε . 20. 麦克斯韦 方程是经典电磁理论的核心。
21.所谓矢量线,乃是这样一些曲线,在曲线上的每一点上,该点的切线方向与矢量场的方向 相同 。
22.由恒定电流产生的磁场称为恒定磁场,恒定磁场是无散场,因此,它可用 矢位(矢势) 函数的旋度来表示。
(完整版)高中物理电磁学总复习

高三物理总复习电磁学复习内容:高二物理(第十三章 电场、第十四章 恒定电流、第十五章 磁场、第十六章 电磁感应、第十七章 变交电流、第十八章 电磁场与电磁波)复习范围:第十三章~第十八章电磁学§.1 第十三章 电场1. (1)电荷守恒定律:电荷既不能创造,也不能消灭,只能从一个物体转移给另一个物体或者从物体的一部分转移到另一部分。
(2)应用起电的三种方式:摩擦起电(前提是两种不同的物质发生摩擦)、感应起电(把电荷移近不带电的导体(不接触导体),使导体带电)、接触带电.注意:①电荷量e 称为元电荷电荷量C 1060.119-⨯=e ;②电子的电荷量e 和电子的质量m 的比叫做电子的比荷C/kg 1076.111⨯=em e。
③两个完全相同的带电金属小球接触时................电荷量分配规律:原带异种电荷的先中和后平分;原带同种电荷的总电荷量平分.2. 库仑定律。
⑴适用对象:点电荷。
注意:①带电球壳可等效点电荷。
当带电球壳均匀带电时,我们可等效在球心处有一个点电荷;球壳不均匀带电荷时,则等效点电荷就靠近电荷多的一侧。
②库仑力也是电场力,它只是电场力的一种。
⑵公式:221r Q Q k F ⋅=(k 为静电力常量等于229/c m N 109.9⋅⨯).3.(1)电场:只要有电荷存在,电荷周围就存在电场(电场是描述自身的物理量...........),电场的基本性质是它对放入其中的电荷有力的作用,这种力叫做电场力. (2)ⅰ。
电场强度(描述自身的物理量........): E = F / q 这个公式适用于一切电场,电场强度E 是矢量,物理学中规定电场中某点的场强方向跟正电荷在该点的电场力的方向相同,即正电荷受的电场力方向,即E 的方向为负电荷受的电场力的方向的反向。
此外F = Eq 与221r Q Q k F ⋅=不同就在于前者适用任何电场,后者只适用于点电荷.注意:①对检验电荷(可正可负)的要求:一是电荷量应当充分小;二是体积也要小。
电磁场与电磁波知识点复习

电磁场与电磁波知识点复习一、电磁场的基本概念电磁场是由电场和磁场相互作用而形成的一种物理场。
电场是由电荷产生的,而磁场则是由电流或变化的电场产生的。
电荷是产生电场的源,库仑定律描述了两个静止点电荷之间的相互作用力与它们电荷量的乘积成正比,与它们之间距离的平方成反比。
电场强度是描述电场强弱和方向的物理量,其定义为单位正电荷在电场中所受到的力。
电流是产生磁场的源,安培定律描述了电流元之间的相互作用。
磁场强度则是描述磁场强弱和方向的物理量。
二、电磁波的产生电磁波是由时变的电场和时变的磁场相互激发而产生,并在空间中以一定的速度传播。
变化的电流和电荷分布都可以产生电磁波。
例如,一个振荡的电偶极子就是一种常见的电磁波源。
当电偶极子中的电荷来回振动时,周围的电场和磁场也随之发生周期性的变化,从而产生电磁波向空间传播。
三、电磁波的性质1、电磁波是横波电磁波中的电场强度和磁场强度都与电磁波的传播方向垂直,这是电磁波作为横波的重要特征。
2、电磁波的传播速度在真空中,电磁波的传播速度恒定,等于光速 c,约为 3×10^8 米/秒。
3、电磁波的频率和波长频率和波长是描述电磁波的两个重要参数,它们之间的关系为:波长=光速/频率。
电磁波的频率范围非常广泛,从低频的无线电波到高频的伽马射线。
4、电磁波的能量电磁波具有能量,其能量密度与电场强度和磁场强度的平方成正比。
四、麦克斯韦方程组麦克斯韦方程组是描述电磁场基本规律的一组方程,包括四个方程:高斯定律、高斯磁定律、法拉第电磁感应定律和安培麦克斯韦定律。
高斯定律描述了电场的通量与电荷量之间的关系;高斯磁定律表明磁场的通量总是为零;法拉第电磁感应定律说明了时变磁场可以产生电场;安培麦克斯韦定律则指出时变电场也可以产生磁场。
这组方程统一了电学和磁学现象,预言了电磁波的存在,并奠定了现代电磁学的基础。
五、电磁波的传播电磁波在不同介质中的传播特性不同。
在均匀介质中,电磁波遵循直线传播规律;当电磁波从一种介质进入另一种介质时,会发生折射和反射现象。
电磁场电磁波复习重点

电磁场电磁波复习重点第一章矢量分析1、矢量的基本运算标量:一个只用大小描述的物理量。
矢量:一个既有大小又有方向特性的物理量,常用黑体字母或带箭头的字母表示。
2、叉乘点乘的物理意义会计算3、通量源旋量源的特点通量源:正负无旋度源:是矢量,产生的矢量场具有涡旋性质,穿过一曲面的旋度源等于(或正比于)沿此曲面边界的闭合回路的环量,在给定点上,这种源的(面)密度等于(或正比于)矢量场在该点的旋度。
4、通量、环流的定义及其与场的关系通量:在矢量场F中,任取一面积元矢量dS,矢量F与面元矢量dS的标量积F.dS定义为矢量F穿过面元矢量dS的通量。
如果曲面 S 是闭合的,则规定曲面的法向矢量由闭合曲面内指向外;环流:矢量场F沿场中的一条闭合路径C的曲线积分称为矢量场F沿闭合路径C的环流。
如果矢量场的任意闭合回路的环流恒为零,称该矢量场为无旋场,又称为保守场。
如果矢量场对于任何闭合曲线的环流不为零,称该矢量场为有旋矢量场,能够激发有旋矢量场的源称为旋涡源。
电流是磁场的旋涡源。
5、高斯定理、stokes定理静电静场高斯定理:从散度的定义出发,可以得到矢量场在空间任意闭合曲面的通量等于该闭合曲面所包含体积中矢量场的散度的体积分,即散度定理是闭合曲面积分与体积分之间的一个变换关系,在电磁理论中有着广泛的应用。
Stokes定理:从旋度的定义出发,可以得到矢量场沿任意闭合曲线的环流等于矢量场的旋度在该闭合曲线所围的曲面的通量,即斯托克斯定理是闭合曲线积分与曲面积分之间的一个变换关系式,也在电磁理论中有广泛的应用。
6、亥姆霍兹定理若矢量场在无限空间中处处单值,且其导数连续有界,源分布在有限区域中,则当矢量场的散度及旋度给定后,该矢量场可表示为亥姆霍兹定理表明:在无界空间区域,矢量场可由其散度及旋度确定。
第二章电磁场的基本规律1、库伦定律(大小、方向)说明:1)大小与两电荷的电荷量成正比,与两电荷距离的平方成反比;2)方向沿q1 和q2 连线方向,同性电荷相排斥,异性电荷相吸引;3)满足牛顿第三定律。
电磁场数学方法总复习

电磁场数学方法第一章 场论1 方向导数定义:方向导数是在一个点M 处沿方向l 的函数()u M 当0ul∂>∂时,函数u 沿l r 方向增加。
当0ul∂<∂时,函数u 沿l r 方向减少。
定理1. 函数(,,)u u x y z =在点0000(,,)M x y z 处可微;cos α,cos βcos γ为l 方向的方向余弦,则函数u 在点0M 处沿l 且由如下公式给出:cos cos cos u u u ul x y zαβγ∂∂∂∂=++∂∂∂∂ 其中,,u u ux y z∂∂∂∂∂∂是在点0M 处的偏导数。
2 梯度方向导数解决了函数()u M 在给定点处沿某个方向的变化率问题。
梯度则解决了函数()u M 在给定点处沿哪个方向的变化率最大的问题。
考察方向导数公式:cos cos cos ||cos(,)u u u uG l G G l l x y zαβγ∂∂∂∂=++=⋅=∂∂∂∂r r r r r 式中u u u G i j k x y z∂∂∂=++∂∂∂r r r r ,cos cos cos l i j k αβγ=++r r r r。
梯度的定义:若在数量场()u M 中的一点M 处,存在这样一个矢量G r,其方向为函数()u M 在M 点处变化率最大的方向,其模也正好是这个最大变化率的数值,则称矢量G ϖ为函数()u M 在点M 处的梯度,记作grad u ,即:()u u u grad u G i j k x y z∂∂∂==++∂∂∂rr r r3 矢量场的通量及散度 通量通量的定义:设有矢量场()A M r ,沿有向曲面S 某一侧的曲面积分n ssA ds A dsΦ==⋅⎰⎰⎰⎰r r称为该矢量穿过曲面S 的通量。
散度的定义:lim lim s M M A dsdivA V v∆∆Ω->∆Ω->⋅∆Φ==∆∆⎰⎰r r r Ò。
工程电磁场 复习资料

工程电磁场_复习资料工程电磁场复习资料一、电磁场的基本概念1、电磁场:是由电场和磁场两种矢量场组成的一种物理场。
2、电磁场的性质:电磁场具有能量、动量和惯性等性质,这些性质可以从麦克斯韦方程组中得到描述。
3、电磁场的波动性:电磁场以波的形式传播,这种波动性表现为电场和磁场在空间中的传播。
4、电磁感应:当导体处于变化的磁场中时,导体内部会产生感应电流,这种现象称为电磁感应。
二、麦克斯韦方程组麦克斯韦方程组是描述电磁场的基本方程组,包括四个基本方程:1、安培环路定律:描述磁场与电流之间的关系。
2、法拉第电磁感应定律:描述电磁感应现象。
3、麦克斯韦方程组的一般形式:描述了电场和磁场在空间中的传播。
4、高斯定律:描述了电荷在空间中的分布。
三、电磁场的边界条件电磁场在两种不同媒质的分界面上会发生反射和折射等现象,这些现象可以用边界条件来描述。
边界条件包括:1、电场强度和磁场强度在分界面上的连续性。
2、电位移矢量和磁感应强度在分界面上的连续性。
3、分界面上没有电荷堆积。
四、电磁场的能量和动量电磁场具有能量和动量,这些量可以用以下公式计算:1、电磁场的能量密度:W=1/2(E^2+B^2)2、电磁场的动量密度:P=E×B3、电磁场的能量流密度:S=E×H五、电磁场的波动性电磁场以波的形式传播,这种波动性可以用波动方程来描述。
波动方程的一般形式为:∇×E=ρ/ε,∇×H=J/εc^2,其中ρ和J分别为电荷密度和电流密度,ε为真空中的介电常数,c为光速。
六、电磁场的散射和衍射当电磁波遇到障碍物时,会发生散射现象;当电磁波通过孔洞或缝隙时,会发生衍射现象。
这些现象可以用费马原理和基尔霍夫公式来描述。
管理学复习资料马工程版一、管理学概述1、管理学定义:管理学是一门研究管理活动及其规律的科学,旨在探索如何有效地组织、协调和控制人的行为,以实现组织目标。
2、管理学的发展历程:管理学作为一门独立的学科,经历了古典管理理论、行为科学理论、现代管理理论等多个发展阶段。
电磁场与电磁波课程主要知识点总复习
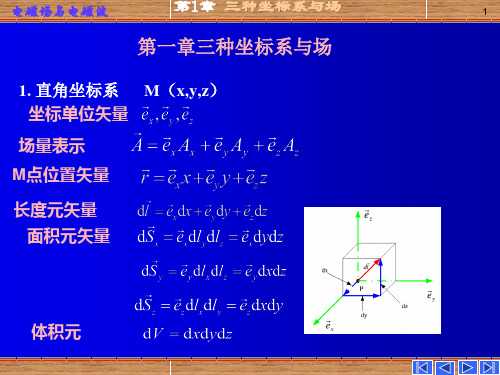
第1章 三种坐标系与场
概念:
| lim u
u u cos u cos u cos
l M0 l0 l x
y
z
Байду номын сангаас
2. 标量场的梯度
3. 矢量场的通量
d S F dS S F endS
F(x, y, z)
en
dS
面积元矢量
电磁场与电磁波
第1章 三种坐标系与场
4. 矢量场的散度
divF lim S F (x, y, z) dS
(1)式称为真空中的高斯定律。它表明在闭合面S的的通量 就等于闭合曲面S所包含自由电荷的总量。
(2)式称为静电系统的守恒定理,说明静电场是一种守恒性 的矢量场---保守场
电磁场与电磁波
第1章 三种坐标系与场
作用:
(1)已知 时根据高斯定理积分方程,求
(2)已知两微分方程,根据亥姆霍兹定理,在给定矢量场的散 度方程与旋度方程确定的条件下,该静电场唯一地确定。
IP R
R x
I
图2 磁介质1的镜 像线电流
2 h 2
z
I I R
x
P
图3 磁介质2 的镜像线电流
电磁场与电磁波
第1章 三种坐标系与场
1、法拉第电磁感应定律
2、位移电流
电磁场与电磁波
第1章 三种坐标系与场
32
3、 麦克斯韦方程组
磁场沿任意闭合回路的环流 ,等于穿过该闭合回路C包 围的任意曲面S的传导电流 与位移电流之和。
第1章 三种坐标系与场 静电场( 区域) 恒定电场(电源外)
本构关系 位函数
边界条件
电磁场与电磁波
第1章 三种坐标系与场
第五章恒定磁场分析
大学物理变化的电磁场总复习内容深入超赞

dt
3.计算互感系数: (1)给任一回路通电流;
(2)计算穿过另一回路的磁通量;
(3)代入定义式或定义方程
例3:长直导线与矩形线圈共面,线圈中通有电
流I(t),计算长直导线中的互感电动势。
问题:长直导线是 解:设长直导线通有电流 I1
回路吗?
矩形线圈内的磁通量
I 1 I(t)
ds l
m S
BdS
=0
Lddtmddt(L)I
LdI dt
I
dL dt
当线圈形状、匝数、介质等不变时,L是常量.
εL
LdI dt
L L
dI dt
自感电动势与电流的变化率成正比
3.自感系数计算 考虑方法同计算电容。
(1)令回路通电流;
B
(2)计算穿过回路的磁通量;
(3)代入定义式或定义方程。
I
例1.计算长直螺线管(N,l,R)的自感系数:
da d
0 I1ldx 2 x
0Ill 2
nda d
o x d a
M m 0l lnd a
I1
M
2 d
dI 0llndadI
dt 2 d dt
三、磁场的能量
L
考虑自感线圈中电流的建立过程:
L
L di dt
K1
在移动dq=idt的过程中,电源反抗
自感电动势做功 dALdqLidt Lidi
在i从0到I过程中,做功
•单位:伏V
正
第十一章 变化的电磁场
§1 电磁感应 §2自感与互感 §3 Maxwell’s 方程组
本章重点:感应电动势、自感、互感 的计算
本章难点:涡旋电场,位移电流,场概念的理解
完整版电磁场理论复习总结

完整版电磁场理论复习总结1.1 标量场和⽮量场1.2 三种常⽤的正交坐标系1.3标量场的梯度哈密顿算符:(⼀e —e —e z)x y z2.梯度的垄本运算公式1) VC-0 (C^S)2) V(Cu)⼆CVw3) V((/ ⼟巧⼆可肿⼟V7附4) V(/a T) = Z/V V +T V;/5) VF(u) = F r(u)Vu6) V(-) = -l(rV?/-i/Vv)v vFF cF7) ^7(^ v) = —Vw + — Vvdu dv式中:U育常報;级⽢为半标变最遢載;3”梯度的重要性质16CJ55 「「⼩V x V/z = 0产⽣场的场源所在的空闾位国点称为源点上记为am或7 场所在的疇间⾫置点称为场贞「记为(x,y\2}或⼫源点到场点的距S?j?=|r-r| 从源点指向场点的⽮量为^ = r-F例3求鸥叫哙呻?刃畑%&R⾐⽰对仗」4运算R表⽰对运算.R^r-r1^J(x-A?)r+(y-/>:BR 、BR 、BR—MY臥叫帝M还W(R) = ARWR = ^-\R(lii dii fir ?S A dS A. A y A zdivA lim ——V 0 V x y zdivA A x A y A z Ax y zA e x( A z A y) e y( A x A z) e z(⼊sy z z x x y1) V Y C=02) Vx(i = A3) V x(H ±B) —V XJ1±V>.54) V x (u = uV y /< + V u KX B)=2J-V XJ4-J4-V X5l f ***** 4;jd' V x Vy - 0! 7)V (VxJ)-O:W屜囲焉唉屋?熾常数,址为标量函数「du电磁总复习第⼀章⽮量分析l ?Eit ⼗dit ?duIt= 0 r ——+ 0 L ——+&——标量场⼼的梯度. ex cy czV u =—yir rotAc'R ex R_y-y r漁—R 忑RVR = -RR'⽮童场的雄度1.4⽮量场的通量与散度三. 散度的运算公式])V C-02)V(Arl) = )tV^4) V (u A) =wV .4 + 4 Vw 沐为常数」为标量函数)- (IA5) V J(rt) - V// —du四、⾼斯定理(散度定理)L v知⼀丄%物理詳5G穿过⼀封闭曲⾓的总谓呈等于⽮虽散度的休秘分1.5⽮量场的环流与旋度-------------------- V VV v ?c A dl rotA nlim --S 0Sr r re x e y e zir irot A Ax y zA x A y A z4-症度计算相关公式:标葷场的梯度的旌度恒为零1G:2D3*酶点录场点df Rmax三、斯托克斯定理物理含义;—个⿂量场旋度的⾯税分導于演⽮量沿此由⾯周界的曲线眦四、⽮量场擬度的重要性质⼙(Vxj^O任意⽮量场I?度的散度等于議⽮量场有两种不同性质的源:(1)散度源(标量)(2)旋度源(⽮量)。
高三电磁场知识点总结详细

高三电磁场知识点总结详细电磁场是物理学中的一个重要概念,对于高三学生来说,电磁场是必修课程中的一个重点内容。
本文将详细总结高三电磁场的知识点,帮助学生们复习和理解相关知识。
第一部分:电磁场基础知识1. 电磁场的概念- 电磁场是由电荷体系形成的以电场和磁场为基本特征的力场。
2. 静电场与静磁场- 静电场:由静止的电荷所产生的电场。
- 静磁场:由静止的电荷所产生的磁场。
3. 电磁感应定律- 法拉第电磁感应定律:导体中的磁通量变化会产生感应电动势。
- 感应电动势的大小与导体中磁通量变化率成正比。
第二部分:电磁场的基本定律1. 库仑定律- 库仑定律描述了两个点电荷间相互作用力的大小与距离的关系。
- 库仑定律公式:F = k * (q1 * q2) / r^22. 电场的叠加原理- 多个电荷同时存在时,它们产生的电场可以通过叠加原理求和得到。
3. 磁场的基本性质- 磁场是由带电粒子运动或者电流产生的。
- 磁场具有方向性,用磁力线表示。
第三部分:电场与电势1. 电势能- 电荷在电场中具有电势能,电势能与电荷的大小、电势差和电场强度有关。
- 电势能的计算公式:Ep = q * V2. 电位- 电位是指某一点的电势能与单位正电荷之比。
- 电位的计算公式:V = U / q3. 静电平衡- 静电平衡要求电场内的电势能相等,即电荷处于平衡状态。
第四部分:电流与磁场1. 安培环路定理- 安培环路定理描述了电流通过闭合回路所产生的磁场的性质。
- 安培环路定理公式:∮B·dl = μ0 * I2. 磁场的磁感应强度- 磁感应强度描述了磁场中的力场作用强度。
- 磁感应强度的计算公式:B = F / (q * v * sinθ)第五部分:电磁感应与电磁波1. 电磁感应现象- 电磁感应现象是指磁场变化时在导体中感应出电流的现象。
2. 法拉第电磁感应定律- 法拉第电磁感应定律描述了磁通量变化导致感应电动势的产生。
- 法拉第电磁感应定律公式:ε = -ΔΦ / Δt3. 麦克斯韦方程组- 麦克斯韦方程组总结了电场和磁场的关系以及它们对物质的作用。
电磁场期末复习资料

____
A.磁场随时间变化
B.回路运动
C.磁场分布不均匀
D.同时选择 A 和 B
10.两个同频同方向传播,极化方向相互垂直的线极化波合成一个椭圆极化波,则一
定有____ __
A.两者的相位差不为 0 和π
B.两者振幅不同
C.两者的相位差不为±π/2
D.同时选择 A 和 B
二、填空题(共 21 分)
第 11 页 共 35页
四、(12 分)同心导体球形电容器内球半径为 a,外球半径为 b,厚度可以忽略。内、外球 之
间的下半部分填充介电常数为 ε 的电介质,内球带电荷 Q,如题图 2-1 所示。试求: (1)空间的场强分场; (2)空间的电位分布; (3)电容器的电容; (4)系统的静电能量。
第 12 页 共 35页
五、(12 分)z < 0 的区域的媒质参数为ε1 = ε0、µ1 = µ0、σ1 = 0 , z > 0 区域的媒 质参数为ε2 = 5ε0、µ2 = 20µ0、σ 2 = 0 。
已知在此表面上反射波电场
,透射波电场
)的表面上, ,且介质内透射波
波长为真空中入射波波长的 ,求介质的相对磁导率 和相对介电常数 。
(4)
一、选择题(共 20 分)
1.在无损耗均匀媒质(电导率为 0,磁导率为μ,介电常数为ε)中,正弦电磁场复矢量
(即向量)H(r)满足亥姆霍兹方程 ∇ 2
ρ H
+
k
2
传播波的电场的 z 分量与 x 方向传播波的电场的 z 分量大小相等、方向相反,则在原点处合
成电场随时间变化的矢端轨迹是
。在轨迹所在的平面上,此轨迹方程为
5、 一个长螺线管的半径为 a,单位长度上密绕 n 匝线圈。若铁芯的磁导率为 u,线圈中通有
电磁场与波复习资料完整版

(2.11) (2.12) (2.13) (2.14)
线密度分布电荷 3.静电场方程 积分形式 :
∫
l
r −r' ρl ( r ')dl ' 3 r −r'
1 N ∑ qi ε 0 i =1
� ∫
S
E ( r )idS =
(2.15) (2.16) (2.17) (2.18)
� ∫ E ( r )idl = 0
1.坡印廷定理 坡印廷定理表征了电磁场能量守恒关系,其微分形式为
−∇i( E × H ) =
积分形式为
∂ 1 1 ( H i B + E i D) + E i J ∂t 2 2
(4.8)
d 1 1 ( H i B + E i D )dV + ∫ E i JdV (4.9) ∫ V dt V 2 2 坡印廷定理的物理意义:单位时间内通过曲面 S 进入体积 V 的电磁能量等于单位时间
ρ ( r ) = lim
C/m3 C/m 2 C/m
(2.1) (2.2) (2.3)
“点电荷”是电荷分布的一种极限情况。当电荷 q 位于坐标原点时,其体密度 ρ ( r ) 应 为
ρ ( r ) = lim
可用 δ 函数表示为
q ⎧ ⎪0 =⎨ ∆V → 0 ∆V ⎪ ⎩∞ ρ ( r ) = qδ ( r )
Wm =
(3.37) (3.38) (3.39)
L= M 21 = ψ 21 I1 µ M= 4π
ψ I
, M 12 =
(3.41) (3.42) (3.43)
∫
c1
ψ 12 I2 dl gdl ∫ c2 r12− r21
电磁场复习要点

电磁场复习要点第⼀章1、⽮量的点乘和叉乘公式、性质,特别是在直⾓坐标系下的计算公式2、三种常⽤正交坐标系的相互转换,各⽅向单位⽮量之间的⽅向关系。
3、场论的基础知识:(1)标量场的梯度的概念、性质、公式、与⽅向导数的关系(2)⽮量场的散度的概念、公式、与通量的关系、散度定理、通量源和⽮量线的特点(3)⽮量场的旋度的概念、公式、与环量的关系、斯托克斯定理、漩涡源和⽮量线的特点(4)两个恒等式(5)亥姆霍兹定理第⼆章1、三⼤实验定律:公式、含义、物理意义2、两个基本假设:有旋电场和位移电流3、麦克斯韦⽅程组微分形式、积分形式及其物理意义4、两种不同介质分界⾯上的边界条件(普通的、理想介质与理想介质、理想导体与理想介质)5、媒质的电磁特性:极化、磁化和传导。
6、三种介质的本构关系对以上公式要求理解,能够灵活运⽤公式进⾏解题。
重点例题:P80页例2.7.1,例2.7.3第三章1、电位函数:引⼊依据,与电场强度之间的关系(积分形式和微分形式),电位参考点的选取原则。
2、电容的定义及其求解3、静电场的能量和能量密度(各种公式)重点查看课本P96页双导体电容的计算步骤。
例3.1.4,例3.1.54、⽮量磁位:引⼊依据,与磁感应强度之间的关系(积分形式和微分形式),⽮量磁位的⽅向。
5、电感的定义,⾃感⼜分内⾃感和外⾃感。
圆截⾯长直导线单位长度的内⾃感是多少6、恒定磁场的能量和能量密度(各种公式)P125页例3.3.77、恒定电场的源量和场量,基本性质。
电阻的求解。
8、什么是边值问题,他的分类,唯⼀性定理及其意义9、边值问题的常⽤解法10、镜像法的原理、求解关键。
接地的⽆限⼤导体平⾯的镜像,具有⼀定夹⾓的接地导体平⾯的镜像。
接地和不接地导体球⾯的镜像。
主要能够求出镜像电荷的个数、位置、⼤⼩。
11、分离变量法的原理。
针对给出问题能够列出位函数满⾜的⽅程和边界条件。
12、有限差分法的主要思想,和主要公式。
第四章1、波动⽅程的意义2、位函数和场量的关系3、坡印廷⽮量的定义,物理意义。
电磁学复习总结(知识点)

电磁学复习总结(知识点)电磁学复总结(知识点)知识点1: 电荷和电场- 电荷是基本粒子的属性,可能为正电荷或负电荷。
- 电场是由电荷产生的力场,它描述了在某一点周围的电荷受到的力。
知识点2: 高斯定律- 高斯定律是电磁学中的重要定律,描述了电场通过一个封闭曲面的总通量与该曲面内的电荷之间的关系。
知识点3: 电势和电势能- 电势是电场在某一点的势能大小,与正电荷的势能增加和负电荷的势能减少相关。
- 电势能是电荷在电场中具有的能量,可以通过电势差来计算。
知识点4: 静电场中的电场分布- 静电场中的电场分布可通过库仑定律计算。
- 静电场中的电场线是指示电场方向的线条,其切线方向为电场的方向。
知识点5: 电容和电- 电容是描述电储存电荷能力的物理量。
- 电是由两个导体之间存在的绝缘介质隔开的装置,用于储存电荷。
知识点6: 电流和电阻- 电流是电荷在单位时间内通过导体横截面的数量。
- 电阻是导体对电流的阻碍程度,可通过欧姆定律计算。
知识点7: 磁场和磁感应强度- 磁场是由电流产生的力场,描述了电流受到的力。
- 磁感应强度是描述磁场强度的物理量,可通过安培定律计算。
知识点8: 磁场中的磁场分布- 磁场中的磁力线是指示磁场方向的线条,其切线方向为磁场的方向。
- 安培环路定律描述了磁场中磁场强度沿闭合路径的总和为零。
知识点9: 电磁感应和法拉第定律- 电磁感应是指磁场与闭合线圈之间产生的感应电动势。
- 法拉第定律描述了感应电动势与磁场变化速率和线圈导线的关系。
知识点10: 自感和互感- 自感是指电流变化时产生的感应电动势。
- 互感是指两个线圈之间产生的相互感应电势。
知识点11: 交流电路和交流电源- 交流电路是指电流方向和大小周期性变化的电路。
- 交流电源是产生交流电的电源,如发电机。
知识点12: 电磁波- 电磁波是由振动的电场和磁场沿空间传播的波动现象。
- 电磁波根据波长可分为不同的频段,如无线电波、微波、可见光等。
电磁场导论总复习

例: 同轴电缆内外导体半径分别为R1和R2长度为l,中间为线
性各向同性电介质,电容率 。已知内外导体间的电压为U,
求:外导体单位面积所受的电场力
解:1.已知条件显化:
①电荷轴对称→等位面同轴圆柱面→E 只有er 方向分量且只与r有关 ②同轴电缆无限长E与z无关 2.由已知条件和要求解的问题确定解题 方法并求解 ①定位 静电场→虚位移法→确定主要计算公式
电力线微分方程: E dl = 0
由E= 可知: 等位面与电力线处处正交(垂直) 等电位面越密处,电场强度越大
2-3 静电场的边值问题
泊松方程
2
场域边界、自然边界、介质分界面衔接条件
2 1
与E1t=E2t等效
1n12n2 与D2nD1n= 等效
当电荷分布在有限区域,场域延伸到无限远处时, 0。称为自然边界条件。
f We g qk 常数
f We g k 常数
a:
We
1 2
n 1
kqk
1
b:
We
2
EDdV
V
② 分解:a: 求qk
b:求E
a: 解:设内导体表面带电量为q
由于
由
DdSq
S
得
D
q
2rl
er
ED 2(2q0)rler4q 0rler
U R 2E d lq R 2d rqln R 2
D2 n –D1 n =
5.2 坡印亭定理与坡印亭矢量
VE eJ d V W tVJ2d V S (E H )d S
电源提供 的电磁功 率(VA)
物理意义
电磁场储 能增加率 (J/S)
工程电磁场总复习PPT课件

q q R d
求得镜像电荷 q
再在球心处放置电荷 q
球面总电 量为零
球面外电荷 q 镜像电荷 q
0
球心处放置镜像电荷 q
q C 4 0 R
5
镜像法原理:以场外虚拟的集中电荷等效边界上的分布电荷
镜像电荷在被研究场域之外,不 会改变内部介质及电荷分布
保证边界 条件不变
镜像电荷
在被研究场域之外 与场源电荷平行对称 与场源电荷大小相等,方向相反
rotE 0
无旋场
L (分界面上无自由面电荷)
边界条件
D2n D1n
1
1
n
12
2
2
n
12
E1t E2t
1 12 2 12
2
折射定理
tg1 1 tg 2 2
1
高斯定理的应用------求对称电荷分布的场强分布
利用高斯定理的解题步骤:
1、对称分析;
2、选择合适的高斯面,求高斯定理等式左端的通量;求高斯定 理等式右端的面内总电荷;(要求面上场强处处相等或分片相等
17
全的电的磁合高磁综电 电磁磁通曲斯场上流场感场连线定以H所E定都B应都续。律涡述律能J定 能 性 旋:,电:产0律 产 原 的表B磁t麦生D生 理 形:明t场克磁电 式麦 :电基斯场场产荷克 表llEH本韦。。生以斯明S方Bd第d电发韦磁ll程一场散d第场组S方的)二是S。(程S方方无J0,式程源Bt表产,场Dtd明S生表),磁传磁d电明S通电导力场电全连磁电线荷电续感(变流总和流性应化和是定原定变的理理变律闭化化
电感
L
I
单位:H(亨利) L Li L0
自感计算的一般步骤:
设 I H B Φ L ( Li , L0 ) A
电磁场总复习一

安培环路定律的应用
真空中一半径为a的无限长导体圆柱,其中 均匀流过电流I,求导体内外的磁感应强度。
1、由于电流均匀分布,所以导体中 的电流密度 2、导体内外的磁感应强度关于圆 柱轴对称,因此利用安培环路定律 求解最为方便。
应用安培环路定律: 在r<a处:
所以
在r>a处:
所以
恒定磁场基本方程p131
电感p150
L L / I
在线性媒质中,一个由导线构成的线圈的自 感只和线圈及其导线的形状、尺寸、周围媒 质及导线材料的磁导率有关,而和电流的量 值无关。对于互感,还需再加一个条件,即 也和两回路的相互位置有关。
电感的求解p153
解:由于D>>a,忽略导线的内自感。单根无限长 导线在距其r处产生的磁感应强度 :
图3.0
磁场能量及力
磁路及其计算
恒定磁场知识结构框图
安培环路定律p129
l
H dl I
其中I是穿过回路l所限定面积的自由电流(不 包括磁化电流)的代数和。电流正负号选取同 真空中安培环路定律。(右手定则)
用安培环路定律求磁场强度
使用安培环路定律,求磁场强度必须根据磁 场的对称性,选择合适的安培环路,使H能提 到积分号外或沿回路的某段H的方向与回路绕 行方向垂直。 解题步骤: (1)分析给定问题中磁场的对称性,当磁场 分布具有对称性(如轴对称、平面对称等) 时,才能用安培环路定律求解。
0 t
静电场中电荷是静止的;恒 定电场中电荷是运动的。
电荷分布不同之处:
基本实验定律 (安培力定律) 磁感应强度(B)(毕奥—沙伐定律)
H 的旋度
基本方程
B 的散度
磁位( m )(J=0)
电磁场复习要点

电磁场复习要点(考试题型:填空15空×2分,单选10题×2分,计算50分)第一章 矢量分析一、重要公式、概念、结论1. 掌握矢量的基本运算(加减运算、乘法运算等)。
2. 梯度、散度、旋度的基本性质,及在直角坐标系下的计算公式。
梯度:xy z u u uu x y z∂∂∂∇=++∂∂∂e e e 散度:y x zA A A x y z∂∂∂∇⋅=++∂∂∂A 旋度:3. 两个重要的恒等式: ()0u ∇⨯∇=,()0∇⋅∇⨯=A4. 亥姆霍兹定理揭示了:研究一个矢量场,必须研究它的散度和旋度,才能确定该矢量场的性质。
5.二、计算:两个矢量的加减法、点乘、叉乘运算以及矢量的散度、旋度的计算。
第二章 电磁场的基本规律 一、重要公式、概念、结论1.电荷和电流是产生电磁场的源量。
2.从宏观效应看,物质对电磁场的响应可分为极化、磁化和传导三种现象。
3. 静电场的基本方程:s lD D ds QE E dl ρ∇•=•=∇⨯=•=⎰⎰表明:静电场是有散无旋场。
电介质的本构关系: 0r D E E εεε== (记忆0ε的值)xyzy y z x z x x y z x yzA A A A A A x y z y z z x x y A A A ∂∂⎫⎫⎛⎛∂∂∂∂∂∂∂⎫⎛∇⨯==-+-+- ⎪⎪⎪ ∂∂∂∂∂∂∂∂∂⎝⎭⎝⎝⎭⎭e e e A e e e4. 恒定磁场的基本方程:l sH J H dl I B B ds ∇⨯=•=∇•=•=⎰⎰ 磁介质的本构关系:0r B H H μμμ== (记忆0μ的值)5. 相同场源条件下,均匀电介质中的电场强度为真空中电场强度值的倍r1ε。
6. 相同场源条件下,均匀磁介质中的磁感应强度是真空中磁感应强度的r μ倍。
7. 电场强度的单位是V/m ;磁感应强度B 的单位是T (特斯拉),或Wb/m 2 8. 电磁感应定律表明:变化的磁场可以激发电场。
电磁场部分复习内容

电场部分:电荷守恒定律:孤立系统正负电荷电量代数和保持不变。
电荷的转移导致系统带电量的变化。
基本电荷电量:电子带电量Ce 191060.1-⨯=,物体带电量ne q =点电荷与库仑定律:r r q q F32141πε=(0εε为为介质介电常数,真空)电场强度:q F E =,∑=++=iz y x E k E j E i E E(1)点电荷电场:r rQ E 30)(41επε或者=,(2)点电荷系:1204i ni ii P r r Q E∑==πε, (3)0204r rdqE dπε=,),(dl dS dV dq λσρ=,线状带电体周围的电场;环状带电体轴线上得电场,圆盘带电体轴线电场,带电体内外电场分布。
电通量与高斯定理:Sd E d e∙=Φ,⎰∙=ΦSd E e,0ε∑⎰⎰=∙=ΦiSeq S d E电场力的功:)(,b a abbaU U q qUr d E q Aab r d E q r d F dA -==∙=∙=∙=⎰静电场的安培环路定理:0=∙⎰Ll d E,电势能:)(Pa Pb p ba ab E E E r d F A --=∆-=∙=⎰ 保,电场力的功:)(a b baabW W W r d E q A --=∆-=∙=⎰,零食能参考位置选择。
电势与电势差:⎰∙==参考零点aa ar d E q W U,⎰∙=-=bab a ab r d E U U U,qdU dA -=点电荷电势:rq Ur04πε=,电荷系电势:∑==ni ii pr q U104πε,连续带电体(体。
面)电势:rdq dU 04πε=。
,等势面, 场强与梯度:标量函数(),,(z y x U )的梯度:kzU j y U i x U z y x gradU∂∂+∂∂+∂∂=),,(。
算符:k zj y i x∂∂+∂∂+∂∂=∇,UgradU ∇=U gradUn nU E -∇=-=∂∂-=0,kzU E j y U E i x U E E z y x)()()(∂∂=+∂∂=+∂∂==电场中的导体与静电平衡:导体内外电场,导体电荷分布电场中的电介质:E E E '+= 0(0E E<),极化强度:EP eχε0=,电位移:P E D+=0ε=E E E rεεεχε==+00)1(,静电场高斯定理:∑⎰⎰=∙=ΦiSD q S d D(真空1=rε)电容与电容器:Uq C ∆=磁场部分:磁性的本源:运动电荷,丹麦物理学家奥斯特发现电流与磁的关系,揭示了电磁本质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附录标量场 ()z y x ,,ϕϕ=一、等值面:()C z y x =,,ϕ 二、方向导数(标量)定义:()P ϕ从点0P 经l 变到点P 的变化率,记作γϕβϕαϕϕcos cos cos zy x l ∂∂+∂∂+∂∂=∂∂ 其中()γβαcos ,cos ,cos 为l 的方向余弦,即γβαcos cos cos z y x l e e e e++=设ze y e x e g z y x∂∂+∂∂+∂∂=ϕϕϕ,则:l l e g g e g l ,cos =⋅=∂∂ϕ 所以当l 与g 方向一致时,l∂∂ϕ有最大值,ϕ增加最快,l 与g 反向,减小最快三、梯度(矢量)定义矢量g作为标量函数ϕ的梯度,记作ϕgrad 。
ze y e x e grad z y x ∂∂+∂∂+∂∂=ϕϕϕϕ梯度的方向就是使ϕ的方向导数取最大值的方向,即增长最快的方向:max⎪⎭⎫⎝⎛∂∂=l g ϕ记哈密顿算子ze y e x e z y x∂∂+∂∂+∂∂≡∇ ,则ϕϕ∇=grad矢量场()z y x A A ,,=一、通量(标量)在矢量场中取一曲面S ,该A在S 上的面积积分称作通量()⎰⎰++=⋅=Φsz y x sdxdy A dzdx A dydz A Sd A若S为一闭合曲面,则其外侧为正。
二、散度(标量)描述S 所围区域V 中某一点附近A的通量:()dV z A y A x A dxdy A dzdx A dydz A S d A V z y x SSz y x ⎰⎰⎰⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂=++=⋅=Φ(高斯定理)记散度:A z A y A x A A div z y x⋅∇=∂∂+∂∂+∂∂==VSd A SV ∆⋅⎰→∆lim通量可以看作V 内各点处散度的体积分,散度是通量在V 中的分布密度 三、环量(标量)L 为一有向闭曲线,A 沿L 的线积分称作A沿L 的环量。
⎰⋅=ΓLl d A四、旋度(矢量)()⎰⎰⎰⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=++=⋅=Γs x y z x y z LLz y x d x d y y A x A d z d x x A z A d y d z z A y A dz A dy A dx A l d A则记A的旋度为A rotSl d A A e y A x A e x A z A e z A y A A rot LS zx y y z x x y z ∆⋅=⨯∇=⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎭⎫ ⎝⎛∂∂-∂∂+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂=⎰→∆0lim环量可以看作S 内各点处旋度的面积分,旋度是环量在S 中的分布密度。
无源场0=⋅∇A,任一点散度为零无源场存在矢势:任一矢量场F 的旋度再取散度恒为零:()0=⨯∇⋅∇F,说明旋度场(F ⨯∇)一定是无源场,换言之,一无源场必有:F A ⨯∇=,满足该式的F称为A 的矢势。
例:恒定磁场B无源(0=⋅∇B ),于是可用磁矢位A 表示:A B ⨯∇=无旋场0=⨯∇A,任一点旋度为0.无旋场A可表示为某一标量函数的梯度场:斯托克斯公式任一标量场的旋度再取梯度后恒为零:()0=∇⨯∇ϕ,说明梯度场(ϕ∇)一定是无旋场,换言之,一无旋场A 必有:ϕ∇=A,ϕ称为A 的位函数。
例:静电场无旋(0=⨯∇E ),于是可用电位ϕ表示:ϕ-∇=E注意:ϕ∇表示梯度,里面的ϕ是一个标量函数,哈密顿算子∇是矢量,所以最后乘出来的梯度ϕ∇是矢量A ⋅∇表示散度,里面的A是矢量函数,所以和矢量∇点乘后的散度A ⋅∇是标量。
另见书本p333-335的计算公式,尤其是各坐标系下的旋度、散度分别怎么求。
陈欣悦第一章 静电场1. 静电场基本方程SVD dS dV ρ⋅=⋅⎰⎰(高斯定理);D ρ∇⋅=;(有源场)0lE dl ⋅=⎰(保守场);0E ∇⨯=;(无旋场)2. 分界面的衔接条件 (1)21n n D D σ-=;(σ 为分界面上分布的自由电荷面密度)(2)12t t E E = ;(3)若两种介质为线性且各向同性,=0σ ,则有111D E ε= ,222D E ε=,11αβ= ,22αβ=,则1122sin sin E E αα= ,111222cos cos E E εαεα=即1122tan tan αεαε=;(4)1212-=nnϕϕεεσ∂∂∂∂ 。
3. 泊松方程:2=-ρϕε∇拉普拉斯方程:2=0ϕ∇ (=0ρ的区域内) 4.镜像法(1) 接地无限大导体平面上方一个点电荷的电场。
镜像电荷-q 。
(2) 接地导体球外电场。
镜像电荷-'Rq q d=-,2R b d=(3) 不接地导体球外电场。
镜像电荷-q'=-R q d,'R q q d=,2R b d=(4) 分界面左右分别充满1ε2ε的介质。
求1ε全空间:q 和q’产生电场,1212'q q εεεε-=+ ;求2ε全空间:q’’产生电场,2122''q q εεε=+ 。
戴琛第二章恒定电场1.电流按体密度分布的电荷,以运动形成电流密度矢量(电流面密度):,则通过任意面积元的电流为按面密度分布的电荷,形成电流线密度矢量按线密度分布的电荷,形成线电流元电流段:体分布面分布线分布()恒定电流:电流密度矢量在各处都不随时间变化的电流。
2.欧姆定律微分形式3.焦耳定律微分形式P(P为功率密度,单位体积的功率损耗)4.电流连续性方程对于恒定电场,即任一闭合面(净)流出的传导电流为05.场强的环路线积分①路线经过电源:为非保守场,为电源电动势②不经过电源:库仑场为保守场6.恒定电场基本方程(电源外)无源(线无头无尾闭合)无旋7.分界面的衔接条件①②③(媒质为各项同性,即与同向)④⑤满足拉普拉斯方程:8.设良导体(),不良导体(),,则电流由良导体流向不良导体,与良导体表面垂直9.导电媒质中的恒定电场与静电场比拟处))或10.镜像法I I γγγγ2121'+-=I I γγγ+=12''2211.求电导步骤UIG d U I l =→∙=→→→⎰当恒定电场与静电场边界条件相同时,可用静电比拟法:γε=G C12.接地电阻深埋接地导体球aR πγ41=✍非深埋接地导体球⎪⎭⎫ ⎝⎛+=h a R 21141πγ (h 为球心到地面距离)✍紧靠地面的半球形接地体aR πγ21=例题李偲第三章 恒定磁场1.媒质的磁化分子磁矩=转矩 T m B =⨯磁化强度矢量 0limi V m M V∆→=∆∑2.总磁化电流=lM dl ⋅⎰(穿过由l 围成的S 面)磁化电流面密度矢量磁化电流线密度3.安培环路定律=I lH dl ⋅⎰4.恒定磁场的基本方程 (1)·d =0SB S ⎰(2) ·d =lH l I ⎰ (3) ·0B ∇= (4) H J ∇⨯=5.分界面上的衔接条件 (1)(正负看与绕行方向是否符合右手螺旋)(2)(3)若两种媒质均为各项周性,分界面无电流: 由铁磁质()非铁磁质()则:(4)(5)6.磁矢位:满足泊松方程7.磁矢位的边值问题(1) (2)(3)1212m m n nϕϕμμ∂∂=∂∂ 8.磁位 在区域则:磁压BMAB Au H dl =⋅⎰9.磁位的边值问题(1) (2)(3)10.镜像法11.圆柱长直导线(内)自感:12.恒定磁场中的能量:13.14.磁场力(虚位移法) (1)|=+|k k m m I I dW Wf dg g ==∂=∂常量常量 (2)-|=-|k k m m dW Wf dg gψψ==∂=∂常量常量王泽电磁感应定律:回路不变,磁场随时间变化d t dt de s⎰∂∂-=-=ψ 感生电动势,变压器电动势磁场不变,回路切割磁力线d dt de l ⋅⨯=-=⎰)(ψ动生电动势,发电机电动势磁场随时间变化,回路切割磁力线ld B v S d t dt de l s⋅⨯+∂∂-=-=⎰⎰)(ψ空间总场强:电荷产生的电场+变化的磁场产生的电场ci E E +=d d t Bdt d d E l sm Li ⋅⨯+∂∂-=-=⋅⎰⎰⎰)(φ)(d t ⨯⨯∇+∂∂-=⨯∇若回路不动:t ∂∂-=⨯∇感应电场i E为非保守场t ∂∂是其涡旋源全电流定律:tJ H S d t S d J l d H SSl∂∂+=⋅∇⇒⋅∂∂+⋅=⋅⎰⎰⎰其中,位移电流t J D ∂∂=上述表明,不仅传导电流可激发磁场,位移电流也可以激发磁场电磁场的基本方程组全电流定律:S d tS d J l d H SSl⋅∂∂+⋅=⋅⎰⎰⎰t J H ∂∂+=⋅∇推广的电磁感应定律:d td sL⎰⎰∂∂-=⋅t B ∂∂-=⨯∇磁通连续性定理: 0=⎰d B S0=⋅∇E高斯定律: q d D S=⎰ ρ=⋅∇分界面上的衔接条件:当0,0==K σ时:2121tan tan εεαα=2121tan tan μμββ=理想导体表面上的边界条件:媒质1:理想导体 媒质2:电介质0,11=∞→E D 因为t B E ∂∂-=⨯∇11所以01=B则σ==-======-n n n t t n n D D D E E B B k t H t H t H 212121221200表明理想导体表面外侧的截止中,磁力线平行于其表面,电力线垂直于其表面动态位:ϕ∇-∂∂-=t 说明包含有旋、无旋两部分:矢量位 ϕ:标量位电磁能流定理(坡印廷定理):dV E dV r J t W d e V V A ⋅+-∂∂-=⋅⨯⎰⎰⎰2)(t W∂∂:体积V 内增加的电磁场能量dVE eV⋅⎰:V 内电源提供的能量⎰VdV r J 2:V 内的焦耳热损耗⨯= 坡印廷矢量,电磁能流密度单位时间内通过垂直于能量传播方向单位面积的电磁能量))(H E t t t S φωφω++= 瞬时值*]Re[)cos()()(1H E H E dt t S T S H E Tow ⨯=-⨯==⎰φφ 有效值向量张凯第五章 准静态电磁场1.电准静态场(ESQ)(忽略电磁感应场B t ∂∂)0E ∇⨯≈;D H J t∂∇⨯=+∂;D ρ∇⋅=; 0B ∇⋅=。
E,D 求解:运用静电场公式,镜像法,电轴法,高斯定理。
2.磁准静态场(MSQ)(忽略电位移电流密度项Dt ∂∂ )H J ∇⨯=;B E t∂∇⨯=-∂ ;D ρ∇⋅=;0B ∇⋅=。
H 求解:运用安培环路定理,镜像法。
当满足条件ωεγ (即良导体),导体中的时变电磁场可按磁准静态场处理。
3.ESQ 与MSQ 的相似点满足泊松方程:2A=J μ∇,2ρϕε∇=-4.电荷弛豫- 0=(x,y,z)eetτρρ弛豫时间:e ετγ=电荷弛豫指导体中的自由电荷体密度随时间指数规律递减。
