工程数学专业指导
工 程 数 学

课程考核方式
课程考核成绩=形成性考核成绩+ 终结性考核成绩
考核成绩满分为10,考核形式为 五次平时作业。每次作业按满分100 分计算,网上公布作业题目。 终结性考核:占课程考核成绩的70%,考核形式为 期末考试,采用半开卷笔试形式, 卷面满分为100分,考试时间为90分 钟。中央电大统一命题,统一考试。
欢迎各位同学参加 工程数学课程的学习!
“河北电大在线教学平台”“工程数学” 主页
登陆:每个学生以自己的名字作为用户名,自己的(8 位数字)生日,如:1985年6月22日出生,密码: 19850622,先注册再进入浏览。 浏览:课程主页上有几个栏目:“课程说明”,“教 学大纲”,“教学设计与实施方案”,考核说明”, “教学辅导”,“形成性考核”等栏目。 “教学辅导”栏目:有各部分重点难点辅导,部分章 节的教学课件。 BBS论坛:公共论坛,学生学习上有问题可以随时发帖, 学生之间可以展开异步讨论,教师定期浏览,回答学 生提出的问题。每学期组织两-三次同步讨论。
课程学习方式
混合学习方式: 自学+面授导学+完成作业+参加期末考试+在线讨论 面授导学: 按照确定的时间,由教师集中上课,主要内容:讲 授课程的重点、难点;作业讲评;答疑解惑。 自学: 学生利用业余时间阅读教材,浏览“河北电大在线 教学平台”“工程数学”主页上教学资源:教学文件, 教学辅导,课件,期末考试的有关信息等,完成作业。 参加BBS课程论坛讨论: 在“工程数学”课程主页上有BBS论坛,学生学习上 有问题可以提问,或回答他人的问题。
面授导学安排(二)
第七、八次:重点辅导“随机变量及其数字特 征” ,指导学生完成第4次作业; 第九次:重点辅导“数理统计”,指导学生完成第 5次作业; 第十次:期末复习。 平时作业收交 自己在”工程数学“课程平台上下载五次作业, 手写完成,下一次上课前交上次作业到教师手中。 按照作业完成情况计入形成性考核成绩。
工程数学实验学习心得范文

工程数学实验学习心得范文工程数学实验学习心得范文篇1第1计:挖掘潜能。
不管你现在情况怎样,你都要相信自己还有巨大的潜能。
从现在到高考进步50名的大有人在,进步80名的也有可能。
.第2计:坚定意志。
高考其实是看谁坚持到最后,谁就笑到最后。
考生应全力以赴知难而进,战胜惰性提升意志.第3计:调好心态。
心态决定成败,高考不仅是知识和智力的竞争,更是心理的竞争。
考生应努力改变最近的不良心态。
第4计:把握自我。
复习时紧跟老师踏踏实实地复习没有错,但也要有自我意识:“我”如何适应老师的要求,如何根据自己的特点搞好最后阶段的复习,如何在“合奏”的前提下灵活处理“独奏”。
第5计:战胜自我。
面对迎考复习的艰辛,面对解题的繁难,面对竞争的压力,面对多变的情绪,只有“战胜自我”,才能海阔天空。
第6计:每日做题。
每日做些题目,让自己保持对问题的敏感,形成模式识别能力。
当然,做题的数量不能多,难度不宜大。
第7计:一次成功。
面对一道题(最好选择陌生的中档题)用心去做,看看能否一下子就理出思绪,一做就成功。
一份试卷,若不能一次成功地解决几道题,就往往会因考试时间不够而造成“隐性失分”。
第8计:讲求规范。
建议考生找几道有评分标准的考题,认真做完,再对照评分标准,看看答题是否严密、规范、恰到好处。
第9计:回到基础。
一般说来,考前不宜攻难题,既没有这么多的时间,也没必要。
要回到基础,把基础打扎实,在考试时才能做到“基础分一分不丢”。
第10计:限时训练。
可以找一组题(比如10道选择题),争取限定一个时间完成;也可以找1道大题,限时完成。
这主要是创设一种考试情境,检验自己在紧张状态下的思维水平。
第11计:激活思维。
可以找一些题,只想思路:第一步做什么,第二步做什么……(不必具体详解)再对照解答,检验自己的思路。
这样做,有利于在短时间里获得更多的解题方向。
第12计:勤于总结。
应当把每一次练习当成巩固知识、训练技能的一次机会。
题是做不完的,关键在于打好基础,勤于总结,寻找规律,一通百通。
工程教育认证补充标准

工程教育认证补充标准地质类专业本补充标准适用于地质工程、勘查技术与工程和资源勘查工程专业。
地质工程专业本补充标准适用于地质工程专业(专业编号081401),含工程地质、岩土钻掘工程等方向。
1.课程体系1.1 课程设置1.1.1数学与自然科学类课程课程设置应使学生具备应用数学、物理和化学的原理和方法解决相关地质问题的能力。
数学类课程应包括高等数学、线性代数、数理统计等;物理类课程应包括大学物理及实验等;化学类课程应包括大学化学或普通化学等。
1.1.2工程基础类课程工程基础类课程应覆盖以下核心内容:工程力学、结构力学、钢筋混凝土结构原理、工程测量、工程(机械)制图、计算机与信息技术基础等,包含其核心概念、基本原理及相关技术与方法。
1.1.3专业基础类课程专业基础类课程应以使学生掌握本专业的共性知识和基本科学方法为目的。
工程地质方向应包括:普通地质学、矿物学、岩石学、构造地质学、地貌学与第四纪地质学、水文地质学等;岩土钻掘工程方向应包括:地质学基础、机械设计基础、液压传动、电工与电子技术、流体力学等。
1.1.4专业类课程工程地质方向包括岩体力学、土力学、工程地质学基础、工程地质勘察、基础工程与地基处理、岩土测试技术、工程地质数值模拟等。
岩土钻掘工程方向包括基础工程学、岩土钻掘工程(艺)、岩土钻掘设备、岩土测试技术、岩土施工工程、钻井液与工程浆液等。
1.2 实践环节具有满足地质工程需要的完备的实践教学体系,主要包括实验课程、课程设计、野外实习,积极开展科技创新等多种形式的实践活动。
(1)实验课程:岩土室内实验、岩土原位测试、材料力学实验、工程勘察技术与工艺实验、地质工程计算机软件应用等。
(2)课程设计:计算机课程设计、钢筋混凝土课程设计、工程地质勘察或岩土钻掘技术课程设计、基础工程课程设计等。
(3)野外实习:野外地质教学实习、专业教学实习、生产实习或毕业实习,应建立相对稳定的实习基地,密切产学研合作,使学生参与到生产实践中。
《工程数学》课程学习指南

《工程数学》课程学习指南工程数学包括两个独立的数学分支——线性代数和概率论。
由于学时的关系,这两部分我们只要求掌握它们最基本的内容,其他内容同学们可根据自己工作和学习中的需要加以自学。
一、线性代数部分¨课程目的《线性代数》部分旨在让学生掌握行列式与矩阵的理论和方法,培养用数学的思想与方法分析问题与解决问题的能力,为后继课程的学习打下良好的数学基础。
¨主要内容n阶行列式的定义、性质与计算;矩阵的定义、性质与运算,矩阵的初等变换与矩阵的秩及求法;向量与向量组的概念及向量组的线性相关性,向量组的秩及求法,线性方程组有解的充分必要条件及有解时解的结构与解法。
¨基本要求第1章行列式本章主要介绍了n阶行列式的概念、性质与计算方法,并且讨论了行列式在解线性方程组中的应用——克莱姆法则。
1.重点内容:行列式的定义、性质与计算;余子式、代数余子式与行列式按一行(列)的展开;克莱姆法则解线性方程组。
2.基本要求:了解:排列的逆序数;行列式的定义;用克莱姆法则解线性方程组的方法。
掌握:行列式的性质;应用行列式的性质计算行列式;行列式按一行(列)展开的方法。
第2章矩阵本章主要介绍了矩阵及其运算、矩阵的可逆及其判定条件与逆矩阵的求法、矩阵的分块、矩阵的初等变换和矩阵的秩及求法。
1.重点内容:矩阵的加法、数乘、乘法、转置的定义及运算法则;初等矩阵与矩阵初等变换的关系;逆矩阵、伴随矩阵的定义及性质,矩阵可逆的条件、逆矩阵的求法;对称矩阵及正交矩阵的定义及特性。
2.基本要求:了解:矩阵及各种运算的定义;矩阵及矩阵的秩的概念;几种特殊矩阵的定义。
掌握:矩阵的乘法;矩阵可逆的概念及矩阵可逆的充分必要条件;逆矩阵的求法;矩阵秩的求法。
第3章n维向量本章主要介绍了n维向量的概念、向量组的线性相关性、向量组的极大无关组与秩、正交向量组与正交矩阵。
1.重点内容:向量的线性组合(线性表示);向量组的线性相关、线性无关的定义,向量组的极大无关组、向量组秩的定义及求法。
高等数学课程建设规划

高等数学课程建设规划数学是研究客观世界数量关系和空间形式的科学。
随着现代科学技术和数学科学的发展,“数量关系”和“空间形式”具备了更丰富的内涵和更广泛的外延。
现代数学内容更加丰富,方法更加综合,应用更加广泛。
数学不仅是一种工具,而且是一种思维模式:不仅是一种知识,而且是一种素养;不仅是一种科学,而且是一种文化,能否运用数学观念定量思维是衡量民族科学文化素质的一个重要标志。
数学教育在培养高素质科学技术人才中具有其独特的、不可替代的重要作用。
高等数学课程是高等学校各专业的一门必修的重要基础与工具课,它不仅为学生研究后继课程和解决实际问题提供了必不可少的数学基础知识和数学方法,而且也为培养学生思维能力,分析解决问题的能力和自学能力,以及使学生形成良好的研究方法提供了不可多得的素材。
因此,高等数学教学质量的好坏直接影响后继课程的教学质量,培养高质量的人才,充分发挥高等数学课程在高等教育中的作用,就必须全面系统的进行高等数学课程建设。
按照初等教育培养方针和课程建设基本要求和标准,结合前两个阶段我校初等数学课程建设的经历,特制定了初等数学课程建设发展规划,其目的是使我校初等数学课程建设步入一个新的循环,再上一个大的台阶,把初等数学课程逐步建设成为师资队伍结构合理,教学水平高,教学文件完备,教学设备先辈的省级精品课程。
一、初等数学课程建设总方针与指导思想我校初等数学课程建设经历了从“明确课程质量标准保证教学基本要求、发挥统考作用、不断提高教学质量”的省优课程建设到“制定规划—组织落实—评价论证”的设岗立项建设及“再规划—再建设—再评价总结”的精品课程建设三个阶段,经过前二个阶段实践,初等数学课程建设取得了可喜成绩,队伍素质明明提高,教师结构日趋合理,教学团队的教学水平稳步提高,教学文件基本美满,教学改革逐步深入,这些成绩说明我校初等数学课程建设事情已步入了有规划、有实践、有评价、有总结的良性循环轨道。
分析、总结初等数学课程建设发展过程,使我们感触课程建设事情是一项长期的系统工程,课程建设质量随着人们认识水平的提高,教学环境的改善而逐步提高,随着课程建设事情的开展,也向我们提出了新的题目和要求,在分析前二1个阶段的经验和问题的基础上,制定了高等数学课程建设的目标:制定科学的建设计划,切实加强教学队伍建设,重视教学内容和课程体系改革,注重使用先进的教学方法和手段,重视教材建设,全面提高教学质量,力争建成省级精品课程。
现代工程数学手册

现代工程数学手册
《现代工程数学手册》是一部非常有价值的参考书籍,它汇集了现代工程中常用的数学知识和技术,为工程师和技术人员提供了全面的指导和帮助。
该手册详细介绍了各种数学概念、公式和算法,并给出了大量的实例和案例分析,使读者能够更好地理解和应用这些数学工具。
它涵盖了线性代数、微积分、微分方程、数值分析、优化算法等多个领域,这些领域都是工程实践中必不可少的数学工具。
此外,《现代工程数学手册》还注重实用性和可操作性,提供了大量的程序代码和软件包,使读者能够轻松地将所学的数学知识应用到实际工程中。
总的来说,《现代工程数学手册》是一部非常实用的参考书籍,对于工程师和技术人员来说是一本不可或缺的指南。
专业名称070104应用数学招生人数10_4
③催化反应工程*或现代炼油工艺*或煤转化工程*
专业名称:081703生物化工招生人数:32
指导教师
研究方向
考试科目
备注
张嗣良
储炬
01.生物过程工程〔微生物过程多尺度研究与优化或生化系统计算分析或重组微生物、初级(次级)产物表达代谢调控机理〕
02.生物工程参数检测与控制
专业名称:080501材料物理与化学招生人数:12
指导教师
研究方向
考试科目
备注
林嘉平
李春忠
刘昌胜
陈国荣
黄葆同
姜复松
01.高分子物理与化学
02.纳米材料科学与工程
03.无机非金属材料
04.生物材料
①英语
②工程数学*或高分子物理*或无机材料研究方法与实验*
③高分子化学*
专业名称:080502材料学招生人数:42
③化工分离工程*或药物制剂与分析*
☆经导师及导师组组长同意,考生可选考其他专业的相关专业课程。
专业名称:082203发酵工程招生人数:9
指导教师
研究方向
考试科目
备注
叶 勤
张嗣良
储 炬
钟建江
张元兴
谭文松
魏东芝
许建和
刘建文
01.微生物工程
02.细胞培养工程
03.生物制药工程
①英语
②微生物学*
③高级生化*或生物化学工程*
02.生物过程工程(生物催化与生物转化)
03.生物医药工程(手性药物和天然药物)
专业名称:081704应用化学招生人数:32
指导教师
研究方向
考试科目
备注
田禾
控制工程数学基础学习指导教辅教材建设的思考

科技信息一、引言自改革开放以来,我国高等教育迅猛发展,已经处于全面提升质量、加强内涵建设的新阶段。
为了适应社会对人才的要求,高等学校掀起了以培养应用型人才为目标的改革浪潮。
在这次浪潮中,如何深化教学改革、加强教材建设、全面提高教学质量成为高校教师所面临的挑战,但这也为教材建设带来了大发展的历史机遇。
教材是体现教学内容和教学要求的知识载体,是保障教学质量的关键,是实现人才培养目标的重要保证。
随着我校教学改革的进一步深入,加强教材建设已成为学校教学工作的一项重要任务。
为了有效地提高教学质量,根据我校生源的实际情况,我们课程组申请了我校2012年“控制工程数学基础学习指导”教材建设项目并获批准。
我校自动化专业是国家级特色建设专业,“控制工程数学基础”课程是我校自动化学院的公共专业基础课,为我校自动化、智能科学技术等专业本科生开设的必修课,是特色课程之一。
通过“控制工程数学基础”这门课程的学习,可为后续专业课程的学习奠定扎实的工程数学基础和基本功训练。
二、教材建设的必要性应用型人才的培养重心是实际的应用能力,但也强调理论对应用能力的支持作用。
在应用型人才培养中,理论知识是用来辅助学生掌握实践技能和应用能力的,因此,掌握好基础理论知识和应用性知识的比例结合问题,是编写教材考虑的重要问题。
工程数学的运用能力是自动化及相关专业从事科研和技术工作的基本功,而在目前的课程体系中,例如傅里叶变换、拉普拉斯变换和z变换是分别在不同学期、不同课程中讲授的,学时又较少,这样就造成学生对这些知识的掌握缺乏系统性和扎实性,在一些专业课的学习中明显地暴露出来了这方面的弱点。
鉴于此,我们在2010年编写了“控制工程数学基础”教材,并由清华大学出版社出版(高等院校电子信息与电气学科特色教材)。
经过10级,11级的使用,对学生系统的掌握控制工程数学相关知识发挥了重要作用。
但是,由于本门课程是在大学一年级开设,学生们学习起来比较吃力。
大一工程数学知识点

大一工程数学知识点工程数学是应用数学的一个分支,它主要研究数学在工程领域中的应用。
作为工程学专业的大一学生,了解和掌握一些基本的工程数学知识点对日后的学习和工作都是非常重要的。
本文将介绍一些大一工程数学的基础知识点。
1.微积分微积分是工程数学的基础,它主要包括导数和积分两个部分。
导数用来研究函数的变化率和切线问题,而积分则用来求曲线下面的面积和曲线长度等问题。
在大一的工程数学中,主要学习一元函数的极限、连续性、导数和不定积分等内容。
2.线性代数线性代数是一门研究向量空间和线性映射的学科。
在工程数学中,线性代数主要用于解决多元线性方程组和矩阵运算等问题。
大一学生需要学习向量的基本运算、矩阵的代数性质、线性方程组的求解方法以及行列式的计算等内容。
3.概率论与数理统计概率论与数理统计是研究随机事件和随机现象的理论和方法。
在工程学中,概率论与数理统计被广泛地应用于可靠性分析、风险评估和数据处理等领域。
大一学生需要学习一些基本的概率分布(如二项分布、正态分布)、统计参数的估计和假设检验等内容。
4.复变函数复变函数是研究复数域上的函数的学科。
在工程数学中,复变函数被广泛地应用于电路分析、信号处理和振动理论等领域。
大一学生需要学习复数的基本运算、复变函数的导数和积分、留数定理以及柯西积分公式等内容。
5.离散数学离散数学是数学中的一个分支,它研究离散对象及其相互关系的学科。
在工程数学中,离散数学主要应用于信息科学和计算机科学中的算法和数据结构等问题。
大一学生需要学习集合论的基本概念、图论的基本概念和算法的基本原理等内容。
总结起来,大一工程数学的知识点主要包括微积分、线性代数、概率论与数理统计、复变函数和离散数学等。
这些知识点是工程学专业的基础,对于学好后续的专业课程和日后的工程实践都具有重要意义。
希望同学们在大一期间能够扎实掌握这些基础知识,为未来的学习和发展打下坚实的基础。
土木工程专业计划指导

工学科:土建类土木工程专业(本科)专业规则一、培养规格与培养目标专业培养规格:本科(专科起点),两年制三年业余学习,最短学习年限不低于两年半。
专业培养目标:本专业培养社会主义建设需要的,德、智、体全面发展的,获得结构工程师基本训练的高级工程技术人才。
毕业生能从事本专业工程结构的设计、建造和管理,具有初步的应用研究和开发能力。
在政治思想道德方面:热爱祖国,拥护党的基本路线,具有全心全意为人民服务的精神;遵纪守法,具有良好的社会公德和职业道德。
在业务知识和能力方面:1.深入掌握本专业所必需的基本理论、基本知识和基本技能;2.具有一般土木工程结构的设计和施工的综合管理能力,以及试验研究能力;3.获得科学研究、技术开发的初步训练;4.具有较强的自主学习能力,以及在土木工程领域获得前沿知识的能力;5.具有一定的外语水平,能够阅读本专业外文资料;6.具有计算机应用的基本能力。
在身体素质方面:身体健康、能精力充沛地工作。
学位目标:工学学士。
二、课程模块设置本专业共设置7个模块,分别是:公共基础课、专业基础课、专业课、通识课、专业拓展课、补修课、实践课。
三、课程设置本专业共设置建筑工程、建筑管理、道路桥梁三个方向专业。
(一)土木工程专业建筑工程方向1.公共基础课该模块最低中央电大考试学分为11学分,模块设置最低学分为18学分。
(1)统设必修课:开放教育入学指南、英语Ⅱ(1)、英语Ⅱ(2)、计算机应用基础(本)。
(2)选修课:学位论文指南。
2.专业基础课该模块最低中央电大考试学分为20学分,模块设置最低学分为23学分。
(1)统设必修课:土木工程CAD、工程数学(本)、土木工程力学(本)、混凝土结构设计原理、工程地质。
(2)选修课:计算机在建筑工程中应用。
3.专业课该模块最低中央电大考试学分为14学分,模块设置最低学分为18学分。
(1)统设必修课:混凝土结构设计(A)、钢结构(本)、工程经济与管理、建筑结构试验。
(2)选修课:高层建筑结构与抗震、高层建筑施工、钢-混凝土组合结构、结构计算软件、特种结构。
工程数学1

工程数学1
工程数学1通常是指大学本科阶段工科专业学生学习的一门数学课程。
这门课程旨在为工科学生提供数学基础知识,使他们能够在工程和科学领域中应用数学工具解决实际问题。
具体内容可能包括但不限于以下主题:
微积分:包括极限、导数、积分等基本概念,以及应用到工程问题的技能,如曲线的切线和曲率等。
线性代数:矩阵、行列式、线性方程组等内容,为工程问题的建模和求解提供数学工具。
常微分方程:解微分方程的基本方法,以及工程和科学领域中常见的微分方程建模问题。
多元统计:多变量函数、偏导数、多元积分等内容,为处理多变量工程问题提供数学支持。
复变函数:复数、复变函数的基本概念,以及在工程和科学中的应用。
离散数学:集合论、图论、逻辑等内容,为计算机科学等领域的学生提供数学基础。
这门课程的目标是培养学生具备将数学知识应用到实际工程问题中的能力,同时提供一个坚实的数学基础,以便他们在后续的工程专业课程中更好地理解和应用相关数学知识。
天津大学数学专业(数学分析与高等代数)考研复习指导资料

对于专业课的复习大概就是这么多,大家在后期复习过程中,也可以再准备一个总结本, 把在复习中遇到的问题和自己的想法记录下来,多总结,多思考,对于最后冲刺是很有帮助 的。这就是今天我为大家做的导学部分。同学们也可以继续关注我们接下来为大家推出的考 研专业课红宝书,那里我将带领大家一起,从基础到冲刺,为同学们提供最可靠、最专业的 服务。谢谢大家! 【主讲人】天津大学本专业在读高分研究生学长 【适用对象】报考对应院系且对应初试科目的不了解的跨校、跨专业、在职考生 【适用专业】1.理学院:基础数学
格瑞斯教育旗下天津考研网,专注考研专业课资料与考研专业课辅导!
第1页共5页
天津考研网()
二、就业前景 学院与东欧、北美、澳洲、亚洲等各国的学术研究机构和著名学府建立了广泛的学术交
流合作关系,与曼彻斯特、拉夫堡、滑铁卢及昆士兰大学等都展开了一系列交流合作。硕士 研究生毕业后就业前景广阔,去向包括出国留学,攻读博士学位,政府部门工作,银行与证 券公司,大型企业等等。 三、录取情况
2、学习阶段
7-9 月份,这一段时间细致复习所有知识点,对整体知识加以把握。重点是对整体框架 的认识。对一些知识点做总结,为下一阶段的复习打好基础。这一阶段对教材的复习尤为重 要,不能放过任何一个知识点,进行全面撒网式的复习,尽量做到面面俱到,没有任何遗漏 的地方,可以准备一个本子,对错题及自己认为重要的题做相应的记录和总结。教材至少要 反复看三遍,理清所有知识点及其之间的关系。
吉林大学导师
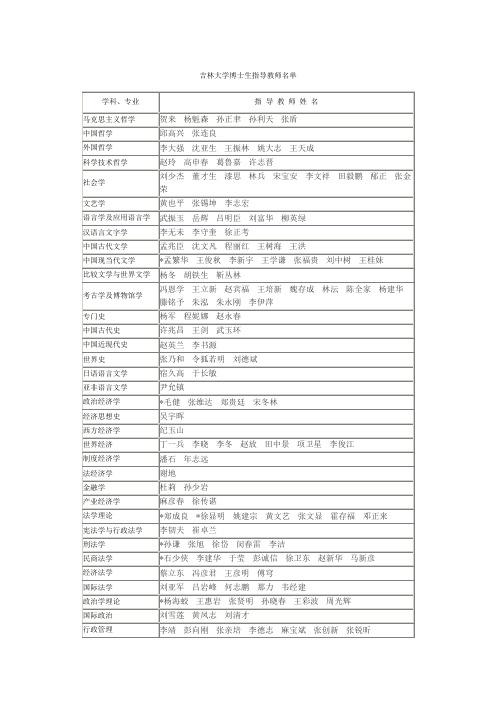
吉林大学博士生指导教师名单学科、专业指导教师姓名马克思主义哲学贺来杨魁森孙正聿孙利天张盾中国哲学邱高兴张连良外国哲学李大强沈亚生王振林姚大志王天成科学技术哲学赵玲高申春葛鲁嘉许志晋社会学刘少杰董才生漆思林兵宋宝安李文祥田毅鹏邴正张金荣文艺学黄也平张锡坤李志宏语言学及应用语言学武振玉岳辉吕明臣刘富华柳英绿汉语言文字学李无未李守奎徐正考中国古代文学孟兆臣沈文凡程丽红王树海王洪中国现当代文学*孟繁华王俊秋李新宇王学谦张福贵刘中树王桂妹比较文学与世界文学杨冬胡铁生靳丛林考古学及博物馆学冯恩学王立新赵宾福王培新魏存成林沄陈全家杨建华滕铭予朱泓朱永刚李伊萍专门史杨军程妮娜赵永春中国古代史许兆昌王剑武玉环中国近现代史赵英兰李书源世界史张乃和令狐若明刘德斌日语语言文学宿久高于长敏亚非语言文学尹允镇政治经济学*毛健张维达郑贵廷宋冬林经济思想史吴宇晖西方经济学纪玉山世界经济丁一兵李晓李冬赵放田中景项卫星李俊江制度经济学潘石年志远法经济学谢地金融学杜莉孙少岩产业经济学麻彦春徐传谌法学理论*郑成良*徐显明姚建宗黄文艺张文显霍存福邓正来宪法学与行政法学李韧夫崔卓兰刑法学*孙谦张旭徐岱闵春雷李洁民商法学*石少侠李建华于莹彭诚信徐卫东赵新华马新彦经济法学蔡立东冯彦君王彦明傅穹国际法学刘亚军吕岩峰何志鹏那力韦经建政治学理论*杨海蛟王惠岩张贤明孙晓春王彩波周光辉国际政治刘雪莲黄凤志刘清才行政管理李靖彭向刚张亲培李德志麻宝斌张创新张锐昕管理科学与工程马飞许正良李全喜毕新华李辉邱长波李春好刘国亮会计学姚梅芳企业管理赵静杰技术经济及管理李京文蔡莉张少杰葛宝山赵树宽卢艳秋李北伟图书馆学王萍李贺徐恺英情报学徐宝祥张向先靖继鹏毕强金融学王铁锋杨惠昶产业经济学沈颂东林秀梅数量经济学张晓峒刘金全金成晓赵振全张屹山石柱鲜高铁梅于维生庞晓波陈守东张世伟孙巍金春雨会计学孙烨毛志宏韩丽荣企业管理于洪彦王克敏金晓彤吕长江吕有晨吴小丁孙乃纪任俊生于桂兰邹国庆张秀娥基础数学*段海豹*王立河*吉山青王春朋袁洪君纪友清史少云廖公夫杜现昆李辉来计算数学*许跃生*张平文李永海邹永魁张树功伍铁如梁学章马驷良马富明刘播包刚概率论与数理统计*史宁中姜铁锋*陈敏*巩馥洲王德辉杨晓云应用数学*辛周平*易英飞*杨彤刘长春徐旭尹景学高文杰李勇工程数学施卫平闫广武吴柏生理论物理吴式枢吕品汪宏年刘广洲金立平粒子物理与原子核物理*孙慧斌马英君陆景彬李险峰凝聚态物理吕天全闫羽郑以松姚斌刘晓梅王文全许大鹏贺天民声学*张碧星光学苏雪梅高锦岳戴振文里佐威张汉壮吴金辉无线电物理张涛应用物理吴汉华韩炜崔海宁无机化学徐如人袁宏明施展庞广生肖丰收刘晓旸陈接胜于吉红孙建敏朱广山冯守华师同顺徐家宁裘式纶宋天佑李国栋李吉学霍启升分析化学苏星光金钦汉丁兰宋文波张忆华张寒琦于爱民孙长青周伟红宋大千有机化学卢然张锁秦李耀先刘在群林英杰母瀛柏旭物理化学*江雷*苏忠民阚秋斌赵敬哲杨文胜张文祥程铁欣王德军吴凤清王子忱杨桦林海波贾明君任咏华高分子化学与物理*闫东航严以京王力彦刘凤岐姜振华沈家骢张万金姜世梅吴立新田文晶林权高歌王贵宾王静媛王策那辉杨柏崔占臣陆丹孙俊奇迟力峰精细化学品化学任玉林陈春海应用化学李俊锋王洪艳邹海峰甘树才微生物学吴永革冯雁孔维于湘晖细胞生物学*盛军房学迅金英花施维生物化学与分子生物学*曲晓刚*王佑春陈霞张应玖王丽萍周慧郝东云生物物理学赵正云李正强微生物与生化药学李又欣微生物与生化药学*刘珂付学奇滕利荣王恩思赵志壮药理学顾景凯固体力学陈塑寰孟广伟徐涛姚国凤宫赫王丽娅机械制造及其自动化赵继王龙山*吴博达王义强张雷王立鼎机械电子工程刘顺安刘昕晖朱喜林程光明贾亚洲赵丁选机械设计及理论阚君武左春柽许纯新王国强成凯秦四成谭庆昌曾平孟繁忠杨志刚马文星工业工程高秀华申桂香孔繁森车辆工程周云山王登峰李幼德程秀生王庆年宋传学李杰管欣初亮史文库李静高镇海郭孔辉宗长富雷雨龙车身工程胡平那景新张君媛动力机械及工程*赵福全*李骏袁兆成林学东郭英男刘忠长高青洪伟李君于秀敏孙万臣材料物理与化学郑伟涛李晓天李敏陈岗于文学孟繁玲材料学贾树胜*刘勇兵蒋青赵明曹占义连建设胡建东李建忱江中浩安健蒋引珊朱永福材料加工工程王春生姜启川刘耀辉赵宇光王强周宏宋玉泉孙大千邱小明于思荣赵熹华李明哲杨慎华蔡中义寇淑清付文智王慧远沈平高分子材料工程张国孙广平张万喜道路与铁道工程刘寒冰郭学东程永春沙庆林王磊交通信息工程及控制杨兆升姜桂艳王殿海交通运输规划与管理*隽志才赵淑芝贾洪飞载运工具运用工程王荣本苏建储江伟金立生交通环境与安全技术王云鹏李显生许洪国李世武农业机械化工程陈秉聪张书慧张守勤马旭殷涌光佟金于建群杨印生周江农业生物环境与能源工程杨贞耐马中苏于海业赵寿经农业电气化与自动化*陈晓光*赵春江*王纪华孙永海吴文福仿生科学与工程任露泉丛茜李建桥韩志武物理电子学赵纯阮圣平马春生秦伟平宋宏伟电路与系统王一丁田小建郭树旭微电子学与固体电子学陈维友张彤赵毅张大明宋俊峰全宝富贾刚杜国同殷景志刘大力张宝林郑杰孙洪波通信与信息系统王树勋王珂司玉娟陈贺新赵继印钱志鸿李月赵晓晖王世刚控制理论与控制工程石要武陈虹田彦涛李元春刘富计算机系统结构邓小铁徐高潮房至一胡亮刘淑芬杨永健计算机软件与理论董蕴美孙吉贵欧阳丹彤张长海刘磊李雄飞计算机应用技术于哲舟欧阳继红刘大有卢奕南王钲旋周春光左万利李文辉许志闻赵宏伟秦贵和申铉京生物信息学宫雷光许东徐鹰梁艳春刘元宁计算机应用技术刘衍珩精密仪器及机械刘光达测试计量技术及仪器高印寒林君程德福田地王忠仁矿物学、岩石学、矿床学金巍孙丰月刘立许文良徐学纯王可勇地球化学葛文春迟效国古生物学与地层学*朱茂炎彭向东张梅生王成文孙春林孙革构造地质学梁一鸿刘正宏刘永江刘志宏李才张兴洲周建波李廷栋第四纪地质学*王宏*郭正堂*刘嘉麒*安芷生数字地质科学薛林福路来君矿产普查与勘探*关凤峻*戴金星王璞珺程日辉刘招君李守义孙景贵地图学与地理信息系统邢立新陈圣波固体地球物理学刘财金旭孟令顺王祝文地球探测与信息技术谢学锦刘国兴吴燕冈韩立国潘保芝郝立波曾昭发孙建国李桐林刘四新滕吉文地学信息工程周云轩姜琦刚地质工程佴磊王清陈剑平殷琨赵大军孙友宏陈晨地质灾害防治工程王常明李广杰水文学及水资源林学钰卞建民卢文喜肖长来梁秀娟地下水科学与工程迟宝明杨悦锁环境科学王宪恩康春莉徐自力刘淼董德明汤洁环境工程赵勇胜张凤君张兰英地球探测与信息技术范继璋生理学*张日辉赵华细胞生物学刘睿智生物化学与分子生物学王丽颖洪敏人体解剖与组织胚胎学陈东免疫学于永利李一台桂香朱迅柳忠辉病原生物学李凡王丽病理学与病理生理学*杨宝学赵雪俭李扬李玉林王琳吴珊孙连坤李荣贵人兽共患疫病学常雅萍药理学杨世杰陈霞陈立放射医学*苏旭金顺子鞠桂芝龚守良刘晓冬医学基因组学*李校堃尉军于雅琴劳动卫生与环境卫生学叶琳卫生毒理学刘娅范洪学牛凤兰李娟孙志伟社会医学与卫生事业管理许树强王伟曹锦丹安力彬免疫学谭岩内科学*杨世忠*孙旗迟宝荣朴云峰高普均孟祥伟许力军华树成宋艳秋姜振宇李薇袁长吉郑杨秦玲李有田孙景辉王峰孔俭吴绥生牛俊奇王冠军神经病学*李新民江新梅刘群吴江冯加纯马涤辉胡林森祝捷临床检验诊断学续薇外科学韩胜皓罗毅男赵刚罗祺王广义刘铜军所剑刘国津范志民佟倜王春喜谷贵山刘一刘建国路来金张舵宫旭傅耀文安君妇产科学付艳岳瑛眼科学宋鄂耳鼻咽喉科学*李晓明祝威病理学与病理生理学高洪文放射医学曲雅勤内科学王育珊金春香马忠森张捷苗里宁李东复孙健刘斌李淑梅许钟镐神经病学胡国华外科学刘军乔士兴邵国光张兴义杨有庚房学东柳克祥妇产科学张为远崔满华眼科学吴雅臻苏冠方郑雅娟耳鼻咽喉科学金春顺生物化学与分子生物学王维忠病理学与病理生理学何成彦张桂珍放射医学杨海山马庆杰内科学王江滨高长斌杨萍毕黎琦神经病学徐忠信外科学赵吉生尹维田王伟华崔树森高忠礼王金成朱庆三田宇孔祥波张学文续哲莉孙辉宋燕张斌杨小玉耳鼻咽喉科学董震急诊医学李洪军口腔临床医学高文信王景云孙新华周延民孙宏晨胡敏生物化学与分子生物学张宏桂金向群杨晓虹李平亚刘忠英周秋丽关铭魏景艳裴瑾病理学与病理生理学李才任立群井玲医学生物工程学王毅孙非颜炜群孙德军药理学睢大员马克思主义理论与思想邓如辛李桂花刘洁冯尚春政治教育马克思主义基本原理高文新徐充马克思主义发展史韩喜平李华庞雅莉马克思主义中国化研究韩广富宋连胜国外马克思主义研究贾中海赵海月思想政治教育杜君动物学刘波李子义赖良学生物化学与分子生物学张永亮张玉静*孙金海欧阳红生动物遗传育种与繁殖周虚赵志辉张嘉保动物营养与饲料科学沈景林基础兽医学*金奇*李春义*杨焕民*胡仲明*李德雪*高宏伟高丰邓旭明柳巨雄岳占碰杨振国预防兽医学*Chritia*张改平*章金刚*肖立华*王兴龙*朱平*冯书章*扈荣良*宣华*涂长春金宁一夏咸柱韩文瑜张西臣丁壮柳增善临床兽医学*朱连勤韦旭斌王哲张乃生人兽共患疫病学*Pascal刘明远植物学杨振明潘洪玉王庆钰原亚萍张世宏世界经济尹小平张慧智庞德良李玉潭张宝仁徐文吉人口、资源与环境经济学王胜今景跃军于潇区域经济学赵儒煜衣保中吴昊朱显平国际政治张景全人口学尹豪世界史李春隆张广翔陈景彦黄定天历史文献学张固也冯胜君张金梁吴良宝丛文俊吴振武中国古代史吕文郁张鹤泉原子与分子物理*王治文金明星胡湛丁大军周雅君刘学深凝聚态物理毛河光贾晓鹏崔田高春晓刘冰冰邹广田崔启良刘洪武杨海滨张明喆马琰铭邹勃李红东王欣物理化学孙家钟黄旭日唐敖庆吴玉清刘靖尧丁益宏吕中元吕文彩任爱民徐蔚青李泽生张红星李菲赵冰吕男田维全说明:1、所有指导教师的详细信息请查阅其所在学院(中心、所)主页。
工程教育认证专业标准

工程教育认证专业标准中国工程教育认证协会说明1. 本标准适用于普通高等学校本科工程教育认证。
2. 本标准由通用标准和专业补充标准组成。
3. 申请认证的专业应当提供足够的证据,证明该专业符合本标准要求。
4. 本标准在使用到以下术语时,其基本涵义是:(1)培养目标:培养目标是对该专业毕业生在毕业后5年左右能够达到的职业和专业成就的总体描述。
(2)毕业要求:毕业要求是对学生毕业时应该掌握的知识和能力的具体描述,包括学生通过本专业学习所掌握的知识、技能和素养。
(3)评估:评估是指确定、收集和准备所需资料和数据的过程,以便对毕业要求和培养目标是否达成进行评价。
有效的评估需要恰当使用直接的、间接的、量化的、非量化的手段,以便检测毕业要求和培养目标的达成。
评估过程中可以包括适当的抽样方法。
(4)评价:评价是对评估过程中所收集到的资料和证据进行解释的过程。
评价过程判定毕业要求与培养目标的达成度,并提出相应的改进措施。
(5)机制:机制是指针对特定目的而制定的一套规范的处理流程,同时对于该流程涉及的相关人员以及各自承担的角色有明确的定义。
5. 本标准中所提到的“复杂工程问题”必须具备下述特征(1),同时具备下述特征(2)-(7)的部分或全部:(1)必须运用深入的工程原理,经过分析才可能得到解决;(2)涉及多方面的技术、工程和其它因素,并可能相互有一定冲突;(3)需要通过建立合适的抽象模型才能解决,在建模过程中需要体现出创造性;(4)不是仅靠常用方法就可以完全解决的;(5)问题中涉及的因素可能没有完全包含在专业工程实践的标准和规范中;(6)问题相关各方利益不完全一致;(7)具有较高的综合性,包含多个相互关联的子问题。
1.通用标准(2017版)1学生1.1具有吸引优秀生源的制度和措施。
1.2具有完善的学生学习指导、职业规划、就业指导、心理辅导等方面的措施并能够很好地执行落实。
1.3对学生在整个学习过程中的表现进行跟踪与评估,并通过形成性评价保证学生毕业时达到毕业要求。
工程图学解题指导(视图)

工程图学解题指导1、平面立体的投影完全由平面组成的立体称为平面立体,如棱柱、棱锥、棱台等。
绘制平面立体的投影,实质上就是绘制组成平面立体的各平面的投影。
只要作出属于平面立体的各棱面、棱线和顶点的投影,并判别可见性,就能绘制其投影图。
画图时,可先画出平面中具有积聚性或反映实形的那些投影,然后再画出其余投影,并判别可见性。
各投影间应保持“长对正、高平齐、宽相等”的投影规律和立体上下、左右、前后六个方位在投影中的对应关系。
在平面立体上取点、线时,应把属于平面立体的棱面作为单独的平面来考虑。
可以利用平面投影的积聚性或平面上作辅助线来作图。
2、平面立体的截切平面立体的截交线是截平面与平面立体表面的共有线,截交线上的点是截平面与立体表面上的共有点。
平面立体的表面具有一定的范围,所以截交线通常是封闭的平面多边形。
多边形的各顶点是平面立体的各棱线或边与截平面的交点,多边形的各边是平面立体的棱面与截平面的交线,或是截平面与截平面的交线。
【例1】已知立体的主、左视图,求俯视图。
分析:假想把左视图的缺口补齐成矩形,可知此立体截切前是长方体。
根据主视图的斜线1’和左视图的线框1”可知截平面是正垂面,正垂面Ⅰ将长方体的左上角去掉。
根据左视图缺口的形状和主视图上的两条虚线,可知长方体中下部分有一个从左到右的通槽。
作图:(1)先画出长方体的俯视图。
(2)根据对正垂面Ⅰ的投影分析,画出正垂面的水平投影。
作图时,在左视图上定出a"、b"、c"、d"、e"、f"、g"、h"、i"、j",并在主视图上定出a、b、c、d、e、f、g、h、i、j,再求出这些点的水平投影,顺序连成左视图线框1”的类似形,即得截面Ⅰ的水平投影。
(3)用虚线画出槽底部的轮廓线,完成俯视图。
【例2】已知四棱台中部开一垂直于V面的三棱柱形通孔,试完成水平投影,作出侧面投影。
工程数学学习指导与习题解析

工程数学学习指导与习题解析
工程数学学习指导
1、正确把握学习的正确思路
解决工程数学中的问题,要掌握知识点的主要定义、基本范畴、公式表示和应用规律,对学习这一知识点要以理解、运用为主,而不能仅停留在记忆和应考题上。
2、注重概念的学习传授
在学习工程数学时应当特别注重概念、法则和方法的学习。
例如,在预备斜率的学习中,我们不仅要记住函数的斜率的公式表达,还要学会它的定义,要深入理解其内涵,能
够将它运用到具体解决问题中去。
3、学会勤加练习
正确把握学习工程数学的正确学习思路不能忽视练习的重要性,练习是检验和转化知
识能力的重要手段。
要经常练习,并有分析思考和加深理解,持之以恒,才能在新知识的
学习中不断提高自己的数学水平。
习题解析
1、求幂函数的导数
解:该函数的定义式为:y=ax^b(a≠0,b为常数)
其求导过程为:
y'=lim(h→0)[(ax^b+h)^b-ax^b]/h
=bax^(b-1)
2、求曲线x=f(y)的切线斜率
解:由题意得曲线的定义式为:x=f(y)
斜率=dy/dx
=f'(y)。
数据科学与工程数学基础

数据科学与工程数学基础标题:数据科学与工程数学基础:揭秘数据世界的奥秘导读:在当今数据驱动的社会中,数据科学和工程数学成为了重要的领域。
本文将从生动有趣的角度,全面解析数据科学与工程数学的基础知识,并为读者提供指导意义,带您一窥数据世界的奥秘。
让我们一起开始这段精彩的探索之旅吧!一、数据科学的畅想与实践数据科学作为一门综合性学科,旨在通过数学、统计学、计算机科学等方法,从数据中发现有价值的信息。
它汇聚了数据分析、机器学习和人工智能等技术,实现了对大规模数据的提取、处理和分析,为决策制定和问题解决提供了强有力的支持。
二、数据科学中的数学基础1.线性代数:线性代数是数据科学的基石,用于处理线性关系,例如矩阵运算、向量空间和线性变换等。
它为机器学习中的特征向量分析、矩阵分解和聚类等重要任务提供了支撑。
2.概率论与数理统计:概率论和数理统计是数据科学中的核心理论,用于描述和分析数据的随机性。
它们为数据的建模和预测提供了理论基础,如贝叶斯推断、假设检验和统计分布等。
3.最优化方法:最优化方法是数据科学中常用的数学工具,用于解决优化问题,如寻找最大值或最小值。
它为机器学习中的模型参数优化、特征选择和模型调优等提供了数学支持。
三、工程数学的威力与应用工程数学作为一门应用数学学科,与数据科学紧密相连,为实际问题的建模、求解和优化提供了数学方法和算法。
1.微积分:微积分是工程数学的基础,用于描述和分析变化。
它在数据科学中应用广泛,例如数据的平滑和拟合、函数的极值计算以及时间序列的分析等。
2.数值计算:数值计算是工程数学中的重要分支,涉及到数值近似、数值求解和数值优化等技术。
在数据科学中,数值计算技术用于处理大规模数据和复杂模型的计算问题。
3.图论与网络分析:图论是工程数学中的重要分支,用于研究图和网络的结构、属性和算法。
在数据科学中,图论和网络分析被广泛应用于社交网络分析、网络流量优化和推荐系统等领域。
四、数据科学与工程数学的指导意义数据科学和工程数学的基础知识不仅仅是理论工具,更是指导实践的重要依据。
工程数学高中语文面试教案

工程数学高中语文面试教案
课程名称:工程数学高中语文面试教案
课时:1课时
教学目标:
1. 学生能够理解工程数学的基本概念和应用。
2. 学生能够运用数学知识解决实际问题。
3. 学生能够通过语文描述清楚数学问题及解决方法。
教学准备:
1. 教师准备PPT或者白板笔记。
2. 学生准备数学工具,如计算器和尺子。
3. 教师准备一些数学应用问题和语文描述题目。
教学步骤:
1. 导入(5分钟)
教师引导学生讨论什么是工程数学,以及它在工程中的应用。
通过引言,激发学生的学习兴趣。
2. 知识讲解(15分钟)
教师通过PPT或白板笔记,讲解工程数学的基本概念和应用,比如线性方程、三角函数等知识点。
教师可以结合实际例子向学生解释这些知识点的重要性。
3. 练习(20分钟)
教师出示一些数学应用问题,让学生利用所学知识解决。
同时,要求学生用语文描述清楚解题思路和方法。
教师可以给予学生适当的提示和指导。
4. 总结(10分钟)
教师对学生的练习情况进行总结,强调工程数学和语文相结合的重要性。
鼓励学生积极学习,提高解决问题的能力。
5. 课堂作业(5分钟)
布置相关的课外作业,让学生继续巩固和拓展所学知识。
教学结束。
注:本教案可根据具体情况调整内容和时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新的 a32 =
旧的a 32 −新的a 31 ∙新的a 12 2−0.5×4 新的a 22
=
4
=0 ,变换第二
2 4 1 4 列后的 0.5 4 ,现在求新的 a23 ,新的 0.5 0 a23 = 旧的a23 -新的a21 ∙ 新的a13 ,即旧的减去(新 的所在的列的第一元素乘以新的所在行的第一个元 素+新的所在的列的第二元素乘以新的所在行的第 二个元素+⋯) ,因为a23 所在的列前面只有一个元素 a13 ,故只需减去a21 a13 就 OK 了,a24 也是这样算, 2 4 1 4 算完后矩阵就变成 0.5 4 1 4 ,a33 的算法和 0.5 0 求a22 类似,即旧的a33 -(新的a13 ∙ a31 + 新的 a23 ∙ a32 ) ,即a33 =2-(0.5× 1+0× 1)=1.5,新的a34 求法与 求a23 、 a24 类似,即a34 =5-(0.5× 4+0× 4)=3,求完 2 4 1 后 即 得 新 矩 阵 0.5 4 1 0.5 0 1.5 Dolittle 分解。 4 4 ,这就基本完成 3 4 4 3
x −x 1
0 −x 1
p(0)+ 多
x −x 0 x 1 −x 0
p(1)= x 式 ,
。但 P(x)是一 故 可 设
次
项
P(x)=在此处键入公式。x+(Ax+B)x(x-1),由其在 0、1 两点的 导数可以确定 余项公式 R(x)= A= ,即求得 P(x)。 B=
f n +1 (ξ ) n+1 ! n j=0(x
2 2
但现在还没有完成,还需要把用第一行的x1 (m+1) =
2-2x2 (m ) -0.5x3 (m) 把第二行的x1 (m+1) 换掉,同理同 理把第三行的x1 (m+1) 、x3 (m +1) 换掉, 然后移项整理 即得 Gauss-Seidel 迭代式 x1 (m+1) = 2-2x2 (m) -0.5x3 (m) x2 (m +1) =-2-6x2 (m ) +0.5x3 (m) x3 (m +1) =2+ 3 x3 (m ) 此即为 Gauss-Seidel 迭代式 4. 试分别建立线性、抛物线插值公式,求 f(1.5)。 xi f(xi )
−1 2 1. 设 X=(2, −5,1) , A= 3 1 −2 2 X ∞ , A 1, A ∞ 。
T
4 求 X 1, X 2, −4 , 3
X 1 =各元素绝对值之和 X 2 =各元素平方之和开根号 A 1 =各列元素绝对值之和中的最大者 A
∞ =各行元素绝对值之和中的最大者
2. 用 Dolittle 分解求线性方程组 2 4 1 x1 4 1 6 2 x2 = 6 1 2 2 x3 5 下面介绍如何进行 Doolittle 分解 2 4 1 4 以上边为例, 增光矩阵A= 1 6 2 6 , 先列变形, 1 2 2 5 后行变形。先对其第一列进行变形,第一列的第二 个和第三个元素分别除以第一个元素即得新的第二 2 个第三个元素 0.5 ,第一行不变,得 0.5 2 4 1 4 ;然后对第二列和第二行进行变 0.5 0.5 换 , 还 是 首 先 第 二 列 , 新 的 a22 = 旧 的 a22 - 新 的 a12 ∙ 新的 a21 ,即 6-0.5× 4=4,然后是求新的a32 ,
φ (x)=x- f ` (x)
f(x)
xk+1 = xk − f ` (xk ) f x = x6 − x − 1 k —> f ` x = 6x 5 − 1 x0 = 1.5
6
f(x )
此即为 newton 法 ⑵由xk+1 = 6 xk + 1知迭代公式为φ(x)= x + 1, 欲判 断其收敛性,则应该判断其是否满足收敛性条件。三 个条件:①在区间[a,b](注:此处为[1,2])上有连续 的一阶导数;②对于 x∈ [a, b],a≤ φ(x) ≤b;③对于 任意 x∈ [a, b], φ· (x) <1。满足以上三个条件,则收 敛。 6. 试用两种不同的插值方法求一个三次多项式 P(x), 使在节点 x0 =0 , x1 =1 上满足条件: p(0)=f(0)=0 , p(1)=f(1)=1, p, (0)= f , (0)=-3, p, (1)= f , (1)=9。 其中, p, (x)、 f , (x)是 P(x)、f(x)的一阶导数,并估计余项。 ⑴ 拉格朗日插值(即第 4 题那种方法) 此处由在x0 、 x1 两点的值可确定一个线性插值函 数,L(x)=x 个 三
2 4 1 x1 把新矩阵上三角拿出来,即 0 4 1 x2 = 0 0 1.5 x3 可很快写出先行方程组的解。 2 4 1 x1 4 3. 已知 3 4 1 x2 = 4 ,试分别写出 Jacobi 1 2 1.5 x3 3
迭
代和 Gauss-Seidel 迭代的计算式。 Jacobi 迭代即把除对角线以外的全部元素移到等号 右边 2x1 + 4x2 + x3 =4 3x1 + x2 + x3 =4 x1 + x2 +1.5x3 =3
x −x 2 x 1 −x 2 16
1 1
x −x 1 x 2 −x 1
2 9
3 23
线性插值(两点确定一条直线,任选两个点,如 1、2) f(x)= f(x1 )+ f(x2 ), 代入计算即得线性插值公式
抛物线插值公式(要取三个点) f(x)=
x −x 2 (x −x 3 ) (x 1 −x 2 )(x 1 −x 3 )
f( x1 )+
x −x 1 (x −x 3 ) (x 2 −x 1 )(x 2 −x 3 )
f( x2 )+
x −x 1 (x −x 2 ) (x 3 −x 1 )(x 3 −x 2 )
f(x3 ),代入即得抛物线插值,注意下
表变化。 5. 设有一非线性方程组x 6 -x-1=0,求 x1. ⑴用 newton 法求近似解,取x0 =1.5 ⑵试分析迭代法xk+1 = 6 xk + 1在[1,2]上的收敛性。 ⑴ 令 f(x)= x 6 -x-1 , newton 法 的 迭 代 函 数 即 为
− xj ),ξ ∈ (a, b),代入
即得余项 R(x)=
f n +1 (ξ ) 2 x (x n+ewton 插值
⋙
2x1 (m+1) =4-4x2 (m) -x3 (m) x2 (m +1) =4-3x1 (m) -x3 (m) 1.5x3 (m +1) =3-x1 (m) -x2 (m) 整理得 x1 (m+1) =2-2x2 (m) -0.5x3 (m) x2 (m +1) =4-3x1 (m) -x3 (m) x3 (m +1) =2-3 x1 (m) -3 x2 (m) 此即为 Jacobi 迭代式,m 代表第几次迭代 Gauss-Seidel 迭代只是把对角线以上的元素移到等号 右边 2x1 (m+1) 3x1 (m+1) + x2 (m+1) x1 (m+1) +x2 (m+1) +1.5x3 (m+1) =4-4x2 (m) -x3 (m) =4--x3 (m) =3
