精选2019年高中数学单元测试试题-数列专题模拟考试(含参考答案)

合集下载

精选新版2019年高中数学单元测试试题-数列专题完整考试题库(含参考答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．设{a n }是有正数组成的等比数列，n S 为其前n 项和。

已知a 2a 4=1, 37S =,则5S = （A ）152 (B)314 (C)334(D)172 （2010辽宁理6）2．已知等差数列{}n a 的前n 项和为55,5,15n S a S ==,则数列11n n a a +⎧⎫⎨⎬⎩⎭的前100项和为（）（）A ．100101B ．99101C ．99100D ．101100（2012大纲理）答案A3．等差数列｛n a ｝和｛n b ｝的前n 项的和分别为n S 和T n ，对一切自然数n 都有132+=n n T S n n ，则=55b a （） A ．32B ．149C ．3120D ．1711（2005）4．已知,22,33x x x ++是一个等比数列的前三项，则其第四项等于（）A ．272- B ．272C ．27D ．27-5．若一个数列的通项公式是an=kn+b (其中b,k 为常数)则下列说法中正确的是 A.数列｛an ｝一定不是等差数列 B.数列｛an ｝是以k 为公差的等差数列 C.数列｛an ｝是以b 为公差的等差数列 D.数列｛an ｝不一定是等差数列6．a+b+c,b+c-a,c+a-b,a+b-c 成等比数列，公比为q,则q+q 2+q 3=( ) A,1 B,2 C,3 D,4第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题7．设n S 是等差数列{}n a *()∈N n 的前n 项和，且14a 1,a 7==，则9S = ．8．对于数列{}n a ，定义数列{}n a ∆满足： )(1*+∈-=∆N n a a a n n n ，，定义数列{}na 2∆满足：)(12*+∈∆-∆=∆N n a a a n n n ，，若数列{}n a 2∆中各项均为1，且0201221==a a ，则1a =____☆____．9．已知数列{}n a 满足221221,2,(1cos )sin 22n n n n a a a a ππ+===+⋅+，则该数列的前10项的和为 ▲ ．10．已知等比数列{}n a 的各均为正数，且21243723,4a a a a a +==，则数列{}n a 的通项公式为。

精选新版2019年高中数学单元测试试题-数列专题完整考试题库(含答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．设S n 是公差为d(d≠0)的无穷等差数列{a n }的前n 项和,则下列命题错误．．的是（）A ．若d<0,则数列{S n }有最大项B ．若数列{S n }有最大项,则d<0C ．若数列{S n }是递增数列,则对任意的n ∈N*,均有S n >0D ．若对任意的n ∈N*,均有S n >0,则数列{S n }是递增数列（2012浙江理）2．已知数列{}n a 对任意的*p q ∈N ，满足p q p q a a a +=+，且26a =-，那么10a 等于（） A ．165-B ．33-C ．30-D ．21-（北京卷6）第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题3．若各项均为正数的等比数列{}n a 满足23123a a a =-，则公比q = ．4．已知各项均为正数的等比数列{}n a ，若4321228a a a a +--=，则872a a +的最小值为___▲___.5．已知等比数列}{n a 中,2,18,73-=-=a a 则=5a .6．设等差数列{}n a ，{}n b 前n 项和分别为n S 和n T ，且231n n S n T n =+，则1111a b =______ 7．数列{}n a 满足111,1(1)n n n a a a a +>-=-，()n N +∈，且122012111a a a +++=2，则201314a a -的最小值为 ▲ ．8．设n S 是公差不为零的等差数列{}n a 的前ｎ项和，若135720,,,a a a a =且成等比数列，则10S = ▲9．在数列{}n a 中12211001,5,(),n n n a a a a a n N a *++===-∈则=10．在等差数列{}n a 中，若2363,26,a a a =+=则8a =11．如果a n ＝nn n 212111+++++ (n ∈N *)，那么a 4－a 3＝ ( ) A ．71 B ．81 C ．5615 D ．56112．若数列{}n a 满足212n na p a +=（p 为正常数，n *∈N ），则称{}n a 为“等方比数列”．甲：数列{}n a 是等方比数列；乙：数列{}n a 是等比数列，则甲是乙条件13．方程()()031623162=++++nx x mx x ·的四个实数根组成一个首项为23的等比数列，则m n -=14．已知数列—1，a 1，a 2，—4成等差数列,—1，b 1,b 2,b 3,—4成等比数列，则212b a a -的值为三、解答题15．数列{}n a 是公差不为零的等差数列，其前n 项和为n S ，且9135S =，3a ，4a ，12a 成等比数列．（1）求数列{}n a 的通项公式；（2）试求所有的正整数m ，使22212m m m a a a +++为数列{}n a 中的项；（3）设,3,c N c ∈≥令1720nn a b c =--，n T 为数列{}n b 的前n 项的和，若214c T ≤，求c的最大值．16．已知nn x a x a x a x a x f ++++= 33221)(，且n a a a a 321,,组成等差数列，n 为正偶数，又n f n f =-=)1(,)1(2。

精选最新版2019年高中数学单元测试试题-数列专题完整考题库(含答案)

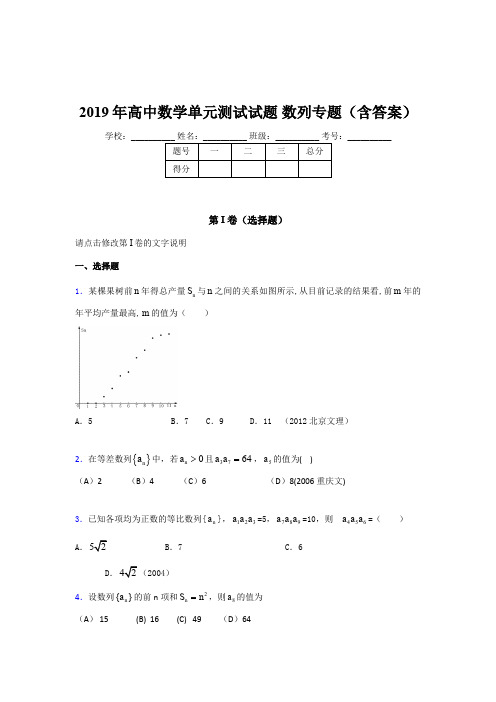
2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．某棵果树前n 年得总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为（）A ．5B ．7C ．9D ．11 （2012北京文理）2．在等差数列{}n a 中，若0n a >且3764a a =，5a 的值为( ) （A ）2 （B ）4 （C ）6 （D ）8(2006重庆文)3．已知各项均为正数的等比数列{n a }，123a a a =5，789a a a =10，则456a a a =（）A ．B ．7C ．6D ．（2004）4．设数列{}n a 的前n 项和2n S n =，则8a 的值为（A ） 15 (B) 16 (C) 49 （D ）645．某人为了观看2008年奥运会，从2001年起，每年5月10日到银行存入a 元定期储蓄，若年利率为p 且保持不变，并约定每年到期存款均自动转为新的一年定期，到2008年将所有的存款及利息全部取回，则可取回的钱的总数（元）为（）A ．7(1)a p +B ．8(1)a p +C ．7[(1)(1)]ap p p+-+ D ．()()811ap p p +-+⎡⎤⎣⎦第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题6．已知数列{}n a 是等差数列，1010=a ，前10项和7010=S ，则其公差=d 。

7．写出数列 ,1330,1320,1312,136,132+++++的一个通项公式，并验证2563是否为该数列中的一项．8．一个等比数列各项均为正数，且它的任何一项都等于它的后面两项的和，则公比q 为_______________。

9．若三角形三边的长依次成递增的等差数列，则最大边与公差之比的取值范围为_____10．在等比数列{}n a 中，若357911243a a a a a =，则7a = .11．在等比数列}{n a 中，32,675==a a ，则6a =_________12．在等差数列{}n a 中，已知前20项之和17020=S ，则=+++161196a a a a 。

精选新版2019年高中数学单元测试试题-数列专题测试题库(含标准答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．在等差数列{a n }中,已知a 4+a 8=16,则该数列前11项和S 11= （）A ．58B ．88C ．143D ．176（2012辽宁理）2．数列}{n a 满足121,12210,2{1<≤-<≤=+n n n n n a a a a a ，若761=a ，则2004a 的值为（）A ．76 B ． 75 C ． 73 D ．713．已知数列{}n a 的前n 项和)(3为常数k k S nn +=，那么下述结论正确的是（）A ．k 为任意实数时，{}n a 是等比数列B ．k = －1时，{}n a 是等比数列C ．k =0时，{}n a 是等比数列D ．{}n a 不可能是等比数列第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题4．已知函数()f x 定义如下表：数列{}n x 满足：． ,3,2,1),(,211===+n x f x x n n , 则201111234201020111(1)i i i x x x x x x x -=-=-+-+-+=∑ ▲ ．5．已知数列{a n }、{b n }都是等差数列，a 1=0、b 1= -4，用S k 、k S '分别表示数列{a n }、{b n }的前k 项和（k 是正整数），若S k +kS '=0，则a k +b k 的值为6．如果a n ＝nn n 212111+++++ (n ∈N *)，那么a 4－a 3＝ ( ) A ．71B ．81C ．5615D ．5617．一个等差数列中a 15=33,a 25=66,则a 35= .8．已知数列{}n a 满足112a =，()1111n n a n a +=-≥，则6a = .9．数列1111,,,,261220--的一个通项公式是___________10．正整数按下列方法分组：{}{}{}{}1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,.....记第n 组中各数之和为n A ；由自然数的立方构成下列数组：{}{}{}{}333333330,1,1,2,2,3,3,4,....记第n 组中后一个数与前一个数的差为,n B则n n A B +=11．已知集合P ={ x | x = 2n ，n ∈N}，Q ={ x | x = 2n ，n ∈N}，将集合P ∪Q 中的所有元素从小到大依次排列，构成一个数列{a n }，则数列{a n }的前20项之和S 20 = ▲ ．12．观察下列等式：2111,22ni i n n ==+∑2321111,326ni in n n ==++∑ 34321111,424ni i n n n ==++∑ 454311111,52330ni in n n n ==++-∑ 5654211151,621212ni i n n n n ==++-∑ 67653111111,722642ni i n n n n n ==++-+∑ ……………………………………212112101,nkk k k k k k k k i ia n a n a n a n a n a +--+--==++++⋅⋅⋅++∑可以推测，当k ≥2（*k N ∈）时，1111, , 12k k k a a a k +-===+ 12k2k a -= .0 （湖北卷15）13．若{}*1112()1nn n na a a a n N a ++==∈-数列满足，，则可得该数列的前2011项的乘积12320102011a a a a a ⋅⋅⋅⋅⋅= ．14．已知数列{n a }的通项公式为22n a n n =+，那么110是它的第_ __项． 15．设7211a a a ≤≤≤≤ ，其中7531,,,a a a a 成公比为q 的等比数列，642,,a a a 成公差为1的等差数列，则q 的最小值是________ 关键字：数列；已知单调；抽取部分数列；求最值16．已知数列{}6,321==a a a n 中且n n n a a a -=++12，那么4a =17．已知数列{}n a 的前n 项和()21n S n n =+则5a 的值为____________18．若等比数列的各项均为正数，前n 项之和为S ，前n 项之积为P ，前n 项倒数之和为M ，下列关系成立的是 .(填序号)①P =S M ②P ＞S M ③2nS P M ⎛⎫= ⎪⎝⎭ ④2P ＞nS M ⎛⎫⎪⎝⎭19．设等差数列{}n a 的前n 项和为n S ,若1≤5a ≤4，2≤6a ≤3，则6S 的取值范围是；20．（2013年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））在正项等比数列}{n a 中,215=a ,376=+a a ,则满足n n a a a a a a 2121>+++的最大正整数n 的值为_____________.21．（5分）（2010•南通模拟）有n 个小球，将它们任意分成两堆，求出这两堆小球球数的乘积，再将其中一堆小球任意分成两堆，求出这两堆小球球数的乘积，如此下去，每次都任选一堆，将这堆小球任意分成两堆，求出这两堆小球球数的乘积，直到不能再分为止，则所有乘积的和为．22．若等差数列{a n }的前n 项和为S n ，a 8＝2a 3，则 S 15S 5的值是 ▲ ．三、解答题23．（本小题满分14分）设数列{}n a 的前n 项和为n S ，对任意*n ∈N 满足2(1)n n n S a a =+，且0n a ≠．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设11,321,n n n a a n c n -+⎧=⎨⨯+⎩为奇数,为偶数，求数列{}n c 的前2n 项和2n T ．24．等比数列{a n }的前n 项和为S n ，公比不为1。

精选最新版2019年高中数学单元测试试题-数列专题测试题库(含答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．在数列{}n a 中，1112,ln 1n n a a a n +⎛⎫==++⎪⎝⎭，则n a ＝ A ．2ln n + B ．()21ln n n +- C ．2ln n n + D ．1ln n n ++(2008江西理)2．等差数列｛n a ｝中，n S 表示前n 项的和，若nn mm S S n m 2222--=，则=n m a a （） A ．11--n mB ．n mC ．22--n mD ．3232--n m （2006）3．等差数列{a n }中，已知a 1＝13，a 2+a 5＝4，a n ＝33，则n 为（） A ．50B ．49C ．48D ．47（2005）4．已知函数()f x 是定义在R 上不恒为0的函数，且对于任意的实数,a b 满足(2)2f =，()()()f ab af b bf a =+，(2)(2),(),,()2n n n n nf f a n N b n N n**=∈=∈，考察下列结论： ①(0)(1)f f = ②()f x 为奇函数 ③数列{}n a 为等差数列 ④数列{}n b 为等比数列，其中正确的个数为( )A ．1B ．2C ．3D ． 45．数列{a n }是实数构成的等比数列,S n =a 1+a 2+…+a n ,则数列{S n }中A.任意一项都不为零B.必有一项为零C.至多有有限项为零D.可以有无数项为零6．等差数列{}n a 中，n a 2110m m m a a a -+-+=≠0，若ｍ＞1且2110m m m a a a -+-+=，2138m S -=，则ｍ的值是（）A ． 10B ． 19C ．20D ．387．国家规定某行业收入税如下：年收入在280万元及以下的税率为p %，超过280万元的部分按(p +2)% 征税，有一公司的实际缴税比例为 (p +0.25)%，则该公司的年收入是 A ．560万元 B ．420万元C ．350万元D ．320万元第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题8．设S n 为等差数列{a n }的前n 项和，已知S 5 = 5，S 9 = 27，则S 7 = ▲ ．9．（5分）（2011•山东）设函数f （x ）=（x ＞0），观察：f 1（x ）=f （x ）=，f 2（x ）=f （f 1（x ））=， f 3（x ）=f （f 2（x ））=，f 4（x ）=f （f 3（x ））=，…根据以上事实，由归纳推理可得：当n ∈N *且n ≥2时，f n （x ）=f （f n ﹣1（x ））=．10．设等差数列{}n a 的前n 项和为n S ，若39S =，636S =，则789a a a ++=11．已知数列{a n }中, 21,212,2n n n n m a n m +=-⎧=⎨=⎩, m 为正整数, 前n 项和为n S ，则S 9= ▲ .12．在等差数列{}n a 中，若42≥S ，93≤S ，则4a 的最大值为 ▲ .13．在等差数列{}n a 中，存在两个不等的正整数,k p ，满足21k a p =+，21p a k =+，设数列{}n a 的前n 项和为n S ，若k p m +=，则m S = （结果用m 表示）.14．已知等差数列{},{}n n a b 的前ｎ项和分别为n S 和n T ，若7453n n S n T n +=+，且2n na b 是整数，则ｎ的值为 ▲15．已知数列{}n a 为等差数列，且17134a a a π++=，则212tan()a a += ___▲___.16．把数列{12n }的所有项按照从大到小，左大右小的原则写成如图所示的数表，第k 行有12k -个数，第k 行的第s 个数（从左数起）记为(k ，s )，则 12010可记为 ▲ ．12 14 16 18 110 112 114 116 118 120 122 124 …17．在等差数列}{n a 中，已知1a ＝1，前5项和5S =35, 则8a 的值是 ▲ .18．某工厂在1997年底制定计划，要使2010年底总产值在原有基础上翻三番，则年产值的平均增长率为_____19．在数列}{n a 中，4,2111-==+n n a a a ，则前n 项和n S 的最大值为______ 20．在11+n n和之间插入n 个正数，使这n +2个正数成等比数列，则插入的n 个正数之积为；21．设函数)10(2log log )(2<<-=x x x f x ,数列{}n a 满足)(2)2(*N n n f n a∈=⑴ 求数列{}n a 的通项公式； ⑵ 判断数列{}n a 的单调性．22．设等差数列112{}0,9,n k k a d a d a a a =的公差不为若是与的等比中项，则k 等于 ▲ ．三、解答题23．设集合I ＝{1,2,3，…，n }(n ∈N +)，选择I 的两个非空子集A 和B ，使B 中最小的数大于A 中最大的数，记不同的选择方法种数为a n ，显然a 1＝0，a 2＝22C ＝1 (1)求a n ；(2)记数列{a n }的前n 项和为S n ，求S n24．某化工企业2007年底投入100万元，购入一套污水处理设备．该设备每年的运转费用是0.5万元，此外每年都要花费一定的维护费，第一年的维护费为2万元，由于设备老化，以后每年的维护费都比上一年增加2万元．（1）求该企业使用该设备x 年的年平均污水处理费用y （万元）；（2）问为使该企业的年平均污水处理费用最低，该企业几年后需要重新更换新的污水处理设备？25．已知分别以21,d d 为公差的等差数列{}n a ,{}n b ,满足120091,409a b ==．（1）若11=d ,且存在正整数m ,使得200920092-=+m m b a ,求2d 的最小值；（2）若0k a =，1600k b =且数列200921121,,,,,,b b b b a a a k k k k ++-,的前项n 和n S 满足200920129045k S S =+,求 {}n a 的通项公式.26．已知数列{}n a 为各项均为正的等比数列，其公比为q ．（1）当q ＝32时，在数列{}n a 中： ①最多有几项在1～100之间？ ②最多有几项是1～100之间的整数？（2）当q ＞1时，在数列{}n a 中，最多有几项是100～1000之间的整数？（参考数据：lg3=0.477，lg2=0.301）．27．已知各项均不为零的数列{a n }的前n 项和为S n ，且满足a 1＝c ，2S n ＝a n a n ＋1＋r ．（1）若r ＝－6，数列{a n }能否成为等差数列？若能，求c 满足的条件；若不能，请说明理由．（2）设32111234212n n n n a a a P a a a a a a --=+++---，2242345221nn n n a a a Q a a a a a a +=+++---，若r ＞c ＞4，求证：对于一切n ∈N*，不等式2n n n P Q n n -<-<+恒成立．28．求等比数列1，2，4，…从第5项到第10项的和.29．设等比数列{a n }的前n 项和为S n ,若S 3+S 6=2S 9,求数列的公比q . 30．若ba a c cb +++1,1,1是等差数列，则a 2，ｂ2，ｃ2是等差数列.。

精选最新版2019年高中数学单元测试试题-数列专题测试版题库(含参考答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．已知等比数列()n a 中21a =，则其前3项的和3S 的取值范围是( ) （Ａ）(],1-∞- （Ｂ）()(),01,-∞+∞（Ｃ）[)3,+∞ （Ｄ）(][),13,-∞-+∞(2008四川理)【解1】：∵等比数列()n a 中21a = ∴当公比为1时，1231a a a ===，33S = ；当公比为1-时，1231,1,1a a a =-==-，31S =- 从而淘汰（Ａ）（Ｂ）（Ｃ）故选D ；【解2】：∵等比数列()n a 中21a = ∴312321111S a a a a q q q q⎛⎫=++=++=++ ⎪⎝⎭∴当公比0q >时，31113S q q =++≥+=；当公比0q <时，31111S q q ⎛⎫=---≤-=- ⎪⎝⎭ ∴(][)3,13,S ∈-∞-+∞ 故选D ；2．已知等差数列{a n }的前n 项和为S n ，a 5=5，S 5=15，则数列的前100项和为(A)100101 (B) 99101(C) 99100 (D) 1011003．[ ]． A ．1001 B ．1000 C ．999 D ．9984．等差数列1，-1,-3,-5,…，-89，它的项数是 A.92 B.47C.46D.455．某大楼有20层，有19人在第一层上了电梯，他们分别要去第2层到20层，每层一人，而电梯只允许停一次，可只使一人满意，其余18人都要上楼或下楼。

假设乘客每向下走一层不满意度为1，每向上走一层不满意度为2。

所有人不满意之和为S ，为使S 最小，电梯应停在第（）层。

A,15 B,14 C,13 D,12第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题6．已知数列}{n a 满足122n n a qa q +=+-（q 为常数，||1q <），若3456,,,a a a a ∈{}18,6,6,30--，则1a = ▲ ．7．已知数列{}n a ，{}n b 满足11a =，22a =，12b =，且对任意的正整数,,,i j k l ，当i j k l +=+时，都有i j k l a b a b +=+，则201011()2010i i i a b =+∑的值是．8．已知等差数列{a n }和{b n }的前n 项和分别为S n ，T n ，且S n T n ＝n2n －1对任意n ∈N*恒成立，则a 10b 5的值为 ▲ ．9．函数()x f 由右表定义：若()221,,5,1N n a f a a a n n ∈===+则2010a 的值为。

精选2019年高中数学单元测试试题-数列专题模拟考核题库(含参考答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．已知等差数列的第k,n,p 项构成等比数列的连续3项,如果这个等差数列不是常数列,则等比数列的公比为A.n k pn -- B.k p n p -- C.p n k n -- D.p k n k --第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题2．已知数列}{n a 满足122n n a qa q +=+-（q 为常数，||1q <），若3456,,,a a a a ∈}{18,6,2,6,30---，则1a= ．3．若数列}{n a 中，22293n a n n =-++（*n ∈N ），那么此数列}{n a 的最大项的值为______．4．设x ，y ，z 是实数，9x ，12y ，15z 成等比数列，且1x ，1y ，1z 成等差数列，则x z z x +的值是 ▲ ．5．在等比数列{}n a 中，已知23=a ，166=a ，则公比=q ★ .6．若数列{}n a 的前n 项和210(123)n S n n n =-=，，，，则数列{}n na 中数值最小的项是第项．7．已知数列{}n a 满足：m a =1（m 为正整数），1,231,nn n n n a a a a a +⎧⎪=⎨⎪+⎩当为偶数时，当为奇数时。

若47a =，则m 所有可能的取值为．56、98．已知数列{}n a 满足()*115132,37n n n a a a n N a +-==∈-,则数列{}n a 的前100项的和为 ▲ . (江苏省苏州市2011年1月高三调研)2009．如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1,2,3,4,5,6的横纵坐标分别对应数列}{n a （n ∈Z *）的前12项，如下表所示：按如此规律下去，则201120102009a a a ++= ▲ .提示：数列为：1,1,-1,2,2,3,-2,4,3,5,-3,6 ，0201120097531=+==+=+a a a a a a ，k a k =2，故201120102009a a a ++=100510．在等比数列}{n a 中，若3223S S =，则公比=q _______11．数列｛n a ｝中，31=a 且n a a n n (21=+是正整数)，则数列的通项公式=n a ；12．数列{}n a 中，nnn a a a 311+=+，21=a ，则=4a （）.A ．252B ．192C ．132D ．7213．已知数列{n a }的前n 项和29n S n n =-，第k 项满足58k a <<，则k =14．等差数列{}n a 中，10120S =，那么29a a += ．三、解答题15．(1) 已知两个等比数列{}n a ，{}n b ，满足11122(0),1,2,a a a b a b a =>-=-=333=-a b .若数列{}n a 唯一，求a 的值；(2)是否存在两个等比数列{}n a ，{}n b ，使得11223344,,,b a b a b a b a ----成公差不为0的等差数列？若存在，求{}n a ，{}n b 的通项公式；若不存在，说明理由.16．已知正项数列}{n a 的前n 项和为n n S S ,是41与2)1(+n a 的等比中项. (1）求证：数列}{n a 是等差数列；（2）若nn n ab 2=，数列}{n b 的前n 项和为n T ，求n T .17．设数列{}n a 的前n 项和为,n S 已知11,a =142n n S a +=+(I ）设12n n n b a a +=-，证明数列{}n b 是等比数列(II ）求数列{}n a 的通项公式。

精选2019年高中数学单元测试试题-数列专题完整考题库(含参考答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．已知等差数列｛n a ｝，n S 表示前n 项的和，,0,0993<>+S a a 则N S S S ,,21中最小的是（） A ．S 4B ．5SC ．S 6D ．9S （2005）2．一个小球从100米高处自由落下,每次着地后又跳回到原高度的一半再落下,设它第n 次着地时,共经过了a n 米,则当n ≥2时,有312100.A --+=n n n a a 212100.B --+=n n n a a n n n a a 2100.C 1+=- 21210021.D --+=n n n a a3．已知{}n a 是等差数列，124a a +=，7828a a +=，则该数列前10项和10S 等于（） A ．64B ．100C ．110D ．120(2008陕西理)第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题4．在圆2250x y x +-=内，过点53,22⎛⎫⎪⎝⎭有n 条长度成等差数列的弦，最小弦长为1a ，最大弦长为n a ，若公差11,53d ⎡⎤∈⎢⎥⎣⎦，那么n 的取值集合是 ▲ ．5．设n S 为数列{}n a 的前n 项和，2n S kn n =+，*n N ∈，其中k 是常数．若对于任意的*m N ∈，m a ，2m a ，4m a 成等比数列，则k 的值为 ▲ ．6．数列{}n a 中，前n 项和23n S n =--，*n N ∈，则{}n a 的通项公式为n a = .7．命题“有的三角形的三个内角成等差数列”的否定是 ▲ .8．若,,,x a b y 成等差数列，,,,x c d y 成等比数列，则2()a b cd+∈ .（结果用区间形式表示）9．已知数列{a n }中, 21,212,2n n n n m a n m +=-⎧=⎨=⎩, m 为正整数, 前n 项和为n S ，则S 9= ▲ .10．当n 为正整数时,函数()N n 表示n 的最大奇因数,如()33N =,()105N =,…,设()()()()()()1234212n n n S N N N N N N =++++⋅⋅⋅+-+,则n S =___________.11．已知0>a 且1≠a ，设数列}{n x 满足)(l o g 1l o g *1N n x x n a n a ∈+=+，且10010021=+++x x x ，则200102101x x x +++ =_____12．若数列{a n }的前n 项和为S n ＝n 2，则 ( ) A ．a n ＝2n ＋1 B ．a n ＝2n －1 C ．a n ＝－2n ＋1 D ．a n ＝－2n －113．在数列{ a n }中，已知a n =2，a n = a n ＋2n ，则a 4 +a 6 +a 8的值为．14．在数列{a n }中，a 1＝3，且a 1n +＝a 2n （n 为正整数），则数列{a n }的通项公式a n ＝_____．123n -15．已知数列{}n a 满足12a =,111n n a a +=-+,则2008a = 16．已知)(1562*∈+=N n n n a n ，则数列{}n a 的最大项是第12项和第13项三、解答题17．（本题满分16分）各项均为正数的等比数列{}n a ，11a =，2416a a =，单调增数列{}n b 的前n 项和为n S ，12b =，且()2*632n n n S b b n N =++∈．⑴ 求数列{}n a 、{}n b 的通项公式； ⑵ 令()*nn nb c n N a =∈，求使得1n c >的所有n 的值，并说明理由； ⑶ 证明{}n a 中任意三项不可能构成等差数列．18．（2013年高考陕西卷（文））设S n 表示数列{}n a 的前n 项和.(Ⅰ) 若{}n a 为等差数列, 推导S n 的计算公式;(Ⅱ) 若11,0a q =≠, 且对所有正整数n , 有11nn q S q-=-. 判断{}n a 是否为等比数列.19．已知各项不为零的等差数列：,,,,,,654321a a a a a a 其公差0≠d .(1) 321,,a a a 能否组成等比数列？请说明理由;(2)在4321,,,a a a a 中删去一项，余下的三项按原来的顺序能否组成等比数列？若能，求出da 1的值，若不能，请说明理由; (3)在654321,,,,,a a a a a a 中删去两项，余下的项按原来的顺序能否组成等比数列？请说明理由.20．设各项均为非负数的数列{}n a 的为前n 项和n n S na λ=（1a ≠2a ，λ∈R ）．（1）求实数λ的值；（2）求数列{}n a 的通项公式（用2n a , 表示）．（3）证明：当2m l p +=（m l p ∈*N ,, ）时，2m l p S S S ⋅≤．21．在首项为a ，公比为q 的等比数列中，设其前n 项和为n s ，若222n n s s x +=，=y )(32n n n s s s +，则x - y = _________．22．设数列{}n a 的前n 项和为n S ,已知121a a ==,(2)n n n b nS n a =++,数列{}n b 是公差为d 的等差数列,*n N ∈.(1) 求d 的值;(2) 求数列{}n a 的通项公式;(3) 求证:2112122()()(1)(2)n n n a a a S S S n n +⋅⋅⋅⋅⋅⋅⋅<++.23．一次函数()f x , 1)0(=f ， )13(),4(),1(f f f 成等比数列， ++)4()2(f f …=+)2(n f _ ____24．已知}{n a 是等比数列，81,262==a a ，则=4a ____________； 25．数列}{n a 满足nn n a a a 2,211+==+，求通项公式和前n 项和。

精编2019年高中数学单元测试试题-数列专题模拟考试(含标准答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．如果-1，a,b,c ,-9成等比数列，那么（） A ．b =3,ac =9 B ．b =-3,ac =9 C ．b =3,ac =-9D ．b =-3,ac =-9(2006北京文)2．已知()1f x bx =+为x 的一次函数，b 为不等于1的常量，且()g n =1(0)[(1)],(1)n f g n n =-≥⎧⎨⎩,设()()()1n a g n g n n N +=--∈，则数列{}n a 为（）A ．等差数列B ．等比数列C ．递增数列D ．递减数列3．设{}n a 是递增等差数列，前三项的和为12，前三项的积为48，则它的首项是（）Ａ．1 Ｂ．2 Ｃ．4 Ｄ．64．已知某数列前n 项之和3n 为，且前n 个偶数项的和为)34(2+n n ，则前n 个奇数项的和为（）A ．)1(32+-n nB ．)34(2-n nC ．23n -D ．321n第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题5．在等差数列51、47、43，……中，第一个负数项为第 ▲ 项.6．已知无穷数列 ,10,,10,10,1051525150-n求证：（1）这个数列成等比数列；（2）这个数列中的任一项是它后面第五项的101；（3）这个数列的任意两项的积仍在这个数列中。

7．在等差数列}{n a 中，若20181563=+++a a a a ，则20S =______8．等差数列}{n a 中，77,1714541074=+++=++a a a a a a ，若13=m a ，则m =_____9．在等比数列}{n a 中，各项都是正数，若4,1987321=++=++a a a a a a ，则数列}{n a 的前15项的和为______10．已知数列}{n a 的通项公式11++=n n a n ，则该数列的前______项之和等于911．等比数列{a n }的前n 项的和为n S ，且S 2009，2S 2010，3S 2011成等差数列，则{a n }的公比为______．12．数列012a a a ，，，…满足：}{1][310n n n a a a a +==+， (][n a 与}{n a 分别表示n a 的整数部分和小数部分），则=2008a ．13．已知数列1,34,59,716,…的一个通项公式是a n =22n -1n. 14．已知数列}{n a 的前n 项和为31n n S =-（*N n ∈），则4a = ▲ 。

精选最新版2019年高中数学单元测试试题-数列专题模拟考核题库(含答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________一、填空题1．等差数列{}n a 中，前m 项(m 为奇数)和为77，其中偶数项之和为33，且181=-m a a ，则通项公式n a =_____▲______。

2．在各项为正数的等比数列{}n a 中，已知424311a a a a ⋅=+，且前n 2项的和等于它的前n 2项中偶数项之和的11倍，则数列{}n a 的通项公式=n a 。

( 3．已知S n 是数列{a n }的前n 项和，且S n = 3n －2，则a n =4．已知数列{}n a 的首项11=a ，且)2(121≥+=-n a a n n ，则6a ＝（）. A ．15 B ．31 C ．62 D ．635．数列{}n a 中，已知a n a nn +-=)1(（a 为常数），且2413a a a =+，求2010a ．6．已知一个等差数列}{n a ，n S 为其前n 项的和，且420,1102010==S S ，则30S =_____7．设数列}{n a 是由正数组成的等比数列，公比为2，且30303212=a a a a ，求30963a a a a 的值。

8．已知三个数成等比数列，它们的积为8-，和为3，则这3个数是_____9．n S 是等差数列{}n a 的前n 项和，),5(,30,2*45N n n a a n ∈≥==-，336=n S ，则=n 。

(10．已知}{n a 是等差数列，若3,244113==+a a a ，则}{n a 的公差是____________； 11．等差数列{}n a 中，若124a a +=, 91036a a +=，则10S = .12．若等比数列{a n }满足：354321=++++a a a a a ，122524232221=++++a a a a a ，则54321a a a a a +-+-的值是________________．13．等差数列的首项为70，公差为9,-则这个数列中绝对值最小的一项是第项 14．等比数列{}n a 中，其前n 项和是n S ，当333S a =时，公比q = ▲ ． 15．已知数列na a n n ++++= 3211:}{满足，则数列}{n a 的前100项的和是 ▲ ．16．已知数列{}n a 满足221221,2,(1cos )sin 22n n n n a a a a ππ+===+⋅+，则该数列的前10项的和为 ▲ ．17．在△ABC 中，a b c , , 分别是角A B C , , 的对边，若222a b c ,, 成等差数列，则cos B 的最小值为．18．函数e x y =的图象在点()e k a k a , 处的切线与x 轴的交点的横坐标为1k a +，其中*k ∈N ，10a =，则135a a a ++= ▲ ．19．已知等差数列}{n a 的前13项之和为413π，则)tan(876a a a ++等于．20．已知0>a 且1≠a ，设数列}{n x 满足)(l o g 1l o g *1N n x x n a n a ∈+=+，且10010021=+++x x x ，则200102101x x x +++ =_____二、解答题21．已知q 和n 均为给定的大于1的自然数.设集合{}0,1,2,1,q M =-，集合{}112,,1,2,,n n i A x x x x q x q x M in -+?==++.（Ⅰ）当2q =，3n =时，用列举法表示集合A ；（Ⅱ）设,s t A Î，112n n s a a q a q -=+++，112n n t b b q b q -=+++，其中,i i a b M Î，1,2,,i n =. 证明：若n n a b <，则s t <.（本小题满分14分）（Ⅰ）22．在数1和100之间插入n 个实数，使得这2n +个数构成递增的等比数列，将这2n +个数的乘积记作n T ，再令,lg n n a T =1n ≥. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设1tan tan ,n n n b a a +=⋅求数列{}n b 的前n 项和n S .(2011年高考安徽卷理科18)（本小题满分13分）【命题意图】：本题考查等比和等差数列，指数和对数运算，两角差的正切公式等基本知识，考查灵活运用知识解决问题的能力，综合运算能力和创新思维能力。

精选新版2019年高中数学单元测试试题-数列专题模拟题库(含参考答案)

2019年高中数学单元测试试题数列专题（含答案）学校：__________ 姓名：__________ 班级：__________ 考号：__________第I 卷（选择题）请点击修改第I 卷的文字说明一、选择题1．设等比数列{}n a 的公比q =2，前n 项和为S n ，则24a S =（） A ．2B ．4C ．215 D ．217(2008宁夏理) 2．已知函数,log )31()(2x x f x-=实数c b a ,,成公差为正数的等差数列，且满足：0)()()(<c f b f a f ；实数d 是方程0)(=x f 的一个解，那么下列四个判断：①;a d <②;b d >③;c d <④c d >中有可能成立的有（）A ．1个B ．2个C ．3个D ．4个3．等比数列{}n a 的各项均为正数，且564718a a a a +=，则3132310log log ...log a a a +++=（） A ．12 B ．10 C ．31log 5+ D ．32log 5+第II 卷（非选择题）请点击修改第II 卷的文字说明二、填空题4．（5分）（2011•山东）设函数f （x ）=（x ＞0），观察：f 1（x ）=f （x ）=，f 2（x ）=f （f 1（x ））=， f 3（x ）=f （f 2（x ））=， f 4（x ）=f （f 3（x ））=，…根据以上事实，由归纳推理可得：当n ∈N *且n ≥2时，f n （x ）=f （f n ﹣1（x ））=．5．已知等差数列{n a }中，,1,16497==+a a a 则12a 的值为 6．已知等差数列{},{}n n a b 的前n 项和分别为n S 和n T ，若7453n n S n T n +=+，且2n nab 是整数，则n 的值为 ▲ ．7．已知数列{1,2,2,3,3,3,4,4,4,4,5，…}的首项是1，随后两项都是2，接下来3项都是3，再接下来4项都是4，…，以此类推，若120,21n n a a -==，则n = 211 . 提示：∵20(120)1123202102n ⨯+-=++++==，211n ∴=. 8．已知ABC ∆ 的一个内角为120o ，并且三边长构成公差为4的等差数列，则ABC ∆的面积为_______________.9．如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1,2,3,4,5,6的横纵坐标分别对应数列}{n a （n ∈Z *）的前12项，如下表所示：按如此规律下去，则201120102009a a a ++= ▲ .提示：数列为：1,1,-1,2,2,3,-2,4,3,5,-3,6 ，0201120097531=+==+=+a a a a a a ，k a k =2，故201120102009a a a ++=100510．等差数列{}n a ,10a =,公差17d =,则8a = .11．若实数c a 1,1,1成等差数列，且22,1,c a 成等比数列，则22ca ca ++=_______12．在等比数列}{n a 中，162,251-=-=a a ，则3a =________13．在等差数列中，若则数列的通项公式为；14．已知数列{a n }是递减的等差数列，且a 3＋a 9＝50，a 5·a 7=616，试求这个数列前多少项和最大，并求这个最大值．15．已知等差数列的前n 项和为7n ２-5n ,则a 100= .16．如图，△12OA A 是等腰直角三角形，1121AO A A ==,以2OA 为直角边作等腰直角三角形△23OA A ，再以3OA 为直角边作等腰直角三角形△34OA A ，如此继续下去得等腰直角三角形 △45OA A ……．则△910OA A 的面积为．三、解答题17．【2014高考山东卷第19题】已知等差数列{}n a 的公差为2，前n 项和为n S ，且124,,S S S 成等比数列.（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）令114(1)n n n n nb a a -+=-，求数列{}n b 的前n 项和n T . 18．（本题满分14分）某校高三有四个班，某次数学测试后，学校随机地在各班抽取部分学生进行测试成绩统计，各班被抽取的学生人数恰好成等差数列，人数最少的班被抽取了22人. 抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示，其中120~130（包括120分但不包括130分）的频率为0.05，此分数段的人数为5人. （1）问各班被抽取的学生人数各为多少人？（2）求平均成绩；（3）在抽取的所有学生中，任取一名学生，求分数不低于90分的概率.19．已知a 为正实数，n 为自然数，抛物线22na y x =-+与x 轴正半轴相交于点A ，设()f n 为该抛物线在点A 处的切线在y 轴上的截距。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019年高中数学单元测试试题数列专题（含答案）
学校：__________ 姓名：__________ 班级：__________ 考号：__________
第I 卷（选择题）
请点击修改第I 卷的文字说明一、选择题
1．已知函数()f x 是定义在R 上不恒为0的函数，且对于任意的实数,a b 满足(2)2f =，
()()()f ab af b bf a =+，(2)(2),(),,()2n n n n n
f f a n N b n N n
**
=∈=∈，考察下列结论： ①(0)(1)f f = ②()f x 为奇函数 ③数列{}n a 为等差数列 ④数列{}n b 为等比数列，其中正确的个数为( )
A ．1
B ．2
C ．3
D ． 4
第II 卷（非选择题）
请点击修改第II 卷的文字说明
二、填空题
2．已知数列,,11,22,5,2⋅⋅⋅则52是该数列的第项
3．已知数列{a n }、{b n }都是等差数列，a 1=0、b 1= -4，用S k 、k
S '分别表示数列{a n }、{b n }的前
k 项和（k 是正整数），若S k +k
S '=0，则a k +b k 的值为
4．数列{a n }的前n 项和为S n ，若S n ＝2
)
13(1-n a ，且a 4＝54，则a 1＝________．
5．已知：数列{a n }中，a 1＝1，a 2＝2，且a n ＋2－a n ＝1＋(－1)n ，求S 10的值．
6．（1）数列1,3,6,10,的一个通项公式为_______________；
（2）数列1357
,
,,,5101726
--的一个通项公式为__________
7．若,,,a b c b c a c a b a b c +++-+-+-成等比数列，公比为q ，则3
2
q q q ++= ；
8．在等差数列}{n a 中，4,84111073=-=-+a a a a a ，则13S =______
9．数列{}n a 中，)2(112,
1,21
121≥+===-+n a a a a a n n n ，则其通项公式为=n a 。

(
10．在等差数列}{n a 中，若01<a 且163S S =，则=n ______时，n S 取得最小值
11．已知数列{}n a 的前n 项和为2
,n S n =某三角形三边之比为234::a a a ，则该三角形最
大角为 120 ． 12．等差数列{}n a ,10a =,公差1
7
d =,则8a = .
13．设等比数列{}n a 的公比2q =，前n 项和为n S ，则42
S a =______________；
14．等差数列}{,022,0,}{112
73n n b a a a d a 数列且公差中=+-≠是等比数列，且
8677,b b a b 则== 。

15．在等差数列{}n a 中，n S 表示其前n 项，若m n S n =，)(n m n
m
S m ≠=，则m n S +的取值范围是 ▲ ．（4，∞+）
16．九章算术》“竹九节”问题：现有一根9节的竹子，自下而下各节的容积成等差数列，上面4节的容积共3升，下面3节的容积共4升，则第5节的容积为升(2011年高考湖北卷理科13)《
17．已知数列{a n }是等差数列，且a 4＋a 7＋a 10＝17，a 8＋a 9＋a 10＝21，若a k ＝13，则k ＝_________．
18．若a >0，b >0，a ，b 的等差中项是12，且m ＝a ＋1a ，n ＝b ＋1
b ，则m ＋n 的最小值为
________．
19．在等差数列}{n a 中，若1471,0S S a =>，则当n =_______时，n S 取得最大值。

三、解答题
20．（本小题满分16分）
设数列{}n a 的各项均为正数，其前n 项的和为S n ,,对于任意正整数m,n,
1m n S +恒成立
（1）若11,a =求234,,a a a 及数列{}n a 的通项公式（2）若()42121a a a a =++，求证：数列{}n a 是等比数列
21． (本小题满分16分)
已知数列{}n a 和{}n b 满足1a m =,1n n a a n λ+=+,24
39
n n n b a =-
+.
(Ⅰ) 当1m =时,求证: 对于任意的实数λ,{}n a 一定不是等差数列； (Ⅱ) 当12
λ=-
,2
9
m ≠
时,试判断{}n b 是否为等比数列；
(Ⅲ) 设n S 为数列{}n b 的前n 项和,在(Ⅱ)的条件下,是否存在实数m ,使得对任意的正整数n ,
都有1233
n S ≤≤?若存在,请m 的取值范围；若不存在,请说明理由.
22．正项数列{a n }的前项和{a n }满足:222
(1)()0n n s n n s n n -+--+=
(1)求数列{a n }的通项公式a n ; (2)令221(2)n n b n a +=
+,数列{b n }的前n 项和为n T .证明:对于任意的*
n N ∈,都有564
n
T <（2013年高考江西卷（理））
23．等比数列{a n }的前n 项和为S n ，公比不为1。

若a 1=1，且对任意的
都有a n ＋2＋a n
＋1
-2a n =0，则S 5=_________________。

24．数列{}n x 满足：2*
110,()n n n x x x x c n N +==-++∈
（I ）证明：数列{}n x 是单调递减数列的充分必要条件是0c <；
（II ）求c 的取值范围，使数列{}n x 是单调递增数列。

【2012高考真题安徽理21】（本小题满分13分）
25．已知等比数列}{n a 的前n 项和n S 满足：
231015=S S ，则=3545S S 7
9
或171
172
． 26．数列{}n a 满足1n a += *21
()n n
a n N a +-
∈，11a =，
①求证：数列⎭
⎬⎫
⎩⎨⎧+11n a 为等差数列；②求数列{}n a 的通项公式。

27．在等差数列}{n a 中，17,6,3
1
641==+=n a a a a 。

求n 28．
1．已知数列的等比数列公比是首项为4
1
,41}{1==q a a n ，设14
132log (*)n
n b a n N +=∈。

（1）求数列{}n b 的通项公式（2）设12||||||n n T b b b =+++，求n T
29．在数列}{n a 中，1)
1(1
11=++=+a n n a a n n ，，求通项公式n a ；
30．两个等差数列5，8，11，……和3，7，11，……都有100项，那么它们共有多少相同的项？。