江苏省无锡市蠡园中学八年级数学《反比例函数复习》学案(无答案)

合集下载

苏科版八年级下册第11章反比例函数单元复习教案

第八讲反比例函数1.反比例函数：一般地，形如：xky =（k 为常数，k ≠0）的函数称为反比例函数，其中 x 是自变量，y 是x 的函数，k 是比例系数．（自变量x 是一切不为0的实数） 2.反比例函数图象及画法：一般地，反比例函数xky =（k 为常数，k ≠0）的图象是由两个分支组成的，是双曲线．这两个分支分别位于第一、三象限或第二、四象限．双曲线两个分支关于原点对称，由于反比例函数中，自变量x ≠0，函数值y ≠0，所以它的图象与 x 轴和y 轴都没有交点，即双曲线的两个分支无限地接近坐标轴，但永远不与坐标轴相交．画反比例函数的图象的基本步骤为： ① 列表；描点；③ 连线． 3.反比例函数性质：4.求反比例函数关系式的基本方法．（1）待定系数法是最基本的方法；（2）若已知两个函数的交点，可把交点坐标直接代入关系式；（3）若有两个函数时，先分别设出解析式（用 k 1， k 2分别表示比例系数），将两个解析式联立建立方程组，利用方程组的相关知识求解；（4）过反比例函数图象上的任意一点作 x 轴的垂线，那么这点与垂足、坐标系原点构成的三角形的面积是一个定值，即22kxy S ==。

命题点1 反比例函数的图象与性质1. 点A (－1，1)是反比例函数y ＝m ＋1x 的图象上一点，则m 的值为( )A. －1B. －2C. 0D. 12. 已知反比例函数y ＝6x ，当1<x <3时，y 的取值范围是( )A. 0<y <1B. 1<y <2C. 2<y <6D. y >63. 若点A (3，－4)、B (－2，m )在同一个反比例函数的图象上，则m 的值为( ) A. 6 B. －6 C. 12 D. －124. 已知y 是x 的反比例函数，当x >0时，y 随x 的增大而减小．请写出一个满足以上条件的函数表达式________．5. 反比例函数y ＝2a －1x 的图象有一支位于第一象限，则常数a 的取值范围是________.6.已知点A (－1，y 1)，B (1，y 2)和C (2，y 3)都在反比例函数y ＝kx(k >0)的图象上，则________<________<________(填y 1，y 2，y 3).命题点2 反比例函数k 的几何意义7. 如图，点A 的坐标是(2，0)，△ABO 是等边三角形，点B 在第一象限．若反比例函数y ＝kx 的图象经过点B ，则k 的值是( )A. 1B. 2C. 3 D ．2 3第7题图第8题图第9题图8. 如图，A 、B 是双曲线y ＝kx 上的两点，过A 点作AC ⊥x 轴，交OB 于D 点，垂足为C ，若△ADO 的面积为1，D 为OB 的中点，则k 的值为( )A. 43B. 83C. 3D. 4 9. 如图，在平面直角坐标系中，过点M (－3，2)分别作x 轴、y 轴的垂线与反比例函数y ＝4x 的图象交于A 、B两点，则四边形MAOB 的面积为________.命题点3 反比例函数与一次函数综合题10. 在同一直角坐标系中，一次函数y ＝kx －k 与反比例函数y ＝kx(k ≠0)的图象大致是( )11. 在平面直角坐标系中，直线y ＝－x ＋2与反比例函数y ＝1x 的图象有唯一公共点．若直线y ＝－x ＋b 与反比例函数y ＝1x的图象有2个公共点，则b 的取值范围是( )A. b ＞2B. －2＜b ＜2C. b ＞2或b ＜－2D. b ＜－2第11题图12. 反比例函数y 1＝mx (x >0)的图象与一次函数y 2＝－x ＋b 的图象交于A ，B 两点，其中A (1，2)．当y 2>y 1时，x的取值范围是( )A ．x <1B ．1<x <2C ．x >2D ．x <1或x >213.如图，直线y ＝kx 与双曲线y ＝2x(x >0)交于点A (1，a )，则k ＝________.第13题图14.如图，在平面直角坐标系中，点M 为x 轴正半轴上一点，过点M 的直线l ∥y 轴，且直线l 分别与反比例函数y ＝8x (x ＞0)和y ＝kx(x ＞0)的图象交于P 、Q 两点，若S △POQ ＝14，则k 的值为________.第14题图15. 在平面直角坐标系xOy 中，直线y ＝kx ＋b (k ≠0)与双曲线y ＝8x 的一个交点为P (2，m )，与x 轴、y 轴分别交于点A 、点B .(1)求m 的值；(2)若P A ＝2AB ，求k 的值.16. 反比例函数y ＝kx(k ≠0)与一次函数y ＝mx ＋b (m ≠0)交于点A (1，2k －1)．(1)求反比例函数的解析式；(2)若一次函数与x 轴交于点B ，且△AOB 的面积为3，求一次函数的解析式.17. 如图，一次函数y ＝x ＋b 的图象与反比例函数y ＝kx 的图象交于点A 和点B (－2，n )，与x 轴交于点C (－1，0)，连接OA .(1)求一次函数和反比例函数的解析式：(2)若点P 在坐标轴上，且满足P A ＝OA ，求点P 的坐标．第17题图18. )如图，已知一次函数y 1＝k 1x ＋b 的图象与x 轴、y 轴分别交于A 、B 两点，与反比例函数y 2＝k 2x 的图象分别交于C 、D 两点，点D (2，－3)，点B 是线段AD 的中点．(1)求一次函数y 1＝k 1x ＋b 与反比例函数y 2＝k 2x 的解析式；(2)求△COD 的面积；(3)直接写出y 1>y 2时自变量x 的取值范围．第18题图第八讲反比例函数命题点1 反比例函数的图象与性质1. B 【解析】由点A (－1，1)是反比例函数图象上一点，可把点A 的坐标代入反比例函数解析式，即可求得m 的值．∵点A (－1，1)在反比例函数y ＝m ＋1x 上，∴把点A (－1，1)代入解析式得，1＝m ＋1－1，解得，m ＝－2，故选择B.2. C 【解析】本题考查反比例函数图象的性质．反比例函数y ＝6x图象在第一、三象限，且在每个象限内y 随x 的增大而减小，当1<x <3时，图象在第一象限，且当x ＝1时，y ＝6; 当x ＝3时，y ＝2. 故当1<x <3时，y 的取值范围是2<y <6.3. A 【解析】设反比例函数的解析式为y ＝kx ，把A (3，－4)代入得k ＝3×(－4)＝－12，所以反比例函数的解析式为：y ＝－12x ，把x ＝－2代入得m ＝－12－2，即m ＝6，故选A.4. y ＝1x (x ＞0)(答案不唯一) 【解析】反比例函数图象在每个象限内y 随x 的增大而减少，则k ＞0.5. a ＞12 【解析】本题考查了反比例函数的图像的位置与其系数的关系．因为反比例函数的图象有一支位于第一象限，所以2a －1＞0，所以a ＞12.6. y 1，y 3，y 2 【解析】本题有三种方法：一是根据反比例函数y ＝kx ，当k ＞0时，图象在第一、三象限；图象在每个象限内y 随x 的增大而减少，且在第三象限y 值为负数，在第一象限y 值为正数，所以y 1＜y 3＜y 2；二是可以取特殊值，如取k ＝1，则y 1＝－1，y 2＝1，y 3＝12，所以y 1＜y 3＜y 2；三是画出y ＝kx (k ＞0)的图象，根据图象可知y 1＜y 3＜y 2.命题点2 反比例函数k 的几何意义7. C 【解析】△ABO 为等边三角形，且OA ＝2，可求得B 点的坐标为(1，3)，又反比例函数y ＝kx 的图象经过点B ，所以k ＝1×3＝3，故选C.8. B 【解析】如解图，过点B 作BE ⊥x 轴于点E ，由反比例函数的比例系数的几何意义得，k ＝2S △AOC ＝2S△BOE，∴S四边形BDCE＝S △AOD ＝1，∵CD ∥BE ，D 是OB 的中点，∴△OCD ∽△OEB ，CD ＝12BE ，∴S △OCD S △OBE ＝(CD BE)2＝14，∴S 四边形BDCE S △OBE＝34，∴S △OBE ＝43S 四边形BDCE ＝43，k ＝2S △AOC ＝2S △OBE ＝83.第8题解图9. 10 【解析】如解图，设AM 与x 轴交于点C ，MB 与y 轴交于点D ，∵点A 、B 分别在反比例函数y ＝4x上，根据反比例函数k 的几何意义，可得S △ACO ＝S △OBD ＝12×4＝2，∵M(－3，2)，∴S 矩形MCOD ＝3×2＝6，∴S 四边形MAOB ＝S △ACO ＋S △OBD ＋S 矩形MCOD ＝2＋2＋6＝10.第9题解图命题点3 反比例函数与一次函数综合题10. A 【解析】本题考查一次函数及反比例函数的图象与性质．11. C 【解析】本题考查反比例函数与一次函数综合问题．∵直线y ＝－x ＋1与y ＝－x ＋b 平行，∴y ＝－x＋b 可以由直线y ＝－x ＋2平移得到．∵直线y ＝－x ＋2与双曲线在第一象限有唯一交点，∴当直线向右平移时，直线y ＝－x ＋b 与双曲线在第一象限有两个交点，∴b ＞2；∵直线向左平移到y ＝－x －2时，直线与双曲线在第三象限有唯一交点，再向左平移时直线与双曲线在第三象限有两个交点，∴此时b ＜－2.由此可知b 的取值范围是b ＞2或b ＜－2.12. B 【解析】先用待定系数法求出反比例函数与一次函数的解析式，再联立方程组求出另一个点B 的坐标，再根据图象得出不等式的解集．把A(1，2)分别代入反比例函数与一次函数的解析式解得m＝2，b＝3，∴y1＝2x，y2＝－x＋3.由⎩⎪⎨⎪⎧y＝2xy＝－x＋3，解得⎩⎪⎨⎪⎧x1＝1y1＝2或⎩⎪⎨⎪⎧x2＝2y2＝1，∴B(2，1)，A(1，2)画出草图如解图，由图象可知，当y2>y1时，1<x<2.第12题解图13. 2【解析】本题考查一次函数与反比例函数结合．把点A坐标(1，a)代入y＝2x，得a＝21＝2，∴点A的坐标为(1，2)，再把点A(1，2)代入y＝kx中，得k＝2.第13题解图14. －20【解析】本题考查反比例函数k的几何意义．由题意可知S△POM＝12×8＝4，S△QOM＝12|k|，∵S△POQ＝S△POM＋S△QOM＝14，∴4＋12|k|＝14，则|k|＝20.∵反比例函数图象在第四象限，∴k＜0，∴k＝－20.15. 解：(1)点P(2，m)在函数y＝8x的图象上，得m＝82，解得m＝4.(2分)(2)由(1)知，点P坐标为(2，4)，代入y＝kx＋b，得4＝2k＋b，即b＝4－2k，∵y＝kx＋b与x、y轴交于A、B两点，∴A(2－4k，0)，B(0，4－2k)，(3分)∴一次函数的图象与y轴交点存在两种情况：即与y轴交于正半轴或负半轴．当一次函数的图象与y轴交于正半轴时，如解图①：过P点作PD⊥x轴于点D，∵PA＝2AB，∴PB＝AB，则OD＝OA＝2.∴4k－2＝2，∴k＝1.图①图②第15题解图当一次函数与y轴交于负半轴时，如解图②：过P点作PD⊥x轴于点D，∵PA＝2AB，∴PD＝2OB＝4，∴OB＝2，∴4－2k＝－2，k＝3.综上，k的值为1或3(5分)16. 解：(1)由已知可知，反比例函数y＝kx过点A(1，2k－1)，∴k1＝2k－1，k＝2k－1，解得k＝1.反比例函数的解析式为y ＝1x.(2分)(2)画出直线的草图如解图．过点A 作AM ⊥x 轴于M.由(1)得点A(1，1)，第16题解图∴点A 到x 轴的距离AM ＝1.(3分)由已知，得S △AOB ＝12×|OB|×|AM|＝3，∴12×|OB|×1＝3，|OB|＝6. ∵点B 在x 轴上，故B(6，0)或 B ′(－6，0)．(5分)①当一次函数的图象过A(1，1)和 B(6，0)时，由⎩⎪⎨⎪⎧m ＋b ＝16m ＋b ＝0，解得⎩⎨⎧m ＝－15b ＝65.此时一次函数解析式为y ＝－15x ＋65.(6分)②当一次函数的图象过A(1，1)和B′(－6，0)时，由⎩⎪⎨⎪⎧m ＋b ＝1－6m ＋b ＝0，解得⎩⎨⎧m ＝17b ＝67，此时一次函数解析式为y ＝17x ＋67.(7分)∴符合条件的一次函数解析式为y ＝－15x ＋65或y ＝17x ＋67.(8分)17. 解：(1)把C(－1，0)代入y ＝x ＋b 得0＝－1＋b ，解得：b ＝1. ∴一次函数的解析式为y ＝x ＋1.(1分)把B(－2，n)代入y ＝x ＋1得n ＝－2＋1＝－1， ∴B(－2，－1)．(2分)把B(－2，－1)代入y ＝k x 得－1＝k－2，解得k ＝2.∴反比例函数的解析式为y ＝2x .(3分)(2)由题意得⎩⎪⎨⎪⎧y ＝x ＋1y ＝2x，(4分)解得⎩⎪⎨⎪⎧x 1＝－2y 1＝－1，⎩⎪⎨⎪⎧x 2＝1y 2＝2. ∴A 点坐标为(1，2)．∵OA ＝PA.∴△OPA 为等腰三角形．当点P 在x 轴上时，P 点坐标为(2，0)；当点P 在y 轴上时，P 点坐标为(0，4). (7分) 18. 解：(1)∵D(2，－3)在y 2＝k 2x 上，∴k 2＝2×(－3)＝－6，故y 2＝－6x.(1分)如解图，作DE ⊥x 轴，垂足为E ，第18题解图∵D(2，－3)，B 是AD 中点， ∴A(－2，0)．∵A(－2，0)，D(2，－3)在一次函数y 1＝k 1x ＋b 图象上，∴⎩⎪⎨⎪⎧－2k 1＋b ＝02k 1＋b ＝－3，解得⎩⎨⎧k 1＝－34b ＝－32.∴y 1＝－34x －32.(3分)(2)由⎩⎨⎧y ＝－34x －32y ＝－6x，解得C(－4，32)，(4分)∴S △COD ＝S △AOC ＋S △AOD ＝12×2×32＋12×2×3＝92.(6分)(3)当x ＜－4或0＜x ＜2时，y 1＞y 2.(8分)。

2021年八年级数学下册 . 反比例函数教学案(无答案)(新版)苏科版

2021年八年级数学下册 11.1 反比例函数教学案（无答案）（新版）苏科版教学目标：1. 结合具体情境体会反比例函数的意义，理解反比例函数的概念；2.能根据实际问题中的条件确定反比例函数的表达式；3．在探索过程中，引导学生体会反比例函数是刻画现实世界中特定数量的一种数学模型教学重点：反比例函数的概念．教学难点：1．讨论两个变量之间的相互关系，从而让学生加深对函数概念的理解；2．通过对反比例函数的简单应用，使学生初步形成数学的建模意识和在函数概念中的运动变化观点．教学过程：一、感情调节：汽车从南京出发开往上海（全程约300km），全程所用时间t（h）随速度v（km/h）的变化而变化.问题：（1）你能用含有v的代数式表示t吗？（2）利用（1）的关系式完成下表：生怎样的变化？（3）速度v是时间t的函数吗？为什么？二．学习过程:自学内容（一）：反比例函数的概念用函数关系式表示下列问题中两个变量之间的关系:（1）一个面积是的长方形的长a(m) 随宽b(m) 的变化而变化则a关于b的关系式为 .（2）京沪线铁路全程为1463km，某列车平均速度为v（km／h），全程运行时间为t（h），则v关于t的关系式为（3）已知三角形的面积S是常数,它的底边长y与底边上的高x之间的关系式为（4）实数m与n的积是—200,m关于n的关系式为3. 交流：（1）这些函数关系式与我们以前学习的正比例函数关系式有什么不同？（2）它们有什么共同特征？（3）你能归纳出反比例函数的概念吗？反比例函数的定义:一般地，形如（k为常数，k≠0）的函数叫做反比例函数，其中x是自变量，y是x的函数，k是比例系数.注意：1．反比例函数也可以表示为y＝kx-1(k为常数，k≠0)的形式．2．反比例函数自变量取值范围：自学内容(二)：典型例题：（例题学习，规范解题过程！）例题讲解：例1.判断下列关系式中y和x是反比例函数关系吗?若是，指出比例系数.（1）；（2）；（3）；（4）；（5） .例2.若函数是反比例函数，求k的值并写出函数的关系式.例3.若y与x成反比例，且x＝－3时，y＝7，求 y与x的函数关系式.。

八年级数学下册第9章反比例函数复习导学案无答案苏科版

反比例函数小结与思考1、反比例函数的定义：________________________________________；2、反比例函数的图象是______________________________________；3、反比例函数的性质：k>0，__________________________________________________;k<0，__________________________________________________;基础训练1、下列函数中，y 是x 反比例函数的是（） A 2x y =B 12y x =+C 12y x=- D 2xy =- 2、已知反比例函数的图像经过点（2，-3），则它的图象一定也经过（）A (－2,－3)B (3,－2)C (－1，-6)D （6，1） 3、下列函数(0)m y x x =>，(1)y m x =-，1(0)m y x x-=>，(1)y m x =-中，其中，当m>1时，y 随x 的增大而减小的有（）A.3个B. 2个C. 1个D. 0个4、已知矩形的面积为8, 那么它的长y 与宽x 之间的关系用图象大致可表示为 ( )．(D)(C)(B)(A )xyxyxyyxOOO O5、在同一直角坐标平面内，如果直线y x =与双曲线2m y x-=没有交点，那么m 的取值范围是( ) A m >2B m <2C m >-2D m <-26、已知点A （x 1，y 1）、B （x 2，y 2）在反比例函数4y x-=的图象上，若x 1<x 2,则（） A y 1<y 2 B y 1=y 2 C y 1>y 2 D 大小无法确定 7、如图,已知关于x 的函数y=k(x-1)和y=-kx(k ≠0), 它们在同一坐标系内的图象大致是( ) 8、如图,点P 是x 轴上的一个动点,过点P 作x 轴的垂线PQ 交双曲线于点Q,连结OQ, 当点P 沿x 轴正半方向运动时,Rt △QOP 面积( )A.逐渐增大B.逐渐减小C.保持不变D.无法确定O y xAO y xCO xBy O xDy9、已知y 与x 成反比例，当x=5时，y=-1，那么当y=3时，x=________；10、已知一次函数y=kx+b 的图象经过第二、三、四象限，则反比例函数1y kbx -= 的图象在第____象限；11、若反比例函数y=(2m-1)22m x - 的图象在第一、三象限,则函数的解析式为___________.12、已知反比例函数32my x-=，当x<0时，y 随x 的增大而减小，则满足上述条件的正整数m =_______; 例题分析1、已知：y=y 1-2y 2,y 1与x 2成反比例，y 2与x 成正比例,当x =-1时，y =5,当x=1时,y = -1，求y 与x 之间的函数关系式；2、如图，一次函数b kx y +=的图像与反比例函数xmy =的图像相交于A 、B 两点， (1)利用图中条件，求反比例函数和一次函数的解析式；(2)根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围；随堂练习1、写出一个反比例函数的解析式，使它的图象不经过第一、三象限，则该函数是____________．2、已知反比例函数y=12kkx-,当x>0时,y 随x 的________而增大.3、函数x k y 22--=图象上三点(-2，1y )，(-1，2y )，(21，3y )，1y ，2y ，3y 的大小为；。

2021年八年级数学下册 . 反比例函数的图像与性质教学案(无答案)(新版)苏科版

2021年八年级数学下册 11.2 反比例函数的图像与性质教学案2（无答案）（新版）苏科版教学目标：1.能简单分析反比例函数的特征；2.用描点的方法画出反比例函数的图像；3．经历画图、观察、猜想、思考等数学活动。

教学重点：画反比例函数的图像．教学难点：1．理解用光滑的曲线顺次连接各点；2．根据图像分析函数具有的一些特征，感受数形结合的思想方法．教学过程：一、感情调节：一次函数y=kx+b(k≠0)的图象是 .当k>0时，y随x的增大而 .当k<0时，y随x的增大而 .二．学习过程:自学内容（一）：画图像1.画出反比例函数y=的图象：1)2)描点：以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点。

3)连线：用光滑的曲线顺次连结各点，即可得到函数y=的图象.2.（1）x、y所取值的符号有什么关系？这个函数的图像会在哪几个象限？（2）x、y的值可以为0吗？这个函数的图像与x轴、y轴有交点吗？（3）当＞0时，随着x的增大，y怎样变化？当＜0时，随着x的增大，y怎样变化？这个函数的图像与x轴、y轴的位置关系有什么特征？自学内容(二)：实践探索一：1.仿照上题在书P127页作出反比例函数y= 的图象2. 观察函数y=和y=的图象，它们有什么相同点和不同点？3．观察：（1）在列表中点（-6，1）与（6，-1）的横纵坐标各有什么特点？你还能找到有这种特点的两点吗？（2）你能大胆猜测反比例函数图象的两支曲线有什么对称关系吗？自学提示：1. 画双曲线时一定要用平滑的曲线2. 图象的不同点从象限、图象上点的横纵坐标，自学内容(三)：典型例题：（例题学习，规范解题过程！）例1.已知反比例函数，当x =1时，y =-8.（1）求k值，并写出函数关系式；（2）点P、Q、R在函数图象上，填空：P(1，), Q(2，), R( ,-2)；（3）点分别是点P、Q、R关于原点的中心对称点，写出点的坐标；例2. 已知正比例函数与反比例函数的图象都过A(，1)点．求:(1)正比例函数的解析式；(2)正比例函数与反比例函数的另一个交点的坐标．三．自主小结:（适时小结，构建、完善知识体系！）四．当堂检测：（当堂检测，熟练掌握新知、新法！）1. 已知函数，当x ＜0时，y _______0，此时，其图象的相应部分在第_____象限.2. 已知反比例函数的图象经过P （－2，m ），则 m ＝＿＿＿＿.3. 已知反比例函数的图象经过点，则这个函数的表达式是 _4. 一个直角三角形的两直角边长分别为，其面积为2，则与之间的关系用图象表示大致为5.已知反比例函数的图象过（2，－2）和（－1，n ），则n 等于（）A ． 3B ． 4C ．6D ． 126．若反比例函数的图象经过点，则这个函数的图象一定经过点（）Ａ．Ｂ．Ｃ．Ｄ．7．反比例函数的图象经过点（2，4），求它的解析式，并画出函数图象，图象分布在哪几个象限？与坐标轴的交点是什么？8．已知反比例函数的图象过点(1,－2)．(1)求这个函数的解析式，并画出图象；(2)若点A (－5,m )在图象上，则点A 关于两坐标轴和原点的对称点是否还在图象上？五．知者加速：（自主加速，你能提高更多！）1．一次函数与反比例函数的图象交点的个数为（）A.0个B.1个C.2个D.无数个2．已知P 为函数y ＝图像上一点，且P 到原点的距离为2，则符合条件的点P 数为 ( )A.0个B.2个C.4个D.无数个七.因人作业：（适度作业是掌握知识、技能的必经之路！）《课课练》P71对应内容.PMZ36161 8D41 赁31612 7B7C 筼31165 79BD 禽27147 6A0B 樋ISC32505 7EF9 绹~21427 53B3 厳7'。

2021年八年级数学下册反比例函数复习教学案(无答案) 苏科版

2021年八年级数学下册反比例函数复习教学案（无答案）苏科版教学目标：1．巩固反比例函数的图象与性质并能运用其与对应的函数关系或之间的内在联系及其几何意义解决有关问题．2．根据所给反比例函数与一次函数的图象解决一些简单的综合问题。

教学重点：所给反比例函数与一次函数的图象解决一些简单的综合问题教学难点：能运用其与对应的函数关系或之间的内在联系及其几何意义解决有关问题．教学设计：交流合作，精讲精练一、回顾旧知复习定义反比例函数的图像与性质二．例题与思考：例11根据图形写出函数的解析式。

2, 并且当 x = 3时 y =1，求 y 与x 的函数关系式。

30) 在同一个直角坐标系中的图象可能是 .例2（如图，一次函数y1（1（2）求出这两个函数的解析式．（3）连结OA、OB，求△ABC的面积拓展提高：当x取何值时，y1=y2当x取何值时，y1>y2当x取何值时，y1<y2例三：一次函数y=ax+by轴交于点M,N垂足分别为C,E ；过点K ，连接CD ．（1）若点 A,B在反比例函数的图象的同一分支上，如图1，试证明:a.S四边形AEDK=S四边形BKCFb.AN=BM（2）若点 A,B分别在反比例函数的图象的不同分支上，课堂小结:请学生谈谈这节课的感受三、巩固练习1．对于函数y＝-,当x＞0时，y 0,y随x增大而.2．反比例函数的图象过点（2，-2），那么函数y与自变量x之间的关系式是________，它的图象在第_______象限内。

3．反比例函数y＝(m-1)的图像在二、四象限，则m的值为.642-2-4-10-5510OAB4．在函数y＝,y＝x+5,y＝-5x的图像中，是中心对称图形，且对称中心是原点的图像有个.5．已知函数，又对应的函数值分别是，若，则有（）A. y1>y2>0B. y2>y1>0C. y1<y2<0D. y2<y1<0一次函数的图象分别与轴、轴交于点，与反比例函数的图象相交于点．过点分别作轴，轴，垂足分别为；过点分别作轴，轴，垂足分别为与交于点，连接EF．（1）若点在反比例函数的图象的同一分支上，如图1，试证明：①；还平行吗？试证明教学反思39917 9BED 鯭•31880 7C88 粈21973 55D5 嗕x28755 7053 灓30094 758E 疎21249 5301 匁36345 8DF9 跹0g26076 65DC 旜-38409 9609 阉26522 679A 枚。

新苏科版八年级下册数学《反比例函数》复习教案

第11章反比例函数教学目标：(一)教学知识点1.经历抽象反比例函数概念的过程、领会反比例函数的意义，理解反比例函数的概念.2.会作反比例函数的图像，并探索和掌握反比例函数的主要性质.3.会从函数图像中获取信息，解决实际问题.(二)能力训练要求1.熟练掌握本章的知识网络结构.2.经历抽象反比例函数概念的过程，理解反比例函数的概念，培养学生的抽象思维能力.3.经历一次函数的图像及其性质的探索过程，在交流中发展学生的合作意识和能力.4.能利用图像解决实际问题.(三)情感与价值观要求通过本章内容的回顾与思考，培养学生的归纳、整理等能力；能利用反比例函数的性质及图像解决实际问题，发展学生的数学应用能力，经历函数图像信息的识别与应用过程，发展学生的形象思维能力.教学重点：反比例函数的概念，会画反比例函数的图像，并掌握其性质.反比例函数的应用.教学难点：探索反比例函数的主要性质.反比例函数的应用.教学方法：师生交流互动法.教学过程：Ⅰ.导入[师]本章的内容已全部学完，请大家先回忆一下，本章学习了哪些主要内容?[生]反比例函数的定义；反比例函数的图像及性质；反比例函数的应用.[师]下面请大家系统全面地进行复习.Ⅱ.重点知识回顾一、本章知识结构[师]由刚才大家的回忆，我们一齐来构造本章内容结构图，好吗?(给学生时间让学生自己构造，然后出示投影片)1.本章内容框架[师]同学们可以根据以上内容框架，用自己的语言归纳总结本章内容.二、举出现实生活中有关反比例函数的实例，并归纳反比例函数概念.[生]例：当三角形的面积是12 cm 2时，它的底边a(cm)是这个底边上的高h(cm)的函数.解：a ＝h24. 在上式中，每给h 一个值，相应地就确定了一个a 的值.因此a 是h 的函数，又它们之间的关系符合y=x k (k≠0),因此，a 是h 的反比例函数.三、说说函数y ＝x 2和y ＝-x2的图像的联系和区别. [生]联系：(1)图像都是由两支曲线组成；(2)它们都不与坐标轴相交；(3)它们都不过原点，既是中心对称图形，又是轴对称图形.区别：(1)它们所在的象限不同，y=x 2的两支曲线在第一和第三象限；y=-x 2的两支曲线在第二和第四象限.(2)y ＝x 2的图像在每个象限内，y 随x 的增大而减小:y=-x2的图像在每个象限内，y 随x 的增大而增大. [师]还有一点.虽然y ＝x 2和y=-x 2的图像不同，但是在这两个函数图像上任取—点，过这两点分别作x 轴、y 轴的平行线，与坐标轴围成的矩形面积相等，都为2.四、画反比例函数图像的步骤，讨论反比例函数图像的性质[生]画图像的步骤有列表，描点，连线.在画反比例函数的图像时应注意：列表时自变量的取值应选取绝对值相等而符号相反的—对一对的数值，并尽量多取一些点，连线时要连成光滑的曲线，而不是折线.反比例函数图像的性质有：1.反比例函数的图像是两支双曲线，当k>0时，图像分别位于第一、三象限；当k<0时，图像分别位于第二、四象限.2.当k>0时.在每一个象限内，y 随x 的增大而减小；当k<0时，在每一个象限，y 随x 的增大而增大.3.因为在y=xk (k≠0)中，x 不能为0，y 也不能为0，所以反比例函数的图像不可能与x 轴相交，也不可能与y 轴相交.4. 在一个反比例函数图像上任取两点P ，Q ，过点P ，Q 分别作x 、轴，y 轴的平行线，与坐标轴围成的矩形面积为S 1，S 2则S 1＝S 25. 反比例函数的图像既是轴对称图形，又是中心对称图形，它有两条对称轴，对称中心是坐标原点.[师]这位同学总结的非常详细，下面进行有关练习.1.下列函数中，其图像位于第一、三象限的有哪些?在其图像所在象限内，y 的值随x 值的增大而增大的是哪些( ) (1)x y 31=(2)x y 2.0= (3)x y 10-= (4)xy 1007-= 2.在函数x y 3=的图像上任取一点P ，过P 分别作x 轴、y 轴的平行线，与坐标轴围成的矩形面积是多少?分析：根据反比例函数图像的根据，当k ＞0时，图像位于第一、三象限，在每一个象限内，y 随x ，的大而减小；当k<0时，正好相反，但在xy 31=中，形式好像和反比例函数的形式不相同，但可以化成xy 31=的形式好像和反比例函数. [生]1.图像位于第一、三象限的有(1)(2).在其图像所在象限内，y 的值随x 值的增大而增大的有(3)(4).2. 由题意可知S=｜k ｜=3.五、你能用反比例函数的知识解决有关问题吗?1.一个圆台物体的上底面积是下底面积的41，当下底面放在桌子上时，对桌面的压强是200 Pa ，倒过来放，对桌面的压强是多少?2.一定质量的CO 2，当体积v ＝5米3时.它的密度ρ＝1.98千克／米3，求(1)ρ与v 的函数关系式；(2)当v=9米3时，CO 2的密度.[师]分析：压强p 与受力面积S ，压力F 之间的关系为p=S F ，因为是同一物体，所以F 是一定的，由于面积不同，所以压强也不同.质量m ，密度ρ和体积v 之间的关系为：ρ=v m 由，由v=5米3，ρ=1.98千克／米3,可知质量m ，实际是已知反比例函数中的k ，就求出了反比例函数关系式.解：1.当下底面放在桌面上时，对桌面的压强为p 1＝S F ＝200Pa,所以倒过来放时，对桌面的压强p 2＝S F S F 441=＝800Pa. 2.设CO 2的质量为m 千克，将v=5米3，ρ=1.98千克／米3代入公式ρ＝v m 中，得m=9.9千克.故所求ρ与v 间的函数关系式为ρ＝v 9.9. (2)当v ＝9米3时，ρ=v 9.9＝1.1(千克／米3)， Ⅲ.课堂练习1.对于函数y=x 2，当x>0时，y_______0，这部分图像在第______象限；对于y ＝-x 2，当x<0时，y____0，这部分图像在第_____象限.2.函数y=x10的图像在第____象限内，在每一个象限内，y 随x 的增大而______. 3.根据下列条件，分别确定函数y ＝x k 的表达式 (1)当x=2时，y ＝-3；(2)点(-31,21-)在双曲线y ＝x k 上. 答案：1.> 一、三 < 二、四2.一、三减小3.(1)y=x6- (2)y=x 61；Ⅳ.课时小结本节课我们从现实世界出发，抽象出反比例函数的概念，比较了反比例函数y=x 2和y=-x 2的图像的联系和区别，归纳了反比例函数的图像和性质，并进一步进行了应用.Ⅴ.课后作业复习题Ⅵ.活动与探究反比例函数图像与矩形的面积若点A 是反比例函数y=xk (k≠0)图像上的任意一点，且AB 垂直x 轴，垂足为B ，AC 垂直于y 轴，垂足为C,则矩形面积S ABOC =｜k ｜.如图(1). 1.如图(2)，P 是反比例函数)y=x k (k≠O)图像上的一点，由P 点分别向x 轴，y 轴引垂线，得阴影部分(矩形)的面积为3，则这个反比例函数的表达式______.2. 如图（3）过双曲线y=x2上两点A 、B 分别作x 轴，y 轴的垂线，若矩形ADDC 与矩形BFOE 的面积分别为S 1,S 2,则S 1与S 2的关系是_____.1.解：由题意得｜k ｜=3.又双曲线的两支分布在第二、四象限，所以k<0，故k ＝-3.∴k=x3 . 2.解：由题意得S 1=S 2=｜k ｜=2.。

苏科版八年级下册11.2反比例函数的图像与性质(2) 学案(无答案)

第3课时11.2反比例函数的图像与性质(2)班级：______姓名：________学习目标：使学生对反比例函数图象和反比例函数的性质加深理解，掌握反比例函数与一次函数的综合应用．学习重点：反比例函数的图象及其性质．学习难点：利用反比例函数的图象解题．一、学前准备1．对于函数y＝6x-，下列说法正确的是()A．它的图像分布在一、三象限B．它的图像既是轴对称图形又是中心对称图形C．当x>0时，y的值随x的增大而增大D．当x<0时，y的值随x的增大而减小2．已知反比例函数2myx-=，当______m时，其图象的两个分支在第二、四象限内；当______m时，其图象在每个象限内y随x的增大而减小．二、合作探索1．已知反比例函数y＝mx的图像经过点（34，－4）．（1）求这个反比例函数的表达式；（2）点（－1，3）在这个函数的图像上吗？（3）该函数的图像在哪几个象限内?y随x怎样变化？（4）若P(1，a)，Q(2，b),比较a、b的大小；（5）若P (x 1，y 1),Q (x 2，y 2)，x 1<x 2<0，比较y 1与y 2的大小；（6）画出函数的图像，当2≤x ≤5时，利用图像求函数值y 的变化范围；（7）当x 1<0<x 2<x 3时，x 1、x 2、x 3分别对应的函数值y 1、y 2、y 3的大小关系是怎样的？（8）当y ≤3时，求x 的取值范围．2．直线y 1＝k 1x ＋b 与双曲线y 2＝2k x相交于A(1，2)、B(m ，－1)两点．(1)求直线和双曲线的解析式；(2)求△AOB 的面积；(3)观察图像，请直接写出不等式y 1>y 2的解集．三、当堂反馈：1．如图，是反比例函数y=2－mx的图象的一支．(1)函数图象的另一支在第几象限？(2)求常数m的取值范围；(3)点A（－3，y1）、B（－1，y2）、C（2，y3）都在这个反比例函数的图象上，比较y1、、y2和y3的大小．yO x2．已知一次函数与反比例函数的图像交于点A(－4，－2)和B(a，4)．(1)求反比例函数的解析式和点B的坐标；(2)根据图像回答，当x在什么范围内时，一次函数的值小于反比例函数的值？四、课后练习1．若双曲线y ＝k x 与直线y ＝2x ＋1的一个交点的横坐标为－1，则k 的值为()A ．－1B ．1C ．－2D ．22．点A(-2,a）,B(-1,b)，C(3,c)在双曲线y=k x （k>0）上，则a,b,c 的大小关系是．3．反比例函数y ＝2x 图像上有两个点为(x 1，y 1)、(x 2，y 2)，且x 1<x 2则下列关系成立的（）A ．y 1>y 2B ．y 1<y 2C ．y 1＝y 2D ．不能确定4．如图，直线y ＝k 1x ＋b 与双曲线y ＝2k x交于A 、B 两点，其横坐标分别为1和5，则不等式k 1x ＋b <2k x的解集是_______．5．设反比例函数y ＝2k x ，(x 1，y 1)，(x 2，y 2)为其图像上两点，若x 1<0<x 2，y 1>y 2，则k 的取值范围是_______．6．正比例函数y 1=2x 的图象与反比例函数y 2=xk 的图象有一个交点的横坐标是3，(1)求k 的值；(2)根据反比例函数的图象，当−3<x <−1时，求y 2的取值范围；(3)当−3<y 2<−1时，求x 的取值范围；(4)当x <3时，求y 2的取值范围；(5)当x 为何值时，y 1>y 2?当x 为何值时，y 1<y 2?7．如图，已知双曲线y ＝k x和直线y ＝mx ＋n 交于点A 和B ，B 点的坐标是(2，－3)，AC 垂直y 轴于点C ，AC ＝32．(1)求双曲线和直线的解析式；(2)求△AOB 的面积．。

苏科版八下数学第11章《反比例函数》复习教案

第11章反比例函数教学目标：(一)教学知识点1.经历抽象反比例函数概念的过程、领会反比例函数的意义，理解反比例函数的概念.2.会作反比例函数的图像，并探索和掌握反比例函数的主要性质.3.会从函数图像中获取信息，解决实际问题.(二)能力训练要求1.熟练掌握本章的知识网络结构.2.经历抽象反比例函数概念的过程，理解反比例函数的概念，培养学生的抽象思维能力.3.经历一次函数的图像及其性质的探索过程，在交流中发展学生的合作意识和能力.4.能利用图像解决实际问题.(三)情感与价值观要求通过本章内容的回顾与思考，培养学生的归纳、整理等能力；能利用反比例函数的性质及图像解决实际问题，发展学生的数学应用能力，经历函数图像信息的识别与应用过程，发展学生的形象思维能力.教学重点：反比例函数的概念，会画反比例函数的图像，并掌握其性质.反比例函数的应用.教学难点：探索反比例函数的主要性质.反比例函数的应用.教学方法：师生交流互动法.教具准备：多媒体课件教学过程：Ⅰ.导入[师]本章的内容已全部学完，请大家先回忆一下，本章学习了哪些主要内容?[生]反比例函数的定义；反比例函数的图像及性质；反比例函数的应用.[师]下面请大家系统全面地进行复习.Ⅱ.重点知识回顾一、本章知识结构[师]由刚才大家的回忆，我们一齐来构造本章内容结构图，好吗?(给学生时间让学生自己构造，然后出示投影片)1.本章内容框架[师]同学们可以根据以上内容框架，用自己的语言归纳总结本章内容.二、举出现实生活中有关反比例函数的实例，并归纳反比例函数概念.[生]例：当三角形的面积是12 cm 2时，它的底边a(cm)是这个底边上的高h(cm)的函数.解：a ＝h24. 在上式中，每给h 一个值，相应地就确定了一个a 的值.因此a 是h 的函数，又它们之间的关系符合y=x k (k≠0),因此，a 是h 的反比例函数.三、说说函数y ＝x 2和y ＝-x2的图像的联系和区别. [生]联系：(1)图像都是由两支曲线组成；(2)它们都不与坐标轴相交；(3)它们都不过原点，既是中心对称图形，又是轴对称图形.区别：(1)它们所在的象限不同，y=x 2的两支曲线在第一和第三象限；y=-x 2的两支曲线在第二和第四象限.(2)y ＝x 2的图像在每个象限内，y 随x 的增大而减小:y=-x2的图像在每个象限内，y 随x 的增大而增大. [师]还有一点.虽然y ＝x 2和y=-x 2的图像不同，但是在这两个函数图像上任取—点，过这两点分别作x 轴、y 轴的平行线，与坐标轴围成的矩形面积相等，都为2.四、画反比例函数图像的步骤，讨论反比例函数图像的性质[生]画图像的步骤有列表，描点，连线.在画反比例函数的图像时应注意：列表时自变量的取值应选取绝对值相等而符号相反的—对一对的数值，并尽量多取一些点，连线时要连成光滑的曲线，而不是折线.反比例函数图像的性质有：1.反比例函数的图像是两支双曲线，当k>0时，图像分别位于第一、三象限；当k<0时，图像分别位于第二、四象限.2.当k>0时.在每一个象限内，y 随x 的增大而减小；当k<0时，在每一个象限，y 随x 的增大而增大.3.因为在y=xk (k≠0)中，x 不能为0，y 也不能为0，所以反比例函数的图像不可能与x 轴相交，也不可能与y 轴相交.4. 在一个反比例函数图像上任取两点P ，Q ，过点P ，Q 分别作x 、轴，y 轴的平行线，与坐标轴围成的矩形面积为S 1，S 2则S 1＝S 25. 反比例函数的图像既是轴对称图形，又是中心对称图形，它有两条对称轴，对称中心是坐标原点.[师]这位同学总结的非常详细，下面进行有关练习.1.下列函数中，其图像位于第一、三象限的有哪些?在其图像所在象限内，y 的值随x 值的增大而增大的是哪些( ) (1)x y 31=(2)x y 2.0= (3)x y 10-= (4)xy 1007-= 2.在函数x y 3=的图像上任取一点P ，过P 分别作x 轴、y 轴的平行线，与坐标轴围成的矩形面积是多少?分析：根据反比例函数图像的根据，当k ＞0时，图像位于第一、三象限，在每一个象限内，y 随x ，的大而减小；当k<0时，正好相反，但在xy 31=中，形式好像和反比例函数的形式不相同，但可以化成xy 31=的形式好像和反比例函数. [生]1.图像位于第一、三象限的有(1)(2).在其图像所在象限内，y 的值随x 值的增大而增大的有(3)(4).2. 由题意可知S=｜k ｜=3.五、你能用反比例函数的知识解决有关问题吗?1.一个圆台物体的上底面积是下底面积的41，当下底面放在桌子上时，对桌面的压强是200 Pa ，倒过来放，对桌面的压强是多少?2.一定质量的CO 2，当体积v ＝5米3时.它的密度ρ＝1.98千克／米3，求(1)ρ与v 的函数关系式；(2)当v=9米3时，CO 2的密度.[师]分析：压强p 与受力面积S ，压力F 之间的关系为p=S F ，因为是同一物体，所以F 是一定的，由于面积不同，所以压强也不同.质量m ，密度ρ和体积v 之间的关系为：ρ=vm 由，由v=5米3，ρ=1.98千克／米3,可知质量m ，实际是已知反比例函数中的k ，就求出了反比例函数关系式. 解：1.当下底面放在桌面上时，对桌面的压强为p 1＝S F ＝200Pa,所以倒过来放时，对桌面的压强p 2＝S F S F 441=＝800Pa. 2.设CO 2的质量为m 千克，将v=5米3，ρ=1.98千克／米3代入公式ρ＝v m中，得m=9.9千克.故所求ρ与v 间的函数关系式为ρ＝v 9.9. (2)当v ＝9米3时，ρ=v 9.9＝1.1(千克／米3)， Ⅲ.课堂练习1.对于函数y=x2，当x>0时，y_______0，这部分图像在第______象限；对于y ＝-x2，当x<0时，y____0，这部分图像在第_____象限. 2.函数y=x10的图像在第____象限内，在每一个象限内，y 随x 的增大而______. 3.根据下列条件，分别确定函数y ＝xk 的表达式 (1)当x=2时，y ＝-3；(2)点(-31,21-)在双曲线y ＝x k 上.答案：1.> 一、三 < 二、四2.一、三减小3.(1)y=x6- (2)y=x 61； Ⅳ.课时小结本节课我们从现实世界出发，抽象出反比例函数的概念，比较了反比例函数y=x 2和y=-x2的图像的联系和区别，归纳了反比例函数的图像和性质，并进一步进行了应用.Ⅴ.课后作业复习题Ⅵ.活动与探究反比例函数图像与矩形的面积若点A 是反比例函数y=xk (k≠0)图像上的任意一点，且AB 垂直x 轴，垂足为B ，AC 垂直于y 轴，垂足为C,则矩形面积S ABOC =｜k ｜.＝图(1). 1.如图(2)，P 是反比例函数)y=x k (k≠O)图像上的一点，由P 点分别向x 轴，y 轴引垂线，得阴影部分(矩形)的面积为3，则这个反比例函数的表达式______.2. 如图（3）过双曲线y=x2上两点A 、B 分别作x 轴，y 轴的垂线，若矩形ADDC 与矩形BFOE 的面积分别为S 1,S 2,则S 1与S 2的关系是_____.1.解：由题意得｜k ｜=3.又双曲线的两支分布在第二、四象限，所以k<0，故k ＝-3.∴k=x3-. 2.解：由题意得S 1=S 2=｜k ｜=2.。

八年级数学《反比例函数-复习课》教案

教
学
流
程
活动流程
活动内容及目的
活动一揭示课题，提出要求、明确任务。
采取“开门见山”的开课形式引入教学，通过多媒体展示“课题”，以此创设教学情境，让学生明白本节学习任务，激发其求知欲，为完成本解学习任务做到心中有数。
活动二提问检查，归整建构（师生合作梳理知识脉络，厘清知识纵横关系，搭建知识结构图）
出示知识点。
教学程序
问题与情境
师生互动
媒体使用与教学评价
活动一揭示课题，提出要求、明确任务。
通过多媒体展示“课题”----《反比例函数复习》
【教师活动】
（1）出示课题
教师并予以明确
【学生活动】
（1）明确课题
【媒体使用】
（1）出示“课题”
【赏析】
（1）学生明确复习任务，激发其求知欲，
活动二提问检查，归整建构（师生合作梳理知识脉络，厘清知识纵横关系，搭建知识结构图）
【赏析】随时搜集掌握评定学生尝试学习效果，及时回授评定的结果，以便有针对性地组织质疑和讲解，帮助学生克服思维障碍，补救知识或方法方面的漏洞。
（2）长和宽在平面直角坐标系中怎么去找？（长和宽应该往坐标轴上靠）
（3）.这个矩形面积应该怎么样计算？可以单独完成也可以和组内同学共同完成。
教师反复进行图形演示，最后给以点拨
【学生活动】
先仔细观察多媒体演示，然后再分四人小组合作交流，得出结论。
做一做让学生独立完成。
【媒体使用】
通过动画设计，有利于节时增效，吸引学生眼球，最大限度地激发学生的学习兴趣，优化课堂结构，提高课堂教学效率。
主要知识回顾，以此引领学生复习反比例函数的概念和三种表达式。
活动三变式训练，查缺补漏。

反比例函数复习教案(恢复)

反比例函数复习学案一、复习目标1、经历抽象反比例函数概念的过程，领会反比例函数的意义，理解反比例函数的概念2、培养学生从函数图象中获取信息的能力，探索并理解反比例函数的主要性质性质。

重点难点分析：重点：反比例函数的概念及性质。

难点：反比例图像的性质二、复习过程★知识点一、反比例函数与正比例函数的联系与区别是什么？思考：在讨论反比例函数的增减性时为什么必须强调在每一个象限内？【设计目的】通过类比让学生填表，掌握反比例与正比例的联系与区别★知识点二、反比例函数的概念1、反比例函数的三种表达式①；②③例1 下面函数中是反比例函数的有 .(填入序号即可)①5y x =； ②x y -=5； ③2x y =； ④2=xy ； ⑤πx y =； ⑥y =26x；⑦12-=x y ； ⑧x y 52-=； ⑨)0(2≠=a a x a y 为常数且；⑩y =1+21x 2. 例2：k 为何值时,函数y =322)(--+k kx k k 是反比例函数?【设计目的】复习反比例的概念★知识点三、反比例图像性质例3若双曲线y ＝－6x 经过点A （m ，－2m ），则m 的值为例4如图，点Ａ是双曲线xk y =与直线y=-x-(k+1)在第二象限内的交点，ＡＢ⊥x 轴于B ，且Ｓ△ABO ＝23.（１）求这两个函数的解析式；（２）求直线与双曲线的两个交点Ａ、Ｃ的坐标(3)x 取何值时，一次函数的值大于反比例函数的值，（4）求△AOC 的面积.【设计目的】通过题目的综合进一步掌握反比例的性质反馈练习 1、点（1，6）在双曲线y= 上，则k=_____．2、一个反比例函数图像过点P （ 5 ，1）和Q （－1 ，2m ）那么m =______3、已知点A(-2,y 1),B(-1,y 2)(1,y 3)都在反比例函数的图象上,则y 1与y 2 , y 3的大小关系反思与收获当堂测评【基础】1、下列各题中，哪些是反比例函数关系。

江苏省无锡市蠡园中学八年级数学下册第九章《反比例函数》单元检测(无答案) 人教新课标版

第九章反比例函数单元检测第十章班级姓名一、选择题（每小题2分，共20分）1、在下列函数中表示y关于x的反比例函数的是--------------------―――---－-（）A、xy2= B、xy2= C、12+=xy D、22xy=2、双曲线xmy21-=（m为常数）当0<x时，y随x的增大而增大，则m取值范围是（）A、0<m B、21<m C、21>m D、21≥m3、已知点（2，5）在反比例函数y=xk的图象上，则下列各点在该函数图象上的是----―（）A、（2，—5）B、（—5，—2）C、（—3，4）D、（4，—3）4、已知反比例函数xy4=，则当14-<<-x时，y的取值范围是--------―――---（）A、41<<y B、24-<<-y C、14-<<-y D、42<<y5、如图所示,点P是反比例函数y=kx图象上一点,过点P分别作x轴、y•轴的垂线,如果构成的矩形面积是4,那么反比例函数的解析式是--――--――- ( )A、y=-2xB、 y=2xC、y=-4xD、y=4x6、反比例函数xy6=图象上有三个点)(11yx，，)(22yx，，)(33yx，，其中3210xxx<<<，则1y，2y，3y 的大小关系是-----------------――--- -------------------( )A．321yyy<< B．312yyy<< C．213yyy<< D．123yyy<<7、函数1kyx-=的图象与直线y x=没有交点，那么k的取值范围是------------（）A．1k> B．1k< C．1k>- D．1k<-8、已知y=1y+2y,其中1y与1x成反比例,且比例系数为1k,而2y与2x成正比例,且比例系数为2k若x＝—1时,y=0 ,则1k、2k的关系是------------------------------―――---( )A、12k k+ =0 B、12k k =1 C、12k k- =0 D、12k k =-19、已知矩形的面积为8，那么它的长y与宽x之间的关系用图像大致可表示为---( )10、一次函数y = kx-k与反比例函数y=kx在同一直角坐标系内的图象大致是------（）yxOC BA二、填空题（每小题3分，共24分）11、函数124y x =-中，自变量x 的取值范围是． 12、如图，反比例函数x ky =)0(<k 的图象与经过原点的直线l 相交于A 、B 两点，已知A 点坐标为)1,2(-，那么B 点的坐标为 .13、y 是x 的反比例函数，且x ＝2时，y ＝7．则y 与x 之间的函数关系式是．14、若双曲线y=(2m-1)22m x - 的图象在第一、三象限，则函数的解析式为 .15、若双曲线x k y 3-=的图象在一、三象限,直线x k y )92(-=过二、四象限,则k 的整数值是．16、若直线y =2x+l 的图象与双曲线图象的一个交点横坐标为l ，则双曲线解析式为．17、如图,△OPQ 是边长为2的等边三角形,若反比例函数的图象过点P,则它的解析式是 .18、两个反比例函数ky x =和1y x =在第一象限内的图象如图所示，点P 在ky x =的图象上，PC ⊥x 轴于点C ，交1y x =的图象于点A ，PD ⊥y 轴于点D ，交1y x =的图象于点B ，当点P 在ky x =的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形PAOB 的面积不会发生变化；③PA 与PB 始终相等；④当点A 是PC 的中点时，点B 一定是PD 的中点．其中一定正确的是三、解答题（第19、20每题8分，第21~24每题10分，共50分）19、近视眼镜的度数y （度）与镜片焦距x （m ）成反比例．已知200度近视眼镜镜片的焦距为0.5m 。

江苏省无锡市蠡园中学八年级数学下册 8.2《分式的基本性质(2)》学案(无答案) 苏科版

课题：§8.2分式的基本性质（2）课型：新授课学习目标（学习重点）：1．理解最简公分母的概念会求出几个分式的最简公分母；2．理解通分的意义，掌握通分的法则．课后作业：一、自我检测题（一）选择题（每小题10分）1．分式的最简公分母是（）A ．aB ．bC ．abD ．b a 22．分式b 2a ，x 3b 2，14ab 的最简公分母是（）A ．24a 2b 3B ．24ab 2C ．12ab 2D ．12a 2b 3（二）填空题（每小题10分）3．x x +21与x x -21的最简公分母是．4．分式()()2222,2,3y x x x y xy y x --+的最简公分母是．（三）解答题（每小题6分）5．不改变分式的值，把下列各式的分子、分母中各项系数都化成整数（1）2a －3b25a ＋53b ；（2）0.25x 2＋0.5y 20.75x 2－2y 2；（3）0.2x －0.4y 15x ＋3y ；（4）0.5m －0.3n2m －3n.6．通分（每小题5分）（1）b a 21，－22ab ；（2）xz xz y x 45,34,2123- （3）y x x -2，y x y+3；（4）221y x -，xy x +21；（5）x x +21，1212++-x x （6）91,62,12--++x xx x x x21,a ab【针对训练（“药方题”）】1、2、3、4（P24.1）；6（P25.3）二、补充训练题（一）基础类1.通分（1）2mn 4m 2－9，2m －32m ＋3；（2）a －1a 2＋2a ＋1，6a 2－1 ；（3）2)(1,a b b a c --（4）a －3，32+a ；（5）)1(,)1(++b b a b a b ；（6）1x 2－4，－x x 2－x －6，x ＋3x 2＋5x ＋6（7）144)12(4,1222+--+a a a a a ；（8）222421,4)1(1a a a a a +---+-；（9）2242,21,21b a ab b a b a -+-（二）拓展类2．已知M x 2－y 2＝2xy －y 2x 2－y 2＋x －y x ＋y ，求M ． 3．已知：1x －1y ＝3，求2x ＋3xy －2y x －2xy －y的值．。

江苏省无锡市梅里中学八年级数学下册《9.1反比例函数》学案(无答案) 苏科版

9.1反比例函数班级姓名学号学习目标1.理解反比例函数的概念，能判断两个变量之间的关系是否是函数关系，进而识别反比例函数.2.能根据已知条件确定反比例函数的表达式.学习重点：1.理解反比例函数的意义.2. 确定反比例函数的表达式学习难点：1.反比例函数表达式的确定.2. 根据已知条件确定反比例函数的表达式.教学过程一、自主探究：1．什么是函数？ 2．什么是一次函数？什么是正比例函数？它们的一般形式是怎样的？3．我们还记得，在小学里学过，什么叫成反比例关系吗？4．如果路程s 一定，那么速度v 和时间t 成什么关系？二、自主合作：1．尝试：汽车从南京出发开往上海（全程约300km ），全程所用时间t(h),随速度v(km/的变化而变化.（1）你能用含v 的代数式表示t 吗？（2）利用（1）的关系式完成下表：v /(km/h)60 80 90 100 120 t /h随着速度的变化，全程所用时间发生怎样的变化？（3）时间t 是速度v 的函数吗？为什么？（4）时间t 是速度v 的一次函数吗？是正比例函数吗？为什么？2．思考：用函数关系式表示下列问题中两个变量之间的关系：（1）一个面积为6400m 2的长方形的长a (m)随宽b (m)的变化而变化；（2）某银行为资助某社会福利厂，提供了20万元的无息贷款，该厂的平均年还款额y （万元）随还款年限x（年）的变化而变化；（3）游泳池的容积为5000m 3,向池内注水，注满水所需时间t (h)随注水速度v (m 3/h)的变化而变化；（4）实数m 与n 的积为-200，m 随n 的变化而变化.3．讨论交流．函数关系式a =6400b 、y = 20x 、t = 5000v 、m =－200n 具有什么共同特征？你还能举出类似的实例吗？ 4．概括总结．一般地，形如y = k x(k 为常数，k ≠0)的函数叫做反比例函数．其中x 是自变量，y 是x 的函数，k 是比例系5.概念巩固:下列关系式中的y 是 x 的反比例函数吗？如果是，比例系数k 是多少？（1）y = 4x ; （2）y = －12x ; （3）y = 1－x; （4） xy = 1; （5）y = x 2; （6）y = ( 2 －3)x －1 反比例函数通常有三种表达式：y = kx，y = kx －1 , xy = k （上述三个式子中k 均为常数且k ≠0）. 三、自主展示：例1：判断下列函数表达式中，表示反比例函数的是哪几个？（1）y = x4 ; （2）y = 34x ; （3）－xy = 3;（4）-3x y + 2 = 0 ; （5）y = 1x2 ; （6）y = 2x + 1 .例2 (1)已知y 是x 的反比例函数，当 x = 3时，y = 2 ,求y 与x 的函数关系式.(2)y = (1＋k)x ︱k ︱－2中，y 是x 的反比例函数，求k 的值.四、自主拓展：1．下列关系式中，是反比例函数的是（）A. y = k xB. y = 2x+1 C. y = －13x D. y = 4x －32.下列各选项中所列举的两个变量之间的关系，是反比例函数关系的是（）A. 斜边长为5的直角三角形中，两直角边之间的关系.B.等腰三角形中，顶角与底角之间的关系.C.圆的面积s 与它的直径d 之间的关系.D. 面积20cm 2的菱形，其中一条对角线长y 与另一条对角线长x 的关系.3．已知y 与x 成反比例函数的关系，且当x = - 2时，y ＝3，（1）求该函数的解析式（2）当x = 4时，求y 的值（3）当y = 2时，求x 的值.归纳总结：反比例函数的五种不同的表现形式：形式1：y 是 x 反比例函数形式2：y = kx (k 为常数，k ≠0)形式3：y = kx －1 (k 为常数，k ≠0)形式4：xy = k(k 为常数，k ≠0)形式5：变量 y 与 x 成反比例，比例系数为k (k ≠0)【课后作业】班级姓名学号 1．函数y = （k ）叫做反比例函数，确定了就可以确定一个反比例函数，自变量的取值范围是 .2．反比例函数y = 2 －12x中的k 值为 . 3.当m 时，y = m+3x是反比例函数，任取一个m 值写出这个反比例函数4.近视眼镜的度数y 度与镜片焦距x 米成反比例，已知400度近视眼镜片的焦距为0.25米，则眼镜度数y 度与镜片焦距x 之间的函数关系式是 .5. 下列各题中：（1）三角形的面积S 一定时，它的底a 与这个底边上的高h 的关系；（2）多边形的内角和与边数的关系；（3）正三角形的面积与边长之间的关系；是反比例函数关系的是: （只填序号）※6.y 与x 成反比例，x 与z 成正比例，则y 与z 成比例. 7.下列函数中是反比例函数的是（）A. x(y －1) = 1B. y = x －1C. y = －1x+1D. y = 1x－3 8.甲地与乙地相距5千米，某人以平均速度v （km/h ）从甲地向乙地行走，设他全程所需时间为t(h),则变量t是v 的（）A. 正比例函数B.反比例函数C.一次函数D.以上都不对9．计划修建铁路s （km ）,铺轨天数a(天),每日铺轨长度b(km/天)，则下列三个结论正确的是（）①当s 一定时，a 是b 的反比例函数；②当a 一定时，s 是b 的反比例函数；③当b 一定时，a 是s 的反比例函数；A. ①B. ②C. ③D. ①②③10. 已知y 与x+2成反比例，且当x=2时,y=3，求（1）y 关于x 的函数解析式；（2）当x=-2时的y 值.11. 一定质量的二氧化碳，当它的体积时，它的密度（1）求与V 的函数关系式；（2）求当时二氧化碳的密度.※12．已知函数y = y1＋y2，y1与x成正比例，y2与x成反比例，且当x =1时，y = 6,当x = 2时，y = 5,求y 与x的函数关系式.【励志故事】愚钝的力量大科学家爱因斯坦曾做过一个实验：他从村子里找了两个人，一个愚钝且软弱，一个聪明且强壮。

江苏省无锡地区八年级数学下册学案反比例函数的应用

班级姓名学习目标：1.能灵活运用反比例函数的知识解决实际问题.2.经历“实际问题——建立模型——拓展应用”的过程培养分析问题，解决问题的能力.补充例题：例1.某蓄水池的排水管每小时排水8m3，6h可将满池水全部排空.⑴蓄水池的容积是多少？.⑵如果增加排水管，使每小时排水量达到Q(m3)，那么将满池水排空所需时间t(h)将如何变化？⑶写出t与Q之间关系式..⑷如果准备在5小时内将满池水排空，那么每小时的排水量至少.⑸已知排水管最多为每小时12 m3，则至少_ ___h可将满池水全部排空.例2.为了预防流行性感冒，某学校对教室采用药熏消毒法进行消毒．已知药物燃烧时，室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例，•药物燃烧后，y与x成反比例(如图所示)．现测得药物8分钟燃毕，此室内空气中每立方米的含药量为6毫克，请你根据题中所提供的信息，解答下列问题：⑴药物燃烧时y关于x的函数关系式为，自变量的取值范围是；⑵药物燃烧后y与x的函数关系式为；⑶研究表明，当空气中每立方米的含药量低于1.6毫克时学生方可进教室，那么从消毒开始，至少需要经过分钟后，学生才能回到教室；⑷研究表明，当空气中每立方米的含药量不低于3毫克且持续时间不低于10•分钟时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？例3.如图,矩形ABCD中,AB＝6,AD＝8,点P在BC边上移动(不与点B、C重合)，设PA=x，点D到PA的距离DE=y.求y与x之间的函数关系式及自变量x的取值范围例4．已知一次函数与反比例函数的图象交于点P(－3,m),Q(2,－3)．（1）求这两个函数的函数关系式；（2（3）当x为何值时，一次函数的值大于反比例函数的值？当x为何值时，一次函数的值小于反比例函数的值？x课后作业：一、填空题1.A 、B 两城市相距720千米，一列火车从A 城去B 城．⑴火车的速度v （千米/时）和行驶的时间t （时）之间的函数关系是．⑵若到达目的地后，按原路匀速原回，并要求在3小时内回到A 城，则返回的速度不能低于．2.有一面积为60的梯形，其上底长是下底长的13，若下底长为x ，高为y ，则y 与x 的函数关系是．3.美国的一种新型汽车可装汽油500L ，若汽车每小时用油量为 xL ．⑴用油时间y （h ）与每小时的用油量之间的函数关系式可表示为．⑵每小时的用油量为25L ，则这些油可用的时间为．⑶如果要使汽车连续行驶50h 不需供油，那么每小时用油量的范围是．3. 如图,直线y=12x+2 分别交x,y 轴于点A,C,P 是该直线上第一象限内的一点,PB ⊥x 轴,B 为垂足,ABP S =9.求过P 点的反比例函数的解析式.4.设∆ABC 中BC 边的长为x(cm)，BC 上的高AD 为y(cm).已知y 关于x 的函数图象过点(3,4). ⑴求y 关于x 的函数解析式和∆ABC 的面积.⑵画出函数的图象，并利用图象，求当2＜x ＜8时y 的取值范围. O y x A CP B附件2：律师事务所反盗版维权声明。

江苏省无锡市蠡园中学八年级数学《1.11.4》学案(无答案)

F EDCBA1．了解轴对称与轴对称图形,会准确画出轴对称图形,找出对称轴、对称点等． 2．能熟练应用轴对称的性质．3．复习线段的垂直平分线，角平分线的性质及推论，并能加以灵活运用．例题：例1．（1）下列说法中，正确的个数是（）①轴对称图形只有一条对称轴，②轴对称图形的对称轴是一条线段，③两个图形成轴对称，这两个图形是全等图形，④全等的两个图形一定成轴对称，⑤轴对称图形是指一个图形，而轴对称是指两个图形而言．A ．1个B ．2个C ．3个D ．4个（2）如图在一个规格为6×12（即6×12个小正方形）的球台上，有两个小球A ，B .若击打小球A ，经过球台边的反弹后，恰好击中小球B ，那么小球A 击出时，应瞄准球台边上的点（） A ．P 1 B ．P 2 C ．P 3 D ．P 4例2．作图题（1）作出图1中△ABC 关于直线l 的对称图形；（2）如图2，∠BAC ＝60°，点P 在边AC 上，试用带刻度的直尺和量角器，在∠BAC 内部找一点O ，使点O 到A 、P 的距离相等，且到∠BAC 的两边的距离相等．图1 图2例3．已知：如图，△ABC 中，△ABC 的外角平分线AD ，交BC 的垂直平分线于D 点，DE ⊥AB 于点E ，DF ⊥AC 于点F ，（1）求证：BE =CF ；（2）若AB =15，AC =7，求AE 的长．课后续助：1．点A 和点B 关于直线l 对称，对直线l 任意一点P ，必有PA ____PBPCBDCBA2．对称图形________有一条对称轴，________有两条对称轴，________有四条对称轴，_______有无数条对称轴.(各填上一个图形即可) ．3．到三角形的三个顶点的距离相等的点是___________的交点．到三角形的三边的距离相等的点是___________的交点．4．如果△ABC 与△A /B /C /关于直线l 对称，且∠A ＝500，∠B /＝700，那么∠C / ＝___ _．5.如图，点P 在∠AOB 内，PM ⊥OA 于M ，PN ⊥OB 于N ，且PM ＝PN ，连结OP ，则OP 是________________．依据是_______________________________． 6．如图，AB ＝AC ，AC 的垂直平分线交BC 于D ，垂足为E ，若AB ＝10，△ABD 的周长为23，求△ABC 的周长．7．如图，有一个三角形纸片ABC ，AB =10cm ，BC =7cm ，AC =6cm ，沿过点B 的直线折叠这个三角形，使顶点C 落在AB 边上的点E 处，折痕为BD ，求△AED 的周长．8．如图，在△ABC 中，∠BAC ＝90°，BE 平分∠ABC ，DE ⊥BC 于D ，DE =DC ．求证：BC ＝AB ＋AE ．9．如图，在四边形ABCD 中，BC ＞BA ，AD =CD ，BD 平分∠ABC ，试说明：∠A +∠C =180°．AC EABD EED C BANM POBA。

江苏省无锡市蠡园中学八年级数学上册《第1章轴对称》复习学案2(无答案) 苏科版

E DCB A课型：复习课学习目标（重点）：1．能将轴对称的知识进行简单的运用．2．掌握线段的垂直平分线和角平分线的性质，并能进行简单运用．3．掌握等腰三角形、等腰梯形的概念和性质，并能用它们解决相关的问题．自助内容：1．填空（1）等腰三角形中，有一个角为50°，则另两角分别为_______________．（2）等腰三角形中，有一个角为100°，则另两角分别为_______________．（3）等腰三角形两边分别为3和7，那么它的周长为___________________．（4）如图，直线MN是线段BC的垂直平分线，MN交BC于D，A是MN上任意一点，连接AB、AC，则△ABC一定是__________三角形；当AB＝5，BD＝3时，△ABC的周长为______；当∠B＝45°时，△ABC是__________ 三角形．（5）如图：等腰梯形ABCD中，AD∥BC，AB=6，AD=5，BC=8，且AB∥DE，则△DEC的周长是____________．2．在Rt△ABC中，∠C=90°，BD平分∠ABC交AC于点D，DE垂直平分线段AB，（1）试找出图中相等的线段，并说明理由．（2）若DE=1cm，BD=2cm，求AC的长．3．在△ABC中，AB=AC，D是BC边上的一点，DE⊥AB，DF⊥AC，垂足分别为E、F，添加一个条件，使DE= DF，并说明理由．解：需添加条件是．理由是：4．如图，在△ABC中，CF⊥AB于F，BE⊥AC于E，M为BC的中点，EF=5，BC=8，判断△EFM的形状并求出它的周长．NMD CBAF ED C BAEFM CBAEDCBA典型例题：例1．在正方形ABCD 上，P 在AC 上，E 是AB 上一定点，则当点P 运动到何处时，△PBE 的周长最小?例2．如图①，△ABC 中，AB =AC ，∠B 、∠C 的平分线交于O 点，过O 点作EF ∥BC 交AB 、AC 于E 、F ．（1）图中有几个等腰三角形?猜想： EF 与BE 、CF 之间有怎样的关系，并说明理由．（2）如图②，若AB ≠AC ，其他条件不变，图中还有等腰三角形吗?如果有，分别指出它们．在第（1）问中EF 与BE 、CF 间的关系还存在吗?（3）如图③，若△ABC 中∠B 的平分线BO 与三角形外角平分线CO 交于O ，过O 点作OE ∥BC 交AB 于E ，交AC 于F ．这时图中还有等腰三角形吗?EF 与BE 、CF 关系又如何?说明你的理由。

中学八年级数学下册《反比例函数》复习教学案

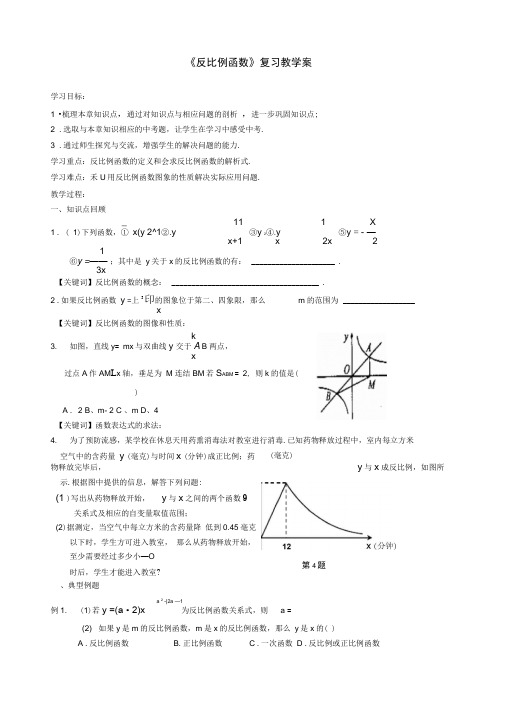
《反比例函数》复习教学案学习目标：1 •梳理本章知识点，通过对知识点与相应问题的剖析，进一步巩固知识点;2 .选取与本章知识相应的中考题，让学生在学习中感受中考.3 .通过师生探究与交流，增强学生的解决问题的能力. 学习重点：反比例函数的定义和会求反比例函数的解析式. 学习难点：禾U 用反比例函数图象的性质解决实际应用问题. 教学过程：一、知识点回顾_11 1X1 . ( 1)下列函数，① x(y 2^1②.y③y 2④.y⑤y = - — x+1x 2x 21⑥y =—— ；其中是 y 关于x 的反比例函数的有： _____________________ .3x【关键词】反比例函数的概念： _____________________________________ . 2 .如果反比例函数 y =上3印的图象位于第二、四象限，那么m 的范围为 __________________x【关键词】反比例函数的图像和性质： k3.如图，直线y = mx 与双曲线y 交于A B 两点，x过点A 作AM L x 轴，垂足为 M 连结BM 若S ABM = 2, 则k 的值是()A . 2B 、m- 2C 、mD 、4 【关键词】函数表达式的求法： 4.为了预防流感，某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中，室内每立方米空气中的含药量 y (毫克)与时间x (分钟)成正比例；药物释放完毕后，y 与x 成反比例，如图所示.根据图中提供的信息，解答下列问题:(1 )写出从药物释放开始， y 与x 之间的两个函数9关系式及相应的自变量取值范围；(2)据测定，当空气中每立方米的含药量降低到0.45毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小—O 时后，学生才能进入教室? 、典型例题a 2 -|2a —1例1.(1)若y =(a • 2)x为反比例函数关系式，则 a =(2) 如果y 是m 的反比例函数，m 是x 的反比例函数，那么 y 是x 的( ) A .反比例函数B .正比例函数C .一次函数D .反比例或正比例函数(毫克)第4题(3) 一函数①它的图像经过点(一1, 1);②它的图像在二、四象限内；③在每个象限内，函数值y随自变量x的增大而增大.则这个函数的解析式可以为___________________________ .k例2. (1)过反比例函数y (k . 0)的图象上的一点分别作x、y轴的垂线段，如果垂线段与x、y轴所x围成的矩形面积是6,那么该函数的表达式是, 若点A( - 3,m)在这个反比例函数的图象上,贝y m= ______ ._______1 _k(2)函数y 的图象与直线y二X没有交点，那么k的取值范围是( )xA. k 1B. k ：1C. k-1D. k ：：—1例3.已知一次函数与反比例函数的图象交于点P( —3,m),Q(2, —3).(1 )求这两个函数的函数关系式；(2)在给定的直角坐标系(如图)中，画出这两个函数的大致图象；(3)当x为何值时，一次函数的值大于反比例函数的值？当x为何值时，一次函数的值小于反比例函数的值？三、归纳总结【课后练习】k1 •已知反比例函数y二一xA .第二、三象限B的图象经过点P(一I , 2)，则这个函数的图象位于2.如下图右一，一次函数y •第一、三象限 C •第三、四象限 D •第二、四象限2的图像交于点A(2,1),B(x1=x—1与反比例函数y 2—1, —2),则使y 1AC// y 轴，△ ABC ()>y 2的x的取值范围是3 的面积记为S ，则 A . S =2B . S =4C . 2 S . 4D . S 44. 如上图右三，在直角坐标系中，点A 是x 轴正半轴上的一个定点，点B 是双曲线y ( x 0 )上x的一个动点，当点 B 的横坐标逐渐增大时，A OAB 的面积将会( )A .逐渐增大B .不变C .逐渐减小D .先增大后减小k5. 已知点A ( X i , y i )、B ( X 2, y 2)是反比例函数y=— ( k > 0)图象上的两点，若X i c 0 c X 2，则有x( )A . y i ::: 0 ■ y2B . y ::: 0 y iC . y i ：： y 2 ：： 0D . y 2 ：： y i ：： 036.已知点A 是反比例函数y 图象上的一点•若 AB 垂直于y 轴，垂足为B ，则△ AOB 的面积xm +i7. 反比例函数 y= ------------- 的图象经过点(2, i ),则m 的值是 ____________x38. 如图，点A 、B 是双曲线y上的点，分别经过 A 、xB 两点向x 轴、y 轴作垂线段，若 S 阴影-i,则S - S 2 = ___________________ .19.如图，一次函数 y x-2的图象分别交x 轴、y 轴于2上一点且PCAOB 的中位线，PC 的延长线交反比例函数三、解答题10. 已知：如图，在平面直角坐标系 / C=90°，点D 在第一象限，中点A. (1、求该反比例函数的解析式；(2、若该反比例函数的图象与 Rt △ OCD 勺另一边DC 交于点B ,求过A B 两点的直线的解析式.A 、B, P 为 AB k亠(k ■ 0) xx O y 中，Rt △ OCD 勺一边0C 在x 轴上，OC=3 DC=4反比例函数的图象经过 0D 的-，贝U k 的值和Q 点的坐标分别为23kii.已知：如图，正比例函数 y =ax 的图象与反比例函数 y的图象交于点 A 3,2 .x(i 、试确定上述正比例函数和反比例函数的表达式；(2、根据图象回答，在第一象限，当x 取何值时，反比例函数的值大于正比例函数的值?(3) Mm, n是反比例函数图象上的一动点，其中0 ：：： m ：：： 3,过点M作直线MN // x轴，交y 轴于点B ;过点A作直线AC // y轴交x轴于点C，交直线MB于点D •当四边形OADM的面积为6时, 请判断线段BM与DM的大小关系，并说明理由.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

班级_____姓名________
课题:反比例函数复习（初二数学下044）课型：复习课学习目标（重点）：
理解反比例函数的性质，掌握如何确定反比例函数表达式．自助内容： 1．知识梳理
（1）反比例函数概念：一般地，如果两个变量x 、y 之间的关系可以表示成y ＝或（k 为常数，k ≠0）的形式，那么称y 是x 的反比例函数．（2）反比例函数的图象和性质
（3）k 的几何含义：反比例函数y ＝
x
(k ≠0)中比例系数k 的几何意义，即过双曲线y ＝
k
x
(k ≠0)上任意一点P 作x 轴、y 轴垂线，设垂足分别为A 、B ，则所得矩形OAPB 的面积为 .
二、知识点应用 1.已知反比例函数k
y x
=的图象经过点(23)，，则此函数的关系式是，这个函数的图象位于象限． 2.在反比例函数1k
y x
-=
的图象的每一条曲线上，y x 都随的增大而增大，则k 的取值范围是．
3.如图，四边形OABC 是边长为1的正方形，反比例函数x
k
y =的图象过点B ，则k 的值为_______．
4．若点A (-2，y 1)、B (-1， y 2)、C (1， y 3)在反比例函数y =
1
x
的图象上，则下列结论正确的是( ) A ．1y >2y >3y B ．3y >1y >2y C ．2y >1y >3y D ．3y >2y >1y
A ．
B ．
C ．
D ．
5.若0ab <，则正比例函数y ax =与反比例函数b
y x
=在同一坐标系中的大致图象可能是（）
课后续助：
一、自我检测题
一、选择（每题5分，共25分）
1．一次函数y ＝kx -2,y 随x 的增大而减小，那么反比例系数y ＝
x
k
（） A ．当x ＞0时，y ＞0 B ．在每个象限内，y 随x 的增大而减小 C ．图像在第一、三象限 D ．图像在第二、四象限 2．已知点M (－2，3 )在双曲线x
k
y =上，则下列各点一定在该双曲线上的是（） A ．(3，-2 ) B ．(-2，-3 ) C ．(2，3 ) D ．(3，2)
3．已知函数)0(<=
k x
k
y ，又x 1、x 2对应的函数值分别是y 1、y 2，若012>>x x ，则有（） A ．y 1>y 2>0 B ．y 2>y 1>0 C ． y 1<y 2<0 D ．y 2<y 1<0 4．函数y =a (x -3)与x
a
y =在同一坐标系中的大致图象是（）
5．一张正方形的纸片，剪去两个一样的小矩形得到一个“E ”图案，如图所示，设小矩形的长和宽分别为x 、y ，剪去部分的面积为20，若210x ≤≤，则y 与x 的函数图象是（）
二、填空（每题5分，共10分）
1．反比例函数y ＝(m -1)2
3m x -的图像在二、四象限，则m 的值为
.
2．点P 在反比例函数1
y x =
(x > 0)的图象上，且横坐标为2. 若将点P 先向右平移两个单位，再向上平移
一个单位后所得的像为点P '
.则在第一象限内，经过点P '的反比例函数图象的解析式是 .
x
x
x
x
B ．
三、解答（1~3每题15分，第4题20分共65分） 1．已知反比例函数与一次函数的图像都经过点（－2，－1），且在x ＝3时两函数值
相等，求这两个函数的解析式.
2.如图，反比例函数x
y 2
=
的图像与一次函数b kx y +=的图像交于点A (m ，2)，点B (－2，n )，一次函数图像与y 轴的交点为C ．
（1）求一次函数解析式；（2）求C 点的坐标；（3）求△AOC 的面积．
3．如图，已知一次函数1
y x m =+（m 为常数）的图象与反比例函数 2k
y
x
=
（k 为常数，0k ≠）的图象相交于点 A （1，3）．
（1）求这两个函数的解析式及其图象的另一交点B 的坐标；（2）观察图象，写出使函数值12y y ≥的自变量x 的取值范围．
4．如图，点P 的坐标为（2，
2
3），过点P 作x 轴的平行线交y 轴于点A ，交双曲线x k y =(x >0)于点N ；作PM ⊥AN 交双曲线x
k
y =(x >0)于点M ，
连结AM 已知PN ＝4．（1）求k 的值；（2）求△APM 的面积．
y m x
=y kx b =+
二、拓展类
1．为预防“手足口病”，某校对教室进行“药熏消毒”．已知药物燃烧阶段，室内每立方米空气中的含药
量y （mg ）与燃烧时间x （分钟）成正比例；燃烧后，y 与x 成反比例（如图所示）．现测得药物10分钟燃烧完，此时教室内每立方米空气含药量为8 mg ．根据以上信息，解答下列问题：（1）求药物燃烧时y 与x 的函数关系式；（2）求药物燃烧后y 与x 的函数关系式；
（3）当每立方米空气中含药量低于1.6 mg 时，对人体无毒害作用．那么从消毒开始，经多长时间学生才可以返回教室？
2．已知：如图，正比例函数y ax =的图象与反比例函数k
y x
=的图象交于点()32A ，．
（1）试确定上述正比例函数和反比例函数的表达式；
（2）根据图象回答，在第一象限内，当x 取何值时，反比例函数的值大于正比例函数的值？（3）()M m n ，是反比例函数图象上的一动点，其中03m <<，过点M 作直线MN x ∥轴，
交y 轴于点B ；过点A 作直线AC y ∥轴交x 轴于点C ，交直线MB 于点D ．当四边形OADM 的面积为6时，请判断线段BM 与DM 的大小关系，并说明理由．
)。