3.公式定义器-练习
第一章 机械运动-课堂作业-2024-2025学年人教版物理八年级上册

第一章机械运动第1节长度和时间的测量知识梳理知识点1长度的单位在国际单位制中,长度的基本单位是,符号是。
长度单位之间的换算关系是1km= m,1m= cm,1m= mm,1m= μm,1nm= m。
知识点2长度的测量(1)选择和使用刻度尺之前要观察刻度尺的、和。
(2)正确使用刻度尺的方法:选、观、放、看、读、记。
(3)读数:正确读取测量数据,视线要正对刻度线,读数时要读到的下一位,一个完整的数据=准确值+估计值十单位。
知识点3时间的测量(1)在国际单位制中,时间的基本单位是,符号是。
还有小时,符号是;分钟,符号是。
(2)机械停表的使用方法:一调(归零);二按(启动);三停;四读。
(3)读数=小盘的分钟读数+大盘的秒读数。
知识点4误差(1)误差是测量值与之间的差异,误差是(填“可以”或“不可以”)消除的。
(2)减小误差的测量方法一般有:①;②;③。
点拨:误差不是错误,错误是能够避免的。
课堂练习1.[知识点2]测量金属块的长度,如下图所示的四种方法中,正确的是()2.[知识点4]误差产生的原因与()A.测量工具有关,但与测量人无关B.测量人有关,但与测量工具无关C.被测物体有关D.测量工具有关,也与测量人有关3.[知识点1]某同学身高是167.4 ,课本每张纸的厚度是73,一支新铅笔的长度是0.175,我国最长的河流长江长约6400。
4.[知识点2]如图所示,用甲、乙两刻度尺测量同一木块的长度,其测量结果分别为:甲测量的结果是,甲尺的分度值是;乙测量的结果是,乙尺的分度值是。
尺测量较准确。
5.[知识点2]测量细铜丝的直径时常采用如图所示的“测多算少”的方法,如图中紧密排绕的铜丝,若这些紧密排绕的铜丝一共有20圈,则铜丝的直径为 mm;如果在将细铜丝缠绕在粗细均匀铅笔上的过程中,没有紧密排列,则测出的细铜丝的直径将(填“偏大”“偏小”或“不变”)。
6.[知识点3]如图甲所示,机械停表的读数是 min s;如图乙所示,电子秒表的读数是。
计算机文化基础试题集10

”习题三(参考)一、判断题1.在汉字系统中,我国国标汉字一律是按拼音顺序排列的。
2.在Windows中,只要选择汉字输入法中的“输入中文符号”,则在“中文半角”状态下也可输出如顿号、引号、句号等全角的中文标点符号。
3.输入汉字的编码方法有很多种,输入计算机后,都按各自的编码方法存储在计算机内部,所以在计算机内部处理汉字信息相当复杂。
4.在用Word 97编辑文本时,若要删除文本区中某段文本的内容,可先选取该段文本,再按Delete键。
5.在Word 97中,建立交叉引用的项目必须在同一个主控文档中。
6.用Word 97制作的表格大小有限制,一般表格的大小不能超过一页。
7.在Word 97中编辑文稿,要产生文绕图的效果,只能在图文框中进行。
8.在Word 97中,使用“查找”命令查找的内容,可以是文本和格式,也可以是它们的任意组合。
9.删除选定的文本内容时,Delete键和退格键的功能相同。
10.Word 97中的“样式”,实际上是一系列预置的排版命令,使用样式的目的是为了确保所编辑的文稿格式编排具有一致性。
11.为了使用户在编排文档版面格式时节省时间和减少工作量,Word 97提供了许多“模板”,所谓“模板”就是文章、图形和格式编排的框架或样板。
12.Word 97中的“宏”是一系列Word命令的集合,可利用宏录制器创建宏,宏录制器不能录制文档正文中的鼠标操作,只能录制键盘操作,但可用鼠标操作来选择命令和选择选项。
13.在Word 97中,把表格加上实线,只能把表格变虚线,通过“格式”菜单中的“边框与底纹”进行。
14.要在每一页中放置相同的水印,必须放在页眉和页脚中。
15.Word 97文档可以保存为“纯文本”类型。
16.在Word 97中隐藏的文字,屏幕中仍然可以显示,但打印时不输出。
二、选择题(题头带*为多选题)1.在微型计算机汉字系统中,一个汉字的机内码占的字节数为。
A.1B.2C.4D.82.100个32×32点阵的汉字字模信息所占的字节数为。
人教版高中物理选修3-1:1.8 电容器的电容 同步课时练习

8电容器的电容记一记电容器的电容知识体系2个公式——电容的定义式和决定式2个前提——电容器的动态分析时U不变和Q不变辨一辨1.其他条件不变时,平行板电容器的电容随极板正对面积的增大而增大.(√)2.其他条件不变时,平行板电容器的电容随极板间距离的增大而增大.(×)3.任何电介质的相对介电常数都大于1.(√)4.某电容器上标有“1.5 μF9 V”的字样,则该电容器的击穿电压为9 V.(×)5.有人说,电容器被击穿后就没有了容纳电荷的本领.(√) 6.两个靠近的导体一定能构成一个电容器.(×)7.电容器的电容跟它两极板间所加电压成反比.(×)想一想1.由电容器电容的定义式:C=QU,能说电容器的电容跟电容器所带电荷量成正比,跟电容器两极间电压成反比吗?提示:不能.因为电容器的电容是描述电容器容纳电荷来■■的物理量,其大小仅由电容器本身性质决定,而与电容器所带电荷量及电容器两极间电压无关.2.电容器所带电荷量的含义是什么?有正、负之分吗提示:电容器所带电荷量是指电容器一极所带电荷量的绝对值,当然不会是负值.3.电容器的额定电压和击穿电压有何区别?提示:电容器的额定电压是电容器正常工作时两极间的电压,而其击穿电压是指电容器中电介质被击穿而使电容器被破坏的极限电压.思考感悟:练一练1.[2019·山东省普通高中学业水平考试]某一型悬的电容器标有16 V,1.01 F的字样,当电容器两极板间的电势差为8 V时,下列判断正确的是()A.电容器的电容是1.01 F,带电量是0.16 CB.电容器的电容是0.11 F,带电量是0.08 CC.电容器的电容是0.005 F,带电量是0.08 CD.电容器的电容是0.005 F,带电量是0.04 C答案:B2.[2019·北京市普通高中学业水平考试]将平行板电容器C、电源E和电阻R等元件连接成如图所示的电路.初始时电容器不带电.闭合开关S,在电源向电容器充电的过程中,下列说法正确的是()A.电容器带电数量增大,两板间电压减小B.电容器带电数量减小,两板间电压增大C.电容器带电数量和两板间电压都增大D.电容器带电数量和两板间电压都减小答案:C3.[2019·广东省普通高中学业水平考试]电容式话筒是利用电容与极板间距离的关系来工作的,如图所示,话筒的振动膜涂有薄薄的金属层,膜后相距几十微米有一个金属片,它们构成电容器的两个极板.声波使振膜发生振动,当声波使振动膜振动时,下列说法正确的有()A.电阻R两端的电压不变B.电容器的电容发生改变C.电容器的带电荷量不变D.声信号被话筒转化为电信号输出答案:BD4.[2019·山西省榆社中学月考]如图,平行板电容器经开关S与电源连接,C点所在的空间位置不变且始终处于由带电平板所激发的匀强电场中,选取B板的电势为零,关于C点电势的变化情况,以下说法正确的是()A.开关S闭合,将A板上移一小段距离,极板间电场强度变弱,C点电势升高B.开关S闭合,将B板上移一小段距离,极板间电场强度变强,C点电势升高C.开关S先闭合后断开,然后将A板上移一小段距离,场强不变,C点电势升高D.开关S先闭合后断开,然后将B板下移一小段距离,场强不变,C点电势升高答案:D要点一对电容器的电容的理解1.(多选)下列关于电容的说法正确的是()A.电容是反映电容器容纳电荷本领的物理量B.电容器A的电容比B的大,说明A的带电荷量比B多C .电容在数值上等于使两极板间的电势差为1 V 时电容器需要带的电荷量D .由公式C =Q U 知,若电容器两极间电压为10 V ,极板带电荷量为2×10-5 C ,则电容器电容大小为5×105 F解析:由电容的定义C =Q U 和物理意义知A 、C 两项正确.答案:AC2.板间距为d 的平行板电容器所带电荷量为Q 时,两极板间电势差为U 1,板间场强为E 1,现将电容器所带电荷量变为2Q ,板间距变为12d ,其他条件不变,这时两极板间电势差为U 2,板间场强为E 2,下列说法正确的是( )A .U 2=U 1,E 2=E 1B .U 2=2U 1,E 2=4E 1C .U 2=U 1,E 2=2E 1D .U 2=2U 1,E 2=2E 1解析:当平行板电容器的其他条件不变,板间距离变为12d 时,电容器的电容为C ′=εr S 4πk d 2=2C ,又知电容器的带电量变为2Q ,则得知U 2=2Q 2C ,即U 2=U 1.根据匀强电场中电势差与场强之间的关系式E =U d 得E 2=U 212d=2E 1,因此C 项正确,其他选项都错误.答案:C3.一个已充电的电容器,若使它的电荷量减少3×10-4 C ,则其电压减少为原来的13,则( )A .电容器原来的带电荷量为9×10-4 CB .电容器原来的带电荷量为4.5×10-4 CC .电容器原来的电压为1 VD .电容器的电容变为原来的13解析:由题意知C =Q U ,C =Q -3×10-4 C 13U,联立解得Q =4.5×10-4C,故B项正确,A项错误.因电容器的电容不知,所以无法得出电容器原来的电压,C项错误.电容是由电容器本身决定的,跟电压和电荷量的变化无关,所以电容器的电容不变,D 项错误.答案:B4.(多选)[2019·枣庄高一检测]带电平行板电容器与静电计相连,如图所示.下列各种情况中能观察到静电计指针偏角增大的是()A.将两极板的间距加大B.将两极板平行错开,使正对面积减小C.在A板的内表面上放置一面积和极板相等、厚度小于极板间距的陶瓷板D.在A板的内表面上放置一面积和极板相等、厚度小于极板间距的铝板解析:将两极板的间距加大,依据C=εr S4πkd,可知电容减小,由电容的定义式C=QU,可知两极板间电压增大,故指针偏角增大,故A项正确.将两极板平行错开,使正对面积减小,依据C=εr S4πkd可知电容减小,由电容的定义式C=QU,可知两极板间电压增大,故指针偏角增大,故B项正确.在A板的内表面上放置一面积和极板相等、厚度小于极板间距的陶瓷板,增大了介电常数,依据C=εr S4πkd可知电容增大,由电容的定义式C=QU可知两极板间电压减小,故指针偏角减小,故C项错误.在极板间放置铝板,相当于减小了极板间距,由C=εr S4πkd知,电容增大,由C=QU知电压减小,则指针偏角减小,故D项错误.故选A、B两项.答案:AB要点二电容器的动态分析问题5.(多选)如图所示,电路中A、B为两块竖直放置的金属板,C 是一只静电计,开关S闭合后,静电计指针张开一个角度,下述做法可使静电计指针张角增大的是()A.使A、B两板靠近一些B.使A、B两板正对面积减小一些C.断开S后,使B板向右平移一些D.断开S后,使A、B正对面积减小一些解析:静电计显示的是A、B两极板间的电压,指针张角越大,表示两板间的电压越高.当合上S后,A、B两板与电源两极相连,板间电压等于电源电压不变,静电计指针张角不变;当断开S后,板间距离增大,正对面积减小,都将使A、B两板间的电容变小,而电容器所带的龟荷量不变,由C=QU可知,板间电压U增大,从而静电计指针张角增大.所以本题的正确答案是C、D.答案:CD6.研究与平行板电容器电容有关因素的实验装置如图所示,下列说法正确的是()A.实验前,只用带电玻璃棒与电容器a板接触,能使电容器带电B.实验中,只将电容器6板向上平移,静电计指针的张角变小C.实验中,只在极板间插入有机玻璃板,静电计指针的张角变大D.实验中,只增加极板带电量,静电计指针的张角变大,表明电容增大解析:当用带电玻璃棒与电容器a板接触,由于静电感应,从而在b板感应出等量的异种电荷,从而使电容器带电,故A项正确;根据电容的决定式:C=εS4πkd,将电容器b板向上平移,即正对面积S减小,则电容C减小,根据C=QU可知,电量Q不变,则电压U增大,则静电计指针的张角变大,故B项错误;根据电容的决定式:C=εS4πkd,只在极板间插入有机玻璃板,则介电系数ε增大,则电容C增大,根据C=QU可知,电量Q不变,则电压U减小,则静电计指针的张角减小,故C项错误;根据电容决定式C=εS4πkd可知,电容C的变化与电量并无关系,因此电量的改变并不会导致电容的变化,故D项错误.答案:A7.传感器是自动控制设备中不可缺少的元件,已经渗透到宇宙开发、环境保护、交通运输以及家庭生活等各种领域.下列为几种电容式传感器,其中通过改变电容器两板间距离而引起电容变化的是()解析:A项改变的是介质,B、D两项改变的是正对面积,C 项改变的是两板间距离,故C项正确.答案:C8.(多选)如图所示,平行板电容器两极板A、B与电池两极相连,一带正电小球悬挂在电容器内部.闭合开关S,充电完毕后悬线偏离竖直方向夹角为θ,则()A.保持S闭合,将A板向B板靠近,则θ增大B.保持S闭合,将A板向B板靠近,则θ不变C.断开S,将A板向B板靠近,则θ增大D.断开S,将A板向B板靠近,则θ不变解析:保持开关S闭合,电容器两端间的电势差不变,带正电的A板向B板靠近,极板间距离减小,电场强度E增大,小球所受的电场力变大,θ增大,故A项正确,B项错误;断开开关S,电容器所带的电量不变,C=εr S4πkd,E=Ud=QCd=4πkQεr S.知d变化,E不变,电场力不变,θ不变,故C项错误,D项正确.答案:AD基础达标1.(多选)[2019·黑龙江鹤岗市第一中学月考]静电计是测量电势差的仪器,指针偏转角度越大,金属外壳和上方金属小球间的电势差越大.实验装置如图所示,在本实验中,静电计指针和A 板等电势,静电计金属壳和B板等电势,因此指针偏转角度越大表示A、B两极板间的电势差越大.现对电容器充电后断开开关,若按图下方的说明来做实验,则()A.图甲中两极板间电势差变大B.图乙中两极板间电势差变大C.图丙中两极板间电势差变小D.图丙中两极板间电势差变大解析:题图甲中,当极板B向上移动时,正对面积减小,根据电容决定式C=εr S4πkd,可知电容减小,电荷量不变,根据U=QC,可知电势差增大,A项正确;题图乙中,电容器板间距离变大,电容减小,电荷量不变,根据U=QC,可知电势差变大,B项正确;题图丙中,插入电介质,电容增大,电荷量不变,根据U=Q C,可知电势差减小,C项正确,D项错误.答案:ABC2.(多选)如图所示,一平行板电容器的两极板与一电压恒定的电源相连,极板水平放置,极板间距为d,在下极板上叠放一厚度为l的金属板,金属板上部空间有一带正电粒子P静止在电容器中,当把金属板从电容器中快速抽出后,粒子P 开始运动,重力加速度为g .则下列判断正确的是( )A .上极板带负电B .粒子开始向上运动C.粒子刚开始运动的加速度大小为l d gD .粒子刚开始运动的加速度大小为l d -lg 解析:金属板抽出前,带正电粒子P 静止在电容器中,粒子受重力和电场力,处于平衡状态,可知上极板带负电,故A 项正确;抽出金属板后,极板间距增大,电压不变,可知电场强度减小,则粒子所受电场力减小,那么粒子向下运动,故B 项错误;开始时粒子受力平衡,有mg =q U d -l,把金属板从电容器中快速抽出后,根据牛顿第二定律,有mg -q U d =ma ,联立解得a =l d g ,故C 项正确,D 项错误.答案:AC3.(多选)[2019·湖南娄底市期中考试]一个电容器的规格是“10 μF 50 V ”,则( )A .这个电容器的电容为10 μFB.这个电容器加上50 V 电压时,电容才是10 μFC .这个电容器的击穿电压高于50 VD .这个电容器没有电压时,电容为0解析:电容器的电容与电容器两极间电压无关,加电压或不加电压时,该电容器电容都是10 μF ,故A 项正确,B 、D 两项错误.50 V 为额定电压,击穿电压高于额定电压,C 项正确.答案:AC4.关于下列四幅图的叙述正确的是( )A.图甲为可变电容器,动片旋出时可以使其与定片的距离增大,从而改变电容B.图乙为莱顿瓶,瓶内外锡箔相当于电容器的两个极板,可以用来储存电荷C.图丙中电容器只要与电源相连,电流表的示数始终不为零D.图丁所示是电解电容器,击穿电压为80 V解析:题图甲所示的电容器为可变电容器,动片旋出时与定片的距离不变,通过减小极板间的正对面积,从而改变电容,故A项错误;题图乙构成一个简易的电容器,能够储存电荷,故B 项正确;题图丙中电容器充电过程中,电流表的示数不为零,电路稳定时电流表的示数为零,故C项错误;题图丁是电解电容器,额定电压为80 V,小于击穿电压,故D项错误.答案:B5.(多选)平行板电容器充电后不断开电源,逐渐增大两极板的正对面积,则正确的选项是()A.电容器电容将逐渐增大B.两极板间的电场强度将逐渐增大C.两极板间电压将保持不变D.两极板上带电荷量不变解析:若电容器与电源连接不断开,则两板间电势差恒定,两板距离也不变,故场强大小也不变;而电容器电容随着正对面积的增大而增大,极板带电荷量随着电容增大也增大.答案:AC6.(多选)如图所示,是一个由电池、电阻R与平行板电容器组成的串联电路,在增大电容器两极板间距离的过程中() A.电阻R中没有电流B.电容器的电容变小C.电阻R中有从a流向b的电流D.电阻R中有从b流向a的电流解析:开始时,图中电容器被充电,A极板带正电,B极板带负电.根据平行板电容器的电容公式C=εr S/4πkd可知,当增大电容器两极板间的距离d时,电容C变小,由于电容器始终与电池相连,电容器极板间的电压U AB保持不变,根据电容的定义式C =Q/U,当C减小时,电容器两极板所带电荷量Q减小,A极板所带的正电荷一部分经R流向电源的正极,即电阻R中有从a流向b的电流,所以B、C两项正确.答案:BC7.一个电容器带电荷量为Q时,两极板间电压为U,若使其带电荷量增加4.0×10-7 C时,它两极板间的电势差增加20 V,则它的电容为()A.1.0×10-8 F B.2.0×10-8 FC.4.0×10-8 F D.8.0×10-8 F解析:电容C=ΔQΔU=4.0×10-720F=2.0×10-8 F,故选B项.答案:B8.用控制变量法,可以研究影响平行板电容器电容的因素(如图所示).设若两极板正对面积为S,极板间的距离为d,静电计指针偏角为θ.实验中,极板所带电荷量不变,若()A.保持S不变,增大d,则θ变大B.保持S不变,增大d,则θ变小C.保持d不变,减小S,则θ变小D.保持d不变,减小S,则θ不变解析:静电计指针偏角体现电容器两板间电压大小.在做选项所示的操作中,电容器电荷量Q保持不变,C=QU=εr S4πkd.保持S不变,增大d,则C减小,U增大,偏角θ增大,A项正确,B项错误;保持d不变,减小S,则C减小,偏角θ也增大,故C、D 两项错误.答案:A9.一空气平行板电容器,极板间正对面积为S,极间距离为d,充以电量Q后两板间电压为U,为使电容器的电容加倍,可采用的办法是()A.将电压变为U/2B.电量变为2QC.将极板正对面积变为2SD.将两极板间的距离减小到d/2解析:电容器的电容与极板带电荷量、两极板间的电压U无关,故A、B两项错误;根据C=εr S/4πkd可知,C、D两项正确.答案:CD10.传感器是一种采集信息的重要器件,如图是一种测定压力的电容式传感器,当待测压力F作用于可动膜片电极上时,可使膜片产生形变,引起电容的变化,将电容器、灵敏电流计和电源串联接成闭合电路,那么()A.当F向上压膜片电极时,电容将减小B.当F向上压膜片电极时,电容将增大C.若电流计有示数,则压力F发生变化D.若电流计有示数,则压力F不发生变化解析:当压力向上时,膜片电极将向上弯曲,使电容器两个极之间距离减小,电容增大,故A项错误,B项正确.当压力F 发生变化时,电容器的电容发生变化,电容器会不断地充放电,所以电流计有示数,当压力不变时,因为电压恒定,电容器带电量不会发生变化,电流计无示数,故C项正确,D项错误.答案:BC11.如图所示为某一电容器中所带电量和两端电压之间的关系图线,若将该电容器两端的电压从40 V降低到36 V,对电容器来说正确的是()A.是充电过程B.是放电过程C.该电容器的电容为5.0×10-2 FD.电容器的电量变化量为0.20 C解析:由Q=CU知,U降低,Q减小,故为放电过程,A项错误,B项正确;由C=Q/U=0.2/40 F=5×10-3 F,可知C项错误;ΔQ=CΔU=5×10-3×4 C=0.02 C,D项错误.答案:B12.如图所示是一种通过测量电容器电容的变化来检测液面高低的仪器原理图.电容器的两个电极分别用导线接到指示器上,指示器可显示出电容的大小,下列关于该仪器的说法中正确的是()A.该仪器中电容器的电极分别是芯柱和导电液体B.芯柱外套的绝缘层越厚,该电容器的电容越大C.如果指示器显示出电容增大,则说明容器中液面升高D.如果指示器显示出电容减小,则说明容器中液面升高解析:电容器的电容与极板带电荷量、两极板间的电压U无关,故A、B两项错误;根据C=εr S/4πkd可知,C、D两项正确.答案:CD能力达标13.计算机键盘上的每一个按键下面都有一个电容传感器,如图所示.电容的计算公式是C =εr S d ,其中常量εr =9.0×10-12 F·m -1,S 表示两金属片的正对面积,d 表示两金属片间的距离.当某一键被按下时,d 发生改变,引起电容器的电容发生改变,从而给电子线路发生相应的信号.已知两金属片的正对面积为50 mm 2,键未被按下时,两金属片间的距离为0.60 mm.只要电容变化达0.25 pF ,电子线路就能发生相应的信号,那么为使按键得到反应,至少需要按下多大距离?解析:先求得未按下时的电容C 1=0.75 pF ,再由C 1C 2=d 2d 1,得ΔC C 2=Δd d 1和C 2=1.00 pF ,得Δd =0.15 mm. 答案:0.15 mm14.如图所示,一平行板电容器接在U =12 V 的直流电源上,电容C =3.0×10-10 F ,两极板间距离d =1.20×10-3 m ,取g =10 m/s 2,求:(1)该电容器所带电荷量;(2)若板间有一带电微粒,其质量为m =2.0×10-3 kg ,恰在板间处于静止状态,则微粒带电荷量多少?带何种电荷?解析:(1)由公式C =Q /UQ =CU =3×10-10×12 C =3.6×10-9 C.(2)若带电微粒恰在极板间静止,则qE =mg ,而E =U /d解得q =mgd /U =2.0×10-3×10×1.20×10-3/12 C =2.0×10-6C ,微粒带负电荷.答案:(1)3.6×10-9 C (2)2.0×10-6 C 负电荷。
机械功与机械能(知识点串讲+针对性练习)

什么是功1.学会从物理现象中归纳简单的规律,知道功的概念。
2.知道做功的两个必要因素。
3.理解功的计算公式W=Fs,知道功的单位,能用功的公式进行有关计算。
教学重点:经历建立机械功概念的过程,学会用公式对功进行简单的计算。
教学难点:理解功的概念,会用功的两个必要因素判断力对物体是否做功。
故事引入:大华同学是一个品学兼优的好学生,不仅学习好,在家里也经常帮爸爸妈妈做一些力所能及的家务。
星期天,大华上午去买了30斤大米,午饭后又帮妈妈收拾碗筷,接着又去井边帮爸爸把一大桶水提回家,累得满头大汗。
大华的爸爸是个物理教师,他说:“大华今天很辛苦、很劳累,但从物理学的角度来看,你今天做这几项家务活时,并没有做功!”。
大华百思不得其解。
大华的爸爸说得对吗?如何从物理学角度来理解这个问题呢?(一)怎样才叫“做功”1.通过实验,体验“做功”学生实验1:用力沿水平方向推着小车前进(如图1所示)。
描述观察到的现象:小车在水平推力作用下,移动了一段距离。
要求:用示意图表示出小车所受的推力以及运动过程情况。
点拨:此例中小车在水平推力F作用下,移动了一段距离S。
学生实验2:用力将地上的物体拿到桌面上来。
描述观察到的现象:物体在力的作用下,向上移动了一段距离。
要求:用示意图表示出物体所受的拉力以及运动过程情况。
点拨:此例中物体在拉力F作用下,向上移动了一段距离S。
2.找找共同点,建立功的概念仔细观察两示意图,比较一下,看看有什么共同点:(1)这两幅图中同学的活动有什么共同点?(2)物体为什么会移动一段距离?(3)移动的距离和力之间有何关系?共同点:物体作用,并沿这个力的方向。
3. 功的概念:物理学中规定:作用在物体上的力,使物体在力的方向上通过了一段距离,就说这个力对物体做了机械功(简称“做功”)(二) 如何判断力是否对物体做功:1.做功的两个必要的因素:(1)作用在物体上的力;(2)物体在力的方向上通过的距离。
2.分析下列物体受到的力,并指出力对物体是否做功。
公式编辑器(Equation 3.0)使用简介
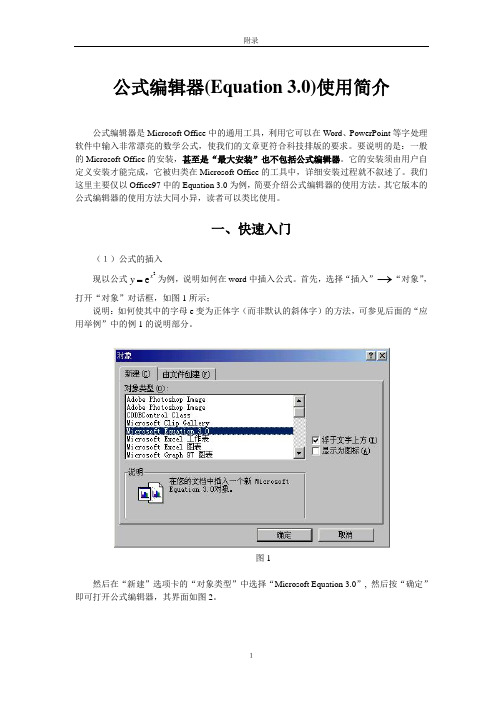
公式编辑器(Equation 3.0)使用简介公式编辑器是Microsoft Office 中的通用工具,利用它可以在Word 、PowerPoint 等字处理软件中输入非常漂亮的数学公式,使我们的文章更符合科技排版的要求。
要说明的是:一般的Microsoft Office 的安装,甚至是“最大安装”也不包括公式编辑器。
它的安装须由用户自定义安装才能完成,它被归类在Microsoft Office 的工具中,详细安装过程就不叙述了。
我们这里主要仅以Office97中的Equation 3.0为例,简要介绍公式编辑器的使用方法。
其它版本的公式编辑器的使用方法大同小异,读者可以类比使用。
一、快速入门(1)公式的插入现以公式2e x y =为例,说明如何在word 中插入公式。
首先,选择“插入”→“对象”,打开“对象”对话框,如图1所示;说明:如何使其中的字母e 变为正体字(而非默认的斜体字)的方法,可参见后面的“应用举例”中的例1的说明部分。
图1然后在“新建”选项卡的“对象类型”中选择“Microsoft Equation 3.0”, 然后按“确定”即可打开公式编辑器,其界面如图2。
图2图2 中大的方框包围的区域是公式编辑器的工作区,是公式对象完成后在文档中占据的区域。
小的虚线框是初始插槽,也就是进行公式输入的地方。
公式编辑器中的光标形状是一条闪烁的竖线和一条闪烁的横线, 光标所在的位置称为插入点。
右边长条状的是公式编辑器的工具栏,我们可以利用它来输入各种符号以及使用各种样板。
现在开始输入,首先输入“y=e”, 这时光标位于“e”的右侧及底部,然后在工具栏上点击第二行的“上标和下标样板”,选择其中的第一种样板,即上标样板,这时在输入区我们可以看到“e”的右上方出现了一个小虚线框,这就是应用上标样板所产生的插槽,在其中输入“x”, 然后再选择一次上标样板,在“x”的右上方又出现一个新的插槽,在其中输入“2”即可。
三角函数诱导公式练习题含答案

三角函数诱导公式练习题含答案三角函数定义及诱导公式练习题1.将120o化为弧度为()A.B.C.D.2.代数式的值为()A. B. C. D. 3.()A.B.C.D.4.已知角α的终边经过点(3a,-4a)(a0),则sin α+cos α等于( ) A. B. C.D.-5.已知扇形的面积为2cm2,扇形圆心角θ的弧度数是4,则扇形的周长为() (A)2cm (B)4cm (C)6cm (D)8cm 6.若有一扇形的周长为60 cm,那么扇形的最大面积为( ) A.500 cm2 B.60 cm2 C.225 cm2 D.30 cm2 7.已知,则的值为()A.B.-C.D.-8.已知,且,则()A、B、C、D、9.若角的终边过点,则_______. 10.已知点P(tanα,cosα)在第二象限,则角α的终边在第________象限.11.若角θ同时满足sinθ0且tanθ0,则角θ的终边一定落在第________象限.12.已知,则的值为.13.已知,,则_____________. 14.已知,则_________. 15.已知tan=3,则 . 16.(14分)已知tanα=,求证:(1)=-;(2)sin2α+sinαcosα=.17.已知(1)求的值;(2)求的值;(3)若是第三象限角,求的值. 18.已知sin(α-3π)=2cos(α-4π),求的值.参考答案1.B 试题分析:,故. 考点:弧度制与角度的相互转化. 2.A. 试题分析:由诱导公式以可得,sin120°cos210°=sin60°×(-cos30°)=-×=,选A. 考点:诱导公式的应用.3.C 试题分析:本题主要考查三角诱导公式及特殊角的三角函数值.由,选C. 考点:诱导公式. 4.A 试题分析:,,.故选 A. 考点:三角函数的定义5.C 设扇形的半径为R,则R2θ=2,∴R2=1R=1,∴扇形的周长为2R+θ·R=2+4=6(cm). 6.C 设扇形的圆心角为,弧长为cm,由题意知,∴ ∴当时,扇形的面积最大;这个最大值为. 应选C. 7.A 试题分析:,=====. 考点:诱导公式. 8.试题分析:.又因为,所以为三象限的角,.选B. 考点:三角函数的基本计算. 9.试题分析:点即,该点到原点的距离为,依题意,根据任意角的三角函数的定义可知. 考点:任意角的三角函数. 10.四由题意,得tanα<0且cosα>0,所以角α的终边在第四象限.11.四由sinθ0,可知θ的终边可能位于第三或第四象限,也可能与y轴的非正半轴重合.由tanθ0,可知θ的终边可能位于第二象限或第四象限,可知θ的终边只能位于第四象限.12.-3 13.试题分析:因为α是锐角所以sin(π-α)=sinα=考点:同角三角函数关系,诱导公式. 14.试题分析:,又,则原式=. 考点:三角函数的诱导公式. 15.45 试题分析:已知条件为正切值,所求分式为弦的齐次式,所以运用弦化切,即将分子分母同除以得. 考点:弦化切16.证明:(1) =-.(2)sin2α+sinαcosα=.(1)原式可以分子分母同除以cosx,达到弦化切的目的.然后将tanx=2代入求值即可. (2)把”1”用替换后,然后分母也除以一个”1”,再分子分母同除以,达到弦化切的目的. 证明:由已知tanα=.(1) ===-.(2)sin2α+sinαcosα====.17.(1);(2);(3). 试题分析:(1)因为已知分子分母为齐次式,所以可以直接同除以转化为只含的式子即可求得;(2)用诱导公式将已知化简即可求得;(3)有,得,再利用同角关系,又因为是第三象限角,所以;试题解析:⑴ 2分.3分⑵ 9分.10分⑶解法1:由,得,又,故,即,12分因为是第三象限角,,所以.14分解法2:,12分因为是第三象限角,,所以.14分考点:1.诱导公式;2.同角三角函数的基本关系. 18.∵sin(α-3π)=2cos(α-4π),∴-sin(3π-α)=2cos(4π-α),∴sinα=-2cosα,且cosα≠0. ∴原式=三角函数的诱导公式1 一、选择题1.如果|cosx|=cos(x+π),则x的取值集合是()A.-+2kπ≤x≤+2kπ B.-+2kπ≤x≤+2kπ C.+2kπ≤x≤+2kπ D.(2k+1)π≤x≤2(k+1)π(以上k∈Z)2.sin(-)的值是()A.B.-C.D.-3.下列三角函数:①sin(nπ+);②cos(2nπ+);③sin(2nπ+);④cos[(2n+1)π-];⑤sin[(2n+1)π-](n∈Z).其中函数值与sin的值相同的是()A.①② B.①③④ C.②③⑤ D.①③⑤ 4.若cos (π+α)=-,且α∈(-,0),则tan(+α)的值为()A.-B.C.-D.5.设A、B、C是三角形的三个内角,下列关系恒成立的是()A.cos(A+B)=cosC B.sin(A+B)=sinC C.tan (A+B)=tanC D.sin=sin 6.函数f(x)=cos(x∈Z)的值域为()A.{-1,-,0,,1} B.{-1,-,,1} C.{-1,-,0,,1} D.{-1,-,,1} 二、填空题7.若α是第三象限角,则=_________.8.sin21°+sin22°+sin23°+…+sin289°=_________.三、解答题9.求值:sin(-660°)cos420°-tan330°cot(-690°).10.证明:.11.已知cosα=,cos(α+β)=1,求证:cos(2α+β)=.12.化简:.13、求证:=tanθ.14.求证:(1)sin(-α)=-cosα;(2)cos(+α)=sinα.参考答案1 一、选择题1.C 2.A 3.C 4.B 5.B 6.B 二、填空题7.-sinα-cosα 8.三、解答题9.+1.10.证明:左边= =-,右边=,左边=右边,∴原等式成立.11.证明:∵cos(α+β)=1,∴α+β=2kπ.∴cos (2α+β)=cos(α+α+β)=cos(α+2kπ)=cosα=.12.解:= = = ==-1.13.证明:左边==tanθ=右边,∴原等式成立.14证明:(1)sin(-α)=sin[π+(-α)]=-sin(-α)=-cosα.(2)cos(+α)=cos[π+(+α)]=-cos(+α)=sinα.三角函数的诱导公式2 一、选择题:1.已知sin(+α)=,则sin(-α)值为()A. B. —C. D. —2.cos(+α)= —,α,sin(-α) 值为()A. B. C. D. — 3.化简:得()A.sin2+cos2 B.cos2-sin2 C.sin2-cos2 D.± (cos2-sin2) 4.已知α和β的终边关于x轴对称,则下列各式中正确的是()A.sinα=sinβ B. sin(α-) =sinβ C.cosα=cosβ D. cos(-α) =-cosβ 5.设tanθ=-2, θ0,那么sinθ+cos(θ-)的值等于(),A. (4+)B. (4-) C. (4±)D. (-4)二、填空题:6.cos(-x)= ,x∈(-,),则x的值为.7.tanα=m,则.8.|sinα|=sin(-+α),则α的取值范围是.三、解答题:9..10.已知:sin(x+)=,求sin(+cos2(-x)的值.11.求下列三角函数值:(1)sin;(2)cos;(3)tan(-);12.求下列三角函数值:(1)sin·cos·tan;(2)sin[(2n+1)π-]. 13.设f(θ)=,求f()的值. 参考答案2 1.C 2.A 3.C 4.C 5.A 6.± 7.8.[(2k-1) ,2k] 9.原式=== sinα 10.11.解:(1)sin=sin(2π+)=sin=. (2)cos=cos (4π+)=cos=. (3)tan(-)=cos(-4π+)=cos=. (4)sin (-765°)=sin[360°×(-2)-45°]=sin(-45°)=-sin45°=-. 注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值. 12.解:(1)sin·cos·tan=sin(π+)·cos(4π+)·tan(π+)=(-sin)·cos·tan=(-)··1=-. (2)sin[(2n+1)π-]=sin(π-)=sin=. 13.解:f(θ)= = = = = = =cosθ-1,∴f()=cos-1=-1=-. 三角函数公式1.同角三角函数基本关系式sin2α+cos2α=1 =tanα tanαcotα=1 2.诱导公式(奇变偶不变,符号看象限) (一)sin(π-α)=sinα sin(π+α)=-sinα cos(π-α)=-cosα cos(π+α)=-cosα tan(π-α)=-tanα tan(π+α)=tanα sin(2π-α)=-sinα sin(2π+α)=sinα cos(2π-α)=cosα cos(2π+α)=cosα tan(2π-α)=-tanα tan(2π+α)=tanα (二)sin(-α)=cosα sin(+α)=cosα cos(-α)=sinα cos(+α)=- sinα tan(-α)=cotα tan(+α)=-cotα sin(-α)=-cosα sin(+α)=-cosα cos(-α)=-sinα cos(+α)=sinα tan(-α)=cotα tan(+α)=-cotα sin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα 3.两角和与差的三角函数cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ sin (α+β)=sinαcosβ+cosαsinβ sin (α-β)=sinαcosβ-cosαsinβ tan(α+β)= tan(α-β)= 4.二倍角公式sin2α=2sinαcosα cos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2α tan2α= 5.公式的变形(1)升幂公式:1+cos2α=2cos2α 1—cos2α=2sin2α (2)降幂公式:cos2α=sin2α=(3)正切公式变形:tanα+tanβ=tan(α+β)(1-tanαtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ) (4)万能公式(用tanα表示其他三角函数值)sin2α=cos2α=tan2α=6.插入辅助角公式asinx+bcosx=sin(x+φ) (tanφ= ) 特殊地:sinx±cosx=sin(x±) 7.熟悉形式的变形(如何变形)1±sinx±cosx 1±sinx 1±cosx tanx+cotx 若A、B是锐角,A+B=,则(1+tanA)(1+tanB)=2 8.在三角形中的结论若:A+B+C=π , =则有tanA +tanB+tanC=tanAtanBtanC tantan+tantan+tantan=1。
小学四年级数学单位换算公式汇总+练习题3套

单位换算题是小学数学学习重点之一。
孩子对单位换算记忆不够深刻,所以总是混淆运用,绕来绕去会出现计算失误,进率错误等问题。
单位换算大全来啦,还有记忆窍门,就算是小马虎也能一目了然,熟记于心。
记得多摘抄、常背诵哦!口诀大化小,往右移,进率有几个“0”,就移几位。
小化大,往左移,进率有几个“0”,就移几位。
长度单位国际单位是“米”(符号“m”),最常见的有千米(km)、米(m)、分米(dm)、厘米(cm)、毫米(mm)。
感性认识指甲厚一毫米,指甲长一厘米,手掌宽一分米,张开手臂长一米。
换算公式1千米(km)=1000米(m),1米(m)=10分米(dm)。
1米(m)=10分米(dm)=100厘米(cm)=1000毫米(mm)1分米(dm)=10厘米(cm)=100毫米(mm)1厘米(cm)=10毫米(mm)熟记口诀米、米、米,是老大,分米分米是老二,厘米厘米是老三,毫米毫米是老四。
米就要比分米大,大多少?是十倍;分米要比厘米大,大多少,也十倍;厘米要比毫米大,大多少,还十倍。
手掌记忆进率伸出一只手,小指、无名指、中指、食指、拇指依次表示毫米、厘米、分米、米、千米。
毫米、厘米、分米、米指缝相等,想象一下只能夹一个蛋,代表进率是10。
而拇指和食指空隙较大,想象一下能夹三个蛋,代表进率是1000。
时间单位1世纪=100年 1年=12个月世纪:计算年代的单位,一百年为一个世纪。
大月(31天)有:1\3\5\7\8\10\12月大月:指阳历(公历)有三十一天的月份,公历每年一﹑三﹑五﹑七﹑八﹑十﹑十二这七个月为大月,均三十一天。
小月(30天)的有:4\6\9\11月小月:指阳历一个月三十天或农历一个月二十九天的月份。
平年2月28天,闰年2月29天平年:阳历或阴历中无闰日的年,或阴阳历中无闰月的年。
平年全年365天,闰年全年366天闰年:阳历或阴历中有闰日的年,或阴阳历中有闰月的年。
1日=24小时1时=60分日:以地球自转周期为基准的时间单位,等于86400s。
整式乘法与因式分解 全章热门考点专练(2个概念3个运算2个公式3个应用4个技巧3种思想)解析版

第9章整式乘法与因式分解全章热门考点专练(2个概念3个运算2个公式3个应用4个技巧3种思想)【知识导图】【知识清单】2个概念【例题1】(22-23八年级上·山东威海·期末)多项式2324223126x y x y x y --的公因式是()A .23x y B .233x y C .223x y D .3xy【答案】C【分析】本题考查了公因式的定义.确定多项式中各项的公因式,可概括为三“定”:①定系数,即确定各项系数的最大公约数;②定字母,即确定各项的相同字母因式(或相同多项式因式);③定指数,即各项相同字母因式(或相同多项式因式)的指数的最低次幂.根据多项式的公因式的确定方法,即可求解.【详解】解:多项式2324223126x y x y x y --的公因式是223x y ,故选C【变式1】(23-24八年级下·山东济南·阶段练习)把多项式33128ab a b +分解因式,应提的公因式是()A .abB .4abC .2abD .24a b【答案】B【分析】本题主要考查了分解因式,观察可知两个单项式的公因式为4ab ,据此可得答案.【详解】解:()3322128432ab a b ab b a +=+,则多项式33128ab a b +分解因式,应提的公因式是4ab ,故选:B【变式2】(23-24七年级下·江苏徐州·期中)把多项式32612x x y -分解因式,应提取的公因式是.【答案】26x 【分析】本题考查了公因式,提公因式26x ,即可求解.【详解】解:把多项式32612x x y -分解因式,应提取的公因式是26x ,故答案为:26x 【变式3】(23-24八年级上·山东东营·阶段练习)()218b a b -与()312a b -的公因式是.【答案】()26a b -【分析】本题考查了公因式;根据公因式的定义,找出系数的最大公约数6,相同因式的最低指数次幂,即可确定公因式.【详解】解:∵18和12的最大公约数是6,∴()218b a b -与()312a b -的公因式是()26a b -,故答案为:()26a b -【例题2】(2023·江苏无锡·模拟预测)下列因式分解正确的是()A .2243(2)1x x x -+=--B .2232(2)()x xy y x y x y -+=--C .42224(2)(2)x x x x x x -=+-D .3244(2)x x x x ++=+【答案】B【分析】此题考查了十字相乘法因式分解,以及提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.根据十字相乘因式分解,提公因式法与公式法因式分解逐项因式分解判断即可.【详解】解:A 、243(1)(3)x x x x -+=--,故本选项不符合题意;B 、2232(2)()x xy y x y x y -+=--,故本选项符合题意;C 、24222(4)(2(2)4)x x x x x x x =--=+-,故本选项不符合题意;D 、无法因式分解,故本选项不符合题意;故选:B【变式1】(2024·甘肃兰州·一模)因式分解:24a -=()A .()()44a a +-B .()()42a a +-C .()()24a a +-D .()()22a a +-【答案】D【分析】本题考查了因式分解的定义以及运用平方差公式进行因式分解,把一个多项式分解成几个整式的乘积的形式,据此即可作答.【详解】解:24a -=()()22a a +-故选:D【变式2】(23-24八年级下·四川成都·阶段练习)下列等式从左到右的变形,是因式分解的是()A .()22326x x x x-=-B .221234m n m n=⋅C .22111x x x x x x ⎛⎫⎛⎫-=+- ⎪⎪⎝⎭⎝⎭D .()()22x y x y x y -=+-D 、()()22x y x y x y -=+-,是因式分解,故本选项符合题意;故选:D【变式3】(2024·广东中山·一模)下列各式从左到右的变形,因式分解正确的是()A .()2a ab a ab+=+B .()233a ab a a b +-=+-C .()222824ab a a b -=-D .()()22824a a a a --=+-【答案】D【分析】本题考查了因式分解的定义,把一个多项式化成几个整式的积的形式叫做因式分解,根据因式分解的定义逐项判断即可.【详解】解:A .从左到右的变形属于整式乘法,不属于因式分解,故本选项不符合题意;B .从左到右的变形不属于因式分解,故本选项不符合题意;C .()()()222824222ab a a b a b b -=-=+-,分解不彻底,故本选项不符合题意;D .从左到右的变形属于因式分解,故本选项符合题意.故选:D3个运算1.单项式乘单项式【例题3】(2024年上海市普陀区中考二模数学试题)下列运算正确的是()A .234a a a +=B .32a a -=C .233a a a ⋅=D .32a a a÷=【答案】C【分析】本题主要考查合并同类项,单项式乘以单项式以及单项式除以单项式,运用相关运算法则求出各选项的结果,再进行判断即可【详解】解:A.34a a a +=,原选项计算错误,不符合题意;B.32a a a -=,原选项计算错误,不符合题意;C.233a a a ⋅=,计算正确,符合题意;D.33a a ÷=,原选项计算错误,不符合题意;故选:C【变式1】(23-24九年级下·甘肃庆阳·阶段练习)计算:()()326ab a --=.【答案】336a b 【分析】本题主要考查单项式乘单项式,直接根据运算法则进行计算即可.【详解】解:()()326ab a--()()()23=61a a b -⨯-⋅⋅⋅336a b =,故答案为:336a b 【变式2】(23-24七年级下·浙江·期中)计算:223a b a ⋅=.【答案】36a b【分析】本题主要考查了单项式乘单项式,直接利用单项式乘单项式运算法则计算得出答案.【详解】解:23236a b a a b ⋅=.故答案为:36a b【变式3】(2024·甘肃陇南·一模)计算:232x x ⋅=.【答案】52x 【分析】本题主要考查了单项式乘以单项式,熟知相关计算法则是解题的关键.【详解】解:23522x x x ⋅=,故答案为:52x2.单项式乘多项式【例题4】(2024·陕西汉中·一模)计算()()3221m m -⋅+的结果是()A .762m m --B .662m m -+C .752m m --D .652m m --【答案】A【分析】本题考查了幂的乘方以及单项式乘多项式,先算幂的乘方,再算单项式乘多项式,即可作答.【详解】解:()()3221m m -⋅+()626m m =-+6621m m m =-⋅-⋅762m m =--,故选:A【变式1】(22-23七年级下·广西崇左·期中)计算:()21x x -=()A .31x -B .3x x -C .3x x+D .2x x-【答案】B【分析】本题考查了单项式乘多项式,根据单项式乘多项式法则(单项式与多项式的每一项都相乘)计算即可.【详解】解:()231x x x x-=-故选:B【变式2】(23-24七年级下·江苏泰州·期中)计算()2323⋅-=x x .计算:()31x x -=.【答案】518x 233x x -/233x x -+【分析】此题考查了积的乘方和单项式乘以单项式运算,单项式乘以多项式运算,应用积的乘方和单项式乘以单项式运算法则进行计算;利用单项式乘以多项式运算法则求解即可.【详解】()2323x x ⋅-3229x x =⋅518x =;()31x x -233x x =-.故答案为:518x ,233x x-【变式3】(2024七年级下·江苏·专题练习)计算()()223235a ab ab =-⋅-.【答案】3233610a b a b -+【分析】根据单项式乘多项式的运算法则(把多项式的每一项都与单项式相乘),即可求解,本题考查了单项式与多项式的乘法,掌握计算法则是解题的关键.【详解】解:()()2233233235610a ab ab a b a b -⋅-=-+.故答案为:3233610a b a b -+.3.多项式乘多项式【例题5】(23-24七年级下·河南周口·阶段练习)定义()*1a b b a =+,例如()()()2*11121x x x x x x +=++=++.则()()2*2x x -+=()A .24x -B .244x x +-C .24x x +-D .22x x +-【答案】D【分析】本题考查新定义运算,多项式乘多项式,根据定义()*1a b b a =+将()()2*2x x -+变形为()()221x x +-+,再按照多项式乘多项式运算法则计算即可.【详解】解:()()()()2*2221x x x x -+=+-+()()21x x =+-222x x x =-+-22x x =+-,故选D【变式1】(23-24七年级下·江苏无锡·阶段练习)下列计算错误的是()A .()()21454x x x x ++=++B .()()2236m m m m -+=+-C .()()245920y y y y +-=+-D .()()236918x x x x -=--+【答案】C【分析】本题主要考查多项式乘法的运算,掌握多项式乘法的运算法则是解题的关键.根据运算法则,逐一对选项进行分析即可.【详解】解:A .2(1)(4)54x x x x ++=++,正确,故该选项不符合题意;B .()()2236m m m m -+=+-,正确,故该选项不符合题意;C .2(4)(5)20y y y y +-=--,错误,故该选项符合题意;D .()()236918x x x x --=-+,正确,故该选项不符合题意.故选:C【变式2】.(22-23七年级下·四川成都·期中)若()()221222x x x mx -+=+-,则m 的值是.【答案】3【分析】本题考查了多项式与多项式的乘法运算,根据多项式与多项式的乘法法则把等号左边化简,然后与右边比较即可求解.【详解】解:∵()()22221224223222x x x x x x x x mx -++--=+-=+-=,∴3m =.故答案为:3【变式3】(2024七年级下·江苏·专题练习)计算:()()34a b a b +-=.【答案】2212a ab b +-【分析】本题考查了多项式乘多项式法则,合并同类项时要注意项中的指数及字母是否相同.根据多项式乘多项式法则,先用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加解答.【详解】解:2222(3)(342)1412a b a b a ab ab b a ab b +-=++=---故答案为:2212a ab b+-2个公式1.平方差公式【例题6】(22-23七年级下·四川成都·期中)下列多项式的乘法中,可以用平方差公式进行计算的是()A .()()22a b b a +-B .()()m n m n -+-C .()()22x y x y -+D .()()11n n ++【答案】A【分析】本题主要考查了平方差公式,解题的关键是根据平方差公式()()22a b a b a b +-=-,逐项进行判断即可.【详解】解:A .()()22224a b b a b a +-=-,则A 符合题意;B .()()m n m n -+-不能用平方差公式计算,则B 不符合题意;C .()()22x y x y -+不能用平方差公式计算,则C 不符合题意;D .()()11n n ++不能用平方差公式计算,则D 不符合题意;故选:A【变式1】(20-21七年级下·浙江杭州·期中)一个长方形的宽为2x y -,长为2x y +,则这个长方形的面积是()A .224x y -B .224x y +C .222x y -D .222x y +【答案】A【分析】本题主要考查平方差公式的应用,掌握平方差公式的结构特征是解题的关键.根据长方形的面积公式进行计算即可.【详解】解:由长方形的面积公式可得,22(2)(2)4x y x y x y +-=-.故选:A【变式2】(23-24七年级下·河南周口·阶段练习)如果一个数()()222121a n n =+--,那么我们称这个数a 为“奇差数”.下列数中为“奇差数”的是()A .56B .82C .94D .126【答案】A【分析】本题考查了平方差公式的应用,首先化简()()2221218a n n n =+--=,再看四个选项中,能够整除8的即为答案.理解“奇差数”的定义,正确化简是解题关键.【详解】解: ()()()()222121212121218a n n n n n n n =+--=++-+-+=,∴“奇差数”是8的倍数,A ,7856=÷,能够被8整除,因此56是“奇差数”;B ,828102÷= ,不能够被8整除,因此82不是“奇差数”;C ,948116÷= ,不能够被8整除,因此94不是“奇差数”;D ,1268156÷= ,不能够被8整除,因此126不是“奇差数”;故选:A【变式3】(23-24九年级下·山东聊城·阶段练习)下列计算正确的是()A .235a b ab +=B .()()22a b a b a b+-=-C .2236a b ab ⋅=D .()235a a =【答案】B【分析】本题考查整式的运算,根据合并同类项,平方差公式,单项式乘单项式,幂的乘方的法则,逐一进行计算,判断即可.【详解】解:A 、2,3a b ,不是同类项,不能合并,不符合题意;B 、()()22a b a b a b +-=-,符合题意;C 、22236a b a b ⋅=,不符合题意;D 、()236a a =,不符合题意;故选:B2.完全平方公式【例题7】(23-24七年级下·江苏徐州·期中)下列计算正确的是()A .236a a a ⋅=B .326()x x -=C .632a a a ÷=D .222()x y x y +=+【答案】B【分析】本题考查了同底数幂的乘除法,积的乘方,完全平方公式;根据以上运算法则进行计算即可求解.【详解】解:A.235a a a ⋅=,故该选项不正确,不符合题意;B.326()x x -=,故该选项正确,符合题意;C.633a a a ÷=,故该选项不正确,不符合题意;D.222()2x y x xy y +=++,故该选项不正确,不符合题意;故选:B【变式1】(23-24八年级下·山东威海·期中)不论x ,y 取何实数,代数式224614x x y y -+-+总是()A .非负数B .正数C .负数D .非正数【答案】B【分析】本题主要考查了完全平方公式的应用,利用完全平方公式把原式变形为()()22231x y -+-+,据此可得答案.【详解】解:224614x x y y -+-+()()2244691x x y y =-++-++()()22231x y =-+-+,∵()()222030x y -≥-≥,,∴()()222311x y -+-+≥,∴224614x x y y -+-+总是正数,故选:B【变式2】(23-24九年级下·河南郑州·期中)下列计算正确的是()A .321a a -=B .()2236m m -=C .2=D .()222244a b a ab b -=-+【答案】D【分析】本题考查了完全平方公式,合并同类项,积的乘方等运算法则,熟练掌握这些法则是解此题的关键.根据合并同类项的法则、积的乘方、完全平方公式进行计算即可.故选D【变式3】(2024·广西桂林·一模)下列运算正确的是()A .()22420x x -=B .()236x x x -⋅=C .()222x y x y +=+D 92=故选:A 3个应用1.应用因式分解解决整除问题【例题8】(2024·浙江嘉兴·一模)若k 为任意整数,则()()222122k k +--的值总能()A .被2整除B .被3整除C .被5整除D .被7整除【答案】B【分析】本题主要考查了因式分解的意义,利用平方差公式把()()222122k k +--因式分解为()341k -,据此可得答案.【详解】解:()()222122k k +--()()()()21222122k k k k =++-+--⎡⎤⎡⎤⎣⎦⎣⎦()341k =-∵k 为任意整数,∴()341k -为整数,∴()341k -一定能被3整除,∴()()222122k k +--的值总能被3整除,故选:B【变式1】(23-24九年级下·河北邯郸·阶段练习)对于任何整数()0a a ≠,多项式()2354a +-都能()A .被9整除B .被a 整除C .被1a +整除D .被1a -整除【答案】C【分析】此题考查了因式分解,利用平方差公式分解,即可做出判断,熟练掌握平方差公式是解本题的关键.【详解】解:原式()()()()3523523371a a a a =+++-=++,则对于任何整数a ,多项式()2354a +-都能被1a +整除.故选:C【变式2】(2024·河南郑州·一模)对任意整数n ,2(21)25n +-都能()A .被3整除B .被4整除C .被5整除D .被6整除【答案】B【分析】根据平方差公式,分解因式后判断,熟练掌握公式法分解因式是解题的关键.【详解】∵()()()()()()2222125215215215432n n n n n n +-=+-=+++-=+-,∴故一定能被4整除,故选B【变式3】(2024·河北邯郸·模拟预测)已知()()844414141-=+-= ,则按此规律推算841-的结果一定能()A .被12整除B .被13整除C .被14整除D .被15整除【答案】D【分析】本题考查了因式分解,根据平方差公式进行因式分解,即可求解.【详解】解:()()()()()()()84442242414141414141414115-=+-=++-=++⨯,故选:D2.应用因式分解解决几何问题【例题9】(23-24七年级下·全国·假期作业)已知,,a b c 为三角形ABC 的三边长,且满足222244b c a c a b -=-,则三角形ABC 的形状为()A .等腰三角形B .直角三角形C .等腰直角三角形D .锐角三角形【答案】A【详解】因为222244b c a c a b -=-,即()()()2222222c b a a b a b -=+-,所以()()()22222220a b a b c b a +---=,()()222220a b a b c -++=,()()()2220a b a b a b c +-++=.因为,,a b c 是三角形的三边长,所以2220,0a b a b c +>++>,所以0a b -=,即a b =,所以三角形ABC 为等腰三角形【变式1】(2024八年级·全国·竞赛)已知ABC 的三边为a 、b 、c ,且满足1111a b c a b c-+=-+,则ABC 的形状为.()()()0a b b c a c ∴--+=,∴a b =或b c =.故答案为:等腰三角形【变式2】(23-24八年级上·全国·课堂例题)(1)若a ,b ,c 是三角形的三边长,且满足关系式2222a bc c ab -=-,试判断这个三角形的形状.(2)若a ,b ,c 是ABC 的三边长,且满足2220a b c ab bc ac ++---=,则ABC 是什么形状?【答案】(1)三角形是等腰三角形;(2)ABC 是等边三角形【分析】本题考查因式分解的应用;(1)把2222a bc c ab -=-通过因式分解求值即可;(2)通过把2222222220a b c ab bc ac ++---=配方后根据非负数的性质判断即可.【详解】(1)∵2222a bc c ab -=-,∴()22220a c ab bc -+-=,∴()()()20a c a c b a c +-+-=,∴()()20a c a c b -++=.∵20a c b ++≠,∴0a c -=,即a c =,∴这个三角形是等腰三角形.(2)∵2220a b c ab bc ac ++---=,∴2222222220a b c ab bc ac ++---=.∴()()()2222222220a b ab b c bc c a ac +-++-++-=,即222()()()0a b b c a c -+-+-=.∴0a b -=,0b c -=,0a c -=,∴a b =,b c =,a c =,∴a b c ==,∴ABC 是等边三角形【变式3】(23-24八年级上·全国·课堂例题)(1)已知ABC 的三边长a ,b ,c 满足22661830a b a b c +--++-=,试判断ABC 的形状.(2)已知a ,b ,c 是ABC 的三边长,且满足2212852a b a b +=+-,求c 的取值范围.∴3.应用因式分解进行简便计算【例题10】(20-21八年级下·陕西汉中·期末)利用因式分解简便计算6999329999⨯+⨯-正确的是()A .()996932991019999⨯+=⨯=B .()9969321991009900⨯+-=⨯=C .()99693219910210098⨯++=⨯=D .()99693299992198⨯+-=⨯=【答案】B【分析】利用提公因式分法将99提公因式进行计算即可判断.【详解】解:69×99+32×99-99=99(69+32-1)=99×100=9900.故选:B .【点睛】本题考查了因式分解的应用,解决本题的关键是掌握因式分解【变式1】(22-23八年级下·贵州贵阳·期中)利用因式分解可以简便计算:5799449999⨯+⨯-分解正确的是()A .()995744⨯+B .()9957441⨯+-C .()9957441⨯++D .()99574499⨯+-【答案】B【分析】利用提取公因式法分解因式即可得.【详解】解:原式57994499199=⨯+⨯-⨯()9957441=⨯+-,故选:B .【点睛】本题考查了因式分解,熟练掌握提取公因式法是解题关键【变式2】(22-23九年级上·广东惠州·开学考试)利用因式分解简便运算:2252.847.2-=.【答案】560【分析】利用平方差法进行因式分解,再进行计算;【详解】原式=()()52.847.252.847.2+⨯-=100 5.6⨯=560.故答案为:560.【点睛】本题考查利用公式法因式分解进行简便运算.熟练掌握公式法因式分解是解题的关键【变式3】(22-23七年级下·湖南怀化·期中)利用因式分解进行简便运算:(1)443424.7 1.365555-⨯+⨯-⨯;(2)22899202899101+⨯+【答案】(1)24-(2)610【分析】(1)运用提公因式法进行因式分解即可求解;(2)运用公式法进行因式分解即可求解.【点睛】本题主要考查因式分解,懂得运用提公因式法和公式法进行因式分解来进行简便运算是解题的关键4个技巧1.巧用乘法公式计算【例题11】(22-23八年级下·河南平顶山·阶段练习)代数式22494610x y x y ++-+中x ,y 取何值时代数式值最小?最小值是多少?【点睛】此题考查了配方法求最值,原式可化为两个完全平方式和一个常数和的形式.利用完全平方公式变形,根据完全平方式恒大于等于0,即可求出最小值,熟练掌握配方法是解题的关键【变式】(22-23七年级下·江苏宿迁·期末)已知2610A x x =-+.(1)当2x =-、0、3时,分别求出A 的值;(2)证明:无论x 取什么值,A 的值都不小于1.【答案】(1)当2x =-时,26A =;当0x =时,10A =;当3x =时,1A =(2)见解析【分析】(1)根据题意可得()2261031A x x x =-+=-+,将2x =-、0、3,分别代入代数式,即可求解;(2)根据题意可得()2261031A x x x =-+=-+,根据平方的非负性,可得1A ≥,即可得证.【详解】(1)解:∵()2261031A x x x =-+=-+∴当2x =-时,()223125126A =--+=+=;当0x =时,()203110A =-+=;当3x =时,()23311A =-+=;(2)证明:∵()2261031A x x x =-+=-+,()230x -≥∴1A ≥,【点睛】本题考查了代数式求值,因式分解的应用,熟练掌握完全平方公式是解题的关键2.先分组在分解【例题12】(21-22八年级下·陕西咸阳·阶段练习)阅读材料:常用的分解因式方法有提公因式法、公式法等.但有的多项式只用上述方法就无法分解,如22424x y x y -+-,细心观察这个式子会发现前两项符合平方差公式,后两项可提取公因式,分解过程为:22424x y x y-+-()()22424x y x y =-+-…分组()()()2222x y x y x y =-++-…组内分解因式()()222x y x y =-++…整体思想提公因式这种分解因式的方法叫分组分解法.根据以上材料,解答下列问题:(1)按上述方法因式分解:①22428x y y x --+;②323927m m m --+;(2)已知a ,b ,c 为ABC 的三边,且2222b ab c ac +=+,试判断ABC 的形状并说明理由.【答案】(1)①()()()222y x x --+;②()2(3)3m m -+;(2)ABC 是等腰三角形,理由见解析;【分析】(1)①本题考查因式分解,根据例题分组提取公因式,再结合公式法因式分解即可得到答案;②本题考查因式分解,根据例题分组提取公因式,再结合公式法因式分解即可得到答案;(2)本题考查因式分解的应用,将2222b ab c ac +=+因式分解即可得到积等于0,即可得到答案;【详解】(1)解:①原式()()22424y x x =---()()()()22222y x x x x =-+--+()()()222y x x =--+;②原式()()2393m m m =---()()239m m =--()2(3)3m m =-+;(2)解:ABC 是等腰三角形,理由如下,2222b ab c ac +=+ ,22220b c ab ac ∴-+-=,()()()20b c b c a b c -++-=,()()20a b c b c ++-=,∵a ,b ,c 为ABC 的三边,0a ∴>,0b >,0c >,20a b c ∴++≠,0∴-=b c ,即b c =,ABC ∴ 是等腰三角形【变式1】(2024八年级下·全国·专题练习)因式分解:2221a ab b -+-.【答案】()()11a b a b -+--【分析】本题主要考查了因式分解,解题的关键是熟练掌握完全平方公式和平方差公式,先根据完全平方公式进行因式分解,然后再用平方差公式进行因式分解.【详解】解:2221a ab b -+-()21=--a b ()()11a b a b =-+--【变式2】(23-24八年级上·四川眉山·期中)因式分解(1)224x y -;(2)2291839x xy y x y -++-.【答案】(1)()()22x y x y +-(2)()()363x y x y -++【分析】本题考查了因式分解:(1)运用平方差公式进行因式分解,即可作答.(2)先分组分解,再进行提公因式,即可作答.【详解】(1)解:224x y -()()22x y x y =+-(2)解:2291839x xy y x y-++-222693939x xy y x y xy y =++--++()()()233333x y x y y x y=+-+++()()3333x y y x y =+-++()()363x y x y =-++【变式3】(23-24八年级上·四川眉山·期中)因式分解:(1)2321025xy y x y -++;(2)3223a a b ab b +--.【答案】(1)2(5)y x y -(2)2()()a b a b +-【分析】本题考查的因式分解,熟知分组分解法与提取公因式法、公式法分解因式是解题的关键.(1)先提取公因式,再利用完全平方公式进行因式分解即可;(2)利用分组分解法因式分解即可.【详解】(1)解:2321025xy y x y-++22(1025)y xy y x =-++2(5)y x y =-;(2)解:3223a ab ab b +--3223()()a ab ab b =+-+22()()a ab b a b =+-+22()()a b a b =+-2()()a b a b =+-3.拆项后用公式法【例题13】(22-23八年级上·贵州黔西·期末)我们已经学过将一个多项式分解因式的方法有提公因式法、运用公式法和十字相乘法,其实分解因式的方法还有分组分解法、拆项法,等等.①分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法叫作分组分解法.例如:()()()2222222424()222x xy y x xy y x y x y x y -+-=-+-=--=-+--.②拆项法,将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法叫作拆项法.例如:()()()()222223214(1)2121213x x x x x x x x x +-=++-=+-=+-++=-+(1)仿照以上方法,按照要求分解因式:①(分组分解法)22441x x y +-+;②(拆项法)268x x -+;(2)已知:a ,b ,c 为ABC 的三条边,222446170a b c a b c ++---+=,求ABC 的周长.【答案】(1)()()2121x y x y ++-+①;()()42x x --②(2)ABC 的周长为7【分析】本题主要考查公式法因式分解:(1)①将22441x x y +-+组成为()22441x x y ++-分解即可.②将268x x -+拆项为()2691x x -+-分解即可;(2)分组拆项配成完全平方式的和形式()()()2226944440a b a b c c ++--+++=-,利用非负性计算即可.【详解】(1)22441x x y +-+①()22441x x y =++-2221()x y =+-()()2121x y x y =++-+268x x -+②2691x x =-+-2(3)1x =--()()3131x x =---+()()42x x =--(2)222446170a b c a b c ++---+=Q ,()()()2224444690a a b b c c ∴-++-++-+=.222(2)(2)(3)0a b c ∴-+-+-=.2a ∴=,2b =,3c =.2237a b c ∴++=++=.ABC ∴ 的周长为7【变式1】(23-24八年级上·山东济宁·期末)观察下面因式分解的过程:432233x x x x +++-4322333x x x x x =+-++-()()222131x x x x x =+-++-()()2231x x x =++-上面因式分解过程的第一步把22x 拆成了223x x -+,这种因式分解的方法称为拆项法.请用上面的方法完成下列题目:(1)22268a b a b -++-;(2)42231x x -+.【答案】(1)()()24a b a b +--+(2)()()221515x x x x +++-【分析】本题考查因式分解,理解题中拆项法是解答的关键.(1)将8-拆成19-,然后重新组合,利用完全平方公式和平方差公式分解因式即可;(2)将223x -拆成22225x x -,然后重新组合,利用完全平方公式和平方差公式分解因式即可.【详解】(1)解:22268a b a b -++-222619a b a b =-+++-()()222169a a b b =++--+()()2213a b =+--()()1313a b a b =++-+-+()()24a b a b =+--+;(2)解:42231x x -+2242251x x x =+-+()4222125x x x =++-()()22215x x =+-()()221515x x x x =+++-【变式2】(23-24八年级上·河北张家口·期末)我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法等等.①分组分解法:例如:()()()()2222222424222x xy y x xy y x y x y x y -+-=-+-=--=---+.②拆项法:例如:()()()()()22222321412121213x x x x x x x x x +-=++-=+-=+-++=-+.仿照以上方法分解因式:(1)22441x x y +-+;(2)2223x xy y +-.(3)解决问题:已知a 、b 、c 、为ABC 的三边长,2254210a b ab b +--+=,且ABC 为等腰三角形,求ABC的周长.【答案】(1)()()2121x y x y +++-(2)()()3x y x y +-(3)ABC 的周长是5【分析】本题考查因式分解及其应用,分组分解法,拆项法因式等知识,掌握完全平方公式和平方差公式是解题的关键.(1)运用分别分组分解法将2441x x ++看出一组,再用平方差公式因式分解即可;(2)运用拆项法将23y -拆成224y y -,再运用(1)的方法因式分解即可;(3)将2254210a b ab b +--+=化成平方和等于0的形式,从而求出a 、b ,再运用等腰三角形的定义分类讨论即可得解.【详解】(1)解:22441x x y +-+22441x x y =++-()2221x y =+-()()2121x y x y =+++-;(2)2223x xy y +-22224x xy y y =++-()224x y y =+-()()22x y y x y y =+++-()()3x y x y =+-;(3)2254210a b ab b +--+= ,22244210a ab b b b --∴+++=,22(2)(1)0a b b ∴-+-=,20a b ∴-=,10b -=,2a ∴=,1b =,ABC 是等腰三角形,c 2∴=或1c =(不符合三角形三边关系,舍去)ABC ∴ 的周长2215=++=【变式3】(2023八年级上·全国·专题练习)利用拆项法,解决下列问题:(1)分解因式:265x x -+;(2)分解因式:2245a ab b +-.【答案】(1)()()15x x --;(2)()()5a b a b +-.【分析】(1)将5拆解成94-,再根据完全平方公式得()2232x --,然后利用平方差公式进一步分解;(2)将25b -拆解成2249b b -,再根据完全平方公式得()2229a b b +-,然后利用平方差公式进一步分解.【详解】(1)原式2694x x =-+-,()2232x =--,()()3232x x =---+,()()15x x =--;(2)原式222449a ab b b =++-,()2229a b b =+-,()()2323b a b a b b =+++-,()()5a b a b =+-.【点睛】此题考查了因式分解的应用,解题时要注意在拆项变形的过程中不要改变式子的值4.换元法【例题14】(23-24八年级上·福建福州·期中)阅读下列材料:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小胡同学用换元法对多项式()()2221234x x x x ---++进行因式分解的过程.解:设22x x y -=,原式()()134y y =-++(第一步)221y y =++(第二步)()21y =+(第三步)()2221x x =-+(第四步)请根据上述材料回答下列问题:(1)小胡同学的解法中,第二步到第三步运用了因式分解的______;A .提取公因式法B .平方差公式法C .完全平方公式法(2)老师说,小胡同学因式分解的结果不彻底,请你写出该因式分解的最后结果;(3)请你用换元法对多项式()()22661881x x x x ++++进行因式分解.【答案】(1)C(2)()41x -(3)()43x +【分析】(1)根据利用完全平方公式()2222a ab b a b ±+=±分解因式即可得;(2)括号里面可以再次用完全平方公式进行因式分解;(3)设26y x x =+,利用换元法和完全平方公式分解因式即可得.【详解】(1)解:()22211y y y ++=+,则第二步到第三步运用了因式分解的完全平方公式法,故选:C .(2)解:原式()2221x x =-+()221x ⎡=⎤⎣⎦-()41x =-,故答案为:()41x -;(3)解:设26y x x =+,()()22661881x x x x ++++则原式()1881y y =++21881y y =++()29y =+()2269x x =++()223x ⎡⎤=+⎣⎦()43x =+.【点睛】本题考查了因式分解——换元法和完全平方公式法,熟练掌握利用公式法分解因式是解题的关键【变式1】(23-24八年级上·全国·课时练习)因式分解:(1)(添项)44x +;(2)(拆项)3234x x -+;(3)(换元)()()2221224x y x y +-+-+.【答案】(1)()()222222x x x x ++-+(2)()()221x x -+(3)()()2268x y x y +-+-【分析】根据分解因式的方法求解即可.【详解】(1)原式()2222222222x x x =+⨯+-⨯()()22222x x =+-()()222222x x x x =++-+.(2)方法一:原式32224x x x =--+()()32224x x x =---()()()2222x x x x =--+-()()222x x x =---()()()221x x x =--+()()221x x =-+.方法二:原式32244x x x =+-+()()()21411x x x x =+--+()()2144x x x =+-+()()212x x =+-.(3)设2x y a +=,则原式()()21224a a =--+21448a a =-+()()68a a =--()()2268x y x y =+-+-.【点睛】此题考查了因式分解的方法,解题的关键是熟练掌握因式分解的方法.因式分解的方法有:提公因式法,平方差公式法,完全平方公式法,十字相乘法等【变式2】(22-23七年级下·江苏镇江·阶段练习)【积累经验】小明在分解因式22(21)(23)4x x x x +-+++时,提出了如下的思路:小明:我发现223x x ++比221x x +-多4,若设221x x m +-=,那么223x x ++就可以表示为m +4.则222(21)(23)4(4)444x x x x m m m m +-+++=++=++=2(2)m +.因为221x x m +-=,所以原式=224(21)(1)x x x ++=+.在解决数学问题时,可以将某个式子看作一个整体,用一个字母去代替它,从而使问题得到简化,这样的方法叫做换元法.换元法的关键是设元.上述问题中,不仅能设221x x m +-=,也可以将22x x +或223x x ++或……设为n .请你任选一种设元的方法,分解因式;【灵活应用】(1)()()12320222342023A =+++⋯++++⋯+,()()1232023232022B =+++⋯+++⋯+,探究A 与B 的数量关系,并说明理由;(2)如图,一户人家有一块长方形土地ABCD ,30AB =,24AD =,其内部有一条宽度为a 的L 型种植区域①,其余部分(长方形)AEFG 为种植区域②,测量区域②的面积为340;阿凡提有两块正方形的土地AGHI 与AJKE 跟这户人家的种植区域②相邻,正方形土地的边长分别为AG 与AE .这户人家对阿凡提的两块地垂涎已久,提出要将自己的土地与阿凡提交换,阿凡提有没有损失呢?请你运用所学的数学知识进行解释.【答案】积累经验:4(1)x +;灵活运用:(1)2023A B -=;(2)没有损失,见解析【分析】积累经验:可以设22x x n +=,将原式中的22x x +全部用n 表示,然后分解因式即可;灵活运用:(1)设2342022a +++⋯+=,把A 、B 各部分用a 表示,然后作差,即可求出A 、B 的关系;(2)设AE x =,AG y =,用含a 的式子分别表示出AE 、AG ,然后根据()2222x y x y xy +=+-表示出交换之后土地的面积,在进行比较即可求解.【详解】积累经验:解:设22x x n +=,则2211x x n +-=-,那么2233x x n ++=+.原式()()134n n =-++=2234n n +-+=2(1)n +因为22x x n +=,所以原式224(21)(1)x x x =++=+灵活运用:解:(1)设2342022a +++⋯+=()()21202320242023A a a a a =++=++()2120232024B a a a a=++=+所以2023A B -=.(2)由题意得,设30AE a x =-=,24AG a y =-=,.则6x y =-,340.xy =所以()222236680716x y x y xy +=+=+=-,即阿凡提的两块土地面积之和为716,而四边形ABCD 的面积为3024720716⨯=>.所以交换土地对阿凡提来说没有损失.【点睛】本题考查了因式分解—换元法、完全平方公式的应用,看懂和理解题例是求解的关键【变式3】(22-23八年级下·山东济南·期末)阅读以下材料,并按要求完成相应任务:在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式结构,而且能使式子的特点更加明显,便于观察如何进行因式分解,我们把这种因式分解的方法称为“换元法”.下面是小涵同学用换元法对多项式()()2241479x x x x +++++进行因式分解的过程.解:设24x x y +=,则原式()()179y y =+++(第一步)2816y y =++(第二步)()24y =+(第三步)()2244x x =++(第四步)请根据上述材料回答下列问题:(1)小涵同学的解法中,第二步到第三步运用了因式分解的A .提取公因式法B .平方差公式法C .完全平方公式法(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果:;请你用换元法对多项式()()229639614x x x x -+-+-进行因式分解.【答案】(1)C(2)()42x +,()431x -【分析】(1)根据利用完全平方公式()2222a ab b a b ±+=±分解因式即可得;(2)利用完全平方公式分解因式即可得出最后结果;设296x x y -=,利用换元法和完全平方公式分解因式即可得.【详解】(1)解:()228164y y y ++=+,则第二步到第三步运用了因式分解的完全平方公式法,故选:C .(2)解:设24x x y +=,则原式()()179y y =+++2816y y =++()24y =+()2244x x =++()222x ⎡⎤=+⎣⎦()42x =+,故答案为:()42x +.对多项式()()229639614x x x x -+-+-,设296x x y -=,则原式()()314y y =+-+2234y y =+-+221y y =++()21y =+()22961x x -=+()2231x ⎡⎤=-⎣⎦()431x =-.【点睛】本题考查了因式分解——换元法和完全平方公式法,熟练掌握利用公式法分解因式是解题的关键3种思想1:整体思想【例题15】(22-23八年级下·贵州六盘水·期末)先阅读下列材料,再解答下列问题:材料:因式分解:()()221x y x y ++++.解:将“()x y +”看成整体,令()x y A +=,则原式()22211A A A =++=+.再将“A ”还原,得原式()21x y =++.上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请解答下列问题:因式分解:()()44a b a b ++-+.【答案】()22a b +-【分析】本题主要考查整体思想的方法进行因式分解,掌握乘法公式,整体思想的方法是解题的关键.根据材料提示,令a b M +=,再结合完全平方公式进行因式分解即可求解.【详解】解:()()44a b a b ++-+令a b M +=,∴原式()44M M =-+。
人教版四年级数学上册典型例题系列之第三单元角的度量 (含答案)

加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好! 经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!12022-2023学年四年级数学上册典型例题系列之第三单元角的度量(解析版)【考点一】判断线段、射线和直线。
【方法点拨】区别图形端点长度延长情况联系线段2可以度量( 不可 )向两端延长射线1不可度量向( 一端 )无限延长直线0不可度量向(两端 )无限延长都是直的,线段、射线都可以看作直线的一部分。
过一点可以画(无数 )条直线。
过两点只能画( 一条 )直线。
从一点出发可以画( 两 )条射线。
【典型例题】下列线中,( A )是直线,( D )射线,( C )是线段。
A. B. C. D.【对应练习1】把3厘米长的线段向两端无限延长,得到的是一条( 直线 ),把一端无限延长,得到的是一条(射线)。
初中数学:《公式法解一元二次方程》练习(含答案)

初中数学:《公式法解一元二次方程》练习(含答案)一、选择题:1.一元二次方程x(x﹣2)=0根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根2.已知b<0,关于x的一元二次方程(x﹣1)2=b的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根 D.有两个实数根3.已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是()A.m≥﹣ B.m≥0 C.m≥1 D.m≥24.关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根,则k的取值范围是()A.k<B.k>C.k<且k≠0 D.k>且k≠0二、填空题5.一元二次方程x2+x=3中,a=______,b=______,c=______,则方程的根是______.6.若x1,x2分别是x2﹣3x+2=0的两根,则x1+x2=______.7.已知三角形两边长是方程x2﹣5x+6=0的两个根,则三角形的第三边c的取值范围是______.8.已知关于x的一元二次方程(k+1)x2﹣2x﹣1=0有两个不相同的实数根,则k的取值范围是______.9.写出一个一元二次方程,使它有两个不相等的实数根______.10.一次二元方程x2+x+=0根的情况是______.11.若关于x的方程ax2+2(a+2)x+a=0有实数解,那么实数a的取值范围是______.12.已知代数式7x(x+5)与代数式﹣6x2﹣37x﹣9的值互为相反数,则x=______.13.已知一次函数y=﹣x+4与反比例函数在同一直角坐标系内的图象没有交点,则k的取值范围是______.14.对于实数a,b,定义运算“﹡”:a﹡b=.例如4﹡2,因为4>2,所以4﹡2=42﹣4×2=8.若x1,x2是一元二次方程x2﹣5x+6=0的两个根,则x1﹡x2=______.三、解答题(共4小题,满分0分)15.用公式法解方程:①4x2﹣4x+1=0②x2﹣x﹣3=0.16.不解方程,判断下列方程的根的情况:①2x2+3x﹣4=0②3x2+2=2x③x2=x﹣1.17.已知关于x的方程mx2﹣(3m﹣1)x+2m﹣2=0,求证:无论m取任何实数时,方程恒有实数根.18.已知关于x的一元二次方程:x2﹣(2k+1)x+4(k﹣)=0.(1)求证:这个方程总有两个实数根;(2)若等腰△ABC的一边长a=4,另两边长b、c恰好是这个方程的两个实数根,求△ABC的周长.《公式法》参考答案与试题解析一、选择题:1.一元二次方程x(x﹣2)=0根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数根【解答】解:原方程变形为:x2﹣2x=0,∵△=(﹣2)2﹣4×1×0=4>0,∴原方程有两个不相等的实数根.故选A.2.已知b<0,关于x的一元二次方程(x﹣1)2=b的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根 D.有两个实数根【解答】解:∵(x﹣1)2=b中b<0,∴没有实数根,故选:C.3.已知关于x的一元二次方程(x+1)2﹣m=0有两个实数根,则m的取值范围是()A.m≥﹣ B.m≥0 C.m≥1 D.m≥2【解答】解;(x+1)2﹣m=0,(x+1)2=m,∵一元二次方程(x+1)2﹣m=0有两个实数根,∴m≥0,故选:B.4.关于x的一元二次方程kx2﹣x+1=0有两个不相等的实数根,则k的取值范围是()A.k<B.k>C.k<且k≠0 D.k>且k≠0 【解答】解:根据题意得k≠0且△=(﹣1)2﹣4k>0,解得k<且k≠0.故选C.二、填空题5.一元二次方程x2+x=3中,a= ,b= 1 ,c= ﹣3 ,则方程的根是x1=﹣1+,x2=﹣1﹣.【解答】解:移项得, x+x﹣3=0∴a=,b=1,c=﹣3∴b2﹣4ac=7∴x1=﹣1+,x2=﹣1﹣.6.若x1,x2分别是x2﹣3x+2=0的两根,则x1+x2= 3 .【解答】解:根据题意得x1+x2=3.故答案为3.7.已知三角形两边长是方程x2﹣5x+6=0的两个根,则三角形的第三边c的取值范围是1<c <5 .【解答】解:∵三角形两边长是方程x2﹣5x+6=0的两个根,∴x1+x2=5,x1x2=6∵(x1﹣x2)2=(x1+x2)2﹣4x1x2=25﹣24=1∴x1﹣x2=1,又∵x1﹣x2<c<x1+x2,∴1<c<5.故答案为:1<c<5.8.已知关于x的一元二次方程(k+1)x2﹣2x﹣1=0有两个不相同的实数根,则k的取值范围是k>﹣2且k≠﹣1 .【解答】解:根据题意得k+1≠0且△=(﹣2)2﹣4(k+1)•(﹣1)>0,解得k>﹣2且k≠﹣1.故答案为k>﹣2且k≠﹣1.9.写出一个一元二次方程,使它有两个不相等的实数根x2+x﹣1=0 .【解答】解:比如a=1,b=1,c=﹣1,∴△=b2﹣4ac=1+4=5>0,∴方程为x2+x﹣1=0.10.一次二元方程x2+x+=0根的情况是方程有两个相等的实数根.【解答】解:∵△=12﹣4×=0,∴方程有两个相等的实数根故答案为方程有两个相等的实数根.11.若关于x的方程ax2+2(a+2)x+a=0有实数解,那么实数a的取值范围是a≥﹣1 .【解答】解:当a=0时,方程是一元一次方程,有实数根,当a≠0时,方程是一元二次方程,若关于x的方程ax2+2(a+2)x+a=0有实数解,则△=[2(a+2)]2﹣4a•a≥0,解得:a≥﹣1.故答案为:a≥﹣1.12.已知代数式7x(x+5)与代数式﹣6x2﹣37x﹣9的值互为相反数,则x= 1±.【解答】解:根据题意得:7x(x+5)﹣6x2﹣37x﹣9=0,这里的:x2﹣2x﹣9=0,这里a=1,b=﹣2,c=﹣9,∵△=4+36=40,故答案为:1±13.已知一次函数y=﹣x+4与反比例函数在同一直角坐标系内的图象没有交点,则k的取值范围是k>4 .【解答】解:依题意可得x2﹣4x+k=0无解,也就是这个一元二次方程无实数根,那么根据根的判别式△=b2﹣4ac=16﹣4k,没有实数根,那么16﹣4k<0,解此不等式可得k>4.故答案为:k>4.14.对于实数a,b,定义运算“﹡”:a﹡b=.例如4﹡2,因为4>2,所以4﹡2=42﹣4×2=8.若x1,x2是一元二次方程x2﹣5x+6=0的两个根,则x1﹡x2= 3或﹣3 .【解答】解:∵x1,x2是一元二次方程x2﹣5x+6=0的两个根,∴(x﹣3)(x﹣2)=0, 解得:x=3或2,①当x1=3,x2=2时,x1﹡x2=32﹣3×2=3;②当x1=2,x2=3时,x1﹡x2=3×2﹣32=﹣3.故答案为:3或﹣3.三、解答题(共4小题,满分0分)15.用公式法解方程:①4x2﹣4x+1=0②x2﹣x﹣3=0.【解答】解:(1)这里a=4,b=﹣4,c=1, ∵△=32﹣16=16,(2)这里a=1,b=﹣,c=﹣3,∵△=2+12=14,∴x=.16.不解方程,判断下列方程的根的情况:①2x2+3x﹣4=0②3x2+2=2x③x2=x﹣1.【解答】解:①△=32﹣4×2×(﹣4)=41>0,所以方程两个不相等的实数根;②方程化为一般式为3x2﹣2x+2=0,△=(﹣2)2﹣4×3×2=0,所以方程有两个相等的实数根;③方程化为一般式为x2﹣x+1=0,△=(﹣)2﹣4××1<0,所以方程无实数根.17.已知关于x的方程mx2﹣(3m﹣1)x+2m﹣2=0,求证:无论m取任何实数时,方程恒有实数根.【解答】证明:当m=0时,原方程为x﹣2=0,解得x=2;当m≠0时,△=(3m﹣1)2﹣4m(2m﹣2)=(m+1)2≥0,所以方程有两个实数根,所以无论m为何值原方程有实数根.18.已知关于x的一元二次方程:x2﹣(2k+1)x+4(k﹣)=0.(1)求证:这个方程总有两个实数根;(2)若等腰△ABC的一边长a=4,另两边长b、c恰好是这个方程的两个实数根,求△ABC的周长.【解答】(1)证明:△=(2k+1)2﹣4×1×4(k﹣)=4k2﹣12k+9=(2k﹣3)2,∵无论k取什么实数值,(2k﹣3)2≥0, ∴△≥0,∴无论k取什么实数值,方程总有实数根;(2)解:∵x=,∴x1=2k﹣1,x2=2,∵b,c恰好是这个方程的两个实数根,设b=2k﹣1,c=2,当a、b为腰,则a=b=4,即2k﹣1=4,解得k=,此时三角形的周长=4+4+2=10;当b、c为腰时,b=c=2,此时b+c=a,故此种情况不存在.综上所述,△ABC的周长为10.。
高中数学《等比数列的概念及通项公式》知识点讲解及重点练习

§4.3等比数列4.3.1等比数列的概念第1课时等比数列的概念及通项公式学习目标 1.通过实例,理解等比数列的概念.2.掌握等比中项的概念并会应用.3.掌握等比数列的通项公式并了解其推导过程.4.灵活应用等比数列通项公式的推广形式及变形.知识点一等比数列的概念1.定义:一般地,如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,通常用字母q表示(q≠0).2.递推公式形式的定义:a na n-1=q(n∈N *且n>1)⎝⎛⎭⎫或a n+1a n=q,n∈N*.思考为什么等比数列的各项和公比q均不能为0?答案由于等比数列的每一项都可能作分母,故每一项均不能为0,因此q也不能为0.知识点二等比中项如果在a与b中间插入一个数G,使a,G,b成等比数列,那么G叫做a与b的等比中项,此时,G2=ab.思考当G2=ab时,G一定是a,b的等比中项吗?答案不一定,如数列0,0,5就不是等比数列.知识点三等比数列的通项公式若等比数列{a n}的首项为a1,公比为q,则a n=a1q n-1(n∈N*).知识点四等比数列通项公式的推广和变形等比数列{a n}的公比为q,则a n=a1q n-1①=a m q n-m②=a1 q·qn.③其中当②中m=1时,即化为①.当③中q>0且q≠1时,y=a1q·qx为指数型函数.1.数列1,-1,1,-1,…是等比数列.( √ )2.若一个数列从第2项起每一项与前一项的比为常数,则该数列为等比数列.( × )3.等比数列的首项不能为零,但公比可以为零.( × )4.常数列一定为等比数列.( × )一、等比数列中的基本运算例1 在等比数列{a n }中:(1)a 1=1,a 4=8,求a n ;(2)a n =625,n =4,q =5,求a 1;(3)a 2+a 5=18,a 3+a 6=9,a n =1,求n .解 (1)因为a 4=a 1q 3,所以8=q 3,所以q =2,所以a n =a 1q n -1=2n -1.(2)a 1=a n q n -1=62554-1=5, 故a 1=5.(3) 因为⎩⎪⎨⎪⎧a 2+a 5=a 1q +a 1q 4=18, ①a 3+a 6=a 1q 2+a 1q 5=9, ② 由②①,得q =12,从而a 1=32. 又a n =1,所以32×⎝⎛⎭⎫12n -1=1,即26-n =20,故n =6.反思感悟 等比数列的通项公式涉及4个量a 1,a n ,n ,q ,只要知道其中任意三个就能求出另外一个,在这四个量中,a 1和q 是等比数列的基本量,只要求出这两个基本量,问题便迎刃而解.跟踪训练1 在等比数列{a n }中:(1)若它的前三项分别为5,-15,45,求a 5;(2)若a 4=2,a 7=8,求a n .解 (1)因为a 5=a 1q 4,而a 1=5,q =a 2a 1=-3, 所以a 5=405.(2)因为⎩⎪⎨⎪⎧ a 4=a 1q 3,a 7=a 1q 6, 所以⎩⎪⎨⎪⎧a 1q 3=2, ①a 1q 6=8, ② 由②①得q 3=4, 从而q =34,而a 1q 3=2,于是a 1=2q 3=12, 所以a n =a 1q n -1=2532n -.二、等比中项的应用例2 如果-1,a ,b ,c ,-9成等比数列,那么b =__________,ac =___________. 答案 -3 9解析 因为b 是-1,-9的等比中项,所以b 2=9,b =±3.又等比数列奇数项符号相同,得b <0,故b =-3,而b 又是a ,c 的等比中项,故b 2=ac ,即ac =9.反思感悟 (1)由等比中项的定义可知G a =b G⇒G 2=ab ⇒G =±ab ,所以只有a ,b 同号时,a ,b 的等比中项有两个,异号时,没有等比中项.(2)在一个等比数列中,从第二项起,每一项(有穷数列的末项除外)都是它的前一项和后一项的等比中项.(3)a ,G ,b 成等比数列等价于G 2=ab (ab >0).跟踪训练2 在等比数列{a n }中,a 1=-16,a 4=8,则a 7等于( )A .-4B .±4C .-2D .±2答案 A解析 因为a 4是a 1与a 7的等比中项,所以a 24=a 1a 7,即64=-16a 7,故a 7=-4.三、等比数列通项公式的推广及应用例3 在等比数列{a n }中.(1)已知a 3=4,a 7=16,且q >0,求a n ;(2)若{a n }为递增数列,且a 25=a 10,2(a n +a n +2)=5a n +1,求通项公式a n .解 (1)∵a 7a 3=q 7-3=q 4=4, ∴q 2=2,又q >0,∴q =2,∴a n =a 3·q n -3=4·(2)n -3=122n +(n ∈N *).(2)由a 25=a 10=a 5·q 10-5,且a 5≠0, 得a 5=q 5,即a 1q 4=q 5,又q ≠0,∴a 1=q .由2(a n +a n +2)=5a n +1得,2a n (1+q 2)=5qa n ,∵a n ≠0,∴2(1+q 2)=5q ,解得q =12或q =2. ∵a 1=q ,且{a n }为递增数列,∴⎩⎪⎨⎪⎧a 1=2,q =2. ∴a n =2·2n -1=2n (n ∈N *).反思感悟 (1)应用a n =a m q n -m ,可以凭借任意已知项和公比直接写出通项公式,不必再求a 1.(2)等比数列的单调性由a 1,q 共同确定,但只要单调,必有q >0.跟踪训练3 已知等比数列{a n }满足a 1=3,a 1+a 3+a 5=21,则a 3+a 5+a 7等于( )A .21B .42C .63D .84答案 B解析 设等比数列{a n }的公比为q ,则由a 1=3,a 1+a 3+a 5=21得3(1+q 2+q 4)=21,解得q 2=-3(舍去)或q 2=2,于是a 3+a 5+a 7=q 2(a 1+a 3+a 5)=2×21=42.四、灵活设元求解等比数列问题例4 (1)有四个数成等比数列,将这四个数分别减去1,1,4,13成等差数列,则这四个数的和是________.答案 45解析 (1)设这四个数分别为a ,aq ,aq 2,aq 3,则a -1,aq -1,aq 2-4,aq 3-13成等差数列.即⎩⎪⎨⎪⎧ 2(aq -1)=(a -1)+(aq 2-4),2(aq 2-4)=(aq -1)+(aq 3-13),整理得⎩⎪⎨⎪⎧a (q -1)2=3,aq (q -1)2=6, 解得a =3,q =2.因此这四个数分别是3,6,12,24,其和为45.(2)有四个实数,前三个数成等比数列,且它们的乘积为216,后三个数成等差数列,且它们的和为12,求这四个数.解 方法一 设前三个数分别为a q,a ,aq , 则a q·a ·aq =216, 所以a 3=216.所以a =6.因此前三个数为6q,6,6q . 由题意知第4个数为12q -6.所以6+6q +12q -6=12,解得q =23. 故所求的四个数为9,6,4,2.方法二 设后三个数为4-d,4,4+d ,则第一个数为14(4-d )2, 由题意知14(4-d )2×(4-d )×4=216, 解得4-d =6.所以d =-2.故所求得的四个数为9,6,4,2.反思感悟 几个数成等比数列的设法(1)三个数成等比数列设为a q,a ,aq . 推广到一般:奇数个数成等比数列设为…,a q 2,a q,a ,aq ,aq 2,… (2)四个符号相同的数成等比数列设为a q 3,a q,aq ,aq 3. 推广到一般:偶数个符号相同的数成等比数列设为…,a q 5,a q 3,a q,aq ,aq 3,aq 5,… (3)四个数成等比数列,不能确定它们的符号是否相同时,可设为a ,aq ,aq 2,aq 3.跟踪训练4 在2和20之间插入两个数,使前三个数成等比数列,后三个数成等差数列,则插入的两个数的和为( )A .-4或352B .4或352C .4D.352答案 B解析 设插入的第一个数为a ,则插入的另一个数为a 22. 由a ,a 22,20成等差数列得2×a 22=a +20. ∴a 2-a -20=0,解得a =-4或a =5.当a =-4时,插入的两个数的和为a +a 22=4.当a =5时,插入的两个数的和为a +a 22=352.1.在等比数列{a n }中,若a 2=4,a 5=-32,则公比q 应为( )A .±12B .±2 C.12D .-2 答案 D解析 因为a 5a 2=q 3=-8,故q =-2. 2.(多选)已知a 是1,2的等差中项,b 是-1,-16的等比中项,则ab 等于( )A .6B .-6C .-12D .12答案 AB解析 ∵a =1+22=32,b 2=(-1)×(-16)=16,b =±4, ∴ab =±6.3.若等比数列的首项为4,末项为128,公比为2,则这个数列的项数为( )A .4B .8C .6D .32答案 C解析 由等比数列的通项公式得,128=4×2n -1,2n -1=32,所以n =6.4.等比数列{a n }中,|a 1|=1,a 5=-8a 2,a 5>a 2,则a n 等于( )A .(-2)n -1B .-(-2n -1) C .(-2)nD .-(-2)n 答案 A解析 设公比为q ,则a 1q 4=-8a 1q ,又a 1≠0,q ≠0,所以q 3=-8,q =-2,又a 5>a 2,所以a 2<0,a 5>0,从而a 1>0,即a 1=1,故a n =(-2)n -1.5.在等比数列{a n }中,a 1=-2,a 3=-8,则数列{a n }的公比为________,通项公式为a n =______________.答案 ±2 (-2)n 或-2n解析 ∵a 3a 1=q 2, ∴q 2=-8-2=4,即q =±2. 当q =-2时,a n =a 1q n -1=-2×(-2)n -1=(-2)n ;当q =2时,a n =a 1q n -1=-2×2n -1=-2n .1.知识清单:(1)等比数列的概念.(2)等比数列的通项公式.(3)等比中项的概念.(4)等比数列的通项公式推广.2.方法归纳:方程(组)思想、构造法、等比数列的设法.3.常见误区:(1)x ,G ,y 成等比数列⇒G 2=xy ,但G 2=xy ⇏x ,G ,y 成等比数列.(2)四个数成等比数列时设成a q 3,a q,aq ,aq 3,未考虑公比为负的情况. (3)忽视了等比数列中所有奇数项符号相同,所有偶数项符号相同而出错.1.在数列{a n }中,若a n +1=3a n ,a 1=2,则a 4为( )A .108B .54C .36D .18答案 B解析 因为a n +1=3a n ,所以数列{a n }是公比为3的等比数列,则a 4=33a 1=54.2.(多选)在等比数列{a n }中,a 1=18,q =2,则a 4与a 8的等比中项为( ) A .-4 B .4 C .-14 D.14答案 AB解析 由题意得a 26=a 4a 8,因为a 1=18,q =2, 所以a 4与a 8的等比中项为±a 6=±4.3.在等比数列{a n }中,a n >0,且a 1+a 2=1,a 3+a 4=9,则a 4+a 5的值为( )A .16B .27C .36D .81答案 B解析 ∵a 1+a 2=1,a 3+a 4=9,∴q 2=9.∴q =3(q =-3舍去),∴a 4+a 5=(a 3+a 4)q =27.4.数列{a n }是公差不为0的等差数列,且a 1,a 3,a 7为等比数列{b n }的连续三项,则数列{b n }的公比为( ) A. 2 B .4 C .2 D.12答案 C解析 因为a 1,a 3,a 7为等比数列{b n }中的连续三项,所以a 23=a 1a 7,设数列{a n }的公差为d ,则d ≠0,所以(a 1+2d )2=a 1(a 1+6d ),所以a 1=2d ,所以公比q =a 3a 1=4d 2d=2. 5.若正项数列{a n }满足a 1=2,a 2n +1-3a n +1a n -4a 2n =0,则数列{a n }的通项公式a n 等于( )A .22n -1B .2nC .22n +1D .22n -3答案 A解析 由a 2n +1-3a n +1a n -4a 2n =0, 得(a n +1-4a n )·(a n +1+a n )=0.又{a n }是正项数列,所以a n +1-4a n =0,a n +1a n=4. 由等比数列的定义知数列{a n }是以2为首项,4为公比的等比数列.由等比数列的通项公式,得a n =2×4n -1=22n -1.6.若{a n }为等比数列,且a 3+a 4=4,a 2=2,则公比q =________.答案 1或-2解析 根据题意,⎩⎪⎨⎪⎧a 1q 2+a 1q 3=4,a 1q =2, 解得⎩⎪⎨⎪⎧ a 1=2,q =1或⎩⎪⎨⎪⎧ a 1=-1,q =-2.7.已知{a n }是等差数列,公差d 不为零.若a 2,a 3,a 7成等比数列,且2a 1+a 2=1,且a 1=________,d =________.答案 23-1 解析 ∵a 2,a 3,a 7成等比数列,∴a 23=a 2a 7,∴(a 1+2d )2=(a 1+d )(a 1+6d ),即2d +3a 1=0.①又∵2a 1+a 2=1,∴3a 1+d =1.②由①②解得a 1=23,d =-1. 8.已知等比数列{a n }的前三项依次为a -1,a +1,a +4,则a n =________.答案 4×⎝⎛⎭⎫32n -1解析 由已知可得(a +1)2=(a -1)(a +4),解得a =5,所以a 1=4,a 2=6,所以q =a 2a 1=64=32, 所以a n =4×⎝⎛⎭⎫32n -1.9.在等比数列{a n }中,a 3=32,a 5=8.(1)求数列{a n }的通项公式a n ;(2)若a n =12,求n . 解 (1)因为a 5=a 3q 2,所以q 2=a 5a 3=14.所以q =±12.当q =12时,a n =a 3q n -3=32×⎝⎛⎭⎫12n -3=28-n ;当q =-12时,a n =a 3q n -3=32×⎝⎛⎭⎫-12n -3.所以a n =28-n 或a n =32×⎝⎛⎭⎫-12n -3.(2)当a n =12时,即28-n =12或32×⎝⎛⎭⎫-12n -3=12,解得n =9.10.在等比数列{a n }中:(1)已知a 3=2,a 5=8,求a 7;(2)已知a 3+a 1=5,a 5-a 1=15,求通项公式a n .解 (1)因为a 5a 3=q 2=82,所以q 2=4,所以a 7=a 5q 2=8×4=32.(2)a 3+a 1=a 1(q 2+1)=5,a 5-a 1=a 1(q 4-1)=15,所以q 2-1=3,所以q 2=4,所以a 1=1,q =±2,所以a n =a 1q n -1=(±2)n -1.11.已知a ,b ,c ,d 成等比数列,且曲线y =x 2-2x +3的顶点是(b ,c ),则ad 等于()A .3B .2C .1D .-2答案 B解析 ∵y =(x -1)2+2,∴b =1,c =2.又∵a ,b ,c ,d 成等比数列,∴ad =bc =2.12.已知等比数列{a n }满足a 1=14,a 3a 5=4(a 4-1),则a 2等于( )A .2B .1 C.12 D.18答案 C解析 方法一 ∵a 3,a 5的等比中项为±a 4,∴a 3a 5=a 24,a 3a 5=4(a 4-1),∴a 24=4(a 4-1),∴a 24-4a 4+4=0,∴a 4=2.又∵q 3=a 4a 1=214=8,∴q =2,∴a 2=a 1q =14×2=12.方法二 ∵a 3a 5=4(a 4-1),∴a 1q 2·a 1q 4=4(a 1q 3-1),将a 1=14代入上式并整理,得q 6-16q 3+64=0,解得q =2,∴a 2=a 1q =12.13.(多选)已知等差数列a ,b ,c 三项之和为12,且a ,b ,c +2成等比数列,则a 等于() A .-2 B .2 C .-8 D. 8答案 BD解析 由已知得⎩⎪⎨⎪⎧ a +c =2b ,a +b +c =12,a (c +2)=b 2,解得⎩⎪⎨⎪⎧a =2,b =4,c =6或⎩⎪⎨⎪⎧a =8,b =4,c =0.故a =2或a =8.14.若数列{a n}的前n项和为S n,且a n=2S n-3,则{a n}的通项公式是________.答案a n=3·(-1)n-1解析由a n=2S n-3得a n-1=2S n-1-3(n≥2),两式相减得a n-a n-1=2a n(n≥2),∴a n=-a n-1(n≥2),又a1=3,故{a n}是首项为3,公比为-1的等比数列,∴a n=3·(-1)n-1.15.已知在等差数列{a n}中,a2+a4=16,a1+1,a2+1,a4+1成等比数列,把各项按如图所示排列.则从上到下第10行,从左到右的第11个数值为________.答案275或8解析设公差为d,由a2+a4=16,得a1+2d=8,①由a1+1,a2+1,a4+1成等比数列,得(a2+1)2=(a1+1)(a4+1),化简得a1-d=-1或d=0,②当d=3时,a n=3n-1.由题图可得第10行第11个数为数列{a n}中的第92项,a92=3×92-1=275.当d=0时,a n=8,a92=8.16.设数列{a n}是公比小于1的正项等比数列,已知a1=8,且a1+13,4a2,a3+9成等差数列.(1)求数列{a n}的通项公式;(2)若b n=a n(n+2-λ),且数列{b n}是单调递减数列,求实数λ的取值范围.解(1)设数列{a n}的公比为q.由题意,可得a n=8q n-1,且0<q<1.由a1+13,4a2,a3+9成等差数列,知8a2=30+a3,所以64q=30+8q2,解得q=12或152(舍去),所以a n=8×⎝⎛⎭⎫12n-1=24-n,n∈N*.(2)b n=a n(n+2-λ)=(n+2-λ)·24-n,由b n>b n+1,得(n+2-λ)·24-n>(n+3-λ)·23-n,即λ<n+1,所以λ<(n+1)min=2,故实数λ的取值范围为(-∞,2).。
第3章Excel公式应用与数据处理

3.4 Excel公式的格式
1. 同一工作表内公式的定义和使用
• 同一工作表内定义公式,直接使用单元格名 称(即单元格地址) • 如:A1、B2
2. 不同工作表公式的定义和引用
F F
引用不同工作表的单元格,需要在单元 格地址前加“工作表名!”。 格式如:工作表名!A1
(1)引用单个工作表的单元格
最大值
最小值 乘积 数值计数
4
5 6 2
数据的最大值
数据的最小值 所有数据的乘积 含有数字的记录或者行的数目
标准偏差
方差 总体标准偏差 总体方差
7
10 8 11
估算总体的标准偏差,数据列为样本
估算总体方差,数据列为样本 总体的标准偏差,数据列为总体 总体方差,数据列为总体
3.7 教学案例
1. 案例要求
1. 定义名称
• (1)直接定义
▫ 选定单元格或区域→输入需要的名称→回车
• (2)快速定义
▫ 选定单元格或区域→公式选项卡→定义的名称(组 )→单击“根据所选内容创建”按钮→打开“以选定区 域创建名称”对话框→选择四个复选框之一→确定
• (3)使用定义命令
▫ 选定单元格或区域→公式→定义的名称→定义名称 →“新建名称”对话框→输入名称(<=255个字符)→ 范围(工作簿或工作表)→确定 ▫ 若给常量/公式定义名称→则在“引用位置”输入“=常 量”或“=公式”。
1. 相对引用
• 相对引用:当复制公式时,即当公式位置改变时 ,公式中的单元格地址也会随之改变。
2. 绝对引用
• 当公式位置改变时,公式中的单元格地址不会随 之改变。这就叫绝对引用。 • 表示:在列标和行号前都加$。如:$A$1 • $:绝对地址标志符号
四年级上册数学第一单元知识点

四年级上册数学第一单元知识点关于任何事物的知识都有五个层次或者要素:事物的名称、定义、形象,有关事物的智识或者知识,以及事物本身——这才是知识的真正目标。
下面小编给大家分享一些四年级上册数学第一单元知识,希望能够帮助大家,欢迎阅读!四年级上册数学第一单元知识1、计数单位:一(个)、十、百、千、万……亿等等,都是计数单位。
相邻两个计数单位之间的进率是十。
2、数位:个位、十位、百位、……亿位等等,都是数位。
数位名称就是在相应的计数单位后添一个“位”字,如:万--万位。
3、数级:个级、万级、亿级……都是数级,一个数级包括四个数位。
4、数位顺序表:含有数级、数位和相应的计数单位的表格叫做数位顺序表,如下。
5、数字表示:某个数位上的数字表示几个这个数位的计数单位。
如:12367 中的2在千位上,表示“2个千”某个数级上的数字表示几个这个数级的计数单位。
如:36472845中的3647在万级上,表示“3647个万”6、大数的读法:①从高位数读起,一级一级往下读。
②万级的数要按照个级的数的读法来读,再在后面加一个万字。
③每级末尾不管有几个零都不读,其他数位有一个“零”或连续几个“零”,都只读一个“零”。
读数注意事项:“2”读作“二”;如果是大数的最高位是十位、十万位、十亿位……且最高位上的数字是“1”时,这个“1”不读,如125046读作“十二万五千零四十六”7、大数的写法:①从高级写起,一级一级往下写。
②当哪一位上一个计数单位也没有,就在哪一位上写0 。
写数注意事项:一定要注意“四位一级”,保证每级有四个数位,不够的要用0补足。
8、读写数检验方法:读数和写数可以互相检验,即读数后再写出来和原数比对,而写数后可以自己读出。
9、写出所组成的数:对照数位顺序表把每个部分的数字分别写入,再用0补足。
10、大数的比较:①位数多的这个数就比较大。
②当这两个数位数相同的时候,我们就应该从左起的第一位比起,也就是从最高位开始比,哪个数最高位上的数大,这个数就大。
狂刷06 平行板电容器-学易试题君之小题狂刷君2019学年高二物理人教版(选修3-1)(解析版)

1 / 19
第一章 静电场
狂刷06 平行板电容器
1.要使平行板电容器的的电容增加,可采用的方法是
A .增大两极板正对面积
B .增大两极板间距
C .增大两板之间的电压
D .使极板带电荷量增加
【答案】A 【解析】根据平行板电容器的决定式4πS
C kd ε=,可知要增加电容,可增大两极板正对面积,或插入电
介质,或减小板间距离,故A 正确,B 错误;电容的定义式为C Q U
=
,运用比值法定义,可知C 与Q 、U 无关,故CD 错误。
2.(2018·福建省闽侯第二中学五校教学联合体高二期末考试)水平放置的平行板电容器与一电池相连。
在电容器的两板间有一带正电的质点处于静止平衡状态。
现将电容器两板间的距离增大,则
A .电容变大,质点向上运动
B .电容变大,质点向下运动
C .电容变小,质点向下运动
D .电容变小,质点保持静止
【答案】
C
【名师点睛】解答本题注意电容器的两种状态,充电后与电源断开则电荷量不变;而与电源相连,则两板间的电势差保持不变。
10.4电容器的电容 同步练习-高二上学期物理人教版(2019)必修第三册

10.4电容器的电容同步练习-2021-2022学年高二上学期物理人教版(2019)必修第三册一.选择题(共12小题)1.(2021春•南京月考)根据电容电容器的电容定义式QCU可知()A.电容器带的电量Q越多,它的电容C就越大,C与Q成正比B.电容器的电容大小与其带电情况无关C.电容器两极板间的电压U越高,它的电容C就越小,C与U成反比D.电容器不带电时,其电容为零2.(2020秋•吕梁期末)一个空气平行板电容器,极板间距离为d,正对面积为S,充以电荷量为Q后,两极板间电压为U,为使电容器的电容加倍,可采用的办法是() A.将电压变为2UB.将带电荷量变为2QC.将极板正对面积变为2SD.将两极间充满介电常数为2的电介质3.(2020秋•武功县期中)平行板电容器充电后断开电源,将其中一块金属板沿远离另一极板的方向平移一小段距离。
如图表示此过程中电容器两极板间电场强度E随两极板间距离d 的变化关系,其中正确的是()A.B.C.D.4.(2020春•洛阳期末)给一个平行板电容器充电后将它与电源断开.再用绝缘工具把电容器两金属板间的距离缓慢拉大.在板间距离增大的过程中下列说法正确的是() A.电容器的带电量增加B.电容器两板间的电压不变C.电容器的电容增加D.电容器两板间的电压增加5.(2021春•白云区校级期末)如图所示,两块大小、形状完全相同的金属板正对水平放置,构成一个平行板电容器。
将两金属板分别与电源两极相连,闭合开关S达到稳定后,在两板间有一带电液滴P恰好处于静止状态,下列判断正确的是()A.保持开关S闭合,减小两极间的距离,板间电压减小B.保持开关S闭合,减小两板间的距离,电容器的电容减小C.断开开关S,减小两板间的距离,液滴静止不动D.断开开关S,减小两板间的距离,板间电场强度增大6.(2021春•十堰期末)如图所示,平行板电容器与直流电源连接,下极板接地,一带电油滴位于电容器中的P点且处于静止状态,现将上极板竖直向上移动一小段距离,则()A.电容器中的电场强度增大B.P点的电势将降低C.电容器的电容减小,极板带电荷量增大D.带电油滴在P点的电势能将减小7.(2021春•锡山区校级期末)如图所示,两块平行放置的金属板A、B与一电源相连,S 闭合后,两板间有一质量为m、带电荷量为q的油滴恰好处于静止状态.下列说法正确的是()A.油滴带负电荷B.若将A板向上平移一小段位移,G中有b a的电流C.若将A板向上平移一小段位移,油滴仍然静止D.若将S断开,油滴立即做自由落体运动8.(2021•浙江模拟)如图所示,一个平行板电容器上极板与电源正极相连,下极板与电源负极相连并接地,P为两极板间的一点,下列操作能使P点电势升高的是()A.开关一直闭合,上极板上升一小段距离B.开关一直闭合,上极板下降一小段距离C.开关闭合后断开,上极板上升一小段距离D.开关闭合后断开,上极板下降一小段距离9.(2021•海淀区校级模拟)如图所示,两块相互靠近的平行金属板组成的平行板电容器,极板N与静电计相连,极板M与静电计的外壳均接地。
高中物理公式 表达式 字母含义 使用条件 范围 总结

(5)初速无论是否为零,匀变速直线运动的质点,在连续相邻的相等的时间间隔内的位移之差为一常数:s = aT2 (a: 匀变速直线运动的加速度 T:每个时间间隔的时间)
9、自由落体运动: V0=0, a=g 10、竖直上抛运动:上升过程是匀减速直线运动,下落过程是匀加速直线运动。全过程是初速度为 VO、加速度为g 的匀减速直线运动。
波长名称产生机理特性与应用1010无线电自由电子的运动波动性显著无线电通讯红外线原子外层电子受激一切物体都能辐射具有热作用遥感技术遥控器可见光紫外线由七种色光组成一切高温物体都能辐射具有化学作用荧光效10伦琴x射线原子外内电子受激粒子性显著穿透本领强射线原子核受激发粒子性显著穿透本领更强4光子说爱因斯坦hc实验基础
(1)
上升最大高度:
H=
Vo 2 2g
第 3 页 共 14 页
(2)
上升的时间:
t=
Vo g
高中物理公式(表达式、字母含义、使用条件、范围)总结
(3) 上升、下落经过同一位置时的加速度相同,而速度等值反向
(4) 上升、下落经过同一段位移的时间相等。
(5)从抛出到落回原位置的时间:t =
2Vo g
(6)适用全过程的公式:
定义式:
E
F q
单位: N / C
点电荷电场场强
:
E
k
Q r
匀强电场场强
:E
U d
3、电势,电势能
: A
E电 q
, E电
q A
第 6 页 共 14 页
高中物理公式(表达式、字母含义、使用条件、范围)总结
顺着电场线方向,电势越来越低。
4、电势差 U,又称电压
:U
W q
2023人教版带答案高中物理必修三第十一章电路及其应用微公式版易错题集锦

2023人教版带答案高中物理必修三第十一章电路及其应用微公式版易错题集锦单选题1、如图所示为测量未知电阻Rx阻值的部分电路,当开关S接a点时,电压表示数为9 V,电流表示数为0.30 A;当开关S接b点时,电压表示数为10 V,电流表示数为0.25 A,则()A.电压表示数相对变化显著B.开关S接在b点时,Rx的测量值更准确C.开关S接在b点时,Rx的测量值小于Rx的真实值D.开关S接在a点时,Rx的测量值大于Rx的真实值答案:BA.由题意可得ΔU U1<ΔI I1电流表示数相对变化显著,A错误;B.由于电流表示数相对变化显著,说明电压表分流作用较大,要选择电流表测量准确的电路,即开关S应接在b点,B正确;CD.开关S接在b点时,Rx的测量值偏大,而S接在a点时,Rx的测量值偏小,CD错误;故选B。
2、电导率σ就是电阻率ρ的倒数,即σ=1ρ。
下列说法中正确的是()A.材料的电导率越小,其导电性能越强B.材料的电导率与材料的形状有关C.电导率的单位是1Ω·mD.电导率大小与温度无关答案:CA.材料的电导率越小,电阻率越大,则其导电性能越弱,选项A错误;B.材料的电导率与材料的形状无关,选项B错误;C.根据R=ρl S则σ=1ρ=LRS则电导率的单位是mΩ⋅m2=1Ω⋅m,选项C正确;D.电阻率大小与温度有关,则电导率大小与温度有关,选项D错误。
故选C。
3、如图所示为两导体a、b的伏安特性曲线,则由图可知a、b的电阻关系为()A.R a>R b B.R a<R b C.R a=R b D.无法判断答案:BI−U图线中斜率表示电阻的倒数,则斜率越大,电阻越小,由于可知,a的斜率大,则a的电阻小,即R a<R b故选B。
4、如图所示,一线圈在匀强磁场中匀速转动,经过图示位置时()A.穿过线圈的磁通量最大,磁通量的变化率最大B.穿过线圈的磁通量最大,磁通量的变化率最小C.穿过线圈的磁通量最小,磁通量的变化率最大D.穿过线圈的磁通量最小,磁通量的变化率最小答案:C题图所示位置线圈平面与磁感线平行,处于垂直于中性面的位置,故穿过线圈的磁通量为零(即最小),而磁通量的变化率即瞬时电动势最大,故选C。
前言上册学过之三个定义公式(精)

前言:上冊學過之三個定義公式1.電流定義:平均每秒流過多少庫侖的電量公式:I(電流)=Q(電量)/時間(t)單位:安培(A)=庫侖(C)/秒(S)2.電位定義:平均每庫侖電量帶有多少焦耳的電能而每庫侖電量經過電阻時損失多少電能叫電位差(電位下降)or 每庫侖電量經過電池時得到多少電能叫電位差)電位上升)公式:V(電壓)=E(電能)/電量(Q)單位:伏特(V)=焦耳(J)/庫侖(C)3.電阻定義:01.電子在導線中移動時,會與導體內部的原子發生碰撞,遭受一些阻礙02.在電器兩端的電壓與流過電器的電流的比值公式:R(電阻)=V(電壓)/I(電流)單位:歐姆(Ω)=伏特(V)/安培(A)電能:在電路中消耗或得到的總電能1.電能差E=電量QX電位差V2.完全公式: E = QV = IVt =I2Rt =V2t/R = Pt< V = IR;Q= It;P為功率>例1. 乾電池提供1.5伏特的電壓,跨接3歐姆的電阻(如右圖所Array示),則:(1)電路電流為多少安培?(2)電池每秒提供的電能是多少?(3)3Ω的電阻上,1分鐘產生熱能多少?例2.有一燈泡接於100伏特的電源,若通過燈絲的電流為1安培,問燈泡每分鐘消耗的電能焦耳例3. 電阻為 2 歐姆和 3 歐姆的二電阻器,將其串聯後和 6V 的電池連結,則在 10 秒內 2 歐姆的電阻器放出焦耳的能量,3 歐姆的電阻器放出焦耳的能量.例4. 承上題,若將此二電阻器並聯,則在 10 秒內 2 歐姆的電阻器放出焦耳的能量,3 歐姆的電阻器放出焦耳的能量例5.將一 100V的電池接在電阻為 2 歐姆的電阻器上,今將此電阻器放入 500克,200C的水中,則在10秒後,可使水溫變為0C(沒有能量散失)例6. 電路圖如右圖所示,求: (1) 總電阻?總電流?(2) 電池在1分鐘內各供應多少電能? (3) 各電阻在1分鐘內各消耗多少電能?電功率:平均一秒消耗或產生多少焦耳的電能1. 計算:電功率 =電器所釋出的電能時間=E/t =V ×Q t =V ×Qt=V ×I =電壓×電流 (因I=Q/t )=I 2R =電流平方×電阻 (因V=IR )=V 2R =電壓平方÷電阻 (因I=V/R )2. 單位: 電功率單位=電壓單位×電流單位=伏特×安培=焦耳庫倫×庫倫秒=焦耳/秒=J/sec =w=瓦特 例6. 電路如圖所示,問: (1) 安培計所測到的電流為多少?(2) 伏特計所測到的電壓為多少? (3) 電阻器R 1 ,R 2 所消耗的電功率各為多少?例7. 電路如圖所示,問:(1)電阻器R 1、R 2 所消耗的電功率各為多少? (2)電池提供的功率? (3) R 1、R 2 及R 3 的電壓比為多少?※討論1:串聯電路 甲、乙兩電阻器的電阻值分別為R 甲,R 乙.串聯,形成如右電路圖,則: (a)甲、乙消耗的電功率比為P 甲:P 乙=R 甲:R 乙 即電功率(P)與電阻器的電阻(R)成正比.(b)電池提供的電功率P 等於各電阻器消耗的電功率之和. P 電池=P 甲 + P 乙 說明: 甲電器所消耗的功率 P 甲 =I 2 × R 甲 (I 為流經甲的電流)乙電器所消耗的功率 P 乙 =I 2 × R 乙 (I 為流經乙的電流) 因甲、乙串聯,所以流經甲,乙的電流大小相等.I 3.0V 12I3.0V21R 甲R 乙故P 甲 :P 乙 =R 甲 ×I 2 : R 乙 ×I 2 =R 甲 : R 乙電池提供的電功率P =P 甲 + P 乙 =R 甲 ×I 2 + R 乙 ×I 2=( R 甲 + R 乙 )×I 2 =R ×I ×I =V ×I※討論2:並聯電路甲、乙兩電阻器的電阻值分別為R 甲,R 乙. 並聯,形成如右電路圖,則甲、乙消耗的電功率比 P 甲:P 乙=R 乙:R 甲,電池提供的電功率P =P 甲+P 乙 說明: 甲電器所消耗的功率 P 甲=V 2R 甲(V 為甲兩端的電壓)乙電器所消耗的功率 P 乙 =V 2R 乙(V 為乙兩端的電壓)因甲、乙並聯,所以甲、乙兩端的電壓大小相等.故P 甲 :P 乙 =V 2R 甲:V 2R 乙=R 乙 : R 甲電池提供的電功率P =P 甲 + P 乙 =V 2R 甲+V 2R 乙=V 2×(1R 甲+1R 乙)=V 2×1R =V ×V R=V ×I 例8.下圖甲的電路中,(1) 在 R 1中,流過的電流為 A ,二端的電壓為 V ,放出的能量為 J (2) 在 R 2中,流過的電流為 A ,二端的電壓為 V ,放出的能量為 J (3) R 1 與 R 2 放出的能量比為 ,可見電阻串聯時,能量和電阻成 比例9.下圖乙的電路中,(1) 在 R 1中,流過的電流為 A ,二端的電壓為 V ,放出的能量為 J (2) 在 R 2中,流過的電流為 A ,二端的電壓為 V ,放出的能量為 J (3) R 1 與 R 2 放出的能量比為 ,可見電阻串聯時,能量和電阻成 比電器的工作電壓與消耗功率的標示及電器電阻:電器上若標有110V AC 50~60Hz 60W 表示:(1)此電器須接110伏特的交流電,此時電器每秒消耗60joul 電能,將其轉換成熱能或光能等. (2)電器的電阻值R =V 2P例8. 有一燈泡標示110V ,AC 60W 若依右圖接上電路.問:(1)燈泡使用1hr ,產生多少熱能?(2)燈泡的電阻為多少?(3)若改接55V 的電壓時,功率為多少?例9. 有甲、乙、丙三個完全相同燈泡標示110V ,AC 20W. 其電路圖如右.問:(1)燈泡電阻值為多少? (2)甲燈泡的功率為多少?(3)乙燈泡的功率為多少? 例10. 電鍋上標示的功率是 800 瓦特,若煮飯時間使用 10 分鐘,表示消耗的能量為 焦耳. 例11. 電鍋上標示的 V 為 110,W 為 880,則(1) 將此電鍋接在 110V 的電源上,每秒產生的能量為 焦耳,此電鍋的電阻為 歐姆,在電路上的電流為 安培(2) 將此電鍋接在 220V 的電源上,每秒產生的能量為 焦耳,在電路上的電流為 安培(假設在此電壓電鍋仍能運作)(3) 將此電鍋接在 55V 的電源上,每秒產生的能量為 焦耳,在電路上的電流為 安培例12. 一電熱器二端之電壓為 100V ,電流為 5A ,則此電熱器的功率為 W ,電阻為 歐姆,5 分鐘內 消耗的能量為 焦耳 例13. 燈泡上註明 200W ,100V ,則(1) 燈泡電阻為歐姆 (2) 流經燈泡的電流為(3) 使用於 80V 的電壓時,電流為 A ,功率為 W 例14.有 AB 二電熱器,A 電熱器標示 100V 和 250W ,B 電熱器標示 100V 和 1000W ,則(1) 將 A B 串聯後接在 100V 之電源,A 的功率為 W ,B 的功率為 W(2) 將 A ,B 並聯後接在 100V 之電源,A 的功率為 W ,B 的功率為 W:交流電源110V AC綜合練習一. 選擇題:( )1. 雅雍裝了一組電路,如圖。
小学三年级数学公式定义整理

一、加法公式:1.相加法则:a+b=b+a(两个数相加顺序可以交换)2.零和法则:a+0=a(任何数与0相加都等于它本身)3.进位法则:当相加的两个数的个位数之和大于等于10时,需要进位。
二、减法公式:1.相减法则:a-b=c,c+b=a(两个数相减得出差,差与被减数之和等于减数)2.零差法则:a-a=0(任何数减去自身都等于0)3.借位法则:当被减数的个位小于减数的个位时,需要向十位借位。
三、乘法公式:1.乘法交换法则:a×b=b×a(两个数相乘的结果与顺序无关)2.结合律:(a×b)×c=a×(b×c)(多个数相乘,括号内的数先相乘,再与括号外的数相乘结果相等)3.乘零法则:a×0=0(任何数与0相乘都等于0)4.乘法法则:各位数分别相乘,十位数与个位数之和再加入进位。
四、除法公式:1.除法交换法则:a÷b≠b÷a(两个数相除的结果与顺序有关)2.除法法则:数a除以数b,商×b+余数=被除数3.除以零没有意义,即a÷0不成立。
五、其他公式:1.两数之积等于其公倍数除以最大公约数:a×b=最大公约数×最小公倍数2. 一元二次方程求根公式:x = (-b±a²-4aa) / (2a) (解一元二次方程ax² + bx + c = 0 的根)以上是小学三年级数学公式的整理。
这些公式能够帮助我们更好地理解和运用数学知识,解决各种数学问题。
在学习过程中,我们可以通过练习和实际应用来巩固和运用这些公式。
数学公式是数学知识的基础,学好了数学公式,才能在数学的道路上越走越远。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公式定义器扩展
目录
公式定义器扩展 (1)
目录 (1)
用于何处? (1)
公式定义器的构成 (1)
公式定义器的类型 (3)
常见的问题 (4)
表单控件初始化值 (5)
步骤一:点击公式定义的按钮 (5)
步骤二:编写逻辑代码 (5)
分支条件表达式 (6)
步骤一:画出流程图 (7)
步骤二:编写条件表达式 (8)
节点处理人 (9)
步骤一:配置节点处理人 (9)
步骤二:调用组织架构的方法 (10)
步骤三:通过逻辑代码来返回 (11)
用于何处?
公式定义器主要用于自定义表单控件的初始值,审批节点的审批人,自动分支的条件表达式等地方。
公式定义器的构成
公式的特点:
1、具有运行上下文。
简单地说,就是变量,参与计算的数据。
如:“$报销金额$”。
2、通过一些逻辑运算符,进行一系列的运算。
对于相对复杂的运算,引入了函数的概
念,方便了公式的编写,如:“$时间.获取时间差$($结束时间$, $开始时间$)”。
3、最终会返回一个结果。
结合下图的公式定义器界面,可以更好地帮助您了解公式定义器。
变量:变量是参与公式计算的数据。
在审批流程模块中,变量可以来自系统预定义的字段,如:标题、创建时间、创建人等;还可以来自自定义表单的字段,如:报销金额、开始时间、结束时间等。
在公式定义器中引用的格式为:“$变量名$”,如:“$报销金额$”。
变量可以在公式定义的左边树变量列表中直接选择引用。
逻辑运算符:
温馨提醒:公式定义器中的逻辑运算符完全符合Java的语法,若您对Java语法了如指掌,
函数:函数是系统预定义好的一些逻辑算法,每个函数包含若干个输入参数(某些函数可能没有输入参数)和一个返回值。
函数的格式:$函数名$(参数1,参数2,……)。
函数可以通过左边树的函数列表进行选择,鼠标放在左边树的函数的时候,会显示该函数的帮助信息。
公式定义器的类型
公式定义器里面的所有变量都有数据类型,函数中的输入输出也有数据类型,公式定义的返回结果也有数据类型。
如何确认一个变量的数据类型?
比如在审批流程模块中,变量可能来自系统预定义的字段,也可能来自表单自定义的字段。
系统预定义的字段来自系统的数据字典(这点开发人员应该非常清楚),在此我就不多加描述。
自定义表单的字段类型如何确定呢?
如何确认函数的参数类型和返回值类型?
当鼠标放在左边树的每个函数节点时,都会提示该函数的简单介绍,信息包括:您该输入什么样的参数,将输出什么样的值。
如何确认公式返回结果类型?
要确认公式返回结果类型,需要从使用公式的场景来理解。
下面举几个场景:
1、流程定义中的条件分支:显然这里应该返回true/false。
2、流程定义中,采用公式定义器来定义处理人:返回值类型为组织架构对象
(或组织架构对象列表)。
3、表单自定义中某个字段的初始值:可以根据该字段的类型确定公式应该返
回什么类型的数据。
返回结果类型的自动转换
另外,公式定义器还能将列表自动转换成单值,或将单值自动转换成列表。
常见的问题
校验失败?
由于公式定义器的语法过于灵活,所以公式定义器的校验方法中,只能简单模拟数据进行校验,所以无法完全校验公式是否可以正常运行。
所以,当您写一些比较复杂的公式的时候,公式定义器可能会提示:“表达式校验未通过!原因可能是由于表达式编写错误,或者校验器无法模拟真实数据导致。
是否仍使用该公式?”当出现该提示的时候,若您确认公式的书写是正确的,可以忽略该提示信息。
常见误区:字符串相等
在编写公式的时候,经常会用到字符串的比较,比如我们需要判断一个城市的字段值是否为深圳,那我们很自然地会将公式写成:
公式解释器中,将字符串看成了是一个对象,这个对象的相等只能采用equals符号。
空指针错误?
字符串、日期、组织架构等都是对象类型,我们可以通过“对象1.equals(对象2)”的方式来比较两个对象是否相等,也可以访问对象的属性/方法,但若这个对象可能没有被赋值,那当访问的时候就会出空指针的错误,所以在使用公式的时候,请尽量保证使用的变量是必填项,避免空指针错误。
解决空指针的方法见“在公式定义器中使用脚本语言”小节。
表单控件初始化值
我们把自定义表单里面的薪资的控件值初始化为一个不大于10000的随机整数。
步骤一:点击公式定义的按钮
步骤二:编写逻辑代码
分支条件表达式
我们根据薪资的数额来决定是否需要老总审批,比如薪资大于8000的要老总来审批,小于
等于8000的就不需要。
步骤一:画出流程图
步骤二:编写条件表达式
节点处理人
公式定义器里面已经内置了一些函数,我们可以在流程,自定义表单中使用它。
比如我们把经理审批节点设置为提交人的直线领导。
步骤一:配置节点处理人
步骤二:调用组织架构的方法
.
步骤三:通过逻辑代码来返回
公式定义器里面允许我们编写逻辑代码。
比如如果创建人没有直线领导,那么我们则固定返回一个人作为审批人。
Word 资料。
