高中数学人教A版必修五课件第二章数列复习
合集下载
新版高中数学人教A版必修5课件：第二章数列 2.3.1
≥
2
题型一 题型二 题型三 题型四
目标导航
Z 知识梳理 HISHISHULI
Z 重难聚焦 HONGNANJUJIAO
D 典例透析 IANLITOUXI
(2)设数列{an}的前n项和为Sn, 点
������,
������������ ������
(均������∈在N函*)数y=3x-2的图象
上,求数列{an}的通项公式.
(2)求此数列的前n项和Sn的最大值.
分析(1)求不等式组
������������ ������������
≥
+1
0, <
0
的正整数解即可;
(2)既可以从项的正负考虑,也可以利用等差数列的前n项和公式
是关于n的二次函数,考虑对应二次函数的最值.
目标导航
Z 知识梳理 HISHISHULI
Z 重难聚焦 HONGNANJUJIAO
又由an=a1+(n-1)d,即-512=1+(4-1)d, 解得d=-171.
反思a1,d,n称为等差数列的三个基本量,an和Sn都可以用这三个基 本量来表示,五个量a1,d,n,an,Sn中可知三求二,即等差数列的通项公 式及前n项和公式中“知三求二”的问题,一般是通过通项公式和前n
项和公式联立方程(组)来求解.这种方法是解决数列运算的基本方
D 典例透析 IANLITOUXI
题型一 题型二 题型三 题型四
解(1)由a1=50,d=-0.6,
知an=50-0.6(n-1)=-0.6n+50.6.
令
������������ ������������
≥
+1
0, <
高二数学人教A版必修5课件：第二章 数列 本章整合
数阵中的数是按一定的规律排成若干行和列,比较多见的是排成等差 数列或等比数列,它重点考查等差数列、等比数列的相关知识,有时也会出 现其他类型的数列.解决此类问题的关键是找出其中的规律,这就要求考生 具有较强的观察分析、归纳猜想的能力以及对数列知识融合迁移的能力. 下面具体讨论一下它的几种题型.
知识网络
答案:n2+n-1
知识网络
专题探究
专题一
专题二
专题三
【应用 7】 德国数学家莱布尼兹发现了如图所示的单位分数三角形
(单位分数是分子为 1、分母为正整数的分数)称为莱布尼兹三角形.
根据前 5 行的规律,写出第 6 行的数从左到右依次是
.
答案:16
,
1 30
,
1 60
,
1 60
,
1 30
,
1 6
知识网络
∴(n+1)an+1-nan=0,即������������������+������ 1 = ������+������ 1,∴n≥2 时,���������������������-���1 = ���������-���1, ∴an=���������������������-���1 ·������������������������--12·…·������������21·a1=���������-���1 ·������������--21·…·12·1=1������.
(3)所求数列的通项可转化为数列 1,0,-1,0,1,…的通项,这恰好是“五点 法”作三角函数的图象的值,从而有 an=3sin���2���π或 an=3cos������2-1π(n∈N*).
专题一
专题二
专题三
知识网络
答案:n2+n-1
知识网络
专题探究
专题一
专题二
专题三
【应用 7】 德国数学家莱布尼兹发现了如图所示的单位分数三角形
(单位分数是分子为 1、分母为正整数的分数)称为莱布尼兹三角形.
根据前 5 行的规律,写出第 6 行的数从左到右依次是
.
答案:16
,
1 30
,
1 60
,
1 60
,
1 30
,
1 6
知识网络
∴(n+1)an+1-nan=0,即������������������+������ 1 = ������+������ 1,∴n≥2 时,���������������������-���1 = ���������-���1, ∴an=���������������������-���1 ·������������������������--12·…·������������21·a1=���������-���1 ·������������--21·…·12·1=1������.
(3)所求数列的通项可转化为数列 1,0,-1,0,1,…的通项,这恰好是“五点 法”作三角函数的图象的值,从而有 an=3sin���2���π或 an=3cos������2-1π(n∈N*).
专题一
专题二
专题三
人教版高中数学必修5：第二章 数列 章末总结PPT优质课件
24 及数列{bn}的前 n 项和 Tn.
数学
(1)证明:因为 lg a1、lg a2、lg a4 成等差数列,
所以 2lg a2=lg a1+lg a4.即 a22 =a1a4.设等差数列{an}的公差为 d, 则(a1+d)2=a1(a1+3d),整理得 d2=a1d. 因为 d≠0,所以 a1=d.所以 a2n =a1+(2n-1)d=2n·d.
3 1 3n1
即 an-a1=
- nn 1 .又因为 a1=1,所以 an= 1 ×3n- nn 1 - 1 .
13
2
2
22
显然 a1=1 也适合上式,所以{an}的通项公式为 an= 1 ×3n- nn 1 - 1 .
2
22
数学
(2)因为 an1 =2n, an
所以 a2 =2, a3 =22, a4 =23,…, an =2n-1,
数学
(2)
an2 (
1 2
)n=(2n -1)
1 2n
.
Sn=1·
1 2
+3×
1 22
+5 ×
1 23
+…+(2n-1)·
1 2n
,①
1 2
Sn=1·
1 22
+3·
1 23
+5 ·
1 24
+…+(2n-1)·
1 2n 1
,②
①-②,得
1 2
Sn=
1 2
+2(
1 22
+
1 23
+
1 2n
)- (2n-1)·
数学
四、数列中的最值
数学
(1)证明:因为 lg a1、lg a2、lg a4 成等差数列,
所以 2lg a2=lg a1+lg a4.即 a22 =a1a4.设等差数列{an}的公差为 d, 则(a1+d)2=a1(a1+3d),整理得 d2=a1d. 因为 d≠0,所以 a1=d.所以 a2n =a1+(2n-1)d=2n·d.
3 1 3n1
即 an-a1=
- nn 1 .又因为 a1=1,所以 an= 1 ×3n- nn 1 - 1 .
13
2
2
22
显然 a1=1 也适合上式,所以{an}的通项公式为 an= 1 ×3n- nn 1 - 1 .
2
22
数学
(2)因为 an1 =2n, an
所以 a2 =2, a3 =22, a4 =23,…, an =2n-1,
数学
(2)
an2 (
1 2
)n=(2n -1)
1 2n
.
Sn=1·
1 2
+3×
1 22
+5 ×
1 23
+…+(2n-1)·
1 2n
,①
1 2
Sn=1·
1 22
+3·
1 23
+5 ·
1 24
+…+(2n-1)·
1 2n 1
,②
①-②,得
1 2
Sn=
1 2
+2(
1 22
+
1 23
+
1 2n
)- (2n-1)·
数学
四、数列中的最值
高中数学第二章数列2.2等差数列第1课时等差数列的概念与通项公式课件新人教A版必修5
3．在等差数列{an}中，若 a1·a3＝8，a2＝3，则公差 d＝( )
A．1 B．－1 C．±1 D．±2 a1（a1＋2d）＝8，
解析：由已知得 a1＋d＝3，
解得 d＝±1. 答案：C
第九页，共32页。
4. lg( 3 ＋ 2 ) 与 lg( 3 － 2 ) 的 等 差 中 项 是 ______________．
第十六页，共32页。
[变式训练] (1)已知数列 3，9，15，…，3(2n－1)，…， 那么 81 是它的第________项( )
A．12 B．13 C．14 D．15 (2)已知等差数列{an}中，a15＝33，a61＝217，试判断 153 是不是这个数列的项，如果是，是第几项？ 解析：(1)an＝3(2n－1)＝6n－3，由 6n－3＝81，得 n ＝14.
第十七页，共32页。
(2)设首项为 a1，公差为 d，则 an＝a1＋(n－1)d， a1＋（15－1）d＝33，
由已知 a1＋（61－1）d＝217，
a1＝－23， 解得
d＝4. 所以 an＝－23＋(n－1)×4＝4n－27，
第十八页，共32页。
令 an＝153，即 4n－27＝153，解得 n＝45∈N*， 所以 153 是所给数列的第 45 项． 答案：(1)C (2)45
答案：(1)× (2)√ (3)√ (4)√
第七页，共32页。
2．已知等差数列{an}中，首项 a1＝4，公差 d＝－2，
则通项公式 an 等于( )
A．4－2n
B．2n－4
C．6－2n
D．2n－6
解析：因为 a1＝4，d＝－2，所以 an＝4＋(n－1)×(－
2)＝6－2n.
高中数学 第二章 数列 2.4 等比数列(二)课件 新人教A版必修5
根据等比数列的性质 a5a6＝a1a10＝a2a9＝a3a8＝a4a7＝9， ∴a1a2…a9a10＝(a5a6)5＝95， ∴log3a1＋log3a2＋…＋log10.
名师点评
抓住各项序号的数字特征，灵活运用等比数列的性质，可以顺利地 解决问题．
1234
4.an＝2n＋3n，判断数列{an}是不是等比数列？ 不是等比数列. ∵a1＝21＋31＝5，a2＝22＋32＝13，a3＝23＋33＝35， ∴a1a3≠a22， ∴数列{an}不是等比数列.
1234
课堂小结
1.解题时，应该首先考虑通式通法，而不是花费大量时间找简便方法. 2.所谓通式通法，指应用通项公式，前n项和公式，等差中项，等比中 项等列出方程(组)，求出根本量. 3.巧用等比数列的性质，减少计算量，这一点在解题中也非常重要.
探究点2 等比数列的性质
命题角度1 序号的数字特征 例2 {an}为等比数列． (1)假设an>0，a2a4＋2a3a5＋a4a6＝25，求a3＋a5；
a2a4＋2a3a5＋a4a6＝a23＋2a3a5＋a25 ＝(a3＋a5)2＝25， ∵an>0， ∴a3＋a5>0， ∴a3＋a5＝5.
(2)假设an>0，a5a6＝9，求log3a1＋log3a2＋…＋log3a10的值．
方法二 设这四个数依次为2qa－a，aq，a，aq(q≠0)，
2qa－a＋aq＝16， 由条件得aq＋a＝12，
解得aq＝＝82，
a＝3， 或q＝13.
当a＝8，q＝2时，所求的四个数为0，4，8，16；
当 a＝3，q＝13时，所求的四个数为 15，9，3，1. 故所求的四个数为0，4，8，16或15，9，3，1.
2．等比数列项的运算性质 在等比数列{an}中，若 m＋n＝p＋q(m，n，p，q∈N*)，则 am·an＝ ap·aq . ①特别地，当 m＋n＝2k(m，n，k∈N*)时，am·an＝ a2k . ②对有穷等比数列，与首末两项“等距离”的两项之积等于首末两项的 积 ，
名师点评
抓住各项序号的数字特征，灵活运用等比数列的性质，可以顺利地 解决问题．
1234
4.an＝2n＋3n，判断数列{an}是不是等比数列？ 不是等比数列. ∵a1＝21＋31＝5，a2＝22＋32＝13，a3＝23＋33＝35， ∴a1a3≠a22， ∴数列{an}不是等比数列.
1234
课堂小结
1.解题时，应该首先考虑通式通法，而不是花费大量时间找简便方法. 2.所谓通式通法，指应用通项公式，前n项和公式，等差中项，等比中 项等列出方程(组)，求出根本量. 3.巧用等比数列的性质，减少计算量，这一点在解题中也非常重要.
探究点2 等比数列的性质
命题角度1 序号的数字特征 例2 {an}为等比数列． (1)假设an>0，a2a4＋2a3a5＋a4a6＝25，求a3＋a5；
a2a4＋2a3a5＋a4a6＝a23＋2a3a5＋a25 ＝(a3＋a5)2＝25， ∵an>0， ∴a3＋a5>0， ∴a3＋a5＝5.
(2)假设an>0，a5a6＝9，求log3a1＋log3a2＋…＋log3a10的值．
方法二 设这四个数依次为2qa－a，aq，a，aq(q≠0)，
2qa－a＋aq＝16， 由条件得aq＋a＝12，
解得aq＝＝82，
a＝3， 或q＝13.
当a＝8，q＝2时，所求的四个数为0，4，8，16；
当 a＝3，q＝13时，所求的四个数为 15，9，3，1. 故所求的四个数为0，4，8，16或15，9，3，1.
2．等比数列项的运算性质 在等比数列{an}中，若 m＋n＝p＋q(m，n，p，q∈N*)，则 am·an＝ ap·aq . ①特别地，当 m＋n＝2k(m，n，k∈N*)时，am·an＝ a2k . ②对有穷等比数列，与首末两项“等距离”的两项之积等于首末两项的 积 ，
高中新课程数学(新课标人教A版)必修五《第二章 数列》归纳整合
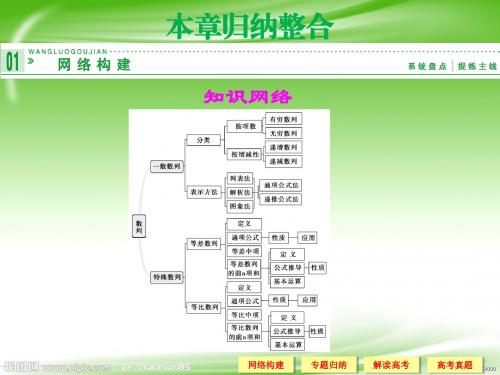
网络构建
专题归纳
解读高考
高考真题
3 且 Sn＝ (an－1)(n∈N*)， 【例4】设 Sn 为数列{an}的前 n 项的和， 2 求数列{an}的通项公式． 3 解：∵Sn＝ (an－1)， 2
3 ∴当 n＝1 时，S1＝a1＝ (a1－1)，解得 a1＝3. 2 3 3 当 n≥2 时，an＝Sn－Sn－1＝ (an－1)－ (an－1－1)，得 2 2 an ＝3， an－1 ∴数列{an}是以 3 为公比的等比数列，且首项 a1＝3. 故数列的通项公式为 an＝3n(n∈N*)．
网络构建 专题归纳 解读高考 高考真题
1 1 1 1 【例5】 求数列 2 ，4 ，6 ，…，2n＋ n＋1的前 n 项和 Sn. 4 8 16 2 1 1 1 1 解 Sn＝2 ＋4 ＋6 ＋…＋2n＋ n＋1 2 4 8 16
1 1 1 1 ＝(2＋4＋6＋…＋2n)＋22＋23＋24＋…＋ n＋1 2
1 1n 21－ n2n＋2 2 2 ＝ ＋ 2 1 1－ 2 1 1 ＝n(n＋1)＋ － n＋1. 2 2
网络构建 专题归纳 解读高考 高考真题
1 2 n 【例6】在数列{an}中，an＝n＋1＋n＋1＋…＋n＋1，又 2 bn＝ ，求数列{bn}的前 n 项的和． a n· an＋1 1 n 解 an＝ (1＋2＋…＋n)＝ ， 2 n＋1
形式均可用累乘法．
(5)构造法(利用数列的递推公式研究数列的通项公式) 若由已知条件直接求an较难，可以通过整理变形等， 从中构造出一个等差数列或等比数列，从而求出通项公 式．
网络构建
专题归纳
解读高考
高考真题
【例1】 已知数列{an}满足an＋1＝an＋3n＋2且a1＝2，求an. 解 ∵a2－a1＝3×1＋2， a3－a2＝3×2＋2， a4－a3＝3×3＋2， … an－an－1＝3×(n－1)＋2， 以上各项相加，得 an－a1＝3[1＋2＋3＋…＋(n－1)]＋2(n－1)
高中数学人教A版必修五教学课件：第二章 《数列》 2.4 第2课时 等比数列的性质
－6 解析：a4a7＝a1· a10＝ ＝－2. 3
答案：B
3． 等比数列{an}中， 若 a9＝－2， 则此数列前 17 项之积为____________．
解析：由题意得 a1a2a3…a15a16a17 ＝(a1a17)· (a2a16)· (a3a15)· …· a9
17 17 ＝a17 9 ＝(－2) ＝－2 .
2 ∴a6 ＝a2· a10，
1 ∴a10＝162 × ＝13 122. 2
2
法三：由公式 ap· aq＝ap＋k· aq－k 得
2 a2· a10＝a2＋4· a10－4＝a6 .
1 ∴a10＝1622× ＝13 122. 2
答案：13 122
探究二
an＋1＝can＋d(c≠1，cd≠0)的递推关系
利用等比数列的性质解题 (1)基本思路：充分发挥项的 “下标”的指导作用，分析等比数列项 与项之间的关系，选择恰当的性质解题． (2)优缺点：简便快捷，但是适用面窄，有一定的思维含量．
1．在等比数列中，若 a2＝2，a6＝162，则 a10＝________.
解析：法一：∵a6＝a2q4，其中 a2＝2，a6＝162， ∴q4＝81， ∴a10＝a6q4＝162×81＝13 122. 法二：∵2,6,10 三数成等差数列， ∴a2，a6，a10 成等比数列．
－
1n－1 4n－1 n－1 第 n 个图形的周长 3 ×(3×4 )＝3×3 .
[感悟提高]
(1)解决此类问题，需要抓住变中的不变量，即数据在改
变，但其变化规律不改变，事实上，给出的图形只是问题的载体，我 们只需从“形”中抽象出“数”，即可将问题归结为等比数列．
a1＝1， 1 ∴ 或 1 q ＝ . q＝2，
高中数学人教A版必修五课件第二章数列复习
2.数列
{a n }
的前
练习
n
项和记作
Sn
,满足
3.已知实数列{an}是等比数列,其中 .已知实数列 是等比数列, 是等比数列
,
S n = 2a n + 3n 12
a7=1,且a4,a5+1,a6成等差数列. , , 成等差数列. 的通项公式; (1)求数列 n}的通项公式; 求数列{a 的通项公式 求数列 (2)数列 n}的前 项和记为 n, 数列{a 的前 项和记为S 的前n项和记为 数列 证明: 证明:Sn<128(n=1,2,3,…). =
- (2)an=amqn-m(m,n∈N*). , ∈
二,等比数列 6. 等比数列的前 项和公式 等比数列的前n项和公式
na1 n Sn = a1(1 q ) 1 q
(q = 1) (q ≠ 1)
二,等比数列
已知
x>0
,
y>0
,
7. 等比数列前 项和的一般形式 等比数列前n项和的一般形式
x,a,b,的前 n 项和公式及 等差, 其推导的方法. 其推导的方法.
知识归纳
一,等差数列 1.等差数列这单元学习了哪些内容? 等差数列这单元学习了哪些内容? 等差数列这单元学习了哪些内容 定 等差数列 通 义 项
前n项和 项和 主要性质
一,等差数列 2. 等差数列的定义,用途及使用时需 等差数列的定义, 注意的问题: 注意的问题 n≥2,an -an-1=d (常数 常数) , 常数 - 3. 等差数列的通项公式如何?结构有 等差数列的通项公式如何? 什么特点? 什么特点? an=a1+(n-1) d - = ∈ an=An+B (d=A∈R) +
新版高中数学人教A版必修5课件：第二章数列 2本章整合
专题三
专题四
(3)解∵an+1= ���������2��� + 2������������, ∴ ������������ + 1 = ������������(������������ + 2).
1 11 1
∴ ������������+1 = 2 ������������ - ������������ + 2 ,
=2
1 ������1
-
1 ������2
+
1 ������2
-
1 ������3
+
…
+
1 ������������
-
1 ������������+1
=2
1 ������1
-
1 ������������+1
.
∵an= 32������-1 − 1, ������1 = 2, ������������ + 1 = 32������ − 1,
∴Sn=1−
2 32������
.
-1
又
Tn=
32������ -1,
∴
������������
2
∴-Sn=1×2+2×22+3×23+…+n×2n.①
∴-2Sn=1×22+2×23+3×24+…+(n-1)×2n+n×2n+1.②
①-②,得 Sn=2+22+23+…+2n-n×2n+1
2(1-2������) = 1-2 − ������ × 2������ + 1 = 2������ + 1 − ������ × 2������ + 1 − 2.
【人教A版】高中数学必修五：第2章《数列》章末总结ppt课件
a3-a2=32-2, a2-a1=3-1. 当n≥2时,以上(n-1)个等式两端分别相加,得
(an-an-1)+(an-1-an-2)+…+(a2-a1)=3n-1+3n-2+…+3-[(n-1)+(n-2)+…+1],
即 an-a1= 3(1 3n1) - n(n 1) .
13
2
又∵a1=1, ∴an= 1 ×3n- n(n 1) - 1 .
根据 an+1= 1 an+1 可得 1 A=1,A=2, ∴an+1-2= 1 (an-2).
2
2
2
令 bn=an-2, 则 b1=a1-2=-1,bn+1= 1 bn, 2
∴数列{bn}是以-1 为首项, 1 为公比的等比数列. 2
∴bn=b1·qn-1=(-1)·
1 2
n
1
=-
1 2
n
该
题型三 数列的求和
【例 4】 (2014 南阳高二期末)已知等差数列{an}中,a2=3,a3=5. (1)求{an}的通项公式;
(2)求数列
1
的前
n
项和
Tn.
anan1
解: (1)an=1+2(n-1)=2n-1.
(2)
1 an an 1
=
1
=1
(2n 1)(2n 1) 2
1 2n
数列
Sn n
是等比数列.
名师导引:分别利用等差、等比数列的定义证明.
该
证明:(1)∵an=2- 1 (n≥2,n∈N*), an 1
bn= 1 , an 1
∴当 n≥2
人教A版高中数学必修五第二章《数列》复习教案-9页word资料
人教A 版高中数学必修五第二章《数列》复习教案1、数列的概念：数列是一个定义域为正整数集N*（或它的有限子集｛1,2，3，…，n ｝）的特殊函数，数列的通项公式也就是相应函数的解析式。
（1）数列}{n a 的通项为1+=bn ana n ，其中b a ,均为正数，则n a 与1+n a 的大小关系为___； （2）已知数列{}n a 中，2n a n n λ=+，且{}n a 是递增数列，求实数λ的取值范围；（3）一给定函数)(x f y =的图象在下列图中，并且对任意)1,0(1∈a ，由关系式)(1n n a f a =+得到的数列}{n a 满足)(*1N n a a n n ∈>+，则该函数的图象是（ ）A B C D2.等差数列的有关概念：（1）等差数列的判断方法：定义法1(n n a a d d +-=为常数）或11(2)n n n n a a a a n +--=-≥。
如设{}n a 是等差数列，求证：以b n =na a a n+++ 21 *n N ∈为通项公式的数列{}n b 为等差数列。
（2）等差数列的通项：1(1)n a a n d =+-或()n m a a n m d =+-。
如(1)等差数列{}n a 中，1030a =，2050a =，则通项n a = ；（2）首项为-24的等差数列，从第10项起开始为正数，则公差的取值范围是______ ；（3）等差数列的前n 和：1()2n n n a a S +=，1(1)2n n n S na d -=+。
如（1）数列 {}n a 中，*11(2,)2n n a a n n N -=+≥∈，32n a =，前n 项和152n S =-，则1a ＝＿，n ＝ ；（2）已知数列 {}n a 的前n 项和212n S n n =-，求数列{||}n a 的前n 项和n T .（4）等差中项：若,,a A b 成等差数列，则A 叫做a 与b 的等差中项，且2a bA +=。
高中数学第二章数列本章整合课件新人教A版必修5
另一种是Sn与an的关系式,记为f(an,Sn)=0,此时,利用an与Sn的关系将已知关系式转 化为关于an的关系式或关于Sn的关系式,再求an或Sn.若求出的是Sn,需再一次利用an 与Sn的关系求an.
专题一
专题二
专题三
1 应用2已知数列{an}中,an>0,Sn是数列{an}的前n项和,且 an+ =2Sn,求 an. ������������ 1 2 解:将 an+ =2Sn 变形为������������ +1=2Snan. ������������
������π 2 ������-1 π(n 2
专题一
专题二
专题三
2.利用an与Sn的关系求通项
an与前n项和Sn关系式有两种形式:一种是Sn与n的关系式,记为Sn=f(n),可由公式
������1 ,������ = 1, an= ������������ -������������ -1 ,������ ≥ 2 直接求出通项an,但要注意n=1与n≥2两种情况能否统一;
④若f(n)是关于n的分式函数,累加后可裂项求和.
专题一
专题二
专题三
应用3已知数列{an}中,a1=1,且an+1-an=3n-n,求数列{an}的通项公式. 分析:由于本例给出了数列{an}中连续两项的差,故可考虑用累加法求解, 解:由an+1-an=3n-n, 得an-an-1=3n-1-(n-1), an-1-an-2=3n-2-(n-2), ……
an-1-an-2=f(n-2),
…… a3-a2=f(2),
a2-a1=f(1).
专题一
专题二
专题三
以上n-1个等式累加得 an-a1=f(n-1)+f(n-2)+…+f(2)+f(1),
专题一
专题二
专题三
1 应用2已知数列{an}中,an>0,Sn是数列{an}的前n项和,且 an+ =2Sn,求 an. ������������ 1 2 解:将 an+ =2Sn 变形为������������ +1=2Snan. ������������
������π 2 ������-1 π(n 2
专题一
专题二
专题三
2.利用an与Sn的关系求通项
an与前n项和Sn关系式有两种形式:一种是Sn与n的关系式,记为Sn=f(n),可由公式
������1 ,������ = 1, an= ������������ -������������ -1 ,������ ≥ 2 直接求出通项an,但要注意n=1与n≥2两种情况能否统一;
④若f(n)是关于n的分式函数,累加后可裂项求和.
专题一
专题二
专题三
应用3已知数列{an}中,a1=1,且an+1-an=3n-n,求数列{an}的通项公式. 分析:由于本例给出了数列{an}中连续两项的差,故可考虑用累加法求解, 解:由an+1-an=3n-n, 得an-an-1=3n-1-(n-1), an-1-an-2=3n-2-(n-2), ……
an-1-an-2=f(n-2),
…… a3-a2=f(2),
a2-a1=f(1).
专题一
专题二
专题三
以上n-1个等式累加得 an-a1=f(n-1)+f(n-2)+…+f(2)+f(1),
新人教A版高中数学必修5第二章数列章末复习课同步课件
2an＋1＝an＋an＋2(n∈N*)⇔{an}是等差
数列 中项公式法
a2n＋1＝anan＋2(an＋1anan＋2≠0) ⇔{an}是
等比数列
an＝pn＋q(p，q 为常数) ⇔{an}是等差 数列 通项公式法 an＝cqn(c，q 均为非零常数) ⇔{an}是 等比数列
Sn＝An2＋Bn(A，B 为常数) ⇔{an}是 前 n 项和公 等差数列
(4)作新数列法：对由递推公式给出的数列，经过变 形后化归成等差数列或等比数列来求通项．
(5)归纳、猜想、证明法． 3．等差数列、等比数列的判断方法 (1)定义法：an＋1－an＝d(常数)⇔{an}是等差数列；aan＋n 1 ＝q(q 为常数，q≠0)⇔{an}是等比数列． (2)中项公式法：2an＋1＝an＋an＋2⇔{an}是等差数列； a2n＋1＝an·an＋2(an≠0)⇔{an}是等比数列．
式法
Sn＝kqn－k(k 为常数，且 q≠0，k≠0， q≠1) ⇔{an}是等比数列
[例 2] (2016·全国卷Ⅲ)已知数列{an}的前 n 项和 Sn＝1 ＋λan，其中 λ≠0.
(1)证明{an}是等比数列，并求其通项公式； (2)若 S5＝3312，求 λ. (1)证明：由题意得 a1＝S1＝1＋λa1， 故 λ≠1，a1＝1－1 λ，a1≠0. 由 Sn＝1＋λan，Sn＋1＝1＋λan＋1 得 an＋1＝Sn＋1－Sn＝λan＋1 －λan，即 an＋1(λ－1)＝λan.
[变式训练] 已知等差数列{an}满足 a3＝2，前 3 项和 S3 ＝92.
(1)求{an}的通项公式； (2)设等比数列{bn}满足 b1＝a1，b4＝a15，求{bn}的前 n 项和 Tn. 解：(1)设{an}的公差为 d，则由已知条件得 a1＋2d＝2， 3a1＋3×2 2d＝92，
2020-2021学年高中数学人教A版必修5第二章数列本章小结 课件(共70张PPT)
2. 通项公式与递推公式
通项公式:
用正整数 n 表示数列的第 n 项 an. an+1-an=f(n) 型, 求通项公式:
n 依次取正整数, 等式累加.
递推公式:
数列的任一项用它的前一项或前两项推出.
F1=1, 如: F2=1,
(斐波拉契数列)
Fn=Fn-1+Fn-2 (n≥3).
3. 前 n 项和
例6. 已知 {an} 是一个公差大于 0 的等差数列, 且
满足 a3a6=55, a2+a7=16.
(1) 求数列 {an} 的通项公式;
(2) 若数列 {an} 和数列 {bn} 满足等式:
an
=
b1 2
+
b2 22
+
b3 23
++
bn 2n
,
求数列 {bn} 的前 n 项和 Sn.
解: (2) 由(1)得
5. 等差中项 a, A, b 成等差, A 是 a, b 的等差中项.
2an = an-k + an+k, m+n = p+q am+an = ap+aq.
6. 等差数列前 n 项和
(关于 n 的二次函数) Sk, S2k-Sk, S3k-S2k, … 成等差数列.
7. 等比数列 定义:
a2=a1·q, a3=a2·q, a4=a3·q, …, an+1=an·q. 通项公式:
+
b3 23
++
bn 2n
,
求数列 {bn} 的前 n 项和 Sn.
解: (2) 由(1)得
①
于是得 an-1=
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
等差数列{an}中，(m、 n、p、q∈N+): ①an＝am＋(n－m)d ； ②若 m＋n＝p＋q，则am＋an＝ap＋aq ； ③由项数成等差数列的项组成的数列仍 是等差数列； ④ 每n项和Sn , S2n－Sn , S3n－S2n … 组成的数列仍是等差数列.
二、等比数列 1. 等比数列的定义
练习 1. 已知: x＞0，y＞0, x，a，b，y成等差数 2 ( a b ) 列，x，c，d，y成等比数列，则 cd 的最小值是 ( ) A. 0 B. 1 C. 2 D. 4
2．数列
{an }
的前
练习
n
项和记作
Sn
，满足
2. 数列{an}的前n项和记作Sn，满足
S n 2an 3n 12
2. 等比数列的通项公式
an a1 q
3. 等比中项
n 1
(a1 , q 0)
二、等比数列
4. 等比数列的判定方法 (1) an＝an－1· q (n≥2)，q是不为零的常数， an－1≠0 {an}是等比数列. (2) an2＝an－1· an＋1(n≥2, an－1, an, an＋1≠0) {an}是等比数列. (3) an＝c· qn (c，q均是不为零的常数) {an}是等比数列.
方法总结
1．数列是特殊的函数，有些题目可结合函数知 识去解决，体现了函数思想、数形结合的思想． 2．等差、等比数列中，a1、an、n、d（q） 、Sn“知 三求二”，体现了方程（组）的思想、整体思想， 有时用到换元法． 3．求等比数列的前 n 项和时要考虑公比是否等 于 1，公比是字母时要进行讨论，体现了分类讨 论的思想． 4．数列求和的基本方法有公式法、化归法、倒 序相加法、错位相减法、并项求和法、分步求和 法、裂项相消法等．
二、等比数列 6. 等比数列的前n项和公式
na1 n S n a1 (1 q ) 1 q
(q 1) (q 1)
二、等比数列
已知
x0
，
y0
，
7. 等比数列前n项和的一般形式
x，a，b，y
成等差数列，
x，c，d，y
成等比数列，则
S n A Aq (q 1)
a7＝1，且a4，a5＋1，a6成等差数列． (1)求数列{an}的通项公式；
(2)数列{an}的前n项和记为Sn，
证明：Sn＜128(n＝1,2,3,…).
练习 4．设数列{an}的前n项和为Sn＝2n2，{bn}
为等比数列，且a1＝b1，b2(a2－a1)＝b1，
(1)求数列{an}和{bn}的通项公式； a (2)设 cn n ，求数列{cn}的前n项和Tn . bn
二、等比数列
5. 等比数列的性质 (1)当q＞1，a1＞0或0＜q＜1，a1＜0时， {an}是递增数列； 当q＞1，a1＜0或0＜q＜1，a1＞0时， {an}是递减数列； 当q＝1时，{an}是常数列； 当q＜0时，{an}是摆动数列.
二、等比数列
5. 等比数列的性质 (1)当q＞1，a1＞0或0＜q＜1，a1＜0时， {an}是递增数列； 当q＞1，a1＜0或0＜q＜1，a1＞0时， {an}是递减数列； 当q＝1时，{an}是常数列； 当q＜0时，{an}是摆动数列. (2)an＝am· qn－m(m、n∈N*).
n
A. 0 B. 1 C. 2 D. 4
二、等比数列 8. 等比数列的前n项和的性质
(1)在等比数列中，若项数为2n(n∈N*)， S 则 偶 q. S奇
二、等比数列 8. 等比数列的前n项和的性质
(1)在等比数列中，若项数为2n(n∈N*)， S 则 偶 q. S奇
(2)Sn，S2n－Sn，S3n－S2n成等比数列.
第二章数列复习
主讲老师：陈震知识结构定义来自数 列通项等差数列
前 n 项和
与函数的关系
等比数列
知识纲要
⑴数列的概念 ，通项公式，数列的 分类，用函数的观点看数列．
⑵等差、等比数列的定义．
⑶等差、等比数列的通项公式． ⑷等差中项、等比中项．
⑸等差、等比数列的前 n 项和公式及 其推导的方法．
知识归纳
一、等差数列 1.等差数列这单元学习了哪些内容？ 定 等差数列 义
通
项
前n项和
主要性质
一、等差数列
2. 等差数列的定义、用途及使用时需 注意的问题: n≥2，an －an－1＝d (常数)
3. 等差数列的通项公式如何？结构有 什么特点？ an＝a1＋(n－1) d
an＝An＋B (d＝A∈R)
一、等差数列
，
Sn＝2an＋3n－12(n∈N*)． (1)证明数列{an－3}为等比数列；
并求出数列{an}的通项公式．
(2)记bn＝nan ，数列{bn}的前n项
和为Tn ，求Tn．
2．数列
{an }
的前
练习
n
项和记作
Sn
，满足
3．已知实数列{an}是等比数列，其中
，
S n 2an 3n 12
4. 等差数列图象有什么特点？ 单调性如何确定？ an a
n
n
n d＞0
d＜ 0
一、等差数列
5. 用什么方法推导等差数列前n项和公式 的?公式内容? 使用时需注意的问题? 前n 项和公式结构有什么特点?
Sn＝An2＋Bn (A∈R)
注意: d＝2A !
一、等差数列
6. 你知道等差数列的哪些性质?