七年级下册数学三角形全等动点问题

合集下载

数学全等三角形动点问题

数学全等三角形动点问题数学这东西，听起来就有点让人打哈欠，尤其是当你碰上了全等三角形动点问题的时候，简直让人想直接躲进床底下。

不过别担心，今天咱们就来聊聊这个话题，轻松点儿，搞笑点儿，保证让你哈哈大笑，顺便脑袋里也装点儿知识。

想象一下，你跟朋友一起去游乐园，前面是个大旋转木马，大家都在排队。

这个木马就像一个个三角形，转来转去，根本停不下来。

好啦，先说说全等三角形。

全等的意思就是两个三角形一模一样，无论你怎么转、怎么动，都还是那样。

就好比双胞胎，真是一看就知道是兄弟姐妹。

你要是把这俩三角形放在一起，哦哟，简直就像是复制粘贴，连角度和边长都跟着一模一样。

这就有意思了，咱们来设想一下：如果这两个三角形有一个动点，那就像是在给它们穿上舞鞋，在舞池里翩翩起舞。

不管怎么转，这舞姿总是那么优雅，简直让人目不暇接。

想象一下这俩三角形之间的关系，简直就是一对恩爱的小情侣。

一个在这里，另一个在那儿，距离虽然不变，但感觉就像在做双人舞。

它们的边长、角度都保持着一致，这就是全等三角形的神奇之处。

想想，如果我们生活中也能有这种“全等”关系，那可真是太好了。

每天都可以找一个人一起“相约”，不管走到哪儿都不会迷路，心里总是有一份安全感。

不过，这个动点问题就有点麻烦了。

你知道，当一个三角形的某个点动起来的时候，其他的就得跟着动。

这就像你在冰箱前，想喝可乐，结果冰箱门关上了，那可真是让人捶心肝。

你得想办法把这动点的位置确定下来，不然整个三角形就乱了套，跟着你在厨房里晃悠，根本停不下来。

数学里的动点就像生活中的那些变化一样，让人琢磨不透。

你以为这个点在这儿，结果它一下子跑到那边，搞得你摸不着头脑。

想想看，谁没有遇到过这种情况呢？就像在约会时，原本想去的餐厅没了位子，你就得随便找个地方，结果最后吃到了你最讨厌的那道菜，真是让人哭笑不得。

再说说这动点问题的性质。

这个动点在三角形里游来游去，就像小猫追蝴蝶一样。

你永远不知道它下一步会往哪儿去，角度变来变去，让人眼花缭乱。

全等三角形之动点问题

全等三角形之动点问题（一）1、已知:如图,在△ABC中,AB=AC=18,BC=12,点D为AB的中点.点P在线段BC上以每秒3个单位的速度由B点向C点运动,同时点Q在线段CA上由C点向A点以每秒a个单位的速度匀速运动.设运动时间为t秒,若某一时刻△BPD与△CQP全等,求t的值与相应的点Q的运动速度a2、如图，在等边ABC∆的顶点A、C处各有一只蜗牛，它们同时出发，分别以每分钟1各单位的速度油A向B和由C向A爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D,E处，请问（1）在爬行过程中，CD和BE始终相等吗？（2）若蜗牛沿着AB和CA的延长线爬行，EB与CD交于点Q，其他条件不变，如图（2）所示，，求证：︒CQE=∠60（3）如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行，连接DE交AC于F”，其他条件不变，则爬行过程中，DF始终等于EF是否正确3、在△ABC中，,∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E(1)当直线MN绕点C旋转到图①的位置时，求证：DE=AD+BE(2)当直线MN绕点C旋转到图②的位置时，求证：DE=AD-BE(3)当直线MN绕点C旋转到图③的位置时，试问：DE、AD、BE有怎样的等量关系?请写出这个等量关系，并加以证BA O DC E图84. 如下图，已知正方形ABCD 中，边长为10厘米，点E 在AB 边上，BE=6厘米．（1）如果点P 在线段BC 上以4厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CD 上由C 点向D 点运动． ①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，△BPE 与△CQP 是否全等，请说明理由； ②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使△BPE 与△CQP 全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿正方形ABCD 四边运动，求经过多长时间点P 与点Q 第一次在正方形ABCD 边上的何处相遇？5、如图7，点O 是线段AD 的中点，分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ，连结AC 和BD ，相交于点E ，连结BC ．求∠AEB 的大小；6、ΔOAB 固定不动，保持ΔOCD 的形状和大小不变，将ΔOCD 绕着点O 旋转（ΔOAB 和ΔOCD 不能重叠），求∠AEB 的大小.C B OD图7AE全等构造角平分线类1如图，在ABC ∆中，2B C ∠=∠，BAC ∠的平分线AD 交BC 与D ．求证：AB BD AC +=．DC B A2如图，在ABC ∆中，AB BD AC +=，BAC ∠的平分线AD 交BC 与D ．求证：2B C ∠=∠．DC B A3如图，ABC ∆中，AB=2AC ，AD 平分BAC ∠，且AD=BD ，求证：CD ⊥AC4如图，在四边形ABCD 中，BC ＞BA,AD ＝CD ，BD 平分ABC ∠，求证： 0180=∠+∠C A5已知ABC ∆中，60A ∠=，BD 、CE 分别平分ABC ∠和ACB ∠，BD 、 CE 交于点O ，试判断BE 、CD 、BC 的数量关系，并加以证明．OED CBA6如图，在ABC ∆中，60B ∠=︒，AD 、CE 分别平分BAC ∠、BCA ∠，且AD 与CE 的交点为F ．求证：FE FD =．CDBACBAFBEDCA7如图，已知在ABC 内，060BAC ∠=，040C ∠=，P ，Q 分别在BC ，CA 上，并且AP ，BQ 分别是BAC ∠，ABC ∠的角平分线。

全等三角形之动点问题(简单题)

一、等腰三角形类：因动点产生的等腰三角形问题1.如图,Rt△ABC在直线l上，且∠ABC= 90°，BC=6cm,AC= 10cm.(1)求AB的长;(2)若有一动点P从点B出发，以2cm/s的速度在直线l上运动,则当t为何值时,△ACP为等腰三角形?二、直角三角形：因动点产生的直角三角形问题2、如图，射线MB上MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P 从M沿射线MB方向以1个单位/秒的速度移动，设P的运动时间为t.求：(1)△PAB为等腰三角形的t值;(2)△PAB为直角三角形的t值;(3) 若AB=5且∠ABM=45。

，其他条件不变，直接写出△PAB为直角三角形的t值三、全等三角形：因动点产生的全等三角形问题3.如图，已知△ABC中，∠B=∠C,AB=AC=10 cm,BC=8 cm,D为AB的中点.点P在线段BC上以3 cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动.(1)若点Q的运动速度与点P的运动速度相等，则经过1 s后，△BPD与△CQP是否全等?请说明理由;(2)若点Q的运动速度与点P的运动速度不相等，则当点Q的运动速度为多少时，能够使△BPD与△CQP全等?四、三角形面积：因动点产生的三角形面积问题4.△ABC中，AB=6cm,BC=8cm,∠B=90°, P从A沿AB向B以1cm/s的速度移动，Q从B沿BC向C以2cm/s的速度移动。

(1)如果P、Q分别从A、B同时出发，几秒后△PBQ的面积等于8cm2?;(2)如果P、Q分别从A、B同时出发，点P到B点后，又继续沿BC向C移动,点Q到达C后，又继续沿CA向A移动,在这一整个移动过程中，是否存在点P、Q,使△PBQ的面积等于9cm2?若存在，试确定P、Q的位置;若不存在，请说明理由。

五、相遇问题：因动点产生的相遇问题5.如图，在△ABC中，AB= BC= AC= 12cm，现有两点M、N分别从点A、点B同时出发，沿△ABC的三边运动，已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时，M、N同时停止运动.(1)点M.N运动几秒后,M、N两点重合?(2)点M.N运动几秒后，可得到等边△AMN?(3)当点M、N在BC边上运动时，能否得到以MN为底边的等腰△AMN?如果能，请求出此时M、N运动的时间.六、最值问题：因动点产生的最值问题6.如图K 13一6，点P,Q分别是△ABC的边AC,AB上的定点，请你在BC上找一点R，使得△PQR的周长最短.。

全等三角形动点问题的解题技巧

全等三角形动点问题的解题技巧全等三角形动点问题的解题技巧1. 引言全等三角形动点问题是解决三角形相关问题的一种重要方法，它可以帮助我们深入理解全等三角形的定义和性质。

在本文中，我们将探讨全等三角形动点问题的解题技巧，并通过具体例子来说明。

2. 全等三角形的定义和性质在开始解决全等三角形动点问题之前，我们首先需要了解全等三角形的定义和性质。

全等三角形指的是具有相等边长和相等角度的两个三角形。

全等三角形有如下性质：2.1 两个全等三角形的对应边对应角均相等。

2.2 两个全等三角形的相应边长比相等。

3. 解题技巧在解决全等三角形动点问题时，我们可以采用以下技巧：3.1 选取适当的动点在全等三角形动点问题中，我们需要选择一个适当的动点来进行分析。

通常情况下，我们可以选取一个顶点或者一个角度作为动点，并通过改变该动点的位置来观察全等三角形的变化。

3.2 确定动点的运动轨迹一旦我们选定了一个动点，我们需要确定它的运动轨迹。

通过观察，我们可以发现，在全等三角形中，动点的运动轨迹通常是一条直线、一条弧线或一个圆。

3.3 利用全等三角形的性质在确定了动点的运动轨迹后，我们需要利用全等三角形的性质来解决问题。

根据全等三角形的定义和性质，我们可以得到一些等式或比例关系，从而推导出所需的结论。

4. 例子分析为了更好地理解全等三角形动点问题的解题技巧，我们以一个具体例子进行分析。

假设我们需要证明一个三角形ABC与另一个三角形A'B'C'全等。

我们可以选择顶点A作为动点，并通过改变点A的位置来观察全等三角形的性质。

4.1 确定动点A的运动轨迹观察发现，当我们固定点B和点C不动时，点A可以在与线段BC平行的直线上自由移动。

点A的运动轨迹是一条平行于BC的直线。

4.2 利用全等三角形的性质由于我们已经确定了点A的运动轨迹，我们可以利用全等三角形的性质来解决问题。

根据全等三角形的性质，我们可以得到如下结论：4.2.1 边AC与A'C'相等4.2.2 角BAC与角B'A'C'相等等等。

全等的三角形里的动点问题

全等的三角形里的动点问题是一个比较复杂的问题，需要结合全等三角形的性质和动点的运动规律来解决。

首先，我们需要明确动点的运动规律，比如是匀速运动还是变速运动，以及运动的速度和方向。

其次，我们需要结合全等三角形的性质，比如边长相等、角度相等，来建立方程或不等式，从而求出动点的轨迹方程或范围。

最后，我们可以利用数学工具来解决方程或不等式，从而得到动点的轨迹或范围。

需要注意的是，全等的三角形里的动点问题往往涉及到多种情况，需要对各种情况进行分类讨论，从而得到完整的答案。

七年级下册三角形全等中的动点问题

三角形与动点问题B，AB上一动点（不与点AAB＝8，D为底边1、如图，在等腰△ACB中，AC＝BC＝5，．DF⊥BC，垂足分别为E，F，则DE＋DF＝重合），DE⊥AC，CF E A B D上一动点，为对角线ACQ为BC边的中点，点P2、在边长为2㎝的正方形ABCD中，点.____________㎝（结果不取近似值），则△PBQ周长的最小值为PQ连接PB、依次，点P按图示方式，沿x轴正方向连续翻转20113、如图，将边长为1的等边△OAP 的坐标．，P50，P2011，P3，P4，…，P2007的位置．试写出P1P3次落在点P1，P2，中，ABC、如图，在等腰Rt△4边上运动，且始终AC、BCAB边上的中点，点D、E分别在ACB=90∠°，AC=CB，F是、EF．AD=CE．连接DE、DF保持CEF）求证：△ADF≌△（1DFE是等腰直角三角形（2）试证明△DFE△ACB△是两个全等的直角三角形，量得它们的斜年包头）如图，已知与、（20095）所示的形状，使点°，将这两个三角形摆成如图（130边长为10cm，较小锐角为CACB△、F、DCB、CF顺时）中的在同一条直线上，且点绕点与点1重合，将图（FGGACEDEAB2针方向旋转到图（）的位置，点在边上，交于点，则线段的长为．（保留根号）cmAA EEBDBD C )(FC ()F 1图（）2图（）6、如图1，若△ABC和△ADE为等边三角形，M，N分别EB，CD的中点，易证：CD=BE，△AMN是等边三角形．（1）当把△ADE绕A点旋转到图2的位置时，CD=BE是否仍然成立？若成立请证明，若不成立请说明理由；（2）当△ADE绕A点旋转到图3的位置时，△AMN是否还是等边三角形？若是，请给出证明，并求出当AB=2AD时，△ADE与△ABC及△AMN的面积之比；若不是，请说明理由．3图图2 1 图8BC?AC?10△ABCAB?ABD 7、如图，已知厘米，为中，的中点．厘米，点CA在线段点运动，同时，点Q秒的速度由厘米/B点向C）如果点（1P在线段BC上以3 点运动．点向A上由C CQP△BPD△是否全等，秒后，与的运动速度与点①若点QP的运动速度相等，经过1 请说明理由；BPD△能够使Q的运动速度为多少时，P②若点Q的运动速度与点的运动速度不相等，当点CQP△全等？与同时出发，都以原来的运动速度从点B以②中的运动速度从点C出发，点PQ（2）若点ABC△△ABC的哪条边上相逆时针沿第一次在P三边运动，求经过多长时间点与点Q 遇？ADQB C上的动点（不包括OBE是边8、如图，在平面直角坐标系中，矩形AOBC在第一象限内，）．F，设C（m，n端点），作∠AEF = 90 ，使EF交矩形的外角平分线BF于点AE；m = n时，如图，求证：EF = （1）若？若存在，请求AEOB上是否还存在点E，使得EF = （2）若m≠n时，如图，试问边的坐标；若不存在，请说明理由．出点EyyyFFCAACACFOBO E ExBBx x△ABCAB?ACBCB、CD重合）上一点（不与是直线年本溪）在，点中，，9.（2009△ADEAD?AE，?DAE??BACCEADAD．以为一边在的右侧作，使，连接．．BC?BAC?90°?BCE?D上，如果，则度；）如图（11，当点在线段????BCE??BAC．，）设（2??，BCD之间有怎样的数量关系？请说明理由；①如图2，当点上移动，则在线段 ??，BCD之间有怎样的数量关系？请直接写出你的结论．在直线上移动，则②当点AAEEC BBC D D2 图图1AAB CB C备用图备用图x y)0,6 ,80 )N ( M ( NlP出发，以轴、．点直线轴分别交于点与，点从点10．如图，ＱOON个单位长度的速1个单位长度的速度沿出发，以每秒→从点方向运动，点2每秒ＱＱＱ、OP、PMM两点同时度沿当点→时，的方向运动．已知点到达点同时出发，t秒．停止运动，设运动时间为ttSS MNPQ的面积为的函数关系式，并写出，求关于的取值范围．）设四边形（1．．．ＱtlP 与）当2平行？为何值时，（yNPxMOＱlABCMN△ABC在厘米的线段厘米，长为11.（2009宁夏）已知：等边三角形1的边长为4ABMABAB重合，点点运动的边与点上沿（运动开始时，点方向以1厘米/秒的速度向NABCM、N△BAB时运动终止）分别作，过点到达点边的垂线，与的其它边交于t QP、MN运动的时间为秒．两点，线段t MNQP MN恰为矩形？并求出该矩形的面为何值时，（1）线段在运动的过程中，四边形积；t MNQP SMN．求四边形在运动的过程中，四边形）线段，运动的时间为的面积为（2tt MNQP S随运动时间的面积的取值范围．变化的函数关系式，并写出自变量CCCQPQPPQB B BM A AA M MNNNACABCDEDABEBE在，边延长线上的一点，如图，连接为正方形的一条对角线，点为BF?BCACCFKBEB?BKFB，交，连接于点，交于作，过点，使上取一点．GBKABH．，交于点于点BH?BG；（1）求证：AMED AEBG?BE?5 （2）求证：F N 1KH436G728C B．。

北师大版初一数学下册全等三角形之动点问题

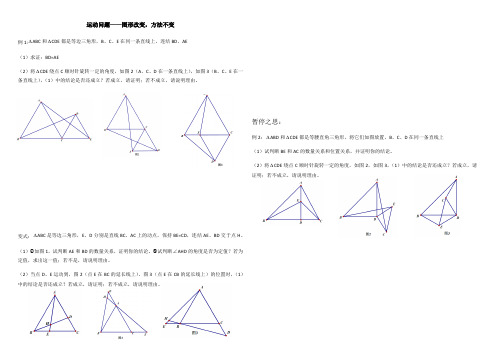
运动问题——图形改变，方法不变例1:∆ABC和∆CDE都是等边三角形，B、C、E在同一条直线上，连结BD、AE（1）求证：BD=AE（2）将∆CDE绕点C顺时针旋转一定的角度，如图2（A、C、D在一条直线上），如图3（B、C、E在一条直线上），（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由。

变式：∆ABC是等边三角形，E、D分别是直线BC、AC上的动点，保持BE=CD，连结AE、BD交于点H。

（1）①如图1，试判断AE和BD的数量关系，证明你的结论。

②试判断∠AHD的角度是否为定值？若为定值，求出这一值；若不是，请说明理由。

（2）当点D、E运动到，图2（点E在BC的延长线上）、图3（点E在CB的延长线上）的位置时，（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由。

暂停之思：例2：∆ABD和∆CDE都是等腰直角三角形，将它们如图放置，B、C、D在同一条直线上（1）试判断BE和AC的数量关系和位置关系，并证明你的结论。

（2）将∆CDE绕点C顺时针旋转一定的角度，如图2，如图3，（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由。

变式：∆ABC 是等腰直角三角形，点D 是直线BC 上一动点，以AD 为直角边在AD 的右侧作等腰RT ∆ADE ，连结CE.（1）试判断BD 和CE 的数量关系和位置关系，并证明你的结论。

（2）将∆ADE 绕点A 顺时针旋转一定的角度，如图2（点D 在CB 的延长线上）；如图3，（点D 在BC 的延长线上）；（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由。

课后作业1、正方形ABCD 和BEFG 如图放置：（1）试判断AE 和CG 的数量关系和位置关系，并证明你的结论。

（2）将正方形BEFG 绕点B 顺时针旋转一定的角度，如图2，（1）中的结论是否还成立？若成立，请证明；若不成立，请说明理由。

2、等腰△ABC 中，AB=AC ，若P 为腰AB 所在直线上任意一点（不与A 、B 重合），以CP 为边作等腰△CPD ，使∠CPD=∠CAB ，PC=PD ，连接DB 交CA 的延长线于F 。

全等三角形的动点问题

当遇到全等三角形中的动点问题时，你如何思考？
方法总结
策略：化动为静
方法：全面审题
图形背景分析运动过程
检验！
分类画出图形表达线段长，建等式。
凡事全力以赴，让自己动作起来时，浑身充满无比的冲劲，使得我们的灵魂几乎也跟不上这样的动作，这是真正用心做事时，最美好的境界
动——让我们全身心的投入静——让我们静下心来审视和消化自己能动能静，动静结合，方能实现自己的理想。
BC上以每秒2cm的速度由点B向点C运动，同时点Q在线段CD上由点C向点D
运动。设点P运动的时间为t秒。（1）请表示线段BP、PC （2）△BPE与△CQP全等，可分为几种情况？
（3）这几种情况下对应边分别为什么？
A
D
E Q
B 2t P 10-2t C
当t为何值时，△BPE与△CQP全等？并求出此时点Q的运动速度。
B
P
C
E
探究新知
如图，在长方形ABCD中，AD=BC=10，AB=CD=4，点E在边BC的延长线上，且CE=3，动点P从点B出发，以每秒2个单位的速度沿BC-CD-DA向终点A运动。设点P的运动时间为ts。
问：当t为何值时，使得△DCE与点D、C、P构成的三角形全等?
A
D
A
PD
P
B
C
EB
C
E
A
2t
A P
t
B Q
AP= ，QB= ；
探究新知
如图，在长方形ABCD中，AD=BC=10，AB=CD=4，点E在边BC的延长线上，
且CE=3，动点P从点B出发，以每秒2个单位的速度沿BC向点C运动。设
点P的运动时间为ts。
A

(完整word版)七年级数学下---全等三角形之动点问题练习

七年级数学下---全等三角形之动点问题练习1、如图，在直角三角形ABC中，∠B＝90°，AB＝5cm，BC＝6cm，点P从点B开始沿BA以1cm／s 的速度向点A运动，同时，点Q从点B开始沿BC以2cm／s的速度向点C运动．几秒后，△PBQ 的面积为9cm2？2、如图所示，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，其中点P运动的速度是1m/s，点Q运动的速度是2m/s，当点Q到达点C 时，P、Q两点都停止运动，设运动时间为t s，解答下列问题：（1）填空：△ABC的面积为；（2）当点Q到达点C时，PQ与AB的位置关系如何？请说明理由．（3）在点P与点Q的运动过程中，△BPQ是否能成为等边三角形？若能，请求出t，若不能，请说明理由． (4)当△BPQ是直角三角形时，求t的值。

3、如图（1），AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A 向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点Q的运动速度为x cm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t 的值；若不存在，请说明理由．4、如图，△ABC中，∠ACB=90°，AC=6，BC=8，点P从A点出发沿A-C-B路径向终点运动，终点为B点；点Q从B点出发沿B-C-A路径向终点运动，终点为A点．点P和Q分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l 于E，QF⊥l于F，问：点P运动多少时间时，△PEC与QFC全等？请说明理由。

七年级下册数学等腰三角形全等动点问题

七年级下册数学等腰三角形全等动点问题引言等腰三角形是中学数学中常见的一个几何图形，也是初学三角函数的重要基础。

而等腰三角形的全等动点问题则是其重要的数学应用之一，本文将对此进行探讨。

等腰三角形简介等腰三角形是指两边（腰）长度相等的三角形，其顶角顶点到底边中点的距离称为它的高。

等腰三角形中，高线既是中线，也是角平分线，且从顶点到底边中点的距离最短。

等腰三角形全等动点问题等腰三角形全等动点问题是指，当已知等腰三角形ABC的底边AB和高CD时，确定其顶点C的位置，使得其全等于另一个已知的等腰三角形A'B'C'。

该问题可以使用解析几何或向量运算等多种方法求解。

解析几何方法通过解析几何方法，可以将等腰三角形ABC和A'B'C'表示为坐标形式，并列出方程组进行求解。

具体而言，设等腰三角形ABC的顶点坐标为(x1, y1)，底边AB所在直线方程为y=kx+b，高CD所在直线方程为y=-1/kx+d，则有：$$\begin{cases}y=kx+b \\y=-\frac{1}{k}x+d \\x-x_1=k\cdot(y-y_1) \\\frac{x-x_1}{y-y_1}=-\frac{1}{k}\end{cases}$$将其中已知量代入，可得未知量x1和y1的值，从而确定等腰三角形ABC的位置。

向量运算方法通过向量运算方法，可以利用向量的基本运算和向量之间的夹角定义，求解等腰三角形ABC的位置。

具体而言，设等腰三角形ABC的底边AB与坐标轴重合，且长为1，高CD与x轴正方向的夹角为θ，则有：$$\begin{cases}\overrightarrow{AC}=-\overrightarrow{A'C'} \\|\overrightarrow{AC}|=|\overrightarrow{A'C'}| \\(\overrightarrow{AC}\cdot\overrightarrow{CD})=0\end{cases}$$将其中已知量代入，根据向量夹角的余弦值可以解出θ，从而确定等腰三角形ABC的位置。

全等三角形的动点问题

全等三角形的动点问题
一、两点同时运动
题1：如图，在△ABC中，AB＝AC＝12cm，∠B＝∠C，BC＝8cm，点D为AB的中点，如果点P在线段BC上以2cm/s的速度由点B向点C运动，同时点Q在线段CA上由点C向点A运动，当一个点停止运动时，另一个点也随之停止运动，当点Q的速度为多少cm/s时，能够在某一时刻使△BPD与△CQP全等。

二、三点同时运动
题2：如图，在长方形ABCD中，AD＝BC＝8，BD＝10，点E从点D出发，以每秒2个单位长度的速度沿DA向点A匀速移动，点F从点C出发，以每秒1个单位长度的速度沿CB向点B匀速移动，点G从点B出发，沿BD向点D匀速移动，三个点同时出发，当有一个点到达终点时，其余两点也随之停止运动，假设移动时间为t秒，求t为何值时，△DEG和△BFG全等。

如图，AB＝12cm，∠CBA=∠DBA=60°，AC=BD=9cm，点P在线段AB上以3cm/s的速度由点B向点A 匀速运动，同时点Q在线段BD上由点B向点D匀速运动，设点Q的速度为xcm/s，当△BPQ与△ACP 全等时，x的值为多少？。

七年级下册期末复习专题--全等三角形动点问题

全等三角形之动点问题典型例题：如图1，点P、Q分别是等边△ABC边AB、BC上的动点（端点除外），点P从顶点A、点Q从顶点B同时出发，且它们的运动速度相同，连接AQ、CP交于点M．（1）求证：△ABQ≌△CAP；（2）当点P、Q分别在AB、BC边上运动时，∠QMC变化吗？若变化，请说明理由；若不变，求出它的度数．（3）如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交点为M，则∠QMC变化吗？若变化，请说明理由；若不变，则求出它的度数．练习题：1.如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：，使△AEH≌△CE B．2.如图，已知△ABC中，AB=AC=12厘米，BC=9厘米，点D为AB的中点．（1）如果点P在线段BC上以3厘米/秒得速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，1秒钟时，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD≌△CQP？(2)若点Q以(1)②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC 的哪条边上相遇？3.如图，边长为6的等边三角形ABC中，D是AB边上的一动点，由A向B运动（A、B不重合），F是BC延长线上的一动点，与D同时以相同的速度由C向BC 延长线方向运动（与C不重合），过点D作DE⊥AC，连接DF交AC于G．（1）当点D运动到AB的中点时，直接写出AE的长；（2）当DF⊥AB时，求AD的长；（3）在运动过程中线段GE的长是否发生变化？如果不变，求出线段GE的长；如果发生改变请说明理由．课后作业：1.如图，在Rt△ABC中，∠BAC＝900，AB=4，AC=10，PQ=BC，P、Q分别在AC和AB的反向延长线上移动，当PC等于多少时，△ABC≌△APQ。

全等三角形之动点问题

全等三角形之动点问题（一）1.已知:如图,线段AB的长为18厘米,动点P从点A出发,沿AB以2厘米/秒的速度向点B运动,动点Q从点B出发,沿BA以1厘米/秒的速度向点A运动.P,Q两点同时出发,当点P到达点B时,点P,Q同时停止运动.设点P运动的时间为t 秒,用t表示线段PQ的长度为_____;若P,Q两点相距6厘米,则经过的时间t=______.2、已知:如图,在等边△ABC中,AB=8,D为边BC上一点,且BD=6.动点P从点C出发沿CA边以每秒2个单位的速度向点A运动,连接AD,BP,设点P运动的时间为t秒.若△BPA≌△ADB,则t的值为3、已知:如图,在长方形ABCD中,AB=DC=6,AD=BC=12,点E为边AD上一点,且AE=10.动点P从点B出发,沿BC边向终点C以每秒2个单位的速度运动,连接AP,DP,设点P运动的时间为t秒.若运动到某一时刻,△DCP≌△CDE,则t的值为4、已知:如图,在△ABC中,AB=AC=18,BC=12,点D为AB的中点.点P在线段BC上以每秒3个单位的速度由B点向C点运动,同时点Q在线段CA上由C点向A点以每秒a个单位的速度匀速运动.设运动时间为t秒,若某一时刻△BPD与△CQP全等,求t的值与相应的点Q的运动速度a5、如图，在等边ABC的顶点A、C处各有一只蜗牛，它们同时出发，分别以每分钟1各单位的速度油A向B和由C向A爬行，其中一只蜗牛爬到终点时，另一只也停止运动，经过t分钟后，它们分别爬行到D,E处，请问（1）在爬行过程中，CD和BE始终相等吗？（2）若蜗牛沿着AB和CA的延长线爬行，EB与CD交于点Q，其他条件不变，如图（2）所示，，求证：︒CQE=∠60（3）如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行，连接DE交AC于F”，其他条件不变，则爬行过程中，DF始终等于EF是否正确6、在△ABC中，,∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E(1)当直线MN绕点C旋转到图①的位置时，求证：DE=AD+BE(2)当直线MN绕点C旋转到图②的位置时，求证：DE=AD-BE(3)当直线MN绕点C旋转到图③的位置时，试问：DE、AD、BE有怎样的等量关系?请写出这个等量关系，并加以证明7.如下图，已知正方形ABCD中，边长为10厘米，点E在AB边上，BE=6厘米．（1）如果点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPE与△CQP是否全等，请说明理由；B O DC E图8 ②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使△BPE 与△CQP 全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿正方形ABCD 四边运动，求经过多长时间点P 与点Q 第一次在正方形ABCD 边上的何处相遇？8、如图7，点O 是线段AD 的中点，分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ，连结AC 和BD ，相交于点E ，连结BC ．求∠AEB 的大小；如图8，ΔOAB 固定不动，保持ΔOCD 的形状和大小不变，将ΔOCD 绕着点O 旋转（ΔOAB 和ΔOCD 不能重叠），求∠AEB 的大小.C B OD 图7AE。

北师大版七年级(下册)三角形全等中的动点问题

A B CDE F 三角形与动点问题1、如图，在等腰△ACB 中，AC ＝BC ＝5，AB ＝8，D 为底边AB 上一动点（不与点A ，B 重合），DE ⊥AC ，DF ⊥BC ，垂足分别为E ，F ，则DE ＋DF ＝．2、在边长为2㎝的正方形ABCD 中，点Q 为BC 边的中点，点P 为对角线AC 上一动点，连接PB 、PQ ，则△PBQ 周长的最小值为____________㎝（结果不取近似值）.3、如图，将边长为1的等边△OAP 按图示方式，沿x 轴正方向连续翻转2011次，点P 依次落在点P1，P2，P3，P4，…，P2007的位置．试写出P1，P3，P50，P2011的坐标．4、如图，在等腰Rt △ABC 中，∠ACB=90°，AC=CB ，F 是AB 边上的中点，点D 、E 分别在AC 、BC 边上运动，且始终保持AD=CE ．连接DE 、DF 、EF ．（1）求证：△ADF ≌△CEF（2）试证明△DFE 是等腰直角三角形5、（2009年）如图，已知ACB △与DFE △是两个全等的直角三角形，量得它们的斜边长为10cm ，较小锐角为30°，将这两个三角形摆成如图（1）所示的形状，使点B C F D 、、、在同一条直线上，且点C 与点F 重合，将图（1）中的ACB △绕点C 顺时针方向旋转到图（2）的位置，点E 在AB 边上，AC 交DE 于点G ，则线段FG 的长为 cm （保留根号）．A EC (F )B图（1）EA GBC (F )D 图（2）6、如图1，若△ABC 和△ADE 为等边三角形，M ，N 分别EB ，CD 的中点，易证：CD=BE ，△AMN是等边三角形．（1）当把△ADE 绕A 点旋转到图2的位置时，CD=BE 是否仍然成立？若成立请证明，若不成立请说明理由；（2）当△ADE 绕A 点旋转到图3的位置时，△AMN 是否还是等边三角形？若是，请给出证明，并求出当AB =2AD 时，△ADE 与△ABC 及△AMN 的面积之比；若不是，请说明理由．7、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点．（1）如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？8、如图，在平面直角坐标系中，矩形AOBC 在第一象限，E 是边OB 上的动点（不包括端点），AQCDB P图1 图2 图3作∠AEF = 90︒，使EF 交矩形的外角平分线BF 于点F ，设C （m ，n ）．（1）若m = n 时，如图，求证：EF = AE ；（2）若m ≠n 时，如图，试问边OB 上是否还存在点E ，使得EF = AE ？若存在，请求出点E 的坐标；若不存在，请说明理由．9.（2009年）在ABC △中，AB AC =，点D 是直线BC 上一点（不与B C 、重合），以AD 为一边在AD 的右侧．．作ADE △，使AD AE DAE BAC =∠=∠，，连接CE ．（1）如图1，当点D 在线段BC 上，如果90BAC ∠=°，则BCE ∠= 度；（2）设BAC α∠=，BCE β∠=．①如图2，当点D 在线段BC 上移动，则αβ，之间有怎样的数量关系？请说明理由； ②当点D 在直线BC 上移动，则αβ，之间有怎样的数量关系？请直接写出你的结论．AEEAC CD DBB图1 图2 AA备用图 B CB C 备用图10．如图，直线l 与x 轴、y 轴分别交于点) 0,8 ( M ，点) 6,0 ( N ．点P 从点N 出发，以每秒1个单位长度的速度沿N →O 方向运动，点Ｑ从点O 出发，以每秒2个单位长度的速度沿O →M 的方向运动．已知点ＱP 、同时出发，当点Ｑ到达点M 时，ＱP 、两点同时停止运动，设运动时间为t 秒．（1）设四边形．．．MNPQ 的面积为S ，求S 关于t 的函数关系式，并写出t 的取值围．（2）当t 为何值时，ＱP 与l 平行？11.（2009）已知：等边三角形ABC 的边长为4厘米，长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M N 、分别作AB 边的垂线，与ABC △的其它边交于P Q 、两点，线段MN 运动的时间为t 秒．（1）线段MN 在运动的过程中，t 为何值时，四边形MNQP 恰为矩形？并求出该矩形的面积；（2）线段MN 在运动的过程中，四边形MNQP 的面积为S ，运动的时间为t ．求四边形MNQP 的面积S 随运动时间t 变化的函数关系式，并写出自变量t 的取值围．如图，AC 为正方形ABCD 的一条对角线，点E 为DA 边延长线上的一点，连接BE ，在BE 上取一点F ，使BF BC =，过点B 作BK BE ⊥于B ，交AC 于点K ，连接CF ，交CPQ BA MN CPQBA M NCPQBAMNABCDE FGH KMN12345678AB 于点H ，交BK 于点G ．（1）求证：BG BH =；（2）求证：AE BG BE +=。

全等三角形--动点问题

全等三角形的动点问题教学重点难点利用熟悉的知识点解决陌生的问题思路：1.利用图形想到三角形全等2.分析题目，了解有几个动点，动点的路程，速度3.结合图形和题目，得出已知或能间接求出的数据4.分情况讨论，把每种可能情况列出来，不要漏5.动点一般都是压轴题，步骤不重要，重要的是思路6.动点类问题一般都有好几问，前一问大都是后一问的提示，就像几何探究类题一样，如果后面的题难了，可以反过去看看前面问题的结论.【典型例题】例1. 如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD 的右侧作正方形ADEF．解答下列问题：（1）如果AB=AC，∠BAC=90°，点D在射线BC上运动时（与点B不重合），如图，线段CF，BD之间的位置关系为_____________，数量关系为______________．请利用图2或图3予以证明（选择一个即可）．例2. 如图，在等腰Rt△ABC中，∠ACB=90°，AC=CB，AC=8，F是AB边上的中点，点D、E分别在AC、BC边上运动，且始终保持AD=CE，连接DE、DF、EF.（1）求证：△ADF≌△CEF.（2）试证明△DFE是等腰直角三角形.（3）在此运动变化的过程中，四边形CDFE的面积是否保持不变？试说明理由．（4）求△CDE面积的最大值．变式如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D、E分别在AC、BC边上运动，且保持AD=CE．连接DE、DF、EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②DE长度的最小值为4；③四边形CDFE的面积保持不变；④△CDE面积的最大值为8．其中正确的结论是（）A．①②③B．①③C．①③④D．②③④例3. 正方形ABCD和正方形AEFG有一公共点A，点G．E分别在线段AD、AB上（如图（1）所示），连接DF、BF．（1）求证：DF=BF（2）若将正方形AEFG绕点A按顺时针方向旋转，连接DG、BE（如图（2）所示），在旋转过程中，请猜想线段DG、BE始终有什么数量关系和位置关系并证明你的猜想．例4.如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点.（1）如果点P在线段BC上以3cm/秒的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？（2）若点Q以②中的速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？变式如图，在等边△ABC中，AB=9cm，点P从点C出发沿CB边向点B点以2cm/s的速度移动，点Q 点从B点出发沿BA边向A点以5cm/s速度移动．P、Q两点同时出发，它们移动的时间为t秒钟．（1）你能用t表示BP和BQ的长度吗？请你表示出来．（2）请问几秒钟后，△PBQ为等边三角形？（3）若P、Q两点分别从C、B两点同时出发，并且都按顺时针方向沿△ABC三边运动，请问经过几秒钟后点P与点Q第一次在△ABC的哪条边上相遇？【拓展提高】1..两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC．（1）请找出图2中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）；（2）证明：DC⊥BE2.如图，在Rt△ABC中，∠BAC=90°，AC=2AB，点D是AC的中点，将一块锐角为45°的直角三角板如图放置，使三角板斜边的两个端点分别与A、D重合，连结BE、EC．试猜想线段BE和EC的数量及位置关系，并证明你的猜想．3. 已知Rt△ABC中，AC=BC，∠C=90°，D为AB边的中点，∠EDF=90°，∠EDF绕D点旋转，它的两边分别交AC、CB（或它们的延长线）于E、F.当∠EDF绕D点旋转到DE⊥AC于E时（如图1），易证12DEF CEF ABCS S S+=△△△．当∠EDF绕D点旋转到DE和AC不垂直时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，S△DEF、S△CEF、S△ABC又有怎样的数量关系？请写出你的猜想，不需证明．4. 如图，AC为正方形ABCD的一条对角线，点E为DA边延长线上的一点，连接BE，在BE上取一点F，使BF=BC，过点B做BK⊥BE与B，交AC于点K，连接CF，交AB于点H，交BK于点G.（1）求证：BH=BG；（2）求证：BE=BG+AE.5.正方形四条边都相等，四个角都是90°．如图，已知正方形ABCD在直线MN的上方，BC在直线MN上，点E是直线MN上一点，以AE为边在直线MN的上方作正方形AEFG．（1）如图1，当点E在线段BC上（不与点B、C重合）时：①判断△ADG与△ABE是否全等，并说明理由；②过点F作FH⊥MN，垂足为点H，观察并猜测线段BE与线段CH的数量关系，并说明理由；（2）如图2，当点E在射线CN上（不与点C重合）时：①判断△ADG与△ABE是否全等，不需说明理由；②过点F作FH⊥MN，垂足为点H，已知GD=4，求△CFH的面积．6.如图1，若△ABC和△ADE为等边三角形，M、N分别为EB、CD的中点，易证：CD=BE，△AMN是等边三角形.（1）当把△ADE绕点A旋转到图2的位置时，CD=BE是否依然成立？若成立请证明，若不成立请说明理由；（2）当△ADE绕点A旋转到图3位置时，△AMN是否还是等边三角形？若是，请给出证明，并求出当AB=2AD时，△ADE与△ABC及△AMN的面积之比；若不是，请说明理由.7.在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧做△ADE，使AD=AE，∠DAE=∠BAC，连接CE.（1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=_________度；（2）设∠BAC=α，∠BCE=β.①如图2，当点D在线段BC上移动，则α，β之间有怎样的数量关系？请说明理由；②当点D在直线BC上移动，则α，β之间有怎样的数量关系？请直接写出你的结论.8.思考与推理如图，在四边形ABCD中，AB=AD=6cm，CB=CD，AB⊥BC，CD⊥AD，∠BCD=120°. ∠PCQ=60°，两边分别交线段AB、AD于点P、Q，把△PBC绕点C顺时针旋转120°得到△MDC.请在图中找出一对全等的三角形并加以证明（△PBC与△MDC除外）.探究与应用在上边的条件下，若∠PCQ绕顶点C在∠BCD内转动，两边始终与线段AB、AD相较于点P、Q，试探究在转动过程中△APQ的周长是否变化，若不变，求它的周长；若变化，请说明理由.9.问题情境：如图1，在直角三角形ABC中，∠BAC=90°，AD⊥BC于点D，可知：∠BAD=∠C（不需要证明）；特例探究：如图2，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB=AC，CF⊥AE于点F，BD⊥AE于点D．证明：△ABD≌△CAF；归纳证明：如图3，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC，∠1=∠2=∠BAC．求证：△ABE≌△CAF；拓展应用：如图4，在△ABC中，AB=AC，AB＞BC．点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为15，则△ACF与△BDE的面积之和为______________.10.如图①，已知△ABC是等腰直角三角形，∠BAC=90°，BC=2，AD是BC边上的高．作正方形DEFG，使点A、C分别在DG和DE上，且DE=BC，且连接AE、BG．（1）试猜想线段BG和AE的数量关系，请直接写出你得到的结论；（2）将正方形DEFG绕点D逆时针方向旋转一定角度后（旋转角度大于0°，或小于90°），DG、DE分别交AB、AC于点M和N（如图②），则（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由．11.如下图，已知正方形ABCD中，边长为10厘米，点E在AB边上，BE=6厘米．（1）如果点P在线段BC上以4厘米/秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D 点运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPE与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPE与△CQP全等？（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿正方形ABCD四边运动，求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇？12.（1）操作发现：如图①，D是等边△ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边△DCF，连接AF．你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论．（2）类比猜想：如图②，当动点D运动至等边△ABC边BA的延长线上时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？（3）深入探究：Ⅰ．如图③，当动点D在等边△ABC边BA上运动时（点D与点B不重合）连接DC，以DC为边在BC 上方、下方分别作等边△DCF和等边△DCF′，连接AF、BF′，探究AF、BF′与AB有何数量关系？并证明你探究的结论．Ⅱ．如图④，当动点D在等边三角形边BA的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论．。

初中七年级数学下全等三角形之动点问题学习练习

七年级数学下- - - 全等三角形之动点问题练习1、如图，在直角三角形ABC中，∠B＝90°，AB＝5cm，BC＝6cm，点P从点B开始沿BA以1cm／s的速度向点A运动，同时，点Q从点B开始沿BC以2cm／s的速度向点C2运动．几秒后，△PBQ的面积为9cm？2、如下图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速运动，此中点P运动的速度是1m/s，点Q运动的速度是2m/s，当点Q抵达点C时，P、Q两点都停止运动，设运动时间为t?s，解答以下问题：（1）填空：△ABC的面积为；（2）当点Q抵达点C时，PQ与AB的地点关系怎样？请说明原因．（3）在点P与点Q的运动过程中，△BPQ能否能成为等边三角形？若能，恳求出不可以，请说明原因．(4)当△BPQ是直角三角形时，求t的值。

t，若3、如图（1），AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．4、（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ能否全等，请说明原因，并判断此时线段PC和线段PQ的地点关系；5、（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其余条件不变．设点Q的运动速度为xcm/s，能否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明原因．4、如图，△ABC中，∠ACB=90°，AC=6，BC=8，点P从A点出发沿A-C-B路径向终点运动，终点为B点；点Q从B点出发沿B-C-A路径向终点运动，终点为 A点．点P和Q 分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时辰，分别过P和Q作PE⊥l于E，QF⊥l于F，问：点P运动多少时间时，△PEC与QFC全等？请说明原因。

北师大版七年级数学下册难点探究专题：全等三角形中的动态问题

难点研究专题：全等三角形中的动向问题◆种类一全等三角形中的动点问题1．如图，在△MAB 中， MA ＝ MB ，过 M 点作直线个动点，在点P 挪动的过程中，若NA ＝ NB ，则∠ PAMMN 交 AB 于 N点．P是直线与∠ PBM 能否相等？说明原因．MN上的一2．如图①，在△ABC 中，∠ BAC ＝ 90°， AB ＝AC( ∠ ABC ＝∠ ACB ＝45°)，点 D 为直线BC 上一动点 (点 D 不与 B， C 重合 )，以 AD 为边在 AD 右边作正方形ADEF ，连结 CF.(1)察看猜想：如图①，当点 D 在线段 BC 上时，①BC 与 CF 的地点关系为________；②线段 BC， CD ，CF 之间的数目关系为______________ ( 将结论直接写在横线上)；(2)数学思虑：如图②，当点 D 在线段CB的延伸线上时，结论①，②能否仍旧建立？若建立，请赐予证明；若不建立，请你写出正确结论再赐予证明．◆种类二全等三角形中的动图问题3．已知等边三角形的三条边相等、三个角都等于60°.如图，△ ABC与△ CDE都是等边三角形，连结 AD ， BE.(1)假如点 B ，C， D 在同一条直线上，如图①所示，试说明：AD ＝ BE ；(2)假如△ ABC 绕 C 点转过一个角度，如图②所示，(1)中的结论还可否建立？请说明原因．◆种类三全等三角形中的翻折问题4．如图，将 Rt△ ABC 沿斜边翻折获得△ ADC ，E，F 分别为 DC ，BC 边上的点，且∠ EAF ＝1 2∠ DAB. 试猜想 DE ， BF， EF 之间有何数目关系，并说明原因．参照答案与分析1．解：∠PAM＝∠PBM.原因以下：∵NA＝NB，MA＝∴△ AMN ≌△BMN (SSS)，∴∠ MAN ＝∠ MBN ，∠ MNA ＝∠ MNB .又∵MB，MN 是公共边，NA＝NB， PN 是公共边，∴△ PAN≌△ PBN(SAS) ，∴∠ PAN＝∠ PBN.∴∠ PAM ＝∠ PBM .2．解： (1)①垂直② BC＝CD＋CF(2)CF ⊥ BC 建立； BC＝ CD ＋ CF 不建立，正确结论： CD ＝ CF＋ BC.证明以下：∵正方形ADEFAD ＝AF ，中，AD ＝ AF ，∠ DAF ＝∠ BAC ＝ 90°，∴∠ BAD ＝∠ CAF.在△ DAB 与△ FAC 中， ∠ BAD ＝∠ CAF ，AB ＝ AC ，∴△ DAB ≌△ FAC(SAS) ，∴∠ ABD ＝∠ ACF ， DB ＝ CF .∵∠ ACB ＝∠ ABC ＝ 45°，∴∠ ABD ＝ 180° － 45°＝ 135°，∴∠ BCF ＝∠ ACF －∠ ACB ＝∠ ABD －∠ ACB ＝ 90°，∴ CF ⊥ BC.∵ CD ＝DB ＋ BC ，DB ＝ CF ，∴ CD ＝ CF ＋ BC.3．解：(1) ∵△ ABC ，△CDE 都是等边三角形， ∴ AC ＝ BC ，CD ＝ DE ，∠ ACB ＝∠ DCE ＝ 60°.∵ 点 B ， C ， D 在同一条直线上，∴∠ ACE ＝ 60°，∴∠ BCE ＝∠ ACD ＝ 120°.在△ ACD 与△ BCE 中，AC ＝ BC ，∵ ∠ ACD ＝∠ BCE ， ∴△ ACD ≌△ BCE(SAS) ．∴ AD ＝ BE.CD ＝ CE ，(2)建立．原因以下：∵∠ ACB ＝∠ DCE ＝ 60°，∴∠ ACB ＋∠ ACE ＝∠ DCE ＋∠ ACE ，即∠ BCE ＝∠ ACD.又∵ AC ＝ BC ，CD ＝ CE ，∴△ ACD ≌△ BCE ，∴ AD ＝BE .4．解： DE ＋ BF ＝EF .原因以下：延伸 CB 至 G ，作∠ 5＝∠ 1，以下图．∵将Rt △ ABC 沿斜边翻折获得△ ADC ，∠ EAF ＝1∠ DAB ，∴ AB ＝ AD ，∠ ABC ＝∠ ADE ＝ 90°，∠ 2＋∠ 3＝∠ 1＋∠4， 2∴∠ ABG ＝ 90°＝ ADE .∵∠ 5＝∠ 1，∴∠ 2＋∠ 3＝∠ 4＋∠ 5，∴∠ GAF ＝∠ EAF .在△ AGB 和△ AED∠ GAB ＝∠ EAD ，中， AB ＝AD ，∴△ AGB ≌△ AED (ASA) ，∴ AG ＝ AE ， BG ＝ DE .在△ AGF 和△ AEF 中，∠ ABG ＝∠ ADE ， AG ＝ AE ，∠ GAF ＝∠ EAF ，∴△ AGF ≌△ AEF(SAS) ，∴ GF ＝ EF ，∴ BG ＋BF ＝ EF ，∴ DE ＋ BF ＝ EF. AF ＝ AF ，。