美国大学生数学建模竞赛数据及评阅分析_吴孟达
大学生数学建模竞赛简介及试题分析

程以及技术含量 5)关于模型的有说服力的检验及精道的优缺点分析 6)由模型得到的关于问题有实际意义的结论 7)某个方面突出的亮点
美国(国际)大学生数学建模竞赛特点
7 是否给出了清晰的摘要。
美国大学生数学建模竞赛论文等级
不合格论文(Unsuccessful Participants)
合格论文(Successful Participants)
乙级论文(Honorablus)
(一等奖)
特级提名论文(Finalist)
赛题内容涉及经济、管理、环境、资源、生态、医学、 安全、未来科技等众多领域。
MCM/ICM 着重强调:
研究问题、解决方案的原创性,团队合作、交流以及结果的合理性。
美国大学生数学建模竞赛题目
每个团队在下列问题中选择且只能选择一个问题, 并提交解决方案。
MCM 问题A(连续) MCM 问题B(离散) MCM 问题C (对于数据的见解) ICM 问题D(运筹学或网络科学) ICM 问题E(环境科学) ICM 问题F (政策)
特级论文(优胜论文)(Outstanding Winner)
评委眼中数学建模竞赛论文 论文的评审流程
提交的论文 不合格论文 合格论文 下一轮论文
淘汰轮
乙级论文
下一轮
摘要与框架
最 评奖轮 终
评
分析与理解
奖 轮
甲级论文 下一轮
结构严谨 条理清晰 简单易读 结果以最简单最明了的方式表达
模型 方法 结果
Are Fingerprints Unique?
我校在美国大学生数学建模竞赛中喜获佳绩

我校在美国大学生数学建模竞赛中喜获佳绩近日,2011年美国大学生数学建模竞赛成绩在竞赛官方网站公布(/undergraduate/contests/mcm/contests/2011/results/),我校的六支参赛队喜获三个一等奖(Meritorious)和一个二等奖(Honorable Mention)。
获得一等奖的代表队分别是由张战国老师指导的宋海滨、王锐、孙玉婷(C 题);由李放歌老师指导的燕姗姗、李军、孙国朋(C题);由杨月莹老师指导的崔迪、朱元杰、房强(B题)。
另外由杨月莹老师指导的李旭、商婷婷、呼建欣(C题)荣获了二等奖。
据悉,美国大学生数学建模竞赛包括数学建模竞赛(MCM:A题和B题)和交叉学科建模竞赛(ICM:C题)。
竞赛以通信形式进行,由3名学生组成一队,在4天时间内自由地收集材料、调查研究,利用计算机、专业软件和互联网等工具,完成一篇包含模型的假设、建立和求解等方面的全英文论文。
论文按时提交美国主办机构,由美国组织专家对全球各地提交的论文进行统一评审。
2011年美国大学生数学建模竞赛吸引了来自包括加拿大、中国、德国、英国在内的17个国家和地区10491名在校大学生参加。
MCM一等奖的获奖率仅为13%,ICM一等奖的获奖率为20%,我校今年的一等奖获奖率与我省其他参赛高校相比名列前茅。
附黑龙江省各高校获奖信息:参赛学校参赛队数优于一等奖一等奖二等奖成功参赛奖哈尔滨工业大学259 2 27 110 120哈尔滨工程大学72 6 29 37东北农业大学 6 3 1 2哈尔滨理工大学11 1 4 6东北林业大学 5 3 2黑龙江大学 4 2 2黑龙江八一农垦大学 5 5理学院。
美国大学生数学建模竞赛对我国高校数学教学的启示

研 究 问题 、 解决 方 案 的 原创 性 、 团队合作、 交 流 以 及
结 果 的合理 性 。MC M 的 宗 旨 是 鼓 励 大 学 师 生 对 范
V o 1 . 1 l N o . 3
Fe b .2 0 1 3
I ) Ol : 1 0 . 3 9 6 9 / j . i s s n . 2 0 9 5 — 3 3 3 X. 2 0 1 3 . 0 3 . 0 2 7
美 国 大 学 生 数 学 建 模 竞 赛 对 我 国 高 校 数 学 教 学 的 启 示
吕小光 , 姜 乐 , 成 青松
( L淮海工学院 理学 院 , 江苏 连云港 2 2 2 0 0 5 ;2 . 电子科技大学 数学科学学 院, 四川 成都 6 3 1 7 l 1 )
摘 要 : 作为数 学建模 领域 内的 国际性权 威 赛事 , 美 国 大 学 生数 学 建 模 竞 赛 受 到 了全 世 界 各 大 高校
当今 社 会 发 展 越 来 越 快 , 各 种 竞 争 压 力 越 来 越 大 , 对人 才 的要求 也 越来越 高 。人 才 的竞争 , 实 际 上 就 是 教 育 的竞 争 、 能 力 发 展 的 竞 争 。 在 传 统 的 教 育
人 ( 本 科 生) 一 组在 四天 时 间 内 , 就 指 定 的 问 题 完 成 从 建 立模 型 、 求解 、 验 证 到 论 文 撰 写 的 全 部 工 作 。 竞
大 洲 的 数 千 名 大 学 生 参 加 。 M CM / I CM 着 重 强 调
建 模 竞 赛 对 高 校 教 师 队 伍 的 能 力 是 一 个 很 大 的 挑 战, 需 要他 们 进一步 提高 能力 和素 质 , 同 时 也 需 要 各
美国大学生数学建模竞赛题解析与研究

推荐
《美国大学生数学建模竞赛题解析与研究(第5辑)》内容新颖、实用性强,可作为指导学生参加美国大学生 数学建模竞赛的主讲教材,也可作为本科生、研究生学习和准备全国大学生、研究生数学建模竞赛的参考书,同 时也可供研究相关问题的科研人员orward by Sol Garfunkel ICM竞赛主席序 Forward by Chris Arney 丛书简介 前言 I Mathematical Modeling for MCM/ICM 2013 Chapter 1 Introduction Chapter 2 General Methodology 2.1 Before the Contest 2.2 Reading the Problem
谢谢观看
图书目录
第1章棒球“最佳击球点”问题 1.1问题分析 1.1.1棒球?球棒 1.1.2分析问题与提出假设 1.2定位球棒的最佳击球点 1.2.1一个初步的想法:定位最佳击球点 1.2.2布罗迪功效模型 1.2.3考虑击球手的舒适度 1.3不同材质球棒的特性分析 1.3.1“软木化”的球棒与普通木质球棒的对比 1.3.2铝制球棒与普通木质球棒的对比
美国大学生数学建模竞赛题解析与研 究
2014年高等教育出版社出版的图书
01 内容简介
03 推荐
目录
02 图书目录 04 目录
《美国大学生数学建模竞赛题解析与研究》是2014年高等教育出版社出版的图书,作者是赵仲孟、王嘉寅。
内容简介
《美国大学生数学建模竞赛题解析与研究(第3辑)》内容简介:本系列丛书是以美国大学生数学建模竞赛 (MCM/ICM)题为主要研究对象,结合竞赛特等奖的论文,对相关的问题进行深入细致的解析与研究。《美国大 学生数学建模竞赛题解析与研究(第3辑)》的主要内容包括:棒球“最佳击球点”问题、重新平衡受人类影响的 生态系统问题、泛太平洋垃圾带问题、犯罪情报分析的建模问题、交通环岛的优化设计问题和能源与移动问题。 《美国大学生数学建模竞赛题解析与研究(第3辑)》可作为指导大学生学习和准备美国大学生数学建模竞赛的主 讲教材,也可作为大学生、研究生学习和准备全国大学生、研究生数学建模竞赛的参考书,同时可供研究相关问 题的人员参考使用。
美国大学生数学建模竞赛的命题与评阅指导课件

2. MCM/ICM 题目的不同之处
• ICM问题通常是全球关注的问题,不依赖于文化背景 • 这就更有利于中国学生。因为某些MCM问题有时
偏重文化与传统的背景,如MCM 2006B,机场轮椅 问题,MCM2021A,交通灯设计,Stop sign(路口暂时 停的标记牌),yield sign〔并道时必需看来车方向〕 在中国没有此类警示牌,MCM2021A, Ultimate Brownie Pan 等,很多中国学生无此概念。 • 参赛的学生根据自己的特长,选择不同类型的题目。
SOL GARFUNKEL, EXECUTIVE DIRECTOR, COMAP
“I hope that you will to work on the exciting and important problems you see here, and that you will join the MCM/ICM contest and rewarding work of increasing the awareness of the importance of Mathematical Modeling.〞
初评过程---论文分类
初评〔第一阶段triage judging〕,也称为鉴别评审阶段。 每篇论文在此阶段中按质量分为以下三类: 第一类是可以进入下一阶段评审的论文; 第二类是满足竞赛要求,但却缺乏以进入下一阶段评
审的论文,这类论文为合格论文; 第三类是不符合竞赛要求的论文,这类论文为不合格
论文。
31
Tianjin University
• Mathematical Modeling for the MCM/ICM Contest , Volume 2
• MCM/ICM评委 • 内容简介 • 1-4章:2021年4个竞赛题的分析、点评与解答 • 第5章:对数学建模研究当前热点问题的拓展 • 实用性强,可供参加美赛的读者参考使用
2022年美国大学生数学建模竞赛(MCMICM)获奖情况数据统计

2022年美国大学生数学建模竞赛(MCMICM)获奖情况数据统计美赛介绍美国大学生数学建模竞赛【MCM】是数学建模领域内的国际性权威赛事,由美国自然基金协会和美国数学应用协会共同主办,美国数学学会、运筹学学会、工业与应用数学学会等多家机构协办。
自 1985 年以来,美国大学生数学建模竞赛已经成功举办38 届,2022 年吸引了来自全球各高校的27205支队伍参加,通过获奖数据分析,可以快速掌握美赛的获奖概率,充分进行备赛拿奖。
奖项说明Outstanding Winners 俗称O奖也叫作特等奖Finalist 俗称F奖也叫作特等奖提名奖Meritorious Winners 俗称M奖也叫作一等奖Honorable Mentions 俗称H奖也叫作二等奖Successful Participants 俗称S奖也叫作成功参赛奖Unsuccessful Participants 俗称U奖也叫作不成功参赛奖Disqualified Teams 俗称D奖被取消评奖资格参赛情况2022年美赛共有参赛队伍27205个参赛学生80693名,2021年参赛队伍26112个,比较起来增加了1093个队伍。
2022MCM与ICM的参加情况:15105个队伍参加MCM(55%)12100个队伍参加ICM(45%)vs2021MCM与ICM的参加情况:10053个队伍参加MCM(38.5%)16059个队伍参加ICM(61.5%)可以发现同比去年MCM参与比上升,ICM参与比则有所下降。
ps:在成绩表里面共有7列,分别是:队号、学校、国家、指导教师、题目、奖项以及附加奖项,其中附加奖项指的是获得列特等奖后,额外获得的奖项。
特大喜讯在这里数模君要公布一个喜讯:2022年数模乐园惊现四支美赛O 奖(outstanding winners)队伍!其中一位更是获得了o奖冠名奖!工业与应用数学学会(SIAM)将指定一个来自 MCM 问题 A 和 B 的优秀团队作为 SIAM 获奖者。
2013美赛结果分析

2013年美国大学生数学建模竞赛结果发布COMAP非常高兴地宣布第29届大学生数学建模竞赛(MCM)结果。
今年共有5636支队伍参加了比赛,分别代表14个国家和地区。
以下11支队伍提交的论文被评定为优胜论文(OUTSTANDING WINNERS):Beijing Univ. of Posts and Telecomm, China(北京邮电大学:郭众鑫、吴帆、王蓓丹;指导教师:贺祖国)Bethel University, Arden Hills, MNColorado College, Colorado Springs, COFudan University, China(复旦大学:王坤睿、许晶、曾溦;指导教师:杨翎)Nanjing University, China(南京大学:陈炜、刘威志、杨岑莹;指导教师:瞿慧)Peking University, China(北京大学:金冲、刘博闻、吴蒙; 指导教师:刘旭峰)Shandong University, China(山东大学:宋炎侃、徐珂、伊凡;指导教师:Hengxu Zhang)Shanghai Jiaotong University, China(上海交通大学:文理斌、吴婧元、王聪; 指导教师:Yuehui Zhang)Tsinghua University, China(清华大学: 高鹏飞、何博硕、邹天忻;指导教师:吴昊)University of Colorado Boulder, Boulder, CO (2)今年的竞赛时间是从2013年1月31日(星期四)到2013年2月4日(星期一)。
在这段时间里,由三名学生组成的本科生或高中生队伍从两个竞赛问题中选择一个,认真研究并建模,最终提交一份解决方案。
今年MCM的主要形式通过网络展开。
参赛队伍需要在规定的时间内通过COMAP的MCM网站注册、获得竞赛材料并下载题目和数据。
今年MCM的两个问题被公认为具有很大的挑战性。
美赛数据及评阅分析
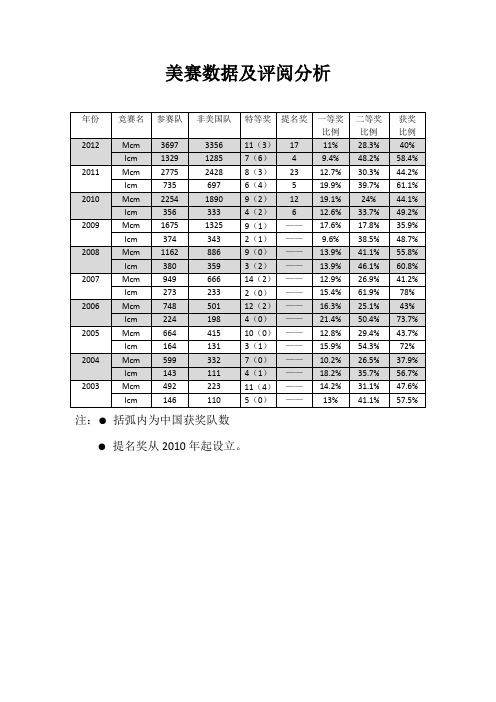
美赛数据及评阅分析注:●括弧内为中国获奖队数●提名奖从2010年起设立。
分析:● 10年间年均增长25%,近5年年均增长33.8%。
●美国参赛队增长不明显,增长队数主要来自于非美国队,这其中主要来自于中国参赛队的增长。
●2012年非美国参赛队占比已经达到了90.8%。
分析:● 10年间年均增长31.6%,近三年年均增长90%。
●10年间美国参赛队几乎未增加,增长队数主要来自于中国参赛队。
●2012年非美国参赛队占比已经达到了96.7%。
分析:●特等奖获奖比例平均为:1.03%●一等奖获奖比例平均为:14.7%●二等奖获奖比例平均为:28%●总获奖比例平均为:43.73%分析:●特等奖获奖比例平均为:1.4%●一等奖获奖比例平均为:15%●二等奖获奖比例平均为:45%●总获奖比例平均为:61.4%据美赛“评委评论”介绍,美赛评阅过程大致分为三轮。
第一轮可以称为“淘汰轮(the triage round)”。
此轮评阅主要以摘要信息以及论文整体结构为评判依据,时间大约是5~10分钟。
每个评委以“通过”“不通过”计分,事先应当设置有大致的“通过”比例(此轮与国内研赛的网评阶段相类似)。
当两位评委意见不一致时可以协商达成一致意见,如果仍不能达成一致意见,则请第三位评委评阅。
有“评论”介绍说:这一轮的淘汰率大约为45%,通过这一轮评审的参赛队大约有80%的获奖概率。
关于如何通过这一轮评审,评委给出的建议是:1、摘要至关重要,必须清晰且信息量充分,评委关心的是你对问题的理解是否准确,你建立的模型及使用的方法是否恰当,以及根据你所建模型得到的主要结果和主要结论是否合理。
过于冗长的技术性描述将阻碍评委对你的结果的关注。
2、你的论文应当有良好的组织架构,以使得评委能够在5~8分钟内理解你的论文的关键信息。
第二轮可以称为“评奖轮(the Preliminary Rounds )”。
每篇论文由若干(应当不超过三名)评委评阅,以5分或10分制计分,每位评委评阅每篇论文的时间大约在15~30分钟之间。
美国大学生建模竞赛特等奖获得者经验分享

参加大学生建模竞赛需要具备哪些方面的能力?有哪些实战经验值得借鉴?获2019年美国大学生数学建模竞赛(MCM)与交叉学科建模竞赛(ICM)特等奖的西交利物浦大学学生团队在经验分享中总结出以下获奖心得:一、以“解决问题”为导向来思考问题,对题目首先要理解到位,而不是急于套用数学模型;二、学生须具备西交利物浦大学所倡导的“学会学习”的能力,尤其是在短时间内快速自学新知识的能力;三、组队的三位同学须在专业能力上优势互补,分工明确、紧密合作。
以下是来自西交利物浦大学获奖团队的经验分享全文:2019年美国大学生数学建模竞赛(MCM)与交叉学科建模竞赛(ICM)成绩公布,西交利物浦大学团队在全球一万多支ICM参赛队伍中脱颖而出,喜获特等奖。
今年全球仅有19支队伍获此殊荣,这也是西交利物浦大学历年参赛所获的最高荣誉。
MCM/ICM(简称“美赛”)由美国数学及其应用联合会主办,是世界范围内极具影响力的数学建模比赛。
今年组委会大幅削减了获奖率,获ICM特等奖(Outstanding Winners)的队伍仅有19支,除西交利物浦大学外,其他获奖团队来自美国杜克大学、中国人民大学、南京大学等。
摘获特等奖的西浦团队由三名大三学生——计算机科学与软件工程系的张啸天(下图左)、数学科学系的王光宇(下图中间)和张一华(下图右)组成。
数学科学系的苏炯龙博士、刘刚博士、马飞博士、费杰博士等老师在赛前为学生提供了指导。
按照竞赛要求,三人团队需在四天时间内就指定问题完成从建立模型、求解、验证到论文撰写的全部工作。
据张啸天介绍,团队选择了关于卢浮宫人流疏散的题目,该题除了需运用到数学建模的相关知识外,还要求参赛者具备良好的运筹学功底,甚至具有一定的建筑学知识。
在团队紧密合作的基础上,三人将卢浮宫的房间抽象化,做成一个可用于数学分析的网络结构模型图,再用图论的知识和数学算法来达到疏散时间最少化;同时运用运筹学算法进行优化,并用遗传算法来改善结果。
吴孟达-谈谈数学建模

1. 直觉——透视现象本质的洞察力
2. 联系——后知识体系的建构
3. 求异——批判精神与深度思考习惯的养成
4. 选择——宏观把握与判断抉择能力
5. 归纳——思维模式的完善
6. 素养——模型检验意识以及对结果的敏感性
20/43
四、关于数学建模课程教学理念的思考
1. 直觉——透视现象本质的洞察力 创新离不开直觉,对现实世界繁杂现象背后的潜在
数学建模——从自然走向理性之路
数学建模——由“知”到“识”的催化平台
2/43
数学建模ABC
A:Assume
B: Borrow C: Criticize
3/43
数学建模的基本要素
The three most fundamental
ideas in mathematical modeling are transience, permanence, and optimality.
结论: 来自可靠的信息源、提及名人并且谈论流行话题
建模启示:对建立评价类模型具有典型意义。
40/43
四、关于数学建模课程教学理念的思考
6. 素养——模型检验意识以及对结果的敏感性
对模型的实用性及合理性的检验意识,以及对数学
表达式和数值结果的敏感性,是是否具有良好工程素养
的表现。
41/43
结 束 语
数学建模课程教学过程中,我们在关注 如何帮助学生掌握数学建模方法的同时,应更
多地关注对学生的系统性思维方式的训练,即
对数学建模思想的理解,以期学生通过学习此
门课程,真正提升自己面对自然现象“量化思
考”的能力。
42/43
的大小,还要取决于输入输出及检索功能的强弱。数学
参加美国大学生数学建模竞赛经验分享

参加美国大学生数学建模竞赛经验分享第一篇:参加美国大学生数学建模竞赛经验分享一、组队篇:团队水平基本决定了最终结果的上限——在美国赛,差团队是无可能做出好结果的(这点与国赛不同)无论队员还是导师,猎取的优先级都应该是这样: 1.2.3.4.没过得奖但有经验的:这种动力最足得过奖的:如果后来参赛成绩还不如之前,对人对己都交代不过去没经验但想得奖的:大多数没经验、想打酱油:不光说队员,还要留意导师,你懂的^_^ 这跟创业组队一样,别在乎现在神马光环,关键看的是将来能够付出多少。
必须保证团队里每个人都有共同的愿景和强大的动力,否则内耗是迟早的事。
高手和好导师都是稀缺资源,下手越早收获可能越大,想找高手:••你必须也是个高手,至少某方面特长能给人信心;必须保证团队间能衷诚合作,互相鼓励/配合——这点与谈恋爱一样,要经一定时间的磨合和考验,才能看得清;•保证每个人的弱点能有效弥补,即便是高手全才也不多,对其弱点如果没有合适的人弥补,结果可能还不如实力平均的队伍;•要能顶得住本校其他队的竞争,比如挖人、争导师、抢机房等等——人才太多没办法,哎~总之,除了主动出击、笨鸟先飞之外,还要求一定的口碑、人脉和组织能力、观察精准、明决善断,敢于取舍。
二、装备篇:•数值工具:各种软件和代码操弄熟练是基本要求,软件不必求多,但每款特色部分一定要尽可能熟。
长的代码尽量拆成短的,而且要调通测试过,关键地方注释好,比赛时,宝贵的时间用来debug是不值的;•信息检索:搜索引擎技巧是根本,其他信息含量都不太高,国内各种数理论坛算是基础,国外各种资源尽量积累(免费论文库、wiki、各大数值软件官网、专业论坛、大牛的blog/twitter、stackoverflow、quora……不会翻墙的要尽量先弄清楚,不然有的资源打不开或者下不到哦),图书馆的国外学术资源也别忽视;••写作软件:有时间精力的同学学一下LaTeX,实在没时间的将就用word转pdf吧;资料积累:钱少的同学可以下outstanding论文,仔细研究(新浪爱问和madio上能下到2011年前的);钱多的可以买comap的杂志,不只为看论文,主要看每题的综述,了解那一题当年的答题情况和阅卷人的思路(我那几年国内有卖的,之后几年没关注了,不清楚现在哪能弄到)。
美国大学生数学建模竞赛试题Problem-E-结果成绩

2016 Interdisciplinary Contest in Modeling®Press Release—April 8, 2016COMAP is pleased to announce the results of the 18th annual Interdisciplinary Contest in Modeling (ICM). This year 5025 teams representing institutions from eight countries participated in the contest. Fourteen teams were designated as OUTSTANDING WINNERS representing the following schools:∙Brown University, USA∙Chongqing University, China∙Communication University of China, China∙Huazhong University of Science and Technology, China, (INFORMS winner)∙NC School of Science and Mathematics, USA,(Vilfredo Pareto Award)∙NC School of Science and Mathematics, USA,(INFORMS winner)∙Northwestern Polytechnical University, China∙Renmin University of China, China∙Rensselaer Polytechnic Institute, USA,(Leonhard Euler Award)∙Shandong University, China∙Sun Yat-Sen University, China, (INFORMS winner)∙United States Military Academy, USA,(Rachel Carson Award)∙University of Colorado Denver, USA∙Xiamen University, ChinaThis year’s conte st ran from Thursday, January 28 to Monday, February 1, 2016. During that time, teams of three students researched, modeled, and communicated a solution to an open-ended interdisciplinary modeling problem. The 2016 ICM was primarily an online contest, where teams registered and obtained contest materials through COMAP’s ICM W ebsite.ICM teams chose one of the following three problems: The D Problem involved measuring the evolution of so ciety’s information networks. By taking a historical perspective of flow of information relative to value of information, the modelers sought to understand the methodology, purpose, andfuncti onality of society’s networks. The E Problem focused on the theme of environmental science. The teams needed to understand the drivers of water scarcity to create intervention strategies for a region to mitigate the water crisis. The new F Problem introduced policy modeling to the ICM. The problem for this first-time topic of policy modeling focused on the Middle East-Europe refugee migration issues. Consistent with other ICM problems, the policy problem challenged teams to utilize a diverse set of disciplinary skills including science, mathematics, politics, government operations, data science, and analysis in their modeling and problem solving. In all three cases, teams searched for pertinent data and grappled with how phenomena internal and external to the system under study needed to be considered. The student teams came up with creative and relevant solutions.These problems also had the ever-present ICM requirements to use thorough data analysis, creative modeling, and scientific methodology, along with effective writing and visualization to communicate their teams' results in a 20-page report. A selection from the Outstanding solution papers will be featured in The UMAP Journal, along with commentaries from the problem authors and judges. This year’s judges remarked that due to the multi-disciplinary nature of the problems, teams were able to solve these problems using a variety of methods and tools. This allowed teams to showcase their strengths in many diverse areas including history, information science, networks, ecology, environmental sciences, health sciences, public policy, dynamical systems, and geo-spatial techniques.2016 ICM Statistics∙5025 Teams participated∙864 Problem D submissions∙3209 Problem E submissions∙952 Problem F submissions∙91 US Teams (2%)∙4934 Foreign Teams (98%) from Australia, Canada, China, Hong Kong SAR, Indonesia, Singapore andUnited Kingdom∙14 Outstanding Winners (1%)∙15 Finalist Winners (1%)∙935 Meritorious Winners (18%)∙2287 Honorable Mentions (45%)∙1649 Successful Participants (33%)∙125 Unsuccessful Participants (2%)ICM is associated with COMAP’s Mathematical Contest in Modeling (MCM), which was held during the same weekend. ICM is designed to develop and advance interdisciplinary problem-solving skills in science, technology, engineering, mathematics (STEM) and the humanities, as well as competence in data science and written communication. Over the years the ICM problems have included topics in environmental science, biology, chemistry, resource management, operations research, information science, public health, and network science. Each team is expected to include advisors and team members who represent a range of disciplinary and interdisciplinary interests in applied problem solving and modeling. To obtain additional information about the ICM and to obtain a complete listing of all the team designations, please visit the ICM Website at: .Major start-up funding for the ICM was provided by a grant from the National Science Foundation (through Project INTERMATH) and COMAP. Additional support is provided by The Institute for Operations Research and the Management Sciences (INFORMS). COMAP's Mathematical Contest in Modeling and Interdisciplinary Contest in Modeling are unique among modeling competitions in that they are the only international contests in which students work in teams to find a solution. Centering its educational philosophy on mathematical modeling, COMAP uses mathematical tools to explore real-world problems. It serves the educational community as well as the world of work by preparing students to become better informed—and prepared—citizens, consumers, workers, and community leaders.Administered byThe Consortium for Mathematicsand Its ApplicationsContest DirectorsChris Arney, United States Military Academy, NY Tina Hartley, United States Military Academy, NY Executive DirectorSolomon A. Garfunkel, COMAP, Inc., MA。
美赛国赛数学建模试卷的分析与体会40页文档

56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。 60、迢迢新秋夕,亭亭月将圆。
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做,明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生,以及整个命运 的,只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
美国数学建模竞赛成绩揭晓

2019美国数学建模竞赛成绩揭晓近日,2019美国大学生数学建模竞赛成绩揭晓。
西交利物浦大学92个队参赛共获一等奖4个、二等奖21个、三等奖67个,获奖总数再创新高。
值得一提的是,今年西交利物浦大学首次有7个队参加交叉学科建模竞赛(ICM),该赛事要求参赛者具有运用数学模型解决跨学科问题的能力,同时对利用计算机处理大批量信息的能力也有着更高的要求。
最终西交利物浦大学有6支参赛队伍获得ICM类二等奖,该获奖比例在全国各高校中名列前茅。
美国大学生数学建模竞赛(MCM)是数学建模领域内的国际性权威赛事,由美国自然基金协会和美国数学应用协会共同主办,美国数学学会、运筹学学会、工业与应用数学学会等多家机构协办。
自1985年以来,美国大学生数学建模竞赛已经成功举办28届,大赛每年吸引了包括哈佛大学、麻省理工学院、北京大学、清华大学等著名高校的优秀学生参与奖项角逐,2019年吸引了来自全球各高校的3000余支队伍参加。
美国大学生数学建模竞赛分一般类型(MCM)和交叉学科(ICM)两类,今年的赛事于美国东部时间2月9日晚上8点在全球通过网络准时开始。
MCM今年共设两个题目:关于树叶分类与重量计算的A 题《TheLeavesofaTree》,关于漂流时间安排与河流容量计算的B题《CampingalongtheBigLongRiver》。
ICM的赛题是C题:从网络通讯记录中找出潜在作案同谋《ModelingforCrimeBusting》。
参赛学生3人组成一队,任选其中一题,利用建立数学模型的方法解决实际问题。
大赛不仅要求参赛选手具备扎实的数学、计算机和论文写作功底,同时对其学术英文表达水平等也提出了相当高的要求。
西交利物浦大学本着“自愿参与、自行组队、不选拔、不排除”的原则,积极为学生搭建参与此高水平国际赛事的平台。
“美国数学建模竞赛为学生们提供了一个培养数学学习与应用能力的机会,相较于比赛成绩,我们更看重的是学生在比赛过程中得到的锻炼机会。
美赛评分标准

美赛评分标准
美国数学建模竞赛(MCM/ICM)的评分标准主要包括以下四个方面:
1. 建模过程:评估参赛者对问题的理解和建模过程,包括问题的定义、假设的合理性、模型的建立和求解过程等。
2. 分析:评估参赛者对问题的深入分析能力,包括数据的处理、模型的验证、结果的解释和预测等。
3. 结论:评估参赛者的结论是否有充分的依据和支持,结论是否准确和有意义。
4. 论文表述:评估参赛者的论文表述能力,包括语言的使用、结构的安排、逻辑的清晰度等。
根据以上四个方面的表现,美国数学建模竞赛的评分标准可以分为以下几个等级:
1. Meritorious(优秀):论文在各方面都非常出色,论据充分、结构清晰、论文表述良好,各方面都达到了要求。
2. Honorable(荣誉):高于平均水平,并包含评申要求的所有要素,达到最基本的要求。
3. Successful(成功):提交了完整论文,但该解答不完整、出现缺陷或弱点。
4. Unsuccessful(失败):未能提交完整的论文或者未能达到最低的参赛要求。
以上信息仅供参考,建议查阅美赛官网获取更准确的信息。
美国大学生数学建模竞赛打分评审标准

美国大学生数学建模竞赛等级评审标准评审要点∙是否对赛题给出了满意的解读方式,并对赛题中可能出现的概念给予了必要的澄清;∙是否明确列出了建模用到的所有条件及假设,并对其合理性给出了解释或论证;∙是否通过对赛题的分析给出了建模的动机或论证了建模的合理性;∙是否设计出了能有效地解答赛题的模型;∙是否对模型给出了稳定性测试;∙是否讨论了模型的优缺点,并给出了清晰的结论;∙是否给出了圆满的摘要。
没有全部完成解答的论文不但是可接受的,而且如果在某些方面有创新并有独到之处,仍然可能获得较好的评审结果。
等级划分参赛论文如果没有按要求讨论赛题,或违反了竞赛规则,则会被定为不合格论(Unsuccessful Participants) 。
其余参赛论文根据评审标准按质量分为5 个级别,由低到高分别为合格论文(Successful Participants)、乙级论文(Honorable Mention)、甲级论文(Meritorious)、特级提名论文(Finalist)、特级论文(Outstanding Winner) (也称为优胜论文)。
任何论文只要对赛题进行了适当的讨论,没有违反竞赛规则,就是合格论文。
只有建模和写作都最优秀的论文才可能评为特级论文。
每个级别的论文所占的百分比如下:∙合格论文,大约50% 的论文属于这个级别。
∙乙级论文,大约30% 的论文属于这个级别。
∙甲级论文,大约10% 到15% 的论文属于这个级别。
∙特级提名论文,大约1% 的论文属于这个级别。
∙特级论文,大约1% 的论文属于这个级别。
除了给论文评级外,MCM/ICM 竞赛还设有INFORMS 奖、SIAM 奖、MAA 奖及Ben Fusaro 奖等4 个奖项,奖励优秀论文。
INFORMS 奖是由美国运筹及管理学协会(the Institute for Operations Research and the Management Sciences) 设立的。
对美国大学生数学建模竞赛的一些认识及感受(2012426)

有固定的模式,要求赛前准备的知识非常多 ,诸如微分方程及数值解,运筹学,图论, 高级算法等。 题目中往往不提供数据或提供很多数据。
6
2012 MCM A:The Leaves of a Tree
"How much do the leaves on a tree weigh?" How might one estimate the actual weight of the leaves (or for that matter any other parts of the tree)? How might one classify leaves? Build a mathematical model to describe and classify leaves. Consider and answer the following:
1999年起,美国数学及其应用联合会又同时推出 交叉学科竞赛(Interdisciplinary Contest in Modeling ),简称 ICM(涉及数学、环境科学、 生物学、化学、资源管理等交叉学科)。
美国大学生数学建模竞赛的宗旨
MCM的宗旨:鼓励大学师生对范围并不固定 的各种实际问题予以阐明、分析并提出解法, 通过这样一种结构,鼓励师生积极参与并强调 实现完整的模型构造的过程。
美国大学生数学建模竞赛题2009--2011
09A Designing a Traffic Circle(交通环岛) 09B Energy and the Cell Phone(能源与手
机) 10A The Sweet Spot((犯罪学) 11A Snowboard Course(单板滑雪场地) 11B Repeater Coordination(中继站的协调)
美国大学生数学建模竞赛概况及备战建议

・自2013年起,全国大学生数学建模竞赛组委会联 合中国工业与应用数学学会数学模型专业委员会,将与美 赛组织者通力合作,共同评阅美赛论文p1。
3美赛备战参考建议
因为参加美赛绝大多数是中国队伍,美赛俨然已成为 “中国大学生数学建模竞赛”的春季赛。但其并不与“中 国式数学建模+中译英”画等号。如果不熟悉美赛的风 格及相关注意事宜,难以在激烈的竞赛中脱颖而出。如何 准备才能在美赛中取得佳绩?笔者结合自身实践与体会, 从以下几方面阐述,抛砖引玉以飨读者。 3.1培养检索英文文献能力 通常情况下,数学建模是在对实际问题做适当简化和 处理的基础上建立模型,这就需要选手熟悉问题的背景和 特点。早期的美赛题目许多来自于美国的社会与生活,如 2005年的“水灾计划”和“收费亭”赛题。这对于不熟 悉美国社会特点的外国选手,尤其是中国学生来说是很难 找到切人点,故常常得到一些不切实际的结果。更糟糕的 是,与赛题相关的中文文献往往寥寥无几,难以满足比赛 的需要,这就要求参赛选手必须习惯检索英文文献。鉴于 Google学术搜索包括了世界上绝大部分出版的学术期刊且 其功能强大、操作简单,所以我们建议选手优先熟悉 Google学术搜索功能及高级学术搜索技巧。 3.2注重文献阅读技巧 有针对地选择文献关键在于选准关键词,这样才能确 保检索内容的全面性。阅读文献时的顺序是先看摘要,通
部时间1月31日20点至2月4 13 20点(北京时间2月1
13
9点至2月5日9点)进行。今年的赛题延续了美赛以
参赛队伍数
Outstanding
5636 11 13 857 1650 3095
往的风格,与之同时也出现了一些新的亮点,在MCM的
Winner
美国大学生数学建模竞赛数据及评阅分析

美国大学生数学建模竞赛数据及评阅分析
吴孟达;毛紫阳;王丹
【期刊名称】《数学建模及其应用》
【年(卷),期】2012(000)004
【摘要】统计了美国大学生数学建模竞赛近十年的参赛数据,对其评阅过程进行了分析,得出了一些有参考价值的结论。
【总页数】4页(P75-78)
【作者】吴孟达;毛紫阳;王丹
【作者单位】国防科技大学理学院数学与系统科学系
【正文语种】中文
【中图分类】O141.4-4
【相关文献】
1.两类体育教练评估模型的分析与比较——以2014年美国大学生数学建模竞赛B 题为例 [J], 赵文才;路荣武;梁霄;
2.两类体育教练评估模型的分析与比较——以2014年美国大学生数学建模竞赛B 题为例 [J], 赵文才;路荣武;梁霄
3.美国大学生数学建模竞赛数据及评阅分析 [J], 吴孟达;毛紫阳;王丹
4.南理工学子在2020年美国大学生数学建模竞赛中取得突破性成绩 [J],
5.2016年美国大学生数学建模竞赛与交叉学科竞赛数据 [J], 朱斌
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
给出了 MCM 和ICM 中国队和美国队参赛队数的变化。
图1分析:
● MCM 参赛队数10年间年均增长25%,近5年年均增长33.8%,增速明显加快。
● 美国参赛队增长不明显,增长队数主要来自于中国参赛队的增长。
收 稿 日 期 :2012-11-09 通 讯 作 者 :吴 孟 达 ,E-mail:mdwu@nudtwmd.com
摘 要:统计了美国大学生数学建模竞赛近十年的参赛数据,对其评阅过程进行 了 分 析,得 出 了 一 些 有 参 考 价 值 的 结论。 关 键 词 :美 国 大 学 生 数 学 建 模 竞 赛 ;中 国 大 学 生 数 学 建 模 竞 赛 ;获 奖 比 例 ;评 阅 过 程
中 图 分 类 号 :O29 文 献 标 志 码 :A 文 章 编 号 :2095-3070(2012)04-0075-04
3 26 1 273 2 373 687 1 854 332 1 282 342 849 357 627 235 466 194 389 125 295 103 195 105
11(3) 7(6) 8(3) 6(4) 9(2) 4(2) 9(1) 2(1) 9(0) 3(2)
图2 ICM 参赛队数变化图 图3 MCM 获奖比例 图4 ICM 获奖比例
2 评 阅 过 程 分 析
据 美 赛 “评 委 评 论 ”介 绍 ,美 赛 评 阅 过 程 大 致 分 为 三 轮 。 第一轮可以称为“淘汰轮(the Triage Round)”。此轮评阅主要以摘要信息以及论文整体结构为 评 判 依 据 ,时 间 大 约 是 5~10 分 钟 。 每 个 评 委 以 “通 过 ”、“不 通 过 ”计 分 ,事 先 应 当 设 置 有 大 致 的 “通 过 ”比 例 (此 轮 与 国内研赛的网评阶段相类似)。当两位 评 委 意 见 不 一 致 时 可 以 协 商 达 成 一 致 意 见,如 果 仍 不 能 达 成 一 致 意 见 ,则 请 第 三 位 评 委 评 阅 。 有 “评 论 ”介 绍 说 ,这 一 轮 的 淘 汰 率 大 约 为 45% ,通 过 这 一 轮 评 审 的 参 赛 队 大 约 有 80% 的 获 奖 概 率 。 关 于 如 何 通 过 这 一 轮 评 审 ,评 委 给 出 的 建 议 是 : 1)摘 要 至 关 重 要 ,必 须 清 晰 且 信 息 量 充 分 。 评 委 关 心 的 是 你 对 问 题 的 理 解 是 否 准 确 ,你 建 立 的 模 型 及 使 用的方法是否恰当,以及根据你所建模型得到的主要结果和主要结论是否合理 。 过 于 冗 长 的 技 术 性 描 述 将 · 76 ·
14(2) 2(0)
12(2) 4(0)
10(0) 3(1) 7(0) 4(1)
11(4) 5(0)
17 4
23 5
12 6
-- -- -- -- -- -- -- -- -- -- -- -- -- --
11% 9.4% 12.7% 19.9% 19.1% 12.6% 17.6% 9.6% 13.9% 13.9% 12.9% 15.4% 16.3% 21.4% 12.8% 15.9% 10.2% 18.2% 14.2% 13%
78% 43% 73.7% 43.7% 72% 37.9% 56.7% 47.6% 57.5%
注:● 特等奖一栏括弧内为中国获奖队数。 ● 提名奖从2010年起设立。
从 表 1 可 以 看 出 ,近 十 年 参 赛 队 主 要 来 自 中 国 和 美 国 ,只 有 很 少 一 部 分 来 自 其 他 国 家 。 图 1 和 图 2 分 别
图1 MCM 参赛队数变化图
图3分析: ● 特等奖获奖比例平均为 1.08%,近五年获奖比例平均 为0.46%。由于参赛规模扩大,此 奖 项 获 奖 比 例 下 降 趋 势 比 较明显。 ● 一等奖获奖比例平均为14.7%。 ● 二等奖获奖比例平均为28%。 ● 总获奖比例平均为43.73%。 ● 获奖比例起伏较大。 图4分析: ● 特等奖获奖比例平 均 为 1.4%,近 五 年 获 奖 比 例 平 均 为 0.76% ,获 奖 比 例 下 降 趋 势 比 较 明 显 。 ● 一等奖获奖比例平均为15% ● 二等奖获奖比例平均为45% ● 总获奖比例平均为61.4% ● 获奖比例起伏较大。 作为比较,全国大学生 数 学 建 模 竞 赛 (以 下 简 称 “国 赛”) 获奖 情 况 统 计 如 下:一 等 奖 获 奖 比 例 平 均 约 为 1.5%,一、二 等 奖 总 获 奖 比 例 平 均 约 为 8% 。
28.3% 48.2% 30.3% 39.7% 24% 33.7% 17.8% 38.5% 41.1% 46.1% 26.9% 61.9% 25.1% 50.4% 29.4% 54.3% 26.5% 35.7% 31.1% 41.1%
40% 58.4% 44.2% 61.1% 44.1% 49.2% 35.9% 48.7% 55.8% 60.8% 41.2%
1 数 据 分 析
美国大学生数学建模竞赛(以下简称“美赛”)创办于 1985 年,已经有 27 年的历史,本文拟对美赛近 10 年 来 的 参 赛 情 况 及 评 阅 过 程 做 一 个 大 致 的 分 析 。 表 1 是 美 赛 近 10 年 参 赛 队 数 及 获 奖 比 例 统 计 。
表 1 美 赛 近 十 年 参 赛 队 数 及 获 奖 比 例 统 计
5分或10分制计分,每位评委评阅每篇论 文 的 时 间 大 约 在 15~30 分 钟 之 间。 然 后 将 所 有 论 文 按 总 分 由 高 到 低 排 序 ,按 既 定 比 例 依 顺 序 确 定 一 、二 等 奖 。
在 此 轮 评 阅 中 ,评 委 最 关 心 的 问 题 是 : 1)参 赛 者 对 问 题 意 义 及 重 心 的 理 解 是 否 准 确 到 位 ; 2)是 否 题 目 中 所 有 问 题 都 得 到 了 回 答 ; 3)模 型 与 建 模 过 程 的 一 致 性 如 何 ,表 述 是 否 清 晰 ; 4)模 型 的 技 术 含 量 如 何 ; 5)由 模 型 得 到 的 结 果 是 否 合 理 ,有 无 合 理 性 及 可 靠 性 检 验 。 第 三 轮 可 以 称 为 “最 终 评 审 轮 (the Final Judging Round)”。 每 道 题 目 在 第 二 轮 中 排 名 最 高 的 二 、三 十 篇 论 文 将 进 入 此 轮 评 审 。 此 轮 评 审 大 约 有 6~8 位 评 委 ,最 终 获 得 特 等 奖 的 论 文 必 须 经 过 所 有 评 委 的 评 审 。 在 此 轮 中 ,评 委 会 仔 细 考 量 论 文 的 模 型 、方 法 与 结 果 ,对 一 篇 特 等 奖 论 文 的 期 望 是 : 1)一 篇 信 息 量 充 分 的 摘 要 ; 2)对 问 题 本 质 的 洞 察 能 力 (very good insight into the problem); 3)文 章 思 路 清 晰 且 有 很 好 的 一 致 性 ; 4)一 个 完 整 而 且 高 质 量 的 模 型 ,包 括 假 设 、建 模 过 程 以 及 技 术 含 量 (it presented a high-quality applica- tion of the complete modeling process); 5)关 于 模 型 的 有 说 服 力 的 检 验 以 及 精 到 的 优 缺 点 分 析 ; Why do you think your model is good?Against what baseline can you compare/validate it? How sensitive is your model to slight changes in the parameters you have chosen?(sensitivity analy- sis) Complete the analysis circle:Are your recommendations practical in the problem context? 6)由 模 型 得 到 的 关 于 问 题 的 有 实 际 意 义 的 结 论 ; 7)某 个 方 面 的 突 出 亮 点 (it demonstrated noteworthy originality and creativity in their modeling effor)。 与 国 赛 相 比 较 ,美 赛 评 阅 过 程 有 以 下 特 点 : 1)遵 循 一 个 原 则 :获 奖 等 级 越 高 的 论 文 被 评 阅 次 数 越 多 。 国 赛 也 有 类 似 的 做 法 ,但 评 阅 次 数 差 异 要 小 一 些。 2)对结果的宽容度较大。例如1999年“大碰撞”,关于小行星碰撞地球 后 可 能 对 人 类 带 来 的 危 害,发 表 的优秀论文中,有的论文说没有影响,有的论文说有毁灭性影响。在历年“评委评 论”中,评 委 多 次 强 调 论 文 的“一致性”,也就是国赛中经常有人提到的要“自圆其说”。评阅中结果重要性的淡化 对 评 委 的 评 阅 水 平 提 出了更高的要求。 3)在 “评 委 评 论 ”中 ,常 常 有 评 委 强 调 考 察 参 赛 论 文 的 “两 个 理 解 ”,即 对 问 题 的 理 解 与 对 所 用 方 法 的 理 解 (Modelers can frequently gain creditability by demonstrating that they understand the problem in its con- text),一 个 理 想 的 模 型 无 非 是 “两 个 理 解 ”的 完 美 结 合 (One key to successful model building is to adapt ex- isting theory or models properly to the problem at hand,whether derived or researched,it is imperative to demonstrate an understanding of the model you are)。 因 此 ,“两 个 理 解 ”在 很 大 程 度 上 体 现 了 参 赛 者 的 建 模 能 力 。 当 然 ,这 样 评 价 学 生 的 建 模 能 力 对 评 委 的 评 阅 能 力 要 求 会 更 高 。 4)与 国 赛 不 同 的 是 ,美 赛 论 文 常 常 需 要 提 交 一 份 2 页 以 内 的 执 行 摘 要 ,其 阅 读 对 象 假 定 为 论 文 成 果 的 应 用 方 ,以 成 果 特 点 介 绍 及 可 操 作 内 容 为 主 ,不 需 要 技 术 细 节 。 这 些 内 容 在 实 际 应 用 课 题 研 究 中 往 往 也 是 课 题 成果应用方所关心的。此环节的设立体现了美赛对可执行结论的重视。美赛优秀论文通常也有单独一节 “The Conclusions”。
