天津市蓟县康中中学2014届高三第二次模拟考试数学(理)试题

合集下载

【政治】天津市蓟县康中中学2014届高三第二次模拟考试试题

天津市蓟县康中中学2014届高三第二次模拟考试试题第I卷选择题（共44分)本大题共11小题，每小题4分，共44分。

在每小题给出的四个选项中。

只有一项是最符合题目要求的。

1．2013年我国省级政协主席全部“退出”同级中共党委常委班子，这有利于A．各民主党派参加国家政权B．完善党的领导方式和执政方式C．开展形式多样的基层民主协商D．发挥社会主义协商民主制度的优势2．刘某从2000年起承包山地，承包期是50年。

由于承包双方担心未来人民币币值变化过大，在合同中做出如下约定：承包费贬值率与升值率按‘1999年12月24K黄金价1 15 5∥克为标准。

以后黄金价按银行售价浮沉，变动在20％以上时按等值24K黄金量计算当年的承包费。

在我国民间，．如果今后能较少订立这类“麻烦"的合同条款，其实现条件应包括①国内物价总水平稳定②国内银行的贷款利率稳定③国际市场黄金价格衡定④人民币汇率稳定A．④B．①④ C．②③ D．③④党的十七大提出，要从各个层次、各个领域扩大公民有序政治参与，最广泛地动员和组织人民依法管理国家事务和社会事务、管理经济和文化事业。

回答5一6题。

3．扩大公民有序政治参与的意义在于①扩大了公民的政治权利②可以使公共决策更加科学化、民主化③有利于保障公民的个人利益④有利于推进民主政治的发展A．①②B．②③C．①④D．②④4．民族区域自治的社会基础是A．各民族大杂居、小聚居、交错杂居的分布特点B．长期统一的多民族国家的历史和现状C．汉族与少数民族的密切关系5．2013年“五一”期间，小黄和父母选择了标价为每人3500元的青藏铁路专线旅游。

小黄用200元在布达拉宫广场的地摊上买了几件富有藏传佛教特色的小饰品，父母则在商场用刷卡消费的方式购买了1000多元的藏医药保健品。

材料中涉及的货币的职能依次是A．价值尺度、支付手段、流通手段B．支付手段、流通手段、价值尺度C．支付手段、价值尺度、流通手段D．价值尺度、流通手段、支付手段6．危机管理是“刀尖上的舞蹈”危机既是“危险”，也是“机会”。

2014级高三二诊数学(理)参考答案及评分意见

数学 ( 理科 ) 参考答案及评分标准
( 一㊁选择题 : 每小题５分 , 共６０分) １． D; ２． A; ３． B; ４． A; ５． D; ; ; ; ; ７． B ８． C ９． D １０． C １１． D; ) 第 Ⅱ 卷( 非选择题 , 共９分０ ( 二㊁填空题 : 每小题５分 , 共２０分) ２ n １３．㊀㊀１４．３２．８; ㊀㊀１５．４; ㊀㊀１６．．－２; n ＋１ ( 三㊁解答题 : 共７０分) B E C E ( 解: 在 әB 据正弦定理 , 有１７． Ⅰ) E C 中, ．＝ s i n øB C E s i n B ２ π , ȵ øB ＝ B E ＝１, C E＝７, ３３ B E ��s i n B ２２１ ʑ s i n øB C E＝．＝＝ C E １４７ ( 由平面几何知识 , 可知 øD Ⅱ) E A ＝ øB C E． π 在R t әA E D中, ȵ øA ＝ , A E ＝５, ２３５７２ ʑc o s øD E A ＝１－s i n øD E A ＝１－＝．２８１４第 Ⅰ 卷( 选择题 , 共６０分) ６． C; １２． A．
ɡ ɡ ɡ
C D２＝ C E２＋D E２－２ C E��D E�� c o s øC E D ＝７＋２８－２ˑ ７ ˑ２７ ˑ ( －
当 x ＝５７０时, ３ˑ５７０＋４３３．２＝６０４．２． y ＝０．
��１０分
高三数学 ( 理科 ) 二诊测试参考答案第㊀共５页) １页(
��１特征量 y 的估计值为６ ʑ 当 x ＝５７０时, ０４．２．２分 ( 解: 如图 , 作 GM ʊ C 交B 连接 MF ．１９． Ⅰ) D, C 于点 M , 作 BH ʊ AD , 交 GM 于 N , 交D C 于H． ȵE F ʊC D ,ʑGM ʊ E F． ʑGN ＝A B ＝３, HC ＝９． ȵA B ʊ GM ʊ D C, NM BM A G ２ ʑ ＝＝＝． HC B C AD ３ ʑNM ＝６． ʑGM ＝GN ＋ NM ＝９． ��４分 ʑGM ��E F． ʑ 四边形 GMF E 为平行四边形． ʑG E ʊ MF ．又 MF ⊂ 平面 B C F, G E ⊄ 平面 B C F, ��６分 ʑG E ʊ 平面 B C F． ( Ⅱ )ȵ 平面 AD E ʅ 平面 C D E F, AD ʅ D E, AD ⊂ 平面 AD E, ʑAD ʅ 平面 C D E F．以 D 为坐标原点 , D C 为x 轴 , D E 为y 轴 , DA 为z 轴建立如图所示的空间直角坐标系D x z． y ʑ E (０, ４, ０) , F (９, ４, ０) , C (１２, ０, ０) , B (３, ０, ４３) ． ң ң , , , ( ) ʑE F ＝９００ E B ＝ (３, ４３) ．－４, 设平面 E B F 的法向量n１＝ (x１ , z１ ) ． y１ , ң x１＝０ n ��E F ＝０, ９由１得． ң ３ x１－４ z１＝０ �� y１＋４３ n１ E B ＝０ ��８分取 y１＝３ , 得 n１＝ (０,３, １) ． ң ң 同理 , F C ＝ (３, ０) , F B ＝ ( －６, －４, ４３) ．－４, , ) 设平面 B C F 的法向量n２＝ ( x２ , z ． y２２ ң ３ x ４ �� －＝０２２ y n F C ＝０, 由２得． ң x２－４ z２＝０－６ y２＋４３ n２ ��F B ＝０ ��１取 x２＝４, 得 n２＝ (４, ０分３, ３３) ． n１ �� n２０ˑ４＋３ ˑ３＋１ˑ３３６３３３９ ʑ c o s＜ n１ , n２＞＝．＝＝＝ n１ | n２ | ２６ | | ２ˑ １６＋９＋２７２ˑ２１３ ��１１分 ȵ 二面角 E －B F －C 为钝二面角 ,

天津市蓟县2014-2015学年高三上学期期末考试(数学理)扫描版

2014—2015高三数学第一学期期末参考答案（理科）一、选择题1. B2. A3. C4. A5. B6. D7. A8. B二、填空题9.π12 10. 90°；1112. π32 13. )21,0( 14. 12三解答题15.（本题满分13分）解：（Ⅰ）()f x =sin cos cos sin cos 46464x x x πππππ--3cos 424x x ππ-)43x ππ- 故()f x 的最小正周期为T = 24ππ=8 (Ⅱ)解法一：在()y g x =的图象上任取一点(,())x g x ，它关于1x =的对称点(2,())x g x - . 由题设条件，点(2,())x g x -在()y f x =的图象上，从而()(23s i n [(2)]43g x f x x ππ=-=-- sin[]243x πππ--cos()43x ππ+ 当304x ≤≤时，23433x ππππ≤+≤，因此()y g x =在区间4[0,]3上的最大值为m a x c o s 32g π== 解法二：因区间4[0,]3关于x = 1的对称区间为2[,2]3，且()y g x =与()y f x =的图象关于 x = 1对称，故()y g x =在4[0,]3上的最大值为()y f x =在2[,2]3上的最大值由（Ⅰ）知()f xsin()43x ππ- 当223x ≤≤时，6436ππππ-≤-≤ 因此()y g x =在4[0,]3上的最大值为max 6g π== . 16. 解：设k A 表示第k 辆车在一年内发生此种事故，123k =，，．由题意知1A ，2A ，3A 独立，且11()9P A =，21()10P A =，31()11P A =．（Ⅰ）该单位一年内获赔的概率为123123891031()1()()()19101111P A A A P A P A P A -=-=-⨯⨯=．（Ⅱ）ξ的所有可能值为0，9000，18000，27000．12312389108(0)()()()()9101111P P A A A P A P A P A ξ====⨯⨯=，123123123(9000)()()()P P A A A P A A A P A A A ξ==++ 123123123()()()()()()()()()P A P A P A P A P A P A P A P A P A =++19108110891910119101191011=⨯⨯+⨯⨯+⨯⨯ 2421199045==， 123123123(18000)()()()P P A A A P A A A P A A A ξ==++ 123123123()()()()()()()()()P A P A P A P A P A P A P A P A P A =++1110191811910119101191011=⨯⨯+⨯⨯+⨯⨯ 273990110==， 123123(27000)()()()()P P A A A P A P A P A ξ===111191011990=⨯⨯=．综上知，ξ的分布列为求ξ的期望有两种解法：解法一：由ξ的分布列得811310900018000270001145110990E ξ=⨯+⨯+⨯+⨯ 299002718.1811=≈（元）．解法二：设k ξ表示第k 辆车一年内的获赔金额，123k =，，，则1ξ有分布列故11900010009E ξ=⨯=．同理得21900090010E ξ=⨯=，319000818.1811E ξ=⨯≈．综上有1231000900818.182718.18E E E E ξξξξ=++≈++=（元）． ……………………………………………………13分17. 解：（Ⅰ）证明：由四边形ABCD 为菱形，∠ABC =60°，可得△ABC 为正三角形.因为 E 为BC 的中点，所以AE ⊥BC . 又 BC ∥AD ，因此AE ⊥AD .因为PA ⊥平面ABCD ，AE ⊂平面ABCD ，所以PA ⊥AE . 而 PA ⊂平面PAD ，AD ⊂平面PAD 且PA ∩AD =A ，所以 AE ⊥平面PAD ，又PD ⊂平面PAD . 所以 AE ⊥PD.（Ⅱ）解：设AB =2，H 为PD 上任意一点，连接AH ，EH .由（Ⅰ）知 AE ⊥平面PAD ，则∠EHA 为EH 与平面PAD 所成的角.在Rt △EAH 中，AE所以当AH 最短时，∠EHA 最大，即当AH ⊥PD 时，∠EHA 最大.此时 tan ∠EHA =AE AH ==因此 AH =.又AD=2，所以∠ADH =45°，所以 PA =2.由（Ⅰ）知AE ，AD ，AP 两两垂直，以A 为坐标原点，建立如图所示的空间直角坐标系，又E 、F 分别为BC 、PC 的中点，所以E 、F 分别为BC 、PC 的中点，所以A （0，0，0），B -1，0），C （C ，1，0），D （0，2，0），P （0，0，2），E0，0），F（1,,122）， ①)0,2,0(),2,1,3(=-=, ∴42222022103||||,cos =⨯⨯+⨯+⨯-=⋅>=<AD BP , 设异面直线PB 与AD 所成角为α，∴414sin =α ②31(3,0,0),(,,1).2AE AF == 设平面AEF 的一法向量为111(,,),m x y z =则⎪⎩⎪⎨⎧=⋅=⋅00m m因此11110,10.2x y z =++= 取11,(0,2,1),z m =-=-则因为 BD ⊥AC ，BD ⊥PA ，PA ∩AC=A ，所以 BD ⊥平面AFC ，故 BD 为平面AFC 的一法向量.又 BD =（），所以 cos ＜m , BD ＞=|BD||||5m BD ==因为二面角E-AF-C 为锐角，18解(Ⅰ)f(x)的定义域为(－∞,1)∪(1,+∞).对f(x)求导数得 f '(x)= ax 2+2－a (1－x)2e －ax.(ⅰ)当a=2时, f '(x)= 2x 2(1－x)2 e －2x, f '(x)在(－∞,0), (0,1)和(1,+ ∞)均大于0, 所以f(x)在(－∞,1), (1,+∞).为增函数.(ⅱ)当0<a <2时, f '(x)>0, f(x)在(－∞,1), (1,+∞)为增函数.(ⅲ)当a>2时, 0<a －2a <1, 令f '(x)=0 ,解得x 1= － a －2a , x 2= a －2a .当x 变化时, f '(x)和f(x)的变化情况如下表:为减函数.(Ⅱ)(ⅰ)当0<a ≤2时, 由(Ⅰ)知: 对任意x ∈(0,1)恒有f(x)>f(0)=1. (ⅱ)当a>2时, 取x 0= 12a －2a ∈(0,1),则由(Ⅰ)知 f(x 0)<f(0)=1(ⅲ)当a ≤0时, 对任意x ∈(0,1),恒有1+x 1－x >1且e －ax ≥1,得f(x)=1+x 1－x e －ax ≥1+x1－x>1. 综上当且仅当a ∈(－∞,2]时,对任意x ∈(0,1)恒有f(x)>1.19. （I ）解：*121(),n n a a n N +=+∈112(1),n n a a +∴+=+{}1n a ∴+是以112a +=为首项，2为公比的等比数列。

天津市蓟县马伸桥中学2014届高三第二次模拟考试数学试题

本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分，考试时间120分钟。

第Ⅰ卷1至2页．第Ⅱ卷3至10页。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷注意事项：1．答第Ⅰ卷前．考生务必将自己的姓名、准考号、科目涂写在答题卡上。

2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后。

再选涂其他答案标号，答在试卷上无效。

3．本卷共10小题，每小题5分，共50分。

参考公式：锥体的体积公式Sh V 31=椎体，其中S 表示锥体的底面积，h 表示锥体的高。

一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。

1.复数1+2ii (i 是虚数单位)的实部是 A ．25- B ．25 C ．15- D ．152.已知x R ∈，则“230x x -”是“()()120x x --≤成立”的A 充分不必要条件B 必要不充分条件C 充分必要条件D 既不充分也不必要条件 3.a b 、是两个非零向量，且a b a b ==-，则与a b +的夹角为A ．300B ．450C ．600D ．9004.(理)设(5n x 的展开式的各项系数之和为M,二项式系数之和为N,若M -N=240,则展开式中3x 的系数为（）A. -150B. 150C. -560D. 560（文）若把函数sin y x x =-的图象向右平移m 个单位（m ＞0）后，所得到的图象关于y 轴对称，则m 的最小值是 A ．6π B ．3π C ．32π D ．65π5．等差数列99637419,27,39,}{S a a a a a a a n 项和则前已知中=++=++的值为 A ．66 B ．99 C ．144 D ．297x=t 6．（理）直线 (t 为参数)与曲线ρ=1的位置关系是( ) y=at+2aA ．相离B ．相交C ．相切D ．不确定(文)直线20ax y a -+=与圆221x y +=的位置关系是（） A ．相离 B ．相交 C ．相切 D ．不确定7．若不等式组0220x y x y y x y a -≥⎧⎪+≤⎪⎨≥⎪⎪+≤⎩，表示的平面区域是一个三角形区域，则a 的取值范围是A.43a ≥B.01a <≤C.413a ≤≤ D.01a <≤或43a ≥8．已知m ，n 为两条不同的直线，βα,为两个不同的平面，βα⊥⊥n m ,，则下列命题中的假命题是A ．若m//n ，则βα//B ．若βα⊥，则n m ⊥C ．若βα,相交，则n m ,相交D ．若n m ,相交，则βα,相交 9．如图所示，墙上挂有边长为a 的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为2a个点的可能性都一样，则它击中阴影部分的概率是 A ．1-4π B ．4π C ．1-8πD ．与a 的取值有关 10.对任意实数,a b ，记{}()max ,()a ab a b b a b ≥⎧⎪=⎨<⎪⎩，若{}()m ax (),()()F x f x g x x R =∈，其中奇函数()y f x =在1x =时有极小值2-，()y g x =是正比例函数，()(0)f x x ≥与()g x 图象如图，则下列关于()y F x =的说法中正确的是A ．()y F x =是奇函数B ．()y F x =有极大值(1)F -和极小值(0)FC ．()y F x =的最小值为2-，最大值为2D ．()y F x =在(3,0)-上是增函数（第14题）第Ⅱ卷注意事项：1．答卷前将密封线内的项目填写清楚。

天津市蓟县届高三模拟考试数学试题及答案 (理)

2014天津蓟县高三数学模拟试卷（理科数学）本试卷共150分。

考试用时150分钟。

注意事项：、准考证号填写在试题卷的答题卡上，并将准考证号条形码粘贴在答题卡上的指定位1.答卷前，考生务必将自己的姓名置.2.选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.非选择题用黑色墨水的签字笔或钢笔直接答在答题卡上.答在试题卷上无效.3.考试结束，监考人员将本试题和答题卡一并收回.一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知复数z满足3(12)12i z i+=+，则z =（）A．3455i+B．3455i-+C．3455i--D．3455i-2．抛物线214y x=的焦点坐标是（）A．1,016⎛⎫⎪⎝⎭ B．10,16⎛⎫⎪⎝⎭ C．（0，1） D．（1，0）3．已知定义在复数集C上的函数)(xf满足⎩⎨⎧∉-∈+=RxxiRxxxf)1(1)(，则()1f i+等于（）A．2- B．0 C.2 D．2i+4．已知函数)2||,0,0)(sin()(πϕωϕω<>>+=AxAxf，其导函数)(xf'的部分图象如图所示，则函数)(xf的解析式为（）第4题A ．)421sin(2)(π+=x x f B ．)421sin(4)(π+=x x f C ．)421sin(2)(π-=x x f D ．)421sin(4)(π-=x x f 5．下列命题中是假命题的是（）A ．),0(,)1()(,342+∞⋅-=∈∃+-且在是幂函数使m m xm x f m R 上递减 B ．有零点函数a x x x f a -+=>∀ln ln )(,02C ．βαβαβαsin cos )cos(,,+=+∈∃使RD ．,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数6．已知m n 、是两条不重合的直线，αβγ、、是三个重合的平面，则//αβ的一个充分条件是（）A ．//,//m m αβB ．,αγβγ⊥⊥C ．,,//m n m n αβ⊂⊂D ．m n 、是异面直线，,//,,//m m n n αββα⊂⊂ 7．已知某程序框图如图所示，则该程序运行后输出的结果为（）A ．15 B ．25 C ．35 D ．458．从星期一到星期六安排甲、乙、丙三人值班，每人值2天班，如果甲不安排在星期一，乙不安排在星期六，那么值班方案种数为（）A ．42B ．30C ．72D ．609．已知函数()y f x =的定义域为R ，当0x <时，()1f x >，且对任意的,R x y ∈，等式()()()f x f y f x y ⋅=+成立，若数列{}n a 满足1(0)a f =，11()(N )(2)n n f a n f a *+=∈--则2009a 的值为（）A ．4016B ．4017C ．4018D ．401910．已知圆Γ：22(4)(3)25x y -+-=，过圆Γ内定点P （2，1）作两条相互垂直的弦AC 和BD ，那么四边形ABCD 面积最大值为（）A ．21 B．．212 D ．42二、填空题：本大题共5小题，每小题4分，共24分.把答案填在题中横线上.11．若1nx x ⎛⎫+ ⎪⎝⎭展开式的二项式系数之和为256，则n =_________，其展开式的常数项等于__________。

天津市蓟县高三数学第二次模拟考试试题理新人教A版

蓟县二中2013届高三第二次模拟考试数学（理）试题一、选择题（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1.i 为虚数单位,复数ii++13= A.i +2 B. i -2 C.2-i D. 2--i2.下列命题中,正确命题的个数为①若0=xy ,则0=x 或0=y ”的逆否命题为“若0≠x 且0≠y ,则0≠xy ； ②函数()2-+=x e x f x的零点所在区间是()2,1；③2=x 是0652=+-x x 的充分不必要条件； A ．0 B ．1 C ．2 D. 3 3.如果执行右面的程序框图，那么输出的S =A ．119 B.719C ．4949D.6004. 在正项等比数列{}n a 中，442=a a ,143=S ,数列{}n b 满足n n a b 2log =,则数列{}n b 的前6项和是A ．0B ．2C ．3 D. 5 5 . 在5)(xa x +二项展开式中,第4项的系数为80,则a 的值为A ．-2B ． 2C ．-2或2D ．22-或22 6.要得到一个奇函数，只需将函数()x x x f 2cos 32sin -=的图象A ．向右平移π6个单位B ．向右平移π3个单位 C ．向左平移π6个单位D ．向左平移π3个单位7.设()xxx f --=22. 若当⎪⎭⎫⎢⎣⎡-∈0,2πθ时，0)3(1cos 12>-+⎪⎭⎫⎝⎛--m f m f θ恒成立，则实数m 的取值范围是 A ．()2,-∞- B.(]),1[2,+∞⋃-∞- C ．()1,2- D.()()+∞⋃-∞-,12,8.定义一种运算⎩⎨⎧>≤=⊗ba b ba ab a ,,，令()()t x x x x f -⊗-+=224(t 为常数),且[]3,3-∈x ，则使函数()x f 最大值为4的t 值是A ．2-或6 B.4或6 C ．2-或4 D.4-或4第Ⅱ卷请在答题卡指定区域．．．．．．．内作答，答在试卷上的无效，解答时应写出文字说明、证明过程或演算步骤。

天津市蓟县康中中学高三数学第二次模拟考试试题理新人教A版

高三第二次模拟考试数学（理）试题一、选择题（本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

）1、复数43i12i++的实部是（A ）2- （B ）2 （C ） 3 （D ）42、下列大小关系正确的是（）（A ）3.0log 34.044.03<< （B ）4.04333.0log 4.0<< （C ）4.03434.03.0log << （D ）34.044.033.0log <<3、如图，一个简单空间几何体的三视图其主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形，则全面积是( )．（A ）324 （B ） 334 （ C ） 12 （ D ） 0. 84、已知变量y x ,满足⎪⎩⎪⎨⎧≤-≤≥,0,2,1y x y x 则y x +的最小值是( )（A ）1 （B ）2 （C ）3 （D ）45、把函数sin ()y x x =∈R 的图象上所有的点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是（）（A ）sin 23y x x π⎛⎫=-∈ ⎪⎝⎭R ，（B ）sin 26x y x π⎛⎫=+∈⎪⎝⎭R ，俯视图（C ）sin 23y x x π⎛⎫=+∈ ⎪⎝⎭R ，（D ）sin 23y x x 2π⎛⎫=+∈ ⎪⎝⎭R ， 6、命题“对任意的32R,1x x x ∈-+0≤”的否定是（）（A ）不存在32R,1x x x ∈-+0≤ （B ）存在32R,1x x x ∈-+0≤（C ）对任意的32R,1x x x ∈-+>0 （D ）存在32R,1x x x ∈-+>07、已知{}n a 是等差数列，48151=+a a ，则=++13833a a a ( ) （A ） 120 （B ）96 （ C ）72 （D ） 488、若m l 、表示互不重合的两条直线，βα、表示互不重合的两个平面，则α//l 的一个充分条件是( ) (A)ββα//,//l (B)m l l m //,,αβα∉=⋂ (C)α//,//m m l(D)ββα⊥⊥l ,9、已知双曲线C116922=-y x 的左右焦点分别为F 1,、F 2,P 为的右支上一点且︳PF 2 ︳=︳F 1,F 2︳则△F 1,F 2P 的面积为（）（A ） 24 （B ） 36 （C ） 48 （D ） 9610、函数R x x x x f ∈+=,)(3，当20πθ≤≤时，0)1()sin (>-+m f m f θ恒成立，则实数m 的取值范围是（）（A ）()1,0 （B ）()0,∞- （ C ） ⎪⎭⎫ ⎝⎛∞-21, （D ） ()1,∞-二、填空题：本大题共6小题。

天津市蓟县2014届高三第一次模拟考试数学(理)试题

3π2ππ22y本试卷共150分。

考试用时150分钟。

注意事项：1.答卷前，考生务必将自己的姓名、准考证号填写在试题卷的答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.非选择题用黑色墨水的签字笔或钢笔直接答在答题卡上.答在试题卷上无效.3.考试结束，监考人员将本试题和答题卡一并收回.一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知复数z 满足3(12)12i z i +=+，则z =（）A ．3455i +B ．3455i -+C ．3455i -- D ．3455i - 2．抛物线214y x =的焦点坐标是A ．1,016⎛⎫⎪⎝⎭B ．10,16⎛⎫ ⎪⎝⎭C ．（0，1）D ．（1，0）3．已知定义在复数集C 上的函数)(x f 满足⎩⎨⎧∉-∈+=R x x i R x xx f )1(1)(，则()1f i +等于A ．2-B ．0C .2D ．2i +4．已知函数)2||,0,0)(sin()(πϕωϕω<>>+=A x A x f ，其导函数)(x f '的部分图象如图所示，则函数)(x f 的解析式为A ．)421sin(2)(π+=x x fB ．)421sin(4)(π+=x x fC ．)421sin(2)(π-=x x fD ．)421sin(4)(π-=x x f5．下列命题中是假命题．．．的是 A ．),0(,)1()(,342+∞⋅-=∈∃+-且在是幂函数使m m xm x f m R 上递减B ．有零点函数a x x x f a -+=>∀ln ln )(,02C ．βαβαβαsin cos )cos(,,+=+∈∃使RD ．,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数6．已知m n 、是两条不重合的直线，αβγ、、是三个重合的平面，则//αβ的一个充分条件是A ．//,//m m αβB ．,αγβγ⊥⊥C ．,,//m n m n αβ⊂⊂D ．m n 、是异面直线，,//,,//m m n n αββα⊂⊂7．已知某程序框图如图所示，则该程序运行后输出的结果为A ．15 B ．25 C ．35 D ．458．从星期一到星期六安排甲、乙、丙三人值班，每人值2天班，如果甲不安排在星期一，乙不安排在星期六，那么值班方案种数为（）A ．42B ．30C ．72D ．609．已知函数()y f x =的定义域为R ，当0x <时，()1f x >，且对任意的,R x y ∈，等式()()()f x f y f x y ⋅=+成立，若数列{}n a 满足1(0)a f =，且11()(N )(2)n n f a n f a *+=∈--则2009a 的值为A ．4016B ．4017C ．4018D ．401910．已知圆Γ：22(4)(3)25x y -+-=，过圆Γ内定点P （2，1）作两条相互垂直的弦AC 和BD ，那么四边形ABCD 面积最大值为（） A ．21 B ．213 C ．212D ．42 二、填空题：本大题共5小题，每小题4分，共24分.把答案填在题中横线上.11．若1nx x ⎛⎫+ ⎪⎝⎭展开式的二项式系数之和为256，则n =_________，其展开式的常数项等于__________。

天津市蓟县擂鼓台中学高三数学第二次模拟考试试题理新人教A版

蓟县擂鼓台中学2014届高三第二次模拟考试数学（理）试题一、选择题（本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的） 1．设复数z 满足12ii z+=，则z = （） A ．2i -+B ．2i --C ．2i -D ．2i +2．在等差数列｛a n ｝中，已知a 1=2,a 2+a 3=13，则a 5等于（） A ．13 B ．14C ．15D ．163．若抛物线22y px =的焦点与双曲线1322=-y x 的右焦点重合，则p 的值为（）． A ．2- B ．2 C ．4- D ．44．21nx x ⎛⎫- ⎪⎝⎭的展开式中，常数项为15，则n =（）A ．3B ．4C ．5D ．65．名工人某天生产同一零件，生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ，则有Ａ．a b c >> B ．a c b >> C ．b a c >>D ．c b a >>6．如右程序框图，输出的结果为（） A ．1 B ．2 C ．4 D ．16 7．．若函数22)(23--+=x x x x f 的一个正数零点附近那么方程022=--+x x x 的一个近似根（精确到0.1）为（）A ．1.2B ．1.3C ．1.4D ．1.58．同时具有性质“①最小正周期是π，②图象关于直线3π=x 对称；③在]3,6[ππ-上是增函数”的一个函数是 A ．)62sin(π+=x yB ．)32cos(π+=x yC ．)62sin(π-=x yD ．)62cos(π-=x y9．m 、R n ∈，a 、b 、c 是共起点的向量，a 、b 不共线，b n a m c +=，则a 、b 、c 的终点共线的充分必要条件是（） A ．1=+nmB ．0=+n mC ．1=-n mD ．1-=+n m10．已知）（x f 是以2为周期的偶函数，当[0,1]x ∈时，()f x x =，那么在区间[1,3]-内，关于x 的方程()1f x kx k =++（k R ∈且1k ≠-）有4个不同的根，则k 的取值范围是（） A ．1(,0)4-B ．1(,0)3-C ．1(,0)2- D ．(1,0)-第Ⅱ卷（非选择题，共100分）二、填空题：本大题共6小题，每小题4分，共24分. 把答案填在题中横线上.11．⎰+30)sin 2(πdx x x ＝。

2014年天津市蓟县高三理科上学期数学期末考试试卷

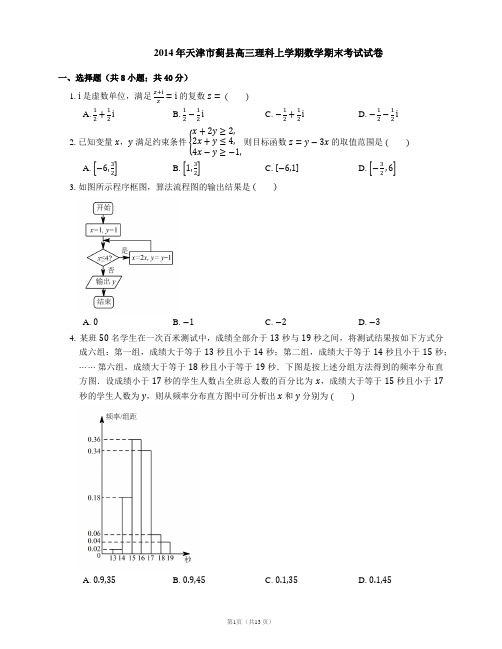
2014年天津市蓟县高三理科上学期数学期末考试试卷一、选择题（共8小题；共40分）1. i是虚数单位，满足z+iz=i的复数z= A. 12+12i B. 12−12i C. −12+12i D. −12−12i2. 已知变量x，y满足约束条件x+2y≥2,2x+y≤4,4x−y≥−1,则目标函数z=y−3x的取值范围是 A. −6,32B. 1,32C. −6,1D. −32,63. 如图所示程序框图，算法流程图的输出结果是 A. 0B. −1C. −2D. −34. 某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；⋯⋯第六组，成绩大于等于18秒且小于等于19秒．下图是按上述分组方法得到的频率分布直方图．设成绩小于17秒的学生人数占全班总人数的百分比为x，成绩大于等于15秒且小于17秒的学生人数为y，则从频率分布直方图中可分析出x和y分别为 A. 0.9,35B. 0.9,45C. 0.1,35D. 0.1,455. 双曲线x2a −y2b=1a>0,b>0的左、右焦点分别是F1，F2，过F1作倾斜角为30∘的直线交双曲线右支于M点，若MF2垂直于x轴，则双曲线的离心率为 A. B. C. D. 336. 已知下列四个命题：①U为全集，A，B是集合，则“存在集合C使得A⊆C，B⊆∁U C”是“A∩B=∅”的充要条件；②已知命题p：若x>y，则−x<−y，命题q：若x>y，则x2>y2，命题p∧¬q为真命题；③命题“对任意x∈R，都有x2≥0”的否定为“不存在x∈R，都有x2<0”；④一物体沿直线以v=2t+3（t的单位：s，v的单位：m/s）的速度运动，则物体在3∼5 s间进行的路程是22 m，其中真命题的个数为 A. 0B. 1C. 2D. 37. 在△ABC中，M是BC的中点，AM=1，点P在AM上且满足AP=2PM，则PA⋅ PB+PC等于 A. −49B. −43C. 43D. 498. 已知两条直线l1:y=m和l2:y=4m+1m>0，l1与函数y=log2x的图象从左至右相交于点A，B，l2与函数y=log2x的图象从左至右相交于C，D，记线段AC和BD在x轴上的投影长度分别为a，b，当m变化时，ba的最小值为 A. 16B. 8C. 82D. 42二、填空题（共6小题；共30分）9. 已知某几何体的三视图如图所示，则该几何体的体积为．10. 如图，△ABC的角平分线AD的延长线交它的外接圆于点E．若△ABC的面积S=12AD⋅AE，则∠BAC=．11. 在直角坐标系xOy中，已知抛物线C的参数方程为x=8t2,y=8t（t为参数），若斜率为1的直线l经过抛物线C的焦点，在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴正半轴为极轴）中，曲线C1的极坐标方程为ρ2−8ρcosθ=r2−16，如果直线l与曲线C1相切，则r=．12. 设△ABC的内角A，B，C所对边的长分别为a，b，c．若b+c=2a，3sin A=5sin B，则角C=．13. 已知f x是定义在−3,3上的偶函数，当x∈0,3时，f x=x2−2x+12，若函数y=f x−a在区间−3,3上有8个零点（互不相同），则实数a的取值范围是．14. 将字母a，a，b，b，c，c排成三行两列，要求每行的字母互不相同，每列的字母也互不相同，则不同的排列方法共有种（用数字作答）．三、解答题（共6小题；共78分）15. 设f x=sinπ4x−π6−2cos2π8x+1．（1）求f x的最小正周期；（2）若函数y=f x与y=g x的图象关于直线x=1对称，求当x∈0,43时，y=g x的最大值．16. 某单位有三辆汽车参加某种事故保险，单位年初向保险公司缴纳每辆900元的保险金、对在一年内发生此种事故的每辆汽车，单位获9000元的赔偿（假设每辆车最多只赔偿一次）．设这三辆车在一年内发生此种事故的概率分别为19，110，111，且各车是否发生事故相互独立，求一年内该单位在此保险中：（1）获赔的概率；（2）获赔金额ξ的分布列与期望．17. 如图，已知四棱锥P−ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60∘，E，F分别是BC，PC的中点．（1）证明：AE⊥PD；（2）设AB=2，若H为PD上的动点，EH与平面PAD所成最大角的正切值为62，①求异面直线PB与AD所成角的正弦值；②求二面角E−AF−C的余弦值．18. 已知函数f x=1+x1−xe−ax，（1）设a>0，讨论y=f x的单调性；（2）若对任意x∈0,1恒有f x>1，求a的取值范围．19. 已知数列a n满足a1=1，a n+1=2a n+1n∈N∗．（1）求数列a n的通项公式；（2）若数列b n满足4b1−14b2−1⋯4b n−1=a n+1b n n∈N∗，证明：数列b n是等差数列；（3）证明：n2−13<a1a2+a2a3+⋯+a na n+1<n2n∈N∗．20. 已知椭圆x2a2+y2b2=1a>b>0的左、右焦点分别是F1−c,0，F2c,0，Q是椭圆外的动点，满足F1Q=2a．点P是线段F1Q与该椭圆的交点，点T在线段F2Q上，并且满足PT⋅TF2= 0，TF2 ≠0．（1）设x为点P的横坐标，证明F1P=a+cax；（2）求点T的轨迹C的方程；（3）试问：在点T的轨迹C上，是否存在点M，使△F1MF2的面积S=b2．若存在，求∠F1MF2的正切值；若不存在，请说明理由．答案第一部分1. B 【解析】因为满足z+iz=i，所以z=ii−1=i−i−1i−1−i−1=12−12i．2. A 【解析】由z=y−3x，得y=3x+z，作出不等式对应的可行域，平移直线y=3x+z，由平移可知当直线y=3x+z经过点A时，直线y=3x+z的截距最大，此时z取得最大值，由2x+y=4,4x−y=−1解得x=12,y=3,即A12,3，代入z=y−3x，得z=3−32=32，即z=y−3x的最大值为32，由平移可知当直线y=3x+z经过点C时，直线y=3x+z的截距最小，此时z取得最小值，由x+2y=2,2x+y=4,解得x=2,y=0,即B2,0，代入z=y−3x，得z=0−6=−6，即z=y−3x的最小值为−6，故−6≤z≤32．3. C 【解析】执行程序框图，可得x=1，y=1，满足条件x≤4，x=2，y=0；满足条件x≤4，x=4，y=−1；满足条件x≤4，x=8，y=−2；不满足条件x≤4，退出循环，输出y的值为−2．4. A5. B【解析】如图在Rt△MF1F2中，∠MF1F2=30∘，F1F2=2c，所以MF1=2ccos30∘=433c，MF2=2c⋅tan30∘=233c，所以2a=MF1−MF2=433c−233c=233c，所以e=ca=3．6. D 【解析】①U为全集，A，B是集合，则“存在集合C使得A⊆C，B⊆∁U C”是“A∩B=∅”的充要条件，正确；②命题p：若x>y，则−x<−y，是真命题；命题q：若x>y，则x2>y2，是假命题；则命题p∧¬q为真命题，正确；③ 命题“对任意 x ∈R ，都有 x 2≥0”的否定为“存在 x ∈R ，都有 x 2<0”，因此不正确；④ 一物体沿直线以 v =2t +3（t 的单位：s ，v 的单位：m/s ）的速度运动，则物体在 3∼5 s 间进行的路程是 ∫352t +3 d t = t 2+3t 35=22，因此正确．综上其中真命题的个数为 3． 7. A8. B【解析】在同一坐标系中作出 y =m ，y =4m +1m >0 ，与 y = log 2x 的图象，设 A ，B ，C ，D 各点的横坐标分别为 x A ，x B ，x C ，x D ，则由 log 2x =m ，解得 x A =2−m ，x B =2m ；由 log 2x =4m +1 m >0 ，解得 x C =2−4，x D =24；所以 a = x A −x C = 2−m −2−4， b = x B −x D = 2m −24，则b=2m −24m +12−m −2−4=2m ⋅24m +1⋅ 2m −24m +1 2m −24 =2m ⋅24m +1=2m +4m +1=2m +1+4−1≥2 m +1 ⋅m +12−1=24−1=23=8,当且仅当 m +1=4m +1，即 m =1 时取“=”号，所以 b a的最小值为 8．第二部分 9. 12π【解析】提示：由三视图可知，该几何体是由左右两个相同的圆柱（底面圆半径为 2，高为 1）与中间一个圆柱（底面圆半径为 1，高为 4）组合而成． 10. 90∘【解析】因为△ABC的角平分线AD的延长线交它的外接圆于E，所以∠BAE=∠CAD，因为∠AEB与∠ACB是同弧上的圆周角，所以∠AEB=∠ACD，所以△ABE∽△ADC，所以ABAE =ADAC，即AB⋅AC=AD⋅AE，因为S=12AB⋅AC⋅sin∠BAC，且S=12AD⋅AE，所以AB⋅AC⋅sin∠BAC=AB⋅AC，所以sin∠BAC=1，又因为∠BAC是三角形内角，所以∠BAC=90∘．11. 2【解析】由抛物线C的参数方程为x=8t2,y=8t（t为参数），得y2=8x，得到焦点坐标为2,0，直线l的方程为：y=x−2，所以x−y−2=0，曲线C1的极坐标方程为ρ2−8ρcosθ=r2−16，所以x−42+y2=r2，因为直线l与曲线C1相切，2=2=r．12. 2π3【解析】由3sin A=5sin B，得3a=5b．又因为b+c=2a，所以a=53b，c=73b，所以cos C=a 2+b2−c22ab=53b2+b2− 73b22×53b×b=−12．因为C∈0,π，所以C=2π3．13. 0,12【解析】函数y=f x−a在区间−3,3上有8个零点（互不相同），可化为函数f x与函数y=a有8个不同的交点，由题意作函数f x与函数y=a的图象如下，故由图象可知，实数 a 的取值范围是 0,12 ．14. 12 第三部分15. （1）f x =sin π4x cos π6−cos π4x sin π6−cos π4x=32sin π4x −32cos π4x= 3 12sin π4x− 32cos π4x= 3sin π4x −π3 ,因为 ω=π4，所以 f x 的最小正周期为 T =2ππ=8；（2）在 y =g x 的图象上任取一点 x ,g x ，它关于 x =1 的对称点 2−x ,g x ，由题设条件，点 2−x ,g x 在 y =f x 的图象上，从而g x =f 2−x= 3sin π4 2−x −π3= 3sin π2−π4x −π3= 3cos π4x +π3,当 0≤x ≤43时，π3≤π4x +π3≤2π3，则 y =g x 在区间 0,43上的最大值为 g x max = 3cos π3= 32． 16. （1）设 A k 表示第 k 辆车在一年内发生此种事故，k =1,2,3，由题意知 A 1，A 2，A 3 独立，且P A 1 =19，P A 2 =110，P A 3 =111，因为该单位一年内获赔的对立事件是 A 1，A 2，A 3 都不发生，所以该单位一年内获赔的概率为 1−1A 2A 3 =1−P A 1 P A 2 P A 3 =1−89×910×1011=311．（2） ξ 的所有可能值为 0，9000，18000，27000． P ξ=0 =P A 1A 2A 3 =P A 1 P A 2 P A 3 =89×910×1011=811，P ξ=9000 =P A 1A 2A 3 +P A 1A 2A 3 +P A 1A 2A 3=P A 1 P A 2 P A 3 +P A 1 P A 2 P A 3 +P A 1 P A 2 P A 3 =19×910×1011+89×110×1011+89×910×111=242=11,Pξ=18000=P A1A2A3+P A1A2A3+P A1A2A3=P A1P A2P A3+P A1P A2 P A3+P A1 P A2P A3=19×110×1011+19×910×111+89×110×111=27=3,Pξ=27000=P A1A2A3=P A1P A2P A3=19×110×111=1990，综上知，ξ的分布列为：ξ090001800027000P81131设ξk表示第k辆车一年内的获陪金额，k=1,2,3，则ξ1有分布列：ξ109000P81所以Eξ1=9000×19=1000．同理得Eξ2=9000×110=900；Eξ3=9000×111≈818.18．综上有Eξ=Eξ1+Eξ2+Eξ3≈1000+900+818.18=2718.18（元）．17. （1）由四边形ABCD为菱形，∠ABC=60∘，可得△ABC为正三角形．因为E为BC的中点，所以AE⊥BC．又BC∥AD，因此AE⊥AD．因为PA⊥平面ABCD，AE⊂平面ABCD，所以PA⊥AE．而PA⊂平面PAD，AD⊂平面PAD，且PA∩AD=A，所以AE⊥平面PAD，又PD⊂平面PAD．所以AE⊥PD．（2）设AB=2，H为PD上任意一点，连接AH，EH．由（1）知：AE⊥平面PAD，则∠EHA为EH与平面PAD所成的角．在Rt△EAH中，AE=3，所以当AH最短时，∠EHA最大，即当AH⊥PD时，∠EHA最大．此时，tan∠EHA=AEAH =3AH=62，因此，AH=．又AD=2，所以∠ADH=45∘，所以PA=2．由（1）知AE，AD，AP两两垂直，以A为坐标原点，建立如图所示的空间直角坐标系，又E，F分别为BC，PC的中点，可得：A0,0,0，B 3,−1,0，C 3,1,0，D0,2,0，P0,0,2，E 3,0,0，F32,12,1，①BP= −3,1,2，AD=0,2,0，所以cos⟨BP,AD⟩=BP⋅ADBP AD =22×2=24，设异面直线PB与AD所成角为α，所以sinα=144．②AE=3,0,0，AF=32,12,1，设平面AEF的一法向量为m=x,y,z，则m⋅AE=0, m⋅AF=0,所以3x=0,32x+12y+z=0,取m=0,2,−1，因为BD⊥AC，BD⊥PA，PA∩AC=A，所以BD⊥平面APC，所以BD⊥平面AFC，故BD为平面AFC的一法向量．又BD= −3,3,0，所以cos⟨m,BD⟩=m ⋅BDm BD =5×12=155，因为二面角E−AF−C为锐角，所以所求二面角的余弦值为155．18. （1）f x的定义域为−∞,1∪1,+∞．对f x求导数得fʹx=ax2−a+21−x2e−ax．（ⅰ）当a=2时，fʹx=2x 21−x2e−2x，fʹx在−∞,0，0,1和1,+∞均大于0，所以f x在−∞,1，1,+∞上为增函数．（ⅱ）当0<a<2时，fʹx>0，f x在−∞,1，1,+∞上为增函数．（ⅲ）当a>2时，0<a−2a <1，令fʹx=0，解得x1=− a−2a，x2=a−2a．当x变化时，fʹx和f x的变化情况如下表：−∞,−a−2a−a−2a−a−2a,a−2aa−2aa−2a,11,+∞fʹx+0−0++ f x↗极大值↘极小值↗↗所以f x在 −∞,− a−2a ，a−2a,1，1,+∞上为增函数，f x在 − a−2a,a−2a上为减函数．（2）（ⅰ）当0<a≤2时，由（1）知：对任意x∈0,1恒有f x>f0=1．（ⅱ）当a>2时，取x0=12a−2a∈0,1，则由（1）知f x0<f0=1，不符合题意；（ⅲ）当a≤0时，对任意x∈0,1，恒有1+x1−x >1且e−ax≥1，得f x=1+x1−xe−ax≥1+x1−x>1．综上，当且仅当a∈−∞,2时，对任意x∈0,1恒有f x>1．19. （1）因为a n+1=2a n+1n∈N∗，所以a n+1+1=2a n+1，所以a n+1是以a1+1=2为首项，2为公比的等比数列．所以a n+1=2n．即a n=2n−1n∈N∗．（2）因为4b1−14b2−1⋯4b n−1=a n+1b n n∈N∗，所以4b1+b2+⋯+b n−n=2nb n．所以2b1+b2+⋯+b n−n=nb n, ⋯⋯①2b1+b2+⋯+b n+b n+1−n+1=n+1b n+1. ⋯⋯②②−①，得2b n+1−1=n+1b n+1−nb n，即n−1b n+1−nb n+2=0, ⋯⋯③nb n+2−n+1b n+1+2=0. ⋯⋯④③−④，得nb n+2−2nb n+1+nb n=0，即b n+2−2b n+1+b n=0，所以b n+2−b n+1=b n+1−b n n∈N∗，所以b n是等差数列．（3）因为a ka k+1=2k−12−1=2k−122k−12<12，k=1,2,⋯,n，所以 a 1a 2+a 2a 3+⋯+a n a n +1<n2．因为a k k +1=2k −1k +1=12−12 2k +1−1 =1−1≥12−13⋅12k , k =1,2,⋯,n ，所以a 12+a 23+⋯+a nn +1≥n −1 1+12+⋯+1n =n 2−13 1−12n>n −1, 所以 n 2−13<a 1a 2+a 2a 3+⋯+a n a n +1<n2n ∈N ∗ ．20. （1）证法一：设点 P 的坐标为 x ,y ．由 P x ,y 在椭圆上，得 F 1P = x +c 2+y 2= x +c 2+b 2−b 2a x 2= a +c ax 2，由 x ≥−a ，知 a +ca x ≥−c +a >0，所以 F 1P =a +c ax ．证法二：设点 P 的坐标为 x ,y ．记 F 1P =r 1， F 2P =r 2，则 r 1= x +c 2+y 2，r 2= x −c 2+y 2．由 r 1+r 2=2a ，r 12−r 22=4cx ，得 F 1P =r 1=a +c ax ．证法三：设点 P 的坐标为 x ,y ．椭圆的左准线方程为 a +cax =0，由椭圆第二定义得 F 1Px +a 2=ca ，即 F 1P =c ax +a 2c = a +c a x．由 x ≥−a ，知 a +cax ≥−c +a >0，所以 F1P =a +c ax ．（2）解法一：设点 T 的坐标为 x ,y ．当 PT=0 时，点 a ,0 和点 −a ,0 在轨迹上．当 PT ≠0 且 TF 2 ≠0 时，由 PT ⋅ TF 2 =0，得 PT ⊥TF 2 ．又PQ=PF2，所以T为线段F2Q的中点．在△QF1F2中，OT=12F1Q=a，所以有x2+y2=a2．综上所述，点T的轨迹C的方程是x2+y2=a2．解法二：设点T的坐标为x,y．当PT=0时，点a,0和点−a,0在轨迹上．当PT ≠0且TF2 ≠0时，由PT⋅TF2=0，得PT⊥TF2．又PQ=PF2，所以T为线段F2Q的中点．设点Q的坐标为xʹ,yʹ，则x=xʹ+c2,y=yʹ2.因此xʹ=2x−c,yʹ=2y. ⋯⋯①由F1Q=2a得xʹ+c2+yʹ2=4a2. ⋯⋯②将①代入②，可得x2+y2=a2．综上所述，点T的轨迹C的方程是x2+y2=a2．（3）解法一：C上存在点M x0,y0使S=b2的充要条件是x02+y02=a2, ⋯⋯③12⋅2c y0=b2. ⋯⋯④由③得y0 ≤a，由④得y0 ≤b2c．所以，当a≥b 2c时，存在点M，使S=b2；当a<b 2c时，不存在满足条件的点M．当a≥b 2c时，MF1=−c−x0,−y0，MF2=c−x0,−y0，由MF1⋅MF2=x02−c2+y02=a2−c2=b2，MF1⋅MF2=MF1 ⋅ MF2cos∠F1MF2，S=12MF1 ⋅ MF2sin∠F1MF2=b2，得tan∠F1MF2=2．解法二：C上存在点M x0,y0使S=b2的充要条件是x02+y02=a2, ⋯⋯③12⋅2c y0=b2. ⋯⋯④由④得y0=b2c．上式代入③得x02=a2−b4c = a−b2ca+b2c≥0，于是，当a≥b 2c时，存在点M，使S=b2；当a<b 2c时，不存在满足条件的点M．当a≥b 2c 时，记k1=k F1M=y0x0+c，k2=k F2M=y0x0−c，由F1F2<2a，知∠F1MF2<90∘，所以tan∠F1MF2=k1−k21+k1k2=2．。

天津市蓟县康中中学2014届高三第二次模拟考试物理试题 Word版含答案

康中中学2014届高三第二次模拟考试物理试题一卷选择题（48分）一、本题共8小题，每小题6分，共48分。

1---5小题为单选题，只有一个正确答案；6---8题在每小题的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确，全部选对的得6分，选不全的得4分，选错或不答的得0分。

1、某消防队员从一平台上跳下，下落2m 后双脚着地，接着他用双腿弯曲的方法缓冲，使自身重心又下降了0.4m ，在着地过程中地面对他双腿的平均作用力是：（）A ．自身重力的4倍 B. 自身重力的8倍 C. 自身重力的6倍 D. 自身重力的10倍2、如图，天车下吊着两个质量都是m 的工件A 和B ，系A 的吊绳较短，系B 的吊绳较长，惹天车运动到P 处突然停止，则两吊绳所受拉力、的大小关系是（）A ．B A F F >B ． B A F F <C ． mg F F B A ==D ． mg F F B A >=3．图2所示，质量为M 的小车放在光滑的水平地面上，右面靠墙，小车的上表面是一个光滑的斜面，斜面的倾角为α设法地重力加速度的g 。

那么，当有一个质量为m 的物体在这个斜面上自由下滑时，小车对右侧墙壁的压力大小是A ．ααcos sin mgB ．ααcos sin mg Mm M+C ．αtan mgD ．αtan mg Mm M+4、两个相互垂直的力F1、F2作用在同一物体上，使物体发生一段位移，已知F1做功为4J ，F2做功为3J ，则他们的合力做功为（）A.5JB.7JC.1JD.3.5J5．如下图所示电路，开关S 原来闭合着，若在t 1时刻突然断开开关S ，则于此时刻前后通过电阻R 1的电流情况用下右图中哪个图像表示比较合适（）6.在高度为h 的同一位置向水平方向同时抛出两个小球A 和B ，若A 球的初速度vA 大于B 球的初速度vB ，则下列说法中正确的是：( )A. A 球比B 球先落地B. 在飞行过程中的任一段时间内，A 球的水平位移总是大于B 球的水平位移C. 若两球在飞行中遇到一堵墙，A 球击中墙的高度大于B 球击中墙的高度D. 在空中飞行的任意时刻，A 球总在B 球的水平正前方，且A 球的速率总是大于B 球的速率 7．一个U 23592原子核在中子的轰击下裂变方程为n Sr X n U 10943810235922++→+，则下列说法正确的是A ．X 原子核中含有86个中子B ．X 原子核中含有141个核子C ．铀核裂变的产物是多种多样的，具有一定的偶然性D ．为了使裂变的链式反应容易进行，最好用纯铀2358．一列简谐横波在0 t 时的波形图如下，若此波的周期为0.2s ，则下列说法中正确的是A ．再经过△t =0.4s 质点P 向右移动0.8mB ．再经过△t =0.4s 质点P 仍在自己平衡位置C ．在波的传播过程中质点Q 与P 的振动情况总是相同的D ．再经过△t =0.2s 后的波形与t =0时的波形是不同的第二卷注意事项：1、用黑色墨水的钢笔或签字笔将答案写在答题卡上。

天津市蓟县蓟州中学2014-2015学年高一第二学期第二次月考数学试卷 word含答案

天津市蓟州中学2014-2015学年第二学期第二次月考高一数学试卷 2015.6.4本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共120分，考试时间90分钟．第Ⅰ卷1至2页，第Ⅱ卷3至4页．祝各位考生考试顺利！第 Ⅰ 卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、考生号、考试科目涂在答题卡上；2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．3．本卷共10小题，每小题4分，共40分．一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 下列两个变量之间的关系是相关关系的是（）A.正方体的棱长和体积B.单位圆中角的度数和所对弧长C.单产为常数时，土地面积和总产量D.日照时间与水稻的亩产量 2.已知等差数列{}n a 满足61020a a +=，则下列选项错误的是（）A.15150S =B.810a =C.1620a =D.41220a a +=3．已知实数y x ,满足约束条件101020x y x y y +-≥⎧⎪--≤⎨⎪-≤⎩，则y x z +=2的最小值是（ )A ．4-B ．2-C ．0D ．24.阅读下面程序框图运行相应的程序，若输入x 的值为-8，则输出y 的值为（）A.0B.1C.18 D.1165．掷两颗均匀的骰子，则点数之和为5的概率等于（）1.18A 1.9B 1.6C 1.12D6. 一名小学生的年龄和身高（单位：cm)的数据如下：由散点图可知，身高y 与年龄x 之间的线性回归直线方程为8.8y x a =+，预测该学生10岁时的身高为（）A.154B.153C.152D.1517.在在ABC ∆中，内角A,B,C 所对应的边分别为,,,c b a ，若32a b =，则2222sin sin sin B AA-的值为（）1.9A -1.3B .1C 7.2D8.对于任意实数x ，一元二次不等式04)2(2)2(2<----x a x a 恒成立，则实数a 取值范围是（）A.()2,∞-B.(]2,∞-C.（－2,2）D.(]2,2-9.某公司10位员工的月工资（单位:元）为x 1，x 2，''',x 10 ，其均值和方差分别为x 和s 2，若从下月起每位员工的月工资增加100元，则这个10位员工下月工资的均值和方差分别为（） A.x ，s 2+1002 B.x +100, s 2+1002 C. x ,s 2 D.x +100, s210.如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为75，30，此时气球的高是60m ，则河流的宽度BC 等于（） A 、1)mB 、1)mC 、1)mD 、1)m第 Ⅱ 卷注意事项：1．用黑色墨水的钢笔或签字笔答题； 2．本卷共9小题，共80分．二、填空题：本大题共5个小题，每小题4分，共20分．请将答案填在题中横线上。

天津市蓟县康中中学届高三模拟考试数学试题及答案(理)

天津市蓟县康中中学2014届高三5月模拟数学（理）试题参考公式：如果事件A B ，互斥，那么球的表面积公式 ()()()P A B P A P B +=+24πS R = 如果事件A B ，相互独立，那么其中R 表示球P(AB)=P(A)P(B)球的体积公式如果事件A 在一次试验中发生的概率是p ，那么34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(012)k k n kn nP k C p p k n -=-=，，，…，第一部分选择题（共50分）一．选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的1、设复数满足关系式+││=2+i ,那么等于( ) (A) -43+i ；(B) 43-i ；(C) -43-i ； (D) 43+i . 2 设函数)(|,3sin |3sin )(x f x x x f 则+=为（）A ．周期函数，最小正周期为3πB ．周期函数，最小正周期为32π C ．周期函数，数小正周期为π2 D ．非周期函数3、设,0,0>>b a 则以下不等式中不恒成立．．．．的是（）A ．4)11)((≥++ba b a ； B ．2332ab b a ≥+； C ．b a b a 22222+≥++； D ．b a b a -≥-||4、如果nx x ⎪⎪⎭⎫ ⎝⎛-3213的展开式中各项系数之和为128，则展开式中1x 3 的系数是（）（A ）7 （B ）－7 （C ）21 （D ）－215、若直线3:-=kx y l 与直线0632=-+y x 的交点位于第一象限，则直线l 的倾斜角的取值范围是（）(A))3,6[ππ, (B))2,6(ππ, (C))2,3(ππ, (D)]2,6[ππ6、如果1a ，2a ，…，8a 为各项都大于零的等差数列，公差0d ≠，则（）（A ）1a 8a 45a a ；（B ）1a 8a 45a a ；（C ）1a +8a 4a +5a ；（D ）1a 8a =45a a . 7、如图所示给出的是计算111124620++++的值的一个程序框图，其中判断框内填入的条件是（）A. 10i >B. 10i <C. 20i >D. 20i <8、函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图，则（）A ．4,2πϕπω==； B ．6,3πϕπω==C ．4,4πϕπω==； D ．45,4πϕπω==9、若椭圆经过原点，且焦点F 1（1，0），F 2（3，0），则其离心率为（）A 、43B 、32 C 、21 D 、41 10、定义函数D x x f y ∈=),(，若存在常数C ，对任意的D x ∈1，存在唯一的D x ∈2，使得C x f x f =+2)()(21，则称函数)(x f 在D 上的均值为C 。

天津市蓟县下仓中学2014届高三第二次模拟考试数学(理)试题

天津市蓟县下仓中学2014届高三第二次模拟考试数学（理）试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分. 共150分。

考试时间120分钟。

参考公式：如果事件A ，B 互斥，那么棱柱的体积公式P(A+B)=P(A)+P(B) V=Sh如果事件A ，B 相互独立，那么其中S 表示棱柱的底面积，h 表示棱柱的高 P(A ·B)=P(A)·P(B) 棱锥的体积公式如果事件A 在一次试验中发生的概率是P ，那么n13V Sh =次独立重复试验中事件A 恰好发生k 次的概率其中s 表示棱锥的底面积，h 表示棱锥的高()()()10,1,2,n kk k n n P k P P k n C -=-=⋅⋅⋅ 棱台的体积公式球的表面积公式24S R π=第I 卷（选择题，共50分）一、选择题（本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的） 1．已知i 是虚数单位，那么=-+2)11(ii A ．i B ．-iC ．1D ．-12．命题“042,2≤+-∈∀x x R x ”的否定为(A) 042,2>+-∈∃x x R x (B) 042,2≥+-∈∀x x R x (C) 042,2≤+-∉∀x x R x (D) 042,2>+-∉∃x x R x 3. 设向量→a 与→b 的夹角为θ，→a =（2，1），→a +3→b =（5，4），则θcos =A .54B .31C .1010D .10103 4．以双曲线1322=-x y 的一个焦点为圆心，离心率为半径的圆的方程是（A ）4)2(22=+-y x (B ) 2)2(22=-+y x (C ) 2)2(22=+-y x (D ) 4)2(22=-+y x 5．化简1cos 2tancot22ααα+-的结果为A. 1sin 22α-B.1sin 22α C.2sin 2α- D. 2sin 2α6．右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是 A ．π32 B ．π16 C ．π12D ．π87．若函数f ( x ) = min {3 + log 41x ,log 2 x }，其中min{p ，q }表示p ，q 两者中的较小者，则f ( x )＜2的解集为 A ．（0，4） B ．（0，+∞）C ．（0，4）∪（4，+∞）D ．（41，+∞） 8．设A 、B 是x 轴上的两点，点P 的横坐标为2，且||||PB PA =，若直线PA 的方程为01=+-y x ，则直线PB 的方程是（）A ．05=-+y xB ．012=--y xC ．042=--y xD ．072=-+y x9. 北京奥运会乒球男团比赛规则如下：每队3名队员，两队之间共需进行五场比赛，其中一场双打，四场单打，每名队员都需比赛两场（双打需两名队员同时上场比赛），要求双打比赛必须在第三场进行，若打满五场，则三名队员不同的出赛顺序安排共有（A ）144 （B ）72 （C ）36 （D ）1810. 已知)(x f ，)(x g 都是定义在R 上的函数，且满足以下条件：①)(x f =x a ·)(x g （0,0≠>a a ）；②)(x g 0≠；③)()()()(''x g x f x g x f ⋅>⋅。

2014年天津市蓟县二中高三模拟题数学(理)试题

2014年天津市蓟县二中高三模拟题数学（理）第Ⅰ卷（共50分）参考公式：球的表面积公式：24πS R =，其中R 是球的半径．如果事件A 在一次试验中发生的概率是p ，那么n 次独立重复试验中事件A 恰好发生k 次的概率：()(1)(012)k kn k n n P k C p p k n -=-= ，，，，．如果事件A B ，互斥，那么()()()P A B P A P B +=+．如果事件A B ，相互独立，那么()()()P AB P A P B = ．一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 如果复数ibi212+-（其中i 为虚数单位，b 为实数）的实部和虚部互为相反数，那么b 等于（ C ） A ．2 B ．32 C ．32- D ．2 2．变量y x ,满足下列条件：⎪⎪⎩⎪⎪⎨⎧≥≥≤+≥+≥+0,024********2y x y x y x y x ，则使y x z 23+=的值最小的()y x ,是( A )A. ( 4.5 ,3 )B. ( 3,6 )C. ( 9, 2 )D. ( 6, 4 )4．执行右面的程序框图，输出的s 是 ( D ) (A) -378 (B) 378 (c) -418 (D) 4185．某几何体的三视图如图所示，根据图中标出的数据．可得这个几何体的表面积为( B )A.344+ B.544+ C.83D.123．“3πθ-=”是“)2cos(2tan θπθ-=”的( A )充分而不必要条件.A 必要而不充分条件.B充分必要条件.C 既不充分也不必要条件.D6．过点（－4，0）作直线L 与圆x 2+y 2+2x －4y －20=0交于A 、B 两点，如果|AB|=8，则L 的方程为 ( D )A 5x +12y+20=0B 5x -12y+20=0C 5x -12y+20=0或x +4=0D 5x +12y+20=0或x +4=0 7．一个社会调查机构就某地居民的月收入调查了20000人，并根据所得数据画出了样本频率分布直方图．为了分析居民的收入与年龄、学历、职业等方面的关系，按月收入用分层抽样方法抽样，若从月收入[3000，3500)(元)段中抽取了30人．则在这20000人中共抽取的人数为 ( A ) A.200 B.100 C.20000 D.408．已知双曲线9322=-y x ,则双曲线右支上的点P 到右焦点的距离与点P 到右准线的距离之比等于( B ) A.2 B.332 C. 2 D.4 9．已知等差数列{}n a 中，有011011<+a a ，且它们的前n 项和n S 有最大值，则使得0n S >的 n 的最大值为（ B ） A ．11 B ．19C ． 20D ．2110 已知函数()y f x =满足：①(1)y f x =+是偶函数；②在[)1,+∞上为增函数若120,0x x <>,且122x x +<-,则1()f x -与2()f x -的大小关系是( C) A 12()()f x f x -=- B 12()()f x f x -<- C 12()()f x f x ->- D 无法确定第Ⅱ卷（非选择题共100分）二、填空题：本大题共6小题．每小题4分。

天津市蓟县康中2014届高三模拟数学理试题

天津市蓟县康中2014届高三模拟数学文试题本卷共10个小题，每小题5分，共50分。

一．选择题：在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 已知集合{}{}|1,|20,A x x B x x =>-=-≤≤则A B =（）A.{}|0x x ≥B. {}|2x x ≥-C. {}|10x x -<≤D. {}|10x x -≤< 2．已知命题1sin ,:≤∈∀x R x p ，则（） A ．1sin ,:≥∈∃⌝R x p B ．1sin ,:≥∈∀⌝R x pC ．1sin ,:>∈∃⌝R x pD ．1sin ,:>∈∀⌝R x p3．若直线==++=-++a y ax ay x a 则垂直与直线,01202)1(2（）A ．－2或0B ．0C ．－2D ．222±4.已知实数x y 、满足条件0022x y x y ≥⎧⎪≥⎨⎪+≤⎩，那么3x y +的最大值是（）A. 1B.3C. 6D. 8 5. 函数()lg 1f x x =+的图像大致是（）6. 在△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，且222222c a b ab =++，则 △ABC 是（）A ．钝角三角形B ．直角三角形C ．锐角三角形D ．等边三角形 7．要得到函数)53sin(2π-=x y 的图明，只需将函数x y 3sin 2=的图象（）A ．向左平移5π个单位B ．向右平移5π个单位C ．向左平移15π个单位 D ．向右平移15π个单位8．以双曲线222=-y x 的右焦点为圆心，且与其渐近线相切的圆的方程是（） A ．02422=--+x y x B ．02422=+-+x y xC ．02422=-++x y xD ．02422=+++x y x第Ⅱ卷（非选择题共100分）二、填空题：本大题共6小题，每小题4分，共24分。