山西省康杰中学届高三5月第三次模拟(数学理)146122

合集下载

山西省康杰中学2017届高三模拟试题(三)(理数)

山西省康杰中学2017届高三模拟试题（三）数学（理科）【满分150分，考试时间为120分钟】一、选择题（5×12＝60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B 铅笔涂黑答题纸上对应题目的答案标号） 1. 已知集合{}{}1|,)1lg(|-≥=-==y y B x y x A ，那么=B A A. []1,0- B. [)1,1-C. ()1,-+∞D. (]0,12. 复数3201611i i i z +⎪⎭⎫ ⎝⎛+-+=（i 为虚数单位）的共轭复数为A. 12i +B. 1i +C. 1i -D. 12i -3. 下列有关命题说法错误的是A. 命题“若1,012==-x x 则”的逆否命题是：“若01,12≠-≠x x 则”B. “1=x ”是“0232=+-x x ”的充分不必要条件 C. 若q p ∧为假命题，则q p ,均为假命题D. 对于命题01,:2<++∈∃x x R x p 使，则01,:2≥++∈∀⌝x x R x p 均有4. 在一次数学竞赛选拔测试中，每人解3道题，至少解对2道题才能通过测试被选上，设某同学解对每道题的概率均为p （10<<p ），且该同学是否解对每道题互相独立，若该同学通过测试被选上的概率恰好是p ，则p 的值为 A.21B.31 C. 32D.525. 如图所示是沿圆锥的两条母线将圆锥削去一部分后得几何体的三视图，其体积为332916+π，则圆锥的母线长为 A. 22B. 32正视图俯视图C. 4D.32+6. 在等差数列{}n a 中，8386=+a a ，则=+105a aA. 16B. 12C. 8D. 47. 函数)1ln()(xx x f -=的图像大致是8. 在ABC ∆中，4,5=⋅=⋅,则=AB A. 9B. 3C. 2D. 19. 已知a 为如图所示的程序框图输出的结果，则二项式6)1(xx a -的展开式中常数项是A. 20B. 52-C. 192-D. 160-10. 已知双曲线)0,0(12222>>=-b a by a x 的左右两个焦点分别为21,F F ,P 是双曲线上的一个动点，满足212F F PF =，直线1PF 与圆222a y x =+相切，则双曲线的离心率为A.45B.3C.332 D.3511. 定义：用{}x 表示不小于x 的最小整数，例如{}{}{}11.1,22.1,22-=-==，已知数列{}n a 满足：n n n a a a a +==+211,1，则=⎭⎬⎫⎩⎨⎧++++++111111201621a a aA. －1B. 0C. 1D. 212. 已知函数)(x f 的定义域为R ，)2()(),()(x f x f x f x f -==-，当[]1,0∈x 时，3)(x x f =，则函数)()cos()(x f x x g -=π在区间⎥⎦⎤⎢⎣⎡-25,21上的所有零点的和为A.7 B . 6 C. 3 D. 2 二、填空题（本大题共4小题，每小题5分，共20分）13. 已知变量y x ,满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≤--≤-00063203y x x y y x ，则2-2yx z =的最小值为 .14. 已知ABC ∆的三个顶点在以O 为球心的球面上，且︒=∠90BAC ，2==AC AB ,球心O 到平面ABC 的距离为1，则球O 的表面积为 .15. 已知抛物线x y 82=的焦点为F ，过点F 作直线l 与抛物线分别交于B A ,两点，若点M 满足）（OB OA OM +=21，过点M 作y 轴的垂线与抛物线交于点P ，若4=PF ，则M 的横坐标为 .16.已知函数)(x f y =在()∞+，0上可导，且满足[])1(0)()(2)1(≠>'+-x x f x x f x 恒成立，2)1(=f ，若曲线)(x f 在点)2,1(处的切线为)(x g y =且2016)(=a g ，则a = .三、解答题（本大题共6小题，满分70分. 解答须写出文字说明、证明过程和演算步骤）17.（本小题满分12分）已知)2cos 3,(cos ,21,sin ,)(x x x x f ==⋅=）（其中，将函数)(x f 的图像向右平移12π个单位，再将所得图像上各点的横坐标缩短到原来的21，纵坐标不变，得到函数)(x g 的图像.（1）若⎥⎦⎤⎢⎣⎡∈125,0πx ，求)(x g 的单调区间；（2）在ABC ∆中，角C B A ,,所对的边分别是c b a ,,，且,3),2,0(,0)(=∈=b B B f π求c a +的范围.18.（本小题满分12分）一超市在销售一批大小相近的某时令水果时，由于存放的时间对口味影响较大，超市根据调研决定最多销售5天，第6天就会扎成果汁。

山西省康杰中学高三数学第三次模拟试题文新人教A版

康杰中学2013年数学（文）模拟训练卷（三）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.第Ⅰ卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，满共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1. 已知集合{}{}2220,(1)1P x x x Q x log x =--≤=-≤，则P Q =I （） A. (-1,3) B. [)1,3-C. (]1,2D. [1,2]2. 设复数121,3z i z i =-=+，其中i 为虚数单位，则12z z 的虚部为（） A.134i + B.134+ C.314i - D. 314- 3. 在ABC ∆中，若tan tan tan tan 1A B A B =++，则cos C 的值是（） A. 22-B. 22C.12D. 12-4. 执行如图所示的程序框图，则输出n 为（） A. 3B.4C. 5D. 65. 设平面α⊥平面β，直线.a β⊄命题P ：“a ∥β”；命题q ：“a ⊥α”，则命题p 成立是命题q 成立的（） A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件6．右图是依据某城市年龄在20岁到45岁的居民上网情况调查而绘制的频率分布直方图，现已知年龄在[)[)[]30,3535,4040,45、、的上网人数呈现递减的等差数列分布，则年龄在[)35,40的网民出现的频率为（） A. 0.04 B.0.06 C.0.2 D.0.3 7．如图所示是一个几体体的三视图，其侧视图是一个边长为a 的等边三角形，俯视图是由两个等边三角形拼成的菱形，则该几何体的体积为（）A. 34aB. 33aC. 32aD. 3a8．若曲线221:20C x y x +-=与曲线2:()0C x y mx m --=有三个不同的公共点，则实数m 的取值范围是（）A.B. (UC. (0,)3D. ((0,)33-U 9．已知等差数列{}n a 的前n 项和n S ，满足201320132013a S ==，则1a ＝（）A.-2014B.-2013C.-2012D.-201110. 已知1,OA OB OA ==u u u r u u u r u u u r与OB uuu r 的夹有为120︒，OC u u u r 与OA u u u r 的夹角为30︒，若(,)OC OA OB R λμλμ=+∈u u u r u u u r u u u r ，则λμ＝（）C.12D.211. 已知若12,F F 分别是双曲线22221(0,0)x y a b a b-=>>的左、右焦点，过1F 且垂直于x 的轴的直线与双曲线交于,A B 两点，若2ABF ∆是锐角三角形，则该双曲线离心率的取值范围是（）A. (1,1)2+B. (1)2++∞C.D. (1)++∞12. 若函数1,0()1,0kx x f x nx x +≤⎧=⎨>⎩，则当0k >时，函数[()]1y f f x =+的零点个数为（）A.1B.2C.3D.4第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分13. 已知向量,a b r r满足2,1,(2)a b b a b ==-⊥r r r r r ，则a b +r r ＝ .14.已知函数2()(1tan )cos f x x x =+的定义域为0,2π⎛⎫⎪⎝⎭，则函数()f x 的值域为 .15. 向平面区域{}22(,)1x y x y +≤内随机投入一点，则该点落在区域2100x y x y +≤⎧⎪≥⎨⎪≥⎩内的概率等于 .16. 如果一个棱柱的底面是正多边形，并且侧棱与底面垂直，这样的棱柱叫做正棱柱，已知一个正六棱柱的各个顶点都在半径为3的球面上，则该正六棱柱的体积的最大值为 .三、解答题：本大题共6小题，满分70分. 解答须写出文字说明、证明过程和演算步骤 17. （本小题满分12分）数列{}n a 的前n 项和n S ，且3(1)2n n S a =-，数列{}n b 满足11,4n n b b +=且14b =(1)求数列{}n a 与{}n b 的通项公式.(2)设数列{}n c 满足2log n n n c a b =⋅，其前n 项和为n T ，求n T18. （本小题满分12分）某学校为了增强学生对数学史的了解，提高学生学习数学的积极性，举行了一次数学史知识竞赛，其中一道题是连线题，要求将4名数学家与他们所著的4本著作一对一边线，规定：每连对一条得5分，连错一条得－2分. 某参赛者随机用4条线把数学家与著作一对一全部连接起来. (1)求该参赛者恰好连对一条的概率. (2)求该参赛者得分不低于6分的概率.19. （本小题满分12分）如图，直四棱柱ABCD －A 1B 1C 1D 1，底面ABCD 为菱形，AB ＝1，AA 1=6,∠ABC ＝60°. (1)求证：AC ⊥BD 1. (2)求四面体D 1AB 1C 的体积.20.（本小题满分12分）已知：圆1O 过点（0，1），并且与直线1y =-相切，则圆1O 的轨迹为C ，过一点(1,1)A 作直线l ，直线l 与曲线C 交于不同两点,M N ，分别在,M N 两点处作曲线C 的切线12,l l ，直线12,l l 的交点为k (1)求曲线C 的轨迹方程.(2)求证：直线12,l l 的交点k 在一条直线上，并求出此直线方程.21.（本小题满分12分）已知函数32()f x ax bx cx =++的导函数为(),()h x f x 的图像在点(2,(2))f --处的切线方程为340x y -+=，且2()03h '-=，又直线y x =是函数()x g x kxe =的图像的一条切线(1)求函数()f x 的解析式及k 的值.(2)若()()1f x g x m ≤-+对于任意[)0,x ∈+∞恒成立，求m 的取值范围. 请考生在22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分. 22.（本小题满分10分）选修4-1：几何证明选讲如图过圆E 外一点A 作一条直线与圆E 交于,B C 两点，且13AB AC =，作直线AF 与圆E 相切于点F ，连接EF 交BC 于点D ，已知圆E 的半径为2，30EBC ∠=︒. (1)求AF 的长. (2)求证：3AD ED =23.（本小题满分10分）修4-4：坐标系与参数方程选讲在直角坐标系xOy 中，曲线1C 的参数方程为3sin x ay a⎧=⎪⎨=⎪⎩ （a 为参数），以原点O为极点，以x 轴正半轴为极轴，建立极坐标系，曲线2C 的极坐标方程为sin()424πρθ+=(1)求曲线1C 的普通方程与曲线2C 的直角坐标方程.(2)设P 为曲线1C 上的动点，求点P 到2C 上点的距离的最小值，并求此时点P 坐标. 24.（本小题满分10分）选修4-5：不等式选讲设函数5(),2f x x x a x R =-+-∈ (1)求证：当12a =-时，不等式1()1nf x >成立. (2)关于x 的不等式()f x a ≥在R 上恒成立，求实数a 的最大值.数学（文）（三）答案1. C {}{}12,13P x x Q x x =-≤≤=<≤，则P Q =I (]1,2.故选C.2. D12z z ===，虚部为14.故选D. 3. B. 由tan tan tan tan 1A B A B ⋅=++可得tan tan 11tan tan A BA B+=--⋅ ，即tan()1A B +=-,所以3,cos 442A B C C ππ+===则，，故选B. 4. B 初始值n=1, s=0，第1次循环后n=2, s=3；第2次循环后n=3, s=12 ；第3次循环后n=4, s=39，此时s>30，因此不进入第4次循环，输出n=4.故选B. 5. B 由题意可知p ⇒q 但q ⇒p ，则p 是q 的必要不充分条件. 故选B.6. C 由[20, 25)的频率为0.01×5=0.05, [25, 30)的频率为0.07×5=0.35,又[35, 40), [40,45]的人数成等差, 则其频率也成等差,又[35, 45]的频率为1-0.05-0.35=0.6, 则[35, 40)的频率为0.2. 故选C.7．A 3213323424a V a a =⨯⨯⨯=. 故选A. 8．D 由()0x y mx m --=可知0,(1)x y m x ==+, 当直线(1)y m x =+与圆2220x y x +-=相切时, 33m =±,当m=0时, 只有两个公共点. 因此33(,0)(0,)33m ∈-⋃, 故选D. 9．D 2013100720132013S a ==,所以10071a =, 则201310072,1006a a d -==1201320122011a a d =-=-. 故选D.10. D 应用向量加法, 三角形法则知12sin 30λμ==o. 11. C 由题意可知222,2b c b ac a<<则, 因此222c a ac -<,不等式两边同时除以2a 得: 2212,210e e e e -<--<即,解得1212e -<<+, 又双曲线的离心率e>1, 因此(1,12)e ∈+, 故选C.12. D 结合图像分析:当0k >时, [()]1f f x =-,则121()(,)()(0,1)f x t f x t k=∈-∞-=∈或, 对于1()f x t =, 存在两个零点12,x x ; 对于2()f x t =存在两个零点34,x x , 共计存在4个零点. 故选D.13.6 由题意可知|b|2-2a·b=0, 又|b|=1, 则2a·b=1, 所以|a +b|2=|a |2+|b|2+2a·b=4+1+1=6,因此|a +b|=614. 12(0,]+ 221()(1tan )cos sin(2)42f x x x x π=+=++, 因为(0,)2x π∈, 所以2sin(2)(,1]42x π+∈-, 所以()f x 的值域为1(0,2+. 15.14π 如图所示:落在阴影部分内的概率为14π.16. 54 设棱柱高为2(03)x x <<, 则底面积264S =⨯,则22362)4V Sh x x x ==⨯⋅=-=-+令20V x '=-+==解得则max 54.V V ==-= 17. 解: (1)对于数列{}n a 有3(1)2n n S a =- ① 113(1)(2)2n n S a n --=-≥ ②由①- ②得113()32n n n n n a a a a a --=-=即,11131,(1)=32n S a a ==-时即,则111333n n nn a a q --=⋅=⋅=;对于数列{}n b 有：11,4n n b b +=可得1214()44n n n b --==. (2)由(1)可知: 242222log 3log 43log 23(42)n nn n n n n n c a b n --=⋅=⋅=⋅=- n T =1232303(2)3...(42)3n n ⋅+⋅+-⋅++-⋅3n T =2312303...(62)3(42)3nn n n +⋅+⋅++-⋅+-⋅－2n T =22123(2)3(2)3...(2)3(42)3nn n +⋅+-⋅+-⋅+-⋅--⋅=2216(2)(33...3)(42)3nn n ++-+++--⋅则n T ＝1119(13)1553(2)3()31322n n n n n -++--++-=+-⋅- 18. 解:记4名数学家分别为a ,b,c,d ,对应的著作分别为A,B,C,D,根据题意,不同的连线方法共对应下列24种情况:c d a b A B C D ⎛⎫⎪ ⎪⎝⎭c d a b A B D C ⎛⎫⎪ ⎪⎝⎭cd a bA CB D ⎛⎫⎪ ⎪⎝⎭c d a bA C DB ⎛⎫⎪ ⎪⎝⎭ cd a b A D B C ⎛⎫⎪ ⎪⎝⎭c d a bA D CB ⎛⎫⎪ ⎪⎝⎭c d a b B A CD ⎛⎫ ⎪ ⎪⎝⎭c d a bB AD C ⎛⎫⎪ ⎪⎝⎭ c d a b B C A D ⎛⎫⎪ ⎪⎝⎭cd a b B C D A ⎛⎫⎪ ⎪⎝⎭cd a b B D A C ⎛⎫⎪ ⎪⎝⎭c d a b B D C A ⎛⎫⎪ ⎪⎝⎭c d a b C A B D ⎛⎫ ⎪ ⎪⎝⎭c d a bC AD B ⎛⎫ ⎪ ⎪⎝⎭c d a bC B AD ⎛⎫ ⎪ ⎪⎝⎭cd a bC BD A ⎛⎫ ⎪ ⎪⎝⎭c d a b C DA B ⎛⎫ ⎪ ⎪⎝⎭c d a b C DB A ⎛⎫ ⎪ ⎪⎝⎭c d a b D AB C ⎛⎫ ⎪ ⎪⎝⎭cd a b D A CB ⎛⎫⎪ ⎪⎝⎭cd a b D B A C ⎛⎫⎪ ⎪⎝⎭c d a b D B CA ⎛⎫⎪ ⎪⎝⎭cd a bD C A B ⎛⎫⎪ ⎪⎝⎭cd a bD C B A ⎛⎫⎪ ⎪⎝⎭ 其中恰好连对一条的情形有如下8种:c d a b A C D B ⎛⎫⎪ ⎪⎝⎭c d a b A D B C ⎛⎫⎪ ⎪⎝⎭cd a bB C A D ⎛⎫⎪ ⎪⎝⎭c d a b B D C A ⎛⎫⎪ ⎪⎝⎭c d a b C AB D ⎛⎫ ⎪ ⎪⎝⎭c d a bC BD A ⎛⎫ ⎪ ⎪⎝⎭c d a b D A CB ⎛⎫ ⎪ ⎪⎝⎭cd a b D B A C ⎛⎫⎪ ⎪⎝⎭ 恰好连对两条的情形有如下6种:cd a bA B D C ⎛⎫⎪ ⎪⎝⎭cd a b A C B D ⎛⎫⎪ ⎪⎝⎭c d a bA D CB ⎛⎫⎪ ⎪⎝⎭cd a b B A CD ⎛⎫⎪ ⎪⎝⎭c d a b C BA D ⎛⎫ ⎪ ⎪⎝⎭c d a b D B CA ⎛⎫⎪ ⎪⎝⎭全部连对的情形只有1种:c d a b A B CD ⎛⎫⎪ ⎪⎝⎭(1)恰好连对1条的概率为81243=; (2)得分不低于6分即全部连对或恰好连对2条的概率为1672424+=. 19. 解: (1)连结BD 交AC 于O.因为四边形ABCD 为平行四边形,且AB=AD,所以四边形ABCD 为菱形, 则AC ⊥BD由直四棱柱ABCD －A 1B 1C 1D 1,所以BB 1⊥平面ABCD, 可知BB 1⊥AC, 又AC ⊥BD ，则AC ⊥平面BB 1D 1D ，又BD 1⊂平面BB 1D 1D ，则AC ⊥BD 1.(2) 111111*********D AB C ABCD A B C D B ABC D ACD A A B D CC B D V V V V V V -=----=111111443ABCD A B C D B ABC V V --=⋅=. 20.解: (1)由定义可知C 的轨迹方程为24x y =.(2)设1122(,),(,)M x y N x y , 直线MN 的方程1(1)y k x -=- 在M 处的切线方程为112()x x y y =+ 在N 处的切线方程为222()x x y y =+ 解得k 点坐标为(1212,24x x x x +) 而21(1)4y k x x y-=-⎧⎨=⎩,整理得24440x kx k -+-=所以2,1k k x k y k ==-故k 点所在直线方程为220x y --=.23. 解: (1)对于曲线1C 有2222cos (cos sin 133sin a y y aαα=⇔+=+==⎩,即1C 的方程为:2213xy+=; 对于曲线2C有2sin()(cos sin)42cos sin880 42x yπρθρθθρθρθ+=+=⇔+=⇔+-=,所以2C的方程为80x y+-=.(2)显然椭圆1C与2C无公共点, 椭圆上点(3cos,sin)Pαα到直线80x y+-=的距离为:|2sin()8||3cos sin8|322dπααα+-+-==当in()13sπα+=时, d取最小值为32,此时点P的坐标为31(,)22.11。

山西省康杰中学高三数学第三次模拟试题理新人教A版

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.第Ⅰ卷（选择题，共60分）一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 设集合{}{}2|2,|2x A x y x x B y y ==-==，则A B ⋂=（）A. (0,2)B. [0,2]C. (1,2]D. (0,2] 2. 在复平面内，已知复数1i z i =-，则其共轭复数z 的对应点位于（） A. 第一象限 B. 第二象限C. 第三象限D. 第四象限 3. 设,x y 满足约条件360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩若目标函数(0,0)z ax by a b =+>>的最大值为12，则23a b+的最小值为（） A. 256 B. 83 C. 113 D. 44. 执行如图所示的程序框图，输出的S 值为（）A. 10B. －6C. 3D. －155. 一个几何体的三视图如图所示，则这个几何体的体积为（）A. (836π+ B. (8236π+ C. (636π+ D. (9236π+ 6. 函数23ln()y x x =+的图象大致是（）7. 已知7270127()x m a a x a x a x -=++++的展开式中4x 的系数是－35，则1237a a a a ++++=（） A. 1 B. 0 C. 2 D. －18.已知平面上不重合的四点P ，A ，B ，C 满足0PA PB PC ++=，且AB AC mAP +=，那么实数m 的值为（）A. 2B. 3C. 4D. 59. 点P 在曲线33cos sin 22y x x =-上移动，设点P 处切线的倾斜角为α，则α的取值范围是（） A. 2[,]33ππ B. 2[0,][,)33πππ⋃ C. 5[,]66ππ D. 5[0,][]66πππ⋃， 10. 函数sin()y x ωϕ=+（0ω>且||2πϕ<）在区间2[,]63ππ上单调递减，且函数值从1减小到－1，那么此函数的图象与y 轴交点的纵坐标为（） A. 22 B. 12 C. 32 D. 62211. 点P 到图形C 上每一个点的距离的最小值称为点P 到图形C 的距离，那么平面内到定圆C 的距离与到定点A 的距离相等的点的轨迹不可能是（）A. 圆B. 椭圆C. 双曲线的一支D. 直线12. 具有性质1()()f f x x=-的函数，我们称为满足“倒负”交换的函数，下列函数（） ①1;y x x =-②1y x x =+；③0(01)0(1)1(1)x y x x x⎧⎪<<⎪==⎨⎪⎪->⎩其中满足“倒负”变换的函数是（） A. ①③ B.①② C.②③ D.①第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题5分，共20分13. 点A 是函数()sin f x x =的图象与x 轴的一个交点（如图所示），若图中阴影部分的面积等于矩形OABC 的面积，那么边AB 的长等于__________.14. 在半径为R 的半球内有一内接圆柱，则这个圆柱的体积的最大值是_____________.15. 在样本的频率分布直方图中，共有5个小长方形，若中间一个小长方形的面积等于其余4个小长方形面积和的14，且样本容量为50，则中间一组的频数为___________. 16. 已知圆22:3,C x y +=直线:360l x y +-=，点00(,)P x y l ∈，使得存在点Q C ∈，使060OPQ ∠=（O 为坐标原点），则0x 的取值范围是__________________.三、解答题：本大题共6小题，满分70分. 解答须写出文字说明、证明过程和演算步骤17. （本小题满分12分）已知数列}{n a 中，n S 为}{n a 的前n 项和，且12n n a S -=. （1）求数列}{n a 的通项公式；（2）设31323log log log n n b a a a =++⋅⋅⋅+，求数列1n b ⎧⎫⎪⎨⎬⎪⎭⎩的前n 项和n T 18. （本小题满分12分）如图，直角梯形ABCD 与等腰直角三角形ABE 所在的平面互相垂直，AB ∥CD ，AB ⊥BC ，AB=2CD=2BC=2，EA ⊥EB.（1）求直线EC 与平面ABE 所成角的正弦值；（2）线段EA 上是否存在点F ，使CE ∥平面FBD ？若存在，求出EF EA；若不存在，请说明理由. 19. （本小题满分12分）有5位同学相约参加某一电视娱乐节目，其中有2人已经参加过，另外3人没有参加过.（1）从这些同学中随机选出2人，求这两位同学中至少有一位参加过此节目的概率.（2）若参加此节目需要预选，参加过此节目的同学通过的概率为12，没有参加过的同学通过预选的概率是13，记通过预选的人数为X. 求X 的分布列和数学期望. 20. （本小题满分10分）设()()ln 1f x x a x ax =+-+（1）0a =时，求()f x 的单调区间；（2）若1a ≥，对任意的1[,1]2x ∈, 求()f x 的最大值.21. （本小题满分10分）设A 、B 分别是直线22y x =和22y x =-上的动点，且||2AB =，设O 为坐标原点，动点P 满足OP OA OB =+.（1）求点P 的轨迹方程；（2）过点(3,0)做两条相互垂直的直线12,l l ，直线12,l l 与点P 的轨迹相交弦分别为CD 、 EF ，设CD 、EF 的弦中点分别为M 、N ，求证：直线MN 恒过一个定点.请考生在第22、23、24三题中任选一题做答，如果多做，则按所做的第一题记分.22. （本小题满分10分）选修4-1：几何证明选讲如图所示，四边形ABCD 是⊙O 的内接四边形，BD 不经过点O ，AC 平分∠BAD ，经过点C 的直线分别交AB 、AD的延长线于E 、F ，且CD 2=AB ·DF.（1）△ABC ～△CDF ；（2）EF 是⊙O 的切线.23. （本小题满分10分）选修4-4：坐标系与参数方程选讲在平面直角坐标系xOy 中，A （1，0），B （2，0）是两个定点，曲线C 的参数方程 2x t =，为（t 为参数）2y t =，（1）将曲线C 的参数方程化为普通方程；（2）以A （1，0）为极点，AB 为长度单位，射线为极轴建立极坐标系，求曲线C 的极坐标方程.24. （本小题满分10分）选修4-5：不等式选讲已知函数()|2|.f x x a a =-+（1）()f x ≤6的解集为{}|23x x -≤≤，求实数a 的值；（2）在（1）的条件下，若存在实数n 使()()f n f n m +-≤成立，求实数m 的取值范围.。

山西省运城市康杰中学高考全真模拟(理科)数学试卷有答案

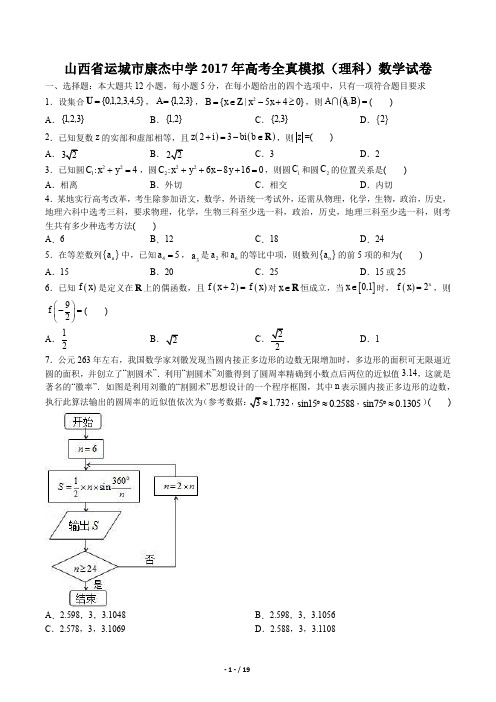
山西省运城市康杰中学2017年高考全真模拟（理科）数学试卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目要求1．设集合0123{45}=U ,,,,,，3{}12A =,,，25{40|}B x x x =∈-+≥Z ，则()A B =U ð( )A ．{123},,B ．{1}2,C ．{2}3,D ．{}22．已知复数z 的实部和虚部相等，且()()2i 3i z b b +=-∈R ，则z =( )A ．B ．C ．3D ．2 3．已知圆2214C x y +=:，圆22268160C x y x y ++-+=:，则圆1C 和圆2C 的位置关系是( )A ．相离B ．外切C ．相交D ．内切4．某地实行高考改革，考生除参加语文，数学，外语统一考试外，还需从物理，化学，生物，政治，历史，地理六科中选考三科，要求物理，化学，生物三科至少选一科，政治，历史，地理三科至少选一科，则考生共有多少种选考方法( ) A ．6B ．12C ．18D ．245．在等差数列{}n a 中，已知45a =，3a 是2a 和6a 的等比中项，则数列{}n a 的前5项的和为( ) A ．15B ．20C ．25D ．15或256．已知()f x 是定义在R 上的偶函数，且()()2f x f x +=对x ∈R 恒成立，当[]0,1x ∈时，()2xf x =，则92f ⎛⎫- ⎪⎝⎭=( )A ．12B C ．2D ．1 7．公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形的面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，其中n 表示圆内接正多边形的边数，执行此算法输出的圆周率的近似值依次为 1.732≈，sin150.2588︒≈，sin750.1305︒≈）( )A ．2.598，3，3.1048B ．2.598，3，3.1056C ．2.578，3，3.1069D ．2.588，3，3.11088．一个几何体的三视图如图所示，则该几何体的体积为( )A ．223B ．203C ．163D ．69．关于函数()[]()2π22cos 0πf x x x =+∈,下列结论正确的是( ) A ．有最大值3，最小值1- B ．有最大值2，最小值2- C ．有最大值3，最小值0 D ．有最大值2，最小值010．点A B C D ,,,在同一个球的球面上，AB BC ==90ABC ∠=，若四面体ABCD 体积的最大值为3，则这个球的表面积为( ) A ．2πB ．4πC ．8πD ．16π11．过抛物线24y x =的焦点F 的直线交抛物线于A B ,两点，且2AF BF =，则直线AB 的斜率为( ) A．B．C．-D．或-12．若函数()213sin221x x f x x -=+++在区间[](),0k k k -＞上的值域为[],m n ，则m n +等于( )A ．0B ．2C ．4D ．6 二、填空题：本大题共4小题，每小题5分13．已知矩形ABCD ，AB=4，AD=1，点E 为DC 的中点，则AE BE ⋅=______．14．为了活跃学生课余生活，我校高三年级部计划使用不超过1200元的资金购买单价分别为90元、120元的排球和篮球．根据需要，排球至少买3个，篮球至少买2个，并且排球的数量不得超过篮球数量的2倍，则能买排球和篮球的个数之和的最大值是______．15．学校艺术节对同一类的,A B C D ,,四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：甲说：“是C 或D 作品获得一等奖”；乙说：“B 作品获得一等奖”；丙说：“A D ,两项作品未获得一等奖”；丁说：“是C 作品获得一等奖”．若这四位同学中只有两位说的话是对的，则获得一等奖的作品是______． 16．我们把满足：()()1n n n n f X X X f X +=-'的数列{}n x 叫做牛顿数列．已知函数()21f x x =-，数列{}n x 为牛顿数列，设1ln1n n n X a X -=+，已知12a =，则3a =______．三、解答题：解答应写出文字说明，证明过程或演算步骤17．如图，D 是直角ABC △斜边BC 上一点，AC =．（1）若30DAC ∠=，求角B 的大小；（2）若2BD DC =，且AD =DC 的长．18．某单位280名员工参加“我爱阅读”活动，他们的年龄在25岁至50岁之间，按年龄分组：第1组[)25,30，第2组[)30,35，第3组[)35,40，第4组[)40,45，第5组[)45,50，得到的频率分布直方图如图所示．（Ⅰ）现要从年龄低于40岁的员工中用分层抽样的方法抽取12人，则年龄在第1，2，3组的员工人数分别是多少？（Ⅱ）为了交流读书心得，现从上述12人中再随机抽取3人发言，设3人中年龄在[)35,40,的人数为ξ，求ξ的数学期望；（Ⅲ）为了估计该单位员工的阅读倾向，现对从该单位所有员工中按性别比例抽取的40人做“是否喜欢阅读国学类书籍”进行调查，调查结果如下表所示：（单位：人）附：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++;19．如图1，菱形ABCD 的边长为12，60BAD ∠=，AC 与BD 交于O 点．将菱形ABCD 沿对角线AC 折起，得到三棱锥B ACD -，点M 是棱BC 的中点，DM =（Ⅰ）求证：平面ODM ⊥平面ABC ；（Ⅱ）求二面角M AD C --的余弦值．20．已知点,A B 分别为椭圆()2222:10x y E a b a b+=>>的左，右顶点，点()0,2P -，直线BP 交E 于点Q ，32PQ QB =且ABP △是等腰直角三角形．（Ⅰ）求椭圆E 的方程；（Ⅱ）设过点P 的动直线l 与E 相交于,M N 两点，当坐标原点O 位于以MN 为直径的圆外时，求直线l 斜率的取值范围． 21．已知函数()ln mx f x x=，曲线()y f x =在点()()22e ,ef 处的切线与直线20x y +=垂直（其中e 为自然对数的底数）．（1）求()f x 的解析式及单调递减区间；（2）若存在[)0e,x ∈+∞，使函数()()1e 2eln ln 22a g x a x x x f x a +=+-⋅⋅≤成立，求实数a 的取值范围． [选修44-：坐标系与参数方程]22．在直角坐标系xOy 中，已知圆2cos :2sin x C y θθ=⎧⎨=⎩（θ为参数），点P 在直线40l x y +-=：上，以坐标原点为极点，x 轴的正半轴为极轴，建立极坐标系．（Ⅰ）求圆C 和直线l 的极坐标方程；（Ⅱ）射线OP 交圆C 于R ，点Q 在射线OP 上，且满足2OP OR OQ =⋅，求Q 点轨迹的极坐标方程． [选修45-：不等式选讲]23．（1）解不等式：211x x --＜；（2）设()21f x x x =-+，实数a 满足1x a -＜，求证：()()()21f x f a a -+＜．山西省运城市康杰中学2017年高考全真模拟（理科）数学试卷答案一．选择题 1~5．CABCA6~10．BBACD11~12．CD二．填空题 13．3- 14．12 15．B 16．8 三．解答题17．解：（1）在ABC △中,根据正弦定理,有sin sin AC DCADC DAC=∠∠．因为AC =,所以sin ADC DAC ∠=∠= 又6060ADC B BAD B ∠=∠+∠=∠+＞, 所以120ADC ∠=,于是1801203030C ∠=--=,所以60B ∠=．（2）设DC x =,则2,3,BD x BC x AC ===．于是sin AC B B AB BC ===．在ABD △中,由余弦定理,得2222cos AD AB BD AB BD B =-∙+,即(2222=642223x x x x +-⨯⨯=,得2x =．故2DC =．18．解：（1）由频率分布直方图得前三组的人数分别为：()0.02528028,28,10.020.020.060.025280112⨯⨯=⎡+++⨯⎤⨯=⎣⎦-所以前三组抽取的人数分别为2812=2,2,82828112⨯++,（2）由上可知,ξ的所有可能取值为0,1,2,3,其概率分别为()383121055C P C ξ===,()128431212515C C P C ξ===,()218431228525C C P C ξ===,()3831214553C P C ξ===,所以,11228140123255555555E ξ=⨯+⨯+⨯+⨯=．（3）假设0H ：“是否喜欢看国学类书籍和性别无关系”,根据表中数据,求得2K 的观测值()240141448 6.8605 6.63522182218k ⨯⨯-⨯=≈>⨯⨯⨯,查表得()26.6350.01P K ≥=,从而能有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系19．（1）证明：∵ABCD 是菱形,∴AD DC OD AC =⊥,,12120ADC AD DC ADC ==∠=△中,,,∴6OD =,又M 是BC 中点,∴16,2OM AB MD ===∵222OD OM MD +=∴DO OM ⊥, ∵,OM AC ⊂面ABC ,OM AC O =, ∴OD ⊥面ABC ,又∵OD ⊂平面ODM ,∴平面ODM ⊥平面ABC ．（2）解：由题意,,OD OC OB OC ⊥⊥,又由（1）知OB OD ⊥,建立如图所示空间直角坐标系, 由条件知：()()()6,0,0,0,,D A M -, 故()()0,93,3,6,6AM AD ==,设平面MAD 的法向量(),,m x y z =,则00m AM m AD ⎧∙=⎪⎨∙=⎪⎩,即3060z x ⎧+=⎪⎨+=⎪⎩,令y =则3,9xz ==,∴()3,m =,由条件知OB ⊥平面ACD ,故取平面ACD 的法向量为()0,0,1n =. 所以,+393cos ,m n m n m n≥=由图知二面角M AD C --为锐二面角, 故二面角M AD C --的余弦值为3120．解：（1）由题意知：ABP △是等腰直角三角形,()220a B =,,, 设()00Q x y ,,由32PQ QB =,则0064,45x y ==-,代入椭圆方程,解得21b =,∴椭圆方程为2214x y +=．（2）由题意可知,直线l 的斜率存在,方程为2y kx =-,设()()1122M x y N x y ,,,,则22214y kx x y =-⎧⎪⎨+=⎪⎩,整理得：()221416120k x kx +-+=, 由韦达定理可知：12122216121414k x x x x k k +==++,, 由直线l 与E 有两个不同的交点,则0△＞,即()()2216412140k k --⨯⨯+＞,解得：234k ＞,①由坐标原点O 位于以MN 为直径的圆外,则0OM ON >,即12120x x y y +＞, 则()()1212121222x x y y x x kx kx +=+--=()()21212124k x x k x x +-⨯++=()222121612401414kk k kk +-⨯+++＞,解得：24k ＜,②综合①②可知：2344k ＜＜,2k ＜或2k -＜＜,直线l 斜率的取值范围32,,2⎛⎛⎫- ⎪ ⎪⎝⎭⎝⎭． 21．解：（1）函数()f x 的定义域为()()0,11,+∞,()()2ln 1ln m x f x x -'=（）,又由题意有：()21e 42m f '==,所以()22,ln x m f x x==．此时,()()()22ln 1ln x f x x -'=,由()0f x '＜得01x ＜＜或1e x ＜＜, 所以函数()f x 的单调递减区间为()01,和()1,e ．（2）因为()()21eln e 2g x a x x a x =+-+, 由已知,若存在[)0x e ∈+∞,,使函数()()21e eln ln 22a g x a x x x f x a +=+-∙∙≤成立, 则只需满足当[)()e min x g x a ∈+∞≤,，即可．又()()21eln e 2g x a x x a x =+-+, 则()()()e x a x g x x--'=,e a ≤,则()0g x '≥在[)e,x ∈+∞上恒成立,∴()g x 在[)e +∞,上单调递增, ∴()()2e e 2ming x g ==-,∴2e 2a ≥-,∵e a ≤, ∴2e e 2a -≤≤．a e ＞,则()g x 在[)e,a 上单调递减,在[),a +∞上单调递增,∴()g x 在[)e +∞,上的最小值是()g a , ∵()()e e g a g a ＜,＞,∴满足题意,综上所述,2e 2a ≥-．22．解：（1）圆2cos 2sin x C y θθ=⎧⎨=⎩：（θ为参数）,可得直角坐标方程：224x y +=, ∴圆C 的极坐标方程2ρ=．点P 在直线40l x y +-=：上,直线l 的极坐标方程4sin cos ρθθ=+．（2）设,P Q R ,的极坐标分别为()()()12,ρθρθρθ,,,,, 因为124=,2sin cos ρρθθ=+,又因为2OP OR OQ =∙,即212=ρρρ∙,∴()2122161==2sin cos ρρρθθ⨯+, ∴8=1sin 2ρθ+．23．（1）解：根据题意,对x 分3种情况讨论：①当0x ＜时,原不等式可化为211x x -+-+＜,解得0x ＞,又0x ＜,则x 不存在, 此时,不等式的解集为∅．②当102x ≤＜时,原不等式可化为211x x -++＜,解得0x ＞,又102x ≤＜, 此时其解集为122x x ⎧⎫≤⎨⎬⎩⎭＜．③当12x ≥时,原不等式化为211x x -+＜ ,解得122x ≤＜, 又由12x ≥,此时其解集为21{|}2x x ≤＜,综上,原不等式的解集为2|}0{x x ＜＜．（2）证明：∵()21f x x x =-+,实数a 满足1x a -＜,故()()2211f x f a x x a a x a x a x a ---+=-∙++-=-＜=()21+2112121x a a x a a a a -+-≤-++=+-＜． ∴()()()21f x f a a -+＜．山西省运城市康杰中学2017年高考全真模拟（理科）数学试卷解析一、选择题.1．【考点】1H ：交、并、补集的混合运算．【分析】利用集合的补集的定义求出集合B 的补集；再利用集合的交集的定义求出A ∩C U B【解答】解：∵2{|5}40B x Z x x -=∈+≥,∴{3}2B =U ,ð ∵集合01234512{}{}3A ==U ,,,,,，，，, ∴{}1,232323{}{}A B ==U ,,,ð, 故选：C ．2．【考点】5A ：复数代数形式的乘除运算．【分析】把已知等式变形,利用复数代数形式的乘除运算化简,再由实部和虚部相等求得b ,得到z ,代入复数模的计算公式得答案．【解答】解：由()2i 3i z b +=-,得()()()()()3bi 2i 6b 2b 3i3bi z===2i 2i 2i 5----+-++-, ∴623b b -=--,解得9b =-． ∴z=33i +,则z 故选：A ．3．【考点】JA ：圆与圆的位置关系及其判定．【分析】把圆的方程化为标准形式,求出圆心和半径,根据两圆的圆心距等于半径之和,可得两个圆关系．【解答】解：圆2214C x y +=：,表示以()10,0C 为圆心,半径等于2的圆．圆22268160C x y x y ++-+=：,即()()22349x y ++-=,表示以()23,4C -为圆心,半径等于3的圆．∴两圆的圆心距523d ==+, ∵两个圆外切．故选：B ．4．【考点】8D ：排列、组合的实际应用．【分析】根据题意,分2种情况讨论：①、从物理,化学,生物三科中选2科,从政治,历史,地理三科中选1科,②、从物理,化学,生物三科中选1科,从政治,历史,地理三科中选2科,分别求出每一种情况下的选法数目,由分类计数原理计算可得答案．【解答】解：根据题意,分2种情况讨论：①、从物理,化学,生物三科中选2科,从政治,历史,地理三科中选1科,则有21339C C ∙=种选法；②、从物理,化学,生物三科中选1科,从政治,历史,地理三科中选2科,则有21339C C ∙=种选法；则一共有9+9=18种选考方法；故选：C ．5．【考点】85：等差数列的前n 项和．【分析】利用等差数列的通项公式和等比中项定义,列出方程组,求出11a =-，2d = ,由此能求出数列{}n a 的前5项的和．【解答】解：∵在等差数列{}n a 中,45a =, 3a 是2a 和2a 的等比中项,∴()()()121113525a d a d a d a d +=⎧⎪⎨+=++⎪⎩, 解得11,2a d =-=,∴数列{}n a 的前5项的和为：()5154=55154152S a d ⨯+=⨯-+⨯=．故选：A ． 6．【考点】3L ：函数奇偶性的性质．【分析】先确定函数()f x 的周期为2,再利用函数()f x 是定义在R 上的偶函数,当[]0,1x ∈时,()2x f x =,即可得出结论．【解答】解：∵()()2f x f x +=对x ∈R 恒成立, ∴()f x 的周期为2.()f x 是定义在R 上的偶函数,∴911222f f f ⎛⎫⎛⎫⎛⎫-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∵当[]0,1x ∈时,()2xf x =,∴122f ⎛⎫= ⎪⎝⎭,故选：B ．7．【考点】EF ：程序框图．【分析】由n 的取值分别为6,12,24,代入即可分别求得S ．【解答】解：当6n =时,16sin602598,2S =⨯⨯︒=．输出2598S =．, 6＜24,继续循环,当12n =时,112sin3032S =⨯⨯︒=,输出3S =,12＜24,继续循环,当24n =时,124sin15 3.10562S =⨯⨯︒=,输出31056S =．,24=24,结束, ∴故选B ． 8．【考点】LF ：棱柱、棱锥、棱台的体积．【分析】由已知中的三视图可得：该几何体是一个正方体切去一个三棱锥所得的组合体,进而得到答案．【解答】解：由已知中的三视图可得：该几何体是一个正方体切去一个三棱锥所得的组合体, 正方体的体积为：8,三棱锥的体积为：13×12×2×2×1=23, 故组合体的体积222833V =-=,故选：A ．9．【考点】GI ：三角函数的化简求值；2H ：正弦函数的图象．【分析】利用二倍角和辅助角公式基本公式将函数化为()sin y A x ωϕ=+的形式,[]0,πx ∈时,求出内层函数的取值范围,结合三角函数的图象和性质,求出()f x 的最大值和最小值．【解答】解：函数()22cos 2x f x x =+．化简可得：()πcos 12sin 16f x x x x ⎛⎫=+=++ ⎪⎝⎭ ∵[]0,πx ∈, ∴ππ7π,666x ⎡⎤+∈⎢⎥⎣⎦，可得πsin ,2611x ⎛⎫+∈ ⎪⎡⎥⎝⎭⎤-⎢⎣⎦x , ∴函数()[]0,3f x ∈,故选：C ．10．【考点】LG ：球的体积和表面积．【分析】根据几何体的特征,判定外接球的球心,求出球的半径,即可求出球的表面积【解答】解：根据题意知,直角三角形ABC △的面积为3．其所在球的小圆的圆心在斜边AC 的中点上,设小圆的圆心为Q ,若四面体ABCD 的体积的最大值,由于底面积ABC S △不变,高最大时体积最大,所以,DQ 与面ABC 垂直时体积最大,最大值为为133ABC S DQ ⨯=△, 即1333DQ ⨯⨯=,∴3DQ =,如图．设球心为O ,半径为R ,则在直角AQO △中,222OA AQ OQ =+,即()2223,2R R R =+-∴=, 则这个球的表面积为：24π216πS =⨯=．故选：D ．11．【考点】8K ：抛物线的简单性质．【分析】当点A 在第一象限,通过抛物线定义及2AF BF =可知B 为CE 中点,通过勾股定理可知|AC =,进而计算可得结论．【解答】解：如图,点A 在第一象限．过A B 、分别向抛物线的准线作垂线,垂足分别为D E 、,过A 作EB 的垂线,垂足为C ,则四边形ADEC 为矩形．由抛物线定义可知,AD AF BE BF ==, 又∵2AF BF =, ∴2AD CE BE ==,即B 为CE 中点, ∴3AB BC =,在Rt ABC △中,AC =,∴直线l 的斜率为AB BC=当点B 在第一象限时,同理可知直线l 的斜率为-∴直线l 的斜率为±故选：C ．12．【考点】34：函数的值域．【分析】由已知函数解析式可得()()6f x f x +-=,结合()f x 在区间[](),0k k k -＞上的值域为[],m n ,即无论k 取什么样的正实数都应有最大值与最小值的和是一个确定的值,令1k =得答案．【解答】解：∵()213sin 221x x f x x -=+++, ∴()()21213sin 23sin 22121x x x x f x x x -----=++-=-=++, ∴()()6f x f x +-=．①又()f x 在区间[](),0k k k -＞上的值域为[],m n ,即无论k 取什么样的正实数都应有最大值与最小值的和是一个确定的值,故可令1k =,由于函数()213sin 221x x f x x -=+++在区间[](),0k k k -＞上是一个增函数, 故()()m n f k f k +=+-由①知,()()6m n f k f k +=+-=．故选：D ．二、填空题：本大题共4小题,每小题5分13．【考点】9R ：平面向量数量积的运算．【分析】根据条件,可分别以,AB AD 所在直线为x 轴,y 轴,建立坐标系,然后可求出点,,A B E 的坐标,进而求出向量,AE BE 的坐标,从而求出,AE BE 的值．【解答】解：分别以边,AB AD 所在直线为,x y 轴,建立如图所示平面直角坐标系,则：()()()0,0,4,0,2,1A B E ；∴()()2,1,2,1AE BE ==-；∴413AE BE =-+=-．故答案为：3﹣．14．【考点】7C ：简单线性规划．【分析】设买排球x 个,篮球y 个,由题意列关于,x y 的不等式组,作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案．【解答】解：设买排球x 个,篮球y 个,买排球和篮球的个数之和z x y =+．则232901201200x y x y x y ≥⎧⎪≥⎪⎨≤⎪⎪+≤⎩, 由约束条件作出可行域如图：联立23440x y x y =⎧⎨+=⎩,解得()8,4A , 化目标函数z x y =+为y x z =-+,由图可知,当直线y x z =-+过点A 时,直线在y 轴上的截距最大,z 有最大值为12．故答案为：12．15．【考点】4F ：进行简单的合情推理．【分析】根据学校艺术节对同一类的,,A B C D ,四项参赛作品,只评一项一等奖,故假设,,A B C D ,分别为一等奖,判断甲、乙、丙、丁的说法的正确性,即可判断．【解答】解：若A 为一等奖,则甲,丙,丁的说法均错误,故不满足题意,若B 为一等奖,则乙,丙说法正确,甲,丁的说法错误,故满足题意,若C 为一等奖,则甲,丙,丁的说法均正确,故不满足题意,若D 为一等奖,则只有甲的说法正确,故不合题意,故若这四位同学中只有两位说的话是对的,则获得一等奖的作品是B故答案为：B16．【考点】8H ：数列递推式．【分析】依题意,可求得()()2+112+111121-11ln ln ln 2ln 21111112n n n n n n n n n n n n X X X X X a a X X X X X +⎛⎫+- ⎪--⎝⎭=====++⎛⎫++- ⎪⎝⎭,即数列{}n a 是以2为公比的等比数列,又12a =,利用等比数列的通项公式即可求得答案．【解答】解：∵()21f x x =-,数列{}n x 为牛顿数列,∴()()2111122n n n n n n n n n f X X X X X X f X X X +⎛⎫-=-=-=+ ⎪'⎝⎭, ∴()()2+112+11112111ln ln ln 2ln 21111112n n n n n n n n n n n n X X X X X a a X X X X X +⎛⎫+- ⎪---⎝⎭=====++⎛⎫++- ⎪⎝⎭, 又12a =,∴数列{}n a 是以2为首项,2为公比的等比数列,∴23228a =⨯=．故答案为：8．三、解答题：解答应写出文字说明,证明过程或演算步骤17．【考点】HP ：正弦定理．【分析】()Ⅰ由正弦定理有sin sin AC DC ADC DAC =∠∠,又AC ,可得sin ADC DAC ∠=∠,结合6060ADC B BAD B ∠=∠+∠=∠+︒︒＞,可求ADC ∠,即可求B 的值． ()Ⅱ设DC x =,则2,3,BD x BC x AC ===．可求sin 33AC B B AB BC ====,由余弦定理即可计算得解DC 的长．【解答】（本题满分为12分）解：()Ⅰ在ABC △中,根据正弦定理,有sin sin AC DC ADC DAC=∠∠．因为AC =,所以sin ADC DAC ∠∠=．又6060ADC B BAD B ∠=∠+∠=∠+︒︒＞,所以120ADC ∠=︒．于是1801203030C ∠=︒-︒-︒=︒,所以60B ∠=︒．()Ⅱ设DC x =,则2,3,BD x BC x AC ==．于是sin AC B B AB BC ===．在ABD △中,由余弦定理,得2222cos AD AB BD AB BD B =-∙+,即(2222=64222x x x x +-⨯=,得2x =．故2DC =．18．【考点】BO ：独立性检验的应用；8B ：频率分布直方图．【分析】()Ⅰ由频率分布直方图得前三组的人数,即可求出年龄在第1,2,3组的员工人数分别是多少； ()Ⅱ由上可知,ξ的所有可能取值为0,1,2,3,求出其概率,即可求ξ的数学期望；()III 求得2K 的观测值,查表得()26635001P K ≥=．．,即可得出结论．【解答】解：()Ⅰ由频率分布直方图得前三组的人数分别为：()0.02528028,28,10.020.020.060.02528⨯⨯=⎡+++⨯⎤⨯=⎣⎦- 所以前三组抽取的人数分别为2812=2,2,82828112⨯++, ()Ⅱ由上可知,ξ的所有可能取值为0,1,2,3,其概率分别为()383121055C P C ξ===,()128431212515C C P C ξ===,()218431228525C C P C ξ===,()3831214553C P C ξ===, 所以,11228140123255555555E ξ=⨯+⨯+⨯+⨯=． ()Ⅲ假设0H ：“是否喜欢看国学类书籍和性别无关系”,根据表中数据, 求得2K 的观测值()240141448 6.8605 6.63522182218k ⨯⨯-⨯=≈>⨯⨯⨯,查表得2 6.6350.01P K ≥=（）,从而能有99%的把握认为该单位员工是否喜欢阅读国学类书籍和性别有关系 19．【考点】MT ：二面角的平面角及求法；LY ：平面与平面垂直的判定．【分析】()Ⅰ推导出,OD AC DO OM ⊥⊥,从而OD ⊥面ABC ,由此能证明平面ODM ABC ⊥平面． ()Ⅱ由,,OD OC OB OC OB OD ⊥⊥⊥,建立空间直角坐标系,利用向量法能求出二面角M AD C --的余弦值．【解答】（本小题满分12分）证明：()Ⅰ证明：∵ABCD 是菱形, ∴AD DC OD AC =⊥,,12120ADC AD DC ADC ==∠=︒△中,,,∴6OD =,又M 是BC 中点,∴16,2OM AB MD ===∵222OD OM MD +=∴DO OM ⊥,∵,OM AC ⊂面ABC ,OM AC O =, ∴OD ⊥面ABC ,又∵OD ⊂平面ODM ,∴平面ODM ⊥平面ABC ．()Ⅱ解：由题意,,OD OC OB OC ⊥⊥,又由（Ⅰ）知OB OD ⊥,建立如图所示空间直角坐标系, 由条件知：()()()6,0,0,0,,D A M - 故()()0,93,3,6,6AM AD ==, 设平面MAD 的法向量(),,m x y z =,则00m AM m AD ⎧=⎪⎨=⎪⎩,即3060z x ⎧+=⎪⎨+=⎪⎩,令y =则3,9x z ==, ∴()3,m =,由条件知OB ⊥平面ACD ,故取平面ACD 的法向量为()0,0,1n =.所以,393cos ,31m nm n m n ≥=由图知二面角M AD C --为锐二面角,故二面角M AD C --20．【考点】4K ：椭圆的简单性质．【分析】()Ⅰ由题意可知：由32PQ QB =,求得Q 点坐标,即可求得椭圆E 的方程； ()Ⅱ设直线2y kx =-,代入椭圆方程,由韦达定理,由0△＞,由坐标原点O 位于以MN 为直径的圆外,则0OM ON ∙>,由向量数量积的坐标公式,即可求得直线l 斜率的取值范围．【解答】解：()Ⅰ由题意知：ABP △是等腰直角三角形,()220a B =,,, 设()00Q x y ,,由32PQ QB=,则0064,45x y ==-,代入椭圆方程,解得21b =, ∴椭圆方程为2214x y +=． ()Ⅱ由题意可知,直线l 的斜率存在,方程为2y kx =-,设()()1122M x y N x y ,,,, 则22214y kx x y =-⎧⎪⎨+=⎪⎩,整理得：()221416120k x kx +-+=, 由韦达定理可知：12122216121414k x x x x k k +==++,, 由直线l 与E 有两个不同的交点,则0△＞, 即()()2216412140k k --⨯⨯+＞,解得：234k ＞,① 由坐标原点O 位于以MN 为直径的圆外,则0OM ON >,即12120x x y y +＞,则()()1212121222x x y y x x kx kx +=+--=()()21212124k x x k x x +-⨯++ =()222121612401414k k k k k +-⨯+++＞, 解得：24k ＜,② 综合①②可知：2344k ＜＜,2k ＜或2k -＜＜直线l斜率的取值范围32,,2⎛⎛⎫- ⎪ ⎪⎝⎭⎝⎭．21．【考点】6H ：利用导数研究曲线上某点切线方程；6B ：利用导数研究函数的单调性．【分析】()1由题意有：()21e 42m f '==,可得()f x 的解析式；()0f x '由＜得01x ＜＜或1e x ＜＜,即可求出单调递减区间； ()2由已知,若存在[)0e,x ∈+∞,使函数()()21e eln ln 22a g x a x x x f x a +=+-∙∙≤成立,则只需满足当[)()e,,min x g x a ∈+∞≤即可【解答】解：()1函数()f x 的定义域为()()0,11,+∞,()()()2ln 1ln m x f x x -'=, 又由题意有：()21e 42m f '==,所以()22,ln x m f x x ==．此时,()()()22ln 1ln x f x x -'=,由()0f x '＜得01x ＜＜或1e x ＜＜, 所以函数()f x 的单调递减区间为()01,和()1,e ． ()2因为()()21eln e 2g x a x x a x =++-,由已知,若存在[)0e x ∈+∞,,使函数()()21e eln ln 22a g x a x x x f x a +=+-≤成立, 则只需满足当[)(),min x e g x a ∈+∞≤,即可．又()()21eln e 2g x a x x a x =+-+, 则()()()e x a x g x x--'=, e a ≤,则()0g x '≥在[)e,x ∈+∞上恒成立,∴()g x 在[)e +∞,上单调递增,∴()()2e e 2min g x g ==-, ∴2e 2a ≥-, ∵e a ≤, ∴2e e 2a -≤≤． e a ＞,则()g x 在[)e,a 上单调递减,在[),a +∞上单调递增,∴()g x 在[)e +∞,上的最小值是()g a ,∵()()e e g a g a ＜,＞,∴满足题意,综上所述,2e 2a ≥-． [选修44-：坐标系与参数方程]22．【考点】QH ：参数方程化成普通方程；4Q ：简单曲线的极坐标方程．【分析】()Ⅰ圆2cos 2sin x C y θθ=⎧⎨=⎩：（θ为参数）,可得直角坐标方程：224x y +=,利用互化公式可得圆C 的极坐标方程．点P 在直线40l x y +-=：上,利用互化公式可得直线l 的极坐标方程． ()Ⅱ设,,P Q R 的极坐标分别为()()()12,ρθρθρθ,,,,,由124=,2sin cos ρρθθ=+,又2•OP OR OQ =,即可得出．【解答】解：()Ⅰ圆2cos 2sin x C y θθ=⎧⎨=⎩：（θ为参数）,可得直角坐标方程：224x y +=, ∴圆C 的极坐标方程2ρ=．点P 在直线40l x y +-=：上,直线l 的极坐标方程4sin cos ρθθ=+． ()Ⅱ设,P Q R ,的极坐标分别为()()()12,ρθρθρθ,,,,, 因为124=,2sin cos ρρθθ=+,又因为2•OP OR OQ =,即212=ρρρ, ∴()2122161==2sin cos ρρρθθ⨯+, ∴8=1sin 2ρθ+． [选修4-5：不等式选讲]23．【考点】4R ：绝对值三角不等式；5R ：绝对值不等式的解法．【分析】()1根据题意,对x 分3种情况讨论：①当0x ＜时,②当102x ≤＜时,③当12x ≥时；在各种情况下．去掉绝对值,化为整式不等式,解可得三个解集,进而将这三个解集取并集即得所求． ()2根据()()2211f x f a x x a a x a x a x a =+=+-<+-----=21211||||21x a a x a a a -+-≤-+-++＜,证得结果．【解答】()1解：根据题意,对x 分3种情况讨论：①当0x ＜时,原不等式可化为211x x -+-+＜,解得0x ＞,又0x ＜,则x 不存在, 此时,不等式的解集为∅．②当102x ≤＜时,原不等式可化为211x x -++＜,解得0x ＞,又102x ≤＜, 此时其解集为122x x ⎧⎫≤⎨⎬⎩⎭＜． ③当12x ≥时,原不等式化为211x x -+＜ ,解得122x ≤＜, 又由12x ≥,此时其解集为21{|}2x x ≤＜, 综上,原不等式的解集为2|}0{x x ＜＜． ()2证明：∵()21f x x x =-+,实数a 满足1x a -＜,故()()2211f x f a x x a a x a x a x a ---+=-∙++-=-＜=()21+2112121x a a x a a a a -+-≤--++=+＜． ∴()()()21f x f a a -+＜．。

山西省康杰中学届高三5月第三次模拟(文综) 146121

2010年5月份康杰中学高三文综模拟试题（三）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分300分，考试时间150分钟。

第Ⅰ卷（选择题）本卷共35小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

读“某地冬至日（12月22日）太阳高度变化曲线图”，回答1—2题。

1．该地的经纬度是（）A．66°S ，120°WB．66.5°S , 120°EC．86°S, 120°ED．80.5°S ， 120°W2．图中的X的数据是（）A．32°B．33°C．32.5°D．33.5°下面左图是风向标示意图，下图是某地近地面水平气压分布示意图。

读图，回答3—4题：3．此时，Q地的风向为（）A．东北风B．东南风C．西南风D．西北风4．此时，最有可能出现阴雨天气的地点是（）A．M地B．N地C．P地D．Q地我海军第三批护航编队经过10余天的航渡，已空越台湾海峡、西沙、南沙，航经马六甲海峡进入印度洋，于2009年8月1日进入亚丁湾、索马里任务海域正式执行扩航任务。

作为前两批护航任务的后续行动，派出海军第三批护航编队对确保护航任务常态化有效进行具有重要意义。

读图，回答5—6题：5．此期间下列现象可信的是（）A．护航舰基本上是逆水到达护航地点B．护航舰逆流行驶过曼德海峡进入红海C．索马里的热带草原一片枯黄D．在曼德海峡沿岸看见成群结队的白色皮肤的索马里人6．关于下列地区地理特征的叙述，正确的是（）A．M地区的自然带呈现地带性分布规律B．N地区处在非洲板块与印度洋板块消亡边界C．J地区分布有大面积的热带稀树草原D．K地区为有大面积的热带草原带读某模式图，回答7—8题。

7．若该图表示农业地域类型的要素及特征，x轴为商品率，Y轴为劳动力，z轴为机械化程度。

下列选项正确的是（）A．①点为水稻种植业②点为游牧业B．①点为水稻种植业③点为商品谷物农业C．②点为水稻种植业④点为大牧场放牧业D．②点为乳畜业④点为大牧场放牧业8．若该图表示工业生产的区位因素，x轴为市场，Y轴为劳动力，z轴为技术。

山西省运城市康杰中学高考数学模拟试题(三)理

【满分150分，考试时间为120分钟】一、选择题(5X 12= 60分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确选项用2B 铅笔涂黑答题纸上对应题目的答案标号) 1 •设复数z 满足(2 i)z 5,则|z| = A., 3B. 2C. . 5D. 52. 已知集合 A ={x|x 2 5x 6 0}, B ={x| y In(x 1)},则 AI B 等于A. [— 1, 6] B. (1,6]C. [-1,+)D. [2, 3]3. 下列说法正确的是A. 命题“若x 2 3x 4 0，则x 4.”的否命题是“若 x 2 3x 4 0,则x 4.B.“ a 0 ”是“函数yx a 在定义域上单调递增”的充分不必要条件.C.X 。

( ,0),3' 4x ).和等于递增，则实数a 的值为C. 5 7.如图，网格纸上小正方形的边长1,粗实线和虚线画出的是某几何体的三视图，该几何体D.若命题p : n N ,3n 500，则 p: n ° N,3n0500.4.在等差数列｛a n ｝中，已知a 4,a 7是函数 f(x) x 2 4x 3的两个零点，贝U ｛a n ｝的前10A. —18B. 9C. 18D. 205.已知函数f (x) a 2 3x 3xR 上的奇函数, 且函数 x ag(x)在(0,)上单调xA. — 1B.C. 1D. 226.已知(1 x) (1 x)...(1nx)2a ° a 〔x a 2Xa 〔 a ?a n 1= 29 n ,那么自然数A. 3B. 4/ 1 1 x厶D. 6na n X ,右的各个面中有若干个是梯形，则这些梯形的面积之和为B. 30 A. 28A . a炷，a:bh2:1B . a1:2C. 32 8. 如图所示是某同学为求 2, 4, 6,…，2016 , 2018的平均数而设计的程序框图，则在该程序框图中的空白判断框和处理框中应填入的内容依次是1（a 0,b 0）的右焦点，P 是y 轴正半轴上一点，以 OP 为直径的圆在第一象限与双曲线的渐近线交于点M （O 为坐标原点），若点P ，M F 三点共线，且MFO 的面积是 PMO 的面积的3倍，则双曲线 C 的离心率为A. , 6B. . 5C. 3D. 210•将函数y cosx sinx 的图像先向右平移（ 0）个单位，再将所得的图像上每个点的11.祖暅原理也就是“等积原理”，它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的，祖暅原理的内容是：夹在两个平行平面间的两个几何体，被平行于这两个平行平面的平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等 .已知，两个平行平面间有三个几何体，分别是三棱锥、四棱锥、圆锥（高度都为h ），其中：三棱锥的底面是正三角形（边长为 a ），四棱锥的底面是有一个角为 60o 的菱形（边长为b ），圆锥的体积为V ，现用平行于这两个平行平面的平面去截三个几何体，如果截得的三个截面的面积相等,那么，下列关系式正确的是D. 36A. i x 1009?,x iB.ix 1009?,x i C.i1009?,x xi 1D.i1009?,x xi 12 29.已知F 是双曲线笃爲a b 横坐标变为原来的 a 倍，得到y ,a 的可能取值为A. C. ,a 2 2 3 1 ,a823 B.,a 281D.,a 2 2x12.已知函数f (x) 2|x| x 2,g(x) — (其中e 为自然对数的底数)，若函数x 2h(x) f[g(x)] k 有4个零点，贝U k 的取值范围为2 12 1 A. ( 1,0)B. (0,1)C. (2 冷,1)D. (0,2 冷)e ee e二、填空题(本大题共 4小题，每小题5分，共20分)rr r_ r r _ r13.已知向量a (1,2)，向量b 在a 方向上的投影为 2,5，且|a b| ,10，则|b| = 球的表面积为三、解答题(本大题共 6小题，满分70分.解答须写出文字说明、证明过程和演算步骤) 17.(本小题满分12分)已知在 ABC 中，角A,B,C 的对边分别为a,b,c 且C0SBC0SC%n Ab c 3sin C(1) 求b 的值；14.已知数列S n ，若 3S n2a n 3n ，则 a .=x 215.实数x, y 满足2x yx 2y0，若 z kxy 的最大值为13,则实数k16.在菱形4.3 , 将 ABD 沿BD 折起到 PBD 的位置，若二面角P BD C 的大小为-3，三棱锥 P BCD 的外接球心为 O ，则三棱锥 P BCD 的外接(2)若cosB . 3sinB 2，求a c的取值范围.18.(本小题满分12分)某闯关游戏规划是：先后掷两枚骰子，将此试验重复n轮，第n轮的点数分别记为x n, y n,如果点数满足x n -6y^，则认为第n轮闯关成功，否则进行下一轮投掷，直到闯关成功，Y n 6游戏结束•（1）求第1轮闯关成功的概率；1（2）如果第i轮闯关成功所获的奖金（单位：元）f（i） 20000歹，求某人闯关获得奖金不超过2500元的概率；（3）如果游戏只进行到第4轮，第4轮后无论游戏成功与否，都终止游戏，记进行的轮数为随机变量X,求X的分布列和数学期望•19. （本小题满分12分）如图，在底面为等边三角形的斜三棱柱」3AB，四边形BGCB为矩形，过AQ作与直线BC1平行的平面AQD交AB于点D .（1）证明：CD AB ；（2）若直线AA1与底面A1B1C1所成的角为60°，求二面角B A1C C1的余弦值.20. （本小题满分12分）如图，已知抛物线C: X2 4y，过点M（0,2）任作一直线与C相交于A,B 两点，过点B作y轴的平行线与直线AO相交于点D（O为坐标原点）.（1）证明：动点D在定直线上；（2）作C的任意一条切线I （不含x轴），与直线y 2相交于点N1，与（1）2 2交于点N2.证明：MN2 MN1为定值，并求此定值.21. （本大题满分12分）已知函数f（x）（x2 2x） lnx ax2 2 .（1）当a 1时，求曲线y f（x）在点（1,f（1））处的切线方程；/./0D VABC A1B1C1中,AA中的定直线相（2）当a 0时，设函数g（x） f （x） x 2，且函数g（x）有且仅有一个零点，若当2 e x e时，g（x） m恒成立，求实数m的取值范围.请考生在第22、23两题中任选一题做答，如果多做，则按所做的第一题记分22.（本题满分10分）选修4—4坐标系与参数方程在直角坐标系x a cos ,xOy中，已知曲线C的参数方程是（为参数，a 0），直y 73 sin线1的参数方程是x 3 t（t为参数），曲线C与直线1的一个公共点在x轴上•y 1 t（1）求曲线C的普通方程；（2）以坐标原点0为极点，x轴的正半轴为极轴建立极坐标系，若点P, Q R在曲线C上且三点2 4 1 1 1的极坐标分别为（1, ）,（2, ——）,（3, ——），求--- 2 一2 —的值•3 3 |0P |2|0Q |2|0R|223.（本小题满分10分）选修4—5：不等式选讲已知函数f（x） | x 2 | | x m |.（1 ）若不等式f （x）1恒成立，求实数m的取值范围；19 16 （2）当m = 1时，函数f （x）的最小值为k，若a b k（a 0,b 0）,求证：丄三 A a b 32018届数学理模拟（三）参考答案C.B.D. x2【解析】【解析】【解析】3x 42 i，所以z .5，故选C.[1,6], B (1,A.若“ x2 3x 4），所以A B （1,6］，故选0 ,则x 4 ”的否命题为“若0 ”，故A错误；B.当a2时，函数y x2在（B.x 4，则,0）上单调递减，故B错误；C.因为任意x （,0）都有3x4x，故C错误。

康杰中学高三数学试卷

一、选择题（每题5分，共50分）1. 下列各数中，无理数是（）A. 2√3B. -√4C. √-1D. √0.252. 已知函数f(x) = x² - 2x + 1，若f(2a - 1) = f(a + 1)，则a的值为（）A. 1B. 2C. 3D. 43. 下列各对点中，一定在直线y = 2x + 1上的是（）A. (1, 3)B. (0, 2)C. (-1, 1)D. (2, 5)4. 已知等差数列{an}的首项a1 = 2，公差d = 3，则第10项an = （）A. 29B. 30C. 31D. 325. 已知函数f(x) = ax² + bx + c（a ≠ 0），若f(-1) = 0，f(2) = 4，则f(3)的值为（）A. 6B. 8C. 10D. 126. 下列不等式中，正确的是（）A. |x| > 2B. |x| ≥ 2C. |x| ≤ 2D. |x| < 27. 已知复数z = 3 + 4i，则|z| = （）A. 5B. 7C. 9D. 118. 已知等比数列{bn}的首项b1 = 3，公比q = 2，则第n项bn = （）A. 3 × 2^(n-1)B. 6 × 2^(n-2)C. 9 × 2^(n-3)D. 12 × 2^(n-4)9. 下列函数中，单调递减的是（）A. y = x²B. y = -x²C. y = 2xD. y = -2x10. 已知向量a = (2, 3)，向量b = (-1, 2)，则向量a - b = （）A. (3, 1)B. (1, 3)C. (-3, -1)D. (-1, -3)二、填空题（每题5分，共50分）11. 已知等差数列{an}的首项a1 = 1，公差d = 2，则第10项an = _______。

12. 已知函数f(x) = 2x - 1，若f(2) = 3，则x = _______。

山西省康杰中学高三5月考题(一)数学理(缺答案)

康杰中学高三五月份考题数学理科（一）本试卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分150分，考试时间1。

第I 卷（选择题共60分）一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1．全集{},034|,2≤+-∈==x x N x A R U{}06|2=-+∈=x x R x B ，则图中阴影表示的集合为（）A ．{}2B ．{}3C ．{}2,3- D ．{}3,2-2．若复数i i iz 41213+=-+（z 是复数，i 为虚数单位），则复数=z （）A ．i +9B ．i -9C ．i +2D ．i -23．已知点),(),sin ,(cos ),,(),,(001303O C B A αα-，若13=+，),(πα0∈，则OC OB 与的夹角为（）A ．6πB ．43π C ．3π D ．2π 4．设等差数列{}n a 的前n 项和为n S ，已知220072009,2011200720091=--=S S a ，则2011S =（）A ．-B ．C ．-D ．5．如图是一个算法的程序框图，该算法输出的结果是（）A ．54 B ．43 C ．32D ．216．若函数123)(+-=a ax x f 在区间[-1，1]上没有零点，则函数x x a x g 3)(1()(3-+= )4+的递减区间是（）A ．)1,(--∞B ．),1(+∞C ．)1,1(-D ．),1()1,(+∞⋃--∞7．已知抛物线)0(22>=p px y 上一点)0)(,1(>m m M 到其焦点的距离为5，双曲线122=-y ax 的左顶点为A ，若双曲线一条渐近线与直线AM 平行，则实数a 等于（）A ．91 B ．41 C ．31 D ．21 8．已知圆C ：)0,0(422≥≥=+y x y x 与函数x x g x x f 2)(,log )(2==的图象分别交于),(11y x A ，),(22y x B ，则2221x x +等于（）A ．16B ．8C ．4D ．2 9．如图所示的是三棱锥D-ABC 的三视图，点O 在三个视图中都是所在边的中点，则异面线线DO 和AB 所成角的余弦值等于（）A ．33 B ．21 C ．3D ．22 10．设第一象限内的点),(y x 满足约束条件⎩⎨⎧≥+-≤--02062y x y x ，若目标函数by ax z += )0,0(>>b a 的最大值为40，则ba 15+的最小值为（）A ．625 B ．49 C ．1D ．411．甲、乙、丙、丁4人站到共有7级的台阶上，若每级台阶最多站3人，同一级台阶上的人不区分站的位置，则不同的站法种数是_____________.A ．2394B ．2401C ．2395D ．2402 12．关于函数xxxx x f 22)(-=和实数n m 、的下列结论中正确的是（）A ．若)()(,3n f m f n m <<-则B ．若)()(,n f m f n m <<则C ．若33),()(n m n f m f <<则D ．若22),()(n m n f m f <<则第Ⅱ卷（非选择题共90分）本卷包括必考题和选考题两部分。

山西省运城市康杰中学2022届高考模拟(五)理科综合化学试题Word版含答案

山西省运城市康杰中学2022届高考模拟〔五〕理科综合化学试题Word版含答案相对原子质量：H—1 C-12 N-14 O-16 Mg-24 Si-28 Cl-35.5 7．中国诗词深受众人喜爱，针对以下一些诗词，从化学角度解读正确的选项是A．王安石的《梅花》“遥知不是雪，唯有暗香来〞描述了物质发生化学变化过程中既有状态变化又有气味的产生B．庾信的《杨柳歌》“独忆飞絮鹅毛下，非复青丝马尾垂〞从化学成分分析现实生活中“飞絮〞“鹅毛〞主要成分都是蛋白质C．赵孟頫的《烟火诗》“纷纷灿烂如星陨，赫赫喧虺似火攻〞描述了颜色反响的现象 D．刘禹锡的《浪淘沙》“千淘万漉虽辛苦，吹尽狂沙始到金〞，说明金在自然界中以游离态存在，其化学性质稳定8. 设NA为阿伏加罗常数的值。

以下说法正确的选项是〔〕 A．7.1g C12与足量NaOH溶液反响转移的电子数为0.2NAB．室温下，1LpH=13的NaOH溶液中，由水电离的OH离子数目为0.1NA C．2.0 g H2O和H2O组成的混合液中含中子数为NAD．60gSiO2和12g金刚石中含有的Si－O键和C－C键的数目均为2NA 9. 如图表示某种有机物的结构,关于它的性质表达中正确的选项是( )A.1 mol该有机物在一定条件下,能与7 mol H2发生成反响B. 该有机物水解的产物互为同分异构体 C 能与Na2CO3反响的官能团有两种D.1 mol该有机物在一定条件下,能与7 mol NaOH反响10. Q、W、X、Y、Z 五种短周期主族元素，它们的原子序数依次增大。

：Q 与X、W 与 Y 分别位于同主族且 W、Y 质子数之和是 Q、X 质子数之和的2倍。

以下说法正确的选项是〔〕 A. 原子半径的大小顺序：W>X>YB. W 的简单气态氢化物的热稳定性比 Y 的弱C. Z 分别与 Q、X 形成的化合物中化学键类型相同D. X 的最高价氧化物对应水化物的碱性在同周期中最强11.以下实验操作及现象,能推出相应结论的是( )选项实验操作及现象结论加118216?常温下,用pH计测得0.1 mol·L NaA溶液的A pH小于0.1 mol·L Na2CO3溶液的pH 取少量久置的Na2SO3溶液,加足量盐酸酸化,再B 参加BaCl2溶液。