人教版初三数学上册22.3实际问题与二次函数——最大利润.3.2实际问题与二次函数

合集下载

人教版九年级上册22.3实际问题与二次函数(最大利润问题)教案教学设计

4.练习：布置一定数量的练习题，巩固学生对最大利润问题的解决方法。
5.总结：对本节课的内容进行总结，强调二次函数在实际问题中的应用。
6.课后作业：布置与最大利润问题相关的作业，让学生在课后进一步巩固所学知识。
教学评价：
1.课堂表现：关注学生在课堂上的参与程度，积极思考、提问的表现。
2.作业完成情况：评价学生对最大利润问题解决方法的掌握程度。
（2）鼓励学生尝试用不同的方法解决同一问题，提高他们的思维灵活性和创新意识。
3.拓展作业：
（1）引导学生关注生活中的最大利润问题，如超市促销、工厂生产等，要求学生运用所学知识进行分析，并提出解决方案。
（2）鼓励学生查找相关资料，了解二次函数在其他领域的应用，如经济学、管理学等。
4.作业要求：
（1）要求学生在作业本上规范书写，保持卷面整洁。
4.通过对最大利润问题的探讨，培养学生的数感和运用数学知识解决实际问题的能力。
（二）过程与方法
1.通过小组合作、讨论交流等形式，培养学生合作探究、解决问题的能力。
2.引导学生运用数学建模的思想，从实际问题中抽象出数学模型，提高学生的数学思维能力。
3.运用数形结合的方法，让学生在解决最大利润问题的过程中，深入理解二次函数的性质和图像。
（2）新课：讲解二次函数在实际问题中的应用，通过例题让学生体会最大利润问题的解决方法。
（3）练习：设计不同难度的练习题，让学生在解决最大利润问题的过程中，巩固所学知识。
（4）总结：对本节课的重点知识进行总结，强调二次函数在实际问题中的应用。
3.教学策略：
（1）关注学生的个体差异，实施分层教学，使每个学生都能在原有基础上得到提高。
三、教学重难点和教学设想
（一）教学重难点

人教版数学九年级上册：22.3 实际问题与二次函数第2课时二次函数与最大利润问题教案

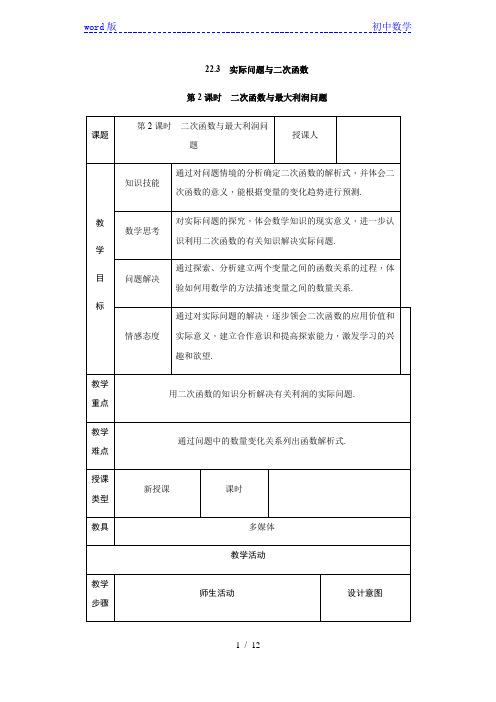
22.3实际问题与二次函数第2课时二次函数与最大利润问题【知识网络】典案二导学设计一、阅读课本：二、学习目标：1．懂得商品经济等问题中的相等关系的寻找方法；2．会应用二次函数的性质解决问题．三、探索新知某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件；每降价1元，每星期可多卖出20件．已知商品的进价为每件40元，如何定价才能使利润最大？分析：调整价格包括涨价和降价两种情况，用怎样的等量关系呢？解：（1）设每件涨价x元，则每星期少卖_________件，实际卖出_________件，设商品的利润为y元．（2）设每件降价x元，则每星期多卖_________件，实际卖出__________件．四、课堂训练1．某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出（100－x）件，应如何定价才能使利润最大？2．蔬菜基地种植某种蔬菜，由市场行情分析知，1月份至6月份这种蔬菜的上市时间x （月份）与市场售价P（元/千克）的关系如下表：上市时间x/（月份）123456市场售价P（元/千克）10.597.56 4.53这种蔬菜每千克的种植成本y（元/千克）与上市时间x（月份）满足一个函数关系，这个函数的图象是抛物线的一段（如图）．（1）写出上表中表示的市场售价P（元/千克）关于上市时间x（月份）的函数关系式；（2）若图中抛物线过A、B、C三点，写出抛物线对应的函数关系式；（3）由以上信息分析，哪个月上市出售这种蔬菜每千克的收益最大？最大值为多少？（收益＝市场售价－种植成本）五、目标检测某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．设每个房间每天的定价增加x元，求：（1）房间每天入住量y（间）关于x（元）的函数关系式；（2）该宾馆每天的房间收费z（元）关于x（元）的函数关系式；（3）该宾馆客房部每天的利润w（元）关于x（元）的函数关系式，当每个房间的定价为多少元时，w有最大值？最大值是多少？。

人教版数学九年级上册说课稿22.3《实际问题与二次函数》

人教版数学九年级上册说课稿22.3《实际问题与二次函数》一. 教材分析《实际问题与二次函数》这一节是人教版数学九年级上册第22.3节的内容。

这部分教材主要让学生理解和掌握二次函数在实际问题中的应用。

通过本节课的学习，学生将能够将所学的二次函数知识应用于解决实际问题，提高他们的数学应用能力。

教材中给出了几个实际问题，让学生通过解决这些问题来理解和掌握二次函数的应用。

二. 学情分析九年级的学生已经学过二次函数的基本知识，他们对二次函数的图像和性质有一定的了解。

但是，将二次函数应用于实际问题可能是他们比较陌生的。

因此，在教学过程中，我需要引导学生将所学的二次函数知识与实际问题联系起来，帮助他们理解和掌握二次函数在实际问题中的应用。

三. 说教学目标1.知识与技能目标：学生能够理解二次函数在实际问题中的应用，并能够运用二次函数解决实际问题。

2.过程与方法目标：学生通过解决实际问题，培养他们的数学思维能力和解决问题的能力。

3.情感态度与价值观目标：学生能够认识到数学在实际生活中的重要性，增强他们对数学的兴趣和自信心。

四. 说教学重难点1.教学重点：学生能够理解二次函数在实际问题中的应用。

2.教学难点：学生能够将所学的二次函数知识应用于解决实际问题，并能够灵活运用。

五. 说教学方法与手段1.教学方法：我将以问题为导向，引导学生通过解决实际问题来理解和掌握二次函数的应用。

我会鼓励学生进行合作学习和讨论，培养他们的数学思维能力和解决问题的能力。

2.教学手段：我将使用多媒体教学手段，如PPT和教学软件，来展示二次函数的图像和实际问题的情境，帮助学生更好地理解和掌握知识。

六. 说教学过程1.导入：我会通过一个简单的实际问题引入本节课的主题，激发学生的兴趣和好奇心。

2.教学新课：我会引导学生回顾二次函数的基本知识，然后向他们介绍二次函数在实际问题中的应用。

我会通过示例和讲解，让学生理解和掌握二次函数的应用方法。

3.学生练习：我会给出几个实际问题，让学生独立解决。

人教版九年级数学上册22.3实际问题与二次函数第2课时《销售利润问题》教案

人教版九年级数学上册22.3实际问题与二次函数第2课时《销售利润问题》教案一. 教材分析本节课是人教版九年级数学上册第22.3节实际问题与二次函数的第2课时，主要内容是销售利润问题。

教材通过引入实际问题，让学生理解和掌握二次函数在实际生活中的应用，培养学生运用数学知识解决实际问题的能力。

本节课的内容与学生的生活实际紧密相连，有利于激发学生的学习兴趣和积极性。

二. 学情分析九年级的学生已经学习了二次函数的基本知识，对于二次函数的图像和性质有一定的了解。

但是，将二次函数应用于实际问题的解决上，可能还存在一定的困难。

因此，在教学过程中，教师需要引导学生将理论知识与实际问题相结合，提高学生运用二次函数解决实际问题的能力。

三. 教学目标1.理解销售利润问题的背景和意义，掌握销售利润问题的解决方法。

2.能够将二次函数知识应用于解决实际问题，提高学生的数学应用能力。

3.培养学生的团队协作能力和问题解决能力，提高学生的数学素养。

四. 教学重难点1.重点：掌握销售利润问题的解决方法，能够将二次函数应用于实际问题的解决。

2.难点：如何引导学生将二次函数与实际问题相结合，提高学生的问题解决能力。

五. 教学方法本节课采用问题驱动的教学方法，通过引入实际问题，引导学生运用二次函数知识进行解决。

同时，采用小组合作学习的方式，鼓励学生积极参与讨论，提高学生的团队协作能力和问题解决能力。

六. 教学准备1.准备相关的实际问题，用于引导学生进行思考和讨论。

2.准备教学课件，用于辅助教学。

七. 教学过程1.导入（5分钟）利用多媒体展示一些生活中的销售利润问题，如商品打折、促销活动等，引导学生关注销售利润问题，激发学生的学习兴趣。

2.呈现（10分钟）呈现一个具体的销售利润问题，如某商品原价为100元，售价为80元，求商品的利润。

引导学生运用二次函数知识进行解决。

3.操练（10分钟）学生分组讨论，每组选取一个销售利润问题进行解决。

教师巡回指导，解答学生的问题，引导学生运用二次函数知识进行解决。

人教版九年级上册22.3 实际问题与二次函数(最大利润问题)教案教学设计

22.3实际问题与二次函数（最大利润问题）教案
（新人教版第二十二章第三节）
一、教学目标：
1.知识和技能目标：通过实际问题与二次函数关系的探究，让学生利用配方等方法解决利润最大值（或最小值）问题
2能力目标：通过观察，思考，交流，进一步提高分析问题、解决问题的能力
3.情感目标：通过生活学习数学，并用数学解决生活中的问题，从而激发学生的学习热情
二、教学重点、难点：
重点：利用二次函数的最大值（或最小值）解决实际问题
难点：如何将实际问题转化为二次函数问题
三、教学过程：。

人教版九年级上册22.3实际问题与二次函数(最大利润问题)(教案)

3.成果分享：每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上，以便全班都能看到。
（五）总结回顾（用时5分钟）
今天的学习，我们了解了二次函数在最大利润问题中的基本概念、重要性和应用。同时，我们也通过实践活动和小组讨论加深了对这一知识点的理解。我希望大家能够掌握这些知识点，并在日常生活中灵活运用。最后，如果有任何疑问或不明白的地方，请随时向我提问。
在学生小组讨论环节，虽然学生们提出了很多有见地的观点，但我感觉他们在分析问题和解决问题的能力上还有待提高。为此，我计划在今后的教学中，多设计一些开放性的问题，引导学生深入思考，培养他们的逻辑思维和分析能力。
总之，在本次教学过程中，我深刻认识到了自身在教学方法和策略上的不足，也看到了学生在学习过程中遇到的困难。在今后的教学中，我将不断调整和改进，努力提高教学效果，让每个学生都能在数学学习的道路上取得更好的成绩。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“二次函数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
2.引导与启发：在讨论过程中，我将作为一个引导者，帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
-二次函数模型的建立：如何根据问题的具体情境，正确地建立二次函数模型，包括确定自变量和因变量，理解函数中各个参数的实际意义。
-实际问题与数学模型的关联：将实际问题抽象成数学模型，理解数学模型背后的实际背景，以及如何将数学结果应用到实际问题中去。
举例：在农产品销售问题中，重点在于让学生理解售价、销售量和成本之间的关系，并将其表达为二次函数的形式。

人教版九年级数学上册第二十二章二次函数《22.3实际问题与二次函数》第1课时教案

人教版九年级数学上册第二十二章二次函数《22.3实际问题与二次函数》第1课时教案一. 教材分析人教版九年级数学上册第二十二章二次函数《22.3实际问题与二次函数》第1课时主要介绍了二次函数在实际问题中的应用。

这部分内容是对前面学习的二次函数知识的巩固和拓展，通过实际问题引导学生将理论知识和实际应用相结合，提高解决问题的能力。

教材通过丰富的例题和练习题，帮助学生掌握二次函数在实际问题中的运用方法。

二. 学情分析九年级的学生已经学习了二次函数的基本知识，对二次函数的图像和性质有了初步的了解。

但是，将二次函数应用于实际问题中，解决实际问题对学生来说还是一个挑战。

因此，在教学过程中，需要关注学生对知识的掌握程度，以及他们在解决实际问题时的思维方式和方法。

三. 教学目标1.了解二次函数在实际问题中的应用。

2.能够将实际问题转化为二次函数问题，利用二次函数解决实际问题。

3.培养学生的数学思维能力和解决问题的能力。

四. 教学重难点1.掌握二次函数在实际问题中的应用。

2.将实际问题转化为二次函数问题。

五. 教学方法采用问题驱动的教学方法，通过引导学生解决实际问题，让学生理解和掌握二次函数在实际问题中的应用。

同时，运用讨论法、案例分析法等，激发学生的学习兴趣，提高学生的参与度。

六. 教学准备1.准备相关的实际问题案例。

2.准备PPT，展示二次函数在实际问题中的应用。

七. 教学过程1.导入（5分钟）通过一个简单的实际问题引出本节课的主题，激发学生的兴趣。

例如：一个农场计划种植两种作物，种植面积一定的条件下，如何安排两种作物的种植面积，使得总收益最大？2.呈现（10分钟）呈现实际问题，引导学生认识到实际问题可以通过二次函数来解决。

通过PPT展示实际问题的图像，让学生观察和分析图像，理解二次函数在实际问题中的应用。

3.操练（10分钟）让学生分组讨论，尝试将实际问题转化为二次函数问题。

每组选择一个实际问题，分析问题中的变量关系，列出二次函数的表达式。

22.3+实际问题与二次函数二商品最大利润问题+课件2023—2024学年人教版数学九年级上册

某商品现在的售价为每件60元，每星期可卖出
300件，已知商品的进价为每件40元，则每星期销售
额是 18000
元，销售利润 6000
元.
数量关系
（1）销售额= 售价×销售量；
（2）利润= 销售额-总成本=单件利润×销售量；
（3）单件利润=售价-进价.
典例精析
例1 某电器商场根据民众健康需要，代理销售某种
• ∴50≤x≤100，
• ∴一周销售量y与x的函数关系式为y=100010x(50≤x≤100)；
例5 某商场销售成本为每件40 元的商品．据
市场调查分析，如果按每件50元销售，一周
能卖出500件；若销售单价每涨1元，每周销
量就减少10 件．设销售单价为x(x≥50)元．
• (2)设一周销售获得毛利润w元，写出w与x
第二十二章
二次函数
22.3 实际问题与二次函数
第5课时商品利润最大问题
导入新课
情境引入
在日常生活中存在着许许多多的与数学知识有关
的实际问题.商品买卖过程中，作为商家追求利润最大
化是永恒的追求.
如果你是商场经理，如何定价才能使商场获得最大利润呢？
讲授新课
一利用二次函数解决商品利润最大问题
探究交流
数的简图，利用简图和性质求出.
小试身手
• 某商家利用网络平台进行“直播带货”，销售一
批成本为每件30பைடு நூலகம்的商品，若销售单价为36元，
则每天可卖出88件，为提高利润，欲对该商品进
行涨价销售，经调查发现：每涨价1元，每天要少
卖出2件，按单价不低于成本价，且不高于50元销
售．
• (1)求该商品每天的销售量y(件)与销售单价x(元)之

初三数学九年级上册：22.3 实际问题与二次函数 22.3.2 实际问题与二次函数(二)——最大利润问题ppt课件

则 y＝(35－ 1 x)x－( 1 x2＋3x＋80)＝－1x2＋32x－80＝－1(x－80)2＋1 200，
10
10
5
5
∵－1＜0，∴当 x＝80 时，函数有最大值 1 200. 5
即当每个周期产销 80 件商品时，产销利润最大，最大值为 1 200 元．
D．180元
8. 生产季节性产品的企业，当它 C 的产品无利润时就会及时停
产．现有一生产季节性产品的企业C ，其一年中获得的利润y和月份n之间的函数关系式为y＝－n2 ＋14n－24，则该企业一年中应
停产的月份房间每天的房价
不得高于340元，设每个房间的
第二十二章二次函数
22．3 实际问题与二次函数
22．3.2 实际问题与二次函数(二)——最大利
武汉专版·九年级上册
3. 一件工艺品的进价为100元，标价135元出售，每天可售出100
件，根据销售统C 计，该工艺品的标价每降价1元，则每天可多售出4件，要使每天获得的利润最
大，则每件的售价应定为( ) A．130元 B．125元 C．131元
10
10
10
w与x的函数关系式； (3)－ 1 ＜0，抛物线开口向下，对称轴为直线 x＝170，又∵0＜x≤160 在对称轴的左侧， 10
(3)一天订住多少个房间时，宾馆 ∴w 随 x 的增大而增大，∴当 x＝160 时，w 的最大值为 10 880 元，此时 y＝34，则当一天订住 34 个房间时，宾馆的最大利润为 10 880 元．
的利润最大？最大利润是多少元？
P·x－C)
(1)直接写出产销成本C与商品件
数x的函数关系式(不要求写自变产销商品件数(x/件)

人教版九年级数学上册22.3实际问题与二次函数第2课时《销售利润问题》教学设计

人教版九年级数学上册22.3实际问题与二次函数第2课时《销售利润问题》教学设计一. 教材分析人教版九年级数学上册第22.3节实际问题与二次函数第2课时《销售利润问题》，主要让学生通过解决实际问题，掌握二次函数在销售利润中的应用。

教材通过引入一个具体的销售利润问题，让学生探究利润与销售数量、销售价格之间的关系，引导学生利用二次函数模型解决问题，培养学生的数学建模能力。

二. 学情分析九年级的学生已经学习了二次函数的基本知识，对二次函数的图像和性质有一定的了解。

但学生在解决实际问题时，可能会对将实际问题转化为数学模型感到困难，对利润、成本等概念在实际问题中的运用还不够熟练。

因此，在教学过程中，需要帮助学生建立数学与实际问题之间的联系，提高学生解决实际问题的能力。

三. 教学目标1.理解销售利润问题的实际背景，掌握利用二次函数解决销售利润问题的方法。

2.能够将实际问题转化为二次函数模型，提高数学建模能力。

3.培养学生的数据分析、逻辑推理和解决问题的能力。

四. 教学重难点1.重点：理解销售利润问题的实际背景，掌握利用二次函数解决销售利润问题的方法。

2.难点：将实际问题转化为二次函数模型，求解最优化问题。

五. 教学方法1.情境教学法：通过引入一个具体的销售利润问题，激发学生的学习兴趣，引导学生主动探究。

2.案例分析法：分析具体案例，让学生了解销售利润问题在实际生活中的应用，培养学生解决实际问题的能力。

3.小组合作学习：鼓励学生分组讨论，共同解决问题，提高学生的团队协作能力。

六. 教学准备1.准备相关案例材料，用于引导学生分析实际问题。

2.准备多媒体教学设备，用于展示案例和教学过程。

七. 教学过程1.导入（5分钟）利用多媒体展示一个实际的销售利润问题，引导学生思考利润与销售数量、销售价格之间的关系。

2.呈现（10分钟）呈现具体案例，让学生分析利润与销售数量、销售价格之间的关系。

引导学生运用二次函数模型解决问题。