桥梁工程箱梁悬臂桥板的结构计算简析
箱梁桥面板计算
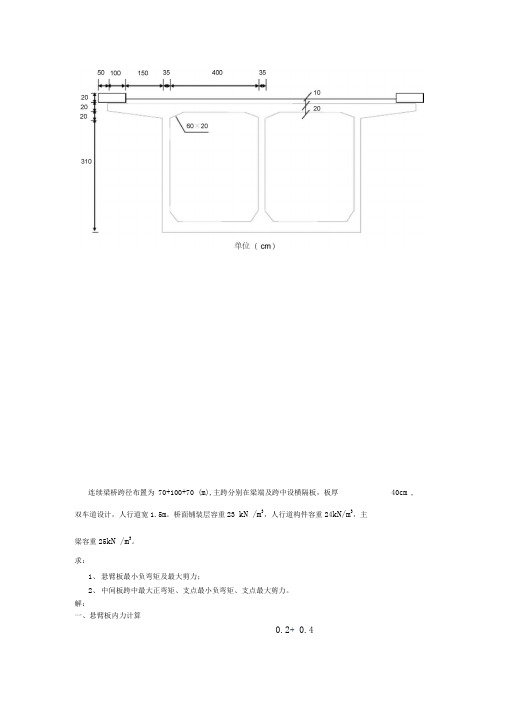
连续梁桥跨径布置为70+100+70 (m),主跨分别在梁端及跨中设横隔板,板厚40cm , 双车道设计,人行道宽1.5m。
桥面铺装层容重23 kN /m3,人行道构件容重24kN/m3,主梁容重25kN /m3。
求:1、悬臂板最小负弯矩及最大剪力;2、中间板跨中最大正弯矩、支点最小负弯矩、支点最大剪力。
解:一、悬臂板内力计算0.2+ 0.4g人二0.2 1 24 = 4.8kN / m g板 1 25 = 7.5kN/mg 铺=0.1 1 23 = 2.3kN / m q「=2.75 1 =2.75kN /m1、悬臂根部最小负弯矩计算 结构自重产生的悬臂根部弯矩:1 5M 支g - -[4.8 1.5 (3-0.75) 2.3 1.5 7.52.5人群荷载产生的悬臂根部弯矩:M 支-2.75 1.5 (3 -0.75) = -9.3kN m汽车荷载产生的悬臂根部弯矩:6 = a 2 2H =0.2 2 0.1 = 0.4m b 1 = b2 ■ 2H = 0.6 ■ 2 0.1 = 0.8m单个车轮作用下板的有效工作宽度:a =印 2b = 0.4 2 (1.5 - 0.1) = 3.2m 1.4m有重叠。
故:a = 3.2 1.4 二 4.6mp 」址=38kN/m ab 1 4.6 0.8M支p内力组合:二―1.3 38 0.8 1 =—39.5kN m基本组合:M ud =1.2 (-42.2) 1.4 (-39.5) 0.8 1.4 (-9.3) = -116.4kN m短期效应组合: M S d=-42.2 0.7 (-39.5)亠1.3 1.0 (-9.3) = -72.8kN m2、悬臂根部最大剪力计算结构自重产生的悬臂根部剪力:Q 支 g =4.8 1.5 2.3 1.5 7.5 2.5 =29.4kN人群荷载产生的悬臂根部剪力:Q 支 r =2.75 1.5 =4.1kN汽车荷载产生的悬臂根部剪力:Q 支p =1.3 38 0.8 =39.5kN内力组合:基本组合:Q ud =1.2 29.4 1.4 39.5 0.8 1.4 4.1 =95.2kN 短期效应组合:Q sd =29.40.7 39.5“1.3 1.04.1=54.8kN、中间桥面板内力计算竺]= -42.2kN m20.5m100l a50m l b =4m2= 50• 2 故按单向板计算内力lb 4把承托面积平摊到桥面板上:0.6 0.2t』0.2 0.23m4g铺=2.3kN /m1、跨中弯矩计算:g板=0.23 1 25 = 5.8kN / m g = 2.3 5.8 二8.1kN /m l = I0 t = 4 0.2 = 4.2m :::10 b =4.35m单个车轮作用下板的有效工作宽度:故:la =印32l」a d34.2 2=0.4 1.8m l = 2.8m3 3= 2.8m 1.4 4.2ma 二a1 t = 0.4 0.2 二0.6m 无重叠P1140P2P3P42a b1 2 0.6 0.8P 140ab1 2 0.8P 1404 0.8=145.8kN / m二87.5kN / m= 43.8kN /mP 140ab1 4.2 0.8=41.7kN / mP5 亠上・=58.3kN/m ab13 0.8P6 二旦=^^"2.5kN/m2ab1 2 1.4 0.8M og 」8.1 4.22=17.9kN m81.4m 有重叠1.3 ./.8■1l = 4.2m145.858.3J2.5hr-87.5 43・8 . 7583ffin 羽4!一■!| I'|:0.4■< •0.7 1 0.80.95M op =1.3 [1 (145.8 -87.5) 0.7 0.11758.3 0.8 0.4] =64.1kN m t 201 1- —, , — , —h 一310 一 15.5 4M 中二 0.5 111.2 =55.6kN m M 支二-0.7 111.2 =-77.8kN m2、支点剪力计算:a a 1 -0.41 2 3 4=1.7^:-l = 2.7m 1.4m 33 32l故:ad =4.1m3a 二 0.6m1Q 支 g 8.1 4=16.2kN111 (54.7 -42.7) 0.45 0.638 42.7 0.8 0.575(109.4 - 72.9) 0.8 0.0922272.9 0.8 0.125] =145.6kN内力组合:基本组合:Q ud =1.2 16.2 1.4 145.6 =223.3kN 短期效应组合:Q sd -16.2 0.7 145.6 “1.3 =94.6kN88 0.7 0.175 41.7 0.4 0.95 21(62.5—58.3) 0.8 0.333M 0=1.2 17.9 1.4 64.1 =111.2kN mQ支p=1.3 [ (145.8 -79.5) 0.8 0.933 79.5 0.8 0.9昇「3/JS^ ---------- 1--------I 二 4m145.8___________________ 0“°.8H 5尸5》1”.8加0.350.19.5 54.7 42.7 72.9109.42.9<TI t m 0.50.9。
悬臂板结构计算
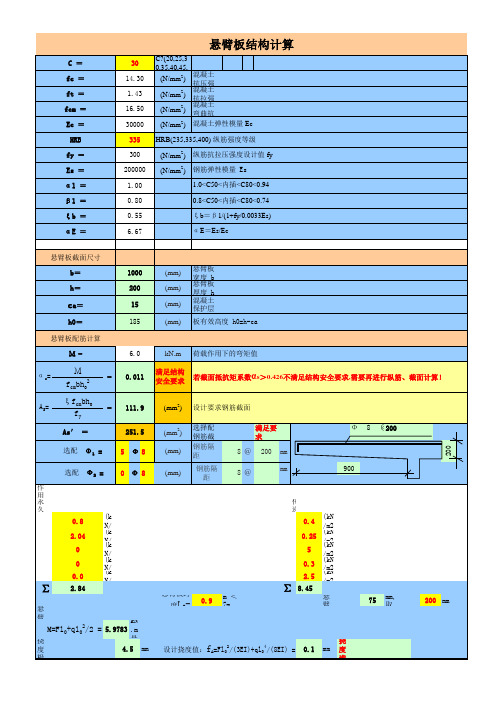
悬臂板截面尺寸 b= h= 1000 200 15 185 (mm) (mm) (mm) (mm) 悬臂板宽度 b 悬臂板厚度 h 混凝土保护层厚度 ca 板有效高度 h0=h-ca
ca=
h0= 悬臂板配筋计算 M= α s=
6.0 = 0.011
kN.m 满足结构 安全要求
荷载作用下的弯矩值 若截面抵抗矩系数αs>0.426不满足结构安全要求,需要再进行纵筋、截面计算!
作用在悬臂板上的荷载 永久性集中荷载标准值: 0.8 2.04 0 0 0.0 (kN/m) 墙面水泥砂浆面层自重 = 厚度×20 (kN/m) 栏河砖自重 = h×17 (kN/m) 栏河贴砖自重 = 厚度×25 (kN/m) 栏河压顶自重= h×25 (kN/m) 栏河上趴满人活荷载
∑
2.84 悬臂板跨度L0= 0.9
悬臂板结构计算
C = fc = ft = fcm = Ec = HRB fy = Es = α 1 = β1 = ξ b = α E = 30 14.30 1.43 16.50 30000 335 300 200000 1.00 0.80 0.55 6.67 C?(20,25,30,35,40,45,50,55) 混凝土等级
∑
m <7m,挠度极限值<l0/200
悬臂板弯矩计算:
2 M=Fl0+ql0 /2 = 5.9783 kN.m
悬臂板弯矩值 设计挠度值:fA=Fl02/(3EI)+ql04/(8EI) =
挠度极限值fA=l0/200 =
4.5
mm
M fcmbh0
2
AS=
ξ fcmbh0 fy
As′ = 选配 Ф 1 = 选配 Ф 2 =
=
《桥梁工程》(上册)第2篇混凝土梁桥第4章悬臂梁桥的设计与计算

令
按此条件求得的
称主广义扇性矩
定义:
约束扭转双力矩 约束扭 转惯矩
3、约束扭转剪应力
微元上Z方向力的平衡
根据截面内外力矩平衡计算
自由扭转 主广义扇性静矩 约束扭转增量
4、约束扭转扭角微分方程
根据截面上内外扭矩平衡
翘曲系数
截面极惯矩
根据截面上纵向位移协调
桥
2、截面形式 • 悬臂部分(锚孔)——吊装时采用肋梁 悬臂施工时采用箱梁 • 挂孔——一般采用肋梁,便于吊装
3、梁高 • 一般采用变高度梁 • 支点梁高/跨中梁高 = 2~2.5 优点:增加支点抗弯能力 不增加很多的弯矩 底缘曲线:抛物线、正弦曲线、圆弧、折 线
4、腹板及顶、底板厚度 • 顶板——满足横向抗弯及纵向抗压要求 一般采用等厚度,主要由横向抗 弯控制 • 腹板——主要承担剪应力和主拉应力 一般采用变厚度腹板,靠近悬臂 端处受构造要求控制,靠近支点 处受主拉应力控制,需加厚。
• 底板——满足纵向抗压要求 一般采用变厚度,悬臂端主要受 构造要求控制,支点主要受纵向 压应力控制,需加厚
5、配筋特点 • 纵向钢筋
– 悬臂上只承担负弯矩,配置负弯矩钢筋 – 锚孔可能承担正或负弯矩需双向配筋 – 节段施工的T形刚构
• 主筋没有下弯时布置在腹板加掖中 • 需下弯时平弯至腹板位置 • 一般在锚固前竖弯,以抵抗剪力
外力剪力流 按开口薄壁 杆件计算
剪切变形:
切口剪切变形协调
最终剪力流
• 闭口多室截面 每室设一个切口,每个切口列一个变 形协调方程
变形协调方程
联合求解可得各室剪力流
最终剪力流
剪切中心 剪力流合力位置 如果外剪力通过剪切 中,截面将只弯曲, 不扭转
简单桥梁结构计算公式

简单桥梁结构计算公式简单桥梁结构是指由简单的梁、桁架等构件组成的桥梁结构。
在设计和施工过程中,需要对桥梁结构进行计算,以保证其安全性和稳定性。
下面将介绍一些常用的简单桥梁结构计算公式。
1. 梁的受力计算公式。
在桥梁结构中,梁是承受荷载的主要构件之一。
梁的受力计算公式可以通过以下公式进行计算:M = -EI(d^2y/dx^2)。
其中,M为梁的弯矩,E为弹性模量,I为截面惯性矩,y为梁的挠度,x为梁的距离。
通过这个公式可以计算出梁在不同位置的弯矩,从而确定梁的受力情况。
2. 桁架的受力计算公式。
桁架是另一种常见的桥梁结构,其受力计算公式可以通过以下公式进行计算:F = σA。
其中,F为桁架的受力,σ为应力,A为受力面积。
通过这个公式可以计算出桁架在受力情况下的应力值,从而确定桁架的受力情况。
3. 桥墩的承载力计算公式。
桥墩是桥梁结构的支撑部分,其承载力计算公式可以通过以下公式进行计算:P = Aσ。
其中,P为桥墩的承载力,A为承载面积,σ为应力。
通过这个公式可以计算出桥墩在承载荷载时的承载能力,从而确定桥墩的稳定性。
4. 桥面板的受力计算公式。
桥面板是桥梁结构的行车部分,其受力计算公式可以通过以下公式进行计算:q = wL/2。
其中,q为桥面板的荷载,w为单位面积荷载,L为荷载长度。
通过这个公式可以计算出桥面板在受力情况下的荷载值,从而确定桥面板的受力情况。
5. 桥梁整体结构的受力计算公式。
桥梁整体结构的受力计算是指对整个桥梁结构进行受力分析,其计算公式可以通过有限元分析等方法进行计算,得出桥梁结构在受力情况下的应力、变形等参数,从而确定桥梁结构的受力情况。
在实际的桥梁设计和施工过程中,需要综合运用以上的计算公式,对桥梁结构进行全面的受力分析和计算,以保证桥梁结构的安全性和稳定性。
同时,还需要考虑桥梁结构的材料、施工工艺等因素,进行合理的设计和施工,从而确保桥梁结构的质量和可靠性。
总之,简单桥梁结构的计算公式是桥梁设计和施工过程中的重要工具,通过合理的计算和分析,可以确保桥梁结构的安全性和稳定性,为人们的出行和物资运输提供良好的保障。
悬臂梁桥的设计与计算PPT课件

Q 0 R
M 0
Re
H
h 2
27
2、45°斜截面的抗拉验算(按轴心受拉构件)
Zj
Rj cos45
Z j1R g( A gw A gH c4 o 5 s A gc v 4 o)5 s s 28
3、最弱斜截面验算(按偏心受拉构件)
判别标准: 边缘应力最大
A
b1
h cos
W
1 6
•
b1
23
中跨——锚梁与挂孔刚度相近时 悬臂与挂孔联合等代为跨度2l2+l3的简支梁
24
第三节 牛腿计算
一、计算截面宽度
25
二、截面内力
N Rs in H cos Q Rcos H s in
M
Re h tg 2来自H h 2 26
三、验算截面内力 1、竖直截面(按抗弯构件验算)
N 0 H
• 腹板——下弯的纵向钢筋 需要时布置竖向预应力钢筋
16
6、牛腿 • 截面小、受力复杂
17
第二节 悬臂梁桥的计算要点
一、恒载内力 • 静定结构 • 变截面 • 手算可采用影响线加栽 • 施工中的内力状态可能出现控制应力
18
二、活载内力
1、纵向——某些截面可能出现正负最不利 弯矩
2、横向
• 箱梁——专门分析
9 石嘴山黄河公路桥 90
10
安徽五河淮河桥
90
30.4
29 .2
5.0
1.9
半立方抛 物线
10
2、截面形式 • 悬臂部分(锚孔)——吊装时采用肋梁
悬臂施工时采用箱梁 • 挂孔——一般采用肋梁,便于吊装
11
3、梁高 • 一般采用变高度梁 • 支点梁高/跨中梁高 = 2~2.5 优点:增加支点抗弯能力
悬臂板结构计算
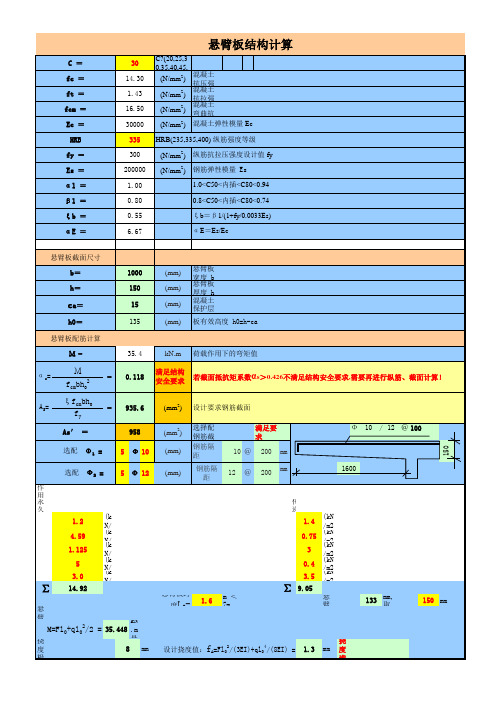
(N/mm2) 混凝土弹性模量 Ec
335 HRB(235,335,400) 纵筋强度等级
300
(N/mm2) 纵筋抗拉压强度设计值 fy
200000 (N/mm2) 钢筋弹性模量 Es
1.00
1.0<C50<内插<C80<0.94
0.80
0.8<C50<内插<C80<0.74
0.55
ξb=β1/(1+fy/0.0033Es)
1.4
(kN /m2
0.75 3
(kN /(mk2N /m2
0.4 3.5
(kN /(mk2N /m2
∑ 9.05
悬
臂
133
mm, 取
150 mm
挠
设计挠度值:fA=Fl02/(3EI)+ql04/(8EI) = 1.3 mm 度
满
悬
臂
kN
M=Fl0+ql02/2 = 35.448 .m
挠
悬
度
8 mm
极
(mm2) 设计要求钢筋截面
(mm2) (mm) (mm)
选择配 钢筋截 钢筋隔 距
钢筋隔 距
满足要 求 10 @ 200 mm
12 @ 200 mm
Ф 10 / 12 @ 100 1600
悬臂板跨
度L0=
1.6
m< 7m,
传
递
C= fc = ft = fcm = Ec =
HRB fy = Es = α1 = β1 = ξb = αE =
悬臂板结构计算
30 14.30 1.43 16.50 30000
C?(20,25,3
0,35,40,45,
带悬臂简支梁计算

带悬臂简支梁计算带悬臂简支梁是一种常见的结构形式,在工程中被广泛应用。
它由一个或多个悬臂梁和简支梁组成,具有较高的承载能力和稳定性。
本文将从结构特点、应力分析、变形分析等方面介绍带悬臂简支梁的计算方法。
我们来了解一下带悬臂简支梁的结构特点。
带悬臂简支梁通常是由梁体和支座组成。
悬臂梁是指在一端固定,另一端自由悬挂的梁结构;而简支梁是指两端都可以自由转动的梁结构。
带悬臂简支梁的支座一般是通过螺栓或焊接固定在基础或者其他结构上。
在进行带悬臂简支梁的计算时,首先需要进行应力分析。
应力分析可以通过静力学和弹性力学的基本原理进行计算。
对于悬臂梁部分,根据力的平衡条件,可以计算出悬臂梁上的剪力和弯矩分布。
而对于简支梁部分,则需要考虑支座的约束力对梁体的影响。
在进行变形分析时,考虑到带悬臂简支梁的结构特点,可以采用梁的挠度和位移的基本理论进行计算。
根据悬臂梁和简支梁的边界条件,可以得到梁在不同位置的挠度和位移。
在实际工程中,带悬臂简支梁的计算可以通过手算、计算软件或有限元分析等多种方法进行。
手算方法适用于一些简单的结构,但对于复杂的结构或者需考虑非线性因素的情况,通常需要借助计算软件或有限元分析进行计算。
需要注意的是,在进行带悬臂简支梁的计算时,要充分考虑结构的安全性和可靠性。
在计算过程中,要合理选择材料参数、荷载参数等,并根据相关规范和标准进行计算。
同时,还要注意悬臂梁和简支梁的连接处是否牢固,是否符合设计要求。
在实际工程应用中,带悬臂简支梁广泛用于桥梁、建筑物、机械设备等领域。
例如,高速公路上的立柱和横梁的连接处,常采用带悬臂简支梁的结构形式。
这种结构形式能够有效分担荷载,提高结构的稳定性和承载能力。
带悬臂简支梁是一种常见的结构形式,在工程中应用广泛。
在进行带悬臂简支梁的计算时,需要进行应力分析和变形分析,并考虑结构的安全性和可靠性。
通过合理的计算方法和工程实践,可以确保带悬臂简支梁的结构设计满足工程要求,并具有良好的承载能力和稳定性。
悬臂板结构计算

满足结构 安全要求
若截面抵抗矩系数αs>0.426不满足结构安全要求,需要再进行纵筋、截面计算!
AS=
ξfcmbh0 fy
=
111.9
As′ =
251.5
选配 Ф1 =
5 Ф8
选配 Ф2 =
0 Ф8
作
用 永
久
0.8
(k N/
2.04 0
(k N(/k N/
0 0.0
(k N(/k N/
∑
2.84
悬
臂
6.67
αE=Es/Ec
200
悬臂板截面尺寸 b= h=
ca=
h0=
1000 200 15 185
(mm) (mm) (mm) (mm)
悬臂板 宽度 b 悬臂板 厚度 h 混凝土 保护层
板有效高度 h0=h-ca
悬臂板配筋计算 M=
6.0
kN.m 荷载作用下的弯矩值
αs=
M fcmbh02
=
0.011
0.3 2.5
(kN /(mk2N /m2
∑ 8.45
悬
臂
75
mm, 取
挠
设计挠度值:fA=Fl02/(3EI)+ql04/(8EI) = 0.1 mm 度
满
200 mm
C= fc = ft = fcm = Ec =
HRB fy = Es = α1 = β1 = ξb = αE =
悬臂板结构计算
30 14.30 1.43 16.50 30000
C?(20,25,3
0,35,40,45,
(N/mm2)
混凝土 抗压强
(N/mm2)
混凝土 抗拉强
(N/mm2)
箱梁悬臂桥板的结构计算简析的开题报告

箱梁悬臂桥板的结构计算简析的开题报告一、选题背景及研究意义:箱梁悬臂桥板是一种常见的钢结构悬臂板,其具有承载能力强、抗风能力强、施工方便等优点,被广泛应用于高速公路、铁路、水库大坝等领域。
本课题旨在研究箱梁悬臂桥板的结构计算及其应用,通过建立相应的数学模型和计算方法,为工程实践提供理论支持和技术指导。
二、研究内容和方法:1.研究箱梁悬臂桥板的结构特点和受力原理,了解其受力形式和应力状态等。
2.研究箱梁悬臂桥板的应力分析和变形计算,掌握其受力分析方法和计算公式。
3.建立箱梁悬臂桥板的数学模型,使用有限元分析软件进行模拟分析,验证理论计算结果。
4.分析箱梁悬臂桥板在不同荷载下的受力性能和变形情况。
5.应用研究成果,设计并实现一座箱梁悬臂桥板工程项目,并进行实际监测和数据分析。
三、预期研究成果及创新点:1.对箱梁悬臂桥板的结构特点和受力原理进行深入研究,提出相应的受力计算方法和理论模型。
2.提出符合国家标准和行业规范的箱梁悬臂桥板设计方案,并进行实际应用和监测,验证理论预测结果的准确性和可靠性。
3.探索箱梁悬臂桥板的优化设计方法和施工技术,提高其工程应用的效率和安全性。
四、研究实施计划:1.第一阶段:文献调研,了解国内外相关研究现状和发展趋势。
制定初步的研究方案和方法。
2.第二阶段:对箱梁悬臂桥板的受力特点和应力状态进行分析和计算,建立相应的数学模型和理论公式。
3.第三阶段:使用有限元分析软件进行数值模拟,分析箱梁悬臂桥板在不同荷载下的变形和应力情况,并与理论计算结果进行比较。
4.第四阶段:根据研究结果,提出相应的设计方案和施工技术,设计并实现一座悬臂桥板工程项目。
5.第五阶段:对悬臂桥板工程项目进行实际监测和数据分析,验证理论计算结果的准确性和可靠性。
修正和优化研究成果,提出相应的改进措施和建议。
悬臂梁 计算公式法

悬臂梁计算公式法悬臂梁计算公式法。
悬臂梁是一种常见的结构形式,它在工程中被广泛应用于桥梁、天桥、楼梯等建筑物中。
悬臂梁的设计和计算是工程设计中的重要内容,合理的计算方法可以确保悬臂梁的稳定性和安全性。
本文将介绍悬臂梁的计算公式法,帮助读者了解悬臂梁的设计原理和计算方法。
悬臂梁的基本原理。
悬臂梁是一种简支梁的特殊形式,它只有一个支点,另一端悬挂在空中。
悬臂梁在受力时会产生弯矩和剪力,因此在设计和计算时需要考虑这些受力情况。
悬臂梁的计算公式法是一种基于力学原理的计算方法,通过公式和理论推导可以得出悬臂梁在受力情况下的各种参数,如弯矩、剪力等。
悬臂梁的计算公式法。
在悬臂梁的计算公式法中,最常用的公式是弯矩和剪力的计算公式。
弯矩是悬臂梁在受力时产生的弯曲力矩,它是悬臂梁设计中需要重点考虑的参数。
剪力则是悬臂梁在受力时产生的剪切力,也是设计中需要考虑的重要参数。
下面将介绍悬臂梁弯矩和剪力的计算公式。
1. 弯矩的计算公式。
悬臂梁的弯矩可以通过以下公式进行计算:M = W L。
其中,M表示弯矩,单位为牛顿·米(N·m);W表示悬臂梁上的集中力或均布载荷,单位为牛顿(N);L表示悬臂梁的长度,单位为米(m)。
在实际工程中,悬臂梁上可能存在多个集中力或均布载荷,需要分别计算每个载荷对应的弯矩,然后将它们叠加得到总的弯矩。
2. 剪力的计算公式。
悬臂梁的剪力可以通过以下公式进行计算:V = W。
其中,V表示剪力,单位为牛顿(N);W表示悬臂梁上的集中力或均布载荷,单位为牛顿(N)。
与弯矩类似,如果悬臂梁上存在多个集中力或均布载荷,需要分别计算每个载荷对应的剪力,然后将它们叠加得到总的剪力。
以上是悬臂梁弯矩和剪力的基本计算公式,通过这些公式可以得出悬臂梁在受力时的弯矩和剪力情况。
在实际工程中,还需要考虑悬臂梁的材料、截面形状、受力情况等因素,以确定悬臂梁的设计方案和参数。
悬臂梁的设计与计算。
在悬臂梁的设计与计算中,需要考虑多种因素,如受力情况、材料特性、截面形状等。
midas 悬臂结构 算例-概述说明以及解释

midas 悬臂结构算例-概述说明以及解释1.引言1.1 概述Midas悬臂结构作为一种重要的结构形式,在工程领域中具有广泛的应用。
悬臂结构以其独特的工作原理和优越的性能,成为各类工程中的重要组成部分。
本文将深入探讨Midas悬臂结构的设计原理、应用领域以及其在工程中的重要性。
通过对Midas悬臂结构的研究与分析,旨在为工程设计提供更多的参考和借鉴,推动悬臂结构在工程实践中的广泛应用和发展。
1.2 文章结构文章结构部分主要是对整篇文章的框架和组织进行介绍,让读者能够清晰地了解文章的内容安排。
本文的结构分为引言、正文和结论三个部分。
在引言部分,我们首先概述了本文要讨论的主题——Midas悬臂结构算例,并介绍了文章的结构安排和目的。
通过引言,读者可以对文章的主题和目的有一个整体的了解。
接下来是正文部分,其中包括三个小节。
首先是Midas悬臂结构的简介,介绍了这种结构的基本概念和特点。
然后是悬臂结构的设计原理,详细讨论了设计这种结构的方法和原则。
最后是悬臂结构的应用领域,探讨了这种结构在工程中的实际应用情况。
最后是结论部分,对前文所述内容进行总结和展望。
我们将总结悬臂结构的优势和应用前景,并对未来发展趋势进行展望。
最后得出结论,强调本文对Midas悬臂结构算例的重要性和价值。
整个结构清晰、逻辑严谨,希望能够为读者提供一份全面而深入的了解。
1.3 目的:本文旨在深入探讨Midas悬臂结构在工程领域中的应用和优势。
通过对悬臂结构的设计原理和应用领域进行分析和总结,希望可以更全面地了解这种结构的特点和适用性。
同时,通过对悬臂结构的优势和发展进行展望,探讨其在未来工程项目中的潜在作用和发展方向。
最终旨在为工程师和设计师提供关于Midas悬臂结构的详尽信息,促进其在实际工程中的应用和推广。
2.正文2.1 Midas悬臂结构简介Midas悬臂结构是一种常用的工程结构形式,其特点是悬挑出一定长度的梁或板,使之只在一端支撑而另一端悬挑。
8_悬臂桥面板计算理论

的函数,则变
∂D( y ) ∂ 2 d 2 D( y ) ∂ 2 w ∂2w 2 + µ 2 = q( x , y ) ∇ w+ D( y )∇ w + 2 2 ∂y ∂y dy ∂y ∂x
常见悬臂板厚度沿方 y向线性变化,若令 y = l0 / 2 处 的 厚 度 为 t c ,相应的弯曲 刚度为
分析曲线图,可以有以下几点看法[3]。 ①按美国AASHTO规范计算值偏大,不经济,似不宜沿用。 ②按魏斯特加公式计算出值偏小,不安全,也不宜采纳。 ③若认为影响面法比较接近实际情况,则对于等厚度悬臂板。 悬臂长度不大时,沙柯公式,JTJ023-85规范建议等均接近影响 面法 ④对于长悬臂板,如悬臂长大于2.5m,JTJ023-85规范建议的 设计结果似偏小,不安全。 (2) 畸变及边梁的影响 文献[3]曾讨论考虑箱梁畸变影响长悬臂变截面带边梁的悬 臂行车道板的计算,指出根部弯矩会减小,并建议了实用计算 方法。 边梁会大大增强荷载的扩散,减小根部内力强度,但其自身 重量引起的内力不可忽视。边梁自身的弯矩亦应引起注意 (3) 建议 ①规范(JTJ023-85)有关有效分布宽度的规定。当悬臂长小 于等于2.5m时,无论变截面或等截面均可利用它进行设计计算
(3)AASHTO规范法 美国公路桥梁标准规范建议的集中力作用下板的有效分布宽度
a = 0.8c + 1.143 + d
∑ Pb ′ m( x,0) = a
荷载点到嵌 固端的距离
(4)魏斯特加(Westergaard)公式
魏斯特加(Westergaard)公式
m ( x, − c ) = −
P
π P 3 Q( x,−c) = cos ϕ πr
桥面板、悬臂板防撞核算解读

目录:页码1,按新规范新防撞箱梁桥面板计算配筋结论: 2 a,桥面板计算结果。
b,悬臂板计算分四种组合计算结果。
2 2,箱梁桥面板计算 5 a, 设计条件及结构尺寸。
b, 各跨公路Ⅰ级横向分布系数 5 c, 2.5m(公)板跨计算实例:影响线、内力、配筋、裂缝。
7 d, 各板跨公路Ⅰ级内力影响线面积9 e, 列表计算各种板跨(公路Ⅰ级)强度计算及裂缝宽度。
10 f, 各跨城-A级横向分布系数及分析单、双轮控制。
11 g, 2.5m(城-A)板跨计算实例:影响线、内力、配筋、裂缝。
12 h, 各跨城-A级内力影响线面积14 i, 列表计算各种板跨(城-A级)强度计算及裂缝宽度。
15 3,悬臂板计算:a,公路Ⅰ级计算条件及原则16 b, 组合式护栏及挂板组合重心图及计算表17 c, 风荷载计算条件及原则18 d, 城-A级计算条件及原则、分析单、双轮控制20 e,计算表:箱梁悬臂板公、城有、无隔音屏公路Ⅰ级A级防撞内力配筋裂缝。
21 箱梁悬臂板公、城有、无隔音屏公路Ⅰ级SB级防撞内力配筋裂缝。
24 箱梁悬臂板公、城有、无隔音屏公路Ⅰ级SA级防撞内力配筋裂缝。
27 箱梁悬臂板公、城有、无隔音屏公路Ⅰ级SS级防撞内力配筋裂缝。
30按新规范箱梁桥面板计算配筋结论:(附Excel表可任意修改) 一、桥面板计算结果:钢筋采用HRB33510Ag=15.39cm裂缝宽度均不控制,未包括箱梁扭矩配筋。
二、悬臂板计算结果:悬臂长度以横桥向不进第二轮为控制计算悬臂总长L=1.25~2.7m(公路Ⅰ级至2.6m)悬臂板均有防撞护栏防撞力根据公路分4等级:A级、SB级、SA级、SS级。
设有两种隔音屏3.5m高(柱间距2m柱底反力3.5kN)、6.0m高(间距柱2m柱底反力10.8kN)悬臂端部厚20 cm (护栏根(L=0.75m)内力控制)悬臂根部厚h 根据防撞等级h=30~40cm对城-A级的防撞力参考公路的防撞等级。
悬臂连续梁桥的计算

悬臂连续梁桥的计算
1.悬挑段的内力计算
悬挑段由于未受到桥墩的约束,其内力计算可以采用简支梁的方法进行。
根据悬挑段的长度、荷载分布和支座反力等信息,可以得到悬挑段的弯矩、剪力和轴力等内力。
2.连续梁段的内力计算
连续梁段的内力计算可以采用静力学原理或结构力学方法。
根据桥梁的几何形状、材料特性和荷载分布,可以利用力平衡方程和变形方程等得到连续梁段各处的内力。
3.荷载的作用效应计算
4.桥梁的抗震设计
在地震区域,悬臂连续梁桥需要进行抗震设计,以保证桥梁在地震作用下具有足够的抗震能力。
抗震设计包括地震荷载的确定、结构的减震措施和抗震性能评估等。
5.结构的受力验算
除了上述几个主要方面的计算,还需要进行杆件的设计和施工方案的确定等。
对于大型的悬挑连续梁桥,还需要进行动力响应和疲劳分析等。
综上所述,悬臂连续梁桥的计算是一项复杂的工作,需要考虑材料的特性、荷载的作用效应以及结构的受力性能等多个方面。
基于这些计算结果,可以进行桥梁的设计和施工,确保桥梁的使用性能和安全性。
悬臂梁 计算公式

悬臂梁计算公式悬臂梁计算公式。
悬臂梁是一种常见的结构形式,广泛应用于工程建筑中。
它的设计和计算是工程设计中的重要内容,对于确保结构的安全性和稳定性至关重要。
在本文中,我们将介绍悬臂梁的计算公式及其应用。
悬臂梁的计算公式主要包括静力学原理和材料力学原理。
静力学原理是指根据平衡条件和力的平衡条件来计算悬臂梁的受力情况,而材料力学原理则是指根据材料的力学性质来计算悬臂梁的受力情况。
下面我们将分别介绍这两方面的计算公式。
首先是静力学原理。
根据力的平衡条件,悬臂梁在受力时会受到弯矩和剪力的作用。
弯矩和剪力是悬臂梁受力的两个基本参数,它们的计算公式如下:1. 弯矩的计算公式。
悬臂梁的弯矩可以根据悬臂梁的受力情况和外力情况来计算。
一般情况下,悬臂梁的弯矩可以使用以下公式来计算:M = F L。
其中,M表示弯矩,F表示作用在悬臂梁上的外力,L表示悬臂梁的长度。
2. 剪力的计算公式。
悬臂梁的剪力也可以根据悬臂梁的受力情况和外力情况来计算。
一般情况下,悬臂梁的剪力可以使用以下公式来计算:V = F。
其中,V表示剪力,F表示作用在悬臂梁上的外力。
以上是悬臂梁在静力学原理下的计算公式。
接下来我们将介绍悬臂梁在材料力学原理下的计算公式。
材料力学原理是指根据材料的力学性质来计算悬臂梁的受力情况。
材料力学原理下的计算公式主要包括应力和应变的计算公式。
1. 应力的计算公式。
悬臂梁在受力时会产生应力,应力的计算公式如下:σ = M y / I。
其中,σ表示应力,M表示弯矩,y表示悬臂梁截面上某点到受力轴线的距离,I表示悬臂梁的惯性矩。
2. 应变的计算公式。
悬臂梁在受力时会产生应变,应变的计算公式如下:ε = σ / E。
其中,ε表示应变,σ表示应力,E表示悬臂梁的弹性模量。
以上是悬臂梁在材料力学原理下的计算公式。
这些计算公式可以帮助工程师和设计师在设计悬臂梁时准确计算悬臂梁的受力情况,确保悬臂梁的结构安全和稳定。
除了上述的计算公式,还需要考虑悬臂梁的边界条件和约束条件,以及材料的强度和稳定性等因素。
8 悬臂桥面板计算理论

Qmax
2P = πc
(2) 半无限宽悬臂板 当荷载位于悬臂行车 道板横向自由边缘附近 时(图),加拿大 Bakht B.给出的集中荷 载产生的悬臂根部弯矩 为
参数
A1 1 kx / l0 m( x,0) = + B1e π ch( A1 x / c)
半 无 限 宽 悬 臂 板
0
k=
l0 A1B1 c 2
c / l0
0.2 1.02 — — — 1.00 — — — 1.00 — — —
0.4
1.03
—
—
—
0.98
—
—
—
0.91
—
—
—
0.6
1.05
0.45
—
—
1.00
0.41
—
—
0.88
0.34
—
—
0.8
1.10
0.63
0.25
—
1.01
0.58
0.23
—
0.85
0.50
0.19
—
1.0
1.18*
0.80
0.91
—
—
—
1.03
—
—
—
1.20
—
—
—
0.4
1.04
—
—
—
1.30
0.33
—
—
1.40
0.57
—
—
0.6
1.14
0.5
—
—
1.49
0.73
—
—
1.61
0.90
—
—
0.8
1.29
0.73
悬臂受力计算

悬臂受力计算悬臂受力计算是力学中一个重要的计算方法,用于分析和计算悬臂结构中的受力情况。
悬臂结构是指一个物体或构件在一端支撑,另一端悬空的结构,常见于桥梁、悬挂物和机械装置等领域。
在设计和工程实践中,了解和计算悬臂受力是必不可少的。
悬臂受力计算的前提是了解结构的几何形状、材料特性和受力情况。
在计算过程中,我们需要考虑以下几个方面:1. 受力分析:首先需要明确悬臂结构所受的外力和内力情况。
外力可以是重力、水平力、垂直力等,而内力则是由于结构自重或其他因素引起的。
通过对受力情况进行分析,我们可以得到悬臂结构受力的具体条件。
2. 弯矩计算:悬臂受力的关键是计算结构所受的弯矩。
弯矩是指在悬臂结构中,由于外力和内力作用,使得结构发生弯曲的力矩。
弯矩的计算需要根据结构形状、材料特性和受力条件进行计算,常用的计算方法有静力学方法、梁理论和有限元分析等。
3. 材料特性:悬臂受力计算还需要考虑结构所使用的材料特性。
不同的材料具有不同的强度、刚度和耐久性等特点,这些特性对悬臂结构的受力情况有重要影响。
在计算过程中,需要根据材料特性确定相应的参数,如弹性模量、抗弯强度和断裂韧性等。
4. 边界条件:悬臂受力计算还需要考虑结构的边界条件。
边界条件是指结构与其他部分的接触或支撑情况。
边界条件的不同将会对悬臂结构的受力分布和变形产生重要影响,因此在计算过程中需要准确确定边界条件。
通过以上几个方面的分析和计算,我们可以得到悬臂结构受力的具体数值和分布情况。
这些计算结果对于结构的设计和安全评估等工作具有重要意义。
悬臂受力计算的目的是为了确保结构在正常使用和极限状态下都能够满足安全要求。
悬臂受力计算的应用非常广泛。
在桥梁工程中,悬臂受力计算可以用于分析和设计桥梁的主梁和悬臂梁等部分的受力情况。
在机械工程中,悬臂受力计算可以用于评估和改进机械装置的受力性能。
在建筑工程中,悬臂受力计算可以用于分析和计算悬挂物的受力情况,如吊篮、天花板和广告牌等。
悬臂板计算过程(1)

工程概况:因工程需要,要在二期车站施工栈板桥西侧的第三道钢筋砼斜撑左侧设置一块1000×200mm的钢筋砼悬臂板,用来放置承载一根直径为600mm的污水管,钢筋砼斜撑连接于冠梁NW47与SW49之间,并在钢筋砼斜撑下面设置了3根4L200×24的临时立柱,用于支撑钢筋砼斜撑。
钢筋砼斜撑、钢筋砼悬臂板和污水管的位置如图1.1所示。
图1.1 污水管放置图
剪力承载力计算书
悬臂板的配筋
水平筋:372Ф18@150
纵向筋:12Ф14@150
梅花形箍筋:620Ф10@300×300
保护层:30mm
混凝土等级:C 30
管自重:2830N
剪力承载力计算:
V ≦V C +V S =0.7f t bh 0+1.25f yv h 0A sv /s
=0.7×1.43N/mm 2×940mm ×140mm+1.25×360N/mm 2
×140mm ×1846mm 2/150mm
=907051N=907.051KN
满载情况下:
水自重:G=γ.V=10KN/m 3×0.3m ×0.3m ×3.14×28m=79.128KN
污水自重:G 污水=79.128KN ×1.2=94.9536KN V=94.9536KN+2.83KN=97.7836KN<907.051KN 故钢筋砼悬臂板可以承载污水管。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1悬臂板受弯分析
在结构设计中往往将复杂的空间结构简化为直观的平面问题来进行考虑,但就复合式箱梁悬臂桥板而言,它是空间结构。因为悬臂板与腹板间结构高度发生突变,导致两者形心跳跃,由于恒活载在箱梁横截面内各部件的内力与应力变化十分复杂。如采用算时,常常把箱梁作为整体空间结构来进行分析,其纵向受力计算通常只考虑了板的整体弯曲结构验算,而忽视了悬臂板受力的不均匀性,其主要受力部位的纵向弯曲往往成为结构计算的盲点。
针对目前箱梁桥板的发展趋向,为满足其安全和可靠的要求,对于悬臂板纵向弯曲受力情况应引起足够重视。目前箱梁桥板工程中常常出现的箱梁腹板根部发生裂缝,根据现场检测:发现其裂缝具有腹板根部粗、两侧逐渐减小的特点;根据分析初步判断是由于设计时只考虑了桥板的整体受力,但却忽视了悬臂板纵向弯曲的问题,因此纵向受力钢筋在底板处虽已配足,但由于纵向受力钢筋在底板处系采取平均布置,而非按实际受力情况布设,从而造成腹板根部局部承载能力不足,并导致横向裂缝的产生。
桥梁工程箱梁悬臂桥板的结构计算简析
箱梁桥板由于整体性好,其混凝土受压区能较好地承受正、负弯矩,在一定的截面面积下还能获得较大的抗弯惯矩,抗扭刚度大,即使在偏心的活载作用下其各梁肋的受力也比较均匀,并能做成各种复杂形状,同时具有立体感强和美观等优点。其主要设计构思是在抗扭刚度大的箱梁上从两处挑出足够长的悬臂,这样不仅满足了使用要求,而且经济指标优越,同时又最大限度地减少了桥墩墩身和基础宽度。因此在江浙运河一带大中跨径桥板设计方面运用广泛,随着现代化城市高架桥的快速发展,目前箱梁的发展也正逐渐趋向大箱配大悬臂板形式。
如图2所示的箱梁悬臂板在恒活载作用下除会发生横向弯曲变形外也常常会发生纵向弯曲变形。由于箱梁悬臂板为薄壁构件,其高度不到梁高的三分之一,但又要传递较大的垂直和水平应力,这就使它成为上部结构中的薄弱部位,并在悬臂根部产生应力集中和开裂的现象。在悬臂板横断面设计时其悬臂长度与端部厚度通常均参照有关图表,并根据横向预加应力或布设钢筋等情况而定,当悬臂过长时恒活载则会在悬臂根部产生很大的剪切力,并导致在悬臂侧腹板产生纵向弯曲应力,所以结构设计时可将此剪切力作为外荷载处理,并根据此剪切力产生的弯矩在
