2018年中考数学模拟试题各地真题271

合集下载

(完整word版)2018中考数学模拟试题含答案(精选5套)

2018年中考数学模拟试卷（一）姓名--------座号--------成绩-------一、选择题（本大题满分36分，每小题3分. ） 1. 2 sin 60°的值等于（） A. 1B.23C. 2D. 32. 下列的几何图形中，一定是轴对称图形的有（）A. 5个B. 4个C. 3个D. 2个3. 据2017年1月24日《桂林日报》报道，临桂县2016年财政收入突破18亿元，在广西各县中排名第二. 将18亿用科学记数法表示为（）A. 1.8×10B. 1.8×108C. 1.8×109D. 1.8×10104. 估计8-1的值在（）A. 0到1之间B. 1到2之间C. 2到3之间D. 3至4之间 5. 将下列图形绕其对角线的交点顺时针旋转90°，所得图形一定与原图形重合的是（） A. 平行四边形 B. 矩形 C. 正方形 D. 菱形 6. 如图，由5个完全相同的小正方体组合成一个立体图形，它的左视图是（）7. 为调查某校1500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取部分学生进行调查，并结合调查数据作出如图所示的扇形统计图. 根据统计图提供的信息，可估算出该校喜爱体育节目的学生共有（） A. 1200名 B. 450名C. 400名D. 300名8. 用配方法解一元二次方程x 2+ 4x – 5 = 0，此方程可变形为（） A. （x + 2）2= 9 B. （x - 2）2 = 9C. （x + 2）2 = 1D. （x - 2）2=19. 如图，在△ABC 中，AD ，BE 是两条中线，则S △EDC ∶S △ABC =（） A. 1∶2B. 1∶4C. 1∶3D. 2∶310. 下列各因式分解正确的是（）A. x 2 + 2x-1=（x - 1）2B. - x 2+（-2）2=（x - 2）（x + 2） C. x 3- 4x = x （x + 2）（x - 2）D. （x + 1）2= x 2 + 2x + 111. 如图，AB 是⊙O 的直径，点E 为BC 的中点，AB = 4，∠BED = 120°，则图中阴影部分的面积之和为（）A. 3B. 23C.23D. 1圆弧角扇形菱形等腰梯形A. B. C. D.（第9题图）（第7题图）12. 如图，△ABC 中，∠C = 90°，M 是AB 的中点，动点P 从点A 出发，沿AC 方向匀速运动到终点C ，动点Q 从点C 出发，沿CB 方向匀速运动到终点B. 已知P ，Q 两点同时出发，并同时到达终点，连接MP ，MQ ，PQ . 在整个运动过程中，△MPQ 的面积大小变化情况是 A. 一直增大B. 一直减小C. 先减小后增大D. 先增大后减小二、填空题（本大题满分18分，每小题3分，） 13. 计算：│-31│= . 14. 已知一次函数y = kx + 3的图象经过第一、二、四象限，则k 的取值范围是 . 15. 在10个外观相同的产品中，有2个不合格产品，现从中任意抽取1个进行检测，抽到合格产品的概率是 .16. 在临桂新区建设中，需要修一段全长2400m 的道路，为了尽量减少施工对县城交通所造成的影响，实际工作效率比原计划提高了20%，结果提前8天完成任务，求原计划每天修路的长度. 若设原计划每天修路x m ，则根据题意可得方程 .17. 在平面直角坐标系中，规定把一个三角形先沿着x 轴翻折，再向右平移2个单位称为1次变换. 如图，已知等边三角形ABC 的顶点B ，C 的坐标分别是（-1，-1），（-3，-1），把△ABC 经过连续9次这样的变换得到△A ′B ′C ′，则点A 的对应点A ′ 的坐标是 .18. 如图，已知等腰Rt △ABC 的直角边长为1，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ……依此类推直到第五个等腰Rt △AFG ，则由这五个等腰直角三角形所构成的图形的面积为 . 三、解答题（本大题8题，共66分，） 19. （本小题满分8分，每题4分）（1）计算：4 cos45°-8+(π-3) +(-1)3；（2）化简：（1 - n m n+）÷22n m m -.20. （本小题满分6分）3121--+x x ≤1， ……① 解不等式组：3（x -1）＜2 x + 1. ……②（第12题图）（第17题图）（第18题图）°21. （本小题满分6分）如图，在△ABC 中，AB = AC ，∠ABC = 72°. （1）用直尺和圆规作∠ABC 的平分线BD 交AC 于点D （保留作图痕迹，不要求写作法）；（2）在（1）中作出∠ABC 的平分线BD 后，求∠BDC 的度数.22. （本小题满分8分）在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：（1）求这50个样本数据的平均数、众数和中位数；（2）根据样本数据，估算该校1200名学生共参加了多少次活动.23. （本小题满分8分）如图，山坡上有一棵树AB ，树底部B 点到山脚C 点的距离BC 为63米，山坡的坡角为30°. 小宁在山脚的平地F 处测量这棵树的高，点C 到测角仪EF 的水平距离CF = 1米，从E处测得树顶部A 的仰角为45°，树底部B 的仰角为20°，求树AB 的高度. （参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）（第21题图）（第23题图）24. （本小题满分8分）如图，PA ，PB 分别与⊙O 相切于点A ，B ，点M 在PB 上，且OM ∥AP ， MN ⊥AP ，垂足为N. （1）求证：OM = AN ；（2）若⊙O 的半径R = 3，PA = 9，求OM 的长.25. （本小题满分10分）某中学计划购买A 型和B 型课桌凳共200套. 经招标，购买一套A 型课桌凳比购买一套B 型课桌凳少用40元，且购买4套A 型和5套B 型课桌凳共需1820元.（1）求购买一套A 型课桌凳和一套B 型课桌凳各需多少元？（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A 型课桌凳的数量不能超过B 型课桌凳数量的32，求该校本次购买A 型和B 型课桌凳共有几种方案？哪种方案的总费用最低？26. （本小题满分12分）在平面直角坐标系中，现将一块等腰直角三角板ABC 放在第二象限，斜靠在两坐标轴上，点C 为（-1，0）. 如图所示，B 点在抛物线y =21x 2 -21x – 2图象上，过点B 作BD ⊥x 轴，垂足为D ，且B 点横坐标为-3.（1）求证：△BDC ≌ △COA ；（2）求BC 所在直线的函数关系式；（3）抛物线的对称轴上是否存在点P ，使△ACP 是以AC 为直角边的直角三角形？若存在，求出所有点P 的坐标；若不存在，请说明理由.（第24题图）（第26题图）2018年初三适应性检测参考答案与评分意见一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DACBCBDABCAC说明：第12题是一道几何开放题，学生可从几个特殊的点着手，计算几个特殊三角形面积从而降低难度，得出答案. 当点P ，Q 分别位于A 、C 两点时，S △MPQ =21S △ABC ；当点P 、Q 分别运动到AC ，BC 的中点时，此时，S △MPQ =21×21AC. 21BC =41S △ABC ；当点P 、Q 继续运动到点C ，B 时，S △MPQ =21S △ABC ，故在整个运动变化中，△MPQ 的面积是先减小后增大，应选C. 二、填空题 13.31； 14. k ＜0； 15. 54（若为108扣1分）； 16. x 2400-x %)201(2400+ = 8；17. （16，1+3）； 18. 15.5（或231）. 三、解答题19. （1）解：原式 = 4×22-22+1-1……2分（每错1个扣1分，错2个以上不给分） = 0 …………………………………4分（2）解：原式 =（n m nm ++-nm n +）·m n m 22- …………2分= nm m +·m n m n m ))((-+ …………3分= m – n …………4分 20. 解：由①得3（1 + x ）- 2（x -1）≤6， …………1分化简得x ≤1. …………3分由②得3x – 3 ＜ 2x + 1， …………4分化简得x ＜4. …………5分 ∴原不等式组的解是x ≤1. …………6分21. 解（1）如图所示（作图正确得3分）（2）∵BD 平分∠ABC ，∠ABC = 72°， ∴∠ABD =21∠ABC = 36°， …………4分∵AB = AC ，∴∠C =∠ABC = 72°， …………5分 ∴∠A= 36°，∴∠BDC =∠A+∠ABD = 36° + 36° = 72°. …………6分 22. 解：（1）观察条形统计图，可知这组样本数据的平均数是 _x =50551841737231⨯+⨯+⨯+⨯+⨯　=3.3， …………1分∴这组样本数据的平均数是3.3. …………2分∵在这组样本数据中，4出现了18次，出现的次数最多， ∴这组数据的众数是4. …………4分∵将这组样本数据按从小到大的顺序排列，其中处在中间的两个数都是3，有233+ = 3. ∴这组数据的中位数是3. ………………6分（2）∵这组数据的平均数是3.3，∴估计全校1200人参加活动次数的总体平均数是3.3，有3.3×1200 = 3900. ∴该校学生共参加活动约3960次. ………………8分 23. 解：在Rt △BDC 中，∠BDC = 90°，BC = 63米，∠BCD = 30°， ∴DC = BC ·cos30° ……………………1分 = 63×23= 9， ……………………2分 ∴DF = DC + CF = 9 + 1 = 10，…………………3分 ∴GE = DF = 10. …………………4分在Rt △BGE 中，∠BEG = 20°， ∴BG = CG ·tan20° …………………5分 =10×0.36=3.6， …………………6分在Rt △AGE 中，∠AEG = 45°，∴AG = GE = 10， ……………………7分 ∴AB = AG – BG = 10 - 3.6 = 6.4.答：树AB 的高度约为6.4米. ……………8分24. 解（1）如图，连接OA ，则OA ⊥AP. ………………1分∵MN ⊥AP ，∴MN ∥OA. ………………2分 ∵OM ∥AP ，∴四边形ANMO 是矩形.∴OM = AN. ………………3分（2）连接OB ，则OB ⊥AP ，∵OA = MN ，OA = OB ，OM ∥BP ， ∴OB = MN ，∠OMB =∠NPM.∴Rt △OBM ≌Rt △MNP. ………………5分 ∴OM = MP.设OM = x ，则NP = 9- x . ………………6分在Rt △MNP 中，有x 2 = 32+（9- x ）2.∴x = 5. 即OM = 5 …………… 8分25. 解：（1）设A 型每套x 元，则B 型每套（x + 40）元. …………… 1分 ∴4x + 5（x + 40）=1820. ……………………………………… 2分∴x = 180，x + 40 = 220.即购买一套A 型课桌凳和一套B 型课桌凳各需180元、220元. ……………3分（2）设购买A 型课桌凳a 套，则购买B 型课桌凳（200 - a ）套.a ≤32（200 - a ）， ∴ …………… 4分 180 a + 220（200- a ）≤40880.解得78≤a ≤80. …………… 5分∵a 为整数，∴a = 78，79，80∴共有3种方案. ………………6分设购买课桌凳总费用为y 元，则y = 180a + 220（200 - a ）=-40a + 44000. …………… 7分 ∵-40＜0，y 随a 的增大而减小，∴当a = 80时，总费用最低，此时200- a =120. …………9分即总费用最低的方案是：购买A 型80套，购买B 型120套. ………………10分2018年中考数学模拟试题（二）姓名---------座号---------成绩-----------一、选择题1、数1,5,0,2-中最大的数是（） A 、1- B 、5 C 、0 D 、22、9的立方根是（）A 、3±B 、3C 、39±D 、393、已知一元二次方程2430x x -+=的两根1x 、2x ，则12x x +=（）A 、4B 、3C 、-4D 、-3 4、如图是某几何题的三视图，下列判断正确的是（） A 、几何体是圆柱体，高为2 B 、几何体是圆锥体，高为2 C 、几何体是圆柱体，半径为2 D 、几何体是圆柱体，半径为2 5、若a b >，则下列式子一定成立的是（）A 、0a b +>B 、0a b ->C 、0ab >D 、0a b> 6、如图AB ∥DE ，∠ABC=20°，∠BCD=80°，则∠CDE=（） A 、20° B 、80° C 、60° D 、100°7、已知AB 、CD 是⊙O 的直径，则四边形ACBD 是（） A 、正方形 B 、矩形 C 、菱形 D 、等腰梯形 8、不等式组302x x +>⎧⎨-≥-⎩的整数解有（）A 、0个B 、5个C 、6个D 、无数个 9、已知点1122(,),(,)A x y B x y 是反比例函数2y x=图像上的点，若120x x >>，则一定成立的是（）A 、120y y >>B 、120y y >>C 、120y y >>D 、210y y >>10、如图，⊙O 和⊙O ′相交于A 、B 两点，且OO ’=5，OA=3， O ’B =4，则AB=( ) A 、5 B 、2.4 C 、2.5 D 、4.8 二、填空题11、正五边形的外角和为 12、计算：3m m -÷=13、分解因式：2233x y -=14、如图，某飞机于空中A 处探测到目标C ，此时飞行高度AC=1200米，从飞机上看地面控制点B 的俯角20α=︒，则飞机A 到控制点B 的距离约为。

2018年中考模拟考试数学试卷(有答案)

11.【答案】
1 12 b c ），则 3a a b c 24 且 2a a b c 24
【解答】设三角形三边长为 a, b, c （ a
8 a 12 ，所以 a 的可能取值为 8,9,10,11 ，满足题意得数组 (a, b, c ) 可能为 (8,8,8) ， (9,9,6) ，(9， 8,7) ，(10,10,4) ，(10,9,5) ，(10,8,6) ，(10,7,7) ，(11,11,2) ，，(11,9,4) ，（11,10,3） (11,8,5) ， (11,7,6) 共 12 组，其中为直角三角形三边长的只有 (10,8,6) ，所以所求概率为
数学试卷第 2页 (共 4 页)
1 2 x bx c 的顶点为 P ，与 x 轴的正半轴交于 A( x1 ,0) 、 B( x2 ,0) 6 3 ) ，若（ x1 x2 ）两点，与 y 轴交于点 C ， PA 是 ABC 的外接圆的切线，设 M (0， 2 AM // BC ，求抛物线的解析式.
2018 年数学试卷
（每小题 6 分，共 48 分。从每小题四个选项中选出一项符合题目要求的答案。）一、选择题 1.若实数 a，b 满足 A ． a 2
1 a ab b 2 2 0 ，则 a 的取值范围是（ 2
B． a 4 C． a 2 或 a 4
） D． 2 a 4 ）
2 2
B．没有实根 D．方程的根有可能取值 a, b, c
4.若 ab 1 ，且有 5a 2018a 9 0 和 9b 2018b 5 0 ，则 A．
9 5
B．
2
5 9
C．
2018 5

2018年中考数学模拟试卷及答案解析

∵CM=BM=1，
又∵PM≤PC+CM，即PM≤3，
∴PM的最大值为3（此时P、C、M共线）．
故选B．
12．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M不与B，C重合），CN⊥DM，CN与AB交于点N，连接OM，ON，MN．下列五个结论：①△CNB≌△DMC；②△CON≌△DOM；③△OMN∽△OAD；④AN2+CM2=MN2；⑤若AB=2，则S△OMN的最小值是，其中正确结论的个数是（）
18．如图，过C（2，1）作AC∥x轴，BC∥y轴，点A，B都在直线y=﹣x+6上，若双曲线y=（x＞0）与△ABC总有公共点，则k的取值范围是．
三、解答题（本大题共8小题，共66分.解答应写出文字说明、证明过程或演算步骤.）
19．（1）计算：|﹣3|+（+π）0﹣（﹣）﹣2﹣2cos60°；
（2）先化简，在求值：（﹣）+，其中a=﹣2+．
【解答】解：从左边看是三个矩形，中间矩形的左右两边是虚线，
故选：B．
4．下列二次根式中，最简二次根式是（）
A．B．C．D．
【考点】74：最简二次根式．
【分析】检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．
【解答】解：A、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故A符合题意；
A．2B．3C．4D．5
【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LE：正方形的性质．
【分析】根据正方形的性质，依次判定△CNB≌△DMC，△OCM≌△OBN，△CON≌△DOM，△OMN∽△OAD，根据全等三角形的性质以及勾股定理进行计算即可得出结论．

2018年中考数学模拟试卷及答案

2018年中考数学模拟试卷及答案2018年中考数学模拟试卷一、选择题（本大题共有6小题，每小题3分，共18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）1.（3分）-3的相反数是（）A．-1 B．3 C．1 D．-32.（3分）下列运算中，正确的是（）A．2x+2y=2xyB．（xy）2÷（xy）3=x-yC．D．2xy-3yx=xy（x2y3）2=x4y53.（3分）一个几何体的表面展开图如图所示，则这个几何体是（）A．四棱锥 B．四棱柱 C．三棱锥 D．三棱柱4.（3分）口袋中装有形状、大小与质地都相同的红球2个，黄球1个，下列事件为随机事件的是（）A．随机摸出1个球，是白球B．随机摸出1个球，是红球C．随机摸出1个球，是红球或黄球D．随机摸出2个球，都是黄球5.（3分）如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（）A．△ABC绕点C顺时针旋转90°，再向下平移3B．△ABC绕点C顺时针旋转90°，再向下平移1C．△ABC绕点C逆时针旋转90°，再向下平移1D．△ABC绕点C逆时针旋转90°，再向下平移36.（3分）如果多项式p=a2+2b2+2a+4b+5，则p的最小值是（）A．1二、填空题（本大题共有10小题，每小题3分，共30分．请把答案直接填写在答题卡相应位置上）7.（3分）9的平方根是38.（3分）若∠α=32°22′，则∠α的余角的度数为57°38′9.（3分）化简：-3的结果是310.（3分）一组数据2、-2、4、1、的方差是5.511.（3分）若关于x的一元二次方程ax2-bx+2=0（a≠0）的一个解是x=1，则3-a+b的值是412.（3分）如图，直线l1∥l2，∠α=∠β，∠1=40°，则∠2=140°13.（3分）圆锥的母线长为6cm，底面圆半径为4cm，则这个圆锥的侧面积为40√5 cm2．14.（3分）如图，⊙O的内接四边形ABCD中，∠A=105°，则∠BOD等于75°15.（3分）如图，Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为点D，若AD=BC，则sin∠A=3/516.（3分）抛物线y=mx2-2mx+m-3（m＞0）在-1＜x＜3位于x轴下方，在3＜x＜4位于x轴上方，则m的值为2三、解答题17.1) $-2+|3\tan30^\circ-1|-(\pi-3)^\circ$2+|\frac{3}{\sqrt{3}}-1|-(\pi-3)^\circ$2+|\sqrt{3}-1|-(\pi-3)^\circ$2+\sqrt{3}-1-(\pi-3)^\circ$2-\sqrt{3}-\pi^\circ$2) $x^2-3x+2=0$x=1$或$x=2$所以方程的解为$x=1$或$x=2$。

2018年中考数学模拟试题及答案(共五套)

中考模拟试卷数学卷一、仔细选一选。

（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的．注意可以用多种不同的方法来选取正确答案． 1.下列四个运算中，结果最小的是（）. A 、2017的相反数 B 、2017的绝对值 C 、2017的0次幂 D 、2017的立方根 2.已知∠α=23°45′，则∠α的余角=（）.A ．66°55′B ．156°15′C ．66°15′D ．156°55′3.若代数式x 2+bx 可以分解因式，则常数b 不可以是（）. A ．﹣1B ．0C ．1D ．24.在代数式x ﹣y, 4a, y+，,yz, ，中有（）.A ．5个整式B ．3个单项式，4个多项式C ．6个整式，4个单项式D ．单项式与多项式的个数相同5.下图是小方送给她外婆的生日蛋糕，则下面关于三种视图判断正确的（）.A.主视图、俯视图、左视图都正确B.主视图、俯视图、左视图都错误C.主视图、左视图正确、俯视图错误D. 左视图、俯视图正确、主视图错误 6.已知⎩⎨⎧>≤-，，a xb x 则的值（）.A.大于0B.小于0C.大于或等于0D.小于或等于07.某超市举办促销活动，促销方式是将原价x 元的衣服以(45x －10) 元出售，则下列说法中，能正确表达该超市促销方式的是（）.A. 原价减去10元后再打8折B. 原价打8折后再减去10元C. 原价减去10元后再打2折D. 原价打2折后再减去10元8．如图为4×4的网格图，A ，B ，C ，D ，O 均在格点上，点O 是（）.(第8题图) A ．△ACD 的外心 B ．△ABC 的外心C ．△ACD 的内心 D ．△ABC 的内心9.在同一直角坐标系中,对于以下四个函数①y=-x-1；②y=x+1；③y=-x+1； ④y=-2（x+1）的图像。

2018年中考数学模拟试卷含解析

2018年中考数学模拟试卷一、选择题（共10小题，每小题3分，满分30分）1．（3分）与﹣2的乘积为1的数是（）A．2 B．﹣2 C．D．﹣2．（3分）下列运算中，正确的是（）A．x3+x3=x6B．x3•x9=x27C．（x2）3=x5D．x÷x2=x﹣13．（3分）据市统计局调查数据显示，我市目前常住人口约为4470000人，数据“4470000”用科学记数法可表示为（）A．4.47×106B．4.47×107C．0.447×107D．447×1044．（3分）若一个多边形的内角和与它的外角和相等，则这个多边形是（）A．三角形B．四边形C．五边形D．六边形5．（3分）如图，已知直线a、b被直线c所截．若a∥b，∠1=120°，则∠2的度数为（）A．50°B．60°C．120° D．130°6．（3分）姜老师给出一个函数表达式，甲、乙、丙三位同学分别正确指出了这个函数的一个性质．甲：函数图象经过第一象限；乙：函数图象经过第三象限；丙：在每一个象限内，y值随x值的增大而减小．根据他们的描述，姜老师给出的这个函数表达式可能是（）A．y=3x B．C．D．y=x27．（3分）初三（1）班12名同学练习定点投篮，每人各投10次，进球数统计如下：这12名同学进球数的众数是（）A．3.75 B．3 C．3.5 D．78．（3分）如图，为了测量某建筑物MN的高度，在平地上A处测得建筑物顶端M的仰角为30°，向N点方向前进16m到达B处，在B处测得建筑物顶端M的仰角为45°，则建筑物MN的高度等于（）A．8（）m B．8（）m C．16（）m D．16（）m 9．（3分）平面直角坐标系xOy中，已知A（﹣1，0）、B（3，0）、C（0，﹣1）三点，D（1，m）是一个动点，当△ACD的周长最小时，△ABD的面积为（）A．B．C．D．10．（3分）如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A1B1C，当A1落在AB边上时，连接B1B，取BB1的中点D，连接A1D，则A1D的长度是（）A．B．2 C．3 D．2二、填空题（共8小题，每小题3分，满分24分）11．（3分）分解因式：x2﹣9=．12．（3分）当a=2016时，分式的值是．13．（3分）甲乙两人8次射击的成绩如图所示（单位：环）根据图中的信息判断，这8次射击中成绩比较稳定的是（填“甲”或“乙”）14．（3分）某学校计划购买一批课外读物，为了了解学生对课外读物的需求情况，学校进行了一次“我最喜爱的课外读物”的调查，设置了“文学”、“科普”、“艺术”和“其他”四个类别，规定每人必须并且只能选择其中一类，现从全体学生的调查表中随机抽取了部分学生的调查表进行统计，并把统计结果绘制了如图所示的两幅不完整的统计图，则在扇形统计图中，艺术类读物所在扇形的圆心角是度．15．（3分）以方程组的解为坐标的点（x，y）在第象限．16．（3分）如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为（结果保留π）17．（3分）如图，正方形ABCD的边长为2，点E，F分别在边AD，CD上，若∠EBF=45°，则△EDF的周长等于．18．（3分）如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF=4．设AB=x，AD=y，则x2+（y﹣4）2的值为．三、解答题（共10小题，满分76分）19．（5分）计算： +|﹣5|﹣（2﹣）0．20．（5分）解不等式组，并写出该不等式组的最大整数解．21．（6分）先化简，再求值：（1﹣）÷，其中x=﹣1．22．（6分）王师傅检修一条长600米的自来水管道，计划用若干小时完成，在实际检修过程中，每小时检修管道长度是原计划的1.2倍，结果提前2小时完成任务，王师傅原计划每小时检修管道多少米？23．（8分）一只不透明的袋子中装有1个红球、1个黄球和1个白球，这些球除颜色外都相同（1）搅匀后从袋子中任意摸出1个球，求摸到红球的概率；（2）搅匀后从袋子中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1个球，求两次都摸到红球的概率．24．（8分）如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．（1）求证：BM=MN；（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．25．（8分）如图，点A（m，4），B（﹣4，n）在反比例函数y=（k＞0）的图象上，经过点A、B的直线与x轴相交于点C，与y轴相交于点D．（1）若m=2，求n的值；（2）求m+n的值；（3）连接OA、OB，若tan∠AOD+tan∠BOC=1，求直线AB的函数关系式．26．（10分）如图1，以△ABC的边AB为直径的⊙O交边BC于点E，过点E作⊙O的切线交AC于点D，且ED⊥AC．（1）试判断△ABC的形状，并说明理由；（2）如图2，若线段AB、DE的延长线交于点F，∠C=75°，CD=2﹣，求⊙O 的半径和BF的长．27．（10分）如图，在矩形ABCD中，AB=6cm，AD=8cm．点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3cm/s，以O为圆心，0.8cm为半径作圆O，点P与点O同时出发，设它们的运动时间为t（单位：s）（0＜t＜）（1）如图1，连接DQ，当DQ平分∠BDC时，t的值为（2）如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；（3）请你继续连行探究，并解答下列问题：①证明：在运动过程中，点O始终在QM所在直线的左侧；②如图3，在运动过程中，当QM与圆O相切时，求t的值；并判断此时PM与圆O是否也相切？说明理由．28．（10分）已知抛物线y=x2﹣2mx+m2+m﹣1（m是常数）的顶点为P，直线l：y=x﹣1．（1）求证：点P在直线l上；（2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；（3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．2018年中考数学模拟试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）与﹣2的乘积为1的数是（）A．2 B．﹣2 C．D．﹣【解答】解：1÷（﹣2）=﹣．故选D．2．（3分）下列运算中，正确的是（）A．x3+x3=x6B．x3•x9=x27C．（x2）3=x5D．x÷x2=x﹣1【解答】解：A、应为x3+x3=2x3，故本选项错误；B、应为x3•x9=x12，故本选项错误；C、应为（x2）3=x6，故本选项错误；D、x÷x2=x1﹣2=x﹣1，正确．故选D．3．（3分）据市统计局调查数据显示，我市目前常住人口约为4470000人，数据“4470000”用科学记数法可表示为（）A．4.47×106B．4.47×107C．0.447×107D．447×104【解答】解：数据“4470000”用科学记数法可表示为4.47×106．故选：A．4．（3分）若一个多边形的内角和与它的外角和相等，则这个多边形是（）A．三角形B．四边形C．五边形D．六边形【解答】解：设多边形的边数为n，根据题意得（n﹣2）•180°=360°，解得n=4．故这个多边形是四边形．故选B．5．（3分）如图，已知直线a、b被直线c所截．若a∥b，∠1=120°，则∠2的度数为（）A．50°B．60°C．120° D．130°【解答】解：如图，∠3=180°﹣∠1=180°﹣120°=60°，∵a∥b，∴∠2=∠3=60°．故选：B．6．（3分）姜老师给出一个函数表达式，甲、乙、丙三位同学分别正确指出了这个函数的一个性质．甲：函数图象经过第一象限；乙：函数图象经过第三象限；丙：在每一个象限内，y值随x值的增大而减小．根据他们的描述，姜老师给出的这个函数表达式可能是（）A．y=3x B．C．D．y=x2【解答】解：y=3x的图象经过一三象限过原点的直线，y随x的增大而增大，故选项A错误；的图象在一、三象限，在每个象限内y随x的增大而减小，故选项B正确；的图象在二、四象限，故选项C错误；y=x2的图象是顶点在原点开口向上的抛物线，在一、二象限，故选项D错误；故选B．7．（3分）初三（1）班12名同学练习定点投篮，每人各投10次，进球数统计如下：这12名同学进球数的众数是（）A．3.75 B．3 C．3.5 D．7【解答】解：观察统计表发现：1出现1次，2出现1次，3出现4次，4出现2次，5出现3次，7出现1次，故这12名同学进球数的众数是3．故选B．8．（3分）如图，为了测量某建筑物MN的高度，在平地上A处测得建筑物顶端M的仰角为30°，向N点方向前进16m到达B处，在B处测得建筑物顶端M的仰角为45°，则建筑物MN的高度等于（）A．8（）m B．8（）m C．16（）m D．16（）m 【解答】解：设MN=xm，在Rt△BMN中，∵∠MBN=45°，∴BN=MN=x，在Rt△AMN中，tan∠MAN=，∴tan30°==，解得：x=8（+1），则建筑物MN的高度等于8（+1）m；故选A．9．（3分）平面直角坐标系xOy中，已知A（﹣1，0）、B（3，0）、C（0，﹣1）三点，D（1，m）是一个动点，当△ACD的周长最小时，△ABD的面积为（）A．B．C．D．【解答】解：由题可得，点C关于直线x=1的对称点E的坐标为（2，﹣1），设直线AE的解析式为y=kx+b，则，解得，∴y=﹣x﹣，将D（1，m）代入，得m=﹣﹣=﹣，即点D的坐标为（1，﹣），∴当△ACD的周长最小时，△ABD的面积=×AB×|﹣|=×4×=．故选（C）10．（3分）如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A1B1C，当A1落在AB边上时，连接B1B，取BB1的中点D，连接A1D，则A1D的长度是（）A．B．2C．3 D．2【解答】解：∵∠ACB=90°，∠ABC=30°，AC=2，∴∠A=90°﹣∠ABC=60°，AB=4，BC=2，∵CA=CA1，∴△ACA1是等边三角形，AA1=AC=BA1=2，∴∠BCB1=∠ACA1=60°，∵CB=CB1，∴△BCB1是等边三角形，∴BB1=2，BA1=2，∠A1BB1=90°，∴BD=DB1=，∴A1D==．故选A．二、填空题（共8小题，每小题3分，满分24分）11．（3分）分解因式：x2﹣9=（x+3）（x﹣3）．【解答】解：x2﹣9=（x+3）（x﹣3）．故答案为：（x+3）（x﹣3）．12．（3分）当a=2016时，分式的值是2018．【解答】解：==a+2，把a=2016代入得：原式=2016+2=2018．故答案为：2018．13．（3分）甲乙两人8次射击的成绩如图所示（单位：环）根据图中的信息判断，这8次射击中成绩比较稳定的是甲（填“甲”或“乙”）【解答】解：由图表明乙这8次成绩偏离平均数大，即波动大，而甲这8次成绩，分布比较集中，各数据偏离平均小，方差小，则S甲2＜S乙2，即两人的成绩更加稳定的是甲．故答案为：甲．14．（3分）某学校计划购买一批课外读物，为了了解学生对课外读物的需求情况，学校进行了一次“我最喜爱的课外读物”的调查，设置了“文学”、“科普”、“艺术”和“其他”四个类别，规定每人必须并且只能选择其中一类，现从全体学生的调查表中随机抽取了部分学生的调查表进行统计，并把统计结果绘制了如图所示的两幅不完整的统计图，则在扇形统计图中，艺术类读物所在扇形的圆心角是72度．【解答】解：根据条形图得出文学类人数为90，利用扇形图得出文学类所占百分比为：30%，则本次调查中，一共调查了：90÷30%=300（人），则艺术类读物所在扇形的圆心角是的圆心角是360°×=72°；故答案为：72．15．（3分）以方程组的解为坐标的点（x，y）在第二象限．【解答】解：，∵①﹣②得，3x+1=0，解得x=﹣，把x的值代入②得，y=+1=，∴点（x，y）的坐标为：（﹣，），∴此点在第二象限．故答案为：二．16．（3分）如图，AB为⊙O的切线，切点为B，连接AO，AO与⊙O交于点C，BD为⊙O的直径，连接CD，若∠A=30°，⊙O的半径为2，则图中阴影部分的面积为π﹣（结果保留π）【解答】解：如图，过O作OE⊥CD于点E，∵AB为⊙O的切线，∴∠DBA=90°，∵∠A=30°，∴∠BOC=60°，∴∠COD=120°，∵OC=OD=2，∴∠ODE=30°，∴OE=1，CD=2DE=2∴S阴影=S扇形COD﹣S△COD=﹣×1×2=π﹣，故答案为：π﹣．17．（3分）如图，正方形ABCD的边长为2，点E，F分别在边AD，CD上，若∠EBF=45°，则△EDF的周长等于4．【解答】解：∵四边形ABCD为正方形，∴AB=BC，∠BAE=∠C=90°，∴把△ABE绕点B顺时针旋转90°可得到△BCG，如图，∴BG=AB，CG=AE，∠GBE=90°，∠BAE=∠C=90°，∴点G在DC的延长线上，∵∠EBF=45°，∴∠FBG=∠EBG﹣∠EBF=45°，∴∠FBG=∠FBE，在△FBG和△EBF中，，∴△FBG≌△FBE（SAS），∴FG=EF，而FG=FC+CG=CF+AE，∴EF=CF+AE，∴△DE F的周长=DF+DE+CF+AE=CD+AD=2+2=4故答案为：4．18．（3分）如图，四边形ABCD为矩形，过点D作对角线BD的垂线，交BC的延长线于点E，取BE的中点F，连接DF，DF=4．设AB=x，AD=y，则x2+（y﹣4）2的值为16．【解答】解：∵四边形ABCD是矩形，AB=x，AD=y，∴CD=AB=x，BC=AD=y，∠BCD=90°．又∵BD⊥DE，点F是BE的中点，D F=4，∴BF=DF=EF=4．∴CF=4﹣BC=4﹣y．∴在直角△DCF中，DC2+CF2=DF2，即x2+（4﹣y）2=42=16，∴x2+（y﹣4）2=x2+（4﹣y）2=16．故答案是：16．三、解答题（共10小题，满分76分）19．（5分）计算： +|﹣5|﹣（2﹣）0．【解答】解：原式=3+5﹣1=7．20．（5分）解不等式组，并写出该不等式组的最大整数解．【解答】解：解不等式①得，x≥﹣2，解不等式②得，x＜1，∴不等式组的解集为﹣2≤x＜1．∴不等式组的最大整数解为：﹣2，﹣1，0，21．（6分）先化简，再求值：（1﹣）÷，其中x=﹣1．【解答】解：原式=•=，当x=﹣1时，原式==．22．（6分）王师傅检修一条长600米的自来水管道，计划用若干小时完成，在实际检修过程中，每小时检修管道长度是原计划的1.2倍，结果提前2小时完成任务，王师傅原计划每小时检修管道多少米？【解答】解：设原计划每小时检修管道x米．由题意，得﹣=2．解得x=50．经检验，x=50是原方程的解．且符合题意．答：原计划每小时检修管道50米．23．（8分）一只不透明的袋子中装有1个红球、1个黄球和1个白球，这些球除颜色外都相同（1）搅匀后从袋子中任意摸出1个球，求摸到红球的概率；（2）搅匀后从袋子中任意摸出1个球，记录颜色后放回、搅匀，再从中任意摸出1个球，求两次都摸到红球的概率．【解答】解：（1）摸到红球的概率=；（2）画树状图为：共有9种等可能的结果数，其中两次都摸到红球的结果数为1，所以两次都摸到红球的概率=．24．（8分）如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．（1）求证：BM=MN；（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．【解答】（1）证明：在△CAD中，∵M、N分别是AC、CD的中点，∴MN∥AD，MN=AD，在RT△ABC中，∵M是AC中点，∴BM=AC，∵AC=AD，∴MN=BM．（2）解：∵∠BAD=60°，AC平分∠BAD，∴∠BAC=∠DAC=30°，由（1）可知，BM=AC=AM=MC，∴∠BMC=∠BAM+∠ABM=2∠BAM=60°，∵MN∥AD，∴∠NMC=∠DAC=30°，∴∠BMN=∠BMC+∠NMC=90°，∴BN2=BM2+MN2，由（1）可知MN=BM=AC=1，∴BN=25．（8分）如图，点A（m，4），B（﹣4，n）在反比例函数y=（k＞0）的图象上，经过点A、B的直线与x轴相交于点C，与y轴相交于点D．（1）若m=2，求n的值；（2）求m+n的值；（3）连接OA、OB，若tan∠AOD+tan∠BOC=1，求直线AB的函数关系式．【解答】解：（1）当m=2，则A（2，4），把A（2，4）代入y=得k=2×4=8，所以反比例函数解析式为y=，把B（﹣4，n）代入y=得﹣4n=8，解得n=﹣2；（2）因为点A（m，4），B（﹣4，n）在反比例函数y=（k＞0）的图象上，所以4m=k，﹣4n=k，所以4m+4n=0，即m+n=0；（3）作AE⊥y轴于E，BF⊥x轴于F，如图，在Rt△AOE中，tan∠AOE==，在Rt△BOF中，tan∠BOF==，而tan∠AOD+tan∠BOC=1，所以+=1，而m+n=0，解得m=2，n=﹣2，则A（2，4），B（﹣4，﹣2），设直线AB的解析式为y=px+q，把A（2，4），B（﹣4，﹣2）代入得，解得，所以直线AB的解析式为y=x+2．26．（10分）如图1，以△ABC的边AB为直径的⊙O交边BC于点E，过点E作⊙O的切线交AC于点D，且ED⊥AC．（1）试判断△ABC的形状，并说明理由；（2）如图2，若线段AB、DE的延长线交于点F，∠C=75°，CD=2﹣，求⊙O 的半径和BF的长．【解答】解：（1）△ABC是等腰三角形，理由是：如图1，连接OE，∵DE是⊙O的切线，∴OE⊥DE，∵ED⊥AC，∴AC∥OE，∴∠1=∠C，∵OB=OE，∴∠1=∠B，∴∠B=∠C，∴△ABC是等腰三角形；（2）如图2，过点O作OG⊥AC，垂足为G，则得四边形OGDE是矩形，∵△ABC是等腰三角形，∴∠B=∠C=75°，∴∠A=180°﹣75°﹣75°=30°，设OG=x，则OA=OB=OE=2x，AG=x，∴DG=OE=2x，根据AC=AB得：4x=x+2x+2﹣，x=1，∴OE=OB=2，在直角△OEF中，∠EOF=∠A=30°，cos30=，OF==2÷=，∴BF=﹣2，⊙O的半径为2．27．（10分）如图，在矩形ABCD中，AB=6cm，AD=8cm．点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC 向点C匀速运动，速度为3cm/s，以O为圆心，0.8cm为半径作圆O，点P与点O同时出发，设它们的运动时间为t（单位：s）（0＜t＜）（1）如图1，连接DQ，当DQ平分∠BDC时，t的值为1（2）如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；（3）请你继续连行探究，并解答下列问题：①证明：在运动过程中，点O始终在QM所在直线的左侧；②如图3，在运动过程中，当QM与圆O相切时，求t的值；并判断此时PM与圆O是否也相切？说明理由．【解答】（1）解：如图1中，∵四边形ABCD是矩形，∴∠A=∠C=∠ADC=∠ABC=90°，AB=CD=6．AD=BC=8，∴BD=，∵PQ⊥BD，∴∠BPQ=90°=∠C，∵∠PBQ=∠DBC，∴△PBQ∽△CBD，∴，∴，∴PQ=3t，BQ=5t，∵DQ平分∠BDC，QP⊥DB，QC⊥DC，∴QP=QC，∴3t=8﹣5t，∴t=1，故答案为1．（2）解：如图2中，作MT⊥BC于T．∵MC=MQ，MT⊥CQ，∴TC=TQ，由（1）可知TQ=（8﹣5t），QM=3t，∵MQ∥BD，∴∠MQT=∠DBC，∵∠MTQ=∠BCD=90°，∴△QTM∽△BCD，∴，∴，∴t=（s），∴t=s时，△CMQ是以CQ为底的等腰三角形．（3）①证明：如图2中，由此QM交CD于E，∵EQ∥BD，∴，∴EC=（8﹣5t），ED=DC﹣EC=6﹣（8﹣5t）=t，∵DO=3t，∴DE﹣DO=t﹣3t=t＞0，∴点O在直线QM左侧．②解：如图3中，由①可知⊙O只有在左侧与直线QM相切于点H，QM与CD 交于点E．∵EC=（8﹣5t），DO=3t，∴OE=6﹣3t﹣（8﹣5t）=t，∵OH⊥MQ，∴∠OHE=90°，∵∠HEO=∠CEQ，∴∠HOE=∠CQE=∠CBD，∵∠OHE=∠C=90°，∴△OHE∽△BCD，∴，∴t=．∴t=s时，⊙O与直线QM相切．连接PM，假设PM与⊙O相切，则∠OMH=PMQ=22.5°，在MH上取一点F，使得MF=FO，则∠FMO=∠FOM=22.5°，∴∠OFH=∠FOH=45°，∴OH=FH=0.8，FO=FM=0.8，∴MH=0.8（+1），由得到HE=，由得到EQ=，∴MH=MQ﹣HE﹣EQ=4﹣﹣=，∴0.8（+1）≠，矛盾，∴假设不成立．∴直线MQ与⊙O不相切．28．（10分）已知抛物线y=x2﹣2mx+m2+m﹣1（m是常数）的顶点为P，直线l：y=x﹣1．（1）求证：点P在直线l上；（2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；（3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．【解答】（1）证明：∵y=x2﹣2mx+m2+m﹣1=（x﹣m）2+m﹣1，∴点P的坐标为（m，m﹣1），∵当x=m时，y=x﹣1=m﹣1，∴点P在直线l上；（2）解：当m=﹣3时，抛物线解析式为y=x2+6x+5，当y=0时，x2+6x+5=0，解得x1=﹣1，x2=﹣5，则A（﹣5，0），当x=0时，y=x2+6x+5=5，则C（0，5），可得解方程组，解得或，则P（﹣3，﹣4），Q（﹣2，﹣3），作ME⊥y轴于E，PF⊥x轴于F，QG⊥x轴于G，如图，∵OA=OC=5，∴△OAC为等腰直角三角形，∴∠ACO=45°，∴∠MCE=45°﹣∠ACM，∵QG=3，OG=2，∴AG=OA﹣OG=3=QG，∴△AQG为等腰直角三角形，∴∠QAG=45°，∵∠APF=90°﹣∠PAF=90°﹣（∠PAQ+45°）=45°﹣∠PAQ，∵∠ACM=∠PAQ，∴∠APF=∠MCE，∴Rt△CME∽Rt△PAF，∴=，设M（x，x2+6x+5），∴ME=﹣x，CE=5﹣（x2+6x+5）=﹣x2﹣6x，∴=，整理得x2+4x=0，解得x1=0（舍去），x2=﹣4，∴点M的坐标为（﹣4，﹣3）；（3）解：解方程组得或，则P（m，m﹣1），Q（m+1，m），∴PQ2=（m+1﹣m）2+（m﹣m+1）2=2，OQ2=（m+1）2+m2=2m2+2m+1，OP2=m2+（m﹣1）2=2m2﹣2m+1，当PQ=OQ时，2m2+2m+1=2，解得m1=，m2=；当PQ=OP时，2m2﹣2m+1=2，解得m1=，m2=；当OP=OQ时，2m2+2m+1=2m2﹣2m+1，解得m=0，综上所述，m的值为，，，，0．。

2018年中考数学模拟试题与答案

2018 年中考数学模拟试题与答案
（试卷满分 120 分，考试时间 120 分钟）
一、选择题（本大题共 12 小题，每小题 3 分，共 36 分．在每小题给出的四个选项中，只有一个是
符合题目要求的．）
1．﹣ 7 的绝对值是（
）
A． 7 B ．﹣ 7
1
C．
7
1
D ．-
7
2．9 的平方根是（
）
A． 3
置的小正方体的个数，则这个几何体的主视图是（
）
A．
B．
C．
D．
6．函数 y=
中自变量 x 的取值范围在数轴上表示正确的是（
）
A．
B
．
C．
D
．
7．把 a2﹣ 4a 多项式分解因式，结果正确的是（
）
A． a（ a﹣4） B ．（ a+2）（a﹣ 2） C ． a（a+2）（ a﹣ 2）
D．（ a﹣ 2） 2﹣ 4
、
是旋转过程中 A、 C的运动轨迹，则图中阴影部分的面积为（
）
A． 4π +2
B ． π﹣2
C ． π +2
D ．4π
12. 如图，点 P 是 ?ABCD边上一动点，沿 A→D→C→Ｂ的路径移动，设 P 点经过的路径长为 x，△ BAP
的面积是 y，则下列能大致反映 y 与 x 的函数关系的图象是（
）
B
．﹣ 3
C ．± 3 D ． 81
3. 下列命题正确的是 ( )
A. 内错角相等
B.
－1 是无理数
C.1 的立方根是± 1
D.
两角及一边对应相等的两个三角形全等
4. 下列计算，正确的是（

2018中考数学模拟试题(带答案)

综合素质自主检测（数学）时间：90 分钟等级：一、选择题（每小题 4 分，共 36 分）1、已知二次函数 y13x2、y21x2、y33x 2，它们的图像开口由小到大的顺序是（）32A、 y1 y2 y3B、 y3 y2y1 C 、 y1y3 y2 D 、 y2 y3 y12、如图，在半径为 2cm 的⊙ O中有长为 2 3 cm的弦 AB，则弦AB所对的圆心角的度数为 ( ) A. 600 B. 90 0C. 120 0 D. 1503、二次函数 y x2bx c 的图象沿 x 轴向左平移 2 个单位，再沿y轴向上平移 3 个单位，得到的图象的函数解析式为y x22x1，则 b 与 c 分别等于（）A、 6， 4 B 、－ 8，14 C 、－ 6，6 D 、－ 8，－ 144、二次函数 y x22x 1 的图象在 x 轴上截得的线段长为（）A、2 2 B 、3 2 C 、2 3 D 、3 35、已知二次函数y ax2bx c(a0) 的图象如图所示，给出以下结论：①a b c 0 ；② a b c 0；③ b 2a 0；④ abc 0 .其中所有正确结论的序号是（）A. ③④B. ②③C.①④D. ①②6、一个圆锥的高为3，侧面展开图是半圆，则圆锥的侧面积是（）（A） 9（B）18（C）27（D）397、函数 y kx26x 3的图象与 x 轴有交点，则k的取值范围是（）A．k3B．k3且 k 0C．k3D．k3且 k08、等边三角形的周长为18，则它的内切圆半径是（）（A）6 3（B）3 3（C） 3（ D）3 39、如图，边长为 12cm 的正方形池塘的周围是草地，池塘边 A、B、C、D处各有一棵树，且 AB=BC=CD=3cm。

现用长 4cm的绳子将一头羊栓在其中的一棵树上，为了使羊在草地上活动区域的面积最大，应将绳子栓在( )A、A 处B、B处C、C处D、D处ABC D11、如图 , 在以 O 为圆心的两个同心圆中 , 大圆的弦 AB 交小圆于 C 和 D 两点,AB=10cm,CD=6cm,则 AC长为12、已知抛物线 y ax 2O 2 x c 与 x 轴的交点都在原点的右侧，则点MACDB（ a,c ）在第象限．13、圆的半径为 2cm，圆内一条弦长为2 3 cm，则弦的中点与弦所对弧的中点间的距离为＿＿＿＿＿＿，这条的弦心距为＿＿＿＿＿＿＿14、如图，有两个同心圆，大圆的弦AB 与小圆相切于点P，大圆的弦CD经过点 P，且 CD=13，PD=4，两圆组成的圆环的面积是______．15、在圆 O中，弦 AB// 弦 CD， AB＝24，CD＝10，弦 AB的弦心距为 5，则AB和 CD之间的距离是。

2018年九年级数学模拟试卷及答案

2018年中考数学模拟试题（一）注意事项：1．本试卷共6页．全卷满分120分．考试时间为120分钟．考生答题全部答在答题卡上，答在本试卷上无效．2．请认真核对监考教师在答题卡上所粘贴条形码的姓名、考试证号是否与本人相符合，再将自己的姓名、考试证号用0.5毫米黑色墨水签字笔填写在答题卡及本试卷上．3．答选择题必须用2B 铅笔将答题卡上对应的答案标号涂黑．如需改动，请用橡皮擦干净后，再选涂其他答案．答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡上的指定位置，在其他位置答题一律无效． 4．作图必须用2B 铅笔作答，并请加黑加粗，描写清楚．一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡．．．相应位置．．．．上） 1．计算│－4＋1│的结果是（ ▲ ）A ．－5B ．－3C ．3D ．52．计算(－xy 2)3的结果是（ ▲ ）A ．x 3y 6B ．－x 3y 6C ．－x 4y 5D ． x 4y 5 3．与17 最接近的整数为（ ▲ ）A ．2B ．3C ．4D ．54．如图，直线l 1∥l 2∥l 3，直线AC 分别交l 1，l 2，l 3于点A ，B ，C ；直线DF 分别交l 1，l 2，l 3于点D ，E ，F ．AC 与DF 相交于点H ，且AH =2，HB =1，BC =5，则 DEEF 的值为（ ▲ ）A ．23B ．25C ．13D ．355．若一组数据2，4，6，8，x 的方差比另一组数据5，7，9，11，13的方差大，则 x 的值可以为（ ▲ ）A ．12B ．10C ．2D ．06．如图，在Rt △ABC 中，∠C =90°，AD 是△ABC 的角平分线，若CD=4，AC=12，则△ABC 的面积为（ ▲ ）A ．48B ．50C ．54D ．60（第4题） A BCD (第6题)二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡．．．相应位置．．．．上） 7．9的平方根是 ▲ ；9的立方根是 ▲ ． 8．使x ＋1 有意义的x 的取值范围是 ▲ ．9．2016年南京全市完成全社会固定资产投资约55000000万元，将55000000用科学记数法表示为 ▲ ． 10．分解因式x 3＋6x 2＋9x 的结果是 ▲ ． 11．计算 33－13的结果是 ▲ ． 12．已知关于x 的方程x 2－3x ＋m ＝0的一个根是2，则它的另一个根是 ▲ ，m 的值是 ▲ ． 13．如图，∠A ＝∠C ，只需补充一个条件 ▲ ，就可得△ABD ≌△CDB ．14. 如图，在△ABC 中，AB 、AC 的垂直平分线l 1、l 2相交于点O ，若∠BAC 等于82°，则∠OBC ＝ ▲ °.15．已知点A （－1，－2）在反比例函数y ＝kx 的图像上，则当x ＞1时，y 的取值范围是 ▲ .16．如图，在半径为2的⊙O 中，弦AB ＝2，⊙O 上存在点C ，使得弦AC ＝22，则∠BOC ＝ ▲ °. 三、解答题（本大题共11小题，共88分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解不等式组⎩⎪⎨⎪⎧ x ＋1≥ 0， x －12＜x 3.，并写出它的整数解．18．（7分）化简：( 2m m 2－4－ 1 m ＋2 )÷1 m 2－2m ．(第14题)A BD（第13题）(第16题)19．（8分）在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m ），绘制出如下两幅统计图．请根据相关信息，解答下列问题：（1）扇形统计图中a ＝ ▲ ，初赛成绩为1.70m 所在扇形图形的圆心角为 ▲ °；（2）补全条形统计图；（3）这组初赛成绩的众数是 ▲ m ，中位数是 ▲ m ；（4）根据这组初赛成绩确定8人进入复赛，那么初赛成绩为1.60m 的运动员杨强能否进入复赛？为什么？20.（8分）在一个不透明袋子中有1个红球、1 个绿球和n 个白球，这些球除颜色外都相同．（1）从袋中随机摸出1个球，记录下颜色后放回袋子中并搅匀，不断重复该试验．发现摸到白球的频率稳定在0.75，则n 的值为 ▲ ；（2）当n ＝2时，把袋中的球搅匀后任意摸出2个球，求摸出的2个球颜色不同的概率．21．（8分）如图，将矩形ABCD 绕点C 旋转得到矩形FECG ，点E 在AD 上，延长ED 交FG 于点H ．（1）求证：△EDC ≌△HFE ；（2）连接BE 、CH ．①四边形BEHC 是怎样的特殊四边形？证明你的结论． ②当AB 与BC 的比值为 ▲ 时，四边形BEHC 为菱形．(第21题)ACDGFEH22．（8分）据大数据统计显示，某省2014年公民出境旅游人数约100万人次，2015年与2016年两年公民出境旅游总人数约264万人次. 若这两年公民出境旅游总人数逐年递增，请解答下列问题：（1）求这两年该省公民出境旅游人数的年平均增长率；（2）如果2017年仍保持相同的年平均增长率，请你预测2017年该省公民出境旅游人数约多少万人次？23．（8分）如图，小明要测量河内小岛B 到河边公路AD 的距离，在点A 处测得∠BAD ＝37°，沿AD 方向前进150米到达点C ，测得∠BCD ＝45°. 求小岛B 到河边公路AD 的距离. （参考数据：sin37°≈ 0.60，cos37° ≈ 0.80，tan37° ≈0.75）24．（8分）已知二次函数y ＝x 2－2m x ＋m 2＋m ＋1的图像与x 轴交于A 、B 两点，点C 为顶点．（1）求m 的取值范围；（2）若将二次函数的图像关于x 轴翻折，所得图像的顶点为D ，若CD ＝8．求四边形ACBD 的面积。

精编2018届数学中考模试卷(含答案解析)四套试卷

a≠０）的图像两个交点关于直线 ∴点 B 的坐标为 (n，m). 故答案为： (n， m).
y=x 对称，点 A 的坐标为 (m， n)，
【分析】反比例函数 y1＝（ k 为常数， k≠０）的图像与一次函数 y2＝－ x＋ a（a 为常数， a≠０）的图像两
个交点关于直线 y=x 对称，再根据点 A 的坐标，就可得出点 B 的坐标。
2018 届数学中考一模试卷
一、单选题
1. 下列各数中，相反数、绝对值、平方根、立方根都等于其本身的是（
A. 0
B. 1
C和. 01
【答案】 A
） D. 和1 － 1
【考点】相反数及有理数的相反数，绝对值及有理数的绝对值，平方根，立方根及开立方
【解析】【解答】解：∵相反数等于它本身的数是
0，平方根等于它本身的数是 0，立方根等于它本身的
，
∴△ AOE≌△ COF（ ASA）
∴ AE＝ CF
∴四边形 AFCE是平行四边形
（ 2）②
【考点】全等三角形的判定与性质，平行四边形的判定与性质
16.如图，以 AB 为直径的半圆沿弦 BC折叠后， AB 与相交于点 D．若
，则∠ B＝ ________ °
【答案】 18
【考点】圆心角、弧、弦的关系，圆周角定理，翻折变换（折叠问题）
【解析】【解答】解：由折叠的性质可得∠ ABC=∠ CBD，
∴
=
，
∵
，
∴
的度数 +
的度数 +
即的度数 ×5=180°，
；数据 6、 7、8、 9、 10 的平均数为 8，方差 S22=
； ∴ S12=S22. 故答案为： =. 【分析】先分别求出这两组数据的平均数，再利用方差的公式求出这两组数据的方差，然后比较大小，即可求解。

九年级2018数学中考模拟试题(卷)与答案

2018年九年级中考模拟试题试卷副标题考试范围：；考试时间：120分钟；命题人：林永章学校：题号-一一二二二-三总分得分注意事项:1 •答题前填写好自己的姓名、班级、考号等信息2 •请将答案正确填写在答题卡上第I 卷（选择题）评卷人得分一•选择题（共10小题，满分30分，每小题3分） 1 • （3分）下列实数中，无理数是（） A. 0 B.二 C. - 2 D •二2. （3分）下列图形中，既是轴对称又是中心对称图形的是（ A.菱形 B •等边三角形C .平行四边形D .等腰梯形4. （3分）一球鞋厂，现打折促销卖出 330双球鞋，比上个月多卖10%设上个月卖出x 双，列出方程（）2A. 10%x=330B. （1 - 10% x=330C. （1 - 10% x=330 D .（ 1+10%）x=3305. （3分）某共享单车前a 公里1元，超过a 公里的，每公里2元，若要使使用该共享单车50%勺人只花1元钱，a 应该要取什么数（） A.平均数 B.中位数 C.众数 D.方差6. （3分）用教材中的计算器依次按键如下，显示的结果在数轴上对应点的位置介于（）之间.绝密★启用前（3分）图中立体图形的主视图是（ 3.B . A.C.D.9. （3分）某校美术社团为练习素描，他们第一次用 120元买了若干本资料，第二次用240元在同一商家买同样的资料，这次商家每本优惠 4元，结果比上次多买了 20本.求第一次买了多少本资料？若设第一次买了 x 本资料，列方程正确的是（ A 加—1刖=4 ■ x-20 "T1 C 垂—迦=4.工 Z-2010. （3分）用棋子摆出下列一组图形: • • • • • •• • • • • • • ••• • •• • • •• • • • •① ②按照这种规律摆下去，第n 个图形用的棋子个数为 A. 3n B. 6n C. 3n+6 D. 3n+3) -■■ =4=4 x+20 )D. x >2)A . 8.x > 1 (3 分) B. x >2 C. x > 1 F 列曲线中不能表示y 是x 的函数的是（ CB. -rl-20评卷人得分二•填空题（共7小题，满分21分，每小题3分）11. （ 3分）2016年南京实现GDP 勺10500亿元，成为全国第11个经济总量超过万亿的城市，用科学记数法表示 10500是 ________ .12. （3分）不透明的布袋里有2个黄球、3个红球、5个白球，它们除颜色外其它都相同，那么从布袋中任意摸出一球恰好为红球的概率是 _________ . 13. （3分）一副三角尺按如图的位置摆放（顶点 C 与F 重合，边CA 与边 FE 叠合，顶点B 、C 、D 在一条直线上）.将三角尺DEF 绕着点F 按顺时针方14. （3分）已知关于x 的方程x 2+px+q=0的两根为-3和-1，则p=q= ______ .15. （3分）如图，在厶ABC 中, AB^AC D E 分别为边 AB AC 上的点.AC=3ADAB=3AE 点F 为BC 边上一点，添加一个条件： ________ ，可以使得△ FDB 与 △ ADE 相似.（只需写出一个）围是 _______.17. （3分）函数y 1=x 与y2—的图象如图所示，下列关于函数y=y 1+y 2的结论: ①函数的图象关于原点中心对称；②当 x V 2时，y 随x 的增大而减小；③当 x >0时，函数的图象最低点的坐标是（2，4），其中所有正确结论的序号第U 卷（非选择题）），如果EF// AB,那么n 的值是元二次方程kx 2-2x+1=0有实数根，则k 的取值范19. (8分)解下列方程: (1)x (x+5) =14;三•解答题（共8小题，满分69分）18. （4 分）（1）计算：竝+ （应-1） 2-訶 + （二）“（7分）（2）先化简，再求值: (互)亠运x-2 i+2 F-4其中x=- 1.2(2) x - 2x - 2=020. (8分)已知：如图，四边形ABCD中，AD// BC, AD=CQ E是对角线BD 上一点，且EA=EC(1)求证：四边形ABCD1菱形；(2)如果BE=BC且/ CBE / BCE=2 3,求证：四边形ABCD是正方形.21. (8分)某公司共25名员工，下表是他们月收入的资料.数是_______ 元.(2)根据上表，可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪一个反映该公司全体员工月收入水平较为合适？说明理由.22. （10分）小强与小刚都住在安康小区，在同一所学校读书，某天早上，小强7：30从安康小区站乘坐校车去学校，途中需停靠两个站点才能到达学校站点，且每个站点停留2分钟，校车行驶途中始终保持匀速，当天早上，小刚7：39从安康小区站乘坐出租车沿相同路线出发，出租车匀速行驶，比小强乘坐的校车早1分钟到学校站点，他们乘坐的车辆从安康小区站出发所行使路程y （千米）与校车行驶时间x （分钟）之间的函数图象如图所示.（1）求点A的纵坐标m的值；（2）小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车？并求此时他们距学校站点的路程.23. ( 12分)综合实践：折纸的思考.【操作体验】用一张矩形纸片折等边三角形.第一步，对折矩形纸片ABC( AB> BC)(图①)，使AB与DC重合，得到折痕EF,把纸片展平(图②).第二步，如图③，再一次折叠纸片，使点C落在EF上的P处，并使折痕经过点B,得到折痕BG折出PB PC,得到△ PBC(1)说明△ PBC是等边三角形.【数学思考】(2)如图④，小明画出了图③的矩形ABCD和等边三角形PBC他发现，在矩形ABC呼把厶PBC经过图形变化，可以得到图⑤中的更大的等边三角形，请描述图形变化的过程.(3)已知矩形一边长为3cm另一边长为a cm,对于每一个确定的a的值, 在矩形中都能画出最大的等边三角形，请画出不同情形的示意图，并写出对应的a 的取值范围.【问题解决】(4)用一张正方形铁片剪一个直角边长分别为4cm和1cm的直角三角形铁圉①圉②图③S® 图⑤24. (12 分)如图，抛物线y=ax2+bx+2 经过点A (- 1, 0), B (4, 0),交y 轴于点C;(1)求抛物线的解析式(用一般式表示)；(2)点D为y轴右侧抛物线上一点，是否存在点D使S A AB冷S A ABD?若存在请直接给出点D坐标；若不存在请说明理由；(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的2018年03月20日123lyz 的初中数学组卷参考答案与试题解析一•选择题（共10小题，满分30分，每小题3分）1. （ 3分）下列实数中，无理数是（ B ） A. 0B. . T C - 2 D.二【解答】解：0，- 2, 是有理数，\7\_ :是无理数，故选：B.2. （3分）下列图形中，既是轴对称又是中心对称图形的是（A ） A. 菱形B .等边三角形C.平行四边形 D.等腰梯形【分析】根据轴对称图形和中心对称图形对各选项分析判断即可得解.【解答】解：A 菱形既是轴对称又是中心对称图形，故本选项正确； B 、等边三角形是轴对称，不是中心对称图形，故本选项错误；C 平行四边形不是轴对称，是中心对称图形，故本选项错误；D 等腰梯形是轴对称，不是中心对称图形，故本选项错误.故选A . D. 【分析】【解答】方体，上面有一个小正方体，在中间. 故选A .4. （ 3分）一球鞋厂，现打折促销卖出 330双球鞋, 比上个月多卖 10%设上个月卖出 x 双，列出方程（D ）A. 10%x=330 B . （ 1- 10%） x=330 C. （ 1 - 10%）2x=330 D. （1+10% x=330【分析】设上个月卖出x 双，等量关系是：上个月卖出的双数x （ 1+10%）=现在卖出的双数，依此列出方程即可.【解答】解：设上个月卖出x 双，根据题意得 (1 + 10% x=330. 故选D.5. （3分）某共享单车前 a 公里1元，超过a 公里的，每公里2元，若要使使用该共享单车 50%勺人只花1元钱，a 应该要取什么数（ B ） A .平均数 B.中位数 C.众数D .方差【分析】由于要使使用该共享单车 50%勺人只花1 元钱，根据中位数的意义分析即可【解答】解：根据中位数的意义，故只要知道中位数就可以了.故选B.计算可得结果介于-2与-1之间. 故选A 7. （ 3分）若代数式. 有意义，则实数x 的取值 ■J 1-1范围是（B ） A . x > 1 B . x >2 C . x > 1 D . x >2【分析】函数的定义：设在一个变化过程中有两个变量x 与y ,对于x 的每一个确定的值，y 都有唯一的值与其对应，那么就说 y 是x 的函数，x 是自变量•由此即根据主视图是从正面看的图形解答. 解：从正面看，共有两层，下面三个小正 6. （3分）用教材中的计算器依次按键如下，显示的结果在数轴上对应点的位置介于（ A ）之间., ,, , , , A B c D K三互 H I =」-4 -2 A 0 IA .B 与C B. C 与D C.E 与F D. A 与 B 【分析】此题实际是求- 2的值.【解答】解：在计算器上依次按键转化为算式为- 【分析】范围；【解答】根据二次根式有意义的条件即可求出故选（B ）解：由题意可知:x > 2 3. （ 3分）图中立体图形的主视图是（A )A .C.(3 分) C )可判断.【解答】解：当给x 一个值时，y 有唯一的值与其对应，就说y 是x 的函数，x 是自变量.选项C 中的曲线，不满足对于自变量的每一个确定的值，函数值有且只有一个值与之对应，即单对应.故C 中曲线不能表示y 是x 的函数，故选C.9. （3分）某校美术社团为练习素描，他们第一次用120元买了若干本资料，第二次用 240元在同一商家买同样的资料，这次商家每本优惠 4元，结果比上次多买了 20本.求第一次买了多少本资料？若设第一次买了 x 本资料，列方程正确的是（ D ）A.240 -120 =4B .240 — 120 =4x-20 Xx+20 KC.120 - 240 =4 D 1201 240=4r-20x W20【分析】E 甘设第- 「次买了 x 本资料，则设第二次买了（ x+20）本资料，由等量关系：第二次比第一次每本优惠4元，即可得到方程.【解答】解：设他上月买了 x 本笔记本，则这次买了（ x+20）本，根据题意得：型-輕L =4.K K +20故选D.10. （3分）用棋子摆出下列一组图形：• • • • • • • • ••• ••••• •••••• • • • ♦ •按照这种规律摆下去，第 n 个图形用的棋子个数为（D ）A. 3nB. 6nC. 3n+6 D . 3n+3【分析】解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论. 【解答】解：•••第一个图需棋子 3+3=6; 第二个图需棋子 3X 2+3=9; 第三个图需棋子 3X 3+3=12; •••第n 个图需棋子3n+3枚. 故选：D.二.填空题（共7小题，满分21分，每小题3分）11. （3分）2016年南京实现 GDP 约10500亿元，成为全国第11个经济总量超过万亿的城市，用科学记数法表示10500是 1.05 X 104 .【分析】科学记数法的表示形式为 a X 10n 的形式，其中1 w |a| v 10, n 为整数.确定n 的值是易错点，由于10500有5位，所以可以确定 n=5-仁4. 【解答】解：10500=1.05 X 104.故答案为：1.05 X 104.12. （3分）不透明的布袋里有 2个黄球、3个红球、 5个白球，它们除颜色外其它都相同，那么从布袋中任意摸出一球恰好为红球的概率是— .-fio]-【分析】由在不透明的袋中装有 2个黄球、3个红球、5个白球，它们除颜色外其它都相同，直接利用概率公式求解，即可得到任意摸出一球恰好为红球的概率. 【解答】解：：•在不透明的袋中装有 2个黄球、3 个红球、5个白球，它们除颜色外其它都相同， •从这不透明的袋里随机摸出一个球，所摸到的球恰好为红球的概率是： --------------------- . 2+3+5 10故答案为：二.1013 （ 3分）一副三角尺按如图的位置摆放（顶点C 与 F 重合，边CA 与边FE 叠合，顶点 B C D 在一条直线上）.将三角尺DEF 绕着点F 按顺时针方向旋转 ”后（0 v n v 180 ）,如果EF// AB,那么n 的值是【分析】分两种情形讨论，分别画出图形求解即可. 【解答】解：①如图1中，EF / AB 时，/ ACE=/ A=45°,•旋转角n=45时，EF / AB.②如图 2 中，EF / AB 时，/ ACE+Z A=180°， • / ACE=135•旋转角 n=360 - 135=225， •/ 0 v n v 180，14 . （3分）已知关于x 的方程x 2+px+q=0的两根为-3 和—1,贝U p= 4 , q= 3 .【分析】由根与系数的关系可得出关于 p 或q 的一元一次方程，解之即可得出结论.【解答】解：•••关于x 的方程x 1 2 3+px+q=0的两根为-3 和-1,•••- 3+ （- 1） =- p , （- 3）X （- 1） =q , ••• p=4, q=3. 故答案为：4; 3.15. （ 3分）如图，在△ ABC 中，为边 AB AC 上的点.AC=3AD 边上一点，添加一个条件： _A ，可以使得△ FDB 与厶ADE 相似.（只需写出一个）或/ BFD=/ A .根据相似三角形的判定方法一一证明即可.【解答】解：DF / AC 或/ BFD=/ A. 理由：I/ A=Z A ,• △ ADE^A ACB•①当 DF// AC 时，△ BDF^A BAG•••△ BDF^A EAD②当/ BFD=/ A 时，•••/ B=/ AED•••△ FBD^^ AED故答案为 DF / AC,或/ BFD=/ A.16. （3分）若关于x 的一元二次方程 kx 2- 2x+仁0 有=3x+2 =-120. （8分）解下列方程： 2 x （x+5） =14；23x - 2x - 2=0【分析】（1）先把方程化为一般式，然后利用因式分解法解方程；（2）利用配方法得到（x - 1） 2=3,然后利用直接开平方法解方程. 【解答】解：（1） x 2+5x - 14=0, （x+7）（x -2） =0, x+7=0 或 x - 2=0, 所以 X 1 = - 7, X 2=2;2（2） x - 2x=2, x 2- 2x+1=3, （x - 1） 2=3,实数根，则 k 的取值范围是 k w 1且 2 0 . 【分析】根据方程根的情况可以判定其根的判别式的取值范围，进而可以得到关于k 的不等式，解得即可，同时还应注意二次项系数不能为 0.【解答】解：•••关于x 的一元二次方程 kx 2- 2x+仁0 有实数根，••△ =b 2- 4ac > 0, 即：4 - 4k > 0, 解得：k w 1,•••关于x 的一元二次方程 kx 2 - 2x+1=0中k 丰0, 故答案为：k w 1且k z 0.17. （3分）函数y 1=x 与y 2—的图象如图所示，下x列关于函数y=y 1+y 2的结论：①函数的图象关于原点中心对称；②当x v 2时，y 随x 的增大而减小；③ 当x >0时，函数的图象最低点的坐标是（ 2, 4）, 其中所有正确结论的序号是 ①③.【分析】结合图形判断各个选项是否正确即可.【解答】解：①由图象可以看出函数图象上的每一个点都可以找到关于原点对称的点，故正确；② 在每个象限内，不同自变量的取值，函数值的变化是不同的，故错误；③ y=x+2= （J 』-」—）2+4 > 4,当且仅当x=2时取 “=”.即在第一象限内，最低点的坐标为（ 2, 4）,故正确；•••正确的有①③.,AB^ AC. D E 分别'AB=3AE 点 F 为 BC DF / AC,或/ BFD=Z AD :=1AC AB 3故答案为：①③.三.解答题（共8小题，满分69分）18. （4 分）计算：顶+ （伍-1）2-押+ 4-）-21【分析】根据负整数指数幕和分数指数幕的意义计算.【解答】解：原式=3 . ：'：+2 - 2家弓+1 - 3+2巳1+2.19. （7分）先化简，再求值：（一）十」x-2 [x+2 / _4其中x= - 1 .【分析】根据分式的运算法则即可求出答案.【解答】解：当x= - 1时,C K+2)(x-2)原式=G+2)(K-2)-仁士卜门，所以 X 1 = 1+ _ ；, X 2=1 -：'；.21. (8分)已知：如图，四边形 ABCD 中, AD// BC, AD=CD E 是对角线 BD 上一点，且 EA=EC (1) 求证：四边形 ABCD 是菱形；(2)如果BE=BC 且/ CBE / BCE=2 3,求证：四边形 ABCD 是正方形.【分析】(1)首先证得厶ADE^A CDE 由全等三角形的性质可得/ ADE=/ CDE 由AD// BC 可得/ ADEN CBD易得/ CDB M CBD 可得BC=CD 易得AD=BC 利用平行线的判定定理可得四边形ABCD 为平行四边形，由AD=CD可得四边形ABCD 是菱形；2)由BE=BC 可得△ BEC 为等腰三角形，可得/ BCE=/ BEC 利用三角形的内角和定理可得/ CBE=180<4【解答】证明：(1 )在厶ADE-与^ CDE 中, rAD=CD • DE 二DE ,(EA=EC•••△ ADE^A CDE •••/ ADE 玄 CDE •/ AD// BC,•••/ ADE 玄 CBD•••/ CDE=/ CBD • BC=CD •/ AD=CD • BC=AD•四边形ABCD 为平行四边形， •/ AD=CD•四边形ABCD 是菱形；(2 )T BE=BC•••/ BCE 玄 BEC •••/ CBE / BCE=2 3 , • •四边形ABCD 是菱形, ••/ ABE=45 , ••/ ABC=90 ,••四边形ABCD 是正方形.22. ( 8分)月收入/元 45000 18000 10000 5500 4800 3400 3000 2200 人数 1 1 1 3 6 1 11 1(1 )3400 3000 元.(2)根据上表，可以算得该公司员工月收入的平均数为6276元.你认为用平均数、中位数和众数中的哪45° 易得/ ABE=45 ,可得/ ABC=90 ,由正方形的判定定理可得四边形ABCD 是正方形.••/ CBE=18<2+34 3=45一个反映该公司全体员工月收入水平较为合适？说明理由.【分析】(1)根据中位数的定义把这组数据从小到大排列起来，找出最中间一个数即可；根据众数的定义找出现次数最多的数据即可；（2）根据平均数、中位数和众数的意义回答.【解答】解：（1）共有25个员工，中位数是第13个数, 则中位数是3400元；3000出现了11次，出现的次数最多，则众数是3000.故答案为3400; 3000;（2）用中位数或众数来描述更为恰当•理由：平均数受极端值45000元的影响，只有3个人的工资达到了6276元，不恰当;23. （10分）小强与小刚都住在安康小区，在同一所学校读书，某天早上，小强7: 30从安康小区站乘坐校车去学校，途中需停靠两个站点才能到达学校站点，且每个站点停留2分钟，校车行驶途中始终保持匀速，当天早上，小刚7: 39从安康小区站乘坐出租车沿相同路线出发，出租车匀速行驶，比小强乘坐的校车早1分钟到学校站点，他们乘坐的车辆从安康小区站出发所行使路程y （千米）与校车行驶时间x （分钟）之间的函数图象如图所示.（1）求点A的纵坐标m的值；（2 ）小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车？并求此时他们距学校站点的路程.【分析】（1）根据速度=路程十时间，可求出校车的速度，再根据m=3+校车速度x（8-6）,即可求出m的值；（2）（方法一）根据时间=路程十速度+4,可求出校车到达学校站点所需时间，进而可求出出租车到达学校站点所需时间，由速度=路程十时间，可求出出租车的速度，再根据相遇时间=校车先出发时间X速度十两车速度差，可求出小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车，结合出租车的速度及安康小区到学校站点的路程，可得出相遇时他们距学校站点的路程.（方法二）观察函数图象结合数量之间的关系，可分别找出点B、C、E、F的坐标，利用待定系数法可分别求出线段BC EF的解析式，联立两函数解析式成方程组可求出交点的坐标，再结合出租车出发的时间及全程的长度即可得出结论.【解答】解：（1）校车的速度为3-4=0.75 （千米/ 分钟），点A的纵坐标m的值为3+0.75 X（8 - 6）=4.5 . 答：点A的纵坐标m的值为4.5 .（2）（方法一）校车到达学校站点所需时间为9十0.75+4=16 （分钟），出租车到达学校站点所需时间为16 -9 -仁6 （分钟）,出租车的速度为9-6=1.5 （千米/分钟），两车相遇时出租车出发时间为0.75 X（9-4）-（1.5 -0.75 ）=5 （分钟），相遇地点离学校站点的路程为9 - 1.5 X 5=1.5 （千米）.答：小刚乘坐出租车出发后经过5分钟追到小强所乘坐的校车，此时他们距学校站点的路程为 1.5千米.（方法二）••• 9 十0.75+4=16 （分钟），•••点C的坐标为（16, 9）. •/点B的坐标为（10, 4.5 ）,•线段BC的解析式为y=0.75x - 3 （10< x< 16）. •••点E的坐标为（15, 9）,点F的坐标为（9, 0）, •线段EF 的解析式为y=1.5x - 13.5 （9< x< 15）.联立两线段解析式成方程组，花萨3 (y=l. 5x-l 3. 5，解得：\=140.5• x - 9=5, 9 - y=1.5 .答：小刚乘坐出租车出发后经过5分钟追到小强所乘坐的校车，此时他们距学校站点的路程为 1.5千米.24. （12分）折纸的思考.【操作体验】用一张矩形纸片折等边三角形.第一步，对折矩形纸片ABCD（ AB> BC）（图①），使AB与DC重合，得到折痕EF,把纸片展平（图②）. 第二步，如图③，再一次折叠纸片，使点C落在EF 上的P 处，并使折痕经过点B,得到折痕BG折出PB PC,得到△ PBC（1）说明△ PBC是等边三角形.【数学思考】(2)如图④，小明画出了图③的矩形ABCD和等边三角形PBC他发现，在矩形ABCD中把厶PBC经过图形变化，可以得到图⑤中的更大的等边三角形，请描述图形变化的过程.(3)已知矩形一边长为3cm另一边长为 a cm,对于每一个确定的a的值，在矩形中都能画出最大的等边三角形，请画出不同情形的示意图，并写出对应的a的取值范围.【问题解决】(4)用一张正方形铁片剪一个直角边长分别为4cm 和1cm的直角三角形铁片，所需正方形铁片的边长的最小值为cm.—5 —出PB=PC PB=CB 得出PB=PC=CB卩可；(2 )由旋转的性质和位似的性质即可得出答案；(3)由等边三角形的性质、直角三角形的性质、勾股定理进行计算，画出图形即可；(4)证明△ AEF^A DCE得出生二仝=丄,设AE=xDC CE 4则AD=CD=4x DE=A B AE=3x 在Rt△ CDE中 ,由勾股定理得出方程，解方程即可.【解答】(1)证明：由折叠的性质得：EF是BC的垂直平分线,BG是PC的垂直平分线,••• PB=PC PB=CB••• PB=PC=CB• △ PBC是等边三角形.(2)解：以点B为中心，在矩形ABCD中把△ PBC逆时针方向旋转适当的角度，得到△P i BG;再以点B为位似中心，将厶P i BC放大，使点C的对应点G落在CD上 ,得到△ P2BC;如图⑤所示；(3)解：本题答案不唯一，举例如图 6 所示,3cm图6(4)解：如图7所示：△ CEF是直角三角形，/CEF=90 , CE=4, EF=1 ,•••/ AEF+Z CED=90 ,•••四边形ABCD是正方形，•••/ A=Z D=90 , AD=CD•••/ DCE+Z CED=90 ,•••/ AEF=Z DCE•△ AEF^^ DCE貳童7，设AE=x 贝U AD=CD=4x• DE=A& AE=3x,在Rt△ CDE中，由勾股定理得: 解得：x*L,••• AD=4X, =_L .故答案为：-25. (12分)如图，抛物线y=ax2+bx+2经过点A (1 , 0), B (4 , 0),交y 轴于点C；(1)求抛物线的解析式(用一般式表示) ；(2 )点D为y轴右侧抛物线上一点，是否存在点D 使S A ABC^S A ABD?若存在请直接给出点D坐标；若不存在请说明理由；3)将直线BC绕点B顺时针旋转45°,与抛物线【分析】(1 )由A、B的坐标，利用待定系数法可求得抛物线解析式；(2 )由条件可求得点D到x轴的距离，即可求得 D 点的纵坐标，代入抛物线解析式可求得D点坐标；(3)由条件可证得BC丄AC,设直线AC和BE交于点F ,过F作FM丄x轴于点M则可得BF=BC利用2 2 2 (3x) + (4x) =4 ,平行线分线段成比例可求得 F 点的坐标，利用待定系数法可求得直线 BE 解析式，联立直线 BE 和抛物线解析式可求得 E 点坐标，则可求得 BE 的长. 【解答】解：（1 ）•••抛物线 y=ax 2+bx+2 经过点 A （- 1, 0）, B (4,0), Ka-b+2=0 ll6a+4b+2=0 •••抛物线解析式为（2）由题意可知亠= ______ ,解得FM=6 • F (2 , 6),且 B (4 , 0),设直线BE 解析式为y=kx+m ，则可得［2k4m ~6，解 L 4k+m=0 得仿-3 得、 ,\b=12•直线BE 解析式为y= - 3x+12 , C( 0, 2), A (- 1, 0), B( 4, 0), 联立直线BE 和抛物线解析式可得• E ( 5 , - 3),• BE= = '•--AB=5, OC=2 AB (=A,AB? OC^X 5 X 2=5, 2 2• S A AB(= △ ABD 3. S A AB =- -X 5= 2 设 D ( x , y ), B ? |y|= — 15 2 X 5|y|= - J ,解得 |y|=3 ,—x 2^—x+2=3 ,解得 x=1 或 x=2 ,此2 2 时D 点坐标为(1, 3)或(2 , 3); 当y= - 3时，由- 当y=3时，由- 丄X 2+3X +2=- 3,解得 x= - 2 (舍2 去）或x=5，此时D 点坐标为（5, - 3）; 综上可知存在满足条件的点 D,其坐标为（1 , 3）或（2, 3）或（5, - 3）; (3)• AO=1 , OC=2 OB=4, AB=5, • AC= = .■: , BC= =2 .■:, :.AC+BC=AB , • △ ABC 为直角三角形，即 BCL AC, 如图，设直线AC 与直线BE 交于点F ,过F 作FM L x 轴于点M, 由题意可知/ FBC=45 , •••/ CFB=45 , • CF=BC=2 !., •—…即1 = 1 ・・ ----- ,即卩 --------OM ||CF | |or 2V5,解得OM=2。

2018年中考数学模拟试卷含答案精品

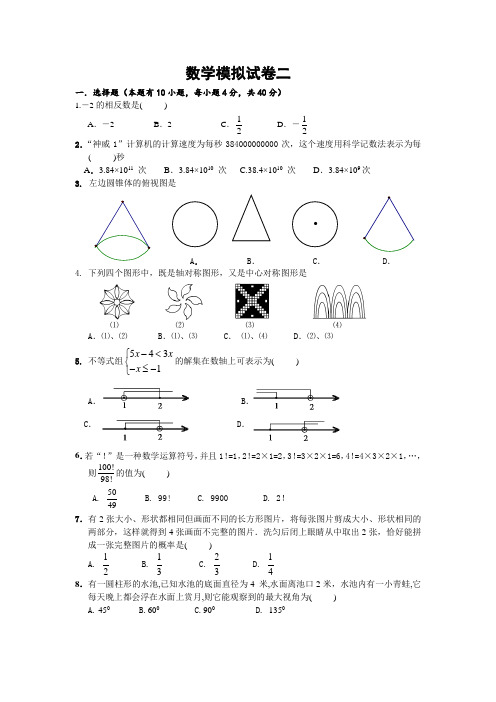
数学模拟试卷二一．选择题（本题有10小题，每小题4分，共40分） 1.－2的相反数是( )A ．－2B ．2C ．12D ．－122．“神威1”计算机的计算速度为每秒384000000000次，这个速度用科学记数法表示为每( )秒 A ．3.84×1011 次 B ．3.84×1010 次 C.38.4×1010 次 D ．3.84×109次 3. 左边圆锥体的俯视图是A ．B ．C ．D ．4. 下列四个图形中，既是轴对称图形，又是中心对称图形是⑴ ⑵ ⑶ ⑷ A ．⑴、⑵ B ．⑴、⑶ C ． ⑴、⑷ D ．⑵、⑶ 5. 不等式组5431x xx -<⎧⎨-≤-⎩的解集在数轴上可表示为( )A ．B ．C ．D ． 6．若“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1，…，则100!98!的值为( ) A. 5049 B. 99! C. 9900 D. 2！7．有2张大小、形状都相同但画面不同的长方形图片，将每张图片剪成大小、形状相同的两部分，这样就得到4张画面不完整的图片．洗匀后闭上眼睛从中取出2张，恰好能拼成一张完整图片的概率是( ) A.12 B. 31 C. 23 D. 148．有一圆柱形的水池,已知水池的底面直径为4 米,水面离池口2米，水池内有一小青蛙,它每天晚上都会浮在水面上赏月,则它能观察到的最大视角为( ) A. 450 B.600 C.900 D. 1350CABD D A B C9．如图8，直线AB CD ，相交于点O ，30AOC ∠=，半径为1cm 的⊙P 的圆心在射线OA 上，且与点O 的距离为6cm ．如果⊙P 以1cm/s 的速度沿由A 向B 的方向移动，那么( )秒种后⊙P 与直线CD 相切．Ａ．4 Ｂ．8 Ｃ．4或6 Ｄ．4或810．将两副三角板如下图摆放在一起，连结AD ，则ADB ∠的余切值为( )A ．1 B1 C ．2 D ．3二．填空题（本题有4小题，每小题4分，共16分）11. “圆形方孔钱”是中国古钱币的突出代表．如图，一枚圆形方孔钱的外圆直径为a ，中间方孔边长为b ，则图示阴影部分面积为． 12.在直角三角形ABC 中，∠ACB=90º，以BC 所在直线为轴旋转一周所得到的几何体是．13．14．如图，四边形A 1B 1C 1O ，A 2B 2C 2C 12，C 3分别在直线y kx b =+(k>0)和x 轴上, 点B 3的坐标是（419，49）,则k+b= ．三、解答题15．（本小题6分）计算：()2015tan 4533π-⎛⎫--+︒+- ⎪⎝⎭.16.（本小题8分）(1) 在下面的方格纸中，以线段AB 为一边，画一个正方形； (2) 如果图中小方格的面积为1平方厘米，你知道(1)中画出的正方形的面积是多大吗？解释你的计算方法．B17．（本小题10分）为迎接2018年奥运会的召开，某市举行一次少年滑冰比赛，各年龄组（1（2）求全体参赛选手年龄的众数、中位数；（3）小明说，他所在年龄组的参赛人数占全体参赛人数的28%. 你认为小明是哪个年龄组的选手?请说明理由.18．（本小题10分）本市某旅游度假区每天的赢利额y（元）与售出的门票x（张）之间的函数关系如图所示.（1）当0≤x≤200，且x为整数时，y关于x的函数解析式为；当200≤x≤300，且x为整数时，y关于x的函数解析式为 . （2）要使旅游度假区一天的赢利超过1000元，试问该天至少应售出多少张门票？（3）请思考并说明图像与y轴交点（0，－1000）的实际意义.19．（本小题10分）已知∠AOB=900，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E．当三角板绕点C旋转到CD与OA垂直时(如图1)，易证得：OD+OE=2OC．当三角板绕点C 旋转到CD与OA不垂直时:（1）在图2情况下上述结论仍成立，请给出证明；（2）在图3情况下，上述结论是否还成立?若成立，请给予证明；若不成立，线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想，不需证明．图1 图2 图320．（本小题12分）如图，已知抛物线y=14x2+1,直线y=kx+b经过点B（0，2）.（1）求b的值；（2）将直线y=kx+b绕着点B旋转到与x轴平行的位置时（如图①），直线与抛物线y=14x2+1相交于两点P1、P2，求出点P1、P2的坐标；（3）将直线y=kx+b绕着点B继续旋转．．．．，与抛物线y=14x2+1相交，其中一个交点为P'（如图②），过点P'作x轴的垂线P'M，点M为垂足。

2018中考数学模拟试题及答案

文档2018 年初中升学模拟考试（一）九年数学试卷题号一二三四五六七八总分得分（考试时间：120分钟；试卷满分：150分）温馨提示：请考生把所有的答案都写在答题卡上，写在试卷上不给分，答题要求见答题卡。

一、选择题（每小题3分，共30分）1．－12的倒数是（）A．2 B．12C．－12D．－22．科学家可以使用冷冻显微术以高分辨率测定溶液中的生物分子结构，使用此技术测定细菌蛋白结构的分辨率达到0.22纳米，也就是0.000 000 000 22米，将0.000 000 000 22用科学记数法表示为（）A．0.22×l0-9 B．2.2×l0-10 C．22×l0-11 D．0.22×l0-83．如图是某几何体的三视图，该几何体是（）A．正方体B．三棱锥C．圆柱D．圆锥第3题图笫4题图4．如图是根据某地某段时间的每天最低温度绘成的折线图，那么这段时间最低温度的中位数，众数分别是（）A．4℃，4℃B．4℃，5℃C．4.5℃，5℃D．4.5C，4℃5．不等式组x1x+12⎧⎨-⎩≤，＞的解集在数轴上可表示为（）6．下列计算，正确的是（）A．2a2＋a＝3a2B．2a－1＝12a(a≠0) C．(－a2)3÷a4＝－a D．2a2·3a3＝6a57．已知四边形ABCD是平行四边形，下列结论中不正确．．．的是（）A．当AB＝BC时，它是菱形B．当AC⊥BD时，它是菱形C．当∠ABC＝90º时，它是矩形D．当AC＝BD时，它是正方形8．小张承包了一片荒山，他想把这片荒山改造成一个苹果园，现在有一种苹果树苗，它的成活率如下表所示：移植棵数(n) 成活数(m) 成活率(m/n) 移植棵数(n) 成活数(m) 成活率(m/n)50 47 0.940 1500 1335 0.890270 235 0.870 3500 3203 0.915400 369 0.923 7000 6335 0.905750 662 0.883 14000 12628 0.902 下面有四个推断：①随着移植棵数的增加，树苗成活的频率总在0.900附近摆动，显示出一定的稳定性，可以估计树苗成活的概率是0.900;②当移植的棵数是1500时，表格记录成活数是1335，所以这种树苗成活的概率是0.890；③若小张移植10000棵这种树苗，则可能成活9000棵；④若小张移植20000棵这种树苗，则一定成活18000棵．其中合理的是（）A．①③B．①④C．②③D．②④9．如图，将矩形ABCD沿着直线BD折叠，使点C落在C′处，P为对角线BD上一点（不与点B，D重合），PM⊥BC′于点M，PN⊥AD于点N。