一元二次方程单元复习

合集下载

一元二次方程专题复习

一元二次方程专题复习（一）直接开平方法→配方法要点一、一元二次方程的解法---配方法1．配方法解一元二次方程： (1)配方法解一元二次方程：将一元二次方程配成的形式，再利用直接开平方法求解，这种解一元二次方程的方法叫配方法.(2)配方法解一元二次方程的理论依据是公式：.(3)用配方法解一元二次方程的一般步骤： ①把原方程化为的形式；②将常数项移到方程的右边；方程两边同时除以二次项的系数，将二次项系数化为1；③方程两边同时加上一次项系数一半的平方；④再把方程左边配成一个完全平方式，右边化为一个常数；⑤若方程右边是非负数，则两边直接开平方，求出方程的解；若右边是一个负数，则判定此方程无实数解. 要点诠释：（1）配方法解一元二次方程的口诀：一除二移三配四开方；（2）配方法关键的一步是“配方”，即在方程两边都加上一次项系数一半的平方. （3）配方法的理论依据是完全平方公式．类型一、用配方法解一元二次方程1.用配方法解方程x 2-7x-1＝0．【答案与解析】将方程变形为x 2-7x ＝1，两边加一次项的系数的一半的平方，得x 2-7x+＝1+，所以有＝1+．直接开平方，得x-＝或x-＝-．所以原方程的根为x ＝+或x ＝-．【总结升华】一般地，用先配方，再开平方的方法解一元二次方程，应按以下步骤进行： (1)把形如ax 2+bx+c ＝0(a ≠0)的方程中二次项的系数化为1； (2)把常数项移到方程的右边；2222()a ab b a b ±+=±(3)方程的两边都加“一次项系数一半的平方”，配方得形如(x+m)2＝n(n ≥0)的方程； (4)用直接开平方的方法解此题．举一反三：【变式】用配方法解方程.(1)x 2-4x-2＝0； (2)x 2+6x+8＝0.要点二、配方法的应用1．用于比较大小：在比较大小中的应用，通过作差法最后拆项或添项、配成完全平方，使此差大于零（或小于零）而比较出大小.2．用于求待定字母的值：配方法在求值中的应用，将原等式右边变为0，左边配成完全平方式后，再运用非负数的性质求出待定字母的取值．3．用于求最值：“配方法”在求最大（小）值时的应用，将原式化成一个完全平方式后可求出最值． 4．用于证明：“配方法”在代数证明中有着广泛的应用，我们学习二次函数后还会知道“配方法”在二次函数中也有着广泛的应用．要点诠释：“配方法”在初中数学中占有非常重要的地位，是恒等变形的重要手段，是研究相等关系，讨论不等关系的常用技巧，是挖掘题目当中隐含条件的有力工具，一定要学好．类型二、配方法在代数中的应用2．若代数式，，则的值（）A ．一定是负数B ．一定是正数C ．一定不是负数D ．一定不是正数【答案】B ；【解析】（作差法）．故选Ｂ．【总结升华】本例是“配方法”在比较大小中的应用，通过作差法最后拆项、配成完全平方，使此差大于零而比较出大小.221078Ma b a =+-+2251N a b a =+++M N -22221078(51)M N a b a a b a -=+-+-+++2222107851a b a a b a =+-+----29127a a =-+291243a a =-++2(32)30a =-+>3．用配方法说明：代数式x2+8x+17的值总大于0.【答案与解析】x2+8x+17＝ x2+8x+42-42+17＝（x+4）2+1∵（x+4）2≥0，∴（x+4）2+1＞0，故无论x取何实数，代数式 x2+8x+17的值总大于0.【总结升华】利用配方法将代数式配成完全平方式后，再分析代数式值得符号.举一反三：【变式】求代数式 x2+8x+17的最小值4．（2014春•滦平县期末）已知x2+y2﹣4x+6y+13＝0，求（x+y）2013的值．【思路点拨】采用配方法求出x、y的值，代入计算即可得到答案．【答案与解析】解：x2+y2﹣4x+6y+13＝0，x2﹣4x+4+y2﹣+6y+9＝0，（x﹣2）2+（y+3）2＝0∴x﹣2＝0，y+3＝0，解得，x＝2，y＝﹣3，（x+y）2013＝﹣1．【总结升华】本题考查的是配方法的应用和非负数的性质的应用，掌握配方法的步骤和几个非负数的和为0，每个非负数都为0是解题的关键．1.一元二次方程的求根公式一元二次方程，当时，.2.一元二次方程根的判别式一元二次方程根的判别式：． ①当时，原方程有两个不等的实数根；②当时，原方程有两个相等的实数根；③当时，原方程没有实数根.3.用公式法解一元二次方程的步骤用公式法解关于x 的一元二次方程的步骤：①把一元二次方程化为一般形式；②确定a 、b 、c 的值（要注意符号）； ③求出的值；④若，则利用公式求出原方程的解；若，则原方程无实根.要点诠释：（1）虽然所有的一元二次方程都可以用公式法来求解，但它往往并非最简单的，一定要注意方法的选用.（2）一元二次方程，用配方法将其变形为：①当时，右端是正数．因此，方程有两个不相等的实根：② 当时，右端是零．因此，方程有两个相等的实根： ③ 当时，右端是负数．因此，方程没有实根.20 (0)ax bx c a ++=≠2224()24b b ac x a a -+=240b ac ∆=->1,22b x a-±=240b ac ∆=-=1,22b x a=-240b ac ∆=-<5．用公式法解下列方程．(1)； (2)．【总结升华】用公式法解一元二次方程的关键是对a 、b 、c 的确定．用这种方法解一元二次方程的步骤是：(1)把方程化为一元二次方程的一般形式；(2)确定a ，b ，c 的值并计算的值；(3)若是非负数，用公式法求解．举一反三：【变式】用公式法解方程6．用公式法解下列方程：(1)； (2) ．【总结升华】首先把每个方程化成一般形式，确定出a 、b 、c 的值，在的前提下，代入求根公式可求出方程的根．23310x x --=2241x x =-24b ac -24b ac -2341x x =+2100x -+=(1)(1)x x +-=240b ac -≥举一反三：【变式】（2014秋•泽州县校级期中）用公式法解方程：5x 2﹣4x ﹣12＝0．【巩固练习】一、选择题1.已知关于x 的一元二次方程，用配方法解此方程，配方后的方程是（）A ．B ．C ．D ． 2．用配方法解下列方程时，配方有错误的是（）A ．化为B ．化为C ．化为D ．化为3．（2015春•张家港市校级期中）若M=2x 2﹣12x+15，N=x 2﹣8x+11，则M 与N 的大小关系为（） A ．M ≥N B ． M ＞N C ． M ≤N D ． M ＜N 4．不论x 、y 为何实数，代数式的值 ( )A ．总小于2B ．总不小于7C ．为任何实数D ．不能为负数 5．已知，则的值等于（）A.4B.-2C.4或-2D.-4或2 6．若t 是一元二次方程的根，则判别式和完全平方式的关系是( )A.△=MB. △＞MC. △＜MD. 大小关系不能确定二、填空题 7．（1）x 2-x+ =（）2；（2）x 2+px+ =（）2. 220x x m --=2(1)1x m -=+2(1)1x m +=+22(1)1x m -=+22(1)1x m +=+22990x x --=2(1)100x -=22740t t --=2781416t ⎛⎫-= ⎪⎝⎭2890x x ++=2(4)25x +=23420x x --=221039x ⎛⎫-= ⎪⎝⎭22247x y x y ++-+438．已知，则的值为． 9．已知4x 2-ax+1可变为（2x-b ）2的形式，则ab=_______．10．将一元二次方程x 2-2x-4=0用配方法化成（x+a ）2=b 的形式为____ ___，∴所以方程的根为_________． 11．把一元二次方程3x 2-2x-3=0化成3(x+m)2=n 的形式是___ ________；若多项式x 2-ax+2a-3是一个完全平方式，则a=_________. 12．（2015春•重庆校级期中）a 2+b 2﹣4a+2b+5=0，则b a 的值为．三、解答题 13. 用配方法解方程.(1) 3x 2-4x-2=0； (2)x 2-4x+6=0．14. 用公式法解下列方程：（2）．15．（2014•甘肃模拟）用配方法证明：二次三项式﹣8x 2+12x ﹣5的值一定小于0．16．已知在⊿ABC 中,三边长a 、b 、c ,满足等式a 2-16b 2-c 2+6ab+10bc=0，求证:a+c=2b223730216b a a b -+-+=a -2(1)210x ax --=；22222(1)()ab x a x b x a b +=+>一元二次方程专题复习（二）温故知新:1.直接开平方法2.配方法3.公式法一、因式分解法因式分解法就是利用因式分解的手段，求出方程的解的方法，这种方法简单易行，是解一元二次方程最常用的方法。

一元二次方程全章复习讲义

一元二次方程内容简介：1. 了解一元二次方程的定义及一元二次方程的一般形式：20(0)ax bx c a ++=≠.2. 掌握一元二次方程的四种解法，并能灵活运用.3. 掌握一元二次方程根的判别式，并能运用它解相应问题.4. 掌握一元二次方程根与系数的关系，会用它们解决有关问题.5. 会解一元二次方程应用题. 知识点一：一元二次方程的定义及一般形式【知识要点】一元二次方程的一般形式：20(0)ax bx c a ++=≠例1、下列方程中是关于x 的一元二次方程的是（）A ()()12132+=+x xB 02112=-+x xC 02=++c bx axD 1222+=+x x x 变式：当k 时，关于x 的方程3222+=+x x kx 是一元二次方程。

例2、方程()0132=+++mx xm m 是关于x 的一元二次方程，则m 的值为。

针对练习：1、方程782=x 的一次项系数是，常数项是。

2、若方程()112=•+-x m x m 是关于x 的一元二次方程，则m 的取值范围是。

知识点二：一元二次方程的解【知识要点】1、当已知一元二次方程的一个根时，要熟练地将这个根代入原方程，并灵活运用得到的等式。

2、在20(0)ax bx c a ++=≠中，x 取特殊值时，a 、b 、c 之间满足的关系式。

例1、已知322-+y y 的值为2，则1242++y y 的值为。

例2、关于x 的一元二次方程()04222=-++-a x x a 的一个根为0，则a 的值为。

例3、一元二次方程()002≠=++a c bx ax 的系数满足b c a =+，则此方程必有一根为。

例4、已知b a ,是方程042=+-m x x 的两个根，c b ,是方程0582=+-m x x 的两个根，则m 的值为。

针对练习：1、已知方程0102=-+kx x 的一根是2，则k 为，另一根是。

一元二次方程复习知识点梳理

一元二次方程总复习考点1：一元二次方程的概念一元二次方程：只含有一个未知数，未知数的最高次数是2，且系数不为 0，这样的方程叫一元二次方程．一般形式：ax 2＋bx+c=0(a ≠0）。

注意：判断某方程是否为一元二次方程时，应首先将方程化为一般形式。

考点2：一元二次方程的解法1.直接开平方法：对形如(x+a ）2=b （b ≥0）的方程两边直接开平方而转化为两个一元一次方程的方法。

X+a=±b∴1x =-a+b 2x =-a-b2.配方法：用配方法解一元二次方程：ax 2＋bx+c=0(k ≠0）的一般步骤是：①化为一般形式；②移项，将常数项移到方程的右边；③化二次项系数为1，即方程两边同除以二次项系数；④配方，即方程两边都加上一次项系数的一半的平方；化原方程为(x+a ）2=b 的形式；⑤如果b ≥0就可以用两边开平方来求出方程的解；如果b ≤0，则原方程无解．3.公式法：公式法是用求根公式求出一元二次方程的解的方法．它是通过配方推导出来的．一元二次方程的求根公式是aac b b x 242-±-=(b 2－4ac ≥0)。

步骤：①把方程转化为一般形式；②确定a ，b ，c 的值；③求出b 2－4ac 的值，当b 2－4ac ≥0时代入求根公式。

4.因式分解法：用因式分解的方法求一元二次方程的根的方法叫做因式分解法．理论根据：若ab=0，则a=0或b=0。

步骤是：①将方程右边化为0；②将方程左边分解为两个一次因式的乘积；③令每个因式等于0，得到两个一元一次方程，解这两个一元一次方程，它们的解就是原一元二次方程的解．因式分解的方法：提公因式、公式法、十字相乘法。

5．一元二次方程的注意事项：⑴ 在一元二次方程的一般形式中要注意，强调a ≠0．因当a=0时，不含有二次项，即不是一元二次方程．⑵ 应用求根公式解一元二次方程时应注意：①先化方程为一般形式再确定a ，b ，c 的值；②若b 2－4ac ＜0，则方程无解．⑶ 利用因式分解法解方程时，方程两边绝不能随便约去含有未知数的代数式．如－2(x ＋4)2 =3（x＋4）中，不能随便约去x ＋4。

一元二次方程复习课(绝对经典)

2
2
关于 x的一元二次方程 x (2k 3) x k 0有
2 2
两个不相等的实数根、
(1)求k的取值范围；（）若 6, 求（） 3 5的值 2 解： )由题意得， (2
2
解得， k1 1, k 2 3 3 k , k 1 4
2 8、x 2 4 x 2 0, 请用配方法转化成（ m） n的 x
形式，则
( x 2) 2
2
9、请写出一个一元二次方程，
它的根为-1和2
(x+1)(x-2)=0
将4个数a、b、c、d排成2行2列，两边各加一条竖线记成
a b a b , 定义 ad bc，这个式子叫做2阶行列式。 c d c d 若 x+1 x-1 1-x x+1 =6则x=
的一个根是-1，则
4 , 另一根为______ x=-3
若a为方程 x2 x 5 0 的解，则 a 2 a 1 的值为 6
6、若a是方程x 3x 3 0的一个根，则
2
3a 9a 2
2
11
2
7、n是方程x m x n 0一个根（n 0）， n m -1
2、若（m+2）x 2 +（m-2） x -2=0是关于x的一元二 ≠－ 2 次方程则m 。
一元二次方程的一般式
ax bx c 0 （a≠0）
2
一元二次方程一般形式二次项系一次项常数项数系数
3x²=1
2y(y-3)= -4
3x²-1=0
2y2-6y+4=0
3 2
0
-6
-1 4

10.《一元二次方程》全章复习与巩固—知识讲解(基础)

《一元二次方程》全章复习与巩固—知识讲解（基础）【学习目标】1.了解一元二次方程及有关概念；2.掌握通过配方法、公式法、因式分解法降次──解一元二次方程；3.掌握依据实际问题建立一元二次方程的数学模型的方法．【知识络】【要点梳理】要点一、一元二次方程的有关概念1.一元二次方程的概念：通过化简后，只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的整式方程，叫做一元二次方程．2.一元二次方程的一般式：3.一元二次方程的解：使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解，也叫做一元二次方程的根. 要点诠释：判断一个方程是否为一元二次方程时，首先观察其是否是整式方程，否则一定不是一元二次方程；其次再将整式方程整理化简使方程的右边为0，看是否具备另两个条件：①一个未知数；②未知数的最高次数为2.对有关一元二次方程定义的题目，要充分考虑定义的三个特点，不要忽视二次项系数不为0．【典型例题】类型一、一元二次方程的有关概念1．下列方程中是关于x 的一元二次方程的是（）A ．2210x x +=B ．20ax bx c ++=C ．(1)(2)1x x -+=D ．223250x xy y --= 【答案】C ；【解析】A ：不是整式方程，故本选项错误；B ：当a =0时，即ax 2+bx +c =0的二次项系数是0时，该方程就不是一元二次方程；故本选项错误；C ：由原方程，得x 2+x-3=0，符一元二次方程的要求；故本选项正确；D ：方程3x 2-2xy -5y 2=0中含有两个未知数；故本选项错误．故选C ．【总结升华】一元二次方程必须满足四个条件：（1）未知数的最高次数是2；（2）二次项系数不为0；（3）是整式方程；（4）含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．举一反三：【高清ID ：388528 关联的位置名称（播放点名称）：利用定义求字母的值】【变式】关于x 的方程22(28)(2)10a a x a x --++-=,当a 时为一元一次方程；当a 时为一元二次方程.【答案】a =4；a ≠4且a ≠-2.要点二、一元二次方程的解法1．基本思想一元二次方程−−−→降次一元一次方程 2．基本解法直接开平方法、配方法、公式法、因式分解法．要点诠释：解一元二次方程时，根据方程特点，灵活选择解题方法，先考虑能否用直接开平方法和因式分解法，再考虑用公式法．【典型例题】类型二、一元二次方程的解法2．用适当的方法解一元二次方程(1) 0.5x2-=0； (2) (x+a)2=；(3) 2x2-4x-1=0； (4) (1-)x2=(1+)x．【答案与解析】(1)原方程可化为0.5x2=∴x2=用直接开平方法，得方程的根为∴x1=，x2=-．(2)原方程可化为x2+2ax+a2=4x2+2ax+∴x2=a2用直接开平方法，得原方程的根为∴x1=a，x2=-a．(3) a=2，b=-4，c=-1b2-4ac=(-4)2-4×2×(-1)=24＞0x=∴x1=，x2=.(4)将方程整理，得(1-)x2-(1+)x=0用因式分解法，得x[(1-)x-(1+)]=0∴ x1=0，x2=-3-2．【总结升华】在以上归纳的几种解法中，因式分解法是最简便、最迅捷的方法，但只有一部分方程可以运用这种方法，所以要善于及时观察标准的二次三项式在有理数范围内是否能直接因式分解，凡能直接因式分解的，应首先采取这种方法．公式法是可以解任何类型的一元二次方程，但是计算过程较繁琐，所以只有选择其他解法不顺利时，才考虑用这种解法．虽然先配方，再开平方的方法也适用于任何类型的一元二次方程，但是对系数复杂的一元二次方程，配方的过程比运用公式更繁琐，所以，配方法适用于系数简单的一元二次方程的求解．举一反三：【变式】解方程． (1)(3x-2)2+(2-3x)＝0； (2)2(t-1)2+t＝1.【答案】(1)原方程可化为：(3x-2)2-(3x-2)＝0，∴ (3x-2)(3x-2-1)＝0．∴ 3x-2＝0或3x-3＝0，∴ 123x =，21x =． (2)原方程可化为：2(t-1)2+(t-1)＝0．∴ (t-1)[2(t-1)+1]＝0．∴ (t-1)(2t-1)＝0，∴ t-1＝0或2t-1＝0．∴ 11t =，212t =．要点三、一元二次方程根的判别式及根与系数的关系1.一元二次方程根的判别式一元二次方程)0(02≠=++a c bx ax 中，ac b 42-叫做一元二次方程)0(02≠=++a c bx ax 的根的判别式，通常用“∆”来表示，即ac b 42-=∆（1）当△>0时，一元二次方程有2个不相等的实数根；（2）当△=0时，一元二次方程有2个相等的实数根；（3）当△<0时，一元二次方程没有实数根.类型三、一元二次方程根的判别式的应用3．（2015•荆门）若关于x 的一元二次方程x 2﹣4x+5﹣a=0有实数根，则a 的取值范围是（）A ．a ≥1B ． a ＞1C ． a ≤1D ．a ＜1【答案】A ；【解析】∵关于x 的一元二次方程x 2﹣4x+5﹣a=0有实数根，∴△=（﹣4）2﹣4（5﹣a ）≥0，∴a ≥1．故选A ．【总结升华】本题考查的是一元二次方程根的判别式，根据方程有两个实数根，得到判别式大于等于零，求出a 的取值范围．【高清ID ：388528 关联的位置名称（播放点名称）：根系关系】2.一元二次方程的根与系数的关系如果一元二次方程)0(02≠=++a c bx ax 的两个实数根是21x x ，，那么a b x x -=+21，ac x x =21. 注意它的使用条件为a ≠0， Δ≥0.要点诠释：1.一元二次方程的根的判别式正反都成立．利用其可以解决以下问题：(1)不解方程判定方程根的情况；(2)根据参系数的性质确定根的范围；(3)解与根有关的证明题．2. 一元二次方程根与系数的应用很多：(1)已知方程的一根，不解方程求另一根及参数系数；(2)已知方程，求含有两根对称式的代数式的值及有关未知数系数；(3)已知方程两根，求作以方程两根或其代数式为根的一元二次方程．类型四、一元二次方程的根与系数的关系4．已知x 1、x 2是关于x 的方程2220x x t -++=的两个不相等的实数根，（1）求t 的取值范围；（2）设2212s x x =+，求s 关于t 的函数关系式．【答案与解析】(1)因为一元二次方程有两个不相等的实数根．所以△＝(-2)2-4(t+2)＞0，即t ＜-1．(2)由一元二次方程根与系数的关系知：122x x +=，122x x t =+，从而2212s x x =+21212()2x x x x =+-222(2)2t t =-+=-，即2(1)s t t =-<-．【总结升华】利用根与系数关系求函数解析式综合题.举一反三：【变式】已知关于x 的一元二次方程222(1)x m x m =--的两实数根为1x ，2x ．（1）求m 的取值范围；（2）设12y x x =+，当y 取得最小值时，求相应m 的值，并求出最小值．【答案】（1）将原方程整理为222(1)0x m x m +-+=．∵ 原方程有两个实数根．∴ 22[2(1)]4840m m m =--=-+≥△，∴ 12m ≤．（2） 1222y x x m =+=-+，且12m ≤．因为y 随m 的增大而减小，故当12m =时，取得最小值1．要点四、列一元二次方程解应用题1.列方程解实际问题的三个重要环节：一是整体地、系统地审题；二是把握问题中的等量关系；三是正确求解方程并检验解的合理性.2.利用方程解决实际问题的关键是寻找等量关系.3.解决应用题的一般步骤：审 (审题目，分清已知量、未知量、等量关系等)；设 (设未知数，有时会用未知数表示相关的量)；列 (根据题目中的等量关系，列出方程)；解 (解方程，注意分式方程需检验，将所求量表示清晰)；验 (检验方程的解能否保证实际问题有意义）；答 (写出答案，切忌答非所问).4.常见应用题型数字问题、平均变化率问题、利息问题、利润(销售)问题、形积问题等.要点诠释：列方程解应用题就是先把实际问题抽象为数学问题（列方程），然后由数学问题的解决而获得对实际问题的解决.类型五、一元二次方程的应用5．如图所示，在长为10cm，宽为8cm的矩形的四个角上截去四个全等的小正方形，使得留下的图形(图中阴影部分)面积是原矩形面积的80%，求所截去的小正方形的边长．【答案与解析】设小正方形的边长为xcm，由题意得4x2＝10×8×(1-80%)．解得x1＝2，x2＝-2．经检验，x1＝2符合题意，x2＝-2不符合题意舍去．∴ x＝2．答：截去的小正方形的边长为2cm．【总结升华】设小正方形的边长为x cm，因为图中阴影部分面积是原矩形面积的80%，所以4个小正方形面积是原矩形面积的20%．举一反三：【变式】（2015春•启东市月考）如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用25m），现在欲砌50m长的墙，砌成一个面积300m2的矩形花园，则BC的长为多少m?【答案】解：设AB=x米，则BC=（50﹣2x）米．根据题意可得，x （50﹣2x ）=300，解得：x 1=10，x 2=15，当x=10，BC=50﹣10﹣10=30＞25，故x 1=10（不合题意舍去），50﹣2x=50﹣30=20．答:BC 的长为20m ．6．某旅行社有100张床位，每床每晚收费10元，空床可全部租出；若每床每晚提高2元，则减少10张床位租出；若每床每晚收费再提高2元，则再减少10张床位租出．以每次提高2元的这种方法变化下去，为了每晚获得1120元的利润，每床每晚应提高多少元?【答案与解析】设每床每晚提高x 个2元，则每床每晚收费为(10+2x)元，每晚出租出去的床位为(100-10x)张，根据题意，得(10+2x)(100-10x)＝1120．整理，得x 2-5x+6＝0．解得，x 1＝2，x 2＝3．∴ 当x ＝2时，2x ＝4；当x ＝3时，2x ＝6．答：每床每晚提高4元或6元均可．【总结升华】这是商品经营问题，总利润＝每张床费×床数．可设每床每晚提高x 个2元，则床费为(10+2x)元，由于每晚每床提高2元，出租出去的床位减少10张，则出租出去的总床位为(100-10x)张，据此可列方程．【巩固练习】一、选择题1.已知1是关于x 的一元二次方程（m ﹣1）x 2+x+1=0的一个根，则m 的值是（）A.1B.﹣1C.0D.无法确定2．若一元二次方程式ax （x ＋1）＋（x ＋1）（x ＋2）＋bx （x ＋2）＝2的两根为0．2，则|3a ＋4b |之值为何（）A ．2B ．5C ．7D ．83．（2015•濠江区一模）某机械厂一月份生产零件50万个，三月份生产零件72万个，则该机械厂二、三月份生产零件数量的月平均增长率为（）A ．2%B ． 5%C ． 10%D ． 20% 4．将代数式x 2+4x-1化成（x+p ）2+q 的形式（）A.（x-2）2+3B.（x+2）2-4C.（x+2）2-5D.（x+2）2+45．若关于x 的一元二次方程2210kx x ++=有实数根，则k 的取值范围是（）．A ．k ＜0B ．k ≤0C ．k ≠1且k ≠0D ．k ≤1且k ≠06．从一块正方形的铁片上剪掉2 cm 宽的长方形铁片，剩下的面积是48 cm 2，则原来铁片的面积是( ) A.64 cm 2 B.100 cm 2 C.121 cm 2 D.144 cm 27．若t 是一元二次方程的根，则判别式和完全平方式的关系是( )A.△=MB. △＞MC. △＜MD. 大小关系不能确定8．如果关于x 的方程ax 2+x-1=0有实数根，则a 的取值范围是( )A ．B ．C ．且D ．且二、填空题9．已知关于x 的方程x 2+mx ﹣6=0的一个根为2，则m = ，另一个根是．10．（2014秋•青海校级期末）有一间长20m ，宽15m 的矩形会议室，在它的中间铺一块地毯，地毯的面积是会议室面积的一半，四周未铺地毯的留空宽度相同，则地毯的长、宽分别为和．11．关于x 的一元二次方程22(1)10a x x a -++-=有一个根为0，则a = .12．阅读材料：设一元二次方程似20ax bx c ++=(a ≠0)的两根为x 1，x 2，则两根与方程系数之间有如下关系：12b x x a +=-，12c x x a =，根据该材料填空：已知x 1，x 2是方程2630x x ++=的两实数根，则2112x x x x +的值为________． 13．已知两个连续奇数的积是15，则这两个数是___________________.14．设x 1，x 2是一元二次方程x 2-3x-2＝0的两个实数根，则2211223x x x x ++的值为________． 15．问题1：设a 、b 是方程x 2＋x －2012＝0的两个实数根，则a 2＋2a ＋b 的值为；问题2：方程x 2－2x －1＝0的两个实数根分别为x 1，x 2，则（x 1―1）（x 2―1）＝；问题3：已知一元二次方程x 2－mx ＋m －2＝0的两个实数根为x 1、x 2且x 1x 2（x 1＋x 2）＝3，则m的值是；问题4：已知一元二次方程x 2-2x+m=0,若方程的两个实数根为X 1,X 2，且X 1+3X 2=3,则m 的值是 .16．某校2010年捐款1万元给希望工程，以后每年都捐款，计划到2012年共捐款4.75万元，则该校捐款的平均年增长率是 .三、解答题17．某两位数的十位数字与个位上的数字之和是5，把这个数的个位上的数字与十位上的数字对调后，所得的新两位数与原两位数的乘积为736，求原来的两位数.18. 恒利商厦九月份的销售额为200万元，十月份的销售额下降了20%，商厦从十一月份起加强管理，改善经营，使销售额稳步上升，十二月份的销售额达到了193.6万元，求这两个月的平均增长率．19．（2015•十堰）已知关于x 的一元二次方程x 2﹣（2m+3）x+m 2+2=0．（1）若方程有实数根，求实数m的取值范围；（2）若方程两实数根分别为x1、x2，且满足x12+x22=31+|x1x2|，求实数m的值．20．某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．（1）求商场经营该商品原来一天可获利润多少元？（2）设后来该商品每件降价x元，商场一天可获利润y元．①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？②求出y与x之间的函数关系式，并通过画该函数图像的草图，观察其图像的变化趋势，结合题意写出当x取何值时，商场获利润不少于2160元？【答案与解析】一、选择题1.【答案】B；【解析】解：根据题意得：（m﹣1）+1+1=0，解得：m=﹣1．故选B．2.【答案】B；【解析】先根据一元二次方程式ax（x＋1）＋（x＋1）（x＋2）＋bx（x＋2）＝2的根确定a．b 的关系式．然后根据a．b的关系式得出3a＋4b＝－5．用求绝对值的方法求出所需绝对值．3.【答案】D；【解析】设平均每月增长的百分率为x，根据题意，得50（1+x）2=72，解得x1=0.2=20%，x2=﹣2.2（不合题意，舍去）故选D．4.【答案】C；【解析】根据配方法，若二次项系数为1，则常数项是一次项系数的一半的平方，若二次项系数不为1，则可先提取二次项系数，将其化为1后再计算．x2+4x-1=x2+4x+4-4-1=（x+2）2-5，故选C．5.【答案】D；【解析】因为方程是一元二次方程，所以k≠0，又因为一元二次方程有实数根，所以△≥0，即△＝4-4k≥0，于是有k≤1，从而k的取值范围是k≤1且k≠0．6．【答案】A；【解析】本题用间接设元法较简便，设原铁片的边长为xcm.由题意，得x(x－2)=48，解得x1=－6(舍去)，x2=8.∴x2=64，即正方形面积为64 cm2.7.【答案】A；【解析】由t是方程的根得at2+bt+c=0,M=4a2t2+4abt+b2=4a(at2+bt)+b2= b2-4ac=△.8．【答案】B ；【解析】注意原方程可能是一元二次方程，也可能是一元一次方程.二、填空题9．【答案】1；﹣3．【解析】根据一元二次方程的解定义，将x =2代入关于x 的方程x 2+mx ﹣6=0，然后解关于m 的一元一次方程；再根据根与系数的关系x 1+x 2=﹣b a解出方程的另一个根． 10．【答案】 15m ，10m ；【解析】设留空宽度为xm ，则（20﹣2x ）（15﹣2x ）=20×15×，整理得：2x 2﹣35x+75=0，即（2x ﹣5）（x ﹣15）=0，解得x 1=15，x 2=2.5，∵20﹣2x ＞0，∴x＜10，∴x=2.5，∴20﹣2x=15，15﹣2x=10．∴地毯的长、宽分别为15m 和10m ．11．【答案】-1；【解析】把x=0代入方程得1a =±,因为10a -≠，所以1a =-.12．【答案】10；【解析】此例首先根据阅读部分，明确一元二次方程根与系数的关系，然后由待求式2112x x x x +变形为2221212121212()2x x x x x x x x x x ++-=，再整体代换．具体过程如下：由阅读材料知 x 1+x 2＝-6，x 1x 2＝3．而222221121212121212()2(6)23103x x x x x x x x x x x x x x ++---⨯+====． 13．【答案】3和5或-3和-5；【解析】注意不要丢解.14．【答案】7；【解析】∵ x 1，x 2是一元二次方程2320x x --=的两实数根，∴ x 1+x 2＝3，x 1x 2＝-2∴ 222222112211221212123(2)()3(2)7x x x x x x x x x x x x x x ++=+++=++=+-= 15．【答案】2011；-2；m=-1或3；m=34. 【解析】由于a ，b 是方程x 2+x-2012=0的两个实数根，根据根与系数的关系可以得到a+b=-1，并且a 2+a-2012=0，然后把a 2+2a+b 可以变为a 2+a+a+b ，把前面的值代入即可求出结果．16．【答案】50%；【解析】设该校捐款的平均年增长率是x ，则，整理，得，解得，答：该校捐款的平均年增长率是50%.三、解答题17.【答案与解析】设原两位数的十位数字为x，则个位数字为（5－x），由题意,得［10x+(5－x)］［10(5－x)+x］=736.整理,得x2－5x+6=0,解得x1=2,x2=3.当x=2时5－x=3,符合题意，原两位数是23.当x=3时5－x=2符合题意，原两位数是32.18.【答案与解析】设这两个月的平均增长率是x．，则根据题意，得200(1－20%)(1+x)2＝193.6，即(1+x)2＝1.21，解这个方程，得x1＝0.1，x2＝－2.1（舍去）．答：这两个月的平均增长率是10%．19.【答案与解析】解：（1）∵关于x的一元二次方程x2﹣（2m+3）x+m2+2=0有实数根，∴△≥0，即（2m+3）2﹣4（m2+2）≥0，∴m≥﹣；（2）根据题意得x1+x2=2m+3，x1x2=m2+2，∵x12+x22=31+|x1x2|，∴（x1+x2）2﹣2x1x2=31+|x1x2|，即（2m+3）2﹣2（m2+2）=31+m2+2，解得m=2，m=﹣14（舍去），∴m=2．20.【答案与解析】⑴若商店经营该商品不降价，则一天可获利润100×（100－80）＝2000（元）⑵ ①依题意得：（100－80－x）（100+10x）＝2160即x2－10x+16=0解得：x1=2,x2=8经检验：x1=2,x2=8都是方程的解，且符合题意.答：商店经营该商品一天要获利润2160元，则每件商品应降价2元或8元.②依题意得：y=（100－80－x）（100+10x）∴y= －10x2+100x+2000=－10(x－5)2+2250画草图（略）观察图像可得：当2≤x≤8时，y≥2160∴当2≤x≤8时，商店所获利润不少于2160元．。

一元二次方程全章复习与巩固—知识讲解

《一元二次方程》全章复习与巩固—知识讲解（提高）【学习目标】1.了解一元二次方程及有关概念；2.掌握通过配方法、公式法、因式分解法降次──解一元二次方程；3.掌握依据实际问题建立一元二次方程的数学模型的方法．【知识网络】【要点梳理】要点一、一元二次方程的有关概念1.一元二次方程的概念：通过化简后，只含有一个未知数(一元)，并且未知数的最高次数是2(二次)的整式方程，叫做一元二次方程．2.一元二次方程的一般式：3.一元二次方程的解：使一元二次方程左右两边相等的未知数的值叫做一元二次方程的解，也叫做一元二次方程的根.要点诠释：判断一个方程是否为一元二次方程时，首先观察其是否是整式方程，否则一定不是一元二次方程；其次再将整式方程整理化简使方程的右边为0，看是否具备另两个条件：①一个未知数；②未知数的最高次数为2.对有关一元二次方程定义的题目，要充分考虑定义的三个特点，不要忽视二次项系数不为0．要点二、一元二次方程的解法1．基本思想一元二次方程−−−→降次一元一次方程2．基本解法直接开平方法、配方法、公式法、因式分解法．要点诠释：解一元二次方程时，根据方程特点，灵活选择解题方法，先考虑能否用直接开平方法和因式分解法，再考虑用公式法．要点三、一元二次方程根的判别式及根与系数的关系 1.一元二次方程根的判别式一元二次方程)0(02≠=++a c bx ax 中，ac b 42-叫做一元二次方程)0(02≠=++a c bx ax 的根的判别式，通常用“∆”来表示，即ac b 42-=∆.（1）当△>0时，一元二次方程有2个不相等的实数根；（2）当△=0时，一元二次方程有2个相等的实数根；（3）当△<0时，一元二次方程没有实数根.2.一元二次方程的根与系数的关系如果一元二次方程)0(02≠=++a c bx ax 的两个实数根是21x x ，，那么a b x x -=+21，ac x x =21.注意它的使用条件为a ≠0， Δ≥0. 要点诠释：1.一元二次方程的根的判别式正反都成立．利用其可以解决以下问题：(1)不解方程判定方程根的情况； (2)根据参系数的性质确定根的范围； (3)解与根有关的证明题．2. 一元二次方程根与系数的应用很多：(1)已知方程的一根，不解方程求另一根及参数系数；(2)已知方程，求含有两根对称式的代数式的值及有关未知数系数；(3)已知方程两根，求作以方程两根或其代数式为根的一元二次方程．要点四、列一元二次方程解应用题1.列方程解实际问题的三个重要环节：一是整体地、系统地审题；二是把握问题中的等量关系；三是正确求解方程并检验解的合理性.2.利用方程解决实际问题的关键是寻找等量关系.3.解决应用题的一般步骤：审 (审题目，分清已知量、未知量、等量关系等)；设 (设未知数，有时会用未知数表示相关的量)；列 (根据题目中的等量关系，列出方程)；解 (解方程，注意分式方程需检验，将所求量表示清晰)；验 (检验方程的解能否保证实际问题有意义）；答 (写出答案，切忌答非所问).4.常见应用题型数字问题、平均变化率问题、利息问题、利润(销售)问题、形积问题等.要点诠释：列方程解应用题就是先把实际问题抽象为数学问题（列方程），然后由数学问题的解决而获得对实际问题的解决.【典型例题】类型一、一元二次方程的有关概念1．已知（m－1）x|m|+1+3x－2＝0是关于x的一元二次方程，求m的值.【答案与解析】依题意得|m|+1＝2，即|m|＝1，解得m＝±1，又∵m－1≠0，∴m≠1，故m＝－1.【总结升华】依题意可知m－1≠0与|m|+1＝2必须同时成立，因此求出满足上述两个条件的m的值即可.特别是二次项系数应为非零数这一隐含条件要注意.举一反三：【变式】若方程2(2)310mm x mx---=是关于x的一元二次方程，求m的值．【答案】根据题意得22,20,mm⎧=⎪⎨-≠⎪⎩解得所以当方程2(2)310mm x mx--=是关于x的一元二次方程时，2m=-．类型二、一元二次方程的解法2．解下列一元二次方程．(1)224(3)25(2)0x x---=； (2)225(3)9x x-=-； (3)2(21)4(21)40x x++++=．【答案与解析】(1)原方程可化为：22[2(3)][5(2)]0x x---=，即(2x-6)2-(5x-10)2＝0，∴ (2x-6+5x-10)(2x-6-5x+10)＝0，即(7x-16)(-3x+4)＝0，∴ 7x-16＝0或-3x+4＝0，∴116 7x=，24 3x=． (2)25(3)(3)(3)x x x-=+-，25(3)(3)(3)0x x x--+-=，∴ (x-3)[5(x-3)-(x+3)]＝0，即(x-3)(4x-18)＝0，∴ x-3＝0或4x-18＝0，∴13x=，292x=．(3)2(21)4(21)40x x++++=，∴2(212)0x++=．即2(23)0x+=，∴1232x x==-．【总结升华】 (1)方程左边可变形为22[2(3)][5(2)]x x---，因此可用平方差公式分解因式；(2)中方程右边分解后为(x-3)(x+3)，与左边中的(x-3)2有公共的因式，可移项后提取公因式(x-3)后解题；(3)的左边具有完全平方公式的特点，可用公式变为(2x+1+2)2＝0再求解．举一反三：【变式】解方程： (1)3x+15＝-2x2-10x； (2)x2-3x＝(2-x)(x-3)．【答案】(1)移项，得3x+15+(2x2+10x)＝0，∴ 3(x+5)+2x(x+5)＝0，即(x+5)(3+2x)＝0，∴ x+5＝0或3+2x＝0，∴15x=-，232x=-．(2)原方程可化为x(x-3)＝(2-x)(x-3)，移项，x(x-3)-(2-x)(x-3)＝0，∴ (x-3)(2x-2)＝0，∴ x-3＝0或2x-2＝0，∴13x=，21x=．类型三、一元二次方程根的判别式的应用3．关于x 的方程2(5)410a x x ---=有实数根．则a 满足（）A ．a ≥1B ．a ＞1且a ≠5C ．a ≥1且a ≠5D ．a ≠5【答案】A ；【解析】①当50a -=，即5a =时，有410x --=，14x =-，有实数根；②当50a -≠时，由△≥0得2(4)4(5)(1)0a --⨯-⨯-≥，解得1a ≥且5a ≠．综上所述，使关于x 的方程2(5)410a x x ---=有实数根的a 的取值范围是1a ≥．答案：A【总结升华】注意“关于x 的方程”与“关于x 的一元二次方程”的区别，前者既可以是一元一次方程，也可以是一元二次方程，所以必须分类讨论，而后者隐含着二次项系数不能为0．4． k 为何值时，关于x 的二次方程2690kx x -+=（1）k 满足时,方程有两个不等的实数根；（2）k 满足时,方程有两个相等的实数根；（3）k 满足时,方程无实数根. 【答案】（1）10k k ≠＜，且；（2）1k =；（3）1k ＞. 【解析】求判别式，注意二次项系数的取值范围. 【总结升华】根据判别式ac b 42-=∆及k ≠0求解.类型四、一元二次方程的根与系数的关系5．已知关于x 的方程222(2)0x m x m --+=，试探求：是否存在实数m 使方程的两个实数根的平方和等于56，若存在，求出m 的值；若不存在，请说明理由．【答案与解析】存在．设方程两根为x 1、x 2，根据题意，得122(2)x x m +=-，212x x m =，221256x x +=，而222121212()2x x x x x x +=+-，于是有[]222(2)256m m --=，整理得28200m m --=，解这个方程得110m =， 22m =-，当10m =时，△＝ 2224[2(2)]41440b ac m m -=---=-<，当2m =-时，△＝2224[2(2)]4480b ac m m -=---=>，所以符合条件的m 的值为-2．【总结升华】由两个实数根的平方和等于56，列出关系式，再由根与系数关系求出m的值，通过判别式去验证m值是否符合题意，从而得出结论.举一反三：【变式】已知关于x的方程2(1)(23)10k x k x k-+-++=有两个不相等的实数根1x、2x．(1)求k的取值范围；(2)是否存在实数k，使方程的两实数根互为相反数如果存在，求出k的值；如果不存在，请说明理由．【答案】(1)根据题意，得△＝(2k-3)2-4(k-1)(k+1)＝224129412130k k k k-+-=-+>，所以1312k<．由k-1≠0，得k≠1.当1312k<且k≠1时，方程有两个不相等的实数根；(2) 不存在．如果方程的两个实数根互为相反数，则12231kx xk -+=-=-，解得32k=．当32k=时，判别式△＝-5＜0，方程没有实数根．所以不存在实数k，使方程的两个实数根互为相反数．类型五、一元二次方程的应用6．甲、乙两人分别骑车从A、B两地相向而行，甲先行1小时后，乙才出发，又经过4小时两人在途中的C地相遇，相遇后两人按原来的方向继续前进.乙在由C 地到达A地的途中因故停了20分钟，结果乙由C地到达A地时比甲由C地到达B 地还提前了40分钟，已知乙比甲每小时多行驶4千米，求甲、乙两人骑车的速度.【答案与解析】设甲的速度为x千米/时，则乙的速度为（x+4）千米/时.根据题意，得54(4)2040460x xx x++=-+解之,得x1=16，x2=－2.经检验：x1=16，x2=－2都是原方程的根，但x2=－2不合题意，舍去.∴当x=16时，x+4=20.答：甲每小时行驶16千米，乙每小时行驶20千米.【总结升华】注意解题的格式，解分式方程应用题要双检验，即验根、符合题意.举一反三：【变式】某工程队在我市实施棚户区改造过程中承包了一项拆迁工程。

人教版九年级数学-一元二次方程全章知识点专题复习(含答案)

一元二次方程全章知识点专题复习【课标要点】1. 理解一元二次方程定义；2. 会解一元二次方程；3. 会根据根的判别式24b ac -判断一元二次方程的根的情况； 4. 会列一元二次方程解决实际问题.⎧⎪⎪⎪⎨⎪⎪⎪⎩解法根的判别式一元二次方程二次三项式的分解因式根与系数的关系实际应用问题第1讲一元二次方程的概念【知识要点】1、一元二次方程的一般形式：200),,,ax bx c a a b c ++=≠（其中是常数. 2、在一般式中，当b ＝0时，则有220c 00ax c ax bx +=+=或当＝时，则有，这两种情况都是一元二次方程.【典型例题】例1判断下列关于x 的方程是不是一元二次方程.22222222213;(2)50;(3)235;(5)2(3)21;511(6)33;(7)2;(8)()10;(9)40:1(10)0.(0)x x x xy x x x x x x x x abx a b x x x x px qx m p =-=--==-=+++=-=+++=-+=+++=≠（）分析：一元二次方程，必须满足：（1）整式方程；（2）含有一个未知数，并且最高次数是2.解：方程（1）、（6）、（7）的左边是分式，不属于整式方程，方程（3）含有两个未知数，方程（4）的左边不是整式，方程（5）经整理候，得－6x ＝1，方程（8）中未确定ab≠0，因此，只有（2）、（9）、（10）是一元二次方程.例2方程25)(3)(3)50.m m m x m x ---+-+=（（1） m 为何值时，此方程为一元二次方程？（2） m 为何值时，此方程为一元一次方程？分析：形如0nax bx c ++=的方程，当n ＝2且a≠0时为一元二次方程；当a ＝0时且b≠0时为一元二次方程.解：（1）当m －2＝2时，m ＝4，这时5)(3)0.m m --≠（当m ＝4时，此方程为一元二次方程.（2）5)(3)0,20,2m 30m m m m --=->-≠当（为自然数，且－时，方程为一元一次方程.由5)(3)0m 5m 3m m m --=≠（得＝或＝，又因为3，∴当m ＝5时，此方程为一元一次方程.例3 为加强防汛工作，市工程队准备对苏州河一段长为2240米的河堤进行加固，由于采用了新的加固模式，现在计划每天加固的长度比原计划增加了20米，因而完成此段加固工程所需天数将比原计划缩短2填，为进一步缩短该段加固工程的时间，如果要求每天加固224米，那么在现在计划的基础上，每天加固的长度还应再增加多少米？（只需列出方程，并整理成一般一元二次方程形式.）分析：根据题意本题有两个关系式：一是计划每天加固的长度比原计划增加了20米，而是实际完成工程任务所需时间比原计划缩短2天，由时间关系列出方程.解：设现在计划每天加固河堤x 米，则原来计划每天加固河堤（x －20）米.根据题意德22402240220x x-=-，整理，得 22022400x x --=【知识运用】一、选择题1．一元二次方程得一般形式是（）A.20x bx c ++= `B.20ax bx c ++=C. 20()ax bx c a o ++== D.以上都不对 2．下列方程为一元二次方程的有（）A.21102x x-+= B. 252ax bx c +=C.()219x -=D.x+y=03.关于x 的方程232232(m n m x mx m x nx px q +=+-+≠其中），经化简整理，化为200)ax bx c a ++=≠（的形式后，二次项系数、一次项系数及常数项分别是（）A.m －n ，p ，qB. m －n ，－p ，qC.m －n ，－p ，－qD.m －n ，p ，－q4．将一元二次方程21x 2x 302-+=－的二次项系数变为正整数，且使方程的根不变的是（）A. 2x 2x 30+=－ B. 2x x 60+=－4C 2x x 60=－4－D 2x x 60-=+4二、填空题5．方程24x 0=是_____元______次方程，二次项系数是______，一次项系数是____，常数项是_______.6.当m__________时，方程2m-1)x 21)x 0m m -+=（－(不是关于x 的一元二次方程；当m___________时，上述方程才是关于x 的一元二次方程；7.若方程22x 3x 1k x +=+是一元二次方程，则k 的取值范围是_________; 三、解答题 8．若方程1(3)x230k k x --+-=是关于x 的一元二次方程，求k 的值.9．若关于x 的一元二次方程22(a-1)x +x+a 10-=的一个根是0，求a 的值.10．某大学改善校园环境，计划在一块长80米，宽60米的矩形场地中央建一矩形网球场，网球场占地面积为3500平方米，四周为宽度相等的步行道，求步行道的宽度，根据题意列出泛称，并将其化为一般形式.第2讲配方法【知识要点】1、直接开平方法解一元二次方程：将方程化成()2b(0)x a b +=≥的形式，则x＝0)a b -±≥.2、配方法解一元二次方程：利用公式222a 2()ab b a b ±+=±，把一元二次方程转化为2()(0)x a b b +=≥，再利用直接开平方法解方程.【典型例题】例1 用配方法解关于x 的一元二次方程： x 0px q ++=2分析：配方法解一元二次方程，关键要搞清配方的目的是什么，即配方要使方程能运用直接开平方法解决，该题是一种字母系数的一元二次方程，故可按上述步骤进行求解，先将其整理成一般形式，二次项系数化为1.因二次项系数为1，所以移项得2x x p q +=-，方程两边配方，然后利用完全平方公式，直接开平方法解出方程.解：22221212x ,x (),244qx ,244q p 400,4x (2)p 40x 23p 40px q p p px q p p p q x pq x q +=-++=-+--->>---<222222移项，得配方，得整理，得（+）＝（1）当时，方程两边直接开平方，得当＝时，＝＝；（）当时,原方程无实数解.例2 用配方法解方程（1）2x 6x 50+-=；（2）24x 7x 20-+=分析：方程经过移项，配方后变为形如2().ax b c +=的方程解：（1）（2）移项，得24x 7x 2-=-化二次项系数为1，例3 试证：不论x 为何实数，多项式424224124x x x x ----的值总大于的值. 分析：比较两个代数式大小通常用做差的方法. 解：∴多项式424224124x x x x ----的值总大于的值. 【知识运用】一、选择题1．已知代数式2224x 228x 5x x +-+-的值为3，则代数式的值为（） A.5B. －5C. 5或－5D.02．将二次三项式22x 4x 6-+进行配方，正确的结果是（）A.24-2（x-1） B.24+2（x-1）C.22-2（x-2）D. 22+2（x-2） 3．方程2(1)9x +=的解是（） A.2x =B. 4x =-C. 122,4x x ==-D. 122,4x x =-=221265,6959,314333x x x x x x x +=++=+=∴+=∴=-+=--2移项，得配方，得即（x ＋）2222127717x ()()48287177x x 864877x x 88x x x -+=-+-∴-∴--∴得即（）＝，＝＝＝4242424222224242(241)(24)23(21)2(1)2x (1)20(241)(24)0x x x x x x x x x x x x x x -----=-+=-++=-+-+>----->对于任何实数，总有即4.已知11120,19,21202020a xb xc x =+=+=+，则代数式222a b c ab bc ac ++---的值是（） A.4 B.3C. 2D. 1二、填空题5．224___9(___3)x -+=-6．将二次三项式2x 2x 2--进行配方，其结果等于__________.7.已知m 是方程2x x 20--=的一个根，则代数式2m m -的值等于______. 三、解答题8．用配方法解下列方程2(1)2360;x x --= 221(2)20;33y y --=2(3)0.40.81;x x -= 2(4)1)0;y y ++=9.用配方法证明21074x x -+-的值恒小于0.10.来自信息产业部的统计数字显示，2019年1月至4月份我国手机产量为4000万台，相当于2018年全年手机产量的80％，预计到2020年年底收机产量将达到9800万台，试求这两年手机产量平均每年的增长率.第3讲公式法【知识要点】1．公式法：一般地，对于一元二次方程221200),b 4ac 0x ax bx c a ++=≠≥，（当－时， 2．2b 4ac 0≥V 当=－，方程可用公式法求解；当2b 4ac 0<V 当=－时，方程无解.【典型例题】例1 用公式法解下列方程21x 100-+=（） 2(2)221x x +=(3)(1)(1)x x +-=分析：首先把每个方程化成一般式，确定a 、b 、c 的值，在2b 4ac 0≥－的前提下，代入求根公式求出方程的根.解：2221222212(2)2210,2,2,1,424?2?(1122(3)10,1,2,1,44?1?(2(4)x x a b c b ac x x x a b c b ac x x +-====--=-±∴=⨯-+-∴===--===-=--=-±∴==⨯∴==Q 移项，得-1)=12>0,-2x=22原方程可化为（-1)=12>0,-（x=222221210,1,1,1,414?1?(x x a b c b ac x x +-====--=-∴=∴===Q 将原方程可化为-1)=5>0,x例2 阅读下面一段材料，并解答问题.22(1)1,4,10,4(411080,(212x x a b c b ac x ==-=-=-⨯⨯>--∴===⨯∴=Q 1=2－＝22220(0)40,4200(0,,,)ax bx c a x b ac b ac b x aa ax bx c a abc ++=≠=-≥--∆=≠∆≥++=≠ 我们知道由一元二次方程运用配方法得其求根公式由平方根的意义知:当时即负数,没有平方根,故代数式就决定了方程根的情况,称它为一元二次方程根的判别式,用记号“”表示,故公式符合条件且0,方可用于求实数根.此外,若均为整数应当222121242,(1)10,:4,?,,?:,b ac b a k x x k x k x x x x k ∆=-∆--+++==∆≥注意当是完全平方时,方程根为有理根;当是完全平方且(是的整数倍时方程的根为整数根. 根据上面得出的结论,请你解答下列问题: 已知关于的方程试求 ⑴为何值时方程有两个实数根 ⑵若方程的两个实数根满足则为何值分析根据上面材料分析当0时方程有实数根,从而确定k 的取值,对[]1222121121212121.:(1),1)4(1)043230.2(2)0,,0,2k-3=0,35k=,0,240,010,10,,x x k k k k x x x x x x x x x x x k k x =∆≥+-+≥-≥∴≥=≥=∆===><-=+=∴+==-∆≥Q 1于⑵中需分类讨论解方程有实数根故0,即-( 化简得时方程有两个实数根由①当时此时即符合要求.②当x 时即与相矛盾故舍去k=-13综上可知:当k=时有22x = 例3 某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如右图),由于地形限制,三级水库处理池的长、宽都不能超过16米,如果池的外围墙建造单价为每米 400元,中间两条间隔墙单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)(1) 当三级污水处理池的总造价为47200元时,求池长x;(2) 如果规定总造价越低就越合算那么根据题目提供的信息以47200元为总造价来修建三级污水处理池是否最合算?请说明理由.分析：可根据三级污水处理池的总造价为47200元列方程.ADBC隔墙隔墙x21212400400:(1)400(2)3002008047200,4007008002008047200,393500,14,25,,14,25,2516(,)10014,16.7x x xx xx x x x x x ⨯++⨯+⨯=⨯++⨯=-+=====><∴ 解由题意得即有化简得解得经检验都是原方程的根但米米不符合题意舍去当池长为米时池宽为米米符合题意当三级污水处理池的总造价为47200(2)1612.5164007008001620080463004720016<⨯⨯++⨯=<∴元时,池长为14米.当以47200元为总造价修建三级污水处理池时,不是最合算. 当池长为米时,池宽为米米,故池长为16米符合题意,这时总造价为当以47200元为总造价修建三级污水处理池时,不是最合算.【知识应用】一、选择题22222401)53200,0,0,x x k k m x x m m m n x mx n n m n --=-++-+=++=≠+1.方程2有两个相等的实数根,则的值为( )A.-1 B.-2 C.1 D.22.若一元二次方程(的常数项为则为( )A.1 B.2 C.1或2 D.53.若是方程的根则的值为( )1A. B.1 C.222235020,______.6.610_______.7.x x x mx m x x x --=++=--=1- D.-124.不解方程,判断方程2的根的情况是( )A.有两个不相等的实数根 B.有两个相等的实数根 C.无实数根 D.不能确定二、填空题5.已知的一个根则方程的另一个根是_____,的值是方程3的两根之和是方程22230530______.x x x --=++=与方程2的公共解是三、解答题,28.已知直角三角形的一条直角边比另一条直角边长2cm,且面积为24cm 求直角三角形的周长.21)(4)240,10,.k x k x k k k +++-+=+≠9.已知方程(有零根其中求的值2210.2)0,a a x ax b x a --++=要使(是关于的一元二次方程求的取值范围.第4讲分解因式法【知识要点】112212121212a xb a x b b b a a x x a a ++≠=-=- 1. 分解因式法:把一个一元一次方:程整理为:()()=0的(0)的形式，方程的解为：；；. 2.注意(1)方程一边一定化为0；（2）常用的方法：①提公因式法；②运用公式法③十字相乘法.【典型例题】260;x x -=例1 用因式分解法解下列方程. (1):(1),,(2),(5)(5),,.x x --分析方程的右边是零左边可以用提公因式法分解方程不要去掉括号更不要两边同时除以或要先移项使方程右边为零212212:60,(6)0,060,0, 6.(2)3(5)2(5)0,(5)[3(5)2]0,(5)(133)0,501330,135,.3x x x x x x x x x x x x x x x x x x -=-=∴=-=∴==---=---=--=∴-=-=∴==解(1)即或原方程可变形为即或 2(2)3(5)2(5)x x -=-例2 用公式法因式分解式解下列方程.2222(4)(43)(2)49(3)16(6)x x x x -=--=+ (1)3221222(1)(2)(1)(4)(43)0[(4)(43)][(4)(43)]0(77)(1)0,770101, 1.(2)7(3)][4(6)]0,7(3)4(6)][7(3)4(x x x x x x x x x x x x x x x x x x ---=∴-+----=∴---=∴-=--=∴==---+=-++--分析:方程先移项再利用因式分解法来解,方程移项后也能因式分解.解:移项,得333或原方程化为[ [126)]0,(113)(345)0,3,15.11x x x x +=+-=∴=-=化简为,1).x x x x +-例3 为解决新疆农牧民出行难的问题今年是新疆投资公路建设力度最大、最多的一年，某公路修筑队接受了改建农村公路96千米的任务，为了尽量减少施工带来的交通不便，实际施工时每天比计划多修1千米，结果提前16天完成任务，问原计划每天修多少千米？分析：如果把修路队原来计划每天修（千米），则实际每天修路是(千米,工作任务可根据工作时间=列方程工作效率解:设原计划每天修路千米,由题意得962129616160(3)(2)03(),2:x x x x x x x =++-=∴+-=∴=-= 化简整理得舍去答原计划每天修2千米.【知识运用】1212121212121200550505244552A. B.4C.,4D.,4225(1)(2)034,A B x x x x x x x x x x x x x x x x x x x x x x x x -======-==--======+-===-一、选择题1.一元二次方（5）＝0的两个根为（）A.，B.，C.，D.，2.方程（）＝5（）的根为（）3.方程的根是，则这个方程为（）.-1,2 .12C D 34,A.(3)(4)0B.(3)(4)0C.(3)(4)0D.(3)(4)0x x x x x x x x x x ==--+=+-=++=--=1,-2 .0,-1,2 .0,1,-24.已知一元二次方程的两根分别为，则这个方程为（）22225123,_____.4_____,.5147.235(23)201(21);(2)(5)59.,3,x x x x x x x x x x y x x x +-+=-=+-++++=-=-=2二、填空题:5.若与的值相等则6.当时代数式的值为零用分解因式法解方程:2()的解是_____.三、解答题8.用适当的方法解方程.1(1)2有一个直角三角形它的边长恰是个连续整数这个三角形的三边长是多少?10.有一个两位数,它的十位数字和个位数字的和是5,把这个两位数的十位数字和个位数字互换后得到另一个两位数,两个两位数的积为736,求原来的两位数.第5讲一元二次方程【知识要点】 1、黄金分割：如,图若点C 把线段分成两条线段AB 和BC ，且满足AC BCAB AC=则称线段AB 被点C 黄金分割，点C 叫做线段AB 的黄金分割点，AC 与AB 的比叫做黄金比.2、列方程解应用题的基本步骤可归纳为：审（审题）；设（设未知数）；列（列方程）解（解方程）；答（答案）.3、列方程解应用题的关键是找出存在的相等关系【典型例题】例1 某商场今年2月份的营业额为400万元，3月份的营业额比2月份增加10％，5月份的营业额达到633.6万元，求3月份到五月份营业额的平均增长率.分析：本题属于平均增长率问题，由已知可设月平均增长率为x ，那么3月份的营业额为400（1＋10％）（1＋x ），5月份营业额为400（1＋10％）（1＋x ）2.解：设平均月增长率为x ，由题意得400（1＋10％）（1＋x ）2＝633.6 整理得：（1＋x ）2＝633.61 1.2440x ∴+=± 0.2x ∴= 所以平均月增长率为20％.例2 一块矩形耕地大小尺寸如图所示，要在这块地上沿东西和南北方向分别挖2条和4条水渠，如果水渠的宽相等，而且要保证余下的可耕地面积为9600米2，那么水渠应挖多宽？分析：这类问题的特点是挖蕖所占用土地面积只与挖蕖的条数、渠道的宽度有关，而与渠道的位置无关，为了研究问题方便可分别把沿东西和南北方向挖的渠道移动到一起，那ABC么剩余可耕的长方形土地的长为（162－2x ）米，宽为（64－4x ）米.解：设水渠应挖x 米宽，以题意，得（162－2x ）（64－4x ）＝9600化简，297960x x -+=解得11x =,296x =（舍去）答：水渠应挖1米宽. 【知识运用】一、选择题1．某商店十月份营业额为5000元，十二月份上升到7200元，平均每月增长的百分率是( ) A ．20% B ．.12％ C ．22％ D.10％2．从正方形的铁皮上，截去2cm 宽的一条长方形，余下的面积是48cm 2,则原来的正方形铁皮的面积是（）A. 9cm 2B.68cm 2C. 8cm 2D. 64cm 23．有一个两位数，它的数字和等于14，交换数字位置后，得到新的两位数比原来的两位数大18，则原来的两位数是（）A ．68 B.86 C.－68 D.－864．随着通讯市场竞争日益激烈，某通讯公司的收集市话收费标准按原标准每分钟降低了a 院后，再次下降25％，现在的收费标准是每分钟b 元，则原收费标准是每分钟（） A. 5(1)4b -元 B. 5()4b a +元 C. 3()4b a +元 D 4()3b a +元. 二、填空题5．三个连续偶数，较小的两个数的平方和等于较大的数的平方，则这三个数为________. 6．一个两位数，它的数字之和为9，如果十位数字为a ，那么这个两位数是________;b 把这个两位数的个位数字与十位数字对调组成一个新数，则这个数与原数的差为________. 7.某种手表的成本在两年内以100元降低到81元，那么平均每年降低成本的百分率是_____. 三、解答题8．某工厂计划用两个月把产量提高21％，如果每月比上个月提高的百分数相同，求这个百分数.9．某人将2000元人民币按一年定期存入银行，到期后支出1000元用来购物，剩下的1000元及应得利息又全部按一年定期存入银行.若存款的利率不变，到期后得本金和利息共1320元，求这种存款方式的年利率.10．某商店如果将进货价为8元的商品按每件10元出售，每天可销售200件.现采用提高售价、减少进货量的方法增加利润，已知这种商品每涨价0.5元，其销售量就减少10件.问售价定为多少时，才能使所赚利润最大，并求出最大利润.第1讲一、1．C 2.C 3.D 4.D 二、5．一、二，4，0，0 6.m=1,m ≠1 7.222a ab b --三、8.根据题意的1230k k ⎧-=⎪⎨-≠⎪⎩①②由①得k －1=－2解得k=3或k=－1,由②得k ≠3,所以k=－19.由于方程的解使方程的左右两边相等，故将方程的解代入原方程后得到关于a 得方程，求出a 得值，但是需要满足原一元二次方程的二次项系数不为零，故只取a=－1. 10．设步行道的宽度为x 米，根据题意得（80－2x ）.(60－2x)=3500整理，得方程的一般形式为703250x -+=2x 第2讲一、1．A 2.B 3.C 4.B二、5．12x,2x ；6.2(1)3x --；7.22m m -=三、8．121233(1)(2)2,31342x y y y y ±±==-==-=--2（）x=29．2711110)002040x --<原式配方得－（ 2210740,10740x x x x +-=+-即－故－的值恒小于 10．设这两年手机产量平均每年的增长率为x ，根据题意得2124000212(1)980040%,8055x x x +====-解得％（舍去）第3讲一、1．B 2..B 3.D 4.A 二、5．24-- 6.2 7.x=－1三、8．设直角三角形的较短的直角边长为xcm ，则较长的直角边长为（x+2）cm.根据题意得：2001)0(4)02402x x k k k k =∴=+⨯++⨯-+=∴=Q 方程有零根即将代入方程得，（2121(2)24248026,8()2810x x x x x x x +=∴+-===-∴+=∴∴解得不符合题意舍去较长直角边为直角三角形的周长为6＋8＋10＝24（cm ）9． 10．要使方程是x 的一元二次方程，则由一元二次方程的定义.有220,2,1a a a a x --≠∴≠≠-且时该方程时关于的一元二次方程第4讲一、1．C 2.A 3.C 4.C 二、5.－ 1或4 6.x ＝－27.260,y y x +-==三、8.（1）y＝12±（2）121x x 5==- 9. 3，4，5 10. 32，23第5讲一、1．C 2.A 3.B 4.D 二、5. 7,6,8 6.9a+9,81－18a 7.10%三、8.设每月提高的百分率为x,原产量为a ，以题意得a(1+x)2=a(1+21%)220(1) 1.210.110% 2.1(10a x x ≠∴+====-∴Q 1解得x 舍去）为％9.设此种存款的年利率为x ，由题意得：【2000（1＋x ）－1000】(1+x)=1320 所以年利率为10％10．设此种商品的售价为x 元，商品所赚利润s 最大.2210.(20010)2040020(10)20000.5102000.x s x x x s x x s -=-⨯=-+∴=--+∴=当时，取最大值。

《一元二次方程》单元测试题及答案

《一元二次方程》单元测试题一、选择题（共8题，每题有四个选项，其中只有一项符合题意。

每题3分,共24分）:1.下列方程中不一定是一元二次方程的是( ）A 。

（a-3）x 2=8 （a ≠3)B 。

ax 2+bx+c=0 C.(x+3）(x —2）232057x +-= 2下列方程中,常数项为零的是（ )A 。

x 2+x=1 B.2x 2—x-12=12；C 。

2(x 2—1）=3(x-1) D 。

2（x 2+1）=x+23。

一元二次方程2x 2-3x+1=0化为(x+a)2=b 的形式，正确的是( ）A 。

23162x ⎛⎫-= ⎪⎝⎭;B 。

2312416x ⎛⎫-= ⎪⎝⎭;C 。

231416x ⎛⎫-= ⎪⎝⎭; D 。

以上都不对 4。

关于x 的一元二次方程()22110a x x a -++-=的一个根是0，则a 值为(）A 1 B 1- C 1或1-D1/25.已知三角形两边长分别为2和9,第三边的长为二次方程x 2—14x+48=0的一根，则这个三角形的周长为( ） A 。

11 B.17 C.17或19 D 。

196.已知一个直角三角形的两条直角边的长恰好是方程22870x x -+=的两个根，则这个直角三角形的斜边长是（）A 、、3 C 、6 D 、97。

使分式2561x x x --+ 的值等于零的x 是（ ) A 。

6 B 。

—1或6 C 。

—1 D.-6 8.若关于y 的一元二次方程ky 2—4y-3=3y+4有实根，则k 的取值范围是（ )A.k>-7/4B.k ≥-7/4 且k ≠0 C 。

k ≥-7/4 D.k>7/4 且k ≠09.已知方程22=+x x ，则下列说中,正确的是（）A 方程两根和是1B 方程两根积是2C 方程两根和是1-D 方程两根积比两根和大210.某超市一月份的营业额为200万元，已知第一季度的总营业额共1000万元, 如果平均每月增长率为x ，则由题意列方程应为( )A 。

《一元二次方程》全章复习与巩固—知识讲解

《一元二次方程》全章复习与巩固—知识讲解一元二次方程是高中数学中的重要内容，它是一种形如ax^2 + bx + c = 0的方程，其中a、b、c为实数，且a ≠ 0。

解一元二次方程的方法有因式分解、配方法和求根公式法。

下面将对这些解法进行讲解。

一、因式分解法如果一元二次方程能够因式分解为两个一次因式的乘积，即 (px + q) (rx + s) = 0，那么方程的解就可以直接得到。

具体步骤如下：1. 将二次方程化简成标准形式：ax^2 + bx + c = 0；2. 因式分解方程：(px + q) (rx + s) = 0；3. 解方程：px + q = 0 或 rx + s = 0；4.求解方程得到x的值。

例如，对方程x^2-5x+6=0应用因式分解法：1.方程已经是标准形式；2.可以将方程改写为(x-2)(x-3)=0；3.解方程得到x-2=0或x-3=0；4.求解方程可得x=2或x=3，这就是原方程的解。

二、配方法对于一元二次方程ax^2 + bx + c = 0，有时候可以通过配方法将方程转化为一个平方差或一个完全平方式。

具体步骤如下：1.当a≠0时，将方程两边同时除以a，化简为x^2+(b/a)x+c/a=0；2. 计算出一个值k，使得(b/a)^2 + 2(b/a)k + k^2 = k^2、其中，2(b/a)k为bx的一半，k^2为(c/a)的相反数的一半；3.将方程变形为(x+k)^2+m=0，即(x+k)^2=-m；4.解方程得到x+k=±√(-m)；5.求解方程得到x的值。

例如，对方程x^2-6x+8=0应用配方法：1.将方程化简为(x-3)^2-1=0；2.得到k=3，使得(-6/2)^2+2(-6/2)k+k^2=1；3.方程变形为(x-3)^2=1；4.解方程得到x-3=±1；5.求解方程可得x=2或x=4，这就是原方程的解。

三、求根公式法一元二次方程的求根公式是美国数学家Vieta发现的，它的公式形式为：x = (-b ± √(b^2 - 4ac)) / 2a。

一元二次方程单元复习(一)(含答案)

一元二次方程单元复习（一）一、单选题(共14道，每道6分)1.下列方程中，是一元二次方程的为( )A. B.C. D.答案：B解题思路：1．解题要点①定义：只含有一个未知数x的整式方程，并且可以化成（a，b，c为常数，）的形式，这样的方程叫做一元二次方程；②定义要点：整式方程，化简整理，一元二次．2．解题过程A．，不满足；B．是一元二次方程；C．中在分母上，不符合整式方程；D．，整理得，不符合二次．试题难度：三颗星知识点：一元二次方程的定义2.x=1是关于x的一元二次方程x2+ax+2b=0的解，则2a+4b=( )A.-2B.-3C.-1D.-6答案：A解题思路：∵x=1是一元二次方程x2+ax+2b=0的解∴1+a+2b=0∴a+2b=-1∴2a+4b=-2试题难度：三颗星知识点：一元二次方程的解3.若关于x的一元二次方程有实数根，则c的值可以为( )A.-1B.-2C.-3D.5答案：D解题思路：思路一：要使该方程有实数根，根据平方根的意义，有思路二：原方程可变形为由题意，解得试题难度：三颗星知识点：解一元二次方程——配方法4.用配方法解方程x2-6x-8=0时，配方结果正确的是( )A.(x-3)2=17B.(x-3)2=14C.(x-6)2=44D.(x-3)2=1答案：A解题思路：原方程可变形为∴∴试题难度：三颗星知识点：解一元二次方程——配方法5.已知x1，x2是一元二次方程x2-2x=0的两个实数根，下列结论一定错误的是( )A.x1≠x2B.x12-2x1=0C.x1+x2=2D.x1·x2=2答案：D解题思路：解得一元二次方程x2-2x=0的两根分别为0和21≠x2；x1+x2=2；x12-2x1=0成立；x1·x2=0．试题难度：三颗星知识点：一元二次方程的解6.已知是方程的一个根，则方程的另一个根及c的值为( )A.，B.，2C.，-1D.，1答案：D解题思路：∵方程有两个根∴∵是方程的一个根∴方程的另一个根为∴试题难度：三颗星知识点：一元二次方程的根与系数的关系7.已知α，β是关于x的一元二次方程的两个不相等的实数根，且满足，则m的值为( )A.3或-1B.3C.1D.-3或1答案：B解题思路：∵α，β是关于x的一元二次方程的两个不相等的实数根∴，∴∵∴∴解得m1=3，m2=-1（舍）试题难度：三颗星知识点：一元二次方程的根的判别式8.若，，，则下列方程中必有两个实数根的是( )A. B.C. D.以上答案都不对答案：C解题思路：∵，，∴，A．，无法判断正负B．，无法判断正负C．，∴方程有两个不相等的实数根试题难度：三颗星知识点：一元二次方程的根的判别式9.若关于x的方程有两个实数根，则m的取值范围为( )A. B.C. D.答案：D解题思路：∵方程有两个实数根∴∴且试题难度：三颗星知识点：一元二次方程的根的判别式10.设菱形的周长为20，两条对角线的长是方程的两个根，则m 的值为( )A. B.C. D.以上答案都不对答案：A解题思路：∵菱形两条对角线的长是方程的两个根∴∵菱形的周长为20∴菱形的边长为5由勾股定理得，∴∴∴解得把分别代入不成立．试题难度：三颗星知识点：一元二次方程的根与系数的关系11.某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元．设该公司5，6两月的营业额的月平均增长率为x，根据题意列方程，则下列方程正确的是( )A.2 500(1+x)2=9 100B.2 500(1+x%)2=9 100C.2 500(1+x)+2 500(1+x)2=9100D.2 500+2 500(1+x)+2 500(1+x)2=9100答案：D解题思路：该公司4月的营业额为2500万元，5，6两月的营业额的月平均增长率为x∴5月份营业额为2500(1+x)，6月份营业额为2500(1+x)2∴第二季度的总营业额为2500+2 500(1+x)+2 500(1+x)2试题难度：三颗星知识点：实际问题与一元二次方程——增长率型12.扬帆中学有一块长30m，宽20m的矩形空地，计划在这块空地上划出四分之一的区域种花，小禹同学设计方案如图所示，求花带的宽度．设花带的宽度为xm，则可列方程为( )A. B.C. D.答案：D解题思路：由题意得，种花之后矩形空地剩下的面积为总面积的四分之三∴试题难度：三颗星知识点：实际问题与一元二次方程——面积型13.某特产店销售开心果，其进价为每千克40元，按每千克60元销售，平均每天可售出100千克．后来经过市场调查发现，单价每降低3元，平均每天的销售量可增加30千克，若该特产店销售这种开心果想要平均每天获利2240元，则每千克开心果的售价应为多少元？若设每千克开心果应降价x元，则x满足的方程为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：实际问题与一元二次方程——经济型14.天山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游，推出了如下收费标准：如果人数不超过25人，人均旅游费用为1000元；如果人数超过25人，每超过1人，人均旅游费用降低20元，但人均旅游费用不低于700元（总人数不超过40人）．某单位组织员工去具有喀斯特地貌特征的黄果树风景区旅游，共支付给旅行社旅游费用27000元，则该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游？( )A.25B.30C.35D.40答案：B解题思路：设该单位这次共有x名员工去具有喀斯特地貌特征的黄果树风景区旅游，①若，则共支付给旅行社的旅游费用为1000x元∴1000x=27000解得，与假设不符。

一元二次方程复习及测试题

第二十一章一元二次方程复习一、自主学习：1、下列方程中，关于X 的一元二次方程是（）A.23(1)2(1)x x +=+B.2112x x+= C.20ax bx c ++= D.2221x x x +=- 2、解下列方程：(1) 241x x -= (2) 222(2)4x x -=- (3)(1)(4)12x x -+=3、某小组同学，新年时每人互送贺年卡一张，已知全组共送贺年卡56张，这个小组共有（）人（A ）7 （B ）8 （C ）14 （D ）44、某辆汽车在公路上行驶，它的行驶路程s(km)和时间t(h)之间的关系式为24s t t =+.那么行驶5km 所需的时间为 h.二、归纳总结：1、一元二次方程的定义及一般形式。

2、一元二次方程的几种解法：3、用配方法、因式分解法等解一元二次方程时，要通过适当的变形先使方程转化为一元一次方程，也就是使未知数从二次变为一次，即降次。

一元二次方程的降次变形，是由一个二次方程得到两个一次方程，因此一个一元二次方程有两个根。

4、对于把实际问题转化为有关一元二次方程的问题，关键是弄清实际问题的背景，找出实际问题中相关数量之间的相等关系，并把这样的关系 “翻译”为一元二次方程。

三、课堂检测：1、方程的220x x -=解是____________________2、方程2430x x --=的解是____________________3、填上适当的数，使等式成立。

224____(____)x x x -+=-4、若x=1是一元二次方程220ax bx +-=的根，则a+b=______5、在参加足球世界杯预选赛的球队中，每两个队都要进行一次比赛，共要比赛45场，若参赛队有x 支队，则可得方程 .6、已知2是关于x 的方程的23202x a -=一个根，则21a -的值是( ) A.3 B.4 C.5 D.67、若关于的一元二次方程的两个根为121,2x x ==，则这个方程是（）A.2320x x +-=B.2320x x --=C.2320x x ++=D.2320x x -+=8、党的十六大提出全面建设小康社会，加快推进社会主义现代化建设，力争国民生产总值到2020年比2000年翻两番.在本世纪的头二十年（2001年－2020年）要实现这一目标，以十年为单位计算，设每个十年国民生产总值的增长率都是x ，那么x 满足的方程为（）（A ）2(1)2x += （B ）2(1)4x += （C ）122x += （D ）(1)2(1)4x x +++=9、解下列方程：（1）2(21)3(21)0x x +++= （2）242x x -= （3）24(5)360x --=10、某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染．请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？11、某商场销售某品牌童装，平均每天可以售出20件，每件盈利40元为了扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施，经调查发现，如果每件童装降价1元，商场平均每天多售出2件，若商场平均每天要盈利1200元每件童装应降价多少元？《一元二次方程》课堂测试题一、选择题(每小题3分，共24分)1、下列方程中，关于x 的一元二次方程是（）A.()()12132+=+x xB.02112=-+x xC.02=++c bx axD.1222-=+x x x 2、方程x x 22=的解为（）A. x ＝2B. x 1＝2-，x 2＝0 C. x 1＝2，x 2＝0 D. x ＝0 3、解方程)15(3)15(2-=-x x 的适当方法是（）A 、直接开平方法B 、配方法C 、公式法D 、因式分解法4、已知m 方程012=--x x 的一个根，则代数式m m -2的值等于（）A.—1B.0C.1D.25、用配方法解下列方程时，配方有错误的是（）A.x 2－2x －99=0化为(x －1)2=100B.x 2+8x +9=0化为(x +4)2=25C.2t 2－7t －4=0化为1681)47(2=-t D.3y 2－4y －2=0化为910)32(2=-y 6、下面是李明同学在一次测验中解答的填空题，其中答对的是（）．A.若x 2=4，则x ＝2B.方程x (2x －1)＝2x －1的解为x ＝1C.若x 2－5xy －6y 2=0（xy≠0）,则y x ＝6或y x ＝－1D.若分式1232-+-x x x 值为零，则x ＝1，2 7、用配方法解一元二次方程02=++c bx ax ，此方程可变形为（） A 、222442a ac b a b x -=⎪⎭⎫ ⎝⎛- B 、222442a b ac a b x -=⎪⎭⎫ ⎝⎛- C 、222442a ac b a b x -=⎪⎭⎫ ⎝⎛+ D 、222442a b ac a b x -=⎪⎭⎫ ⎝⎛+ 8、从正方形的铁皮上，截去2cm 宽的一条长方形，余下的面积是48cm 2，则原来的正方形铁皮的面积是（）A.9cm 2B.68cm 2C.8cm 2D.64cm 2二、填空题(每小题3分，共18分)9、把方程（2x+1）（x —2）=5－3x 整理成一般形式后，得，其中二次项系数是，一次项系数是，常数项是。

一元二次方程复习题

一元二次方程复习题一. 知识归纳1 一元二次方程概念ax 2+bx +c =0(a ≠0)2 解法①直接开平方法②配方法③公式法④因式分解法3 根的判别式⊿△=b 2-4ac4 根与系数关系1x + 2x =ab-, 1x ·2x =a c二. 填空题1方程02=x 的解为__________，方程()()040022≥-≠=++ac b a c bx ax 的解为________若关于x 的二次方程(m +1)x 2-3x +2=0有两个相等的实数根，则m =______.2设方程0432=-+x x 的两根分别为1x ，2x ，则1x + 2x =______，1x ·2x =________ =+2221x x ________, ()221x x -=________, 121213x x x x ++=___________3 若方程x 2-5x +m =0的一个根是1，则m =________4 两根之和等于－3，两根之积等于－7的最简系数的一元二次方程是________5 已知方程2x 2+(k -1)x -6=0的一个根为2，则k =_______6若关于x 的一元二次方程mx 2+3x-4=0有实数根，则m 的值为______ 7方程无实根，则 ______8如果是一个完全平方公式，则 ______。

9若方程的两根之差的绝对值是8，则 ______。

10若方程的两根之比为3，则_____。

11在实数范围内分解因式：=-52x ___ _，12-+x x =____________122--x x =______________132--x x =____________12若a ，b 为实数，且()0232=-+-+ab b a ，则以a ，b 为根的一元二次方程是_______________13以方程0122=--x x 的两根的相反数为根的一元二次方程是______________ 三. 选择题1下列方程（1）－x 2+2=0 （2）2x 2－3x =0 （3）－3x 2=0 （3）x 2+x1=0 （5）232+x ＝5x （6）2x 2－3=（x －3）（x 2+1）中是一元二次方程的有（）A 、2个B 、3个C 、4个D 、5个2下列配方正确的是（）(1) x 2+3x =（x +23）2－23 （2）x 2+2x +5=（x +1）2+4 （3）x 2－21x +43=（x －41）2+161 （4）3x 2+6x +1=3（x +1）2－23方程（x －1）2+（2x +1）2=9x 的一次项系数是（）A 、2B 、5C 、－7D 、7 4方程x 2－3x +2－m =0有实根，则m 的取值范围是（） A 、m ＞－41 B 、m ≥41 C 、m ≥－41 D 、m ＞41 5方程（m +1）x 2－（2m +2）x +3m －1=0有一个根为0，则m 的值为（） A 、32 B 、31 C 、－32 D 、－316方程()()1231=+-x x 化为02=++c bx ax 形式后，a 、b 、c 的值为（）（A ）1，–2，-15 （B ）1，-2，15（C ）-1，2，15 （D ）–1，2，–15 7方程()()02322=-+x x 的解的个数是（）（A ）1 （B ）2 （C ）3 （D ）48若方程07532=--x x 的两根为x 1，x 2，下列表示根与系数关系的等式中，正确的是（）(A)7,52121-=⋅=+x x x x （B ）37,352121=⋅-=+x x x x（C ）37,352121=⋅=+x x x x （D ）37,352121-=⋅=+x x x x9以215-和215+为根的一元二次方程是（）（A ）0152=+-x x （B ）02522=+-x x （C ）0152=++x x （D ）02522=++x x 10如果一元二次方程02=++c bx ax 的两个根是x 1，x 2，那么二次三项式c bx ax ++2分解因式的结果是（）（A ）()()212x x x x c bx ax --=++ （B ）()()212x ax x ax c bx ax --=++（C ）()()212x x x x a c bx ax ++=++ （D ）()()212x x x x a c bx ax --=++11在实数范围内，1842++x x 可以分解为（）（A ）()()3232++-+x x （B ）⎪⎪⎭⎫⎝⎛---⎪⎪⎭⎫ ⎝⎛+--232232x x （C ）()()322322++-+x x （D ）()()32232241++-+x x12已知方程()031222=+--m x m x 的两个根是互为相反数，则m 的值是（）（A ）1±=m （B ）1-=m （C ）1=m （D ）0=m13如果关于x 的方程3ax 2－23（a －1）x +a =0有实数根，则a 的取值范围是（）A 、a <21且a ≠0 B 、a ≥21 C 、a ≤21且a ≠0 D 、a ≤21 14若方程2x （kx －4）－x 2+6=0没有实数根，则k 的最小整数值是（） A 、1 B 、2 C 、3 D 、415一元二次方程一根比另一根大8，且两根之和为6，那么这个方程是（）A 、x 2－6x －7=0B 、x 2－6x +7=0C 、x 2+6x －7=0D 、x 2+6x +7=016已知方程07822=+-x x 的两根恰好是一个直角三角形的两条直角边的长，则这个直角三角形的斜边的长是（）（A ）9（B ）6 （C ）3（D ）317若一元二次方程02=++q px x 的两根之比为3∶2，则q p ,满足的关系式是（）（A ）q p 2532= （B ）q p 2562= （C ）q p 3252= (D) q p 6252= 18方程x 2-2x-m=0有两个正实根，则m 的取值范围是（） A 、0<m<1 B 、m>0 C 、－１≤m ＜０Ｄ、m ＜－１ 19一元二次方程ax 2+bx+c=0（a ≠0）的两根之和为m ，两根平方和为n ，则c bm an ++2121 的值为（）A 、0B 、22n m + C 、2m D 、2n 20已知关于x 的一元二次方程032=+-m x x 的两根21x x 、满足161112221=+x x ，则m 的值为（）A 、4B 、－36C 、4或－36D 、－36或－421若一元二次方程的两根21x x 、满足下列关系：=+++22121x x x x 0,05222121=+--x x x x ，则这个一元二次方程（）A 、032=++x x B 、032=--x x C 、032=+-x x D 、032=-+x x 四. 解方程1、04)221(2=-+x 2、0662=++x x3、06)32(5)32(2=+---x x4、22)3(4)23(-=+x x 5、06122=+-x x6、34124)3(2-+=-x x五. 在实数范围内分解因式 1、592-x2、3742--x x3、22582y xy x +-六. 解答题1已知方程0132=--x x 的两个根是21,x x ，求代数式（1）()()1121--x x ；（2）111221+++x xx x 的值。

一元二次方程单元复习

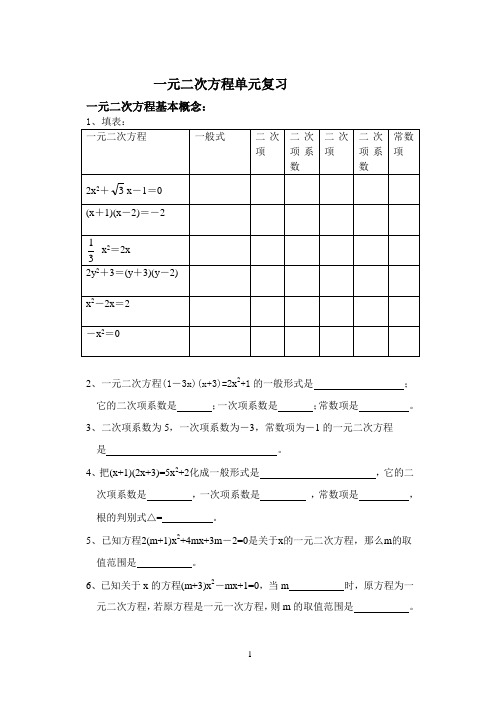
一元二次方程单元复习一元二次方程基本概念：1、填表：2、一元二次方程(1－3x)(x+3)=2x2+1的一般形式是；它的二次项系数是；一次项系数是；常数项是。

3、二次项系数为5，一次项系数为－3，常数项为－1的一元二次方程是。

4、把(x+1)(2x+3)=5x2+2化成一般形式是，它的二次项系数是，一次项系数是，常数项是，根的判别式△= 。

5、已知方程2(m+1)x2+4mx+3m－2=0是关于x的一元二次方程，那么m的取值范围是。

6、已知关于x的方程(m+3)x2－mx+1=0，当m 时，原方程为一元二次方程，若原方程是一元一次方程，则m的取值范围是。

7、把方程a(x 2+x)+b(x 2－x)=1－c 写成关于x 的一元二次方程的一般形式是，它的二次项系数是、它是一元二次方程的条件是。

一次项系数是，常数项是。

8、已知关于x 的一元二次方程(2m －1)x 2+3mx+5=0有一根是x=－1，则m= 。

9、已知关于x 的方程(2k+1)x 2－4kx+(k －1)=0，问：(1)k 为时，此方程是一元一次方程；此时方程的根为； (2)k 为时，此方程是一元二次方程；此时一元二次方程的二次项系数是，一次项系数是，常数项为。

10、当k 时，关于x 的方程(k+1)x 2+(2k －1)x+3=0是一元二次方程。

11、方程2x 2=8的实数根是。

12、方程4(x －3)2=36的实数根是。

13、方程(x 2－4)(x+3)=0的解是。

解方程：14、240x -=； 15、2410y -=；16、m 2－3m －4＝0； 17、2690x x -+=；18、24210y y --=； 19、220n n --=；20、2122030x x -+=； 21、22320x x --=；22、(2)(1)70x x +-=； 23、224(21)9(4)x x -=+；24、(2x ＋1)2－3＝2(2x ＋1)； 25、(1－x) 2＝1－x 2；26、()()323212x x -+= 27、24120x x --=28、26730x x +-= 29、22510x x +-=30、方程53x 0.22-的解是。

《一元二次方程》全章复习

《一元二次方程》全章复习1．一元二次方程的有关概念2．配方法的应用3．根判别式，根与系数的关系4．一元二次方程的解法：1）直接开平方法 2)因式分解法 3）配方法 4）公式法5．实际问题：1）传播与数字问题 2）增长率与销售问题 3）有关面积的问题【巩固练习】1.下列方程是一元二次方程的是（） A.211x x x-=+ B.224x xy y -+= C.20ax bx c +=+ D.(x 1)1x x -=- 2.在一元二次方程2410x x --=中，二次项系数和一次项系数分别为（）A.1，4B.1，-4C.-1，-4D.2,4x x -3.在一元二次方程260x kx --=中，已知一个根为3x =，则实数k 的值为（）A.1B.-1C.2D.-24.关于x 的一元二次方程22(a 1)10x x a -++-=的一个根是0，则a 的值为（）A.1B.-1C.1或-1D.12 5.若关于x 的一元二次方程220x x m -+=没有实数根，则实数m 的取值范围是（）A.m <1B.m > -1C.m < -1D.m > 16. 若关于x 的方程2(m 1)02x m mx +-+=有两个不等的实数根，则m 的取值范围是7. 已知2410x x a +=-可变为2(2)x b -的形式，则ab=8. 若关于x 的方程2(2)10x x m m +++=-有两个相等的实数根，则m=9.已知一个矩形长比宽多2cm ，其面积为82cm ，则此长方形的周长是10. 若方程2310x x b +=+无解，则b 应满足的条件是11. 若关于x 的方程22(21)20k x x k -+-+=+有实数根，则k 的取值范围是 12. 若分式2817x x x -+-的值为0，则x= 13. 关于x 的方程22202x x a b a +-=+的根是14. 若关于x 的方程260x x k +=+的两根之差为2，则k=15. 已知关于x 的方程22(31)0x x m m --+=有两根为12,x x ，且121134x x +=-，则m= 16.用恰当的方法解下列方程：（1）21(3)13x += （2）2(21)2(2x 1)x +=+（3）(x 8)16x += （4）2280x x +-=（5）22(32)(2x 1)x +=- （5）2(21)4(21)40y y +-++=17.已知,αβ是方程2250x x +-=的两个实数根，求22ααβα++的值18.已知12,x x 是方程2214160x x +-=的两个实数根，求下列代数式的值，（1）212()x x - （2）2112x x x x + （3）12(2)(2)x x -- （4）12x x -19.已知关于x 的方程222(a 1)740x x a a +-+--=的两根为12,x x ，且满足12123340x x x x --+=，求a 的值20.实数k 在什么范围取值时，方程22(k 1)0kx kx -+-=有两个正的实数根21.若关于x 的方程2430x x k -+-=的两根为12,x x ，且满足123x x =，试求出方程的两个实数根及k 的值23.若n > 0，关于x 的方程21(m 2n)04x x mn --+=有两个相等的正的实数根，求m n24.如果2246130x x y y -++=，求(xy)z25.水果店花500元进了一批水果，按40%的利润定价，无人购买．决定打折出售，但仍无人购买，结果又一次打折后才售完．经结算，这批水果共盈利67元．若两次打折相同，每次打了几折？26.如图，在△ABC中，AB=10m，BC= 40m，∠C=90°，点P从点A开始沿AC边向点C以2m/s的速度匀速移动，同时另一点Q由C点开始以3m/s的速度沿着CB匀速移动，几秒时，△PCQ的面积等于450m2?25.某汽车销售公司6月份销售某厂家的汽车，在一定范围内，每部汽车的进价与销售量有如下关系：若当月仅售出1部汽车，则该部汽车的进价为27万元，每多售出1部，所有售出的汽车的进价均降低0.1万元/部，月底厂家根据销售量一次性返利给销售公司，销售量在10部以内（含10部），每部返利0.5万元；销售量在10部以上，每部返利1万元．（1）若该公司当月售出3部汽车，则每部汽车的进价为_________ 万元；（2）如果汽车的售价为28万元/部，该公司计划当月盈利12万元，那么需要售出多少部汽车？（盈利=销售利润+返利）。

一元二次方程小结与复习

∴x1=3
33 x 2
x2=0
返回
用配方法解方程。
①x2-2x-3=0 解:x2-2x=3 ②3x2-2x-5=0 解: 3x2-2x=5
2 3 2 2x 3 5 x= 3 1 5 1 2= +( )2 x+( 3 ) 3 3 1 16 2= (x- 3 ) 9 1 4 x- 3 =± 3 1 4 x= 3± 3 5
返回
知识回顾
二、一元二次方程的解法
1. 一元二次方程的解.
满足方程，有根就是两个 2.一元二次方程的几种解法 (1)直接开平方法(2)因式分解法 (3) 配方法 (4)公式法
二、一元二次方程的解法
1、直接开平方法。（x+m）2=n（n≥ 0）
练习
2、配方法。 ①化——将二次项系数化为1。 ②移——将常数项移到方程的右边。 ③配——在方程两边同时加上一次项系数一半的平
方，使原方程变为（x+m）2=n （n≥ 0）
的形式。 ④开——用直接开平方法解出方程。
练习
解下列方程。
x2=3 解：x=± 3 (x+1)2=5 解：x+1=± 5 x=-1± 5 (2x-3)2=9 解：2x-3=±3 2x=3±3
∴x1= 3
x2=- 3
∴ x1=-1+ 5
x2=-1- 5
数字问题
1、若一个三位数的个位数字是a，十位数字是b，百位数字是c，则这个三位数可表示为 100c+10b+a 。
2.有一个两位数,它的十位数字与个位数字的和是5.把这个两位数的十位数字与个位数字互换后得到另一个两位数,两个两位数的积为763.求原来的两位数.
解 : 设这个两位数的个位数字为x, 根据题意, 得

一元二次方程单元复习练习(Word版含答案)

由（1）知，点A，B分别在反比例函数（x＜0），（x＞0）的图象上，
∴S△ACO＝ × ＝1 ，S△ODB＝ ×3＝．∵∠AOB＝90°，
∴∠AOC＋∠BOD＝90°，∵∠AOC＋∠OAC＝90°，∴∠OAC＝∠BOD．
又∵∠ACO＝∠ODB＝90°，∴△ACO∽△ODB．
∴ ＝＝，∴ ＝± （舍负取正），即＝．
（2）①利用润滑用油量每减少1kg，用油的重复利用率将增加1.6%，进而求出答案；
②首先表示出用油的重复利用率，进而利用乙车间技术革新后实际耗油量下降到12kg，得出等式求出答案．
试题解析：（1）根据题意可得：70×（1﹣60%）=28（kg）；
（2）①60%+1.6%（90﹣80）=76%；
②设润滑用油量是x千克，则
∴在Rt△AOB中，tan∠OBA＝＝．
4．已知关于x的一元二次方程有两个实数根．
求k的取值范围；
设方程两实数根分别为，，且满足，求k的值．
【答案】（1）；（2）．
【解析】
【分析】
根据方程有实数根得出，解之可得．
利用根与系数的关系可用k表示出和的值，根据条件可得到关于k的方程，可求得k的值，注意利用根的判别式进行取舍．
2009年底汽车数量为14.4×90%+y，
2010年底汽车数量为（14.4×90%+y）×90%+y，
∴（14.4×90%+y）×90%+y≤15.464，
∴y≤2．
答：每年新增汽车数量最多不超过2万辆．
考点：一元二次方程—增长率的问题
2．机械加工需用油进行润滑以减小摩擦，某企业加工一台设备润滑用油量为90kg，用油的重复利用率为60%，按此计算，加工一台设备的实际耗油量为36kg，为了倡导低碳，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际油耗量进行攻关．

一元二次方程单元复习

一元二次方程专题复习

一元二次方程全章复习讲义

一元二次方程复习知识点梳理

一元二次方程复习课(绝对经典)

10.《一元二次方程》全章复习与巩固—知识讲解(基础)

一元二次方程全章复习与巩固—知识讲解

人教版九年级数学-一元二次方程全章知识点专题复习(含答案)

《一元二次方程》单元测试题及答案

《一元二次方程》全章复习与巩固—知识讲解

一元二次方程单元复习(一)(含答案)

一元二次方程复习及测试题

一元二次方程复习题

一元二次方程单元复习

《一元二次方程》全章复习

一元二次方程小结与复习

一元二次方程单元复习练习(Word版 含答案)

一元二次方程单元复习练习(Word版含答案)