SVM Guide
svm训练参数

svm训练参数
在使用支持向量机(SVM)进行训练时,有一些重要的参数需要
选择。
以下是一些常见的SVM训练参数:
1. C参数(惩罚参数):控制了决策边界的平滑度。
较小的C值将产生较大的决策边界间隔,较大的C值将产生更小的决策边界间隔。
选择C的值取决于数据集的特征。
2. 核函数:SVM可以使用不同的核函数来进行非线性分类。
常见的核函数包括线性核函数、多项式核函数和径向基函数(RBF)核函数。
选择适当的核函数取决于数据集的特性。
3. gamma参数(RBF核函数特有):控制了决策边界的曲率。
较
高的gamma值将产生更复杂的决策边界,较低的gamma值将产生更简
单的决策边界。
4. degree参数(多项式核函数特有):控制了多项式核函数的
阶数。
较高的阶数可以使决策边界更复杂,但可能导致过拟合。
5. coef0参数(多项式和sigmoid核函数特有):控制了多项式核函数和sigmoid核函数的影响。
较大的coef0值将产生更复杂的决
策边界。
这些参数的选择通常需要通过交叉验证等方法来进行调整,以获
得最佳分类性能。
大数据十大经典算法SVM-讲解PPT

contents
目录
• 引言 • SVM基本原理 • SVM模型构建与优化 • SVM在大数据处理中的应用 • SVM算法实现与编程实践 • SVM算法性能评估与改进 • 总结与展望
01 引言
算法概述
SVM(Support Vector Machine,支持向量机)是一种监督学习模型,用于数据 分类和回归分析。
性能评估方法
01
准确率评估
通过计算模型在测试集上的准确率来评估SVM算法的性能,准确率越
高,说明模型分类效果越好。
02
混淆矩阵评估
通过构建混淆矩阵,可以计算出精确率、召回率、F1值等指标,更全面
地评估SVM算法的性能。
03
ROC曲线和AUC值评估
通过绘制ROC曲线并计算AUC值,可以评估SVM算法在不同阈值下的
核函数是SVM的重要组成部分 ,可将数据映射到更高维的空 间,使得原本线性不可分的数 据变得线性可分。常见的核函 数有线性核、多项式核、高斯 核等。
SVM的性能受参数影响较大, 如惩罚因子C、核函数参数等 。通过交叉验证、网格搜索等 方法可实现SVM参数的自动调 优,提高模型性能。
SVM在文本分类、图像识别、 生物信息学等领域有广泛应用 。通过具体案例,可深入了解 SVM的实际应用效果。
SVM算法实现步骤
模型选择
选择合适的SVM模型,如CSVM、ν-SVM或One-class SVM等。
模型训练
使用准备好的数据集对SVM模 型进行训练,得到支持向量和 决策边界。
数据准备
准备用于训练的数据集,包括 特征提取和标签分配。
参数设置
设置SVM模型的参数,如惩罚 系数C、核函数类型及其参数 等。
《支持向量机SVM》课件

多分类SVM
总结词
多类分类支持向量机可以使用不同的核函数和策略来解决多 类分类问题。
详细描述
多类分类支持向量机可以使用不同的核函数和策略来解决多 类分类问题。常用的核函数有线性核、多项式核和RBF核等 。此外,一些集成学习技术也可以与多类分类SVM结合使用 ,以提高分类性能和鲁棒性。
03
SVM的训练与优化
细描述
对于非线性数据,线性不可分SVM通 过引入核函数来解决分类问题。核函 数可以将数据映射到更高维空间,使 得数据在更高维空间中线性可分。常 用的核函数有线性核、多项式核和径 向基函数(RBF)。
通过调整惩罚参数C和核函数参数, 可以控制模型的复杂度和过拟合程度 。
详细描述
多分类支持向量机可以通过两种策略进行扩展:一对一(OAO)和一对多(OAA)。 在OAO策略中,对于n个类别的多分类问题,需要构建n(n-1)/2个二分类器,每个二分 类器处理两个类别的分类问题。在OAA策略中,对于n个类别的多分类问题,需要构建
n个二分类器,每个二分类器处理一个类别与剩余类别之间的分类问题。
鲁棒性高
SVM对噪声和异常值具有 一定的鲁棒性,这使得它 在许多实际应用中表现良 好。
SVM的缺点
计算复杂度高
对于大规模数据集,SVM的训练时间可能会很长,因为其需要解决一 个二次规划问题。
对参数敏感
SVM的性能对参数的选择非常敏感,例如惩罚因子和核函数参数等, 需要仔细调整。
对非线性问题处理有限
SVM的优点
分类效果好
SVM在许多分类任务中表 现出了优秀的性能,尤其 在处理高维数据和解决非 线性问题上。
对异常值不敏感
SVM在训练过程中会寻找 一个最优超平面,使得该 平面的两侧的类别距离最 大化,这使得SVM对异常 值的影响较小。
FANUC伺服调整教材

①设定1902#0#1=0
#7 1902 #6 #5 #4 #3 #2 #1 ASE #0 FMD
#1:ASE
#0:FMD
FSSB的设定方式为自动设定方式时 0:自动设定未完成。 1:自动设定已经完成。 0:FSSB的设定方式为自动方式。 1:FSSB的设定方式为手动方式。
14
BEIJING-FANUC
2020
2001 1820 2084/2085 2022 2023 2024 1821
18
BEIJING-FANUC
第一章 伺服电机规格及初始化
1、初始化设定位
设定初始化设定位
#7 初始化 设定位 #1:DGP 0:进行伺服参数的初始设定。 1:结束伺服参数的初始设定。 #6 #5 #4 #3 #2 #1 DGP #0
3
BEIJING-FANUC
目录
四、自动增益调整
五、加工条件选择功能 第四章:SERVO GUIDE软件的使用及调试方法 一、Servo Guide软件介绍 二、Servo Guide连接 三、 Servo Guide调整步骤 第五章:伺服调整实例分析 一、工件表面光洁度调整案例
16
BEIJING-FANUC
第一章 伺服电机规格及初始化
四、伺服初始化
伺服初始化是在完成了FSSB连接与设定的基础上进行电机的一转移动量以 及电机种类的设定。伺服电机必须经过初始化相关参数正确设定后才能够 正常运行。
设定参数3111后,伺服设定画面能够显示。
第一章 伺服电机规格及初始化
②按伺服电机连接顺序设定参数1023的值。 1023 伺服轴号
设定控制轴为放大器连接的第几个伺服轴,通常控制轴号与伺服轴号设定 相同。
SVM支持向量机PPT

增量学习与在线学习
增量学习是指模型能够随着新数据的不断加入而进行自我更 新和调整的能力。在线学习则是增量学习的一种特殊形式, 它允许模型在实时数据流上进行学习和更新。
随着大数据时代的到来,增量学习和在线学习在许多领域中 变得越来越重要。未来的SVM研究将更加注重增量学习和在 线学习方面的研究,以提高SVM在处理大规模、高维数据集 时的效率和准确性。
SVM
如前所述,SVM通过找到能够将不同类别的数据点最大化分隔的决策边界来实现分类。 SVM具有较弱的表示能力和学习能力,但具有较好的泛化能力。
比较
神经网络和SVM在分类问题上有不同的优势和局限性。神经网络适合处理复杂和高度非 线性问题,而SVM在处理大规模和线性可分数据集时表现更佳。选择哪种算法取决于具 体问题和数据特性。
与贝叶斯分类器比较
贝叶斯分类器
贝叶斯分类器是一种基于概率的分类方法。它通过计算每个类别的概率来对新的输入数据进行分类。贝叶斯分类器具 有简单和高效的特点,但需要较大的训练样本。
SVM
如前所述,SVM通过找到能够将不同类别的数据点最大化分隔的决策边界来实现分类。SVM具有较好的泛化能力和 处理大规模数据集的能力,但计算复杂度较高。
svm支持向量机
contents
目录
• SVM基本概念 • SVM分类器 • SVM优化问题 • SVM应用领域 • SVM与其他机器学习算法的比较 • SVM未来发展方向
01 SVM基本概念
定义
定义
SVM(Support Vector Machine) 是一种监督学习模型,用于分类和 回归分析。
FANUC系统调试作业指导书
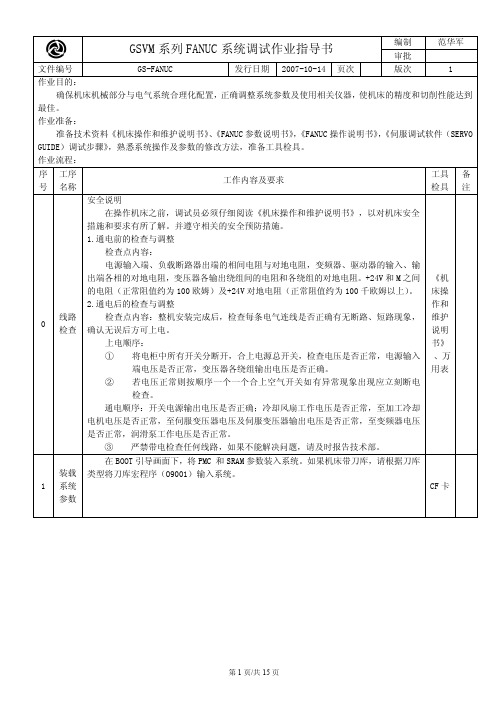
K1.2 K2.0 K2.1
润滑泵使 能
10 把刀库
K1.2=0 润滑泵受系统控制 K1.2=1 润滑泵不受系统控制 K2.0=1(K0.7=K2.1=K2.2=K2.3=0) 斗笠式刀库 D0=10 K2.0=K0.7=1(K2.1=K2.2=K2.3=0)圆盘式刀库 C2=10
16 把刀库
K2.1=1(K0.7=K2.0=K2.2=K2.3=0)斗笠式刀库 D0=16 K2.1=K0.7=1(K2.0=K2.2=K2.3=0)圆盘式刀库 C2=16
地址
Y2.0 Y2.1 Y2.2 Y2.3 Y2.4 Y2.5 Y2.6 Y2.7 Y3.0 Y3.1 Y3.2 Y3.3 Y3.4 Y3.5 Y3.6 Y3.7 Y5.3
电机电压是否正常,至伺服变压器电压及伺服变压器输出电压是否正常,至变频器电压
是否正常,润滑泵工作电压是否正常。
③ 严禁带电检查任何线路,如果不能解决问题,请及时报告技术部。
在 BOOT 引导画面下,将 PMC 和 SRAM 参数装入系统。如果机床带刀库,请根据刀库
装载 类型将刀库宏程序(O9001)输入系统。
书》
4. 检查工作灯、报警灯、就绪灯、排屑器、冷却泵、润滑泵、松刀按钮、刀库马达、 《 发
刀臂马达,要求动作正确。 机床 5. 对 RS232 通讯接口进行试验,要求通讯可靠。 8 功能 6. 对机床的润滑、冷却油路进行检查,要求密封可靠,冷却充分, 检查 7. 润滑良好,油路系统不得有渗漏现象。
那科 参数 说明 书》
4020/4133
1320/1321
1420
主轴转速3744/4020
GSVM5030 258/258/258 500/300/300 6000
svm向量机的使用流程

SVM向量机的使用流程1. 简介SVM(Support Vector Machine,支持向量机)是一种常用的机器学习算法,广泛应用于分类和回归问题。
它基于统计学习理论中的结构风险最小化原则,在数据平面上构建出一个最优的超平面,用于分类不同类别的样本数据。
2. 基本原理SVM基于以下两个关键概念:2.1 最大间隔分类器SVM试图寻找一个超平面,使得不同类别的样本点能够被它们之间的最大间隔所分开。
这样的超平面称为最大间隔分类器。
2.2 支持向量支持向量是距离最大间隔分类器最近的样本点,它们对于定义超平面和分类决策起到关键的作用。
3. 使用流程SVM的使用流程主要包括以下几个步骤:3.1 数据准备首先,需要准备用于训练和测试的数据。
数据应该包含已知类别的样本点,并且每个样本点都应该由一些特征组成。
3.2 数据预处理在使用SVM之前,需要对数据进行预处理。
这包括特征选择、特征缩放和数据标准化等步骤,以确保数据的质量和一致性。
3.3 模型训练使用训练集来训练SVM模型。
在训练过程中,SVM将根据具体的核函数和超参数来寻找最优的超平面。
使用测试集对训练完成的SVM模型进行评估。
常用的评估指标包括准确率、精确率、召回率和F1值等。
3.5 模型优化根据评估结果,可以调整SVM模型的超参数,以优化模型的性能。
常见的超参数包括核函数类型、正则化系数等。
3.6 模型应用训练完成并优化的SVM模型可以用于预测新样本的类别。
通过输入新样本的特征,SVM将输出预测的类别。
4. 实例演示下面以一个简单的二分类问题为例,演示SVM的使用流程:4.1 数据准备准备一个包含两个类别的样本数据集,每个类别有若干个样本点。
每个样本点都有一些特征,比如身高、体重等。
4.2 数据预处理对数据进行特征选择,保留与分类相关性较高的特征。
然后,进行特征缩放和数据标准化,以确保不同特征的量纲一致。
4.3 模型训练使用训练集对SVM模型进行训练。
svm基本结构

支持向量机(SVM)是一种广泛使用的监督学习算法,主要用于分类任务。
SVM的基本结构可以分为以下几个核心部分:1. 数据集:SVM算法输入的是一个包含多个样本的数据集,每个样本由一组特征和一个标签组成。
2. 特征空间:SVM的第一步是将原始数据映射到一个更高维度的特征空间。
这样做通常是为了找到一个合适的分离超平面,该超平面能够最好地分隔不同的类别。
3. 支持向量:在特征空间中,最靠近分离超平面的训练样本点被称为支持向量。
这些点是决定超平面位置的关键因素。
4. 分离超平面:SVM的目标是找到一个超平面,它能够最大化两个类别之间的间隔(即支持向量之间的距离)。
5. 软间隔:在实际应用中,可能存在一些难以精确分类的样本。
为了提高模型的泛化能力,SVM允许存在一些违反分类规则的样本,即引入软间隔的概念,允许一定的误分类。
6. 最优边界:除了寻找一个合适的分离超平面之外,SVM也致力于使离群点(即那些距离超平面最近的点)尽可能远离决策边界。
7. 核函数:当数据不是线性可分的时候,SVM通过使用核技巧将数据映射到更高维的空间,使之变得线性可分。
常用的核函数包括线性核、多项式核、径向基函数(RBF)核和sigmoid 核。
8. 正则化:为了避免过拟合,SVM可以通过引入正则化项来控制模型的复杂度。
常见的正则化技术包括L1正则化和L2正则化。
9. 优化问题:SVM的目标函数可以通过拉格朗日乘子法转换成一个凸优化问题,该问题可以通过各种优化算法求解,例如序列最小优化(SMO)算法。
SVM的结构和原理使得它非常适合处理中小规模的数据集,并且在许多实际应用中取得了很好的性能。
然而,当面对非常大的数据集时,SVM可能会遇到计算效率和存储效率的问题。
机器学习算法掌握SVM分类器的关键步骤

机器学习算法掌握SVM分类器的关键步骤机器学习算法中,支持向量机(Support Vector Machine, SVM)是一种被广泛应用于分类和回归问题的方法。
它通过在特征空间中找到一个最优超平面来实现数据的划分。
本文将介绍掌握SVM分类器的关键步骤,帮助读者更好地理解和应用这个算法。
一、数据预处理在应用SVM分类器之前,需要对数据进行预处理。
这包括如下几个方面的步骤:1. 数据收集:收集与问题相关的数据,并将其整理为合适的格式,如矩阵或数据框。
2. 数据清洗:对数据进行清洗,处理缺失值、异常值等问题,确保数据的质量和可靠性。
3. 特征选择:根据问题的需求,选择与目标变量相关性高的特征,剔除对模型无意义或冗余的特征。
4. 特征缩放:对于特征值的范围差异较大的情况,使用特征缩放方法(如标准化或归一化)将其缩放到相同的范围内,以避免某些特征对模型训练的影响过大。
二、选择合适的SVM核函数SVM分类器的核心思想是通过一个超平面将数据划分为不同的类别。
在选择合适的核函数时,需要考虑问题的性质以及数据的分布情况。
1. 线性核函数:适用于线性可分的问题,即数据可以完全被一个超平面分割开。
2. 多项式核函数:适用于非线性问题,通过将数据映射到更高维的特征空间,将问题转化为线性可分的问题。
3. 高斯核函数(径向基函数):适用于非线性问题,可以处理数据在低维空间中呈现复杂结构的情况。
4. Sigmoid核函数:适用于二分类问题,但在一般情况下效果相对较差。
根据问题的特点选择合适的核函数,能够有效提高SVM分类器的性能。
三、模型训练与参数调优1. 模型训练:使用训练数据集对SVM分类器进行训练。
通过求解优化问题,找到能够使分隔超平面与不同类别的样本点之间的间隔最大化的超平面。
2. 超参数调优:SVM分类器中存在一些关键的超参数,如正则化参数C、核函数的参数等。
通过交叉验证等方法,寻找最优的超参数组合,以提高模型的泛化能力和分类性能。
多分类SVM分类器优化技巧

多分类SVM分类器优化技巧支持向量机(Support Vector Machine,SVM)是一种高效的分类算法,一般应用于二分类问题。
然而,在现实生活中,我们常常遇到需要将样本分为多个类别的问题。
这时就需要使用多分类SVM分类器。
本文将介绍一些优化技巧,以提高多分类SVM分类器的性能。
1. One-vs-All 方法One-vs-All 方法是一种简单有效的方法,用于将多分类问题转化为二分类问题。
该方法的思路是,对于有 k 个类别的问题,构造 k 个二分类学习器,每次将其中一个类别作为正例,剩余的 k-1 个类别作为负例。
训练完成后,对于一个待分类的样本,将其输入到 k 个分类器中,选择分类器输出中置信度最高的类别作为预测类别。
One-vs-All 方法的优点是简单易理解,但是分类器的数量较多,对于大规模数据集计算量较大。
2. One-vs-One 方法One-vs-One 方法是一种常用的多分类方法。
与 One-vs-All 方法不同,它的思路是通过构造 k(k-1)/2 个二分类学习器,每次仅将两个类别之间的样本作为正负例进行训练。
训练完成后,对于一个待分类的样本,将其输入到 k(k-1)/2 个分类器中,统计每个类别在分类器输出中的数量,选择具有最大数量的类别作为预测类别。
One-vs-One 方法相对于 One-vs-All 方法计算量较小,但是需要训练大量的分类器,对于数据集较大的问题,计算量依然非常大。
3. 多类核函数多类核函数是一种直接将多个类别映射到一个高维空间的方式。
通过在高维空间中构造一个多类别核函数,可以将多分类问题转化为在高维空间中的二分类问题。
多类核函数的优点是计算量小,但是需要对核函数进行特殊设计,使得其能够处理多类别问题。
4. 类别平衡技巧有时候,样本分布可能不均衡,导致分类器对样本量较多的类别预测结果较为准确,而对样本量较少的类别预测结果误差较大。
这时候,需要使用类别平衡技巧来解决这个问题。
SVM原理简介

SVM原理简介SVM是我在做模式识别的时候⽤得最多的⼀种分类器。
以下是我通过学习后对SVM原理的理解与总结,记录下来以便⾃⼰复习。
1、SVM原理概述SVM是从线性可分情况下的最优分类⾯发展⽽来的,图⼀中三⾓形点和圆形点分别代表两类样本,假设:,i=1,...,n,我们要寻找⼀个分类超平⾯H:,使得:假设分别为过各类中离分类超平⾯最近的样本并且平⾏于分类超平⾯的超平⾯,它们之间的距离叫做分类间隔。
最优分类超平⾯要求不但能把两类样本正确分开,⽽且要求分类间隔最⼤。
易知分类间隔为2/||W||,使分类间隔最⼤,等价于与使||W||最⼩。
所以求最优分类超平⾯求解下例问题:H1,H2上的训练样本点就称作⽀持向量。
图⼀利⽤Lagrange优化⽅法可以把上述最优分类⾯问题转化为其对偶问题:其中αi为与每个样本对应的Lagrange乘⼦,容易证明解中有⼀部分(通常是少部分),若αi不为零,对应的样本就是⽀持向量。
解上述问题后得到的最优分类函数是:在线性不可分的情况下,可以增加⼀个松弛项,使求解最优分类超平⾯变为下述问题:即折衷考虑最少分错样本与最⼤分类间隔,得到⼴义最优分类超平⾯,其中C为惩罚系数。
对应的对偶问题变为:对于⾮线性问题,可以通过⾮线性变换转化为某个⾼维空间中的线性问题,在变换空间求解最优分类⾯。
在最优分类⾯中采⽤适当的内积函数K(x i,x j)就可以实现某⼀⾮线性变换后的线性分类:分类函数变为:这就是⽀持向量机。
总结起来,SVM的基本思想如图⼆所⽰:图⼆2、核函数⽬前研究最多的核函数主要有四类:通常来讲,RBF核函数可以作为⼀个SVM模型的最佳选择。
RBF核通过⾮线性映射将样本映射到⼀个⾼维空间中,因此,相较于线性核函数,它能很好地处理类别标签与属性之间为⾮线性关系的情况。
⽽且,线性核可以看做RBF核的⼀种特殊情况,在某些参数下,线性核具有与RBF核相同的表现。
另外,研究显⽰sigmoid核在某些参数下也与RBF核具有相同表现。
FANUC伺服调整教材

ai 系列
SV: 伺服模块 SP: 主轴模块 PS: 电源模块
AC 主轴电机
iI 系列
7
BEIJING-FANUC
第一章 伺服电机规格及初始化
高速、高输出、高可靠性 最适合工作机械 注塑成型机、电动冲压机 部分型号列表
30i-A
由参数983 复合型机床 设定机床类型
6
ai
αi系列
BEIJING-FANUC
第一章 伺服电机规格及初始化
二、各类伺服放大器规格和电机的特性
1、ai系列
最高驱动性能、高可靠性的伺服、主轴系统 适用于所有的工作机械 输出功率范围宽、转速范围大
FANUC 系列 0i -D 30i /31i /32i
2020
2001 1820 2084/2085 2022 2023 2024 1821
18
BEIJING-FANUC
第一章 伺服电机规格及初始化
1、初始化设定位
设定初始化设定位
#7 初始化 设定位 #1:DGP 0:进行伺服参数的初始设定。 1:结束伺服参数的初始设定。 #6 #5 #4 #3 #2 #1 DGP #0
第一章 伺服电机规格及初始化
②按伺服电机连接顺序设定参数1023的值。 1023 伺服轴号
设定控制轴为放大器连接的第几个伺服轴,通常控制轴号与伺服轴号设定 相同。
SVM
SVM
SVM
轴 X Y Z B
C B
1020 88 89 90 66 67
1022 1 2 3 0 0
①设定1902#0#1=0
#7 1902 #6 #5 #4 #3 #2 #1 ASE #0 FMD
svm概念

svm概念SVM概念简述什么是SVM•SVM是支持向量机(Support Vector Machine)的缩写。
•是一种广泛应用于分类和回归问题中的监督学习模型。
SVM原理•SVM的基本原理是寻找一个超平面,使得将训练样本划分到不同的类别时,间隔最大化。
•超平面将分类问题转化为一个凸优化的问题。
•SVM通过使用核函数实现非线性分类。
SVM相关概念支持向量•在SVM中,支持向量是距离超平面最近的样本点。
•支持向量决定了超平面的位置和边界。
分离超平面•SVM寻找一个超平面,将不同类别的样本完全分离。
•超平面是n维空间中的一个(n-1)维子空间。
间隔•间隔指的是离超平面最近的样本点到超平面的距离。
•SVM通过最大化间隔来提高分类器的鲁棒性。
核函数•核函数是一种将输入从原始特征空间映射到高维特征空间的函数。
•通过使用核函数,可以在低维度下实现高维度的分类。
软间隔与松弛因子•在现实情况下,数据往往是线性不可分的。
•为了解决这个问题,SVM引入了软间隔和松弛因子的概念,允许一些样本点位于超平面错误的一侧。
SVM应用领域•机器学习中常用的分类算法之一,适用于多种领域。
•在图像分类、文本分类、生物信息学等领域有广泛应用。
•具有较强的鲁棒性和预测能力。
以上是对SVM概念及其相关内容的简要概述,SVM作为一种重要的分类算法,在实际应用中展现了出色的性能和效果。
SVM优点•SVM具有较强的鲁棒性,对于噪声和异常点有较好的处理能力。
•在高维空间中可以有效地处理线性不可分的问题。
•可以通过选择不同的核函数应用于非线性分类问题。
•可以通过调整软间隔和松弛因子来平衡分类的精确性和泛化能力。
SVM缺点•SVM对大规模数据集的训练效率较低。
•对于非线性问题,选择合适的核函数和调整相关参数需要一定的经验和尝试。
•SVM对输入数据的缩放较为敏感。
SVM算法步骤1.收集训练数据集,并对数据进行预处理,如数据清洗、缩放等。
2.选择合适的核函数,并确定相关参数。
如何使用SVM算法优化推荐系统

如何使用SVM算法优化推荐系统推荐系统是一种非常威力的工具,在我们日常生活中广泛应用。
从购物网站到数字音乐媒体,推荐系统不仅可以大大促进用户的购买和使用体验,而且还可以帮助企业做出更为精准的决策。
近年来,支持向量机(Support Vector Machine,SVM)算法在推荐系统中的应用日益广泛,并且效果显著。
本文将会介绍什么是推荐系统以及什么是SVM算法,之后探讨如何使用SVM算法优化推荐系统。
推荐系统是什么?推荐系统是指在Internet信息服务中,通过历史用户行为数据和其他相关信息来预测用户可能感兴趣的商品或服务的一种信息过滤系统。
推荐系统的基本作用是预测用户可能感兴趣的商品或服务,并将它们提供给用户。
推荐系统的核心是推荐算法,推荐算法是通过对用户历史行为数据的分析、挖掘及机器学习来实现的,推荐系统最广泛的应用是在网络购物网站,比如大家熟知的淘宝、京东等电商平台。
什么是SVM算法?支持向量机(Support Vector Machine,SVM)又称为支持向量网络,是一种非常流行的监督学习算法,它可以用于分类、回归和异常检测。
SVM算法基于最大间隔分离超平面来进行分类,通过求解二次规划问题来找到最优超平面。
SVM算法的优点是:能够有效地处理高维数据,具有良好的泛化性能,不受数据特征空间的限制。
SVM算法的缺点是:对于大规模训练数据的运算量比较大,可能会受到噪声数据的影响。
如何使用SVM算法优化推荐系统?在推荐系统中,使用SVM算法可以通过以下步骤来实现:1. 数据预处理数据预处理是指在训练模型之前的数据预处理过程,主要包括数据清洗、数据集成、数据转换、数据规约等步骤。
在推荐系统中,我们需要对用户历史数据进行预处理,例如去重、空值填充、数据类型转换等。
2. 数据划分和特征提取在数据预处理完成之后,我们需要将数据集分为训练集和测试集,并且提取出有意义的特征。
在推荐系统中,用户历史行为数据通常包括用户ID、商品ID、时间等特征。
机器学习代码实战——SVM(支持向量机)(使用不同核函数)

机器学习代码实战——SVM(支持向量机)(使用不同核函数)支持向量机(Support Vector Machine, SVM)是一种常用的机器学习方法,它可以应用于分类和回归问题。
SVM通过构建一个超平面或决策边界来在不同类别之间进行分类,从而找到最佳的分类结果。
在SVM中,我们可以使用不同的核函数来改变超平面的形状和效果。
下面将介绍SVM 的基本原理以及如何使用不同核函数来解决分类问题。
SVM的基本原理是找到一个超平面来将不同类别的样本分割开来,最大化边界的宽度。
这个超平面的选择要求离它最近的训练点与该超平面的距离最大化,这些训练点被称为支持向量。
SVM的目标是找到一个最优的决策边界,使得其能够正确分类训练样本,并且对未知数据具有较好的泛化能力。
SVM可以使用不同的核函数来改变超平面的形状。
核函数是一种将输入空间映射到高维特征空间的函数,它可以将线性可分的样本在低维特征空间中转化为非线性可分的样本,从而提高分类的准确性。
常用的核函数有线性核函数、多项式核函数和高斯核函数。
线性核函数是最简单的核函数,它在原始特征空间上直接进行线性分割。
当数据集是线性可分的时候,使用线性核函数可以获得较好的分类效果。
线性核函数可以通过设置kernel参数为'linear'来使用。
多项式核函数可以在原始特征空间中引入高阶项,从而实现非线性分割。
多项式核函数可以通过设置kernel参数为'poly'来使用,并且可以通过degree参数来控制多项式的阶数。
高斯核函数(也称为径向基函数)将数据从原始特征空间映射到无穷维的特征空间中。
高斯核函数可以通过设置kernel参数为'rbf'来使用,并且可以通过gamma参数来控制高斯核函数的宽度。
除了上述三种常用的核函数之外,SVM还支持其他核函数,如sigmoid核函数和核对角线核函数等。
每种核函数都有不同的特点和适用场景,选择合适的核函数是SVM应用中的一项重要任务。
svmcgforregress函数

svmcgforregress函数如何使用SVR模型进行回归分析引言:回归分析是统计学中一种重要的分析方法,用于分析自变量与因变量之间的关系。
在回归分析中,我们希望根据自变量的取值,精确预测因变量的数值。
支持向量机(Support Vector Machine,SVM)是一种机器学习算法,在分类问题中广泛应用。
然而,SVM还可以应用于回归问题,这就是支持向量机回归(Support Vector Machine for Regression,SVR)。
本文将介绍使用SVR模型进行回归分析的步骤,并给出一个详细的实例来帮助读者深入理解和应用SVR模型。
章节一:SVR模型简介首先,我们需要了解SVR模型的基本概念和原理。
SVR模型与SVM分类器类似,但是目标不同。
SVR模型旨在找到一个函数,该函数可以尽可能地拟合样本,并使预测值与真实值之间的误差最小化。
具体而言,SVR模型通过在特征空间中找到一条线(或者高维空间中的超平面),使得函数与真实值之间的误差限制在一个可接受的范围内。
章节二:SVR模型的核函数在应用SVR模型之前,我们需要选择核函数。
决定核函数的选择是SVR 模型中非常重要的一步。
核函数用于将样本映射到高维特征空间,以便在高维空间中找到线性可分的超平面。
常用的核函数有线性核、多项式核和径向基核等。
章节三:数据预处理在进行回归分析之前,我们需要对数据进行预处理。
预处理步骤包括数据清洗、特征选择和数据归一化等。
数据清洗用于去除异常值和缺失值,以保证数据的质量。
特征选择是为了挑选出与因变量具有较强相关性的自变量。
数据归一化可以使得不同特征之间的数值范围相似,避免某个特征对模型的影响过大。
章节四:构建SVR模型在进行SVR模型的构建之前,我们需要将数据集划分为训练集和测试集。
训练集用于建立模型,测试集用于评估模型的性能。
接下来,我们需要确定模型的超参数,例如核函数类型、正则化参数和松弛变量参数等。
通过网格搜索、交叉验证等方法,选择最优的超参数组合。
svm实验目的与要求

svm实验目的与要求
一、实验目的:
1. 了解 SVM 的基本原理和工作机制。
2. 学习如何使用 SVM 算法进行分类或回归任务。
3. 探索 SVM 在不同数据集上的性能和效果。
4. 比较不同 SVM 模型的参数设置和超参数调优的影响。
5. 研究 SVM 在处理高维数据和非线性问题时的优势。
6. 应用 SVM 算法解决实际问题,如图像识别、文本分类等。
二、实验要求:
1. 数据集准备:选择一个合适的数据集,根据实验目的选择分类或回归问题的数据集。
2. 数据预处理:对数据集进行必要的预处理,包括数据清洗、特征选择、特征缩放等。
3. SVM 模型构建:使用适当的 SVM 算法库或编程实现 SVM 模型。
4. 模型训练与调优:选择合适的核函数(如线性核、径向基核、多项式核等),并调整模型的参数,如惩罚参数 C 和核函数参数。
5. 模型评估:使用交叉验证或留一法等技术对训练好的模型进行评估,计算准确率、召回率、F1 分数等指标。
6. 模型应用:将训练好的 SVM 模型应用于测试数据集或实际问题中,进行预测或分类。
7. 结果分析与比较:分析实验结果,比较不同 SVM 模型的性能,探讨可能的改进方向。
8. 实验报告撰写:记录实验过程、结果和结论,包括数据集描述、算法实现、模型评估以及结果分析等内容。
需要注意的是,SVM 实验的具体目的和要求可能因应用场景和数据集的不同而有所变化。
在实际实验中,应根据具体情况进行相应的调整和扩展。
svm高维矩阵参数寻优

svm高维矩阵参数寻优SVM (支持向量机) 是一种经典的机器学习算法,在许多领域中都被广泛应用。
本文将讨论如何寻找SVM模型中高维矩阵参数的最优值,以提高模型的性能和准确性。
首先,我们需要明确高维矩阵参数在SVM模型中的作用。
在SVM中,样本数据通过一种非线性映射(称为核函数) 映射到高维空间中,以便构建一个最优的超平面来区分不同的类别。
这个高维矩阵参数实际上表示了在映射后的高维空间中不同数据点之间的相似性。
通过调整高维矩阵参数的值,我们可以改变这种相似性的计算方式,从而影响最终的模型性能。
以下是一步一步的过程,以帮助您寻找SVM模型中高维矩阵参数的最优值:第一步:数据准备和预处理在开始寻找SVM模型的最优参数之前,我们需要准备和预处理数据。
这包括加载和标记数据集,将数据划分为训练集和测试集,以及对数据进行必要的归一化和标准化处理。
第二步:选择核函数和参数空间SVM模型中的核函数是非线性映射的关键。
常用的核函数包括线性核、多项式核和高斯核等。
我们需要根据数据集的特点和需求选择适当的核函数。
另外,核函数还有一些参数,如多项式核的阶数和高斯核的带宽。
选择合适的参数空间是为了覆盖所有可能的参数组合。
第三步:建立评估指标为了衡量模型的性能,我们需要选择合适的评估指标。
在分类问题中,常见的评估指标包括准确率、召回率、F1得分和AUC等。
根据具体的应用场景选择合适的评估指标,并确定评估指标的优化方向。
第四步:网格搜索和交叉验证网格搜索是一种常用的参数寻优方法。
它通过枚举参数空间中的所有可能组合,计算每个组合在交叉验证中的评估指标,并选择评估指标最优的参数组合。
通过交叉验证,我们可以减少模型在特定数据集上的过拟合风险。
第五步:参数优化和模型调整根据网格搜索的结果,我们可以确定最优的高维矩阵参数。
然后,我们可以使用这些参数来优化SVM模型,并进行模型调整。
模型调整包括调整正则化参数、优化训练算法和增加训练样本等操作,以更好地拟合数据和提高模型的性能。
servo guide常见问题总结

Servo guide调整常见问题总结----参考《servo guide总结》在机床现场实际的调整servo guide和在实验室调整的区别很大,由于实验室没有机床所以模拟起来难免会有很多地方太理想。
实际的调整出来的曲线和我们的想象区别还是很大的。
下面从调整的步骤上来一一说明一下:Servo guide调整开始之前,我们要记得先把原始参数拷贝下来,以防万一,另外螺补和反向间隙的值都要清除(全清0)才开始正式的调整。
但是调完之后需要恢复螺补和反向间隙。
一.HRV3的应用在需要应用HRV3时,一般先看版本,只要伺服版本在90B0(先按MDI键盘的system 键再用软键选择屏幕上的“系统”,再选择“系统”,翻页即可以找到伺服版本号)以上的均可以。
将参数2013#0设为1即可实现相应轴的HRV3控制,但是要注意,同一个SVM 控制下的轴一定要设定相同,有插补关系的轴一定要设定相同,同一根光缆必须设定相同。
因为HRV3改变的是电流环响应周期,如果有插补关系或同一SVM控制的轴的设定不同,必然会导致456报警。
所以一般用HRV3控制时,我们一般把所有的轴均设为HRV3控制。
另外,在使用HRV3控制时,我们很容易犯一个错误,就是很多时候,我们在现场调试,有时为了方便或是别的原因,在设定HRV3之前都做一个伺服参数的重新设定,这时再设定2013#0为1,然后重启发现诊断700#1不为1,也就是说没有实现设定,但是又没有出现报警,这是为什么呢?其实,很多时候都是因为我们忘了做FSSB的设定了,只要把FSSB重新设定一下(指的是将FSSB的轴和放大器设定都确定一次,也就是在FSSB的轴和放大器画面分别按oprt->setting即可)再就是,要使HRV3有效,除了上述的操作外,还必须用G5.4Q1激活。
二.调整过程一般开始我们都是振动机床来观察幅频响应特性,以为下面的调整做好基础准备。
调整时一般调整的过程是从内到外,也就是先电流环再速度环最后位置环。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
An Idiot’s guide to Support vectormachines (SVMs)R. Berwick, Village IdiotSVMs: A NewGeneration of Learning Algorithms •Pre 1980:–Almost all learning methods learned linear decision surfaces.–Linear learning methods have nice theoretical properties •1980’s–Decision trees and NNs allowed efficient learning of non-linear decision surfaces–Little theoretical basis and all suffer from local minima •1990’s–Efficient learning algorithms for non-linear functions based on computational learning theory developed–Nice theoretical properties.Key Ideas•Two independent developments within last decade–Computational learning theory–New efficient separability of non-linearfunctions that use “kernel functions”•The resulting learning algorithm is an optimization algorithm rather than a greedy search.Statistical Learning Theory•Systems can be mathematically described as a system that–Receives data (observations) as input and–Outputs a function that can be used to predictsome features of future data.•Statistical learning theory models this as a function estimation problem •Generalization Performance (accuracy in labeling test data) is measuredOrganization•Basic idea of support vector machines –Optimal hyperplane for linearly separablepatterns–Extend to patterns that are not linearlyseparable by transformations of original data tomap into new space –Kernel function •SVM algorithm for pattern recognition Unique Features of SVM’s andKernel Methods•Are explicitly based on a theoretical model of learning•Come with theoretical guarantees about their performance•Have a modular design that allows one to separately implement and design their components•Are not affected by local minima•Do not suffer from the curse of dimensionalitySupport Vectors•Support vectors are the data points that lie closest to the decision surface•They are the most difficult to classify•They have direct bearing on the optimum location of the decision surface•We can show that the optimal hyperplane stems from the function class with the lowest “capacity” (VC dimension).Recall: Which Hyperplane?•In general, lots of possiblesolutions for a,b,c.•Support Vector Machine(SVM) finds an optimalsolution. (wrt what cost?)Support Vector Machine (SVM)Support vectors Maximize margin•SVMs maximize the margin around the separating hyperplane.•The decision function is fully specified by a subset of training samples, the support vectors .•Quadratic programming problem•Text classification method du jour Separation by Hyperplanes•Assume linear separability for now:–in 2 dimensions, can separate by a line–in higher dimensions, need hyperplanes•Can find separating hyperplane by linear programming (e.g. perceptron):–separator can be expressed as ax + by = cLinear Programming / PerceptronFind a,b,c, such thata x+b y≥c for red pointsa x+b y≤c for green points.Which Hyperplane?In general, lots of possiblesolutions for a,b,c.Which Hyperplane?•Lots of possible solutions for a,b,c.•Some methods find a separating hyperplane,but not the optimal one (e.g., perceptron)•Most methods find an optimal separatinghyperplane•Which points should influence optimality?–All points•Linear regression•Naïve Bayes–Only “difficult points” close to decisionboundary•Support vector machines•Logistic regression (kind of)Support Vectors again for linearlyseparable case•Support vectors are the elements of the training set that would change the position of the dividing hyper plane if removed.•Support vectors are the critical elements of the training set•The problem of finding the optimal hyper plane is an optimization problem and can be solved by optimization techniques (use Lagrange multipliers to get into a form that can be solved analytically).X X X XXXSupport Vectors: Input vectors for which w 0T x + b 0= 1 or w 0T x + b 0= -1ρ0d +d -Definitions Define the hyperplane H such that:x i •w +b ≥+1 when y i =+1x i •w +b ≤-1 when y i =-1d+ = the shortest distance to the closest positive pointd-= the shortest distance to the closest negative pointThe margin of a separating hyperplane is d ++ d -.HH1 and H2 are the planes:H1: x i •w +b = +1H2: x i •w +b = -1The points on the planes H1 and H2 are the Support Vectors H1H2Moving a support vectormoves the decisionboundaryMoving the other vectors has no effect The algorithm to generate the weights proceeds in such a way that only the support vectors determine the weights and thus the boundary Maximizing the margind+d-We want a classifier with as big margin as possible.Recall the distance from a point(x 0,y 0) to a line:Ax+By+c = 0 is|A x 0+B y 0+c|/sqrt(A 2+B 2)The distance between H and H1 is:|w•x +b|/||w||=1/||w||The distance between H1 and H2 is: 2/||w||In order to maximize the margin, we need to minimize ||w||. With the condition that there are no datapoints between H1 and H2:x i •w +b ≥+1 when y i =+1x i •w +b ≤-1 when y i =-1 Can be combined into y i (x i •w) ≥1H1H2HWe now must solve a quadratic programming problem •Problem is: minimize||w||, s.t. discrimination boundary is obeyed, i.e., min f(x) s.t. g(x)=0, wheref: ½||w||2andg: y i(x i•w)-b = 1 or[y i(x i•w)-b] -1=0This is a constrained optimization problem Solved by Lagrangian multipler methodflatten paraboloid2-x2-2y2Intuition:intersection of two functions at atangent point.flattened paraboloid2-x2-2y2with superimposed constraint x2 +y2 = 1flattened paraboloid f: 2-x2-2y2=0with superimposed constraint g: x+y= 1Maximize when the constraint line g is tangent to the inner ellipse contour line of fflattened paraboloid f:2-x2-2y2=0 with superimposed constraint g: x+y= 1; at tangent solution p, gradient vectors of f,g are parallel (no possible move to incr f that also keeps you in region g) Maximize when the constraint line g is tangent to the inner ellipse contour line of fTwo constraints1.Parallel normal constraint (= gradient constrainton f, g solution is a max)2.G(x)=0 (solution is on the constraint line)We now recast these by combining f, g as theLagrangianRedescribing these conditions •Want to look for solution point p where•Or, combining these two as the Langrangian L & requiring derivative of L be zero:()()()0f pg p g x λ∇=∇=(,)()()(,)0L x f x g x x λλλ=−∇=How Langrangian solves constrainedoptimization(,)()() where(,)0L x f x g x x λλλ=−∇=Partial derivatives wrt x recover the parallel normal constraintPartial derivatives wrt λrecover the g (x,y )=0In general, (,)()()i i i L x f x g x λλ=+∑In general(,)()() a function of variables for the ', for the . Differentiating gives equations, each set to 0. The eqns differentiated wrt each give the gradient conditions; the i i i i L x f x g x n m n x s m n m n x ααα=+++∑ eqns differentiated wrt each recover the constraints i i m g αGradient max of f constraint condition gIn our case, f (x ): ½|| w ||2; g(x ): y i (w .x i +b)-1=0 so Lagrangian isL= ½|| w ||2-Σαi [y i (w .x i +b)-1]Lagrangian Formulation•In the SVM problem the Lagrangian is •From the derivatives = 0 we get()212110,l lP i i i ii i i L y b iααα==≡−⋅++≥∀∑∑w x w 11,0l li i i i i i i y y αα====∑∑w xThe Lagrangian trick Reformulate the optimization problem:A ”trick” often used in optimization is to do an Lagrangian formulation of the problem.The constraints will be replaced by constraints on the Lagrangian multipliers and the training data will occur only as dot products.Gives us the task:Max L = ∑αi –½∑αiαj x i•x j,Subject to:w= ∑αi y i xi∑αi y i= 0What we need to see: x i and x j(input vectors) appear only in the formof dot product –we will soon see why that is important.The Dual problem•Original problem:fix value of f and find α•New problem:Fix the values of α, and solve the(now unconstrained) problem max L(α, x)•Ie, get a solution for each α, f*(α)•Now minimize this over the space of α•Kuhn-Tucker theorem: this is equivalent tooriginal problemAt a solution p•The the constraint line g and the contour lines of f must be tangent•If they are tangent, their gradient vectors (perpindiculars) are parallel•Gradient of g must be 0 –I.e., steepest ascent & so perpendicular to f•Gradient of f must also be in the same direction as gInner productsThe task:Max L = ∑αi –½∑αiαj x i•x j,Subject to:w= ∑αi y i x i∑αi y i= 0Inner productInner productsWhy should inner product kernels be involved in pattern recognition?--Intuition is that they provide some measure of similarity --cf Inner product in 2D between 2 vectors of unit length returns the cosine of the angle between them.e.g. x= [1, 0]T, y= [0, 1]TI.e. if they are parallel inner product is 1x T x= x.x= 1If they are perpendicular inner product is 0x T y= x.y= 0But…are we done???Not Linearly SeparableFind a line that penalizespoints on “the wrong side”.x x x x x xx ϕ(o)X Fϕϕ(x)ϕ(x)ϕ(x)ϕ(x)ϕ(x)ϕ(x)ϕ(x)ϕ(o)ϕ(o)ϕ(o)ϕ(o)ϕ(o)ϕ(o)o o o o ooTransformation to separateNon Linear SVMsa b()()()2x a x b x a b x ab−−=−++{}2,x x x6•The idea is to gain linearly separation by mapping the data to a higher dimensional space –The following set can’t be separated by a linear function, but can be separated by a quadratic one–So if we map we gain linear separation Problems with linear SVM=-1=+1What if the decision function is not linear? What transform would separate these?Ans: polar coordinates!Non-linear SVM 1The Kernel trick =-1=+1Imagine a function φthat maps the data into another space:φ=Rd →Η=-1=+1Remember the function we want to optimize: L dual = ∑αi –½∑αi αj x i •x j ,x i and x j as a dot product. We will have φ(x i ) •φ(x j ) in the non-linear case.If there is a ”kernel function”K such as K(xi,xj) = φ(xi) •φ(xj), we do not need to know φexplicitly. One example: Rd ΗφWe’ve already seen a nonlineartransform…•What is it???•tanh(β0x T x i + β1)Examples for Non Linear SVMs()(),1pK =⋅+x y x y (){}222,exp K σ−=−x y x y ()(),tanh K κδ=⋅−x y x y 1st is polynomial (includes x•x as special case)2nd is radial basis function (gaussians)3rd is sigmoid (neural net activation function)Inner Product KernelsMercer’s theorem issatisfied only for some values of β0and β1tanh(β0x T x i + β1)Two layer perceptron The width σ2is specified apriori exp(1/(2σ2)||x-x i ||2)Radial-basis functionnetworkPower p is specified apriori by the user (x T x i + 1)p Polynomial learningmachineComments Inner Product KernelK(x,x i ), I = 1, 2, …, NType of Support Vector MachineNon-linear svm2The function we end up optimizing is:Max Ld = ∑αi–½∑αiαj K(xi•x j),Subject to:w= ∑αi y i x i∑αi y i= 0Another kernel example: The polynomial kernelK(xi,xj) = (xi•xj + 1)p, where p is a tunable parameter. Evaluating K only require one addition and one exponentiation more than the original dot product.Examples for Non Linear SVMs2 –Gaussian KernelLinearGaussianNonlinear rbf kernel Admiral’s delight w/ difft kernelfunctionsOverfitting by SVMBuilding an SVM Classifier •Now we know how to build a separator for two linearly separable classes•What about classes whose exemplary examples are not linearly separable?。
