有限元线法
第1章有限元法简介
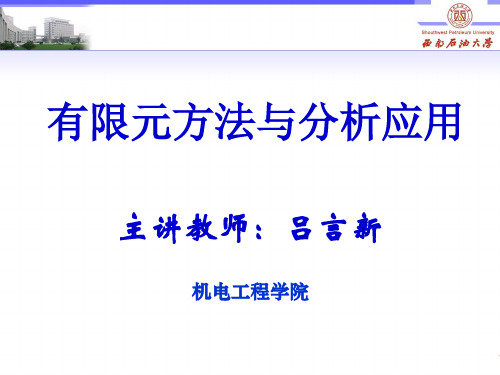
Fix uix k ii 0 F v iy iy 0 0 K = = F jx u jx k ji 0 F jy v jy 0 0
k ij 0 uix 1 v 0 0 iy EA 0 l 1 k jj 0 u jx 0 0 0 v jy
钱学森
钱伟长
胡海昌
杨桂通
徐芝伦
软件名称
简介
MSC/Nastran
LS-Dyna MSC/Dytran MSC/Marc ANSYS FLUENT ABAQUS
著名结构分析程序,最初由NASA研制。
动力学分析程序(大多为显式算法) 非线性分析软件 通用结构分析软件(耦合场分析) 流场分析软件 非线性分析软件(非协调单元,非线性 直接解算方法)
令杆件两端节点分别产生单位位移,可以计算产生这样的单 位位移所需要的力,而力的大小就是刚度系数。 EA 首先取 ui 1,u j 0, 此 时 需 要 压 力 ui。 按 照 局 部 坐 标 系 l EA EA 和力的规定, Fi ui,F j ui, 则 l l EA EA ui l k , k
单元2 3
F3 10N
x
考虑y方向的单元刚度矩阵
Fi k ii k ij ui EA 1 1 ui = u l F u k k 1 1 jj j j ji j
若考虑y方向,则有:
——宏观假设
弹性力学的基本假定
2、线弹性(Linear elastic)
物体的变形与外力作用的关系是线性的, 除去外力,物体可回复原状 ,而且这个关系和 时间无关,也和变形历史无关,称为完全线弹 性材料
线性和非线性有限元

目
CONTENCT
录
• 线性有限元方法 • 非线性有限元方法 • 线性与非线性有限元的比较 • 线性与非线性有限元的实例分析 • 未来研究方向与展望
01
线性有限元方法
定义与原理
定义
线性有限元方法是一种数值分析方法,用于求解偏微分方程的近 似解。它将复杂的求解区域离散化为有限个小的、简单的子区域 ,即有限元,然后对每个有限元进行求解,最终得到原偏微分方 程的近似解。
THANK YOU
感谢聆听
在实际应用中,应根据问题的特性和需求选择合适 的有限元方法。对于复杂的问题,可能需要结合多 种有限元方法进行求解。
05
未来研究方向与展望
线性有限元方法的改进与优化
80%
高效求解算法
研究更快速、稳定的线性有限元 求解算法,提高计算效率。
100%
自适应网格生成
发展更智能、自动的网格生成技 术,以适应复杂几何形状和边界 条件。
线性有限元
由于线性有限元基于线性方程组进行求解,因此计算复杂度 相对较低,适用于求解一些较简单的问题,如弹性力学问题 。
非线性有限元
非线性有限元需要求解非线性方程组,计算复杂度较高,但 能够处理更复杂的问题,如塑性力学、流体力学等领域的问 题。
精度比较
线性有限元
对于一些简单的问题,线性有限元可以给出较为精确的结果。然而,对于一些 复杂的问题,线性有限元可能无法准确描述非线性行为。
80%
多物理场耦合
研究线性有限元在多物理场耦合 问题中的应用,如流体-结构、电 磁-热等。
非线性有限元方法的改进与优化
高阶非线性有限元
发展高阶非线性有限元方法, 以更精确地描述复杂非线性行 为。
第8章 接触问题的有限元法

18
小滑动和有限滑动 当选用小滑动公式时,ABAQUS从模拟开始就
建立从属表面和主控表面的关系。ABAQUS确定主 控表面的哪个部分与从属表面的每一个节点发生关 系。这种关系在整个分析中保持不变。如果分析包 括几何非线性,小滑动公式需要考虑主控表面的任 何转动与变形对接触力的影响。如果不包括几何非 线性问题,可忽略主控表面的任何转动和变形,认 为加载路径是固定的。
一对接触面的法线方向应该相反,如果法线方向 错误,ABAQUS理解为过盈接触,因此无法收敛。
17
从属表面和主控表面
ABAQUS采用主控—从属接触算法:从属表面 的节点不能穿透主控表面的任何部分。这种算法对 主控表面没有限制,它可以穿透从属表面。为了获 得接触模拟的最好结果,必须认真和准确地定义从 属和主控表面:
力引起的等效节点力向量
和罚系数有关的矩阵
F 'k+1 = −Λ'T T N cd c − Λ'd '
整体坐标系下接触力等效节点力向量
对称阵 F k+1 = −(N c )T T Λ'T T N cd c − (N c )T T Λ'd '
F k+1 = −Kcd c + F̃ k+1 --系统的等效节点接触力向量
采用有限元法分析接触问题时,需要分别对接触 物体进行有限元网格剖分,并规定在初始接触面上, 两个物体对应节点的坐标位置相同,形成接触对。整 体和局部坐标系下,两个物体由于接触载荷引起的等 效节点力矢量分别记为
3
{ } F Ι = F1Ι , F2Ι , F3Ι T
第九章 有限元线性方程组的解法

i ≥ j)
(9-9)
讨论: 1 从式(9—9)看出,在按行列由Kij计算lij时,计算完lij后,Kij 就失去存在的作用,同时所用到lip、ljp和lpp排列顺序都在Kij之前,因 此可将分解后得到的元素lij存贮在Kij单元中,即原来存贮[K]的内存 单元,现在可用来存贮[L]矩阵,以减少对内存贮量的要求。 2 由于这里只存贮下三角形带内元素,所以在利用式(9—9) 由Kij计算lij时,求和号内各元素的列号应从第i行和第j列上第一个非 零元素所在列号(i1和j1)中最大的列号开始。 3 从式(9—8)看出,在分解[K]时,每行的第一个非零元素其 值保持不变,因此在分解总刚时,每行可从第二个非零元素的列号 开始,这样lij的最后递推公式为
2.检查哪些自由度已集成完毕,以集成完毕的自由度i作为主 元对其它行列的元素进行消元修正。 图(b)中,自由度4已等成完毕,是不活动变量,现在作为主 元,用
×
表示。主元行元素 × ,不再变化,对其它行列元素进行
消元修正。 自由度 2 扫描单元① 4 5 波前 Байду номын сангаас前三角形 (a) K × × P × × ×
δ i = ∆i −
讨论:
j =i +1
∑l
n
ji x j
lii
(9-13)
(i = n − 1, n − 2,L,1)
∆ 1.因为 δ i 与 ∆ i 相对应,而且一旦求出 δ i 后, i就失去作用,因
此把求得的 δ i 存贮在 ∆ i 的内存单元中,即存贮在结点荷载的内存 单元中。 2. lij必须是带内元素,因此它的列号i必不小于该行的第一个非 零元素的列号j1。
0 l ij = K ij −
有限元线法二次参数单元的温度场分析

有限元线法二次参数单元的温度场分析近年来,有限元线法(FEM)的发展迅速,因其对不同形状的构件的实际性能进行精确分析的能力而备受关注。
在FEM中,二次参数单元(QUAD)是一种重要的有限元种类,被广泛用于温度场分析。
本文将着重讨论QUAD单元在温度场分析方面的应用,详细阐述其优势和缺陷,并从理论出发,介绍QUAD单元有效的计算方法。
QUAD单元以二次矩形形式出现,在温度场分析中,可以快速准确地解决结构的热力学响应问题。
QUAD单元的优势在于,其使用的网格拓扑简单,即只需定义网格点的位置,而无需定义每个网格单元的节点,这极大地减少了模型拓扑定义的难度;同时,QUAD单元可以将复杂曲面转化为矩形网格,这使计算可以非常有效地进行,具有同等准确性。
QUAD单元在温度场分析中具有显著的优势,但也存在一些缺点。
由于它们是二次参数单元,因此边界上的节点只保留一个节点,它们受到网格系统的影响,因此在它们的计算结果中可能存在一定的误差。
另外,由于QUAD单元的节点分布是均匀的,颗粒分布难以准确地表述,从而影响其准确性。
要有效地解决结构的温度场分析,我们需要一种能够准确表达温度场的方法。
为此,基于QUAD单元,我们可以提出有效的数值计算方法,以及更先进的有限元方法。
首先,根据坐标变换公式,我们可以将整个构件变换到以矩形有限元模型表示,即由正方形单元组成的四边形网格模型。
此外,使用坐标转换公式,还可以将几何形状任意分布的温度场表示为矩形模型,并通过定义某些特性参数,使其能够准确表达温度变化的趋势。
然后,根据有限元理论,计算在QUAD网格上的温度响应,并利用Galerkin 法求解整体温度场分析问题,从而得到QUAD单元在温度场分析中的准确计算结果。
除了使用坐标转换公式,我们还可以采用更先进的有限元方法,例如通用有限元(GEM)、直接有限元(DFEM)等,以较高的准确度求解温度场分析问题。
GEM及DFEM方法可以使用任意形状的有限元,克服QUAD单元的一些缺点,在温度场分析中实现更高的精度和可靠性;此外,它们也能够准确描述热结构件的温度场变化特征,从而使整个热分析过程更加便捷。
材料力学弹性力学有限元课程学习思路步骤

材料力学弹性力学有限元课程学习思路步骤解决问题的思路和步骤(基本方程)根据胡克定律(Hooke's law),在弹性限度内,材料的应力与应变成线性关系。
在处理具体的杆件问题时,根据材料性质和变形情况的不同,可将问题分为三类:①线弹性问题。
在杆变形很小,而且材料服从胡克定律的前提下,对杆列出的所有方程都是线性方程,相应的问题就称为线性问题。
对这类问题可使用叠加原理,即为求杆件在多种外力共同作用下的变形(或内力),可先分别求出各外力单独作用下杆件的变形(或内力),然后将这些变形(或内力)叠加,从而得到最终结果。
②几何非线性问题。
若杆件变形较大,就不能在原有几何形状的基础上分析力的平衡,而应在变形后的几何形状的基础上进求解一个弹性力学问题,就是设法确定弹性体中各点的位移、应变和应力共15 个函数。
从理论上讲,只有15个函数全部确定后,问题才算解决。
但在各种实际问题中,起主要作用的常常只是其中的几个函数,有时甚至只是物体的某些部位的某几个函数。
所以常常用实验和数学相结合的方法,就可求解。
直角坐标系下的弹性力学的基本方程为:有限元方法(FEM)的理论基础是变分原理和加权余量法。
仍然遵从平衡方程、几何方程、本构方程、协调方程,其解满足应力边界条件、位移边界条件。
其基本求解思想是把计算域划分为有限个互不重叠的单元,在每个单元内,选择一些合适的节点作为求解函数的插值点,将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程离散求解。
采用不同的权函数和插值函数形式,便构成不同的有限元方法。
行分析。
这样,力和变形之间就会出现非线性关系,这类问题称为几何非线性问题。
③物理非线性问题。
在这类问题中,材料内的变形和内力之间(如应变和应力之间)不满足线性关系,即材料不服从胡克定律。
在几何非线性问题和物理非线性问题中,叠加原理失效。
解决这类问题可利用卡氏第一定理、克罗蒂-恩盖塞定理或采用单位载荷法等。
有限元中的半解析法

如图1(a)所示,有一矩形薄板,设每条边界的支承条件相同,图中表示了三种支承情况,图1(b)用一些与边界线平行的直线将板分割成若干窄长的条带以此组成有限元分析中的单元。下面介绍这种条带单元位移场的建立思路。
图1矩形薄板与有限条离散示意图
1.1确定位移模式
对于薄板来说,挠度ω可用分离变量形式表示
(1)
(8)
式中
(3)参数FEMOL的能量泛函的确定:结构中每个单元的能量为∏e,它是η的函数。则整个求解域的能量为:
(9)
(4)建立常微分方程体系:常微分方程建立后,经过一系列的处理后即可用求解器(Solver)来求未知节线位移函数。
有限线元法中,由于引入参数单元,是可用于不规则区域的求解;由于未知节线位移是通过解常微分方程组得到的,其自然精度要比其他方法高。也是一种很有效的半解析方法。
fm(y)=[N1N2][δT1mδT2m]T(5)
若为內节线的高阶条元,记内节线位移参数与形函数为δ3m、N3则
fm(y)=[N1N2N3][δT1mδT2mδT3m]T
其余的可类推。
若仅以节线位移为参数时,则
fm(y)=[ ][ω1mω2m]T
当以节线位移和转角为参数时,有
fm(y)=[N1N2N3N4][ωT1mδT1mω2mδ2m]T
1.4有限条法的不足
虽然样条法在实际中有广泛的应用,但依然有一定的局限性:
(1)条元不可能在长边方向连接有限元或其它单元。
(2)当结构的某一边界并非同一支承情况,如矩形板的四条边线,每条边上均同时存在多种支承情况,显然在边界条件不同的相邻条元间,由于Xm(x)不同,当然不可能保证位移间的协调性,因此,有限条将无法使用。
有限元线法在热传导问题中的发展现状

有限元线法在热传导问题中的发展现状有限元线法在热传导问题中的发展现状一、介绍1、有限元线法(FEM),是一种将力学系统的几何性质和材料属性结合在一起的解析方法,是解决力学问题的主要方法之一。
2、其在热传导问题中,可以用来计算温度场、热流和热量传递过程。
二、发展历程1、 1960年,R. Kosloff 等人首次将有限元法用于热传导问题,他们使用有限元积分方法,解决了半空间热传导问题。
2、 1970 年,R. S. Averill 和G. Y. Yu在其著作"Finite Element Analysis Of Thermal Transport Problems"中,系统地论述了有限元法用于热传导的数学模型,使此方法在热学领域应用得到突飞猛进。
3、 1980 年, J. J. Roques 和J. Legais 提出了原子键链分子动力学(AMBER) 模型新方法,解决了边界和凝聚态体中由热传导和热扩散引起的温度变化问题。
4、 2000 年,Y. S. Li、R. S. Elliott以及R. K. Marcus等人在《Wiley Periodicals Inc. Applied Numerical Mathematics》${2004}$年出版的一篇文章中,深入研究了FEM在热传导中的理论与方法,能够有效地解决非线性热传导问题。
三、近年发展1、朝着更容易使用、节约时间的方向发展,有限元线法的发展方向有:(1) 自动生成程序:自动生成识别器系统,用于自动生成、确定和交互使用有限元法程序。
(2) 基于网格优化的程序:改进网格,自动优化有限元法下的固有源状态精度。
(3) 热传导分析器:可用于热传导问题中复杂场景的几何建模,以及对复杂热源场特性的分析。
2、先进的微网格热传导分析:采用微网格技术为基础,基于微结构的理论和方法,进行高精度热传导分析。
3、柔性的多物理场分析:分析热源交互作用的特性,提供热传导源中温度场的分析。
