Lingo教程四 LINGO的函数模板
LINGO基本语法和编程ppt课件

f对
x, j
y j
是非线性的,
所以在新建料场时是NLP模型。先解NLP模型,而把现有临时料场的位置作
为初始解告诉LINGO。
本例中集合的概念
利用集合的概念,可以定义需求点DEMAND和供应点 SUPPLY两个集合,分别有6个和2个元素(下标)。但决 策变量(运送量) 与c ij 集合DEMAND和集合SUPPLY都 有关系的。该如何定义这样的属性?
在实际问题中,输入的数据通常是原始数据,不一定 能在模型中直接使用,可以在这个段对这些原始数据进 行一定的“预处理”,得到模型中真正需要的数据。
例如
Calc: TotalWeight = @sum(Box(i): zl(i)*js(i)); EndCalc
注意计算段只能对常量进行计算,不能对需要 通过解优化程序求解出来的变量进行计算。
1 2 3 456
a 1.25 8.75 0.5 5.75 3 7.25
b 1.25 0.75 4.75 5 6.5 7.75
d3
5
4
7 6 11
建立模型
记工地的位置为(a ,b ) ,水泥日用量为d,i1, 6;料场
ii
i
位置为(
x
j
,
y
j
)
,日储量为
e j
,
j 1,2
;从料场
j 向工地i
的
运送量为c ij 。
集合的基本用法
例四这理属个些解性SA季需(LIIL度求ANCtG的必tOrO帆须i公b建u船按司t模e需时需)语求满要的言量足决概最分。定念重别每下。要是个四的季4个0是度条季理正,度解常6的0集的条帆合生,船(产7生5S能条产et)力,量及2是。5其条4下0, 条帆船,每条船的生产费用为400美元。如果加班生产, 每条船的生产费用为450美元。每个季度末,每条船的 库存费用为20美元。假定生产提前期为0,初始库存为 10条船。如何安排生产可使总费用最小?
第04讲 Lingo软件入门

第4讲 Lingo 软件入门司守奎烟台市,海军航空工程学院数学教研室Email :sishoukui@4.1 初识Lingo 程序Lingo 程序书写实际上特别简捷,数学模型怎样描述,Lingo 语言就对应地怎样表达。
首先介绍两个简单的Lingo 程序。
例4.1 求解如下的线性规划问题:121212112max726450,128480,s.t.3100,,0z x x x x x x x x x =++≤⎧⎪+≤⎪⎨≤⎪⎪≥⎩ Lingo 求解程序如下max =72*x1+64*x2; x1+x2<=50;12*x1+8*x2<=480; 3*x1<=100;说明:Lingo 中默认所有的变量都是非负的,在Lingo 中就不需写出对应的约束。
例4.2 抛物面22y x z +=被平面1=++z y x 截成一椭圆,求原点到这椭圆的最短距离。
该问题可以用拉格朗日乘子法求解。
下面我们把问题归结为数学规划模型,用Lingo 软件求解。
设原点到椭圆上点),,(z y x 的距离最短,建立如下的数学规划模型:⎩⎨⎧+==++++.,1s.t.min 22222y x z z y x z y xLingo 求解程序如下: min =(x^2+y^2+z^2)^(1/2); x+y+z=1; z=x^2+y^2;@free (x); @free (y);说明:Lingo 中默认所有变量都是非负的,这里y x ,的取值是可正可负的,所以使用Lingo 函数free 。
例4.3 求解如下的数学规划模型:⎪⎪⎩⎪⎪⎨⎧==∑∑∑===.,1s.t.min9912100100110012i ii i i ix x x x用Lingo 求解上述数学规划问题,使用集合和函数比较方便,使用集合的目的是为了定义向量,集合使用前,必须先定义;Lingo 程序中的标量不需要定义,直接使用即可。
sets :var/1..100/:x; endsetsmin =@sqrt (@sum (var(i):x(i)^2)); @sum (var(i):x(i))=1;x(100)=@sum (var(i)|i#le#99:x(i)^2); @for (var(i)|i#le#99:@free (x(i)));说明:如果不使用集合和函数,全部使用标量x1,x2,…,x100,最后一个约束就要写99遍,@free(x1); …; @free (x99)。
LINGO基本用法与运算函数

例如,目标函数中有求和表达式ΣCijXij(i从1 到10,j从1到20),若用直接输入的方式,将有 200个系数与200个变量相乘再相加,需要输入 长长一大串,既不便于输入,又不便于修改, 别人看不懂,可读性较差.
LINGO提供了建模语言,能够用较少语 句描述目标函数和约束条件,为建立大规 模数学规划模型提供了方便.我们以一个 运输规划模型为例说明其用法。
办法是用现成软件求解.LINGO是专门
用来求解各种规划问题的软件包,其功
能十分强大,是解决最优化问题的最佳
选择。
LINGO的基本用法和运算 函数
§1.1 LINGO 入门
LINGO的基本用法和运算 函数
一、概况
LINGO 是 美 国 LINDO 系 统 公 司 ( Lindo SystemInc)开发的求解数学规划系列软件中的一 个(其它软件为LINDO,GINO,What’s Best等 等),的主要功能是求解大型线性、非线性和整数 规 划 , 目 前 的 版 本 是 11.0 . 可 以 从 Internet 网 址 http://下载该软件的安装文件lingo11.exe,执行该 文件即可在计算机内安装LINGO 软件系统,首次 运行该软件时,要求用户输入密码,如果输入了正 确的密码,则该软件就成了正式版,如果密码不对 或不输入密码,则该软件就成为演示版.
1.目标函数(求某个数学表达式的最大值或最 小值);
2. 决策变量,即目标函数值取决于哪些变量;
3. 约束条件,即对变量附加一些条件限制(等 式或不等式).
LINGO的基本用法和运算 函数
例1:某工厂有两条生产线,分别用来生产 M和P两种型号的产品,利润分别为200元/个 和300元/个,生产线的最大生产能力分别为 每日100和120,生产线每生产一个M产品需 要1个劳动日进行调试、检测等工作,而每个 P产品需要2个劳动日,该厂每天只有160个 劳动日可用,假如原材料等其它条件不受限 制,问应如何安排生产计划,使获得的利润 最大?
LINGO快速入门

概率函数
• 7.@phg(pop,g,n,x) • 超几何(Hypergeometric)分布的累积分布函数。pop表示产品总数,g是正
品数。从所有产品中任意取出n(n≤pop)件。pop,g,n和x都可以是非整数, 这时采用线性插值进行计算。
变量界定函数
• 变量界定函数实现对变量取值范围的附加限制,共4种: • @bin(x) 限制x为0或1 • @bnd(L,x,U) 限制L≤x≤U • @free(x) 取消对变量x的默认下界为0的限制,即x可
以取任意实数 • @gin(x) 限制x为整数 • 在默认情况下,LINGO规定变量是非负的,也就是说下界
• @smax(x1,x2,...,xn)返回 x1 , x2 , … , xn 中的 最大值
• @smin(x1,x2,...,xn)返回 x1 , x2 , … , xn 中的最 小值
例 给定一个直角三角形,求包含该三角形的最小正方形。
解:如图所示。ABCDDAEabx
求最小的正方形就相当于求如下的最优化问题:
• data:
• sex,age = 1 16
•
0 14
•
0 17
•
0 13;
• friend = 0.3 0.5 0.6;
• enddata
基本运算符
• ^ 乘方 •﹡ 乘 •/ 除 •﹢ 加 •﹣ 减
: LINGO具有9种逻辑运算符
• #not# 否定该操作数的逻辑值,# not #是一个一元运算符 • #eq# 若两个运算数相等,则为 true ;否则为 flase • #ne# 若两个运算符不相等,则为 true ;否则为 flase • #gt# 若左边的运算符严格大于右边的运算符,则为 true ;否则
lingo的格式

lingo的格式
5. 条件语句:使用else语句来进行条件判断,例如:
if (condition) { // do something
} else { // do something else
}
lingo的格式
6. 循环语句:使用for循环或者while循环来进行循环操作,例如:
for (var i = 0; i < 10; i++) { // do something
}
while (condition) { // do something
}
lingo的格式
7. 函数定义:使用function关键字来定义函数,例如: function myFunction(param1, param2) { // do something }
8. 对象和属性:可以使用对象和属性来组织和访问数据,例如: var myObject = { property1: value1, property2: value2 }; var myValue = myObject.property1;
lingo的格式
Lingo是一种计算机编程语言,其格式可以根据具体的上下文和使用环境而有所不同。以 下是一般情况下Lingo的基本格式:
1. 语句分隔符:每个语句以分号(;)作为结束符号。 2. 注释:可以使用双斜杠(//)或者斜杠星号(/*...*/)来添加注释。 3. 变量声明:使用var关键字来声明变量,例如:var myVariable。 4. 数据类型:Lingo支持多种数据类型,包括整数(integer)、浮点数(float)、布尔 值(boolean)、字符串(string)等。
lingo的格式
以上是Lingo的一般格式,具体的语法和规则可能会根据不同的版本和应用程序而有所变 化。在实际编写Lingo代码时,建议参考相关的文档和教程,以确保正确使用语言的特性和 语法。
2024年度LINGO基本教程完整版PPT大纲

2024/2/2
1
目录
2024/2/2
• 引言 • LINGO编程基础 • 线性规划问题求解 • 整数规划与非线性规划问题求解 • 约束条件处理技巧 • 优化算法介绍与应用 • 实际问题建模与求解案例分析 • 课程总结与展望
2
01
引言
Chapter
2024/2/2
拉格朗日乘子法
引入拉格朗日乘子,构造拉格朗 日函数,将等式约束问题转化为 无约束优化问题。
罚函数法
将等式约束条件转化为某种形式 的罚函数,加入到目标函数中, 通过求解无约束优化问题得到近 似解。
2024/2/2
22
不等式约束条件处理方法
积极约束法
将不等式约束条件转化为等式约束条件,引 入松弛变量,构造新的目标函数进行求解。
24
06
优化算法介绍与应用
Chapter
2024/2/2
25
梯度下降法原理及在LINGO中实现
01
梯度下降法基本原理
通过迭代求解目标函数的最小值,每次迭代沿着当前位置的负梯度方向
前进一段距离,直到达到最小值或满足停止条件。
2024/2/2
02 03
LINGO中实现梯度下降法
在LINGO中,可以使用内置函数或自定义程序来实现梯度下降法。需要 定义目标函数、梯度函数和迭代步长等参数,并通过循环迭代来逼近最 小值。
在LINGO中,可以使用内置函数或自定义程序来实现牛顿 法。需要定义目标函数、一阶导数和二阶导数等参数,并 通过循环迭代来逼近根。
牛顿法的优缺点
牛顿法具有收敛速度快、精度高等优点,但需要计算二阶 导数矩阵,计算量较大,且对初始值有一定要求。
LINGO使用教程
LINGO 使用教程LINGO 是用来求解线性和非线性优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO 高效的求解器可快速求解并分析结果。
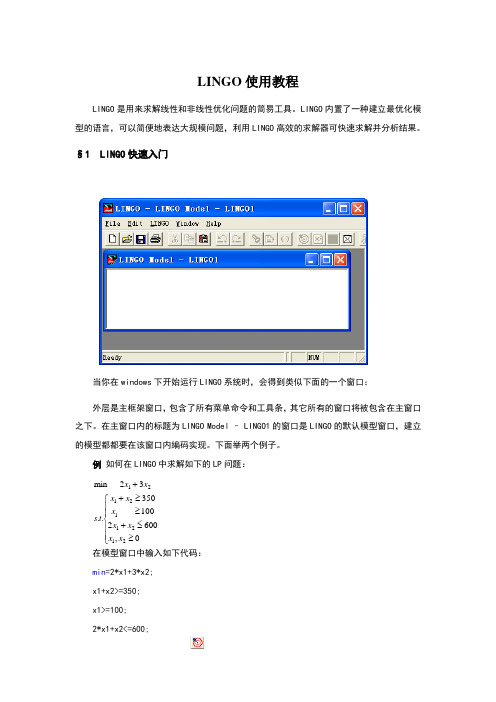
§1 LINGO 快速入门当你在windows 下开始运行LINGO 系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例 如何在LINGO 中求解如下的LP 问题: ⎪⎪⎩⎪⎪⎨⎧≥≤+≥≥++0,6002100350..32min212112121x x x x x x x t s x x 在模型窗口中输入如下代码:min =2*x1+3*x2; x1+x2>=350; x1>=100; 2*x1+x2<=600;然后点击工具条上的按钮即可。
例使用LINGO软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如下表。
使用LINGO软件,编制程序如下:model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
LINGO教程(PDF)
2.3 模型的集部分 集部分是 LINGO 模型的一个可选部分。在 LINGO 模型中使用集之前,必须在集部分事先 定义。集部分以关键字“sets:”开始,以“endsets”结束。一个模型可以没有集部分,或 有一个简单的集部分,或有多个集部分。一个集部分可以放置于模型的任何地方,但是一个 集及其属性在模型约束中被引用之前必须定义了它们。 2.3.1 定义原始集 为了定义一个原始集,必须详细声明: ·集的名字
外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。 在主窗口内的标题为 LINGO Model – LINGO1 的窗口是 LINGO 的默认模型窗口,建立的模型 都都要在该窗口内编码实现。下面举两个例子。
例 1.1 如何在 LINGO 中求解如下的 LP 问题:
min 2x1 + 3x2 s.t.
现在我们将深入介绍如何创建集,并用数据初始化集的属性。学完本节后,你对基于建 模技术的集如何引入模型会有一个基本的理解。
2.1 为什么使用集 集是 LINGO 建模语言的基础,是程序设计最强有力的基本构件。借助于集,能够用一个
共 53 页 2
LINGO 教程
单一的、长的、简明的复合公式表示一系列相似的约束,从而可以快速方便地表达规模较大 的模型。
2.2 什么是集 集是一群相联系的对象,这些对象也称为集的成员。一个集可能是一系列产品、卡车或 雇员。每个集成员可能有一个或多个与之有关联的特征,我们把这些特征称为属性。属性值 可以预先给定,也可以是未知的,有待于 LINGO 求解。例如,产品集中的每个产品可以有一 个价格属性;卡车集中的每辆卡车可以有一个牵引力属性;雇员集中的每位雇员可以有一个 薪水属性,也可以有一个生日属性等等。 LINGO 有两种类型的集:原始集(primitive set)和派生集(derived set)。 一个原始集是由一些最基本的对象组成的。 一个派生集是用一个或多个其它集来定义的,也就是说,它的成员来自于其它已存在的 集。
lingo教程

lingo教程Lingo是一个强大且易于学习的编程语言,用于Adobe Director,一个用于创建互动式多媒体应用程序的软件。
在这个Lingo教程中,我们将介绍一些基本的Lingo语法和使用方法。
首先,让我们从Lingo的变量和数据类型开始。
Lingo支持许多数据类型,包括数字,字符串,布尔值和列表。
要声明一个变量,可以使用“variableName = value”的语法。
例如,要声明一个名为“score”的变量,并将其设置为10,可以使用以下代码:```score = 10```要输出变量的值,可以使用“put”命令。
例如:```put score```这将在屏幕上显示变量的值。
Lingo还支持条件语句和循环。
条件语句用于根据条件执行不同的操作。
例如,以下代码将检查“score”变量的值,并根据其值执行不同的操作:if score > 10 thenput "High score!"elseput "Low score."end if```循环用于重复执行一组操作。
例如,以下代码将显示从1到10的所有数字:```repeat with i = 1 to 10put iend repeat```Lingo还支持函数和自定义命令。
函数用于执行特定的操作并返回一个值。
例如,以下代码定义了一个名为“addNumbers”的函数,它将两个数字相加并返回结果:```function addNumbers(num1, num2)return num1 + num2end addNumbers```要使用这个函数,可以使用以下代码:put addNumbers(5, 3)```这将输出结果为8。
自定义命令用于执行一系列的操作,但不返回任何值。
例如,以下代码定义了一个名为“showMessage”的自定义命令,它将显示一个消息框,并将输入的文本作为参数:```on showMessage(text)alert textend showMessage```要使用这个自定义命令,可以使用以下代码:```showMessage("Hello, world!")```这将显示一个消息框,其中包含文本“Hello, world!”。
lingo中的常用函数格式

一、数学函数LINGO提供了大量的标准数学函数:@abs(x):返回x的绝对值@sin(x):返回x的正弦值,x采用弧度制@cos(x):返回x的余弦值@tan(x):返回x的正切值@exp(x):返回常数e的x次方@log(x):返回x的自然对数@lgm(x):返回x的gamma函数的自然对数(当x为整数时lgm(x)=log(x-1)当x不为整数时,采用线性插值得到结果)。
@sign(x) :如果x<0返回-1;否则,返回1@floor(x):返回x的整数部分。
当x>=0时,返回不超过x的最大整数;当x<0时,返回不低于x的最大整数。
@pow(x,y):指数函数,返回x的y次方的值。
@sqr(x):平方函数,返回x的平方(既x*x)的值。
@sqrt(x):平方根函数,返回x的正的平方根的值。
@sign(x):符号函数,返回x的符号值(x<0时返回-1,x>=0时返回+1)。
@mod(x,y):模函数,返回x对y取模的结果,既x除以y的余数,这里x和y应该是整数@smax(x1,x2,…,xn):返回x1,x2,…,xn中的最大值@smin(x1,x2,…,xn):返回x1,x2,…,xn中的最小值二、变量定界函数@BND(L,X,U):限制L<=X<=U。
注意LINGO中没有与LINDO命令SLB,SUB类似的函数@SLB和@SUB@BIN(X):限制X为0或1。
@FREE(X):取消对X的符号限制(即可取负数、0或正数)。
@GIN(X):限制X为正数。
三、概率函数1.@pbn(p,n,x)二项分布的累积分布函数。
当n和(或)x不是整数时,用线性插值法进行计算。
2.@pcx(n,x)自由度为n的χ2分布的累积分布函数。
3.@peb(a,x)当到达负荷为a,服务系统有x个服务器且允许无穷排队时的Erlang繁忙概率。
4.@pel(a,x)当到达负荷为a,服务系统有x个服务器且不允许排队时的Erlang繁忙概率。
第四讲 LINGO编程举例及Options选项卡主要参数说明

第四讲LINGO编程举例及Options选项卡主要参数说明一、LINGO编程举例例1水资源分配问题。
某水库可分配的水资源量为7个单位,分配给3个用户,各用户在分配一定单位水资源后产生的效益如下表所示,求最优分配方案。
水资源量 1 2 3 4 5 6 7用户1 5 15 40 80 90 95 100 用户2 5 15 40 60 70 73 75 用户3 4 26 40 45 50 51 53解用ijc表示上表所表示的效益矩阵,引入决策矩阵X表示水资源分配情况,其元素ijx的取值为0或1,1ijx=表示给用户i分配j单位水资源。
则目标函数是分配方案的总效益最大,约束条件用两条:①水资源总量7个单位;②每个用户得到的水资源量只能是从0到7共八个数字中的一个,即711, 1,2,3 ijjx i =≤=∑,等价于矩阵X的每行元素之和不能超过1。
于是建立本问题的0-1规划模型如下:3711713711max 1, 1,2,3,..7, 1,2,3,1,2,,7,01, 1,2,3,1,2,,7ij iji j ij j ij i j ij z c x x i s t j x i j x i j ======⎧≤=⎪⎪⎪⋅===⎨⎪⎪===⎪⎩∑∑∑∑∑或Global optimal solution found at iteration: 0 Objective value: 120.0000Variable Value Reduced CostX( 1, 1) 0.000000 -5.000000X( 1, 2) 0.000000 -15.00000X( 1, 3) 0.000000 -40.00000X( 1, 4) 1.000000 -80.00000X( 1, 5) 0.000000 -90.00000X( 1, 6) 0.000000 -95.00000X( 1, 7) 0.000000 -100.0000X( 2, 1) 0.000000 -5.000000X( 2, 2) 0.000000 -15.00000X( 2, 3) 1.000000 -40.00000X( 2, 4) 0.000000 -60.00000X( 2, 5) 0.000000 -70.00000X( 2, 6) 0.000000 -73.00000X( 2, 7) 0.000000 -75.00000X( 3, 1) 0.000000 -4.000000X( 3, 2) 0.000000 -26.00000X( 3, 3) 0.000000 -40.00000X( 3, 4) 0.000000 -45.00000X( 3, 5) 0.000000 -50.00000X( 3, 6) 0.000000 -51.00000例2旅行售货商(TSP )模型的一个实例有一个旅行售货商,从某个城市出发,要遍访若干城市各一次且仅一次,最后返回原出发城市(称能到每个城市一次且仅一次的路线为一个巡回)。
lingo教程(有样例)

Lingo 模型Lingo 是较好的最优化建模工具(详细使用说明见Lingo模型参考),Lingo 模型由两部分组成:(一) 目标(objective):最优化目标。
(二)限制条件(constraint). (下载网址:)1.我的食谱由四种食品组成:,果仁巧克力,冰淇淋,可乐,奶酪.一块果仁巧克力价格为50 美分,一杯冰淇淋价格为20美分, 一瓶可乐价格为30美分, 一快奶酪价格为80美分.我每天的营养最低需求: 500 卡路里,6 盎司巧克力,10 盎司〔讲评〕师:该问题的目标是什么?生:食谱中饮食的成本最低师:限制条件?生:满足每天卡路里,巧克力,糖,脂肪的最低需求师:选择哪些变量?生:果仁巧克力,冰淇淋,可乐,奶酪的数量( 参考模型:lingo-LP1.lg4)讨论:如果巧克力冰淇淋的价格变为原来的两倍,食谱将如何改动?练习:1.1.你决意生产两种糖果:硬糖和软糖,糖果仅由糖,坚果,和巧克力制成.你现在有100盎司糖,20盎司坚果,30盎司巧克力.软糖须含有至少20%的坚果.硬糖须含有至少10%的坚果和10%的巧克力.一盎司的软糖售价为25美分, 一盎司的硬糖售价为20美分. 试安排生产计划( 参考模型:lingo-LP1-1.lg4)1.2.某公司生产 A, B, C 三种产品,售价分别为: A, $10;B,$56;C,$100.生产一单位A,需1小时的劳力; 生产一单位 B,需2小时的劳力加上2单位的A; 生产一单位 C,需3小时的劳力加上1单位的B.现有40小时的劳力, 试安排生产计划.( 参考模型:lingo-LP1-2.lg4)2.Donovan公司生产一种电子产品.已知明年四季度的需求(须按时交货):季度1,4000件; 季度2,2000件; 季度3,3000件; 季度4,10000件;公司员工每年有一个季度休假,每个员工年薪为$30,000,每季度最多可生产500件产品.每个季度末公司须为每件存货付存储费$30.公司现有600件产品,如何安排明年的生产?〔讲评〕师:该问题的目标是什么?生:员工年薪与存储费总和最低师:限制条件?生:每季度初的库存与该季度生产量的和须满足该季度的需求师:如何表示员工总数?生甲:各季度上班的员工x(1),x(2),x(3),x(4)总和生乙:甲的总和是员工总数的3倍,因为每个员工工作3个季度。
Lingo教程四 LINGO的函数模板

Lingo教程四 LINGO的函数有了前几节的基础知识,再加上本节的内容,你就能够借助于LINGO建立并求解复杂的优化模型了。
LINGO有9种类型的函数:1.基本运算符:包括算术运算符、逻辑运算符和关系运算符2.数学函数:三角函数和常规的数学函数3.金融函数:LINGO提供的两种金融函数4.概率函数:LINGO提供了大量概率相关的函数5.变量界定函数:这类函数用来定义变量的取值范围6.集操作函数:这类函数为对集的操作提供帮助7.集循环函数:遍历集的元素,执行一定的操作的函数8.数据输入输出函数:这类函数允许模型和外部数据源相联系,进行数据的输入输出9.辅助函数:各种杂类函数4.1 基本运算符这些运算符是非常基本的,甚至可以不认为它们是一类函数。
事实上,在LINGO中它们是非常重要的。
4.1.1 算术运算符算术运算符是针对数值进行操作的。
LINGO提供了5种二元运算符:^乘方﹡乘/除﹢加﹣减LINGO唯一的一元算术运算符是取反函数“﹣”。
这些运算符的优先级由高到底为:高﹣(取反)^﹡/低﹢﹣运算符的运算次序为从左到右按优先级高低来执行。
运算的次序可以用圆括号“()”来改变。
例4.1算术运算符示例。
2﹣5/3,(2﹢4)/5等等。
4.1.2 逻辑运算符在LINGO中,逻辑运算符主要用于集循环函数的条件表达式中,来控制在函数中哪些集成员被包含,哪些被排斥。
在创建稀疏集时用在成员资格过滤器中。
LINGO具有9种逻辑运算符:#not# 否定该操作数的逻辑值,#not#是一个一元运算符#eq# 若两个运算数相等,则为true;否则为flase#ne# 若两个运算符不相等,则为true;否则为flase#gt# 若左边的运算符严格大于右边的运算符,则为true;否则为flase#ge# 若左边的运算符大于或等于右边的运算符,则为true;否则为flase#lt# 若左边的运算符严格小于右边的运算符,则为true;否则为flase#le# 若左边的运算符小于或等于右边的运算符,则为true;否则为flase#and# 仅当两个参数都为true时,结果为true;否则为flase#or# 仅当两个参数都为false时,结果为false;否则为true这些运算符的优先级由高到低为:高 #not##eq# #ne# #gt# #ge# #lt# #le#低 #and# #or#例4.2逻辑运算符示例2 #gt#3 #and#4 #gt# 2,其结果为假(0)。
lingo用法

Lingo 是一种专门用于线性规划和整数规划的建模和求解语言。
它提供了一种简洁的方式来描述数学模型,并使用线性规划算法求解这些模型。
下面是Lingo 的一些基本用法示例:
1. 变量定义:
- 定义实数变量:`X = 0.5;`
- 定义整数变量:`INT_VAR Y;`
2. 目标函数定义:
- 最小化目标函数:`MIN = 2*X + 3*Y;`
- 最大化目标函数:`MAX = -X + 4*Y;`
3. 约束条件定义:
- 等式约束:`EQUATION C1: X + Y = 10;`
- 不等式约束:`INEQUATION C2: X >= 5;`
- 范围约束:`5 <= Y <= 20;`
4. 求解模型:
- 使用默认求解器求解:`SOLVE;`
- 指定求解器和参数:`SOLVE WITH LP_METHOD=3;` 以上是Lingo 的一些基本用法示例,实际上,Lingo 还提供了更多的功能和语法,用于描述更复杂的数学模型和问题。
它可以处理
线性规划、整数规划、混合整数规划等多种类型的问题,并提供了丰富的优化算法和工具来求解这些问题。
lingo入门教程

lingo入门教程Lingo是一种广泛应用于计算机编程和计算机科学领域的编程语言。
它是用于Adobe Director(一种多媒体应用程序)中的脚本语言,用于控制多媒体元素和动画。
Lingo的语法比较简单易懂,有助于创建交互式和多媒体项目。
下面是一些Lingo的基本概念和用法。
1. 变量(Variables): 在Lingo中,变量用于存储数据值。
变量可以是数字、文本或其他数据类型。
要创建变量,可以使用关键字`global`或`local`,后跟变量名和初始值(可选)。
例如:```global myVariable = 10local myText = "Hello World"```2. 条件语句(Conditional statements): 条件语句用于根据条件执行特定的代码块。
常用的条件语句有`if-then`和`if-then-else`。
例如:```if myVariable > 5 thenalert "Value is greater than 5"elsealert "Value is less than or equal to 5"end if```3. 循环(Loops): 循环用于重复执行一段代码块,直到满足指定条件为止。
Lingo提供了`repeat`和`repeat while`循环语句。
例如:```repeat with i = 1 to 5put iend repeat```4. 函数(Functions): 函数是一组预定义的代码,用于执行特定的任务。
Lingo提供了许多内置函数,如`alert`、`put`等。
您还可以创建自己的函数。
例如:```on multiplyNumbers(a, b)return a * bend multiplyNumbersput multiplyNumbers(2, 4) -- 输出8```这些只是Lingo的一些基本概念和用法。
Lingo计算四元一次方程组

Lingo计算四元一次方程组
用Lingo解方程①每个方程必须以分号“;”结束。
②请注意:Lingo的所有符号都是英文格式下的符号。
③ Lingo的加减乘除分别是:+、-、*、/。
特别注意:(1)2*x+1=1在Lingo中不可以简写为2x+1=1,乘号不能省略。
(2)注意除号“/”的形状,如同函数y=x的图像,而不是y = -x。
Lingo变量① Lingo默认所有变量为大于0的数字,因而非负的条件不必多写。
②万一遇到一个变量可以小于0,可以使用一个函数叫做@free,来使其定义域为R。
③ m和M等价,Lingo不区分大小写,所以mmm、mMm、MMM被视作同一个变量。
所以,在Lingo的使用过程中,全程使用小写为宜。
④在变量命名方面还是尽量字母在前的命名方式。
例如:x , x1 , max_x。
注意:在读取矩阵中的元素的时候,第一个元素是
x(1),不是x1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Lingo教程四 LINGO的函数有了前几节的基础知识,再加上本节的内容,你就能够借助于LINGO建立并求解复杂的优化模型了。
LINGO有9种类型的函数:1.基本运算符:包括算术运算符、逻辑运算符和关系运算符2.数学函数:三角函数和常规的数学函数3.金融函数:LINGO提供的两种金融函数4.概率函数:LINGO提供了大量概率相关的函数5.变量界定函数:这类函数用来定义变量的取值范围6.集操作函数:这类函数为对集的操作提供帮助7.集循环函数:遍历集的元素,执行一定的操作的函数8.数据输入输出函数:这类函数允许模型和外部数据源相联系,进行数据的输入输出9.辅助函数:各种杂类函数4.1 基本运算符这些运算符是非常基本的,甚至可以不认为它们是一类函数。
事实上,在LINGO中它们是非常重要的。
4.1.1 算术运算符算术运算符是针对数值进行操作的。
LINGO提供了5种二元运算符:^乘方﹡乘/除﹢加﹣减LINGO唯一的一元算术运算符是取反函数“﹣”。
这些运算符的优先级由高到底为:高﹣(取反)^﹡/低﹢﹣运算符的运算次序为从左到右按优先级高低来执行。
运算的次序可以用圆括号“()”来改变。
例4.1算术运算符示例。
2﹣5/3,(2﹢4)/5等等。
4.1.2 逻辑运算符在LINGO中,逻辑运算符主要用于集循环函数的条件表达式中,来控制在函数中哪些集成员被包含,哪些被排斥。
在创建稀疏集时用在成员资格过滤器中。
LINGO具有9种逻辑运算符:#not# 否定该操作数的逻辑值,#not#是一个一元运算符#eq# 若两个运算数相等,则为true;否则为flase#ne# 若两个运算符不相等,则为true;否则为flase#gt# 若左边的运算符严格大于右边的运算符,则为true;否则为flase#ge# 若左边的运算符大于或等于右边的运算符,则为true;否则为flase#lt# 若左边的运算符严格小于右边的运算符,则为true;否则为flase#le# 若左边的运算符小于或等于右边的运算符,则为true;否则为flase#and# 仅当两个参数都为true时,结果为true;否则为flase#or# 仅当两个参数都为false时,结果为false;否则为true这些运算符的优先级由高到低为:高 #not##eq# #ne# #gt# #ge# #lt# #le#低 #and# #or#例4.2逻辑运算符示例2 #gt#3 #and#4 #gt# 2,其结果为假(0)。
4.1.3 关系运算符在LINGO中,关系运算符主要是被用在模型中,来指定一个表达式的左边是否等于、小于等于、或者大于等于右边,形成模型的一个约束条件。
关系运算符与逻辑运算符#eq#、#le#、#ge#截然不同,前者是模型中该关系运算符所指定关系的为真描述,而后者仅仅判断一个该关系是否被满足:满足为真,不满足为假。
LINGO有三种关系运算符:“=”、“<=”和“>=”。
LINGO中还能用“<”表示小于等于关系,“>”表示大于等于关系。
LINGO并不支持严格小于和严格大于关系运算符。
然而,如果需要严格小于和严格大于关系,比如让A严格小于B:A<B,那么可以把它变成如下的小于等于表达式:A+ε<=B,这里ε是一个小的正数,它的值依赖于模型中A小于B多少才算不等。
下面给出以上三类操作符的优先级:高#not# ﹣(取反)^﹡/﹢﹣#eq# #ne# #gt# #ge# #lt# #le##and# #or#低 <= = >=4.2 数学函数LINGO提供了大量的标准数学函数:@abs(x) 返回x的绝对值@sin(x) 返回x的正弦值,x采用弧度制@cos(x) 返回x的余弦值@tan(x) 返回x的正切值@exp(x) 返回常数e的x次方@log(x) 返回x的自然对数@lgm(x) 返回x的gamma函数的自然对数@sign(x) 如果x<0返回-1;否则,返回1@floor(x) 返回x的整数部分。
当x>=0时,返回不超过x的最大整数;当x<0时,返回不低于x的最大整数。
@smax(x1,x2,…,xn)返回x1,x2,…,xn中的最大值@smin(x1,x2,…,xn)返回x1,x2,…,xn中的最小值例4.3给定一个直角三角形,求包含该三角形的最小正方形。
解:如图所示。
求最小的正方形就相当于求如下的最优化问题:LINGO代码如下:model:sets:object/1..3/: f;endsetsdata:a, b = 3, 4; !两个直角边长,修改很方便;enddataf(1) = a * @sin(x);f(2) = b * @cos(x);f(3) = a * @cos(x) + b * @sin(x);min = @smax(f(1),f(2),f(3));@bnd(0,x,1.57);end在上面的代码中用到了函数@bnd,详情请见4.5节。
4.3 金融函数目前LINGO提供了两个金融函数。
1.@fpa(I,n)返回如下情形的净现值:单位时段利率为I,连续n个时段支付,每个时段支付单位费用。
若每个时段支付x单位的费用,则净现值可用x乘以@fpa(I,n)算得。
@fpa的计算公式为净现值就是在一定时期内为了获得一定收益在该时期初所支付的实际费用。
例4.4 贷款买房问题贷款金额50000元,贷款年利率5.31%,采取分期付款方式(每年年末还固定金额,直至还清)。
问拟贷款10年,每年需偿还多少元?LINGO代码如下:50000 = x * @fpa(.0531,10);答案是x=6573.069元。
2.@fpl(I,n)返回如下情形的净现值:单位时段利率为I,第n个时段支付单位费用。
@fpl(I,n)的计算公式为细心的读者可以发现这两个函数间的关系:4.4 概率函数1.@pbn(p,n,x)二项分布的累积分布函数。
当n和(或)x不是整数时,用线性插值法进行计算。
2.@pcx(n,x)自由度为n的χ2分布的累积分布函数。
3.@peb(a,x)当到达负荷为a,服务系统有x个服务器且允许无穷排队时的Erlang繁忙概率。
4.@pel(a,x)当到达负荷为a,服务系统有x个服务器且不允许排队时的Erlang繁忙概率。
5.@pfd(n,d,x)自由度为n和d的F分布的累积分布函数。
6.@pfs(a,x,c)当负荷上限为a,顾客数为c,平行服务器数量为x时,有限源的Poisson服务系统的等待或返修顾客数的期望值。
a是顾客数乘以平均服务时间,再除以平均返修时间。
当c和(或)x不是整数时,采用线性插值进行计算。
7.@phg(pop,g,n,x)超几何(Hypergeometric)分布的累积分布函数。
pop表示产品总数,g是正品数。
从所有产品中任意取出n(n≤pop)件。
pop,g,n和x都可以是非整数,这时采用线性插值进行计算。
8.@ppl(a,x)Poisson分布的线性损失函数,即返回max(0,z-x)的期望值,其中随机变量z服从均值为a的Poisson分布。
9.@pps(a,x)均值为a的Poisson分布的累积分布函数。
当x不是整数时,采用线性插值进行计算。
10.@psl(x)单位正态线性损失函数,即返回max(0,z-x)的期望值,其中随机变量z服从标准正态分布。
11.@psn(x)标准正态分布的累积分布函数。
12.@ptd(n,x)自由度为n的t分布的累积分布函数。
13.@qrand(seed)产生服从(0,1)区间的拟随机数。
@qrand只允许在模型的数据部分使用,它将用拟随机数填满集属性。
通常,声明一个m×n的二维表,m表示运行实验的次数,n表示每次实验所需的随机数的个数。
在行内,随机数是独立分布的;在行间,随机数是非常均匀的。
这些随机数是用“分层取样”的方法产生的。
例4.5model:data:M=4; N=2; seed=1234567;enddatasets:rows/1..M/;cols/1..N/;table(rows,cols): x;endsetsdata:X=@qrand(seed);enddataend如果没有为函数指定种子,那么LINGO将用系统时间构造种子。
14.@rand(seed)返回0和1间的伪随机数,依赖于指定的种子。
典型用法是U(I+1)=@rand(U(I))。
注意如果seed不变,那么产生的随机数也不变。
例4.6 利用@rand产生15个标准正态分布的随机数和自由度为2的t分布的随机数。
model:!产生一列正态分布和t分布的随机数;sets:series/1..15/: u, znorm, zt;endsets!第一个均匀分布随机数是任意的;u( 1) = @rand( .1234);!产生其余的均匀分布的随机数;@for(series( I)| I #GT# 1:u( I) = @rand( u( I - 1)));@for( series( I):!正态分布随机数;@psn( znorm( I)) = u( I);!和自由度为2的t分布随机数;@ptd( 2, zt( I)) = u( I);!ZNORM 和 ZT 可以是负数;@free( znorm( I)); @free( zt( I)););end4.5 变量界定函数变量界定函数实现对变量取值范围的附加限制,共4种:@bin(x) 限制x为0或1@bnd(L,x,U) 限制L≤x≤U@free(x) 取消对变量x的默认下界为0的限制,即x可以取任意实数@gin(x) 限制x为整数在默认情况下,LINGO规定变量是非负的,也就是说下界为0,上界为+∞。
@free取消了默认的下界为0的限制,使变量也可以取负值。
@bnd用于设定一个变量的上下界,它也可以取消默认下界为0的约束。
4.6 集操作函数LINGO提供了几个函数帮助处理集。
1.@in(set_name,primitive_index_1 [,primitive_index_2,…])如果元素在指定集中,返回1;否则返回0。
例4.7全集为I,B是I的一个子集,C是B的补集。
sets:I/x1..x4/;B(I)/x2/;C(I)|#not#@in(B,&1):;endsets2.@index([set_name,] primitive_set_element)该函数返回在集set_name中原始集成员primitive_set_element的索引。
如果set_name被忽略,那么LINGO 将返回与primitive_set_element匹配的第一个原始集成员的索引。
