Folding dynamics of the helical structures in a minimal model
2-4 范德瓦尔斯结合
例如: —— 惰性元素具有球对称,结合时排列最紧密以使势能最低 —— Ne、Ar、Kr、Xe的晶体都是面心立方 —— 透明的绝缘体,熔点特低 —— 分别为24K、84K、117K和161K
固体物理(Solid Physics) 重庆交通大学
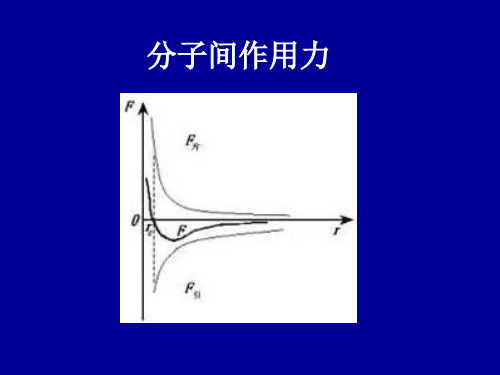
范德瓦尔斯力的本质
1.葛生力(Keesom,亦称静电力)
葛生力:极性分子的永久偶极矩间的静电相互作 用。 最初,人们对范德瓦耳斯键的本质的认识来源于 葛生力(由Keesom1912年提出而得名)。 显然这种静电吸引力大小与偶极矩取向有关。
固体物理(Solid Physics) 重庆交通大学
有金属键的特点。(石墨是一种良导体,可做电
极等) Ⅲ.层与层之间以范德瓦尔斯键结合。(结合力 弱,所以石墨质地疏松,在层与层之间可插入其 它物质,制成石墨插层化合物。)
——石墨是共价键、金属键和分子键的混合键。
固体物理(Solid Physics)
重庆交通大学
2.SiO2、P2O5、B2O3等是形成玻璃的主要形
晶体总的势能
1 12 6 U ( r ) N ( 4 )[ A12 ( ) A6 ( ) ] 2 r r
—— 非极性分子晶体的晶格常数、结合能和体变模量
dU 0 晶格常数 dr r r0
d 2U 平衡状态体变模量 K (V ) 2 V0 dV
晶体的结合能 W U ( r0 )
—— 原子的极化率
2 p p p 两个电偶极子之间的相互作用能 E 1 2 1 6 3 r r
—— 作用能与p1的平方成正比,对时间的平均值不为零 —— 力随距离增加下降很快,两个原子之间的相互作用很弱 两个原子的相互作用势能
A B u( r ) 6 12 间作用力(分子键)成键;通过电偶极
聚集态结构NEW专题知识讲座
聚乙烯单晶monocrystal
聚甲醛单晶旳螺旋形生长
PEO单晶旳多种形态
G. Reiter
单晶构造示意图
球晶Spherulite
球晶旳成长过程
正交偏振光显微镜图像——Maltase 黑十字
纤维状晶体与串晶(“糖葫 芦”“羊肉串”)fibous crystal
串晶
伸直链晶体extended chain crystal
弗洛里(1910-1985) Paul John Flory
成就:是高分子科学理论旳主要开拓者和奠基人之一。 1936年用几率措施得到缩聚产物旳分子量分布(见高聚物旳分子 量分布),现称弗洛里分布。1942年对柔性链高分子溶液旳热力 学性质,提出混合熵公式,即著名旳弗洛里-哈金斯晶格理论,由 此能够阐明高分子溶液旳渗透压、相分离和交联高分子旳溶胀现 象等。1965年他提出溶液热力学旳相应态理论,可合用于从小分 子溶液到高分子溶液旳热力学性质。在柔性链高分子溶液方面, 1949年找到了溶液中高分子形态符合高斯链形态,溶液热力学性 质符合理想溶液性质旳温度-溶剂条件。此温度现称弗洛里温度 或θ-温度,此溶剂通称θ-溶剂。1951年得出著名旳特征粘数方程 式。1956年提出刚性链高分子溶液旳临界轴比和临界浓度,在此 浓度以上将出现线列型液晶相。在高分子汇集态构造方面,他 1953年就从理论上推断高聚物非晶态固体中柔性链高分子旳形态 应与θ-溶剂中旳高斯线团相同,十几年后为中子散射试验所证明。 他还建立了高聚物和共聚物结晶旳热力学理论。他在内旋转异构 体理论方面补充了近邻键内旋转旳相互作用,使构象旳计算到达 实际应用所需旳精确性,能够从分子链旳化学构造定量地计算与 高分子链构象统计有关旳多种数值。
结晶模型——折叠链片晶模型 folded chain lamellae structure model
化学Chapter 1,2

Generalized Displacements
L
y ( x) = ∑ bn sin
n =1
x
∞
nπ x L
b1 sin b2 sin
πx
L 2π x L 3π x L
b3 sin
Deflected shape of the structure is expressed as the sum of a series of specified displacement patterns
ω=
1 k 2 m
Compliance
Example 2 A l/2 l/2 l/2 B l/2
F =1
&& FI = my
C m y
1 1 l 2 l 1 l l 2 l l3 ( ⋅l ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ ⋅ ) = δ11 = 2 3 2 2 2 2 3 2 8EI EI 2
l3 && && y = (−my ) ⋅ δ11 = (− my ) ⋅ 8 EI
y(t)
y(t)
&& & my d (t ) + cy d (t ) + ky st + ky d (t ) = F (t ) + W && & my d (t ) + cy d (t ) + ky d (t ) = F (t ) Subscript d is omitted, still represent dynamic && & my (t ) + cy (t ) + ky (t ) = F (t ) displacement
蛋白质折叠

蛋白质折叠与生物信息流
在生物体内,生物信息流动可分为两个部分: 第一部分是存储于DNA序列中的遗传信息通过
转录和翻译传入蛋白质的一级序列中,这是一 维信息之间的传递,三联子密码介导了这一传 递过程 第二部分是肽链经过疏水塌缩、空间盘曲、侧 链聚集等折叠过程形成蛋白质的天然构象,同 时获得生物活性,从而将生命信息表达出来 蛋白质折叠是一维信息向三维信息的转化过程
Ellis1987年提出了蛋白质“辅助性组装学说”。体内蛋 白质折叠往往需要其他辅助因子参与,并伴有ATP的 水解。因此,蛋白质折叠是一个热力学过程,也受动 力学控制。
有的学者基于有些相似氨基酸序列的蛋白质具有不同 的折叠结构,而一些不同氨基酸序列的蛋白质在结构 上却相似的现象,提出了mRNA二级结构可能作为一 种遗传密码从而影响蛋白质结构的假说。
疏水簇以非特异性布朗运动方式扩散、碰撞、相互黏附, 导致大的结构生成并增加稳定性。
进一步碰撞形成具有疏水核心和二级结构的类熔球态中 间体。
球形中间体调整为致密的、无活性的类似天然结构的高 度有序熔球态结构。
最后无活性高度有序熔球态转变为完整有活力的天然态。
成核-凝聚-生长模型
(Nuclear-Condensation-Growth Model)
拼版模型 (Jig-Saw Puzzle Model)
中心思想是多肽链可以沿多条不同的途径进行 折叠, 在沿每条途径折叠的过程中都是天然结 构越来越多, 最终形成天然构象
每条途径的折叠速度都较快, 与单一途径折叠 方式相比, 多肽链速度较快, 另一方面, 外界 生理生化环境的微小变化或突变等因素可能会 给单一折叠途径造成较大的影响 这些变化可能 给某条折叠途径带来影响, 但不影响另外的折 叠途径, 因而不会从总体上干扰多肽链的折叠
蛋白质折叠的热力学和动力学

蛋白质折叠的热力学和动力学药学院 10489629 苟宝迪蛋白质是一种生物大分子,基本上是由20种氨基酸以肽键连接成肽链。
肽链在空间卷曲折叠成为特定的三维空间结构。
有的蛋白质由多条肽链组成,每条肽链称为亚基,亚基之间又有特定的空间关系,称为蛋白质的四级结构。
所以蛋白质分子有非常特定的复杂的空间结构。
诺贝尔奖得主Anfinsen认为每一种蛋白质分子都有自己特有的氨基酸的组成和排列顺序,由这种氨基酸排列顺序决定它的特定的空间结构。
具有完整一级结构的多肽或蛋白质, 只有当其折叠形成正确的三维空间结构才可能具有正常的生物学功能. 如果这些生物大分子的折叠在体内发生了故障, 形成错误的空间结构, 不但将丧失其生物学功能, 甚至会引起疾病.蛋白质异常的三维空间结构可以引发疾病,疯牛病、老年性痴呆症、囊性纤维病变、家族性高胆固醇症、家族性淀粉样蛋白症、某些肿瘤、白内障等等都是“折叠病”。
蛋白质折叠的研究(图1[1]),是生命科学领域的前沿课题之一。
不仅具有重大的科学意义,而且在医学和在生物工程领域具有极大的应用价值。
图1蛋白质折叠的热力学研究蛋白质折叠的研究,比较狭义的定义就是研究蛋白质特定三维空间结构形成的规律、稳定性和与其生物活性的关系。
这里最根本的科学问题就是多肽链的一级结构到底如何决定它的空间结构?X-射线晶体衍射是至今为止研究蛋白质结构最有效的方法, 所能达到的精度是其它任何方法所不能比拟的. 但是, 蛋白质分离纯化技术要求高, 蛋白质晶体难以培养,晶体结构测定的周期较长, 从而制约了蛋白质工程的进展. 随着近代物理学、数学和分子生物学的发展, 特别是计算机技术的进步, 人们开始用理论计算的方法, 利用计算机来预测蛋白质的结构. 同源模建方法是最常用、最有效的蛋白质结构预测方法. 但是, 利用同源模建方法预测蛋白质结构时, 需用同源蛋白质的已知结构作为模板. 当缺乏这种模板结构时, 预测则很难奏效. 这是该方法的天生缺陷. 是否能从蛋白质序列出发, 直接预测蛋白质的结构?从理论上最直接地去解决蛋白质的折叠问题,就是根据测得的蛋白质的一级序列预测由Anfinsen原理决定的特定的空间结构。
化工热力学

nM f (T , P, n1 , n2 )
微分此式:
d (nM ) [ (nM ) (nM ) (nM ) ] P ,n dT [ ]T ,n dP [ ]T , P ,n j 1 dn1 T P n1
[
(nM ) ]T , P ,n j 2 dn2 n2
对于单相体系,总内能可写成:
nU U t f (nS , nV , n1、n2 ni nN )
全微分为:
(nU ) (nU ) d (nU ) d (nS ) d (nV ) (nS ) nV ,n (nV ) nS ,n (nU ) dni i ni nS ,nV ,n
M ( xi M i )
(4-21)
上两式为偏摩尔量的加和公式。
结论:① 对于纯组分 ② 对于溶液 xi =1,
M1 M
Mi Mi
3.偏摩尔性质间的关系
Hi Ui PVi Ai Ui T Si Gi Hi T Si
dUi Td Si PdVi
d H i Td Si Vi dP
其中,由于体系中只有i 组分变化,故n对ni的导数 等于1。因为此时ni变化多少,n变化多少。
M xk M [( )T , p , x j [ i ,k ] ( )] xk ni k ni T , p ,n j [ i ] xk M [( )T , p , x j [ i ,k ] ( )] xk n k 1 M xk ( )T , p , x j [ i ,k ] n k xk M M i M n( )T , p ,n j [ i ] ni
在恒T,恒P下 (nM ) (nM ) d nM [ ]T , P ,n j 1 dn1 [ ]T , P ,n j 2 dn2 n1 n2
范德华莫尔超晶格中的共振杂化激子异质结构

范德华莫尔超晶格中的共振杂化激子异质结构下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!引言近年来,范德华莫尔超晶格中的共振杂化激子异质结构研究备受关注。
文献翻译--陈建领

外文资料译文多晶体金属多层膜的变形机制图1引言在塑性方面金属多层膜代表了一种探索长度尺度的理想工具。
他们还提供了用控制界面和结构来生产接近理论强度的合成材料的机会。
一些作者依据Hall-Petch和Orowan强化机制探索了长度尺度的影响。
Embury和Fisher 早期绘制的珠光体机制图表明,Hall-Petch在单相金属晶粒细化加强模型也适用于有作为阻碍距离的界面间隔的双相材料。
更多最近的研究,例如Embury-Hirth,Anderson等,Chu和Barnett和Nix 表明在纳米级多层膜的力学行为可能受单个位错行为(Orowan的层间位错弯曲模型),而不是逆着界面的堆积位错。
Masumura等人的另一项最近的研究表明在单相纳米材料中晶粒尺寸低于临界晶粒尺寸,基础的扩散机制,如Coble蠕变可能会执行,并可能导致伴随晶粒细化的软化。
为简便起见,通常这些模型,无论是有单晶成份层的多层膜或多层膜的单相细晶材料都很发达。
了解多晶多层膜的力学性能构成由于两个层厚度和面晶粒的尺寸可能影响屈服强度的一个额外的复杂性。
虽然平面晶粒的大小可能改变层厚度,没有普遍的关系使我们在只知道层厚度时能够计算出晶粒尺寸,反之亦然。
这些参数之间的关系通常是通过详细的微观结构的特性来决定。
因此,对于给定的多晶金属多层膜,我们如何获取关于层厚度和晶粒大小值执行不同的组合,变形机制见解?在本次调查中,我们提出一个简单的分析,使我们在这些不同的机制运作时能够获得微观尺度的极限值。
我们提出的结论在层厚度和晶粒大小的二维图形的形式,包括不同的变形机制的运作。
这些图形的目的是用于解释尺寸强化或多层膜软化机制,相同的方法,像Ashby的变形温度和压力机制图一样,都是依赖金属变形行为。
Frost试图扩展Ashby的变形机制图,他的的铝薄膜变形机制图表明,由于薄膜层的更高的循环应力,预测应变率数量级比实测应变率高几个数量级。
因此,需要开展更多工作纳入薄膜和大块多晶体的变形行为的基本差别,机制图是压力,温度和微观尺度的一个函数。
毕业设计论文塑料注射成型

Modeling of morphology evolution in the injection moldingprocess of thermoplastic polymersR.Pantani,I.Coccorullo,V.Speranza,G.Titomanlio* Department of Chemical and Food Engineering,University of Salerno,via Ponte don Melillo,I-84084Fisciano(Salerno),Italy Received13May2005;received in revised form30August2005;accepted12September2005AbstractA thorough analysis of the effect of operative conditions of injection molding process on the morphology distribution inside the obtained moldings is performed,with particular reference to semi-crystalline polymers.The paper is divided into two parts:in the first part,the state of the art on the subject is outlined and discussed;in the second part,an example of the characterization required for a satisfactorily understanding and description of the phenomena is presented,starting from material characterization,passing through the monitoring of the process cycle and arriving to a deep analysis of morphology distribution inside the moldings.In particular,fully characterized injection molding tests are presented using an isotactic polypropylene,previously carefully characterized as far as most of properties of interest.The effects of both injectionflow rate and mold temperature are analyzed.The resulting moldings morphology(in terms of distribution of crystallinity degree,molecular orientation and crystals structure and dimensions)are analyzed by adopting different experimental techniques(optical,electronic and atomic force microscopy,IR and WAXS analysis).Final morphological characteristics of the samples are compared with the predictions of a simulation code developed at University of Salerno for the simulation of the injection molding process.q2005Elsevier Ltd.All rights reserved.Keywords:Injection molding;Crystallization kinetics;Morphology;Modeling;Isotactic polypropyleneContents1.Introduction (1186)1.1.Morphology distribution in injection molded iPP parts:state of the art (1189)1.1.1.Modeling of the injection molding process (1190)1.1.2.Modeling of the crystallization kinetics (1190)1.1.3.Modeling of the morphology evolution (1191)1.1.4.Modeling of the effect of crystallinity on rheology (1192)1.1.5.Modeling of the molecular orientation (1193)1.1.6.Modeling of theflow-induced crystallization (1195)ments on the state of the art (1197)2.Material and characterization (1198)2.1.PVT description (1198)*Corresponding author.Tel.:C39089964152;fax:C39089964057.E-mail address:gtitomanlio@unisa.it(G.Titomanlio).2.2.Quiescent crystallization kinetics (1198)2.3.Viscosity (1199)2.4.Viscoelastic behavior (1200)3.Injection molding tests and analysis of the moldings (1200)3.1.Injection molding tests and sample preparation (1200)3.2.Microscopy (1202)3.2.1.Optical microscopy (1202)3.2.2.SEM and AFM analysis (1202)3.3.Distribution of crystallinity (1202)3.3.1.IR analysis (1202)3.3.2.X-ray analysis (1203)3.4.Distribution of molecular orientation (1203)4.Analysis of experimental results (1203)4.1.Injection molding tests (1203)4.2.Morphology distribution along thickness direction (1204)4.2.1.Optical microscopy (1204)4.2.2.SEM and AFM analysis (1204)4.3.Morphology distribution alongflow direction (1208)4.4.Distribution of crystallinity (1210)4.4.1.Distribution of crystallinity along thickness direction (1210)4.4.2.Crystallinity distribution alongflow direction (1212)4.5.Distribution of molecular orientation (1212)4.5.1.Orientation along thickness direction (1212)4.5.2.Orientation alongflow direction (1213)4.5.3.Direction of orientation (1214)5.Simulation (1214)5.1.Pressure curves (1215)5.2.Morphology distribution (1215)5.3.Molecular orientation (1216)5.3.1.Molecular orientation distribution along thickness direction (1216)5.3.2.Molecular orientation distribution alongflow direction (1216)5.3.3.Direction of orientation (1217)5.4.Crystallinity distribution (1217)6.Conclusions (1217)References (1219)1.IntroductionInjection molding is one of the most widely employed methods for manufacturing polymeric products.Three main steps are recognized in the molding:filling,packing/holding and cooling.During thefilling stage,a hot polymer melt rapidlyfills a cold mold reproducing a cavity of the desired product shape. During the packing/holding stage,the pressure is raised and extra material is forced into the mold to compensate for the effects that both temperature decrease and crystallinity development determine on density during solidification.The cooling stage starts at the solidification of a thin section at cavity entrance (gate),starting from that instant no more material can enter or exit from the mold impression and holding pressure can be released.When the solid layer on the mold surface reaches a thickness sufficient to assure required rigidity,the product is ejected from the mold.Due to the thermomechanical history experienced by the polymer during processing,macromolecules in injection-molded objects present a local order.This order is referred to as‘morphology’which literally means‘the study of the form’where form stands for the shape and arrangement of parts of the object.When referred to polymers,the word morphology is adopted to indicate:–crystallinity,which is the relative volume occupied by each of the crystalline phases,including mesophases;–dimensions,shape,distribution and orientation of the crystallites;–orientation of amorphous phase.R.Pantani et al./Prog.Polym.Sci.30(2005)1185–1222 1186R.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221187Apart from the scientific interest in understandingthe mechanisms leading to different order levels inside a polymer,the great technological importance of morphology relies on the fact that polymer character-istics (above all mechanical,but also optical,electrical,transport and chemical)are to a great extent affected by morphology.For instance,crystallinity has a pro-nounced effect on the mechanical properties of the bulk material since crystals are generally stiffer than amorphous material,and also orientation induces anisotropy and other changes in mechanical properties.In this work,a thorough analysis of the effect of injection molding operative conditions on morphology distribution in moldings with particular reference to crystalline materials is performed.The aim of the paper is twofold:first,to outline the state of the art on the subject;second,to present an example of the characterization required for asatisfactorilyR.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221188understanding and description of the phenomena, starting from material description,passing through the monitoring of the process cycle and arriving to a deep analysis of morphology distribution inside the mold-ings.To these purposes,fully characterized injection molding tests were performed using an isotactic polypropylene,previously carefully characterized as far as most of properties of interest,in particular quiescent nucleation density,spherulitic growth rate and rheological properties(viscosity and relaxation time)were determined.The resulting moldings mor-phology(in terms of distribution of crystallinity degree, molecular orientation and crystals structure and dimensions)was analyzed by adopting different experimental techniques(optical,electronic and atomic force microscopy,IR and WAXS analysis).Final morphological characteristics of the samples were compared with the predictions of a simulation code developed at University of Salerno for the simulation of the injection molding process.The effects of both injectionflow rate and mold temperature were analyzed.1.1.Morphology distribution in injection molded iPP parts:state of the artFrom many experimental observations,it is shown that a highly oriented lamellar crystallite microstructure, usually referred to as‘skin layer’forms close to the surface of injection molded articles of semi-crystalline polymers.Far from the wall,the melt is allowed to crystallize three dimensionally to form spherulitic structures.Relative dimensions and morphology of both skin and core layers are dependent on local thermo-mechanical history,which is characterized on the surface by high stress levels,decreasing to very small values toward the core region.As a result,the skin and the core reveal distinct characteristics across the thickness and also along theflow path[1].Structural and morphological characterization of the injection molded polypropylene has attracted the interest of researchers in the past three decades.In the early seventies,Kantz et al.[2]studied the morphology of injection molded iPP tensile bars by using optical microscopy and X-ray diffraction.The microscopic results revealed the presence of three distinct crystalline zones on the cross-section:a highly oriented non-spherulitic skin;a shear zone with molecular chains oriented essentially parallel to the injection direction;a spherulitic core with essentially no preferred orientation.The X-ray diffraction studies indicated that the skin layer contains biaxially oriented crystallites due to the biaxial extensionalflow at theflow front.A similar multilayered morphology was also reported by Menges et al.[3].Later on,Fujiyama et al.[4] investigated the skin–core morphology of injection molded iPP samples using X-ray Small and Wide Angle Scattering techniques,and suggested that the shear region contains shish–kebab structures.The same shish–kebab structure was observed by Wenig and Herzog in the shear region of their molded samples[5].A similar investigation was conducted by Titomanlio and co-workers[6],who analyzed the morphology distribution in injection moldings of iPP. They observed a skin–core morphology distribution with an isotropic spherulitic core,a skin layer characterized by afine crystalline structure and an intermediate layer appearing as a dark band in crossed polarized light,this layer being characterized by high crystallinity.Kalay and Bevis[7]pointed out that,although iPP crystallizes essentially in the a-form,a small amount of b-form can be found in the skin layer and in the shear region.The amount of b-form was found to increase by effect of high shear rates[8].A wide analysis on the effect of processing conditions on the morphology of injection molded iPP was conducted by Viana et al.[9]and,more recently, by Mendoza et al.[10].In particular,Mendoza et al. report that the highest level of crystallinity orientation is found inside the shear zone and that a high level of orientation was also found in the skin layer,with an orientation angle tilted toward the core.It is rather difficult to theoretically establish the relationship between the observed microstructure and processing conditions.Indeed,a model of the injection molding process able to predict morphology distribution in thefinal samples is not yet available,even if it would be of enormous strategic importance.This is mainly because a complete understanding of crystallization kinetics in processing conditions(high cooling rates and pressures,strong and complexflowfields)has not yet been reached.In this section,the most relevant aspects for process modeling and morphology development are identified. In particular,a successful path leading to a reliable description of morphology evolution during polymer processing should necessarily pass through:–a good description of morphology evolution under quiescent conditions(accounting all competing crystallization processes),including the range of cooling rates characteristic of processing operations (from1to10008C/s);R.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221189–a description capturing the main features of melt morphology(orientation and stretch)evolution under processing conditions;–a good coupling of the two(quiescent crystallization and orientation)in order to capture the effect of crystallinity on viscosity and the effect offlow on crystallization kinetics.The points listed above outline the strategy to be followed in order to achieve the basic understanding for a satisfactory description of morphology evolution during all polymer processing operations.In the following,the state of art for each of those points will be analyzed in a dedicated section.1.1.1.Modeling of the injection molding processThefirst step in the prediction of the morphology distribution within injection moldings is obviously the thermo-mechanical simulation of the process.Much of the efforts in the past were focused on the prediction of pressure and temperature evolution during the process and on the prediction of the melt front advancement [11–15].The simulation of injection molding involves the simultaneous solution of the mass,energy and momentum balance equations.Thefluid is non-New-tonian(and viscoelastic)with all parameters dependent upon temperature,pressure,crystallinity,which are all function of pressibility cannot be neglected as theflow during the packing/holding step is determined by density changes due to temperature, pressure and crystallinity evolution.Indeed,apart from some attempts to introduce a full 3D approach[16–19],the analysis is currently still often restricted to the Hele–Shaw(or thinfilm) approximation,which is warranted by the fact that most injection molded parts have the characteristic of being thin.Furthermore,it is recognized that the viscoelastic behavior of the polymer only marginally influences theflow kinematics[20–22]thus the melt is normally considered as a non-Newtonian viscousfluid for the description of pressure and velocity gradients evolution.Some examples of adopting a viscoelastic constitutive equation in the momentum balance equations are found in the literature[23],but the improvements in accuracy do not justify a considerable extension of computational effort.It has to be mentioned that the analysis of some features of kinematics and temperature gradients affecting the description of morphology need a more accurate description with respect to the analysis of pressure distributions.Some aspects of the process which were often neglected and may have a critical importance are the description of the heat transfer at polymer–mold interface[24–26]and of the effect of mold deformation[24,27,28].Another aspect of particular interest to the develop-ment of morphology is the fountainflow[29–32], which is often neglected being restricted to a rather small region at theflow front and close to the mold walls.1.1.2.Modeling of the crystallization kineticsIt is obvious that the description of crystallization kinetics is necessary if thefinal morphology of the molded object wants to be described.Also,the development of a crystalline degree during the process influences the evolution of all material properties like density and,above all,viscosity(see below).Further-more,crystallization kinetics enters explicitly in the generation term of the energy balance,through the latent heat of crystallization[26,33].It is therefore clear that the crystallinity degree is not only a result of simulation but also(and above all)a phenomenon to be kept into account in each step of process modeling.In spite of its dramatic influence on the process,the efforts to simulate the injection molding of semi-crystalline polymers are crude in most of the commercial software for processing simulation and rather scarce in the fleur and Kamal[34],Papatanasiu[35], Titomanlio et al.[15],Han and Wang[36],Ito et al.[37],Manzione[38],Guo and Isayev[26],and Hieber [25]adopted the following equation(Kolmogoroff–Avrami–Evans,KAE)to predict the development of crystallinityd xd tZð1K xÞd d cd t(1)where x is the relative degree of crystallization;d c is the undisturbed volume fraction of the crystals(if no impingement would occur).A significant improvement in the prediction of crystallinity development was introduced by Titoman-lio and co-workers[39]who kept into account the possibility of the formation of different crystalline phases.This was done by assuming a parallel of several non-interacting kinetic processes competing for the available amorphous volume.The evolution of each phase can thus be described byd x id tZð1K xÞd d c id t(2)where the subscript i stands for a particular phase,x i is the relative degree of crystallization,x ZPix i and d c iR.Pantani et al./Prog.Polym.Sci.30(2005)1185–1222 1190is the expectancy of volume fraction of each phase if no impingement would occur.Eq.(2)assumes that,for each phase,the probability of the fraction increase of a single crystalline phase is simply the product of the rate of growth of the corresponding undisturbed volume fraction and of the amount of available amorphous fraction.By summing up the phase evolution equations of all phases(Eq.(2))over the index i,and solving the resulting differential equation,one simply obtainsxðtÞZ1K exp½K d cðtÞ (3)where d c Z Pid c i and Eq.(1)is recovered.It was shown by Coccorullo et al.[40]with reference to an iPP,that the description of the kinetic competition between phases is crucial to a reliable prediction of solidified structures:indeed,it is not possible to describe iPP crystallization kinetics in the range of cooling rates of interest for processing(i.e.up to several hundreds of8C/s)if the mesomorphic phase is neglected:in the cooling rate range10–1008C/s, spherulite crystals in the a-phase are overcome by the formation of the mesophase.Furthermore,it has been found that in some conditions(mainly at pressures higher than100MPa,and low cooling rates),the g-phase can also form[41].In spite of this,the presence of different crystalline phases is usually neglected in the literature,essentially because the range of cooling rates investigated for characterization falls in the DSC range (well lower than typical cooling rates of interest for the process)and only one crystalline phase is formed for iPP at low cooling rates.It has to be noticed that for iPP,which presents a T g well lower than ambient temperature,high values of crystallinity degree are always found in solids which passed through ambient temperature,and the cooling rate can only determine which crystalline phase forms, roughly a-phase at low cooling rates(below about 508C/s)and mesomorphic phase at higher cooling rates.The most widespread approach to the description of kinetic constant is the isokinetic approach introduced by Nakamura et al.According to this model,d c in Eq.(1)is calculated asd cðtÞZ ln2ðt0KðTðsÞÞd s2 435n(4)where K is the kinetic constant and n is the so-called Avrami index.When introduced as in Eq.(4),the reciprocal of the kinetic constant is a characteristic time for crystallization,namely the crystallization half-time, t05.If a polymer is cooled through the crystallization temperature,crystallization takes place at the tempera-ture at which crystallization half-time is of the order of characteristic cooling time t q defined ast q Z D T=q(5) where q is the cooling rate and D T is a temperature interval over which the crystallization kinetic constant changes of at least one order of magnitude.The temperature dependence of the kinetic constant is modeled using some analytical function which,in the simplest approach,is described by a Gaussian shaped curve:KðTÞZ K0exp K4ln2ðT K T maxÞ2D2(6)The following Hoffman–Lauritzen expression[42] is also commonly adopted:K½TðtÞ Z K0exp KUÃR$ðTðtÞK T NÞ!exp KKÃ$ðTðtÞC T mÞ2TðtÞ2$ðT m K TðtÞÞð7ÞBoth equations describe a bell shaped curve with a maximum which for Eq.(6)is located at T Z T max and for Eq.(7)lies at a temperature between T m(the melting temperature)and T N(which is classically assumed to be 308C below the glass transition temperature).Accord-ing to Eq.(7),the kinetic constant is exactly zero at T Z T m and at T Z T N,whereas Eq.(6)describes a reduction of several orders of magnitude when the temperature departs from T max of a value higher than2D.It is worth mentioning that only three parameters are needed for Eq.(6),whereas Eq.(7)needs the definition offive parameters.Some authors[43,44]couple the above equations with the so-called‘induction time’,which can be defined as the time the crystallization process starts, when the temperature is below the equilibrium melting temperature.It is normally described as[45]Dt indDtZðT0m K TÞat m(8)where t m,T0m and a are material constants.It should be mentioned that it has been found[46,47]that there is no need to explicitly incorporate an induction time when the modeling is based upon the KAE equation(Eq.(1)).1.1.3.Modeling of the morphology evolutionDespite of the fact that the approaches based on Eq.(4)do represent a significant step toward the descriptionR.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221191of morphology,it has often been pointed out in the literature that the isokinetic approach on which Nakamura’s equation (Eq.(4))is based does not describe details of structure formation [48].For instance,the well-known experience that,with many polymers,the number of spherulites in the final solid sample increases strongly with increasing cooling rate,is indeed not taken into account by this approach.Furthermore,Eq.(4)describes an increase of crystal-linity (at constant temperature)depending only on the current value of crystallinity degree itself,whereas it is expected that the crystallization rate should depend also on the number of crystalline entities present in the material.These limits are overcome by considering the crystallization phenomenon as the consequence of nucleation and growth.Kolmogoroff’s model [49],which describes crystallinity evolution accounting of the number of nuclei per unit volume and spherulitic growth rate can then be applied.In this case,d c in Eq.(1)is described asd ðt ÞZ C m ðt 0d N ðs Þd s$ðt sG ðu Þd u 2435nd s (9)where C m is a shape factor (C 3Z 4/3p ,for spherical growth),G (T (t ))is the linear growth rate,and N (T (t ))is the nucleation density.The following Hoffman–Lauritzen expression is normally adopted for the growth rateG ½T ðt Þ Z G 0exp KUR $ðT ðt ÞK T N Þ!exp K K g $ðT ðt ÞC T m Þ2T ðt Þ2$ðT m K T ðt ÞÞð10ÞEqs.(7)and (10)have the same form,however the values of the constants are different.The nucleation mechanism can be either homo-geneous or heterogeneous.In the case of heterogeneous nucleation,two equations are reported in the literature,both describing the nucleation density as a function of temperature [37,50]:N ðT ðt ÞÞZ N 0exp ½j $ðT m K T ðt ÞÞ (11)N ðT ðt ÞÞZ N 0exp K 3$T mT ðt ÞðT m K T ðt ÞÞ(12)In the case of homogeneous nucleation,the nucleation rate rather than the nucleation density is function of temperature,and a Hoffman–Lauritzen expression isadoptedd N ðT ðt ÞÞd t Z N 0exp K C 1ðT ðt ÞK T N Þ!exp KC 2$ðT ðt ÞC T m ÞT ðt Þ$ðT m K T ðt ÞÞð13ÞConcentration of nucleating particles is usually quite significant in commercial polymers,and thus hetero-geneous nucleation becomes the dominant mechanism.When Kolmogoroff’s approach is followed,the number N a of active nuclei at the end of the crystal-lization process can be calculated as [48]N a ;final Zðt final 0d N ½T ðs Þd sð1K x ðs ÞÞd s (14)and the average dimension of crystalline structures can be attained by geometrical considerations.Pantani et al.[51]and Zuidema et al.[22]exploited this method to describe the distribution of crystallinity and the final average radius of the spherulites in injection moldings of polypropylene;in particular,they adopted the following equationR Z ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi3x a ;final 4p N a ;final 3s (15)A different approach is also present in the literature,somehow halfway between Nakamura’s and Kolmo-goroff’s models:the growth rate (G )and the kinetic constant (K )are described independently,and the number of active nuclei (and consequently the average dimensions of crystalline entities)can be obtained by coupling Eqs.(4)and (9)asN a ðT ÞZ 3ln 24p K ðT ÞG ðT Þ 3(16)where heterogeneous nucleation and spherical growth is assumed (Avrami’s index Z 3).Guo et al.[43]adopted this approach to describe the dimensions of spherulites in injection moldings of polypropylene.1.1.4.Modeling of the effect of crystallinity on rheology As mentioned above,crystallization has a dramatic influence on material viscosity.This phenomenon must obviously be taken into account and,indeed,the solidification of a semi-crystalline material is essen-tially caused by crystallization rather than by tempera-ture in normal processing conditions.Despite of the importance of the subject,the relevant literature on the effect of crystallinity on viscosity isR.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221192rather scarce.This might be due to the difficulties in measuring simultaneously rheological properties and crystallinity evolution during the same tests.Apart from some attempts to obtain simultaneous measure-ments of crystallinity and viscosity by special setups [52,53],more often viscosity and crystallinity are measured during separate tests having the same thermal history,thus greatly simplifying the experimental approach.Nevertheless,very few works can be retrieved in the literature in which(shear or complex) viscosity can be somehow linked to a crystallinity development.This is the case of Winter and co-workers [54],Vleeshouwers and Meijer[55](crystallinity evolution can be drawn from Swartjes[56]),Boutahar et al.[57],Titomanlio et al.[15],Han and Wang[36], Floudas et al.[58],Wassner and Maier[59],Pantani et al.[60],Pogodina et al.[61],Acierno and Grizzuti[62].All the authors essentially agree that melt viscosity experiences an abrupt increase when crystallinity degree reaches a certain‘critical’value,x c[15]. However,little agreement is found in the literature on the value of this critical crystallinity degree:assuming that x c is reached when the viscosity increases of one order of magnitude with respect to the molten state,it is found in the literature that,for iPP,x c ranges from a value of a few percent[15,62,60,58]up to values of20–30%[58,61]or even higher than40%[59,54,57].Some studies are also reported on the secondary effects of relevant variables such as temperature or shear rate(or frequency)on the dependence of crystallinity on viscosity.As for the effect of temperature,Titomanlio[15]found for an iPP that the increase of viscosity for the same crystallinity degree was higher at lower temperatures,whereas Winter[63] reports the opposite trend for a thermoplastic elasto-meric polypropylene.As for the effect of shear rate,a general agreement is found in the literature that the increase of viscosity for the same crystallinity degree is lower at higher deformation rates[62,61,57].Essentially,the equations adopted to describe the effect of crystallinity on viscosity of polymers can be grouped into two main categories:–equations based on suspensions theories(for a review,see[64]or[65]);–empirical equations.Some of the equations adopted in the literature with regard to polymer processing are summarized in Table1.Apart from Eq.(17)adopted by Katayama and Yoon [66],all equations predict a sharp increase of viscosity on increasing crystallinity,sometimes reaching infinite (Eqs.(18)and(21)).All authors consider that the relevant variable is the volume occupied by crystalline entities(i.e.x),even if the dimensions of the crystals should reasonably have an effect.1.1.5.Modeling of the molecular orientationOne of the most challenging problems to present day polymer science regards the reliable prediction of molecular orientation during transformation processes. Indeed,although pressure and velocity distribution during injection molding can be satisfactorily described by viscous models,details of the viscoelastic nature of the polymer need to be accounted for in the descriptionTable1List of the most used equations to describe the effect of crystallinity on viscosityEquation Author Derivation Parameters h=h0Z1C a0x(17)Katayama[66]Suspensions a Z99h=h0Z1=ðx K x cÞa0(18)Ziabicki[67]Empirical x c Z0.1h=h0Z1C a1expðK a2=x a3Þ(19)Titomanlio[15],also adopted byGuo[68]and Hieber[25]Empiricalh=h0Z expða1x a2Þ(20)Shimizu[69],also adopted byZuidema[22]and Hieber[25]Empiricalh=h0Z1Cðx=a1Þa2=ð1Kðx=a1Þa2Þ(21)Tanner[70]Empirical,basedon suspensionsa1Z0.44for compact crystallitesa1Z0.68for spherical crystallitesh=h0Z expða1x C a2x2Þ(22)Han[36]Empiricalh=h0Z1C a1x C a2x2(23)Tanner[71]Empirical a1Z0.54,a2Z4,x!0.4h=h0Zð1K x=a0ÞK2(24)Metzner[65],also adopted byTanner[70]Suspensions a Z0.68for smooth spheresR.Pantani et al./Prog.Polym.Sci.30(2005)1185–12221193。
固体力学英语词汇翻译(1)

固体力学英语词汇翻译(1)固体力学英语词汇翻译(1)固体力学英语词汇翻译(1)弹性力学elasticity弹性理论theory of elasticity均匀应力状态homogeneous state of stress应力不变量stress invariant应变不变量strain invariant应变椭球strain ellipsoid均匀应变状态homogeneous state of strain应变协调方程equation of strain compatibility拉梅常量lame constants各向同性弹性isotropic elasticity旋转圆盘rotating circular disk楔wedge开尔文问题kelvin problem布西内斯克问题boussinesq problem艾里应力函数airy stress function克罗索夫-穆斯赫利什维利法kolosoff-muskhelishvili method基尔霍夫假设kirchhoff hypothesis板plate矩形板rectangular plate圆板circular plate环板annular plate波纹板corrugated plate加劲板stiffened plate,reinforced plate中厚板plate of moderate thickness弯[曲]应力函数stress function of bending 壳shell扁壳shallow shell旋转壳revolutionary shell球壳spherical shell[圆]柱壳cylindrical shell锥壳conical shell环壳toroidal shell封闭壳closed shell波纹壳corrugated shell扭[转]应力函数stress function of torsion 翘曲函数warping function半逆解法semi-inverse method瑞利--里茨法rayleigh-ritz method松弛法relaxation method莱维法levy method松弛relaxation量纲分析dimensional analysis自相似[性] self-similarity影响面influence surface接触应力contact stress赫兹理论hertz theory协调接触conforming contact滑动接触sliding contact滚动接触rolling contact压入indentation各向异性弹性anisotropic elasticity颗粒材料granular material散体力学mechanics of granular media 热弹性thermoelasticity超弹性hyperelasticity粘弹性viscoelasticity对应原理correspondence principle褶皱wrinkle塑性全量理论total theory of plasticity 滑动sliding微滑microslip粗糙度roughness非线性弹性nonlinear elasticity 大挠度large deflection突弹跳变snap-through有限变形finite deformation格林应变green strain阿尔曼西应变almansi strain弹性动力学dynamic elasticity运动方程equation of motion准静态的quasi-static气动弹性aeroelasticity水弹性hydroelasticity颤振flutter弹性波elastic wave简单波simple wave柱面波cylindrical wave水平剪切波horizontal shear wave 竖直剪切波vertical shear wave 体波body wave无旋波irrotational wave畸变波distortion wave膨胀波dilatation wave瑞利波rayleigh wave等容波equivoluminal wave勒夫波love wave界面波interfacial wave边缘效应edge effect塑性力学plasticity可成形性formability金属成形metal forming耐撞性crashworthiness结构抗撞毁性structural crashworthiness拉拔drawing破坏机构collapse mechanism回弹springback挤压extrusion冲压stamping穿透perforation层裂spalling塑性理论theory of plasticity安定[性]理论shake-down theory运动安定定理kinematic shake-down theorem 静力安定定理static shake-down theorem率相关理论rate dependent theorem载荷因子load factor加载准则loading criterion加载函数loading function加载面loading surface塑性加载plastic loading塑性加载波plastic loading wave 简单加载simple loading比例加载proportional loading 卸载unloading卸载波unloading wave冲击载荷impulsive load阶跃载荷step load脉冲载荷pulse load极限载荷limit load中性变载nentral loading拉抻失稳instability in tension 加速度波acceleration wave本构方程constitutive equation 完全解complete solution名义应力nominal stress过应力over-stress真应力true stress等效应力equivalent stress流动应力flow stress应力间断stress discontinuity应力空间stress space主应力空间principal stress space静水应力状态hydrostatic state of stress对数应变logarithmic strain工程应变engineering strain等效应变equivalent strain应变局部化strain localization应变率strain rate应变率敏感性strain rate sensitivity应变空间strain space有限应变finite strain塑性应变增量plastic strain increment累积塑性应变accumulated plastic strain永久变形permanent deformation内变量internal variable应变软化strain-softening理想刚塑性材料rigid-perfectly plastic material刚塑性材料rigid-plastic material理想塑性材料perfectl plastic material材料稳定性stability of material应变偏张量deviatoric tensor of strain应力偏张量deviatori tensor of stress应变球张量spherical tensor of strain应力球张量spherical tensor of stress路径相关性path-dependency线性强化linear strain-hardening应变强化strain-hardening随动强化kinematic hardening各向同性强化isotropic hardening强化模量strain-hardening modulus幂强化power hardening塑性极限弯矩plastic limit bending moment塑性极限扭矩plastic limit torque弹塑性弯曲elastic-plastic bending弹塑性交界面elastic-plastic interface弹塑性扭转elastic-plastic torsion粘塑性viscoplasticity非弹性inelasticity理想弹塑性材料elastic-perfectly plastic material极限分析limit analysis极限设计limit design极限面limit surface上限定理upper bound theorem上屈服点upper yield point下限定理lower bound theorem下屈服点lower yield point界限定理bound theorem初始屈服面initial yield surface后继屈服面subsequent yield surface屈服面[的]外凸性convexity of yield surface 截面形状因子shape factor of cross-section 沙堆比拟sand heap analogy屈服yield屈服条件yield condition屈服准则yield criterion屈服函数yield function屈服面yield surface塑性势plastic potential能量吸收装置energy absorbing device能量耗散率energy absorbing device塑性动力学dynamic plasticity塑性动力屈曲dynamic plastic buckling塑性动力响应dynamic plastic response塑性波plastic wave运动容许场kinematically admissible field静力容许场statically admissible field流动法则flow rule速度间断velocity discontinuity滑移线slip-lines滑移线场slip-lines field移行塑性铰travelling plastic hinge塑性增量理论incremental theory of plasticity米泽斯屈服准则mises yield criterion普朗特--罗伊斯关系prandtl- reuss relation特雷斯卡屈服准则tresca yield criterion洛德应力参数lode stress parameter莱维--米泽斯关系levy-mises relation亨基应力方程hencky stress equation赫艾--韦斯特加德应力空间haigh-westergaard stress space 洛德应变参数lode strain parameter德鲁克公设drucker postulate盖林格速度方程geiringer velocity equation结构力学structural mechanics结构分析structural analysis结构动力学structural dynamics拱arch三铰拱three-hinged arch抛物线拱parabolic arch圆拱circular arch穹顶dome空间结构space structure空间桁架space truss雪载[荷] snow load风载[荷] wind load土压力earth pressure地震载荷earthquake loading弹簧支座spring support支座位移support displacement支座沉降support settlement超静定次数degree of indeterminacy 机动分析kinematic analysis结点法method of joints截面法method of sections结点力joint forces共轭位移conjugate displacement影响线influence line三弯矩方程three-moment equation单位虚力unit virtual force刚度系数stiffness coefficient柔度系数flexibility coefficient力矩分配moment distribution力矩分配法moment distribution method力矩再分配moment redistribution分配系数distribution factor矩阵位移法matri displacement method单元刚度矩阵element stiffness matrix单元应变矩阵element strain matrix总体坐标global coordinates贝蒂定理betti theorem高斯--若尔当消去法gauss-jordan elimination method 屈曲模态buckling mode复合材料力学mechanics of composites复合材料composite material纤维复合材料fibrous composite单向复合材料unidirectional composite泡沫复合材料foamed composite颗粒复合材料particulate composite层板laminate夹层板sandwich panel正交层板cross-ply laminate斜交层板angle-ply laminate层片ply多胞固体cellular solid膨胀expansion压实debulk劣化degradation脱层delamination脱粘debond纤维应力fiber stress层应力ply stress层应变ply strain层间应力interlaminar stress比强度specific strength强度折减系数strength reduction factor 强度应力比strength -stress ratio横向剪切模量transverse shear modulus 横观各向同性transverse isotropy正交各向异orthotropy剪滞分析shear lag analysis短纤维chopped fiber长纤维continuous fiber纤维方向fiber direction纤维断裂fiber break纤维拔脱fiber pull-out纤维增强fiber reinforcement致密化densification最小重量设计optimum weight design网格分析法netting analysis混合律rule of mixture失效准则failure criterion蔡--吴失效准则tsai-w u failure criterion达格代尔模型dugdale model断裂力学fracture mechanics概率断裂力学probabilistic fracture mechanics格里菲思理论griffith theory线弹性断裂力学linear elastic fracture mechanics, lefm 弹塑性断裂力学elastic-plastic fracture mecha-nics, epfm 断裂fracture脆性断裂brittle fracture解理断裂cleavage fracture蠕变断裂creep fracture延性断裂ductile fracture晶间断裂inter-granular fracture准解理断裂quasi-cleavage fracture 穿晶断裂trans-granular fracture裂纹crack裂缝flaw缺陷defect割缝slit微裂纹microcrack折裂kink椭圆裂纹elliptical crack深埋裂纹embedded crack[钱]币状裂纹penny-shape crack预制裂纹precrack短裂纹short crack表面裂纹surface crack裂纹钝化crack blunting裂纹分叉crack branching裂纹闭合crack closure裂纹前缘crack front裂纹嘴crack mouth裂纹张开角crack opening angle,coa裂纹张开位移crack opening displacement, cod 裂纹阻力crack resistance固体力学英语词汇翻译(1) 相关内容:。
何曼君高分子物理名词解释完整版

几何异构(顺反异构):由于主链双键的碳原子上的取代基不能绕双键旋转,当组成双键的两个碳原子同时被两个不同的原子或基团取代时,即可形成顺式、反式两种构型,它们称作几何异构。
键接异构(顺序异构):是指结构单元在高分子链中的连接方式。一般头-尾相连占主导优势,而头-头(或尾-尾)相连所占比例较低。
(2)侧基:侧基的极性越大,极性基团数目越多,相互作用越强,单键内旋转越困难,分子链柔顺性越差。非极性侧基的体积越大,内旋转位阻越大,柔顺性越差。对称性侧基,可使分子链间的距离增大,相互作用减弱,柔顺性大。侧基对称性越高,分子链柔顺性越好。
(3)支化:1、短支链使分子链间距离加大,分子间作用力减弱,从而对链柔性具有一定改善作用。2、长支链则起到阻碍单键内旋转作用,导致链柔性下降。
4.柔顺性的比较(分子结构对柔顺性的影响)
答:由于分子内旋转是导致分子链柔顺性的根本原因,而高分子链的内旋转又受其分子结构的制约,因而分子链的柔顺性与其分子结构密切相关。分子结构对柔顺性的影响有:
(1)主链结构:1、主链完全由C-C键组成的碳链高分子都具有较大的柔性。如PE、PP和乙丙橡胶等。2、当主链中含C-O,C-N,Si-O键时,柔顺性好。(这是因为O、N原子周围的原子比C原子少,内旋转的位阻小;而Si-O-Si的键角也大于C-C-C键,因而其内旋转位阻更小,即使在低温下也具有良好的柔顺性。如::-Si-O->-C-O->-C-C-。)3、当主链中含非共轭双键时,虽然双键本身不会内旋转,但却使相邻单键的非键合原子(带*原子)间距增大使内旋转较容易,柔顺性好。4、当主链中由共轭双键组成时,由于共轭双键因p电子云重叠不能内旋转,因而柔顺性差,是刚性链。如聚乙炔、聚苯。5、在主链中引入不能内旋转的芳环、芳杂环等环状结构,可提高分子链的刚性。
带旋转自由度的四边形平板壳单元

边界上 的参数 F在 节点 i 为 - 1, 在节点 j 为 + 1, 取值范围为 - 1 [ F[ 1; l ij 是 ij 边的长度 . 1. 3 切线刚度推导 推导采用的是 U. L. 列式 . 几何方程为 9u 9x 9v 9y 9u 9v + 9y 9x 9H x 9x
y 9H 9y
a ( 4 , 5) = [ N 9 ( F ) - N 5( F ) ] sinA cos A a ( 4 , 9) = N 7 ( F ) cos A a ( 4 , 10) = N 6 ( F ) sin A+ N 10 ( F ) cos A a ( 4 , 11) = [ N 10 ( F ) - N 6( F ) ] sin A cos A a ( 5 , 1) = N 8 ( F ) sinA a ( 5 , 2) = [ N 9 ( F ) - N 5( F ) ] sinA cos A a ( 5 , 3) = N 5 ( F ) cos2 A+ N 9 ( F ) sin2 A a ( 5 , 9) = N 7 ( F ) sinA a ( 5 , 10) = [ N 10 ( F ) - N 6( F ) ] sin A cos A a ( 5 , 11) = N 6 ( F ) cos2 A+ N 10 ( F ) sin2 A a ( 6 , 1) = N 7 ( F ) sinA a ( 6 , 2) = - N 7 ( F ) cos A a ( 6 , 6) = N 9 ( F ) a ( 6, 7) = N 8 ( F ) sinA a ( 6 , 8) = - N 8 ( F ) cos A a ( 6 , 12) = N 10 ( F ) a 中未给出的值为 0. N 1 ( F ) ~ N 10 ( F )为
高分子物理名词解释

一、概念与名词第一章高分子链的结构高聚物的结构指组成高分子的不同尺度的结构单元在空间相对排列,包括高分子的链结构和聚集态结构。
高分子链结构表明一个高分子链中原子或基团的几何排列情况。
聚集态结构指高分子整体的内部结构,包括晶态结构、非晶态结构、取向态结构、液晶态结构和织态结构。
近程结构指单个大分子内一个或几个结构单元的化学结构和立体化学结构。
远程结构指单个高分子的大小和在空间所存在的各种形状称为远程结构化学结构除非通过化学键的断裂和生成新的化学键才能改变的分子结构为化学结构。
物理结构而一个分子或其基团对另一个分子的相互作用构型分子中各原子在空间的相对位置和排列叫做构型,这种化学结构不经过键的破坏或生成是不能改变的。
旋光异构结构单元-CH2--C*HR-型的高分子,由于每一个结构单元含有一个C*,因此,它们在高分子链中有三中键接方式,即全同、间同、无规立构,此即为旋光异构。
全同立构结构单元-CH2--C*HR-型的高分子,由于每一个结构单元含有一个C*,因此,它们在高分子链中有三种键接方式,若高分子链中C*的异构体是相同的,此即为全同立构。
间同立构结构单元-CH2--C*HR-型的高分子,由于每一个结构单元含有一个C*,因此,它们在高分子链中有三种键接方式,若高分子链中C*的两种异构体是交替出现的,此即为间同立构。
无规立构结构单元-CH2--C*HR-型的高分子,由于每一个结构单元含有一个C*,因此,它们在高分子链中有三种键接方式,若高分子链中C*的两种异构体是无规则出现的,此即为无规立构。
有规立构全同和间同立构高分子统称为有规立构。
等规度全同立构高分子或全同立构高分子和间同立构高分子在高聚物中的百分含量。
几何异构当主链上存在双键时,而组成双键的两个碳原子同时被两个不同的原子或基团取代时,即可形成顺反异构,此即为几何异构。
顺反异构当主链上存在双键时,而组成双键的两个碳原子同时被两个不同的原子或基团取代时,即可形成顺反异构,此即为几何异构。
蛋白质折叠过程中的动力学和热力学研究

蛋白质折叠过程中的动力学和热力学研究蛋白质是生命体中最重要的分子之一。
它们是生化反应的催化剂和信使,构成生命机体的各种功能元件。
蛋白质的功能与结构息息相关。
而蛋白质的结构又直接由其折叠状态决定。
越来越多的研究表明,蛋白质折叠过程中的动力学和热力学是影响蛋白质结构及功能的重要因素。
对于一个蛋白质分子来说,其折叠状态决定了它的生物学功能。
尽管所有蛋白质都是由氨基酸组成的,但它们之间的相互作用可以形成多样化的结构和功能。
研究表明,引起蛋白质折叠的力包括范德华力、氢键、静电相互作用和水化作用等。
折叠过程中,蛋白质分子会自发地寻求最佳构象,使其自由能降至最小,从而加强其稳定性和生物学功能。
折叠过程中的热力学是影响蛋白质结构的重要因素。
蛋白质的熵趋向于增加,而它的内能则趋向于减小。
因此,折叠蛋白质的自由能需要在熵减与内能减的平衡中达到最小值。
不同的氨基酸序列和环境条件会导致蛋白质折叠过程中自由能曲线的变化。
这也就意味着,不同的蛋白质可能需要不同的营养物质来保持其稳定结构和正常功能。
此外,环境因素如酸碱度和温度,也会对蛋白质的稳定性产生影响。
动力学在折叠过程中也扮演了重要角色。
蛋白质的折叠速率、稳定性和膜蛋白的结构都与动力学有关。
针对动力学问题,科学家们使用了各种技术与方法。
例如,利用分子动力学模拟(molecular dynamics)和核磁共振技术(NMR),分析蛋白质分子的结构和动力学行为。
分子动力学模拟是预测蛋白质结构的重要工具,可以模拟蛋白质在任何条件下的构象,从而了解折叠过程中的动力学细节。
另外,NMR不仅可以提供关于蛋白质结构的信息,也可解析蛋白质的动力学。
在蛋白质折叠研究领域,最近几年出现了许多新的技术和方法。
其中一些新技术,如单分子荧光技术,可以观测单个蛋白质的折叠过程。
此外,某些实验室开发的新分析方法,如质谱法和生物信息学,能够增加对蛋白质折叠的认识。
这些研究成果不仅提高了折叠的可控性,也为制备未知结构蛋白质提供了路线。
Von-Karman板方程的摄动—复变函数解法

Von-Karman板方程的摄动—复变函数解法
刘平;付功义
【期刊名称】《四川建筑科学研究》
【年(卷),期】2015(041)006
【摘要】板的大挠度方程由Von-Karman于1909年推导出来,这便是著名的Von-Karman大挠度方程组. 但是,由于Von-Karman方程为八阶非线性耦合方程,求解十分困难,至今尚无精确解. 为求解Von-Karman方程,一般采用瑞利李兹法、能量法、迦辽金法及摄动法以求得近似解. 复变函数最初由原苏联科学家柯索洛夫引入解弹性平面问题,而后由穆什维海尔院士集大成,解决弹性平面问题及一系列孔洞及复杂边界问题,后由萨文、卢尔瓦兹等一批原苏联科学家引入到求解板的小挠度方程问题中. 本文进一步将复变函数推广到板的大挠度方程中,得出Von-Karman方程在复变函数下的表达式;另外,给出了求解大挠度板复变函数方法的一般步骤,并求解出固支边界圆板的渐近解.
【总页数】5页(P6-10)
【作者】刘平;付功义
【作者单位】江苏科技大学,江苏镇江 212003;上海交通大学,上海 200240
【正文语种】中文
【中图分类】TU33
【相关文献】
1.工科复变函数中一道作业题不同解法的讨论 [J], 李景和
2.基于复变函数解法的桁材开孔腹板弹性屈曲分析 [J], 杨源; 莫中华; 唐文勇; 孙启荣; 沈亚明
3.复变函数的matlab解法探究 [J], 张春玲;魏永亮;冯贵平
4.奇异摄动方程的样条函数解法 [J], 钱芝蓁;耿秀芬;张伟江
5.正交各向异性板平面剪切型裂纹应力强度因子的复变-变分解法 [J], 崔德渝;张行因版权原因,仅展示原文概要,查看原文内容请购买。
力学专业英语部分翻译(孟庆元)

1、应力和应变应力和应变的概念可以通过考虑一个棱柱形杆的拉伸这样一个简单的方式来说明。
一个棱柱形的杆是一个遍及它的长度方向和直轴都是恒定的横截面。
在这个实例中,假设在杆的两端施加有轴向力F,并且在杆上产生了均匀的伸长或者拉紧。
通过在杆上人工分割出一个垂直于其轴的截面mm,我们可以分离出杆的部分作为自由体【如图1(b)】。
在左端施加有拉力P,在另一个端有一个代表杆上被移除部分作用在仍然保存的那部分的力。
这些力是连续分布在横截面的,类似于静水压力在被淹没表面的连续分布。
力的集度,也就是单位面积上的力,叫做应力,通常是用希腊字母,来表示。
假设应力在横截面上是均匀分布的【如图1(b)】,我们可以很容易的看出它的合力等于集度,乘以杆的横截面积A。
而且,从图1所示的物体的平衡,我们可以看出它的合力与力P必须的大小相等,方向相反。
因此,我们可以得出等式(1)可以作为棱柱形杆上均匀应力的方程。
这个等式表明应力的单位是,力除以面积。
当杆被力P拉伸时,如图所示,产生的应力是拉应力,如果力在方向是相反,使杆被压缩,它们就叫做压应力。
使等式(1)成立的一个必要条件是,应力,必须是均匀分布在杆的横截面上。
如果轴向力P作用在横截面的形心处,那么这个条件就实现了。
当力P没有通过形心时,杆会发生弯曲,这就需要更复杂的分析。
目前,我们假设所有的轴向力都是作用在横截面的形心处,除非有相反情况特别说明。
同样,除非另有说明,一般也假设物体的质量是忽略的,如我们讨论图1的杆一样。
轴向力使杆产生的全部伸长量,用希腊字母δ表示【如图1(a)】,单位长度的伸长量,或者应变,可以用等式来决定。
L是杆的总长。
注意应变ε是一个无量纲的量。
只要应变是在杆的长度方向均匀的,应变就可以从等式(2)中准确获得。
如果杆处于拉伸状态,应变就是就是压应变,这也就意味着杆上临近的横截面是互相靠近的。
当材料的应力和应变显示的是线性关系时,也就是线弹性。
这对多数固体材料来说是极其重要的性质,包括多数金属,塑料,木材,混凝土和陶瓷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Abstract
The folding of a polypeptide is an example of the cooperative effects of the amino-acid residues. Of recent interest is how a secondary structure, such as a helix, spontaneously forms during the collapse of a peptide from an initial denatured state. The Monte Carlo implementation of a recent helix-forming model enables us to study the entire folding process dynamically. As shown by the computer simulations, the foldability and helical propagation are both strongly correlated to the nucleation properties of the sequence. 64.60Cn, 87.15.By, 64.70.Kb
monomers can attain when forming a bond. A Monte Carlo (MC) procedure is implemented after that point, and the entire chain begins to collapse to the ordered helical state (Fig. 2a right). The process allows us to examine the kinetics of domain growth of the ordered segments. The key features of the helical-forming model are kept the same as in our previous study; however, some minor changes have been implemented to tailor the model towards a more realistic helix folding experiment. When randomly chosen, the rotation of a monomer about the axis defined by the two nearest neighbors is attempted according to the Metropolis rule [12]. The bond angles can now fluctuate slightly around 2π/3 with an energy cost [13], which maintains a worm-like backbone and allows for small local movements. The second change is the replacement of the square-well potential for the monomer-monomer interaction in our original work by the Lennard-Jones model which allows for a more smooth dynamic motion when two monomers interact [14]. Our last change breaks the symmetry between left and right handed helices. The vector u ˆ described in Fig. 1 is tilted to make a correct right hand bonding in a helical state after accounting for the pitch of the helix [15]. In the first set of numerical experiments (Model I), chains with number of residues N = 19, 25, 31, 37, 43, and 49 were considered. With each N , forty folding events were performed with the allowed maximum folding time tmax listed in Table 1. Fig. 2a is a time lapse image of a typical folding event (N = 49), where the left plot corresponds to an initial configuration, equilibrated at T = ∞, and the last plot a completely folded state. From the observation of these folding events, three important features emerge. (1) For shorter chains (N < 31) there is no clear indication of a preferred nucleation site; the entire chain folds directly to the ordered helix state. Almost all of the events that did not fold into the preferred helical state acquire intermediate, poorly wrapped globular states. (2) For longer chains, the entire folding event accompanies a nucleation propagation process, an expected mechanism for a cooperative system. As demonstrated in Fig. 2a, the nucleation starts at the ends of the chain and gradually heads towards the center, which is 3
Folding dynamics of the helical structure observed in a minimal model
arXiv:cond-mat/0201374v1 [cond-mat.soft] 21 Jan 2002
Josh P. Kemp and Jeff Z.Y. Chen
Typeset using REVTEX 1
Attempting to understand the complex functional nature of proteins is one of the most challenging problems in molecular biology. In the past 10 years, considerable effort has been made to show that these molecules are far from atypical polymer chains made of disordered amino-acids. Despite the seemingly disordered nature of the sequence, every protein possesses some remarkably similar basic characteristics. Much of the current knowledge has been derived from computer simulations of simplified protein models [2–5]. One of the ultimate goals of theoretical modeling is to offer a base for quantitative comparison with experimental structural determinations. Therefore, it would be advantageous to generalize minimal models in an off-lattice, three-dimensional setting. For example, in an off-lattice G¯ o-type model [4], a heteropolymer with interactions between residues is constructed in such a way that the interaction matrix is chosen to yield the desired native state. [4,6,7]. The essence of these lattice and off-lattice models is that protein structures are created out of heterogeneity of the sequence. There is no doubt that heterogeneity plays a dominant role in structure selection; however, secondary structures are known to originate from a number of other important effects such as hydrogen bonding. This suggests that additional considerations should be made in theoretical models in order to capture structural and dynamical properties that go beyond the heterogeneity consideration in a sequence. In a recent Letter, we have stressed the need to include a directional biased residueresidue potential energy in order to design a significantly ordered native state, using the helical structure as an example [8]. In particular, we have shown that an almost perfect helical native structure could be produced from a homopolymer backbone with a squarewell potential that prefers parallel bond angle planes (Fig. 1). This preference, written in a very compact mathematical form, can be thought of as a simple adaptation of much more complex hydrogen-bonding and dipole potential energies [8–11]. In this Letter, we present the folding dynamics study of helix-forming polymers based on thiumerical experiment, a denatured initial configuration is wellequilibrated at high temperature (Fig. 2a left), and is then quenched below the coil-helix transition temperature at T = 0.6ǫ/kB , where ǫ is the maximum attractive energy that two 2
