分式1
7.1分式(1)

第一关:已知肉骨头每斤8元,花 了n元,问可以买多少斤?
n n÷8 8
第一关:已知肉骨头每斤8元,花了n 元,问可以买多少斤?
n n÷8 8
第二关:若肉骨头每斤n元,花了8元,
问可以买多少斤? 8 8÷n n
第三关:若花40元买了a斤香蕉和b 斤橙子,问这两种水果的平均价格是 第五关:若买了4元/斤的香蕉a斤, 多少? 5元/斤的橙子b斤, 40 问这两中水果的平均价格是多少? 40÷(a+b)
小猪每秒比小狗多走了(b-a)米,
所以小猪赶上小狗的时间是:
6a 6a÷(b-a)= b a(秒).
当b=6,a=5时,小猪追上小狗的时间是 6a 65 = 6 5 30 (秒)。 ba 6a 答:小猪赶上小狗的时间是 b a 秒.当b=6,a=5, 时,求小猪追上小狗的时间是30秒。
3 xB)9 2 ( A) x 1 ( x 的值为零. X=3 3.当___时,分式
(C ) x 1或x 2
x2
谢谢朋友们!
( D) x 1且x 2
小猪以b米每秒的速度继续前进, 突然它看到了在它前面6a米的地 方有一只小狗正以a米每秒的速度 前进(b>a) ,求小猪追上小狗需要多 少时间?
பைடு நூலகம்
分式中字母的取值不能使分母为零。 当分母为零时,分式就没有意义。
2x 3 分式 x2
有意义,x应取什么数?
解:当分式的分母为0时,分式无意义. ∴当x+2=0时,即当x=-2时, 分式无意义. ∴x应该取除-2外的任何实数.
2x 1 对于分式 3x 5
(1)当x取什么数时,分式有意义?
(2)当X=1时,分式的值是多少?
分式1

分式1分式的概念:一般地,如果A、B表示两个整式,且B中含有字母,那么式子A / B 就叫做分式,其中A称为分子,B 称为分母。
分式是不同于整式的一类代数式。
分式条件1.分式有意义条件:分母不为0。
2.分式值为0条件:分子为0且分母不为0。
3.分式值为正(负)数条件:分子分母同号得正,异号得负。
4.分式值为1的条件:分子=分母≠0。
5.分式值为-1的条件:分子分母互为相反数,且都不为0。
分式的基本性质分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变。
用式子表示为:(A,B,C为整式,且B、C≠0)运算法则:约分根据分式基本性质,可以把一个分式的分子和分母的公因式约去,这种变形称为分式的约分。
约分的关键是确定分式中分子与分母的公因式。
约分步骤:1.如果分式的分子和分母都是单项式或者是几个因式乘积的形式,将它们的公因式约去。
2.分式的分子和分母都是多项式,将分子和分母分别分解因式,再将公因式约去。
公因式的提取方法:系数取分子和分母系数的最大公约数,字母取分子和分母共有的字母,指数取公共字母的最小指数,即为它们的公因式。
最简分式:一个分式不能约分时,这个分式称为最简分式。
约分时,一般将一个分式化为最简分式。
根据分数的基本性质,异分母的分数可以通分,使几个分数的的分母相同;同样,根据分式的基本性质,分式也可以进行类似的变形,使几个异分母分式的分母相同,而分式的值不变。
通分:把几个异分母分式分别化为与原分式值相等的同分母分式,叫做分式的通分。
它与约分是互逆运算。
通分步骤:先求出所有分式分母的最简公分母,再将所有分式的分母变为最简公分母。
同时各分式按照分母所扩大的倍数,相应扩大各自的分子。
最简公分母的确定方法:系数取各因式系数的最小公倍数,相同字母的最高次幂及单独字母的幂的乘积。
同分母加减同分母的分式相加减,分母不变,分子相加减。
用字母表示为:。
异分母加减异分母的分式相加减,通分化为同分母的分式,然后再按同分母分式的加减法法则进行计算。
1.1 分式(1)

类比分数来学习分式
1、分数
5 π 有意义吗? , 有意义吗? 0 0
a+1 2、分式 2a 有意义的条件是什么? 有意义的条件是什么? a+1 3、分式 2a 中 ,a 可取多少值? 可取多少值? a+1 4、计算a=1, a=2时,分式 计算a =2时 值分别是多少? 值分别是多少? 2a
补充例题
2、什么叫做分式? 什么叫做分式?
P59,然后作答. P59,然后作答. 如果整式A除以整式B 可以表示成的形式. 如果整式A除以整式B, 可以表示成的形式. A 且除式B中含有字母, 分式(fraction) 且除式B中含有字母,那么称式子 B 为分式(fraction). 其中, 其中,A叫做分式的 分子 ,B叫做分式的 分母 .
例1 当x取什么值时,下列分式有意义? 取什么值时,下列分式有意义? x −1 x 2x ⑴ x−2 , ⑵ 4x + 1 , ⑶ | x | −3 解⑴: 由分母 x-2=0,得 x=2. 2=0, x ≠2时 所以当 x≠2时, 分式 有意义. 有意义. x−2
1 +1=0, 解⑵ :由分母 4x+1=0,得 x= - . 4 1 x −1 所以当 x≠- 时, 分式 有意义. 有意义. 4 4x + 1
x − 2 的值为零. 的值为零. 2x − 1 4、已知,当x=5时,分式 2 x + k 的值等于零, 已知, =5时 的值等于零, 3x − 2 则k =-10 .
⑵ 当x =2 时,分式
感悟与反思
1、这节课你有哪些收获? 这节课你有哪些收获? 2、目前 ,你学到了哪些式子?能举几个例子吗? 你学到了哪些式子?能举几个例子吗? 3、区分整式与分式的依据?分式有意义有条件吗? 区分整式与分式的依据?分式有意义有条件吗? 学习方法指导: 学习方法指导: 分式是表示具体情景中数量的模型, 分式是表示具体情景中数量的模型,分式是分 所以其性质与运算是完全类似的. 数的代数化 ,所以其性质与运算是完全类似的. 数学(分式)与现实世界密切联系. 数学(分式)与现实世界密切联系. 以前用字母表示数量关系是整式, 以前用字母表示数量关系是整式,以后表示数 量关系的式子可以是分式. 量关系的式子可以是分式.
分式(1)(分式概念、基本性质)

分式(1)(分式概念、基本性质) 一、基础知识梳理:1.分式的概念:一般地,如果A ,B 表示两个整式,并且B 中含有字母,那么式子BA做分式。
A 叫做分子,B 叫做分母. 分式的概念要注意以下几点:(1)分式是两个整式相除的商,其中分母是除式,分子是被除式,而分数线则可以理解为除号,还含有括号的作用;(2)分式的分子可以含字母,也可以不含字母,但分母必须含有字母;(3)分式有意义的条件是分母不能为0.2.分式的基本性质:分式的分子分母同时乘以或除以同一个不为0的整式,分式的值不变.3.分式的约分(1)约分的概念:把一个分式的分子与分母的公因式约去,叫做分式的约分. (2)分式约分的依据:分式的基本性质.(3)分式约分的方法:把分式的分子与分母分解因式,然后约去分子与分母的公因式. 4.最简分式的概念:一个分式的分子与分母没有公因式时,叫做最简分式. 二、针对性练习: (一)、填空题: 1.对于分式122x x -+(1)当________时,分式的值为0 ;(2)当________时,分式的值为1;(3)当________时,分式无意义; (4)当________时,分式有意义.2.填充分子,使等式成立;()222(2)a a a -=++; ()22233x x x -=-+- 3.填充分母,使等式成立:()2223434254x x x x -+-=--- ; ()21a a a c ++=(a ≠0). 4.化简:233812a b c a bc =_______;6425633224a b c a b c = ;224488a ba b-=- ;223265a a a a ++=++ ;()()x y a y x a --322= . 5.不改变分式的值,把下列各式的分子和分母中各项系数都化为整数:0.010.50.30.04x y x y -=+ ;y x y x 6.02125.054-+= ;=-+b a ba 41323121 . 6.不改变分式的值,使下列各分式的分子、分母中最高次项的系数都是正数:(1)2211x x x y +++-= ; (2)343223324x x x x -+---= .7.(1)已知:34y x =,则2222352235x xy y x xy y-++-= . (2)已知0345x y m==≠,则x y m x y m +++-= . 8.若||x x x x -+-=+123132成立,则x 的取值范围是 . (二)、选择题:9.在下列有理式221121a x x m n x y x y ya b ,,,,++-+-()()中,分式的个数是( ) A. 1B. 2C. 3D. 410.把分式xx y+(x ≠0,y ≠0)中的分子、分母的x ,y 同时扩大2倍,那么分式的值 ( ) A .扩大2倍 B .缩小2倍 C .改变 D .不改变 11.下列等式正确的是 ( )A .22b b a a =B .1a b a b -+=--C .0a b a b +=+D .0.10.330.22a b a ba b a b--=++12.与分式a ba b-+--相等的是 ( )A .a b a b +- B .a b a b -+ C .a b a b +-- D a ba b--+ 13.下列等式从左到右的变形正确的是 ( )A .b a =11b a ++B b bm a am =C .2ab b a a= D .22b b a a =14.不改变分式的值,使21233xx x --+-的分子、分母中的最高次项的系数都是正数,则分式可化为 ( )A .22133x x x -+- B .22133x x x +++ C .22133x x x ++- D .22133x x x --+ 15.将分式253xyx y -+的分子和分母中的各项系数都化为整数,应为 ( )A .235x y x y -+ B .151535x y x y -+ C .1530610x y x y -+ D .253x yx y-+16.下列各式正确的是 ( )A .c c a b a b -=-++ B .c c a b b a -=-+- C .c c a b a b -=-++ D .c ca b a b-=-+- 17.不改变分式的值,分式22923a a a ---可变形为 ( )A .31a a ++ B .31a a -- C .31a a +- D .31a a -+ 18.不改变分式的值,把分式23427431a a a a a a -++--+-中的分子和分母按a 的升幂排列,是其中最高项系数为正,正确的变形是 ( )A .23437431a a a a a a -++-+- B .23347413a a a a a a -+--++C .23434731a a a a a a +-+--+-D .23347413a a a a a a -++--++19.已知a b ,为有理数,要使分式ab的值为非负数,a b ,应满足的条件是( ) A. a b ≥≠00, B. a b ≤<00,C. a b ≥>00,D. a b ≥>00,,或a b ≤<00,20.已知113a b-=,求2322a ab b a ab b ----的值( ) A. 12 B. 23 C. 95D. 4(三)、解答题:21.已知:3x y -=20,求x xy y x xy y 2222323-++-的值.22.已知:x x 210--=,求x x441+的值. 23.化简:x x x x x x 32325396512++-++-. 24.把分式1882483222a b ab a b++++化为一个整式和一个分子为常数的分式的和,并且求出这个整式与分式的乘积等于多少?25. 已知:x y y y +=--=22402,,求y xy-的值.26. 已知:a b c ++=0,求a b c b c a c a b()()()1111113++++++的值. 27.已知:,ac zc b y b a x -=-=-求z y x ++的值.28.已知:,0,1=++=++z cy b x a c z b y a x 求222222cz b y a x ++的值.。
分式1 分式定义和分式的基本性质

分式定义和分式的基本性质一、基础知识:1. 分式定义:(1)、代数式:用运算符号(包括加、减、乘、除、乘方、开方)把数或表示数的字母连结而成的式子叫做代数式;单独一个数或一个字母 代数式;(2)、单项式:只含 运算的代数式叫做单项式;单独一个数或一个字母 单项式; 单项式中的叫做单项式的系数,单项式中所有字母指数的叫做单项式的次数;(3)、多项式:几个 的和叫做多形式;多形式中的每个单项式叫做多形式的 ,多形式里含有几项,就把这个多形式叫做 ,其中次数最高的项的次数叫做这个多形式的 ,不含字母的项叫做 ; (4)、整式: 和 统称为整式;(5)、分式:一般地,如果A 、B 表示两个整式,并且B 中含有 ,那么代数式 叫做分式,其中A 是分式的分子,B 是分式的分母。
2.分式的基本性质:(1)、分式的基本性质:分式的分子和分母都乘(或除以) 一个不等于 的整式,分式的值 ; 即A B =A×CB×C , A B =A÷CB÷C (其中C 是不等于0的整式); (2)、有关概念:①分式的约分:根据分式的基本性质,把一个分式的分子和分母分别除以它们的 ,叫做分式的约分;约分的目的是把分式 ;②最简分式:分子和分母没有 的分式叫做最简分式;③分式的通分:根据分式的基本性质,把几个 分母的分式变形成 分母的分式,叫做分式的通分,变形后的分母叫做这几个分式的公分母;④最简公分母:几个分式中各分母系数(都是整数)的最小 与所有字母的最高次幂的 叫做这几个分式的最简公分母。
二、经典例题: 题型一:考查分式的定义例1、下列代数式中:yx yx y x y x b a b a y x x -++-+--1,,,21,22π,分式有: 个。
变式训练:下列各式中哪些是分式:9x+4, x 7 , 209y +, 54-m , 238y y -,91-x题型二:考查分式有意义的条件 例2、当x 有何值时,下列分式有意义(1)44+-x x (2)122-x (3)xx 11-变式训练:当x 有何值时,下列分式有意义 (1)232+x x(2)3||6--x x题型三:考查分式的值为0的条件 例3、当x 取何值时,下列分式的值为0. (1)31+-x x(2)42||2--x x (3)653222----x x x x变式训练:当x 取何值时,下列分式的值为0. (1)x x 37+ (2)xx 3217- (3)x 2−1x 2−x题型四:考查分式的值为正、负的条件例4、(1)当x 时,分式x-84为正; (2)当x 时,分式2)1(35-+-x x 为负;变式训练:当x 时,分式32+-x x 为非负数. 题型五:化分数系数、小数系数为整数系数例5、不改变分式的值,把分子、分母的系数化为整数. (1)y x yx 41313221+- (2)ba ba +-04.003.02.0变式训练:不改变分式的值,把分子、分母的系数化为整数. yx yx 5.008.02.003.0+-题型六:分数的系数变号例6、不改变分式的值,把下列分式的分子、分母的首项的符号变为正号. (1)yx yx --+- (2)ba a---(3)b a ---变式训练:不改变分式的值,使下列分式的分子和分母都不含“-”号.(1) 233ab y x -- (2) 2317ba ---题型七:约分例7、将下列各式 化为最简分式:(1)c ab bc a 2321525- (2)96922++-x x x (3)yx y xy x 33612622-+-变式训练:将下列各式 化为最简分式:(1)ac bc 2 (2)22)(y x xyx ++ (3)b a b ab a +++36922题型八:通分例8、通分:(1)xab ,yac ; (2)yx (y +1) ,xy (y +1); (3)aab−b ,bab +a.变式训练:通分:(1)cb ac a b ab c 225,3,2--; (2)a b b b a a 22,--;题型九:化简求值题例9、已知:511=+y x ,求yxy x yxy x +++-2232的值. 变式训练:已知:311=-b a ,求a ab b b ab a ---+232的 ;例10、已知:21=-x x ,求221xx +的值. 变式训练:已知:31=+x x ,求1242++x x x 的值.例11、若0)32(|1|2=-++-x y x ,求yx 241-的值.变式训练:若0106222=+-++b b a a ,求ba ba 532+-的值.三、巩固练习:1.当x 取何值时,下列分式有意义:(1)3||61-x(2)1)1(32++-x x2.当x 为何值时,下列分式的值为零: (1)4|1|5+--x x(2)562522+--x x x3.解下列不等式 (1)012||≤+-x x (2)03252>+++x x x4.不改变分式的值,把分式b a ba 10141534.0-+的分子、分母的系数化为整数. 5.如果21<<x ,试化简x x --2|2|xx x x |||1|1+---.6.分式11−x ,11+x ,12x1+x 的最简公分母为四、课后作业:1.当x 取何值时,分式x111+有意义:2当x 为何值时,分式 的值为零x x x --213.约分: (1)2)(xy yy x + (2)222)(y x y x --(3)b a abc ab 22369+ (4)122362+-x x4.通分:(1)22,21,1222--+--x x x x xx x ; (2)aa -+21,25.已知:31=+x x ,求1242++x x x 的值.。
分式(一)

专题二:分式分式的基本概念,基本性质,运算法则;部分分式:把一个分式写成几个简单分式的代数和,称为将分式化为部分分式,它是分式运算的常用技巧。
分式运算的技巧还有:换元法、整体法、逐项求和、拆项求和等。
解数学题是运用已知条件去探求未知结论的一个过程。
如何运用已知条件是解题顺畅的重要前提,对已知条件的运用有下列途径: (1) 直接运用条件; (2) 变形运用条件; (3) 综合运用条件; (4) 挖掘隐含条件.在解某些含多个字母的代数式问题时,如果已知与未知之间的联系不明显,为了沟通已知与未知之间的联系,则可考虑引入一个参数,参数的引入,可起到沟通变元、消元的功能.一、基本概念与计算: 例1、要使分式xx -11有意义,则x 的取值范围是 . 例2、 112525,_______2x xy y x y x xy y -++==++已知则例3、,,00,111111a b c a b c b c c a a b≠++=已知,且则a(+)+b(+)+c(+)的值是_____例4、111111221112()()113a baba b a b a b-⨯-⨯-++已知a,b 为整数,且满足=,求a+b 的值.例5、方程11422x x +=-的一个根是4,则它的另一个根是_________例6、已知,,a b c 均为实数,且257(1)(2)112x a b cx x x x x -=++---+-, 求abc 的值。
例7、 方程2(21)5160x x x -+--+=的所有根的和是( ) 例8 方程111+6x y= 有( )组正整数解. 例9、13217219211211215217292x x x xx x x x----+=+----练习一:1.x 取______________值时, 112122x +++有意义.2. 当3221,(1)(1)(1)0a a x a x a <-+++-+=时,方程的根的情况是( ) A 两负根 B 一正一负,且负根的绝对值大 C 一正一负,且正根的绝对值大 D 没有实数根3、若分式322(4)(4)2218812512a a a a m m a a -----+--- 的值与 a 的取值无关,求m 的值。
10.1 分式(1)

探索规律,揭示新知
做一做
(1)一个n边形,若每个内角都相等,则每个内角为度.
(2)小明用a元钱去购买练习本,原价每本b元,现在每本降价1元,那么现在可以购买本练习本.
刚才我们一起列出了代数式:、、、、、、.
这些代数式有什么共同的特征?
(2x-3)为0的x的值是多少?(由分母2x-3=0,得x=)
所以只要x≠,分式就有意义.
解:由分母2x-3=0,得x=;
所以当x≠时,分式有意义.
教学
环节
学生自学共研的内容方法
(按环节设计自学、讨论、训练、探索、创新等内容)
教师施教提要
(启发、精讲、活动等)
再次
优化
随堂
练习
课堂
小结
达标
检测
练习.
1.列代数式,并说明列出的代数式是否为分式.
如果它的宽是am,那么这块玻璃的长是m.
教学
环节
学生自学共研的内容方法
(按环节设计自学、讨论、训练、探索、创新等内容)
教师施教提要
(启发、精讲、活动等)
再次优化合作探究图片2:小丽买瓜子的情境.
小丽用n元人民币买了m袋相同包装的瓜子,你能写出每袋瓜子的价格吗?
(是(n÷m)元,通常用元来表示.)
图片3:学生去公园旅行.
某校八年级学生步行到距学校12公里的郊外去旅行,一班的学生组成前队步行速度为x千米/时,一班到达目的地的时间用了时,二班的学生组成后队,速度比一队每小时快2千米,则他们到达目的地的时间为h.
图片4:棉田问题.
有两块棉田,一块面积为aha,产棉花mkg;另一块面积为bha,产棉花nkg.这两块棉田平均每公顷产棉花多少千克?
8年级--分式1

专题:反比例函数1、分式定义则分式无意义;如果________且________不为零时,则分式的值为零. (3)分式的分子、分母和分式本身的符号改变其中任何________个,分式的值不变.2、分式的化简与计算(1)分式约分的主要步骤是:把分式的分子与分母________,然后约去分子与分母的公因式.的积.(3)分式的乘除法法则表示为:_______; ________.1、分式性质下列各式中 ①38n m ++m 2 ②1+x +y 2-z 1 ③π213-x ④x 1分式有 ,整式有 . 2.当a=2时,分式aa 21+的值为 . 3.()()23+÷-m m 写成分式为____________,且当m≠_____时分式有意义.4.当x= 时,分式135-+x x 无意义;当x= 时,这个分式的值为零. 5.当x 时,分式1212+-x x有意义;当x= 时,这个分式的值为零.6.当x= 时,分式123-+x x 的值为零;当分式23+-x x =0时,x= . 7.用分式填空:(1)小明t 小时走了s 千米的路,则小明的速度是 千米/时;(2)某食堂有煤m 吨,原计划每天烧煤a 吨,现每天节约用煤b (a b <)吨,则这批煤可比原计划多烧________天;(3)小明参加打靶比赛,有a 次打了m 环,b 次打了n 环,则此次打靶的平均成绩是________; (4)一箱苹果售价p 元,总重m 千克,箱重n 千克,则每千克苹果的售价是______元;8.已知有理式:x 4、4a 、yx -1、43x 、21x 2、a 1+4,其中分式有 ( ) A .2个 B .3个 C .4个 D .5个9.在一段坡路,小明骑自行车上坡的速度为每小时v 1千米,下坡时的速度为每小时v 2千米,则他在这段路上、下坡的平均速度是每小时( ).A .221v v +千米B .2121v v v v +千米C .21212v v v v +千米 D .无法确定10.当x 为任意实数时,下列分式中一定有意义的是( )A .21x x - B .112-+x x C .112+-x x D .21+-x x11.当x 取什么数时,下列分式有意义.(1)912-x (2)ax 45-12.当x 取什么值时,下列分式的值为零.(1)242+-x x (2)2)1)(2(--+x x x13.当x=2时分式ax x --314没有意义,求a 的值.14.若分式2122-++x x x 的值为负数,求x 的取值范围.15.当x 取何整数时,分式14-x 的值是整数.16.已知:3223222⨯=+,8338332⨯=+,154415442⨯=+,245524552⨯=+,…若ab a b ⨯=+21010符合前面式子的规律,求a+b 的值.下列说法正确的是( )A.如果A ,B 是整式,那么BA就叫做分式; B.只要分式的分子为零,则分式的值就为零;C.只要分式的分母为零,则分式必无意义;D.因为x x 2不是分式,而是整式.2.在x 1,21,212+x ,πxy 3,a+m 1中,分式的个数有( )A. 2个B. 3个C. 4个D. 5个3.使分式12--a aa 有意义的a 取值应是( )A. 任意实数B. a 1-≠C. a 1≠D. a 0≠或14.要使分式1122+-a a 有意义,则a 取值应是( )A .-1 B. 1 C. 1± D. 任意实数 5.当x=2时,下列各式的值为0的是( )A. 2322+--x x x B. 21-x C. 942--x x D. 12-+x x6.对于分式13-+x ax 中,当x=-a 时,下列结论正确地是( )A. 分式无意义B. 分式值为0C. 当a 31-≠时,分式的值为0D. 当a 31≠时,分式的值为07.下列各式从左到右的变形不正确的是( )A.y y 3232-=-. B. x y x y 66=-- C. y x y x 4343-=- D. yxy x 3838-=-- 8.下列各个算式中正确的是( )A .22a b a b =;B. b a ba b a +=++22;C. Y X Y Y X Y +=+22;D. xy y x xy y x 23613121-=-9.把分式则分式的值倍都扩大中,2b ,a 2ba a+( ) A .扩大4倍 B.扩大2倍 C. 缩小2倍 D. 不变 10.下列等式成立的是( )A .b a b a b a -=-+22B b a ba ba b ab a +-=-+-2222 C .a b b a b ab a -=-+-222 D ()b a a b b a --=--1211.在-3x,52,53,8,7,32,22ba y x xy y x y x -+--中,是分式的是 .12.要使分式321-+a a 有意义,则a 的值应是 ;要使分式142--a a 的值为零,则a 的值应为 .13.分式xx -1,当 时,其值为0;当 时,分式无意义;当 时,分式的值为正数.14,化简=abbca 15252 . 15,当x=3时,分式44422+--x x x 的值为 .2.分式的乘除法.计算:(1)c b aa b 2242⋅=________;(2)x y 62÷231x= . 2.若代数式1324x x x x ++÷++有意义,则x 的取值范围是__________. 3.计算()341815ax abx ÷= . 4.若5=b a ,则abb a 22+= .5.下列变形错误的是( ) A .46323224y y x y x -=- B .1)()(33-=--x y y xC .9)(4)(27)(12323b a x b a b a x -=-- D .y xa xy a y x 3)1(9)1(32222-=-- 6.计算2322nmm n m n ÷÷-的结果为( )A .22nm B .32nm -C .4mn -D .n -7.已知x 为整数,且分式2221x x +-的值为整数,则x 可取的值有( ) A .1个 B .2个 C .3个 D .4个8.计算:(1)xyyx x xy -÷-)2( (2) 43222(((a bc ab c c b a ÷-⋅-(3)24244422223-+-÷+-+-x x x x x x x x (4)22211(11-+⋅-÷--m m m m m m m9.先化简,再求值(1)xx x x x x x 39396922322-+⋅++-,其中x =31-.(2)xx x x x x x +-÷++223122,其中x=-2. (3)x x x x x 144421422++÷--,其中41-=x .10.若21<<x ,化简xxx x x x +-----1122.A.326x xx = B.0=++y x y x C.1-=-+-y x yx D.b a x b x a =++ 2.下列分式运算,结果正确的是( )A.n m m n n m =∙3454;B.bc ad d c b a =∙ C . 222242b a a b a a -=⎪⎭⎫ ⎝⎛-; D.3334343y x y x =⎪⎪⎭⎫ ⎝⎛ 3.已知a-b 0≠,且2a-3b=0,则代数式ba ba --2的值是( ) A.-12 B.0 C.4 D.4或-124.已知72=y x ,则222273223yxy x y xy x +-+-的值是( ) A.10328 B.1034 C.10320 D.1037 5.化简x xy x 1∙÷等于( ) A.1 B.xy C.x y D.yx 6.如果y=1-x x,那么用y 的代数式表示x 为( ) A. 1+-=y y x B. 1--=y y x C. 1+=y y x D. 1-=y y x 7.若将分式xx x +22化简得1+x x ,则x 应满足的条件是( )A. x>0B. x<0C.x 0≠D. x 1-≠8.22442bc a a b -⋅; 9.化简222210522yx ab b a y x -⋅+; 10.化简x x x x x ÷+++1222;11.若m 等于它的倒数,求分式22444222-+÷-++m mm m m m 的值;12.若分式4321++÷++x x x x 有意义,求x 的取值范围;13.计算-()4425m n m n n m -÷⎪⎪⎭⎫ ⎝⎛-⋅⎪⎭⎫ ⎝⎛;14.计算22322358154mab m b a -÷; 15.计算(xy-x 2)xy y x -÷.不改变分式本身的符号和分式的值,使下列各组里第二个分式的分母和第一个分式的分母相同(1)6132a a a +-+,4532a a a --+-(2)7123x x x ---()(),3423x x x ---()()(3)x y x y x ---()()232,x y x y x --322()2.计算:(1)423223423b a d c cd ab ⋅ (2)m m m m m --⋅-+-3249622 (3)(xy -x 2)÷xy y x - (4)24244422223-+-÷+-+-x x x x x x x x3.先化简,再求值(1)xx x x x x x 39396922322-+⋅++-,其中x =-31. (2)22441y x y x y x +÷-+,其中x =8,y =11.。
《分式(1)》教学设计方案
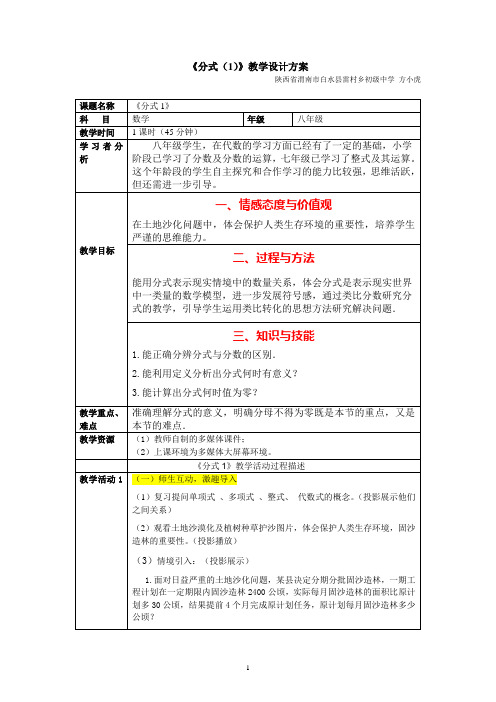
1.面对日益严重的土地沙化问题,某县决定分期分批固沙造林,一期工程计划在一定期限内固沙造林2400公顷,实际每月固沙造林的面积比原计划多30公顷,结果提前4个月完成原计划任务,原计划每月固沙造林多少公顷?
这一问题中有哪些等量关系?
如果设原计划每月固沙造林x公顷,那么原计划完成一期工程需要____________个月,实际完成一期工程用了____________个月;
答案:C
说明:当x = a时,分子x−a = 0,但需满足分式有意义,即分母2x−3≠0,x≠
∴当a≠ 时,分式值为0,因此,答案为C.
2.分式 有意义,则x的值为( )
A.x≠−1 B.x≠−2 C.x≠1 D.x≠−1,x≠−2且x≠1
答案:D
说明: 有意义,需满足x+1≠0且x− ≠0,得x≠−1且 ≠0,
2.能利用定义分析出分式何时有意义?
3.能计算出分式何时值为零?
教学重点、难点
准确理解分式的意义,明确分母不得为零既是本节的重点,又是本节的难点.
教学资源
(1)师自制的多媒体课件;
(2)上课环境为多媒体大屏幕环境。
《分式1》教学活动过程描述
教学活动1
(一)师生互动,激趣导入
(2)观看土地沙漠化及植树种草护沙图片,体会保护人类生存环境,固沙造林的重要性。(投影播放)
《分式(1)》教学设计方案
陕西省渭南市白水县雷村乡初级中学方小虎
课题名称
《分式1》
科目
数学
年级
八年级
教学时间
1课时(45分钟)
学习者分析
八年级学生,在代数的学习方面已经有了一定的基础,小学阶段已学习了分数及分数的运算,七年级已学习了整式及其运算。这个年龄段的学生自主探究和合作学习的能力比较强,思维活跃,但还需进一步引导。
分式(一)

学好分式三步走:1.分式的概念,分式何时有意义,何时值为零2.分式的基本性质,约分,通分3.分式的加、减、乘、除、乘方运算1.分式的概念,分式何时有意义,何时值为零①分式的定义:一般地,如果A 、B 表示两个整式,并且B 中含有字母,那么式子A B 叫做分式,其中A 叫分子,B 叫分母且B ≠0 。
②分式有意义(或分式存在)的条件:分式的分母不等于零即B ≠0 。
③分式的值为零的条件:分式的值为零是指分式在有意义的前提下分式的分子为零。
即当A =0且B ≠0时,0A B=。
【例1】 ⑴若分式25x -有意义,则x 的取值范围是( ) ⑵分式211x x --的值为0,则x 的值为( )【例2】 ⑴下列式子:1x ,23a a b -,3x y +,42a π-,2x x x-,其中是分式的有( ) A .1个 B .2个C .3个D .4个⑵当x ___时,分式2x x +有意义; 当x ___时,分式211x +有意义;⑶当x 为何值时,下列分式的值为0? ①213x x -+; ②2656x x x ---分式(一)③221634x x x -+- ④288x x +⑤()22255x x --2.分式的基本性质,约分,通分①分式的基本性质:分式的分子与分母同乘以(或除以)一个不等于0的整式,分式的值不变。
()0A A M A M M B B M B M÷==÷×≠×②利用分式的基本性质,约去分子和分母的公因式,但不改变分式的值,这样的分式变形叫做分式的约分。
分子分母中没有公因式的分式叫做最简分式。
③通分:利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,把几个分式变成分母相同的分式.为了通分,要先确定各分式的公分母,一般取各分母的所有因式的最高次幂的积作公分母,它叫做最简公分母。
【例3】 ⑴化简222a b a ab-+的结果为( ) ⑵化简2244xy y x x --+的结果为( )【例4】⑴下列式子中,正确的是( )A.B.C.D.a b a b c ca b a b c c a b a b c ca b a b c c ---=---+=-----=---+=-⑵若x ,y 的值扩大为原来的3倍,下列分式的值如何变化? ①x y x y +- ②xy x y- ③22x y x y -+⑶不改变分式的值,把分式的分子和分母各项系数都化为整数: ①1223________1134x y x y -=+ ②0.20.03_______0.04a b a b-=+3.分式的加、减、乘、除、乘方运算 分式的乘法a c a c b d b d⋅⋅=⋅ 分式的除法a c a d a d b d b c b c⋅÷=⋅=⋅ 分式的乘方n n n a a b b ⎛⎫= ⎪⎝⎭同分母分式相加减a b a b c c c ±±= 异分母分式相加减a c ad bc ad bc b d bd bd bd±±=±= 0指数幂01(0)a a =≠ 负整数指数幂1(0)p pa a a -=≠【例5】 化简22226211962x x x x x x x x -++++÷-+--【例6】 先化简再求值:2221412211a a a a a a --⋅÷+-+-其中a 满足20a a -=【例7】已知2310x x -+=,求:221x x +。
分式(一)分式的基本性质

分式(一)分式的基本性质【知识要点】1.用A ,B 表示两个整式,A ÷B 就可以表示成A B 的形式,如果B 中含有字母,式子AB就叫做分式。
对分式的概念要注意以下两点:①分母中应含有字母;②分母的值不能为零,若为零,则该分式就没有意义。
2.整式和分式统称为有理式。
3.分式的基本性质:分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变。
用式子表示是,A A M A A MB B M B B M⨯÷==⨯÷(其中M 是不等于零的整式)。
4.分式的符号变换法则:分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变。
【典型例题】例1 下列各式中,哪些是整式?哪些是分式?(1)1a ; (2)1x x +; (3)1()3x y +; (4)2212x y -; (5)x y x y +-;(6)5a ; (7)xπ; (8)0.3732a x y ++; (9)1323y x +-; (10)5(3)x y m x +-例2 x 取何值时,下列分式有意义?(1)132x x ++ (2)(1)(5)(1)(2)x x x x +--- (3)15x - (4)213x x -+例3 x 取何值时,下列分式没有意义? (1)261x x +; (2)2(2)(3)9x x x ---; (3)2111x-例4 x 取何值时,下列分式的值为零? (1)31x x + (2)55x x -+ (3)211x x +-例5 x为何值时,分式532xx-+的值为正?例6 不改变分式的值,把下列各式的分子与分母中的各项系数化为整数。
(1)0.030.20.080.5x yx y-+;(2)22110.32310.25x yx xy+++;(3)13225m nm n+-例7 不改变分式的值,使下列分式的分子与分母都不含有“-”号。
(1)23xy---;(2)2nm-(3)25ba-(4)21()nxy+---例8 不改变分式243422231253x x x xx x y xy x y+--+-++-的值,使分子与分母中的最高次项的系数为正数。
八年级数学上册第1章分式1.1分式第1课时分式的概念教案湘教版

第1章分式1。
1 分式第1课时分式的概念【知识与技能】1.了解分式的概念,明确分式和整式的区别。
2。
使学生能够求出分式有意义的条件.【过程与方法】让学生经历用字母表示实际问题中数量关系的过程,体会分式是表示现实世界中的一类量的数学模型。
【情感态度】培养学生观察、归纳、类比的思维,让学生学会自主探索,合作交流。
【教学重点】理解分式有意义的条件,分式的值为零的条件.【教学难点】能熟练地求出分式有意义的条件,分式的值为零的条件。
一、情景导入,初步认知下列式子中哪些是整式?【教学说明】因为分式概念的学习是学生通过观察,比较分式与整式的区别从而获得的,所以必须熟练掌握整式的概念.二、思考探究,获取新知 1.思考:(1)某长方形画的面积为Sm 2,长为8m ,则它的宽为____m. (2)某长方形画的面积为Sm 2,长为xm ,则它的宽为____m 。
(3)如果两块面积为x 公顷,y 公顷的稻田,分别产稻谷akg ,bkg,那么这两块稻田平均每公顷产稻谷_____kg.【教学说明】要给学生一定的思考时间,让学生积极投身于问题情景中,根据学生的情况,教师可以给予适当的提示和引导.2.讨论内容:前面出现的代数式如下,它们有什么共同特征?它们与整式有什么不同?【教学说明】让学生通过观察、归纳、总结出整式与分式的异同,从而得出分式的概念.【归纳结论】 一般地,一个整式f 除以一个非零整式g (g中含有字母)所得的商记作f g ,那么代数式f g 叫做分式.3.当x 取什么值时,分式223x x --的值满足下列条件:(1)不存在;(2)等于0。
解:(1)当分母2x-3=0时,即x=32时,分子的值为32-2≠0,因此x=32时,分式223x x --的值不存在。
(2)当x —2=0,即x=2时,分式223x x --的值等于0。
【教学说明】让学生通过观察,归纳、总结出整式与分式的异同,从而得到分式的概念。
三、运用新知,深化理解1.下列各式中,哪些是整式?哪些是分式?解:(2)、(4)是整式,(1)、(3)是分式. 2.若分式13x -有意义,则x 的取值范围是( )A.x ≠3 B 。
分式(一)分式的概念与计算

分式(一)分式的概念与计算学习目标1.学习分式的概念性质2.熟练掌握分式的通分与拆分技巧,3.巩固乘法公式与因式分解技巧专题简介分式是新人教版大纲中,八年级上学期内容,基础知识简单,但是相关专题中会涉及众多代数技巧,难度会陡然真大.分式的概念与计算是历年中考必考内容,在中考中考察方式较为基础.但是在各类竞赛中,特别是全国初中数学联赛中分式的各类恒等变形技巧是考察重点,同时也是难点之一.分式作为代数式中承上启下的知识点学好的关键在于温故而知新,只要熟练掌握,整式恒等变形的技巧,分式学习就会很轻松,只是在整式技巧的基础下,额外增加了通分、拆分取倒等新技巧的综合.专题分类1、分式的基本概念与性质:___________________2、分式的基本运算:_________________________3、分式的拆分:_____________________________模块一:分式的基本概念和性质知识导航一、分式的基本概念【例1】(1)代数式1312,,,,34a b m nbx a+-+π中,分式有( )A.1个B.2个C.3个D.4个(2)使代数式3234x xx x++÷--有意义的x的值是___________.x________时,分式1111x++有意义.不论x为何值,分式21 2x x c++总有意义,则c____________.(3)已知分式22153x xx+--的值为零,那么x的值是_____________.当_____________分式21 5x x -+的值为正数;当x满足_____________时,12xx+<-.(4)当x _______时,分式233x x --的值为1;如果分式121x x -+的值为-1,则x 的值是_________. (5)当x _________时,分式48x -的值为正数;当_______时,分式48xx--的值为负数. 【练1】(1)要使分式11x x-有意义,求x 的取值范围;(2)分式22123x x x ---有意义,求x 的取值范围;(3)已知分式()()811x x x -+-的值为0,求x 的值.【例2】(1)将分式2x x y+中的x 、y 的值同时扩大3倍,则扩大后分式的值( )A.扩大3倍B.缩小3倍C.保持不变D.扩大32倍 (2)若()()()()2223328x m x x x m ---=---成立,则m 的值为_____. (3)约分3232430x y x y -=________;26231x xx ++=________.(4)分式()23121,,7322x y xy x y x x y---的最简公分母为________. 【练2】通分:(1)()2222,,1121x x x x x x x +---+;(2)()()()()()()111,,a b a c b c b a c a c b ------分式的基本运算基础夯实【例3】计算:(1)()2322x y x x y xy x y ⎛⎫⎛⎫-÷+⋅ ⎪ ⎪-⎝⎭⎝⎭(2)2212239a aa a a a -+÷---(3)2233x y x yx y x x y x x ⎡⎤+-⎛⎫---÷⎪⎢⎥+⎝⎭⎣⎦ 【练3】计算:()22221031525965a a a a a a a-+÷-⋅-+-.【例4】已知:2380x x +-=,求代数式21441212x x x x x x -+-⋅--++的值. 【练4】(1)已知220x-=,求代数式()222111x x x x -+-+的值. (2)已知12x y =,求2222222x x y yx xy y x y x y-⋅+-++-的值. 强化挑战【例5】化简:2222222211222a b a ab b ab a b a b ab ⎡⎤-⎛⎫+÷+⋅⎢⎥ ⎪++-+⎝⎭⎢⎥⎣⎦【练5】化简:()()()()()()222222222222a b c b c a c a b a c ba b cb c a ------+++-+-+-.【例6】化简:2232233223222244113a b a b a a b ab b a a b ab b a b a b a b +++--+++-+--+-.巅峰突破【例7】化简:()()4222223366422412b a a a b b a ab b a b a b a a b b ---⎛⎫-÷ ⎪-+----+⎝⎭.【练7】化简:()442432164242416844m m m m m m m m m m -+-+÷⨯÷+++--+.模块三:分式的拆分 知识导航分式计算技巧——分式的拆分分式拆分的基本模型11a b ab a b+=+,这种模型在计算中运用分式广泛!而复杂的题型通常将这种性质包容在其中.如:()()b ca b a c ---冷眼看,不是符合基本模型,若对分子稍加边形则里面出现基本模型.()a b a c c b ---=-,所以原式变为()()()()11a b a c a b a c a b c a---=+----题型1分式拆分 基础夯实【例8】化简:2221113256712x x x x x x ++++++++ 【练8】化简:22222111113256712920x x x x x x x x x x +++++++++++++ 强化挑战【例9】化简:222222a b c b c a c a ba ab ac bc b ab bc ac c ac bc ab------++--+--+--+.【练9】化简:()()()()()()222a bc b ac c aba b a c b c b a c a c b ---++++++++.题型2部分分式 基础夯实【例10】仿照例子解题: 例子:若215111M N xx x x -+=+--恒成立,求M 、N 的值. 解题过程如下:∵215111M N xx x x -+=+--,∴M (x -1)+N (x +1)=1-5x 则Mx -M +Nx +N =1-5x , 即Mx +Nx +N -M =-5x +1 故(M +N )x +(N –M ) =-5x +1, ∴51M N N M +=-⎧⎨-=⎩解得:32M N =-⎧⎨=-⎩请你按照上面的方法解题:若28224M N x x x x -+=+--恒成立,求M 、N 的值. 【练10】已知()()237231111x x A Bx x x x -+=++-+-+,其中A 、B 为常数,求4A -2B 的值.强化挑战 题型2 分离常数【例12】阅读下面材料,并解答问题.材料:讲分式42231x x x --+-+拆分成一个整式与一个分式(分子为整数)的和的形式.解:由分母为-x 2+1,可设-x 4-x 2+3=(-x 2+1)(x 2+a )+b则-x 4-x 2+3=(-x 2+1)(x 2+a )+b =-x 4-ax 2+x 2+a +b =-x 4-(a -1)x 2+(a +b ).∵对应任意x ,上述等式均成立, ∴113a ab -=⎧⎨+=⎩,∴a =2,b =1. ∴()()()()222242222222121123112+11111x x x x x x x x x x x x -+++-++--+==+=+-+-+-+-+-+. 这样,分式42231x x x --+-+被拆成了一个整式22x +与一个分式211x -+的和. 解答:(1)将分式422681x x x --+-+拆成一个整式与一个分式(分子为整数)的和的形式.(2)试说明422681x x x --+-+的最小值为8.第4讲 七年级尖端班课后作业 分式(一)概念与计算【习1】当x 为何值时,下列分式的值为零?(1)1x x+(2)211x x -+(3)33x x --(4)237x x ++(5)2231x x x +--(6)2242x x x-+【习2】x 为何值时,分式1122x x+-+有意义? 【习3】如果分式61x+的值为正整数,则正整数x 的值的个数是( ) A.2个 B.3个C.4个D.5个【习4】如果把223xyx y-中的x 和y 都扩大5倍,那么分式的值( )A.扩大5倍B.不变C.缩小5倍D.扩大4倍【习5】不改变分式的值,将下列各分式中的分子、分母的系数化为整数,其结果不正确的为( )A.113223113223a ba b a b a b ++=-- B.1.30.813820.7207x y x yx y x y--=--C.134624172748x yx y x y x y --=++ D.135320.55x y x y x x --= 【习6】先化简:22211a a a a a a --⎛⎫-÷⎪+⎝⎭,然后给a 选择一个你喜欢的数代入求值. 【习7】计算:()2226634443x x x x x x x -+-÷+⋅-+- 【习8】3232242312111x x x x x x x x x ⎛⎫-⎛⎫-÷-÷ ⎪ ⎪+-++⎝⎭⎝⎭【习9】(第9届希望杯试题)化简:422423216424(2)416844m m m m m m m m m m -+-+÷⨯÷+++--+=__________.【习10】求代数式的值:2222242x x xx x x -÷++-+,其中12x =. 【习11】先化简,再求值:3221691322x x x xx x x x -+-⋅----,其中x =-6 【习12】先化简,再求值:2223193693x x x x x x x x x+--⎛⎫-÷ ⎪--+-⎝⎭,其中x =2 【习13】化简:2481124811111x x x x x -----++++.【习14】计算:22216103224x x x x x x x ----++---. 【习15】化简:()()()()()()a b b c c a a b b c c a a b b c c a a b b c c a ------+++++++++. 【习16】化简:222222b c c a a b a ab ac bc b ab bc ac c bc ac ab a b b c c a---++-----+--+--+---.【习17】将下列分式写成部分分式的和的形式:2342x x x +--【习18】已知22x +与2b x -的和等于244x x -,求a ,b .。
1分式PPT课件(北京课改版)

分式的分母不能为0,
即当B≠0时,分式
A B
有意义。
分式在什么条件下无意义呢?
A
当B=0时,分式 B 无意义。
例题
例1 (1)当x
时,分式
2 3x
有意义?
解:要使分式 2 有意义,
3x
必须 3x≠0,
即x≠0
2
所以当x≠0时,分式
有意义。 3x
(2)当x (3)当b
x
时,分式 x 1有意义;
1
时,分式 5 3b有意义;
思考
1.长方形的面积为10cm²,长为7cm。
10
宽应为__7__cm;
S
长方形的面积为S,长为a,宽应为___a___;
S
?
a
2、把体积为200cm³的水倒入底面积为 33cm²
200 的圆柱形容器中,水面高度为__3_3__cm;
把体积为V的水倒入底面积为S的圆柱形
v 容器中,水面高度为___s___。 S
分析1:∵2x2 +1 >0,∴1-x<0, ∴x>1
分析2:x>1或x< 2
3
课堂小结:本节课你有什么收获?
❖分式的概念 ❖分式有意义及无意义的条件 ❖分式值为0的条件 ❖分式值的正负 ❖你学会了什么数学方法?
再 见
请大家视察式子
S
v
,
,
90
a
s
30+v
60 30 v ,有什么共同点?
它们与分数有什么相同点和不同点?
相同点
不同点
与分数都具有
A B
的情势
分数的分子A与分母B都是 整数,而这些式子中A和B
初一数学分式 (1)

分式1. 分式的定义:如果A、B表示两个整式,并且B中含有字母,那么式子叫做分式。
分式有意义的条件是分母不为零,分式值为零的条件分子为零且分母不为零2.分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。
()3.分式的通分和约分:关键先是分解因式4.分式的运算:分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
分式除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
分式乘方法则:分式乘方要把分子、分母分别乘方。
分式的加减法则:同分母的分式相加减,分母不变,把分子相加减。
异分母的分式相加减,先通分,变为同分母分式,然后再加减混合运算:运算顺序和以前一样。
能用运算率简算的可用运算率简算。
5. 任何一个不等于零的数的零次幂等于1,即;当n为正整数时,(6.正整数指数幂运算性质也可以推广到整数指数幂.(m,n是整数)(1)同底数的幂的乘法:;(2)幂的乘方:;(3)积的乘方:;(4)同底数的幂的除法:( a≠0);(5)商的乘方:();(b≠0)7. 分式方程:含分式,并且分母中含未知数的方程——分式方程。
解分式方程的过程,实质上是将方程两边同乘以一个整式(最简公分母),把分式方程转化为整式方程。
解分式方程时,方程两边同乘以最简公分母时,最简公分母有可能为0,这样就产生了增根,因此分式方程一定要验根。
解分式方程的步骤:(1)能化简的先化简(2)方程两边同乘以最简公分母,化为整式方程;(3)解整式方程;(4)验根.增根应满足两个条件:一是其值应使最简公分母为0,二是其值应是去分母后所的整式方程的根。
分式方程检验方法:将整式方程的解带入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解。
列方程应用题的步骤是什么?(1)审;(2)设;(3)列;(4)解;(5)答.应用题有几种类型;基本公式是什么?基本上有五种:(1)行程问题:基本公式:路程=速度×时间而行程问题中又分相遇问题、追及问题.(2)数字问题在数字问题中要掌握十进制数的表示法.(3)工程问题基本公式:工作量=工时×工效.(4)顺水逆水问题v顺水=v静水+v水.v逆水=v静水-v水.。
1.1分式1

§1.1 分式(1)宁海中学张燕波一、教材分析:本节课的主要内容是分式的概念以及掌握分式有意义、无意义、分式值为0的条件。
它是在学生掌握了整式的四则运算、多项式的因式分解,并以分数知识为基础,对比引出分式的概念,把学生对“式”的认识由整式扩充到有理式。
学好本节知识是为进一步学习分式知识打下扎实的基础,是以后学习函数、方程等问题的关键。
二、学情分析:学生已经对整式进行了探索,通过分数的学习,学生可能会用分数的定义去理解分式。
但是在分式中,它的分母不是具体的数,而是含有字母的整式。
为了学生能切实掌握所学知识,在教学中对于教材中的例题和练习题,作了适当的延伸拓展和变式处理。
还特别设计了反馈练习。
三、教学目标(一)知识与技能目标1.使学生了解分式的概念,明确分母不为零是分式概念的组成部分。
2.使学生能够求出分式有意义的条件。
(二)过程与方法目标1.通过对分式与分数的类比,学生亲身经历探究整式扩充到分式的过程,初步学会运用类比转化的思想方法研究数学问题。
2.学生通过类比方法的学习,提高了对事物之间是普遍联系又是变化发展的辩证观点的再认识。
(三)情感与价值目标1.在土地沙化问题中,体会保护人类生存环境的重要性,培养学生严谨的思维能力。
2.通过联系实际探究分式的概念,能够体会到数学的应用价值。
3.在合作学习过程中增强与他人的合作意识。
四、教学重点和难点:重点:分式的概念。
难点:理解和掌握分式有意义、分式值为零时的条件。
五、教学方法与学法教学方法:探索—发现教学法学法引导:自主探索、研讨发现六、教具准备:课件七、教学过程:八、板书设计:1.1分式一、知识点:二、例题:三、练习:分式的定义分式有意义、无意义、分式值为0的条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分式测试题
一、选择题(每小题3分,共30分)
1、在x 1、8x 、212+x 、πxy 3、y
x +π、m a 1+中分式的个数有( ) A 、2个 B 、3个 C 、4个 D 、5个
2、无论x 取什么数时,总是有意义的分式是 ( )
A .
122+x x B.12+x x C.133+x x D.2
5x x - 3、化简x
y x x 1⋅÷的结果是( ) A 、 1 B 、 xy C 、 x y D 、 y x 4、下列计算正确的是( )
A 、 23231=⎪⎭⎫ ⎝⎛--
B 、 b a b a +=+211
C 、 b a b a b a +=--22
D 、02010
=⎪⎭⎫ ⎝⎛- 5、下列约分正确的是( )
A 、326x x x =;
B 、0=++y x y x ;
C 、x xy x y x 12=++;
D 、2
14222=y x xy 6、把分式xy
y x -中的x 、y 的值都扩大2倍,则分式的值( ) A 、 不变 B 、 扩大2倍 C 、 扩大4倍 D 、 缩小一半
7、下列等式的变形一定成立的是( )
.A 、 b b c a a c +=+ .B 、()()x y b b x y a a +=+ .C 、 22b b a a = .D 、()()
b b x y a a x y -=- 8、下列等式成立的是( )
A 、(-3)-2 =-9
B 、(-3)-2 =9
1 C 、(a 12)
2 =a 14 D 、0.0000000618=6.18710-⨯ 9、把分式方程11
2=+-x x x 化为整式方程正确的是( ) A 、1)1(22=-+x x B 、1)1(22
=++x x C 、)1()1(22+=-+x x x x D 、)1()1(22+=+-x x x x
10、一件工作,甲单独做a 小时完成,乙单独做b 小时完成,则甲、乙两人合作完成需要( )小时。
A 、b a 11+
B 、ab 1
C 、b
a +1 D 、b
a a
b + 二、认真填一填(共30分,每小题3分) 11、当x 时,分式6213-+x x 有意义;当x 时,分式9
6922++-x x x 的值等于0. 12、计算:a
b b b a a -+-= . 13、计算:
x x 1-÷⎪⎭⎫ ⎝⎛-x 11= 14、÷
-)(2a a 1
-a a = 15、当x 时,两分式44-x 与1
3-x 的值相等。
16、分式x 1,422-x x ,x y -23的最简公分母是 17、用科学记数法表示:-0.0000000102= ;
18、不改变分式0.50.20.31
x y ++的值,使分式的分子分母各项系数都化为整数,结果是 。
19、某住宅小区原来a 天用水m 吨,安装了循环用水装置后这些水可多用5天,现在每天比原来少用水 吨。
20、已知0142=+-a a ,那么2
21a a += 三、解答题(共小题,共60分)
21、计算:(1)y x y y x x --- (5分) (2)y
x x x y xy x 22+⋅+ (6分)
22、计算:)11(2)(y
x y x xy y x xy y x x -÷-∙---(7分)
23、计算:()30225174-+⎪⎪⎭⎫ ⎝
⎛+--÷13- (6分)
24、解方程
22121--=--x
x x (6分)
25、先化简,再求值 222434111211
x x x x x x x x ---÷+=-++- ,其中(7分)
26、八年级学生去距离学校10千米的博物馆参观,一部分同学骑自行车先走,过了20分后,其余同学乘汽车出发,结果他们同时到达。
已知汽车的速度是骑车同学速度的2倍,求骑车同学的速度。
(8分)
27、学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?(8分)
28、先观察下列等式,然后用你发现的规律解答下列问题:(本小题7分) 由
211121211-==⨯,312161321-==⨯,4
131121431-==⨯…… (1)计算211⨯+321⨯+431⨯+541⨯+651⨯+761⨯+871⨯= (n 为正整数)。
(3分)
(2)化简:()()()()()
32121111+++++++x x x x x x +……+()()201220111++x x 。
(4分)。
