Lecture10-字符串匹配
python匹配字符串详解

python匹配字符串详解Python是一种强大的编程语言,它提供了丰富的功能和库,用于处理字符串匹配。
在本文中,我们将深入探讨如何使用Python进行字符串匹配。
1. 简介让我们简单介绍一下字符串匹配的概念。
字符串匹配是指在一段文本中查找特定模式的过程。
这个模式可以是一个单词、一个短语、一个正则表达式,甚至是一个字符串序列。
Python提供了多种方法来进行字符串匹配,包括简单的模式匹配、正则表达式和字符串算法。
2. 简单的模式匹配在Python中,我们可以使用`in`运算符来判断一个字符串是否包含另一个字符串。
例如,我们可以使用以下代码判断一个字符串是否包含特定的单词:```pythontext = "Hello, world!"if "world" in text:print("包含")else:print("不包含")```除了`in`运算符,Python还提供了`startswith()`和`endswith()`函数来判断一个字符串是否以特定的前缀或后缀开头。
这些函数非常实用,可以帮助我们快速判断字符串的开头和结尾。
3. 正则表达式正则表达式是一种强大的工具,用于在文本中查找和匹配模式。
Python内置了`re`模块,提供了丰富的正则表达式功能。
我们可以使用正则表达式来进行更复杂的字符串匹配。
例如,我们可以使用以下代码来匹配一个字符串中的所有数字:```pythonimport retext = "Hello 123 world 456"pattern = r"\d+" # 匹配一个或多个数字result = re.findall(pattern, text)print(result)```输出结果为:`['123', '456']`。
python字符串匹配算法

python字符串匹配算法一、引言在计算机科学中,字符串匹配是指在文本中查找特定模式的子串。
这种操作在很多实际应用中都非常重要,例如在文件搜索、数据过滤、自然语言处理等领域。
Python提供了一些内置函数和库,可以方便地进行字符串匹配。
二、基本算法1. 朴素字符串匹配算法(Naive String Matching):这是一种简单的字符串匹配算法,通过遍历文本串,逐个字符地与模式串进行比较,以确定是否存在匹配。
2. 暴力匹配算法(Brute Force):这是一种基于字符比较的字符串匹配算法,通过逐个字符地比较文本串和模式串,直到找到匹配或者遍历完整个文本串为止。
3. KMP算法(Knuth-Morris-Pratt Algorithm):这是一种高效的字符串匹配算法,通过记忆已经比较过的字符,减少不必要的重复比较,从而提高匹配速度。
三、Python实现1. 朴素字符串匹配算法:在Python中,可以使用`str.find()`方法或`str.index()`方法来查找模式串在文本串中的位置。
示例如下:```pythontext = "Hello, world!"pattern = "world"index = text.find(pattern)if index != -1:print("Pattern found at index", index)else:print("Pattern not found")```2. 暴力匹配算法:在Python中,可以使用`re`模块来实现暴力匹配算法。
示例如下:```pythonimport retext = "Hello, world! This is a test."pattern = "world"matches = re.findall(pattern, text)if matches:print("Pattern found in text")else:print("Pattern not found in text")```3. KMP算法:在Python中,可以使用`re`模块中的`search()`方法来实现KMP算法。
字符串模式匹配

实验7、字符串查找目的掌握字符串模式匹配的经典算法。
问题描述分别用简单方法和KMP方法实现index在文本串中查找指定字符串的功能。
步骤1.定义字符串类型2.实现简单的index操作,从文本串中查找指定字符串。
3.实现KMP方法的index操作,从文本串中查找指定字符串。
4.[选]建立一个文本文件,读入每一行来测试自己完成的练习,观察并理解程序的各个处理。
设备和环境PC计算机、Windows操作系统、C/C++开发环境结论能够理解和掌握字符串模式匹配的典型算法。
思考题1.对KMP算法分别用手工和程序对某个模式串输出next和nextval。
朴素算法:#include<stdio.h>#include<string.h>#define NOTFOUND -1#define ERROR -2#define MAXLEN 100//字符串的最大长度char S[MAXLEN+10],T[MAXLEN+10],st[MAXLEN+10];//串S和串Tint S0,T0; //S0:串S的长度 T0:串T的长度int pos; //pos的起始位置void Init(char *S,int &S0)//读入字符串{int len,i;New_Input:scanf("%s",st);//读入字符串len=strlen(st);if (len>MAXLEN)//如果字符串的长度大于规定的字符串最大长度 {printf("This String is too long,Please Input a new one.nn");goto New_Input;//重新读入字符串}for (i=1;i<=len;i++) S[i]=st[i-1];S[len+1]='';S0=len;}int Index(char *S,char *T,int pos){if (pos<1 || pos>S0) return ERROR; // 输入数据不合法int i=pos,j=1;while (i<=S0 && j<=T0){if (S[i]==T[j]) {i++; j++;}else {i=i-j+2; j=1;}//不匹配时,对应S移到下一位进行匹配}if (j>T0) return i-T0; //返回S中找到的位置else return NOTFOUND;}int main(){int ret;//函数返回值Init(S,S0);Init(T,T0);scanf("%d",&pos);ret=Index(S,T,pos); //在S串中从pos这个位置起,找到第一个与T匹配的子串的起始位置if (ret==NOTFOUND) printf("Not Found.n");else if(ret==ERROR) printf("The Input Data is Error.n");else printf("In S,from %dth is equal to T.n",ret);return 0;}KMP:#include<stdio.h>#include<string.h>#define NOTFOUND -1#define ERROR -2#define MAXLEN 100//字符串的最大长度char S[MAXLEN+10],T[MAXLEN+10],st[MAXLEN+10]; //串S和串Tint S0,T0; //S0:串S的长度 T0:串T的长度int pos; //pos的起始位置int next[MAXLEN+10];void Init(char *S,int &S0)//读入字符串{int len,i;New_Input:scanf("%s",st);//读入字符串len=strlen(st);if (len>MAXLEN)//如果字符串的长度大于规定的字符串最大长度{printf("This String is too long,Please Input a new one.nn");goto New_Input; //重新读入字符串}for (i=1;i<=len;i++) S[i]=st[i-1];S[len+1]='';S0=len;}void Get_next(char *S,int *next){int i=1,j=0;next[1]=0;while (i<T0)if (j==0 || T[i]==T[j]) {i++; j++; next[i]=next[j];}else j=next[j];}int Index_KMP(char *S,char *T,int pos){int i=pos,j=1;while (i<=S0 && j<=T0)if (j==0 || S[i]==T[j]) {i++; j++;}else j=next[j];if (j>T0) return i-T0;else return NOTFOUND;}int main(){int ret;//函数返回值Init(S,S0);Init(T,T0);scanf("%d",&pos);Get_next(T,next);ret=Index_KMP(S,T,pos); //在S串中从pos这个位置起,找到第一个与T匹配的子串的起始位置if (ret==NOTFOUND) printf("Not Found.n");else if (ret==ERROR) printf("The Input Data is Error.n");else printf("In S,from %dth is equal to T.n",ret);return 0;}扩张KMP:#include<stdio.h>#include<string.h>#define NOTFOUND -1#define ERROR -2#define MAXLEN 100 //字符串的最大长度char S[MAXLEN+10],T[MAXLEN+10],st[MAXLEN+10]; //串S和串Tint S0,T0; //S0:串S的长度 T0:串T 的长度int pos; //pos的起始位置int nextval[MAXLEN+10];void Init(char *S,int &S0)//读入字符串{int len,i;New_Input:scanf("%s",st); //读入字符串len=strlen(st);if (len>MAXLEN) //如果字符串的长度大于规定的字符串最大长度{printf("This String is too long,Please Input a new one.nn");goto New_Input; //重新读入字符串}for (i=1;i<=len;i++) S[i]=st[i-1];S[len+1]='';S0=len;}void Get_nextval(char *S,int *nextval){int i=1,j=0;nextval[1]=0;while (i<T0)if (j==0 || T[i]==T[j]){i++; j++;if (T[i]!=T[j]) nextval[i]=j;else nextval[i]=nextval[j];}else j=nextval[j];}int Index_KMP(char *S,char *T,int pos){int i=pos,j=1;while (i<=S0 && j<=T0)if (j==0 || S[i]==T[j]) {i++; j++;}else j=nextval[j];if (j>T0) return i-T0;else return NOTFOUND;}int main(){int ret;//函数返回值Init(S,S0);Init(T,T0);scanf("%d",&pos);Get_nextval(T,nextval);ret=Index_KMP(S,T,pos); //在S串中从pos这个位置起,找到第一个与T匹配的子串的起始位置if (ret==NOTFOUND) printf("Not Found.n");else if (ret==ERROR) printf("The Input Data is Error.n");else printf("In S,from %dth is equal to T.n",ret);return 0;}。
字符串匹配

1.生成next[]数组。时间复杂度O(m) 2.利用next[]数组进行匹配。时间复杂度O(n)
求给定字符串(长度S<=400000)所有满足前缀 和后缀相同的长度。 求给定字符串(长度S<=10^6)最多是由其一个 子串重复多少次得到的。 求给定字符串(长度S<=10^6)的所有由其一个 子串重复>=2次得到的前缀,输出前缀长度和重复 次数。
四、后缀数组
若待匹配串难以确定,需要在原串中找到符合特定 条件的串? 匹配串在原串中的每次出现其实就是一个“后缀的 前缀” 那么我们可以把原串的所有后缀按照字典序进行排 序,这样任何待匹配串都能仅在一遍线性扫描中得 到结果
后缀数组sa[]:sa[k]代表排序后第k小的后缀的起 始位置。 名次数组rank[]:rank[k]代表起始位置为k的后缀 的名次。 两者可以相互推出。因此我们通过计算rank[]来得 到sa[]。
三、hash
比较两个字符串是否相等需要O(len)的时间。而比 较两个int类型的数据是否相等只需要O(1)的时间。 如果构建一个函数f:string->int,在需要比较字符 串A和B时通过比较f(A)和f(B)代替,就可以极大降 低时间复杂度。此函数即为hash函数。 通常可以将字符串看作k进制数,并对p取模后得到 其hash函数值,k和p通常是质数。 为降低出错概率,可设多组hash函数,只有全部匹 配成功时才接受。
给定一个长度不超过n的长字符串A和若干个长度不 超过m的短字符串B1…Bm 对于每个短字符串,找出它在长字符串中出现的所 有位置。 例:ababcababcabc ababc 则返回0,5
字符串匹配算法

字符串匹配算法本系列文章主要介绍几种常用的字符串比较算法,包括但不限于蛮力匹配算法,KMP算法,BM算法,Horspool算法,Sunday算法,fastsearch算法,KR算法等等。
本文主要介绍KMP算法和BM算法,它们分别是前缀匹配和后缀匹配的经典算法。
所谓前缀匹配是指:模式串和母串的比较从左到右,模式串的移动也是从左到右;所谓后缀匹配是指:模式串和母串的的比较从右到左,模式串的移动从左到右。
看得出来前缀匹配和后缀匹配的区别就仅仅在于比较的顺序不同。
下文分别从最简单的前缀蛮力匹配算法和后缀蛮力匹配算法入手,详细的介绍KMP算法和BM算法以及它们的实现。
KMP算法首先来看一下前缀蛮力匹配算法的代码(以下代码从linux源码string.h中抠出),模式串和母串的比较是从左到右进行(strncmp()),如果找不到和模式串相同的子串,则从左到右移动模式串,距离为1(s++)。
[cpp]view plaincopyprint?1.char* strstr(registerconst char *s, registerconst char *wanted)2.{3. registerconst size_t len = strlen(wanted);4.if(len == 0) return(char*)s;5.while(*s != *wanted || strncmp(s, wanted, len))6.if(*s++ == '\0')7.return(char*)NULL;8.return(char*)s;9.}KMP算法中的KMP分别是指三个人名:Knuth、Morris、Pratt,其本质也是前缀匹配算法,对比前缀蛮力匹配算法,区别在于它会动态调整每次模式串的移动距离,而不仅仅是加一,从而加快匹配过程。
下图通过一个直观的例子展示前缀蛮力匹配算法和KMP算法的区别,前文提过,这二者唯一的不同在于模式串移动距离。
C语言中的字符串匹配算法实现

C语言中的字符串匹配算法实现在C语言中,字符串匹配算法用于判断一个字符串是否包含另一个字符串。
本文将介绍几种常见的字符串匹配算法及其实现。
一、暴力匹配算法(Brute-Force Algorithm)暴力匹配算法是最简单直观的字符串匹配算法,也被称为朴素字符串匹配算法。
算法思想:从主字符串的第一个字符开始,依次与模式字符串的字符逐个比较,如果出现字符不匹配的情况,则主字符串的指针后移一位,再从下一个字符开始重新比较。
实现代码示例:```c#include <stdio.h>#include <string.h>int bruteForceMatch(char *str, char *pattern) {int len1 = strlen(str);int len2 = strlen(pattern);int i = 0, j = 0;while(i < len1 && j < len2) {if(str[i] == pattern[j]) {i++;j++;} else {i = i - j + 1;j = 0;}}if(j == len2) {return i - len2; // 返回匹配位置的索引} else {return -1; // 未找到匹配}}int main() {char str[] = "Hello, world!";char pattern[] = "world";int index = bruteForceMatch(str, pattern);if(index >= 0) {printf("匹配成功,匹配位置为:%d\n", index);} else {printf("未找到匹配\n");}return 0;}```上述示例代码中,我们使用了一个bruteForceMatch函数来实现暴力匹配算法。
字符串模式匹配算法综述

字符串模式匹配算法综述摘要:字符串匹配问题是在给定符号序列(称为文本)中按照一定的匹配条件,搜索给定符号序列或给定符号序列集合中元素(称为模式)出现位置的搜索问题。
该问题是计算机科学的基础问题之一,被广泛的应用于各种涉及文字和符号处理的领域中,是网络安全、信息检索、计算生物学等重要领域的关键问题。
本文主要介绍了BF 算法、KMP 算法、BM 算法、BMH 算法、AC 算法和 AC-BM 算法。
关键词:模式匹配,BF算法,KMP算法,改进算法,BM算法,AC算法,ACH算法。
0.前言字符串是一种线性表,它在计算机应用系统中如文本编辑、情报检索、自然语言翻译有着广泛的应用。
在这些应用中常常需要在一堆文字符串中检测是否有某一指定的字符串。
设Pattern(下文简称 P)和Text(下文简称 T)是给定的两个字符串,在字符串T中寻找等于P的子串的过程称为模式匹配,其中字符串T称为主串,字符串P称为模式串。
如果在字符串T中找到等于P的子串,则称匹配成功,否则匹配失败。
比较著名的模式匹配算法有BF算法、KMP算法、AC算法和BM算法,本文对所述算法进行探讨。
随着计算机技术的快速发展,计算机网络在国民经济中发挥了日益重要的作用,己成为人们日常生活中不可缺少的一部分。
同时,网络安全也日益引起人们的关注。
1.模式匹配算法1.1 单模式匹配算法1.1.1 BF(Bruce Force)算法1.算法思想从文本字符串 T 的第一个字符起和模式字符串 P 中的第一个字符开始比较,若相等,逐个比较后续字符,否则从文本字符串的下一个字符起再重新和模式字符串的第一个字符比较。
2.算法描述对于文本字符串n k m i k T T T T T ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅--10模式字符串mj P P P ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅0 (1)P 和 T 从左端对齐,使得 0P 与 0T 对齐;(2)从左到右匹配 P 与 T 的字符,直到出现不匹配的情况,则执行(3),或是 P 己被完全匹配的情况则结束比较;(3)将 P 右移一个字符,重新从P 的第一个字符开始匹配;(4)重复上述(2)过程,直到 P 被完全匹配,或 P 移到 T 的右端。
字符串匹配

字符串匹配一、需求分析:1、输入时首先输入一个主串,然后每次输入一个子串进行查找,范围:每个字符串的长度为0<=length<=100。
2、输出的形式,输出查找出的子串在主串中的位置,所有位置均找出。
3、功能,实现字符串匹配。
4、测试数据,主串:aabcdjijikkklpopopguhiji,子串1:po, 子串2:ij, 子串3:eba。
二、概要设计:各函数的调用关系:三、详细设计:见源码:zifuchuanpipei.cpp文件的实现#include<iostream>using namespace std;int getsubpos(char* p,char* subp,int pos) //字符串匹配函数{for(int i=pos;*(p+i)!='\0';i++) //遍历主串{for(int j=0;*(subp+j)!='\0';j++) //遍历子串{if(*(p+i+j)!=*(subp+j)){break;}}if(j==strlen(subp)) return i;}return -1;}int main() //main函数{char a[2][100];int b,j,i;int num; //位置个数记录gets(a[0]);while(gets(a[1])){b=0;j=strlen(a[0]);i=0;num=0;while(1){b=getsubpos(a[0],a[1],b);if(b!=-1) cout<<"第"<<++num<<"个位置为:"<<b<<endl;else if(i!=1){cout<<"未找到"<<endl;break;}else break;i=1;b++;}}return 0;}四、调式分析:1、调式时指针出现错误导致非法访问内存,程序崩溃,最终修改了指针,解决了问题。
字符串匹配算法的原理和实现

字符串匹配算法的原理和实现随着互联网应用的广泛普及,各种搜索引擎、数据挖掘等技术越来越受到人们的关注。
在很多应用中,我们需要对文本进行匹配,即在一段文本中查找某个字符串是否出现过,或者查找多个字符串在文本中的位置。
这就需要用到字符串匹配算法,本文将介绍字符串匹配算法的原理和实现。
一、暴力匹配算法暴力匹配算法是最朴素的字符串匹配算法,也称为朴素算法或者蛮力算法。
它的原理非常简单,就是从文本的第一个字符开始依次比较,如果匹配失败,则将文本的指针后移一位,开始下一次比较。
具体实现可以用以下代码表示:```int search(string pattern, string text) {int n = text.length();int m = pattern.length();for(int i = 0; i < n - m + 1; i++) {int j;for(j = 0; j < m; j++) {if(pattern[j] != text[i+j]) {break;}}if(j == m) {return i;}}return -1;}```该算法的时间复杂度为O(nm),其中n和m分别是文本和模式串的长度。
当模式串非常短时,该算法的效率还可以接受,但是当模式串很长时,算法效率就会变得很低,甚至比较文本中的每个字符都慢。
因此,我们需要更加快速和高效的算法来实现字符串匹配。
二、KMP算法KMP算法全称为Knuth-Morris-Pratt算法,它是一种比暴力匹配算法更加高效的字符串匹配算法,可以在O(n+m)的时间复杂度内完成字符串匹配。
KMP算法的基本思想是利用匹配失败后的信息来避免无谓的比较,具体过程如下:1.计算模式串的前缀函数(Prefix Function)。
前缀函数的定义是:对于模式串P的每个位置i(0 <= i < m),对应的前缀函数(Pi)表示模式串的第0个位置到第i个位置的最长的,既是最前面的,也是最后面的,与整个模式串P的某个前缀相等的后缀的长度。
字符串匹配算法

字符串匹配算法公告:CSDN新版博客排名规则公示,请各位用户周知字符串匹配算法(一)简介分类:算法2008-10-29 15:223587人阅读评论(8)收藏举报注:本文大致翻译自EXACT STRING MATCHING ALGORITHMS,去掉一些废话,增加一些解释。
文本信息可以说是迄今为止最主要的一种信息交换手段,而作为文本处理中的一个重要领域——字符串匹配,就是我们今天要说的话题。
(原文还特意提及文本数据数量每18个月翻一番,以此论证算法必须要是高效的。
不过我注意到摩尔定律也是18个月翻番,这正说明数据的增长是紧紧跟随处理速度的,因此越是使用高效的算法,将来待处理的数据就会越多。
这也提示屏幕前的各位,代码不要写得太快了……)字符串匹配指的是从文本中找出给定字符串(称为模式)的一个或所有出现的位置。
本文的算法一律输出全部的匹配位置。
模式串在代码中用x[m]来表示,文本用y[n]来,而所有字符串都构造自一个有限集的字母表Σ,其大小为σ。
根据先给出模式还是先给出文本,字符串匹配分为两类方法:第一类方法基于自动机或者字符串的组合特点,其实现上,通常是对模式进行预处理;第二类方法对文本建立索引,这也是现在搜索引擎采用的方法。
本文仅讨论第一类方法。
文中的匹配算法都是基于这样一种方式来进行的:设想一个长度为m的窗口,首先窗口的左端和文本的左端对齐,把窗口中的字符与模式字符进行比较,这称为一趟比较,当这一趟比较完全匹配或者出现失配时,将窗口向右移动。
重复这个过程,直到窗口的右端到达了文本的右端。
这种方法我们通常叫sliding window。
对于穷举法来说,找到所有匹配位置需要的时间为O(mn),基于对穷举法改进的结果,我们按照每一趟比较时的比较顺序,把这些算法分为以下四种:1从左到右:最自然的方式,也是我们的阅读顺序2从右到左:通常在实践中能产生最好的算法3特殊顺序:可以达到理论上的极限4任意顺序:这些算法跟比较顺序没关系(例如:穷举法)一些主要算法的简单介绍如下:从左到右采用哈希,可以很容易在大部分情况下避免二次比较,通过合理的假设,这种算法是线性时间复杂度的。
匹配字符串正则

匹配字符串正则
正则表达式是一种强大的文本匹配工具,可以用来匹配字符串中符合特定规则的内容。
在实际的开发中,经常会用到正则表达式来进行字符串的处理。
正则表达式可以用来匹配字符串中的各种元素,如数字、字母、空格、符号等等。
使用正则表达式的时候,可以通过特定的符号和语法来构建匹配规则,从而实现对字符串的筛选和提取。
在正则表达式中,一些常见的匹配符号包括:
- d:匹配数字
- w:匹配字母、数字、下划线
- s:匹配空格、制表符、换行符等空白字符
- .:匹配任意字符
- *:匹配前一个字符0次或多次
- +:匹配前一个字符1次或多次
- ?:匹配前一个字符0次或1次
- {n}:匹配前一个字符恰好n次
- {n,m}:匹配前一个字符至少n次,最多m次
除了这些基本符号,正则表达式还可以使用一些特殊的语法来处理字符串,如正则表达式的分组、捕获、反向引用等等。
总之,正则表达式是一种非常强大的字符串匹配工具,掌握它可以让我们在开发中更加高效和便捷。
- 1 -。
字符匹配算法

字符匹配算法
字符匹配算法是计算机科学中非常重要的算法之一。
它的目的是在一个字符串中找到另一个字符串的出现位置。
这个问题看起来非常简单,但是在实际应用中,需要考虑到很多因素,比如字符串长度、匹配算法的效率等。
传统的字符匹配算法是暴力搜索算法,它的时间复杂度为O(n*m),其中n为目标字符串的长度,m为模式串的长度。
这种算法在大规模数据下的效率较低,因此需要寻找更加高效的算法。
常用的高效算法有KMP算法、Boyer-Moore算法、Rabin-Karp算法等。
其中KMP算法是应用最广泛的一种,它的时间复杂度为O(n+m)。
这种算法通过预处理模式串来实现快速匹配,其核心思想是利用已经匹配的信息来减少不必要的比较。
Boyer-Moore算法的时间复杂度为O(n),它通过预处理模式串来减少比较次数。
Rabin-Karp算法则采用哈希函数来将字符串转化为
数字,然后通过比较数字来判断是否匹配。
在实际应用中,需要根据具体问题的要求来选择合适的字符匹配算法。
例如,对于需要频繁进行字符串匹配的问题,可以选择KMP算法;对于需要快速匹配较长的模式串的问题,可以选择Boyer-Moore 算法;对于字符串集较大的问题,则可以选择Rabin-Karp算法。
总之,字符匹配算法是计算机科学中非常重要的一部分,它可以帮助我们解决很多实际问题。
在面对不同的问题时,我们需要选择合适的算法来提高效率。
字符串匹配问题
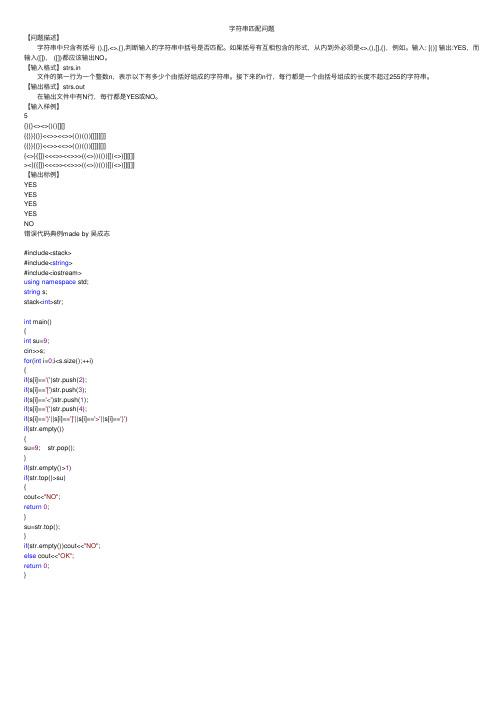
字符串匹配问题【问题描述】字符串中只含有括号 (),[],<>,{},判断输⼊的字符串中括号是否匹配。
如果括号有互相包含的形式,从内到外必须是<>,(),[],{},例如。
输⼊: [()] 输出:YES,⽽输⼊([]), ([])都应该输出NO。
【输⼊格式】strs.in⽂件的第⼀⾏为⼀个整数n,表⽰以下有多少个由括好组成的字符串。
接下来的n⾏,每⾏都是⼀个由括号组成的长度不超过255的字符串。
【输出格式】strs.out在输出⽂件中有N⾏,每⾏都是YES或NO。
【输⼊样例】5{}{}<><>()()[][]{{}}{{}}<<>><<>>(())(())[[]][[]]{{}}{{}}<<>><<>>(())(())[[]][[]]{<>}{[]}<<<>><<>>>((<>))(())[[(<>)]][[]]><}{{[]}<<<>><<>>>((<>))(())[[(<>)]][[]]【输出标例】YESYESYESYESNO错误代码典例made by 吴成志#include<stack>#include<string>#include<iostream>using namespace std;string s;stack<int>str;int main(){int su=9;cin>>s;for(int i=0;i<s.size();++i){if(s[i]=='(')str.push(2);if(s[i]=='[')str.push(3);if(s[i]=='<')str.push(1);if(s[i]=='{')str.push(4);if(s[i]==')'||s[i]==']'||s[i]=='>'||s[i]=='}')if(str.empty()){su=9; str.pop();}if(str.empty()>1)if(str.top()>su){cout<<"NO";return0;}su=str.top();}if(str.empty())cout<<"NO";else cout<<"OK";return0;}。
浅谈数据结构-字符串匹配

浅谈数据结构-字符串匹配是数据结构中字符串的⼀种基本运算,给定⼀个⼦串,要求在某个字符串中找出与该⼦串相同的所有⼦串,这就是模式匹配。
假设P是给定的⼦串,T是待查找的字符串,要求从T中找出与P相同的所有⼦串,这个问题成为模式匹配问题。
P称为模式,T称为⽬标。
如果T中存在⼀个或多个模式为P的⼦串,就给出该⼦串在T中的位置,称为匹配成功;否则匹配失败。
蛮⼒算法(BF算法)算法思想从⽬标串T的的第⼀个字符起与模式串P的第⼀个字符⽐较。
若相等,则继续对字符进⾏后续的⽐较;否则⽬标串从第⼆个字符起与模式串的第⼀个字符重新⽐较。
直⾄模式串中的每个字符依次和⽬标串中的⼀个连续的字符序列相等为⽌,此时称为匹配成功,否则匹配失败。
算法性能假设模式串的长度为m,⽬标串的长度为n:N为外循环,M为内循环。
BF算法存在回溯,严重影响到效率,最坏的情况的是N*M,所以算法的复杂度为O(mn).暴⼒算法中⽆法利⽤已知的信息,也就是模式串的信息,减少匹配。
⽐如在第四步中,t[5]和p[4]不匹配,然后⼜回溯(图有点问题),t[3]和P[0]肯定不同,因为之前匹配过了,我们得知t[3]=p[1],⽽p[0]和p[1]不同。
代码int bf(const char *text, const char *find){//异常判断if (*text == '/0' || *find == '/0'){return -1;}int find_len = strlen(find);int text_len = strlen(text);if (text_len < find_len){return -1;}//去除const属性char *s =const_cast<char*>(text);char *p = s;char *q = const_cast<char*>(find);//执⾏BF算法while (*p != '\0'){//匹配成功,指针前移if (*p == *q){p++;q++;}//否则,回溯,通过记录之前的指针位置,重新赋值。
字符串匹配的KMP算法

字符串匹配的KMP算法是计算机的基本任务之⼀。
举例来说,有⼀个字符串"BBC ABCDAB ABCDABCDABDE",我想知道,⾥⾯是否包含另⼀个字符串"ABCDABD"?许多算法可以完成这个任务,(简称KMP)是最常⽤的之⼀。
它以三个发明者命名,起头的那个K就是著名科学家Donald Knuth。
这种算法不太容易理解,⽹上有很多,但读起来都很费劲。
直到读到的⽂章,我才真正理解这种算法。
下⾯,我⽤⾃⼰的语⾔,试图写⼀篇⽐较好懂的KMP算法解释。
1.⾸先,字符串"BBC ABCDAB ABCDABCDABDE"的第⼀个字符与搜索词"ABCDABD"的第⼀个字符,进⾏⽐较。
因为B与A不匹配,所以搜索词后移⼀位。
2.因为B与A不匹配,搜索词再往后移。
3.就这样,直到字符串有⼀个字符,与搜索词的第⼀个字符相同为⽌。
4.接着⽐较字符串和搜索词的下⼀个字符,还是相同。
5.直到字符串有⼀个字符,与搜索词对应的字符不相同为⽌。
6.这时,最⾃然的反应是,将搜索词整个后移⼀位,再从头逐个⽐较。
这样做虽然可⾏,但是效率很差,因为你要把"搜索位置"移到已经⽐较过的位置,重⽐⼀遍。
7.⼀个基本事实是,当空格与D不匹配时,你其实知道前⾯六个字符是"ABCDAB"。
KMP算法的想法是,设法利⽤这个已知信息,不要把"搜索位置"移回已经⽐较过的位置,继续把它向后移,这样就提⾼了效率。
8.怎么做到这⼀点呢?可以针对搜索词,算出⼀张《部分匹配表》(Partial Match Table)。
这张表是如何产⽣的,后⾯再介绍,这⾥只要会⽤就可以了。
9.已知空格与D不匹配时,前⾯六个字符"ABCDAB"是匹配的。
查表可知,最后⼀个匹配字符B对应的"部分匹配值"为2,因此按照下⾯的公式算出向后移动的位数: 移动位数 = 已匹配的字符数 - 对应的部分匹配值因为 6 - 2 等于4,所以将搜索词向后移动4位。
字符串匹配算法总结

Brute Force(BF或蛮力搜索) 算法:这是世界上最简单的算法了。
首先将匹配串和模式串左对齐,然后从左向右一个一个进行比较,如果不成功则模式串向右移动一个单位。
速度最慢。
那么,怎么改进呢?我们注意到Brute Force 算法是每次移动一个单位,一个一个单位移动显然太慢,是不是可以找到一些办法,让每次能够让模式串多移动一些位置呢?当然是可以的。
我们也注意到,Brute Force 是很不intelligent 的,每次匹配不成功的时候,前面匹配成功的信息都被当作废物丢弃了,当然,就如现在的变废为宝一样,我们也同样可以将前面匹配成功的信息利用起来,极大地减少计算机的处理时间,节省成本。
^_^注意,蛮力搜索算法虽然速度慢,但其很通用,文章最后会有一些更多的关于蛮力搜索的信息。
KMP算法首先介绍的就是KMP 算法。
这个算法实在是太有名了,大学上的算法课程除了最笨的Brute Force 算法,然后就介绍了KMP 算法。
也难怪,呵呵。
谁让Knuth D.E. 这么world famous 呢,不仅拿了图灵奖,而且还写出了计算机界的Bible <The Art of Computer Programming>( 业内人士一般简称TAOCP). 稍稍提一下,有个叫H.A.Simon 的家伙,不仅拿了Turing Award ,顺手拿了个Nobel Economics Award ,做了AI 的爸爸,还是Chicago Univ 的Politics PhD ,可谓全才。
KMP 的思想是这样的:利用不匹配字符的前面那一段字符的最长前后缀来尽可能地跳过最大的距离比如模式串ababac 这个时候我们发现在c 处不匹配,然后我们看c 前面那串字符串的最大相等前后缀,然后再来移动下面的两个都是模式串,没有写出来匹配串原始位置ababa c移动之后aba bac因为后缀是已经匹配了的,而前缀和后缀是相等的,所以直接把前缀移动到原来后缀处,再从原来的c 处,也就是现在的第二个b 处进行比较。
字符串匹配

先看数据结构书上的KMP算法网上找的别人对KMP的理解这种由D.E.Knuth,J.H.Morris和V.R.Pratt同时发现的改进的模式匹配算法简称为KMP算法。
大概学过信息学的都知道,是个比较难理解的算法,今天特把它搞个彻彻底底明明白白。
注意到这是一个改进的算法,所以有必要把原来的模式匹配算法拿出来,其实理解的关键就在这里,一般的匹配算法:个人理解:所谓的KMP中的前缀函数,也就是求next或者nextval,其实是模式串自己匹配自己的一个过程,next存储的就是模式串自己匹配自己时,第i个字符在自己中出现的最后位置(因为要尽快匹配)!int Index(String S,String T,int pos)//参考《数据结构》中的程序{i=pos;j=1;//这里的串的第1个元素下标是1while(i<=S.Length && j<=T.Length){if(S[i]==T[j]){++i;++j;}else{i=i-j+2;j=1;}//**************(1)}if(j>T.Length) return i-T.Length;//匹配成功else return 0;}匹配的过程非常清晰,关键是当‘失配’的时候程序是如何处理的?回溯,没错,注意到(1)句,为什么要回溯,看下面的例子:S:aaaaabababcaaa T:ababcaaaaabababcaaaababc.(.表示前一个已经失配)回溯的结果就是aaaaabababcaaaa.(babc)如果不回溯就是aaaaabababcaaaaba.bc这样就漏了一个可能匹配成功的情况aaaaabababcaaaababc为什么会发生这样的情况?这是由T串本身的性质决定的,是因为T串本身有前后'部分匹配'的性质。
如果T为abcdef这样的,大没有回溯的必要。
改进的地方也就是这里,我们从T串本身出发,事先就找准了T自身前后部分匹配的位置,那就可以改进算法。
字符串的匹配问题(本科生教材)

pq-1 pq
ti-q … tj-q+ next[q]-1 … … tj- next[q] … tj-2, tj-1 tj p0 p1 … pnext[q]-1 … … … pq
与最长前、后缀矛盾
?
4、求前缀函数
由 p 的 前 缀 函 数 的 定 义 易 知 next[0]=-1 next[1]=0 。 用数学归纳法来计算前缀函数next的值: 对于任何q>1,如果我们已经计算出: next[0], next[1],…, next[q] 那么如何计算next[q+1]呢?
2、例2
求串‘ababababca’的前缀函数π[]
a b Next[] -1 0 a 0 b 1 a 2 b 3 a 4 b 5 c 6 a 0
c d a b a b a b a b ? a b a b a b a b c c d a b a b a b a b ? ? ? a b a b a b a b c
最后1个位 置不匹配!
可能存 在匹配 的位置
c d a b a b a b a b ? ? ? ? ?
a b a b a b a b c c d a b a b a b a b ? ? ? ? ? a b a b a b a b c
当p.c[q]与t.c[j]不相等时,模式串p向右滑动 多少个位置,再比较,既不丢失可能的匹配, 又不做回溯? 以例2为例,展示匹配和滑动的过程!
tj-q … tj-q+ next[q]-1 … tj- next[q] … tj-2, tj-1 tj p0 p1 … pnext[q]-1 … pq- next[q] …
模板向后滑动
最大后缀
pq-1 pq
tj-q … tj-q+ next[q]-1 …tj- next[q] … tj-2, tj-1 tj
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
前缀函数计算
• Prefix-function
COMPUTE-PREFIX-FUNCTION(P) 1 m ← length[P] 2 π[1] ← 0 3k←0 4 for q ← 2 to m 5 do while k > 0 and P[k + 1] ≠ P[q] 6 do k ← π[k] 7 if P[k + 1] = P[q] 8 then k ← k + 1 9 π[q] ← k 10 return π
10
KMP算法的时间复杂度
• KMP,第5行循环n次,6-7行最坏情况下要循环m次。如 下面的例子。 • 因此,最坏情况的时间复杂度似乎为O(nm)
T=a b c a a a a a b P= aaaaaa π[i]=0,1,2,3,4,5 匹配失败时,执行 q ← π[q]共m-1次。
• 然而依据平摊分析,若q ← π[q]重复m-1次,意味着之前q ← q + 1 重复了m-1次,i=i+1重复了m-1次,而且在此过 程中q←π[q]没被执行一次。因此纵观整个for循环,i=i+1 被重复多少次, q←π[q]就被重复多少次,因此整个时间 复杂度为O(n)。
3
思考题
• Exercises 32.1-2,Suppose that all characters in the pattern P are different. Show how to accelerate NAIVE-STRING-MATCHER to run in time O(n) on an n-character text T. • Exercises 32.1-4,Suppose we allow the pattern P to contain occurrences of a gap character ⋄ that can match an arbitrary string of characters (even one of zero length). For example, the pattern ab⋄ba⋄c occurs in the text cabccbacbacab as • Note that the gap character may occur an arbitrary number of times in the pattern but is assumed not to occur at all in the text. Give a polynomial-time algorithm to determine if such a pattern P occurs in a given text T , and analyze the running time of your algorithm.
6
前缀函数的计算(1)
• 已知模式P[1 ‥ q]与文本字符T[s+1 ‥ s+q]匹配,那么满 足P[1 ‥ k]= T[s’+1‥ s’+k]的最小位移s’ > s是多少(其中 s’+k = s+q)? • 对于新的位移s’ ,无需把P的前k个字符与T中相应的字符 进行比较,因为前面的等式已保证它们匹配。
4
Knuth-Moriis-Pratt算法
• 由Knuth,Morris,Pratt设计。匹配时间为 O(n),用到辅助函数π[1…m]。
5
Knuth-Moriis-Pratt2.10: The prefix function π. (a) q = 5 个字符匹配 成功。 (b) 利用5个字符匹配成功的信息可知, s + 1的位 移是无效的,而s′ = s + 2 可能是有效的。 (c) 前缀函数π 可以预计算,此处P的最长前缀也是P5的一个真后缀P3。 如 π[5] = 3。意味着在位移s有 q个字符匹配成功,则下一 个可能有效的位移为 s′ = s + (q - π[q])。
• 用模式与自身比较,预先计算出这些必要的信息,如图 32-10c可以把等式32.5解释为满足Pk是Pq后缀的最大的 k<q。
7
前缀函数的计算(2)
• 前缀函数定义如下,给定模式 P[1 ‥ m],前缀函 数是: • π : {1, 2, . . . , m} → {0, 1, . . . , m - 1} 且满足: • π[q] = max {k : k < q and Pk ⊐ Pq}. • 即 π[q] 是Pq的真后缀P 的最长前缀的长度。
8
KMP算法
• KMP
KMP-MATCHER(T, P) 1 n ← length[T] 2 m ← length[P] 3 π ← COMPUTE-PREFIX-FUNCTION(P) 4 q ← 0 ▹Number of characters matched. 5 for i ← 1 to n ▹Scan the text from left to right. 6 do while q > 0 and P[q + 1] ≠ T[i] 7 do q ← π[q] ▹Next character does not match. 8 if P[q + 1] = T[i] 9 then q ← q + 1 ▹Next character matches. 10 if q = m ▹Is all of P matched? 11 then print "Pattern occurs with shift" i - m 12 q ← π[q] ▹Look for the next match.
字符串匹配
高文宇 gwyy@
1
字符串匹配算法比较
• Figure 32.2:字符串匹配算法比较
2
朴素的字符串匹配
• naive string-matching algorithm
NAIVE-STRING-MATCHER(T, P) 1 n ← length[T] 2 m ← length[P] 3 for s ← 0 to n - m 4 do if P[1 ‥ m] = T[s + 1 ‥ s + m] 5 then print "Pattern occurs with shift" s
11
再见
• 再见
12
