专题复习《坐标法解立体几何体解答题》

合集下载

高中数学立体几何大题题库答案

立体几何解答题题库答案1.（1）作法:取BC 的中点H ,连接AH ,则直线AH 即为要求作的直线l ．证明如下:,PA AB PA AC ⊥⊥,且AB AC A =,PA ∴⊥平面ABC ．平面//α平面PAB ,且α平面11PAC P A =,平面PAB平面PAC PA =． 11P A ∴⊥平面ABC ,11PA AH ∴⊥．又AB AC =,H 为BC 的中点,则AH BC ⊥,从而直线AH 即为要求作的直线l ．（2）α将三棱锥P ABC -分成体积之比为8:19的两部分,∴四面体111P A B C 的体积与三棱锥P ABC -分成体积之比为8:27,又平面//α平面PAB ,11123AC B C PC AC BC PC ∴===．易证//PA 平面111P A B ,则P 到平面111P A B 的距离1d 即为A 到平面111P A B 的距离,111d AA ∴==又D 为1B C 的中点,D ∴到平面111P A B 的距离21112d AC ==, 故四棱锥111A PPDB -的体积()1211422323V d d =⨯+⨯⨯⨯=． 2.(1)由几何体的三视图可知,底面ABCD 是边长为4的正方形,PA ⊥平面ABCD ,PA ∥EB ,且PA ＝,BE ＝,AB ＝AD ＝CD ＝CB ＝4,∴V P －ABCD ＝13PA ×S ABCD ＝13××4×4┉┉┉┉┉┉┉┉┉┉┉┉4分（2）证明:连结AC 交BD 于O 点,取PC 中点F ,连结OF ,∵EB ∥PA ,且EB ＝12PA ,又OF ∥PA ,且OF ＝12PA ,∴EB ∥OF ,且EB ＝OF ,∴四边形EBOF 为平行四边形,∴EF ∥BD .又EF ⊂平面PEC ,BD ⊄平面PEC ,所以BD ∥平面PEC .┉┉┉┉┉┉┉┉┉┉┉┉8分解法二:可取PA 的中点Q,证明平面PEC ∥平面BDQ.BD ⊂平面BDQ.所以BD ∥平面PEC .(3)存在,点M 为线段BC 上任意一点. 证明如下:连结BP ,∵EBAB ＝BA PA ∠EBA ＝∠BAP ＝90°, ∴△EBA ∽△BAP ,∴∠PBA ＝∠BEA ,∴∠PBA ＋∠BAE ＝∠BEA ＋∠BAE ＝90°,∴PB ⊥AE . 又∵BC ⊥平面APEB ,∴BC ⊥AE ,∴AE ⊥平面PBC ,∴点M 为线段BC 上任意一点,均可使得AE ⊥PM. ┉┉┉┉┉┉┉┉┉┉12分3.（Ⅰ）在梯形ABCD 中,∵CD AB //,CB AD =,∴=∠BAD 60ABC ∠=,∴=∠ADC 120=∠BCD ,∵1==DC AD .∴=∠CAD 30=∠ACD ,∴ 90=∠ACB ,∴AC BC ⊥.（4分）∵平面ACFE ⊥平面ABCD ,平面 ACFE 平面ABCD AC =,∴⊥BC 平面ACFE .（Ⅱ）在ADC ∆中,-+=222DC AD AC ADC DC AD ∠⋅cos 23=,∴3=AC .分别以CF CB CA ,,为x 轴,y 轴,z 轴建立平面直角坐标系, 设h CF =,则)0,0,0(C ,)0,0,3(A ,)0,1,0(B ,)0,0,21(D ,),0,0(h F ,则)0,1,21(-=BD ,),1,0(h BF -=,易知平面BCF 的一个法向量为)0,0,1(=m , ∵平面BDF 的法向量为),,(z y x =,∴⎪⎩⎪⎨⎧=⋅=⋅,0,0BF n BD n 即⎪⎩⎪⎨⎧=+-=-,0,021hz y y x 令1=z ,则h x 2=,h y =, ∴平面BDF 的法向量为)1,,2(h h =,∵二面角D BF C --的平面角的余弦值为66, ∴>=<n m ,cos 1522+h h66=,解得1=h ,即1=CF .（10分）所以六面体ABCDEF 的体积为:=ABCDEF V ACFE B V -ACFE D V -+BC S ACFE ⨯=正方形31D ACFE y S ⨯+正方形3121211311131=⨯⨯+⨯⨯=.（12分）4.（1）证明:取AD 的中点O,连OC,OP∵∆PAD 为等边三角形,且O 是边AD 的中点∴AD PO ⊥∵平面PAD ⊥底面ABCD ,且它们的交线为AD∴ABCD PO 平面⊥∴PO BA ⊥∵O PO AD AD BA =⊥ 且,∴PAD AB 平面⊥∴AB PD ⊥（2）设点M 到平面ACD 的距离为h ∵31==--ACD M ACM D V V ∴3131=⋅∆h S ACD ∴11ACD h S ∆== ∵31==OP h CP CM∴λ== 5.（I ）连PM 、MB ∵PD ⊥平面ABCD ∴PD ⊥MD222222222323a AM AB BM a MD PD PM =+==+=∴又 ∴PM=BM 又PN=NB ∴MN ⊥PB,22,BC a PC a BC a DC PD ==∴===得NC ⊥PB MN NC N = ∴PB ⊥平面MNC⊂PB 平面PBC∴平面MNC ⊥平面PBC（II ）取BC 中点E,连AE,则AE//MC ∴AE//平面MNC,A 点与E 点到平面MNC 的距离相等取NC 中点F,连EF,则EF 平行且等于21BN ∵BN ⊥平面MNC ∴EF ⊥平面MNC,EF 长为E点到平面MNC 的距离 ∵PD ⊥平面ABCD,PD BC ∴⊥ 又BC ⊥DC BC ∴⊥面PCD ∴BC ⊥PC.24121,222a PB BN EF a PC BC PB ====+=∴ 即点A 到平面MNC 的距离为2a 6.（2）连接A 1B ,设A 1B ∩AB 1=F ,连接EF ．在直三棱柱ABC －A 1B 1C 1中,四边形AA 1B 1B 为平行四边形,所以F 为A 1B 的中点．又因为E 是BC 的中点,所以EF ∥A 1C ．因为EF 在平面AB 1E 内,A 1C 不在平面AB 1E 内,所以A 1C ∥平面AB 1E ．7.证明:（1）∵ABCD 为矩形,∴BC ⊥AB,又∵平面ABCD ⊥平面AEBF,BC ⊂平面ABCD,平面ABCD∩平面AEBF=AB, ∴BC ⊥平面AEBF, ……………（2分）又∵AF ⊂平面AEBF,∴BC ⊥AF. ……………（3分）∵∠AFB=90°,即AF ⊥BF,且BC 、BF ⊂平面BCF,BC∩BF=B , ∴AF ⊥平面BCF. ……………（5分）又∵AF ⊂平面ADF,∴平面ADF ⊥平面BCF. ………………………………（6分）（2）∵BC ∥AD,AD ⊂平面ADF,∴BC ∥平面ADF.∵ABE ∆和ABF ∆均为等腰直角三角形,且BAE AFB ∠=∠=90°,∴∠FAB=∠ABE=45°,∴AF ∥BE,又AF ⊂平面ADF,∴BE ∥平面ADF,∵BC∩BE=B ,∴平面BCE ∥平面ADF.延长EB 到点H,使得BH =AF,又BC //AD,连CH 、HF,易证ABHF 是平行四边形, ∴HF //AB //CD,∴HFDC 是平行四边形,∴CH ∥DF.过点B 作CH 的平行线,交EC 于点G,即BG ∥CH ∥DF,（DF ⊂平面CDF ）∴BG ∥平面CDF,即此点G 为所求的G 点. ………………………………（9分）又22AF BH ==,∴EG=23EC ,又2ABE ABF S S ∆∆=, 2444433333G ABE C ABE C ABF D ABF B ADF G ADF V V V V V V ------=====, 故43G ABE G ADF V V --=..………………………………（12分） 8.（1）证明: 四边形ABCD 为菱形 AC BD ⊥∴,………………1分又Q 面ACFE ⋂面ABCD =ACABCD BD 平面⊂∴………………2分面ABCD ⊥面ACFE C………………3分ACFE BD 面⊥∴,………………4分Q ACFE CH 面⊂ ………………5分CH BD ⊥∴………………………………6分（2）在FCG ∆中,GF CH CH CF CG ⊥===,23,3 所以︒=∠120GCF ,………………6分3=GF ………………8分ACFE BD 面⊥ ,ACFE GF 面⊂GF BD ⊥∴,………………9分3322121=⨯⨯=⋅=∆GF BD S BDF …………………………………. 10分又BD CH ⊥∴,GF CH ⊥,G GF BD =⋂∴,BDF GF BD 平面⊂∴,∴CH ⊥平面BDF . . . . . . . . . . . . . 12分232333131=⋅⋅=⋅⋅==∆--CH S V V BDF BDF C BDC F ……………………………14分 9.（1）证明:取BD 的中点O ,连接OE ,OG在BCD ∆中,因为G 是BC 的中点,所以OG ∥DC 且112OG DC ==,……………1分因为EF ∥AB ,AB ∥DC ,1EF =,所以EF ∥OG 且EF OG =,……………………2分所以四边形OGFE 是平行四边形,所以FG ∥OE , ………………………3分又FG ⊄平面BED ,OE ⊂平面BED ,所以FG ∥平面BED ． ……………………………4分（2）证明:在ABD ∆中,1AD =,2AB =,60BAD ∠=,由余弦定理得BD ==…………………………5分因为222314BD AD AB +=+==,所以BD AD ⊥. …………………………6分因为平面AED ⊥平面ABCD ,BD ⊂平面ABCD ,平面AED 平面ABCD AD =, 所以BD ⊥平面AED . ……………………………7分（3）解法1:由（1）FG ∥平面BED ,所以点F 到平面BED 的距离等于点G 到平面BED 的距离, ……………………8分设点G 到平面BED 的距离为h ,过E 作EM DA ⊥,交DA 的延长线于M ,则EM ⊥平面ABG ,所以EM 是三棱锥E ABG -的高． ……………………9分由余弦定理可得2cos 3ADE ∠=,所以sin ADE ∠=,sin EM DE ADE =⋅∠=. …………………………10分12DBG S DB BG ∆=⋅=12BDE S BD DE ∆=⋅= 因为G BDE E DBG V V--=,………………………………11分即1133BDE DBG S h S EM ∆∆⋅=⋅,解得h = 所以点F 到平面BED 的距离为65． ………………………………12分解法2:因为EF ∥AB ,且12EF AB =, 所以点F 到平面BED 的距离等于点A 到平面BED 的距离的12, ……………8分由（2）BD ⊥平面AED .因为BD ⊂平面BED ,所以平面BED ⊥平面AED ．过点A 作AH DE ⊥于点H ,又因为平面BED 平面AED ED =,故⊥AH 平面BED . 所以AH 为点A 到平面BED 的距离．…………………9分在ADE ∆中,6,3,1===AE DE AD , 由余弦定理可得2cos 3ADE ∠=所以sin ADE ∠=, …………………10分因此35sin =∠⋅=ADE AD AH , ……………………………………………………11分所以点F 到平面BED 的距离为65． ………………………………………………12分10.（1）设O 为AC 的中点,连接OS ,OD ,∵SA SC =,∴OS AC ⊥,∵DA DC =,∴DO AC ⊥,又,OS OD ⊂平面SOD ,且OS OD O =,AC ⊥平面SOD ,又SD ⊂平面SOD ,∴AC SD ⊥.（2）连接BD ,在ASC ∆中,∵SA SC =,60ASC ∠=,O 为AC 的中点,∴ASC ∆为正三角形,且2AC =,OS =∵在ASC ∆中,2224DA DC AC +==,O 为AC 的中点,∴90ADC ∠=,且1OD =,∵在SOD ∆中,222OS OD SD +=,∴SOD ∆为直角三角形,且90SOD ∠=,∴SO OD ⊥又OS AC ⊥,且ACDO O =,∴SO ⊥平面ABCD . ∴B SAD S BAD V V --=13BAD S SO ∆=⋅⋅1132AD CD SO =⨯⋅⋅⋅11323=⨯=. 11.证明(1)因为∠BAD ＝∠CDA ＝90°,所以//AB CD ,四边形ABCD 为直角梯形,2CD =又PC PD ==222CD PC PD +=PD PC ∴⊥又,,AD CD AD PAD ⊥⊂,CD,PCD ABCD PCD ABCD ⊥=平面平面平面平面 AD PCD ∴⊥平面又PC PBC ⊂平面 ,AD PC ∴⊥,,,PD PC PD PA A PD PA PAD ⊥=⊂点平面PC PAD ∴⊥平面,PC PBC ⊂平面所以平面P AD ⊥平面PBC ……………………4分(2)30°…………………………………8分(3)存在E 为PC 中点,即PE =满足条件……………………………12分 12.（1)证明:∵四边形11BB C C 是菱形,∴11B C BC ⊥,∵11,AB B C AB BC B ⊥⋂=, ∴1B C ⊥平面1ABC ,又AO ⊂平面1ABC ,∴1B C AO ⊥．∵1AB AC =,O 是1BC 的中点,∴1AO B C ⊥,∵11B C BC O ⋂=,∴AO ⊥平面11BB C C …………… ……6分（2）菱形11BB C C 的边长为2,又1160,B BC BB C ∠=︒∴∆是等边三角形,则12B C =. 由（1）知,1AO B C ⊥,又O 是1B C 的中点,1AB AC ∴=,又1160,B AC AB C ∠=︒∴∆是等边三角形,则112AC AB B C ===.在Rt ACO ∆中,22AO ===分11111122sin1201332C ABC A BCC BCC V V S AO --∆∴==⋅=⨯⋅⋅⋅=……………12分 13.（Ⅰ）证明:∵四边形ABCD 是菱形,∴AC BD ⊥.又∵PA ⊥平面ABCD ,BD ⊂≠平面ABCD ,∴PA BD ⊥．又PA AC A =,PA ⊂≠平面PAC ,AC ⊂≠平面PAC ,∴BD ⊥平面PAC ,∵BD ⊂≠平面PBD ,∴平面PBD ⊥平面PAC .（Ⅱ）解:BCD 11=221=3223C BDM M V V --=⨯⨯⨯⨯ 14. （1）证明:因为底面ABCD 为矩形,所以AD ∥BC ．AD BCAD ADF BC ADF BC ADF ⎫⎪⊂⇒⎬⎪⊄⎭∥平面∥平面平面,BC ADFBC BCPQ BC PQ BCPQ ADF PQ ⎫⎪⊂⇒⎬⎪=⎭∥平面平面∥平面平面,PQ BC PQ ABCD PQ ABCD BC ABCD ⎫⎪⊄⇒⎬⎪⊂⎭∥平面∥平面平面．（2）解:由CD ⊥BE ,CD ⊥CB ,易证CD ⊥CE ,由BC ⊥CD ,BC ⊥FD ,易证BC ⊥平面CDFE ,所以CB ⊥CE ,即CD ,CE ,CB 两两垂直．连接FB ,FC ,则CD ＝2,BC ＝3,1(23)123F ABCD V -=⨯⨯⨯=, 111(31)1322F BCE V -=⨯⨯⨯⨯=, 15222ABCDEF F ABCD F BCE V V V --=+=+=．15.（1）证明:因为AB =1BC =,090ABC ∠=,所以2AC =,060BCA ∠=,在△ACD 中,AD =2AC =,060ACD ∠=,由余弦定理可得:2222cos AD AC CD AC CD ACD =+-∠解得:CD =4所以222AC AD CD +=,所以△ACD 是直角三角形,又E 为CD 的中点,所以12AE CD CE == 又060ACD ∠=,所以△ACE 为等边三角形,所以060CAE BCA ∠==∠,所以//BC AE ,又AE ⊂平面SAE ,BC ⊄平面SAE ,所以BC ∥平面SAE .（2）解:因为SA ⊥平面ABCD ,所以SA 同为三棱锥S BCE -与四棱锥S ABED -的高.由（1）可得0120BCE ∠=,122CE CD ==,所以1sin 2BCE S BC CE BCE ∆=⨯⨯∠1122=⨯⨯=.BCE ABED ABCD S S S ∆=-四边形四边形ABC ACD BCD S S S ∆∆∆=+-111222=+⨯⨯=.所以::1:4BCE ABED S S ∆==四边形故:三棱锥S BCE -与四棱锥S BEDA -的体积比为1:4.16.（Ⅰ）取PA 的中点G,连FG,由题可知:BF=FP ,则FG //AB FG = 12AB ,又CE= ED ,可得:DE//AB 且DE = 12AB , ∴ FG //DE 且FG = DE ,∴四边形DEFG 为平行四边形,则EF //DG且EF =DG ,DG ⊂平面PAD ；EF ⊄平面PAD,∴ EF//平面PAD ⋯⋯⋯4分（Ⅱ）由PD ⊥平面ABCD ,PD ⊂平面PAD ,∴ 平面PAD ⊥平面ABCD,且交线为AD,又底面ABCD 是矩形,∴ BA ⊥ AD,∴BA ⊥ 平面PAD ,∴平面PAB ⊥平面PAD,其交线为PA ,又PD=AD,G 为PA 的中点,∴DG ⊥ PA,∴ DG ⊥平面PAB ,由（Ⅰ）知:EF // DG , ∴ EF ⊥平面PAB ⋯⋯⋯8分（Ⅲ）由得,AD=PD=1,F 为PB 的中点,∴ AEF P V -= AEF B V - = ABE F V -= ABE P V -21=PD S ABE ⋅⋅⋅∆3121 = 112213121⋅⋅⋅⋅⋅= 122⋯⋯⋯⋯12分 17.(1)见解析；（2.解:（1）证明:∵OD ABCD ⊥平面,PA QD ∥,∴PA ABCD ⊥平面,又∵BC ABCD ⊂平面,∴PA BC ⊥,又BC AB ⊥,PA PAB ⊂平面,AB PAB ⊂平面,PAAB A =,∴BC PAB ⊥平面,又∵BC QBC ⊂平面,∴平面PAB QBC ⊥平面. --------------------------518.（1）证明:∵平面PAD 垂直矩形平面ABCD ,∴CD ⊥平面PAD取DC 中点H,连接EH,EH ⊥CD,连接FH,则FH ⊥CD则CD ⊥平面EHF,∴平面EHF//平面PAD,又EF ∈平面EHF∴EF 平行PAD ； …………4分（2）证明:∵平面PAD 垂直矩形平面ABCD ,角CDA=90度,CD ⊥平面PAD,又平面PAD∩平面PDC 于PD,又DC ∈平面PDC,∴平面PDC 垂直平面PAD ………8分分19.（1）连结AB 1交A 1B 于点O,则O 为AB 1中点, D AC OD B CCD A BD B C A BD B C A BD∴⊂⊄∴１１１１１１是的中点又平面，平面平面20.（1）证明:连接BD ,交AC 于F ,连接EF .∵四边形ABCD 为正方形∴F 为BD 的中点∵E 为PB 的中点,∴EF ∥PD 又∵PD ⊄面ACE ,EF ⊂面ACE ,∴PD ∥平面ACE .（2）.取AB 中点为G ,连接EG .∵E 为PB 的中点,∴EG ∥P A∵PA ⊥平面ABCD ,∴EG ⊥平面ABCD ,即EG 是三棱锥E ADC -的高,在Rt PAB ∆中,PB =4AB =,则4PA =, 2EG =,∴三棱锥E ADC -的体积为1116442323⨯⨯⨯⨯=. 21.（Ⅰ）证明:∵四边形ABCD 是矩形,∴CD ⊥BC .∵平面PBC ⊥平面ABCD ,平面PBC ∩平面ABCD =BC ,CD ⊂平面ABCD ,∴CD ⊥平面PBC ,∴CD ⊥PB .∵PB ⊥PD ,CD ∩PD =D ,CD 、PD ⊂平面PCD ,∴PB ⊥平面PCD .∵PB ⊂平面P AB ,∴平面P AB ⊥平面PCD .（Ⅱ）取BC 的中点O ,连接OP 、OE .∵PB ⊥平面PCD ,∴PB PC ⊥,∴112OP BC ==, ∵PB PC =,∴PO BC ⊥．∵平面PBC ⊥平面ABCD ,平面PBC ∩平面ABCD =BC ,PO ⊂平面PBC ,∴PO ⊥平面ABCD ,∵AE ⊂平面ABCD ,∴PO ⊥AE .∵∠PEA =90O , ∴PE ⊥AE .∵PO ∩PE=P ,∴AE ⊥平面POE ,∴AE ⊥OE .∵∠C=∠D =90O , ∴∠OEC =∠EAD ,∴Rt OCE Rt EDA ∆∆,∴OC CE ED AD=． ∵1OC =,2AD =,CE ED =,∴CE ED ==111332A PED P AED AED V V S OP AD ED OP --==⋅=⨯⋅⋅112132=⨯⨯= 22.（1）证明:因为23λ=,所以23CE CS =,在线段CD 上取一点F 使23CF CD =,连接EF,BF,则EF ∥SD 且DF ＝1．因为AB ＝1,AB ∥CD,∠ADC ＝90°,所以四边形ABFD 为矩形,所以CD ⊥BF ．又SA ⊥平面ABCD,∠ADC ＝90°,所以SA ⊥CD,AD ⊥CD ．因为AD∩SA ＝A,所以CD ⊥平面SAD, PCBAE DO所以CD ⊥SD,从而CD ⊥EF ．因为BF∩EF ＝F,所以CD ⊥平面BEF ．又BE ⊂平面BEF,所以CD ⊥BE ．（2）解:由题设得,111()2332S BCD BCD V S SA CD AD SA -=⋅=⨯⨯⨯⨯=△,又因为SB ==BD ==SD =,所以12SBD S SD =⋅=△,设点C 到平面SBD 的距离为h,则由V S —BCD ＝V C —SBD 得h =,因为13CE CS =,所以点E 到平面SBD 的距离为23h =．23.证明:（1）∵几何体1111ABCD A B C D -为四棱柱,∴四边形11BCC B 为平行四边形,即BC ∥11B C ,且BC =11B C ,……………2分又∵底面ABCD 为等腰梯形,∴BC ∥AM ,即AM ∥11B C , ………………………3分又∵22AD AB BC ==,且M 为边AD 的中点,∴AM BC =,即AM =11B C ,……………4分则四边形11AMC B 为平行四边形,即1C M ∥1AB , ………………………………5分又∵1C M ⊄平面11A ABB ,1A B ⊂平面11A ABB ,∴1C M ∥平面11A ABB , ……………………………………………………7分（2）∵BC ∥AM ,且AM BC =,∴四边形AMCB 为平行四边形, 又∵2AD AM AB ==,∴四边形AMCB 为茭形,则BM ⊥AC , ……………9分又∵1CB ⊥底面ABCD ,且BM ⊂底面ABCD ,∴BM ⊥1CB , ……………11分又∵1AC CB C =,且AC ⊂平面1ACB ,1CB ⊂平面1ACB ,∴BM ⊥平面1ACB , ……………………………………………………13分又∵BM ⊂底面1B BM ,∴平面1B BM ⊥平面1ACB ……………………………14分 24.（Ⅰ）证明:取BC 中点M ,连接,DM PM可知1MD AB ==且MD BC ⊥又,2PB PC BC ⊥=,∴在Rt PBC ∆有1PM = 又2PD =,222PD PM MD ∴=+,即MD PM ⊥ ………………………3分又,,MD BC PM BC M PM ⊥=⊂平面PBC ,BC ⊂平面PBCMD ∴⊥平面PBC , ………………………5分又MD ⊂平面ABCD∴平面PBC ⊥平面ABCD ………………………6分（Ⅱ）设点D 到平面PAB 的距离为h,PC PB PC PB =⊥,PM BC ∴⊥ 又平面PBC ⊥平面ABCD ,且平面PBC 平面ABCD BC =PM ∴⊥面ABCD ………………………8分1111||1113326P ABD ABD V PM S -∆∴==⨯⨯⨯⨯=………………………9分在PAB ∆中有1,PB AB PA ===,222,PB AB PA PB AB ∴+=∴⊥∴2PAB S ∆=…………………10分1113326D ABP ABP V S h h -∆=⋅=⨯=,2h ∴=所以点D 到平面PAB.………………………12分 25.（1）因为//BC 平面SDM, BC ⊂平面ABCD,平面SDM 平面ABCD=DM,所以DM BC //,因为DC AB //,所以四边形BCDM 为平行四边形,又CD AB 2=,所以M 为AB 的中点．因为AM λ=,12λ∴=．（2）因为BC ⊥SD , BC ⊥CD ,所以BC ⊥平面SCD ,又因为BC ⊂平面ABCD ,所以平面SCD ⊥平面ABCD ,平面SCD 平面ABCD CD =,在平面SCD 内过点S 作SE ⊥直线CD 于点E ,则SE ⊥平面ABCD , 在Rt △SEA 和Rt △SED 中,因为SA SD =,所以AE DE ==, 又由题知45EDA ∠=,所以AE ED ⊥,由已知求得AD =,所以1AE ED SE ===,连接BD,则111133S ABD V -=⨯⨯=三棱锥,又求得△SAD所以由B ASD S ABD V V --=三棱锥三棱锥点B 到平面SAD ．26.（1）由已知,平面ABCD, ∵平面, 又∵,∴平面．因平面EBD,则平面平面BDE ．（2）法1:记AC 交BD 于点O,连PO,由（1）得平面平面BDP,且交于直线PO, 过点E 作于H,则平面PBD, ∴为BE 与平面PBD 所成的角． ∵,∴． ∴．又,则．于是,直线BE与平面PBD所成角的正弦值是．法2:（等体积法）∵,∴E点到平面PBD的距离为．又,则．于是,直线BE与平面PBD所成角的正弦值是．27.（1）又又（2）设,则.过作,为垂足,为中点....四棱锥P-ABCD的侧面积为:,。

坐标法解立体几何解答题

坐标法解立体几何解答题教学目的：1、熟练掌握空间向量的有关知识；2、能灵活运用坐标法解决立体几何解答题的有关问题；3、进一步提高学生的空间想象能力和运算能力。

教学重点：1、建立适当的空间直角坐标系；2、正确写出点的坐标；3、求平面的法向量；4、灵活运用坐标法解决空间角、空间距离等问题教学难点：求平面的法向量授课类型：专题复习教学方法：启发引导式教具准备：幻灯片20张教学过程：一、复习引入：空间向量解决立体几何问题主要有两个基本方法：坐标法与基底法。

本节课着重研究利用坐标法解决立体几何解答题。

1、空间向量的有关知识：(幻灯片投影)（1）设点)z ,y ,B(x )z ,y ,A(x 222111、，则),,(121212z z y y x x AB ---=→；（2）设向量),,(),,,(222111z y x b z y x a ==→→，则 ① 212121z z y y x x b a ++=⋅→→；② →a ∥),,(),,(222111z y x z y x b a b λλ=⇔⋅=⇔→→→； ③ 0212121=++=⋅⇔⊥→→→→z z y y x x b a b a ；（3）设向量),,(z y x a =→，则222z y x a ++=→；（4）→→→→→→→→⋅>=<ba b a b a ,cos b a 的夹角：、向量；2、坐标法解决立体几何解答题的步骤：(幻灯片投影) （1）建立适当的空间直角坐标系；（2）写出相应的点的坐标；l （3）解决问题：(幻灯片投影) （一）求空间角问题：空间的角主要有：异面直线所成的角；直线和平面所成的角；二面角。

① 求异面直线所成的角：设a 、b 分别为异面直线a 、b 的方向向量，则两异面直线所成的角α=arccos ||||||a ba b 。

② 求线面角：设l 是斜线l 的方向向量，n 是平面α的法向量，则斜线l 与平面α所成的角2,,2ππθ-><><-=→→→→n l n l 或③ 求二面角：法一：在α内a l ⊥，在β内b l ⊥，其方向如图，则二面角l αβ--的平面角ba b a ⋅⋅=arccosα法二：设m n 、是二面角l αβ--的两个半平面的法向量，其方向一个指向内侧，另一个指向外侧，则二面角l αβ--的平面角nm n m ⋅⋅=arccosα（二）求空间距离问题构成空间的点、线、面之间有七种距离，这里着重介绍点面距离的求法。

坐标法解立体几何习题及解析

坐标法解立体几何1空间直角坐标系：（1）若空间的一个基底的三个基向量互相垂直，且长为1，这个基底叫单位正交基底，用{,,}i j k 表示；（2）在空间选定一点O 和一个单位正交基底{,,}i j k ，以点O 为原点，分别以,,i j k 的方向为正方向建立三条数轴：x 轴、y 轴、z 轴，它们都叫坐标轴．我们称建立了一个空间直角坐标系O xyz -，点O 叫原点，向量 ,,i j k 都叫坐标向量．通过每两个坐标轴的平面叫坐标平面，分别称为xOy 平面，yOz 平面，zOx 平面；2．空间直角坐标系中的坐标：在空间直角坐标系O xyz -中，对空间任一点A ，存在唯一的有序实数组(,,)x y z ，使OA xi yj zk =++，有序实数组(,,)x y z 叫作向量A 在空间直角坐标系O xyz -中的坐标，记作(,,)A x y z ，x 叫横坐标，y 叫纵坐标，z 叫竖坐标．3．空间向量的直角坐标运算律：（1）若123(,,)a a a a =，123(,,)b b b b =，则112233(,,)a b a b a b a b +=+++，112233(,,)a b a b a b a b -=---，123(,,)()a a a a R λλλλλ=∈，112233a b a b a b a b ⋅=++，112233//,,()a b a b a b a b R λλλλ⇔===∈，1122330a b a b a b a b ⊥⇔++=．（2）若111(,,)A x y z ，222(,,)B x y z ，则212121(,,)AB x x y y z z =---．一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标4模长公式：若123(,,)a a a a =，123(,,)b b b b =，则222123||a a a a a a =⋅=++，222123||b b b b b b =⋅=++．5．夹角公式：112233222222123123cos ||||a ba b a b a a a b b b ⋅⋅==⋅++++．异面直线所成的夹角：6．两点间的距离公式：若111(,,)A x y z ，222(,,)B x y z ，则2222212121||()()()AB AB x x y y z z ==-+-+-，或222,212121()()()A B d x x y y z z =-+-+-7、法向量①直线的法向量：在直线L 上取一个定向量，则与垂直的非零向量叫直线L 的法向量②平面的法向量：与平面α垂直的非零向量叫平面α的法向量．构造直线或平面的法向量，在求空间角与距离时起到了桥梁的作用，在解题过程中只须求出而不必在图形中作出来．在空间直角坐标系下，构造关于法向量坐标的三元一次方程组，得到直线（或平面）的法向量坐标的一般形式，再取特值. 其向上或向下的方向可根据竖坐标的符号来确定. 一、平面的法向量例1 已知AB =（2，2，1），AC =（4，5，3），求平面ABC 的法向量解：设面ABC 的法向量(,,)n x y z =，则n ⊥AB 且n ⊥，即n ·AB =0，且n ·=0，即2x +2y +z=0且4x +5y +3z=0，解得1,2,x z y z ⎧=⎪⎨⎪=-⎩∴n =z （21，－1，1）点评：一般情况下求法向量用待定系数法由于法向量没规定长度，仅规定了方向，所以有一个自由度，可把n 的某个坐标设为1，再求另两个坐标平面法向量是垂直于平面的向量，故法向量的相反向量也是法向量。

(第三个解答题)立体几何

线面垂直⇒面面平行
垂直关系垂直关系 3．面面垂直的判断定理．
β l α
l⊥α, l⊂β⇒β⊥α ⊥ ⊂
线面垂直⇒面面垂直
垂直关系垂直关系 4．面面垂直的性质．
α l m β
α⊥β,α∩β=m,l⊂β,l⊥m α β ⊂ ⊥ ⇒ l⊥α ⊥
面面垂直⇒线面垂直
要想让我们减轻学习的负担，要想让我们减轻学习的负担，只有一个办法，有一个办法，就是提升自己的学习成提升自己的学习能力。绩，提升自己的学习能力。
α β n m
α∥β,γ∩α=m, γ∩β=n γ α β ⇒m∥n ∥ 面面平行⇒线线平行
垂直关系垂直关系 1．线面垂直的判断定理．
l aP
α
b
l⊥a, l⊥b, ⊥ ⊥ a∩b=P, ⇒l⊥α ⊥ a⊂α,b⊂α ⊂ ⊂ 线线垂直⇒线面垂直
垂直关系垂直关系 2．线面垂直的性质（1）．线面垂直的在空间四边形 ABCD 中，E、F、G、．如图，、、、 H 分别是 AB、BC、CD、DA 上的中点，上的中、、、求证：为平行四边形. 求证：四边形 EFGH 为平行四边形
A E B F C G H D
一、定理的熟悉
变式 1：如图，在空间四边形 ABCD 中，E、F、：如图，、、 G、H 分别是 AB、BC、CD、DA 上的点，若四上的点，、、、、为平行四边形，边形 EFGH 为平行四边形， l 求证：求证：AC//平面 EFGH. 平面
A
O B
C
l⊥a, ,l⊥b, ⇒ l⊥a ⊥α⊥ α l⊥ a⊂ ⊥ ⊂ ⊥ a∩b=P, ⇒l⊥α ⊥ a⊂α,b⊂α ⊂ ⊂
一、定理的熟悉
5．已知平面α⊥ 平面γ，平面β⊥平面γ ，．平面γ 平面γ 平面α∩平面β=l，求证：l⊥平面γ. ，求证： ⊥平面γ l α

立体几何解答题专项训练-2022届高三数学三轮冲刺复习

(1)求证:EF⊥平面BCF；
(2)点M在线段EF上运动，当点M在什么位置时，平面MAB与平面FCB所成锐二面角最大？并求此时锐二面角的余弦值。
16、在四棱锥P﹣ABCD中，侧面PAB为等边三角形，底面ABCD为直角梯形，AB∥CD，∠DAB＝90°，PB＝PC＝2，CD＝AD＝1，E为线段AB的中点，过直线CE的平面与线段PA，PD分别交于点M，N．
（1）求证：MN⊥PB；
（2）若直线PC与平面CEMN所成的角的余弦值为，求的值．
17、如图所示，正方形所在平面与梯形所在平面垂直，，，， .
(1)求证:EF∥平面SAD.
(2)若G为线段AB上一动点,求平面EFG与平面ABCD间最小锐二面角的余弦值.
15、如图1所示，在矩形中，，，为中点，将沿折起，使点到点处，且平面平面，如图2所示.
（1）求证：；
（2）在棱上取点，使平面平面，求直线与平面所成角的正弦值.
立体几何解答题专项训练
1、在如图所示的几何体中，四边形是正方形，四边形是梯形，，，平面平面，且 .
(1)求证：平面；
(2)求平面与平面所成角的大小；
(3)已知点在棱上，且异面直线与所成角的余弦值为，求点到平面的距离.
2、如图，在梯形ABCD中，AB∥CD，∠BCD= ，四边形ACFE为矩形，且CF⊥平面ABCD，AB=CD=BC=CF=1。
（1）证明：平面平面 .
（2）若，求二面角的余弦值.
11、如图1，已知为等边三角形，四边形为平行四边形，，把沿向上折起，使点E到达点P位置，如图2所示；且平面平面．
（1）证明：；
（2）在（1）的条件下求二面角的余弦值．

专题8.7 高考解答题热点题型-立体几何(解析版)

高考理科数学一轮复习：题型全归纳与高效训练突破专题8.7高考解答题热点题型---立体几何目录一、题型综述 (1)二题型全归纳 (1)题型一空间点、线、面的位置关系及空． (1)题型二平面图形的折叠问题 (7)题型三立体几何中的探索性问题 (10)三、高效训练突破 (15)一、题型综述立体几何是每年高考的重要内容，基本上都是一道客观题和一道解答题，客观题主要考查考生的空间想象能力及简单的计算能力．解答题主要采用证明与计算相结合的模式，即首先利用定义、定理、公理等证明空间线线、线面、面面的平行或垂直关系，再利用空间向量进行空间角的计算求解．重在考查考生的逻辑推理及计算能力，试题难度一般不大，属中档题，且主要有以下几种常见的热点题型．二题型全归纳题型一空间点、线、面的位置关系及空．1证明点共面或线共面的常用方法(1)直接法：证明直线平行或相交，从而证明线共面．(2)纳入平面法：先确定一个平面，再证明有关点、线在此平面内．．(3)辅助平面法：先证明有关的点、线确定平面α，再证明其余元素确定平面β，最后证明平面α，β重合．2．证明空间点共线问题的方法(1)公理法：一般转化为证明这些点是某两个平面的公共点，再根据公理3证明这些点都在这两个平面的交线上(2)纳入直线法：选择其中两点确定一条直线，然后证明其余点也在该直线上．3．证明线共点问题的常用方法先证其中两条直线交于一点，再证其他直线经过该点．4.求异面直线所成角的方法(1)几何法①作：利用定义转化为平面角，对于异面直线所成的角，可固定一条，平移一条，或两条同时平移到某个特殊的位置，顶点选在特殊的位置上．①证：证明作出的角为所求角．①求：把这个平面角置于一个三角形中，通过解三角形求空间角．(2)向量法建立空间直角坐标系，利用公式|cos θ|＝|m ·n ||m ||n |求出异面直线的方向向量的夹角．若向量夹角是锐角或直角，则该角即为异面直线所成角；若向量夹角是钝角，则异面直线所成的角为该角的补角．【例1】如图，AE ①平面ABCD ，CF ①AE ，AD ①BC ，AD ①AB ，AB ＝AD ＝1，AE ＝BC ＝2.(1)求证：BF ①平面ADE ；(2)求直线CE 与平面BDE 所成角的正弦值；(3)若二面角E －BD －F 的余弦值为13，求线段CF 的长．【解题思路】由条件知AB ，AD ，AE 两两垂直，可以A 为坐标原点建立空间直角坐标系，用空间向量解决．(1)寻找平面ADE 的法向量，证明BF →与此法向量垂直，即得线面平行．(2)CE →与平面BDE 的法向量所成角的余弦值的绝对值，即为直线CE 和平面BDE 所成角的正弦值；(3)设CF ＝h ，用h 表示二面角E －BD －F 的余弦值，通过解方程得到线段长．【规范解答】 (1)证明：以A 为坐标原点，AB 所在的直线为x 轴，AD 所在的直线为y 轴，AE 所在的直线为z 轴，建立如图所示的空间直角坐标系．则A (0,0,0)，B (1,0,0)，设F (1,2，h )．依题意，AB →＝(1,0,0)是平面ADE 的一个法向量，又BF →＝(0,2，h )，可得BF →·AB →＝0，又直线BF ①平面ADE ，所以BF ①平面ADE .(2)依题意，D (0,1,0)，E (0,0,2)，C (1,2,0)，则BD →＝(－1,1,0)，BE →＝(－1,0,2)，CE →＝(－1，－2,2)．设n ＝(x ，y ，z )为平面BDE 的法向量，则⎩⎪⎨⎪⎧ n ·BD →＝0，n ·BE →＝0，即⎩⎪⎨⎪⎧－x ＋y ＝0，－x ＋2z ＝0，不妨令z ＝1，可得n ＝(2,2,1)．因此有cos 〈CE →，n 〉＝CE →·n |CE →||n |＝－49. 所以直线CE 与平面BDE 所成角的正弦值为49. (3)设m ＝(x 1，y 1，z 1)为平面BDF 的法向量，则⎩⎪⎨⎪⎧ m ·BD →＝0，m ·BF →＝0，即⎩⎪⎨⎪⎧－x 1＋y 1＝0，2y 1＋hz 1＝0，不妨令y 1＝1，可得m ＝⎝⎛⎭⎫1，1，－2h . 由题意，有|cos 〈m ，n 〉|＝|m ·n ||m ||n |＝⎪⎪⎪⎪4－2h 3 2＋4h2＝13，解得h ＝87.经检验，符合题意．所以线段CF 的长为87. 【例2】.如图，在三棱锥P ABC 中，P A ①底面ABC ，①BAC ＝90°.点D ，E ，N 分别为棱P A ，PC ，BC 的中点，M 是线段AD 的中点，P A ＝AC ＝4，AB ＝2.(1)求证：MN ①平面BDE ；(2)已知点H 在棱P A 上，且直线NH 与直线BE 所成角的余弦值为721，求线段AH 的长．【解析】：如图，以A 为原点，分别以AB →，AC →，AP →的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系．依题意可得A (0，0，0)，B (2，0，0)，C (0，4，0)，P (0，0，4)，D (0，0，2)，E (0，2，2)，M (0，0，1)，N (1，2，0)．(1)证明：DE →＝(0，2，0)，DB →＝(2，0，－2)．设n ＝(x ，y ，z )为平面BDE 的法向量，则⎩⎪⎨⎪⎧n ·DE →＝0，n ·DB →＝0，即⎩⎪⎨⎪⎧2y ＝0，2x －2z ＝0. 不妨设z ＝1，可取n ＝(1，0，1)．又MN →＝(1，2，－1)，可得MN →·n ＝0.因为MN ①平面BDE ，所以MN ①平面BDE .(2)依题意，设AH ＝h (0≤h ≤4)，则H (0，0，h )，进而可得NH →＝(－1，－2，h )，BE →＝(－2，2，2)．由已知，得|cos 〈NH →，BE →〉|＝|NH →·BE →||NH →||BE →|＝|2h －2|h 2＋5×23＝721，整理得10h 2－21h ＋8＝0，解得h ＝85或h ＝12. 所以，线段AH 的长为85或12. 【例3】如图，在几何体ACD －A 1B 1C 1D 1中，四边形ADD 1A 1与四边形CDD 1C 1均为矩形，平面ADD 1A 1①平面CDD 1C 1，B 1A 1①平面ADD 1A 1，AD ＝CD ＝1，AA 1＝A 1B 1＝2，E 为棱AA 1的中点．(1)证明：B 1C 1①平面CC 1E ；(2)求直线B 1C 1与平面B 1CE 所成角的正弦值．【解析】(1)证明：因为B 1A 1①平面ADD 1A 1，所以B 1A 1①DD 1，又DD 1①D 1A 1，B 1A 1∩D 1A 1＝A 1，所以DD 1①平面A 1B 1C 1D 1，又DD 1①CC 1，所以CC 1①平面A 1B 1C 1D 1.因为B 1C 1①平面A 1B 1C 1D 1，所以CC 1①B 1C 1.因为平面ADD 1A 1①平面CDD 1C 1，平面ADD 1A 1∩平面CDD 1C 1＝DD 1，C 1D 1①DD 1，所以C 1D 1①平面ADD 1A 1.经计算可得B 1E ＝5，B 1C 1＝2，EC 1＝3，从而B 1E 2＝B 1C 21＋EC 21，所以在①B 1EC 1中，B 1C 1①C 1E .又CC 1，C 1E ①平面CC 1E ，CC 1∩C 1E ＝C 1，所以B 1C 1①平面CC 1E .(2)如图，以点A 为坐标原点，建立空间直角坐标系，依题意得A (0，0，0)，C (1，0，1)，B 1(0，2，2)，C 1(1，2，1)，E (0，1，0)，则CE →＝(－1，1，－1)，B 1C →＝(1，－2，－1)．设平面B 1CE 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧m ·B 1C →＝0，m ·CE →＝0，即⎩⎪⎨⎪⎧x －2y －z ＝0，－x ＋y －z ＝0，消去x 得y ＋2z ＝0，不妨设z ＝1，可得m ＝(－3，－2，1)为平面B 1CE 的一个法向量，易得B 1C 1→＝(1，0，－1)，设直线B 1C 1与平面B 1CE 所成角为θ，则sin θ＝|cos 〈m ，B 1C 1→〉|＝⎪⎪⎪⎪⎪⎪m ·B 1C 1→|m |·|B 1C 1→|＝⎪⎪⎪⎪⎪⎪－414×2＝277，故直线B 1C 1与平面B 1CE 所成角的正弦值为277. 题型二平面图形的折叠问题【解法】解决平面图形翻折问题的关键是抓住“折痕”，准确把握平面图形翻折前后的两个“不变”．(1)与折痕垂直的线段，翻折前后垂直关系不改变；(2)与折痕平行的线段，翻折前后平行关系不改变．【例1】如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把①DFC 折起，使点C 到达点P 的位置，且PF ①BF .(1)证明：平面PEF ①平面ABFD ；(2)求DP 与平面ABFD 所成角的正弦值．【解题思路】(1)①翻折前后的不变关系，四边形ABFE 是矩形．①证明BF ①平面PEF .①证明平面PEF ①平面ABFD .(2)解法一：①建系：借助第(1)问，过P 作平面ABFD 的垂线为z 轴，垂足为原点，EF 所在直线为y 轴，建系．①求直线DP 的方向向量和平面ABFD 的法向量．①由公式计算所求角的正弦值．解法二：①作：过P 作PH ①EF 交EF 于点H ，连接DH .①证：证明PH ①平面ABFD ，得①PDH 为直线DP 与平面ABFD 所成角．①算：在Rt①PDH 中，PD 的长度是正方形ABCD 的边长，①PHD ＝90°，易知要求sin①PDH ，关键是求PH ；由此想到判断①PEF 的形状，进一步想到证明PF ①平面PED .【规范解答】(1)证明：由已知可得，BF ①PF ，BF ①EF ，又PF ∩EF ＝F ，所以BF ①平面PEF .又BF ①平面ABFD ，所以平面PEF ①平面ABFD .(2)解法一：作PH ①EF ，垂足为H .由(1)得，PH ①平面ABFD .以H 为坐标原点，HF →的方向为y 轴正方向，建立如图所示的空间直角坐标系Hxyz ，设正方形ABCD 的边长为2.由(1)可得，DE ①PE .又DP ＝2，DE ＝1，所以PE ＝ 3.又PF ＝1，EF ＝2，故PE ①PF .所以PH ＝32，EH ＝32，则H (0,0,0)，P ⎝⎛⎭⎫0，0，32， D ⎝⎛⎭⎫－1，－32，0，DP →＝⎝⎛⎭⎫1，32，32，HP →＝⎝⎛⎭⎫0，0，32为平面ABFD 的一个法向量．设DP 与平面ABFD 所成角为θ，则sin θ＝|HP →·DP →||HP →||DP →|＝343＝34. 所以DP 与平面ABFD 所成角的正弦值为34. 解法二：因为PF ①BF ，BF ①ED ，所以PF ①ED ，又PF ①PD ，ED ∩PD ＝D ，所以PF ①平面PED ，所以PF ①PE ，设AB ＝4，则EF ＝4，PF ＝2，所以PE ＝23，过P 作PH ①EF 交EF 于点H ，因为平面PEF ①平面ABFD ，所以PH ①平面ABFD ，连接DH ，则①PDH 即为直线DP 与平面ABFD 所成的角，因为PE ·PF ＝EF ·PH ，所以PH ＝23×24＝3，因为PD ＝4，所以sin①PDH ＝PH PD ＝34，所以DP 与平面ABFD 所成角的正弦值为34. 题型三立体几何中的探索性问题【技巧要点】对命题条件的探索的三种途径途径一：先猜后证，即先观察与尝试给出条件再证明．途径二：先通过命题成立的必要条件探索出命题成立的条件，再证明充分性．途径三：将几何问题转化为代数问题【例1】(2020·湖北“四地七校”联考)在四棱锥P －ABCD 中，底面ABCD 是边长为22的正方形，平面P AC ①底面ABCD ，P A ＝PC ＝2 2.(1)求证：PB ＝PD ；(2)若点M ，N 分别是棱P A ，PC 的中点，平面DMN 与棱PB 的交点为点Q ，则在线段BC 上是否存在一点H ，使得DQ ①PH ？若存在，求BH 的长；若不存在，请说明理由．【解题思路】 (1)要证PB ＝PD ，想到在①PBD 中，证明BD 边上的中线垂直于BD ，联系题目条件想到用面面垂直的性质证明线面垂直．(2)借助第(1)问的垂直关系建立空间直角坐标系，求平面DMN 的法向量n ，分别依据P ，B ，Q 共线和B ，C ，H 共线，设PQ →＝λPB →和BH →＝tBC →，利用垂直关系列方程先求λ再求t ，确定点H 的位置．【规范解答】 (1)证明：记AC ∩BD ＝O ，连接PO ，①底面ABCD 为正方形，①OA ＝OC ＝OB ＝OD ＝2.①P A ＝PC ，①PO ①AC ，①平面P AC ①底面ABCD ，且平面P AC ∩底面ABCD ＝AC ，PO ①平面P AC ，①PO ①底面ABCD .①BD ①底面ABCD ，①PO ①BD .①PB ＝PD .(2)存在．以O 为坐标原点，射线OB ，OC ，OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系如图所示，由(1)可知OP ＝2.可得P (0,0,2)，A (0，－2,0)，B (2,0,0)，C (0,2,0)，D (－2，0,0)，可得M (0，－1,1)，N (0,1,1)，DM →＝(2，－1,1)，MN →＝(0，2,0)．设平面DMN 的法向量n ＝(x ，y ，z )，①DM →·n ＝0，MN →·n ＝0，①⎩⎪⎨⎪⎧2x －y ＋z ＝0，2y ＝0. 令x ＝1，可得n ＝(1,0，－2)．记PQ →＝λPB →＝(2λ，0，－2λ)，可得Q (2λ，0,2－2λ)，DQ →＝(2λ＋2,0,2－2λ)，DQ →·n ＝0，可得2λ＋2－4＋4λ＝0，解得λ＝13. 可得DQ →＝⎝⎛⎭⎫83，0，43. 记BH →＝tBC →＝(－2t,2t,0)，可得H (2－2t,2t,0)，PH →＝(2－2t,2t ，－2)，若DQ ①PH ，则DQ →·PH →＝0，83(2－2t )＋43×(－2)＝0，解得t ＝12. 故BH ＝ 2.故在线段BC 上存在一点H ，使得DQ ①PH ，此时BH＝ 2.【例2】如图，在四棱锥PABCD中，P A①平面ABCD，底面ABCD为菱形，E为CD的中点．(1)求证：BD①平面P AC；(2)若①ABC＝60°，求证：平面P AB①平面P AE；(3)棱PB上是否存在点F，使得CF①平面P AE？说明理由．【解】(1)证明：因为P A①平面ABCD，所以P A①BD.因为底面ABCD为菱形，所以BD①A C.又P A∩AC＝A，所以BD①平面P A C.(2)证明：因为P A①平面ABCD，AE①平面ABCD，所以P A①AE.因为底面ABCD为菱形，①ABC＝60°，且E为CD的中点，所以AE①CD，所以AB①AE.又AB∩P A＝A，所以AE ①平面P AB .因为AE ①平面P AE ，所以平面P AB ①平面P AE .(3)棱PB 上存在点F ，使得CF ①平面P AE .取F 为PB 的中点，取G 为P A 的中点，连接CF ，FG ，EG .则FG ①AB ，且FG ＝12AB . 因为底面ABCD 为菱形，且E 为CD 的中点，所以CE ①AB ，且CE ＝12AB . 所以FG ①CE ，且FG ＝CE .所以四边形CEGF 为平行四边形．所以CF ①EG .因为CF ①平面P AE ，EG ①平面P AE ，所以CF ①平面P AE .【例3】图1是由矩形ADEB ，Rt①ABC 和菱形BFGC 组成的一个平面图形，其中AB ＝1，BE ＝BF ＝2，①FBC ＝60°.将其沿AB ，BC 折起使得BE 与BF 重合，连接DG ，如图2.(1)证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ①平面BCGE ；(2)求图2中的二面角B －CG －A 的大小．【解析】：(1)证明：由已知得AD ①BE ，CG ①BE ，所以AD ①CG ，故AD ，CG 确定一个平面，从而A ，C ，G ，D 四点共面．由已知得AB ①BE ，AB ①BC ，故AB ①平面BCGE .又因为AB ①平面ABC ，所以平面ABC ①平面BCGE .(2)作EH ①BC ，垂足为H .因为EH ①平面BCGE ，平面BCGE ①平面ABC ，所以EH ①平面ABC .由已知，菱形BCGE 的边长为2，①EBC ＝60°，可求得BH ＝1，EH ＝ 3.以H 为坐标原点，HC →的方向为x 轴的正方向，建立如图所示的空间直角坐标系H xyz ，则A (－1，1，0)，C (1，0，0)，G (2，0，3)，CG →＝(1，0，3)，AC →＝(2，－1，0)．设平面ACGD 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧CG →·n ＝0AC →·n ＝0，即⎩⎨⎧x ＋3z ＝0，2x －y ＝0. 所以可取n ＝(3，6，－3)．又平面BCGE 的法向量可取为m ＝(0，1，0)，所以cos n ，m ＝n ·m |n ||m |＝32. 因此二面角B CG A 的大小为30°.三、高效训练突破1.(2020·深圳模拟)已知四棱锥PABCD，底面ABCD为菱形，PD＝PB，H为PC上的点，过AH的平面分别交PB，PD于点M，N，且BD①平面AMHN.(1)证明：MN①PC；(2)当H为PC的中点，P A＝PC＝3AB，P A与平面ABCD所成的角为60°，求AD与平面AMHN所成角的正弦值．【解析】(1)证明：连接AC、BD且AC∩BD＝O，连接PO.因为ABCD为菱形，所以BD①AC，因为PD＝PB，所以PO①BD，因为AC∩PO＝O且AC、PO①平面P AC，所以BD①平面P AC，因为PC①平面P AC，所以BD①PC，因为BD①平面AMHN，且平面AMHN∩平面PBD＝MN，所以BD①MN，MN①平面P AC，所以MN①P C.(2)由(1)知BD ①AC 且PO ①BD ，因为P A ＝PC ，且O 为AC 的中点，所以PO ①AC ，所以PO ①平面ABCD ，所以P A 与平面ABCD 所成的角为①P AO ，所以①P AO ＝60°，所以AO ＝12P A ，PO ＝32P A ，因为P A ＝3AB ，所以BO ＝36P A . 以OA →，OD →，OP →分别为x ，y ，z 轴，建立空间直角坐标系，如图所示．设P A ＝2，所以O (0，0，0)，A (1，0，0)，B (0，－33，0)，C (－1，0，0)，D (0，33，0)，P (0，0，3)，H (－12，0，32)，所以BD →＝(0，233，0)，AH →＝(－32，0，32)，AD →＝(－1，33，0)．设平面AMHN 的法向量为n ＝(x ，y ，z )，所以⎩⎪⎨⎪⎧n ·BD →＝0，n ·AH →＝0，即⎩⎨⎧233y ＝0，－32x ＋32z ＝0，令x ＝2，则y ＝0，z ＝23，所以n ＝(2，0，23)，设AD 与平面AMHN 所成角为θ，所以sin θ＝|cos 〈n ，AD →〉|＝|n ·AD →|n ||AD →||＝34. 所以AD 与平面AMHN 所成角的正弦值为34. 2．(2020·河南联考)如图所示，在四棱锥P －ABCD 中，底面ABCD 为平行四边形，平面P AD ①平面ABCD ，①P AD 是边长为4的等边三角形，BC ①PB ，E 是AD 的中点．(1)求证：BE ①PD ；(2)若直线AB 与平面P AD 所成角的正弦值为154，求平面P AD 与平面PBC 所成的锐二面角的余弦值．【解析】：(1)证明：因为①P AD 是等边三角形，E 是AD 的中点，所以PE ①AD .又平面P AD ①平面ABCD ，平面P AD ∩平面ABCD ＝AD ，PE ①平面P AD ，所以PE ①平面ABCD ，所以PE ①BC ，PE ①BE .又BC ①PB ，PB ∩PE ＝P ，所以BC ①平面PBE ，所以BC ①BE .又BC ①AD ，所以AD ①BE .又AD ∩PE ＝E 且AD ，PE ①平面P AD ，所以BE ①平面P AD ，所以BE ①PD .(2)由(1)得BE ①平面P AD ，所以①BAE 就是直线AB 与平面P AD 所成的角．因为直线AB 与平面P AD 所成角的正弦值为154，即sin①BAE ＝154 ，所以cos①BAE ＝14. 所以cos①BAE ＝AE AB ＝2AB ＝14，解得AB ＝8，则BE ＝AB 2－AE 2＝215.由(1)得EA ，EB ，EP 两两垂直，所以以E 为坐标原点，EA ，EB ，EP 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则点P (0，0，23)，A (2，0，0)，D (－2，0，0)，B (0，215，0)，C (－4，215，0)，所以PB →＝(0，215，－23)，PC →＝(－4，215，－23)．设平面PBC 的法向量为m ＝(x ，y ，z )，由⎩⎪⎨⎪⎧PB →·m ＝0，PC →·m ＝0，得⎩⎨⎧215y －23z ＝0，－4x ＋215y －23z ＝0，解得⎩⎨⎧x ＝0，z ＝5y . 令y ＝1，可得平面PBC 的一个法向量为m ＝(0，1，5)．易知平面P AD 的一个法向量为n ＝(0，1，0)，设平面P AD 与平面PBC 所成的锐二面角的大小为θ，则cos θ＝⎪⎪⎪⎪m ·n |m ||n |＝⎪⎪⎪⎪⎪⎪（0，1，5）·（0，1，0）6×1＝66. 所以平面P AD 与平面PBC 所成的锐二面角的余弦值为66. 3.(2020·云南师范大学附属中学3月月考)如图，在直三棱柱ABC A 1B 1C 1中，①ABC 是边长为2的正三角形，AA 1＝26，D 是CC 1的中点，E 是A 1B 1的中点．(1)证明：DE ①平面A 1BC;(2)求点A 到平面A 1BC 的距离．【解析】 (1)证明：如图取A 1B 的中点F ，连接FC ，FE .因为E ，F 分别是A 1B 1，A 1B 的中点，所以EF ①BB 1，且EF ＝12BB 1. 又在平行四边形BB 1C 1C 中，D 是CC 1的中点，所以CD ①BB 1，且CD ＝12BB 1，所以CD ①EF ，且CD ＝EF . 所以四边形CFED 是平行四边形，所以DE ①CF .因为DE ①/平面A 1BC ，CF ①平面A 1BC ，所以DE ①平面A 1BC .(2)法一：(等体积法)因为BC ＝AC ＝AB ＝2，AA 1＝26，三棱柱ABC A 1B 1C 1为直三棱柱，所以V 三棱锥A 1－ABC ＝13S ①ABC ×AA 1＝13×34×22×26＝2 2. 又在①A 1BC 中，A 1B ＝A 1C ＝27，BC ＝2，BC 边上的高h ＝ A 1B 2－⎝⎛⎭⎫12BC 2＝33，所以S ①A 1BC ＝12BC ·h ＝3 3. 设点A 到平面A 1BC 的距离为d ，则V 三棱锥A －A 1BC ＝13S ①A 1BC ×d ＝13×33×d ＝3d . 因为V 三棱锥A 1－ABC ＝V 三棱锥A －A 1BC ，所以22＝3d ，解得d ＝263，所以点A 到平面A 1BC 的距离为263. 法二：(向量法)由题意知，三棱柱ABC A 1B 1C 1是正三棱柱．取AB 的中点O ，连接OC ，OE .因为AC ＝BC ，所以CO ①AB .又平面ABC ①平面ABB 1A 1，平面ABC ∩平面ABB 1A 1＝AB ，所以CO ①平面ABB 1A 1.因为O 为AB 的中点，E 为A 1B 1的中点，所以OE ①AB ，所以OC ，OA ，OE 两两垂直．如图，以O 为坐标原点，以OA ，OE ，OC 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系，则C (0，0，3)，A (1，0，0)，A 1(1，26，0)，B (－1，0，0)．则BA 1→＝(2，26，0)，BC →＝(1，0，3)．设平面A 1BC 的法向量为n ＝(x ，y ，z )，则由⎩⎪⎨⎪⎧n ①BA 1→，n ①BC →，可得⎩⎪⎨⎪⎧n ·BA 1→＝2x ＋26y ＝0，n ·BC →＝x ＋3z ＝0，整理得⎩⎨⎧x ＋6y ＝0，x ＋3z ＝0，令x ＝6，则y ＝－1，z ＝－ 2. 所以n ＝(6，－1，－2)为平面A 1BC 的一个法向量．而BA →＝(2，0，0)，所以点A 到平面A 1BC 的距离d ＝|BA →·n ||n |＝6×26＋1＋2＝263. 4．(2020·湖北十堰4月调研)如图，在三棱锥P －ABC 中，M 为AC 的中点，P A ①PC ，AB ①BC ，AB ＝BC ，PB ＝2，AC ＝2，①P AC ＝30°.(1)证明：BM ①平面P AC ；(2)求二面角B －P A －C 的余弦值．【答案】：见解析(1)证明：因为P A ①PC ，AB ①BC ，所以MP ＝MB ＝12AC ＝1，又MP 2＋MB 2＝BP 2，所以MP ①MB .因为AB ＝BC ，M 为AC 的中点，所以BM ①AC ，又AC ∩MP ＝M ，所以BM ①平面P AC .(2)法一：取MC 的中点O ，连接PO ，取BC 的中点E ，连接EO ，则OE ①BM ，从而OE ①AC . 因为P A ①PC ，①P AC ＝30°，所以MP ＝MC ＝PC ＝1. 又O 为MC 的中点，所以PO ①AC .由(1)知BM ①平面P AC ，OP ①平面P AC ，所以BM ①PO . 又BM ∩AC ＝M ，所以PO ①平面ABC .以O 为坐标原点，OA ，OE ，OP 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，如图所示，由题意知A ⎝⎛⎭⎫32，0，0，B ⎝⎛⎭⎫12，1，0，P ⎝⎛⎭⎫0，0，32，BP →＝⎝⎛⎭⎫－12，－1，32，BA →＝(1，－1，0)，设平面APB 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·BP→＝－12x －y ＋32z ＝0，n ·BA →＝x －y ＝0，令x ＝1，得n ＝(1，1，3)为平面APB 的一个法向量，易得平面P AC 的一个法向量为π＝(0，1，0)，cos 〈n ，π〉＝55，由图知二面角B －P A －C 为锐角，所以二面角B －P A －C 的余弦值为55. 法二：取P A 的中点H ，连接HM ，HB ，因为M 为AC 的中点，所以HM ①PC ，又P A ①PC ，所以HM ①P A .由(1)知BM ①平面P AC ，则BH ①P A ，所以①BHM 为二面角B －P A －C 的平面角．因为AC ＝2，P A ①PC ，①P AC ＝30°，所以HM ＝12PC ＝12.又BM ＝1，则BH ＝BM 2＋HM 2＝52，所以cos①BHM ＝HM BH ＝55，即二面角B －P A －C 的余弦值为55.5．(2020·合肥模拟)如图，在多面体ABCDEF 中，四边形ABCD 是正方形，BF ①平面ABCD ，DE ①平面ABCD ，BF ＝DE ，M 为棱AE 的中点．(1)求证：平面BDM ①平面EFC ；(2)若DE ＝2AB ，求直线AE 与平面BDM 所成角的正弦值．【答案】：见解析(1)证明：连接AC ，交BD 于点N ，连接MN ，则N 为AC 的中点，又M 为AE 的中点，所以MN ①EC . 因为MN ①平面EFC ，EC ①平面EFC ，所以MN ①平面EFC .因为BF ，DE 都垂直底面ABCD ，所以BF ①DE . 因为BF ＝DE ，所以四边形BDEF 为平行四边形，所以BD ①EF .因为BD ①平面EFC ，EF ①平面EFC ，所以BD ①平面EFC .又MN ∩BD ＝N ，所以平面BDM ①平面EFC . (2)因为DE ①平面ABCD ，四边形ABCD 是正方形，所以DA ，DC ，DE 两两垂直，如图，建立空间直角坐标系D xyz .设AB ＝2，则DE ＝4，从而D (0，0，0)，B (2，2，0)，M (1，0，2)，A (2，0，0)，E (0，0，4)，所以DB →＝(2，2，0)，DM →＝(1，0，2)，设平面BDM 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·DB →＝0，n ·DM →＝0，得⎩⎪⎨⎪⎧2x ＋2y ＝0，x ＋2z ＝0.令x ＝2，则y ＝－2，z ＝－1，从而n ＝(2，－2，－1)为平面BDM 的一个法向量．因为AE →＝(－2，0，4)，设直线AE 与平面BDM 所成的角为θ，则 sin θ＝|cos 〈n ·AE →〉|＝⎪⎪⎪⎪⎪⎪n ·AE →|n |·|AE →|＝4515，所以直线AE 与平面BDM 所成角的正弦值为4515.6.(2020·河南郑州三测)如图①，①ABC 中，AB ＝BC ＝2，①ABC ＝90°，E ，F 分别为边AB ，AC 的中点，以EF 为折痕把①AEF 折起，使点A 到达点P 的位置(如图①)，且PB ＝BE .(1)证明：EF ①平面PBE ；(2)设N 为线段PF 上的动点(包含端点)，求直线BN 与平面PCF 所成角的正弦值的最大值．【解析】：(1)证明：因为E ，F 分别为边AB ，AC 的中点，所以EF ①BC . 因为①ABC ＝90°，所以EF ①BE ，EF ①PE ，又BE ∩PE ＝E ，所以EF ①平面PBE . (2)取BE 的中点O ，连接PO ，因为PB ＝BE ＝PE ，所以PO ①BE .由(1)知EF ①平面PBE ，EF ①平面BCFE ，所以平面PBE ①平面BCFE . 又PO ①平面PBE ，平面PBE ∩平面BCFE ＝BE ，所以PO ①平面BCFE .过点O 作OM ①BC 交CF 于点M ，分别以OB ，OM ，OP 所在的直线为x 轴，y 轴，z 轴建立空间直角坐标系，如图所示，则B ⎝⎛⎭⎫12，0，0，P ⎝⎛⎭⎫0，0，32，C ⎝⎛⎭⎫12，2，0， F ⎝⎛⎭⎫－12，1，0，PC →＝⎝⎛⎭⎫12，2，－32， PF →＝⎝⎛⎭⎫－12，1，－32，由N 为线段PF 上一动点，得PN →＝λPF →(0≤λ≤1)，则可得N ⎝⎛⎭⎫－λ2，λ，32（1－λ），BN →＝⎝⎛⎭⎫－λ＋12，λ，32（1－λ）.设平面PCF 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧PC →·m ＝0，PF →·m ＝0，即⎩⎨⎧12x ＋2y －32z ＝0，－12x ＋y －32z ＝0，取y ＝1，则x ＝－1，z ＝3，所以m ＝(－1，1，3)为平面PCF 的一个法向量．设直线BN 与平面PCF 所成的角为θ，则sin θ＝|cos 〈BN →，m 〉|＝|BN →·m ||BN →|·|m |＝25·2λ2－λ＋1＝25·2⎝⎛⎭⎫λ－142＋78≤25·78＝47035(当且仅当λ＝14时取等号)，所以直线BN 与平面PCF 所成角的正弦值的最大值为47035.7．(2020·山东淄博三模)如图①，已知正方形ABCD 的边长为4，E ，F 分别为AD ，BC 的中点，将正方形ABCD 沿EF 折成如图①所示的二面角，且二面角的大小为60°，点M 在线段AB 上(包含端点)，连接AD .(1)若M 为AB 的中点，直线MF 与平面ADE 的交点为O ，试确定点O 的位置，并证明直线OD ①平面EMC ； (2)是否存在点M ，使得直线DE 与平面EMC 所成的角为60°？若存在，求此时二面角M EC F 的余弦值；若不存在，说明理由．【答案】见解析【解析】：(1)因为直线MF ①平面ABFE ，故点O 在平面ABFE 内，也在平面ADE 内，所以点O 在平面ABFE 与平面ADE的交线(即直线AE )上(如图所示)．因为AO ①BF ，M 为AB 的中点，所以①OAM ①①FBM ，所以OM ＝MF ，AO ＝BF ，所以AO ＝2. 故点O 在EA 的延长线上且与点A 间的距离为2. 连接DF ，交EC 于点N ，因为四边形CDEF 为矩形，所以N 是EC 的中点．连接MN ，则MN 为①DOF 的中位线，所以MN ①OD ，又MN ①平面EMC ，OD ①/ 平面EMC ，所以直线OD ①平面EMC . (2)由已知可得EF ①AE ，EF ①DE ，又AE ∩DE ＝E ，所以EF ①平面ADE .所以平面ABFE ①平面ADE ，易知①ADE 为等边三角形，取AE 的中点H ，则易得DH ①平面ABFE ，以H 为坐标原点，建立如图所示的空间直角坐标系，则E (－1，0，0)，D (0，0，3)，C (0，4，3)，F (－1，4，0)，所以ED →＝(1，0，3)，EC →＝(1，4，3)．设M (1，t ，0)(0≤t ≤4)，则EM →＝(2，t ，0)，设平面EMC 的法向量为m ＝(x ，y ，z )，则⎩⎪⎨⎪⎧m ·EM →＝0，m ·EC →＝0①⎩⎨⎧2x ＋ty ＝0，x ＋4y ＋3z ＝0，取y ＝－2，则x ＝t ，z ＝8－t 3，所以m ＝⎝ ⎛⎭⎪⎫t ，－2，8－t 3为平面EMC 的一个法向量．要使直线DE 与平面EMC 所成的角为60°，则82t 2＋4＋（8－t ）23＝32，所以23t 2－4t ＋19＝32，整理得t 2－4t ＋3＝0，解得t＝1或t ＝3，所以存在点M ，使得直线DE 与平面EMC 所成的角为60°，取ED 的中点Q ，连接QA ，则QA →为平面CEF 的法向量，易得Q ⎝⎛⎭⎫－12，0，32，A (1，0，0)，所以QA →＝⎝⎛⎭⎫32，0，－32.设二面角M －EC －F 的大小为θ，则|cos θ|＝|QA →·m ||QA →|·|m |＝|2t －4|3t 2＋4＋（8－t ）23＝|t －2|t2－4t ＋19. 因为当t ＝2时，cos θ＝0，平面EMC ①平面CDEF ，所以当t ＝1时，cos θ＝－14，θ为钝角；当t ＝3时，cos θ＝14，θ为锐角．综上，二面角M －EC －F 的余弦值为±14.。

(完整版)立体直角坐标系常见题型

(完整版)立体直角坐标系常见题型立体直角坐标系常见题型（完整版）本文档将介绍立体直角坐标系中常见的题型及解答方法。

一、点的坐标计算1. 已知点P在立体直角坐标系中的坐标为(x₁, y₁, z₁)，则点P'关于y轴的对称点的坐标为(x₁, -y₁, z₁)。

2. 已知点P、Q在立体直角坐标系中的坐标分别为(x₁, y₁, z₁)和(x₂, y₂, z₂)，则线段PQ的中点的坐标为((x₁+x₂)/2, (y₁+y₂)/2, (z₁+z₂)/2)。

3. 若点P在立体直角坐标系中的坐标为(x₁, y₁, z₁)，则点P关于x轴、y轴、z轴的对称点的坐标分别为(-x₁, y₁, z₁)、(x₁, -y₁, z₁)、(x₁, y₁, -z₁)。

二、直线与平面1. 已知直线L过点P(x₁, y₁, z₁)且与向量a = (a₁, a₂, a₃)平行，则直线L的参数方程可表示为：x = x₁ + a₁ty = y₁ + a₂tz = z₁ + a₃t2. 已知平面π过点P(x₁, y₁, z₁)且法向量为n = (n₁, n₂, n₃)，则平面π的方程可表示为：n₁(x - x₁) + n₂(y - y₁) + n₃(z - z₁) = 0三、向量运算1. 向量a = (a₁, a₂, a₃)的模长计算公式为：|a| = sqrt(a₁² + a₂² + a₃²)2. 向量a与向量b的点积计算公式为：a·b = a₁b₁ + a₂b₂ + a₃b₃3. 向量a与向量b的叉积计算公式为：a ×b = (a₂b₃ - a₃b₂, a₃b₁ - a₁b₃, a₁b₂ - a₂b₁)四、空间中的图形1. 球的方程：已知球心为C(x₁, y₁, z₁)且半径为r，则球的方程为：(x - x₁)² + (y - y₁)² + (z - z₁)² = r²2. 锥面的方程：已知顶点为V(x₁, y₁, z₁)且开口方向为向量a = (a₁, a₂, a₃)，则锥面的方程可表示为：((x - x₁)/a₁)² + ((y - y₁)/a₂)² + ((z - z₁)/a₃)² = 0以上为立体直角坐标系常见题型及解答方法的简要介绍。

2023届高考数学总复习：立体几何复习题附答案

a，
在 Rt△FCM 中，tan∠FCM ．
，
∴sin∠FCM ，
故直线 CF 与平面 ACDE 所成角的正弦值为． 2．如图，在三棱柱 ABC﹣A1B1C1 中，BC⊥平面 AA1C1C，D 是 AA1 的中点，△ACD 是边长
为 1 的等边三角形．（1）证明：CD⊥B1D；（2）若 BC ，求二面角 B﹣C1D﹣B1 的大小．
，令
由（1）知，平面 B1C1D 的一个法向量为
，得
，，，
，，，
故 th＜，＞
，
所以二面角 B﹣C1D﹣B1 的大小为 30°．
第3页共3页
在直角梯形 AEFB 中，有 AF EF，BF
쳌
∴AF2+BF2＝AB2，即 AF⊥BF．
∵BC∩BF＝B，BC、BF⊂平面 BCF，
∴AF⊥平面 BCF．
EF，AB＝2EF，
（2）解：∵AE⊥平面 ABC，AE⊂平面 ACDE，∴平面 ACDE⊥平面 ABC，
又平面 ABC∥平面 DEF，∴平面 ACDE⊥平面 DEF．
【解答】解：（1）证明：因为△ACD 是边长为 1 的等边三角形，所以∠ADC＝60°，∠ DA1C1＝120° 因为 D 是 AA1 的中点，所以 AD＝A1D＝A1C1＝1，即△A1C1D 是等腰三角形，则∠A1DC1＝30°，故∠CDC1＝90°，即 CD⊥C1D，因为 BC⊥平面 AA1C1C，BC∥B1C1，所以 B1C1⊥平面 AA1C1C，因为 CD⊂平面 AA1C1C，所以 B1C1⊥CD，因为 B1C1∩C1D＝C1，B1C1⊂平面 B1C1D，C1D⊂平面 B1C1D，所以 CD⊥平面 B1C1D，因为 B1D⊂平面 B1C1D，所以 CD⊥B1D；

专题08 立体几何解答题常考全归类(精讲精练)(原卷版)

专题08 立体几何解答题常考全归类【命题规律】空间向量是将空间几何问题坐标化的工具，是常考的重点，立体几何解答题的基本模式是论证推理与计算相结合，以某个空间几何体为依托，分步设问，逐层加深．解决这类题目的原则是建系求点、坐标运算、几何结论．作为求解空间角的有力工具，通常在解答题中进行考查，属于中等难度．【核心考点目录】核心考点一：非常规空间几何体为载体核心考点二：立体几何探索性问题核心考点三：立体几何折叠问题核心考点四：立体几何作图问题核心考点五：立体几何建系繁琐问题核心考点六：两角相等（构造全等）的立体几何问题核心考点七：利用传统方法找几何关系建系核心考点八：空间中的点不好求核心考点九：创新定义【真题回归】1．（2022·天津·统考高考真题）直三棱柱111ABC A B C 中，112,,AA AB AC AA AB AC AB ===⊥⊥，D 为11A B 的中点，E 为1AA 的中点，F 为CD 的中点．(1)求证：//EF 平面ABC ；(2)求直线BE 与平面1CC D 所成角的正弦值；(3)求平面1ACD 与平面1CC D 所成二面角的余弦值．2．（2022·全国·统考高考真题）如图，四面体ABCD 中，,,AD CD AD CD ADB BDC ⊥=∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2,60AB BD ACB ==∠=︒，点F 在BD 上，当AFC △的面积最小时，求CF 与平面ABD 所成的角的正弦值．3．（2022·浙江·统考高考真题）如图，已知ABCD 和CDEF 都是直角梯形，//AB DC ，//DC EF ，5AB =，3DC =，1EF =，60BAD CDE ∠=∠=︒，二面角F DC B --的平面角为60︒．设M ，N 分别为,AE BC 的中点．(1)证明：FN AD ⊥；(2)求直线BM 与平面ADE 所成角的正弦值．4．（2022·全国·统考高考真题）如图，PO 是三棱锥-P ABC 的高，PA PB =，AB AC ⊥，E 是PB 的中点．(1)证明：//OE 平面PAC ；(2)若30ABO CBO ∠=∠=︒，3PO =，5PA =，求二面角C AE B --的正弦值．5．（2022·全国·统考高考真题）如图，四面体ABCD 中，,,AD CD AD CD ADB BDC ⊥=∠=∠，E 为AC 的中点．(1)证明：平面BED ⊥平面ACD ；(2)设2,60AB BD ACB ==∠=︒，点F 在BD 上，当AFC △的面积最小时，求三棱锥F ABC -的体积．6．（2022·全国·统考高考真题）在四棱锥P ABCD -中，PD ⊥底面,,1,2,ABCD CD AB AD DC CB AB DP =====∥(1)证明：BD PA ⊥；(2)求PD 与平面PAB 所成的角的正弦值．7．（2022·北京·统考高考真题）如图，在三棱柱111ABC A B C 中，侧面11BCC B 为正方形，平面11BCC B ⊥平面11ABB A ，2AB BC ==，M ，N 分别为11A B ，AC 的中点．(1)求证：MN ∥平面11BCC B ；(2)再从条件①、条件②这两个条件中选择一个作为已知，求直线AB 与平面BMN 所成角的正弦值．条件①：AB MN ⊥；条件②：BM MN =．注：如果选择条件①和条件②分别解答，按第一个解答计分．8．（2022·全国·统考高考真题）如图，直三棱柱111ABC A B C 的体积为4，1A BC 的面积为(1)求A 到平面1A BC 的距离；(2)设D 为1A C 的中点，1AA AB =，平面1A BC ⊥平面11ABB A ，求二面角A BD C --的正弦值．【方法技巧与总结】1、用综合法求空间角的基本数学思想主要是转化与化归，即把空间角转化为平面角，进而转化为三角形的内角，然后通过解三角形求得．求解的一般步骤为：（1）作图：作出空间角的平面角．（2）证明：证明所给图形是符合题设要求的．（3）计算：在证明的基础上计算得出结果．简称：一作、二证、三算．2、用定义作异面直线所成角的方法是“平移转化法”，可固定一条，平移另一条；或两条同时平移到某个特殊的位置，顶点选在特殊的位置上．3、求直线与平面所成角的常见方法（1）作角法：作出斜线、垂线、斜线在平面上的射影组成的直角三角形，根据条件求出斜线与射影所成的角即为所求．（2）等积法：公式θ=sin h l，其中θ是斜线与平面所成的角，h 是垂线段的长，是斜线段的长，其中求出垂线段的长（即斜线上的点到面的距离）既是关键又是难点，为此可构造三棱锥，利用等体积法来求垂线段的长．（3）证垂法：通过证明线面垂直得到线面角为90°．4、作二面角的平面角常有三种方法（1）棱上一点双垂线法：在棱上任取一点，过这点分别在两个面内作垂直于棱的射线，这两条射线所成的角，就是二面角的平面角．（2）面上一点三垂线法：自二面角的一个面上一点向另一面引垂线，再由垂足向棱作垂线得到棱上的点（即垂足），斜足与面上一点连线和斜足与垂足连线所夹的角，即为二面角的平面角．（3）空间一点垂面法：自空间一点作与棱垂直的平面，截二面角得两条射线，这两条射线所成的角就是二面角的平面角．【核心考点】核心考点一：非常规空间几何体为载体【规律方法】关键找出三条两两互相垂直的直线建立空间直角坐标系．【典型例题】例1．（2022·陕西安康·统考一模）如图，已知AB 为圆锥SO 底面的直径，点C 在圆锥底面的圆周上，2BS AB ==，6BAC π∠=，BE 平分SBA ∠，D 是SC 上一点，且平面DBE ⊥平面SAB .(1)求证：SA BD ⊥；(2)求二面角E BD C --的正弦值.例2．（2022·安徽·校联考二模）如图，将长方形11OAAO （及其内部）绕1OO 旋转一周形成圆柱，其中11,2OA O O ==，劣弧11A B 的长为,6AB π为圆O 的直径.(1)在弧AB 上是否存在点C （1,C B 在平面11OAAO 的同侧），使1BC AB ⊥，若存在，确定其位置，若不存在，说明理由；(2)求平面11A O B 与平面11B O B 夹角的余弦值.例3．（2022·山东东营·胜利一中校考模拟预测）如图，,AB CD 分别是圆台上､下底面的直径，且AB CD ，点E 是下底面圆周上一点，AB =(1)证明：不存在点E 使平面AEC ⊥平面ADE ；(2)若4DE CE ==，求二面角D AE B --的余泫值.例4．（2022·河北·统考模拟预测）如图，在圆台1OO 中，上底面圆1O 的半径为2，下底面圆O 的半径为4，过1OO 的平面截圆台得截面为11ABB A ，M 是弧AB 的中点，MN 为母线，cos NMB ∠=(1)证明：1AB ⊥平面1AOM ； (2)求二面角M NB A --的正弦值.核心考点二：立体几何探索性问题【规律方法】与空间向量有关的探究性问题主要有两类：一类是探究线面的位置关系；另一类是探究线面角或二面角满足特定要求时的存在性问题．处理原则：先建立空间直角坐标系，引入参数（有些是题中已给出），设出关键点的坐标，然后探究这样的点是否存在，或参数是否满足要求，从而作出判断．【典型例题】例5．（2022·上海虹口·统考一模）如图，在三棱柱111ABC A B C 中，底面ABC 是以AC 为斜边的等腰直角三角形，侧面11AAC C 为菱形，点1A 在底面上的投影为AC 的中点D ，且2AB =．(1)求证：1BD CC ⊥；(2)求点C 到侧面11AA B B 的距离；(3)在线段11A B 上是否存在点E ，使得直线DE 与侧面11AA B B 请求出1A E 的长；若不存在，请说明理由．例6．（2022春·山东·高三山东省实验中学校考阶段练习）如图，在三棱柱111ABC A B C 中，1AB C 为等边三角形，四边形11AA B B 为菱形，AC BC ⊥，4AC =，3BC =.(1)求证：11AB AC ⊥；(2)线段1CC 上是否存在一点E ，使得平面1AB E 与平面ABC 的夹角的余弦值为14？若存在，求出点E 的位置；若不存在，请说明理由.例7．（2022春·黑龙江绥化·高三海伦市第一中学校考期中）如图1，在矩形ABCD 中，AB ＝2，BC ＝1，E 是DC 的中点，将DAE 沿AE 折起，使得点D 到达点P 的位置，且PB ＝PC ，如图2所示．F 是棱PB 上的一点．(1)若F 是棱PB 的中点，求证：//CF 平面P AE ；(2)是否存在点F ，使得二面角F AE C --？若存在，则求出PF FB 的值；若不存在，请说明理由．例8．（2022·广东韶关·统考一模）已知矩形ABCD 中，4AB =，2BC =，E 是CD 的中点，如图所示，沿BE 将BCE 翻折至BFE △，使得平面BFE ⊥平面ABCD .(1)证明：BF AE ⊥；(2)若(01)DP DB λλ=<<是否存在λ，使得PF 与平面DEF 求出λ的值；若不存在，请说明理由.核心考点三：立体几何折叠问题【规律方法】1、处理图形翻折问题的关键是理清翻折前后长度和角度哪些发生改变，哪些保持不变．2、把空间几何问题转化为平面几何问题，把握图形之间的关系，感悟数学本质．【典型例题】例9．（2022春·江苏南通·高三期中）已知梯形ABCD 中，//AD BC ，π2∠=∠=ABC BAD ，24AB BC AD ===，E ，F 分别是AB ，CD 上的点，//EF BC ，AE x =，G 是BC 的中点，沿EF 将梯形ABCD 翻折，使平面AEFD ⊥平面EBCF ．(1)当2x =时①求证：BD EG ⊥；②求二面角D BF C --的余弦值；(2)三棱锥D FBC -的体积是否可能等于几何体ABE FDC -体积的一半？并说明理由．例10．（2022春·辽宁·高三辽宁实验中学校考期中）如图1，在平面四边形ABCD 中，已知ABDC ，AB DC ∥，142AD DC CB AB ====，E 是AB 的中点．将△BCE 沿CE 翻折至△PCE ，使得2DP =，如图2所示．(1)证明：DP CE ⊥；(2)求直线DE 与平面P AD 所成角的正弦值．例11．（2022春·湖南长沙·高三宁乡一中校考期中）如图，平面五边形P ABCD 中，PAD 是边长为2的等边三角形，//AD BC ，AB ＝2BC ＝2，AB BC ⊥，将PAD 沿AD 翻折成四棱锥P －ABCD ，E 是棱PD 上的动点（端点除外），F ，M 分别是AB ，CE 的中点，且PC =(1)证明：AB FM ⊥；(2)当直线EF 与平面P AD 所成的角最大时，求平面ACE 与平面P AD 夹角的余弦值．例12．（2022·四川雅安·统考模拟预测）如图①，ABC 为边长为6的等边三角形，E ，F 分别为AB ，AC 上靠近A 的三等分点，现将AEF △沿EF 折起，使点A 翻折至点P 的位置，且二面角P EF C --的大小为120°（如图②）．(1)在PC 上是否存在点H ，使得直线//FH 平面PBE ？若存在，确定点H 的位置；若不存在，说明理由． (2)求直线PC 与平面PBE 所成角的正弦值．核心考点四：立体几何作图问题【规律方法】（1）利用公理和定理作截面图（2）利用直线与平面平行的性质定理作平行线（3）利用平面与平面垂直作平面的垂线【典型例题】例13．（2022·贵州·校联考模拟预测）如图，已知平行六面体1111ABCD A B C D -的底面ABCD 是菱形，112CD CC AC ===，3DCB π∠=且113cos cos 4C CD C CB ∠=∠=.(1)试在平面ABCD 内过点C 作直线l ，使得直线//l 平面1C BD ，说明作图方法，并证明：直线11//l B D ； (2)求点C 到平面1A BD 的距离.例14．（2022秋·河北石家庄·高一石家庄市第十五中学校考期中）如图为一块直四棱柱木料，其底面ABCD 满足：AB AD ⊥，AD BC ∥．(1)要经过平面11CC D D 内的一点P 和棱1BB 将木料锯开，在木料表面应该怎样画线？（借助尺规作图，并写出作图说明，无需证明）(2)若2AD AB ==，11BC AA ==，当点P 是矩形11CDD C 的中心时，求点1D 到平面1APB 的距离．例15．（2022·全国·高三专题练习）如图多面体ABCDEF 中，面FAB ⊥面ABCD ，FAB 为等边三角形，四边形ABCD 为正方形，//EF BC ，且332EF BC ==，H ，G 分别为CE ，CD 的中点.（1）求二面角C FH G --的余弦值；（2）作平面FHG 与平面ABCD 的交线，记该交线与直线AB 交点为P ，写出APAB的值（不需要说明理由，保留作图痕迹）.例16．（2022·全国·高三专题练习）四棱锥P ABCD -中，底面ABCD 是边长为2的菱形，23DAB π∠=.ACBD O =,且PO ⊥平面ABCD ，PO =点,F G 分别是线段.PB PD 上的中点，E 在PA 上.且3PA PE =.（Ⅰ）求证：//BD 平面EFG ；（Ⅰ）求直线AB 与平面EFG 的成角的正弦值；（Ⅰ）请画出平面EFG 与四棱锥的表面的交线，并写出作图的步骤.核心考点五：立体几何建系繁琐问题【规律方法】利用传统方法解决【典型例题】例17．如图，已知三棱柱-111ABC A B C 的底面是正三角形，侧面11BB C C 是矩形，M ，N 分别为BC ，11B C 的中点，P 为AM 上一点．过11B C 和P 的平面交AB 于E ，交AC 于F ．（1）证明：1//AA MN ，且平面⊥1A AMN 平面11EB C F ；（2）设O 为△111A B C 的中心．若//AO 平面11EB C F ，且=AO AB ，求直线1B E 与平面1A AMN 所成角的正弦值．例18．如图，在锥体-P ABCD 中，ABCD 是边长为1的菱形，且∠=︒60DAB ，==PA PD ，=2PB ，E ，F 分别是BC ，PC 的中点（1）证明：⊥AD 平面DEF （2）求二面角--P AD B 的余弦值．例19．（2022春·福建南平·高三校考期中）在三棱柱111ABC A B C 中，AB AC ⊥，1B C ⊥平面ABC ，E 、F 分别是棱AC 、11A B 的中点.(1)设G 为11B C 的中点，求证：//EF 平面11BCC B ；(2)若2AB AC ==，直线1BB 与平面1ACB 所成角的正切值为2，求多面体1B EFGC -的体积V .核心考点六：两角相等（构造全等）的立体几何问题【规律方法】构造垂直的全等关系【典型例题】例20．如图，已知三棱柱-111ABC A B C 的底面是正三角形，侧面11BB C C 是矩形，M ，N 分别为BC ，11B C 的中点，P 为AM 上一点．过11B C 和P 的平面交AB 于E ，交AC 于F ．（1）证明：1//AA MN ，且平面⊥1A AMN 平面11EB C F ；（2）设O 为△111A B C 的中心．若//AO 平面11EB C F ，且=AO AB ，求直线1B E 与平面1A AMN 所成角的正弦值．例21．如图，在锥体-P ABCD 中，ABCD 是边长为1的菱形，且∠=︒60DAB ，==PA PD ，=2PB ，E ，F 分别是BC ，PC 的中点（1）证明：⊥AD 平面DEF （2）求二面角--P AD B 的余弦值．核心考点七：利用传统方法找几何关系建系【规律方法】利用传统方法证明关系，然后通过几何关系建坐标系．【典型例题】例22．如图：长为3的线段PQ 与边长为2的正方形ABCD 垂直相交于其中心()O PO OQ >．（1）若二面角P AB Q --的正切值为3-，试确定O 在线段PQ 的位置；（2）在（1）的前提下，以P ，A ，B ，C ，D ，Q 为顶点的几何体PABCDQ 是否存在内切球？若存在，试确定其内切球心的具体位置；若不存在，请说明理由．例23．在四棱锥P ABCD -中，E 为棱AD 的中点，PE ⊥平面ABCD ，//AD BC ，90ADC ∠=︒，2ED BC ==，3EB =，F 为棱PC 的中点．（Ⅰ）求证：//PA 平面BEF ；（Ⅰ）若二面角F BE C --为60︒，求直线PB 与平面ABCD 所成角的正切值．例24．三棱柱111ABC A B C -中，AB AC ⊥，2AB AC ==，侧面11BCC B 为矩形，123A AB π∠=，二面角1A BC A --的正切值为12．（Ⅰ）求侧棱1AA 的长；（Ⅰ）侧棱1CC 上是否存在点D ，使得直线AD 与平面1A BC ，若存在，判断点的位置并证明；若不存在，说明理由．核心考点八：空间中的点不好求【规律方法】方程组思想【典型例题】例25．（2022·江苏南京·模拟预测）已知三棱台111ABC A B C 的体积为143，且π2ABC ∠=，1A C ⊥平面11BB C C . (1)证明：平面11A B C ⊥平面111A B C ；(2)若11AC B C =，11112A B B C ==，求二面角1B AA C --的正弦值.例26．（2022春·浙江·高三浙江省新昌中学校联考期中）如图，在四棱台1111ABCD A B C D -中，底面ABCD 是边长为2的菱形，3DAB π∠=，平面11BDD B ⊥平面ABCD ，点1,O O 分别为11,B D BD 的中点，1111,,O B A AB O BO ∠∠=均为锐角.(1)求证：1AC BB ⊥；(2)若异面直线CD 与1AA ，四棱锥1A ABCD -的体积为1，求二面角1B AA C --的平面角的余弦值.例27．（2022春·辽宁沈阳·高三沈阳市第一二〇中学校考期中）如图，在几何体ABCDE 中，底面ABC 为以AC为斜边的等腰直角三角形.已知平面ABC ⊥平面ACD ，平面ABC ⊥平面,//BCE DE 平面,ABC AD DE ⊥.(1)证明；DE ⊥平面ACD ；(2)若22AC CD ==，设M 为棱BE 的中点，求当几何体ABCDE 的体积取最大值时,AM 与CD 所成角的余弦值.核心考点九：创新定义【规律方法】以立体几何为载体的情境题都跟图形有关，涉及在具体情境下的图形阅读，需要通过数形结合来解决问题．图形怎么阅读一是要读特征，即从图形中读出图形的基本特征；二是要读本质，即要善于将所读出的信息进行提升，实现“图形→文字→符号”的转化；三是要有问题意识，带着问题阅读图形，将研究图形的本身特征和关注题目要解决的问题有机地融合在一起；四是要有运动观点，要“动手”去操作，动态地去阅读图形．【典型例题】例28．（2022·安徽合肥·合肥一六八中学校考模拟预测）已知顶点为S 的圆锥面（以下简称圆锥S ）与不经过顶点S 的平面α相交，记交线为C ，圆锥S 的轴线l 与平面α所成角θ是圆锥S 顶角（圆S 轴截面上两条母线所成角θ的一半，为探究曲线C 的形状，我们构建球T ，使球T 与圆锥S 和平面α都相切，记球T 与平面α的切点为F ，直线l 与平面α交点为A ，直线AF 与圆锥S 交点为O ，圆锥S 的母线OS 与球T 的切点为M ，OM a =，MS b =．(1)求证：平面SOA ⊥平面α，并指出a ，b ，θ关系式； (2)求证：曲线C 是抛物线．例29．（2022·全国·高三专题练习）类比于二维平面中的余弦定理，有三维空间中的三面角余弦定理；如图1，由射线PA ，PB ，PC 构成的三面角-P ABC ，APC α∠=，BPC β∠=，APB γ∠=，二面角A PC B --的大小为θ，则cos cos cos sin sin cos γαβαβθ=+．（1）当α、π0,2β⎛⎫∈ ⎪⎝⎭时，证明以上三面角余弦定理；（2）如图2，四棱柱1111ABCD A B C D -中，平面11AA C C ⊥平面ABCD ，160A AC ∠=︒，45BAC ∠=︒， ①求1A AB ∠的余弦值；②在直线1CC 上是否存在点P ，使//BP 平面11DA C ？若存在，求出点P 的位置；若不存在，说明理由．例30．（2022·全国·校联考模拟预测）蜂房是自然界最神奇的“建筑”之一，如图1所示．蜂房结构是由正六棱柱截去三个相等的三棱锥H ABC -，J CDE -，K EFA -，再分别以AC ，CE ，EA 为轴将ACH ∆，CEJ ∆，EAK ∆分别向上翻转180︒，使H ，J ，K 三点重合为点S 所围成的曲顶多面体（下底面开口），如图2所示．蜂房曲顶空间的弯曲度可用曲率来刻画，定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和，而每一顶点的曲率规定等于2π减去蜂房多面体在该点的各个面角之和（多面体的面角是多面体的面的内角，用弧度制表示）．（1）求蜂房曲顶空间的弯曲度；（2）若正六棱柱的侧面积一定，当蜂房表面积最小时，求其顶点S 的曲率的余弦值．【新题速递】1．（2022·重庆沙坪坝·重庆八中校考模拟预测）如图，在三棱柱111ABC A B C 中，1BC CC =，1AC AB =.(1)证明：平面1ABC ⊥平面11BCC B ；(2)若BC =，1AB B C =，160CBB ∠=︒，求直线1BA 与平面111A B C 所成角的正弦值.2．（2022·四川达州·统考一模）如图，三棱柱111ABC A B C -中，底面ABC 为等腰直角三角形，112AB AC BB ===，，160ABB ∠=.(1)证明: 1AB B C ⊥；(2)若12B C =，求1AC 与平面1BCB 所成角的正弦值.3．（2022·陕西宝鸡·统考一模）如图在四棱锥P ABCD -中，PA ⊥底面ABCD ，且底面ABCD 是平行四边形.已知2,1,PA AB AD AC E ====是PB 中点.(1)求证：平面PBC ⊥平面ACE ；(2)求平面PAD 与平面ACE 所成锐二面角的余弦值.4．（2022·广东广州·统考一模）如图，已知四棱锥P ABCD -的底面ABCD 是菱形，平面PBC ⊥平面ABCD ，30,ACD E ∠=为AD 的中点，点F 在PA 上，3AP AF =.(1)证明：PC //平面BEF ；(2)若PDC PDB ∠∠=，且PD 与平面ABCD 所成的角为45，求平面AEF 与平面BEF 夹角的余弦值.5．（2022·上海奉贤·统考一模）如图，在四面体ABCD 中，已知BA BD CA CD ===.点E 是AD 中点.(1)求证：AD ⊥平面BEC ；(2)已知95,arccos,625AB BDC AD ∠===，作出二面角D BC E --的平面角，并求它的正弦值.6．（2022·上海浦东新·统考一模）如图，三棱锥-P ABC 中，侧面P AB 垂直于底面ABC ，PA PB =，底面ABC 是斜边为AB 的直角三角形，且30ABC ∠=︒，记O 为AB 的中点，E 为OC 的中点.(1)求证：PC AE ⊥；(2)若2AB =，直线PC 与底面ABC 所成角的大小为60°，求四面体P AOC 的体积.7．（2022·四川成都·石室中学校考模拟预测）如图，在四棱锥P ABCD -中，AB BD BP ===PA PD ==90APD ∠=︒，E 是棱PA 的中点，且BE 平面PCD(1)证明：CD ⊥平面PAD ；(2)若1CD =，求二面角A PB C --的正弦值.8．（2022春·江苏徐州·高三期末）如图，四棱锥P ABCD -中，PA ⊥底面ABCD ，AD ∥BC ，N 为PB 的中点.(1)若点M 在AD 上，2AM MD =，34AD BC =，证明：MN 平面PCD ； (2)若3PA AB AC AD ====，4BC =，求二面角D AC N --的余弦值.9．（2022·陕西汉中·统考一模）如图，多面体ABCDEF 中，四边形ABCD 为菱形，60,ABC FA ∠=⊥平面,ABCD ED FA ∥，且22AB FA ED ===.(1)求证：BD FC ⊥；(2)求二面角F AC E --的大小.10．（2022·陕西汉中·统考一模）如图，多面体ABCDEF 中，四边形ABCD 为菱形，60,ABC FA ∠=⊥平面,ABCD FA ED ∥，且22AB FA ED ===.(1)求证：BD FC ⊥；(2)求点A 到平面FBD 的距离.11．（2022·四川广安·广安二中校考模拟预测）APD △是等腰直角三角形，AP PD ⊥且AD =ABCD 是直角梯形，AB BC ⊥，DC BC ⊥，且222AB BC CD ===，平面APD ⊥平面ABCD .(1)求证：AP ⊥平面BPD ；(2)若点E 是线段PB 上的一个动点，问点E 在何位置时三棱锥D APE -.12．（2022·四川南充·统考一模）在平面五边形ABCDE 中（如图1），ABCD 是梯形，//AD BC ，2AD BC ==AB =90ABC ∠=︒，ADE 是等边三角形．现将ADE 沿AD 折起，连接EB ，EC 得四棱锥E ABCD -（如图2）且CE =(1)求证：平面EAD ⊥平面ABCD ；(2)在棱EB 上有点F ，满足13EF EB =，求二面角E AD F --的余弦值．13．（2022·贵州贵阳·贵阳六中校考一模）如图，在四棱锥P ABCD -中，DA AB ⊥，PD PC ⊥，PB PC ⊥，1AB AD PD PB ====，4cos 5DCB ∠=.(1)求证：BD ⊥平面PAC .(2)设E 为BC 的中点，求PE 与平面ABCD 所成角的正弦值.14．（2022春·广东广州·高三校考期中）如图所示，在四棱锥P ABCD -中，PC ⊥底面ABCD ，四边形ABCD 是直角梯形，AB AD ⊥，//,222AB CD PC AB AD CD ====，点E 在侧棱PB 上.(1)求证：平面EAC ⊥平面PBC ；(2)若平面PAC 与平面ACE PE BE 的值.。

专题九：坐标法解立体几何题

空间向量在立体几何中的应用空间向量是高中数学中的重要内容之一，是处理空间线线、线面、面面位置关系和夹角的重要工具，是高考考查的重要内容之一.运用向量方法研究立体几何问题思路简单，模式固定，避免了几何法中作辅助线的问题，从而降低了立体几何问题的难度.本文将空间向量在立体几何中的应用的重要考点和解题方法作以解析.【考点及要求】1.理解直线的方向向量与平面法向量.2.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系.3.能用向量方法证明证明直线和平面位置关系的一些定理（包括三垂线定理）.4.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角计算问题，了解向量方法在研究集合问题中的应用.【考点归纳分析】考点1.利用空间向量证明空间垂直问题利用空间向量证明空间线线、线面、面面垂直问题是高考考查的重点内容，考查形式灵活多样，常与探索性问题、平行问题、空间角问题结合，考查形式可以是小题，也可以是解答题的一部分，或解答题的某个环节，题目容易，是高考中的重要得分点. 例1已知三棱锥P －ABC 中，PA ⊥面ABC ，AB ⊥AC ，PA=AC=12AB ，N 为AB 上一点，AB=4AN,M,S 分别为PB,BC 的中点.证明：CM ⊥SN ；审题要津：本题空间坐标系易建立，可用坐标法.证明：设PA=1，以A 为原点，射线AB ，AC ，AP 分别为x ，y ，z 轴正向建立空间直角坐标系如图，则P （0,0,1），C （0,1,0），B （2,0,0），M （1,0,12），N （12,0,0），S （1,12,0） 111(1,1,),(,,0)222CM SN =-=-- , 因为110022CM SN ∙=-++= ，所以CM ⊥SN . 【点评】对坐标系易建立的空间线线垂直判定（证明）问题，常用向量法，即通过证明所证直线的方向向量的数量积为0证明两直线垂直.例2在长方体1111ABCD A BC D -中，E 、F 分别是棱BC ,1CC 上的点，CF =AB =2CE , 1::AB AD AA = 1:2:4.证明AF ⊥平面1A ED审题要津：本题空间坐标系易建立，可用坐标法.解析：如图所示，建立空间直角坐标系，点A 为坐标原点，设1AB =,依题意得(0,2D ,(1,2,1)F ,1(0,0,4)A ,31,,02E ⎛⎫ ⎪⎝⎭已知(1,2,1)AF = ,131,,42EA ⎛⎫=-- ⎪⎝⎭ ,11,,02ED ⎛⎫=- ⎪⎝⎭ 于是AF ·1EA =0，AF ·ED =0.因此，1AF EA ⊥,AF ED ⊥,又1EA ED E ⋂=所以AF ⊥平面1A ED【点评】对坐标系易建立的空间线面垂直问题，通常用向量法，先求出平面的法向量和直线的方向向量，证明平面法向量与直线的方向向量平行或者直接用向量法证明直线与平面内两条相交直线垂直，再用线面垂直判定定理即可.例 3 （2010年山东文）在如图所示的几何体中，四边形ABCD 是正方形，MA ⊥平面ABCD ，//PD MA ，E 、G 、F 分别为MB 、PB 、PC 的中点，且2AD PD MA ==.求证：平面EFG ⊥平面PDC .审题要津：本题空间坐标系易建立，可用坐标法. 解析：以A 为原点，向量DA ,AB ,AM 分别为x 轴、y 轴、z 轴的正方向，如图建立坐标系，设AM=1，则AD=AB=PD=2,则B(0,2,0),C (－2,2,0),D(－2,0,0),P(－2,0,2), M(0,0,1),则E(0,1,12),G(－1,1,1),F(－2,1,1)， ∴EG =(-1,0,12),GF =(－1,0,0),设平面EFG 的法向量m =（x ，y ，z ），则 EG ∙ m =12x z -+=0且GF ∙ m =x -=0，取y =1，则x =z =0，∴m =（0，1,0）, 易证面PDC 的法向量为DA =(2,0,0), ∵DA ∙ m =200100⨯+⨯+⨯=0, ∴m ⊥DA , ∴平面EFG ⊥平面PDC 【点评】对于易建立空间坐标系的面面垂直问题，常向量法，即先建立坐标系，求出两个平面的法向量，通过证明这两个平面的法向量垂直，即得面面垂直.考点2.利用空间向量处理空间平行关系空间线线、线面、面面平行关系问题是高考考查的另一个重点内容，考查的形式灵活多样，常与探索性问题、垂直问题、空间角问题结合，可以是小题，也可以是解答题的一个小题，题目的难度一般不大，是高考中的得分点之一.例4（2010 湖南理18）在正方体1111ABCD A BC D -，E 是棱1DD 的中点。

专题06 立体几何(解答题)

专题06 立体几何（解答题）1．【2019年高考全国Ⅰ卷文数】如图，直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点.（1）证明：MN ∥平面C 1DE ；（2）求点C 到平面C 1DE 的距离．【答案】（1）见解析；（2）41717. 【解析】（1）连结1,B C ME .因为M ，E 分别为1,BB BC 的中点，所以1 ME B C ∥，且112ME B C =. 又因为N 为1A D 的中点，所以112ND A D =. 由题设知11=A B DC ∥，可得11=BC A D ∥，故=ME ND ∥，因此四边形MNDE 为平行四边形，MN ED ∥. 又MN ⊄平面1C DE ，所以MN ∥平面1C DE . （2）过C 作C 1E 的垂线，垂足为H .由已知可得DE BC ⊥，1DE C C ⊥，所以DE ⊥平面1C CE ，故DE ⊥CH. 从而CH ⊥平面1C DE ，故CH 的长即为C 到平面1C DE 的距离，由已知可得CE =1，C 1C =4，所以117C E =，故417CH =.从而点C 到平面1C DE 的距离为41717.【名师点睛】该题考查的是有关立体几何的问题，涉及的知识点有线面平行的判定，点到平面的距离的求解，在解题的过程中，注意要熟记线面平行的判定定理的内容，注意平行线的寻找思路，再者就是利用线面垂直找到距离问题，当然也可以用等积法进行求解.2．【2019年高考全国Ⅱ卷文数】如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，AB =3，求四棱锥11E BB C C -的体积．【答案】（1）见详解；（2）18.【解析】（1）由已知得B 1C 1⊥平面ABB 1A 1，BE ⊂平面ABB 1A 1，故11B C BE ⊥．又1BE EC ⊥，所以BE ⊥平面11EB C ．（2）由（1）知∠BEB 1=90°. 由题设知Rt △ABE ≌Rt △A 1B 1E ，所以1145AEB A EB ︒∠=∠=，故AE =AB =3，126AA AE ==.作1EF BB ⊥，垂足为F ，则EF ⊥平面11BB C C ，且3EF AB ==．所以，四棱锥11E BB C C -的体积1363183V =⨯⨯⨯=．【名师点睛】本题主要考查线面垂直的判定，以及四棱锥的体积的求解，熟记线面垂直的判定定理，以及四棱锥的体积公式即可，属于基础题型.3．【2019年高考全国Ⅲ卷文数】图1是由矩形ADEB ，Rt △ABC 和菱形BFGC 组成的一个平面图形，其中AB =1，BE =BF =2，∠FBC =60°．将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2．（1）证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ；（2）求图2中的四边形ACGD 的面积.【答案】（1）见解析；（2）4.【解析】（1）由已知得AD BE ，CG BE ，所以AD CG ，故AD ，CG 确定一个平面，从而A ，C ，G ，D 四点共面．由已知得AB⊥BE，AB⊥BC，故AB⊥平面BCGE．又因为AB⊂平面ABC，所以平面ABC⊥平面BCGE．（2）取CG的中点M，连结EM，DM.因为AB∥DE，AB⊥平面BCGE，所以DE⊥平面BCGE，故DE⊥CG.由已知，四边形BCGE是菱形，且∠EBC=60°得EM⊥CG，故CG⊥平面DEM．因此DM⊥CG．在Rt△DEM中，DE=1，EM=3，故DM=2．所以四边形ACGD的面积为4．【名师点睛】本题是很新颖的立体几何考题，首先是多面体折叠问题，考查考生在折叠过程中哪些量是不变的，再者折叠后的多面体不是直棱柱，突出考查考生的空间想象能力.-中，PA⊥平面ABCD，底部ABCD为菱形，E 4．【2019年高考北京卷文数】如图，在四棱锥P ABCD为CD的中点．（1）求证：BD⊥平面PAC；（2）若∠ABC=60°，求证：平面PAB⊥平面PAE；（3）棱PB上是否存在点F，使得CF∥平面PAE？说明理由．【答案】（1）见解析；（2）见解析；（3）存在，理由见解析.【解析】（1）因为PA⊥平面ABCD，⊥．所以PA BD又因为底面ABCD为菱形，所以BD AC ⊥．所以BD ⊥平面PAC ．（2）因为PA ⊥平面ABCD ，AE ⊂平面ABCD ，所以PA ⊥AE ．因为底面ABCD 为菱形，∠ABC =60°，且E 为CD 的中点，所以AE ⊥CD ．所以AB ⊥AE ．所以AE ⊥平面PAB ．所以平面PAB ⊥平面PAE ．（3）棱PB 上存在点F ，使得CF ∥平面PAE ．取F 为PB 的中点，取G 为PA 的中点，连结CF ，FG ，EG ．则FG ∥AB ，且FG =12AB ．因为底面ABCD 为菱形，且E 为CD 的中点，所以CE ∥AB ，且CE =12AB ．所以FG ∥CE ，且FG =CE ．所以四边形CEGF 为平行四边形．所以CF ∥EG ．因为CF ⊄平面PAE ，EG ⊂平面PAE ，所以CF ∥平面PAE ．【名师点睛】本题主要考查线面垂直的判定定理，面面垂直的判定定理，立体几何中的探索问题等知识，意在考查学生的转化能力和计算求解能力.5．【2019年高考天津卷文数】如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，PCD △为等边三角形，平面PAC ⊥平面PCD ，,2,3PA CD CD AD ⊥==.（1）设G ，H 分别为PB ，AC 的中点，求证：GH ∥平面PAD ；（2）求证：PA ⊥平面PCD ；（3）求直线AD 与平面PAC 所成角的正弦值. 【答案】（1）见解析；（2）见解析；（33【解析】（1）连接BD ，易知AC BD H =，BH DH =.又由BG=PG ，故GH PD ∥.又因为GH ⊄平面P AD ，PD ⊂平面P AD ，所以GH ∥平面P AD .（2）取棱PC 的中点N ，连接DN .依题意，得DN ⊥PC ，又因为平面PAC ⊥平面PCD ，平面PAC 平面PCD PC =，所以DN ⊥平面P AC ，又PA ⊂平面P AC ，故DN PA ⊥. 又已知PA CD ⊥，CD DN D =，所以PA ⊥平面PCD .（3）连接AN ，由（2）中DN ⊥平面P AC ，可知DAN ∠为直线AD 与平面P AC 所成的角，因为PCD △为等边三角形，CD =2且N 为PC 的中点，所以3DN =又DN AN ⊥，在Rt AND △中，3sin DN DAN AD ∠==所以，直线AD 与平面P AC 所成角的正弦值为33.【名师点睛】本小题主要考查直线与平面平行、直线与平面垂直、平面与平面垂直、直线与平面所成的角等基础知识.考查空间想象能力和推理论证能力.6．【2019年高考江苏卷】如图，在直三棱柱ABC－A1B1C1中，D，E分别为BC，AC的中点，AB=BC．求证：（1）A1B1∥平面DEC1；（2）BE⊥C1E．【答案】（1）见解析；（2）见解析.【解析】（1）因为D，E分别为BC，AC的中点，所以ED∥AB.在直三棱柱ABC−A1B1C1中，AB∥A1B1，所以A1B1∥ED.又因为ED⊂平面DEC1，A1B1 平面DEC1，所以A1B1∥平面DEC1.（2）因为AB=BC，E为AC的中点，所以BE⊥AC.因为三棱柱ABC−A1B1C1是直棱柱，所以CC1⊥平面ABC.又因为BE ⊂平面ABC ，所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1，AC ⊂平面A 1ACC 1，C 1C ∩AC =C ，所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1，所以BE ⊥C 1E .【名师点睛】本小题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识，考查空间想象能力和推理论证能力.7．【2019年高考浙江卷】如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ，90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点. （1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.【答案】（1）见解析；（2）35．【解析】方法一：（1）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC ．又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ，则A 1E ⊥BC ．又因为A 1F ∥AB ，∠ABC =90°，故BC ⊥A 1F ．所以BC ⊥平面A 1EF ．因此EF ⊥BC ．（2）取BC 中点G ，连接EG ，GF ，则EGFA 1是平行四边形．由于A 1E ⊥平面ABC ，故A 1E ⊥EG ，所以平行四边形EGFA 1为矩形．由（1）得BC ⊥平面EGFA 1，则平面A 1BC ⊥平面EGFA 1，所以EF 在平面A 1BC 上的射影在直线A 1G 上．连接A 1G 交EF 于O ，则∠EOG 是直线EF 与平面A 1BC 所成的角（或其补角）．不妨设AC =4，则在Rt △A 1EG 中，A 1E =23，EG =3. 由于O 为A 1G 的中点，故11522A G EO OG ===，所以2223cos 25EO OG EG EOG EO OG +-∠==⋅．因此，直线EF 与平面A 1BC 所成角的余弦值是35．方法二：（1）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC . 又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ．如图，以点E 为原点，分别以射线EC ，EA 1为y ，z 轴的正半轴，建立空间直角坐标系E –xyz ．不妨设AC =4，则A 1（0，0，23），B （3，1，0），1(3,3,23)B ，33(,,23)22F ，C (0，2，0)．因此，33(,,23)22EF =，(3,1,0)BC =-．由0EF BC ⋅=得EF BC ⊥．（2）设直线EF 与平面A 1BC 所成角为θ．由（1）可得1=(310)=(0223)BC AC --，，，，，．设平面A 1BC 的法向量为n ()x y z =，，，由100BC A C ⎧⋅=⎪⎨⋅=⎪⎩n n ，得3030x y y z ⎧-+=⎪⎨-=⎪⎩，取n (131)=，，，故||4sin |cos |=5|||EF EF EF θ⋅==⋅，n n n |，因此，直线EF 与平面A 1BC 所成的角的余弦值为35．【名师点睛】本题主要考查空间点、线、面位置关系，直线与平面所成的角等基础知识，同时考查空间想象能力和运算求解能力.8．【2018年高考全国Ⅰ卷文数】如图，在平行四边形ABCM 中，3AB AC ==，90ACM =︒∠，以AC为折痕将△ACM 折起，使点M 到达点D 的位置，且AB DA ⊥．（1）证明：平面ACD ⊥平面ABC ；（2）Q 为线段AD 上一点，P 为线段BC 上一点，且23BP DQ DA ==，求三棱锥Q ABP -的体积．【答案】（1）见解析；（2）1.【解析】（1）由已知可得，BAC ∠=90°，BA AC ⊥．又BA ⊥AD ，所以AB ⊥平面ACD ．又AB ⊂平面ABC ，所以平面ACD ⊥平面ABC ．（2）由已知可得，DC =CM =AB =3，DA =32又23BP DQ DA ==，所以22BP = 作QE ⊥AC ，垂足为E ，则QE =∥13DC ．由已知及（1）可得DC ⊥平面ABC ，所以QE ⊥平面ABC ，QE =1．因此，三棱锥Q ABP -的体积为1111322451332Q ABP ABP V QE S -=⨯⨯=⨯⨯⨯⨯︒=△．【名师点睛】该题考查的是有关立体几何的问题，涉及到的知识点有面面垂直的判定以及三棱锥的体积的求解，在解题的过程中，需要清楚题中的有关垂直的直线的位置，结合线面垂直的判定定理证得线面垂直，之后应用面面垂直的判定定理证得面面垂直，需要明确线线垂直、线面垂直和面面垂直的关系，在求三棱锥的体积的时候，注意应用体积公式求解即可.解答本题时，（1）首先根据题的条件，可以得到BAC ∠=90°，即BA AC ⊥，再结合已知条件BA ⊥AD ，利用线面垂直的判定定理证得AB ⊥平面ACD ，又因为AB ⊂平面ABC ，根据面面垂直的判定定理，证得平面ACD ⊥平面ABC ；（2）根据已知条件，求得相关的线段的长度，根据第一问的相关垂直的条件，求得三棱锥的高，之后借助于三棱锥的体积公式求得三棱锥的体积. 9．【2018年高考全国Ⅱ卷文数】如图，在三棱锥P ABC -中，22AB BC ==，4PA PB PC AC ====，O 为AC 的中点．（1）证明：PO ⊥平面ABC ；（2）若点M 在棱BC 上，且2MC MB =，求点C 到平面POM 的距离．【答案】（1）见解析；（2）455．【解析】（1）因为AP =CP =AC =4，O 为AC 的中点，所以OP ⊥AC ，且OP =23．连结OB ．因为AB =BC =22AC，所以△ABC 为等腰直角三角形，且OB ⊥AC ，OB =12AC =2．由222OP OB PB +=知，OP ⊥OB ．由OP ⊥OB ，OP ⊥AC 知PO ⊥平面ABC ．（2）作CH ⊥OM ，垂足为H ．又由（1）可得OP ⊥CH ，所以CH ⊥平面POM ．故CH 的长为点C 到平面POM 的距离．由题设可知OC =12AC =2，CM =23BC =23，∠ACB =45°．所以OM =253，CH =sin OC MC ACB OM ⋅⋅∠=455．所以点C 到平面POM 45【名师点睛】立体几何解答题在高考中难度低于解析几何，属于易得分题，第一问多以线面的证明为主，解题的核心是能将问题转化为线线关系的证明，解答本题时，连接OB ，欲证PO ⊥平面ABC ，只需证明,PO AC PO OB ⊥⊥即可；本题第二问可以通过作出点到平面的距离线段求解，即过点C 作CH OM ⊥，垂足为M ，只需论证CH 的长即为所求，再利用平面几何知识求解即可，本题也可利用等体积法解决.10．【2018年高考全国Ⅲ卷文数】如图，矩形ABCD 所在平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点．（1）证明：平面AMD ⊥平面BMC ；（2）在线段AM 上是否存在点P ，使得MC ∥平面PBD ？说明理由．【答案】（1）见解析；（2）存在，理由见解析.【解析】（1）由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ．因为M 为CD 上异于C ，D 的点，且DC 为直径，所以DM ⊥CM ．又BC ∩CM =C ，所以DM ⊥平面BMC ．而DM ⊂平面AMD ，故平面AMD ⊥平面BMC ．（2）当P 为AM 的中点时，MC ∥平面PBD ．证明如下：连结AC 交BD 于O ．因为ABCD 为矩形，所以O 为AC 中点．连结OP ，因为P 为AM 中点，所以MC ∥OP ．MC ⊄平面PBD ，OP ⊂平面PBD ，所以MC ∥平面PBD ．【名师点睛】本题主要考查面面垂直的证明，利用线线垂直得到线面垂直，再得到面面垂直，第二问先断出P 为AM 中点，然后作辅助线，由线线平行得到线面平行，考查学生空间想象能力，属于中档题.11．【2018年高考北京卷文数】如图，在四棱锥P −ABCD 中，底面ABCD 为矩形，平面P AD ⊥平面ABCD ，P A ⊥PD ，P A =PD ，E ，F 分别为AD ，PB 的中点.（1）求证：PE ⊥BC ；（2）求证：平面P AB ⊥平面PCD ；（3）求证：EF ∥平面PCD .【答案】（1）见解析；（2）见解析；（3）见解析.【解析】（1）∵PA PD =，且E 为AD 的中点，∴PE AD ⊥. ∵底面ABCD 为矩形，∴BC AD ∥， ∴PE BC ⊥.（2）∵底面ABCD 为矩形，∴AB AD ⊥. ∵平面PAD ⊥平面ABCD ，∴AB ⊥平面PAD . ∴AB PD ⊥.又PA PD ⊥，∴PD ⊥平面PAB ，∴平面PAB ⊥平面PCD . （3）如图，取PC 中点G ，连接,FG GD .∵,F G 分别为PB 和PC 的中点，∴FG BC ∥，且12FG BC =. ∵四边形ABCD 为矩形，且E 为AD 的中点， ∴1,2ED BC DE BC =∥，∴ED FG ∥，且ED FG =，∴四边形EFGD 为平行四边形， ∴EF GD ∥.又EF ⊄平面PCD ，GD ⊂平面PCD ， ∴EF ∥平面PCD .【名师点睛】证明面面关系的核心是证明线面关系，证明线面关系的核心是证明线线关系.证明线线平行的方法：（1）线面平行的性质定理；（2）三角形中位线法；（3）平行四边形法. 证明线线垂直的常用方法：（1）等腰三角形三线合一；（2）勾股定理逆定理；（3）线面垂直的性质定理；（4）菱形对角线互相垂直.12．【2018年高考天津卷文数】如图，在四面体ABCD 中，△ABC 是等边三角形，平面ABC ⊥平面ABD ，点M 为棱AB 的中点，AB =2，AD =23，∠BAD =90°．（1）求证：AD ⊥BC ；（2）求异面直线BC 与MD 所成角的余弦值；（3）求直线CD 与平面ABD 所成角的正弦值．【答案】（1）见解析；（2）1326；（3）34．【解析】（1）由平面ABC ⊥平面ABD ，平面ABC ∩平面ABD =AB ，AD ⊥AB ，可得AD ⊥平面ABC ，故AD ⊥BC ．（2）取棱AC 的中点N ，连接MN ，ND ．又因为M 为棱AB 的中点，故MN ∥BC ．所以∠DMN （或其补角）为异面直线BC 与MD 所成的角．在Rt △DAM 中，AM =1，故DM 22=13AD AM +AD ⊥平面ABC ，故AD ⊥AC ．在Rt △DAN 中，AN =1，故DN 22=13AD AN +在等腰三角形DMN 中，MN =1，可得1132cos MNDMN DM ∠==．所以，异面直线BC 与MD 所成角的余弦值为1326．（3）连接CM ．因为△ABC 为等边三角形，M 为边AB 的中点，故CM ⊥AB ，CM =3．又因为平面ABC ⊥平面ABD ，而CM ⊂平面ABC ，故CM ⊥平面ABD ．所以，∠CDM 为直线CD 与平面ABD 所成的角．在Rt △CAD 中，CD =22AC AD +=4．在Rt △CMD 中，3sin 4CM CDM CD ∠==．所以，直线CD 与平面ABD 所成角的正弦值为34．【名师点睛】本小题主要考查异面直线所成的角、直线与平面所成的角、平面与平面垂直等基础知识．考查空间想象能力、运算求解能力和推理论证能力．13．【2018年高考江苏卷】在平行六面体1111ABCD A B C D -中，1111,AA AB AB B C =⊥．求证：（1）AB ∥平面11A B C ；（2）平面11ABB A ⊥平面1A BC ．【答案】（1）见解析；（2）见解析.【解析】（1）在平行六面体ABCD -A 1B 1C 1D 1中，AB ∥A 1B 1．因为AB⊄平面A1B1C，A1B1⊂平面A1B1C，所以AB∥平面A1B1C．（2）在平行六面体ABCD-A1B1C1D1中，四边形ABB1A1为平行四边形．又因为AA1=AB，所以四边形ABB1A1为菱形，因此AB1⊥A1B．又因为AB1⊥B1C1，BC∥B1C1，所以AB1⊥BC．又因为A1B∩BC=B，A1B⊂平面A1BC，BC⊂平面A1BC，所以AB1⊥平面A1BC．因为AB1⊂平面ABB1A1，所以平面ABB1A1⊥平面A1BC．【名师点睛】本题可能会出现对常见几何体的结构不熟悉导致几何体中的位置关系无法得到运用或者运用错误，如柱体的概念中包含“两个底面是全等的多边形，且对应边互相平行，侧面都是平行四边形”，再如菱形对角线互相垂直的条件，这些条件在解题中都是已知条件，缺少对这些条件的应用可导致无法证明.解答本题时，（1）先根据平行六面体得线线平行，再根据线面平行判定定理得结论；（2）先根据条件得四边形ABB1A1为菱形，再根据菱形对角线相互垂直，以及已知垂直条件，利用线面垂直判定定理得线面垂直，最后根据面面垂直判定定理得结论.14．【2018年高考浙江卷】如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=1，AB=BC=B1B=2．（1）证明：AB1⊥平面A1B1C1；（2）求直线AC1与平面ABB1所成的角的正弦值．【答案】（1）见解析；（2）3913. 【解析】方法一：（1）由11112,4,2,,AB AA BB AA AB BB AB ===⊥⊥得11122AB A B ==，所以2221111A B AB AA +=.故111AB A B ⊥.由2BC =，112,1,BB CC ==11,BB BC CC BC ⊥⊥得115B C =，由2,120AB BC ABC ==∠=︒得23AC =，由1CC AC ⊥，得113AC =，所以2221111AB B C AC +=，故111AB B C ⊥.因此1AB ⊥平面111A B C .（2）如图，过点1C 作111C D A B ⊥，交直线11A B 于点D ，连结AD .由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB ，由111C D A B ⊥得1C D ⊥平面1ABB ，所以1C AD ∠是1AC 与平面1ABB 所成的角.由1111115,22,21BC A B AC ==1111116cos 77C A B C A B ∠=∠=，所以13C D ，故11139sin C D C AD AC ∠==.因此，直线1AC 与平面1ABB 所成的角的正弦值是3913. 方法二：（1）如图，以AC 的中点O 为原点，分别以射线OB ，OC 为x ，y 轴的正半轴，建立空间直角坐标系O -xyz .由题意知各点坐标如下：111(0,3,0),(1,0,0),(0,3,4),(1,0,2),3,1),A B A B C --因此11111(1,3,2),(1,3,2),(0,23,3),AB A B AC ==-=- 由1110AB A B ⋅=得111AB A B ⊥. 由1110AB AC ⋅=得111AB AC ⊥. 所以1AB ⊥平面111A B C .（2）设直线1AC 与平面1ABB 所成的角为θ.由（1）可知11(0,23,1),(1,3,0),(0,0,2),AC AB BB === 设平面1ABB 的法向量(,,)x y z =n .由10,0,AB BB ⎧⋅=⎪⎨⋅=⎪⎩n n 即30,20,x z ⎧+=⎪⎨=⎪⎩可取(3,1,0)=-n .所以111|39sin |cos ,|13|||AC AC AC θ⋅===⋅n |n n |. 因此，直线1AC 与平面1ABB 39. 【名师点睛】本题主要考查空间点、线、面位置关系，直线与平面所成的角等基础知识，同时考查空间想象能力和运算求解能力.15．【2017年高考全国Ⅰ文数】如图，在四棱锥P −ABCD 中，AB//CD ，且90BAP CDP ∠=∠=．（1）证明：平面PAB ⊥平面PAD ；（2）若PA =PD =AB =DC ，90APD ∠=，且四棱锥P −ABCD 的体积为83，求该四棱锥的侧面积．【答案】（1）见解析；（2）326+．【解析】（1）由已知90BAP CDP ==︒∠∠，得AB AP ⊥，CD PD ⊥．由于AB CD ∥，故AB PD ⊥，从而AB ⊥平面PAD ．又AB ⊂平面PAB ，所以平面PAB ⊥平面PAD ．（2）在平面PAD 内作PE AD ⊥，垂足为E ．由（1）知，AB ⊥平面PAD ，故AB PE ⊥，可得PE ⊥平面ABCD ．设AB x =，则由已知可得2AD x =，22PE x =．故四棱锥P ABCD -的体积31133P ABCD V AB AD PE x -=⋅⋅=．由题设得31833x =，故2x =．从而2PA PD ==，22AD BC ==22PB PC ==．可得四棱锥P ABCD -的侧面积为21111sin 606232222PA PD PA AB PD DC BC ⋅+⋅+⋅+︒=+ 【名师点睛】证明面面垂直，先由线线垂直证明线面垂直，再由线面垂直证明面面垂直；计算点面距离时，如直接求不方便，应首先想到转化，如平行转化、对称转化、比例转化等，找到方便求值时再计算，可以减少运算量，提高准确度，求点面距离有时能直接作出就直接求出，不方便直接求出的看成三棱锥的高，利用等体积法求出．解答本题时，（1）由AB AP ⊥，AB PD ⊥，得AB ⊥平面PAD 即可证得结果；（2）设AB x =，则四棱锥P ABCD -的体积31133P ABCD V AB AD PE x -=⋅⋅=，解得2x =，可得所求侧面积．16．【2017年高考全国Ⅱ卷文数】如图，四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面ABCD ，1,2AB BC AD BAD ==∠90.ABC =∠=︒ （1）证明：直线BC ∥平面PAD ;（2）若△PCD 的面积为27，求四棱锥P ABCD -的体积.【答案】（1）见解析；（2）43.【解析】（1）在平面ABCD 内，因为∠BAD =∠ABC =90°，所以BC ∥AD . 又BC PAD ⊄平面，AD PAD ⊂平面，故BC ∥平面P AD .（2）取AD 的中点M ，连结PM ，CM ，由12AB BC AD ==及BC ∥AD ，∠ABC =90°得四边形ABCM 为正方形，则CM ⊥AD .因为侧面P AD 为等边三角形且垂直于底面ABCD ，平面P AD ∩平面ABCD =AD ，所以PM ⊥AD ，PM ⊥底面ABCD ，因为CM ABCD⊂底面，所以PM⊥CM.设BC=x，则CM=x，CD=2x，PM=3x，PC=PD=2x.取CD的中点N，连结PN，则PN⊥CD，所以142PN x=.因为△PCD的面积为27，所以114227 22x x⨯⨯=，解得x=−2（舍去），x=2，于是AB=BC=2，AD=4，PM=23，所以四棱锥P−ABCD的体积()22412343 32V⨯+=⨯⨯=.【名师点睛】解答本题时，（1）先由平面几何知识得BC∥AD，再利用线面平行的判定定理证得结论；（2）取AD的中点M，利用线面垂直的判定定理证明PM⊥底面ABCD，从而得四棱锥的高，再通过平面几何计算得底面直角梯形的面积，最后代入锥体体积公式即可.垂直、平行关系证明中应用转化与化归思想的常见类型：(1)证明线面、面面平行，需转化为证明线线平行.(2)证明线面垂直，需转化为证明线线垂直.(3)证明线线垂直，需转化为证明线面垂直.17．【2017年高考全国Ⅲ卷文数】如图，四面体ABCD中，△ABC是正三角形，AD=CD．（1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB=BD．若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．【答案】（1）见解析；（2）1:1【解析】（1）取AC的中点O，连结DO，BO.因为AD=CD，所以AC⊥DO.又由于△ABC是正三角形，所以AC ⊥BO . 从而AC ⊥平面DOB ，故AC ⊥BD . （2）连结EO .由（1）及题设知∠ADC =90°，所以DO =AO . 在Rt △AOB 中，222BO AO AB +=.又AB =BD ，所以222222BO DO BO AO AB BD +=+==，故∠DOB =90°. 由题设知△AEC 为直角三角形，所以12EO AC =. 又△ABC 是正三角形，且AB =BD ，所以12EO BD =.故E 为BD 的中点，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，四面体ABCE 的体积为四面体ABCD 的体积的12，即四面体ABCE 与四面体ACDE 的体积之比为1:1.【名师点睛】解答本题时，（1）取AC 的中点O ，由等腰三角形及等边三角形的性质得OD AC ⊥，OB AC ⊥，再根据线面垂直的判定定理得⊥AC 平面OBD ，即得AC ⊥BD ；（2）先由AE ⊥EC ，结合平面几何知识确定12EO AC =，再根据锥体的体积公式得所求体积之比为1:1.垂直、平行关系证明中应用转化与化归思想的常见类型：（1）证明线面、面面平行，需转化为证明线线平行. （2）证明线面垂直，需转化为证明线线垂直. （3）证明线线垂直，需转化为证明线面垂直.18．【2017年高考北京卷文数】如图，在三棱锥P –ABC 中，PA ⊥AB ，PA ⊥BC ，AB ⊥BC ，PA =AB =BC =2，D 为线段AC 的中点，E 为线段PC 上一点．（1）求证：PA ⊥BD ；（2）求证：平面BDE ⊥平面PAC ；（3）当PA ∥平面BDE 时，求三棱锥E –BCD 的体积．【答案】（1）见解析；（2）见解析；（3）13. 【解析】（1）因为PA AB ⊥，PA BC ⊥，所以PA ⊥平面ABC ，又因为BD ⊂平面ABC ，所以PA BD ⊥.（2）因为AB BC =，D 为AC 中点，所以BD AC ⊥，由（1）知，PA BD ⊥，所以BD ⊥平面PAC ，所以平面BDE ⊥平面PAC .（3）因为PA ∥平面BDE ，平面PAC 平面BDE DE =，所以PA DE ∥.因为D 为AC 的中点，所以112DE PA ==，2BD DC ==由（1）知，PA ⊥平面ABC ，所以DE ⊥平面ABC . 所以三棱锥E BCD -的体积1163V BD DC DE =⋅⋅=. 【名师点睛】线线、线面的位置关系以及证明是高考的重点内容，而其中证明线面垂直又是重点和热点，要证明线面垂直，根据判定定理可转化为证明线与平面内的两条相交直线垂直，也可根据性质定理转化为证明面面垂直.解答本题时，（1）要证明线线垂直，一般转化为证明线面垂直；（2）要证明面面垂直，一般转化为证明线面垂直、线线垂直；（3）由13BCD V S DE =⨯⨯△即可求解.19．【2017年高考天津卷文数】如图，在四棱锥P ABCD -中，AD ⊥平面PDC ，AD BC ∥，PD PB ⊥，1AD =，3BC =，4CD =，2PD =．（1）求异面直线AP 与BC 所成角的余弦值；（2）求证：PD ⊥平面PBC ；（3）求直线AB 与平面PBC 所成角的正弦值．【答案】（1）55；（2）见解析；（3）55．【解析】（1）如图，由已知AD //BC ，故DAP ∠或其补角即为异面直线AP 与BC 所成的角．因为AD ⊥平面PDC ，所以AD ⊥PD ．在Rt △PDA 中，由已知，得225AP AD PD =+=，故5cos 5AD DAP AP ∠==．所以，异面直线AP 与BC 所成角的余弦值为55．（2）因为AD ⊥平面PDC ，直线PD ⊂平面PDC ，所以AD ⊥PD ．又因为BC //AD ，所以PD ⊥BC ，又PD ⊥PB ，所以PD ⊥平面PB C ．（3）过点D 作AB 的平行线交BC 于点F ，连结PF ，则DF 与平面PBC 所成的角等于AB 与平面PBC 所成的角．因为PD ⊥平面PBC ，故PF 为DF 在平面PBC 上的射影，所以DFP ∠为直线DF 和平面PBC 所成的角．由于AD //BC ，DF //AB ，故BF =AD =1，由已知，得CF =BC –BF =2．又AD ⊥DC ，故BC ⊥DC ，在Rt △DCF 中，可得2225DF CD CF =+=，在Rt △DPF 中，可得5sin 5PD DFP DF ∠==．所以，直线AB 与平面PBC 所成角的正弦值为55．【名师点睛】线线、线面的位置关系以及证明是高考的重点考查内容，而证明线面垂直又是重点和热点，要证明线面垂直，根据判断定理转化为证明直线与平面内的两条相交直线垂直即可，而线线垂直又可通过线面垂直得到，用几何法求线面角，关键是找到斜线的射影，斜线与其射影所成的角就是线面角．解答本题时，（1）异面直线所成的角一般都转化为相交线所成的角，因为AD BC ∥，所以DAP ∠或其补角即为异面直线AP 与BC 所成的角，本题中AD ⊥PD ，进而可得AP 的长，所以cos ADDAP AP∠=；（2）要证明线面垂直，根据判断定理，证明直线与平面内的两条相交直线垂直即可；（3）根据（2）中的结论，作DF AB ∥，连结PF ，则DFP ∠为直线DF 和平面PBC 所成的角．20．【2017年高考山东卷文数】由四棱柱ABCD −A 1B 1C 1D 1截去三棱锥C 1−B 1CD 1后得到的几何体如图所示，四边形ABCD 为正方形，O 为AC 与BD 的交点，E 为AD 的中点，A 1E ⊥平面ABCD . （1）证明：1A O ∥平面B 1CD 1;（2）设M 是OD 的中点，证明：平面A 1EM ⊥平面B 1CD 1.【答案】（1）见解析；（2）见解析.【解析】（1）取11B D 的中点1O ，连接111,CO AO ，由于1111ABCD A B C D -是四棱柱，所以1111,AO OC AO OC =∥，因此四边形11AOCO 为平行四边形，所以11A O O C ∥，又1O C ⊂平面11B CD ，1AO ⊄平面11B CD ，所以1A O ∥平面11B CD .（2）因为AC BD ⊥，E ，M 分别为AD 和OD 的中点，所以EM BD ⊥，又1A E ⊥平面ABCD ，BD ⊂平面ABCD ，所以1,A E BD ⊥ 因为11,B D BD ∥所以11111,,EM B D A E B D ⊥⊥ 又1,A E EM ⊂平面1A EM ，1A E EM E =，所以11B D ⊥平面1,A EM 又11B D ⊂平面11B CD ，所以平面1A EM ⊥平面11B CD .【名师点睛】证明线面平行时，先直观判断平面内是否存在一条直线和已知直线平行，若找不到这样的直线，可以考虑通过面面平行来推导线面平行，应用线面平行性质的关键是如何确定交线的位置，有时需要经过已知直线作辅助平面来确定交线．在应用线面平行、面面平行的判定定理和性质定理进行平行转化时，一定要注意定理成立的条件，严格按照定理成立的条件规范书写步骤，如把线面平行转化为线线平行时，必须说清经过已知直线的平面与已知平面相交，则直线与交线平行．-中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E，21．【2017年高考江苏卷】如图，在三棱锥A BCDF(E与A，D不重合)分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【答案】（1）见解析；（2）见解析.⊥，【解析】（1）在平面ABD内，因为AB⊥AD，EF AD∥．所以EF AB又因为EF⊄平面ABC，AB⊂平面ABC，所以EF∥平面ABC．⊥，（2）因为平面ABD⊥平面BCD，平面ABD平面BCD=BD，BC⊂平面BCD，BC BD所以BC⊥平面ABD．因为AD⊂平面ABD，所以BC⊥AD．=，AB⊂平面ABC，BC⊂平面ABC，又AB⊥AD，BC AB B所以AD⊥平面ABC，又因为AC⊂平面ABC，所以AD⊥AC．【名师点睛】垂直、平行关系证明中应用转化与化归思想的常见类型：（1）证明线面、面面平行，需转化为证明线线平行；（2）证明线面垂直，需转化为证明线线垂直；（3）证明线线垂直，需转化为证明线面垂直．22．【2017年高考浙江卷】如图，已知四棱锥P–ABCD，△PAD是以AD为斜边的等腰直角三角形，BC AD∥，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．（1）证明：CE ∥平面PAB ；（2）求直线CE 与平面PBC 所成角的正弦值．【答案】（1）见解析；（2）8．【解析】本题主要考查空间点、线、面位置关系，直线与平面所成的角等基础知识，同时考查空间想象能力和运算求解能力.满分15分.（1）如图，设P A 中点为F ，连接EF ，FB ．因为E ，F 分别为PD ，P A 中点，所以EF AD ∥且12EF AD =，又因为BC AD ∥，12BC AD =，所以 EF BC ∥且EF BC =，即四边形BCEF 为平行四边形，所以CE BF ∥，因此CE ∥平面P AB ．（2）分别取BC ，AD 的中点为M ，N ．连接PN 交EF 于点Q ，连接MQ ．因为E ，F ，N 分别是PD ，P A ，AD 的中点，所以Q 为EF 中点，在平行四边形BCEF 中，MQ//CE ．由△P AD 为等腰直角三角形得PN ⊥AD ．由DC ⊥AD ，N 是AD 的中点得BN ⊥AD ．PABCDE所以AD⊥平面PBN，由BC//AD得BC⊥平面PBN，那么平面PBC⊥平面PBN．过点Q作PB的垂线，垂足为H，连接MH．MH是MQ在平面PBC上的射影，所以∠QMH是直线CE与平面PBC所成的角．设CD=1．在△PCD中，由PC=2，CD=1，PD=2得CE=2，在△PBN中，由PN=BN=1，PB=3得QH=14，在Rt△MQH中，QH=14，MQ=2，所以sin∠QMH=28，所以直线CE与平面PBC所成角的正弦值是28．【名师点睛】本题主要考查线面平行的判定定理、线面垂直的判定定理及面面垂直的判定定理，属于中档题．证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行．②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面．本题（1）是就是利用方法①证明的．另外，本题也可利用空间向量求解线面角．。

坐标法解立体几何

（一）本周学习与研究中的三个重点1、空间右手直角坐标系及其在空间右手直角坐标系下的向量坐标运算．空间直角坐标系是在仿射坐标系的基础上，选取空间任意一点O和一个单位正交基底{}（按右手系排列）建立的坐标系．具体选择坐标系时，注意O点的任意性，一方面既要有利于作图的直观性，另一方面又要注意有关要求点的坐标容易表示．在空间右手直角坐标系下的点，向量坐标是唯一的，这一点的理解和证明可仿照向量分解定理的唯一性理解和证明．由此说明相等的向量其坐标是唯一的，这为后面的解题中常常需要进行向量的平移提供理论依据．空间向量的坐标运算，加法、减法和数量积等与平面向量类似，具有类似的运算法则，同学们学习中可类比的学习．虽然一个向量在不同空间的表达方式不同，但其实质没变，即向量在平面上是用唯一确定的有序实数对表示，即=(x,y)，而在空间则用唯一确定的有序实数组表示，即=(x,y,z)．如向量的数量积在二维、三维空间都是这样定义的．不同点仅是向量在不同空间具有不同的表达形式．如在平面上,,在空间=(a,a2,a3), ，不论在平面或空间都有．12、空间两向量平行、垂直的充要条件空间两向量平行时与平面两向量平行的表达式不一样，但实质是一致的，即对应坐标成比例，且比值为λ，空间两向量垂直的充要条件形式与平面向量里类似，仅多了一项基向量而已．3、空间两向量的夹角公式，距离公式，中点坐标公式（1）（2）（3）为AB的中点，则由可知夹角公式在平面向量正文里没有涉及，但可根据数量积的定义推出．这里应注意两向量夹角范围是：0°≤θ≤180°，当θ=0°时，表示两向量为同向共线向量，当θ=90°时，表示两向量垂直，当θ=180°时，表示两向量为反向共线向量．两点间的距离公式是长度公式的推广．其推导过程是首先根据向量的减法，推出向量的坐标表示，然后再用长度公式推出．这几个公式都与坐标原点的选取无关．（二）本周学习与研究中的两个难点1、空间任意一点的坐标确定空间任一点P的坐标确定办法如下：过P分别作三个坐标平面的平行平面（或垂面），分别交坐标轴于A、B、C三点，|x|=OA，|y|=OB，|z|=OC，当方向相同时，x>0，反之x<0，同理，可确定y、z．具体理解，可以以长方体作为模型，以其一共点的三条棱，建立空间直角坐标系来理解．这其中同学们应准确判断一点在各坐标平面内的射影的坐标，并比较它们间的关系，以及一些特殊点，如落在坐标轴上的点的坐标形式等．2、距离公式，夹角公式的应用应用距离公式、夹角公式解决立体几何问题，关键在于选择建立适当的空间直角坐标系．它们在立体几何中的应用有：计算两异面直线所成角时，当用几何方法较困难时，可以建立适当的空间直角坐标系后，利用向量方法求解，此时应注意异面直线所成的角的范围与向量夹角范围的区别；求线段的长度时，有时用几何方法较难构造三角形，此时，可考虑应用向量方法，表示出线段两端点的坐标，然后再用两点间的距离加以解决．。

解答立体几何问题的常用方法

备考指南立体几何问题侧重于考查同学们的空间想象、逻辑推理以及运算能力.求解立体几何问题的常用方法主要有几何法和向量法.掌握并合理运用这两种解题方法，有利于迅速找到解题的思路.下面结合实例，谈一谈解答立体几何问题的常用方法.一、几何法几何法是解答立体几何问题的常用方法，也是比较重要的方法.在运用几何法求解立体几何问题时，要根据空间中点、线、面之间的位置关系，寻找平行、垂直关系，灵活运用立体几何中的定义、公理、判定定理和性质定理来分析、解答问题.例1.如图1所示，已知四棱锥P-ABCD的底面ABCD是边长为3的菱形，PD=3,PA=PC=23，点Q是PD的中点.（1）求证：直线PB∥平面ACQ；（2）求证：平面PAD⊥平面ABCD.证明：（1）连接BD交AC于点O，连接OQ，根据菱形ABCD的性质可知O为BD的中点，因为Q是PD的中点，所以OQ是ΔPBD的中位线，可得OQ∥PB.又OQ⊂平面ACQ，PB⊄平面ACQ，由线面平行的判定定理得PB∥平面ACQ.（2）在ΔPAD中，PD2+DA2=32+(3)2=12=(23)2 =PA2，所以PD⊥DA.同理可证PD⊥DC.因为DA⋂DC=D，由线面垂直的判定定理得PD⊥平面ABCD.因为PD⊂平面PAD，所以由面面垂直的判定定理得平面PAD⊥平面ABCD.在解答立体几何中有关线线、线面、面面平行和垂直的问题时，往往需要首先根据图形理清点、线、面之间的位置关系，然后运用线线、线面、面面平行和垂直的定义、判定定理、性质定理来解题.对于第一个问题，需首先想到运用线面平行的判定定理；对于第二个问题，要证明面面垂直，往往需先想到运用面面垂直的判定定理，则需根据线面垂直的判定定理证明线面垂直，只需根据勾股定理证明线线垂直.二、向量法1.基底法基底法是指根据向量的基本定理，将各个向量用基底表示出来，通过向量运算来解题.运用基底法解题，需先根据立体几何图形的特点和位置关系，选择一组合适的向量，将其作为基底，再根据向量的基本定理，将各个向量用基底表示出来，利用向量的数量积公式、模的公式、共线定理等进行求解.例2.已知正四面体ABCD的各条棱长均为1，点E、F分别是BC、AD的中点，则AE∙CF=（）. A.0 B.12 C.1 D.-12解：如图2所示，设向量AB=a ,AC=b , AD=c ，因为正四面体的各条棱长均为1，所以a ∙b =a ∙c =b ∙c =1×1×cos60°=12，且||||b 2=1.因为点E、F分别是BC、AD的中点，所以AE=a +b 2， CF=-b +c 2，所以AE∙CF=æèçöø÷a +b 2∙æèçöø÷-b +c 2=-12a ∙b +14a ∙c -12||||b 2+14b ∙c=-12×12+14×12-12×1+14×12=-12.故本题选D.以AB=a 、AC=b 、 AD=c 为基底，并用这些基底将AE、CF表示出来，即可根据向量的数量积公式，求得AE∙CF的表达式及值.运用基底法解题的关键在于根据题意和图形的特点，选取合适的基底.图1图2552.坐标法有些立体几何问题中的图形为特殊图形，如正方体、直棱柱、长方体、正棱锥、圆锥、圆柱等，此时可采用坐标法求解.首先要根据这些图形的特点，找到两条或三条垂直且交于一点的直线，将其作为坐标轴，建立空间直角坐标系；然后求得相关点的坐标、直线的方向向量以及平面的法向量，通过向量的坐标运算求得问题的答案.若用a 、b 表示直线a 、b 的方向向量，用m 、n 表示平面α、β的法向量，则（1）直线a 、b 所成角的余弦值为：cos θ=||||||cos a ,b =||||||||||a ∙b ||a ||||b ；（2）直线a 与平面α所成角的正弦值为：sin θ=||cos a,m =||||||||a∙m ||a ||m ；（3）平面α、β的二面角的余弦值为：cos θ=cos m ,n =m ∙n ||m ||n 或cos θ=-cos m ,n =-m ∙n ||m ||n （依平面角与法向量夹角的大小而定）；（4）若A 为平面α外一点，P 为平面α上任意一点，则A 到平面α的距离为：d =|||||||| AP ∙n ||n.例3.据《九章算术》中的记载可知，堑堵是底面为直角三角形，侧棱垂直于底面的三棱柱；阳马是底面为矩形，一条侧棱垂直于底面的四棱锥；鳖臑是四个面均为直角三角形的四面体.如图3，在堑堵ABC -A 1B 1C 1中，AC ⊥BC .（Ⅰ）求证：四棱锥B -A 1ACC 1为阳马，并判断四面体A 1-CBC 1是否为鳖臑，若是，请写出各个面的直角（只写出结论）；（Ⅱ）若A 1A =AB =2，当阳马B -A 1ACC 1的体积最大时，求二面角C -A 1B -C 1的余弦值.图3解：(Ⅰ)由堑堵ABC -A 1B 1C 1的定义知A 1A ⊥底面ABC ，所以BC ⊥A 1A ，因为BC ⊥AC ，A 1A ⋂AC =A ，所以BC ⊥平面A 1ACC 1.由堑堵ABC -A 1B 1C 1的定义知，四边形A 1ACC 1为矩形，因此四棱锥B -A 1ACC 1为阳马.易知四面体A 1-CBC 1为鳖臑，四个面的直角分别是∠A 1CB ,∠A 1C 1C ,∠BCC 1,∠A 1C 1B .（Ⅱ）因为A 1A =AB =2，由（Ⅰ）知阳马B -A 1ACC 1的体积为V =13S 矩形A 1ACC 1∙BC =13×A 1A ×AC ×BC =23AC ×BC≤13(AC 2+BC 2)=13×AB 2=43，所以当AC =BC =2时，V max =43，此时直线CA ,CB ,CC 1两两互相垂直，可建立如图4所示的空间直角坐标系C -xyz .易知点C (0,0,0),B (0,2,0),A 1(2,0,2),C 1(0,0,2)，所以 CA 1=(2,0,2),CB =(0,2,0),BA 1=(2,-2,2)，BC 1=(0,-2,2).设平面CA 1B 的法向量为n =(x ,y ,z )，则ìíîn ∙CA 1=0，n ∙ CB =0，可得ìíî2x +2z =0，2y =0，令x =2，则z =-1,y =0，则n =(2,0,-1)；同理可得平面C 1A 1B 的一个法向量m =(0,2,1).所以cos <n ,m >=n ∙m ||n ||m =-13×3=-13.由图4知，二面角C -A 1B -C 1为锐二面角，故二面角C -A 1B -C 1的余弦值为13.利用坐标法求解有关夹角或距离问题，关键是建立合适的空间直角坐标系.通常要使更多的点落在坐标轴上，这样便于计算.有时可通过添加辅助线来画出其中的一条坐标轴.相比较而言，几何法和基底法的适用范围较广，对于大部分的题目，都可以采用几何法和基底法求解；而坐标法的适用范围较窄，只适用于求解方便建立空间直角坐标系的题目.但运用坐标法求解立体几何问题较为便捷，只需通过简单的向量运算即可.（作者单位：安徽省宁国市宁国中学）备考指南图456。

立体几何解答题

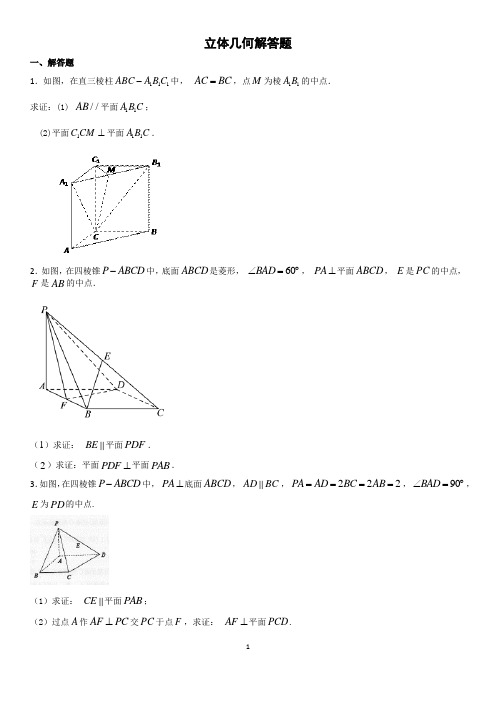
立体几何解答题一、解答题1．如图，在直三棱柱111ABC A B C -中， AC BC =，点M 为棱11A B 的中点．求证：(1) //AB 平面11A B C ；(2)平面1C CM ⊥平面11A B C ．2．如图，在四棱锥P ABCD -中，底面ABCD 是菱形， 60BAD ∠=︒， PA ⊥平面ABCD ， E 是PC 的中点， F 是AB 的中点．（1）求证： BE 平面PDF ．（2）求证：平面PDF ⊥平面PAB ．3．如图，在四棱锥P ABCD -中， PA ⊥底面ABCD ， AD BC ， 222PA AD BC AB ====， 90BAD ∠=︒， E 为PD 的中点.（1）求证： CE 平面PAB ；（2）过点A 作AF PC ⊥交PC 于点F ，求证： AF ⊥平面PCD .4．如图，平行四边形ABCD 中，，将BCD ∆沿BD 折起到EBD ∆的位置，使平面EBD ⊥平面ABD .（1）求证： AB DE ⊥（2）求三棱锥E ABD -的侧面积.5．如图，正方体1111ABCD A B C D -中， ,E F 分别是1,BB CD 的中点.（1）求证： 1D F ⊥平面ADE ；（2）求异面直线EF 与1BD 所成角的余弦值.6．如图，三棱锥A BPC -中，,，为中点，为PB 中点，且PMB ∆为正三角形。

（Ⅰ）求证： DM //平面APC ；（Ⅱ）求证： BC ⊥平面APC ；（Ⅲ）若4BC =, 10AB =，求三棱锥D BCM -的体积。

7．如图所示，在四棱锥P ABCD -中，底面ABCD 是矩形，侧棱PA ⊥平面ABCD ， E 、F 分别是AB ， PC 的中点， PA AD =．求证：（1）EF 平面PAD ．（2）EF ⊥平面PCD ．8．如图，在四棱锥P −ABCD 中,AB ⊥平面PAD ,DC//AB ，DC =2AB ,E 为棱PA 上一点.（1）设O 为AC 与BD 的交点, 若PE =2AE , 求证:OE//平面PBC ；（2）若DE ⊥AP , 求证：PB ⊥DE ．9．如图，在直三棱柱111ABC A B C -中， AC BC ⊥，点D 是AB 的中点．求证：（1）1AC BC ⊥；（2）1//AC 平面1B CD ．10．如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点，求证：PA平面BDE；（1）//（2）BD⊥平面PAC.11．如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点.(1) 证明：AE⊥平面PCD；(2) 求PB和平面PAD所成的角的大小.12．如图在正方体中ABCD−A1B1C1D1中，（1）求异面直线BC1与CD1所成的角；（2）求直线D1B与底面ABCD所成角的正弦值；（3）求二面角D1−AC−D大小的正切值.参考答案1．（1）见解析（2）见解析【解析】试题分析：（1）AB 与平面11A B C 内的11A B 平行，所以//AB 平面11A B C .（2）通过证明1CC ⊥ 11A B ， 1C M ⊥ 11A B 可得11A B ⊥平面1C CM ．结合11A B ⊂平面11A B C ，可得平面1C CM ⊥平面11A B C ．试题解析：（1）在三棱柱111ABC A B C -中， 11//AB A B ，又AB ⊄平面11A B C ， 11A B ⊂平面11A B C ，所以//AB 平面11A B C ．（2）在直三棱柱111ABC A B C -中， 1CC ⊥平面111A B C ，又11A B ⊂平面111A B C ，所以1CC ⊥ 11A B ．因为AC BC =，所以1111AC B C =．又因为点M 为棱11A B 的中点，所以1C M ⊥ 11A B ．又1CC ⋂ 11C M C =， 1CC ， 1C M ⊂平面1C CM ，所以11A B ⊥平面1C CM ．又11A B ⊂平面11A B C ，所以平面1C CM ⊥平面11A B C ．点睛：本题第一问考查的是直线与平面平行的判定。

二轮复习第34讲利用坐标法解决立体几何的角度与距离问题

第34讲利用坐标法解决立体几何的角度与距离问题一．选择题(共1小题)1．(2021•南岗区校级期中)如图，三棱锥A -BCD 中，∠DAB =∠DAC =∠BAC =90°，AB =AD =AC =1，M ，N 分别为CD ，BC 的中点，则异面直线AM 与DN 所成角余弦值为( )A ．16B ．36C ．56D ．56【解答】解：三棱锥A -BCD 中，∠DAB =∠DAC =∠BAC =90°，建立空间直角坐标系，如图所示：由于AB =AD =AC =1，M ，N 分别为CD ，BC 的中点，所以A (0，0，0)，M 0,12,12 ，D (0，0，1)，N 12,12，0 ，则AM =0,12,12 ，DN =12,12,-1 ，所以异面直线AM 与DN 所成角余弦值cos θ=AM ∙DN |AM ||DN |=36．故选：B ．二．解答题(共21小题)2．(2021•凉山州模拟)如图，在四棱锥P -ABCD 中，底面为直角梯形，AD ⎳BC ，∠BAD =90°，PA ⊥底面ABCD ，且PA =AD =AB =2BC ，M 、N 分别为PC ，PB 的中点．(1)求证：PB ⊥DM ；(2)求二面角A -MD -C 的正弦值．【解答】解：(1)证明：∵PA ⊥面ABCD ，AD ⊂面ABCD ，∴AD ⊥PA ，∵∠BAD =90°，∴AD ⊥AB ，PA ∩AB =A ，PA ，AB ⊂面PAB ，∴AD ⊥面PAB ，∵PB ⊂面PAB ，∴AD ⊥PB ，又ΔPAB 中，AP =AB ，N 为PB 的中点，∴AN ⊥PB ，AN ∩AD =A ，AN ，AD ⊂平面AND ，∴PB ⊥面AND ，又N ，M 分别为PB ，PC 的中点，∴MN ⎳BC ，BC ⎳AD ，∴MN ⎳AD ，∵N ∈面AND ，∴M ∈面AND ，∴MN ⊂面AND ，∴PB ⊥DM ．(2)解：以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴，建立空间直角坐标系，设PA =AD =AB =2BC =2，则A (0，0，0)，P (0，0，2)，C (2，1，0)，D (0，2，0)，M 1，12，1，设面AMD 的法向量m =(x ，y ，z )，AD =(0，0，2)，AM =1，12，1 ，AD ∙m =2y =0AM ∙m =x +12y +z =0 ，取x =1，得m =(1，0，-1)，设面CMD 的法向量n =(x ，y ，z )，DC =(2，-1，0)，DM =1，-32，1 ，DC ∙n =2x -y =0DM ∙n =x -32y +z =0，取x =1，得n =(1，2，2)，cos <m ,n >=m ∙n |m |∙|n |=-132，∴二面角A -MD -C 的正弦值为：1--132 2=346．3．(2021•荔湾区校级期末)如图，在平行四边形ABCD 中，AB =2BC ，∠ABC =120°，E 为线段AB 的中点，将ΔADE 沿在直线DE 翻折成△A DE ，使平面A DE ⊥平面BCD ，F 为线段A C 的中点．(1)求证：BF ⎳平面A DE ．(2)设M 为线段DE 的中点，求直线FM 与平面A DE 所成角的大小．(3)若BC =2，求三棱锥A -DEF 的体积．【解答】解：(1)证明：取CD 中点G ，连结GF ，BG ，∵在平行四边形ABCD 中，AB =2BC ，∠ABC =120°，E 为线段AB 的中点，将ΔADE 沿在直线DE 翻折成△A DE ，使平面A DE ⊥平面BCD ，∴GF ⎳A ′D ，BG ⎳DE ，∵GF ∩BG =G ，A ′D ∩DE =D ，∴平面A ′DE ⎳平面BGF ，∵BF ⊂BGF ，∴BF ⎳平面A DE ．(2)解：取CD 中点G ，连结EG 、AG 、DE ，A ′M ，设BC =2，则四边形AEGD 是边长为2的菱形，且∠DAE =60°，∴MA ⊥ME ，∵由平面A DE ⊥平面BCD ，F 为线段A C 的中点．∴A ′M ⊥平面AEGD ，以M 为原点，MA 为x 轴，ME 为y 轴，MA ′为z 轴，建立空间直角坐标系，则M (0，0，0)，A ′(0，0，3)，D (0，-1，0)，C (-23，1，0)，F -3，12，32 ，FM =3，-12，-32，平面A ′DE 的法向量m =(1，0，0)，设直线FM 与平面A DE 所成角为θ，则sin θ=|FM ∙n ||FM |∙|n |=32，∴θ=60°．∴直线FM 与平面A DE 所成角的大小为60°．(3)解：∵BC =2，∴由(2)得F -3，12,32 ，平面A ′DE 的法向量m =(1，0，0)，∵MF =-3,12,32 ，∴点F 到平面A ′DE 的距离d =|MF ∙m ||m |=3．∵S △A ′DE =12×2×3=3，∴三棱锥A -DEF 的体积：V A ′-DEF =V F -A ′DE =13×3×3=1．4．(2021•和平区校级月考)如图，四棱锥P -ABCD 中，ΔPAD 是以AD 为斜边的等腰直角三角形，BC ⎳AD ，CD ⊥AD ，PC =AD =2DC =2CB =2，E 为PD 的中点．(1)证明：CE ⎳平面PAB ；(2)求直线CE 与平面PAB 间的距离．【解答】(1)证明：取PA 的中点M ，连接BM 、EM ，∵E 为PD 的中点，∴EM ⎳AD ，EM =12AD =BC ，∴四边形BCEM 为平行四边形，∴CE ⎳BM ，∵CE ⊄平面PAB ，BM ⊂平面PAB ，∴CE ⎳平面PAB ．(2)解：∵CE ⎳平面PAB ，∴点E 到平面PAB 的距离即为所求．PC =AD =2DC =2CB =2，取AD 的中点N ，连接BN 、PN ，则四边形BCDN 为矩形，BN =CD =1∵ΔPAD 是以AD 为斜边的等腰直角三角形，∴PN ⊥AD ，PN =12AD =1，∵BN ⊥AD ，PN ∩BN =N ，PN 、BN ⊂平面PNB ，∴AD ⊥平面PNB ，∵BC ⎳AD ，∴BC ⊥平面PNB ，∵BC ⊂平面ABCD ，∴平面ABCD ⊥平面PNB ，以B 为原点，BC 、BN 分别为x 、y 轴，在平面PNB 内，作Bz ⊥平面ABCD ，建立如图所示的空间直角坐标系，则B (0，0，0)，A (1，-1，0)，D (1，1，0)∵BC ⊥平面PNB ，∴BC ⊥PB ，在Rt ΔPBC 中，PB =PC 2-BC 2=22-12=3，∵BN =PN =1，∴∠PNB =120°，∴点P 32，0，32 ，E 54，12，34 ，∴BP =32，0，32 ，BA =(1，-1，0)，BE =54，12，34 ，设平面PAB 的法向量为n =(x ，y ，z )，则n ⋅BP =0n ⋅BA =0 ，即32x +32z =0x -y =0，令x =1，则y =1，z =-3，∴n =(1，1，-3)，∴点E 到平面PAB 的距离d =n ⋅BE |n |=54+12-3×341+1+3=55，故直线CE 与平面PAB 间的距离为55．5．(2021•沙坪坝区校级月考)如图，在四棱锥P -ABCD 中，ΔPAD 是以AD 为斜边的等腰直角三角形，BC ⎳AD ，CD ⊥AD ，PC =3，AD =2DC =2CB =2，E 为PD 上一点．(1)若E 为PD 的中点，证明：CE ⎳平面PAB ；(2)若直线CE 与底面ABCD 所成角的正弦值为1111，求二面角P -AB -E 的正弦值．【解答】(1)证明：取线段PA 的中点M ，连结EM ，BM ，因为线段PD 的中点为E ，线段PA 的中点为M ，所以EM ⎳AD 且EM =12AD ，又四边形ABCD 中，BC ⎳AD ，AD =2BC ，所以EM ⎳BC ，EM =BC ，所以四边形BCEM 为平行四边形，所以CE ⎳BM ，因为BM ⊂平面PAB ，CE ⊄平面PAB ，所以CE ⎳平面PAB ；(2)解：已知ΔPAD 是以AD 为斜边的等腰直角三角形，AD =2，所以PD =2，因为PC =3,CD =1，所以PC 2=PD 2+CD 2，由勾股定理的逆定理可得，CD ⊥PD ，又CD ⊥AD ，AD ∩PD =D ，AD ，PD ⊂平面PAD ，所以CD ⊥平面PAD ，因为CD ⊂平面ABCD ，所以平面ABCD ⊥平面PAD ，取AD 的中点O ，连结PO ，OB ，则PO ⊥AD ，又PO ⊂平面PAD ，平面ABCD ∩平面PAD =AD ，所以PO ⊥平面ABCD ，四边形ABCD 中，BC ⎳AD ，AD =2BC ，所以四边形BCDO 是平行四边形，所以BO ⎳CD ，BO =CD ，所以BO ⊥AD ，以O 为坐标原点，以OB ，OD ，OP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系如图所示，所以A (0，-1，0)，B (1，0，0)，C (1，1，0)，D (0，1，0)，P (0，0，1)，则DP =(0,-1,1),CD =(-1,0,0)，设DE =λDP =(0,-λ,λ),λ∈(0,1)，所以CE =CD +DE =(-1,-λ,λ)，平面ABCD 的法向量可取n =(0,0,1)，因为直线CE 与底面ABCD 所成角的正弦值为1111，所以1111=CE ⋅n |CE ||n | ，即1111=|λ|1+2λ2，解得λ=13，所以CE =-1,-13,13 ，则E 0,23,13 ，所以AE =0,53,13 ,AB =(1,1,0)，设平面ABE 的法向量为m =(x ,y ,z )，所以m ⋅AE =0m ⋅AB =0 ，所以53y +13z =0x +y =0，令y =1，则x =-1，z =-5，所以m =(-1,1,-5)，又AP =(0,1,1)，设平面PAB 的法向量为p =(a ,b ,c )，则有p ⋅AP =0p ⋅AB =0，所以b +c =0a +b =0 ，令b =1，则c =-1，a =-1，所以p =(-1,1,-1)，所以cos <m ,p >=m ⋅p |m ||p |=79，所以sin <m ,p >=1-cos 2<m ,p >=429，所以二面角P -AB -E 的正弦值为429．6．(2021•江苏一模)如图，在四棱锥P -ABCD 中，ΔPAD 是以AD 为斜边的等腰直角三角形，BC ⎳AD ，AB ⊥AD ，AD =2AB =2BC =2，PC =2，E 为PD 的中点．(1)求直线PB 与平面PAC 所成角的正弦值；(2)设F 是BE 的中点，判断点F 是否在平面PAC 内，并请证明你的结论．【解答】解：(1)取AD 中点O ，连接OP 、OC ，ΔPAD 是以AD 为斜边的等腰直角三角形，所以OP ⊥AD ，OP =OA =OD =1，因为BC ⎳AD ，AB ⊥AD ，AD =2AB =2BC =2，所以四边形ABCO 为边长为1的正方形，所以OC ⊥AD ，又因为PC =2，所以PC 2=OP 2+OC 2，所以PO ⊥OC ，所以OA 、OC 、OP 两两垂直，建立如图所示的空间直角坐标系，A (1，0，0)，B (1，1，0)，C (0，1，0)，P (0，0，1)，平面PAC 的法向量为n =(1，1，1)，PB =(1，1，-1)，所以直线PB 与平面PAC 所成角的正弦值为|PB ⋅n ||PB |⋅|n |=13⋅3=13．(2)连接AF ，D (-1，0，0)，E -12，0，12 ，F 14，12，14 ，AF =-34，12，14 ，点F 到平面PAC 的距离为|AF ⋅n ||n |=03=0，所以点F 在平面PAC 内．7．(2021•房山区一模)如图，四棱锥P -ABCD 中，ΔPAD 是以AD 为斜边的等腰直角三角形，PD =CD =2，PC =2，BC =//12AD ，CD ⊥AD ．(Ⅰ)求证：CD ⊥平面PAD ；(Ⅱ)若E 为PD 中点，求CE 与面PBC 所成角的正弦值；(Ⅲ)由顶点C 沿棱锥侧面经过棱PD 到顶点A 的最短路线与PD 的交点记为F ．求该最短路线的长及PF FD的值．【解答】(Ⅰ)证明：∵PD =CD =2，PC =2，∴CD 2+PD 2=PC 2，∴CD ⊥PD ，又∵CD ⊥AD ，PD ∩AD =D ，∴CD ⊥平面PAD ．(Ⅱ)解：取AD 的中点O ，连接OP ，OB ，∵PA =PD ，∴PO ⊥AD ．∵CD ⊥平面PAD ，PO ⊂平面PAD ，∴PO ⊥CD ，又AD ∩CD =D ，∴PO ⊥平面ABCD ，∵BC =//12AD ，CD ⊥AD ．∴四边形BCDO 是矩形，∴OB ⊥OD ．以点O 为坐标原点建立空间直角坐标系O -xyz ，如图所示则C (2,1,0)，P (0，0，1)，D (0，1，0)，B (2,0,0)，E 0，12，12 ，∴CE =-2,-12,12 ，PB =(2,0,-1),BC =(0,1,0)，设面PBC 的法向量n =(x ,y ,z )，则n ⋅PB =0n ⋅BC =0 ，即2x -z =0y =0，令x =1可得n =(1，0，2)．∴cos <CE ,n >=CE ⋅n |CE ||n |=-2252⋅3=-1515．设CE 与面PBC 所成角为θ，∴sin θ=|cos <CE , n >|=1515．(Ⅲ)解：∵CD ⊥平面PCD ，PD ⊂面PAD ，∴CD ⊥PD ，∴ΔPDC 为等腰直角三角形，作出平面APD 和平面PCD 的侧面展开图，如图所示：连接AC 交PD 于F ，则AC 为最短路线，∵∠APD =∠PDC =90°，∴AP =//DC ，∴四边形ADC ′P 为平行四边形，∴F 与E 重合，∴最短路线长为2AF =2AP 2+PF 2=2×102=10，此时PF FD =1．8．(2021春•湖北期末)如图，四棱锥S -ABCD 中，AB ⎳CD ，BC ⊥CD ，侧面SAB 为等边三角形，AB =BC =4，CD =SD =2．(1)求证：SD ⊥AB ；(2)求AB 与平面SBC 所成的角的正弦值．【解答】解：(1)证明：∵四棱锥S -ABCD 中，AB ⎳CD ，BC ⊥CD ，侧面SAB 为等边三角形，AB =BC =4，CD =SD =2．∴AD =42+(4-2)2=25，SA =AB =4，∴SA 2+SD 2=AD 2，∴SD ⊥SA ，同理得SD ⊥SB ，∵SA ∩SB =S ，∴SD ⊥平面SAB ，∵AB ⊂平面SAB ，∴SD ⊥AB ．(2)解：以D 为原点，在平面ABCD 内过D 作DC 的垂线为x 轴，DC 为y 轴，过D 作平面ABCD 的垂线为z 轴，建立空间直角坐标系，A (4，-2，0)，B (4，2，0)，C (0，2，0)，S (1，0，3)，CB =(4，0，0)，CS =(1，-2，3)，AB =(0，4，0)，设平面SBC 的一个法向量是n =(x ，y ，z )，则n ⋅CB =4x =0n ⋅CS =x -2y +3z =0，取z =2，得n =(0，3，2)，设AB 与平面SBC 所成的角为θ，则sin θ=|n ⋅AB ||n |⋅|AB |=437⋅4=217．∴AB 与平面SBC 所成的角的正弦值为217．9．(2021•天山区校级期末)如图，在三棱锥P -ABC 中，AB ⊥BC ，AB =BC =12PA ，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ．(1)求证：OD ⎳平面PAB ；(2)求直线OD 与平面PBC 所成角的正弦值．【解答】证明：(1)∵点O ，D 分别是AC ，PC 的中点，∴OD ⎳PA又∵OD ⊄平面PAB ，PA ⊂平面PAB ∴OD ⎳平面PAB ；(2)连接OB ，∵AB =BC ，点O 是AC 的中点，∴OB ⊥AC又∵OP ⊥底面ABC ．故可以O 为坐标原点，建立如图所示的空间直角坐标系令AB =BC =12PA =1，AB ⊥BC ，则OA =OB =OC =22，OP =142则O (0，0，0)，B 22，0，0 ，C 0，22，0 ，P 0，0，142 ，D 0，24，144 ∴OD =0，24，144 ，BC =-22，22，0 ，PC =0，22，-142 设m=(x ，y ，z )是平面PBC 的一个法向量则m ∙BC =0m ∙PC=0，即-22x +22y =022y -142z =0令z =1，则m=(7，7，1)直线OD 与平面PBC 所成角θ满足：sin θ=|m ∙OD ||m |∙|OD |=21030故直线OD 与平面PBC 所成角的正弦值为2103010．(2012秋•小店区校级月考)如图，四边形ABCD中(图1)，E是BC的中点，DB=2，DC=1，BC=5，AB=AD=2．将(图1)沿直线BD折起，使二面角A-BD-C为60°(如图2)(1)求证：AE⊥平面BDC；(2)求异面直线AB与CD所成角的余弦值；(3)求点B到平面ACD的距离．【解答】解：(1)如图1取BD中点M，连接AM，ME．因AB=AD=2．∴AM⊥BD(3)⋯(1分)因DB=2，DC=1，BC=5满足：DB2+DC2=BC2，所以ΔBCD是BC为斜边的直角三角形，BD⊥DC，因E是BC的中点，所以ME为ΔBCD的中位线ME// 12CD，∴ME⊥BD，ME=12⋯(2分)∴∠AME是二面角A-BD-C的平面角，∴∠AME=60°⋯(3分)∵AM⊥BD，ME⊥BD且AM、ME是平面AME内两相交于M的直线∴BD ⊥平面AEM ∵AE ⊂平面AEM ，∴BD ⊥AE ⋯(4分)因AB =AD =2．，DB =2，∴ΔABD 为等腰直角三角形，∴AM =12BD =1，AE 2=AM 2+ME 2-2AM ∙ME ∙cos ∠AME =1+14-2×1×12×cos60°=34∴AE=32∴AE 2+ME 2=1=AM 2，∴AE ⊥ME ⋯(6分)∴BD ∩ME ，BD ⊂面BDC ，ME ⊂面BDC ，∴AE ⊥平面BDC ⋯(7分)(2)如图2，以M 为原点MB 为x 轴，ME 为y 轴，建立空间直角坐标系，(8分)则由(1)及已知条件可知B (1，0，0)，E 0,12,0 ，A 0,12,32 ，D (-1，0，0)，C (-1，1，0)，AB =1,-12,-32,CD =(0,-1,0)，⋯(9分)设异面直线AB 与CD 所成角为θ，则cos θ=AB ∙CD|AB | ∙|CD |⋯(10分)=122×1=24．⋯(11分)(3)由AD =-1,-12,-32,CD =(0,-1,0)，可知n =(3,0,-2)满足，n ∙AD =0,n ∙CD =0，n是平面ACD 的一个法向量，⋯(12分)记点B 到平面ACD 的距离d ，则AB 在法向量n方向上的投影绝对值为d则d =AB ∙n|n|⋯(13分)，所以d =3+0+3(3)2+0+(-2)2=2217⋯(14分)11．(2010•浙江)如图，在矩形ABCD 中，点E ，F 分别在线段AB ，AD 上，AE =EB =AF =23FD =4．沿直线EF 将ΔAEF 翻折成△A ′EF ，使平面A ′EF ⊥平面BEF ．(Ⅰ)求二面角A ′-FD -C 的余弦值；(Ⅱ)点M ，N 分别在线段FD ，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使C 与A ′重合，求线段FM 的长．【解答】解：(Ⅰ)取线段EF 的中点H ，连接A ′H ，因为A ′E =A ′F 及H 是EF 的中点，所以A ′H ⊥EF ，又因为平面A ′EF ⊥平面BEF ．如图建立空间直角坐标系A -xyz 则A ′(2，2，22)，C (10，8，0)，F (4，0，0)，D (10，0，0)．故FA ′ =(-2，2，22)，FD =(6，0，0)．设n=(x ，y ，z )为平面A ′FD 的一个法向量，-2x +2y +22z =06x =0，取z =2，则n =(0,-2,2)．又平面BEF 的一个法向量m=(0,0,1)，故cos ‹n ,m >=n ⋅m |n |⋅|m |=33．所以二面角的余弦值为33(Ⅱ)设FM =a ，则M (4+a ，0，0)，因为翻折后，C 与A 重合，所以CM =A ′M ，故，(6-a )2+82+02=(-2-a )2+22+(22)2，得a =214，经检验，此时点N 在线段BC 上，所以FM=21 4．方法二：(Ⅰ)解：取线段EF的中点H，AF的中点G，连接A′G，A′H，GH．因为A′E=A′F及H是EF的中点，所以A′H⊥EF又因为平面A′EF⊥平面BEF，所以A′H⊥平面BEF，又AF⊂平面BEF，故A′H⊥AF，又因为G、H是AF、EF的中点，易知GH⎳AB，所以GH⊥AF，于是AF⊥面A′GH，所以∠A′GH为二面角A′-DH-C的平面角，在Rt△A′GH中，A′H=22，GH=2，A G=23所以cos∠A GH=3 3．故二面角A′-DF-C的余弦值为3 3．(Ⅱ)解：设FM=x，因为翻折后，C与A′重合，所以CM=A′M，而CM2=DC2+DM2=82+(6-x)2，A′M2=A′H2+MH2=A′H2+MG2+GH2=(22)2+(2+x)2+22，故(6-x)2+82+02=(-2-x)2+22+(22)2得x=21 4，经检验，此时点N在线段BC上，所以FM=21 4．12．(2021•五莲县期中)如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，BE ⎳CF ，∠BCF =∠CEF =90°．AD =3，EF =2．(1)求证：AE ⎳平面DCF ；(2)当AB 的长为何值时，二面角A -EF -C 的大小为60°．【解答】证明：(1)过E 作EG ⊥CF 于G ，连接DG ，则四边形BCGE 为矩形．又ABCD 为矩形，∴AD 平行且等于EG ，∴四边形ADGE 为平行四边形，∴AE ⎳DG ，∵AE ⊄平面DCF ，DG ⊂平面DCF ，∴AE ⎳平面DCF ．解：(2)分别以直线BE 、BC 、BA 所在的直线为x 轴，y 轴，z 轴，建立空间直角坐标系，依题意可得：B (0，0，0)，C (0，3，0)，E (3，0，0)，F (4，3，0)，设AB =m ，则A (0，0，m )．AE =(3，0，-m )，EF =(1，3，0)，平面CEF 的法向量m=(0，0，1)．设平面AEF 的法向量n=(x ，y ，z )，则n ⋅AE=3x -mz =0n ⋅EF =x +3y =0 ，取z =9，得n =(3m ，-3m ，9)(8分)∵二面角A -EF -C 的大小为60°，∴cos60°=|n ⋅m ||n |⋅|m |=912m 2+81，解得m =92．∴当AB =92时，二面角A -EF -C 的大小为60°．(12分)13．(2014秋•成都校级月考)在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC ⊥BC ，AC =BC =BD =2AE ，M 是AB 的中点．(Ⅰ)求证：CM ⊥EM ；(Ⅱ)求CM 与平面CAE 所成角的大小；(Ⅲ)求平面ABC 与平面CDE 所成锐二面角的余弦值．【解答】证明：(Ⅰ)分别以CB ，CA 所在直线为x ，y 轴，过点C 且与平面ABC 垂直的直线为z 轴，建立如图所示的空间直角坐标系C -xyz 设AE =a ，则M (a ，-a ，0)，E (0，-2a ，a )，所以CM =(a ，-a ，0)，EM =(a ，a ，-a )，∴CM ∙EM=a ×a +(-a )×a +0×(-a )=0，∴CM ⊥EM ．解：(2)平面CAE 的法向量n=(1，0，0)，CM =(a ，-a ，0)，设CM 与平面CAE 所成角为θ，则sin θ=|CM ∙n ||CM |∙|n |=a 2a =22，θ=45°，∴直线CM 与平面CAE 所成的角为45°．(3)D (2a ，0，2a )，CD =(2a ，0，2a )，CE=(0，-2a ，a )，设平面CDE 的法向量m=(x ，y ，z )，则m ∙CE=-2ay +az =0m ∙CD=2ax +2az =0，令y =1，得m =(-2，1，2)，平面ABC 的法向量p=(0，0，1)，设平面ABC 与平面CDE 所成锐二面角为θ，则cos θ=|m ∙p ||m |∙|p |=23．∴平面ABC 与平面CDE 所成锐二面角的余弦值为23．14．(2021•天津二模)如图，DC ⊥平面ABC ，EB ⎳DC ，AC =BC =EB =2DC =4，∠ACB =90°，P 、Q 分别为AE ，AB 的中点．(1)证明：PQ ⎳平面ACD ．(2)求异面直线AB 与DE 所成角的余弦值；(3)求平面ACD 与平面ABE 所成锐二面角的大小．【解答】(1)证明：∵P 、Q 分别是AE 、AB 的中点，∴PQ ⎳BE ，PQ =12BE ，又DC ⎳BE ，DC =12BE ，∴PQ ⎳DC ，∵PQ ⊄平面ACD ，DC ⊂平面ACD ，∴PQ ⎳平面ACD ；(2)解：∵DC ⊥平面ABC ，∠ACB =90°，以点C 为坐标原点，分别以CD ，CA ，CB的方向为x ，y ，z 轴的正方向建立空间直角坐标系．则C (0，0，0)，A (0，4，0)，B (0，0，4)，D (2，0，0)，E (4，0，4)，AB =(0,-4,4)，DE =(2,0,4)，∴cos <AB ,DE >=AB ∙DE|AB |∙|DE |=105，∴异面直线AB 与DE 所成角的余弦值105；(3)解：由(Ⅱ)可知AB =(0,-4,4)，AE=(4,-4,4)，设平面ABE 的法向量为n=(x ,y ,z )．则n ∙AB=-4y +4z =0n ∙AE=4x -4y +4z =0，取z =1，得n =(0,1,1)．由已知可得平面ACD 的法向量为CB=(0，0，4)，∴cos <n ,CB >=n ∙CB |n |∙|CB |=22．故所求平面ACD 与平面ABE 所成锐二面角的大小为45°．15．(2011•浙江)如图，在三棱锥P -ABC 中，AB =AC ，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上，已知BC =8，PO =4，AO =3，OD =2(Ⅰ)证明：AP ⊥BC ；(Ⅱ)在线段AP 上是否存在点M ，使得二面角A -MC -B 为直二面角？若存在，求出AM 的长；若不存在，请说明理由．【解答】解：以O 为原点，以AD 方向为Y 轴正方向，以射线OP 的方向为Z 轴正方向，建立空间坐标系，则O (0，0，0)，A (0，-3，0)，B (4，2，0)，C (-4，2，0)，P (0，0，4)(I )则AP =(0，3，4)，BC =(-8，0，0)由此可得AP ⋅BC=0∴AP ⊥BC即AP ⊥BC(II )设PM =λPA ，λ≠1，则PM=λ(0，-3，-4)BM =BP +PM =BP +λPA=(-4，-2，4)+λ(0，-3，-4)AC =(-4，5，0)，BC =(-8，0，0)设平面BMC 的法向量a=(a ，b ，c )则BM ⋅a =0BC ⋅a =0-4a -(2+3λ)b +(4-4λ)c =0-8a =0令b =1，则a =0，1，2+3λ4-4λ平面APC 的法向量b=(x ，y ，z )则AP ⋅b =0AC ⋅b =0 即3y +4z =0-4x +5y =0令x =5则b=(5，4，-3)由a ⋅b =0得4-3⋅2+3λ4-4λ=0解得λ=25故AM =3综上所述，存在点M 符合题意，此时AM =316．(2015秋•江西月考)如图，在三棱柱ABC -A 1B 1C 1中，∠BAC =90°，AB =AC =2，AA 1=A 1B =A 1C =6．(1)证明：平面ABC ⊥平面A 1BC ；(2)在线段BB 1上是否存在点E ，使得二面角E -A 1C -B 的余弦值为105？若存在确定点E 的位置，若不存在，说明理由．【解答】证明：(Ⅰ)设BC 的中点为O ，∵A 1B =A 1C =6，BC =AB 2+AC 2=22，∴A 1O ⊥BC ，且A 1O =2，又∠BAC =90°，AB =AC =2，∴AO ⊥BC ，且AO =2，∴AO 2+A 1O 2=2+4=AA 12，∴A 1O ⊥AO ，∴A 1O ⊥面ABC ，又A 1O ⊂平面A 1BC ，∴平面A 1BC ⊥平面ABC ．解：(Ⅱ)如图，以OA ，OB ，OA 1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，则A (2,0,0)，B (0，2，0)，C (0，-2，0)，A 1(0，0，2)，平面A 1BC 的法向量m =(1，0，0)，设BE =λBB 1 =λAA 1 ，(0≤λ≤1)，则BE =(-2λ，0，2λ)，点E 的坐标为(-2λ，2，2λ)，设平面EA 1C 的法向量为n =(x ，y ，z )，由n ⊥CA 1 ，n ⊥CE ，得2y +2z =0-2λx +22y +2λz =0 ，取z =1，得n =-22λ+2，-2，1 ，∵|cos <m ,n >|=105，∴105=2-22λ 2-22λ 2+2+1，解得λ=1，∴在线段BB 1上存在点E ，使得二面角E -A 1C -B 的余弦值为105，且点E 与点B 1重合．17．(2021春•东湖区校级期中)如图，在三棱柱ABC -A 1B 1C 1中，∠BAC =90°，AB =AC =2，A 1A =4，A 1在底面ABC 的射影为BC 的中点，D 是B 1C 1的中点．(1)证明：A 1D ⊥平面A 1BC ；(2)求二面角B -A 1D -B 1的平面角的正切值．【解答】(1)证明：∵AB =AC =2，D 是B 1C 1的中点．∴A 1D ⊥B 1C 1，∵BC ⎳B 1C 1，∴A 1D ⊥BC ，∵A 1O ⊥面ABC ，A 1D ⎳AO ，∴A 1O ⊥AO ，A 1O ⊥BC∵BC ∩AO =O ，A 1O ⊥A 1D ，A 1D ⊥BC∴A 1D ⊥平面A 1BC(2)解，如图，以BC 中点O 为坐标原点，以OB 、OA 、OA 1所在直线分别为x 、y 、z 轴建系．则BC =2AC =22,A 1O =AA 21-AO 2=14，易知A 1(0,0,14),B (2,0,0),C (-2,0,0)，A (0,2,0),D (0,-2,14),B 1(2,-2,14)，A 1D =(0,-2,0)，BD =(-2,-2,14)设平面A 1BD 的法向量为m =(x ,y ,z )，由，m ∙A 1D =0m ∙BD =0 得-2y =0-2x -2y +14z =0 ，取z =1，得m =(7,0,1)又平面A 1DB 1的法向量为n =(0,0,1)，∴cos <m ,n >=11×22=24∴二面角A 1-BD -B 1的平面角的正切值7．18．(2021•舒城县校级开学)如图，已知多面体ABC -A 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面ABC ，∠ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2．(1)证明：AB 1⊥A 1C 1；(2)求直线AC 1与平面ABB 1所成的角的正弦值．【解答】(1)证明：以A 为原点，AC ，AA 1所在直线分别为y ，z 轴，在平面ABC 内作Ax ⊥AC ，建立如图所示的空间直角坐标系，则A (0，0，0)，B 1(1，3，2)，A 1(0，0，4)，C 1(0，23，1)，∴AB 1 =(1，3，2)，A 1C 1 =(0，23，-3)，∴AB 1 ⋅A 1C 1 =3×23+2×(-3)=0，即AB 1⊥A 1C 1．(2)解：由(1)可知，AC 1 =(0，23，1)，AB =(1，3，0)，AB 1 =(1，3，2)，设平面ABB 1的法向量为n =(x ，y ，z )，则n ⋅AB =0n ⋅AB 1 =0 ，即x +3y =0x +3y +2z =0，令y =1，则x =-3，z =0，∴n =(-3，1，0)，设直线AC 1与平面ABB 1所成的角为θ，则sin θ=|cos <n ，AC 1 >|=n ⋅AC 1 |n |⋅|AC 1 |=232×13 =3913，故直线AC 1与平面ABB 1所成的角的正弦值为3913．19．(2021•滁州期末)如图，已知在直四棱柱(侧棱垂直底面的棱柱)ABCD -A 1B 1C 1D 1中，AD ⊥DC ，AB ⎳DC ，DC =DD 1=2AD =2AB =2(1)求证：DB ⊥平面B 1BCC 1．(2)求BC 1与平面A 1BD 所成的角的余弦值；(3)求二面角A 1-DB -C 1的正弦值．【解答】证明：(1)以D 为原点，DA 、DC 、DD 1所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则D (0，0，0)，B (1，0，0)，C 1(0，2，2)，C (0，2，0)，DB =(1，1，0)，BC =(-1，1，0)，BB 1 =(0，0，2)，DB ∙BC =-1+1+0=0，∴BD ⊥BC ，DB ∙BB 1 =0，∴BD ⊥BB 1，∵BB 1∩BC =B ，∴DB ⊥平面B 1BCC 1．解：(2)设n =(x ，y ，z )为平面A 1BD 的一个法向量，DA 1 =(1，0，2)，DB =(1，1，0)，则n ∙DA 1 =x +2z =0n ∙DB =x +y =0 ，取z =1，得n =(-2，2，1)，又BC 1 =(-1，1，2)，设BC 1与平面A 1BD 所面A 1BD 所成角为θ，则sin θ=|n ∙BC 1 ||n |∙|BC 1 |=63，∴BC 1与平面A 1BD 所成的角的余弦值为63．(3)由(2)知平面A 1BD 的一个法向量为n =(-2，2，1)，设m =(x ，y ，z )为平面C 1BD 的一个法向量，BC 1 =(-1，1，2)，DB =(1，1，0)，则n ∙BC 1 =-x +y +2z =0n ∙DB =x +y =0，取x =-1，得m =(1，-1，1)，设二面角A 1-DB -C 1的平面角为θ，则|cos θ|=m ∙n |m |∙|n |=333=33，∴sin θ=1-33 2=63．∴二面角A 1-DB -C 1的正弦值为63．20．(2015秋•辽宁校级月考)如图，在四棱锥P -ABCD 中，PA ⊥面ABCD ，AB =BC =2，AD =CD =7，PA =3，G 为线段PC 上的点，∠ABC =120°(Ⅰ)证明：BD ⊥面PAC ；(Ⅱ)求PC 与面PBD 所成的角；(Ⅲ)若G 满足PC ⊥面GBD ，求PG GC的值．【解答】解：(1)设AC ∩BD =O ，∵AB =BC =2，AD =CD =7，∴ΔABD ≅ΔCBD ，∴∠ABD =∠CBD ，∴ΔABO ≅ΔCBO ，∴BD ⊥AC ，∵PA ⊥面ABCD ，∴PA ⊥BD ，∵PA ∩AC =A ，∴BD ⊥面PAC ．解：(2)以O 为坐标原点，以OC 和OD 所在直线为x 轴和y 轴，建立空间直角坐标系Oxyz ，P (-3，0，3)，B (0，-1，0)，D (0，2，0)，C (3，0，0)，设面PBD 的法向量为n =(x ,y ,z )，则PB =(3,-1,-3)，BD =(0,3,0)，PC =(23,0,-3)，由n ⊥PB n ⊥BD，得3x -y -3z =03y =0 ，取x =1，得n =(1,0,1)，∴cos ‹PC ,n ›=PC ∙n |PC |∙|n |=1010，∴sin θ=|cos ‹PC ,n ›|=1010，即PC 与面PBD 所成角为arcsin 1010，(3)设G (x ，y ，z )，CG =λCP ，得(x -3,y ,z )=λ(-23,0,23)得x =3-23λy =0z =3λ，即G (3-23λ,0,3λ)，∴BG =(3-23λ,1,3λ)由BG ⊥PC ，得λ=25，即PG GC =32．21．(2021•龙岗区校级期中)如图，在三棱台ABC -DEF 中，平面ACFD ⊥平面ABC ，∠ACB =∠ACD =45°，DC =2BC ．(1)证明：BC ⊥BD ；(2)求二面角F -CD -B 的正弦值．【解答】(1)证明：如图，过点D 作DO ⊥AC ，交AC 与点O ，连接OB ，由∠ACD =45°，DO ⊥AC ，所以CD =2CO ，由平面ACFD ⊥平面ABC ，平面ACFD ∩平面ABC =AC ，DO ⊂平面ACFD ，故DO ⊥平面ABC ，又BC ⊂平面ABC ，所以DO ⊥BC ，由∠ACB =45°，BC =12CD =22CO ，则BO ⊥BC ，又DO ∩BO =O ，DO ，BO ⊂平面BDO ，所以BC ⊥平面BDO ，又DB ⊂平面BDO ，故BC ⊥DB ；(2)解：以点O 为坐标原点，建立空间直角坐标系如图所示，设CD =2BC =22，则O (0，0，0)，B (1，1，0)，C (0，2，0)，D (0，0，2)，所以OC =(0,2,0),BC =(-1,1,0),CD =(0,-2,2)，OD =(0,2,0)，设平面BCD 的法向量为n =(x ,y ,z )，则n ⋅BC =0n ⋅CD =0 ，即-x +y =0-2y +2z =0，令x =1，则y =z =1，故n =(1,1,1)，设平面FCOD 的法向量为m =(a ,b ,c )，则m ⋅OC =0m ⋅OD =0 ，即2c =02b =0，令x =1，则m =(1,0,0)，所以|cos <m ,n >|=|m ⋅n ||m ||n |=11×3=33，故二面角F -CD -B 的正弦值为1-33 2=63．22．(2021•新疆模拟)如图，在四棱锥A -BCDE 中，平面ABC ⊥平面BCDE ，∠CDE =∠BED =90°，AB =CD =2，DE =BE =1，AC =2．(1)求证：DB ⊥平面ABC ；(2)求平面ABE 与平面ADC 所成二面角大小的余弦值．【解答】证明：(1)以D 为原点，DE 为x 轴，DC 为y 轴，在过D 作平面BCDE 垂线为z 轴，建立空间直角坐标系，则D (0，0，0)，B (1，1，0)，A (0，2，2)，C (0，2，0)，DB =(1，1，0)，CA =(0，0，2)，CB =(1，-1，0)，DB ∙CA =0，DB ∙CB =0，∴DB ⊥CA ，DB ⊥CB ，∵CA ∩CB =C ，∴DB ⊥平面ABC ．解：(2)平面ADC 的法向量n =(1，0，0)，E (1，0，0)，EA =(-1，2，2)，EB =(0，1，0)，设平面ABE 的法向量m =(x ，y ，z )，则m ∙EA =-x +2y +2z =0m ∙EB =y =0，取z =1，得m =(2,0,1)，设平面ABE 与平面ADC 所成二面角大小为θ，则cos θ=|m ∙n ||m |∙|n |=23=63．∴平面ABE 与平面ADC 所成二面角大小的余弦值为63．。

第34讲利用坐标法解决立体几何的角度与距离问题(解析版)

第34讲利用坐标法解决立体几何的角度与距离问题参考答案与试题解析一．选择题（共1小题）1．（2021•南岗区校级期中）如图，三棱锥A BCD -中，90DAB DAC BAC ∠=∠=∠=︒，1AB AD AC ===，M ，N 分别为CD ，BC 的中点，则异面直线AM 与DN 所成角余弦值为( )A ．16B C D ．56【解答】解：三棱锥A BCD -中，90DAB DAC BAC ∠=∠=∠=︒，建立空间直角坐标系，如图所示：由于1AB AD AC ===，M ，N 分别为CD ，BC 的中点，所以(0A ，0，0)，11(0,,)22M ，(0D ，0，1)，11(,22N ，0)，则11(0,,)22AM =，11(,,1)22DN =-，所以异面直线AM 与DN 所成角余弦值3cos ||||||AM DN AM DN θ== 故选：B ．二．解答题（共21小题）2．（2021•凉山州模拟）如图，在四棱锥P ABCD -中，底面为直角梯形，//AD BC ，90BAD ∠=︒，PA ⊥底面ABCD ，且2PA AD AB BC ===，M 、N 分别为PC ，PB 的中点．（1）求证：PB DM ⊥；（2）求二面角A MD C --的正弦值．【解答】解：（1）证明：PA ⊥面ABCD ，AD ⊂面ABCD ，AD PA ∴⊥， 90BAD ∠=︒，AD AB ∴⊥， PAAB A =，PA ，AB ⊂面PAB ，AD ∴⊥面PAB ，PB ⊂面PAB ，AD PB ∴⊥，又PAB ∆中，AP AB =，N 为PB 的中点，AN PB ∴⊥， ANAD A =，AN ，AD ⊂平面AND ，PB ∴⊥面AND ，又N ，M 分别为PB ，PC 的中点， //MN BC ∴，//BC AD ，//MN AD ∴，N ∈面AND ，M ∴∈面AND ，MN ∴⊂面AND ，PB DM ∴⊥．（2）解：以A 为原点，AB 为x 轴，AD 为y 轴，AP 为z 轴，建立空间直角坐标系，设22PA AD AB BC ====，则(0A ，0，0)，(0P ，0，2)，(2C ，1，0)，(0D ，2，0)，(1M ，12，1)，设面AMD 的法向量(m x =，y ，)z ， (0AD =，0，2)，(1AM =，12，1)， 20102AD m y AM m x y z ⎧==⎪⎨=++=⎪⎩，取1x =，得(1m =，0，1)-，设面CMD 的法向量(n x =，y ，)z ，(2DC =，1-，0)，(1DM =，32-，1)，20302DC n x y DM n x y z ⎧=-=⎪⎨=-+=⎪⎩，取1x =，得(1n =，2，2)， cos ,||||32m n m n m n <>==-∴二面角A MD C --．3．（2021•荔湾区校级期末）如图，在平行四边形ABCD 中，2AB BC =，120ABC ∠=︒，E 为线段AB 的中点，将ADE ∆沿在直线DE 翻折成△A DE '，使平面A DE '⊥平面BCD ，F 为线段A C ''的中点．（1）求证：//BF 平面A DE '．（2）设M 为线段DE 的中点，求直线FM 与平面A DE '所成角的大小．（3）若2BC =，求三棱锥A DEF '-的体积．【解答】解：（1）证明：取CD 中点G ，连结GF ，BG ，在平行四边形ABCD 中，2AB BC =，120ABC ∠=︒，E 为线段AB 的中点，将ADE ∆沿在直线DE 翻折成△A DE '，使平面A DE '⊥平面BCD ，//GF A D ∴'，//BGDE， GFBG G =，A DDE D '=，∴平面//A DE '平面BGF ，BF BGF ⊂，//BF ∴平面A DE '．（2）解：取CD 中点G ，连结EG 、AG 、DE ，A M '，设2BC =，则四边形AEGD 是边长为2的菱形，且60DAE ∠=︒，MA ME ∴⊥，由平面A DE '⊥平面BCD ，F 为线段A C ''的中点．A M ∴'⊥平面AEGD ，以M 为原点，MA 为x 轴，ME 为y 轴，MA '为z 轴，建立空间直角坐标系，则(0M ，0，0)，(0A '，0，(0D ，1-，0)，(C -，1，0)，(F ，12，(3FM =，12-，，平面A DE '的法向量(1m =，0，0)，设直线FM 与平面A DE '所成角为θ，则||3sin ||||FM n FM n θ==，60θ∴=︒． ∴直线FM 与平面A DE '所成角的大小为60︒．（3）解：2BC =，∴由（2）得(F 12，平面A DE '的法向量(1m =，0，0)，1(2MF =-，∴点F 到平面A DE '的距离||3||MF m d m ==． 122A DES'=⨯∴三棱锥A DEF '-的体积：113A DEF F A DE V V '--'===．4．（2021•和平区校级月考）如图，四棱锥P ABCD -中，PAD ∆是以AD 为斜边的等腰直角三角形，//BC AD ，CD AD ⊥，222PC AD DC CB ====，E 为PD 的中点．（1）证明：//CE 平面PAB ；（2）求直线CE与平面PAB间的距离．【解答】（1）证明：取PA的中点M，连接BM、EM，E为PD的中点，//EM AD∴，12EM AD BC==，∴四边形BCEM为平行四边形，//CE BM∴，CE⊂/平面PAB，BM⊂平面PAB，//CE∴平面PAB．（2）解：//CE平面PAB，∴点E到平面PAB的距离即为所求．222PC AD DC CB====，取AD的中点N，连接BN、PN，则四边形BCDN为矩形，1BN CD==PAD∆是以AD为斜边的等腰直角三角形，PN AD∴⊥，112PN AD==，BN AD⊥，PN BN N=，PN、BN⊂平面PNB，AD∴⊥平面PNB，//BC AD，BC∴⊥平面PNB，BC⊂平面ABCD，∴平面ABCD⊥平面PNB，以B为原点，BC、BN分别为x、y轴，在平面PNB内，作Bz⊥平面ABCD，建立如图所示的空间直角坐标系，则(0B，0，0)，(1A，1-，0)，(1D，1，0)BC⊥平面PNB，BC PB∴⊥，在Rt PBC∆中，PB===1BN PN==，120PNB∴∠=︒，∴点3(2P ，0，5(4E ，12， ∴3(2BP =，0，(1BA =，1-，0)，5(4BE =，12，设平面PAB 的法向量为(n x =，y ，)z ，则00n BP n BA ⎧⋅=⎪⎨⋅=⎪⎩，即3020x x y ⎧+=⎪⎨⎪-=⎩，令1x =，则1y =，z =∴(1n =，1，，∴点E 到平面PAB的距离514||||||n BE d n +⋅==，故直线CE 与平面PAB． 5．（2021•沙坪坝区校级月考）如图，在四棱锥P ABCD -中，PAD ∆是以AD 为斜边的等腰直角三角形，//BC AD ，CD AD ⊥，PC 222AD DC CB ===，E 为PD 上一点．（1）若E 为PD 的中点，证明：//CE 平面PAB ；（2）若直线CE 与底面ABCD ，求二面角P AB E --的正弦值．【解答】（1）证明：取线段PA 的中点M ，连结EM ，BM ，因为线段PD 的中点为E ，线段PA 的中点为M ，所以//EM AD 且12EM AD =，又四边形ABCD 中，//BC AD ，2AD BC =，所以//EM BC ，EM BC =，所以四边形BCEM 为平行四边形，所以//CE BM ，因为BM ⊂平面PAB ，CE⊂/平面PAB ，所以//CE 平面PAB ；（2）解：已知PAD ∆是以AD 为斜边的等腰直角三角形，2AD =，所以PD 1PC CD ==，所以222PC PD CD =+，由勾股定理的逆定理可得，CD PD ⊥，又CD AD ⊥，AD PD D =，AD ，PD ⊂平面PAD ，所以CD ⊥平面PAD ，因为CD ⊂平面ABCD ，所以平面ABCD ⊥平面PAD ，取AD 的中点O ，连结PO ，OB ，则PO AD ⊥，又PO ⊂平面PAD ，平面ABCD ⋂平面PAD AD =，所以PO ⊥平面ABCD ，四边形ABCD 中，//BC AD ，2AD BC =，所以四边形BCDO 是平行四边形，所以//BO CD ，BO CD =，所以BO AD ⊥，以O 为坐标原点，以OB ，OD ，OP 所在直线分别为x 轴，y 轴，z 轴建立空间直角坐标系如图所示，所以(0A ，1-，0)，(1B ，0，0)，(1C ，1，0)，(0D ，1，0)，(0P ，0，1)，则(0,1,1),(1,0,0)DP CD =-=-，设(0,,),(0,1)DE DP λλλλ==-∈，所以(1,,)CE CD DE λλ=+=--，平面ABCD 的法向量可取(0,0,1)n =，因为直线CE 与底面ABCD，||||||CE n CEn ⋅=，解得13λ=，所以11(1,,)33CE =--，则21(0,,)33E ，所以51(0,,),(1,1,0)33AE AB ==，设平面ABE 的法向量为(,,)m x y z =，所以00m AE m AB ⎧⋅=⎪⎨⋅=⎪⎩，所以51033y z x y ⎧+=⎪⎨⎪+=⎩，令1y =，则1x =-，5z =-，所以(1,1,5)m =--，又(0,1,1)AP =，设平面PAB 的法向量为(,,)p a b c =，则有00p AP p AB ⎧⋅=⎪⎨⋅=⎪⎩，所以00b c a b +=⎧⎨+=⎩，令1b =，则1c =-，1a =-，所以(1,1,1)p =--，所以7cos ,||||9m p m p m p ⋅<>==，所以242sin ,1,m p cos m p <>=-<>=，所以二面角P AB E --．6．（2021•江苏一模）如图，在四棱锥P ABCD -中，PAD ∆是以AD 为斜边的等腰直角三角形，//BC AD ，AB AD ⊥，222AD AB BC ===，PC =E 为PD 的中点．（1）求直线PB 与平面PAC 所成角的正弦值；（2）设F 是BE 的中点，判断点F 是否在平面PAC 内，并请证明你的结论．【解答】解：（1）取AD 中点O ，连接OP 、OC ，PAD ∆是以AD 为斜边的等腰直角三角形，所以OP AD ⊥，1OP OA OD ===，因为//BC AD ，AB AD ⊥，222AD AB BC ===，所以四边形ABCO 为边长为1的正方形，所以OC AD ⊥，又因为PC =，所以222PC OP OC =+，所以PO OC ⊥，所以OA 、OC 、OP 两两垂直，建立如图所示的空间直角坐标系， (1A ，0，0)，(1B ，1，0)，(0C ，1，0)，(0P ，0，1)，平面PAC 的法向量为(1n =，1，1)，(1PB =，1，1)-，所以直线PB 与平面PAC 所成角的正弦值为||13||||3PB n PB n ⋅==⋅⋅．（2）连接AF ，(1D -，0，0)，1(2E -，0，1)2，1(4F ，12，1)4，3(4AF =-，12，1)4，点F到平面PAC的距离为||||3AF nn⋅==，所以点F在平面PAC内．7．（2021•房山区一模）如图，四棱锥P ABCD-中，PAD∆是以AD为斜边的等腰直角三角形，PD CD==2PC=，//12BC AD=，CD AD⊥．（Ⅰ）求证：CD⊥平面PAD；（Ⅱ）若E为PD中点，求CE与面PBC所成角的正弦值；（Ⅲ）由顶点C沿棱锥侧面经过棱PD到顶点A的最短路线与PD的交点记为F．求该最短路线的长及PFFD的值．【解答】（Ⅰ）证明：PD CD=2PC=，222CD PD PC∴+=，CD PD∴⊥，又CD AD⊥，PD AD D=，CD∴⊥平面PAD．（Ⅱ）解：取AD的中点O，连接OP，OB，PA PD=，PO AD∴⊥．CD⊥平面PAD，PO⊂平面PAD，PO CD∴⊥，又AD CD D=，PO∴⊥平面ABCD，//12BC AD =，CD AD ⊥．∴四边形BCDO 是矩形，OB OD ∴⊥．以点O 为坐标原点建立空间直角坐标系O xyz -，如图所示则C ，(0P ，0，1)，(0D ，1，0)，B ，(0E ，12，1)2， ∴11(,)22CE =--，(2,0,1),(0,1,0)PB BC =-=，设面PBC 的法向量(,,)n x y z =，则0n PB n BC ⎧⋅=⎪⎨⋅=⎪⎩，即00z y -==⎪⎩，令1x =可得(1n=，0．22cos ,||||5CE nCE n CE n -⋅∴<>===⋅设CE 与面PBC 所成角为θ，∴15sin |cos ,|CE n θ=<>=．（Ⅲ）解：CD ⊥平面PCD ，PD ⊂面PAD ， CD PD ∴⊥，PDC ∴∆为等腰直角三角形，作出平面APD 和平面PCD 的侧面展开图，如图所示：连接AC 交PD 于F ，则AC 为最短路线，90APD PDC '∠=∠=︒，//AP DC '∴=，∴四边形ADC P '为平行四边形，F ∴与E 重合，∴最短路线长为22AF ==，此时1PF FD=．8．（2021春•湖北期末）如图，四棱锥S ABCD -中，//AB CD ，BC CD ⊥，侧面SAB 为等边三角形，4AB BC ==，2CD SD ==．（1）求证：SD AB ⊥；（2）求AB 与平面SBC 所成的角的正弦值．【解答】解：（1）证明：四棱锥S ABCD -中，//AB CD ，BC CD ⊥，侧面SAB 为等边三角形，4AB BC ==，2CD SD ==．AD ∴=4SA AB ==，222SA SD AD ∴+=，SD SA ∴⊥，同理得SD SB ⊥， SASB S =，SD ∴⊥平面SAB ，AB ⊂平面SAB ，SD AB ∴⊥．（2）解：以D 为原点，在平面ABCD 内过D 作DC 的垂线为x 轴，DC 为y 轴，过D 作平面ABCD 的垂线为z 轴，建立空间直角坐标系，(4A ，2-，0)，(4B ，2，0)，(0C ，2，0)，(1S ，0，，(4CB =，0，0)，(1CS =，2-，(0AB =，4，0)，设平面SBC 的一个法向量是(n x =，y ，)z ，则4020n CB x n CS x y ⎧⋅==⎪⎨⋅=-=⎪⎩，取2z =，得(0n =2)，设AB 与平面SBC 所成的角为θ，则||4sin ||||7n AB n AB θ⋅===⋅．AB ∴与平面SBC ．9．（2021•天山区校级期末）如图，在三棱锥P ABC -中，AB BC ⊥，12AB BC PA ==，点O ，D 分别是AC ，PC 的中点，OP ⊥底面ABC ．（1）求证：//OD 平面PAB ；（2）求直线OD 与平面PBC 所成角的正弦值．【解答】证明：（1）点O ，D 分别是AC ，PC 的中点， //OD PA ∴又OD ⊂/平面PAB ，PA ⊂平面PAB //OD ∴平面PAB ；（2）连接OB ，AB BC =，点O 是AC 的中点， OB AC ∴⊥又OP ⊥底面ABC ．故可以O 为坐标原点，建立如图所示的空间直角坐标系令112AB BC PA ===，AB BC ⊥，则2OA OB OC ===，2OP =则(0O ，0，0)，B 0，0)，(0C ，0)，(0P ，0，(0D∴(0OD =，(BC =-，0)，(0PC =，设(m x =，y ，)z 是平面PBC 的一个法向量则00m BC m PC ⎧=⎪⎨=⎪⎩，即00y y ⎧+=⎪⎪-=令1z =，则(7m =，1) 直线OD 与平面PBC 所成角θ满足： ||210sin ||||m OD m OD θ== 故直线OD 与平面PBC10．（2012秋•小店区校级月考）如图，四边形ABCD 中（图1)，E 是BC 的中点，2DB =，1DC =，BC ，AB AD ==1)沿直线BD 折起，使二面角A BD C --为60︒（如图2)（1）求证：AE ⊥平面BDC ；（2）求异面直线AB 与CD 所成角的余弦值；（3）求点B 到平面ACD 的距离．【解答】解：（1）如图1取BD 中点M，连接AM，ME．因AB AD==AM BD∴⊥（3）⋯（1分）因2DB=，1DC=，BC=满足：222DB DC BC+=，所以BCD∆是BC为斜边的直角三角形，BD DC⊥，因E是BC的中点，所以ME为BCD∆的中位线1//2ME CD，ME BD ∴⊥，12ME=⋯（2分）AME∴∠是二面角A BD C--的平面角，60AME∴∠=︒⋯（3分）AM BD⊥，ME BD⊥且AM、ME是平面AME内两相交于M 的直线BD∴⊥平面AEM AE⊂平面AEM，BD AE∴⊥⋯（4分）因AB AD==，2DB=，ABD∴∆为等腰直角三角形，∴112AM BD==，22212cos124AE AM ME AM ME AME=+-∠=+-⨯2221AE ME AM∴+==，AE ME∴⊥⋯（6分）BD M E∴，BD⊂面BDC，ME⊂面BDC，AE∴⊥平面BDC⋯（7分）（2）如图2，以M为原点MB为x轴，ME为y轴，建立空间直角坐标系，（8分）则由（1）及已知条件可知(1B ，0，0)，1(0,,0)2E ，1(0,2A ，(1D -，0，0)，(1C -，1，0)， 13(1,,),(0,1,0)2AB CD =--=-，⋯（9分）设异面直线AB 与CD 所成角为θ，则cos ||||||AB CDAB CD θ=⋯（10分）1==⋯（11分）（3）由13(1,,),(0,1,0)2AD CD =---=-，可知(3,0,2)n =-满足，0,0n AD n CD ==，n 是平面ACD 的一个法向量，⋯（12分）记点B 到平面ACD 的距离d ，则AB 在法向量n 方向上的投影绝对值为d 则||||AB nd n =⋯（13分），所以7d ==（14分）11．（2010•浙江）如图，在矩形ABCD 中，点E ，F 分别在线段AB ，AD 上，243AE EB AF FD ====．沿直线EF 将AEF ∆翻折成△A EF '，使平面A EF '⊥平面BEF ．（Ⅰ）求二面角A FD C '--的余弦值；（Ⅱ）点M ，N 分别在线段FD ，BC 上，若沿直线MN 将四边形MNCD 向上翻折，使C 与A '重合，求线段FM 的长．【解答】解：（Ⅰ）取线段EF 的中点H ，连接A H '，因为A E A F '='及H 是EF 的中点，所以A H EF '⊥，又因为平面A EF '⊥平面BEF ．如图建立空间直角坐标系A xyz -则(2A '，2，，(10C ，8，0)， (4F ，0，0)，(10D ，0，0)．故(2FA '=-，2，，(6FD =，0，0)．设(n x =，y ，)z 为平面A FD '的一个法向量，22060x y x ⎧-++=⎪⎨=⎪⎩，取z =，则(0,n =-．又平面BEF 的一个法向量(0,0,1)m =，故3cos ,||||n m n m n m ⋅〈>==⋅．（Ⅱ）设FM a =，则(4M a +，0，0)，因为翻折后，C 与A 重合，所以CM A M ='，故，222222(6)80(2)2a a -++=--++，得214a =，经检验，此时点N 在线段BC 上，所以214FM =．方法二：（Ⅰ）解：取线段EF 的中点H ，AF 的中点G ，连接A G '，A H '，GH ．因为A E A F '='及H 是EF 的中点，所以A H EF '⊥又因为平面A EF '⊥平面BEF ，所以A H '⊥平面BEF ，又AF ⊂平面BEF ，故A H AF '⊥，又因为G 、H 是AF 、EF 的中点，易知//GH AB ，所以GH AF ⊥，于是AF ⊥面A GH '，所以A GH ∠'为二面角A DH C '--的平面角，在Rt △A GH '中，A H '=，2GH =，A G '=所以cos A GH '∠=．故二面角A DF C '--．（Ⅱ）解：设FM x =，因为翻折后，C 与A '重合，所以CM A M ='，而222228(6)CM DC DM x =+=+-，222222222(2)2A M A H MH A H MG GH x '='+='++=+++，故222222(6)80(2)2x x -++=--++ 得214x =，经检验，此时点N 在线段BC 上，所以214FM =．12．（2021•五莲县期中）如图，矩形ABCD 和梯形BEFC 所在平面互相垂直，//BE CF ，90BCF CEF ∠=∠=︒．AD =2EF =．（1）求证：//AE 平面DCF ；（2）当AB 的长为何值时，二面角A EF C --的大小为60︒．【解答】证明：（1）过E 作EG CF ⊥于G ，连接DG ，则四边形BCGE 为矩形．又ABCD 为矩形，AD ∴平行且等于EG ，∴四边形ADGE 为平行四边形，//AE DG ∴，AE ⊂/平面DCF ，DG ⊂平面DCF ，//AE ∴平面DCF ．解：（2）分别以直线BE 、BC 、BA 所在的直线为x 轴，y 轴，z 轴，建立空间直角坐标系，依题意可得：(0B ，0，0)，(0C 0)，(3E ，0，0)，(4F 0)，设AB m =，则(0A ，0，)m ．(3AE =，0，)m -，(1EF =0)，平面CEF 的法向量(0m =，0，1)．设平面AEF 的法向量(n x =，y ，)z ，则30n AE x mz n EF x ⎧⋅=-=⎪⎨⋅==⎪⎩，取9z =，得(3n m =，，9)（8分）二面角A EF C --的大小为60︒， ||cos60||||12n m n m m ⋅∴︒==⋅92m =． ∴当92AB =时，二面角A EF C --的大小为60︒．（12分）13．（2014秋•成都校级月考）在如图所示的几何体中，EA ⊥平面ABC ，DB ⊥平面ABC ，AC BC ⊥，2AC BC BD AE ===，M 是AB 的中点．（Ⅰ）求证：CM EM ⊥；（Ⅱ）求CM 与平面CAE 所成角的大小；（Ⅲ）求平面ABC 与平面CDE 所成锐二面角的余弦值．【解答】证明：（Ⅰ）分别以CB ，CA 所在直线为x ，y 轴，过点C 且与平面ABC 垂直的直线为z 轴，建立如图所示的空间直角坐标系C xyz -设AE a =，则(M a ，a -，0)，(0E ，2a -，)a ，所以(CM a =，a -，0)，(EM a =，a ，)a -，∴()0()0CM EM a a a a a =⨯+-⨯+⨯-=，CM EM ∴⊥．解：（2）平面CAE 的法向量(1n =，0，0)，(CM a =，a -，0)，设CM 与平面CAE 所成角为θ，则||sin ||||2CM n CM n aθ===，45θ=︒，∴直线CM 与平面CAE 所成的角为45︒．（3）(2D a ，0，2)a ，(2CD a =，0，2)a ，(0CE =，2a -，)a ，设平面CDE 的法向量(m x =，y ，)z ，则20220m CE ay az m CD ax az ⎧=-+=⎪⎨=+=⎪⎩，令1y =，得(2m =-，1，2)，平面ABC 的法向量(0p =，0，1)，设平面ABC 与平面CDE 所成锐二面角为θ，则||2cos ||||3m p m p θ==．∴平面ABC 与平面CDE 所成锐二面角的余弦值为23．14．（2021•天津二模）如图，DC ⊥平面ABC ，//EB DC ，24AC BC EB DC ====，90ACB ∠=︒，P 、Q 分别为AE ，AB 的中点．（1）证明：//PQ 平面ACD ．（2）求异面直线AB 与DE 所成角的余弦值；（3）求平面ACD 与平面ABE 所成锐二面角的大小．【解答】（1）证明：P 、Q 分别是AE 、AB 的中点， //PQ BE ∴，12PQ BE =，又//DC BE ，12DC BE =， //PQ DC ∴，PQ ⊂/平面ACD ，DC ⊂平面ACD ， //PQ ∴平面ACD ；（2）解：DC ⊥平面ABC ，90ACB ∠=︒，以点C 为坐标原点，分别以CD ，CA ，CB 的方向为x ，y ，z 轴的正方向建立空间直角坐标系．则(0C ，0，0)，(0A ，4，0)，(0B ，0，4)，(2D ，0，0)，(4E ，0，4)， (0,4,4)AB =-，(2,0,4)DE =，10cos ,||||AB DE AB DE AB DE ∴<>==，∴异面直线AB 与DE ；（3）解：由（Ⅱ）可知(0,4,4)AB =-，(4,4,4)AE =-，设平面ABE 的法向量为(,,)n x y z =．则4404440n AB y z n AE x y z ⎧=-+=⎪⎨=-+=⎪⎩，取1z =，得(0,1,1)n =．由已知可得平面ACD 的法向量为(0CB =，0，4)， 2cos ,||||n CB n CB n CB ∴<>== 故所求平面ACD 与平面ABE 所成锐二面角的大小为45︒．15．（2011•浙江）如图，在三棱锥P ABC -中，AB AC =，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上，已知8BC =，4PO =，3AO =，2OD = （Ⅰ）证明：AP BC ⊥；（Ⅱ）在线段AP 上是否存在点M ，使得二面角A MC B --为直二面角？若存在，求出AM 的长；若不存在，请说明理由．【解答】解：以O 为原点，以AD 方向为Y 轴正方向，以射线OP 的方向为Z 轴正方向，建立空间坐标系，则(0O ，0，0)，(0A ，3-，0)，(4B ，2，0)，(4C -，2，0)，(0P ，0，4) ()I 则(0AP =，3，4)，(8BC =-，0，0)由此可得0AP BC ⋅=∴AP BC ⊥即AP BC ⊥()II 设PM PA λ=，1λ≠，则(0PM λ=，3-，4)- (4BM BP PM BP PA λ=+=+=-，2-，4)(0λ+，3-，4)- (4AC =-，5，0)，(8BC =-，0，0)设平面BMC 的法向量(a a =，b ，)c 则00BM a BC a ⎧⋅=⎪⎨⋅=⎪⎩ 4(23)(44)080a b c a λλ--++-=⎧⎨-=⎩令1b =，则(0a =，1，23)44λλ+- 平面APC 的法向量(b x =，y ，)z 则00AP b AC b ⎧⋅=⎪⎨⋅=⎪⎩ 即340450y z x y +=⎧⎨-+=⎩令5x =则(5b =，4，3)- 由0a b ⋅= 得2343044λλ+-⋅=- 解得25λ=故3AM =综上所述，存在点M 符合题意，此时3AM =16．（2015秋•江西月考）如图，在三棱柱111ABC A B C -中，90BAC ∠=︒，2AB AC ==，111AA A B AC ===．（1）证明：平面ABC ⊥平面1A BC ；（2）在线段1BB 上是否存在点E ，使得二面角1E AC B --？若存在确定点E 的位置，若不存在，说明理由．【解答】证明：（Ⅰ）设BC 的中点为O ，11A B A C ==，BC = 1AO BC ∴⊥，且12A O =，又90BAC ∠=︒，2AB AC ==，AO BC ∴⊥，且AO =，2221124AO AO AA ∴+=+=， 1AO AO ∴⊥，1AO ∴⊥面ABC ，又1A O ⊂平面1A BC ，∴平面1A BC ⊥平面ABC ．解：（Ⅱ）如图，以OA ，OB ，1OA 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，则A ，(0B0)，(0C，0)，1(0A ，0，2)，平面1A BC 的法向量(1m =，0，0)，设11BE BB AA λλ==，(01)λ，则(BE =-，0，2)λ，点E 的坐标为(，2)λ，设平面1EAC 的法向量为(n x =，y ，)z ，由1n CA ⊥，n CE ⊥，得2020z x z λ+=++=⎪⎩，取1z =，得22(n =-+1)，10|cos ,|m n <>=，∴=解得1λ=，∴在线段1BB 上存在点E ，使得二面角1E AC B --，且点E 与点1B 重合．17．（2021春•东湖区校级期中）如图，在三棱柱111ABC A B C -中，90BAC ∠=︒，2AB AC ==，14A A =，1A 在底面ABC 的射影为BC 的中点，D 是11B C 的中点．（1）证明：1A D ⊥平面1A BC ；（2）求二面角11B A D B --的平面角的正切值．【解答】（1）证明：2AB AC ==，D 是11B C 的中点．111A D B C ∴⊥，11//BC B C ，1A D BC ∴⊥，1A O ⊥面ABC ，1//A D AO ，1AO AO ∴⊥，1AO BC ⊥ BCAO O =，11AO A D ⊥，1A D BC ⊥ 1A D ∴⊥平面1A BC（2）解，如图，以BC 中点O 为坐标原点，以OB 、OA 、1OA 所在直线分别为x 、y 、z 轴建系．则1BC AO =易知1(A B C ，1(0,A D B ，1(0,A D =，(BD =-设平面1A BD 的法向量为(,,)m x y z =，由，100m A D m BD ⎧=⎪⎨=⎪⎩得00⎧=⎪⎨+=⎪⎩，取1z =，得(7,0,1)m =又平面11A DB 的法向量为(0,0,1)n =，cos ,412m n ∴<>==⨯∴二面角11A BD B --18．（2021•舒城县校级开学）如图，已知多面体111ABC A B C -，1A A ，1B B ，1C C 均垂直于平面ABC ，120ABC ∠=︒，14A A =，11C C =，12AB BC B B ===．（1）证明：111AB AC ⊥；（2）求直线1AC 与平面1ABB 所成的角的正弦值．【解答】（1）证明：以A 为原点，AC ，1AA 所在直线分别为y ，z 轴，在平面ABC 内作Ax AC ⊥，建立如图所示的空间直角坐标系，则(0A ，0，0)，1(1B 2)，1(0A ，0，4)，1(0C ，1)，∴1(1AB =2)，11(0A C =，3)-，∴11132(3)0AB A C ⋅=⨯⨯-=，即111AB AC ⊥．（2）解：由（1）可知，1(0AC =，1)，(1AB =0)，1(1AB =2)，设平面1ABB 的法向量为(n x =，y ，)z ，则100n AB n AB ⎧⋅=⎪⎨⋅=⎪⎩，即020x x z ⎧=⎪⎨+=⎪⎩，令1y =，则x =0z =，∴(3n =-，1，0)，设直线1AC 与平面1ABB 所成的角为θ，则sin |cos n θ=<，111||||||||2n AC AC n AC ⋅>===⋅⨯，故直线1AC 与平面1ABB ． 19．（2021•滁州期末）如图，已知在直四棱柱（侧棱垂直底面的棱柱）1111ABCD A B C D -中，AD DC ⊥，//AB DC ，1222DC DD AD AB ====（1）求证：DB ⊥平面11B BCC ．（2）求1BC 与平面1A BD 所成的角的余弦值；（3）求二面角11A DB C --的正弦值．【解答】证明：（1）以D 为原点，DA 、DC 、1DD 所在直线分别为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，则(0D ，0，0)，(1B ，0，0)，1(0C ，2，2)，(0C ，2，0)， (1DB =，1，0)，(1BC =-，1，0)，1(0BB =，0，2)， 1100DB BC =-++=，BD BC ∴⊥，10DB BB =，1BD BB ∴⊥， 1BB BC B =，DB ∴⊥平面11B BCC ．解：（2）设(n x =，y ，)z 为平面1A BD 的一个法向量， 1(1DA =，0，2)，(1DB =，1，0)，则1200n DA x z n DB x y ⎧=+=⎪⎨=+=⎪⎩，取1z =，得(2n =-，2，1)，又1(1BC =-，1，2)，设1BC 与平面1A BD 所面1A BD 所成角为θ，则11||6sin ||||n BC n BC θ== 1BC ∴与平面1A BD ．（3）由（2）知平面1A BD 的一个法向量为(2n =-，2，1)，设(m x =，y ，)z 为平面1C BD 的一个法向量， 1(1BC =-，1，2)，(1DB =，1，0)，则1200n BC x y z n DB x y ⎧=-++=⎪⎨=+=⎪⎩，取1x =-，得(1m =，1-，1)，设二面角11A DB C --的平面角为θ，则|cos |||||||33m n m n θ===，sin θ∴==． ∴二面角11A DB C --．20．（2015秋•辽宁校级月考）如图，在四棱锥P ABCD -中，PA ⊥面ABCD ，2AB BC ==，AD CD ==PA ，G 为线段PC 上的点，120ABC ∠=︒（Ⅰ）证明：BD ⊥面PAC ；（Ⅱ）求PC 与面PBD 所成的角；（Ⅲ）若G 满足PC ⊥面GBD ，求PGGC的值．【解答】解：（1）设ACBD O =，2AB BC ==，AD CD =ABD CBD ∴∆≅∆，ABD CBD ∴∠=∠，ABO CBO ∴∆≅∆，BD AC ∴⊥，PA ⊥面ABCD ，PA BD ∴⊥，PAAC A =，BD ∴⊥面PAC ．解：（2）以O 为坐标原点，以OC 和OD 所在直线为x 轴和y 轴，建立空间直角坐标系Oxyz ，(P 0，(0B ，1-，0)，(0D ，2，0)，C 0，0)，设面PBD 的法向量为(,,)n x y z =，则(3,1,PB =-，(0,3,0)BD =，(23,0,PC =， n PBn BD⎧⊥⎪⎨⊥⎪⎩由，得030y y -==⎪⎩，取1x =，得(1,0,1)n =， ∴10cos ,10||||PC n PC n PC n 〈〉==，∴10sin |cos ,|PC n θ=〈〉=，即PC 与面PBD所成角为，（3）设(G x ，y ，)z ，CG CP λ=，得(,)(x y z λ=-得0x y z ⎧=⎪=⎨⎪=⎩，即)G ， ∴(3)BG =由BG PC ⊥，得25λ=，即32PG GC =．21．（2021•龙岗区校级期中）如图，在三棱台ABC DEF -中，平面ACFD ⊥平面ABC ，45ACB ACD ∠=∠=︒，2DC BC =．（1）证明：BC BD ⊥；（2）求二面角F CD B --的正弦值．【解答】（1）证明：如图，过点D 作DO AC ⊥，交AC 与点O ，连接OB ，由45ACD ∠=︒，DO AC ⊥，所以CD =，由平面ACFD ⊥平面ABC ，平面ACFD ⋂平面ABC AC =，DO ⊂平面ACFD ，故DO ⊥平面ABC ，又BC ⊂平面ABC ，所以DO BC ⊥，由45ACB ∠=︒，12BC CD ==，则BO BC ⊥，又DOBO O =，DO ，BO ⊂平面BDO ，所以BC ⊥平面BDO ，又DB ⊂平面BDO ，故BC DB ⊥；（2）解：以点O 为坐标原点，建立空间直角坐标系如图所示，设2CD BC ==则(0O ，0，0)，(1B ，1，0)，(0C ，2，0)，(0D ，0，2)，所以(0,2,0),(1,1,0),(0,2,2)OC BC CD ==-=-，(0,2,0)OD =，设平面BCD 的法向量为(,,)n x y z =，则00n BC n CD ⎧⋅=⎪⎨⋅=⎪⎩，即0220x y y z -+=⎧⎨-+=⎩，令1x =，则1y z ==，故(1,1,1)n =，设平面FCOD 的法向量为(,,)m a b c =，则00m OC m OD ⎧⋅=⎪⎨⋅=⎪⎩，即2020c b =⎧⎨=⎩，令1x =，则(1,0,0)m =，所以|||cos ,|||||13m n m n m n ⋅<>===⨯故二面角F CD B --=．22．（2021•新疆模拟）如图，在四棱锥A BCDE -中，平面ABC ⊥平面BCDE ，90CDE BED ∠=∠=︒，2AB CD ==，1DE BE ==，AC =（1）求证：DB ⊥平面ABC ；（2）求平面ABE 与平面ADC 所成二面角大小的余弦值．【解答】证明：（1）以D 为原点，DE 为x 轴，DC 为y 轴，在过D 作平面BCDE 垂线为z 轴，建立空间直角坐标系，则(0D ，0，0)，(1B ，1，0)，(0A ，2，(0C ，2，0)，(1DB =，1，0)，(0CA =，0，(1CB =，1-，0)， 0DB CA =，0DB CB =，DB CA ∴⊥，DB CB ⊥，CA CB C =，DB ∴⊥平面ABC ．解：（2）平面ADC 的法向量(1n =，0，0)，(1E ，0，0)，(1EA =-，2，(0EB =，1，0)，设平面ABE 的法向量(m x =，y ，)z ，则200m EA x y m EB y ⎧=-++=⎪⎨==⎪⎩，取1z =，得(2,0,1)m =，设平面ABE 与平面ADC 所成二面角大小为θ，则||2cos ||||3m n m n θ===．∴平面ABE 与平面ADC ．。

立体几何空间直角坐标系解法典型例题

学习必备欢迎下载立体几何坐标解法典型例题1、如图，正三棱柱ABC A1B1C1的所有棱长都为2 ， D 为CC1中点．（Ⅰ）求证： AB1⊥平面 A1 BD ；A A1（Ⅱ）求二面角 A A1D B 的大小；（Ⅲ）求点 C 到平面A BD的距离．C D C1 1B B12、如图，在 Rt△ AOB 中，OAB π，斜边 AB 4 ．Rt△AOC可以通过Rt△AOB以直线AO 6为轴旋转得到，且二面角 B AO C 的直二面角．D是AB的中点．A（1）求证：平面COD平面AOB；（2）求异面直线AO与CD所成角的大小．DEO BC3．(2010 ·海松江区模拟上 )设在直三棱柱 ABC－ A1 B1C1中，AB＝ AC＝ AA1＝ 2，∠ BAC＝90°，E， F 依次为 C1C， BC 的中点．(1)求异面直线 A1 B、 EF 所成角θ的正弦值；(2)求点 B1到平面 AEF 的距离．4.四棱锥 S ABCD 中，底面ABCD为平行四边形，侧面SBC底面ABCD．已知∠ABC 45，AB 2，BC 2 2，SA SB3．（Ⅰ）证明SABC ；（Ⅱ）求直线SD 与平面SAB所成角的大小．SCB D A5．如图，点 P 是单位正方体 ABCD － A 1B 1C 1D 1 中异于 A 的一个顶点，则 → →的值为AP ·AB ( )A ． 0B ． 1C ．0或1D ．任意实数5．在棱长为 1 的正方体 ABCD －A 1B 1C 1D 1 中， M 、N 分别为 A 1B 1 和 BB 1 的中点，那么直线AM 与 CN 所成角的余弦值等于 ( )310 A. 2 B. 1032 C.5D.5<二 >选择题辨析[注]：①两条异面直线在同一平面内射影一定是相交的两条直线 .（×）②直线在平面外，指的位置关系：平行或相交③若直线 a 、b 异面， a 平行于平面， b 与的关系是相交、平行、在平面内 .④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线 .（×）⑥在同一平面内的射影长相等，则斜线长相等 . （×）⑦ a, b 是夹在两平行平面间的线段，若 a b ，则 a, b 的位置关系为相交或平行或异面.[注]：①直线 a 与平面内一条直线平行，则 a ∥ . （×）②直线 a 与平面内一条直线相交，则a 与平面相交 . （×）③若直线 a 与平面平行，则内必存在无数条直线与a 平行 .（√）④两条平行线中一条平行于一个平面，那么另一条也平行于这个平面 . （×）⑤平行于同一直线的两个平面平行 .（×） ⑥平行于同一个平面的两直线平行 . （×）⑦直线 l 与平面、所成角相等，则 ∥. （×）[注]： ①垂直于同一平面的两个平面平行 . （×）．．．．②垂直于同一直线的两个平面平行. （√） ③垂直于同一平面的两条直线平行 . （√）。

用坐标方法解决立体几何问题 ppt课件

500kgkg50060kgabxayabc坐标分别为则正三角形的顶点建立空间直角坐标系轴的单位长度轴正方向方向为平面坐标为原点平面解
用坐标方法解决立体几何问题
如图，一块均匀的正三角形面的钢板的质量
为 500kg ，在它的顶点处分别受力 F1, F2, F3 ，每个力与同它相邻的三角形的两边之间的
A
D
O
B
E
C
用坐标方法解决立体几何问题
用坐标方法解决立体几何问题
用坐标方法解决立体几何问题
用坐标方法解决立体几何问题
坐标分别A为 (0,0,0),B(0,1,0),C( 3, 1,0). 22zFF1
3
C
F
2
O
A
用坐标方法解决x立体几何问题
500kg
B
y
例2 如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC,E是PC的中点，作 EF⊥PB交PB于点F.
(1)求证：PA//平面EDB
(2)求证：PB⊥平面EFD
P
(3)求二面角C-PB-D的大小。
F
E
D A
用坐标方法解决立体几何问题
C B
解：如图所示建立空间直角坐标系，点D为坐标原点，设DC=1
(1)证明：连结AC,AC交BD于点G,连结EG
依题意得A(1,0,0),P(0,0,1),
Z
11
E(0, , ) 22
P
因为底面ABCD是正方形，
角都是 60 ，且 F1 F2 F3 200kg .这块钢板在这些力的作用下将会怎样运动？这三
个力最小为多少时，才能提起这块钢板？
F3
F1
C
F2

空间坐标法解立体几何专题

例1（2011届景德镇市二检卷文19）正四棱柱1111D C B A ABCD -中，底面边长为6，侧棱长为4，E 、F 分别为棱AB 、BC 的中点（1）求证：平面EF B 1⊥平面11BDD B （2）求点1D 到平面EF B 1的距离d知识点：怎样用向量表示点到平面的距离？如图，PO ⊥α于O ，A 是平面α内任意一点，点P 到平面α的距离设为d ，n 为平面α的一个法向量，则有： ==||PO d θcos ||PA ==例1解：怎样用坐标法求点到平面的距离？例1第2问如图建立空间坐标系，分析：要求点1D 到平面 EF B 1的距离d ，由公式：d ||11n B D ⋅=，只要求出11B D 的坐标和平面EF B 1的一个法向量n 坐标，11B D 坐标很好求，因为1D 坐标为：（0，0，4），1B 坐标为（6，6，4），所以11B D 坐标为：（6，6，0）；下面求平面EF B 1的一个法向量n 坐标分析：如何求平面的一个法向量n 坐标？根据法向量的含义，法向量和平面垂直，故法向量和平面内任何一条直线都垂直，根据直线和平面垂直的判定定理，知道只要和两个不共线的向量垂直即可，在本题中可推出法向量n⊥E B 1，F B n 1⊥，所以01=⋅E B n ，01=⋅F B n ，由于1B 坐标为（6，6，4），E 坐标为（3，6，0），F 坐标为（6，3，0），所以E B 1的坐标为：（3-，0，4-），F B 1的坐标为：（0，3-，4-），利用坐标法，得到：⎩⎨⎧=--=--043043z y z x ，由于法向量有长有短，方向可以朝上，还可以朝下，所以法向量有无数多个，但法向量不可以是零向量，故z 不能取0，为简单起见，取3=z ，得：4-=x ，4-=y ，所以法向量n =4(-，4-，3）代入公式d ||n B D ⋅=，得点1D 到平面EF B 1的距离为：41414841483)4()4(|30)4(6)4(6|222==+-+-⨯+-⨯+-⨯=d例2（2010全国卷一6）直三棱柱111C B A ABC -中，若︒=∠90BAC ，1AA AC AB ==，则异面直线1BA 与1AC 所成的角等于（）A.30°B. 45°C. 60°D. 90°知识点：怎样用向量表示两条异面直线所成的角？=θcos cos |a <，>b |=例2解：怎样用坐标法求两条异面直线所成的角？解答例2：如图建立空间坐标系，设异面直线1BA 与1AC 所成的角为θ，则||cos 1111AC BA ⋅=θAB=a ，易求点B 坐标：（0，a ，)0，点1A 坐标：0(，0，a ），点A 坐标：（0，0，0），点1C 坐标： a (，0，a ），所以 0(1=BA ，a -，a ），=1AC a (，0，a ） 2120)(0|00|cos 22222222==+++-+⨯+⨯-⨯=aaaa aa a a a a θ∴︒=60θ故选C例3（2010江西卷20）如图，BC D ∆与M C D ∆都是边长为2的正三角形，平面M C D ⊥平面B C D ，AB ⊥平面B C D ，AB =. （1）求直线A M 与平面B C D 所成的角的大小；（2）求平面A C M 与平面B C D 所成的二面角的正弦值.知识点：怎样用向量表示直线和平面所成的角？见右下图，设直线PA 和平面α所成的角为θ，则θAPO ∠-︒=90，而PAO ∠可看成向量PA 和向量PO 的夹角，n 为平面α的一个法向量，显然n 与向量PO 共线，故法向量n 和向量PA 的夹角与向量PA 和向量PO 的夹角相等或互补，即PA <，>PO PA =<，>n 或PA <-π，>n ，所以)90sin(sin APO ∠-︒=θAPO ∠=cosPA <=cos ，>PO<=cos |PA ，>n |=例3解：怎样用坐标法求直线和平面所成的角？例3的第（1）问如图建立空间坐标系，设直线A M 与平面B C D所成的角的大小为θ， ∵AB ⊥平面B C D∴BA 是平面BCD 的一个法向量故sin =θ点A 坐标：（0，0，32）点B 坐标：（0，0，0）点M 坐标：（23，23，3）（注明：先作MO ⊥CD 于O ，过点C 作CE ⊥BD 于E ，CG ⊥y 轴于G ，过点O 作OF ⊥BD 于F ，OH ⊥y 轴于H ，再利用坐标定义求出点M 坐标）于是AM 23(=，23，3-)，BA =（0，0，32）∴222222)32(00)3()23()23(|323023023|sin ++-++⨯-⨯+⨯=θ1266=22=∴︒=45θ知识点：怎样用向量表示二面角平面角？如图：PA ⊥平面α，PB ⊥平面β，则PA ⊥l ，PB ⊥l ，所以l ⊥平面PAB ，设平面PAB 向四周延展后交l 于点C ，并连CA 、CB ，则有：CA ⊥l ，CB ⊥l ，故∠ACB 是二面角平面角；另一方面，四边形PBCA 内角和等于360°，而 ∠CBP =∠CAP=90°，所以二面角平面角∠ACB 与∠APB 互补作向量PB ，向量PA ，则∠APB 等于向量PB 、向量 PA 的夹角设1n 、2n 分别是平面α、β的法向量，它们的夹角1n <，>2n 与PA <，>PB 相等或互补设二面角平面角的大小为θ，则θ=1n <，>2n 或θ=-π1n <，>2n 例3解：怎样用坐标法求二面角的大小？例3的第（2）问求平面A C M 与平面B C D 所成的二面角的正弦值.分析：容易知道平面BCD 的一个法向量为1n =（0，0，1）所以只要求平面ACM 的法向量坐标即可。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

(2) a b a b (x1, y1, z1) (x2 , y2 , z2 ),
(3) a b a b x1x2 y1 y2 z1z2 0
3、设 a (x, y, z), 则 a x2 y2 z2
4、向量a、b的夹角：cos
a, b
a b
ab
返回
1、建立适当的空间直角坐标系
B
cos m, n
m n
1
1,
mn
3 3 3
二面角A
A1B
C的平面角的余弦值为1 3
。
3、如图，已知四棱锥P ABCD的底面是边长为2的菱形，且BAD 600，PA 平面ABCD，且PA 1，E、F分别是 BC、PA的中点。（1）求证：BF 平面PED；（2）求二面角P DE A的大小；（3）求点C到平面PED的距离。
（1）求证： AF 平面PEC；（2）求平面 PEC和平面PAD所成的
二面角的大小；（3）求点 D到平面 P E C的距离。
P1
3 A3
D
z P
6
F 3
B
(1)证明： A为P1D的中点， AB
3
C
CD, AB P1D,
A
3
D
即AB PA, AB AD AB 平面PAD,
E
y
CD 平面PAD,CD AD,CD PD,
(1)证明：如图，以CA为x轴，CB为y轴，
建立空间直角坐标系C xyz，则
A1
2P
C(0,0,0)、A( 2,0,0)、B(0,1,0)、Q( 2 , 1 ,0)、
22
M
(0,1,
1 2
)、A1
(
2,0,1), 设P(x,0,1)，
1
ቤተ መጻሕፍቲ ባይዱ
PQ (
21
1
x, ,1), CM (0,1, ),
A x
z A1 建立空间直角坐标系A xyz，
设AB a, AA1 m,则B（a，0，0），A1(0,0, m)
B1
C1
C(
a， 3 22
a,0),
A1B
(a,0,m),
A1C
(
a 2
,
3 a,m), 2
A
由
A1B
A1C, 得
A1B
A1C
a
（
a） 2
0
3 a (m)2 0, 2
B x
C
m
2 a,
x
PDA为二面角P CD B的平面角，
B
C
即PDA 450，
PA AD 3, PA AD, 故PA 平面ABCD,
6、如图，已知正方形ABCD和矩形ACEF所在的平面互相垂
直，AB 2, AF 1, M是线段EF的中点。
（1）求证：AM 平面BDE；（2）求二面角A DF B的大小；
n2
n1
cos n1, n2 | n1 n2 | , (其中n1、n2为二面角两个面的平面角） | n1 | | n2 |
n1, n2 或 n1, n2
2、两直线平行
3、两直线垂直
4、直线与平面平行
5、直线与平面垂直
SA n 6、点S到平面的距离： d
n
A Bn
n
Sn A
1、四棱锥S ABCD中, DAB ABC 900, SA 平面ABCD,
y
2
4、直三棱柱ABC A1B1C1中，AB AC， BAC 1200，BA1C 900。（1）求A1B与AC所成的角的余弦值；（2）求二面角C A1B A的大小。
z
A1
B1
C1
y A
B
C
O
x
5、在直角梯形 P1DCB中，P1D CB, 且P1D 6, BC 3，DC 6, A是P1D的中点，沿 AB把平面P1AB折起到平面 PAB的位置，使二面角P CD B成450角，设E、F分别是线段 AB、PD的中点。
（3）试在线段AC上确定一点P，使得PF与BC所成的角是600。
(1)证明：平面ACEF ABCD平面，而FA AC, 平面ACEF ABCD平面 AC，E FA 平面ABCD,
P(x, x,0)
M z
F
1
yD
C
P O
2
x
B
2
A
6、如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB 2, AF 1, M是线段EF的中点。（1）求证：AM 平面BDE；（2）求二面角A DF B的大小；（3）试在线段AC上确定一点P，使得PF与BC所成的角是600。
SA AB BC a, AD 2a.求证：平面SAC 平面SCD;
(2)求A到平面SCD的距离；（3）求SD和AC所成的角。
(1)证明：如图，以AB为x轴，AD为y轴，
z
S
建立空间直角坐标系A xyz，则
A(0,0,0)、C(a, a,0)、D(0,2a,0)、S(0,0, a),
a
设 m (x1, y1, z1)是平面SAC的法向量，则
m AB 2x1 y1 0 0
设 n (x2 , y2 , z2 )是平面A1BC的法向量，A1
P
z C1
则 n BC, n CA1,
B1
而 BC （0，1，0），CA1 （ 2，0，1），
M
n
BC
0
y2
0
0
A x
C
n CA1 2x2 1 z2 0
Q
取x2 1，得y2 0, z2 2, n (1,0, 2 )
22
2
B1 M
Q
PQCM (
2
x） 0
1
1 （ 1）
1
0， PQ
CM
B
2
2
2
y
z C1
C
1
（2）设 m (x1, y1, z1)是平面AA1B的法向量，则
m AA1, m AB,而 AA1 （0，0，1），AB （ 2，1，0），
m
AA1
0
0
z1
0
取x1 1，得y1 2, z1 0,m (1, 2,0)
A
a
2a
Dy
m AC, m SA,
Ba
C
x
而 AC (a, a,0),SA (0,0, a),
m m
AC ax1 ay1 0
SA 0 0 az1 0
0
取x1 1，得y1 1, z1 0,m (1,1,0)
设 n (x2, y2, z2 )是平面SCD的法向量，则 n SD, n CD,
z
SA n
A到平面SCD的距离d
2a 6 a
S
n
63
A
D
(3) SD (0,2a,a), AC (a, a,0),
y
cos SD, AC
SD AC
2a2
10 B
5a 2a 5 x
C
2、在直ABC A1B1C1三棱柱中，AC BC, AA1 BC 1,
AC 2,点M是的BB1中点，Q是AB的中点。（1）若P是A1C1上的一动点，求证：PQ CM；（2）求二面角A A1B C的余弦值。
而 SD (0,2a,a), CD (a, a,0),
n
SD
0
2ay2
az2
0
n SA ax2 ay2 0 0
取y2 1，得x2 1, z2 2, n (1,1,2)
m n 11 (1)1 0 2 0,平面SAC 平面SCD.
(2）由（1）知 n (1,1,2)是平面SCD的法向量，
zP
x D
6a E C O
x 2 2a
F(x, yF,0)(其中2xa,yy,02a)
F A
y
2a
y
B
8、如图，在底面为菱形的四棱锥P ABCD中，ABC 600， PA AC a, PB PD 2a,点E在PD上，且PE：ED 2：1. （1）求证：PA 平面ABCD; （2）求面EAC与面DAC所成的二面角的大小。
2、写出相应点的坐标 3、解决问题：
1、空间角
（1）两异面直线AB与CD的夹角：
为锐角或直角
cos AB,CD
AB CD
, AB,CD 或 AB,CD
AB CD
（2）直线 l与平面所成的角：
AB, n
或
AB, n
2
2
A
sin cos AB, n
AB n
AB n
Bn
（3）二面角的平面角：
E
z
M
P(0, y,0)
1
C P
xD
2
F
B
2
Ay
7、如图，正四棱锥P ABCD中，侧棱PA与底面ABCD
所成的角的正切值为 6 。 2
（1）求侧面PAD与底面ABCD所成的二面角的大小；（2）若E是PB的中点，求异面直线PD与AE所成角的余弦值；（3）问在棱AD上是否存在一点F，使EF 侧面PBC，若存在，使确定点F的位置；若不存在，说明理由。
z P
F
D
A x
2
C
E
B
（1，3，0）
y
CP n
d
z
n
D
C
E
x
P（ 3，0，1）
F
A
2
B y
4、直三棱柱ABC A1B1C1中，AB AC，
BAC 1200，BA1C 900。
（1）求A1B与AC所成的角的余弦值；
（2）求二面角C A1B A的大小。如图，以AB为x轴，AA1为z轴，