无向图深度遍历邻接矩阵报告
选择题

苏州市职业大学20 ─20 学年第学期试卷标准答案及评分标准《》(集中/分散A/B卷开/闭卷笔试/上机)2002-2003下《计算机应用基础》考试题(适用班级:02级学生)本卷满分100 分考试时间为1.5 小时出题老师:干雪芳、庄卓试卷考试形式:闭卷班级______________ 学号_________ 姓名________一、单项选择题 (每题1分,共142分)1. 向一个有128个元素的顺序表中插入一个新元素并保持原来顺序不变,平均要移动()个元素。
A.64B.63C.63.5D.7【答案】A2. 线性表是具有n个()的有限序列(n≠0)。
A.表元素B.字符C.数据元素D.数据项【答案】C3. 下列哪种排序方法在最坏的情况下的时间复杂度是O(n*log2n)()。
A .直接插入排序 B. 堆排序 C. 简单选择排序 D. 快速排序【答案】B4. 数组A[5][6]的每个元素占5个单元,将其按行优先次序存储在起始地址为1000的连续的内存单元中,则元素A[4][4]的地址为()。
A.1140B.1145C.1120D.1125【答案】A5. 从一个栈顶指针为HS的链栈中删除一个结点时,用x保存被删结点的值,则执行()。
A.x=HS;HS=HS->next;B.x=HS->data;C.HS=HS->next;x=HS->data;D.x=HS->data;HS=HS->next;【答案】D6. 已知含6个顶点(v0,v1,v2,v3,v4,v5)的无向图的邻接矩阵如图所示,则从顶点v0出发进行深度优先遍历可能得到的顶点访问序列为()。
A.(v0,v1,v2,v5,v4,v3)B.(v0,v1,v2,v3,v4,v5)C.(v0,v1,v5,v2,v3,v4)D.(v0,v1,v4,v5,v2,v3)【答案】A7. 如下陈述中正确的是()。
A.串是一种特殊的线性表B.串的长度必须大于零C.串中元素只能是字母D.空串就是空白串【答案】A8. 在一个长度为n的顺序表中插入一个元素时,等概率情况下的平均移动元素的次数是()。
《数据结构》实验指导书

1.单链表的类型定义
#include <stdio.h>
typedef int ElemType;//单链表结点类型
typedef struct LNode
{ElemType data;
struct LNode *next;
2.明确栈、队列均是特殊的线性表。
3.栈、队列的算法是后续实验的基础(广义表、树、图、查找、排序等)。
六、实验报告
根据实验情况和结果撰写并递交实验报告。
实验四 串
一、预备知识
1.字符串的基本概念
2.字符串的模式匹配算法
二、实验目的
1.理解字符串的模式匹配算法(包括KMP算法)
typedef struct
{ElemType *base;
int front,rear;
} SqQueue;
4.单链队列的类型定义
typedef struct QNode
{QElemType data;
typedef struct list
{ElemType elem[MAXSIZE];//静态线性表
int length; //顺序表的实际长度
} SqList;//顺序表的类型名
五、注意问题
1.插入、删除时元素的移动原因、方向及先后顺序。
4.三元组表是线性表的一种应用,通过它可以更好地理解线性表的存储结构。同时矩阵又是图的重要的存储方式,所以这个实验对更好地掌握线性表对将来对图的理解都有极大的帮助。
六、实验报告
根据实验情况和结果撰写并递交实验报告。
实验六 树和二叉树
一、预备知识
1.二叉树的二叉链表存储结构
无向图的基本算法

marked = new boolean[graph.V()]; id = new int[graph.V()]; for (int i =0; i < graph.V(); i++) {
View Code 试验一个算法最简单的办法是找一个简单的例子来实现。
深度优先路径查询 有了这个基础,我们可以实现基于深度优先的路径查询,要实现路径查询,我们必须定义一个变量来记录所探索到的路径。所以在上面 的基础上定义一个edgesTo变量来后向记录所有到s的顶点的记录,和仅记录从当前节点到起始节点不同,我们记录图中的每一个节点到开 始节点的路径。为了完成这一日任务,通过设置edgesTo[w]=v,我们记录从v到w的边,换句话说,v-w是最后一条从s到达w的边。 edgesTo[]其实是一个指向其父节点的树。
}
View Code
广度优先算法的搜索步骤如下:
广度优先搜索首先是在距离起始点为1的范围内的所有邻接点中查找有没有到达目标结点的对象,如果没有,继续前进在距离起始点为
2的范围内查找,依次向前推进。
连通分量 使用深度优先遍历计算图的所有连通分量。
package Graph; public class CC {
public int GetVerticals () {
return verticals; }
public int GetEdges() {
return edges; }
public void AddEdge(int verticalStart, int verticalEnd) {
数据结构课程设计实践报告

数据结构实验报告实验名称:结构图提交文档学生姓名:提交文档学生学号:同组成员名单:指导教师姓名:结构图一、实验目的和要求1、设计目的1.掌握图的相关概念,包括图,有向图,无向图,完全图,子图,连通图,度,入度,出度,简单回路和环等定义。
2.重点掌握图的各种存储结构,包括邻接矩阵和邻接表等。
3.重点掌握图的基本运算,包括创建图,输出图,深度优先遍历,广度优先遍历等。
4.掌握图的其他运算,包括最小生成树,最短路径,拓扑排序和关键路径等算法。
5. 灵活运用图这种数据结构解决一些综合应用问题。
2、设计内容和要求1、编写一个程序algo8-1.cpp,实现不带权图和带权图的邻接矩阵与邻接表的相互转换算法、输出邻接矩阵与邻接表的算法,并在此基础上设计一个程序exp8-1.cpp实现如下功能:①建立如图1所示的有向图G的邻接矩阵,并输出;②由有向图G的邻接矩阵产生邻接表,并输出;③再由②的邻接表产生对应的邻接矩阵,并输出。
图12、编写一个程序algo8-2.cpp,实现图的遍历运算,并在此基础上设计一个程序exp8-2.cpp完成如下功能:①输出图1所示的有向图G从顶点0开始的深度优先遍历序列(递归算法);②输出图1所示的有向图G从顶点0开始的深度优先遍历序列(非递归算法);③输出图1所示的有向图G从顶点0开始的广度优先遍历序列。
3、设计一个程序exp8-3.cpp,采用邻接表存储图,并输出图8.1(a)中从指定顶点1出发的所有深度优先遍历序列。
二、运行环境(软、硬件环境)软件环境:Visual C++6.0运行平台: Win32硬件:普通个人pc机三、实验过程描述文件graph.h中定义了图的邻接矩阵表示类型和邻接表表示类型,该头文件在以下三个实验中都会使用到。
其代码如下:#ifndef GRAPH_H_INCLUDED#define GRAPH_H_INCLUDEDtypedef int InfoType;#define MAXV 100 //最大顶点个数#define INF 32767 //INF表示无限大//以下定义邻接矩阵类型typedef struct{int no;InfoType info;}VertexType;typedef struct{int edges[MAXV][MAXV];int n,e;VertexType vexs[MAXV];}MGraph;//以下定义邻接表类型typedef struct ANode{int adjvex;struct ANode* nextarc;InfoType info;}ArcNode;typedef int Vertex;typedef struct VNode{Vertex data;ArcNode* firstarc;}VNode;typedef VNode AdjList[MAXV];typedef struct{AdjList adjlist;int n,e;}ALGraph;#endif // GRAPH_H_INCLUDED实验①源程序。
邻接矩阵的深度优先遍历算法

邻接矩阵的深度优先遍历算法简介邻接矩阵是一种常用的图表示方法,它使用一个二维数组来表示图中各个节点之间的关系。
深度优先遍历(Depth First Search,DFS)是一种常用的图遍历算法,它通过递归或栈的方式依次访问图中的所有节点。
本文将介绍邻接矩阵的深度优先遍历算法,并提供相应的代码实现。
邻接矩阵邻接矩阵是一种二维数组,它的行和列分别代表图中的各个节点。
如果两个节点之间存在边,则对应位置上的元素为1;否则为0。
对于无向图来说,邻接矩阵是对称的;而对于有向图来说,邻接矩阵不一定对称。
下面是一个示例的邻接矩阵:A B C DA 0 1 0 1B 1 0 1 1C 0 1 0 0D 1 1 0 0深度优先遍历算法算法思想深度优先遍历算法从起始节点开始,递归或使用栈的方式依次访问与当前节点相邻的未访问过的节点,直到所有节点都被访问过为止。
算法步骤1.创建一个栈,并将起始节点入栈;2.创建一个数组,用于记录已经访问过的节点;3.当栈不为空时,执行以下操作:–从栈顶弹出一个节点,标记为已访问,并输出该节点;–遍历该节点的邻居节点,如果邻居节点未被访问,则将其入栈;4.重复步骤3,直到栈为空。
算法实现def dfs(adj_matrix, start_node):stack = [start_node]visited = [False] * len(adj_matrix)while stack:node = stack.pop()visited[node] = Trueprint(node)for i in range(len(adj_matrix)):if adj_matrix[node][i] == 1 and not visited[i]:stack.append(i)示例假设有以下图的邻接矩阵:A B C DA 0 1 0 1B 1 0 1 1C 0 1 0 0D 1 1 0我们以A作为起始节点进行深度优先遍历,那么遍历的顺序将会是A、B、C、D。
图练习与答案
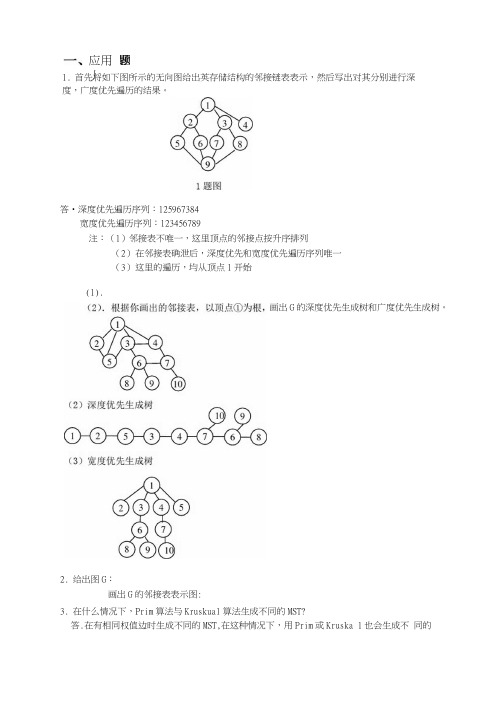
1. 首先将如下图所示的无向图给出英存储结构的邻接链表表示,然后写出对其分别进行深度,广度优先遍历的结果。
答•深度优先遍历序列:125967384宽度优先遍历序列:123456789注:(1)邻接表不唯一,这里顶点的邻接点按升序排列(2) 在邻接表确泄后,深度优先和宽度优先遍历序列唯一 (3) 这里的遍历,均从顶点1开始 2. 给出图G :画岀G 的邻接表表示图:3. 在什么情况下,Prim 算法与Kruskual 算法生成不同的MST?答.在有相同权值边时生成不同的MST,在这种情况下,用Prim 或Kruska 1也会生成不 同的应用丿 画出G 的深度优先生成树和广度优先生成树。
(1).HST4・已知一个无向图如下图所示,要求分别用Prim和Kruskal算法生成最小树(假设以①为起点,试画出构适过程)。
答.Prim算法构造最小生成树的步骤如24题所示,为节省篇幅,这里仅用Kruskal算法, 构造最小生成树过程如下:(下图也可选(2, 4)代替(3, 4), (5, 6〉代替⑴5))5.G=(V,E)是一个带有权的连通图,则:(1). ifi回答什么是G的最小生成树:(2). G为下图所示,请找出G的所有最小生成树。
答.(1)最小生成树的左义见上而26题(2)最小生成树有两棵。
邙艮于篇幅,下而的生成树只给岀顶点集合和边集合,边以三元组(Vi,Vj,W)形式),其中 W代表权值。
V (G) ={1, 2, 3, 4, 5} E1(G) = {(4, 5, 2), (2, 5, 4), (2, 3, 5), (1, 2,7) }:E2(G)={(4, 5, 2), (2, 4, 4), (2, 3, 5), (b 2、7) }6.请看下边的无向加权图。
(1).写出它的邻接矩阵。
(2).按Prim算法求其最小生成树, 并给出构造最小生成树过程中辅助数组的各分量值。
辅助数组各分量值:7.已知世界六大城市为:(Pe)、纽约(N)、巴黎(Pa).伦敦(L)、东京仃).墨西哥(M), 下表给泄了这六大城市之间的交通里程:世界六大城市交通里程表(单位:百公里)(1) .画岀这六大城市的交通网络图;(2) .画出该图的邻接表表示法;(3) .画岀该图按权值递增的顺序来构造的最小(代价)生成树.8.已知顶点1-6和输入边与权值的序列(如右图所示):每行三个数表示一条边的两个端点和貝权值,共11行。
数据结构第七章课后习题答案 (1)

7_1对于图题7.1(P235)的无向图,给出:(1)表示该图的邻接矩阵。
(2)表示该图的邻接表。
(3)图中每个顶点的度。
解:(1)邻接矩阵:0111000100110010010101110111010100100110010001110(2)邻接表:1:2----3----4----NULL;2: 1----4----5----NULL;3: 1----4----6----NULL;4: 1----2----3----5----6----7----NULL;5: 2----4----7----NULL;6: 3----4----7----NULL;7: 4----5----6----NULL;(3)图中每个顶点的度分别为:3,3,3,6,3,3,3。
7_2对于图题7.1的无向图,给出:(1)从顶点1出发,按深度优先搜索法遍历图时所得到的顶点序(2)从顶点1出发,按广度优先法搜索法遍历图时所得到的顶点序列。
(1)DFS法:存储结构:本题采用邻接表作为图的存储结构,邻接表中的各个链表的结点形式由类型L_NODE规定,而各个链表的头指针存放在数组head中。
数组e中的元素e[0],e[1],…..,e[m-1]给出图中的m条边,e中结点形式由类型E_NODE规定。
visit[i]数组用来表示顶点i是否被访问过。
遍历前置visit各元素为0,若顶点i被访问过,则置visit[i]为1.算法分析:首先访问出发顶点v.接着,选择一个与v相邻接且未被访问过的的顶点w访问之,再从w 开始进行深度优先搜索。
每当到达一个其所有相邻接的顶点都被访问过的顶点,就从最后访问的顶点开始,依次退回到尚有邻接顶点未曾访问过的顶点u,并从u开始进行深度优先搜索。
这个过程进行到所有顶点都被访问过,或从任何一个已访问过的顶点出发,再也无法到达未曾访问过的顶点,则搜索过程就结束。
另一方面,先建立一个相应的具有n个顶点,m条边的无向图的邻接表。
数据结构- 图

7.2 图的存储表示
一、图的数组(邻接矩阵)存储表示 二、图的邻接表存储表示 三、有向图的十字链表存储表示 四、无向图的邻接多重表存储表示
28
一、图的数组(邻接矩阵)存储表示
定义:矩阵的元素为
1
aij
0
若(vi , v j )或 vi , v j E 否则
v1
v2
v3
v4
v5
无向图G2
} ArcNode;
39
顶点的结点结构
data firstarc
typedef struct VNode { VertexType data; // 顶点信息 ArcNode *firstarc; // 指向第一条依附该顶点的弧 } VNode, AdjList[MAX_VERTEX_NUM];
40
谓词 P(v,w) 定义了弧 <v,w>的意义或信息。
3
由于“弧”是有方向的,因此称由顶点集和弧集构成的图为有 向图。
例如: G1 = (V1, VR1) A
B
E
其中 V1={A, B, C, D, E} VR1={<A,B>, <A,E>,
<B,C>, <C,D>, <D,B>, <D,A>, <E,C> }
24
插入或删除顶点
InsertVex(&G, v); //在图G中增添新顶点v。 DeleteVex(&G, v);
// 删除G中顶点v及其相关的弧。
25
插入和删除弧 InsertArc(&G, v, w); // 在G中增添弧<v,w>,若G是无向的, //则还增添对称弧<w,v>。 DeleteArc(&G, v, w);
实验五 图的基本操作

实验五图的基本操作一、实验目的1、使学生可以巩固所学的有关图的基本知识。
2、熟练掌握图的存储结构。
3、熟练掌握图的两种遍历算法。
二、实验内容本次实验提供4个题目,难度相当,学生可以根据自己的情况选做,其中题目一是必做题,其它选作!题目一:图的遍历(必做)[问题描述]对给定图,实现图的深度优先遍历和广度优先遍历。
[基本要求]以邻接表为存储结构,实现连通无向图的深度优先和广度优先遍历。
以用户指定的结点为起点,分别输出每种遍历下的结点访问序列。
【测试数据】由学生依据软件工程的测试技术自己确定。
题目二:在图G中求一条从顶点 i 到顶点 s 的简单路径[测试数据]自行设计[题目三]:在图G中求一条从顶点 i 到顶点 s 且长度为K的简单路径[测试数据]自行设计三、实验前的准备工作1、掌握图的相关概念。
2、掌握图的逻辑结构和存储结构。
3、掌握图的两种遍历算法的实现。
四、实验报告要求1、实验报告要按照实验报告格式规范书写。
2、实验上要写出多批测试数据的运行结果。
3、结合运行结果,对程序进行分析。
一.实验内容定义结构体QueueNode,并完成队列的基本操作,利用队列先进先出的性质,在广度优先遍历时将队列作为辅助工具来完成广度优先遍历。
void EnQueue(QueueList* Q,int e)函数实现进队操作,if-else语句完成函数的具体操作void DeQueue(QueueList* Q,int* e)函数实现出队操作,if-else语句完成函数的具体操作void CreatAdjList(Graph* G)函数用来完成创建图的操作,其中使用两次for循环语句第一次用循环语句输入顶点,第二次建立无向图中的边和表,流程图如图表1所示void dfs(Graph *G,int i,int visit[])函数是从第i个顶点出发递归的深度优先遍历图G深度优先搜索:dfs():寻找v的还没有访问过的邻接点,循环找到v的所有的邻接点,每找到一个都以该邻接点为新的起点递归调用深度优先搜索,找下一个邻接点。
数据结构课程设计-图的遍历和构建

摘要图(Graph)是一种复杂的非线性结构。
图可以分为无向图、有向图。
若将图的每条边都赋上一个权,则称这种带权图网络。
在人工智能、工程、数学、物理、化学、计算机科学等领域中,图结构有着广泛的应用。
在图结构中,对结点(图中常称为顶点)的前趋和后继个数都是不加以限制的,即结点之间的关系是任意的。
图中任意两个结点之间都可能相关。
图有两种常用的存储表示方法:邻接矩阵表示法和邻接表表示法。
在一个图中,邻接矩阵表示是唯一的,但邻接表表示不唯一。
在表示的过程中还可以实现图的遍历(深度优先遍历和广度优先遍历)及求图中顶点的度。
当然对于图的广度优先遍历还利用了队列的五种基本运算(置空队列、进队、出队、取队头元素、判队空)来实现。
这不仅让我们巩固了之前学的队列的基本操作,还懂得了将算法相互融合和运用。
目录第一章课程设计目的..................................................................................... 错误!未定义书签。
第二章课程设计内容和要求....................................................................... 错误!未定义书签。
2.1课程设计内容.................................................................................. 错误!未定义书签。
2.1.1图的邻接矩阵的建立与输出ﻩ错误!未定义书签。
2.1.2图的邻接表的建立与输出............................................... 错误!未定义书签。
2.1.3图的遍历的实现.................................................................... 错误!未定义书签。
数据结构实验报告-无向图的邻接矩阵存储结构

数学与计算机学院课程设计说明书课程名称: 数据结构与算法课程设计课程代码: 6014389 题目: 无向图的邻接矩阵存储结构年级/专业/班: 2010级软件4班学生姓名: 吴超学号: 312010*********开始时间: 2011 年 12 月 9 日完成时间: 2011 年 12 月 30 日课程设计成绩:指导教师签名:年月日数据结构课程设计任务书学院名称:数学与计算机学院课程代码:__6014389______ 专业:软件工程年级:2010一、设计题目无向图的邻接矩阵存储结构二、主要内容图是无向带权图,对下列各题,要求写一算法实现。
1)能从键盘上输入各条边和边上的权值;2)构造图的邻接矩阵和顶点集。
3)输出图的各顶点和邻接矩阵4)插入一条边5)删除一条边6)求出各顶点的度7)判断该图是否是连通图,若是,返回1;否则返回0.8)使用深度遍历算法,输出遍历序列。
三、具体要求及应提交的材料用C/C++语言编程实现上述内容,对每个问题写出一个算法实现,并按数学与计算机学院对课程设计说明书规范化要求,写出课程设计说明书,并提交下列材料:1)课程设计说明书打印稿一份2)课程设计说明书电子稿一份;3)源程序电子文档一份。
四、主要技术路线提示用一维数组存放图的顶点信息,二维数组存放各边信息。
五、进度安排按教学计划规定,数据结构课程设计为2周,其进度及时间大致分配如下:六、推荐参考资料[1] 严蔚敏,吴伟民.数据结构.清华大学出版社出版。
[2] 严蔚敏,吴伟民. 数据结构题集(C语言版) .清华大学出版社.2003年5月。
[3]唐策善,李龙澎.数据结构(作C语言描述) .高等教育出版社.2001年9月[4] 朱战立.数据结构(C++语言描述)(第二版本).高等出版社出版.2004年4月[5]胡学钢.数据结构(C语言版) .高等教育出版社.2004年8月指导教师签名日期年月日系主任审核日期年月日目录引言 (7)1 需求分析 (7)1.1任务与分析 (7)1.2测试数据 (8)2 概要设计 (8)2.1 ADT描述 (8)2.2程序模块结构 (9)2.3各功能模块 (11)3详细设计 (11)3.1类的定义 (11)3.2 初始化 (12)3.3 图的构建操作 (13)3.4 输出操作 (13)3.5 get操作 (14)3.6 插入操作 (14)3.7 删除操作 (15)3.8 求顶点的度操作 (15)3.10 判断连通操作 (17)3.11 主函数 (17)4 调试分析 (17)4.1 测试数据 (20)4.2调试问题 (20)4.3 算法时间复杂度 (20)4.4 经验和心得体会 (21)5用户使用说明 (21)6测试结果 (21)6.1 创建图 (21)6.2插入节点 (22)6.3 深度优先遍历 (22)6.4 求各顶点的度 (22)6.5 输出图 (23)6.6 判断是否连通 (23)6.7 求边的权值 (24)6.8 插入边 (24)6.9 删除边 (25)结论 (26)致谢 (27)摘要随着计算机的普及,涉及计算机相关的科目也越来越普遍,其中数据结构是计算机专业重要的专业基础课程与核心课程之一,为适应我国计算机科学技术的发展和应用,学好数据结构非常必要,然而要掌握数据结构的知识非常难,所以对“数据结构”的课程设计比不可少。
无向图的深度优先遍历序列

#include <stdio.h>#define MAXVERTEXNUM 20#define TRUE 1#define FALSE 0typedef char VertexType;typedef int VRType;typedef int Status;typedef int InfoType;typedef enum {DG,DN,UDG,UDN} GraphKind;typedef struct ArcCell { // 弧的定义VRType adj; // VRType是顶点关系类型。
// 对无权图,用1或0表示相邻否;// 对带权图,则为权值类型。
InfoType *info;} ArcCell,AdjMatrix[MAXVERTEXNUM][MAXVERTEXNUM]; typedef struct { // 图的定义VertexType vexs[MAXVERTEXNUM]; // 顶点信息 AdjMatrix arcs; // 弧的信息int vexnum, arcnum; // 顶点数,弧数GraphKind kind; // 图的种类标志} MGraph;int visited[MAXVERTEXNUM];int LocateVex(MGraph G, VertexType v){int i;for(i=0; i<G.vexnum; i++)if(G.vexs[i]==v)return i;return -1;}void CreateMGraph(MGraph &G){ //建立无向图int i,j,k;char v1,v2;printf("\n输入顶点数和边数(用逗号隔开) : ");scanf("%d,%d",&G.vexnum, &G.arcnum);getchar();for (i=0 ; i< G.vexnum; ++i){printf("输入顶点 %d 的值 : ",i+1);scanf("%c",&G.vexs[i]);getchar();}for (i=0 ; i< G.vexnum; ++i)for(j=0 ; j< G.vexnum; ++j)G.arcs[i][j].adj=0;for(k=1;k<=G.arcnum;k++){printf("输入第 %d 条边的起始顶点和终止顶点(用逗号隔开): ",k); scanf("%c,%c",&v1,&v2);i=LocateVex(G,v1) ; j= LocateVex(G,v2) ;G.arcs[i][j].adj=1;G.arcs[j][i].adj=1;getchar();}} //ENDvoid DFS(MGraph G,int i);void DFSTraverse(MGraph G){ // 对图 G 作深度优先遍历。
邻接矩阵的深度优先遍历算法

邻接矩阵的深度优先遍历算法简介邻接矩阵是一种常见的图存储结构,它使用二维数组来表示图中各个顶点之间的关系。
而深度优先遍历算法是一种常用的图遍历算法,用于遍历和搜索图的各个顶点。
本文将介绍邻接矩阵的深度优先遍历算法,包括其基本思想、实现步骤以及应用场景等内容。
基本思想深度优先遍历算法(Depth-First Search,DFS)是一种针对图和树的遍历算法,它通过从起始顶点开始,逐个探索图中的顶点,并沿着某一条路径一直深入,直到无法继续为止,然后回溯到前一顶点继续探索其它路径,直到所有顶点都被访问过为止。
邻接矩阵是一种常见的图表示方法,它通过一个二维数组来表示图中各个顶点之间的关系。
邻接矩阵中的每个元素表示两个顶点之间是否存在一条边,具体而言,如果顶点i和顶点j之间存在一条边,则邻接矩阵中下标为(i, j)和(j, i)的元素值为1;否则,它们的元素值为0。
邻接矩阵的深度优先遍历算法是通过对邻接矩阵进行遍历,找出与起始顶点相连接的顶点,并依次对这些顶点进行深度优先遍历。
实现步骤邻接矩阵的深度优先遍历算法可以使用递归或迭代的方式来实现。
下面分别介绍这两种实现方法的具体步骤。
递归实现1.创建一个数组visited,用来记录每个顶点是否已被访问过,初始时所有元素都设为0。
2.选择一个起始顶点v,并将visited[v]设置为1,表示该顶点已被访问过。
3.遍历邻接矩阵中与v相连的所有顶点w,如果visited[w]为0,则递归调用深度优先遍历函数,将w作为新的起始顶点。
4.重复步骤3,直到所有顶点都被访问过为止。
迭代实现1.创建一个数组visited,用来记录每个顶点是否已被访问过,初始时所有元素都设为0。
2.创建一个栈,用来存储待访问的顶点。
3.选择一个起始顶点v,并将visited[v]设置为1,表示该顶点已被访问过。
4.将v入栈。
5.当栈不为空时,执行以下操作:–出栈一个顶点u,访问它。
–遍历邻接矩阵中与u相连的所有顶点w,如果visited[w]为0,则将w入栈,并将visited[w]设置为1。
图的遍历深度优先遍历和广度优先遍历

4
5
f
^
对应的邻接表
终点2作为下次的始点, 由于1点已访问过,跳过, 找到4,记标识,送输出, 4有作为新的始点重复上 述过程
1 2 4
5
输出数组 resu
3.邻接表深度优先遍历的实现
template <class TElem, class TEdgeElem>long DFS2(TGraphNodeAL<TElem, TEdgeElem> *nodes,long n,long v0, char *visited, long *resu,long &top) {//深度优先遍历用邻接表表示的图。nodes是邻接表的头数组,n 为结点个数(编号为0~n)。 //v0为遍历的起点。返回实际遍历到的结点的数目。 //visited是访问标志数组,调用本函数前,应为其分配空间并初 始化为全0(未访问) //resu为一维数组,用于存放所遍历到的结点的编号,调用本函 数前,应为其分配空间 long nNodes, i; TGraphEdgeAL<TEdgeElem> *p; nNodes=1;
1 2
4
图 20-1有向图
5
3
1 2 3 4 5
1 0 1 0 1 0
2 1 0 0 0 0
3 0 0 0 0 0
4 0 1 0 0 0
5 1 0 1 0 0
1 2 3 4 5
1 1 0 1 1
1 2 4 5
所示图的邻接矩阵g
访问标识数组 visited
输出数组 resu
例如从1点深度优先遍历,先把1设置访问标志,并置入输出数组resu,然后从邻接 矩阵的第一行,扫描各列,找到最近的邻接点2,将其设置访问标志,并进入输出数 组,接着从邻接矩阵的2行扫描,找到第一个构成边的点是1,检查访问标识数组, 发现1已经访问过,跳过,找第二个构成边 的点4,设置访问标识,进入输出数组, 再从邻接矩阵的第4行扫描,寻找构成边的点,除1外在无其他点,返回2行,继续 寻找,也无新点,返回1,找到5,将5置访问标志,进入输出数组,1行再无其他新 点,遍历结束,返回遍历元素个数为4 。
邻接矩阵和点坐标-概述说明以及解释

邻接矩阵和点坐标-概述说明以及解释1. 引言1.1 概述邻接矩阵和点坐标是图论中常用的两种表示图结构的方法。
邻接矩阵是一种二维数组,用于表示图中顶点之间的连接关系,而点坐标则是通过在平面上定义每个顶点的位置来表示图的结构。
邻接矩阵是图的一种静态表示方式,它将图中的顶点和边映射到一个矩阵中。
在邻接矩阵中,矩阵的行和列分别对应于图中的顶点,而矩阵元素的值表示对应顶点之间是否存在边。
邻接矩阵的优点是易于理解和实现,特别适用于稠密图,但对于稀疏图而言,其空间复杂度较高。
相对于邻接矩阵的静态表示方式,点坐标则提供了一种更加直观和灵活的图表示方法。
点坐标通过给图中的每个顶点指定一个坐标来确定图的结构。
这些坐标可以体现顶点之间的相邻关系以及它们在平面上的位置。
点坐标的使用使得图可以在平面上直观地绘制出来,并且可以方便地计算顶点之间的距离和角度等信息。
邻接矩阵和点坐标在图的表示和分析中扮演着重要的角色。
它们有着各自的特点和适用场景,可以相互转换和结合使用,从而为图论的相关问题的解决提供了多种方法和思路。
本篇文章将对邻接矩阵和点坐标的原理、应用和优缺点进行详细介绍和讨论。
在文章的后续部分中,我们将分别对邻接矩阵和点坐标进行深入探讨,并通过具体实例来解释其使用方法和技巧。
最后,我们将对这两种方法进行对比和总结,并展望它们在未来图论研究中的潜在发展方向。
1.2 文章结构文章结构部分的内容可以包括以下信息:文章结构部分旨在介绍文章的整体结构和各个章节的内容安排。
本文的结构分为引言、正文和结论三个部分。
引言部分主要从概述、文章结构和目的三个方面介绍了本文的主题和目标。
概述部分介绍了邻接矩阵和点坐标的概念以及它们在图论和几何学中的重要性。
文章结构部分主要包含了两个章节:邻接矩阵和点坐标。
邻接矩阵章节会详细介绍邻接矩阵的定义、性质、应用等内容。
邻接矩阵是一种常见的图表示方法,它可以通过矩阵来表示图中节点之间的连接关系,是图论中的重要基础概念。
编写程序实现图的各种基本运算

仲恺农业工程学院实验报告纸计算机科学与工程学院(院、系)专业班组课《数据结构》实验报告一、上机实验的问题和要求(需求分析):[ 题目]编写程序实现图的各种基本预算,并在此基础上设计主函数,使其完成如下功能:(1)建立无向图。
(2)输出无向图对应的邻接矩阵(3)实现深度遍历和广度遍历。
二、源程序及注释以及运行结果[ 源程序] 程序名://text8-2.c#include<stdio.h>#include<stdlib.h>#define MAXV 100int a[MAXV][MAXV];int Visited[MAXV];typedef char InfoType;typedef char Vertex;typedef struct ArcNode //弧的结点的数据结构{int adjvex; //该弧所指向的顶点的位置,即终点位置struct ArcNode *nextarc; //指向下一条弧的指针InfoType info; //该弧的相关信息}ArcNode;typedef struct VNode{Vertex data; //顶点信息ArcNode *firstarc; //指向第一条依附该顶点的弧的指针}VNode,AdjList[MAXV];typedef struct{AdjList adjlist;int n,e; //图中的顶点数n和边数e}ALGraph; //图的类型void createALGraph(ALGraph &G) //创建图{int i;int j;int k;for(i=0;i!=G.n;i++){G.adjlist[i].data=i+1;}printf("请输入某边的相邻顶点(vi-vj)的下标(如:1 2):\n");for(i=0;i!=G.e;i++){scanf("%d %d",&j,&k);a[j-1][k-1]=1;a[k-1][j-1]=1;}int mark;ArcNode *p;ArcNode *q;for(i=0;i!=G.n;i++){mark=0;for(j=0;j!=G.n;j++)if(j==i)continue;else if(a[i][j]==1){if(mark==0){p=(ArcNode *)malloc(sizeof(ArcNode));p->adjvex=j;p->nextarc=NULL;G.adjlist[i].firstarc=p;mark=1;}else{q=(ArcNode *)malloc(sizeof(ArcNode));q->adjvex=j;q->nextarc=NULL;p->nextarc=q;p=p->nextarc;q=NULL;}}elsecontinue;}}//createAlGraphint firstAdjvex(ALGraph G,int v){if(G.adjlist[v].firstarc!=NULL)return G.adjlist[v].firstarc->adjvex;else return -1;}int nextAdjvex(ALGraph G,int v,int w){ArcNode *r;r=(ArcNode *)malloc(sizeof(ArcNode));r=G.adjlist[v].firstarc;while(r->nextarc!=NULL){if(r->adjvex==w)return r->nextarc->adjvex;elser=r->nextarc;}r=NULL;return -1;}void DFS(ALGraph G,int v)//深度优先遍历{int w;Visited[v]=true;printf("%d ",G.adjlist[v].data);for(w=firstAdjvex(G,v);w>=0;){if(!Visited[w])DFS(G,w);w=nextAdjvex(G,v,w);}}//深度优先遍历void DSTaverse(ALGraph G,int v){int i;for(i=0;i!=G.n;i++)Visited[i]=false;printf("从第一个位置深度优先遍历结果为:\n");if(!Visited[v])DFS(G,v);for(v=0;v!=G.n;v++)if(!Visited[v])DFS(G,v);}//广度优先遍历void BFS(ALGraph *G,int v){ArcNode *p;int queue[MAXV],front=0,rear=0;int visited[MAXV];int w,i;for(i=0;i<G->n;i++)visited[i]=0;printf("%d ",v);visited[v]=1;rear=(rear+1)%MAXV;queue[rear]=v;while(front!=rear){front=(front+1)%MAXV;w=queue[front];p=G->adjlist[w].firstarc;while(p!=NULL){if(visited[p->adjvex]==0){printf("%d ",p->adjvex);visited[p->adjvex]=1;rear=(rear+1)%MAXV;queue[rear]=p->adjvex;}p=p->nextarc;}}printf("\n");}void main(){ALGraph G;int i,j;printf("\n 图有关的信息的输入:\n");while(1){printf("请输入图的顶点个数和边的条数:");scanf("%d %d",&G.n,&G.e);if(G.n<=1||G.e<=0){printf("输入出错,请重新输入!\n");continue;} else{createALGraph(G);printf("该图的邻接矩阵如下:\n");for(i=0;i<G.n;i++){for(j=0;j<G.n;j++)printf("%d ",a[i][j]);if(j=G.n)printf("\n");}DSTaverse(G,0);//先深度优先遍历printf("\n");printf("从第一个位置广度优先遍历结果为:\n");BFS(&G,0);//广度优先遍历printf("\n");break;}}}五、[ 运行结果]如。
邻接矩阵表示图-深度-广度优先遍历

*问题描述:建立图的存储结构(图的类型可以是有向图、无向图、有向网、无向网,学生可以任选两种类型),能够输入图的顶点和边的信息,并存储到相应存储结构中,而后输出图的邻接矩阵。
1、邻接矩阵表示法:设G=(V,E)是一个图,其中V={V1,V2,V3…,Vn}。
G的邻接矩阵是一个他有下述性质的n阶方阵:1,若(Vi,Vj)∈E 或<Vi,Vj>∈E;A[i,j]={0,反之图5-2中有向图G1和无向图G2的邻接矩阵分别为M1和M2:M1=┌0 1 0 1 ┐│ 1 0 1 0 ││ 1 0 0 1 │└0 0 0 0 ┘M2=┌0 1 1 1 ┐│ 1 0 1 0 ││ 1 1 0 1 │└ 1 0 1 0 ┘注意无向图的邻接是一个对称矩阵,例如M2。
用邻接矩阵表示法来表示一个具有n个顶点的图时,除了用邻接矩阵中的n*n个元素存储顶点间相邻关系外,往往还需要另设一个向量存储n个顶点的信息。
因此其类型定义如下:VertexType vertex[MAX_VERTEX_NUM]; // 顶点向量AdjMatrix arcs; // 邻接矩阵int vexnum, arcnum; // 图的当前顶点数和弧(边)数GraphKind kind; // 图的种类标志若图中每个顶点只含一个编号i(1≤i≤vnum),则只需一个二维数组表示图的邻接矩阵。
此时存储结构可简单说明如下:type adjmatrix=array[1..vnum,1..vnum]of adj;利用邻接矩阵很容易判定任意两个顶点之间是否有边(或弧)相联,并容易求得各个顶点的度。
对于无向图,顶点Vi的度是邻接矩阵中第i行元素之和,即n nD(Vi)=∑A[i,j](或∑A[i,j])j=1 i=1对于有向图,顶点Vi的出度OD(Vi)为邻接矩阵第i行元素之和,顶点Vi 的入度ID(Vi)为第i列元素之和。
即n nOD(Vi)=∑A[i,j],OD(Vi)=∑A[j,i])j=1j=1用邻接矩阵也可以表示带权图,只要令Wij, 若<Vi,Vj>或(Vi,Vj)A[i,j]={∞, 否则。
实验四图的实现及遍历

实验四图的实现及遍历题目:(1)采用邻接矩阵作为图的存储结构,完成有向图和无向图的DFS和BFS操作;(2)采用邻接链表作为图的存储结构,完成有向图和无向图的DFS和BFS操作。
班级:0421001 姓名:杨欢学号:2010211971 完成日期:2011.12.3一、需求分析掌握有向图和无向图的概念;掌握邻接矩阵和邻接链表建立图的存储结构;掌握DFS 及BFS对图的遍历操作;了解图结构在人工智能、工程等领域的广泛应用。
实验要求:1、分析、理解程序。
2、调试程序。
设计一个有向图和一个无向图,任选一种存储结构,完成有向图和无向图的DFS(深度优先遍历)和BFS(广度优先遍历)的操作。
二、概要设计1,分析理解,调试程序2 ,设计一个无向图G,如右图所示3,设计一个有向图K,如右下图所示4,分别对无向图G和有向图K进行邻接矩阵存储和邻接链表存储,再分别进行深度优先遍历和广度优先遍历。
附加程序代码邻接矩阵作为存储结构的程序示例#include"stdio.h"#include"stdlib.h"#define MaxVertexNum 100 //定义最大顶点数typedef struct{char vexs[MaxVertexNum]; //顶点表int edges[MaxVertexNum][MaxVertexNum]; //邻接矩阵,可看作边表int n,e; //图中的顶点数n和边数e}MGraph; //用邻接矩阵表示的图的类型//=========建立邻接矩阵=======void CreatMGraph(MGraph *G){int i,j,k;char a;printf("Input VertexNum(n) and EdgesNum(e): ");scanf("%d,%d",&G->n,&G->e); //输入顶点数和边数scanf("%c",&a);printf("Input Vertex string:");for(i=0;i<G->n;i++){scanf("%c",&a);G->vexs[i]=a; //读入顶点信息,建立顶点表}for(i=0;i<G->n;i++)for(j=0;j<G->n;j++)G->edges[i][j]=0; //初始化邻接矩阵printf("Input edges,Creat Adjacency Matrix\n");for(k=0;k<G->e;k++) { //读入e条边,建立邻接矩阵scanf("%d%d",&i,&j); //输入边(Vi,Vj)的顶点序号G->edges[i][j]=1;G->edges[j][i]=1; //若为无向图,矩阵为对称矩阵;若建立有向图,去掉该条语句 }}//=========定义标志向量,为全局变量=======typedef enum{FALSE,TRUE} Boolean;Boolean visited[MaxVertexNum];//========DFS:深度优先遍历的递归算法======void DFSM(MGraph *G,int i){ //以Vi为出发点对邻接矩阵表示的图G进行DFS搜索,邻接矩阵是0,1矩阵int j;printf("%c",G->vexs[i]); //访问顶点Vivisited[i]=TRUE; //置已访问标志for(j=0;j<G->n;j++) //依次搜索Vi的邻接点if(G->edges[i][j]==1 && ! visited[j])DFSM(G,j); //(Vi,Vj)∈E,且Vj未访问过,故Vj为新出发点}void DFS(MGraph *G){int i;for(i=0;i<G->n;i++)visited[i]=FALSE; //标志向量初始化for(i=0;i<G->n;i++)if(!visited[i]) //Vi未访问过DFSM(G,i); //以Vi为源点开始DFS搜索}//===========BFS:广度优先遍历=======void BFS(MGraph *G,int k){ //以Vk为源点对用邻接矩阵表示的图G进行广度优先搜索int i,j,f=0,r=0;int cq[MaxVertexNum]; //定义队列for(i=0;i<G->n;i++)visited[i]=FALSE; //标志向量初始化for(i=0;i<G->n;i++)cq[i]=-1; //队列初始化printf("%c",G->vexs[k]); //访问源点Vkvisited[k]=TRUE;cq[r]=k; //Vk已访问,将其入队。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
65.printf("\n");
66.visited[v]=TRUE;
67.for(j=0;j<G.vexnum;j++)
68.if(!visited[j]&&G.arcs[v][j].adj==1)
69.DepthFirstSearch(G,j);
10.#define FALSE 0
11.#define TRUE 1
12.#define MAX_VERTEX_NUM 100
13.int visited[MAX_VERTEX_NUM];
14.typedef int AdjType;
15.typedef int VertexData;
16.typedef enum{DG,DN,UDG,UDN}GraphKind;
3.模块划分
(1) 创建一个无向图以邻接矩阵为存储结构:void CreateUDN(AdjMatrix *G)
(2) 邻接矩阵的定位:int LocateVertex(AdjMatrix *G,VertexData v)
(3)深度优先遍历:void DepthFirstSearch(AdjMatrixG,int v)
17.typedef struct ArcNode{
18.AdjType adj;
19.} ArcNode;
20.typedef struct{
21.VertexData vertex[MAX_VERTEX_NUM];
22.ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
46.{ scanf("%d",&G->vertex[i]);
47.}
48.for(k=0;k<G->arcnum;k++)
49.{
50.printf("输入一条弧的两个顶点:");
51.scanf("%d,%d",&v1,&v2);
52.getchar();
53.i=LocateVertex(G,v1);
无向图的深度遍历实验报告
系别
计算机系
班级
学号
课程名称
数据结构
实验日期
实验名称
图的遍历
成绩
实验目的:
1.掌握图的结构特征,以及邻接矩阵和邻接表存储结构的特点和实现。2.掌握在邻接矩阵或邻接表存储结构下图的深度优先和广度优先遍历算法思想及其程序实现。
实验条件:
计算机一台,Visual C++6.0
实验容:
76.}
77.
78.int main()
79.{int i,j;
80.AdjMatrix G;
81.GreateUDN(&G);
82.printf("此无向图的深度遍历为:");
83.TraverseGraph(G);
84.printf("输出邻接矩阵\n");
85.for(i=0;i<G.vexnum;i++)
(4)无向图的遍历:void TraverseGraph(AdjMatrixG)
(5)主函数:void main()
4.详细设计
5.#include <stdio.h>
6.#include <stdlib.h>
7.#include<math.h>
8.#define OK 1
9.#define ERROR 0
54.j=LocateVertex(G,v2);
55.G->arcs[i][j].adj=1;
56.G->arcs[j][i].adj=1;
57.}
58.return(OK);
59.}
60.
61.
62.void DepthFirstSearch(AdjMatrix G,int v)
63.{ int j;
typedef struct
{
VertexData vertex[MAX_VERTEX_NUM];//为顶点的集合
ArcNode arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
int vexnum,arcnum;//vexnum为顶点数,arcnum为弧数
}AdjMatrix; //邻接矩阵的定义
30.return (j);
31.}
32.
33.int GreateUDN(AdjMatrix *G)
34.{ int i,j,k;
35.VertexData v1,v2;
36.printf("输入图的顶点数和弧数:\n");
37.scanf("%d,%d",&G->vexnum,&G->arcnum);
86.{
87.for(j=0;j
89.printf("%d ",G.arcs[i][j].adj);
90.}
91.printf("\n");}
92.return 0;
93.}
94.
95.测试数据及结果
第一组测试:
输入数据:顶点:1,2
38.getchar();
39.for(i=0;i<G->vexnum;i++)
40.{
41.for(j=0;j<G->vexnum;j++)
42.G->arcs[i][j].adj=FALSE;
43.}
44.printf("输入图的顶点:\n");
45.for(i=0;i<G->vexnum;i++)
70.}
71.void TraverseGraph(AdjMatrix G)
72.{ int i;
73.for(i=0;i<G.vexnum;i++) visited[i]=FALSE;
74.for(i=0;i<G.vexnum;i++)
75.if(!visited[i]) DepthFirstSearch(G,i);
1.问题描述
以邻接矩阵或邻接表为存储结构,利用深度优先搜索算法或广度优先搜索算法遍历一个无向图。给出遍历序列,若该图不连通,给出其连通分量的个数和各连通分量的遍历序列。
2.数据结构类型定义
采用邻接矩阵为存储结构:
typedef struct ArcNode
{
int adj;
}ArcNode;//邻接矩阵元素的定义
23.int vexnum,arcnum;
24.}AdjMatrix;
25.int LocateVertex(AdjMatrix *G,VertexData v)
26.{ int j=ERROR,k;
27.for(k=0;k<G->vexnum;k++)
28.if(G->vertex[k]==v)
29.{j=k;break;}
