匝道计算程序
匝道专用计算(两条)

一匝道 起点 ZH HY1 YH1 HY2 YH2 HZ 终点 二匝道 起点 ZH HY1 YH1 HY2 YH2 HZ 终点 K000+090.000 K000+160.000 K000+223.715 K000+271.881 K000+384.032 K000+444.032 K000+544.032 9987.403 9968.981 9910.603 9880.438 9922.316 9981.363 10081.363 10059.378 10125.341 10136.791 10100.904 10007.909 10000.000 10000.000 1.000 50.000 50.000 75.000 75.000 1.000 0.000 桩 号 坐 X(M) 标 Y(M) 半径R(M)
请输入中桩到 左 边桩垂距(M)= 3.50 请输入中桩到 右 边桩垂距(M)= 3.50
请输入自定义逐桩距
ห้องสมุดไป่ตู้ 切线方位角
备 注
输
入
说
明
匝道的组成:起点直线-缓和曲线(ZH)-圆 曲线(HY1)-卵形曲线(YH1)-圆曲线(HY2)缓和曲线(YH2)-直线(HZ)-终点。 1、切线方位角: 136°08′20.6″ 按 136.08206 格式输入。 2、半径输入:缓和曲线接直线端输入“1”, 其余按设计参数输入,直线不作规定。 3、起点或终点无直线段可不作输入,但ZH-HZ 间各行必须输入。如:接直线端无缓和曲线 92.17262 132.23516 205.24336 251.24185 337.04542 0.00000 0.00000 ,HY1、YH1输入同一点参数过度。 4、自定义逐桩距的取值:请按以下线性设计 逐桩点个数及线段长度选择 2、 2.5、5、 10、 20、25、50米7个级数。 直线、圆曲线50个逐桩点,如果自定义 逐桩距为5米,可计算250米长的直线和圆 曲线; 完整缓和曲线50个逐桩点; 不完整缓和曲线40个逐桩点,如果自定义 逐桩距为5米 ,可计算200米长的不完整 缓和曲线。 如果要同时计算两条匝道,请根据长匝道中 的最长线段自定义逐桩距,使其完整显示。
fx-5800p匝道(线元法)测量程序

fx-5800p匝道(线元法)测量程序1.ZDZS(匝道正算程序)Do:〝1.AZD 2.BZD 3.CZD 4.DZD 5.EZ D↙ZD=〝?→Z[1]:Lpwhile Z[1]>6 Or Z[1]≤0(零):〝X0(零)=〞?J:〝Y0(零)=〞?N↙J→Z[2]:N→Z[3]↙LbI 0(零):〝K=〞?S:90→T(如将90→T改为〝Q°=〞?T可计算斜交):〝D=〞?Z:Z[1]=1=>Prog〝AZD〞: Z[1]=2=>Prog〝BZD〞: Z[1]=3=>Prog〝CZD〞: Z[1]=4=>Prog〝DZD〞: Z[1]=5=>Prog 〝EZD〞↙〝X=〞:X+Zcos(F+T)→X◢〝Y=〞:Y+Zsin(F+T)→Y◢Prog〝A〞:Goto 0(零)↙本程序中输入及显示说明:输入部分:ZD=? 输1为运行A匝道、输2为运行B匝道、输3为运行C匝道、输4为运行D匝道、输5为运行E匝道;X0=? 输入测站点X坐标;Y0=? 输入测站点Y坐标;K=? 输入待求点桩号;D=? 输入待求点距中桩距离。
(以线路前进方向区分左右、当待求点位于中桩时D=0(零);当待求点位于中桩左侧时D取负值;当待求点位于中桩右侧时D取正值。
)显示部分:X= 显示待求点X坐标;Y= 显示待求点Y坐标;FWJ= 显示测站点至待求点方位角(即水平角);HD= 显示测站点至待求点水平距离。
若测站X0坐标输入0(零)时、不论测站Y0坐标输入多少,都不显示FWJ=、HD=两项。
2.ZDFS(匝道反算程序)Do:〝1.AZD 2.BZD 3.CZD 4.DZD 5.EZ D↙ZD=〝?→Z[1]:Lpwhile Z[1]>6 Or Z[1]≤0(零)↙LbI 0(零):〝K=〞?S:〝X=〞?I:〝Y=〞?J: Z[1]=1=>Prog 〝AZD〞: Z[1]=2=>Prog〝BZD〞: Z[1]=3=>Prog〝CZD〞: Z[1]=4=>Prog〝DZD〞: Z[1]=5=>Prog〝EZD〞:Porg〝E〞:O(欧)+W→S:〝K=〞:S◢〝D=〞:Z◢Goto 0(零)↙本程序中输入及显示说明:输入部分:ZD=? 输1为运行A匝道、输2为运行B匝道、输3为运行C匝道、输4为运行D匝道、输5为运行E匝道;K=? 输入待求点大概桩号;X=? 输入待求点X坐标;Y=? 输入待求点Y坐标。
匝道的计算公式与认识

18.有时设计院没有给出匝道最后一段缓和曲线的结束半径,那么在积木法计算前就需要计算最后一段缓和曲线的结束半径。
公式如下:其中 A 是缓和曲线参数、R 是半径ls 是缓和曲线长度。
回旋线是公路路线设计中最常见的一种缓和曲线。
我国的标准规定缓和曲线采用回旋线。
它的基本公式为:A*A=r*l其中:A是回旋线参数。
r是回旋线上某点的曲率半径(m)l是回旋线上某点到原点的曲线长在回旋线上的任意点上,r是随着l 的变化而变化的。
但是在缓和曲线的终点处,l=Ls,r=R,则上式可写为A*A=R*Ls则 -------A=√R*Ls在设计上可以由已知R和Ls计算A,也可以按各种条件选择R和A,再计算Ls.至于用于计算坐标,你可以综合所有的已知条件进行计算,它只是提供一个计算和你进行复核的条件。
对互通立交端部的一点认识随着经济和交通运输事业的飞速发展,高等级公路的普遍修建,作为高等级公路车辆出入门户的互通式立交也开始大量修建。
立体交叉中主线与交叉线处于不同高程上,需用道路将其互相联系,便于各方向车流四通八达,这些起联系作用的道路通常称为匝道。
匝道两端与主线、交叉线连接区域称之为匝道端部。
匝道端部范围,包括匝道出入口,三角区,变速车道等部分。
匝道的端部形式,就其出入口位置不同,有左出入口和右出入口;就其主线或交叉线几何形状不同,有直线和曲线等。
匝道端部形式多样,几何关系以及设计都较繁琐,而且都应满足各自不同的技术要求,如设计不当,将造成对车辆行驶不利,容易引发事故阻碍交通。
本文就结合自己的设计经验,针对匝道端部设计做一些探讨。
一、匝道端部路线平、纵面要求1、路线平面要求从主线流出的车辆,在进入匝道的短暂运行过程中,其驾驶过程较为复杂,分流、转向、减速对司机都有一定的操作要求,同时司机产生心理压力也有影响。
因此,出口处应为车辆行驶创造良好条件,对路线平面应有较高要求,入口处一般也应如此。
我国公路《规范》规定,驶入匝道的分流点应具有较大的曲率半径,并使曲率变化适应行驶速度的变化。
广东省高速公路匝道里程计算方法

广东省高速公路的收费里程计算方式
高速公路收费里程包含主线收费里程和匝道收费里程.主线收费里程直接等于主线的长度。
匝道收费里程按照匝道的平均长度折半计算。
一、收费站匝道里程计算
收费站的匝道收费里程等于收费站的所有匝道长度平均折半,每条匝道长度按照收费站中心桩号起计算至高速主线连接处(收费站与市政路相连的长度不计入收费里程)。
二、互通立交匝道里程计算
互通立交的匝道收费里程等于所有匝道长度平均折半(枢纽互通及T型互通的匝道取消收费)。
1.枢纽互通的高接高匝道取消收费。
高接高互通立交的主线桩号,取高速相交处的中心桩号(如遇特殊情况单独研究),高接高互通立交的匝道统一为0,不计入收费里程。
2.T型连接的互通立交匝道取消收费,互通立交的主线桩号调整至两条主线相交的虚拟点。
3.双喇叭互通的匝道可保留继续收费。
立交匝道中桩坐标计算EXCEL程序
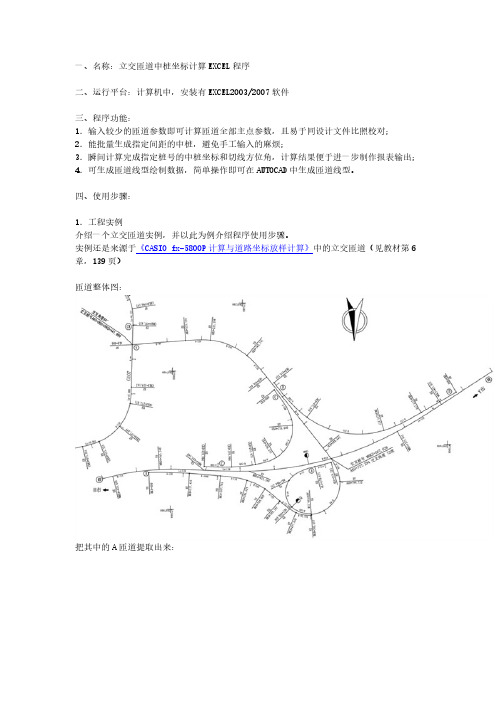
一、名称:立交匝道中桩坐标计算EXCEL程序二、运行平台:计算机中,安装有EXCEL2003/2007软件三、程序功能:1.输入较少的匝道参数即可计算匝道全部主点参数,且易于同设计文件比照校对;2.能批量生成指定间距的中桩,避免手工输入的麻烦;3.瞬间计算完成指定桩号的中桩坐标和切线方位角,计算结果便于进一步制作报表输出;4.可生成匝道线型绘制数据,简单操作即可在AUTOCAD中生成匝道线型。
四、使用步骤:1.工程实例介绍一个立交匝道实例,并以此为例介绍程序使用步骤。
实例还是来源于《CASIO fx-5800P计算与道路坐标放样计算》中的立交匝道(见教材第6章,139页)匝道整体图:把其中的A匝道提取出来:A匝道相关的参数表也提取出来:.2.打开EXCEL计算程序,输入A匝道的相关参数图中浅绿色部分是输入的原始数据部分。
这里原始数据的输入是难点和关键,一定要准确验证,否则后面的工作全是无用功。
这里就数据输入作详细解读如下:(1)第一行,“匝道”后面的单元格可输入匝道编号,这个不参与计算,仅作提示,使界面清晰明了。
(2)数据第一列,是节点栏,“节点”是我起的名字,含义是两种不同线元交界的点,如ZH、ZY、HZ、GQ、YZ等特征点都是节点,匝道的起、终点也是节点,注意QZ不是节点。
这一栏就填节点的名称,注意不要漏了。
(3)节点桩号栏。
这个在设计文件上可以找到,需要强调的是输入时按数字输入,如输入153.194,回车后会自动显示为K0+153.194格式,千万不可按桩号格式K**+***的格式输入,否则会出错。
(4)半径1、半径2两栏。
节点除匝道起、终点外,都是对前后两个线元起承接作用的点,一般情况下,其曲率半径是连续的,但也有例外,如ZY点,节点前承直线终点,半径无穷大,后接圆曲线,半径为R。
因此,在节点处曲率半径连续的情况下,就在半径1中填写半径值,半径2中空着就行(当然填一个与半径1一样的值也没事),而当节点出曲率半径不连续的情况下,就分别在半径1和半径2中相应填写两个不同的半径值。
最新4850匝道程序汇总

4 85 0 匝道程序程序说明卡西欧4800或4850计算主线及其匝道中边桩坐标,高程,反算任意点桩号及其距中距离,以及边坡超欠挖情况。
主程序1ZA DAO (用N值判断那条线路)N=0 1,2,3,4,5,6,7,8,9"/ b|0 : {K} : N: N=0=>prog ZHU XIAN':工>N=1=>prog AZA':工>N=2=>prog BZA':工>N=3=>prog CZA”:工>N=4=>prog DZA”:工>N=5=>prog EZA,:工>N=6=>prog FZA':工>N=7=>prog GZA:工>N=8=>prog HZA”:工>N=9=>prog AS':<」(被交道阿森主线)主程序:2“ N0-9H” (用N值判断那条线路的高程)N=0 1,2,3,4,5,6,7,8,9"/ b|0 : {K} : N: N=0=>prog ZHU XIAN H”工>N=1=>prog AZ H”:工>N=2=>prog BZ H”:工>N=3=>prog CZ H”:. <」桩距ZHUANG JU (由三维坐标反算桩号和边桩距离及其坡角)仅供学习与交流,如有侵权请联系网站删除谢谢2{X: Y:H}:Z[38]=1XXP=':Y YP兰:HH仝:NN仝:QKQ= :ZKZ仝:Z[21]=X : Z[22]=Y : Z[23]=H:<」/ b|0 : Z[24]=Q : Z[25]=Z :K=Q Prog ZA DAOZ[26]=Z[12]:Z[27]=Z[13]:<K=Z: Prog ZA DAO :Z[28]=Z[12]:Z[29]=Z[13]:< pol((Z[28]-Z[26]),(Z[29]-Z[27])):Z[30]=l:J<0=>Z[31]=J+360:丰 >Z[31]=J: ?pol((Z[21]-Z[26]),(Z[22]-Z[27])):Z[32]=IJ<0=>Z[33]=J+360:丰 >Z[33]=J: ?(Z[31]-Z[33])v-270=>Z[34]=-1:Z[35]=(360-Z[33]+Z[31]) :丰 > (Z[31]-Z[33])<0=>Z[34]=1:Z[35]=(Z[33卜Z[31]) :丰 >(Z[31]-Z[33])>270=>Z[34]=1:Z[35]=360-Z[31]+Z[33] :丰 >(Z[31] -Z[33])>0=>Z[34]=-1:Z[35]=Z[31 卜Z[33]: ????Z[36]=Q+Z[32]*cosZ[35]:Z[37]=Z[32]*si nZ[35]Z[38]=Z[38]+1(计数器:初始值为1)<」Z[38]=2=> 50M‘ :Q=Z[36卜50:Z=Z[36]+50:Goto 0 :工>Z[38]=3=> fn”Q=Z[36卜1 : Z=Z[36]+1:Goto 0 :工>Z[38]=4=> 0.1m”:Q=Z[36]-0.1:Z=Z[36]+0.1:Goto 0 :工>ZHUANG HAO'N」K=Z[36] ▲Z[34]<0=> ZUO=:Z[37] ▲工> YOU”Z[37] ▲Prog NO-9H”J“QIAO HAN (桥涵任意角点)/ b|0:prog: ZA DAO :/ b|1:{FST}:Z[70]=F+S+T:(输入顺序为FST)仅供学习与交流,如有侵权请联系网站删除谢谢3Z[71]= V (S A2+T A2-2* V(S A2)* V (T八2)*cos(180-F)):Z[72]= V(SA2+TA2-2* V心八2)* V(TA2)*cosF ):Z[73]=cos -t(TA2+Z[71]A2/4-Z[72]A2/4)/ V仃八2亿[71])): Z[74]=cos -1(SA2+Z[72F2/4-Z[71]A2/4)/ V心八2亿[72])): S> 0 =>Goto 2:丰 >Goto 3:/ b|2:T>0 =>Z[75]=Z[11]+Z[73]:S=Z[71]:Goto 4:丰 >T<0 =>Z[75]=Z[11]+F+Z[74]:S=Z[72]:Goto 4: ?/ b|3:T<0 =>Z[75]=Z[11]+180+Z[73]:S=Z[71]:Goto 4: 丰 >T>0 =>Z[75]=Z[11]+180+F+Z[74]:S=Z[72]:Goto 4:/ b|4:Z[75]>360=>Z[75]=Z[75]-360: 丰 >Z[75]=Z[75]: ?Z[76]=Z[12]+S*cosZ[75]:Z[77]=Z[13]+S*si nZ[75]:“ X=” v」Z[76] ▲“ Y=” v」Z[77] ▲Goto 1:<」子程序:1ZHY”直缓圆中边桩坐标计算程序)Z[1]=Abs(K-Z):Z[2]=1/R:Z[3]=(R-S)/(2HRS):Z[4]=i80/ n:Z[5]=0.1739274226:Z[6]=0.3260725774:Z[7]=0.0694318442:Z[8]=0.3300094782:Z[9]=1 -Z[8]:Z[10]=1 -Z[7]:X=O+Z[1](Z [5] cos(U+GZ[4]Z[7]Z[1](Z[2]+Z[7]Z[1]Z [ 3]))+Z[6] cos(U+GZ[4]Z[8]Z[1](Z[2]+Z[8]Z[1]Z [ 3]))+Z[6] cos(U+GZ[4]Z[9]Z[1](Z[2]+Z[9]Z[1]Z [ 3]))+Z[5] cos(U+GZ[4]Z[10]Z[1](Z[2]+Z[10]Z[1]Z[3]))<Y=P+Z[1](Z[5]si n(U+GZ[4]Z[7]Z[1](Z[2]+Z[7]Z[1]Z[3]))+Z[6]si n(U+GZ[4]Z[8]Z[1](Z[2]+Z[8]Z[1]Z [ 3]))+Z[6]si n(U+GZ[4]Z[9]Z[1](Z[2]+Z[9]Z[1]Z [ 3]))+Z[5]si n(U+GZ[4]Z[10]Z[1](Z[2]+Z[10]Z[1]Z[3]))vZ[11]=U+GZ[4]Z[1](Z[2]+Z[1]Z[2]):Z[12]=X:Z[13]=Y:“ AN= v」Z[11] f DM2 (注:(f DM2)命令为十进制转换六十进制并显示度分秒。
匝道积木法放样

匝道计算程序(积木法)所有曲线都可以算曲线任意里程中边桩坐标正反算(CASIO fx-4800P计算器)程序一、程序功能本程序由一个主程序(TYQXJS)和两个子程——正算子程序(SUB1)、反算子程序(SUB 2)序构成,可以根据曲线段——直线、圆曲线、缓和曲线(完整或非完整型)的线元要素(起点坐标、起点里程、起点切线方位角、线元长度、起点曲率半径、止点曲率半径)及里程边距或坐标,对该曲线段范围内任意里程中边桩坐标进行正反算。
另外也可以将本程序中核心算法部分的两个子程序移植到其它相关的程序中,用于对曲线任意里程中边桩坐标进行正反算。
本程序也可以在CASIO fx-4500P计算器及CASIO fx-4850P计算器上运行。
二、源程序1.主程序(TYQXJS)"1.SZ => XY":"2.XY => SZ":N:U"X0":V"Y0":O"S0":G"F0":H"LS":P"R0":R" RN":Q:C=1÷P:D=(P-R)÷(2HPR):E=180÷π:N=1=>Goto 1:≠>Goto 2Δ←┘Lbl 1:{SZ}:SZ:W=Abs(S-O):Prog "SUB1":X"XS"=X◢Y"YS"=Y◢Goto 1←┘Lbl 2:{XY}:XY:I=X:J=Y:Prog "SUB2":S"S"=O+W◢Z"Z"=Z◢Goto 22. 正算子程序(SUB1)A=0.1739274226:B=0.3260725774:K=0.0694318442:L=0.330 0094782:F=1-L:M=1-K:X=U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD)) +Bcos(G+QEFW(C+FWD))+Acos(G+QEMW(C+MWD))):Y=V+W(Asin(G+QEKW(C+K WD))+Bsin(G+QELW(C+LWD))+Bsin(G+QEFW(C+FWD))+Asin(G+QEMW(C+MWD))):F=G+QEW(C+WD)+90:X=X+ZcosF:Y=Y+ZsinF3. 反算子程序(SUB2)T=G-90:W=Abs((Y-V)cosT-(X-U)sinT):Z=0:Lbl 0:Prog "SUB 1":L=T+QEW(C+WD):Z=(J-Y)cosL-(I-X)sinL:AbsZ<1E-6=>Goto1:≠>W=W+Z:Got o 0Δ←┘Lbl 1:Z=0:Prog "SUB1":Z=(J-Y)÷sinF三、使用说明1、规定(1) 以道路中线的前进方向(即里程增大的方向)区分左右;当线元往左偏时,Q=-1;当线元往右偏时,Q=1;当线元为直线时,Q=0。
匝道坐标计算程序

匝道坐标计算程序(辛甫生公式)L1 LbI0:{EG}:A“XA”:B“YA”:C“CA”:D“1/RA”:E“1/RB”:F“KA”:G“KB”L2 LbI1:{HORS}:H“KI”:O“DL”:R“DR”:S“PJ”:H>G => Goto2△L3 P=(E-D)/Abs(G-F):Q=Abs(H-F):I=P×Q:T=D+IL4 J=C+(I+2D)Q×90/π⊿M=C+(I/4+2D)Q×45/(2π):N=C+(3I/4+2D)Q×135/(2π)L5 K=C+(I/2+2D)Q×45/πL6 X=A+Q(cosC+cosJ+4(cosM+cosN)+2cosK)/12⊿L7 Y=B+Q(sinC+sinJ+4(sinM+sinN)+2sinK)/12⊿L8 U“XL”=X+Ocos(J-180+S)⊿V“YL”=Y+Osin(J-180+S)⊿L9 W“XR”=X+Rcos(J+S)⊿Z“YR”=Y+Rsin(J+S)⊿L10 A=X:B=Y:C=J:D=T:F=H:Goto1L11 LbI2:A=X:B=Y:D=E:F=G:C=J:Goto0数据输入说明:① XA、YA、CA分别为A点(起始点)的X、Y坐标及方位角。
② 1/RA、1/RB分别为A点和B点的曲率,以1/R表示。
曲线左偏时取“-”;曲线右偏时取“+”;直线时为0;缓和曲线时: 1/RA为0或是〒1/RA、1/RB为0或是〒1/RB;圆曲线时均为〒1/R。
【左“-”右“+”】③ KA、KB分别为曲线原起点A和终点B的里程桩号。
④ XL、YL、XR、YR分别为左边桩和右边桩的X、Y坐标。
⑤ DL、DR分别为左、右边桩距中桩的水平距离。
⑥ 当一个曲线计算完后,即KI>KB时,程序显示1/RB和KB,此时需输入下一个曲线原终点的曲率和桩号。
⑦ 计算无缓和曲线时,不能由直线段直接计算而应将KA、1/RA输入LR点桩号和〒1/R。
5800B匝道程序

B匝道WN(不运行)"ZS=1,FS=2"?N: 1÷P→C:(P-R)÷(2HPH)→D:180÷π→E: If N=1: Then Goto 1: Else Goto 2: IfEnd←┚LbI 1:1→I:0→Z:Abs(K-O)→W: Prog"ZS"←┚F-90→F←┚"JJ"?K:"PJ"?L: "ZX=":Z[7]+Lcos(F+K)→Z[3]◢"ZY=": Z[8]+Lsin(F+K)→Z[4]◢"QXFWJ="DMS◢Abs(Z)→Z:Goto 8←┚LbI 2:"X"?I:"Y"?J: Prog"FS":"FSZH=":O+W→K◢"FSJL=":Z◢Lbl 8正算子程序(ZS)(不运行)1÷P→C:(P-R)÷(2HPR)→D: 180÷π→E0.1739274226→A:0.3260725774→B:0.0694318442→K:0.3300094782→L:1-L→F:1-K→M:U+W(Acos(G+QEKW(C+KWD))+Bcos(G+QELW(C+LWD))+Bcos(G+QEFW(C+FWD))+Acos(G+QEMW(C+MWD)))→Z[7]:V+W(Asin(G+QEKW(C+KWD))+Bsin(G+QELW(C+LWD))+Bsin(G+QEFW(C+FWD))+Asin(G+QEMW(C+MWD)))→Z[8]:G+QEW(C+WD)+90→F:Z[7]+ZcosF→Z[7]:Z[8]+ZsinF→Z[8]3反算子程序(FS)(不运行)G-90→T:Abs((Z[8]-V)cosT-(Z[7]-U)sinT)→W:0→Z←┚Lbl 0←┚prog"ZS":T+QEW(C+WD)→L:(J-Z[8])cosL-(I-Z[7])sinL →Z:If Abs(Z)<0.001: Then Goto1:Else W+Z→W:IfEnd :Goto 0←┚Lbl 1:0→Z:Prog"ZS":(J-Y)÷sinF→ZZX-WN(运行主程序,该程序适用于匝道,对全段完整非完整曲线计算太过麻烦)"CZX"?S(仪站X坐标):"CZY"?W(仪站Y坐标)LbI 0: "K"?K: If K≤352.207(第1条单一曲线的终点下面同上): Then Goto A:Else If K≤407.762 And K>352.207: Then Goto B:Else If K≤472.013 And K>407.762: Then Goto C:Else If K≤509.191And K>472.013: Then Goto D: IfEnd: IfEnd: IfEnd:IfEnd←┚LbI A:181.659(起点X坐标)→U:5253.471(起点Y坐标)→V:0起点桩号→O:291°6'46"(方位角)→G:352.207(曲线长度)→H: 10^45(起点半径)→P: 10^45 (止点半径)→R:0(路线左右偏,左负右正直线输0)→Q:Prog "WN":Goto WLbI B:308.527→U:4924.907→V:352.207→O:291°6'46"→G:55.556→H: 10^45 →P:45 →R:+1→Q:Prog "WN":Goto WLbI C:338.166→U:4879.028→V:407.762→O: 326°28'50"→G:64.251→H: 45 →P:45 →R:+1→Q:Prog "WN":Goto WLbI D:396.608→U:4886.601→V:472.013→O: 48°17'14"→G:37.178→H:45 →P:64.05 →R:+1→Q:Prog "WN":Goto WLbI W:"PJ1"?T←┚(该项是只左右边桩再左右偏距,输0为不再左右偏,适用于桥梁桥台、盖梁、涵洞八字墙等放样,以路线前进方向,前-,后+)If T=0:Then Z[3]→Z: Z[4]→M: Goto P: Else Goto V: IfEnd←┚LbI V:"JJ1"?O←┚(左右边桩再偏夹角,用180°减去路线夹角)"X1=": Z[3]+Tcos(F+K+O)→U◢"Y1=" :Z[4]+Tsin(F+K+ O)→V◢U→Z: V→M: GotoP←┚LbI P:Pol(Z-S,M-W): If J≤0:Then J+360°→J: IfEnd←┚"JL=":I◢(仪站至测点的距离)"FWJ="DMS◢(仪站至测点的方位角)Goto01.规定以道路中线前进方向(即里程增大的方向)区分左右;当线元往左偏时Q=-1;当元线往右偏时,Q=1:当元线为直线时,Q=0°2.当所求点位于中线时,Z=0;当位于中线左侧时,Z取负值:当位于中线右侧时,Z取正值°当线元为直线时,其起点、止点的曲率半径为无穷大,以10的45次方代替°3.当线元为圆曲线时,无论其起点、止点与什么线元相接,其曲率半径均等于圆弧的半径°4.当线元为完整的缓和曲线时,起点与直线相接时,曲率半径为无穷大,以10的45次方代替°与圆曲线相接时,曲率半径等于圆曲线的半径,止点跟直线相接时,曲率半径为无穷大,以10的45次方代替;与圆曲线相接时,曲率半径等于圆曲线的半径°5.当线元为非完整缓和曲线时,起点与直线相接时,曲率半径等于设计规定的值;与圆曲线衔接时,曲率半径等于圆曲线的半径°止点与直线相接时,曲率半径等于设计规定的值;与圆曲线衔接时,曲率半径等于圆曲线的半径°二、输入与显示说明1.输入部分:2.. 输入3.ZS=1,FS=2,选择计算方式,输入1正算;输入2反算4.数据库的输入5.U?线元起点的X坐标6.V?线元起点的Y坐标7.O?线元起点的里程8.G?线元的起点切点方位角9.H?线元的长度10.P?线元起点的曲率的半径11.R?线元止点的曲率的半径.12.ZY?线元左右偏标志(左偏Q=-1,右偏Q=1,直线段Q=0)13.计算时:14.K?正算时所求的里程15.JJ?夹角,(正交90°,斜交直接输角度)16.PJ?偏距(左负右正)17..结果18.ZX=正算时,计算得出的测点的X坐标19.ZY=正算时,计算得出的测点的Y坐标20.QXFWJ=正算时,测点对应中线点的切线方位角21.PJ1?:左右桩号再偏距离,不需要时输022.JJ1? :左右边桩再偏角度23.JL=仪站与测点的距离24.FWJ=仪站与测点的方位角25.反算时输入:26.X?反算时所求点的X坐标27.Y?反算时所求点的Y坐标28.结果29.FSZH=反算时,计算得出的所求点的里程30.FSJL=反算时,计算得出的所求点的边距(负为左偏,正为右偏)。
线元法(积木法)匝道坐标正反算放样程序

Cls :"1Z 2A 3B"?→I ↙(注:此处""内为线路名,有几条线路就加入几条!)Cls:"K Or –K To Shu"?K:If K≥0:Then↙I=1=>Prog"P. Z"↙I=2=>Prog"P. A"↙I=3=>Prog"P. B"↙………………………(注:此处必须与上述""内为线路名和下面的数据库子程序名对应,有几条线路就加入几条!)Mat B[1,1]→A: Mat B[1,2]→L: Mat B[1,3]→U: Mat B[1,4]→V: MatB[1,5]→W: Mat B[1,6]→P: Mat B[1,7]→Q: Mat B[1,8]→G↙Else Cls:"K0"?A:"KN"?L :"X0"?U :"Y0"?V :"F0"?W :"R0"?P :"RN"?Q:"ZX:-1,+1,0"?G:IfEnd :Cls↙1→O: Prog "XY-B"↙Cls:"1.ZS 2.FS"? →I: I=2=>Goto 3↙Cls:"XC"?H:"YC"?Z↙LbI 1 : Cls:"K×+×××"?K↙If K>L Or K<A : Then Cls: Locate 6,2,"K OUT !"◢Stop: IfEnd↙LbI 2: Cls:90→B: Cls:"RJ Or 0 To K"?B:B=0 =>Goto 1:"Z"?T↙Prog "XY-A"↙X+Tcos(M+B)→X↙Y+Tsin(M+B)→Y↙360Frac((M+360)÷360→M↙Pol(X-H,Y-Z : 360Frac((J+360)÷360→J↙2→O: Prog "XY-B":Goto 2↙LbI 3 : Cls: "X"?C:"Y"?D↙LbI 4 : If K>L Or K<A : Then Cls: Locate 6,2,"K OUT !"◢Stop:IfEnd↙Prog "XY-A"↙(D-Y)sin(M)+(C-X)cos(M)→H↙If Abs(H)>X10-3 :Then K+H→K:Goto 4:IfEnd↙(D-Y)÷cos(M)→T↙3→O: Prog "XY-B":Goto 3↙子程序1名: XY-A5→N: G(Q-1-P-1)÷Abs(L-A)→F: Abs(K-A)÷N→R: 90R÷π→S:W+(FNR+2GP-1)NS→M:1→E↙U+R÷6×(Cos (W)+Cos (M) +4∑(Cos (W+((E+0.5)FR+2GP-1)×(E+0.5)S),E,0,(N-1))+2∑(Cos (W+((EFR+2GP-1)ES,E,1,(N-1)))→X ↙V+R÷6×(sin (W)+sin (M) +4∑(sin (W+((E+0.5)FR+2GP-1)×(E+0.5)S),E,0,(N-1))+2∑(sin (W+((EFR+2GP-1)ES,E,1,(N-1)))→Y↙子程序2名: XY-BCls :Fix 3:If O=1:Then "XY RESULTS:": "K0=":"KN=":"F0=": Locate 5,2,A : Locate 5,3,L : Locate 5,4,W◢Cls :"X0=":"Y0=":"R0=":"RN=": Locate 5,1,U : Locate 5,2,V : Locate 5,3,GP : Locate 5,4,GQ◢IfEnd↙If O=2:Th en↙Cls :"K×××=":"Z=":"X=":"Y=": Locate 6,1, K : Locate 4, 2, T : Locate 4,3, X : Locate 4,4, Y◢If T=0 :Then Cls :"QF(Z)=": Locate 8,1, M:M▼DMS◢IfEnd↙Cls :"K×××=":"S=": Locate 6,1, K : Locate 4, 2, I :"F=":J:J▼DMS◢IfEnd↙If O=3:Then "X=":"Y=":"K×××=":"Z=": Locate 4,1,C: Locate 4, 2, D : Locate 6,3,K :Locate 4,4,T◢IfEnd:Cls↙线路线元数据库子程序格式:数据库采用给矩阵变量Mat B赋值的形式,使数据组织更加简洁,极大的减少了线路数据库子程序的输入量,节约了计算器空间程序说明:程序线元判断原则:(1) 以道路中线的前进方向(即里程增大的方向)区分左右;(2) 当所求点位于中线时,Z=0;当位于中线左侧时,Z取负值;当位于中线右侧时,Z取正值。
匝道程序 2

立交匝道中边桩坐标放样正反算程序主程序:(RAMP)Deg : Fix 3 : 10→Dim Z↙0.1739274226→Z[1] : 0.0694318442→Z[2] : 0.3260725774→Z[3] : 0.3300094782→Z[4] ↙Z[3]→Z[5] : 1- Z[4]→Z[6] : Z[1]→Z[7] : 1-Z[2]→Z[8]↙“RAMP?[1-N]”?→Z[9]↙(输入匝道代码,比如数字1,2,3...代表a,b,c匝道,并存储在变量Z[9]中)If Z[9]=0 : then“XA”?W :“YA”?Y :“FWJ”?Q:“RS”?A :“RE”?B :“KS”?S : “KE”?E : IfEnd ↙(若Z[9]=0 时,则手工输入原始数据:线元起点X﹑Y坐标,方位角,线元起﹑终点曲率,起﹑终点桩号)Cls :“ZS[1],FS[2]”?→Z[10]:Z[10]=2 =>Goto 2↙“XS”?U :“YS”?V↙(输入测站点坐标)Lbl 0:“KP”?P↙(输入待计算的中桩桩号)Z[9]>0=>Prog“RAMP-DATA”↙(调用匝道数据库子程序)Prog“RAMP-ZBJS”↙(调用子程序计算中桩坐标)Lbl 1:90→H:“YJ”?H : H=0 =>Goto 0 :?D↙(输入右角及距离,若右角为0则返回桩号输入)F+Dcos(Z+H)→R : G+Dsin(Z+H)→T↙(坐标计算)Pol(R-U,T-V) : J<0=>J+360→J↙1→O :Prog“RAMP-XS”: Goto 1↙(调用计算结果显示子程序)Lbl 2:“XB”?U :“YB”?V :“KP”?P↙(坐标反算,输入X,Y,估算的桩号)Lbl 3:Z[9]>0=>Prog“RAMP-DATA”↙Prog“RAMP-ZBJS”↙(调用子程序计算中桩坐标)(V-G)cos(Z-90)-(U-F)sin(Z-90)→H↙If Abs(H)>0.001 : Then P+H→P : Goto 3: IfEnd↙(G-V)÷sin(Z-90)→D↙2→O : Prog“RAMP-XS”: Goto 2↙(调用计算结果显示子程序)子程序1:(RAMP-ZBJS)坐标计算E-S →C : P-S →L : 180÷π→M : (B-A)÷2÷C →N ↙0→F : 0→G : 0→Z:For 0→K To 3:(计算X,Y 坐标值)F+LZ[2K+1]cos(Q+MALZ[2K+2]+MN(LZ[2K+2])2)→F:(计算X,Y 坐标值)G+LZ[2K+1]sin(Q+MALZ[2K+2]+MN(LZ[2K+2])2)→G:(计算X,Y 坐标值)Next :W+F →F : Y+G →G:(计算X,Y 坐标值)Q+MAL+MNL 2→Z:(计算切线方位角)Z<0=>Z+360→Z : Z>360=>Z-360→Z ↙子程序2(RAMP-XS)显示 Cls :If O =1 :Then ↙“X=” :Locate4,1,R: “Y=”: Locate4,2,T : Fix4 : “A=” : Locate4,3,J 。
匝道程序

匝道计算程序立交匝道中边桩坐标放样正反算程序ramp(0911改进版)一、前言本人编著《casio fx-5800p计算与道路坐标放样计算》中,有关立交匝道坐标放样计算程序有三个:1.p132,立交匝道坐标放样计算程序ramp-1,它的特点是手工输入线元基础数据,可计算该线元范围内的中、边桩坐标和极坐标放样数据,无坐标反算功能;2.p136,道路(立交)坐标反算计算程序ramp-2,它的特点是手工输入线元基础数据,可在该线元范围内根据坐标反算对应中桩及据中桩距离。
3.p147,立交匝道坐标放样计算程序ramp-3,它的特点是采用了数据库子程序保存立交匝道的各线元的基础数据,而不需要手工输入了,运行一次程序可计算一条匝道而不只是一个线元的中、边桩坐标和极坐标放样数据,同样无坐标反算功能。
2009年3月22日,我在qq空间中发布了ramp-3程序的更新版,并取名为ramp-4,该程序的特点是在ramp-3功能的基础上,增加了坐标反算功能,参见链接:/qqblog/595077/1237737328.htm。
今天发布的立交匝道中边桩坐标放样正反算程序ramp(0911版)是我的立交匝道计算的最新成果,具备前面所有版本程序的全部功能。
与ramp-4 程序比较,ramp(0911版)程序的主要改进之处有:1.鉴于卡西欧编程计算器积分函数计算误差的争议(参见日志:/qqblog/595077/1242886367.htm),本程序坐标积分计算改为采用gauss-legendre积分法(四节点)进行计算,计算速度与采用计算器内部积分函数相比,速度无明显区别,但程序代码相对多一些;2.匝道线元数据库子程序改为矩阵变量的形式,使数据组织更加简洁,数据输入更加快捷;3.计算结果显示输出采用了满屏四行输出的形式,一屏可同时显示四个计算结果(或关键数据);4.可调用数据库子程序,也可手工输入线元基础数据进行计算(参见程序运行框图);5.考虑到立交匝道各线元基础数据数量大、不易根据设计图表准确确定等特点,特编写了在计算机上运行的“立交匝道参数辅助计算excel程序”,帮助用户准确、快速编写匝道数据库子程序。
高速公路--匝道计算

高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l 0——对应的缓和曲线长度R——圆曲线半径——曲线起点处的半径R1——曲线终点处的半径R2——曲线起点处的曲率P1——曲线终点处的曲率P2α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i(上坡为“+”,下坡为“-”)1(上坡为“+”,下坡为“-”)②第二坡度:i2③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K③曲线终点桩号:K1④曲线起点坐标:x0,y⑤曲线起点切线方位角:α⑥曲线起点处曲率:P(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
匝道计算

B值 = G值 =
0.326072577 0.330009478
C值= 0.00066823 H值= 0.93056816
D值= I值=
6.17282E6.17282E-05 0.069431844
E值=
57.29577951
249° 05′47.5″ 起点方位角 249° 05′47.5″
K0+000 3275092.037 533114.707 K0+020 3275085.181 533095.920 K0+040 3275079.518 533076.745 K0+060 3275076.038 533057.066 K0+080 3275075.767 533037.097 K0+100 3275079.68 533017.531
Hale Waihona Puke 3275092.037 533114.707 249°05′47.5″ 249.0965278 3275085.181 533095.92 251°16′37.1″ 251.2769644 3275079.518 533076.745 256°17′12.5″ 256.2868134 3275076.038 533057.066 264°07′33.9″ 264.1260748 3275075.767 533037.097 274°47′41.1″ 274.7947486 3275079.68 533017.531 288°17′34.2″ 288.2928348
3275092.037 533114.707 249
曲线、直线坐标计算 曲线、
说明:本程序适用于匝道坐标,可任意一段曲线内坐标及方位角(包括卵形曲线),也可算直线段坐标 当半径无穷大时输入=10的45次方(=10^45),运行直线时,Rq和Rz输=10^45,L输大于零的数就行 待求点 桩号 待求点中桩坐标 X Y 距起点 中桩0 左+,右- ,中桩0 距离 0 0 0 0 0 0 0 20 40 60 80 100 边距 待求点坐标 X Y 方位角转换 °′″ 方位角 百进制( 百进制( 度)
线元法计算器兼匝道程序(精编文档).doc

【最新整理,下载后即可编辑】5800 计算程序主程序QXJSLbI 0: “1.SZ=>XY”:“2.XY=>SZ”“3.GC=>SQX”:? Q :Q=1=> Goto1:Q=2=>Goto2:Q=3 => Goto3LbI 1: “CE:X”?G:“CEY:”?H:Prog“XLXY”: LbI A: “K= ” ?S: Prog“KM”:“-B,0,B=”? Z: “σ右交角=”?M:Prog“SUB1”: Fix 4:Cls“X=”: Locate3,1,N◢“Y=”: Locate3,1,E◢Prog“JI”:Goto ALbI 2: “X=”? B: “Y=”? C:B→N: C→E:Prog“SUB2”: “K =”:S◢“-B,0,B=”:Z◢Goto 0LbI 3: 0→B: “H-B”?B:B→Z[9]: LbI D: Prog“XLXY”: “KM”?Z: Prog“KM”:“-B,0,B”?D:Prog“H”Fix 5:“H=”:H-Z[9] →H◢“I=”: I◢Goto D说明:Q: 代表正反算及竖曲线,其中1 为正算,2 为反算;3代表竖曲线;S: 代表里程;Z :代表偏移距离;M :代表偏移角度(以线路前进方向为X 方向,顺时针转为正;N :X 坐标;E :Y 坐标;F :切线方位角;SUB1 正算子程序0.5 (1÷R-1÷P)÷L→D:S-O→XU+∫(cos(A+(X÷P+DX2)×180÷π,0,X)→NV+∫( sin(A+(X÷P+DX2)×180÷π,0,X)→EA+(X÷P+DX2)×180÷π→FN+Zcos(F+M) →N:E+Zsin(F+M) →EReturnSUB2 反算子程序Lbl 1:0→Z :1→Q :Prog“KM”: Prog“SUB1”Pol(N-B+10^(-46), E-C+10^(-46)):Isin(F-90-J) →W:S+W→SIf Abs(W)>0.0001 :Then Goto1Lbl 2: 0→Z :Prog“SUB1”:(C-E) ÷sin(F+90) →Z次程序JIClstatPol(N-G,-E-H):ClsIf J<0:Then J+360→Y:Ease J→Y:Ifend“F J L=”:I◢“F W J=”:Y▲ DMS ◢XLXZ(线路选择)1→I:“XLXZ:Z=1:A=2,B=3,C=4,D=5,E=6,F=7,L=8”?I: I →Z[1]: IF I =0:Then Goto 0:Else Goto 1:IfEndLbI 0 : “F”?A: “QDZH”?O: “X”?U: “Y”?V: “R1”?P: “R2”?R:“L”?L: Goto 1LbI 1SUB0 ( 数据库)Goto1 ↙Lbl 1IF S<157687.528:Then157547.528→o :2884169.2517→U:471475.6573→V:98 °32 ′43.08 ″→A:10^45→P:10000;→R:140→L: Return:IfEnd 说明:S :里程;O 为线元起点里程;U 为线元起点X 坐标;V 为线元起点Y 坐标;A 线元起点切线方位角;P 线元起点半径(左转为负右转为正);R 线元终点半径(左转为负右转为正)高程计算子程序(H)程序名:HP rog “S1”:C-T→F:Z-F→S:C+T→E:G-TI→Q:If T=O:Then Q+S I→H:Goto 0:Else If Z<F:Then Q+SI→H:Goto 0:Else If Z≤E:T hen Q+SI+S2÷2÷R→H:Goto 0:LbI 0:H:If D=0:Then Goto I:Else Prog“I”:H+V→H:Goto ILbI I高程超高计算程序(I)程序名:IIf Z[3]=1:Then Prog “I1”:Goto 1: IfEndLbI 1: If W=1:Then Goto Z:Else Goto X: IfEndLbI Z:If S=0:Then Abs(D)×M→V:Goto 2:Else Abs(D)×((N-M)×(Z-C)÷S+M)→V:Goto 2:IfEnd:LbI X:If S=0:Then Abs(D)×M→V:Goto 2:Else Abs(D)×(((3((Z-C)÷S)2-2((Z-C)÷S)∧(3))×(N-M))+M)→V:Goto 2:IfEndLbI 2:Abs(D)→E:V÷E→I:I(E-K)→V②-1程序名:S1(线路1高程竖曲线要素子程序)If Z[1]=1:Then Goto 1:Else If Z[1]=2:Then Prog“SA”: Else I f Z[1]=3:Then Prog “SB”: Else If Z[1]=4: Then Prog“SC”: Else If Z[1]=5:Then Prog“SD”: Else If Z[1]=6: Then Prog“S E”: Else If Z[1]=7:Then Prog“SF”: Else If Z[1]=8:Then Pro g“SL”:IfEndGoto 1LbI 1If Z≤26157.8:Then -200000→R:157.8→T:26000→C:37.1→G:0.012 22→I:Return:IfEnd程序字母说明:R-竖曲线半径(分正负:凹曲线为正,凸曲线为负);T-竖曲线切线长(标段结尾或开头没有竖曲线的输0);C-竖曲线交点桩号;G-交点桩号高程(未竖曲线调整的);I-竖曲线前纵坡③-1程序名:I1(线路1高程超高参数子程序)If Z[1]=1:Then Goto L:Else If Z[1]=2:Then Prog“IA”: Else I f Z[1]=3:Then Prog “IB”: Else If Z[1]=4: Then Prog“IC”: Else If Z[1]=5:Then Prog“ID”: Else If Z[1]=6: Then Prog“I E”: Else If Z[1]=7:Then Prog“IF”: Else If Z[1]=8:Then Pro g“IL”:IfEnd1.5→K:If D<0:Then Goto L:Else Goto R:IfEnd:LbI LIf Z≤26735.555:Then 1→W: 120→S:26615.555→C:-0.02→M:0.02→N:Goto 0:IfEndLbI RIf Z≤26735.555:Then 1→W:0→S:-0.02→M: Goto 0:IfEndLbI 0字程序中字母表示说明:K-中央分隔带半幅宽(中桩标高至中桩中线距离,无分隔带则为0)本线路中为0;W-超高方式参数(W=1为一般直线方式超高,W=2为三次抛物线方式超高);S-超高渐变段距离(不是渐变段则输入0);C-超高渐变段起点桩号(不是渐变段,无需输入);M-超高段起点横坡,N-超高渐变段终点横坡(不是渐变段,无需输入)H (高程主程序)Fix 3 :Lb1 3: “ K=” ?Z: Prog“SQX”:(P-Q) ÷ Abs(P-Q) →W If Z<(H-T):Then(H-Z) × P →X:Goto 2:IfEndIf Z ≥ (H-T) And Z<H:Then (H-Z) × P+(Z-H+T)2÷ (2WR)→X:Else (H+T-Z)2÷ (2WR)-(Z-H) × Q→X: Goto 2:IfEn dLb1 2: ” GAO CHENG= ” D-X →X ◢Goto 3SQX (竖曲线数据库)Goto 1Lb1 1IfZ≤157893.75:Then25000→R:93.75→T:157800→H:421.977→D:-0. 0045→P:0.003→Q:Return:IfEnd说明:Z代表竖曲线终点里程,R 代表竖曲线半径;T 代表竖曲线切长;D 代表变坡点标高(未改正之前);P 代表前段坡度,上坡为正,下坡为负;Q 代表后段坡度,上坡为正,下坡为负;。
匝道验算

本计算以C匝道桥第1联30+32*2+30箱梁第2跨为例,对荷载进行计算及对支架体系进行验算。
该跨的验算具有代表性。
本方案设计均采用容许应力法计算,不计结构、荷载及材料等安全系数。
(1)、荷载计算1、荷载分析根据本工程现浇箱梁的结构特点,在施工过程中将涉及到以下荷载形式;1.1、q1—模板自重q1取1.5kn/m2;1.2、q2—箱梁自重荷载,新浇钢筋混凝土密度取26kn/m3;1.3、q3—施工人员、施工材料及设备荷载,一般按2kn/m2进行取值。
按分布荷载计算,计算模板及直接支承模板的小棱时取2.5kn/m2,计算直接支承小棱的梁时取1.2kn/m2,计算支架立柱时取1.0kn/m2;1.4、q4—振捣荷载,对水平面模板q4=2.0kn/m2;垂直于模板q4=4.0kn/m21.5、q5—新浇混凝土对侧模的压力(按规范要求每层浇筑高度控制在30cm 以内计算侧压力)。
1.6、q6—倾倒混凝土产生的水平荷载,查《路桥施工计算手册》表8-1,q6=2.0kn/m2;1.7、q7—支架自重,支架自重根据支架立杆设计间距、横杆步距、扣件、剪刀撑等钢管组合计算。
2、荷载组合模板、支架设计计算的荷载组合荷载组合受力结构强度计算(承载力)刚度验算(稳定性)底模q1+ q2+ q3+ q4 q1+ q2侧模q4+q 5+ q6 q6底模下纵桥向方木q1+ q2+ q3+ q4 q1+ q2立杆托顶横桥向方木q1+ q2+ q3+ q4 q1+ q2支架q1+ q2+ q3+ q4+ q7 q1+ q2 q3+ q4+ q7 地基q1+ q2+ q3+ q4+ q73、荷载计算3.1箱梁自重—q2计算根据工程现浇箱梁结构特点,通过认真分析,选取具有代表性及最不利荷载的断面,进行箱梁自重计算。
经分析:本段箱梁断面外尺寸相同,端横梁C1#、C2#、C30#、C5#、C6#墩梁高1.8m,部分为实心结构,混凝土结构自重最大。
2车道高架桥上匝道计算书

2车道高架桥上匝道计算书我们需要了解高架桥匝道的基本设计要求。
匝道的宽度应根据交通流量和车道数来确定,一般情况下,高架桥匝道至少应具备两个车道,以满足车辆的通行需求。
匝道的坡度和弯度也需要根据实际情况进行设计,以确保车辆能够平稳地通过匝道。
在进行高架桥匝道的计算时,我们需要考虑以下几个方面:1. 匝道的纵向坡度:匝道的纵向坡度对车辆的行驶速度和能量消耗有一定影响。
一般情况下,匝道的纵向坡度应控制在合理范围内,以确保车辆能够平稳通过。
2. 匝道的横向坡度:匝道的横向坡度对车辆的操控和安全性有一定影响。
匝道的横向坡度应根据实际情况进行设计,以确保车辆能够稳定行驶。
3. 匝道的弯道半径:匝道的弯道半径是决定车辆通过匝道时是否需要减速的重要参数。
弯道半径过小会导致车辆无法平稳通过,而弯道半径过大则会增加匝道的占地面积。
4. 匝道的减速带:为了保证车辆能够安全减速并进入匝道,设计中通常会设置减速带。
减速带的长度和坡度应根据车辆的行驶速度和匝道的设计要求进行确定。
除了以上几个关键参数,高架桥匝道的设计还需要考虑其他因素,例如视线要求、交通标志标线、排水系统等。
在实际的高架桥匝道计算中,我们可以使用各种工程软件和计算方法进行设计和分析。
这些软件和方法可以帮助工程师们更加准确地进行匝道的设计和计算,以满足交通流量和安全性的要求。
总结起来,高架桥上的匝道是城市交通中重要的组成部分,其设计和计算对于交通流的顺畅和安全至关重要。
匝道的宽度、坡度、弯道半径、减速带等参数需要根据实际情况进行设计,并使用合适的工程软件和计算方法进行分析。
通过合理的设计和计算,我们可以确保高架桥匝道的安全性和通行效率,为城市交通的发展做出贡献。
