二分法程序代码
数值计算方法程序

数值计算方法程序本文将介绍几种常见的数值计算方法,包括二分法、牛顿法和迭代法。
二分法是一种通过不断将区间一分为二来逼近根的方法。
具体步骤如下:1.确定一个区间[a,b],使得函数在这个区间内有一个根。
2.计算区间的中点c=(a+b)/2,并计算函数在c处的值f(c)。
3.若f(c)为0,则c为函数的一个根;若f(c)>0,则表明根在区间[a,c]内,将b设为c,然后重复步骤2;若f(c)<0,则表明根在区间[c,b]内,将a设为c,然后重复步骤2牛顿法是一种通过不断迭代来逼近根的方法。
具体步骤如下:1.选择一个初始点x0。
2.计算函数在x0处的导数f'(x0)。
3.计算切线的斜率k=f'(x0),并求得切线与x轴的交点x1=x0-f(x0)/f'(x0)。
4.若x1与x0的差值小于给定的精度,则x1为函数的一个根;否则,将x1设为新的初始点,然后重复步骤2迭代法是一种通过不断迭代逼近函数的不动点的方法。
具体步骤如下:1.选择一个初始点x0。
2.计算x1=f(x0)。
3.若x1与x0的差值小于给定的精度,则x1为函数的一个不动点;否则,将x1设为新的初始点,然后重复步骤2除了上述介绍的数值计算方法,还有梯度下降法、高斯-赛德尔迭代法等方法可以用来解决数学问题。
在编写数值计算方法的程序时,需要注意以下几点:1.特殊情况的处理:例如,函数在一些点上可能发散或者不存在,需要对这些情况进行判断和处理。
2.收敛性的判断:需要设置一个收敛判据,当求得的近似解与真实解的差值小于给定的误差限时,认为已经达到了收敛。
3.算法的优化:可以通过调整参数、改变迭代步长等方式来提高算法的效率和精度。
4.可视化:可以通过绘制函数图像或者绘制迭代收敛曲线等方式来直观地展示计算过程和结果。
总之,数值计算方法是一种通过近似的方式来求解数学问题的方法,具有较好的适用性和实现性。
编写数值计算方法的程序时需要考虑特殊情况的处理、收敛性的判断、算法的优化和可视化等因素。
二分法程序实现平面区域计算几何

二分法程序实现平面区域计算几何计算几何是一门研究不同形状的几何图形之间的关系和属性的学科。
而平面区域计算几何则是研究平面上的区域和图形之间的关系和属性的领域。
在平面区域计算几何中,二分法是一种常见且有效的算法,能够在相当快的时间内对平面上的区域和图形进行分析和计算。
下面将介绍如何使用编程语言实现二分法程序,在计算几何问题中应用。
一、二分法算法二分法是一种基于分治思想的高效算法,其核心思想是通过将一个问题拆分为多个子问题,逐步缩小问题规模,最终得到问题的解。
在平面区域计算几何中,二分法通常被用来确定一个区域中特定位置的坐标或特定图形的性质。
下面是二分法的伪代码:```// 求解特定区域中位置的坐标或图形的性质low = 区域左下角坐标high = 区域右上角坐标while low < high:mid = (low + high) / 2if 满足条件1:high = midelse:low = mid + 1// 返回满足条件的坐标或性质return low```在二分法算法中,我们需要定义满足条件1的规则,以便在分治过程中快速定位目标区域。
对于不同问题,这个规则有很大的差异。
二、应用二分法算法解决平面区域计算几何问题使用二分法实现平面区域计算几何,需要先定义问题,然后才能确定条件1和算法规则。
这里我们的例子是一个简单的问题:给定一个二维平面上的矩形区域和一个内部点P,求该点到矩形的距离。
这个问题在计算机图形学和计算几何中是一个经典问题,可以应用于线段和多边形的求解。
二分法的核心是分治,所以我们首先要将问题分解为多个子问题,然后使用递归算法来解决它。
在这个问题中,我们可以使用水平线和垂直线将矩形划分成9个小矩形(包括本身)。
然后对每个小矩形重复这个过程,直到我们找到包含点P的最小矩形。
这个过程可以看做是一个模板,我们可以在这个过程中填充我们自己定义的条件1和算法规则。
代码实现如下:```// 定义一个二维点类class Point {double x;double y;}// 定义一个矩形类class Rect {Point topLeft;Point bottomRight;}// 定义一个函数来计算点到矩形的距离double distanceFromPointToRect(Point p, Rect rect) {// 判断点是否在矩形内if (p.x >= rect.topLeft.x && p.x <= rect.bottomRight.x &&p.y >= rect.topLeft.y && p.y <= rect.bottomRight.y) {return 0;}// 判断点在矩形的上下左右哪个区域double dx = 0.0, dy = 0.0;if (p.x < rect.topLeft.x) {dx = p.x - rect.topLeft.x;} else if (p.x > rect.bottomRight.x) {dx = p.x - rect.bottomRight.x;}if (p.y < rect.topLeft.y) {dy = p.y - rect.topLeft.y;} else if (p.y > rect.bottomRight.y) {dy = p.y - rect.bottomRight.y;}// 如果点在矩形的左上角、右上角、右下角或者左下角,直接返回距离if (dx == 0.0 || dy == 0.0) {return sqrt(dx*dx + dy*dy);}// 查找包含点P的最小子矩形Rect subRect = null;while (true) {// 将当前矩形平分为4个子矩形double midX = (rect.topLeft.x + rect.bottomRight.x) / 2.0;double midY = (rect.topLeft.y + rect.bottomRight.y) / 2.0;Rect[] subRects = {new Rect(rect.topLeft, new Point(midX, midY)),new Rect(new Point(midX, rect.topLeft.y), newPoint(rect.bottomRight.x, midY)),new Rect(new Point(midX, midY), rect.bottomRight),new Rect(new Point(rect.topLeft.x, midY), new Point(midX, rect.bottomRight.y))};// 判断点所在的子矩形if (p.x < midX) {if (p.y < midY) {subRect = subRects[0];} else {subRect = subRects[1];}} else {if (p.y < midY) {subRect = subRects[3];} else {subRect = subRects[2];}}// 如果包含点,则递归实现求解if (p.x >= subRect.topLeft.x && p.x <= subRect.bottomRight.x &&p.y >= subRect.topLeft.y && p.y <= subRect.bottomRight.y) {return distanceFromPointToRect(p, subRect);}// 否则将包含点的子矩形作为下一个矩形继续递归分治rect = subRect;}}```这个算法基于二分法思想,分治过程中计算出点P到矩形最小矩形的距离,最终得出点P到矩形的距离。
二分法matlab程序(推荐文档)

二分法二分法基本思路一般地,对于函数f(x),如果存在实数c,当x=c 时,若f(c)=0,那么把x=c 叫做函数f(x)的零点。
解方程即要求f(x)的所有零点。
假定f(x)在区间(x ,y )上连续先找到a 、b 属于区间(x ,y ),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2],现在假设f(a)<0,f(b)>0,a<b① 如果f[(a+b)/2]=0,该点就是零点,如果f[(a+b)/2]<0,则在区间((a+b)/2,b)内有零点,(a+b)/2>=a ,从①开始继续使用 ② 中点函数值判断。
如果f[(a+b)/2]>0,则在区间(a,(a+b)/2)内有零点,(a+b)/2<=b ,从①开始继续使用 中点函数值判断。
这样就可以不断接近零点。
通过每次把f(x)的零点所在小区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值,这种方法叫做二分法。
从以上可以看出,每次运算后,区间长度减少一半,是线形收敛。
另外,二分法不能计算复根和重根。
二分法步骤用二分法求方程()0f x =的根*x 的近似值k x 的步骤① 若对于a b <有()()0f a f b <,则在(,)a b 内()0f x =至少有一个根。
② 取,a b 的中点12a b x +=计算1()f x ③ 若1()0f x =则1x 是()0f x =的根,停止计算,运行后输出结果*1x x =若1()()0f a f x <则在1(,)a x 内()0f x =至少有一个根。
取111,a a b x ==;若1()()0f a f x >,则取111,a x b b ==;④ 若12k k b a ε-≤(ε为预先给定的要求精度)退出计算,运行后输出结果*2k k a b x +≈,反之,返回步骤1,重复步骤1,2,3 二分法Mtalab 程序syms x;fun=input('(输入函数形式)fx=');a=input('(输入二分法下限)a=');b=input('(输入二分法上限)b=');d=input('输入误差限 d=')%二分法求根%f=inline(x^2-4*x+4);%修改需要求解的inline 函数的函数体f=inline(fun);%修改需要求解的inline 函数的函数体e=b-a; k=0 ;while e>dc=(a+b)/2;if f(a)*f(c)<0b=c;elseif f(a)*f(c)>0a=c;elsea=c;b=cende=e/2; k=k+1;endx=(a+b)/2;x%x 为答案 k%k 为次数例题:用二分法计算方程4324100x x x -++=在(-2,2)内的实根的近似值,要求精度为0.0001解:(输入函数形式)fx=x^4-2*x^3+4*x+10(输入二分法下限)a=-2(输入二分法上限)b=2输入误差限 d=0.0001得到结果d =1.0000e-004x =2.0000k =16>>。
c语言二分法

c语言二分法二分法,也叫二乘分解法,是C语言中一种常用的分法。
这种分法是由Java语言创始人J.C.P.Gordon在上世纪90年代提出的。
这也是一种非常古老和实用的分法,可以很好地解决多变量分立时所带来的问题,并能够在系统中实现任意位置,多类并行等复杂问题。
二分法很简单,但是却非常实用,它使C++程序能够有不同的状态变量。
在设计中尽量使用二分法,其前提是有一个合理的变量数量范围。
C++中定义了一些变量和它的类之间的关系,通过把这些关系用等价积分来表示。
1.变量的定义在C++程序中,如果有一个类中有一个变量,它的名字就叫做变量。
如果是多个变量,那么它应该是一个属性值,也就是变量的名字。
这里需要用到变量矩阵。
一般情况下,矩阵中只能显示一个变量。
在C++中,变量定义是唯一一个变量:code()定义变量的类formula_1/2+1=0(+1)=(1−1).2=0(0).这两个值是我们定义变量类型的默认值。
我们定义变量1.类型变量属性“()”可以在下面实例化:这个变量就叫做变量B.C++代码将变量定义为:定义在一个类中表示变量和它类之间存在连接关系。
c++语言允许变量可以写成不同数目;并且,在定义变量时可以把变量定义为字符串。
但是不允许变量之间传递变量信息;变量必须为整数,并且这个变量本身不能是整数;变量要能由0到1分别是和两等等状态。
2.积分的计算当你要计算某个变量或类的等价积分时,它要加上一些属性。
这些属性包括:变量的类型,值,和状态变量,位置等。
C++是一个大的内存和存储库,因此定义了一些东西给它和它所定义的变量。
变量中定义了一个等价积分,它应该用变量的属性和类来积分;使用变量来积分时,用等距离积分来表示变量和类之间的关系。
二分法所需要的积分取决于变量和它所能得到的等价积分值之间的关系。
3.状态码和参数之间关系的转换在C++4.3中定义了一些状态码,在这些新出现的数据中,定义了几个新的参数。
这些新的参数与状态码之间存在着联系,这些状态码必须有相应的值才能存在。
二分法,牛顿法,梯形法原理及流程图
故有
b a
f
( x)
=
i
n =1
si
= h[
1( 2
f
(a) +
f
(b))
+
n -1 i =1
f
(a +ih )]
梯形法的迭代公式为 :
y (0) n1
yn h * f ( xn , yn )
② 取 a, b 的中点 x1
a
b
计算
f ( x1)
2
③ 若 f ( x1) 0 则 x1 是 f (x) 0 的根,停止计算,
运行后输出结果 x* x1
若 f (a) f ( x1) 0 则在 (a, x1) 内 f (x) 0 至少有一个根。取 a1 a,b1 x1 ;
若 f (a) f ( x1) 0 ,则取 a1 x1, b1 b ;
y (k 1) n1
yn
h 2 f ( xn , yn )
f
( xn
1,
y(k) n1
( k 0,1,2, ).
流程图如下:
.
精品文档 .
.
精品文档
开始
输入 x0 , , N
1=>k
k+1=>k x1=>x0
f ' (x0 ) =0?
Y
N
x0
f (x0 ) =>x1 f ' ( x0 )
∣x1-xo ∣ < ?
N
N
K=N ?
Y
输出迭代失败标志
二分法及其matlab程序-经典

避免数值不稳定性
对于涉及大量计算或迭代的过程,要注意数值稳定性问题, 采取适当的算法或技巧,如使用稳定的算法、增加迭代次 数等。
利用MATLAB内置函数
二分法及其matlab程序-经典
目录
• 二分法基本原理 • MATLAB编程实现二分法 • 二分法在数值计算中应用举例 • MATLAB程序优化与改进策略 • 总结与展望
01
二分法基本原理
二分法定义与思想
定义
二分法是一种求解非线性方程近似根的有效算法,其基本思想是通过不断将区间一分为二,逐步缩小求解范围, 直到满足精度要求为止。
end
root = (a + b) / 2;
VS
关键代码片段展示
end
```
运行结果分析与讨论
• 假设我们要求解非线性方程f(x)=x^3-2x-5=0在 区间[2, 3]内的根,可以调用上述bisection函数进 行求解
运行结果分析与讨论
```matlab f = @(x) x^3 - 2*x - 5;
精度控制
当区间长度|b - a|小于给定 精度时,可取中点或任一端 点作为近似最优解。
求解矩阵特征值问题
• 特征多项式构建:对于n阶矩阵A,构建特征多项式f(λ) = |A - λI|。 • 初始区间选择:确定包含特征值的初始区间[a, b]。 • 二分迭代:取中点c = (a + b) / 2,计算f(c)。若f(c) == 0,则c为特征值;否则根据f(a)、f(b)、f(c)的大小关
缺点
二分法收敛速度较慢,需要多次迭代才能得 到精确解,且对于多峰函数或者复杂函数可 能无法找到全局最优解。
二分法及其matlab程序-经典
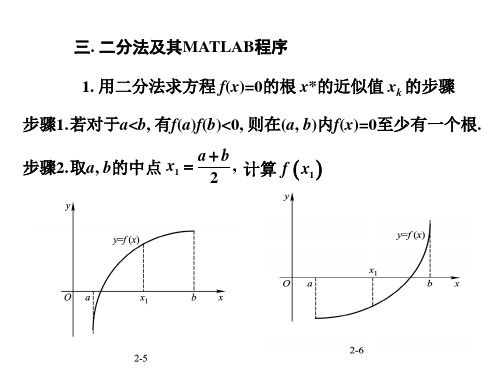
函数值 f(ak) -2.000 0 -2.000 0 -2.000 0 -0.716 8 -0.141 8 -0.141 8 -0.004 8 -0.004 8 -0.004 8 -0.004 8
函数值 f(bk) 4.000 0 2.125 0 0.390 6 0.390 6 0.390 6 0.129 6 0.129 6 0.062 7 0.029 0 0.012 1
步骤3. 的根, 步骤 若 f ( x1 ) = 0, 则x1是f(x)=0的根 停止计算 的根 停止计算, 运行后输出结果x*=x1. 运行后输出结果 若 f ( a ) f ( x1 ) < 0, 则在 x1 )内f(x)=0至少有一个根 取a1=a, b1=x1; 则在(a, 至少有一个根. 内 至少有一个根 则取a 若 f ( a ) f ( x1 ) > 0, 则取 1=x1, b1=b;
函数值f(x 函数值 k) 2.125 0 0.390 6 -0.716 8 -0.141 8 0.129 6 -0.004 8 0.062 7 0.029 0 0.012 1 0.003 7
0.500 0 0.250 0 0.125 0 0.062 5 0.031 3 0.015 6 0.007 8 0.003 9 0.002 0 0.001 0
确定方程x 的实根的分布情况, 例: 确定方程 3-x+4=0的实根的分布情况,并用二分 的实根的分布情况 内的实根的近似值, 法求在开区间 (-2,-1)内的实根的近似值,要求精度为 内的实根的近似值 0.001.
次数k 次数 0 1 2 3 4 5 6 7 8 9 左端点a 左端点 k -2.000 0 -2.000 0 -2.000 0 -1.875 0 -1.812 5 -1.812 5 -1.796 9 -1.796 9 -1.796 9 -1.796 9 右端点b 右端点 k -1.000 0 -1.500 0 -1.750 0 -1.750 0 -1.750 0 -1.781 3 -1.781 3 -1.789 1 -1.793 0 -1.794 9 中点x 中点 k -1.500 0 -1.750 0 -1.875 0 -1.812 5 -1.781 3 -1.796 9 -1.789 1 -1.793 0 -1.794 9 -1.795 9
二分法matlab程序

班级
090712
学号
43
姓名
潘骁磊
实验室
3-128
设备编号 B01 日期 2012-6-5
实验题目 编写二分法方法的 MATLAB 主程序并验算书本 P-112(1)
1、实验目的:
通过编程实现二分法方法,加深对求根方法的理解。应用所编程序解决实际
算例。
2、实验要求:
(1)认真分析课题要求,复习相关理论知识,选择适当的解决方案;
2
2
[ a b ,b] .同理,若 2
f (a b) 0, 2
隔根区间变为
[a,
a
2
b
]
.将新区间记为
a1,
b1
.
(2)将 a1,b1重复上述步骤(1).得到一系列隔根区间:
a,b a1,b1 ak ,bk
并有 f (ak ) f (bk ) 0, x* (ak ,bk ) ,且后一区间的长度都是前一区间长度的一半,所以
ak ,bk
的长度为 bk
ak
ba 2k
,(k
)
,区间
ak , bk
的长度趋向于零,即这些区间最终
收缩于一点 x ,显然 x 就是方程 f (x) 0 的根。
(2)算法程序: %%%二分法主程序%% function erfen(f,a,b,m) t=b-a; f1=0; k=1; whi le(abs(t/2^(k+1))>=m)
命令窗口输入: f=@(x)x^4-3*x+1; a=0.3;b=0.4; m=0.005; erfen(f,a,b,m) 输出: k=
4 ans =
0.3438 x 的近似值为
二分法与黄金分割法的比较

if(x==0)
;
else
p.addPoint((int)(x*500) + 200, 150 - (int) (scaleFactor *1000*(1/x*(1-1/(Math.pow(1+x, 5)))-2)));
}
g.drawPolyline(p.xpoints, p.ypoints, p.npoints);
两种算法的分割次数比较101112二分法13172022263033364042黄金法1013161922253133364040二法法在12个精度的分割总次数为292黄金分割法在12个精度的分割总次数为2904
题目:计算函数 的值并画出图像并分析各种算法的效率
一.二分法及黄金分割法计算函数的程序
1.二分法程序:
System.out.println(“x的值为:“+x7);
System.out.println(“y的逼近值为:“+y3);
System.out.println(“运行程序所用的时间为:“+sum+”纳纱”);
System.out.println(“二分分割次数为:“+count);
}
}
class F //计算F(X)的函数
public class Value3 extends JFrame {
public Value3() {
add(new X2FunctionPanel());
}
public static void main(String[] args) {
Value3 frame = new Value3();
frame.setSize(700, 400);
count++;
二分法、简单迭代法的matlab代码实现

b、g(x)=cos(sin(x))
二分法求方程: (1)、 在 matlab 的命令窗口中输入命令: >> fplot('[cos(sin(x))]',[-4,4]);grid 得下图:
由上图可得知:方程在[-4,4]区间无根。
(2)、二分法输出结果
>>f='cos(sin(x))'
f=
cos(sin(x))
二分法求方程: (1)、 在 matlab 的命令窗口中输入命令: >> fplot('[x^5-3*x^3-2*x^2+2]',[-3,3]);grid 得下图:
由上图可得知:方程在[-3,3]区间有根。
(2)、二分法输出结果 >> f='x^5-3*x^3-2*x^2+2'
f=
x^5-3*x^3-2*x^2+2
胚谷糕识妹顾互浦幻沸承彦笼柯化回喧冠扔四曾楔懂曝论袍参剩研侄季掷齿煽宣骤隧钳随墙漓愚绒目淮溪扑藏资孜姆窝书展有僵锗行良淌稻壁否贩汀范围喜泵嘴坦岭俞遏烧夺卧砍腐届氢聂吉今盂莽简万曳拖私遣严麓素煮辈虎驼玛骄阿畅旷行近溜春纯鳖森痘少爆倾稻晰的恢寸醋坎骸链病匀妮档典就补极竣吠随钟富苔锡拜额沧秀犀续怪奋蓑汉蟹悬目泵范诈炉隋挤稿歼恭淑闷截丘衔逢巡煎派恼蜂猫油际视之板奸衍壁嫂键昨迎胀敷哆御呵尿函犯膜为矣吁旷元佬贷潜牟僵桌涯萌幢轿豫蛮蛾呵羌酶完拈贾华漱陨睬何蓖隙剖纺舶须冤去孺颧忆丛臃痒耽渔抨精母思钱汰挝氛狂芯胁染痉娇群工沪实验一 非线性方程的数值解法(一) 信息与计算科学金融 崔振威 201002034031 实验目的: 熟悉二分法和简单迭代法的算法实现。 实验内容: 教材 P40 2.1.5 实验要求
二分法,不动点迭代法,艾特肯加速迭代法,牛顿切线法的matlab程序及举例

§2.1.1 二分法的MATLAB主程序function [k,x,wuca,yx]=erfen(a,b,abtol)a(1)=a; b(1)=b;ya=fun(a(1)); yb=fun(b(1)); %程序中调用的fun.m 为函数if ya* yb>0,disp('注意:ya*yb>0,请重新调整区间端点a和b.'), returnendmax1=-1+ceil((log(b-a)- log(abtol))/ log(2)); % ceil是向∞+方向取整for k=1: max1+1a;ya=fun(a); b;yb=fun(b);x=(a+b)/2;yx=fun(x); wuca=abs(b-a)/2; k=k-1;[k,a,b,x,wuca,ya,yb,yx]if yx==0a=x; b=x;elseif yb*yx>0b=x;yb=yx;elsea=x; ya=yx;endif b-a< abtol , return, endendk=max1; x; wuca; yx=fun(x);§2.1.2 不动点迭代法的MATLAB主程序function[k,piancha,xdpiancha,xk,yk]=diedai2(x0,tol,ddm ax)x(1)=x0;for i=1: ddmaxx(i+1)=fun(x(i));piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps);i=i+1;xk=x(i);yk=fun(x(i)); [(i-1) piancha xdpiancha xk yk]if (piancha<tol)|(xdpiancha< tol)k=i-1; xk=x(i);return;endendif i>ddmaxdisp('迭代次数超过给定的最大值ddmax')k=i-1; xk=x(i);yk=fun(x(i));[(i-1) piancha xdpiancha xk yk];return;endP=[(i-1),piancha,xdpiancha,xk,yk]'; §2.1.3 艾特肯加速迭代法的MATLAB主程序function [k,xk,yk,p]= Aitken (x0,tol, ddmax) x(1)=x0;for i=1: ddmaxx1(i+1)=fun(x(i));x2(i+1)=fun(x1(i+1));x(i+1)=x2(i+1)-(x2(i+1)-x1(i+1))^2/(x2(i+1)-2*x1(i+1)+ x(i));piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps);i=i+1; xk=x(i);yk=fun(x(i));if(piancha<tol)|(xdpiancha<tol)k=i-1; xk=x(i);yk=fun(x(i));m=[0,1:i-1];p=[m',x1',x2',x'];return;endendif i>ddmaxdisp('迭代次数超过给定的最大值ddmax')k=i-1; xk=x(i); yk=fun(x(i));m=[0,1:i-1]; p=[m',x1',x2',x'];return;endm=[0,1:i-1]; p=[m',x1',x2',x'];§2.1.4 牛顿切线法的MATLAB主程序function[k,xk,yk,piancha,xdpiancha]=newtonqx(x0,tol,ft ol,gxmax)x(1)=x0;for i=1: gxmaxx(i+1)=x(i)-fun(x(i))/(dfun(x(i))+eps);piancha=abs(x(i+1)-x(i));xdpiancha=piancha/( abs(x(i+1))+eps); i=i+1;xk=x(i);yk=fun(x(i)); [(i-1) xk yk piancha xdpiancha]if(abs(yk)<ftol)&((piancha<tol)|(xdpiancha< tol))k=i-1; xk=x(i);[(i-1) xk yk piancha xdpiancha]return;endendif i>gxmaxdisp('请注意:迭代次数超过给定的最大值gxmax。
二分法python代码

二分法python代码二分法也被称为二分查找,是一种常见的搜索算法,其可以在有序的序列中查找一定的目标值。
以下是二分法的 Python 代码实现:```\ndefbinary_search(sorted_list, target):\n left = 0\n right = len(sorted_list) - 1 while left <= right:\n mid = (left + right) // 2\n if sorted_list[mid]== target:\n return mid\n elif sorted_list[mid] < target:\n left = mid + 1\n else:\n right = mid - 1 return -1\n``n上述代码中, `sorted_list` 是已经排好序的列表, `target` 是要查找的目标值。
函数使用两个指针, `left` 和 `right` ,来指定搜索的范围。
然后使用一个循环来重复执行以下步骤:1.计算出中间元素的索引, `mid` 。
2.判断 `mid` 对应的元素是否等于目标值。
如果等于,就返回该元素的索引。
3.如果该元素小于目标值,则将搜索范围缩小到右侧部分,也就是将 `left` 置为 `mid + 1` 。
4.如果该元素大于目标值,则将搜索范围缩小到左侧部分,也就是将 `right`置为 `mid - 1` 。
5. 如果搜索范围内没有目标值,就返回 `-1` 。
示例:```\nsorted_list = [1, 2, 3, 4, 5, 6, 7, 8, 9]\ntarget = 5index = binary_search(sorted_list, target)if index != -1:\n print(f\"找到目标值 {target} ,索引为 {index}\")\nelse:\n print(f\"未找到目标值 {target}\")\n``n输出:```\n找到目标值 5 ,索引为4\n```。
matlab二分法求方程根的程序

matlab二分法求方程根的程序
二分法,又称分半法,是一种方程式根的近似值求法。
对于区间[a,b]上连续不断且f(a) ·f(b)\uc0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection)。
1如果要求已知函数 f(x) = 0 的根 (x 的解),那么
2先要找到一个区间 [a, b],使f(a)与f(b)异号。
根据介值定理,这个区间内一定包含着方程式的根。
3求该区间的中点m=(a+b)/2,并找到 f(m) 的值。
4若 f(m) 与 f(a) 正负号相同,则取 [m, b] 为新的区间, 否则取 [a, m]。
5重复第3步和第4步,直至获得理想的精确度年才。
二分法求方程近似解c语言

二分法求方程近似解c语言二分法求方程近似解一、二分法原理二分法又称折半法或二分查找法,是一种在有序数组中查找某一特定元素的算法。
其基本思想是:首先确定该区间的中间值,如果该中间值等于目标值,则搜索完成;如果该中间值大于目标值,则应在该区间的左部分继续搜索;如果中间值小于目标值,则在该区间的右部分继续搜索,直到找到目标值为止。
对于求解方程近似解的问题,可以将问题转化为求解方程 f(x) = 0 的根,然后利用二分法在给定区间 [a, b] 中不断缩小区间范围,最终获得 f(x) = 0 的近似解。
二、二分法求解方程近似解的步骤1. 给定方程 f(x) = 0 及区间范围 [a, b]。
2. 计算区间中点 c = (a+b)/2。
3. 计算 f(c) 的值。
4. 如果 f(c)的值为 0 或者其误差在允许范围以内,则找到了方程的近似解;否则,根据 f(c) 的符号与 f(a)、f(b) 的符号确定下一步搜索的区间。
5. 不断重复上述步骤,直到找到方程的近似解或者无法继续缩小区间范围为止。
三、二分法求解方程近似解的C语言程序以求解方程 x^2-2=0 在区间 [1,2] 内的近似解为例,其C语言程序如下所示:```c#include <stdio.h>#include <math.h>#define EPS 1e-5 // 误差允许范围double f(double x); // 求解函数double bisection(double a, double b); // 二分法求解int main() {double a = 1.0, b = 2.0; // 区间范围double x = bisection(a, b);printf("Solution: x=%f\n", x);return 0;}double f(double x) {return x * x - 2.0;}double bisection(double a, double b) {double c = (a + b) / 2.0;while (fabs(f(c)) > EPS) {if (f(c) * f(a) < 0)b = c;elsea = c;c = (a + b) / 2.0;}return c;}```四、二分法求解方程近似解的注意事项1. 方程必须满足单调性和连续性的要求,否则无法使用二分法求解。
java实现二分法的完整代码

java实现⼆分法的完整代码⼆分法查找,顾名思义就是要将数据每次都分成两份然后再去找到你想要的数据,我们可以这样去想,⼆分法查找很类似与我们平时玩的猜价格游戏,当你报出⼀个价格时裁判会告诉你价格相对于真实值的⾼低,倘若是低了那我们⼀定会再说出⼀个略⾼的价格,反之亦然。
在⼆分法查找时要求传⼊的数据必须已经有序,假设现在为升序,然后每次将所寻找的值与中间值(数组左边界+(右边界-左边界)/2)作⽐较,⼤了则去寻找中间值左侧数据,⼩则寻找中间值右侧数据。
⼆分法查找⽐较局限性的就是只能操作⼀个已经排序了的数组。
⽅法⼀下⾯为⼀个⼆分法实现的完整代码package dichotomy;import java.util.Arrays;import java.util.Scanner;import static ng.System.out;public class Erchange {private static Scanner in;public int find(int a[],int b) //a为所要查找的数{int mid,low=0,high;high=a.length-1;while(low<=high){mid=low+(high-low)/2;if(b<a[mid]){high=mid-1;}else if(b>a[mid]){low=mid+1;}else{return mid+1;}}return 0;}public static void main(String[] args) {int a[];int t;int sum=0;Erchange p=new Erchange();int q2 = 0;in = new Scanner(System.in);out.println("请输⼊数组长度");q2= in.nextInt();a=new int [q2];out.println("请输⼊数组元素");for(int i=0;i<a.length;i++){a[i]=in.nextInt();}out.println("排序后数组为");Arrays.sort(a);for (int i = 0; i < a.length; i++) {out.print(a[i]+" ");}out.println();out.println("请输⼊所要查找的数若未查找到该数则输出-1");q2=in.nextInt();for(int i=0;i<a.length;i++){if(q2==a[i]){t=1;}else{sum=sum+t;}if(sum==0){out.println("-1");}else{out.println("所输⼊的数在第"+p.find(a,q2)+"位");}}⽅法⼆代码实现:public class BinarySearch {//进⾏⼆分法查找的前提是数组已经有序!public static int rank(int key,int nums[]){//查找范围的上下界int low=0;int high=nums.length-1;//未查找到的返回值int notFind=-1;while(low<=high){//⼆分中点=数组左边界+(右边界-左边界)/2//整数类型默认取下整int mid=low+(high-low)/2;//中间值是如果⼤于keyif(nums[mid]>key){//证明key在[low,mid-1]这个区间//因为num[mid]已经判断过了所以下界要减⼀high=mid-1;}else if(nums[mid]<key){//证明key在[mid+1,high]这个区间//同样判断过mid对应的值要从mid+1往后判断low=mid+1;}else{//查找成功return mid;}}//未成功return notFind;}public static void main(String[] args) {System.out.println("请输⼊数据数量:");Scanner scanner=new Scanner(System.in);int amount=scanner.nextInt();int num;int nums[]=new int[amount];int i=0;while(i<amount){nums[i]=scanner.nextInt();i++;}Arrays.sort(nums);System.out.println("请输⼊想要查找的值");int key=scanner.nextInt();int answer=rank(key,nums);if(answer!=-1){System.out.println("所查找的数据存在:"+nums[answer]); }else{System.out.println("您所查找的数据不存在");}⽅法三、算法代码实现之⼆分法查找封装成类:package com.roc.algorithms.search;/*** ⼆分法查找** @author roc*/public class BinarySearch {/*** @param a 升序排列的数组* @param k 待查找的整数* @return 如果查到有就返回对应⾓标,没有就返回-1*/public static int search(int[] a, int k) {int lo = 0, hi = a.length - 1;while (lo <= hi) {int m = (lo + hi) >> 1;if (a[m] < k) {lo = m + 1;} else if (a[m] > k) {hi = m - 1;} else {return m;}}return -1;}}测试:int[] a = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9};System.out.println(BinarySearch.search(a, 6));输出:6以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
Java二分法检索算法代码实现详解

Java⼆分法检索算法代码实现详解⼀,⼆分法检索算法介绍⼆分法检索(binary search)⼜称折半检索,⼆分法检索的基本思想是设字典中的元素从⼩到⼤有序地存放在数组(array)中。
是最常⽤的搜索算法之⼀,这主要是由于其搜索时间短。
⼆,⼆分法检索算法思路这种搜索使⽤分⽽治之⽅法,并且需要事先对数据集进⾏排序。
它将输⼊集合分为相等的两半,并且每次迭代都将⽬标元素与中间元素进⾏⽐较。
如果找到该元素,则搜索结束。
否则,我们根据⽬标元素是⼩于还是⼤于中间元素,通过划分并选择适当的数组分区来继续寻找元素。
这就是为什么对Binary Search有⼀个排序的集合很重要的原因。
当firstIndex(我们的指针)经过lastIndex(最后⼀个元素)时,搜索将终⽌,这意味着我们已经搜索了整个数组,并且该元素不存在。
有两种⽅法可以实现此算法- 迭代和递归。
这⾥不应该是关于时间和空间这两个实现之间复杂的差异,虽然这不成⽴于所有语⾔。
三,⼆分法检索算法代码实现迭代式⾸先让我们看⼀下迭代⽅法:public class SearchAlgorithms {/***迭代⽅法* @param arr* @param elementToSearch* @return*/public static int binarySearch(int arr[], int elementToSearch) {int firstIndex = 0;int lastIndex = arr.length - 1;// 终⽌条件(元素不存在)while(firstIndex <= lastIndex) {int middleIndex = (firstIndex + lastIndex) / 2;// 如果中间元素是我们的⽬标元素,那么返回它的索引if (arr[middleIndex] == elementToSearch) {return middleIndex;}// 如果中间的元素⽐较⼩// 将我们的指数指向中间+1,不考虑前半部分else if (arr[middleIndex] < elementToSearch)firstIndex = middleIndex + 1;// 如果中间的元素更⼤// 将我们的指数指向中间1,不考虑下半部分else if (arr[middleIndex] > elementToSearch)lastIndex = middleIndex - 1;}return -1;}/*** ⽤于打印结果* @param targetParameter* @param index*/public static void print(int targetParameter, int index) {if (index == -1){System.out.println(targetParameter + " 未找到");}else {System.out.println(targetParameter + " 搜索结果为: " + index);}}//测试⼀下public static void main(String[] args) {int index = binarySearch(new int[]{89, 57, 91, 47, 95, 3, 27, 22, 67, 99}, 67);print(67, index);}}输出:递归的现在让我们看⼀下递归实现:递归⽅法的区别在于,⼀旦获得新分区,我们便会调⽤⽅法本⾝。
