优化设计复习
优化设计复习题(原)

word 教育资料优化设计复习题一、单项选择题(在每小题列出的选项中只有一个选项是符合题目要求的)1.多元函数F(X)在点X *附近偏导数连续, F ’(X *)=0且H(X *)正定,则该点为F(X)的( ) ①极小值点 ②极大值点 ③鞍点 ④不连续点 2.F(X)为定义在n 维欧氏空间中凸集D 上的具有连续二阶偏导数的函数,若H(X)正定,则称F(X)为定义在凸集D 上的( ) ①凸函数 ②凹函数 3.黄金分割法中,每次缩短后的新区间长度与原区间长度的比值始终是一个常数,此常数是( ) ①0.382 ②0.186 ③0.618 ④0.816 4.在单峰搜索区间[x 1,x 3](x 1<x 3)内,取一点x 2,用二次插值法计算得x 4(在[x 1,x 3]内),若x 2>x 4,并且其函数值F (x 4)<F(x 2),则取新区间为( ) ①[x 1,x 4] ②[x 2,x 3] ③[x 1,x 2] ④[x 4,x 3] 5.用变尺度法求一n 元正定二次函数的极小点,理论上需进行一维搜索的次数最多为( ) ①n 次 ②2n 次 ③n+1次 ④2次6.下列特性中,梯度法不具有的是( ) ①二次收剑性 ②要计算一阶偏导数 ③对初始点的要求不高 ④只利用目标函数的一阶偏导数值构成搜索方向 8.对于极小化F(X),而受限于约束g μ(X)≤0(μ=1,2,…,m)的优化问题,其内点罚函数表达式为( ) ① Ф(X,r (k))=F(X)-r(k)11/()gX u u m=∑② Ф(X,r (k))=F(X)+r(k)11/()gX u u m =∑③ Ф(X,r (k))=F(X)-r(k)max[,()]01gX u u m=∑④ Ф(X,r (k))=F(X)-r (k)min[,()]01g X u u m=∑9.外点罚函数法的罚因子为( ) ①递增负序列 ②递减正序列 ③递增正序列 ④递减负序列 10.函数F (X )为在区间[10,20]内有极小值的单峰函数,进行一维搜索时,取两点13和16,若F (13)<F (16),则缩小后的区间为( ) ①[10,16] ②[10,13] ③[13,16] ④[16,20] 11.多元函数F (X )在X *处存在极大值的充分必要条件是:在X *处的Hesse 矩阵( ) ①等于零 ②大于零 ③负定 ④正定 12.对于函数F (x )=x 21+2x 22,从初始点x (0)={1,1}T 出发,沿方向s (0)={-1,-2}T进行一维搜索,最优步长因子为( )①10/16 ②5/9 ③9/34 ④1/213.目标函数F (x )=x 21+x 22-x 1x 2,具有等式约束,其等式约束条件为h(x)=x 1+x 2-1=0,则目标函数的极小值为( ) ①1 ②0.5 ③0.25 ④0.1 14. 优化设计的自由度是指( )① 设计空间的维数 ② 可选优化方法数 ③ 所提目标函数数 ④ 所提约束条件数 15. 在无约束优化方法中,只利用目标函数值构成的搜索方法是( ) ①梯度法 ② Powell 法 ③共轭梯度法 ④变尺度法 17. 利用0.618法在搜索区间[a,b ]内确定两点a 1=0.382,b 1=0.618,由此可知区间[a,b ]的值是( ) ①[0,0.382] ② [0.382,1] ③ [0.618,1]④ [0,1]18. 已知函数F(X)=x 12+x 22-3x 1x 2+x 1-2x 2+1,则其Hesse 矩阵是( ) ① ⎥⎦⎤⎢⎣⎡--2332 ② ⎥⎦⎤⎢⎣⎡2332③ ⎥⎦⎤⎢⎣⎡2112 ④ ⎥⎦⎤⎢⎣⎡--3223 19. 对于求minF(X)受约束于g i (x)≤0(i=1,2,…,m)的约束优化设计问题,当取λi ≥0时,则约束极值点的库恩—塔克条件为( )①()i i 1F X g (X)mi λ=∇=∇∑,其中λi 为拉格朗日乘子② ()i i 1F X =g (X)mi λ=-∇∇∑,其中λi 为拉格朗日乘子③ ()i i 1F X g (X)qi λ=∇=∇∑,其中λi 为拉格朗日乘子,q 为该设计点X 处的约束面数④()i i 1F X g (X)qi λ=-∇=∇∑,其中λi 为拉格朗日乘子,q 为该设计点X 处的约束面数20. 在共轭梯度法中,新构造的共轭方向S (k+1)为( ) ① S (k+1)= ∇F(X (k+1))+β(k)S (K),其中β(k)为共轭系数② S (k+1)=∇F(X (k+1))-β(k)S (K),其中β(k)为共轭系数 ③ S (k+1)=-∇F(X (k+1))+β(k)S (K),其中β(k)为共轭系数④ S (k+1)=-∇F(X (k+1))-β(k)S (K),其中β(k)为共轭系数 21. 用内点罚函数法求目标函数F(X)=ax+b 受约束于g(X)=c-x ≤0的约束优化设计问题,其惩罚函数表达式为( ) ① (k)1ax b r c-x+-,r (k)为递增正数序列② (k)1ax b r c-x +-,r (k)为递减正数序列 ③ (k)1ax b r c-x ++,r (k)为递增正数序列word 教育资料④ (k)1ax b r c-x++,r (k)为递减正数序列22. f(x)在区间[x 1,x 3]上为单峰函数,x 2为区间中的一点,x 4为利用二次插值法求得的近似极值点,若x 4-x 2<0,且f(x 4)≥f(x 2),则新的搜索区间为( )① [x 1,x 4] ② [x 2,x 3] ③ [x 1,x 2] ④[x 4,x 3]23. 已知F(X)=x 1x 2+2x 22+4,则F(X)在点X (0)=⎭⎬⎫⎩⎨⎧-11的最大变化率为( )① 10 ② 4 ③ 2 ④ 1024.试判别矩阵1111⎡⎣⎢⎤⎦⎥,它是( )矩阵 ①单位 ②正定矩 ③负定 ④不定 ⑤半正定 ⑥半负定 25.约束极值点的库恩——塔克条件为:-∇=∇=∑F X g Xii qi()()**λ1,当约束函数是g i (X)≤0和λi>0时,则q 应为( )①等式约束数目 ②不等式约束数目 ③起作用的等式约束数目 ④起作用的不等式约束数目26.在图示极小化的约束优化问题中,最优点为( ) ①A ②B ③C ④D27.内点罚函数(X,r (k))=F(X)-r (k)101g X g X u u u m(),(())≤=∑,在其无约束极值点X ·(r (k))逼近原目标函数的约束最优点时,惩罚项中( ) ①r (k)趋向零,11g X u u m()=∑不趋向零 ②r (k)趋向零,11g X u u m()=∑趋向零 ③r (k)不趋向零,11g X u u m()=∑趋向零 ④r (k)不趋向零,11g X u u m()=∑不趋向零 29.0.618法在迭代运算的过程中,区间的缩短率是( )①不变的 ②任意变化的 ③逐渐变大 ④逐渐变小 30.对于目标函数F(X)受约束于g u (X) ≤0(u=1,2,…,m)的最优化设计问题,外点法惩罚函数的表达式是( )①()()(k)(k)2()1X,M F X M {max[(),0]},mk u u g X M =Φ=+∑为递增正数序列②()()(k)(k)2()1X,M F X M {max[(),0]},mk u u g X M =Φ=+∑为递减正数序列③()()(k)(k)2()1X,M F X M {min[(),0]},mk u u g x M =Φ=+∑为递增正数序列 ④()()(k)(k)2()1X,MF X M {min[(),0]},mk uu g x M=Φ=+∑为递减正数序列31.对于二次函数F(X)=12X T AX+b T X+c,若X *为其驻点,则▽F(X *)为( )①零 ②无穷大 ③正值 ④负值 32.在约束优化方法中,容易处理含等式约束条件的优化设计方法是( )①可行方向法 ②复合形法 ③内点罚函数法 ④外点罚函数法33.已知F(X)=(x 1-2)2+x 22,则在点X (0)=00⎧⎨⎩⎫⎬⎭处的梯度为( )①∇=⎧⎨⎩⎫⎬⎭F X ()()000 ②∇=-⎧⎨⎩⎫⎬⎭F X ()()020 ③∇=⎧⎨⎩⎫⎬⎭F X ()()040 ④∇=-⎧⎨⎩⎫⎬⎭F X ()()04034.Powell 修正算法是一种( )①一维搜索方法②处理约束问题的优化方法③利用梯度的无约束优化方法④不利用梯度的无约束优化方法 二、多项选择题(在每小题列出的多个选项中有两个以上选项是符合题目要求的,多选、少选、错选均无分) 35.下列矢量组中,关于矩阵A=105051--⎡⎣⎢⎤⎦⎥..共轭的矢量组是( )①s 1={0 1} ,s 2={1 0}T②s 1={-1 1}T ,s 2={1 1}T③s 1={1 0}T ,s 2={1 2}T④s 1={1 1}T ,s 2={1 2}T⑤.s 1={1 2}T ,s 2={2 1}T36. 对于只含不等式约束的优化设计问题,可选用的优化方法有( )① Powell 法 ② 变尺度法 ③ 内点罚函数法 ④ 外点罚函数法E. 混合罚函数法37. 根据无约束多元函数极值点的充分条件,已知驻点X*,下列判别正确的是( )①若Hesse矩阵H(X*)正定,则X*是极大值点②若Hesse矩阵H(X*)正定,则X*是极小值点③若Hesse矩阵H(X*)负定,则X*是极大值点④若Hesse矩阵H(X*)负定,则X*是极小值点⑤若Hesse矩阵H(X*)不定,则X*是鞍点38.下述Hesse矩阵中,正定矩阵为()①3335⎡⎣⎢⎤⎦⎥②313153337⎡⎤⎢⎥-⎢⎥-⎢⎥⎣⎦③3445⎡⎣⎢⎤⎦⎥④245434542⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦⑤523222327⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦39.F(X)在区间[a,b]上为单峰函数,区间内函数情况如图所示:F1=F2。
2024高考总复习优化设计二轮用书地理(适用于新高考新教材)思维方式一 区域认知

【示例剖析】 第(1)题,地理事物主要分为点、线、面三种情况。可考查 点与点、点与线、点与面、线与线、线与面、面与面,共6种空间分布特
征( C32 排列组合)。此题考查的是面与面的空间分布特征。主要答题格式
有纬度位置、海陆位置、相对位置。本题图中没有纬度,所以不用写纬度 位置。但有海陆位置,根据图例可以叙述闽语主要分布在广东省东部沿海 及雷州半岛地区。其他图例可根据相对位置关系来写。答案还要有总体 空间分布特点,此题没有时间因素的特点。(注意:相对位置关系以广东省 还是广州市为依据。)
【示例剖析】
第(1)题,
步骤
分析
定要素 地形要素对地貌、水文、气候的影响,进而对里海产生影响
明机制
地形隆起改变了地貌分布和地貌类型;改变了水系特征和水文特征; 阻挡水汽进入,使气候变干
山脉隆起,使里海与古地中海分离,使原来是海域的地方成为湖泊,原
联情境
来的洋盆成为湖盆;里海再也无法与古地中海进行水体交换,汇水面 积大大减少;山脉隆起阻挡了西风从海洋带来的水汽,使里海流域降
(2)尺度效应 ①内涵:大尺度上的地理事象是小尺度上地理事象产生的背景;小尺度上的 地理事象构成大尺度上地理事象的诱因;局地尺度与全球尺度之间相互影 响,互为因果;从不同尺度观察地理事象的特点得出的结果并不相同;在一 种尺度上获取的信息并不一定适用于另一种尺度。 ②举例:因气候暖湿化,卓乃湖水位上涨而溢出,造成清水河以上河段(卓乃 湖、库赛河、库赛湖、海丁诺尔、盐湖)贯通,使长江水系北源流程延长拓 展。(小尺度上的地理事象构成大尺度上地理事象的诱因)
③举例:青藏高原的种植业主要分布于雅鲁藏布江谷地和湟水谷地,属于河 谷农业,主要影响因素是热量,即河谷内地势低,气温高,热量较充足,得以发 展种植业。此事象产生的背景是青藏高原地势高,高原面气候寒冷,热量不 足,不能发展种植业。青藏高原这个大尺度区域的热量条件是河谷农业小 尺度种植业发展的背景。(大尺度上的地理事象是小尺度上地理事象产生 的背景)
2024年高考总复习优化设计一轮用书数学配人教A版(适用于新教材)课时规范练34
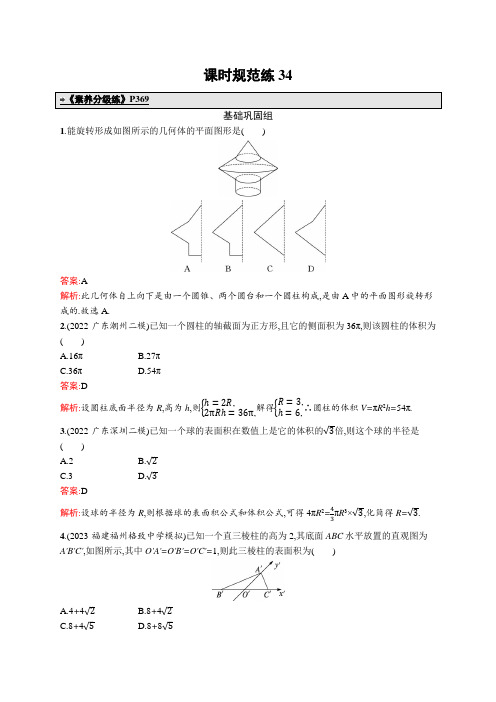
课时规范练34《素养分级练》P369基础巩固组1.能旋转形成如图所示的几何体的平面图形是( )答案:A解析:此几何体自上向下是由一个圆锥、两个圆台和一个圆柱构成,是由A 中的平面图形旋转形成的.故选A .2.(2022·广东潮州二模)已知一个圆柱的轴截面为正方形,且它的侧面积为36π,则该圆柱的体积为( ) A.16π B.27πC.36πD.54π答案:D解析:设圆柱底面半径为R ,高为h ,则{ℎ=2R ,2πRℎ=36π,解得{R =3,ℎ=6,∴圆柱的体积V=πR 2h=54π.3.(2022·广东深圳二模)已知一个球的表面积在数值上是它的体积的√3倍,则这个球的半径是( ) A.2 B.√2C.3D.√3答案:D解析:设球的半径为R ,则根据球的表面积公式和体积公式,可得4πR 2=43πR 3×√3,化简得R=√3. 4.(2023·福建福州格致中学模拟)已知一个直三棱柱的高为2,其底面ABC 水平放置的直观图为A'B'C',如图所示,其中O'A'=O'B'=O'C'=1,则此三棱柱的表面积为( )A.4+4√2B.8+4√2C.8+4√5D.8+8√5答案:C解析:由斜二测画法可得底面的平面图如图所示,其中OA=2OB=2OC=2,所以AB=AC=√5,所以此三棱柱的表面积S=2×12×2×2+(2+2√5)×2=8+4√5.5.(2022·山东菏泽一模)如图1,在高为h的直三棱柱容器ABC-A1B1C1中,AB=AC=2,AB⊥AC.现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为A1B1C(如图2),则容器的高h为()图1图2A.3B.4C.4√2D.6答案:A解析:在图1中V水=12×2×2×2=4,在图2中,V水=V ABC-A1B1C1−V C-A1B1C1=12×2×2×h-1 3×12×2×2×h=43h,∴43h=4,∴h=3.6. (2022·广东佛山二模)如图,某几何体由共底面的圆锥和圆柱组合而成,且圆柱的两个底面圆周和圆锥的顶点均在体积为36π的球的球面上,若圆柱的高为2,则圆锥的侧面积为()A.2√6πB.4√6πC.16πD.16π3答案:B解析:依题意,作球的剖面图,其中,O 是球心,E 是圆锥的顶点,EC 是圆锥的母线.设球的半径为R ,则43πR 3=36π,R=3.∵圆柱的高为2,∴OD=1,DE=3-1=2,DC=√32-12=2√2,母线EC=√22+8=2√3.∴圆锥的侧面积S=12·EC ·2π·DC=12×2√3×2π×2√2=4√6π.故选B .7.(2022·全国甲,理9)甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若S 甲S 乙=2,则V 甲V 乙=( )A.√5B.2√2C.√10D.5√104答案:C如图,甲、乙两个圆锥的侧面展开图刚好拼成一个圆,设圆的半径(即圆锥的母线长)为3,则圆的周长为6π,甲、乙两个圆锥的底面半径分别为r 1,r 2,高分别为h 1,h 2,则2πr 1=4π,2πr 2=2π,则r 1=2,r 2=1,由勾股定理得,h 1=√5,h 2=2√2,所以V 甲V 乙=13πr 12ℎ113πr 22ℎ2=2√512×2√2=√10.故选C .8.(多选)(2023·广东广州高三检测)某班级到一工厂参加社会实践劳动,加工出如图所示的圆台O 1O 2,在轴截面ABCD 中,AB=AD=BC=2 cm,且CD=2AB ,则( )A.该圆台的高为1 cmB.该圆台轴截面面积为3√3 cm 2C.该圆台的体积为7√3π3cm 3 D.一只小虫从点C 沿着该圆台的侧面爬行到AD 的中点,所经过的最短路程为5 cm 答案:BCD解析:如图,作BE⊥CD交CD于点E,易得CE=CD-AB2=1,则BE=√22-12=√3,则圆台的高为√3 cm,故A错误;圆台的轴截面面积为12×(2+4)×√3=3√3(cm2),故B正确;圆台的体积为13×√3×(π+4π+√π·4π)=7√3π3(cm3),故C正确;由圆台补成圆锥,可得大圆锥的母线长为4 cm,底面半径为2 cm,侧面展开图的圆心角θ=2π·24=π,设P为AD的中点,连接CP,可得∠COD=π2,OC=4,OP=3,则CP=√42+32=5,从点C沿着该圆台的侧面爬行到AD的中点,所经过的最短路程为5 cm,故D正确.故选BCD.9. (2023·湖南长沙一中高三检测)在棱长为2的正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AB,BC,CD,DA的中点,将该正方体挖去两个四分之一圆锥,得到如图所示的几何体,则该几何体的体积为.答案:8-π3解析:∵该几何体为正方体挖去两个四分之一圆锥,圆锥底面圆半径R=1,高h=2,∴该几何体的体积V=23-12×13×π×12×2=8-π3.10.(2022·福建漳州一模)某中学开展劳动实习,学习加工制作包装盒.现将一张足够用的正方形硬纸片加工制作成轴截面的顶角为60°,高为6的圆锥形包装盒,若在该包装盒中放入一个球形冰淇淋(内切),则该球形冰淇淋的表面积为.答案:16π解析:如图,由题意知,∠BAC=60°,AO1=6,故在Rt△AO1C中,AC=4√3,O1C=2√3.设内切球球心为O,半径为R,则OD=OO1=R.在Rt△ADO中,∠OAD=30°,所以2R=6-R,解得R=2.所以该球形冰淇淋的表面积S=4πR2=16π.综合提升组11. (2022·山东青岛二模)《九章算术》中记录的“羡除”是算学和建筑学术语,指的是一段类似隧道形状的几何体.如图,羡除ABCDEF 中,底面ABCD 是正方形,EF ∥平面ABCD ,EF=2,其余棱长都为1,则这个几何体的外接球的体积为( )A.√2π3B.4π3C.8√2π3D.4π答案:B解析:连接AC ,BD 交于点M ,取EF 的中点O ,连接OM ,则OM ⊥平面ABCD ,取BC 的中点G ,连接FG ,作GH ⊥EF ,垂足为H ,如图所示.由题意可知,HF=12,FG=√32,所以HG=√FG 2-HF 2=√22,所以OM=HG=√22.又AM=√22,所以OA=√OM 2+AM 2=1.又OE=1,所以OA=OB=OC=OD=OE=OF=1,即这个几何体的外接球的球心为O ,半径为1,所以这个几何体的外接球的体积为V=43×π×13=43π.12. (2022·山东泰安三模)如图,已知三棱柱ABC-A 1B 1C 1的底面是等腰直角三角形,AA 1⊥底面ABC ,AC=BC=2,AA 1=4,点D 在上底面A 1B 1C 1(包括边界)上运动,则三棱锥D-ABC 的外接球表面积的最大值为( )A.81π4B.24πC.243π16D.8√6π答案:B解析:因为△ABC 为等腰直角三角形,AC=BC=2,所以△ABC 的外接圆的圆心为AB 的中点O 1,且AO 1=√2.连接O 1与A 1B 1的中点E ,则O 1E ∥AA 1,所以O 1E ⊥平面ABC.设球的球心为O ,由球的截面性质可得O 在O 1E 上,设OO 1=x ,DE=t (0≤t ≤√2),球的半径为R.因为OA=OD=R ,所以√2+x 2=√(4-x)2+t2,所以t2=8x-14.又0≤t≤√2,所以74≤x≤2.因为R2=2+x2,所以8116≤R2≤6,所以三棱锥D-ABC的外接球表面积的最大值为24π.13.(多选)(2022·山东滨州二模)在边长为4的正方形ABCD中,如图1所示,E,F,M分别为BC,CD,BE的中点,分别沿AE,AF及EF所在直线把△AEB,△AFD和△EFC折起,使B,C,D三点重合于点P,得到三棱锥P-AEF,如图2所示,则下列结论正确的是()图1图2A.PA⊥EFB.三棱锥M-AEF的体积为4C.三棱锥P-AEF外接球的表面积为24πD.过点M的平面截三棱锥P-AEF的外接球所得截面的面积的取值范围为[π,6π]答案:ACD解析:由题意,将三棱锥补形为长方体,其中PA=4,PE=2,PF=2,如图所示.对于A,因为AP⊥PE,AP ⊥PF,PE∩PF=P,PE,PF⊂平面PEF,所以AP⊥平面PEF,又EF⊂平面PEF,所以PA⊥EF,故A正确;对于B,因为M为PE的中点,所以V M-AEF=12V P-AEF=12V A-PEF=12×13×12×2×2×4=43,故B错误;对于C,三棱锥P-AEF的外接球即为补形后长方体的外接球,所以外接球的直径2R=√22+22+42=2√6,所以三棱锥P-AEF外接球的表面积为S=4πR2=24π,故C正确;对于D,过点M的平面截三棱锥P-AEF的外接球所得截面为圆,其中最大截面为过球心O的大圆,此时截面圆的面积为πR2=π(√6)2=6π,最小截面为过点M且垂直于球心O与M连线的圆,此时截面圆半径r=√R 2-OM 2=√6-5=1,截面圆的面积为πr 2=π,所以过点M 的平面截三棱锥P-AEF 的外接球所得截面的面积的取值范围为[π,6π],故D 正确.故选ACD .14.十字贯穿体(如图1)是美术素描学习中一种常见的教具.如图2,该十字贯穿体由两个全等的正四棱柱组合而成,且两个四棱柱的侧棱互相垂直,若底面正方形边长为2,则这两个正四棱柱公共部分所构成的几何体的内切球的体积为 .图1图2答案:4π3解析:该几何体的直观图如图所示,这两个正四棱柱公共部分所构成的几何体为两个全等的四棱锥S-ABCD 和P-ABCD.设内切球的半径为R ,AC 的中点为H ,由题意,H 为内切球的球心,连接BH ,SH ,可知SH 即为四棱锥S-ABCD 的高,在Rt △ABH 中,BH=√AB 2-AH 2=√6-2=2.又AC=SB=2√2,∴S 四边形ABCD =12×2√2×2×2=4√2.又BH=SH ,∴V S-ABCD =13SH ·S 四边形ABCD =13×2×4√2=8√23.由八个侧面的面积均为2√2,∴13R ×2√2×8=2×8√23,得R=1.故几何体的内切球的体积为4π3.创新应用组15.如图,“十字歇山”是由两个直三棱柱重叠后的景象,重叠后的底面为正方形,直三棱柱的底面是顶角为120°,腰为3的等腰三角形,则该几何体的体积为( )A.23B.24C.26D.27答案:D解析:该几何体由直三棱柱AFD-BHC 及直三棱柱DGC-AEB 组成,作HM ⊥CB 于M ,如图.因为CH=BH=3,∠CHB=120°,所以CM=BM=3√32,HM=32.因为重叠后的底面为正方形,所以AB=BC=3√3.在直棱柱AFD-BHC 中,AB ⊥平面BHC ,则AB ⊥HM.由AB ∩BC=B ,可得HM ⊥平面ADCB.设重叠后的EG 与FH 的交点为I,则V I -BCDA =13×3√3×3√3×32=272,V AFD-BHC =12×3√3×32×3√3=814,则该几何体的体积V=2V AFD-BHC -V I -BCDA =2×814−272=27.。
2024高考总复习优化设计二轮用书地理(适用于新高考新教材)热考7 生物与环境

(2023·福建漳州质量检测)鸟类学家发现短翅蝗莺、煤山雀等属于不具备 长距离飞行能力的高山鸟类,由于大时间尺度的气温变化,原来只分布于我 国青藏高原边缘西南山地,后来也出现在相距上千千米的武夷山地,这种现 象被称为“武夷山现象”。据此完成6~7题。 6.从这些鸟类只分布于青藏高原边缘西南山地到出现“武夷山现象”,可推 测( D ) A.冰期这些鸟类分布区收缩 B.间冰期这些鸟类分布区稳定 C.经历冰期—间冰期—冰期 D.经历间冰期—冰期—间冰期 7.在武夷山脉与台湾山脉的某些鸟类也有类似现象,说明台湾海峡( A ) A.曾经出露为陆地 B.曾经完全冰封 C.由山地沉降而成 D.由板块张裂形成
1 2 3 4 5 6 7 8 9 10 11
解析 第6题,鸟类开始只分布于青藏高原边缘西南山地,是由于间冰期高山 地区温度适宜,鸟类适合生存;冰期到来温度下降,食物减少,鸟类向低海拔 山地迁徙,鸟类分布区扩大;后来进入间冰期,部分鸟类又飞回西南山地,说 明分布区不稳定,但也有鸟类已经适应了武夷山的气候而没有迁回,D正确。 第7题,从题干可知短翅蝗莺、煤山雀等不具备长距离飞行能力,如果中途 没有休息点而要到达台湾山脉是不可能的,所以曾经在武夷山和台湾山脉 之间应该是有陆地的,A正确;完全冰封不利于鸟类的长距离飞行,B错误;台 湾海峡位于亚欧板块和太平洋板块的交界处,由板块挤压而成,C、D错误。
1 2 3 4 5 6 7 8 9 10 11
解析 第(1)题,相比于热带雨林而言,温带雨林所在地区纬度偏高,热量不足, 植被的垂直结构更为简单,植物种类较少(丰富度较低/多样性较少),且在植 被类型上,多为耐寒性更强的针叶林。 第(2)题,从地理位置的角度来看,该区域位于美洲板块与太平洋板块的交 界地带,板块消亡边界附近地壳运动活跃。从外力的角度来讲,该区域受海 浪、风浪、波浪等侵蚀影响强。同时,纬度较高,受冰川侵蚀作用强,使得 海岸线蜿蜒曲折。 第(3)题,主要分析该区域适合罕见或濒危动物生存的自然环境。结合所学 知识可知,该区域受阿拉斯加暖流影响,冬季气候温和,为动物的生存发展 提供了良好的生存环境。同时,结合前面分析可知,该区域为温带雨林,
优化设计复习题

一、 填空题二、 用最速下降法求()()2211f x =100)1x x -+-(x 最优解时,设()[]00.5,0.5T x =-,第一步迭代的搜索方向为 T 100]- [103。
三、 机械优化设计采用数学的规划法,其核心一是最佳步长,二是搜索方向。
四、 当优化问题是凸规划的情况下,在任何局部最优解就是全域最优解。
五、 应用外推法来确定搜索区间时,最后得到的三点,即为搜索区间的始点,中间点和终点,他们的函数值形成趋势高--低--高。
六、 包含n 个设计变量的优化问题,称为 n 维优化问题。
七、 函数12TT x Hx B x c ++的梯度为_________。
八、 设G 为n n ⨯对称正定矩阵,若n 维空间中有两个非零向量0d ,1d ,满足()010d Gd=,则0d ,1d 之间存在共轭关系。
九、 与负梯度成锐角的方向为函数值下降 方向,与梯度成直角的方向为函数值的不变方向。
十、 设计变量、目标函数、约束条件是优化设计问题的数学模型的基本要素。
十一、 对于无约束二元函数()12,f x x ,若在()01234,x x x =点处取得极小值,其必要条件是在0x 点的梯度为0,充分条件是在0x 点的海赛矩阵正定。
十二、 K-T 条件可以叙述为在极值点处目标函数的负梯度为起作用的各约束函数梯度的非负线性组合。
十三、 用黄金分割法求一元函数()21036f x x x =-+的极值点,初始搜索区间[][],10,10a b =-,经第一次区间消去后得到新区间【-2.36,10】。
十四、 优化设计问题的数学模型的基本要素有设计变量,目标函数,约束条件。
十五、 牛顿法搜索方向k d =()()21()k k f x f x --∇∇,其计算是 大,且要求初始在级极小点附近位置。
十六、 将函数()2112121210460f x x x x x x x =+---+表示成12TT x Hx B x c ++的形式为 。
优化设计复习资料概论

优化设计复习资料一:填空题(40分)1,机械优化设计方法:解析法 数值计算法。
2,优化设计问题基本方法:数学解析法 图解法 数值迭代法。
3,数值迭代法的基本步骤:建立搜索方向→计算最优步骤→判断是否为最优解。
(方向)步长kk k n d a x x )(1+=+。
4,二元及多元函数的极值条件:0)(=∇x f ,负定(大)正定(小)/)(0=x G 。
5,迭代法基本思想:步步逼近 步步下降。
数值迭代法终止准则:点距足够小 函数下降量足够小准则 函数梯度充分小准则。
6,优化设计包括的内容:建立优化设计问题的数学模型 选择恰当的优化方法 编程求解最优的设计参数。
7,求解不等式约束问题的基本思想:将不等式问题转化成等式问题 具体做法:引入松弛变量。
8,无约束问题取得极值的条件:0)(=X f 0)(''>x f 即梯度为0,且海赛矩阵正定或负定。
9,二元偏导和方向导数的关系:10系统可靠性设计方向:预测法 分配法。
02190=+θθ 11,两幅图干涉越小,可靠性越高。
(图看书)12,设计螺栓的设计准则:受拉→静力或疲劳拉伸强度 受剪切或压溃→挤压强度 剪切强度。
13,随机方向法基本思路:随机选择初始点→随机选择探索方向→随机选择探索步长。
1212cos cos x x x f f f x x dθθ∂∂∂=+∂∂∂14,优化问题的几何解析:无约束问题 等式约束化问题 不等式约束化问题。
15.优化设计三要素:设计变量 约束条件 目标函数。
16,惩罚函数包括:内点 外点 混合惩罚函数。
17,约束定义及其分类:约束条件:在优化设计中,对设计变量取值时的限制条件,称为约束条件或设计约束,简称约束。
分为:等式约束 不等式约束 。
18,约束优化方法:直接解法 间接解法。
19,守剪螺栓强度:抗剪切强度 压溃强度。
20,的地方方向是函数值变化最快方向重合时值最大,方向和时,)()(1),cos(x f D x f d f ∇=∇儿)(x f ∇的模函数变化率的最大值。
2024高考总复习优化设计二轮用书地理(适用于新高考新教材)专项练题型一

4.(2023·福建高考预测卷)阅读图文材料,完成下列各题。 云南省贡山独龙江乡是我国唯一的独龙族聚居地,境内最高峰4 969米,最 低点1 170米,森林覆盖率高达93%,是“野生动植物天然博物馆”。长期以来, 独龙族人通过毁林烧荒轮种玉米、芋头、土豆维持一家人口粮,通过伐木、 采挖野生药材、捕猎换钱贴补家用。2011年独龙江乡开始推广“林+蜂”模 式,在不砍树的前提下种植多年生草本植物草果(药食两用中药材),同时在 草果地招引独龙蜂,收获蜂蜜。2018年年底独龙江乡独龙族实现整族脱贫。 下图为独龙江乡的位置及水系图。
1234
第(3)题,由材料可知,该引水式水电站引用河流上游的水至河段下游,集中 落差并经压力管道,引水至厂房进行发电。由于尼洋河流域洪水期输沙量 大,河床床沙多为砾石、卵石,即尼洋河输沙中大粒径比重大,在发电过程 中容易对发电设备(电站)造成危害,故为了减少悬沙进入电站,应将双坝设 计的另一道坝修建在引水式水电站的坝前位置。
1234
第(4)题,读图可知,与其他河流相比,寿溪流程短,流域面积小。由上文可知, 聚落布局与水源、水热条件、地形、土壤等因素有关,因此可以从这些角 度继续分析。如该地纬度较低,蒸发量大,降雨量小,水源较少,水热条件较 差;河流流程短,流量小,河流沉积作用较弱,土壤较为贫瘠,地形较为崎岖等。
1234
1234
2.(2023·广东佛山一模)阅读图文材料,完成下列各题。 2010年以来,我国钢铁工业取得了举世瞩目的成绩。2020年我国粗钢产量 超过10亿吨,连续4年占全球粗钢产量比例超过一半。我国铁矿石品质一 般,生产成本较高,钢铁生产高度依赖进口铁矿石。西非铁矿石资源丰富, 但地质勘查工作程度低,各国基础设施薄弱。中国是投资西非铁矿最多的 国家。下图示意西非铁矿资源(图中百分数为铁矿石品位)和中资企业铁 矿项目(序号1、2、3、4、5)分布。
2024年高考总复习优化设计一轮用书数学配人教A版(适用于新教材)课时规范练23

课时规范练23《素养分级练》P307基础巩固组1.函数y=2cos 2x+π6的部分图象大致是( )答案:A解析:由y=2cos 2x+π6可知,函数的最大值为2,排除D;因为函数图象过点π6,0,排除B;又因为函数图象过点-π12,2,排除C,故选A .2.将函数y=sin 2x 的图象向右平移φ个单位长度后,得到函数y=cos 2x+π6的图象,则φ的值可以是( )A.π12 B.π6C.π3D.2π3答案:D解析:y=cos 2x+π6=sin 2x+π6+π2=sin 2x+2π3,将函数y=sin 2x 的图象向右平移φ个单位长度后,得到函数y=sin[2(x-φ)]=sin(2x-2φ)的图象,由题意可得2π3=2k π-2φ(k ∈Z ),可得φ=k π-π3(k ∈Z ),当k=1时,φ=2π3,故选D .3.(2023·黑龙江大庆高三期末)某智能降噪耳机工作的原理是利用芯片生成与噪音的相位相反的声波,通过两者叠加抵消掉噪音,如图所示,若噪音的声波曲线的解析式为y=A sin(ωx+φ)(其中A>0,ω>0,0<φ<2π)的振幅为1,周期为2,初相为π2,则用来降噪的声波曲线的解析式是( )A.y=sin πxB.y=-cos πxC.y=-sin πxD.y=cos πx答案:B解析:由题意知,A=1,ω=π,φ=π2,噪音的声波曲线的解析式为y=sin πx+π2,而降噪声波曲线可以看成将噪音声波曲线向左平移半个周期得到的曲线,故降噪声波曲线的解析式为y=sin πx+π+π2=-cos πx ,故选B .4.(2022·四川内江高三模拟)已知函数f (x )=A cos(ωx+φ)A>0,ω>0,|φ|<π2,将函数f (x )的图象向左平移3π4个单位长度,得到函数g (x )的部分图象如图所示,则fπ3=( )A.12B.-12C.√32D.-√32答案:A解析:平移不改变振幅和周期,所以由图象可知A=1,2πω×34=π6--7π12=3π4,解得ω=2,函数f (x )的图象向左平移3π4个单位长度,得g (x )=cos 2x+3π4+φ.当x=π6时,2×π6+3π2+φ=3π2+2k π,k ∈Z ,且|φ|<π2,得φ=-π3,所以f (x )=cos 2x-π3,fπ3=cos π3=12.故选A .5.(2023·陕西咸阳高三二模)如图,A ,B 是函数f (x )=2sin(ωx+φ)ω>0,|φ|<π2的图象与x 轴的两个交点,若|OB|-|OA|=4π3,则ω=( )A.1B.12C.2D.23答案:B解析:由图象可知,点(0,1)在函数图象上,所以2sin φ=1,因为|φ|<π2,所以φ=π6,f (x )=2sin ωx+π6.令2sinωx+π6=0,解得ωx+π6=k π,k ∈Z ,x=kπ-π6ω,k ∈Z ,因为ω>0,所以当k=0时,解得x A =-π6ω,当k=1时,x B =5π6ω,所以|OB|-|OA|=5π6ω−π6ω=4π3,解得ω=12,故选B .6.(多选)(2023·海南海口高三月考)将函数f (x )=√3cos ωx+π3-1的图象向左平移π4个单位长度得到函数g (x )的图象与f (x )图象重合,则ω的值可以为( ) A.-4 B.8 C.12 D.16答案:BD解析:由题意得g (x )=√3cos ωx+π4+π3-1=√3cos ωx+ωπ4+π3-1,由于函数g (x )的图象与f (x )图象重合,故ωπ4=2k π(k ∈Z ),ω=8k (k ∈Z ).当k=1时,ω=8;当k=2时,ω=16.由于k 取整数,故ω=8k 不会取到-4或12.故选BD .7.(多选)(2023·福建宁德高三期中)函数f (x )=cos(ωx+φ)(ω>0,0≤φ<2π)的部分图象如图所示,则( )A.ω=3B.函数f (x )在3π5,14π5上单调递增C.φ=6π5D.函数f (x )图象的对称轴为直线x=kπ3−π15(k ∈Z ) 答案:AD解析:由图象知函数的周期T=2×13π30−π10=2π3=2πω,解得ω=3,所以A 正确;由题图得3×π10+φ=2k π+π2(k ∈Z ),因为0≤φ<2π,所以φ=π5,所以C 错误;f (x )=cos 3x+π5,当2k π≤3x+π5≤2k π+π(k ∈Z )时,函数f (x )单调递减,取k=1,得f (x )的一个单调递减区间为3π5,14π15,所以B 错误;函数f (x )图象的对称轴为直线3x+π5=k π(k ∈Z ),即x=kπ3−π15(k ∈Z ),所以D 正确.故选AD .8.设函数f (x )=sin(ωx+φ)ω>0,|φ|<π2在一个周期内的图象经过A -5π18,0,B -π9,-1,Cπ9,0,D2π9,1这四个点中的三个点,则φ= .答案:-π6 解析:因为-π9--5π18=122π9--π9=π6,所以f (x )在一个周期内的图象不可能经过点C ,则T=π6×4=2πω,解得ω=3.因为f 2π9=1,所以2π9×3+φ=π2+2k π(k ∈Z ),φ=-π6+2k π(k ∈Z ).又|φ|<π2,所以φ=-π6.9.(2023·山东济南高三月考)已知函数f (x )=cos 2x+sin 2x-π2,将函数f (x )的图象先向右平移π12个单位长度,再向下平移1个单位长度得到函数g (x )的图象,则函数g (x )图象的对称轴为直线 . 答案:x=kπ2+π12(k ∈Z ) 解析:f (x )=cos 2x+sin 2x-π2=2cos 2x=1+cos 2x ,由题意可得g (x )=cos 2x-π12=cos 2x-π6,令2x-π6=k π(k ∈Z ),解得x=kπ2+π12(k ∈Z ).综合提升组10.(2023·山东东营高三期中)将函数y=a sin x+b cos x 图象上所有点的纵坐标不变,横坐标变为原来的12,然后将所得图象向左平移π6个单位长度,可得函数y=2cos 2x+π6的图象,则a+b=( ) A.2 B.0 C.√3+1 D.1-√3答案:C解析:先将y=2cos 2x+π6的图象向右平移π6个单位长度,得y=2cos 2x-π6+π6=2cos 2x-π6,然后纵坐标不变,横坐标变为原来的2倍,得y=2cos x-π6=2√32cos x+12sin x =sin x+√3cos x ,故a=1,b=√3,所以a+b=1+√3,故选C .11.(多选)(2023·河北保定高三模拟)已知P (1,2√3)是函数f (x )=A sin(ωx+φ)A>0,ω>0,|φ|<π2图象的一个最高点,B ,C 是与P 相邻的两个最低点.若△PBC 为等边三角形,则下列说法正确的是( ) A.A=2B.f (x )的最小正周期为8C.φ=π4D.将f (x )图象上所有点向右平移1个单位长度后得到g (x )的图象,(2,0)是g (x )图象的一个对称中心 答案:BC解析:设BC 的中点为D ,与P 相邻且函数f (x )的图象与x 轴的交点为E ,F ,即E ,F 为函数f (x )图象的两个对称中心,连接PD ,则由题意知A=2√3,故选项A 错误;易知|PD|=4√3,∠BPD=π6,所以|BD|=4,|PB|=|BC|=8,则f (x )的最小正周期为8,故选项B 正确;因为ω=2π8=π4,则π4×1+φ=π2+2k π,k∈Z ,又|φ|<π2,所以φ=π4,故选项C 正确;因为f (x )=2√3sinπ4x+π4,则将f (x )图象上所有点向右平移1个单位长度后得到g (x )=2√3sin π4x 的图象,易知(2,0)不是g (x )图象的对称中心,故选项D 错误.故选BC .12.如图是一个半径为R 的水车,一个水斗从点A (1,-√3)出发,沿圆周按逆时针方向匀速旋转,且旋转一周用时6秒.经过t 秒后,水斗旋转到P 点,设点P 的坐标为(x ,y ),其纵坐标满足y=f (t )=R sin(ωt+φ)t ≥0,ω>0,|φ|<π2.若当t ∈[0,m )时,函数f (t )恰有2个极大值,则m 的取值范围是 .答案:172,292解析:根据点A 的坐标(1,-√3)可得圆周的半径R=√1+3=2.又旋转一周用时6秒,即周期T=6,从而得ω=2πT =π3,∴f (t )=2sin π3t+φ.又当t=0时,在函数图象上y=-√3,∴f (0)=2sinπ3×0+φ=-√3,即sin φ=-√32. 又|φ|<π2,∴φ=-π3, ∴f (t )=2sinπ3t-π3.根据三角函数的性质,f (t )在[0,m )内恰有两个极大值时,有5π2<π3m-π3≤9π2, 解得172<m ≤292.创新应用组13.(2023·浙江金华高三月考)已知函数f (x )=cos 2x 图象向右平移π12个单位长度后得到g (x )的图象.若对于任意的x 1∈-π3,π6,总存在x 2∈[m ,n ],使得f (x 1)=g (x 2),则|m-n|的最小值为 . 答案:π3解析:函数f (x )=cos 2x 图象向右平移π12个单位长度后得到g (x )=cos 2x-π6的图象.因为x 1∈-π3,π6,所以2x 1∈-2π3,π3,所以f (x 1)=cos 2x 1∈-12,1.因为对于任意的x 1∈-π3,π6,总存在x 2∈[m ,n ],使得f (x 1)=g (x 2),所以g (x 2)的取值范围应包含-12,1.根据余弦函数的性质,为使|m-n|取最小值,只需函数g (x )在x ∈[m ,n ]上单调且值域为-12,1即可.由2k π-2π3≤2x-π6≤2k π(k ∈Z )可得k π-π4≤x ≤k π+π12(k ∈Z ),因此|m-n|的最小值为-π4−π12=π3.。
优化设计复习二

15、梯度法属于无约束优化问题求解算法中的( )。 A直接法 B间接法 C人工智能优化法 16、一般情况下,用powell法求解无约束优化问题时,比坐标轮法求解速 度( )。 A慢 B一样 C快 17、( )属于一维优化方法。 A二次插值法 B罚函数法 C牛顿法 18、牛顿法是以( )为搜索方向的约束优化方法。 A共轭方向 B牛顿方向 C 梯度方向 19、复合形法的搜索方向一般是以( )为依据。 A最坏点 B 次坏点 C 最好点 20、Powell基本算法存在( )现象。 A 理论上不收敛 B 退化 C 共轭方向组不能保证线性独立 21、K-T”条件是( )取得极值的必要条件。 A约束优化问题 B 无约束优化问题 C 非线性规划问题
复习二
1、属于无约束优化问题求解算法中的直接法是:( )。 A 梯度法 B牛顿法 C POWELL法 D变尺度法 2. 复合形法中,映射点(迭代新点)XR需满足的条件为( ) 要求。 A适用性和可行性 B 可行性 C适用性 D映射性 3. 按类型划分,罚函数法属于( )。 A 一维优化方法 B无约束优化方法 C 直接法 D约束优化方法 4. 对于只含有不等式约束的优化问题,满足每一个设计约束的设 计点,称为( )。 A边界点 B非可行点 C 外点 D内点 5. 多元函数梯度的概念是:( ) A以其各二阶偏导数为分量的一个列向量 B以其各一阶偏导数为分量的 一个列向量 C以其各二阶偏导数为分量的一个行向量 D以其各一阶偏导数为分量的 一个行向量
8设计的发展经历了3个阶段,包 括: 、 、 。 9、提高价值可以从三个方面着手: 、 、 。 10、创造性思维的四对基本类型: 。 11、判定约束非线性规划优化问题中的某迭代点是否为约束极值 点的必要条件,一般采用 进行检验。 12、坐标轮换法若用于求解二维无约束问题,则遇到在极值点附 近等值线形状是 时,有效;是 时,显效 时,无效。 13、梯度法又称 ,其原因为梯度法以 为搜索方 向。 14、黄金分割法的区间缩短率每次都 ,大小为 。
高考总复习优化设计二轮用书化学H湖南专版(适用于新高考新教材)第2编 高考关键能力专项

(二)陌生、复杂文字信息的获取与加工
1.主要特征
此类题目的情境一般为学术探索情境和化学史料情境;外观特征主要有两
点:一是题目所给的情境和信息是全新的,是学生没有接触过的;二是一般
以新物质、新概念、新理论和新规律的形式呈现。
2.常见考向
常见有以下四个考向:一是以新物质为载体的考查;二是以新概念为载体的
同周期元素从左到右第一电离能呈增大趋势→第一电离能F>O>C→所以错误。
C项,基于物质性质的类别判断:
Q为Al元素→Q的氧化物为Al2O3→Al2O3为两性氧化物→所以正确。
D项,基于结构简式的配位键判断
总结提升
1.掌握表示物质组成的化学用语中关键信息获取与加工的一般方法
第一步,确定表示物质组成式子的类型。
主要考查定量分析和定量计算。
(二)表格类关键信息的获取与加工
1.主要形式
除图示外,表格在高考试题中也属于常见形式,主要有以下四种:一是元素
周期表;二是条件数据表格;三是物理常数表格;四是实验数据表格。
2.常见考向
常见有以下四个考向:一是“位—构—性”的综合推断题中的根据元素周期
表的分析判断;二是元素及其化合物综合题等大题中的根据条件数据表格
,m为正整数)
。
思路指导 新物质—基于物质组成的分析判断
(1)背景信息:题干中第一句话。
(2)关键信息:题给物质的类别“无环氮多烯”。信息的获取与加工过程如下:
关键信 宏观物质 氮烷、氮烯和无环氮多烯
息获取 组成结构 每有一个双键,烯比烷少2个H原子
信息
加工
(3)干扰信息:当看到“氮烷”时,易根据烷烃的通式简单地迁移,认为氮烷的
在N—Al、N—Ga两种化学键,判断只含有极性共价键;
优化设计复习资料有答案

优化设计复习资料有答案现代设计方法参考书目: 1、陈继平. 现代设计方法,华中科技大学出版社。
2、高健. 机械设计优化基础,科学出版社,2007,9 3、刘惟信. 机械最优化设计,第二版,清华大学出版社。
第一章习题例2 某工厂生产甲乙两种产品。
生产每种产品所需的材料、工时、电力和可获得的利润,以及能够提供的材料、工时和电力见表。
试确定两种产品每天的产量,以使每天可能获得的利润最大。
设每天生产甲产品x1件,乙x2件,利润为f(x1,x2) f(x1,x2)=60x1+120x2 每天实际消耗的材料、工时和电力分别用函数g1(x1,x2)、g2(x1,x2)、g3(x1,x2)表示:g1(x1,x2)=9x1+4x2g2(x1,x2)=3x1+10x2g3(x1,x2)=4x1+5x2 于是上述问题可归结为:求变量x1,x2 使函数f(x1,x2)= 60x1+120x2极大化满足条件g1(x1,x2)=9x1+4x2≤360 g2(x1,x2)=3x1+10x2≤300g3(x1,x2)=4x1+5x2≤200g4(x1,x2)=x1≥0g5(x1,x2)=x2≥0 例3 一种承受纯扭矩的空心传动轴,已知传递的扭矩为T,试确定此传动轴的内外径,以使其用料最省。
例:求下列非线性规划优化问题优化设计的迭代算法1、下降迭代算法的基本格式k?1kk迭代公式k 基本原理:从某一初始设计开始,沿某个搜索方向以适当步长得到新的可行的设计,如此反复迭代,直到满足设计要求,迭代终止。
?X??XSk?1kS(k)——第k 步的搜索方向,是一个向量;X? X*??X?X*αk——第k步的步长因子,是一个数,它决定在方向S(k)上所取的步长大小。
简单的说:是一个搜索、迭代、逼近的过程。
最关键的是搜索的方向和步长。
迭代算法的基本步骤:1,选定初始点X(0),令k=0; 2、在X(k)处选定下降方向S(k);, 3、从X(k)出发沿S(k)一维搜索,找到X(k+1)=X(k)+αkS(k), 使得f(X(k+1))例:f (X)=x12+4x22,已知初始点X(0)=[1,1]T,搜索方向S(o)=[-2,-4]T,求X(1)=? ?12??1?2??(1)(0)(0) X?X??S1???4??1?4??(1)229f(X)?(1?2?)?4(1?4?)α? 36 8? ? 17X(1)??1 17迭代终止条件:迭代法收敛性1)线性收敛性二次收敛性超线性收敛性终止迭代收敛准则。
三年级语文优化设计专项复习第58页答案

三年级语文优化设计专项复习第58页答案1、下列各句中加点词的解释,全部正确的一项是()[单选题] *A.足以极视听之娱极:十分引壶觞以自酌引:举起、端起B.所以兴怀,其致一也致:达到策扶老以流憩策:拄着C.况修短随化,终期于尽期:期望感吾生之行休休:停止D.齐彭殇为妄作殇:未成年而死去的人善万物之得时善:羡慕(正确答案)2、“每当夏月塘荷盛开时,我每天至少有几次徘徊在塘边”中“徘徊”的读音是“pái huái”。
[判断题] *对(正确答案)错3、下列选项中加着重号字注音有错误的一项是()[单选题] *A、一幢房屋dòng 眉黛hēi(正确答案)B、一声嗥叫háo 灵动língC、旮旮旯旯gā点缀zhuìD、一抹金黄mǒ盛开shèng4、下列词语中,加着重号字的注音不正确的一项是()[单选题] *A、精湛(zhàn)竣工(jùn)眷属(juàn)B、书籍(jí)违背(wéi)拜谒(yè)C、喘息(quǎn)祭祀(sì)糟粕(pà)(正确答案)D、抵御(yù)阴霾(mái)束缚(fù)5、下列选项中加着重号字注音正确的一项是()[单选题] *A、嗜好shì厌恶èB、崇高chóng 熔化róng(正确答案)C、补偿chǎng结缘yuánD、包揽lǎn 苦难nán6、下列各句中加点词的解释,全部正确的一项是()[单选题] *A.不爱珍器重宝肥饶之地爱:喜爱以致天下之士致:招致,招引B.惠文、武、昭襄蒙故业蒙:继承追亡逐北北:败逃的军队(正确答案)C.原庄宗之所以得天下原:推其根本数十伶人困之困:困乏D.纵一苇之所如如:自如举天下杰,莫能与之争举:全,整个7、5.下列各组词语的字形及加点字的注音全部正确的一项是()[单选题] * A.黝黑(yǒu)俯瞰(kàn)花团锦簇(cù)拈轻怕重(niān)(正确答案) B.称职(chèng)契约(qì)锲而不舍(qiè)吹毛求疵(zī)C.豢养(huàn)翘首(qiào)戛然而止(jiá)强词夺理(qiáng)D.睥睨(bì)盘桓(huán)如坐针毡(zān)惟妙惟肖(xiào)8、1《致橡树》的作者是舒婷,中国当代朦胧诗派的代表诗人之一。
2024高考总复习优化设计二轮用书地理(适用于新高考新教材)滚动突破练二

9.该公司布局在小县城主要考虑( C ) A.用水用地便宜 B.科技水平较高
C.劳动力成本低 D.自然环境优美
10.随着人工智能学习层次的提升,所需求的数据更加专业化,为此该公司
需要( A )
A.提高从业人员素质
B.加大科技研发投入
C.增加公司员工数量
D.投入更多高端设备
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
第13题,2012—2020年高速公路开通,东京湾区大面积县域人口由净流入变 为净流出,而影响人口流动的主要因素是经济因素,人口由流入到流出,说 明该区域提供的就业机会减少,工资待遇下降,为了寻求更好的就业机会和 工资待遇,人口流出,所以2012—2020年高速公路开通,东京湾区边缘地区 人均收入水平变化趋势是下降,B正确。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
1.墨西哥成为美国最大的移民来源国,主要是因为两国( D ) A.地域文化相似 B.人口数量差距大 C.产业雷同度高 D.经济发展差距大 2.1980—2020年墨西哥北部六州年GDP总量及占比均有较快增长,主要得 益于( A ) A.制造业发展速度快 B.中心城市辐射带动强 C.科技与创新能力强 D.现代服务业迅速发展
4.甲、乙、丙三种模式分别表示( D ) A.双城式、副中心式、飞地式 B.飞地式、双城式、副中心式 C.副中心式、双城式、飞地式 D.飞地式、副中心式、双城式 5.三种模式中,高铁新城对中心城区起促进作用( A ) A.最小的是甲模式 B.最小的是乙模式 C.最小的是丙模式 D.三种模式一样大 6.与甲模式相比,乙模式土地利用最突出的优势是( C ) A.类型多样 B.成本低 C.利用率高 D.面积大
2024年高考总复习优化设计一轮用书数学配人教A版(适用于新教材)课时规范练51

课时规范练51《素养分级练》P330基础巩固组1.(2022·江苏南京三模)为庆祝中国共青团成立100周年,某校计划举行庆祝活动,共有4个节目,要求A节目不排在第一个,则节目安排的方法数为()A.9B.18C.24D.27答案:B解析:由题意,先从后面3个节目中选择一个安排A节目,然后其他3个节目任意排在剩下的3个位置,共有C31A33=18种方法.2.(2023·陕西交大附中模拟)将4个9和2个6随机排成一行,则2个6不相邻共有()种不同的排法.A.240B.120C.20D.10答案:D解析:若2个6不相邻,只需将2个6插入4个9所形成5个空的2个空中,故不同的排法种数为C52=10.3.(2022·广东汕头三模)2022年北京冬季奥运会期间,从3名男志愿者和2名女志愿者中选4名去支援“冰壶”“花样滑冰”“短道速滑”三项比赛志愿者工作,其中冰壶项目需要一男一女两名,花样滑冰和短道速滑各需要一名,男女不限.则不同的支援方法的种数是()A.36B.24C.18D.42答案:A解析:第一步从3名男志愿者和2名女志愿者各选一名志愿者去支援冰壶项目,选法共有C31C21=6种;第二步从剩余的3人中选一人去支援花样滑冰,选法共有C31=3种;第三步从剩余的2人中选一人去支援短道速滑,选法共有C21=2种.依据分步乘法计数原理可知,不同的支援方法的种数是6×3×2=36.4.(2022·河北秦皇岛二模)“学习强国”学习平台是立足全体党员、面向全社会的优质平台,现日益成为人们了解国家动态,紧跟时代脉搏的热门APP.该款软件主要设有“阅读文章”“视听学习”两个学习版块和“每日答题”“每周答题”“专项答题”“挑战答题”四个答题版块.某人在学习过程中,将六大版块各完成一次,则“挑战答题”版块与其他三个答题版块在完成顺序上均不相邻的学习方法种数为()A.144B.72C.96D.36答案:A解析:当“挑战答题”版块在首或尾时,则与“挑战答题”版块相邻的只能是“阅读文章”或“视听学习”版块,其他任意排,共有A21A21A44=96种不同的排法;当“挑战答题”版块不在首尾时,则与“挑战答题”版块相邻的只能是“阅读文章”和“视听学习”版块,其他任意排,共有A22A44=48种不同的排法.所以“挑战答题”版块与其他三个答题版块在完成顺序上均不相邻的学习方法种数为96+48=144.5.(2022·山东淄博三模)若A m3=6C m4(m∈N*,m≥4),则m=.答案:7解析:因为A m 3=6C m 4(m ∈N *,m ≥4),所以m (m-1)(m-2)=6×m (m -1)(m -2)(m -3)4!,即6(m-3)=4!,解得m=7.6.(2022·湖南邵阳、郴州二模)一次考试后,学校准备表彰在该次考试中表现优异的10位同学,其中有2位是高三(1)班的同学,现要选4人去“表彰会”上作报告,若高三(1)班的2人同时参加,则2人作报告的顺序不能相邻,则要求高三(1)班至少有1人参加的作报告的方案共有 种(用数字作答).答案:3 024解析:若高三(1)班只有1人参加,则有C 21C 83A 44=2 688种不同的方案;若高三(1)班2人都参加,则有C 82A 22A 32=336种不同方案,故共有3 024种不同的方案.综合提升组7.(多选)(2023·海南华侨中学高三检测)身高各不相同的六位同学A ,B ,C ,D ,E ,F 站成一排照相,则说法正确的是( )A.A ,C ,D 三位同学从左到右按照由高到矮的顺序站,共有A 66A 33种站法B.A 与C 同学不相邻,共有A 44·A 52种站法C.A ,C ,D 三位同学必须站在一起,且A 只能在C 与D 的中间,共有A 33A 44种站法D.A 不在排头,B 不在排尾,共有A 66-2A 55+A 44种站法答案:ABD解析:A:6个人全排列有A 66种方法,A ,C ,D 全排列有A 33种方法,所以A ,C ,D 从左到右按高到矮的排列有A 66A 33种方法,故A 正确;B:先排列除A 与C 外的4个人,有A 44种方法,4个人排列共有5个空,利用插空法将A 和C 插入5个空,有A 52种方法,所以共有A 44·A 52种方法,故B 正确;C:A ,C ,D 必须排在一起且A 在C ,D 中间的排法有2种,将这3人捆绑在一起,与其余3人全排列,有A 44种方法,所以共有2A 44种方法,故C 错误;D:6个人全排列有A 66种方法,当A 在排头时,有A 55种方法,当B 在排尾时,有A 55种方法,当A 在排头且B 在排尾时,有A 44种方法,所以A 不在排头,B 不在排尾的情况共有A 66-2A 55+A 44种,故D 正确.故选ABD .8.(2023·江苏无锡模拟)甲、乙、丙、丁、戊共5名同学进行劳动技术比赛,决出第1名到第5名的名次,已知甲和乙都没有得到冠军,并且乙不是第5名,则这5个人的名次排列情况共有 种.答案:54解析:因为甲和乙都没有得到冠军,并且乙不是第5名,当甲是第5名时,则乙可以为第2,3,4名,有3种情况,剩下的3人全排列有A 33=6种,此时,由分步乘法计数原理得共有3×6=18种情况; 当甲不是第5名时,则甲乙排在第2,3,4名,有A 32=6种情况,剩下的3人全排列有A 33=6种,此时,由分步乘法计数原理得共有6×6=36种情况.所以这5个人的名次排列情况共有18+36=54种情况.9.有2男2女共4名学生被分派去A ,B ,C 三个公司实习,每个公司至少1人,且A 公司只收女生,则不同的分派方法数为 .答案:14解析:由题意,第一类,A 公司收1个女生,有C 21=2种分派方案,则B ,C 公司分派人数可以为1,2或者2,1共2种分派方案,共C 32+C 31=6种,所以一共有2×6=12种分派方案,第二类,A 公司收2个女生,只有1种分派方案,则B ,C 公司的分派人数只能是1,1,则有C 21=2种分派方案,根据分类加法计数原理共有12+2=14种.创新应用组10.(2023·湖北高三开学考试)如图,某城市的街区由12个全等的矩形组成(实线表示马路),CD 段马路由于正在维修,暂时不通,则从A 到B 的最短路径有( )A.23条B.24条C.25条D.26条 答案:D解析:先假设CD 是实线,则从A 到B ,向上3次,向右4次,最短路径有A 77A 33A 44=35条,其中经过CD 的路径,即先从A 到C ,然后C 到D ,最后D 到B 的最短路径有3×3=9条,所以,当CD 不通时,最短路径有35-9=26条.11.(2023·广东珠海模拟)3名女生和4名男生随机站成一排,则每名女生旁边都有男生的概率为 .答案:2235解析:依题意所有可能情况总数为A 77,若女生都不相邻,首先将4个男生全排列,再将3个女生插入所形成的5个空中的3个空,则有A 44A 53种排法;若有两个女生相邻,首先从3个女生中选出2个并排列作为一个整体A ,将4个男生全排列,再将整体A 插入中间3个空中的1个,再将另一个女生插入4个空中的1个空,则有C 32A 22A 44C 31C 41种排法,故每名女生旁边都有男生的概率P=A 44A 53+C 32A 22A 44C 31C 41A 77=2235.。
优化设计复习资料

优化设计复习资料一:填空题(40分)1,机械优化设计方法:解析法 数值计算法。
2,优化设计问题基本方法:数学解析法 图解法 数值迭代法。
3,数值迭代法的基本步骤:建立搜索方向→计算最优步骤→判断是否为最优解。
(方向)步长kk k n d a x x )(1+=+。
4,二元及多元函数的极值条件:0)(=∇x f ,负定(大)正定(小)/)(0=x G 。
5,迭代法基本思想:步步逼近 步步下降。
数值迭代法终止准则:点距足够小 函数下降量足够小准则 函数梯度充分小准则。
6,优化设计包括的内容:建立优化设计问题的数学模型 选择恰当的优化方法 编程求解最优的设计参数。
7,求解不等式约束问题的基本思想:将不等式问题转化成等式问题 具体做法:引入松弛变量。
8,无约束问题取得极值的条件:0)(=X f 0)(''>x f 即梯度为0,且海赛矩阵正定或负定。
9,二元偏导和方向导数的关系:10系统可靠性设计方向:预测法 分配法。
02190=+θθ 11,两幅图干涉越小,可靠性越高。
(图看书)12,设计螺栓的设计准则:受拉→静力或疲劳拉伸强度 受剪切或压溃→挤压强度 剪切强度。
13,随机方向法基本思路:随机选择初始点→随机选择探索方向→随机选择探索步长。
1212cos cos x x x f f f x x dθθ∂∂∂=+∂∂∂14,优化问题的几何解析:无约束问题 等式约束化问题 不等式约束化问题。
15.优化设计三要素:设计变量 约束条件 目标函数。
16,惩罚函数包括:内点 外点 混合惩罚函数。
17,约束定义及其分类:约束条件:在优化设计中,对设计变量取值时的限制条件,称为约束条件或设计约束,简称约束。
分为:等式约束 不等式约束 。
18,约束优化方法:直接解法 间接解法。
19,守剪螺栓强度:抗剪切强度 压溃强度。
20,的地方方向是函数值变化最快方向重合时值最大,方向和时,)()(1),cos(x f D x f d f ∇=∇儿)(x f ∇的模函数变化率的最大值。
五年级下优化设计期末综合复习(四)答案人教版答案

五年级下优化设计期末综合复习(四)答案人教版答案语文:一、看拼音,写词语。
túsū() hǎibīn() xuányá()háomài() bàozhú() pāndēnɡ()ánɡshǒutǐnɡxiōnɡ()zhǎndīnɡjiétiě()二、将下列词语补充完整。
( )神()注( )七()八气()山() ( )天()地痛不()生( )善()施三、用“”画出词语中的错别字,并改正。
居高临下() 热泪盈眶() 不翼而飞() 冲锋陷阵() 神态各异() 川流不息()四、按要求写词语。
1.写出表示高兴、快乐的词语:、、。
2.写出表示伤心、痛苦的词语:、、。
3.分别写出下列词的近义词与反义词。
富有~( )→()惊慌~( )→()五、按要求写句子。
1.天空中的小星星在闪耀。
(改为拟人句)2.五位壮士的英雄壮举怎能不让人钦佩呢?(改为陈述句)3.从天而降的石块把敌人砸得屁滚尿流。
(改为“被”字句)4.崎岖的山路上留下了许多具敌人的尸体。
(缩句)5.我用了整整一个月左右的时间学会了电脑。
(修改病句)六、说说下列句子使用的修辞手法。
1.五位壮士的口号声惊天动地,气吞山河。
( )2.许多小枞树披着浓霜,一动不动地站在那里。
( )3.石头像雹子一样,带着五位壮士的决心,带着中国人民的仇恨,向日寇头上砸去。
( )七、根据课本内容填空。
1.默写古诗《春日》及其作者。
2.五位壮士在狼牙山顶峰,着群众和部队主力远去的方向。
他们回头还在向上爬的日寇,脸上露出。
3.一两字, 楼外青山。
别君容易。
柳、花可可,云淡淡、月。
长安迷望眼。
八、阅读短文,回答问题。
(一)狼牙山五壮士(节选)五位壮士一面向顶峰攀登,一面依托大树和岩石向敌人射击。
山路上又留下了许多具日寇的尸体。
到了狼牙山峰顶,五位壮士居高临下,继续向紧跟在身后的敌人射击。
不少敌人坠落山涧,粉身碎骨。
2022年优化设计一轮复习电子版(1)

2022年优化设计一轮复习电子版(1)一、基础知识回顾1. 设计原理:包括设计的基本概念、设计流程、设计原则等。
2. 设计方法:介绍常用的设计方法,如迭代设计、模块化设计等。
3. 设计工具:介绍常用的设计工具,如CAD软件、仿真软件等。
二、案例分析1. 案例一:分析一个成功的设计案例,探讨其设计思路、设计方法和设计成果。
2. 案例二:分析一个失败的设计案例,探讨其设计过程中的问题,并提出改进建议。
三、实践操作1. 设计任务:根据给定的设计需求,进行一次实际的设计操作。
2. 设计评价:对设计成果进行评价,分析其优缺点,并提出改进建议。
四、复习要点1. 重点知识:列出复习的重点知识,帮助大家有针对性地进行复习。
2. 易错点:分析常见的易错点,提醒大家注意。
3. 试题解析:提供一些典型的试题,并进行详细的解析,帮助大家更好地理解和掌握知识。
2022年优化设计一轮复习电子版(1)五、设计创新思维1. 创新思维:介绍设计创新的基本概念,激发大家的创新思维。
2. 创新方法:介绍常用的设计创新方法,如头脑风暴、思维导图等。
3. 创新案例:分析一些成功的设计创新案例,探讨其创新思路和创新成果。
六、设计项目管理1. 项目管理:介绍设计项目的基本概念,包括项目目标、项目计划、项目执行等。
2. 项目管理工具:介绍常用的项目管理工具,如甘特图、项目管理软件等。
3. 项目案例分析:分析一些成功的设计项目案例,探讨其项目管理经验。
七、设计伦理与可持续发展1. 设计伦理:介绍设计伦理的基本概念,强调设计师的社会责任。
2. 可持续发展:介绍可持续发展的基本概念,探讨设计在可持续发展中的作用。
3. 案例分析:分析一些成功的设计案例,探讨其如何实现设计伦理和可持续发展。
八、设计趋势与未来展望1. 设计趋势:介绍当前设计领域的主要趋势,如智能化、绿色化等。
3. 案例分析:分析一些具有前瞻性的设计案例,探讨其如何引领设计趋势。
九、复习策略与时间管理1. 复习策略:提供一些有效的复习策略,帮助大家提高复习效率。
2022年优化设计一轮复习电子版(1)

2022年优化设计一轮复习电子版(1)随着科技的快速发展,电子版资料已经成为了我们学习和工作的重要工具。
而优化设计作为一门学科,也需要不断地进行复习和巩固。
因此,我们为您准备了这份2022年优化设计一轮复习电子版,帮助您更好地掌握相关知识。
在开始复习之前,我们需要明确复习的目的。
我们要通过复习巩固已学过的知识点,加深对优化设计原理和方法的理解。
我们要通过复习提高自己的实践能力,将理论知识应用到实际问题中。
我们要通过复习拓展自己的知识面,了解优化设计的最新发展动态。
1. 注重基础知识的复习。
优化设计是一门涉及多学科知识的综合性学科,基础知识的学习和掌握是至关重要的。
2. 理论联系实际。
通过解决实际问题,将理论知识应用到实践中,加深对理论知识的理解和掌握。
3. 多角度思考。
优化设计问题往往有多种解决方案,我们要学会从不同角度思考问题,找到最优解。
4. 持续学习。
优化设计是一个不断发展的领域,我们要保持学习的热情,不断更新自己的知识体系。
希望这份2022年优化设计一轮复习电子版能够帮助您更好地复习和巩固优化设计相关知识,提高自己的实践能力。
祝您学习顺利!2022年优化设计一轮复习电子版(1)随着科技的快速发展,电子版资料已经成为了我们学习和工作的重要工具。
而优化设计作为一门学科,也需要不断地进行复习和巩固。
更好地掌握相关知识。
在开始复习之前,我们需要明确复习的目的。
我们要通过复习巩固已学过的知识点,加深对优化设计原理和方法的理解。
我们要通过复习提高自己的实践能力,将理论知识应用到实际问题中。
我们要通过复习拓展自己的知识面,了解优化设计的最新发展动态。
1. 注重基础知识的复习。
优化设计是一门涉及多学科知识的综合性学科,基础知识的学习和掌握是至关重要的。
2. 理论联系实际。
通过解决实际问题,将理论知识应用到实践中,加深对理论知识的理解。
3. 多角度思考。
优化设计问题往往有多种解决方案,我们要学会从不同角度思考问题,找到最优解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k 1
Xk0
---多元函数求极值 的牛顿法迭代公式。
2 f X k —— 海赛矩阵
原始牛顿方向
16
2015年4月26日1时33分
对于二次函数 ,其展开到二次项的泰勒展开式就是其
本身,海赛矩阵G是一个常矩阵,其中各元素均为常数。因 此,无论从任何点出发,只需一步就可找到极小点。 如果某一迭代方法能使二次型函数在有限次迭代内达到
k k k 2 k 1
f X k 1 f X k k d k min f X k d k
20
2015年4月26日1时33分
可以看出原始牛顿法就相当于阻尼牛顿法的步长
因子取成固定值1的情况。阻尼牛顿法每次迭代都在牛 顿方向上进行一维搜索,避免了迭代后函数值上升的现 象,从而保持了牛顿法二次收敛的特性,而对初始点的 选取并没有苛刻的要求。
间 接 法
无 约 束 优 化 方 法
最速下降法 牛顿法 共轭方向法 共轭梯度法 变尺度法
利用目标函数的导数 信息
直 接 法
坐标轮换法 鲍威尔方法 单型替换法
利用目标函数 值信息
3
2015年4月26日1时33分
2、最速下降法的原理
(1)使 d f X ,按此规律不断走步,形成迭代算法:
可以看出二者的对角形矩阵不同,前者的等值线 为一族椭圆,后者的等值线为一族同心圆,这说明 对角形矩阵是表示度量的矩阵或者是表示尺度的矩 阵,最速下降法的收敛速度和变量的尺度有很大关 系。
13
2015年4月26日1时33分
梯度法的特点:
(1)理论明确,程序简单,对初始点要求不严格; (2)对一般函数而言,梯度法的收敛速度并不快,因为最速 下降法仅仅是指某点的一个局部性质; (3)梯度法相邻两次搜索方向的正交性决定了迭代全过程的 搜索路径呈锯齿形,在远离极小点时逼近速度较快,而在接近 极小点时逼近速度较慢; (4)梯度法的收敛速度与目标函数的性质密切相关。对于等 值线(面)为同心圆(球)的目标函数,一次搜索即可达到极 小点。
0 为一维搜索最佳步长,应满足极值必要条件
0 8(2 40 ) 5000(2 1000 ) 0
626 0 0.02003072 31252
8
2015年4月26日1时33分
则第一次迭代设计点位置和函数值
1.919877 2 4 0 X 2 2 100 0.3071785 10 0
21
2015年4月26日1时33分
(2)阻尼牛顿法的计算步骤
1)给定初始点 X 0 ,收敛精度 ,置 k 0
f X 2)计算 f X 、 f X 、
k 2 k 2 k 1
f X k d f X
k 2 k 1
0 1 50
代入牛顿法迭代公式可得:
0 过一次迭代即求得极小点和函数极小值。
2015年4月26日1时33分
从牛顿法迭代公式的推演中可以看到,迭代点的位置是
按照极值条件确定的,其中并未含有沿下降方向搜寻的概念。
2 0 f X 0 50
2 0
1 2 1 2 0 f X 0
1 1 2 2 1 0 2 0 0 X X f X f X 2 0
23
2015年4月26日1时33分
函数只有在函数极值点附近,才能很接近一个二次
X k 1 X k k f X k
(k 0,1, 2 )
(2)其步长因子 k 取一维搜索的最佳步长,即
k k k k min f x k 1 f x a f x min f x a f x k k
7
2015年4月26日1时33分
例:求目标函数 f X x12 25x22 的极小点 解法1:取初始点
f X 0 104
X 2, 2 ,则初始点处的函数值
0 T
及梯度分别为:
2 4 2 4 0 X 1 X 0 0f X 0 0 2 100 2 100 0
6
2015年4月26日1时33分
方法特点
1)初始点可任选,每次迭代计算量小,存储量少,程序
简短。即使从一个不好的初始点出发,开始的几步迭代,
目标函数值下降很快,然后慢慢逼近局部极小点; 2)任意相邻两点的搜索方向是正交的,它的迭代路径为 绕道逼近极小点。当迭代点接近极小点时,步长变得很小, 越走越慢。
因此对于非二次函数,如果采用上述牛顿迭代公式,有时会 使函数值上升。因此需要对牛顿法进行改进,引人数学规划
法的搜寻概念,产生了阻尼牛顿法。
19
2015年4月26日1时33分
阻尼牛顿法
在牛顿法中,迭代点的位置是按照极值条件确定,并未 含有沿下降方向搜寻的概念,因此采用牛顿迭代公式,对 于非二次函数,有时会使函数值上升。
x
k 1
x k s
k
k
(k 0,1,2, )
2
x k 1 x k ak f ( x k ) (k 0,1,2, )
2015年4月26日1时33分
用直接法寻找极小点时,不必求函数的导数,只要计 算目标函数值。这类方法较适用于解决变量个数较少的(n ≤20)问题,一般情况下比间接法效率低。间接法除要计算 目标函数值外,还要计算目标函数的梯度,有的还要计算 其海赛矩阵。
2015年4月26日1时33分
机械优化设计
金山职业技术学院 骆志高
1
2015年4月26日1时33分
最速下降法(梯度法)
1、基本思想
函数的负梯度方向是函数值在该点下降最快的方向。 将n维问题转化为一系列沿负梯度方向用一维搜索方法寻 优的问题,即利用负梯度作为搜索方向,故称为最速下降 法或梯度法。 搜索方向取该点的负梯度方向即 d f X ,使函 数值在该点附近的范围内下降最快。
2x 4 f X 0 1 50 x2 100
0 0 min (2 4 )2 25(2 100 )2 min f X 1 min f X f X
的下一个近似点,根据极值必要条件:
k 2 k X k 1 0 即 f X f X
对于多元函数 f X ,设 X k 为 f X 极小点 X 的第一 个近似点, f X 泰勒展开,保留到二次项,得:
X
k 1
X
k
2
X f X f X (k 0,1, 2 )
3)求 X k 1 X k d k k
1 ,停机; 4)检查收敛精度。若 X k 1 X k ,则 X X k
否则置 k k 1 返回到2),继续进行搜索。
22
2015年4月26日1时33分
基于以下两方面的原因, 给牛顿法的运用带来
一定局限性: 使用条件苛刻,对于二阶不可微的f(X)也不适用。 若迭代点的海赛矩阵为奇异,则无法求逆矩阵,不 能构造牛顿法方向; 为了保证牛顿方向是目标函数下降方向,海赛矩阵 的逆阵必须正定;
最速下降法的搜索路径
锯齿现象,如图所示
5
2015年4月26日1时33分
在接近极小点的位置,由于锯齿现象使每次迭代 行进的距离缩短,因而收敛速度减慢,这种情况似乎 与“最速下降”的名称相矛盾,这主要是因为梯度是 函数的局部性质(从局部上看,在一点附近函数的下 降是快的),但从整体上看则走了许多弯路,函数的 下降并不算快。
4
2015年4月26日1时33分
由上式可知,在最速下降 法中,相邻两个迭代点上的函 数梯度相互垂直。而搜索方向 就是负梯度方向,因此相邻两 个搜索方向互相垂直。
梯度法的搜索路线:
最速下降法中,迭代点向 函数极小点靠近的过程,走的
是曲折的路线。这一次的搜索
方向与前一次的搜索方向互相 垂直,形成“之”字形的直齿
1
f X 1 3.686164
经过10次迭代后,得到最优解:
X 0, 0
T
f X
是一段锯齿形路线,如下图。
0
9
该问题的目标函数的等值线为一族椭圆,迭代点走的
2015年4月26日1时33分
等直线为椭圆的迭代过程
10
2015年4月26日1时33分
解法2:引入变化
y1, y2 y12 y22
15
'
2015年4月26日1时33分
1、牛顿法
f x x 1 k k T k k T f x f x x x x x 2 f x k x x k 2 设 X k 1 为 X 的极小点,它作为 f X 极小点 X
极小点,称此迭代方法是二次收敛的。因此牛顿方法是二次
收敛的。
17
2015年4月26日1时33分
2 2 f x , x x 25 x 用牛顿法求 例: 1 2 1 2 的极小值
解:取初始点
0
X 0 2, 2 ,则
T
2 x1 4 f X 50 x2 X 0 100
0 2 4 0 Y , 0 0 10 200
1
0
26 0.5 52
Y1 0
经过坐标(尺度)变化后,只需要经过一次迭代,就可找到 最优解: T f X 0 X 0, 0
