MATLAB实训时域和频域
matlab信号频域分析实验报告

matlab信号频域分析实验报告Matlab信号频域分析实验报告引言:信号频域分析是一种重要的信号处理技术,通过将信号从时域转换到频域,可以更好地理解信号的频率特性和频谱分布。
本实验旨在利用Matlab软件进行信号频域分析,探索信号的频域特性,并通过实验结果验证频域分析的有效性。
一、实验目的本实验的主要目的是通过Matlab软件进行信号频域分析,了解信号的频域特性和频谱分布,验证频域分析的有效性。
二、实验原理信号频域分析是将信号从时域转换到频域的过程,常用的频域分析方法有傅里叶变换和功率谱估计等。
傅里叶变换可以将信号分解为不同频率的正弦和余弦分量,从而得到信号的频谱分布。
功率谱估计则可以估计信号在不同频率上的功率。
三、实验步骤1. 生成信号:首先,使用Matlab生成一个包含多个频率分量的复合信号。
可以选择正弦信号、方波信号或者其他复杂信号。
2. 时域分析:利用Matlab的时域分析函数,如plot()和stem(),绘制信号的时域波形图。
观察信号的振幅、周期和波形特征。
3. 频域分析:使用Matlab的傅里叶变换函数fft(),将信号从时域转换到频域。
然后,利用Matlab的频域分析函数,如plot()和stem(),绘制信号的频域谱图。
观察信号的频率分量和频谱分布。
4. 功率谱估计:使用Matlab的功率谱估计函数,如pwelch()或periodogram(),估计信号在不同频率上的功率。
绘制功率谱图,观察信号的功率分布。
四、实验结果与分析通过实验,我们生成了一个包含多个频率分量的复合信号,并进行了时域分析和频域分析。
实验结果显示,信号的时域波形图反映了信号的振幅、周期和波形特征,而频域谱图则展示了信号的频率分量和频谱分布。
在时域波形图中,我们可以观察到信号的振幅和周期。
不同频率分量的信号在时域波形图中呈现出不同的振幅和周期,从而反映了信号的频率特性。
在频域谱图中,我们可以观察到信号的频率分量和频谱分布。
实验二-典型环节的时域分析和频域分析

一、 实验名称:典型环节的时域分析和频域分析二、实验目的:(1) 理解、掌握matlab 模拟典型环节的根本方法,包括:比例环节、积分环节、一阶微分环节、惯性环节和振荡环节等。
(2) 熟悉各种典型环节的阶跃响应曲线和频域响应曲线 (3) 理解参数变化对动态特性的影响三、 实验要求:(1) 一人一机,独立完成实验内容 。
(2) 根据实验结果完成实验报告,并用A4纸打印后上交。
四、 时间:2022年11月21日 五、 地点:信自楼234实验报告:一、比例环节的时域分析和频域分析 比例环节的传递函数:()G s k(1) 当k=1:3:10时,绘制系统的阶跃响应曲线,分析k值的影响情况。
程序:for k=1:3:10;num=k;den=1;G=tf(num,den);figure(1);step(G); hold on; %翻开第1个图形窗口,绘制系统的阶跃响应曲线 endfigure(1); legend('k=1','k=4','k=7','k=10'); 曲线:结果分析:时域响应的结果就是把输入信号放大k 倍。
如图,输入信号为幅值为1的阶跃信号,因此,输出是幅值为k 的阶跃信号。
程序:for k=1:3:10;num=k;den=1;G=tf(num,den);figure(1);bode(G);hold on; %翻开第1个图形窗口,绘制系统的阶跃响应曲线 endfigure(1); legend('k=1','k=4','k=7','k=10');曲线:结果分析:比例环节对幅频有影响,输出信号的幅值为输入信号的20*lgk倍。
比例环节对相位没有影响,如图显示,相位特性为一条0度的程度线。
二、积分环节的时域分析和频域分析积分环节的传递函数:1 ()G ss=(1) 当k=1:3:10时,绘制系统()kG ss=的阶跃响应曲线,分析曲线特点。
实验三利用MATLAB进行系统频域分析

实验三利用MATLAB进行系统频域分析系统频域分析是指通过对系统的输入输出信号进行频域分析,从而分析系统的频率响应特性和频率域特征。
利用MATLAB进行系统频域分析可以方便地实现信号的频谱分析、滤波器设计等功能。
下面将介绍如何利用MATLAB进行系统频域分析的基本步骤。
一、信号频谱分析1. 将信号导入MATLAB环境:可以使用`load`函数导入数据文件,或者使用`audioread`函数读取音频文件。
2. 绘制信号的时域波形图:使用`plot`函数绘制信号的时域波形图,以便对信号的整体特征有一个直观的了解。
3. 计算信号的频谱:使用快速傅里叶变换(FFT)算法对信号进行频谱分析。
使用`fft`函数对信号进行频域变换,并使用`abs`函数计算频谱的幅度。
4. 绘制信号的频谱图:使用`plot`函数绘制信号的频谱图,以便对信号的频率特征有一个直观的了解。
二、滤波器设计1.确定滤波器类型和要求:根据系统的要求和信号的特性,确定滤波器的类型(如低通滤波器、高通滤波器、带通滤波器等)和相应的频率响应要求。
2. 设计滤波器:使用MATLAB中的滤波器设计函数(如`fir1`、`butter`、`cheby1`等)来设计滤波器。
这些函数可以根据指定的滤波器类型、阶数和频率响应要求等参数来生成相应的滤波器系数。
3. 应用滤波器:使用`filter`函数将滤波器系数应用到信号上,得到滤波后的信号。
三、系统频率响应分析1. 生成输入信号:根据系统的要求和实际情况,生成相应的输入信号。
可以使用MATLAB中的信号生成函数(如`square`、`sine`、`sawtooth`等)来生成基本的周期信号,或者使用`randn`函数生成高斯白噪声信号。
2.绘制输入信号的频谱图:使用前面提到的信号频谱分析方法,绘制输入信号的频谱图。
3. 输入信号与输出信号的频域分析:使用`fft`函数对输入信号和输出信号进行频谱分析,并使用`abs`函数计算频谱的幅度。
实验二 时域采样与频域采样及MATLAB程序

实验二 时域采样与频域采样一 实验目的1 掌握时域连续信号经理想采样前后的频谱变化,加深对时域采样定理的理解2 理解频率域采样定理,掌握频率域采样点数的选取原则二 实验原理1 时域采样定理对模拟信号()a x t 以T 进行时域等间隔采样,形成的采样信号的频谱ˆ()aX j Ω会以采样角频率2()s s TπΩΩ=为周期进行周期延拓,公式为: 1ˆˆ()[()]()a a a s n X j FT x t X j jn T +∞=-∞Ω==Ω-Ω∑ 利用计算机计算上式并不容易,下面导出另外一个公式。
理想采样信号ˆ()a xt 和模拟信号()a x t 之间的关系为: ˆ()()()a a n xt x t t nT δ+∞=-∞=-∑ 对上式进行傅里叶变换,得到:ˆ()[()()()()j t j t a a a n n X j x t t nT e dt x t t nT e dt δδ+∞+∞+∞+∞-Ω-Ω-∞-∞=-∞=-∞Ω=-=-∑∑⎰⎰在上式的积分号内只有当t nT =时,才有非零值,因此:ˆ()()jn T aa n X j x nT e +∞-Ω=-∞Ω=∑上式中,在数值上()()a x nT x n =,再将T ω=Ω代入,得到:ˆ()()()jn j aa T T n X j x n e X e ωωωω+∞-=Ω=Ω=-∞Ω==∑上式说明采样信号的傅里叶变换可用相应序列的傅里叶变换得到,只要将自变量ω用T Ω代替即可。
2 频域采样定理对信号()x n 的频谱函数()j X e ω在[0,2π]上等间隔采样N 点,得到2()()j k N X k X e ωπω== 0,1,2,,1k N =-则有: ()[()][()]()N N N i x n IDFT X k x n iN R n +∞=-∞==+∑即N 点[()]IDFT X k 得到的序列就是原序列()x n 以N 为周期进行周期延拓后的主值序列, 因此,频率域采样要使时域不发生混叠,则频域采样点数N 必须大于等于时域离散信号的长度M (即N M ≥)。
信号分析实验一内容

实验一连续时间信号的时域和频域分析一. 实验目的:1. 熟悉MATLAB 软件平台。
2. 掌握MATLAB 编程方法、常用语句和可视化绘图技术。
3. 编程实现常用信号及其运算MATLAB 实现方法。
4. 编程实现常用信号的频域分析。
二. 实验原理:1、连续时间信号的描述:(1)向量表示法连续信号是指自变量的取值范围是连续的,且对于一切自变量的取值,除了有若干个不连续点之外,信号都有确定的值与之对应。
严格来说,MATLAB 并不能处理连续信号,而是用等时间间隔点的样值来近似表示连续信号。
当取样时间间隔足够小时,这些离散的样值就能较好地近似连续信号。
矩阵是MATLAB 进行数据处理的基本单元,矩阵运算是MATLAB 最重要的运算。
通常意义上的数量(也称为标量)在MATLAB 系统中是作为1×1 的矩阵来处理的,而向量实际上是仅有一行或者一列的矩阵。
通常用向量表示信号的时间取值范围,如t = -5:5,但信号x(t)、向量t 本身的下标都是从1 开始的,因此必须用一个与向量x 等长的定位时间变量t,以及向量x,才能完整地表示序列x(t)。
在MATLAB 可视化绘图中,对于以t 为自变量的连续信号,在绘图时统一用plot 函数;而对n 为自变量的离散序列,在绘图时统一用stem 函数。
(2)符号运算表示法符号对象(Symbolic Objects 不同于普通的数值计算)是Matlab 中的一种特殊数据类型,它可以用来表示符号变量、表达式以及矩阵,利用符号对象能够在不考虑符号所对应的具体数值的情况下能够进行代数分析和符号计算(symbolic math operations),例如解代数方程、微分方程、进行矩阵运算等。
符号对象需要通过sym 或syms 函数来指定, 普通的数字转换成符号类型后也可以被作为符号对象来处理.我们可以用一个简单的例子来表明数值计算和符号计算的区别: 2/5+1/3 的结果为0.7333(double 类型数值运算), 而sym(2)/sym(5)+sym(1)/sym(3)的结果为11/15, 且这里11/15 仍然是属于sym 类型, 是符号数。
基于MATLAB自动控制系统时域频域分析与仿真

基于MATLAB自动控制系统时域频域分析与仿真MATLAB是一款强大的数学软件,也是自动控制系统设计的常用工具。
它不仅可以进行时域分析和频域分析,还可以进行相关仿真实验。
本文将详细介绍MATLAB如何进行自动控制系统的时域和频域分析,以及如何进行仿真实验。
一、时域分析时域分析是指对系统的输入信号和输出信号进行时域上的观察和分析,以了解系统的动态特性和稳定性。
MATLAB提供了一系列的时域分析工具,如时域响应分析、稳态分析和步骤响应分析等。
1.时域响应分析通过时域响应分析,可以观察系统对于不同的输入信号的响应情况。
在MATLAB中,可以使用`lsim`函数进行系统的时域仿真。
具体步骤如下:- 利用`tf`函数或`ss`函数创建系统模型。
-定义输入信号。
- 使用`lsim`函数进行时域仿真,并绘制系统输出信号。
例如,假设我们有一个二阶传递函数模型,并且输入信号为一个单位阶跃函数,可以通过以下代码进行时域仿真:```num = [1];den = [1, 1, 1];sys = tf(num, den);t=0:0.1:10;u = ones(size(t));[y, t, x] = lsim(sys, u, t);plot(t, y)```上述代码中,`num`和`den`分别表示系统的分子和分母多项式系数,`sys`表示系统模型,`t`表示时间序列,`u`表示输入信号,`y`表示输出信号。
通过绘制输出信号与时间的关系,可以观察到系统的响应情况。
2.稳态分析稳态分析用于研究系统在稳态下的性能指标,如稳态误差和稳态标准差。
在MATLAB中,可以使用`step`函数进行稳态分析。
具体步骤如下:- 利用`tf`函数或`ss`函数创建系统模型。
- 使用`step`函数进行稳态分析,并绘制系统的阶跃响应曲线。
例如,假设我们有一个一阶传递函数模型,可以通过以下代码进行稳态分析:```num = [1];den = [1, 1];sys = tf(num, den);step(sys)```通过绘制系统的阶跃响应曲线,我们可以观察到系统的稳态特性。
matlab频域分析实验报告

Matlab频域分析实验报告引言频域分析是一种常用的信号处理技术,可以帮助我们理解信号的频率特性和频率成分。
在本实验中,我们将使用Matlab进行频域分析,并通过实际的信号示例来说明其应用。
实验目标本实验的目标是通过Matlab进行频域分析,了解信号的频率特性,并能够对信号进行频域滤波、谱估计和频域增强。
实验步骤步骤一:加载信号数据首先,我们需要加载信号数据。
在Matlab中,我们可以使用load()函数来加载数据文件。
假设我们的信号数据文件名为signal.mat,则可以使用以下代码进行加载:load('signal.mat');步骤二:绘制时域波形图加载信号数据后,我们可以通过绘制时域波形图来观察信号的时域特性。
可以使用plot()函数来绘制信号的时域波形图。
以下是示例代码:plot(signal);xlabel('时间');ylabel('信号幅度');title('信号的时域波形图');步骤三:进行傅里叶变换为了将信号转换到频域,我们需要进行傅里叶变换。
在Matlab中,可以使用fft()函数对信号进行傅里叶变换。
以下是示例代码:signal_freq = fft(signal);步骤四:绘制频域幅度谱进行傅里叶变换后,我们可以绘制信号的频域幅度谱来观察信号的频率特性。
可以使用abs()函数来计算频域幅度,并使用plot()函数来绘制频域幅度谱图。
以下是示例代码:signal_freq_amp = abs(signal_freq);plot(signal_freq_amp);xlabel('频率');ylabel('幅度');title('信号的频域幅度谱');步骤五:频域滤波频域分析不仅可以帮助我们观察信号的频率特性,还可以进行频域滤波。
例如,我们可以通过在频域中将低幅度的频率成分设置为0来实现低通滤波。
《MATLAB》连续时间信号的频域分析和连续时间系统的时域分析实验报告
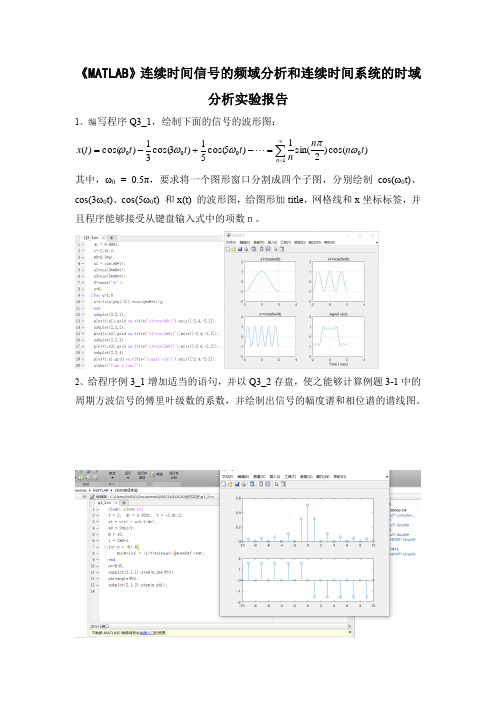
《MATLAB 》连续时间信号的频域分析和连续时间系统的时域分析实验报告1、编写程序Q3_1,绘制下面的信号的波形图:其中,ω0 = 0.5π,要求将一个图形窗口分割成四个子图,分别绘制cos(ω0t)、cos(3ω0t)、cos(5ω0t) 和x(t) 的波形图,给图形加title ,网格线和x 坐标标签,并且程序能够接受从键盘输入式中的项数n。
2、给程序例3_1增加适当的语句,并以Q3_2存盘,使之能够计算例题3-1中的周期方波信号的傅里叶级数的系数,并绘制出信号的幅度谱和相位谱的谱线图。
-+-=)5cos(51)3cos(31)cos()(000t t t t x ωωω∑∞==10)cos()2sin(1n t n n nωπ3.3反复执行程序例3_2,每次执行该程序时,输入不同的N值,并观察所合成的周期方波信号。
通过观察,你了解的吉布斯现象的特点是什么?3.4分别手工计算x1(t) 和x2(t) 的傅里叶级数的系数。
1.利用MATLAB 求齐次微分方程,,起始条件为,,时系统的零输入响应、零状态响应和全响应。
2. 已知某LTI 系统的方程为:其中,。
利用MATLAB 绘出范围内系统零状态响应的波形图。
3.已知系统的微分方程如下,利用MATLAB 求系统冲激响应和阶跃响应的数值解,并绘出其时域波形图。
(1)'''()2''()'()'()y t y t y t x t ++=()()t x t e u t -=(0)1y -='(0)1y -=''(0)2y -=''()5'()6()6()y t y t y t x t ++=()10sin(2)()x t t u t π=05t ≤≤''()3'()2()()y t y t y t x t ++=(2)''()2'()2()'()y t y t y t x t ++=。
MTALAB实验三 控制系统的时域、频域和根轨迹分析

实验三 控制系统的时域、频域和根轨迹分析一、 实验目的1、掌握如何使用Matlab 进行系统的时域分析2、掌握如何使用Matlab 进行系统的频域分析3、掌握如何使用Matlab 进行系统的根轨迹分析二、 实验内容:1、时域分析1.1、某系统的开环传递函数为43220()83640G s s s s s=+++试编程求系统在单位负反馈下的阶跃响应曲线,并求最大超调量。
>> G=tf([20],[1 8 36 40 0]); G=feedback(G,1); step(G)Step ResponseTime (sec)A m p l i t u d e024681012140.20.40.60.811.21.41.2、典型二阶系统222()2nn nG s s s ωξωω=++ 编程求:当6,n ωξ=分别取值为0.2、0.4、0.6、0.8、1.0、1.5、2.0时的单位阶跃响应曲线。
>>s=tf('s');wn=6;zet=[0.2,0.4,0.6,0.8,1.0,1.5,2.0]; for i=1:7G=wn^2/(s^2+2*wn*zet(:,i)*s+wn^2);step(G),hold on end00.51 1.52 2.53 3.54 4.550.20.40.60.811.21.41.6Step ResponseTime (sec)A m p l i t u d e1.3、典型二阶系统传递函数为:222()2nn nG s s s ωξωω=++ 绘制当:0.7,n ξω=分别取2、4、6、8、10、12时的单位阶跃响应曲线。
>> s=tf('s');zet=0.7;wn=[2:2:12];for i=1:6G=wn(:,i)^2/(s^2+2*wn(:,i)*zet*s+wn(:,i)^2);step(G),hold onend00.51 1.52 2.53 3.54 4.50.20.40.60.811.21.4Step ResponseTime (sec)A m p l i t u d e2、根轨迹分析根据下面负反馈系统的开环传递函数,绘制系统根轨迹,并分析使系统稳定的K 值范围。
matlab 时域 频域 指标

在 MATLAB 中,时域和频域是信号处理领域中常用的两个概念。
以下是与时域和频域相关的一些指标:
时域指标:
1.时域信号表示:在 MATLAB 中,时域信号可以使用向量表示,其中向量的
元素表示信号在不同时间点的取值。
例如:
2.信号幅值:信号在时域的幅值表示信号在不同时间点的振幅。
可以使用plot
函数来绘制信号波形:
3.信号能量和功率:信号在时域的能量可以通过对信号的幅值的平方进行积
分得到。
功率是能量除以时间。
频域指标:
1.傅里叶变换: MATLAB 提供了fft函数用于计算信号的离散傅里叶变换
(DFT)。
2.频谱表示:频谱表示信号在频域中的成分。
可以使用plot函数来绘制频谱
图:
3.主要频率:频谱中最高峰对应的频率通常表示信号的主要频率。
4.带宽:频谱中主要频率附近的宽度。
这些指标提供了一种全面了解信号在时域和频域中的特性的方法。
在MATLAB 中,通过使用信号处理工具箱和绘图函数,可以轻松地对时域和频域进行分析。
matlab频域分析实验报告

matlab频域分析实验报告Matlab频域分析实验报告引言频域分析是信号处理领域中的重要内容,它能够帮助我们理解信号在频域上的特性和行为。
而Matlab作为一款强大的数学计算软件,可以帮助我们进行频域分析,并且提供了丰富的工具和函数来实现这一目的。
本实验报告将介绍使用Matlab进行频域分析的方法和步骤,并通过实验数据展示其应用效果。
实验目的本实验旨在通过Matlab软件进行频域分析,掌握信号在频域上的特性和行为,了解频域分析在实际应用中的重要性和价值。
实验内容1. 信号生成:首先,我们使用Matlab生成一个具有特定频率和幅度的信号,以便进行后续的频域分析。
2. 时域分析:接下来,我们将对生成的信号进行时域分析,包括波形图和功率谱密度图的绘制,以便了解信号在时域上的特性。
3. 频域分析:然后,我们将使用Matlab提供的FFT函数对信号进行频域分析,得到信号在频域上的频谱图,并分析其频率成分和能量分布情况。
4. 频率响应:最后,我们将对信号进行频率响应分析,通过滤波器设计和频率域滤波来改变信号的频域特性,并观察其对信号的影响。
实验结果通过以上实验步骤,我们得到了生成信号的波形图和功率谱密度图,以及信号的频谱图和频率响应分析结果。
通过对这些结果的分析,我们可以清晰地了解信号在时域和频域上的特性和行为,以及频率响应对信号的影响。
结论本实验通过Matlab频域分析工具,帮助我们深入了解信号在频域上的特性和行为,为我们进一步应用频域分析提供了重要的参考和指导。
同时,Matlab的强大功能和丰富的工具库,为频域分析提供了便利和支持,使得我们能够更加高效地进行信号处理和分析工作。
因此,频域分析在实际应用中具有重要的意义和价值。
总结通过本实验,我们深入了解了Matlab频域分析的方法和步骤,以及其在实际应用中的重要性和价值。
频域分析对于理解信号的特性和行为具有重要意义,而Matlab作为一款强大的数学计算软件,为我们提供了丰富的工具和函数来实现频域分析,从而帮助我们更好地进行信号处理和分析工作。
用Matlab进行信号与系统的时频域分析

专 业
学 生 姓 导 单 位
日 期
一、实验目的
1、了解matlab中相关函数的调用,以及其参数设定方式。学会调试代码运行过程中出现的错误。
2、熟悉掌握时域、频域的相关知识,加深对书本知识的理解。
二、实验任务
1、完成实验内容的三个小题,分析解决调试代码过程中出现的问题。
图形:
代码:
(二)信号的频域分析
上机题3.求周期矩形脉冲信号的频谱图,已知
图形:
代码:
五、实验思考题
对于上机题3,改变信号的周期,比较他们的计算结果。
T=0.4s T=0.5s
T=0.8s T=1s
六、实验小结
本次试验虽然时间很短,只有两节课时间,但是我却从中学到了很多。下面我就这次试验总结自己的感悟。
最后,这次试验不仅让我熟悉了matlab中关于信号的函数,还让我重新复习了信号相关的知识,感觉收获颇丰,希望这样的信号实验能越来越多。
第一,实现做好准备。这次实验前,许多同学都不知道实验要做什么内容,在老师提醒下,才开始找资料。这些事应该在实验前就做好了,这导致了最后有同学没有做完。这让我明白了,好的开始是成功的一半,天上不会掉馅饼,准备很重要。第二,细节决定成败。在上面的代码中,有很多错误只是抄写不准确,导致之前所有的代码都要重新打一遍,非常浪费时间,这完全可以避免。同样的,在学习中,有解许多题目时,往往一个小错就可能导致整个题目都是是错的,非常可惜。第三,学会找错。其实本次matlab实验还比较简单,大部分错误都是字符打错了。但是,我在过程中就发现了一个问题,比如第一题在最后一行代码输入之后,前面的两个图形都不见了。我问到其他同学,有些人遇到同样的问题,有些人则没有。而解决办法则是重新输入,不知道这是不是因为软件自身的原因,我重新输入之后,程序又运行正常了。这让那个我明白了在学习是要善于发现问题,在解决问题过程中让自己对知识了解得更透彻。同时这也让我明白了同学合作的重要性。
matlab 信号分析实验报告

matlab 信号分析实验报告Matlab 信号分析实验报告引言:信号分析是一门重要的学科,它涉及到从原始信号中提取有用信息的技术和方法。
Matlab作为一种强大的数学计算工具,被广泛应用于信号分析领域。
本实验报告将介绍我在信号分析实验中使用Matlab所做的工作和实验结果。
一、实验目的本次实验的主要目的是通过Matlab对不同类型的信号进行分析,包括时域分析、频域分析和滤波处理。
通过这些实验,我们可以更好地理解信号分析的基本概念和方法,并掌握Matlab在信号分析中的应用技巧。
二、实验内容1. 时域分析时域分析是对信号在时间上的变化进行分析,主要包括信号的幅度、频率、相位等特征。
在实验中,我们使用Matlab绘制了一段正弦信号的波形图,并计算了其均值、方差和峰值等统计量。
通过这些分析,我们可以了解信号的基本特性。
2. 频域分析频域分析是对信号在频率上的变化进行分析,主要包括信号的频谱、频率分量等特征。
在实验中,我们使用Matlab对一段音频信号进行频谱分析,并绘制了其频谱图。
通过这些分析,我们可以了解信号的频率分布情况,进一步理解信号的特性。
3. 滤波处理滤波处理是对信号进行去噪或频率调整的处理方法。
在实验中,我们使用Matlab对一段包含噪声的信号进行滤波处理,并比较了滤波前后的信号波形和频谱。
通过这些分析,我们可以了解滤波处理对信号的影响,以及如何选择合适的滤波器进行处理。
三、实验结果1. 时域分析结果通过Matlab绘制正弦信号的波形图,我们可以观察到信号的周期性变化,并计算了其均值为0、方差为0.5和峰值为1的统计量。
这些结果表明该正弦信号的幅度和频率都比较稳定。
2. 频域分析结果通过Matlab绘制音频信号的频谱图,我们可以观察到信号在不同频率上的能量分布情况。
通过分析频谱图,我们可以判断音频信号中的主要频率分量,并进一步了解音频信号的特性。
3. 滤波处理结果通过Matlab对带噪声的信号进行滤波处理,我们可以观察到噪声被有效去除,并比较了滤波前后的信号波形和频谱。
用matlab进行信号与系统的时频域分析

课程实验报告题 目:用Matlab 进行 信号与系统的时、频域分析学 院 学 生 姓 名 班 级 学 号 指 导 教 师 开 课 学 院 日 期 用Matlab 进行信号与系统的时、频域分析 一、 实验目的进一步了解并掌握Matlab 软件的程序编写及运行;掌握一些信号与系统的时、频域分析实例;了解不同的实例分析方法,如:数值计算法、符号计算法;通过使用不同的分析方法编写相应的Matlab 程序;通过上机,加深对信号与系统中的基本概念、基本理论和基本分析方法的理解。
二、 实验任务了解数值计算法编写程序,解决实例;在Matlab 上输入三道例题的程序代码,观察波形图;通过上机实验,完成思考题;完成实验报告。
三、主要仪器设备硬件:微型计算机软件:Matlab四、 实验内容(1) 连续时间信号的卷积已知两个信号)2()1()(1---=t t t x εε和)1()()(2--=t t t x εε,试分别画出)(),(21t x t x 和卷积)()()(21t x t x t y *=的波形。
程序代码:T=0.01;t1=1;t2=2;t3=0;t4=1;t=0:T:t2+t4;x1=ones(size(t)).*((t>t1)-(t>t2));x2=ones(size(t)).*((t>t3)-(t>t4));y=conv(x1,x2)*T;subplot(3,1,1),plot(t,x1);ylabel('x1(t)');subplot(3,1,2),plot(t,x2);ylabel('x2(t)');subplot(3,1,3),plot(t,y(1:(t2+t4)/T+1));ylabel('y(t)=x1*x2');xlabel('----t/s');(2)已知两个信号)()(t e t x t ε-=和)()(2/t te t h t ε-=,试用数值计算法求卷积,并分别画出)(),(t h t x 和卷积)()()(t h t x t y *=的波形。
matlab 信号频谱分析实验报告

matlab 信号频谱分析实验报告Matlab 信号频谱分析实验报告引言:信号频谱分析是一项重要的技术,用于研究信号在频域上的特性。
在实际应用中,我们经常需要对信号进行频谱分析,以了解信号的频率成分和频谱特征。
本实验利用Matlab软件进行信号频谱分析,通过实验数据和结果展示,探索信号频谱分析的原理和应用。
实验一:时域信号与频域信号的关系在信号处理中,时域信号和频域信号是两个重要的概念。
时域信号是指信号在时间上的变化,频域信号则是指信号在频率上的变化。
通过傅里叶变换,我们可以将时域信号转换为频域信号,从而获得信号的频谱信息。
实验中,我们首先生成一个简单的正弦信号,并绘制其时域波形图。
然后,利用Matlab中的傅里叶变换函数对信号进行频谱分析,得到其频域波形图。
通过对比时域和频域波形图,我们可以观察到信号在不同频率上的能量分布情况。
实验二:频谱分析的应用频谱分析在许多领域中具有广泛的应用。
在通信领域中,频谱分析可以用于信号调制和解调、频率选择性传输等方面。
在音频处理中,频谱分析可以用于音乐合成、音频效果处理等方面。
在图像处理中,频谱分析可以用于图像压缩、图像增强等方面。
本实验中,我们以音频处理为例,展示频谱分析的应用。
首先,我们选取一段音频信号,并绘制其时域波形图。
然后,通过傅里叶变换,将信号转换为频域信号,并绘制其频域波形图。
通过观察频域波形图,我们可以了解音频信号在不同频率上的能量分布情况,从而进行音频效果处理或音频识别等应用。
实验三:信号滤波与频谱分析信号滤波是信号处理中常用的技术,用于去除信号中的噪声或干扰。
在频谱分析中,我们可以通过滤波器对信号进行滤波,从而改变信号的频谱特性。
本实验中,我们选取一段含有噪声的信号,并绘制其时域波形图。
然后,利用滤波器对信号进行滤波,并绘制滤波后的时域波形图和频域波形图。
通过对比滤波前后的波形图,我们可以观察到滤波器对信号频谱的影响,以及滤波效果的好坏。
结论:通过本实验,我们深入了解了Matlab在信号频谱分析中的应用。
matlab数值积分的实现:时域积分和频域积分

matlab数值积分的实现:时域积分和频域积分积分操作主要有两种方法:时域积分和频域积分,积分中常见的问题就是会产生二次趋势。
关于积分的方法,在国外一个论坛上有人提出了如下说法,供参考。
Double integration of raw acceleration data is a pretty poorestimate for displacement. The reason is that at each integration, youare compounding the noise in the data.If you are dead set on working in the time-domain, the best results come from the following steps.Remove the mean from your sample (now have zero-meansample)Integrate once to get velocity using some rule (trapezoidal, etc.)Remove the mean from the velocityIntegrate again to get displacement.Remove the mean. Note, if you plot this, you will see drift over time.To eliminate (some to most) of the drift (trend), use a least squares fit (high degree depending on data) to determine polynomial coefficients.Remove the least squares polynomial function from your data.A much better way to get displacement from acceleration data is to work in the frequency domain. To do this, follow these steps...Remove the mean from the accel. dataTake the Fouriertransform (FFT) of the accel. data.Convert the transformed accel. data to displacement data by dividing each element by -omega^2, where omega is the frequency band.Now take the inverse FFT to get back to the time-domain and scale your result.This will give you a much better estimate of displacement.说到底就是频域积分要比时域积分效果更好,实际测试也发现如此。
matlab 时域变频域

matlab 时域变频域
MATLAB中可以使用傅里叶变换将时域信号转换为频域信号。
所谓时域信号是指信号随时间变化的情况,而频域信号则是将信号分解为一系列的正弦和余弦波之和,每一个正弦和余弦波都有自己的频率,幅值和相位。
在MATLAB中进行时域变频域转换的过程,一般可以使用fft函数来实现。
该函数接受一个时域信号向量作为输入,并返回该信号对应的频域信号向量。
具体实现可以参考下面的示例代码:
time_domain_signal = sin(linspace(0, pi, 1000)); frequency_domain_signal = fft(time_domain_signal);
plot(abs(frequency_domain_signal));
在这个示例中,我们首先通过linspace函数创建了一个包含1000个等间隔采样点的向量,然后使用sin函数生成了对应的时域信号。
接着,我们调用了fft函数,将时域信号转换为频域信号,并使用plot函数画出了频域信号的模值。
需要注意的是,在将时域信号转换为频域信号时,我们需要确保该信号是周期性的,并且采样点数是2的幂次方。
如果信号周期不是整数倍,则需要使用周期延拓的方法将信号补完整,否则会出现频域泄漏的现象。
同时,如果采样点数不是2的幂次方,则需要使用fft 函数的补零功能,将采样点数补成2的幂次方。
用Matlab画出信号的时域波形及频谱,观察它们的关系

实验结果
f 3 (t) t[u (t 1) u (t 1)]
f '3 (t ) f 4 (t )
MATLAB编程 R=0.05; h=0.001; t=-1.2:R:1.2; y=t.t>=-1-t.t>=1; f4=diffy/h; subplot1,2,1,plott,f1 Xlabel't',ylabel'f4' axis-2,2,-0.5,1.5; N=1000; k=-N:N; W1=40; W=kW1/N; F=yexp-jt'WR; F=realF; subplot1,2,2,plotW,F Xlabel'W',ylabel'Fjw'
信号与系统课程实践考察
级:
班
学号: 姓名:
指导老师:
f1(t)sa(2t)
一 实验题目
f1(t)sa(2t) f2(t)u(t2)u(t2)
f3(t)t[u(t 1 ) u(t 1 )]
f4 (t )
df3 (t ) dt
试用MATLAB画出它们的时域波形及频谱,观察 它们的关系.
二 实验目的
1 正确运用傅立叶变换
2用Matlab编程观察周期信 号的合成过程.进一步理解 周期信号的傅里叶级数分 解特性.
3.学习用Matlab绘制周期 信号频谱的方法.
f1(t)sa(2t)
Eg(t)Esa(2z)
F(t`) 2f()
1. 根据对称性 MATLAB编程 R=0.05; t=-1.2:R:1.2; t1=2t; f1=sinct1; subplot1,2,1,plott,f1 Xlabel't',ylabel'f1' axis-2,2,-0.5,1.5; N=1000; k=-N:N; W1=40; W=kW1/N; F=f1exp-jt'WR; F=realF; subplot1,2,2,plotW,F Xlabel'W',ylabel'Fjw'
matlab 时域变频域

matlab 时域变频域
Matlab是一款用于科学计算和数据可视化的软件平台,它可以
方便地进行信号处理和频域分析。
在 Matlab 中,时域和频域都是重要的概念,其中时域表示信号随时间的变化,而频域表示信号在不同频率下的变化。
Matlab 提供了多种函数和工具箱,用于将时域信号转换为频域
信号。
其中最常用的是傅里叶变换(FFT)和快速傅里叶变换(FFT)。
这些函数可以将信号从时域转换为频域,以便更好地分析和处理信号。
在 Matlab 中,可以通过以下步骤将时域信号转换为频域信号:
1. 采集信号:先采集需要分析的信号数据。
2. 信号预处理:对采集的信号进行预处理,如去除噪声、滤波等。
3. 信号采样:对信号进行采样,以便进行频域分析。
4. 频域分析:使用 Matlab 中的 FFT 或其他函数将信号转换为频域信号,并进行分析。
5. 频域滤波:对频域信号进行滤波处理,以去除不需要的频率
分量。
6. 频域反变换:将处理后的频域信号反变换回时域信号,以便
进行进一步的处理和分析。
总之,Matlab 提供了强大的工具和函数,用于将时域信号转换
为频域信号,以更好地分析和处理信号。
通过熟练掌握这些工具和函数,可以更加高效地进行信号处理和分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实训报告
课程名称MATLAB实训报告名称时域和频域学院电子
班级
学号
学生姓名
实验目的:
1、熟悉并学会使用MATLAB的可视化界面环境;
2、熟悉并学会MATLAB的程序设计;
3、了解一阶系统和二阶系统相对于阶跃信号输入的时域和频域特性;实验过程:
在进入系统后,会出现如下图
一阶系统时域
T=2时的曲线
T=1.6时的曲线
T=1时的曲线
T=0.4时的曲线
汇总得下图
由图得,T越大,反应速度越快一阶系统的频域
取T=0.3时的曲线
T=1时的曲线
T=5时的曲线
汇总:T值取得越大,其零极点分布越靠右二阶系统的时域
ζ=0.2,Wn=1时曲线
ζ=0.707,Wn=1时曲线
ζ=1,Wn=10时曲线
ζ=2,Wn=10时曲线
二阶系统,ζ越大,系统反应越慢,在0,707附近最佳二阶系统的频域
Wn=10不变,改变ζ的值
ζ=1时曲线
ζ=0.707时曲线
ζ= 1.5时曲线
Wn=5时曲线
Wn=2时曲线
Wn=1时曲线
当ζ不变时,Wn越大,零极点分布图为一条竖直线
体会
通过学习MATLAB我又一次锻炼了自己的思维.它学起来得心应手也让我明白了学习一门语言(c语言)对学习其他语言的帮助指导作用.同时,它也加强了我
理论联系实际的能力.这是一个专业课的基础工具,学好它是必要的.。
