A Fourier-Mukai Transform for Stable Bundles on K3 Surfaces
Fourier Transform and applications - University of Central Florida傅立叶变换及应用-中佛罗里达大学

Applications: Frequency Domain In Images
Spatial frequency of an image refers to the rate at which the pixel intensities change
In picture on right:
Introduction to the Frequency Domain zone.ni/devzone/conceptd.nsf/webmain/F814BEB1A040CDC68625684600508C88
Fourier Transform Filtering Techniques olympusmicro/primer/java/digitalimaging/processing/fouriertransform/index.html
Time Domain and Frequency Domain
In 1807, Jean Baptiste Joseph Fourier showed that any periodic signal could be represented by a series of sinusoidal functions
Fast Fourier Transform
Applications
Summary References
Transforms
Transform:
In mathematics, a function that results when a given function is multiplied by a so-called kernel function, and the product is integrated between suitable limits. (Britannica)
Fourier Transform Basics

f t
F n e f t e
j 2 pnt
dn dt
F n
j 2 pnt
Waves: 5
PROPERTIES OF FOURIER TRANSFORMS
Fourier transforms are sometimes of use in physics due to their direct physical interpretation (see later), but often their usefulness is more indirect
In particular, a great usefulness comes from their help in solving awkward differential equations
Here we list several general transform properties of benefit in this and other contexts (Note that these properties are listed here without proofs. Most proofs follow from the defining equations)
The othorgonality relations:
0 2p
0
cos m cos n d 0 p
mn mn mn mn
0 2p
0
sin m sin n d 0 p
0 2p
0
sin m cos n d 0 (all m,n)
Waves: 5
Waves: 5
lec09

Lecture 9: Fourier Transform Basics
Chapter objectives
1. Understand how Fourier transform theory is applied to image processing. 2. Be able to ‘attaching meaning’ to Fourier spectrum. 3. Familiar with the procedures of performing frequency domain filtering using various filters.
f(x) F(u) e
j2 ux
du
2017/12/26
Chapter 4 Frequency Domain Enhancement
11
Lecture 9: Fourier Transform Basics
Discrete Fourier Transform The discrete Fourier transform (DFT) of f(x), x=0,1,2,…,M-1, is: 1 M1 F (u ) f(x ) e j2 ux M For u=0,1,2,…,M-1. M x 0 The inverse discrete Fourier transform (IDFT) is obtained by:
Discrete Fourier Transform

Discrete Fourier transformIn mathematics, the discrete Fourier transform (DFT) is a specific kind of Fourier transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function (which is often a function in the time domain). But the DFT requires an input function that is discrete and whose non-zero values have a limited (finite) duration. Such inputs are often created by sampling a continuous function, like a person's voice. Unlike the discrete-time Fourier transform (DTFT), it only evaluates enough frequency components to reconstruct the finite segment that was analyzed. Using the DFT implies that the finite segment that is analyzed is one period of an infinitely extended periodic signal; if this is not actually true, a window function has to be used to reduce the artifacts in the spectrum. For the same reason, the inverse DFT cannot reproduce the entire time domain, unless the input happens to be periodic (forever). Therefore it is often said that the DFT is a transform for Fourier analysis of finite-domain discrete-time functions. The sinusoidal basis functions of the decomposition have the same properties.The input to the DFT is a finite sequence of real or complex numbers (with more abstract generalizations discussed below), making the DFT ideal for processing information stored in computers. In particular, the DFT is widely employed in signal processing and related fields to analyze the frequencies contained in a sampled signal, to solve partial differential equations, and to perform other operations such as convolutions or multiplying large integers. A key enabling factor for these applications is the fact that the DFT can be computed efficiently in practice using a fast Fourier transform (FFT) algorithm.FFT algorithms are so commonly employed to compute DFTs that the term "FFT" is often used to mean "DFT" in colloquial settings. Formally, there is a clear distinction: "DFT" refers to a mathematical transformation or function, regardless of how it is computed, whereas "FFT" refers to a specific family of algorithms for computing DFTs. The terminology is further blurred by the (now rare) synonym finite Fourier transform for the DFT, which apparently predates the term "fast Fourier transform" (Cooley et al., 1969) but has the same initialism.DefinitionThe sequence of N complex numbers x0, ..., xN−1is transformed into the sequence of N complex numbers X, ...,XN−1by the DFT according to the formula:where i is the imaginary unit and is a primitive N'th root of unity. (This expression can also be written in termsof a DFT matrix; when scaled appropriately it becomes a unitary matrix and the Xkcan thus be viewed as coefficients of x in an orthonormal basis.)The transform is sometimes denoted by the symbol , as in or or .The inverse discrete Fourier transform (IDFT) is given byA simple description of these equations is that the complex numbers represent the amplitude and phase of thedifferent sinusoidal components of the input "signal" . The DFT computes the from the , while theIDFT shows how to compute the as a sum of sinusoidal components with frequency cycles per sample. By writing the equations in this form, we are making extensive use of Euler's formula to express sinusoids in terms of complex exponentials, which are much easier to manipulate. In the same way, by writingin polar form, we obtain the sinusoid amplitude and phase from the complex modulus and argument of, respectively:where atan2 is the two-argument form of the arctan function. Note that the normalization factor multiplying the DFT and IDFT (here 1 and 1/N) and the signs of the exponents are merely conventions, and differ in some treatments. The only requirements of these conventions are that the DFT and IDFT have opposite-sign exponents and that theproduct of their normalization factors be 1/N. A normalization of for both the DFT and IDFT makes the transforms unitary, which has some theoretical advantages, but it is often more practical in numerical computation to perform the scaling all at once as above (and a unit scaling can be convenient in other ways).(The convention of a negative sign in the exponent is often convenient because it means that is the amplitude of a "positive frequency" . Equivalently, the DFT is often thought of as a matched filter: when looking for a frequency of +1, one correlates the incoming signal with a frequency of −1.)In the following discussion the terms "sequence" and "vector" will be considered interchangeable.PropertiesCompletenessThe discrete Fourier transform is an invertible, linear transformationwith C denoting the set of complex numbers. In other words, for any N > 0, an N-dimensional complex vector has a DFT and an IDFT which are in turn N-dimensional complex vectors.OrthogonalityThe vectors form an orthogonal basis over the set of N-dimensional complex vectors:where is the Kronecker delta. This orthogonality condition can be used to derive the formula for the IDFT from the definition of the DFT, and is equivalent to the unitarity property below.The Plancherel theorem and Parseval's theoremIf Xk and Ykare the DFTs of xnand ynrespectively then the Plancherel theorem states:where the star denotes complex conjugation. Parseval's theorem is a special case of the Plancherel theorem and states:These theorems are also equivalent to the unitary condition below.PeriodicityIf the expression that defines the DFT is evaluated for all integers k instead of just for , then the resulting infinite sequence is a periodic extension of the DFT, periodic with period N.The periodicity can be shown directly from the definition:Similarly, it can be shown that the IDFT formula leads to a periodic extension.The shift theoremMultiplying by a linear phase for some integer m corresponds to a circular shift of the output : is replaced by , where the subscript is interpreted modulo N (i.e., periodically). Similarly, a circularshift of the input corresponds to multiplying the output by a linear phase. Mathematically, if represents the vector x thenifthenandCircular convolution theorem and cross-correlation theoremThe convolution theorem for the continuous and discrete time Fourier transforms indicates that a convolution of two infinite sequences can be obtained as the inverse transform of the product of the individual transforms. With sequences and transforms of length N, a circularity arises:The quantity in parentheses is 0 for all values of m except those of the form , where p is any integer. At those values, it is 1. It can therefore be replaced by an infinite sum of Kronecker delta functions, and we continue accordingly. Note that we can also extend the limits of m to infinity, with the understanding that the x and y sequences are defined as 0 outside [0,N-1]:which is the convolution of the sequence with a periodically extended sequence defined by :Similarly, it can be shown that :which is the cross-correlation of andA direct evaluation of the convolution or correlation summation (above) requiresoperations for an outputsequence of length N. An indirect method, using transforms, can take advantage of the efficiency of the fast Fourier transform (FFT) to achieve much better performance. Furthermore, convolutions can be used to efficiently compute DFTs via Rader's FFT algorithm and Bluestein's FFT algorithm.Methods have also been developed to use circular convolution as part of an efficient process that achieves normal (non-circular) convolution with an or sequence potentially much longer than the practical transform size (N ).Two such methods are called overlap-save and overlap-add [1] .Convolution theorem dualityIt can also be shown that :which is the circular convolution of and .Trigonometric interpolation polynomial The trigonometric interpolation polynomialN even ,for N odd,where the coefficients X k are given by the DFT of x n above, satisfies the interpolation propertyfor .For even N , notice that the Nyquist componentis handled specially.This interpolation is not unique: aliasing implies that one could add N to any of the complex-sinusoid frequencies(e.g. changing to ) without changing the interpolation property, but giving different values in between the points. The choice above, however, is typical because it has two useful properties. First, it consistsof sinusoids whose frequencies have the smallest possible magnitudes, and therefore minimizes the mean-squareslope of the interpolating function. Second, if the are real numbers, then is real as well.In contrast, the most obvious trigonometric interpolation polynomial is the one in which the frequencies range from0 to (instead of roughly to as above), similar to the inverse DFT formula. This interpolation does not minimize the slope, and is not generally real-valued for real ; its use is a common mistake.The unitary DFTAnother way of looking at the DFT is to note that in the above discussion, the DFT can be expressed as a Vandermonde matrix:whereis a primitive Nth root of unity. The inverse transform is then given by the inverse of the above matrix:With unitary normalization constants , the DFT becomes a unitary transformation, defined by a unitary matrix:where det() is the determinant function. The determinant is the product of the eigenvalues, which are always oras described below. In a real vector space, a unitary transformation can be thought of as simply a rigid rotation of the coordinate system, and all of the properties of a rigid rotation can be found in the unitary DFT.The orthogonality of the DFT is now expressed as an orthonormality condition (which arises in many areas of mathematics as described in root of unity):If is defined as the unitary DFT of the vector thenand the Plancherel theorem is expressed as:If we view the DFT as just a coordinate transformation which simply specifies the components of a vector in a new coordinate system, then the above is just the statement that the dot product of two vectors is preserved under a unitary DFT transformation. For the special case , this implies that the length of a vector is preserved aswell—this is just Parseval's theorem:Expressing the inverse DFT in terms of the DFTA useful property of the DFT is that the inverse DFT can be easily expressed in terms of the (forward) DFT, via several well-known "tricks". (For example, in computations, it is often convenient to only implement a fast Fourier transform corresponding to one transform direction and then to get the other transform direction from the first.) First, we can compute the inverse DFT by reversing the inputs:(As usual, the subscripts are interpreted modulo N; thus, for , we have .)Second, one can also conjugate the inputs and outputs:Third, a variant of this conjugation trick, which is sometimes preferable because it requires no modification of the data values, involves swapping real and imaginary parts (which can be done on a computer simply by modifying pointers). Define swap( ) as with its real and imaginary parts swapped—that is, if thenswap( ) is . Equivalently, swap( ) equals . ThenThat is, the inverse transform is the same as the forward transform with the real and imaginary parts swapped for both input and output, up to a normalization (Duhamel et al., 1988).The conjugation trick can also be used to define a new transform, closely related to the DFT, that is involutary—that is, which is its own inverse. In particular, is clearly its own inverse: . A closely related involutary transformation (by a factor of (1+i) /√2) is , since thefactors in cancel the 2. For real inputs , the real part of is none other than the discrete Hartley transform, which is also involutary.Eigenvalues and eigenvectorsThe eigenvalues of the DFT matrix are simple and well-known, whereas the eigenvectors are complicated, not unique, and are the subject of ongoing research.Consider the unitary form defined above for the DFT of length N, whereThis matrix satisfies the matrix polynomial equation:This can be seen from the inverse properties above: operating twice gives the original data in reverse order, so operating four times gives back the original data and is thus the identity matrix. This means that the eigenvalues satisfy the equation:Therefore, the eigenvalues of are the fourth roots of unity: is +1, −1, +i, or −i.Since there are only four distinct eigenvalues for this matrix, they have some multiplicity. The multiplicitygives the number of linearly independent eigenvectors corresponding to each eigenvalue. (Note that there are N independent eigenvectors; a unitary matrix is never defective.)The problem of their multiplicity was solved by McClellan and Parks (1972), although it was later shown to have been equivalent to a problem solved by Gauss (Dickinson and Steiglitz, 1982). The multiplicity depends on the value of N modulo 4, and is given by the following table:Multiplicities of the eigenvalues λ of the unitary DFT matrix U as a function of thetransform size N (in terms of an integer m).size N λ = +1 λ = −1λ = -iλ = +i4m m + 1m m m− 14m + 1m + 1m m m4m + 2m + 1m + 1m m4m + 3m + 1m + 1m + 1mOtherwise stated, the characteristic polynomial of is:No simple analytical formula for general eigenvectors is known. Moreover, the eigenvectors are not unique because any linear combination of eigenvectors for the same eigenvalue is also an eigenvector for that eigenvalue. Various researchers have proposed different choices of eigenvectors, selected to satisfy useful properties like orthogonality and to have "simple" forms (e.g., McClellan and Parks, 1972; Dickinson and Steiglitz, 1982; Grünbaum, 1982; Atakishiyev and Wolf, 1997; Candan et al., 2000; Hanna et al., 2004; Gurevich and Hadani, 2008).A straightforward approach is to discretize the eigenfunction of the continuous Fourier transform, namely the Gaussian function. Since periodic summation of the function means discretizing its frequency spectrum and discretization means periodic summation of the spectrum, the discretized and periodically summed Gaussian function yields an eigenvector of the discrete transform:•.A closed form expression for the series is not known, but it converges rapidly.Two other simple closed-form analytical eigenvectors for special DFT period N were found (Kong, 2008):For DFT period N = 2L + 1 = 4K +1, where K is an integer, the following is an eigenvector of DFT:•For DFT period N = 2L = 4K, where K is an integer, the following is an eigenvector of DFT:•The choice of eigenvectors of the DFT matrix has become important in recent years in order to define a discrete analogue of the fractional Fourier transform—the DFT matrix can be taken to fractional powers by exponentiating the eigenvalues (e.g., Rubio and Santhanam, 2005). For the continuous Fourier transform, the natural orthogonal eigenfunctions are the Hermite functions, so various discrete analogues of these have been employed as the eigenvectors of the DFT, such as the Kravchuk polynomials (Atakishiyev and Wolf, 1997). The "best" choice of eigenvectors to define a fractional discrete Fourier transform remains an open question, however.The real-input DFTIf are real numbers, as they often are in practical applications, then the DFT obeys the symmetry:The star denotes complex conjugation. The subscripts are interpreted modulo N.Therefore, the DFT output for real inputs is half redundant, and one obtains the complete information by onlylooking at roughly half of the outputs . In this case, the "DC" element is purely real, and for even N the "Nyquist" element is also real, so there are exactly N non-redundant real numbers in the first half + Nyquist element of the complex output X.Using Euler's formula, the interpolating trigonometric polynomial can then be interpreted as a sum of sine and cosine functions.Generalized/shifted DFTIt is possible to shift the transform sampling in time and/or frequency domain by some real shifts a and b, respectively. This is sometimes known as a generalized DFT (or GDFT), also called the shifted DFT or offset DFT, and has analogous properties to the ordinary DFT:Most often, shifts of (half a sample) are used. While the ordinary DFT corresponds to a periodic signal in both time and frequency domains, produces a signal that is anti-periodic in frequency domain ( ) and vice-versa for . Thus, the specific case of is known as an odd-time odd-frequency discrete Fourier transform (or O2 DFT). Such shifted transforms are most often used for symmetric data, to represent different boundary symmetries, and for real-symmetric data they correspond to different forms of the discrete cosine and sine transforms.Another interesting choice is , which is called the centered DFT (or CDFT). The centered DFT has the useful property that, when N is a multiple of four, all four of its eigenvalues (see above) have equal multiplicities (Rubio and Santhanam, 2005)[2]The discrete Fourier transform can be viewed as a special case of the z-transform, evaluated on the unit circle in the complex plane; more general z-transforms correspond to complex shifts a and b above.Multidimensional DFTThe ordinary DFT transforms a one-dimensional sequence or array that is a function of exactly one discrete variable n. The multidimensional DFT of a multidimensional array that is a function of d discretevariables for in is defined by:where as above and the d output indices run from . This is more compactly expressed in vector notation, where we define andas d-dimensional vectors of indices from 0 to , which we define as:where the division is defined as to be performed element-wise, and thesum denotes the set of nested summations above.The inverse of the multi-dimensional DFT is, analogous to the one-dimensional case, given by:As the one-dimensional DFT expresses the input as a superposition of sinusoids, the multidimensional DFTexpresses the input as a superposition of plane waves, or sinusoids. The direction of oscillation in space is . The amplitudes are . This decomposition is of great importance for everything from digital image processing (two-dimensional) to solving partial differential equations. The solution is broken up into plane waves.The multidimensional DFT can be computed by the composition of a sequence of one-dimensional DFTs along each dimension. In the two-dimensional case the independent DFTs of the rows (i.e., along ) arecomputed first to form a new array . Then the independent DFTs of y along the columns (along ) are computed to form the final result . Alternatively the columns can be computed first and then the rows. Theorder is immaterial because the nested summations above commute.An algorithm to compute a one-dimensional DFT is thus sufficient to efficiently compute a multidimensional DFT. This approach is known as the row-column algorithm. There are also intrinsically multidimensional FFT algorithms.The real-input multidimensional DFTFor input data consisting of real numbers, the DFT outputs have a conjugate symmetry similar to the one-dimensional case above:where the star again denotes complex conjugation and the -th subscript is again interpreted modulo (for).ApplicationsThe DFT has seen wide usage across a large number of fields; we only sketch a few examples below (see also the references at the end). All applications of the DFT depend crucially on the availability of a fast algorithm to compute discrete Fourier transforms and their inverses, a fast Fourier transform.Spectral analysisWhen the DFT is used for spectral analysis, the sequence usually represents a finite set of uniformly-spacedtime-samples of some signal , where t represents time. The conversion from continuous time to samples (discrete-time) changes the underlying Fourier transform of x(t) into a discrete-time Fourier transform (DTFT), which generally entails a type of distortion called aliasing. Choice of an appropriate sample-rate (see Nyquist frequency) is the key to minimizing that distortion. Similarly, the conversion from a very long (or infinite) sequence to a manageable size entails a type of distortion called leakage, which is manifested as a loss of detail (aka resolution) in the DTFT. Choice of an appropriate sub-sequence length is the primary key to minimizing that effect. When the available data (and time to process it) is more than the amount needed to attain the desired frequency resolution, a standard technique is to perform multiple DFTs, for example to create a spectrogram. If the desired result is a power spectrum and noise or randomness is present in the data, averaging the magnitude components of the multiple DFTs is a useful procedure to reduce the variance of the spectrum (also called a periodogram in this context); two examples of such techniques are the Welch method and the Bartlett method; the general subject of estimating the power spectrum of a noisy signal is called spectral estimation.A final source of distortion (or perhaps illusion) is the DFT itself, because it is just a discrete sampling of the DTFT, which is a function of a continuous frequency domain. That can be mitigated by increasing the resolution of the DFT. That procedure is illustrated in the discrete-time Fourier transform article.•The procedure is sometimes referred to as zero-padding, which is a particular implementation used in conjunction with the fast Fourier transform (FFT) algorithm. The inefficiency of performing multiplications and additions with zero-valued "samples" is more than offset by the inherent efficiency of the FFT.•As already noted, leakage imposes a limit on the inherent resolution of the DTFT. So there is a practical limit to the benefit that can be obtained from a fine-grained DFT.Data compressionThe field of digital signal processing relies heavily on operations in the frequency domain (i.e. on the Fourier transform). For example, several lossy image and sound compression methods employ the discrete Fourier transform: the signal is cut into short segments, each is transformed, and then the Fourier coefficients of high frequencies, which are assumed to be unnoticeable, are discarded. The decompressor computes the inverse transform based on this reduced number of Fourier coefficients. (Compression applications often use a specialized form of the DFT, the discrete cosine transform or sometimes the modified discrete cosine transform.)Partial differential equationsDiscrete Fourier transforms are often used to solve partial differential equations, where again the DFT is used as an approximation for the Fourier series (which is recovered in the limit of infinite N). The advantage of this approach is that it expands the signal in complex exponentials e inx, which are eigenfunctions of differentiation: d/dx e inx = in e inx. Thus, in the Fourier representation, differentiation is simple—we just multiply by i n. (Note, however, that the choice of n is not unique due to aliasing; for the method to be convergent, a choice similar to that in the trigonometric interpolation section above should be used.) A linear differential equation with constant coefficients is transformed into an easily solvable algebraic equation. One then uses the inverse DFT to transform the result back into the ordinary spatial representation. Such an approach is called a spectral method.Polynomial multiplicationSuppose we wish to compute the polynomial product c(x) = a(x) · b(x). The ordinary product expression for the coefficients of c involves a linear (acyclic) convolution, where indices do not "wrap around." This can be rewritten as a cyclic convolution by taking the coefficient vectors for a(x) and b(x) with constant term first, then appending zeros so that the resultant coefficient vectors a and b have dimension d > deg(a(x)) + deg(b(x)). Then,Where c is the vector of coefficients for c(x), and the convolution operator is defined soBut convolution becomes multiplication under the DFT:Here the vector product is taken elementwise. Thus the coefficients of the product polynomial c(x) are just the terms 0, ..., deg(a(x)) + deg(b(x)) of the coefficient vectorWith a fast Fourier transform, the resulting algorithm takes O (N log N) arithmetic operations. Due to its simplicity and speed, the Cooley–Tukey FFT algorithm, which is limited to composite sizes, is often chosen for the transform operation. In this case, d should be chosen as the smallest integer greater than the sum of the input polynomialdegrees that is factorizable into small prime factors (e.g. 2, 3, and 5, depending upon the FFT implementation).Multiplication of large integersThe fastest known algorithms for the multiplication of very large integers use the polynomial multiplication method outlined above. Integers can be treated as the value of a polynomial evaluated specifically at the number base, with the coefficients of the polynomial corresponding to the digits in that base. After polynomial multiplication, a relatively low-complexity carry-propagation step completes the multiplication.Some discrete Fourier transform pairs Some DFT pairs NoteShift theoremReal DFTfrom the geometric progression formulafrom the binomial theoremis a rectangular window function of W pointscentered on , where W is an odd integer, and is asinc-like functionDiscretization and periodic summation of the scaledGaussian functions for . Since either or islarger than one and thus warrants fast convergence ofone of the two series, for large you may choose tocompute the frequency spectrum and convert to the timedomain using the discrete Fourier transform.Derivation as Fourier seriesThe DFT can be derived as a truncation of the Fourier series of a periodic sequence of impulses.GeneralizationsRepresentation theoryThe DFT can be interpreted as the complex-valued representation theory of the finite cyclic group. In other words, asequence of n complex numbers can be thought of as an element of n -dimensional complex space orequivalently a function from the finite cyclic group of order n to the complex numbers,This latter may be suggestively written to emphasize that this is a complex vector space whose coordinates are indexed by the n -element setFrom this point of view, one may generalize the DFT to representation theory generally, or more narrowly to the representation theory of finite groups.More narrowly still, one may generalize the DFT by either changing the target (taking values in a field other than the complex numbers), or the domain (a group other than a finite cyclic group), as detailed in the sequel.Other fieldsMany of the properties of the DFT only depend on the fact that is a primitive root of unity, sometimesdenoted or (so that ). Such properties include the completeness, orthogonality, Plancherel/Parseval, periodicity, shift, convolution, and unitarity properties above, as well as many FFT algorithms. For this reason, the discrete Fourier transform can be defined by using roots of unity in fields other than the complex numbers, and such generalizations are commonly called number-theoretic transforms (NTTs) in the case of finite fields. For more information, see number-theoretic transform and discrete Fourier transform (general).Other finite groupsThe standard DFT acts on a sequence x0, x1, …, xN−1of complex numbers, which can be viewed as a function {0, 1,…, N− 1} → C. The multidimensional DFT acts on multidimensional sequences, which can be viewed as functionsThis suggests the generalization to Fourier transforms on arbitrary finite groups, which act on functions G→ C where G is a finite group. In this framework, the standard DFT is seen as the Fourier transform on a cyclic group, while the multidimensional DFT is a Fourier transform on a direct sum of cyclic groups.AlternativesAs with other Fourier transforms, there are various alternatives to the DFT for various applications, prominent among which are wavelets. The analog of the DFT is the discrete wavelet transform (DWT). From the point of view of time–frequency analysis, a key limitation of the Fourier transform is that it does not include location information, only frequency information, and thus has difficulty in representing transients. As wavelets have location as well as frequency, they are better able to represent location, at the expense of greater difficulty representing frequency. For details, see comparison of the discrete wavelet transform with the discrete Fourier transform.Notes[1]T. G. Stockham, Jr., "High-speed convolution and correlation," in 1966 Proc. AFIPS Spring Joint Computing Conf. Reprinted in DigitalSignal Processing, L. R. Rabiner and C. M. Rader, editors, New York: IEEE Press, 1972.[2]Santhanam, Balu; Santhanam, Thalanayar S. "Discrete Gauss-Hermite functions and eigenvectors of the centered discrete Fourier transform"(/Proceedings/ICASSP 2007/pdfs/0301385.pdf), Proceedings of the 32nd IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2007, SPTM-P12.4), vol. III, pp. 1385-1388.References•Brigham, E. Oran (1988). The fast Fourier transform and its applications. Englewood Cliffs, N.J.: Prentice Hall.ISBN 0-13-307505-2.•Oppenheim, Alan V.; Schafer, R. W.; and Buck, J. R. (1999). Discrete-time signal processing. Upper Saddle River, N.J.: Prentice Hall. ISBN 0-13-754920-2.•Smith, Steven W. (1999). "Chapter 8: The Discrete Fourier Transform" (/ch8/1.htm). The Scientist and Engineer's Guide to Digital Signal Processing (Second ed.). San Diego, Calif.: California Technical Publishing. ISBN 0-9660176-3-3.•Cormen, Thomas H.; Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein (2001). "Chapter 30: Polynomials and the FFT". Introduction to Algorithms (Second ed.). MIT Press and McGraw-Hill. pp. 822–848.ISBN 0-262-03293-7. esp. section 30.2: The DFT and FFT, pp. 830–838.。
Fourier Transform

Fourier transformIn mathematics, the Fourier transform is the operation that decomposes a signal into its constituent frequencies. Thus the Fourier transform of a musical chord is a mathematical representation of the amplitudes of the individual notes that make it up. The original signal depends on time, and therefore is called the time domain representation of the signal, whereas the Fourier transform depends on frequency and is called the frequency domain representation of the signal. The term Fourier transform refers both to the frequency domain representation of the signal and the process that transforms the signal to its frequency domain representation.More precisely, the Fourier transform transforms one complex-valued function of a real variable into another. In effect, the Fourier transform decomposes a function into oscillatory functions. The Fourier transform and its generalizations are the subject of Fourier analysis. In this specific case, both the time and frequency domains are unbounded linear continua. It is possible to define the Fourier transform of a function of several variables, which is important for instance in the physical study of wave motion and optics. It is also possible to generalize the Fourier transform on discrete structures such as finite groups. The efficient computation of such structures, by fast Fourier transform, is essential for high-speed computing.DefinitionThere are several common conventions for defining the Fourier transform of an integrable function ƒ: R→ C (Kaiser 1994). This article will use the definition:for every real number ξ.When the independent variable x represents time (with SI unit of seconds), the transform variable ξ representsfrequency (in hertz). Under suitable conditions, ƒ can be reconstructed from by the inverse transform:for every real number x.For other common conventions and notations, including using the angular frequency ω instead of the frequency ξ, see Other conventions and Other notations below. The Fourier transform on Euclidean space is treated separately, in which the variable x often represents position and ξ momentum.IntroductionThe motivation for the Fourier transform comes from the study of Fourier series. In the study of Fourier series, complicated functions are written as the sum of simple waves mathematically represented by sines and cosines. Due to the properties of sine and cosine it is possible to recover the amount of each wave in the sum by an integral. In many cases it is desirable to use Euler's formula, which states that e2πiθ = cos 2πθ + i sin 2πθ, to write Fourier series in terms of the basic waves e2πiθ. This has the advantage of simplifying many of the formulas involved and providing a formulation for Fourier series that more closely resembles the definition followed in this article. This passage from sines and cosines to complex exponentials makes it necessary for the Fourier coefficients to becomplex valued. The usual interpretation of this complex number is that it gives both the amplitude (or size) of the wave present in the function and the phase (or the initial angle) of the wave. This passage also introduces the need for negative "frequencies". If θ were measured in seconds then the waves e2πiθ and e−2πiθ would both complete one cycle per second, but they represent different frequencies in the Fourier transform. Hence, frequency no longer measures the number of cycles per unit time, but is closely related.There is a close connection between the definition of Fourier series and the Fourier transform for functions ƒ which are zero outside of an interval. For such a function we can calculate its Fourier series on any interval that includes the interval where ƒ is not identically zero. The Fourier transform is also defined for such a function. As we increase the length of the interval on which we calculate the Fourier series, then the Fourier series coefficients begin to look like the Fourier transform and the sum of the Fourier series of ƒ begins to look like the inverse Fourier transform. To explain this more precisely, suppose that T is large enough so that the interval [−T/2,T/2] contains the interval onis given by:which ƒ is not identically zero. Then the n-th series coefficient cnComparing this to the definition of the Fourier transform it follows that since ƒ(x) is zero outside [−T/2,T/2]. Thus the Fourier coefficients are just the values of the Fourier transform sampled on a grid of width 1/T. As T increases the Fourier coefficients more closely represent the Fourier transform of the function.Under appropriate conditions the sum of the Fourier series of ƒ will equal the function ƒ. In other words ƒ can be written:= n/T, and Δξ = (n + 1)/T − n/T = 1/T. where the last sum is simply the first sum rewritten using the definitions ξnThis second sum is a Riemann sum, and so by letting T → ∞ it will converge to the integral for the inverse Fourier transform given in the definition section. Under suitable conditions this argument may be made precise (Stein & Shakarchi 2003).could be thought of as the "amount" of the wave in the Fourier series of In the study of Fourier series the numbers cnƒ. Similarly, as seen above, the Fourier transform can be thought of as a function that measures how much of each individual frequency is present in our function ƒ, and we can recombine these waves by using an integral (or "continuous sum") to reproduce the original function.The following images provide a visual illustration of how the Fourier transform measures whether a frequency is present in a particular function. The function depicted oscillates at 3 hertz (if t measures seconds) and tends quickly to 0. This function was specially chosen to have a real Fourier transform which can easily be plotted. The first image contains its graph. In order to calculate we must integrate e−2πi(3t)ƒ(t). The second image shows the plot of the real and imaginary parts of this function. The real part of the integrand is almost always positive, this is because when ƒ(t) is negative, then the real part of e−2πi(3t) is negative as well. Because they oscillate at the same rate, when ƒ(t) is positive, so is the real part of e−2πi(3t). The result is that when you integrate the real part of the integrand you get a relatively large number (in this case 0.5). On the other hand, when you try to measure a frequency that is not present, as in the case when we look at , the integrand oscillates enough so that the integral is very small. The general situation may be a bit more complicated than this, but this in spirit is how the Fourier transform measures how much of an individual frequency is present in a function ƒ(t).Original function showingoscillation 3 hertz.Real and imaginary parts of integrand for Fourier transformat 3 hertzReal and imaginary parts of integrand for Fourier transformat 5 hertz Fourier transform with 3 and 5hertz labeled.Properties of the Fourier transformAn integrable function is a function ƒon the real line that is Lebesgue-measurable and satisfiesBasic propertiesGiven integrable functions f (x ), g (x ), and h (x ) denote their Fourier transforms by, , andrespectively. The Fourier transform has the following basic properties (Pinsky 2002).LinearityFor any complex numbers a and b , if h (x ) = aƒ(x ) + bg(x ), thenTranslationFor any real number x 0, if h (x ) = ƒ(x − x 0), thenModulationFor any real number ξ0, if h (x ) = e 2πixξ0ƒ(x ), then.ScalingFor a non-zero real number a , if h (x ) = ƒ(ax ), then. The case a = −1 leads to the time-reversal property, which states: if h (x ) = ƒ(−x ), then.ConjugationIf , thenIn particular, if ƒ is real, then one has the reality conditionAnd ifƒ is purely imaginary, thenConvolutionIf , thenUniform continuity and the Riemann–Lebesgue lemmaThe rectangular function is Lebesgue integrable.The sinc function, which is the Fourier transform of the rectangular function, is bounded andcontinuous, but not Lebesgue integrable.The Fourier transform of an integrable function ƒ is bounded and continuous, but need not be integrable – for example, the Fourier transform of the rectangular function, which is a step function (and hence integrable) is the sinc function, which is not Lebesgue integrable, though it does have an improper integral: one has an analog to thealternating harmonic series, which is a convergent sum but not absolutely convergent.It is not possible in general to write the inverse transform as a Lebesgue integral. However, when both ƒ and are integrable, the following inverse equality holds true for almost every x:Almost everywhere, ƒ is equal to the continuous function given by the right-hand side. If ƒ is given as continuous function on the line, then equality holds for every x.A consequence of the preceding result is that the Fourier transform is injective on L1(R).The Plancherel theorem and Parseval's theoremLet f(x) and g(x) be integrable, and let and be their Fourier transforms. If f(x) and g(x) are also square-integrable, then we have Parseval's theorem (Rudin 1987, p. 187):where the bar denotes complex conjugation.The Plancherel theorem, which is equivalent to Parseval's theorem, states (Rudin 1987, p. 186):The Plancherel theorem makes it possible to define the Fourier transform for functions in L2(R), as described in Generalizations below. The Plancherel theorem has the interpretation in the sciences that the Fourier transform preserves the energy of the original quantity. It should be noted that depending on the author either of these theorems might be referred to as the Plancherel theorem or as Parseval's theorem.See Pontryagin duality for a general formulation of this concept in the context of locally compact abelian groups.Poisson summation formulaThe Poisson summation formula provides a link between the study of Fourier transforms and Fourier Series. Given an integrable function ƒ we can consider the periodic summation of ƒ given by:where the summation is taken over the set of all integers k. The Poisson summation formula relates the Fourier series of to the Fourier transform of ƒ. Specifically it states that the Fourier series of is given by:Convolution theoremThe Fourier transform translates between convolution and multiplication of functions. If ƒ(x) and g(x) are integrablefunctions with Fourier transforms and respectively, then the Fourier transform of the convolution is given by the product of the Fourier transforms and (under other conventions for the definition of theFourier transform a constant factor may appear).This means that if:where ∗ denotes the convolution operation, then:In linear time invariant (LTI) system theory, it is common to interpret g(x) as the impulse response of an LTI systemwith input ƒ(x) and output h(x), since substituting the unit impulse for ƒ(x) yields h(x) = g(x). In this case, represents the frequency response of the system.Conversely, if ƒ(x) can be decomposed as the product of two square integrable functions p(x) and q(x), then theFourier transform of ƒ(x) is given by the convolution of the respective Fourier transforms and .Cross-correlation theoremIn an analogous manner, it can be shown that if h(x) is the cross-correlation of ƒ(x) and g(x):then the Fourier transform of h(x) is:As a special case, the autocorrelation of function ƒ(x) is:for whichEigenfunctionsOne important choice of an orthonormal basis for L2(R) is given by the Hermite functionswhere are the "probabilist's" Hermite polynomials, defined by Hn(x) = (−1)n exp(x2/2) D n exp(−x2/2). Under this convention for the Fourier transform, we have thatIn other words, the Hermite functions form a complete orthonormal system of eigenfunctions for the Fourier transform on L2(R) (Pinsky 2002). However, this choice of eigenfunctions is not unique. There are only four different eigenvalues of the Fourier transform (±1 and ±i) and any linear combination of eigenfunctions with the same eigenvalue gives another eigenfunction. As a consequence of this, it is possible to decompose L2(R) as a directsum of four spaces H0, H1, H2, and H3where the Fourier transform acts on Hksimply by multiplication by i k. Thisapproach to define the Fourier transform is due to N. Wiener (Duoandikoetxea 2001). The choice of Hermite functions is convenient because they are exponentially localized in both frequency and time domains, and thus give rise to the fractional Fourier transform used in time-frequency analysis (Boashash 2003).Fourier transform on Euclidean spaceThe Fourier transform can be in any arbitrary number of dimensions n. As with the one-dimensional case there are many conventions, for an integrable function ƒ(x) this article takes the definition:where x and ξ are n-dimensional vectors, and x·ξ is the dot product of the vectors. The dot product is sometimes written as .All of the basic properties listed above hold for the n-dimensional Fourier transform, as do Plancherel's and Parseval's theorem. When the function is integrable, the Fourier transform is still uniformly continuous and the Riemann–Lebesgue lemma holds. (Stein & Weiss 1971)Uncertainty principleGenerally speaking, the more concentrated f(x) is, the more spread out its Fourier transform must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we "squeeze" a function in x, its Fourier transform "stretches out" in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.The trade-off between the compaction of a function and its Fourier transform can be formalized in the form of an Uncertainty Principle by viewing a function and its Fourier transform as conjugate variables with respect to the symplectic form on the time–frequency domain: from the point of view of the linear canonical transformation, the Fourier transform is rotation by 90° in the time–frequency domain, and preserves the symplectic form.Suppose ƒ(x) is an integrable and square-integrable function. Without loss of generality, assume that ƒ(x) is normalized:It follows from the Plancherel theorem that is also normalized.The spread around x = 0 may be measured by the dispersion about zero (Pinsky 2002) defined byIn probability terms, this is the second moment of about zero.The Uncertainty principle states that, if ƒ(x ) is absolutely continuous and the functions x ·ƒ(x ) and ƒ′(x ) are square integrable, then(Pinsky 2002).The equality is attained only in the case (hence ) where σ > 0is arbitrary and C 1 is such that ƒ is L 2–normalized (Pinsky 2002). In other words, where ƒ is a (normalized) Gaussian function, centered at zero.In fact, this inequality implies that:for any in R (Stein & Shakarchi 2003).In quantum mechanics, the momentum and position wave functions are Fourier transform pairs, to within a factor of Planck's constant. With this constant properly taken into account, the inequality above becomes the statement of the Heisenberg uncertainty principle (Stein & Shakarchi 2003).Spherical harmonicsLet the set of homogeneous harmonic polynomials of degree k on R n be denoted by A k . The set A k consists of the solid spherical harmonics of degree k . The solid spherical harmonics play a similar role in higher dimensions to the Hermite polynomials in dimension one. Specifically, if f (x ) = e −π|x |2P (x ) for some P (x ) in A k , then. Let the set H k be the closure in L 2(R n ) of linear combinations of functions of the form f (|x |)P (x )where P (x ) is in A k . The space L 2(R n ) is then a direct sum of the spaces H k and the Fourier transform maps each space H k to itself and is possible to characterize the action of the Fourier transform on each space H k (Stein & Weiss 1971). Let ƒ(x ) = ƒ0(|x |)P (x ) (with P (x ) in A k ), then whereHere J (n + 2k − 2)/2 denotes the Bessel function of the first kind with order (n + 2k − 2)/2. When k = 0 this gives a useful formula for the Fourier transform of a radial function (Grafakos 2004).Restriction problemsIn higher dimensions it becomes interesting to study restriction problems for the Fourier transform. The Fourier transform of an integrable function is continuous and the restriction of this function to any set is defined. But for a square-integrable function the Fourier transform could be a general class of square integrable functions. As such, the restriction of the Fourier transform of an L 2(R n ) function cannot be defined on sets of measure 0. It is still an active area of study to understand restriction problems in L p for 1 < p < 2. Surprisingly, it is possible in some cases to define the restriction of a Fourier transform to a set S , provided S has non-zero curvature. The case when S is the unit sphere in R n is of particular interest. In this case the Tomas-Stein restriction theorem states that the restriction of the Fourier transform to the unit sphere in R n is a bounded operator on L p provided 1 ≤ p ≤ (2n + 2) / (n + 3).One notable difference between the Fourier transform in 1 dimension versus higher dimensions concerns the partial sum operator. Consider an increasing collection of measurable sets E R indexed by R ∈ (0,∞): such as balls of radius R centered at the origin, or cubes of side 2R . For a given integrable function ƒ, consider the function ƒR defined by:Suppose in addition that ƒ is in L p (R n ). For n = 1 and 1 < p < ∞, if one takes E R = (−R, R), then ƒR converges to ƒ in L p as R tends to infinity, by the boundedness of the Hilbert transform. Naively one may hope the same holds true forn > 1. In the case that ERis taken to be a cube with side length R, then convergence still holds. Another naturalcandidate is the Euclidean ball ER= {ξ : |ξ| < R}. In order for this partial sum operator to converge, it is necessary that the multiplier for the unit ball be bounded in L p(R n). For n ≥ 2 it is a celebrated theorem of Charles Fefferman that the multiplier for the unit ball is never bounded unless p = 2 (Duoandikoetxea 2001). In fact, when p≠ 2, thisshows that not only may ƒR fail to converge to ƒ in L p, but for some functions ƒ ∈ L p(R n), ƒRis not even an element ofL p.GeneralizationsFourier transform on other function spacesIt is possible to extend the definition of the Fourier transform to other spaces of functions. Since compactly supported smooth functions are integrable and dense in L2(R), the Plancherel theorem allows us to extend the definition of the Fourier transform to general functions in L2(R) by continuity arguments. Further : L2(R) →L2(R) is a unitary operator (Stein & Weiss 1971, Thm. 2.3). Many of the properties remain the same for the Fourier transform. The Hausdorff–Young inequality can be used to extend the definition of the Fourier transform to include functions in L p(R) for 1 ≤ p≤ 2. Unfortunately, further extensions become more technical. The Fourier transform of functions in L p for the range 2 < p < ∞ requires the study of distributions (Katznelson 1976). In fact, it can be shown that there are functions in L p with p>2 so that the Fourier transform is not defined as a function (Stein & Weiss 1971).Fourier–Stieltjes transformThe Fourier transform of a finite Borel measure μ on R n is given by (Pinsky 2002):This transform continues to enjoy many of the properties of the Fourier transform of integrable functions. One notable difference is that the Riemann–Lebesgue lemma fails for measures (Katznelson 1976). In the case that dμ = ƒ(x) dx, then the formula above reduces to the usual definition for the Fourier transform of ƒ. In the case that μ is the probability distribution associated to a random variable X, the Fourier-Stieltjes transform is closely related to the characteristic function, but the typical conventions in probability theory take e ix·ξ instead of e−2πix·ξ (Pinsky 2002). In the case when the distribution has a probability density function this definition reduces to the Fourier transform applied to the probability density function, again with a different choice of constants.The Fourier transform may be used to give a characterization of continuous measures. Bochner's theorem characterizes which functions may arise as the Fourier–Stieltjes transform of a measure (Katznelson 1976). Furthermore, the Dirac delta function is not a function but it is a finite Borel measure. Its Fourier transform is a constant function (whose specific value depends upon the form of the Fourier transform used).Tempered distributionsThe Fourier transform maps the space of Schwartz functions to itself, and gives a homeomorphism of the space to itself (Stein & Weiss 1971). Because of this it is possible to define the Fourier transform of tempered distributions. These include all the integrable functions mentioned above, as well as well-behaved functions of polynomial growth and distributions of compact support, and have the added advantage that the Fourier transform of any tempered distribution is again a tempered distribution.The following two facts provide some motivation for the definition of the Fourier transform of a distribution. First let ƒ and g be integrable functions, and let and be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula (Stein & Weiss 1971),Secondly, every integrable function ƒ defines a distribution Tƒby the relationfor all Schwartz functions φ.In fact, given a distribution T, we define the Fourier transform by the relationfor all Schwartz functions φ.It follows thatDistributions can be differentiated and the above mentioned compatibility of the Fourier transform with differentiation and convolution remains true for tempered distributions.Locally compact abelian groupsThe Fourier transform may be generalized to any locally compact abelian group. A locally compact abelian group is an abelian group which is at the same time a locally compact Hausdorff topological space so that the group operations are continuous. If G is a locally compact abelian group, it has a translation invariant measure μ, called Haar measure. For a locally compact abelian group G it is possible to place a topology on the set of characters so that is also a locally compact abelian group. For a function ƒ in L1(G) it is possible to define the Fourier transform by (Katznelson 1976):Locally compact Hausdorff spaceThe Fourier transform may be generalized to any locally compact Hausdorff space, which recovers the topology but loses the group structure.Given a locally compact Hausdorff topological space X, the space A=C(X) of continuous complex-valued functions on X which vanish at infinity is in a natural way a commutative C*-algebra, via pointwise addition, multiplication, complex conjugation, and with norm as the uniform norm. Conversely, the characters of this algebra A, denoted are naturally a topological space, and can be identified with evaluation at a point of x, and one has an isometric isomorphism In the case where X=R is the real line, this is exactly the Fourier transform. Non-abelian groupsThe Fourier transform can also be defined for functions on a non-abelian group, provided that the group is compact. Unlike the Fourier transform on an abelian group, which is scalar-valued, the Fourier transform on a non-abelian group is operator-valued (Hewitt & Ross 1971, Chapter 8). The Fourier transform on compact groups is a major tool in representation theory (Knapp 2001) and non-commutative harmonic analysis.Let G be a compact Hausdorff topological group. Let Σ denote the collection of all isomorphism classes of finite-dimensional irreducible unitary representations, along with a definite choice of representation U(σ) on theHilbert space Hσ of finite dimension dσfor each σ ∈ Σ. If μ is a finite Borel measure on G, then the Fourier–Stieltjestransform of μ is the operator on Hσdefined bywhere is the complex-conjugate representation of U(σ) acting on Hσ. As in the abelian case, if μ is absolutely continuous with respect to the left-invariant probability measure λ on G, then it is represented asfor some ƒ ∈ L 1(λ). In this case, one identifies the Fourier transform of ƒ with the Fourier –Stieltjes transform of μ.The mapping defines an isomorphism between the Banach space M (G ) of finite Borel measures (see rca space) and a closed subspace of the Banach space C ∞(Σ) consisting of all sequences E = (E σ) indexed by Σ of (bounded) linear operators E σ : H σ → H σ for which the normis finite. The "convolution theorem" asserts that, furthermore, this isomorphism of Banach spaces is in fact an isomorphism of C * algebras into a subspace of C ∞(Σ), in which M (G ) is equipped with the product given by convolution of measures and C ∞(Σ) the product given by multiplication of operators in each index σ.The Peter-Weyl theorem holds, and a version of the Fourier inversion formula (Plancherel's theorem) follows: if ƒ ∈ L 2(G ), thenwhere the summation is understood as convergent in the L 2 sense.The generalization of the Fourier transform to the noncommutative situation has also in part contributed to the development of noncommutative geometry. In this context, a categorical generalization of the Fourier transform to noncommutative groups is Tannaka-Krein duality, which replaces the group of characters with the category of representations. However, this loses the connection with harmonic functions.AlternativesIn signal processing terms, a function (of time) is a representation of a signal with perfect time resolution, but no frequency information, while the Fourier transform has perfect frequency resolution, but no time information: the magnitude of the Fourier transform at a point is how much frequency content there is, but location is only given by phase (argument of the Fourier transform at a point), and standing waves are not localized in time – a sine wave continues out to infinity, without decaying. This limits the usefulness of the Fourier transform for analyzing signals that are localized in time, notably transients, or any signal of finite extent.As alternatives to the Fourier transform, in time-frequency analysis, one uses time-frequency transforms or time-frequency distributions to represent signals in a form that has some time information and some frequency information – by the uncertainty principle, there is a trade-off between these. These can be generalizations of the Fourier transform, such as the short-time Fourier transform or fractional Fourier transform, or can use different functions to represent signals, as in wavelet transforms and chirplet transforms, with the wavelet analog of the (continuous) Fourier transform being the continuous wavelet transform. (Boashash 2003). For a variable time and frequency resolution, the De Groot Fourier Transform can be considered.Applications Analysis of differential equationsFourier transforms and the closely related Laplace transforms are widely used in solving differential equations. The Fourier transform is compatible with differentiation in the following sense: if f (x ) is a differentiable function withFourier transform , then the Fourier transform of its derivative is given by . This can be used to transform differential equations into algebraic equations. Note that this technique only applies to problems whose domain is the whole set of real numbers. By extending the Fourier transform to functions of several variables partial differential equations with domain R n can also be translated into algebraic equations.。
Motion Estimation

. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
2 Introduction to Digital Video 2.1 Definitions and terminology . . . . . 2.1.1 Images . . . . . . . . . . . . . 2.1.2 Video sequences . . . . . . . 2.1.3 Video interlacing . . . . . . . 2.1.4 Contrast . . . . . . . . . . . . 2.1.5 Spatial frequency . . . . . . . 2.2 Digital image processing . . . . . . . 2.2.1 Fourier transform . . . . . . . 2.2.2 Convolution . . . . . . . . . . 2.2.3 Digital filters . . . . . . . . . 2.2.4 Correlation . . . . . . . . . . 2.3 MPEG-2 video compression . . . . . 2.3.1 The discrete cosine transform 2.3.2 Quantization . . . . . . . . . 2.3.3 Motion compensation . . . . 2.3.4 Efficient representation . . .
ii
c Philips Electronics N.V. 2001
no classification
Fourier-Transform

and substitute y = x + c. Property 1.2. The Fourier transform of f ( Ax) is (1/|A|) fˆ( A−1ξ ). Proof. Write down the Fourier transform as
be given, and let h then be a step function with f − h L1 ≤ . Since we already know about step-functions, we know there exists R such that
|ξ | ≥ R =⇒ |hˆ (ξ )| ≤ .
Let f ∈ L1(( )ޒthe space of complex-valued, integrable functions on )ޒ. The Fourier transform of f is the function fˆ defined by
fˆ(ξ ) = e−2πixξ f (x ) dx.
The integrand belongs to L1 in the above definition, because its norm is the same as that of f . So the definition makes sense.
Example. If f = χ[−1,1], then
1
fˆ(ξ) = e−2πi xξ dx
−1
1 = − 2πiξ
e−2πi xξ
1 x=−1
sin(2π ξ )
= πξ .
The function sin(2π ξ )/(π ξ ) is not integrable: the Fourier transform of an L1 function is not L1 in general.
fourier transform的原理

fourier transform的原理Fourier Transform的原理Fourier Transform(傅里叶变换)是一种数学工具,用于将一个函数或信号从时间域转换到频率域。
它是由法国数学家Jean-Baptiste Joseph Fourier 在19世纪提出的。
傅里叶变换在信号处理、图像处理、通信等领域都有广泛的应用。
傅里叶级数在介绍傅里叶变换之前,我们首先了解一下傅里叶级数。
傅里叶级数是傅里叶变换的基础,用于将周期性函数表示为一系列正弦和余弦函数的和。
傅里叶级数的公式如下:f(x)=a0+∑[a n cos(2πnxT)+b n sin(2πnxT)]∞n=1其中,a n和b n是函数f(x)的傅里叶系数,T是函数f(x)的周期。
连续傅里叶变换傅里叶级数适用于周期性函数,但对于非周期性函数,我们需要使用连续傅里叶变换。
连续傅里叶变换将一个非周期性函数f(t)转换为一个连续的频谱F(ω),其公式如下:F(ω)=∫f∞−∞(t)e−iωt dt连续傅里叶变换将时域信号转换为频域信号,其中ω表示角频率。
离散傅里叶变换在实际应用中,我们通常处理的是离散的数字信号。
离散傅里叶变换(DFT)是连续傅里叶变换的一种离散形式,将一个离散的信号序列x(n)转换为离散的频谱X(k),其公式如下:X(k)=∑xN−1n=0(n)e−i2πknN其中,k表示频率索引,N表示信号的长度。
快速傅里叶变换离散傅里叶变换的计算复杂度为O(N2),当N较大时,计算时间将会变得非常长。
为了提高计算效率,我们引入了快速傅里叶变换(FFT)。
FFT 是一种高效的算法,能够将离散傅里叶变换的计算复杂度降低到O(NlogN),使得大规模的信号处理成为可能。
傅里叶变换的应用傅里叶变换在信号处理和频谱分析中有着广泛的应用。
它可以用于图像压缩、音频处理、信号滤波、图像恢复等领域。
例如,在音频处理中,我们可以使用傅里叶变换将时域的声音信号转换为频域的频谱,以便对声音进行频谱分析和滤波处理。
Discrete Fourier transform
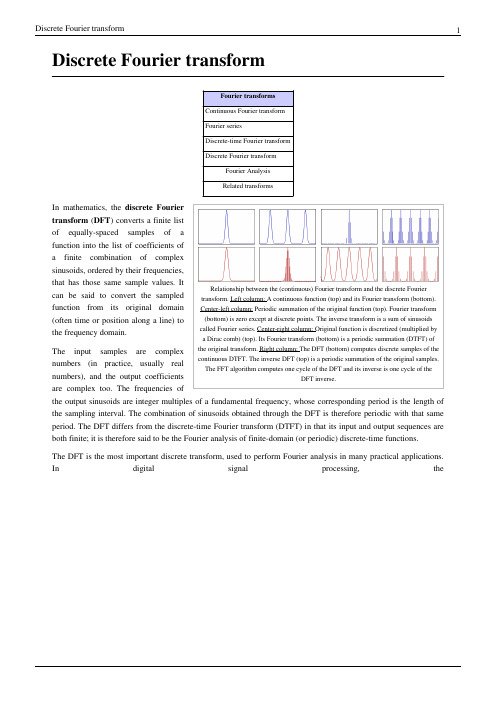
Discrete Fourier transformRelationship between the (continuous) Fourier transform and the discrete Fourier transform. Left column: A continuous function (top) and its Fourier transform (bottom).Center-left column: Periodic summation of the original function (top). Fourier transform (bottom) is zero except at discrete points. The inverse transform is a sum of sinusoids called Fourier series. Center-right column: Original function is discretized (multiplied by a Dirac comb) (top). Its Fourier transform (bottom) is a periodic summation (DTFT) of the original transform. Right column: The DFT (bottom) computes discrete samples of the continuous DTFT. The inverse DFT (top) is a periodic summation of the original samples.The FFT algorithm computes one cycle of the DFT and its inverse is one cycle of the DFT inverse.In mathematics, the discrete Fouriertransform (DFT ) converts a finite listof equally-spaced samples of afunction into the list of coefficients ofa finite combination of complexsinusoids, ordered by their frequencies,that has those same sample values. Itcan be said to convert the sampledfunction from its original domain(often time or position along a line) tothe frequency domain.The input samples are complexnumbers (in practice, usually realnumbers), and the output coefficientsare complex too. The frequencies ofthe output sinusoids are integer multiples of a fundamental frequency, whose corresponding period is the length of the sampling interval. The combination of sinusoids obtained through the DFT is therefore periodic with that same period. The DFT differs from the discrete-time Fourier transform (DTFT) in that its input and output sequences are both finite; it is therefore said to be the Fourier analysis of finite-domain (or periodic) discrete-time functions.The DFT is the most important discrete transform, used to perform Fourier analysis in many practical applications.In digital signal processing, theIllustration of using Dirac comb functions and the convolution theorem to model the effects of sampling and/or periodic summation. At lower left is a DTFT, the spectral result of sampling s(t) at intervals of T. The spectral sequences at (a) upper right and (b)lower right are respectively computed from (a) one cycle of the periodic summation ofs(t) and (b) one cycle of the periodic summation of the s(nT) sequence. The respectiveformulas are (a) the Fourier series integral and (b) the DFT summation. Its similarities to the original transform, S(f), and its relative computational ease are often the motivationfor computing a DFT sequence.function is any quantity or signal thatvaries over time, such as the pressureof a sound wave, a radio signal, ordaily temperature readings, sampledover a finite time interval (oftendefined by a window function). Inimage processing, the samples can bethe values of pixels along a row orcolumn of a raster image. The DFT isalso used to efficiently solve partialdifferential equations, and to performother operations such as convolutionsor multiplying large integers.Since it deals with a finite amount ofdata, it can be implemented incomputers by numerical algorithms oreven dedicated hardware. Theseimplementations usually employefficient fast Fourier transform (FFT)algorithms;[1] so much so that the terms "FFT" and "DFT" are often used interchangeably. The terminology isfurther blurred by the (now rare)synonym finite Fourier transform forthe DFT, which apparently predatesthe term "fast Fourier transform" but has the same initialism.DefinitionThe sequence of N complex numbers x 0, ..., x N −1 is transformed into an N -periodic sequence of complex numbersaccording to the DFT formula:(Eq.1)The transform is sometimes denoted by the symbol , as in or or .[2]Eq.1 can be interpreted or derived in various ways, for example:•It completely describes the discrete-time Fourier transform (DTFT) of an N-periodic sequence, which comprises only discrete frequency components. (Discrete-time Fourier transform#Periodic data)•It can also provide uniformly spaced samples of the continuous DTFT of a finite length sequence. (Sampling the DTFT)•It is the cross correlation of the input sequence, x n , and a complex sinusoid at frequency k /N . Thus it acts like a matched filter for that frequency.•It is the discrete analogy of the formula for the coefficients of a Fourier series:(Eq.2)which is the inverse DFT (IDFT).Each is a complex number that encodes both amplitude and phase of a sinusoidal component of function . The sinusoid's frequency is k/N cycles per sample. Its amplitude and phase are:where atan2 is the two-argument form of the arctan function. The normalization factor multiplying the DFT and IDFT (here 1 and 1/N) and the signs of the exponents are merely conventions, and differ in some treatments. The only requirements of these conventions are that the DFT and IDFT have opposite-sign exponents and that the product of their normalization factors be 1/N. A normalization of for both the DFT and IDFT, for instance, makes the transforms unitary.In the following discussion the terms "sequence" and "vector" will be considered interchangeable.PropertiesCompletenessThe discrete Fourier transform is an invertible, linear transformationwith C denoting the set of complex numbers. In other words, for any N > 0, an N-dimensional complex vector has a DFT and an IDFT which are in turn N-dimensional complex vectors.OrthogonalityThe vectors form an orthogonal basis over the set of N-dimensional complex vectors:where is the Kronecker delta. (In the last step, the summation is trivial if , where it is 1+1+⋅⋅⋅=N, and otherwise is a geometric series that can be explicitly summed to obtain zero.) This orthogonality condition can be used to derive the formula for the IDFT from the definition of the DFT, and is equivalent to the unitarity property below.The Plancherel theorem and Parseval's theoremIf Xk and Ykare the DFTs of xnand ynrespectively then the Plancherel theorem states:where the star denotes complex conjugation. Parseval's theorem is a special case of the Plancherel theorem and states:These theorems are also equivalent to the unitary condition below.PeriodicityIf the expression that defines the DFT is evaluated for all integers k instead of just for , then the resulting infinite sequence is a periodic extension of the DFT, periodic with period N.The periodicity can be shown directly from the definition:Similarly, it can be shown that the IDFT formula leads to a periodic extension.Shift theoremMultiplying by a linear phase for some integer m corresponds to a circular shift of the output : is replaced by , where the subscript is interpreted modulo N (i.e., periodically). Similarly, a circularshift of the input corresponds to multiplying the output by a linear phase. Mathematically, if represents the vector x thenifthenandCircular convolution theorem and cross-correlation theoremThe convolution theorem for the discrete-time Fourier transform indicates that a convolution of two infinite sequences can be obtained as the inverse transform of the product of the individual transforms. An important simplification occurs when the sequences are of finite length, N. In terms of the DFT and inverse DFT, it can be written as follows:which is the convolution of the sequence with a sequence extended by periodic summation:Similarly, the cross-correlation of and is given by:A direct evaluation of either summation (above) requires operations for an output sequence of length N. An indirect method, using transforms, can take advantage of the efficiency of the fast Fourier transform(FFT) to achieve much better performance. Furthermore, convolutions can be used to efficiently compute DFTs via Rader's FFT algorithm and Bluestein's FFT algorithm.Methods have also been developed to use circular convolution as part of an efficient process that achieves normal (non-circular) convolution with an or sequence potentially much longer than the practical transform size (N).Two such methods are called overlap-save and overlap-add.[3]Convolution theorem dualityIt can also be shown that :which is the circular convolution of and .Trigonometric interpolation polynomial The trigonometric interpolation polynomialforN even ,forN odd,where the coefficients X k are given by the DFT of x n above, satisfies the interpolation propertyfor .For even N , notice that the Nyquist component is handled specially.This interpolation is not unique : aliasing implies that one could add N to any of the complex-sinusoid frequencies(e.g. changing to ) without changing the interpolation property, but giving different values in between the points. The choice above, however, is typical because it has two useful properties. First, it consistsof sinusoids whose frequencies have the smallest possible magnitudes: the interpolation is bandlimited. Second, if the are real numbers, then is real as well.In contrast, the most obvious trigonometric interpolation polynomial is the one in which the frequencies range from0 to (instead of roughly to as above), similar to the inverse DFT formula. This interpolation does not minimize the slope, and is not generally real-valued for real ; its use is a common mistake.The unitary DFTAnother way of looking at the DFT is to note that in the above discussion, the DFT can be expressed as a Vandermonde matrix:whereis a primitive Nth root of unity. The inverse transform is then given by the inverse of the above matrix:With unitary normalization constants, the DFT becomes a unitary transformation, defined by a unitary matrix:where det() is the determinant function. The determinant is the product of the eigenvalues, which are always oras described below. In a real vector space, a unitary transformation can be thought of as simply a rigid rotation of the coordinate system, and all of the properties of a rigid rotation can be found in the unitary DFT.The orthogonality of the DFT is now expressed as an orthonormality condition (which arises in many areas of mathematics as described in root of unity):If is defined as the unitary DFT of the vector thenand the Plancherel theorem is expressed as:If we view the DFT as just a coordinate transformation which simply specifies the components of a vector in a new coordinate system, then the above is just the statement that the dot product of two vectors is preserved under a unitary DFT transformation. For the special case , this implies that the length of a vector is preserved aswell—this is just Parseval's theorem:Expressing the inverse DFT in terms of the DFTA useful property of the DFT is that the inverse DFT can be easily expressed in terms of the (forward) DFT, via several well-known "tricks". (For example, in computations, it is often convenient to only implement a fast Fourier transform corresponding to one transform direction and then to get the other transform direction from the first.) First, we can compute the inverse DFT by reversing the inputs:(As usual, the subscripts are interpreted modulo N; thus, for , we have .)Second, one can also conjugate the inputs and outputs:Third, a variant of this conjugation trick, which is sometimes preferable because it requires no modification of the data values, involves swapping real and imaginary parts (which can be done on a computer simply by modifying pointers). Define swap( ) as with its real and imaginary parts swapped—that is, if thenswap( ) is . Equivalently, swap( ) equals . ThenThat is, the inverse transform is the same as the forward transform with the real and imaginary parts swapped for both input and output, up to a normalization (Duhamel et al., 1988).The conjugation trick can also be used to define a new transform, closely related to the DFT, that is involutary—that is, which is its own inverse. In particular, is clearly its own inverse: . A closely related involutary transformation (by a factor of (1+i) /√2) is , since thefactors in cancel the 2. For real inputs , the real part of is none other than the discrete Hartley transform, which is also involutary.Eigenvalues and eigenvectorsThe eigenvalues of the DFT matrix are simple and well-known, whereas the eigenvectors are complicated, not unique, and are the subject of ongoing research.Consider the unitary form defined above for the DFT of length N, whereThis matrix satisfies the matrix polynomial equation:This can be seen from the inverse properties above: operating twice gives the original data in reverse order, so operating four times gives back the original data and is thus the identity matrix. This means that the eigenvalues satisfy the equation:Therefore, the eigenvalues of are the fourth roots of unity: is +1, −1, +i, or −i.Since there are only four distinct eigenvalues for this matrix, they have some multiplicity. The multiplicitygives the number of linearly independent eigenvectors corresponding to each eigenvalue. (Note that there are N independent eigenvectors; a unitary matrix is never defective.)The problem of their multiplicity was solved by McClellan and Parks (1972), although it was later shown to have been equivalent to a problem solved by Gauss (Dickinson and Steiglitz, 1982). The multiplicity depends on the value of N modulo 4, and is given by the following table:Multiplicities of the eigenvalues λ of the unitary DFT matrix U as a function of thetransform size N (in terms of an integer m).size Nλ = +1λ = −1λ = -iλ = +i4m m + 1m m m− 14m + 1m + 1m m m4m + 2m + 1m + 1m m4m + 3m + 1m + 1m + 1mOtherwise stated, the characteristic polynomial of is:No simple analytical formula for general eigenvectors is known. Moreover, the eigenvectors are not unique because any linear combination of eigenvectors for the same eigenvalue is also an eigenvector for that eigenvalue. Various researchers have proposed different choices of eigenvectors, selected to satisfy useful properties like orthogonality and to have "simple" forms (e.g., McClellan and Parks, 1972; Dickinson and Steiglitz, 1982; Grünbaum, 1982; Atakishiyev and Wolf, 1997; Candan et al., 2000; Hanna et al., 2004; Gurevich and Hadani, 2008).A straightforward approach is to discretize the eigenfunction of the continuous Fourier transform, namely the Gaussian function. Since periodic summation of the function means discretizing its frequency spectrum and discretization means periodic summation of the spectrum, the discretized and periodically summed Gaussian function yields an eigenvector of the discrete transform:•.A closed form expression for the series is not known, but it converges rapidly.Two other simple closed-form analytical eigenvectors for special DFT period N were found (Kong, 2008):For DFT period N = 2L + 1 = 4K +1, where K is an integer, the following is an eigenvector of DFT:•For DFT period N = 2L = 4K, where K is an integer, the following is an eigenvector of DFT:•The choice of eigenvectors of the DFT matrix has become important in recent years in order to define a discrete analogue of the fractional Fourier transform—the DFT matrix can be taken to fractional powers by exponentiating the eigenvalues (e.g., Rubio and Santhanam, 2005). For the continuous Fourier transform, the natural orthogonal eigenfunctions are the Hermite functions, so various discrete analogues of these have been employed as the eigenvectors of the DFT, such as the Kravchuk polynomials (Atakishiyev and Wolf, 1997). The "best" choice of eigenvectors to define a fractional discrete Fourier transform remains an open question, however.Uncertainty principleIf the random variable is constrained by:then may be considered to represent a discrete probability mass function of n, with an associated probability mass function constructed from the transformed variable:For the case of continuous functions P(x) and Q(k), the Heisenberg uncertainty principle states that:where and are the variances of and respectively, with the equality attained in the case of a suitably normalized Gaussian distribution. Although the variances may be analogously defined for the DFT, an analogous uncertainty principle is not useful, because the uncertainty will not be shift-invariant. Nevertheless, a meaningful uncertainty principle has been introduced by Massar and Spindel.[4]However, the Hirschman uncertainty will have a useful analog for the case of the DFT.[] The Hirschman uncertainty principle is expressed in terms of the Shannon entropy of the two probability functions. In the discrete case, the Shannon entropies are defined as:andand the Hirschman uncertainty principle becomes:[]The equality is obtained for equal to translations and modulations of a suitably normalized Kronecker comb ofperiod A where A is any exact integer divisor of N. The probability mass function will then be proportional to a suitably translated Kronecker comb of period B=N/A.[]The real-input DFTIf are real numbers, as they often are in practical applications, then the DFT obeys the symmetry:where denotes complex conjugation.It follows that X0 and XN/2are real-valued, and the remainder of the DFT is completely specified by just N/2-1complex numbers.Generalized DFT (shifted and non-linear phase)It is possible to shift the transform sampling in time and/or frequency domain by some real shifts a and b, respectively. This is sometimes known as a generalized DFT (or GDFT), also called the shifted DFT or offset DFT, and has analogous properties to the ordinary DFT:Most often, shifts of (half a sample) are used. While the ordinary DFT corresponds to a periodic signal in both time and frequency domains, produces a signal that is anti-periodic in frequency domain ( ) and vice-versa for . Thus, the specific case of is known as an odd-time odd-frequency discrete Fourier transform (or O2 DFT). Such shifted transforms are most often used for symmetric data, to represent different boundary symmetries, and for real-symmetric data they correspond to different forms of the discrete cosine and sine transforms.Another interesting choice is , which is called the centered DFT (or CDFT). The centered DFT has the useful property that, when N is a multiple of four, all four of its eigenvalues (see above) have equal multiplicities (Rubio and Santhanam, 2005)[5]The term GDFT is also used for the non-linear phase extensions of DFT. Hence, GDFT method provides a generalization for constant amplitude orthogonal block transforms including linear and non-linear phase types. GDFT is a framework to improve time and frequency domain properties of the traditional DFT, e.g. auto/cross-correlations, by the addition of the properly designed phase shaping function (non-linear, in general) to the original linear phase functions (Akansu and Agirman-Tosun, 2010).[6]The discrete Fourier transform can be viewed as a special case of the z-transform, evaluated on the unit circle in the complex plane; more general z-transforms correspond to complex shifts a and b above.Multidimensional DFTThe ordinary DFT transforms a one-dimensional sequence or array that is a function of exactly one discrete variable n. The multidimensional DFT of a multidimensional array that is a function of d discretevariables for in is defined by:where as above and the d output indices run from . This ismore compactly expressed in vector notation, where we define andas d-dimensional vectors of indices from 0 to , which we define as:where the division is defined as to be performed element-wise, and the sum denotes the set of nested summations above.The inverse of the multi-dimensional DFT is, analogous to the one-dimensional case, given by:As the one-dimensional DFT expresses the input as a superposition of sinusoids, the multidimensional DFT expresses the input as a superposition of plane waves, or multidimensional sinusoids. The direction of oscillation inspace is . The amplitudes are . This decomposition is of great importance for everything from digitalimage processing (two-dimensional) to solving partial differential equations. The solution is broken up into planewaves.The multidimensional DFT can be computed by the composition of a sequence of one-dimensional DFTs along each dimension. In the two-dimensional case the independent DFTs of the rows (i.e., along ) arecomputed first to form a new array . Then the independent DFTs of y along the columns (along ) are computed to form the final result . Alternatively the columns can be computed first and then the rows. Theorder is immaterial because the nested summations above commute.An algorithm to compute a one-dimensional DFT is thus sufficient to efficiently compute a multidimensional DFT. This approach is known as the row-column algorithm. There are also intrinsically multidimensional FFT algorithms.The real-input multidimensional DFTFor input data consisting of real numbers, the DFT outputs have a conjugate symmetry similar to the one-dimensional case above:where the star again denotes complex conjugation and the -th subscript is again interpreted modulo (for).ApplicationsThe DFT has seen wide usage across a large number of fields; we only sketch a few examples below (see also the references at the end). All applications of the DFT depend crucially on the availability of a fast algorithm to compute discrete Fourier transforms and their inverses, a fast Fourier transform.Spectral analysisWhen the DFT is used for spectral analysis, the sequence usually represents a finite set of uniformly spacedtime-samples of some signal , where t represents time. The conversion from continuous time to samples (discrete-time) changes the underlying Fourier transform of x(t) into a discrete-time Fourier transform (DTFT), which generally entails a type of distortion called aliasing. Choice of an appropriate sample-rate (see Nyquist rate) is the key to minimizing that distortion. Similarly, the conversion from a very long (or infinite) sequence to a manageable size entails a type of distortion called leakage, which is manifested as a loss of detail (aka resolution) in the DTFT. Choice of an appropriate sub-sequence length is the primary key to minimizing that effect. When the available data (and time to process it) is more than the amount needed to attain the desired frequency resolution, a standard technique is to perform multiple DFTs, for example to create a spectrogram. If the desired result is a power spectrum and noise or randomness is present in the data, averaging the magnitude components of the multiple DFTs is a useful procedure to reduce the variance of the spectrum (also called a periodogram in this context); two examples of such techniques are the Welch method and the Bartlett method; the general subject of estimating the power spectrum of a noisy signal is called spectral estimation.A final source of distortion (or perhaps illusion) is the DFT itself, because it is just a discrete sampling of the DTFT, which is a function of a continuous frequency domain. That can be mitigated by increasing the resolution of theDFT. That procedure is illustrated at Sampling the DTFT.•The procedure is sometimes referred to as zero-padding, which is a particular implementation used in conjunction with the fast Fourier transform (FFT) algorithm. The inefficiency of performing multiplications and additions with zero-valued "samples" is more than offset by the inherent efficiency of the FFT.•As already noted, leakage imposes a limit on the inherent resolution of the DTFT. So there is a practical limit to the benefit that can be obtained from a fine-grained DFT.Filter bankSee FFT filter banks and Sampling the DTFT.Data compressionThe field of digital signal processing relies heavily on operations in the frequency domain (i.e. on the Fourier transform). For example, several lossy image and sound compression methods employ the discrete Fourier transform: the signal is cut into short segments, each is transformed, and then the Fourier coefficients of high frequencies, which are assumed to be unnoticeable, are discarded. The decompressor computes the inverse transform based on this reduced number of Fourier coefficients. (Compression applications often use a specialized form of the DFT, the discrete cosine transform or sometimes the modified discrete cosine transform.) Some relatively recent compression algorithms, however, use wavelet transforms, which give a more uniform compromise between time and frequency domain than obtained by chopping data into segments and transforming each segment. In the case of JPEG2000, this avoids the spurious image features that appear when images are highly compressed with the original JPEG.Partial differential equationsDiscrete Fourier transforms are often used to solve partial differential equations, where again the DFT is used as an approximation for the Fourier series (which is recovered in the limit of infinite N). The advantage of this approach is that it expands the signal in complex exponentials e inx, which are eigenfunctions of differentiation: d/dx e inx = in e inx. Thus, in the Fourier representation, differentiation is simple—we just multiply by i n. (Note, however, that the choice of n is not unique due to aliasing; for the method to be convergent, a choice similar to that in the trigonometric interpolation section above should be used.) A linear differential equation with constant coefficients is transformed into an easily solvable algebraic equation. One then uses the inverse DFT to transform the result back into the ordinary spatial representation. Such an approach is called a spectral method.Polynomial multiplicationSuppose we wish to compute the polynomial product c(x) = a(x) · b(x). The ordinary product expression for the coefficients of c involves a linear (acyclic) convolution, where indices do not "wrap around." This can be rewritten as a cyclic convolution by taking the coefficient vectors for a(x) and b(x) with constant term first, then appending zeros so that the resultant coefficient vectors a and b have dimension d > deg(a(x)) + deg(b(x)). Then,Where c is the vector of coefficients for c(x), and the convolution operator is defined soBut convolution becomes multiplication under the DFT:Here the vector product is taken elementwise. Thus the coefficients of the product polynomial c(x) are just the terms 0, ..., deg(a(x)) + deg(b(x)) of the coefficient vectorWith a fast Fourier transform, the resulting algorithm takes O (N log N) arithmetic operations. Due to its simplicity and speed, the Cooley–Tukey FFT algorithm, which is limited to composite sizes, is often chosen for the transform operation. In this case, d should be chosen as the smallest integer greater than the sum of the input polynomial degrees that is factorizable into small prime factors (e.g. 2, 3, and 5, depending upon the FFT implementation).Multiplication of large integersThe fastest known algorithms for the multiplication of very large integers use the polynomial multiplication method outlined above. Integers can be treated as the value of a polynomial evaluated specifically at the number base, with the coefficients of the polynomial corresponding to the digits in that base. After polynomial multiplication, a relatively low-complexity carry-propagation step completes the multiplication.ConvolutionWhen data is convolved with a function with wide support, such as for downsampling by a large sampling ratio, because of the Convolution theorem and the FFT algorithm, it may be faster to transform it, multiply pointwise by the transform of the filter and then reverse transform it. Alternatively, a good filter is obtained by simply truncating the transformed data and re-transforming the shortened data set.Some discrete Fourier transform pairsSome DFT pairsNoteShift theoremReal DFTfrom the geometric progression formulafrom the binomial theoremis a rectangular window function of W pointscentered on n=0, where W is an odd integer, andis a sinc-like function (specifically, is a Dirichletkernel) ArrayDiscretization and periodic summation of the scaledGaussian functions for . Since either oris larger than one and thus warrants fast convergenceof one of the two series, for large you may chooseto compute the frequency spectrum and convert to thetime domain using the discrete Fourier transform.。
Fourier transform

Fourier transformThe Fourier transform, named after Joseph Fourier, is a mathematical transform with many applications in physics and engineering. Very commonly it transforms a mathematical function of time, f(t), into a new function, sometimesdenoted by or F, whose argument is frequency with units of cycles/sec (hertz) or radians per second. The new function is then known as the Fourier transform and/or the frequency spectrum of the function f. The Fourier transform is also a reversible operation. Thus, given the function one can determine the original function, f. (See Fourier inversion theorem.) f and are also respectively known as time domain and frequency domainrepresentations of the same "event". Most often perhaps, f is a real-valued function, and is complex valued, where a complex number describes both the amplitude and phase of a corresponding frequency component. In general, f is also complex, such as the analytic representation of a real-valued function. The term "Fourier transform" refers to both the transform operation and to the complex-valued function it produces.In the case of a periodic function (for example, a continuous but not necessarily sinusoidal musical sound), the Fourier transform can be simplified to the calculation of a discrete set of complex amplitudes, called Fourier series coefficients. Also, when a time-domain function is sampled to facilitate storage or computer-processing, it is still possible to recreate a version of the original Fourier transform according to the Poisson summation formula, also known as discrete-time Fourier transform. These topics are addressed in separate articles. For an overview of those and other related operations, refer to Fourier analysis or List of Fourier-related transforms.DefinitionThere are several common conventions for defining the Fourier transform ƒof an integrable function f : R→ C (Kaiser 1994, p. 29), (Rahman 2011, p. 11). This article will use the definition:, for every real number ξ.When the independent variable x represents time (with SI unit of seconds), the transform variable ξ represents frequency (in hertz). Under suitable conditions, f is determined by ƒvia the inverse transform:for every real number x.The statement that f can be reconstructed from ƒis known as the Fourier inversion theorem, and was first introduced in Fourier's Analytical Theory of Heat (Fourier 1822, p. 525), (Fourier & Freeman 1878, p. 408), although what would be considered a proof by modern standards was not given until much later (Titchmarsh 1948, p. 1). The functions f and ƒoften are referred to as a Fourier integral pair or Fourier transform pair (Rahman 2011, p. 10).For other common conventions and notations, including using the angular frequency ω instead of the frequency ξ, see Other conventions and Other notations below. The Fourier transform on Euclidean space is treated separately, in which the variable x often represents position and ξ momentum.IntroductionThe Fourier transform relates the function's time domain, shown in red, to the function's frequency domain, shown in blue. The component frequencies, spread across the frequencyspectrum, are represented as peaks in thefrequency domain.The motivation for the Fourier transform comes from the study ofFourier series. In the study of Fourier series, complicated but periodicfunctions are written as the sum of simple waves mathematicallyrepresented by sines and cosines. The Fourier transform is an extensionof the Fourier series that results when the period of the representedfunction is lengthened and allowed to approach infinity.(Taneja 2008,p. 192)Due to the properties of sine and cosine, it is possible to recover theamplitude of each wave in a Fourier series using an integral. In manycases it is desirable to use Euler's formula, which states that e 2πi θ=cos(2πθ) + i sin(2πθ), to write Fourier series in terms of the basic waves e 2πiθ. This has the advantage of simplifying many of the formulas involved, and provides a formulation for Fourier series thatmore closely resembles the definition followed in this article.Re-writing sines and cosines as complex exponentials makes itnecessary for the Fourier coefficients to be complex valued. The usual interpretation of this complex number is that it gives both the amplitude (or size) of the wave present in the function and the phase (or the initial angle) of the wave. These complex exponentials sometimes contain negative "frequencies". If θ is measured in seconds, then the waves e 2πiθ and e −2πiθ both complete one cycle per second, but they represent different frequencies in the Fourier transform. Hence, frequency no longer measures the number of cycles per unit time, but is still closely related.There is a close connection between the definition of Fourier series and the Fourier transform for functions f which are zero outside of an interval. For such a function, we can calculate its Fourier series on any interval that includes the points where f is not identically zero. The Fourier transform is also defined for such a function. As we increase the length of the interval on which we calculate the Fourier series, then the Fourier series coefficients begin to look like the Fourier transform and the sum of the Fourier series of f begins to look like the inverse Fourier transform. To explain this more precisely, suppose that T is large enough so that the interval [−T /2,T /2] contains the interval on which f is not identically zero. Then the n -th series coefficient c nis given by:Comparing this to the definition of the Fourier transform, it follows that c n = ƒ(n /T ) since f (x ) is zero outside[−T /2,T /2]. Thus the Fourier coefficients are just the values of the Fourier transform sampled on a grid of width 1/T .As T increases the Fourier coefficients more closely represent the Fourier transform of the function.Under appropriate conditions, the sum of the Fourier series of f will equal the function f . In other words, f can bewritten:where the last sum is simply the first sum rewritten using the definitions ξn = n /T , and Δξ = (n + 1)/T − n /T = 1/T .This second sum is a Riemann sum, and so by letting T → ∞ it will converge to the integral for the inverse Fourier transform given in the definition section. Under suitable conditions this argument may be made precise (Stein &Shakarchi 2003).In the study of Fourier series the numbers c n could be thought of as the "amount" of the wave present in the Fourier series of f . Similarly, as seen above, the Fourier transform can be thought of as a function that measures how much of each individual frequency is present in our function f , and we can recombine these waves by using an integral (or"continuous sum") to reproduce the original function.ExampleThe following images provide a visual illustration of how the Fourier transform measures whether a frequency is present in a particular function. The function depicted f (t ) = cos(6πt ) e -πt 2 oscillates at 3 hertz (if t measures seconds)and tends quickly to 0. (The second factor in this equation is an envelope function that shapes the continuous sinusoid into a short pulse. Its general form is a Gaussian function). This function was specially chosen to have a real Fourier transform which can easily be plotted. The first image contains its graph. In order to calculate ƒ(3) we must integrate e −2πi (3t )f (t ). The second image shows the plot of the real and imaginary parts of this function. The real part of the integrand is almost always positive, because when f (t ) is negative, the real part of e −2πi (3t ) is negative as well.Because they oscillate at the same rate, when f (t ) is positive, so is the real part of e −2πi (3t ). The result is that when you integrate the real part of the integrand you get a relatively large number (in this case 0.5). On the other hand,when you try to measure a frequency that is not present, as in the case when we look at ƒ(5), the integrand oscillates enough so that the integral is very small. The general situation may be a bit more complicated than this, but this in spirit is how the Fourier transform measures how much of an individual frequency is present in a function f (t ).Original function showingoscillation 3 hertz.Real and imaginary parts of integrand for Fourier transformat 3 hertzReal and imaginary parts of integrand for Fourier transformat 5 hertz Fourier transform with 3 and 5hertz labeled.Properties of the Fourier transformHere we assume f (x ), g (x ) and h(x ) areintegrable functions , are Lebesgue-measurable on the real line, and satisfy:We denote the Fourier transforms of these functions by , andrespectively.Basic propertiesThe Fourier transform has the following basic properties: (Pinsky 2002).LinearityFor any complex numbers a and b , if h (x ) = af (x ) + bg (x ), thenTranslationFor any real number x 0, ifthenModulationFor any real number ξ0if then ScalingFor a non-zero real number a , if h (x ) = f (ax ), thenThe case a = −1 leads to the time-reversal property, which states: if h (x ) = f (−x ), thenConjugationIf thenIn particular, if f is real, then one has the reality conditionAnd if f is purely imaginary, thenInvertibility and periodicityUnder suitable conditions on the function f, it can be recovered from its Fourier transform Indeed, denoting the Fourier transform operator by so then for suitable functions, applying the Fourier transform twice simply flips the function: which can be interpreted as "reversing time". Since reversing time is two-periodic, applying this twice yields so the Fourier transform operator is four-periodic, and similarly the inverse Fourier transform can be obtained by applying the Fourier transform three times:In particular the Fourier transform is invertible (under suitable conditions).More precisely, defining the parity operator that inverts time,one has that:These equalities of operators require careful definition of the space of functions in question, defining equality offunctions (equality at every point? equality almost everywhere?) and defining equality of operators – that is, defining the topology on the function space and operator space in question. These are not true for all functions, but are true under various conditions, which are the content of the various forms of the Fourier inversion theorem.This four-fold periodicity of the Fourier transform is similar to a rotation of the plane by 90°, particularly as the two-fold iteration yields a reversal, and in fact this analogy can be made precise. While the Fourier transform can simply be interpreted as switching the time domain and the frequency domain, with the inverse Fourier transform switching them back, more geometrically it can be interpreted as a rotation by 90° in the time–frequency domain (considering time as the x-axis and frequency as the y-axis), and the Fourier transform can be generalized to the fractional Fourier transform, which involves rotations by other angles. This can be further generalized to linearcanonical transformations, which can be visualized as the action of the special linear group SL2(R) on the time–frequency plane, with the preserved symplectic form corresponding to the uncertainty principle, below. This approach is particularly studied in signal processing, under time–frequency analysis.Uniform continuity and the Riemann–Lebesgue lemmaThe rectangular function is Lebesgue integrable. The Fourier transform may be defined in some cases for non-integrablefunctions, but the Fourier transforms of integrable functions haveseveral strong properties.The Fourier transform, ƒ, of any integrable function f is uniformlycontinuous and (Katznelson 1976). By theRiemann–Lebesgue lemma(Stein & Weiss 1971),However, ƒneed not be integrable. For example, the Fourier transformof the rectangular function, which is integrable, is the sinc function,which is not Lebesgue integrable, because its improper integrals behave analogously to the alternating harmonic series, in converging to a sum without being absolutely convergent.The sinc function, which is the Fourier transform of the rectangular function, is bounded andcontinuous, but not Lebesgue integrable.It is not generally possible to write the inverse transform as a Lebesgueintegral. However, when both f and ƒ are integrable, the inverseequalityholds almost everywhere. That is, the Fourier transform is injective onL 1(R ). (But if f is continuous, then equality holds for every x .)Plancherel theorem and Parseval's theoremLet f (x ) and g (x ) be integrable, and let ƒ(ξ) andbe their Fourier transforms. If f (x ) and g (x ) are also square-integrable, then we haveParseval's theorem (Rudin 1987, p. 187):where the bar denotes complex conjugation.The Plancherel theorem, which is equivalent to Parseval's theorem, states (Rudin 1987, p. 186):The Plancherel theorem makes it possible to extend the Fourier transform, by a continuity argument, to a unitary operator on L 2(R ). On L 1(R )∩L 2(R ), this extension agrees with original Fourier transform defined on L 1(R ), thus enlarging the domain of the Fourier transform to L 1(R ) + L 2(R ) (and consequently to L p (R ) for 1 ≤ p ≤ 2). The Plancherel theorem has the interpretation in the sciences that the Fourier transform preserves the energy of the original quantity. Depending on the author either of these theorems might be referred to as the Plancherel theorem or as Parseval's theorem.See Pontryagin duality for a general formulation of this concept in the context of locally compact abelian groups.Poisson summation formulaThe Poisson summation formula (PSF) is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. It has a variety of useful forms that are derived from the basic one by application of the Fourier transform's scaling and time-shifting properties. The frequency-domain dual of the standard PSF is also called discrete-time Fourier transform, which leads directly to:• a popular, graphical, frequency-domain representation of the phenomenon of aliasing, and• a proof of the Nyquist-Shannon sampling theorem.Convolution theoremThe Fourier transform translates between convolution and multiplication of functions. If f (x ) and g (x ) are integrable functions with Fourier transforms and respectively, then the Fourier transform of the convolution is given by the product of the Fourier transformsand (under other conventions for the definition of theFourier transform a constant factor may appear).This means that if:where ∗denotes the convolution operation, then:In linear time invariant (LTI) system theory, it is common to interpret g(x) as the impulse response of an LTI system with input f(x) and output h(x), since substituting the unit impulse for f(x) yields h(x) = g(x). In this case, represents the frequency response of the system.Conversely, if f(x) can be decomposed as the product of two square integrable functions p(x) and q(x), then theFourier transform of f(x) is given by the convolution of the respective Fourier transforms and .Cross-correlation theoremIn an analogous manner, it can be shown that if h(x) is the cross-correlation of f(x) and g(x):then the Fourier transform of h(x) is:As a special case, the autocorrelation of function f(x) is:for whichEigenfunctionsOne important choice of an orthonormal basis for L2(R) is given by the Hermite functionswhere Hen(x) are the "probabilist's" Hermite polynomials, defined byUnder this convention for the Fourier transform, we have that.In other words, the Hermite functions form a complete orthonormal system of eigenfunctions for the Fourier transform on L2(R) (Pinsky 2002). However, this choice of eigenfunctions is not unique. There are only four different eigenvalues of the Fourier transform (±1 and ±i) and any linear combination of eigenfunctions with the same eigenvalue gives another eigenfunction. As a consequence of this, it is possible to decompose L2(R) as a directsum of four spaces H0, H1, H2, and H3where the Fourier transform acts on Heksimply by multiplication by i k.Since the complete set of Hermite functions provides a resolution of the identity, the Fourier transform can be represented by such a sum of terms weighted by the above eigenvalues, and these sums can be explicitly summed. This approach to define the Fourier transform is due to N. Wiener (Duoandikoetxea 2001). Among other properties, Hermite functions decrease exponentially fast in both frequency and time domains, and they are thus used to define a generalization of the Fourier transform, namely the fractional Fourier transform used in time-frequency analysis (Boashash 2003). In physics, it was introduced by Condon (Condon 1937).Fourier transform on Euclidean spaceThe Fourier transform can be in any arbitrary number of dimensions n . As with the one-dimensional case, there are many conventions. For an integrable function f (x ), this article takes the definition:where x and ξ are n -dimensional vectors, and x · ξ is the dot product of the vectors. The dot product is sometimes written as .All of the basic properties listed above hold for the n -dimensional Fourier transform, as do Plancherel's and Parseval's theorem. When the function is integrable, the Fourier transform is still uniformly continuous and the Riemann –Lebesgue lemma holds. (Stein & Weiss 1971)Uncertainty principleGenerally speaking, the more concentrated f (x ) is, the more spread out its Fourier transform ƒ(ξ) must be. In particular, the scaling property of the Fourier transform may be seen as saying: if we "squeeze" a function in x , its Fourier transform "stretches out" in ξ. It is not possible to arbitrarily concentrate both a function and its Fourier transform.The trade-off between the compaction of a function and its Fourier transform can be formalized in the form of an uncertainty principle by viewing a function and its Fourier transform as conjugate variables with respect to the symplectic form on the time –frequency domain: from the point of view of the linear canonical transformation, the Fourier transform is rotation by 90° in the time –frequency domain, and preserves the symplectic form.Suppose f (x ) is an integrable and square-integrable function. Without loss of generality, assume that f (x ) is normalized:It follows from the Plancherel theorem that ƒ(ξ) is also normalized.The spread around x = 0 may be measured by the dispersion about zero (Pinsky 2002, p. 131) defined byIn probability terms, this is the second moment of |f (x )|2 about zero.The Uncertainty principle states that, if f (x ) is absolutely continuous and the functions x ·f (x ) and f ′(x ) are square integrable, then(Pinsky 2002).The equality is attained only in the case (hence ) where σ > 0 is arbitrary and C 1 is such that f is L 2–normalized (Pinsky 2002). In other words, where f is a (normalized) Gaussian function with variance σ2, centered at zero, and its Fourier transform is a Gaussian function with variance σ−2.In fact, this inequality implies that:for any x 0, ξ0 ∈ R (Stein & Shakarchi 2003, p. 158).In quantum mechanics, the momentum and position wave functions are Fourier transform pairs, to within a factor of Planck's constant. With this constant properly taken into account, the inequality above becomes the statement of the Heisenberg uncertainty principle (Stein & Shakarchi 2003, p. 158).A stronger uncertainty principle is the Hirschman uncertainty principle which is expressed as:where H(p) is the differential entropy of the probability density function p(x):where the logarithms may be in any base which is consistent. The equality is attained for a Gaussian, as in the previous case.Spherical harmonicsLet the set of homogeneous harmonic polynomials of degree k on R n be denoted by A k . The set A k consists of the solid spherical harmonics of degree k . The solid spherical harmonics play a similar role in higher dimensions to the Hermite polynomials in dimension one. Specifically, if f (x ) = e −π|x |2P (x ) for some P (x ) in A k , then. Let the set H k be the closure in L 2(R n ) of linear combinations of functions of the form f (|x |)P (x )where P (x ) is in A k . The space L 2(R n ) is then a direct sum of the spaces H k and the Fourier transform maps each space H k to itself and is possible to characterize the action of the Fourier transform on each space H k (Stein & Weiss 1971). Let f (x ) = f 0(|x |)P (x ) (with P (x ) in A k ), then whereHere J (n + 2k − 2)/2 denotes the Bessel function of the first kind with order (n + 2k − 2)/2. When k = 0 this gives a useful formula for the Fourier transform of a radial function (Grafakos 2004).Restriction problemsIn higher dimensions it becomes interesting to study restriction problems for the Fourier transform. The Fourier transform of an integrable function is continuous and the restriction of this function to any set is defined. But for a square-integrable function the Fourier transform could be a general class of square integrable functions. As such, the restriction of the Fourier transform of an L 2(R n ) function cannot be defined on sets of measure 0. It is still an active area of study to understand restriction problems in L p for 1 < p < 2. Surprisingly, it is possible in some cases to define the restriction of a Fourier transform to a set S , provided S has non-zero curvature. The case when S is the unit sphere in R n is of particular interest. In this case the Tomas-Stein restriction theorem states that the restriction of the Fourier transform to the unit sphere in R n is a bounded operator on L p provided 1 ≤ p ≤ (2n + 2) / (n + 3).One notable difference between the Fourier transform in 1 dimension versus higher dimensions concerns the partial sum operator. Consider an increasing collection of measurable sets E R indexed by R ∈ (0,∞): such as balls of radius R centered at the origin, or cubes of side 2R . For a given integrable function f , consider the function f R defined by:Suppose in addition that f ∈ L p (R n ). For n = 1 and 1 < p < ∞, if one takes E R = (−R , R ), then f R converges to f in L p as R tends to infinity, by the boundedness of the Hilbert transform. Naively one may hope the same holds true for n > 1.In the case that E R is taken to be a cube with side length R , then convergence still holds. Another natural candidate is the Euclidean ball E R = {ξ : |ξ| < R }. In order for this partial sum operator to converge, it is necessary that the multiplier for the unit ball be bounded in L p (R n ). For n ≥ 2 it is a celebrated theorem of Charles Fefferman that the multiplier for the unit ball is never bounded unless p = 2 (Duoandikoetxea 2001). In fact, when p ≠ 2, this shows that not only may f R fail to converge to f in L p , but for some functions f ∈ L p (R n ), f R is not even an element of L p .Fourier transform on function spacesOn L p spacesOn L1The definition of the Fourier transform by the integral formulais valid for Lebesgue integrable functions f; that is, f∈ L1(R).The Fourier transform : L1(R) → L∞(R) is a bounded operator. This follows from the observation thatwhich shows that its operator norm is bounded by 1. Indeed it equals 1, which can be seen, for example, from the(R) of continuous functions that tend to transform of the rect function. The image of L1 is a subset of the space Czero at infinity (the Riemann–Lebesgue lemma), although it is not the entire space. Indeed, there is no simple characterization of the image.On L2Since compactly supported smooth functions are integrable and dense in L2(R), the Plancherel theorem allows us to extend the definition of the Fourier transform to general functions in L2(R) by continuity arguments. The Fourier transform in L2(R) is no longer given by an ordinary Lebesgue integral, although it can be computed by an improper integral, here meaning that for an L2 function f,where the limit is taken in the L2 sense. Many of the properties of the Fourier transform in L1 carry over to L2, by a suitable limiting argument.Furthermore : L2(R) → L2(R) is a unitary operator (Stein & Weiss 1971, Thm. 2.3). For an operator to be unitary it is sufficient to show that it is bijective and preserves the inner product, so in this case these follow from the Fourier inversion theorem combined with the fact that for any f,g∈L2(R) we haveIn particular, the image of L2(R) is itself under the Fourier transform.On other L pThe definition of the Fourier transform can be extended to functions in L p(R) for 1 ≤ p≤ 2 by decomposing such functions into a fat tail part in L2 plus a fat body part in L1. In each of these spaces, the Fourier transform of a function in L p(R) is in L q(R), where is the Hölder conjugate of p. by the Hausdorff–Young inequality. However, except for p = 2, the image is not easily characterized. Further extensions become more technical. The Fourier transform of functions in L p for the range 2 < p < ∞ requires the study of distributions (Katznelson 1976). In fact, it can be shown that there are functions in L p with p > 2 so that the Fourier transform is not defined as a function (Stein & Weiss 1971).Tempered distributionsOne might consider enlarging the domain of the Fourier transform from L1+L2 by considering generalized functions,or distributions. A distribution on R is a continuous linear functional on the space Cc(R) of compactly supported smooth functions, equipped with a suitable topology. The strategy is then to consider the action of the Fouriertransform on Cc(R) and pass to distributions by duality. The obstruction to do this is that the Fourier transform doesnot map Cc (R) to Cc(R). In fact the Fourier transform of an element in Cc(R) can not vanish on an open set; see theabove discussion on the uncertainty principle. The right space here is the slightly larger space of Schwartz functions.The Fourier transform is an automorphism on the Schwartz space, as a topological vector space, and thus induces an automorphism on its dual, the space of tempered distributions(Stein & Weiss 1971). The tempered distribution include all the integrable functions mentioned above, as well as well-behaved functions of polynomial growth and distributions of compact support.For the definition of the Fourier transform of a tempered distribution, let f and g be integrable functions, and let and be their Fourier transforms respectively. Then the Fourier transform obeys the following multiplication formula (Stein & Weiss 1971),Every integrable function f defines (induces) a distribution Tfby the relationfor all Schwartz functions φ.So it makes sense to define Fourier transform of Tfbyfor all Schwartz functions φ. Extending this to all tempered distributions T gives the general definition of the Fourier transform.Distributions can be differentiated and the above mentioned compatibility of the Fourier transform with differentiation and convolution remains true for tempered distributions.Feichtinger's algebraFeichtinger's algebra Sis defined as the space of functions whose short-time Fourier transform is absolutelyintegrable i.e. contained in L1(R2). The Fourier transform is a homeomorphism on it. The space Sis contained in L1∩ C(R), but is a larger space than the space of Schwartz functions. It is a Banach algebra under both multiplication and convolution.GeneralizationsFourier–Stieltjes transformThe Fourier transform of a finite Borel measure μ on R n is given by (Pinsky 2002, p. 256):This transform continues to enjoy many of the properties of the Fourier transform of integrable functions. One notable difference is that the Riemann–Lebesgue lemma fails for measures (Katznelson 1976). In the case that dμ = f(x)dx, then the formula above reduces to the usual definition for the Fourier transform of f. In the case that μ is the probability distribution associated to a random variable X, the Fourier-Stieltjes transform is closely related to the characteristic function, but the typical conventions in probability theory take e ix·ξ instead of e−2πix·ξ (Pinsky 2002). In the case when the distribution has a probability density function this definition reduces to the Fourier transform。
Fourier Transform Pairs外文翻译
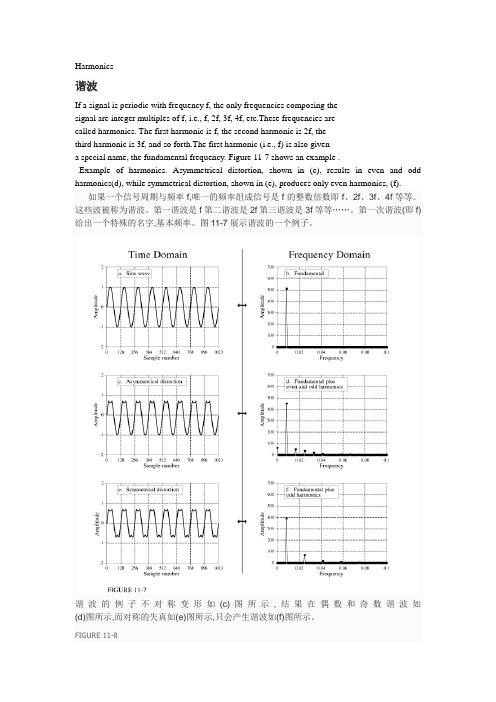
Harmonics谐波If a signal is periodic with frequency f, the only frequencies composing thesignal are integer multiples of f, i.e., f, 2f, 3f, 4f, etc.These frequencies arecalled harmonics. The first harmonic is f, the second harmonic is 2f, thethird harmonic is 3f, and so forth.The first harmonic (i.e., f) is also givena special name, the fundamental frequency. Figure 11-7 shows an example .Example of harmonics. Asymmetrical distortion, shown in (c), results in even and odd harmonics(d), while symmetrical distortion, shown in (e), produces only even harmonics, (f).如果一个信号周期与频率f,唯一的频率组成信号是f的整数倍数即f、2f、3f、4f等等。
这些波被称为谐波。
第一谐波是f第二谐波是2f第三谐波是3f等等……。
第一次谐波(即f) 给出一个特殊的名字,基本频率。
图11-7展示谐波的一个例子。
谐波的例子不对称变形如(c)图所示,结果在偶数和奇数谐波如(d)图所示,而对称的失真如(e)图所示,只会产生谐波如(f)图所示。
FIGURE 11-8Harmonic aliasing. Figures (a) and (b) show a distorted sine wave and its frequency spectrum, Harmonics with a frequency greater than 0.5 will become aliased to a frequency between 0 and 0.5. (c) displays the same frequency spectrum on a logarithmic scale, revealing many aliased peaks with very low amplitude.图11 - 8谐波混淆。
Fourier Series and Transform

Fourier series
For any function f(x) with period 2π (f(x) = f(2π +x)), we can describe the f(x) in terms of an infinite sum of sines and cosines
a0 ∞ f ( x ) = + ∑ ( am cos mx + bm sin mx ), 2 m=1
+
=
Fourier series
Period function
example (cont…)
⎧ 1 f ( x) −π < x < 0
The Fourier series is:
f ( x) =
4 sin x sin 3 x sin 5 x ( + + + ...) π 1 3 5
+
=
Fourier series
Period function
example (cont…)
⎧ 1 f ( x) = ⎨ ⎩− 1 0< x <π −π < x < 0
The Fourier series is:
f ( x) =
4 sin x sin 3 x sin 5 x ( + + + ...) π 1 3 5
π
−π
∫ cos nxdx = 0,
π
π
−π
∫ sin nxdx = 0
π
−π
∫ sin mx cos nxdx = 0
⎧0 ∫ cos mx cos nxdx = ⎨ −π ⎩π
m≠n m=n
傅里叶变换Fouriertransform

傅立叶变换
例题2 将矩形脉冲 f (t) = h rect(t/2T)展开为傅立叶积分。 解: 先求出 f (t) 的傅立叶变换 代入傅立叶积分公式,得
例题3 求对称指数函数f(t)的傅立叶变换 傅立叶变换
狄拉克函数
本章小结
傅立叶级数 周期函数的三角展开公式; 基本三角函数的性质。 傅立叶变换 非周期函数的三角展开公式; 傅立叶变换的性质。 狄拉克函数 狄拉克函数概念; 狄拉克函数性质; 狄拉克函数功能。
作 业
P73 6-2 (3) (1) (3) (1)
实施:
展开公式
困难
展开系数 cn 为无穷小; 幂指数 nx/L 不确定。
解决方法: 把 nπ/L 作为新变量,即定义ωn = nπ/L ; 把 cnL/π作为新的展开系数,即定义F(ωn)=cnL/π. 公式的新形式: 展开公式:
展开系数:
取极限: 傅立叶变换:
傅立叶积分:
傅立叶变换
傅立叶变换
傅立叶变换
傅立叶变换的性质 一般假定 f(x) → F(ω), g(x) → G(ω) 奇偶虚实性 f(x)为偶函数,F(ω)=∫f(x)cos(ωx)dx/(2π)为实函数; f(x)为奇函数,F(ω)=-i∫f(x)sin(ωx)dx/(2π)为虚函数 线性性质 k f(x) → k F(ω); f(x)+g(x) → F(ω)+ G(ω) 分析性质 f ’(x) → iωF(ω);
典型周期函数(周期为2π)
傅立叶级数
添加标题
理论意义:把复杂的周期函数用简单的三角级数表示;
01
添加标题
Lecture 4 Fourier transform theory

Z cos(2 ! x) cபைடு நூலகம்s(2 ! x)dx = 0
1 2
for !1 6= !2, because the function being integrated is actually a cosine function itself (2 cos A cos B = cos(A + B ) + cos(A ? B )) and so it has equal areas above and below the x-axis. Thus, we project our given function f onto our basis functions e?2 i!x to get the Fourier amplitudes F (!) for each frequency !:
Amplitude of sinewave
A1/2
A1/2
-3f -5f -f f
3f 5f frequency
Figure 3: The amplitude of the sine waves at each frequency for a square wave.
So what does the Fourier transform really mean? When we calculate the Fourier transform of an image, we treat the intensity signal across the image as a function, not just an array of values. The Fourier transform describes a way of decomposing a function into a sum of orthogonal basis functions in just the same way as we decompose a point in Euclidean space into the sum of its basis vector components. For example, a vector v in 3-space is described in terms of 3 orthogonal unit vectors i, j and k, and we can write v as the sum of its projections onto these 3 basis vectors: v = xi + yj + zk: Given the vector v, we can calculate the components of v in each of the i, j, and k directions by calculating the dot product (or inner product or projection) of v and each of these basis vectors. Thus
Fourier Transform - Tufts University傅里叶变换-塔夫斯大学 10页PPT文档
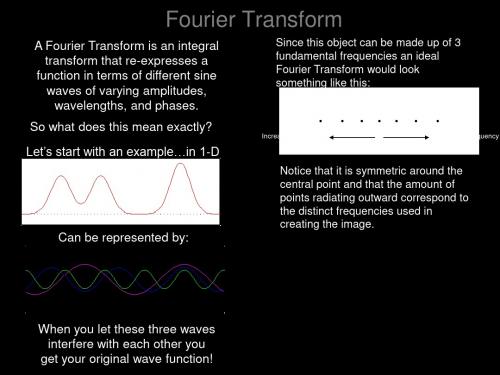
Where F(w) is original function and f(t) is the transformed function
Since Computers don’t like infinite integrals a Fast Fourier Transform makes it simpler:
frequency.
x-y coordinate system
This image exclusively has 8 cycles in the horizontal direction.
Fourier Transform
You will notice that the second example is a little more smeared out. This is because
dots refer to the frequency of a component wave.)
Fourier Transform Images are from: /~brayer/vision/fourier.html
Let’s Bring it Up a Few Notches
taking the reciprocal of the distances between a dot and the center of the image.
no preferred long range order.
The power of FT is that it allows you to take a seemingly complicated image which has an apparent order that is difficult to determine see and break it up
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
arXiv:alg-geom/9405006v2 5 Aug 1996
´ndez Ruip´ C. Bartocci,⋆ U. Bruzzo,♯ and D. Herna erez¶ ⋆ Dipartimento di Matematica, Universit` a di Genova, Italia ♯ Scuola Internazionale Superiore di Studi Avanzati (SISSA — ISAS), Trieste, Italia ¶ Departamento de Matem´ atica Pura y Aplicada, Universidad de Salamanca, Espa˜ na Revised — 6 August 1996
1991 Mathematics Subject Classification. 14F05, 32L07, 32L25, 58D27. Key words and phrases. Fourier-Mukai transform, stable bundles, K3 surfaces, instantons. Research partly supported by the Italian Ministry for University and Research through the research projects ‘Metodi geometrici e probabilistici in fisica matematica’ and ‘Geometria delle variet` a differenziabili,’ by the Spanish DGICYT through the research projects PB91-0188 and PB92-0308, by EUROPROJ, and by the National Group GNSAGA of the Italian Research Council.
LБайду номын сангаас
This space, which is a quasi-projective subscheme of the moduli space of simple sheaves over X , has been extensively studied by Mukai [19-20]. In particular, he proved the following crucial result: if MH (v ) = Y is nonempty and compact of dimension two, then it is a K3 surface, isogenous to the original K3 surface X . If X is a K3 surface satisfying these conditions and a few additional assumptions, we can prove our first result (already announced in [2]), by exploiting the relationship between stable bundles and instanton bundles (the so-called Hitchin-Kobayashi correspondence). Theorem 1. Let F be a µ-polystable IT1 locally free sheaf of zero degree on X . The Fourier-Mukai transform of F is a µ-polystable locally free sheaf on Y . For a wide family of K3 surfaces X , we can choose v so that X = MH (v ) is a K3 surface isomorphic to X . The nonemptiness of MH (v ) in this case has been proved in [4] by direct methods. Then we prove that the Fourier-Mukai transform is invertible, just as in the case of abelian surfaces: Theorem 2. Let F be an WITi sheaf on X . Then its Fourier-Mukai transform F = Ri π ˆ∗ (π ∗ F ⊗ Q) is a WIT2−i sheaf on X , whose Fourier-Mukai transform R2−i π∗ (ˆ π ∗ F ⊗ Q∗ ) is isomorphic to F . Furthermore, the Fourier-Mukai transform of a stable bundle is stable: Theorem 3. Let F be a zero-degree µ-stable bundle on X , with v (F ∗ ) = v . Then
Abstract. We define a Fourier-Mukai transform for sheaves on K3 surfaces over C, and show that it maps polystable bundles to polystable ones. The rˆ ole of “dual” variety to the given K3 surface X is here played by a suitable component X of the moduli space of stable sheaves on X . For a wide class of K3 surfaces X can be chosen to be isomorphic to X ; then the Fourier-Mukai transform is invertible, and the image of a zero-degree stable bundle F is stable and has the same Euler characteristic as F.
1. Introduction and preliminaries Mukai’s functor may be defined within a fairly general setting; given two schemes X , Y (of finite type over an algebraically closed field k ), and an element Q in the derived category D(X × Y ) of OX ×Y -modules, Mukai [18] defined a functor SX →Y from the derived category D− (X ) to D− (Y ), SX →Y (E ) = Rπ ˆ∗ (Q⊗π ∗ E ) (here π : X × Y → X and π ˆ : X × Y → Y are the natural projections). Mukai has proved that, when X is an abelian variety, Y = X its dual variety, and Q the Poincar´ e bundle on X × X , the functor SX →X gives rise to an equivalence of categories. If one is interested in transforming sheaves rather than complexes one can introduce (following Mukai) the notion of WITi sheaves: an OX -module E
L
2
´ ´ C. BARTOCCI, U. BRUZZO AND D. HERNANDEZ RUIPEREZ
is said to be WITi if its Fourier-Mukai transform is concentrated in degree i, i.e. Hk R π ˆ∗ (Q⊗π ∗ E ) = 0 for all k = i. Let X is be a polarized abelian surface and X is its dual. If F is a µ-stable vector bundle of rank ≥ 2 and zero degree, then it is WIT1 , and its Mukai transform F is again a µ-stable bundle (with respect to a suitable polarization on X ) of degree zero. This result was proved by Fahlaoui and Laszlo [10] and Maciocia [14], albeit Schenk [21] and Braam and van Baal [7] had previously obtained a completely equivalent result in the differential-geometric setting: the Nahm-Fourier transform of an instanton on a flat four-torus (with no flat factors) is an instanton over the dual torus (cf. also [9], and, for a detailed proof of the equivalence of the two approaches, [3]). The key remark which makes it possible to relate the algebraic-geometric treatment to the differential-geometric one is that the Fourier-Mukai transform is interpretable as the index of a suitable family of elliptic operators parametrized by the target space X , very much in the spirit of Grothendieck-Illusie’s approach to the definition of index of a relative elliptic complex. The Fourier-Mukai transform can be studied also in the case of nonabelian varieties. The general idea is to consider a variety X , some moduli space Y of ‘geometric objects’ over X , and (if possible) a ‘universal sheaf’ Q over the product X × Y . In the present paper we consider the case of a smooth algebraic K3 surface X over C with a fixed ample line bundle H on it; the rˆ ole of dual variety is here played by the moduli space Y = MH (v ) of Gieseker-stable sheaves (with respect to H ) E on X having a fixed v , where v (E ) = ch(E ) td(X ) = (r, α, s) ∈ H 0 (X, Z) ⊕ H 1,1 (X, Z) ⊕ H 4 (X, Z) .
