人教B版 高中数学 选修4-4 极坐标与参数方程 知识点归纳、题型归纳(含答案)
人教高中数学选修 4-4 极坐标与参数方程 知识点
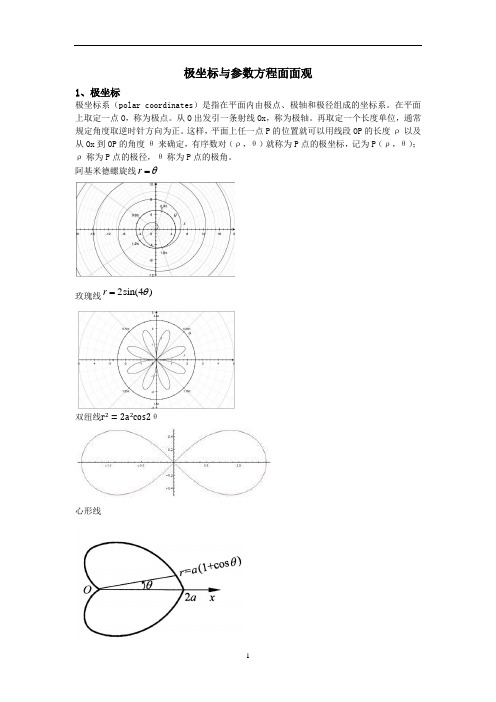
极坐标与参数方程面面观1、极坐标极坐标系(polar coordinates)是指在平面内由极点、极轴和极径组成的坐标系。
在平面上取定一点O,称为极点。
从O出发引一条射线Ox,称为极轴。
再取定一个长度单位,通常规定角度取逆时针方向为正。
这样,平面上任一点P的位置就可以用线段OP的长度ρ以及从Ox到OP的角度θ来确定,有序数对(ρ,θ)就称为P点的极坐标,记为P(ρ,θ);ρ称为P点的极径,θ称为P点的极角。
阿基米德螺旋线rθ=玫瑰线2sin(4) rθ=双纽线r2=2a2cos2θ心形线极坐标中的直线一般方程a ρcos θ+b ρcos θ+c =0(θ为倾斜角)极坐标中的圆圆心在极点,半径为R :ρ=R (θ任意)半径为R 的圆过(R,0)点:ρ=2Rcos θ.圆心(a ,α)半径为r :r 2=ρ2+a 2−2a ρcos (α−θ)ρ^2-2R ρ(sin θ+cos θ)+R^2=0圆心在(a ,π2)处且过极点:ρ=2asin θ(θ∈[0,π]) 椭圆、双曲线、抛物线统一的极坐标方程为: θρcos 1e ep -=.(p 是定点F 到定直线的距离,p >0 ).当0<e <1时,方程表示椭圆;当e >1时,方程表示双曲线,若ρ>0,方程只表示双曲线右支,若允许ρ<0,方程就表示整个双曲线;当e=1时,方程表示开口向右的抛物线.2、参数方程 定义:一般的,在平面直角坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数't’的函数{x=f(t),y=g(t)}并且对于't‘的每一个允许值,由上述方程组所确定的点M (x,y)都在这条曲线上,那么上述方程则为这条曲线的参数方程,联系x ,y 的变数't‘叫做变参数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。
(注意:参数是联系变数x ,y 的桥梁,可以是一个有物理意义和几何意义的变数,也可以是没有实际意义的变数)圆的参数方程它的参数方程为:cos ()sin x a r y b r θθθ=+⎧⎨=+⎩为参数(θ∈ [0,2π) ) (a,b) 为圆心坐标,r 为圆半径。
高中数学选修4—4(坐标系与参数方程)知识点总结

坐标系与参数方程知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x xy y的作用下,点P(x,y)对应到点(,)P x y,称为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.2.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点O,叫做极点,自极点O引一条射线Ox,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标设M是平面内一点,极点O与点M的距离|OM|叫做点M的极径,记为;以极轴Ox为始边,射线OM为终边的角xOM叫做点M的极角,记为.有序数对(,)叫做点M的极坐标,记作(,)M.一般地,不作特殊说明时,我们认为0,可取任意实数.特别地,当点M在极点时,它的极坐标为(0,)(∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02,那么除极点外,平面内的点可用唯一的极坐标(,)表示;同时,极坐标(,)表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M是坐标平面内任意一点,它的直角坐标是(,)x y,极坐标是(,)(0),于是极坐标与直角坐标的互化公式如表:点M直角坐标(,)x y极坐标(,)互化公式cossinxy222tan(0)x yyxx在一般情况下,由tan确定角时,可根据点M所在的象限最小正角.4.常见曲线的极坐标方程曲线图形极坐标方程圆心在极点,半径为r的圆(02) r圆心为(,0)r,半径为r的圆2cos()22 r圆心为(,)2r,半径为r的圆2sin(0) r过极点,倾斜角为的直线(1)()()R R 或(2)(0)(0)和过点(,0)a ,与极轴垂直的直线cos()22a 过点(,)2a ,与极轴平行的直线sin(0)a 注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2),(,),(,),都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,点(,)44M 可以表示为5(,2)(,2),444444或或(-)等多种形式,其中,只有(,)44的极坐标满足方程.二、参数方程1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t yg t ①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t ,把它代入普通方程,求出另一个变数与参数的关系()y g t ,那么()()x f t yg t 就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致.注:普通方程化为参数方程,参数方程的形式不一定唯一。
(完整版)高中数学选修4—4(坐标系与参数方程)知识点总结

e 44
th
(
,
2
)或(或 (,-
2 ))
44
44
, 5
等多种形式,其中,只有
(
,
)
的极坐标满足方程
.
44
44
in 二、参数方程
gs 1.参数方程的概念
thin x f (t)
ll 一般地,在平面直角坐标系中,如果曲线上任意一点的坐标
x,
y
都是某个变数
t
的函数
y
g
(t
)
①,并且对于
t
a 的曲线的参数方程的形式也不同。
ing 3.圆的参数
ir be 如图所示,设圆O 的半径为 r
,点 M
从初始位置
M0
出发,按逆时针方向在圆 O 上作匀速圆周运动,设
M
(x,
y)
x ,则
y
r cos r sin
(为参数)
。
the 这就是圆心在原点 O ,半径为 r 的圆的参数方程,其中 的几何意义是 OM0 转过的角度。
bein (1)极坐标系如图所示,在平面内取一个定点 O ,叫做极点,自极点 O 引一条射线 Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正 eir 方向(通常取逆时针方向),这样就建立了一个极坐标系. th 注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系, in 而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系. ings (2)极坐标:设 M 是平面内一点,极点 O 与点 M 的距离|OM|叫做点 M 的极径,记为 ;以极轴 Ox 为始边,射线 OM 为终边的角 xOM 叫做点 M 的极角,记 th 为 .有序数对 (, ) 叫做点 M 的极坐标,记作 M (, ) .
高中数学选修4—4(坐标系与参数方程)知识点总结

坐标系与参数方程 知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x xy yλλϕμμ'=>⎧⎨'=>⎩的作用下,点P(x,y)对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 2.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标:设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0,θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:点M直角坐标(,)x y 极坐标(,)ρθ互化公式cos sin x y ρθρθ=⎧⎨=⎩222tan (0)x y yx xρθ=+=≠ 在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4.常见曲线的极坐标方程曲线 图形 极坐标方程圆心在极点,半径为r 的圆(02)r ρθπ=≤<圆心为(,0)r ,半径为r 的圆2cos ()22r ππρθθ=-≤<圆心为(,)2r π,半径为r 的圆2sin (0)r ρθθπ≤<过极点,倾斜角为α的直线(1)()()R R θαρθπαρ=∈=+∈或 (2)(0)(0)θαρθπαρ=≥=+≥和过点(,0)a ,与极轴垂直的直线cos ()22a ππρθθ=-<<过点(,)2a π,与极轴平行的直线sin (0)a ρθθπ=<<注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2),(,),(,),ρθρπθρπθρπθ+-+--+都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=.二、参数方程 1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t =,把它代入普通方程,求出另一个变数与参数的关系()y g t =,那么()()x f t y g t =⎧⎨=⎩就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致.注:普通方程化为参数方程,参数方程的形式不一定唯一。
高中数学选修4—4(坐标系与参数方程)知识点总结

坐标系与参数方程知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x x y yλλϕμμ'=>⎧⎨'=>⎩的作用下,点P(x,y)对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.2.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系. (2)极坐标:设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数.特别地,当点M 在极点时,它的极坐标为(0,θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:点M直角坐标(,)x y 极坐标(,)ρθ互化公式cos sin x y ρθρθ=⎧⎨=⎩ 222tan (0)x y yx xρθ=+=≠ 在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4.常见曲线的极坐标方程曲线 图形 极坐标方程圆心在极点,半径为r 的圆(02)r ρθπ=≤<圆心为(,0)r ,半径为r 的圆2cos ()22r ππρθθ=-≤<圆心为(,)2r π,半径为r 的圆2sin (0)r ρθθπ≤<过极点,倾斜角为α的直线(1)()()R R θαρθπαρ=∈=+∈或 (2)(0)(0)θαρθπαρ=≥=+≥和过点(,0)a ,与极轴垂直的直线cos ()22a ππρθθ=-<<过点(,)2a π,与极轴平行的直线sin (0)a ρθθπ=<<注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2),(,),(,),ρθρπθρπθρπθ+-+--+都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=.二、参数方程 1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t =,把它代入普通方程,求出另一个变数与参数的关系()y g t =,那么()()x f t y g t =⎧⎨=⎩就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致.注:普通方程化为参数方程,参数方程的形式不一定唯一。
高中数学选修4—4(坐标系与参数方程)知识点总结

--坐标系与参数方程 知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x x y yλλϕμμ'=>⎧⎨'=>⎩的作用下,点P(x,y)对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 2.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系. (2)极坐标:设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:--点M直角坐标(,)x y 极坐标(,)ρθ互化公式cos sin x y ρθρθ=⎧⎨=⎩222tan (0)x y yx xρθ=+=≠ 曲线 图形 极坐标方程圆心在极点,半径为r 的圆(02)r ρθπ=≤<圆心为(,0)r ,半径为r 的圆2cos ()22r ππρθθ=-≤<圆心为(,)2r π,半径为r 的圆2sin (0)r ρθθπ≤< 过极点,倾斜角为α的直线(1)()()R R θαρθπαρ=∈=+∈或(2)(0)(0)θαρθπαρ=≥=+≥和过点(,0)a ,与极轴垂直的直线cos ()22a ππρθθ=-<<过点(,)2a π,与轴平行的直线注:由于(,),(,2ρθρπ点的直角坐标的唯一性明显不同示形式,只要求至少有一个能满足极坐标方程即可--,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=.二、参数方程 1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t =,把它代入普通方程,求出另一个变数与参数的关系()y g t =,那么()()x f t y g t =⎧⎨=⎩就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致.注:普通方程化为参数方程,参数方程的形式不一定唯一。
(推荐)高中数学选修4-4(坐标系与参数方程)知识点总结

坐标系与参数方程 知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x xy yλλϕμμ'=>⎧⎨'=>⎩的作用下,点P(x,y)对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 2.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标:设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数.特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:点M直角坐标(,)x y 极坐标(,)ρθ互化公式cos sin x y ρθρθ=⎧⎨=⎩222tan (0)x y yx xρθ=+=≠ 在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4.常见曲线的极坐标方程曲线 图形 极坐标方程圆心在极点,半径为r 的圆(02)r ρθπ=≤<圆心为(,0)r ,半径为r 的圆2cos ()22r ππρθθ=-≤<圆心为(,)2r π,半径为r 的圆2sin (0)r ρθθπ≤<过极点,倾斜角为α的直线(1)()()R R θαρθπαρ=∈=+∈或 (2)(0)(0)θαρθπαρ=≥=+≥和过点(,0)a ,与极轴垂直的直线cos ()22a ππρθθ=-<<过点(,)2a π,与极轴平行的直线sin (0)a ρθθπ=<<注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2),(,),(,),ρθρπθρπθρπθ+-+--+都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=.二、参数方程 1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t =,把它代入普通方程,求出另一个变数与参数的关系()y g t =,那么()()x f t y g t =⎧⎨=⎩就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致.注:普通方程化为参数方程,参数方程的形式不一定唯一。
高中数学选修4—4(坐标系与参数方程)知识点总结

坐标系与参数方程知识点1.平面直角坐标系中的坐标伸缩变换设点 P(x,y) 是平面直角坐标系中的任意一点x x ( 0),在变换:y (的作用y 0)下 , 点 P(x,y) 对应到点 P ( x , y ) ,称为平面直角坐标系中的坐标伸缩变换, 简称伸缩变换.2. 极坐标系的概念(1) 极坐标系如图所示, 在平面内取一个定点O ,叫做极点,自极点 O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向 ), 这样就建立了一个极坐标系 .注: 极坐标系以角这一平面图形为几何背景, 而平面直角坐标系以互相垂直的两条数轴为几何背景 ; 平面直角坐标系内的点与坐标能建立一一对应的关系, 而极坐标系则不可. 但极坐标系和平面直角坐标系都是平面坐标系.(2) 极坐标设 M是平面内一点 , 极点O与点 M的距离 |OM|叫做点 M的极径 , 记为; 以极轴Ox为始边, 射线OM为终边的角xOM 叫做点M的极角,记为. 有序数对(, ) 叫做点M的极坐标,记作M(, ).一般地 , 不作特殊说明时, 我们认为0,可取任意实数.特别地 , 当点M在极点时 , 它的极坐标为(0,)(∈ R).和直角坐标不同, 平面内一个点的极坐标有无数种表示.如果规定0,02, 那么除极点外, 平面内的点可用唯一的极坐标( ,) 表示; 同时 , 极坐标(, ) 表示的点也是唯一确定的.3. 极坐标和直角坐标的互化(1) 互化背景 : 把直角坐标系的原点作为极点 ,x 轴的正半轴作为极轴 , 并在两种坐标系中取相同的长度单位 , 如图所示 :(2) 互化公式 : 设M是坐标平面内任意一点 , 它的直角坐标是(x, y) , 极坐标是( , ) (0),于是极坐标与直角坐标的互化公式如表:点 M直角坐标( x, y)极坐标(, )x cos 2 x2 y2互化公式y( x 0) y sin tanx在一般情况下 , 由tan 确定角时 , 可根据点M所在的象限最小正角 .4. 常见曲线的极坐标方程曲线图形极坐标方程圆心在极点, 半径r (0 2 )为 r 的圆圆心为 (r ,0) ,半径2r cos ( ) 为 r 的圆2 2圆心为 (r , ) ,半22r sin(0)径为 r 的圆过极点 , 倾斜角为 (1) ( R)或 ( R)的直线(2)(0)和( 0)过点 (a,0) , 与极轴cosa()垂直的直线22过 点 (a, ) , 与 极2sina(0 )轴平行的直线注 : 由于平面上点的极坐标的表示形式不唯一, 即( , ),( ,2),( ,),( , ), 都表示同一点的坐标, 这与点的直角坐标的唯一性明显不同. 所以对于曲线上的点的极坐标的多种表示形式 , 只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,点M( ,)可以表示为4 4( ,2 )或( , 4 2 )或(- ,5)等多种形式 ,其中,只有 (, ) 的极坐标满足方 4 44 4 44 4程.二、参数方程1. 参数方程的概念一般地 , 在平面直角坐标系中 , 如果曲线上任意一点的坐标x, y 都是某个变数 t 的函数 x f (t )M ( x, y) 都在这条曲线上 ,y① , 并且对于 t 的每一个允许值 , 由方程组①所确定的点g(t )那么方程①就叫做这条曲线的参数方程, 联系变数 x, y 的变数 t 叫做参变数 , 简称参数 , 相对于参数方程而言 , 直接给出点的坐标间关系的方程叫做普通方程.2. 参数方程和普通方程的互化(1) 曲线的参数方程和普通方程是曲线方程的不同形式 , 一般地可以通过消去参数而从参数方程得到普通方程 .(2) 如果知道变数 x, y 中的一个与参数 t 的关系 , 例如 x f (t) , 把它代入普通方程 , 求 出另一个变数与参数的关系y g(t) , 那么x f (t )y就是曲线的参数方程 , 在参数方程与g(t )普通方程的互化中 , 必须使 x, y 的取值范围保持一致 .注: 普通方程化为参数方程,参数方程的形式不一定唯一。
(完整)高中数学选修4-4-极坐标与参数方程-知识点与题型,推荐文档

选做题部分极坐标系与参数方程一、极坐标系1. 极坐标系与点的极坐标(1) 极坐标系:如图4 —4—1所示,在平面内取一个』点0,叫做极点,自极点0引一条射线Ox叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.(2) 极坐标:平面上任一点M的位置可以由线段0M的长度p和从Ox到0M的角度9来刻画,这两个数组成的有序数对M的极坐标.其中p称为点M的极径,9称为点M的极角.2.极坐标与直角坐标的互化点M直角坐标(x,y)极坐标(p, 9互化公式题型一极坐标与直角坐标的互化1、已知点P的极坐标为(..2,—),则点P的直角坐标为 ()4A. (1, 1)B. (1, -1 )C. (-1,1)D. (-1,-1 )2、设点P的直角坐标为(3,3),以原点为极点,实轴正半轴为极轴建立极坐标系(0 2 ),则点P的极坐标为( )A. (3.2, —) B . ( 3 2, —) C . (3, — ) D . ( 3, — )4 4 4 43•若曲线的极坐标方程为p= 2sin 0+ 4cos 9,以极点为原点,极轴为x轴正半轴建立直角坐标系,则该曲线的直角坐标方程为___________ .4.在极坐标系中,过点(1,0)并且与极轴垂直的直线方程是( )A.p= cos 0B.p= sin 9 C . p cos 0= 1 D . p sin 0= 15. __________________________________________ 曲线C的直角坐标方程为x2+ y2—2x = 0,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为_________________________________________ .n6.在极坐标系中,求圆p= 2cos 9与直线9= 4(p>0)所表示的图形的交点的极坐标.题型二极坐标方程的应用由极坐标方程求曲线交点、距离等几何问题时,如果不能直接用极坐标解决,可先转化为直角坐标方程,然后求解.1. 在极坐标系中,已知圆C经过点PC 2,专),圆心为直线P sin B—n J与极轴的交点,求圆C的直角坐标方程.n2. 圆的极坐标方程为p= 4cos B,圆心为C,点P的极坐标为4,-3,则|CP| = _________ .n3. 在极坐标系中,已知直线I的极坐标方程为p sin 0 +石=1,圆C的圆心的极坐标n是C1,4,圆的半径为1.(i)则圆C的极坐标方程是 __________ ;(ii)直线I被圆C所截得的弦长等于 _____________n4. 在极坐标系中,已知圆C:p= 4cos 0被直线I : p sin 0—"6 = a截得的弦长为2念,则实数a的值是__________ .、参数方程1.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式•一般地,可以通过消去参数而 从参数方程得到普通方程.⑵如果知道变数x , y 中的一个与参数t 的关系,例如x = f(t),把它代入普通方程,求x = f t ,出另一个变数与参数的关系 y = g(t),那么,就是曲线的参数方程.y = g t2.题型一参数方程与普通方程的互化【例1】把下列参数方程化为普通方程:,1x = 1 + ,⑵y = 5 +题型二直线与圆的参数方程的应用x = 1 + t ,x = 2cos 0+ 2,1、已知直线I 的参数方程为(参数t € R),圆C 的参数方程为(参y = 4— 2ty = 2sin 0数0€ [0,2 n ])求直线I 被圆C 所截得的弦长.卜1+导2、曲线C 的极坐标方程为:p =acos 0( a > 0),直线I 的参数方程为:i _If(1)求曲线C 与直线I 的普通方程;(2)若直线I 与曲线C 相切,求a 值.x = 3+ cos 0, ⑴ y = 2-sin 03、在直角坐标系xoy中,曲线C的参数方程为「些曲",(a为参数),以原点OI y=sinCT为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为P sin (日+号)二吋(I)求曲线C的普通方程与曲线C2的直角坐标方程;(□)设P为曲线C上的动点,求点P到C2上点的距离最小值.综合应用1、曲线2 5t 1 2t(t 为参数)与坐标轴的交点是(2 1 1 1 5A (0,—)、(一,0)B (0, —)、(一,0)C (0, 4)、(8,0)D (0, —)、(8,0)5 2 5 2 9/ 2 si n 23、参数万程(为参数)化为普通方程为y sin 2A . y x 2 B.y x 2C. y x 2(2 x 3)D. y x 2(0 y 1)3.判断下列结论的正误.(2)若点P 的直角坐标为(1, 3),则点P 的一个极坐标是(2,—石)((3)在极坐标系中,曲线的极坐标方程不是唯一的 ( )(1)平面直角坐标系内的点与坐标能建立一一对应关系,在极坐标系中点与坐标也是 一对应关系(4.参数方1t (t为参数)表示的曲线是(A.一条直5•与参数方程为B.两条直线C. 一条射线(t为参数)等价的普通方程为(D •两条射线A. x22y_4B . x22y1(0 x 1)4C. x21(0 2) D . x22y1(0 x 1,0 y 2)4x15.参数方程y tan为参数所表示的曲线是cotA.直线B.两条射线C .线段 D.圆16.下列参数方程t是参数)与普通方程 2y x表示同一曲线的方程是:x tA. rB.y t x si n21 ysintC.1 cos2t x1 cos2ty tant8、已知曲线C 的极坐标方程是2cos 2sin 0,以极点为平面直角坐标系的原8. 在极坐标系有点 M(3, 3),若规定极径 V 0,极角 [0,2],则M 的极坐标为 ________ ;若规定极径 V 0,极角 (-,),贝U M 的极坐标为 __________________ . _________39. ORF 2的一个顶点在极点 0,其它两个顶点分别为R 5,— , P 2 4 —,则 ORP 24 12的面积为 ______________ 。
(完整)高中数学选修4—4(坐标系与参数方程)知识点总结,推荐文档

坐标系与参数方程 知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换的作用下,点P(x,y)对应到点,称为平面直角坐标系中的坐标(0):(0)x x y yλλϕμμ'=>⎧⎨'=>⎩A A (,)P x y '''ϕ伸缩变换,简称伸缩变换.2.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点,叫做极点,自极点引一条射线,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正O O Ox 方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标:设M 是平面内一点,极点与点M 的距离|OM|叫做点M 的极径,记为;以极轴为始边,射线为终边的角叫做点M 的极角,记O ρOx OM xOM ∠为.有序数对叫做点M 的极坐标,记作.θ(,)ρθ(,)M ρθ一般地,不作特殊说明时,我们认为可取任意实数.0,ρ≥θ特别地,当点在极点时,它的极坐标为(0, )(∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.M θθ如果规定,那么除极点外,平面内的点可用唯一的极坐标表示;同时,极坐标表示的点也是唯一确定的.0,02ρθπ>≤<(,)ρθ(,)ρθ3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设是坐标平面内任意一点,它的直角坐标是,极坐标是(),于是极坐标与直角坐标的互化公式如表:M (,)x y (,)ρθ0ρ≥点M 直角坐标(,)x y 极坐标(,)ρθ互化公式cos sin x y ρθρθ=⎧⎨=⎩222tan (0)x y y x xρθ=+=≠在一般情况下,由确定角时,可根据点所在的象限最小正角.tan θM 4.常见曲线的极坐标方程曲线图形极坐标方程圆心在极点,半径为的圆r (02)r ρθπ=≤<圆心为,半径(,0)r 为的圆r 2cos ()22r ππρθθ=-≤<圆心为,半(,)2r π径为的圆r 2sin (0)r ρθθπ≤<过极点,倾斜角为的直线α(1)()()R R θαρθπαρ=∈=+∈或(2)(0)(0)θαρθπαρ=≥=+≥和过点,与极轴(,0)a 垂直的直线cos ()22a ππρθθ=-<<过点,与极(,)2a π轴平行的直线sin (0)a ρθθπ=<<注:由于平面上点的极坐标的表示形式不唯一,即都表示同一点的坐标,这与点的直角坐标的唯一性明(,),(,2),(,),(,),ρθρπθρπθρπθ+-+--+显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程点可以表示为,ρθ=(,)44M ππ等多种形式,其中,只有的极坐标满足方程.5(,2)(,2),444444ππππππππ+-或或(-)(,)44ππρθ=二、参数方程1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标都是某个变数的函数①,并且对于的每一个允许值,由方程组①所确定的,x y t ()()x f t y g t =⎧⎨=⎩t 点都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数的变数叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐(,)M x y ,x y t 标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数中的一个与参数的关系,例如,把它代入普通方程,求出另一个变数与参数的关系,那么就是曲线,x y t ()x f t =()y g t =()()x f t y g t =⎧⎨=⎩的参数方程,在参数方程与普通方程的互化中,必须使的取值范围保持一致.,x y 注:普通方程化为参数方程,参数方程的形式不一定唯一。
高中数学选修4—4(坐标系与参数方程)知识点总结

坐标系与参数方程 知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x x y yλλϕμμ'=>⎧⎨'=>⎩的作用下,点P(x,y)对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换. 2.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系. (2)极坐标:设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=.二、参数方程 1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t =,把它代入普通方程,求出另一个变数与参数的关系()y g t =,那么()()x f t y g t =⎧⎨=⎩就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致.注:普通方程化为参数方程,参数方程的形式不一定唯一。
高中数学选修4—4(坐标系与参数方程)知识点总结

坐标系与参数方程 知识点1.平面直角坐标系中的坐标伸缩变换设点P(x,y)是平面直角坐标系中的任意一点,在变换(0):(0)x xy yλλϕμμ'=>⎧⎨'=>⎩g g 的作用下,点P(x,y)对应到点(,)P x y ''',称ϕ为平面直角坐标系中的坐标伸缩变换,简称伸缩变换.2.极坐标系的概念 (1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数. 特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.3.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:点M直角坐标(,)x y极坐标(,)ρθ互化公式cos sin x y ρθρθ=⎧⎨=⎩222tan (0)x y yx xρθ=+=≠ 在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 4.常见曲线的极坐标方程 曲线图形极坐标方程圆心在极点,半径为r 的圆(02)r ρθπ=≤<圆心为(,0)r ,半径为r 的圆2cos ()22r ππρθθ=-≤<圆心为(,)2r π,半径为r 的圆2sin (0)r ρθθπ≤<过极点,倾斜角为α的直线(1)()()R R θαρθπαρ=∈=+∈或 (2)(0)(0)θαρθπαρ=≥=+≥和过点(,0)a ,与极轴垂直的直线cos ()22a ππρθθ=-<<过点(,)2a π,与极轴平行的直线sin (0)a ρθθπ=<<注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2),(,),(,),ρθρπθρπθρπθ+-+--+都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=.二、参数方程 1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标,x y 都是某个变数t 的函数()()x f t y g t =⎧⎨=⎩①,并且对于t 的每一个允许值,由方程组①所确定的点(,)M x y 都在这条曲线上,那么方程①就叫做这条曲线的参数方程,联系变数,x y 的变数t 叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数,x y 中的一个与参数t 的关系,例如()x f t =,把它代入普通方程,求出另一个变数与参数的关系()y g t =,那么()()x f t y g t =⎧⎨=⎩就是曲线的参数方程,在参数方程与普通方程的互化中,必须使,x y 的取值范围保持一致.注:普通方程化为参数方程,参数方程的形式不一定唯一。
高中数学选修4-4-极坐标与参数方程-知识点与题型

选做题部分 极坐标系与参数方程一、极坐标系1.极坐标系与点的极坐标(1)极坐标系:如图4-4-1所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.(2)极坐标:平面上任一点M 的位置可以由线段OM 的长度ρ和从Ox 到OM 的角度θ来刻画,这两个数组成的有序数对(ρ,θ)称为点M 的极坐标.其中ρ称为点M 的极径,θ称为点M 的极角. 2.极坐标与直角坐标的互化点M 直角坐标(x ,y ) 极坐标(ρ,θ)互化公式题型一 极坐标与直角坐标的互化1、已知点P 的极坐标为)4,2(π,则点P 的直角坐标为 ( )A.(1,1)B.(1,-1)C.(-1,1)D.(-1,-1)2、设点P 的直角坐标为(3,3)-,以原点为极点,实轴正半轴为极轴建立极坐标系(02)θπ≤<,则点P 的极坐标为( )A .3)4πB .5()4π-C .5(3,)4πD .3(3,)4π-3.若曲线的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x 轴正半轴建立直角坐标系,则该曲线的直角坐标方程为________.4.在极坐标系中,过点(1,0)并且与极轴垂直的直线方程是( ) A .ρ=cos θ B .ρ=sin θ C .ρcos θ=1 D .ρsin θ=15.曲线C 的直角坐标方程为x 2+y 2-2x =0,以原点为极点,x 轴的正半轴为极轴建立极坐标系,则曲线C 的极坐标方程为________.6. 在极坐标系中,求圆ρ=2cos θ与直线θ=π4(ρ>0)所表示的图形的交点的极坐标.题型二 极坐标方程的应用由极坐标方程求曲线交点、距离等几何问题时,如果不能直接用极坐标解决,可先转化为直角坐标方程,然后求解.1.在极坐标系中,已知圆C 经过点P(2,π4),圆心为直线ρsin ⎝ ⎛⎭⎪⎫θ-π3=-32与极轴的交点,求圆C 的直角坐标方程.2.圆的极坐标方程为ρ=4cos θ,圆心为C ,点P 的极坐标为⎝ ⎛⎭⎪⎫4,π3,则|CP|=________.3.在极坐标系中,已知直线l 的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ+π4=1,圆C 的圆心的极坐标是C ⎝ ⎛⎭⎪⎫1,π4,圆的半径为1.(i)则圆C 的极坐标方程是________; (ii)直线l 被圆C 所截得的弦长等于________.4.在极坐标系中,已知圆C :ρ=4cos θ被直线l :ρsin ⎝ ⎛⎭⎪⎫θ-π6=a 截得的弦长为23,则实数a 的值是________.二、参数方程1.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式.一般地,可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数x ,y 中的一个与参数t 的关系,例如x =f (t ),把它代入普通方程,求出另一个变数与参数的关系y =g (t ),那么,⎩⎪⎨⎪⎧x =f t ,y =gt就是曲线的参数方程.2.常见曲线的参数方程和普通方程 点的轨迹普通方程参数方程直线y -y 0=tan α(x -x 0)⎩⎪⎨⎪⎧x =x 0+t cos αy =y 0+t sin α (t 为参数)题型一 参数方程与普通方程的互化 【例1】把下列参数方程化为普通方程: (1)⎩⎪⎨⎪⎧x =3+cos θ,y =2-sin θ;(2)⎩⎪⎨⎪⎧x =1+12t ,y =5+32t .题型二 直线与圆的参数方程的应用1、已知直线l 的参数方程为⎩⎪⎨⎪⎧x =1+t ,y =4-2t (参数t ∈R ),圆C 的参数方程为⎩⎪⎨⎪⎧x =2cos θ+2,y =2sin θ(参数θ∈[0,2π]),求直线l 被圆C所截得的弦长.2、曲线C的极坐标方程为:ρ=acosθ(a>0),直线l的参数方程为:(1)求曲线C与直线l的普通方程;(2)若直线l与曲线C相切,求a值.3、在直角坐标系xoy中,曲线C1的参数方程为,(α为参数),以原点O为极点,x轴正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为.(Ⅰ)求曲线C1的普通方程与曲线C2的直角坐标方程;(Ⅱ)设P为曲线C1上的动点,求点P到C2上点的距离最小值.综合应用 1、曲线25()12x tt y t=-+⎧⎨=-⎩为参数与坐标轴的交点是( )A 21(0,)(,0)52、 B 11(0,)(,0)52、 C (0,4)(8,0)-、 D 5(0,)(8,0)9、3、参数方程222sin sin x y θθ⎧=+⎪⎨=⎪⎩(θ为参数)化为普通方程为( ) A .2y x =- B .2y x =+ C .2(23)y x x =-≤≤ D .2(01)y x y =+≤≤ 3.判断下列结论的正误.(1)平面直角坐标系内的点与坐标能建立一一对应关系,在极坐标系中点与坐标也是一一对应关系( )(2)若点P 的直角坐标为(1,-3),则点P 的一个极坐标是(2,-π3)( )(3)在极坐标系中,曲线的极坐标方程不是唯一的( ) (4)极坐标方程θ=π(ρ≥0)表示的曲线是一条直线( )4.参数方程为1()2x t t t y ⎧=+⎪⎨⎪=⎩为参数表示的曲线是( )A .一条直线B .两条直线C .一条射线D .两条射线5.与参数方程为)x t y ⎧=⎪⎨=⎪⎩为参数等价的普通方程为( ) A .214y +=2x B .21(01)4y x +=≤≤2xC .21(02)4y y +=≤≤2x D .21(01,02)4y x y +=≤≤≤≤2x15.参数方程()为参数θθθ⎩⎨⎧+==cot tan 2y x 所表示的曲线是( )A .直线B .两条射线C .线段D .圆16.下列参数方程(t 是参数)与普通方程y x 2=表示同一曲线的方程是: ( )A .x t y t ==⎧⎨⎩2B .x t y t ==⎧⎨⎩sin sin 2C .x t y t ==⎧⎨⎪⎩⎪D .⎪⎩⎪⎨⎧=+-=t y t t x tan 2cos 12cos 13.由参数方程()⎪⎭⎫⎝⎛<<-⎩⎨⎧=-=202tan 21sec 22ππθθθ为参数,y x 给出曲线在直角坐标系下的方程是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选修4—4 极坐标与参数方程
一、伸缩变换
设),(y x P 是平面直角坐标系中任意一点,在变换⎩⎨⎧='='y
y x x μλϕ: )0()0(>>μλ的作用下,点),(y x P 对应),(y x P ''',称ϕ为平面直角坐标系中的伸缩变换。
练习
1.将1422=+y x 的横坐标压缩为原来的2,纵坐标伸长为原来的2
1倍,则曲线的方程变为 。
2.在平面直角坐标系中,方程122=+y x 所对应的图形经过伸缩变换⎩⎨
⎧='='y
y x x 32,后的图形所对应的方程是 .
二、极坐标
(一)极坐标系与极坐标
1、极坐标系:在平面上取一个定点O ,由O 点出发的一条射线Ox 一个长度单位及计算
角度的正方向(通常取逆时针方向),合称为一个极坐标系.O 点称为极点,Ox 称为极轴.
2、极坐标:平面上任一点M 的位置可以由线段OM 的长度ρ和从Ox 到OM 的角度θ
来刻画.这两个数组成的有序数对),(θρ称为点M 的极坐标.ρ称为极径,θ
称为极角.
注:①在通常情况下,总认为0≥ρ,只在事先说明的情况下,才允许取0<ρ; ①极点O 的坐标为:),0(θ)(R ∈θ
①点),(θρ与),(θπρ+关于极点O 对称;
点),(θρ与),(θρ-关于极轴对称
①点),(θρ,)2,(θπρ+k ,)2.(ππρ+-k (允许ρ小于0时)表示同一点.
(二)极坐标与直角坐标的关系
设M 为平面上的点,它的直角坐标为),(y x ,极坐标为),(θρ,关系如下:
⎪⎪⎪⎩
⎪⎪⎪⎨⎧=+===x y y x y x θρθρθρtan sin cos 2
22)0(≠x 注:在极坐标系中,αθ=)0(≥ρ表示以极点为起点的一条射线;αθ=)(R ∈ρ表示以极点为起点的一条直线.
练习
1、点M 的直角坐标为)1,3(--化为极坐标为 .
2、极坐标为(1,π)的点M 的直角坐标为 .
3、将以下极坐标方程化为对应的直角坐标方程
(1)ρ=2cosθ﹣4sinθ (2)ρsin 2θ=4cosθ
(3)ρ=4cosθ (4)1)3cos(=-
πρx
(5)ααρ222cos 3sin 42+=
(6)34πθ= )(R ∈ρ
(7)2=ρ
4、在直角坐标系xOy 中,圆C 的直角坐标方程为1)1(22=+-y x ,以O 为极点,x 轴的非负半轴为极轴建立极坐标系.
(1)求圆C 的极坐标方程;
(2)直线l 的极坐标方程是33)3sin(2=+
πθρ,射线OM :3πθ=与圆C 的交点为P O ,,
与直线l 的交点为Q ,求线段PQ 的长.
5、在直角坐标系xOy 中,直线1C :2-=x ,圆2C :1)2()1(22=-+-y x ,以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系.
(1)求1C 、2C 的极坐标方程;
(2)若直线3C 的极坐标方程为4πθ=)(R ∈ρ,设2C 与3C 的交点为N M ,,求MN C 2∆的面积.
三、参数方程
(一)参数方程:
在平面上取定了一个直角坐标系xOy ,把坐标y x ,表示为第三个变量t 的函数⎩
⎨⎧==)()(t g y t f x b t a ≤≤,如果对于t 的每一个值(b t a ≤≤),由方程组所确定的点),(y x M 都在一条曲线上;而这条曲线上的任一点),(y x M 都可由t 的某个值通过方程组得到,称方程组就叫做这条曲线的参数方程,其中,变量t 称为参数.
(二)直线的参数方程
1、直线的标准参数方程:直线l 过点),(00y x M ,倾斜角为α的参数方程为
⎩⎨⎧+=+=α
αsin cos 00t y y t x x 推导如下:设直线的点斜式方程为:)(00x x k y y -=-,其中αtan =k )2(πα≠
代入得
)(tan 00x x y y -=-α )(cos sin 00x x y y -=
-α
α 即ααsin cos 00y y x x -=-,
令上式的比值为t ,整理得⎩
⎨⎧+=+=ααsin cos 00t y y t x x 2、t 的几何意义:表示直线上任一点A 到定点0M 的距离.
①当点A 在0M 的上方时,0>t ;
①当点A 在0M 的下方时,0<t ;
①当点A 与0M 重合时,0=t ;
3、结论:直线l 的参数方程为⎩
⎨⎧+=+=ααsin cos 00t y y t x x )(为参数t ,其中),(00y x M ,B A ,为直线l 上的任一 点,且B A ,对应的参数分别为21,t t
①A 到0M 的距离为1t ,B 到0M 的距离为2t
①B A ,两点之间的距离为:21t t AB -=
①点B A ,中点对应的参数为:2
21t t + ①0M 为B A ,中点时:021=+t t ①⎪⎩⎪⎨⎧+⋅-+=-=+=+2
1212212121004)(t t t t t t t t t t B M A M )0()0(2121>⋅<⋅t t t t 2100t t B M A M ⋅=⋅
4、运用直线l 的标准参数方程求弦长和弦的中点坐标(直线l 与曲线相交于不同的两点时): 将直线l 的标准参数方程⎩⎨⎧+=+=α
αsin cos 00t y y t x x 代入圆锥曲线方程,得到关于t 的二次方程,
得到⎪⎩⎪⎨⎧⋅+>∆2
1210t t t t ,所以弦长=21221214)(t t t t t t ⋅-+=-,弦的中点对应的参数为221t t +代入直线直线l 的标准参数方程⎩⎨
⎧+=+=α
αsin cos 00t y y t x x 中,得到弦的中点坐标.
5、直线l 的一般参数方程: 过点),(00y x M ,斜率a b k =的直线参数方程为:⎩
⎨⎧+=+=bt y y at x x 00 )(为参数t。
