二次函数与相似三角形综合题20160203
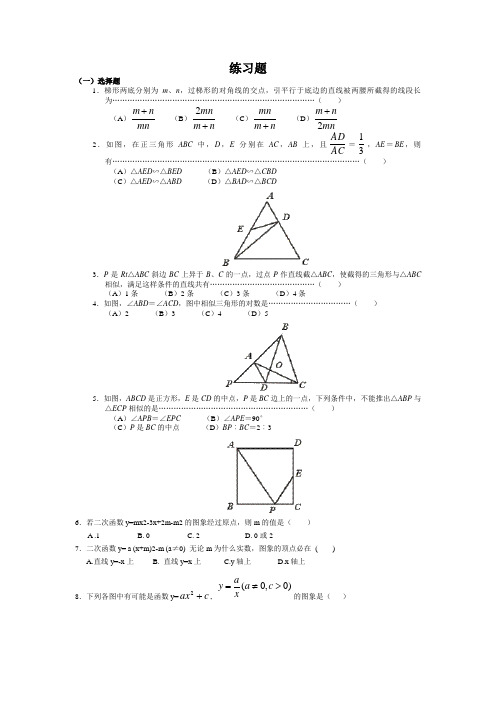
中考数学总复习《二次函数与相似三角形问题综合》专项检测卷(带答案)

中考数学总复习《二次函数与相似三角形问题综合》专项检测卷(带答案)学校:___________姓名:___________班级:___________考号:___________1.如图,在平面直角坐标系中,抛物线2y x bx c =++与x 轴交于点()2,0A -和()1,0B .(1)求抛物线的函数表达式;(2)直线43y x h =-+经过点B ,交抛物线于另一点C .P 是线段BC 上一点,过点P 作直线PQ y ∥轴交抛物线于点Q ,且PB PQ =,求点P 的坐标;(3)M ,N 是抛物线上的动点(不与点B 重合),直线BM ,BN 分别交y 轴于点E ,F ,若EBF EOB ∽△△,求证:直线MN 经过一个定点.2.如题,在平面直角坐标系xOy 中,抛物线22y ax bx =++与x 轴交于点()1,0A -,点()4,0B ,与y 轴交于点C ,连接AC ,BC .(1)求抛物线的解析式.(2)点D 为抛物线的对称轴上一动点,当ACD 周长最小时,求点D 的坐标.(3)点E 是OC 的中点,射线AE 交抛物线于点F ,P 是抛物线上一动点,过点P 作y 轴的平行线,交射线AF 与点G ,是否存在点P 使得PFG △与AOE △相似?若存在,求出点P 的坐标;若不存在,请说明理由.3.如图,在平面直角坐标系中,抛物线212y x bx c =-++与x 轴交于点()2,0A -和()4,0B ,与y 轴交于点C ,连接BC .(1)求抛物线的解析式;(2)P 是第一象限内抛物线上的一个动点,过点P 作直线l x ⊥轴于点(),0M m ,交BC 于点N ,连接CM PB PC ,,.PCB 的面积记为1S ,BCM 的面积记为2S ,当12S S 时,求m 的值;(3)在(2)的条件下,点Q 在抛物线上,直线MQ 与直线BC 交于点H ,当HMN △与BCM 相似时,请直接写出点Q 的坐标.4.如图,在平面直角坐标系中,已知抛物线214y x bx c =-++与x 轴分别相交于()2,0A -,()8,0B 两点.(1)求该抛物线的解析式;(2)点D 是第一象限内该抛物线上的动点,过点D 作x 轴的垂线交BC 于点E ,交x 轴于点F . ①求DE BF +的最大值;①若G 是AC 的中点,以点C D E 为顶点的三角形与AOG 相似 求点D 的坐标. 5.如图 抛物线223y x x =-++交x 轴于A B 两点 交y 轴于点C 连接AC BC .(1)求ABC 的面积;(2)点M 为y 轴上一点 是否存在点M 使得MBC 与ABC 相似?若存在 请求出点M 的坐标;若不存在 请说明理由;(3)点P 为抛物线上一点(点P 与点B 不重合) 且使得PAC △中有一个角是45︒ 请直接写出点P 的坐标.6.在平面直角坐标系xOy 中 把与x 轴交点相同的二次函数图象称为“共根抛物线”.如图 抛物线1L :245y x x =-++的顶点为D 交x 轴于点A B (点A 在点B 左侧) 交y 轴于点C .抛物线2L 与1L 是“共根抛物线” 其顶点为P .(1)若抛物线2L 经过点()38-,求抛物线L 1对应的函数关系式; (2)连接BC .设点Q 是抛物线1L 上且位于其对称轴右侧的一个动点 若DPQ 与BOC 相似 求其“共根抛物线”2L 的顶点Р的坐标.7.如图 直线23y x c =-+与x 轴交于点()3,0A 与y 轴交于点B 抛物线243y x bx c =-++经过点A B .(1)求点B 的坐标和抛物线的解析式;(2)(),0M m 为x 轴上一动点 过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P N .①点M 在线段OA 上运动 若以B P N 为顶点的三角形与APM ∆相似 求点M 的坐标; ①点M 在x 轴上自由运动 若三个点M P N 中恰有一点是其它两点所连线段的中点(三点重合除外) 则称M P N 三点为“共谐点”.请直接写出使得M P N 三点成为“共谐点”的m 的值.8.如图 二次函数2y ax bx c =++(0a <)的图象与x 轴交于()1,0A - B 两点 与y 轴交于点C 已知3OB OA = OC OB =.(1)求该二次函数的表达式;(2)点M 为抛物线对称轴上一动点 是否存在点M 使得BM CM -有最大值 若存在 请直接写出其最大值及此时点M 坐标 若不存在 请说明理由.(3)连接AC P 为第一象限内抛物线上一点 过点P 作PD x ⊥轴 垂足为D 连接PA 若PDA 与COA 相似 请求出满足条件的P 点坐标:若没有满足条件的P 点 请说明理由.9.如图 在平面直角坐标系中 二次函数的图象交坐标轴于()20A -,()40B , ()08C ,三点 点P 是直线BC 上方抛物线上的一个动点.(1)求这个二次函数的解析式;(2)动点P 运动到什么位置时 PBC 的面积最大 求此时P 点坐标及PBC 面积的最大值;(3)在y 轴上是否存在点Q 使以O B Q 为顶点的三角形与AOC 相似?若存在 请直接写出点Q 的坐标;若不存在 请说明理由.10.如图 已知抛物线经过()40A ,()10B , ()02C -,三点.(1)求该抛物线的解析式;(2)若P 是直线4x =右侧的抛物线上一动点 过点P 作PM x ⊥轴 垂足为M 是否存在点P 使得以A P M 为顶点的三角形与OAC 相似?若存在 请求出符合条件的点P 的坐标;若不存在 请说明理由11.综合与探究:如图 在平面直角坐标系中 抛物线24y ax bx =+-与x 轴交于点()1,0A - ()3,0B 与y 轴交于点C 连接BC .若在第四象限的抛物线上取一点M 过点M 作MD x ⊥轴于点D 交直线BC 于点E .(1)求抛物线的表达式;(2)试探究抛物线上是否存在点M 使ME 有最大值?若存在 求出点M 的坐标和ME 的最大值;若不存在 请说明理由;(3)连接 CM 试探究是否存在点M 使得以M C E 为顶点的三角形和BDE △相似?若存在 请求出点M 的坐标;若不存在 请说明理由.12.综合与探究如图 抛物线213222y x x =-++的图象与x 轴交于A B 两点 点A 在点B 的左侧 与y 轴交于点C 连接BC .(1)求点B C 的坐标.(2)C '是点C 关于抛物线对称轴的对称点 D 是BC 线段上一点 已知25BD BC = 求直线C D '的解析式.(3)若C 关于x 轴的对称点为M 连接BM N 是线段AB 上的动点 过点N 作x 轴的垂线交抛物线于点P 交直线BM 于点Q 当以B P Q 为顶点的三角形与BOM 相似时 请直接写出点P 的坐标.13.如图 抛物线26y ax bx =+-与y 轴交于点A 与x 轴交于点()3,0B - ()1,0C P 是线段AB 下方抛物线上的一个动点 过点Р作x 轴的垂线 交x 轴于点H 交AB 于点D .设点P 的横坐标为()30t t -<<.(1)求抛物线的解析式.(2)用含t 的式子表示线段PD 的长 并求线段PD 长度的最大值.(3)连接AP 当DPA 与DHB △相似时 求点P 的坐标.14.如图 抛物线经过点()2,0A - ()3,3B -和坐标原点O 顶点为C .(1)求抛物线的表达式;(2)求证:BOC 是直角三角形;(3)若点P 是抛物线上第一象限内的一个动点 过点P 作PM x ⊥轴 垂足为M 是否存在点P 使得以P M A 为顶点的三角形与BOC 相似?若存在 求出点P 的坐标;若不存在 请说明理由.15.在平面直角坐标系中 抛物线()26160y ax ax a a =--≠与x 轴的两个交点分别为A B 、与y 轴相交于点C 连接BC 已知点()04C ,.(1)求A B 、两点坐标和抛物线的解析式;(2)设点P 是抛物线上在第一象限内的动点(不与C B 、重合) 过点P 作PD BC ⊥ 垂足为点D .①点P 在运动过程中 线段PD 的长度是否存在最大值?若存在 求出最大值以及此时点D 的坐标;若不存在 请说明理由:①当以P D C 、、为顶点的三角形与COA 相似时 求点P 的坐标.参考答案:1.(1)解:将()2,0A - ()1,0B 代入2y x bx c =++得:()2202201b c b c⎧=--+⎪⎨=++⎪⎩ 解得:12=⎧⎨=-⎩b c ∴抛物线的函数表达式为:22y x x =+-;(2)解:将()1,0B 代入43y x h =-+ 得:4013h =-⨯+ 解得:43h = ∴直线BC 的解析式为:4433y x =-+ 联立直线BC 与抛物线得:244332y x y x x ⎧=-+⎪⎨⎪=+-⎩ 解得:103529x y ⎧=-⎪⎪⎨⎪=⎪⎩或10x y =⎧⎨=⎩ 1052,39C ⎛⎫∴- ⎪⎝⎭设44,33P m m⎛⎫-+⎪⎝⎭则()2,2Q m m m+-PB PQ=()()2224444123333m m m m m⎛⎫⎛⎫-+-+-+-+-⎪ ⎪⎝⎭⎝⎭()22257101933m m m-=--+即()257101333m m m--=--+或()257101333m m m-=--+解得:1m=或53m=-或5m=-P是线段BC上一点()1,0B1052,39C⎛⎫-⎪⎝⎭53m∴=-532,39P⎛⎫∴-⎪⎝⎭;(3)解:设()()()2211122212,2,,21,1 M x x x N x x x x x+-+-≠≠直线MN的解析式为y kx n=+即2111222222x x kx nx x kx n⎧+-=+⎨+-=+⎩解得:()121212k x xn x x=++⎧⎨=-+⎩∴直线MN的解析式为:()()121212y x x x x x=++-+直线BM的解析式为y k x n''=+即21112x x k x nk n⎧+-=+'=+'''⎨⎩解得:()1122k xn x=+⎧⎨=-+''⎩∴直线BM的解析式为:()()1122y x x x=+-+当0x=时()12y x=-+()10,2E x∴--直线BN的解析式为y k x n''''=+即222220x x k x n k n '''⎧+-=+⎨=+'''''⎩解得:()2222k x n x =+⎧⎨=-+''''⎩∴直线BN 的解析式为:()()2222y x x x =+-+当0x =时 ()22y x =-+()20,2F x ∴--12EF x x ∴=-EBF EOB ∽△△EF BE BE OE∴= 112BE OE x ==+()21121122x x x x ∴++=-⋅+即()221111212542x x x x x x x ++=+-- ∴()121252x x x x =--+∴()()()()()()121212121212125223y x x x x x x x x x x x x x x ⎡⎤=++-+=++---+=++++⎣⎦ ∴当2x =-时 1y =∴直线MN 经过一个定点()2,1-.2.(1)解:把点()1,0A - ()4,0B 分别代入22y ax bx =++得2016420a b a b -+=⎧⎨++=⎩解得1232a b ⎧=-⎪⎪⎨⎪=⎪⎩①抛物线的解析式为213222y x x =-++. (2)①()1,0A - ()4,0B①对称轴为直线14322x -+== 点A 关于对称轴的对称点为点B 连接BC 交对称轴于点D 连接AD 此时AD CD +最小当0x =时 2y =①点()0,2C .设直线BC 的解析式为2y kx =+ 代入()4,0B 得420k += ①12k =- ①直线BC 的解析式为122y x =-+ 当32x =时 54y = ①点35,24D ⎛⎫ ⎪⎝⎭. (3)存在.①()0,2C E 是OC 的中点∴()0,1E .又()1,0A -①直线AE 的解析式为1y x =+ 1OE OA ==. 联立2132221y x x y x ⎧=-++⎪⎨⎪=+⎩得2132122x x x -++=+. 解得12x = 21x =-(舍).当2x =时 3y =.①()2,3F . 设213,222P n n n ⎛⎫-++ ⎪⎝⎭则(),1G n n +. ①2213112112222PG n n n n n =-++--=-++. 分以下两种情况:①如图2 若FPG AOE ∽△△ 则90FPG PF PG =.①PF x ∥轴.①2PF n =-. ①2112122n n n -=-++.解得1n =或2n =(舍).①()1,3P .①如图3 若PFG AOE ∽△△ 则90PFG ∠=︒ PF FG =.过点F 作FH PG ⊥于点H 则2PG FH = 即()21112222n n n ⎛⎫--++=- ⎪⎝⎭.解得3n =或2n =(舍).①()3,2P .综上 点P 的坐标为()1,3或()3,2.3.(1)解:抛物线212y x bx c =-++与x 轴交于()20A -,()40B ,两点 ∴()221220214402b c b c ⎧-⨯--+=⎪⎪⎨⎪-⨯++=⎪⎩解得:14b c =⎧⎨=⎩①抛物线的函数表达式为2142y x x =-++; (2)解:抛物线2142y x x =-++与y 轴交于点C ∴()0,4C∴4OC =设直线BC 的解析式为y kx d =+ 把()4,0B ()0,4C 代入 得: 404k d d +=⎧⎨=⎩解得14k d =-⎧⎨=⎩ ∴直线BC 的解析式为4y x =-+直线l x ⊥轴 (),0M m21,42P m m m ⎛⎫∴-++ ⎪⎝⎭(),4N m m -+ ()221144222PN m m m m m ∴=-++--+=-+ 221111244222B C S PN x x m m m m ⎛⎫∴=⋅-=⨯-+⨯=-+ ⎪⎝⎭()4,0B ()0,4C (),0M m()211448222C S BM y m m ∴=⋅=⨯-⨯=- 12S S2482m m m ∴-+=-解得2m =或4m =(P 与B 重合 舍去)m ∴的值为2;(3)解:()4,0B ()0,4COB OC ∴= BOC ∴是等腰直角三角形45CBO ∴∠=︒BMN ∴是等腰直角三角形45BNM MBN ∴∠=∠=︒HMN 与BCM 相似 且45MNH CBM ∠=∠=︒H ∴在MN 的右侧 且NH MN BC BM=或NH MN BM BC = 设(),4H t t -+ 由(2)知()2,0M ()2,2N ()4,0B ()4,0CBC ∴= 2BM = 2MN =2NH - 当NHMNBC BM =时 如图:∴222242t -=解得6t =或2t =-(此时H 在MN 左侧 舍去)()6,2H ∴-由()2,0M ()6,2H - 同(2)得直线MH 解析式为112y x =-+2112142y x y x x ⎧=-+⎪⎪⎨⎪=-++⎪⎩解得x y ⎧=⎪⎪⎨⎪=⎪⎩或x y ⎧=⎪⎪⎨⎪=⎪⎩①点Q 的坐标为⎝⎭或⎝⎭;当NH MNBM BC =时 如图:∴222242t -=解得32t =(舍去)或52t =5322H ⎛⎫∴ ⎪⎝⎭, 由()2,0M 5322H ⎛⎫ ⎪⎝⎭, 同(2)得直线MH 解析式为36y x =- 236142y x y x x =-⎧⎪⎨=-++⎪⎩解得261266x y ⎧=-+⎪⎨=-+⎪⎩2261266x y ⎧=--⎪⎨=--⎪⎩①点Q 的坐标为(226,1266-+-+或(226,1266----.综上所述 点Q 的坐标为333133+-⎝⎭或333133-+⎝⎭或(226,1266-+-+或(226,1266----. 4.(1)将()2,0A - ()8,0B 代入抛物线214y x bx c =-++ 得()221220418804b c b c ⎧-⨯--+=⎪⎪⎨⎪-⨯++=⎪⎩解得324b c ⎧=⎪⎨⎪=⎩ ∴该抛物线的解析式为213442y x x =-++. (2)①由抛物线的解析式为213442y x x =-++ 得()0,4C .设直线BC 的解析式为y kx t =+ 将()8,0B ()0,4C 代入得80,4,k t t +=⎧⎨=⎩解得1,24,k t ⎧=-⎪⎨⎪=⎩ ∴直线BC 的解析式为142y x =-+. 设第一象限内的点D 的坐标为213,442m m m ⎛⎫-++ ⎪⎝⎭ 则1,42E m m ⎛⎫-+ ⎪⎝⎭ 2213114424224DE m m m m m ⎛⎫⎛⎫∴=-++--+=-+ ⎪ ⎪⎝⎭⎝⎭8BF m =- ()()2211282944DE BF m m m m ⎛⎫∴+=-++-=--+ ⎪⎝⎭. 104-< ∴当2m =时 DE BF +有最大值 为9.①()2,0A - ()8,0B ()0,4C2OA ∴= 8OB = 4OC = 10AB =22220AC OA OC ∴=+= 22280BC OB OC =+= 2210100AB == 222AC BC AB ∴+=90ACB ∴∠=︒90CAB CBA ∴∠+∠=︒.DF x ⊥轴于点F90FEB CBA ∴∠+∠=︒CAB FEB DEC ∴∠=∠=∠.以点C D E 为顶点的三角形与AOG 相似 只需OA AG DE CE =或OA AG CE DE =. G 是AC 的中点 ()2,0A - ()0,4C()1,2G ∴- 2OA =12AG AC == 由①知2124DE m m =-+ 1,42E m m ⎛⎫-+ ⎪⎝⎭CE ∴=. 当OA AG DE CE =时22124m m =-+解得4m =或0m =(舍去) ()4,6D ∴. 当OAAGCE DE =时 251524m m m -+解得3m =或0m =(舍去) 253,4D ⎛⎫∴ ⎪⎝⎭.综上所述 以点C D E 为顶点的三角形与AOG 相似点D 的坐标为()4,6或253,4⎛⎫ ⎪⎝⎭. 5.(1)解:对于抛物线223y x x =-++ 当0x =时 可有3y = 即(0,3)C 当0y =时 可有2230x x -++= 解得11x =- 23x =即(1,0)A - (3,0)B①3OC = 3(1)4AB =--= ①1143622ABC S AB OC =⋅=⨯⨯=;(2)解:存在 点M 的坐标为30,2⎛⎫- ⎪⎝⎭ 或()01M -,理由如下:①(1,0)A - (3,0)B (0,3)C ①221310AC =+= 4AB = 223332BC =+如下图 当BCA CMB ∽时则有BCABCM BC = 3232①92CM = ①93322OM CM OC =-=-= ①30,2M ⎛⎫- ⎪⎝⎭;当BAC CMB ∽时 如图:则有BC ABCM BC = 4CM =①4CM =①1OM CM OC =-=则()01M -, 综上:30,2M ⎛⎫- ⎪⎝⎭或()01M -,(3)解:根据题意 点P 与点B 不重合;且45APC ∠=︒ 如图结合二次函数的对称性 且=45ABC ∠︒ ①45BAP ∠=︒①CP AB ∥则3P C y y ==①223y x x =-++①对称轴()2121x =-=⨯- 则()112C P x x += 则2P x =①P 的坐标为()23,当45PAC ∠=︒时 如下图设AP 交y 轴于点H 过点H 作HN AC ⊥于点N ①45PAC ∠=︒①9045NHA PAC PAC ∠=︒-∠=︒=∠ ①HN NA =①(1,0)A - (0,3)C①1OA = 3OC = ①1tan 3NH OA ACO CN OC ∠=== 设HN NA t == 则3CN t = 2AH t = ①310AC t t =+解得10t =①52AH t = ①2212OH AH OA =-=①10,2H ⎛⎫ ⎪⎝⎭设直线AH 的解析式为111(0)y k x b k =+≠ 将点(1,0)A - 10,2H ⎛⎫ ⎪⎝⎭代入 可得111012k b b =-+⎧⎪⎨=⎪⎩ 解得111212k b ⎧=⎪⎪⎨⎪=⎪⎩①直线AH 的解析式为1122y x =+ 联立直线AH 的解析式1122y x =+与抛物线解析式223y x x =-++ 可得2112223y x y x x ⎧=+⎪⎨⎪=-++⎩ 解得=1x -(舍去)或52x =①点57,24P ⎛⎫ ⎪⎝⎭; 当45ACP ∠=︒时 如下图 设CP 交x 轴于点T 过点T 作TK BC ⊥于点K ①(3,0)B (0,3)C ①3OB OC == ①190452OCB CBT ∠=∠=⨯︒=︒ ①45ACP OCB ∠=∠=︒ 即ACO OCP OCP PCB ∠+∠=∠+∠①ACO PCB ∠=∠ ①1tan tan 3TK BCP ACO CK ∠==∠= ①45KBT ∠=︒①9045KTB KBT KBT ∠=︒-∠=︒=∠①KB KT =设KT KB t == 则3CK t = 2BT t ①332BC t t =+=解得32t = ①322BT t ==①3,02T ⎛⎫ ⎪⎝⎭ 设直线CT 的解析式为222(0)y k x b k =+≠ 将点(0,3)C 3,02T ⎛⎫ ⎪⎝⎭代入 可得2223302b k b =⎧⎪⎨=+⎪⎩解得2223k b =-⎧⎨=⎩ ①直线CT 的解析式为23y x =-+联立直线CT 的解析式23y x =-+与抛物线解析式223y x x =-++可得22323y x y x x =-+⎧⎨=-++⎩解得0x =(舍去)或4x =①点(4,5)P -.综上所述 点P 坐标为(2,3) 57,24⎛⎫ ⎪⎝⎭或(4,5)-. 6.(1)解:在抛物线1L :245y x x =-++中令0y = 则2450x x -++=解得11x =- 25x = 即()10A -, ()50B , 根据题意 设抛物线L 2的函数关系式为()()15y a x x =+-将点()38-,代入得()()83135a =-+-- 解得12a = ①抛物线2L 的函数关系式为()()2115152222y x x x x =+-=--;(2)解:由题意得 5OB OC ==①BOC 为等腰直角三角形①抛物线1L :()224529y x x x =-++=--+①顶点()29D ,由题意可知PDQ ∠不可能为直角①当90DPQ ∠=︒时 如图 DPQ BOC ∽或DPQ COB ∽ 则DP QP =设Q 2()45m m m -++,①2QP m =- ()2945DP m m =--++①()22945m m m -=--++ 解得12m =(舍去) 23m = ①当3m =时 2458m m -++=①()28P ,①当90DQP ∠=︒时 如图 DPQ BCO ∽或DPQ CBO ∽ 过点Q 作QM DP ⊥垂足为点M 则DM QM MP ==由①可知()28M ,①1MP DM ==①()27P ,综上所述:点P 的坐标为()28P ,或()27P ,.7.(1)解:23y x c =-+与x 轴交于点()3,0A 与y 轴交于点B 02c 解得2c =(0,2)B ∴抛物线243y x bx c =-++经过点A B ∴12302b c c -++=⎧⎨=⎩ 解得1032b c ⎧=⎪⎨⎪=⎩ ∴抛物线解析式为2410233y x x =-++; (2)解:①由(1)可知直线解析式为223y x =-+ (,0)M m 为x 轴上一动点 过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P N2,23P m m ⎛⎫∴-+ ⎪⎝⎭2410,233N m m m ⎛⎫-++ ⎪⎝⎭ 223PM m 3AM m 22410242243333PN m m m m m ⎛⎫=-++--+=-+ ⎪⎝⎭BPN △和APM △相似 且BPN APM ∠=∠90BNP AMP 或90NBP AMP ∠=∠=︒当90BNP ∠=︒时 则有BN MN ⊥N ∴点的纵坐标为224102233m m ∴-++= 解得0m =(舍去)或52m = 502M ⎛⎫∴ ⎪⎝⎭,; 当90NBP ∠=︒时 过点N 作NC y ⊥轴于点C则90NBC BNC ∠+∠=︒ NC m = 22410410223333BC m m m m =-++-=-+ 90NBP ∠=︒90NBC ABO ∴∠+∠=︒ABO BNCRt Rt NCB BOA ∴∽△△ ∴NC CB OB OA= ∴24103323m m m -+= 解得0m =(舍去)或118m = 1108M ⎛⎫∴ ⎪⎝⎭,; 综上可知当以B P N 为顶点的三角形与APM △相似时 点M 的坐标为502⎛⎫ ⎪⎝⎭,或1108⎛⎫ ⎪⎝⎭,; ①由①可知(,0)M m 2,23P m m ⎛⎫-+ ⎪⎝⎭ 2410,233N m m m ⎛⎫-++ ⎪⎝⎭M P N 三点为“共谐点”∴有P 为线段MN 的中点、M 为线段PN 的中点或N 为线段PM 的中点当P 为线段MN 的中点时 则有22410222333m m m ⎛⎫-+=-++ ⎪⎝⎭解得3m =(舍去)或0.5m =;当M 为线段PN 的中点时 则有22410220333m m m ⎛⎫-++-++= ⎪⎝⎭解得3m =(舍去)或1m =-;当N 为线段PM 的中点时 则有22410222333m m m ⎛⎫-+=-++ ⎪⎝⎭解得3m =(舍去)或14m =-; 综上可知当M P N 三点成为“共谐点”时m 的值为0.5或1-或14-. 8.(1)解:(1,0)A -1OA ∴=3OB OA = OC OB =3OB OC ∴==.(3,0)∴B (0,3)C二次函数()2<0y ax bx c a =++的图象经过点A B C∴09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩ 解得:123a b c =-⎧⎪=⎨⎪=⎩∴该二次函数的表达式为223y x x =-++;(2)解:①()222314y x x x =-++=--+①抛物线对称轴为直线1x =延长AC 交对称轴于点M 此时BM CM AM CM AC -=-=有最大值①()1,0A - (0,3)C ①221310AC =+=设直线AC 的解析式为3y mx =+ 代入()1,0A -得03m =-+ 解得3m =①直线AC 的解析式为33y x =+①当1x =时 336y =+=①点M 坐标为()16,;答:BM CM - 点M 坐标为()16,; (3)解:设2(,23)P m m m -++PD x ⊥轴 P 为第一象限内抛物线上一点 0m ∴> OD m = 223PD m m =-++ 1AD OA OD m ∴=+=+ PDA 与COA 相似 ∴OA AD OC PD =或OA PD OC AD= ∴211323m m m +=-++或212331m m m -++=+. 解得:10m = 21m =-或31m =- 483m =.0m >83m ∴=. PDA ∴与COA 相似 满足条件的P 点坐标为81139⎛⎫⎪⎝⎭,. 9.(1)解:①(0,8)C 则设抛物线解析式为28y ax bx =++把A 、B 两点坐标代入可得428016480a b a b -+=⎧⎨++=⎩解得:12a b =-⎧⎨=⎩①抛物线解析式为228y x x =-++;(2)解:①点P 在抛物线上①可设()228P t t t -++,过P 作PE x ⊥轴于点E 交直线BC 于点F 如图①(40)B ,(08)C , 设直线BC 解析式为8y kx =+则048k =+解得2k =-①直线BC 解析式为28y x =-+①(28)F t t -+,①()2228(28)4PF t t t t t =-++--+=-+ ①1111()2222PBC S PF OE PF BE PF OE BE PF OB =⋅+⋅=⋅+=⋅△ ()221442(2)82t t t =-+⨯=--+ ①当2t =时 PBC S 最大值为8 此时2288t t -++=①当P 点坐标为(2,8)时 PBC 的最大面积为8; (3)解:设(0)Q m ,①=90AOC ︒∠①分AOC QOB ∽△△和AOC BOQ ∽△△两种情况 当AOC QOB ∽△△时①OA OC OQ OB= 即284m = 解得1m =±①点Q 的坐标为()01,或()01-,; 当AOC BOQ ∽△△时 ①OA OC OB OQ= 即284m = 解得16m =±①点Q 的坐标为()016,或()016-,; 综上 点Q 的坐标为()016,或()016-,或()01,或()01-,. 10.(1)解:①该抛物线过点()02C -,①可设该抛物线的解析式为22y ax bx =+-.将()40A ,()10B ,代入 得1642020a b a b +-=⎧⎨+-=⎩解得1252a b ⎧=-⎪⎪⎨⎪=⎪⎩①此抛物线的解析式为215222y x x =-+-; (2)解:存在;设P 点的横坐标为m 则P 点的纵坐标为215222m m -+- 由题意 4m > 如图 4AM m =- 215222PM m m =-+①90COA PMA ∠=∠=︒ ①12PM OC AM OA ==或①2PM OA AM OC ==当12PM OC AM OA ==时 则21522422m m m ⎛⎫-+=- ⎪⎝⎭ 解得:1224m m ==, (都不符合题意 舍去); 当2PM OA AM OC==时 则()21522422m m m -+=- 解得:1254m m ==,(4m =不符合题意舍去)此时 2152222m m -+-=- 则()52P -, 综上所述 符合条件的点P 为()52-,. 11.(1)解:把点()1,0A - ()3,0B 代入24y ax bx =+-中得:409340a b a b --=⎧⎨+-=⎩解得:4383a b ⎧=⎪⎪⎨⎪=-⎪⎩则抛物线的表达式为则抛物线的表达式为:248433y x x -=-; (2)存在 理由如下:由抛物线解析式可知:点()0,4C - 设BC 的表达式为:4y kx =-将点B 的坐标代入上式得:034k =- 解得:43k = 则直线BC 的表达式为:443y x =- 设点4,43E x x ⎛⎫- ⎪⎝⎭ 则点248,433M x x x ⎛⎫-- ⎪⎝⎭则224484(4)(4)43333ME x x x x x =----=-+ ①403-< 故ME 有最大值 当32x =时 ME 的最大值为3 此时 点3,52M ⎛⎫- ⎪⎝⎭; (3)存在 理由如下:DEB CEM M C E ∠=∠,,,为顶点的三角形和BDE △相似 ①当CME ∠为直角时则点C 、M 关于抛物线对称轴对称 而抛物线的对称轴为32x =则点()3,4M -;①当90ECM ∠=︒时 如图:由(1)得()0,4C - 设直线BC 的解析式为: 14y k x =- 把()3,0B 代入得1340k -=143k ∴= 设直线CM 的解析式为:24y k x =- 易知:121k k234k ∴=- 故直线CM 的表达式为:344y x =-- 联立抛物线表达式和上式得:248344334x x x --=-- 解得:0x =(舍去)或2316x =即点23325(,)1664M -; 综上 点M 的坐标为:23325,1664⎛⎫-⎪⎝⎭或()3,4-12.(1)解:令2132022x x -++= 解得11x =- 24x =①点A 在点B 的左侧①()10A -,()40B , 将0x =代入213222y x x =-++ 可得:2y =①()02C ,; (2)证明:如图 过点D 作DD x '⊥轴于点D根据题意 可得:DD OC '∥①BDD BCO '∽ ①25BD DD BD BO CO BC ''=== ①()40B ,()02C , ①4BO = 2CO =①2425BD DD ''== 解得85BD '= 45DD '= ①125OD BO BD ''=-=①12455D ⎛⎫ ⎪⎝⎭, 由抛物线213222y x x =-++ 可知对称轴为直线32x = ①点C 、C '关于抛物线对称轴对称①()32C ',设直线C D '的解析式为()0y kx b k =+≠把()32C ',、12455D ⎛⎫ ⎪⎝⎭,代入解析式 可得:3212455k b k b +=⎧⎪⎨+=⎪⎩ 解得:24k b =⎧⎨=-⎩ ①直线C D '的解析式为24y x =-;(3)解:①()02C ,①点C 关于x 轴的对称点M 的坐标为()02-,设直线BM 的解析式为()0y ax n a =+≠把()40B ,()02M -,代入解析式 可得:402a n n +=⎧⎨=-⎩ 解得:122a n ⎧=⎪⎨⎪=-⎩ ①直线BM 的解析式为122y x =- 设点N 的坐标为()0m , 则213222P m m m ⎛⎫-++ ⎪⎝⎭,、()12142Q m m m ⎛⎫--≤≤ ⎪⎝⎭, ①PQ x ⊥轴①OM PQ ∥①BMO BQP ∠=∠①90BOM ∠=︒ 而90BQP ∠<︒①可分以下两种情况:①如图2 连接BP 当90QBP MOB ∠=∠=︒时 PBQ BOM ∽①BPQ QBN ∠=∠①90BNP QNB ∠=∠=︒①BNP QNB ∽ ①PN NBBN NQ = ①21324221422m m mm m++-=-- ①()21324221442m m mm m ++-=-- ①21322224m m m ++=-解得:4m =或3m =检验:当4m =时 40m -= 等式不成立 且点B 、P 、Q 重合 BPQ 不存在此情况舍去;将3m =代入213222y x x =-++ 可得2y =①()32P ,; ①如图3 当90BPQ MOB ∠=∠=︒时 此时点P 与点A 、点N 重合 BOM BPQ ∽此时1m =- 点P 的坐标为()10-,; 综上所述 以点B 、P 、Q 为顶点的三角形与BOM 相似时 点P 的坐标为()32,或()10-,.13.(1)解:①抛物线26y ax bx =+-与x 轴交于点()3,0B -()1,0C ①936060a b a b --=⎧⎨+-=⎩解得:24a b =⎧⎨=⎩①抛物线为:2246y x x =+-;(2)解:①2246y x x =+-当0x =时 y =-6①()0,6A -设直线AB 为y kx n =+①630n k n =-⎧⎨-+=⎩ 解得:26k n =-⎧⎨=-⎩①直线AB 为26y x =--设点P 的横坐标为()30t t -<<.①()2,246P t t t +- (),26D t t --①222624626PD t t t t t =----+=--当()63222t -=-=-⨯-时 PD 的最大值为:233926222⎛⎫⎛⎫-⨯--⨯-= ⎪ ⎪⎝⎭⎝⎭. (3)解:如图 连接AP①BDH ADP ∠=∠ 而DPA 与DHB △相似①分两种情况讨论:当DPA DHB ∽时 ①DP AP DH BH= 90APD BHD ∠=∠=︒ ①AP x ∥轴 OH AP =①A P 关于抛物线的对称轴对称①()3,0B - ()1,0C①抛物线的对称轴为直线3112x -+==- 而()0,6A - ①()2,6P --;如图 当DHB DAP ∽时 过A 作AQ PH ⊥于Q①AQ OH = 6AO QH ==设AQ OH n ==①DHB DAP ∽①90DHB DAP ∠=∠=︒①90ADP APD APQ QAP ∠+∠=∠+∠=︒①PAQ ADP ∠=∠由PH y ∥轴 可得ADP BAO ∠=∠①PAQ BAO ∠=∠ ①31tan tan 62PAQ BAO ∠=∠== ①12PQ AQ 即12PQ n = ①1,62P n n ⎛⎫--- ⎪⎝⎭ ①()()2124662n n n -+⨯--=-- 解得:74n =(0n =舍去) ①755,48P ⎛⎫-- ⎪⎝⎭. 综上:()2,6P --或755,48P ⎛⎫-- ⎪⎝⎭. 14.(1)解:设抛物线的解析式为2(0)y ax bx c a =++≠ 将点(2,0)A - (3,3)B - (0,0)O 代入可得:4209330a b c a b c c -+=⎧⎪-+=⎨⎪=⎩解得:120a b c =⎧⎪=⎨⎪=⎩所以函数解析式为:22y x x =+;(2)证明:①()22211y x x x =+=+-①抛物线的顶点C 的坐标为()1,1--①()0,0O ()3,3B -①()()22303018OB =--+-= ()()2210102OC =--+--=()()22313120BC =---+--=⎡⎤⎡⎤⎣⎦⎣⎦ ①222OB OC BC +=①BOC 是直角三角形;(3)解:假设存在点P 使以P M A 为顶点的三角形与BOC 相似 如图设(,)P x y 由题意知0x > 0y > 且22y x x =+由(2)知 BOC 为直角三角形 90COB ∠=︒ 且:1:3OC OB = ①若PMA COB ∽ 则AM PM BO CO= 即223(2)x x x +=+ 得 113x = 22x =-(舍去) 当13x =时 79y = 即1(3P 7)9; ①若PMA BOC ∽AM PM OC BO= 即:223(2)x x x +=+ 得:13x = 22x =-(舍去)当3x =时 15y = 即(3,15)P .①存在 当点P 坐标为17,39⎛⎫ ⎪⎝⎭或(3,15) 使得以P M A 为顶点的三角形与BOC 相似. 15.(1)解:①2616y ax ax a =--经过()04C ,①164a -= 解得14a =- ①213442y x x =-++; 令0y = 即2134=042x x -++ 解得:122,8x x =-=①()()2,0,8,0A B -(2)设直线BC 的关系式为y kx b =+ ()8,0B ()04C ,①408b k b =⎧⎨=+⎩解得124k b ⎧=-⎪⎨⎪=⎩. ①直线BC 的方程为142y x =-+. 如图 过点P 作PG x ⊥轴于点G PG ,交CB 于点E①PG CO ∥①PED OCB ∠=∠又90PDE COB ∠=∠=︒①PDE BOC ∽△△ ①PD PE BO BC= ①8,4BO CO ==①BC =①BO PD PE PE BC =⨯ ①当线段PE 最长时 PD 的长度最大. 设213(4)42P t t t -++, 则1(,4)2E t t -+. 即213442PG t t =-++ 142EG t =-+. ①22112(4)444PE PG EC t t t =-=-+=--+()08t <<. 当4t =时 PE 有最大值是4 此时P 点坐标为()46,.①25854PD == 设1,42D m m ⎛⎫-+ ⎪⎝⎭ ①()2221854462m m ⎛⎫-+-+-= ⎪⎝⎭⎝⎭ 解得12125m m == ①111214442255m -+=-⨯+= 即点D 的坐标为121455⎛⎫ ⎪⎝⎭,. ①①284OA OB OC ===,,①2222420AC =+= ()2228100AB =+= 2224880BC =+=. 可得222AC BC AB =+.①90ACB ∠=︒.①COA BOC ∽.故当PDC △与COA 相似时 则PDC △与BOC 相似. ①PCD CBO ∠∠=或PCD BCO ∠∠=.(i )如图 当PCD CBO ∠=∠时即PDC COB ∽①PCD CBO ∠=∠①CP AB ∥①()04C ,①4P y =. ①2134442t t -++= 解得1260x x ==,(舍)即PDC COB ∽时 (64)P ,; (ii )当PCD BCO ∠=∠时 即PDC BOC ∽如图 过点P 作PG x ⊥轴于G 与直线BC 交于F①PF OC ∥①PFC BCO ∠=∠①PCD PFC ∠=∠①PF PC =. 设213(4)42P n n n -++, 则2124PF n n =-+ 过点P 作y 轴的垂线 垂足为N在Rt PNC △中 22222243213131344421644PC PN NC n n n n n n ⎡⎤=+=+-++-=-+⎢⎥⎣⎦() ①22PF PC = 即2243211313(2)41644n n n n n -+=-+ 解得120=3=n n , (舍).即PDC BOC ∽时 25(3)4P ,. ①当PDC △与COA 相似时 点P 的坐标为(64)P ,或2534P ⎛⎫ ⎪⎝⎭,.。
二次函数与相似三角形综合经典例题.docx
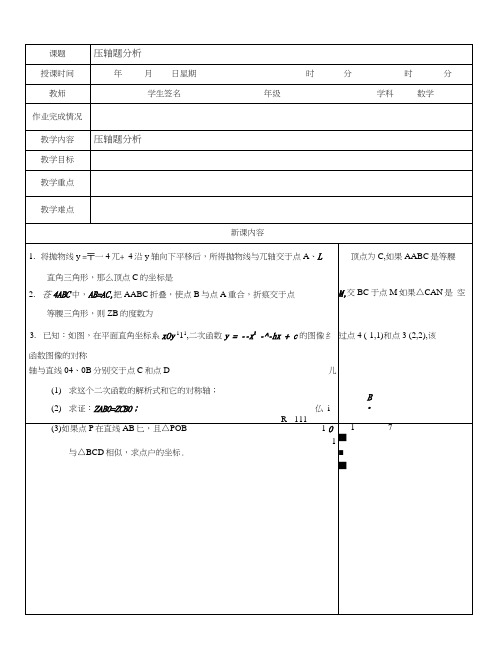
4.如图,MOB的顶点4、3在二次函数y = -|x2+Z?x + |的图像上,又点A、B
分别在y轴和兀轴上,tan ZABO= 1.
(1)求此二次函数的解析式;(4分)
(2)过点A作AC // B O交上述函数图像于点C,
点P在上述函数图像上,当APOC与AABO相似时,求点P的坐标.(8分)
5.如图,在Rt\ABC中,ZACB = 90° , CE是斜边4B上的中线,AB = 10, tanA = 的一动
点,过点P作PQ丄CB,交CB延长线于点Q,
设EP = x, BQ = y .
(1)求y关于兀的函数关系式及定义域;(4分)
(2)联结当PB平分ZCPQ时,求PE的长;(4分)
(3)过点B作BF丄交PQ于F,当ABEF和相似时,求兀的值.(6分)
D
(备用图)B
,点P是CE延长线上
24.(本题満分12分,其中第⑴小題3分,第(2)小題4分,第⑶小题5分)如RL 已知
点川(1,0人B(3,0)、C(0,1).
(只若二次曲数图像经过点乩C和点D⑴冷)三点・求这个二次诵数的解析式• (<
27涼ZACR的正切值.
(3)若点E在线段BC上,与A*BC相似,求出点E的坐标.
24.(木分门分〉
如图10,梯OABC. 8C//OA. iilOA在*紬正半救上.边OC在》轴正半納上•戍〃(3* 4).
4ir«5.
(1>求ZB/tO的正切備。
<2>知果二次除敵A = 的酌*经过O、/1斷点・余这个二次宙敷的解析
式并浪割怕厦点M的坐标、
<3)点0在x紬上・tXA{?. /5.O及(2)中的点M为顶点的三角影与△
求MQ的坐标.
学习情况
课后作业。
二次函数与相似三角形问题(含答案)
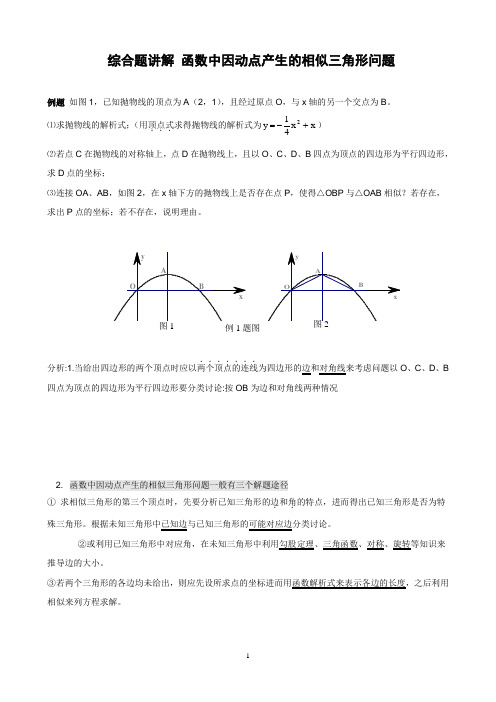
综合题讲解 函数中因动点产生的相似三角形问题例题 如图1,已知抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B 。
⑴求抛物线的解析式;(用顶点式...求得抛物线的解析式为x x 41y 2+-=) ⑵若点C 在抛物线的对称轴上,点D 在抛物线上,且以O 、C 、D 、B 四点为顶点的四边形为平行四边形,求D 点的坐标;⑶连接OA 、AB ,如图2,在x 轴下方的抛物线上是否存在点P ,使得△OBP 与△OAB 相似?若存在,求出P 点的坐标;若不存在,说明理由。
分析:1.当给出四边形的两个顶点时应以两个顶点的连线.......为四边形的边和对角线来考虑问题以O 、C 、D 、B 四点为顶点的四边形为平行四边形要分类讨论:按OB 为边和对角线两种情况2. 函数中因动点产生的相似三角形问题一般有三个解题途径① 求相似三角形的第三个顶点时,先要分析已知三角形的边.和角.的特点,进而得出已知三角形是否为特殊三角形。
根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
例1题图图1O AByxOAByx图2y xEQ PC B OA 例题2:如图,已知抛物线y=ax 2+4ax+t (a >0)交x 轴于A 、B 两点,交y 轴于点C ,抛物线的对称轴交x 轴于点E ,点B 的坐标为(-1,0). (1)求抛物线的对称轴及点A 的坐标;(2)过点C 作x 轴的平行线交抛物线的对称轴于点P ,你能判断四边形ABCP 是什么四边形?并证明你的结论;(3)连接CA 与抛物线的对称轴交于点D ,当∠APD=∠ACP 时,求抛物线的解析式.练习1、已知抛物线2y ax bx c =++经过53(33)02P E ⎛⎫⎪ ⎪⎝⎭,,,及原点(00)O ,.(1)求抛物线的解析式.(由一般式...得抛物线的解析式为225333y x x =-+) (2)过P 点作平行于x 轴的直线PC 交y 轴于C 点,在抛物线对称轴右侧且位于直线PC 下方的抛物线上,任取一点Q ,过点Q 作直线QA 平行于y 轴交x 轴于A 点,交直线PC 于B 点,直线QA 与直线PC 及两坐标轴围成矩形OABC .是否存在点Q ,使得OPC △与PQB △相似?若存在,求出Q 点的坐标;若不存在,说明理由.(3)如果符合(2)中的Q 点在x 轴的上方,连结OQ ,矩形OABC 内的四个三角形OPC PQB OQP OQA ,,,△△△△之间存在怎样的关系?为什么?练习2、如图,四边形OABC 是一张放在平面直角坐标系中的矩形纸片,点A 在x 轴上,点C 在y 轴上,将边BC 折叠,使点B 落在边OA 的点D 处。
二次函数与相似三角形问题含答案

函数中因动点产生的相似三角形问题综合题讲解 1、如图,已知抛物线与交于A(-1,0)、E(3,0)两点,与轴交于点xy B(0,3)。
(1)求抛物线的解析式;(2)设抛物线顶点为D,求四边形的面积;(3)△与△是否相似?如果相似,请给以证明;如果不相似,请说明理由。
??35经过及原点 2、已知抛物线.2,,,P(E3)03cy?ax??bx,(0O0)???? 2??(1)求抛物线的解析式.(2)过点作平行于轴的直线交轴于点,在抛物线对称轴右侧且xy C PCP1 / 24位于直线下方的抛物线上,任取一点,过点作直线平行于轴交xy QQQA PC轴于点,交直线于点,直线与直线及两坐标轴围成矩形QA PCABPC是否存在点,使得与相似?若存在,求出点的坐标;.PQB △QQ OABCOPC△若不存在,说明理由.(3)如果符合(2)中的点在轴的上方,连结,矩形内的四个x QOQ OABC y系?之间存在怎样的关三角形OQAOQP,△△OPC,△PQB,C为什么?Ox3 、如图所示,已知抛物线与轴交于A、B两点,与轴交于点C.2x1?y?x y(1)求A、B、C三点的坐标.(2)过点A作∥交抛物线于点P,求四边形的面积.(3)在轴上方的抛物线上是否存在一点M,过M作轴于点G,使以A、xx?yM、G三点为顶点的三角形与相似.若存在,请求出M点的坐标;否则,?P请说明理由.2 / 24x A BC4、在平面直角坐标系中,已知二次函数的图象与轴交于两点(点在点的左边),与轴交于点,其顶点2x0)??c(ay?ax?bxxOy的横坐标为1,y C BAB,A和.且过点12)3,?(?(23),)(1)求此二次函数的表达式;(由一般式得抛物线的解析式为232x?y??x?...(2)若直线与线段交于点(不与点重合),则是否存0)?kx(kl:y?DBCCB,在这样的直线,使得以为顶点的三角形与相似?若存在,求l BAC,D△B,O出该直线的函数表达式及点的坐标;若不存在,请说明理由;D3)(0C,0)B(3,0),1A(?,,(3)若点是位于该二次函数对称轴右边图象上不与顶点重合的任意一Pxl的横坐的大小(不必证明)与,并写出此时点点,试比较锐角PACO?PCO?C 的取值范围.标x p3 / 24AyB32 A三点,B、Cx++c与坐标轴交于A 5、如图,已知抛物线y =、43x-3与x轴交于点Q,点)1,0,过点C的直线y=P 点的坐标为(-t4是线段上的一个动点,过P作⊥于点H.若=5t,且0<t<1.(1)填空:点C的坐标是_ _,b=_ _,c=_ _;(2)求线段的长(用含t的式子表示);(3)依点P的变化,是否存在t的值,使以P、H、Q为顶点的三角形与4 / 24△相似?若存在,求出所有t的值;若不存在,说明理由.yQ H x BAOPC6、如图,抛物线经过三点.2) C(0,0)A(4,,B(1,,0)(1)求出抛物线的解析式;(2)P是抛物线上一动点,过P作轴,垂足为M,是否存在P点,x?PM使得以A,P,M为顶点的三角形与相似?若存在,请求出符合条件OAC△的点P的坐标;若不存在,请说明理由;(3)在直线上方的抛物线上有一点D,使得的面积最大,求出点D DCA△的坐标.5 / 241上的轴的直线,抛物线已知,如图1,过点作平行于 7、??2x1?E0,xy?l4两点的横坐标分别为1和4,直线交轴于点,过点分别作y?FABBB、A、A直线的垂线,垂足分别为点、,连接.Cl DDFCF、(1)求点的坐标;F、A、B(2)求证:;DF?CF1对称轴右侧图象上的一动点,过点作交)(3点是抛物线2xy POPQ ⊥PP4是否存在点使得与相似?若存在,请求出所有符轴于点,x OPQ△Q PCDF△合条件的点的坐标;若不存在,请说明理由.P6 / 24y取得最小值-1,并且抛物线与c=2时,抛物线y=++2轴交当 8、x .、BA3),与x轴交于点(于点C0,)求该抛物线的关系式;(1的大与yy)都在该抛物线上,试比较y1y,),N(x+,M(2)若点(x2121小;yE作,过点为线段上一动点(A、C两端点除外)D(3)是线段的中点,E.问:是否存在△与△相似?若存在,求出F轴的平行线与抛物线交于点yC 点E的坐标;若不存在,则说明理由.3 EDFA BO x7 / 24图象的对称轴交于点一次函数-2x的图象与二次函数-2B.x+3x、9如图,;)写出点B的坐标(12部分上的一个动点,将图象在y轴右侧x(2)已知点P是二次函数-+3x..若以为直角边. 轴于yC、D两点分别交2x直线-沿y 轴向上平移,x轴、 . P的△与△相似,则点的坐标为D COB8 / 2410、如图,抛物线与轴交于两点A(-1,0),B(1,0),与2x1??bxy?ax y 轴交于点C.(1)求抛物线的解析式;(2)过点B作∥与抛物线交于点D,求四边形的面积;(3)在轴下方的抛物线上是否存在一点M,过M作⊥轴于点N,使以A、M、xx N为顶点的三角形与△相似?若存在,则求出点M的坐标;若不存在,请说明理由.9 / 24轴只有一个公共点.111、已知:函数的图象与 1)求这个函2x数关系式;(2为A,P,与)如图所示,设二次函数1图象的顶点为By轴的交点为(2.. P点的坐标;图象上的一点,若以线段为直径的圆与直线相切于点B,求M,试探索点中,若圆与x轴另一交点关于直线的对称点为M)在(3(2)yM是否在抛物线1上,若在抛物2点的坐标;若不在,请说明理线上,求出由.AOxB10 / 24????与CC:的交点为, CA, B,12、如图,设抛物线点A的坐标是,点B的横坐标是-2.)4(2,(1)225??51y??a?y?axx?12211求的值及点B的坐标;a(2)点D在线段上,过D作x轴的垂线,垂足为点H,在的右侧作正三角形.记过C顶点M的直线为,且与x轴交于点N.ll2①若过△的顶点G,点D的坐标为(1, 2),求点N的横坐标;l②若与△的边相交,求点N的横坐标的取值范围. l,现将纸片折叠,使点在线段上运动,设31,点P13、如图,在矩形中,x为折痕与矩形边的交点)F,再将纸片还原。
中考数学总复习《二次函数与相似三角形》专项测试题

中考数学总复习《二次函数与相似三角形》专项测试题1.如图所示,已知以M 为顶点的抛物线2y x bx c =-++交x 轴于A ,B 两点,交y 轴于点C ,直线BC 的表达式为3y x =-+.(1)求抛物线的表达式.(2)连接AC ,在x 轴上方的抛物线上有一点D ,若ABD ACO ∠=∠,求点D 的坐标;(3)若点P 为抛物线位于第一象限图象上一动点,过P 作PQ BC ⊥,求PQ 的最大值;(4)在x 轴上是否存在一点N ,使得以A ,C ,N 为顶点的三角形与BCM 相似?若存在,请求出点N 的坐标;若不存在,请说明理由.2.在平面直角坐标系中,经过原点的抛物线的顶点是()1,1-,与x 轴交于另一点A ,与直线4y x =+交于点B 和C (B 在左侧),点P 是直线BC 下方抛物线上不与O ,A 重合的一动点,过点P 作BC 的平行线交x 轴于点Q ,设点P 的横坐标为m .(1)请直接写出解析式和点A ,B ,C 的坐标;(2)如图,若抛物线的对称轴为直线l ,点P 在直线l 的右侧,PQ 与直线l 交于点M ,当M 为PQ 的中点时,求m 的值;(3)线段PQ 的长记为d .①求d 关于m 的函数解析式;①若2d ≥d 关于m 的函数图象,直接写出m 的取值范围. 3.如图,抛物线2134y x x =--与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C .直线l 与抛物线交于A ,D 两点,与y 轴交于点E ,点D 的坐标为()4,3-.(1)请直接写出A ,B 两点的坐标及直线l 的函数表达式;(2)若点P 是抛物线上的点,点P 的横坐标为()0m m ≥,过点P 作PM x ⊥轴,垂足为M ,PM 与直线l 交于点N .当PN MN =时,求点P 的坐标;(3)若点Q 是y 轴上的点,且45ADQ ∠=︒,求点Q 的坐标.4.在平面直角坐标系xOy 中,已知抛物线F :2y x bx c =-++经过点(3,1)A --,与y 轴交于点(02)B ,.(1)求抛物线的函数表达式;(2)在直线AB 上方抛物线上有一动点C ,连接OC 交AB 于点D ,求CD OD 的最大值及此时点C 的坐标. 5.如图,抛物线21382y x x =--与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为点D ,连接AC BC BC ,,与抛物线的对称轴交于点E .(1)求点A ,B ,C 的坐标.(2)若点P 是第四象限内抛物线上一动点,当三角形PAB 的面积为60时,求点P 的坐标.(3)若点Q 是对称轴右侧抛物线上的动点,试探究在射线ED 上是否存在一点H ,使以H ,Q ,E 为顶点的三角形与BOC 相似.若存在,直接写出点H 的坐标;若不存在,请说明理由.6.综合探究如图(1)所示,在平面直角坐标系xOy 中,已知菱形ABCD 的顶点A 在y 轴正半轴上,顶点B ,C ,D 在二次函数²y ax =(a 为常数,且0a ≠)的图象上,且AD y ⊥轴,BC 与y 轴交于点E 23BC =(1)求AE 的长.(2)求a 的值.(3)如图(2)所示,F 是射线BA 上的一动点,点C ,D 同时绕点F 按逆时针方向旋转90︒得点C D '',,当AC D ''△是直角三角形时,求BF 的长.7.如图,在平面直角坐标系xOy 中,抛物线2y ax bx c =++过点()1,0A -,()2,0B 和()0,2C ,连接BC ,()(),0P m n m >为抛物线上一动点,过点P 作PN x ⊥轴交直线BC 于点M ,交x 轴于点N .(1)求抛物线和直线BC 的解析式;(2)如图1,连接CP CN ,,当CPN △是直角三角形时,求m 的值;(3)如图2,连接OM ,当OCM 为等腰三角形时,求m 的值;(4)点P 在第一象限内运动过程中,若在y 轴上存在点Q ,使得以O ,P ,Q 为顶点的三角形与以B ,C ,N 为顶点的三角形相似(其中点P 与点C 相对应),请直接写出m 的值.8.如图,抛物线23y ax bx =--与x 轴交于A ,B 两点,且3OB OA =,与y 轴交于点C ,连接AC ,抛物线对称轴为直线=1x -,D 为第三象限内抛物线上一动点,过点D 作DE OB ⊥于点E ,与BC 交于点F ,设点D 的横坐标为m .(1)求抛物线的表达式;(2)当线段DF 的长度最大时,求D 点的坐标;(3)抛物线上是否存在点D ,使得以点O ,D ,E 为顶点的三角形与AOC △相似?若存在,求出m 的值;若不存在,请说明理由.9.如图,抛物线22y ax x c =-+(a 、c 为常数,0a ≠)与x 轴交于A 、()2,0B 两点(点A 在点B 左侧),与y 轴交于点C ,OA=4,连接AC .(1)求抛物线的函数表达式;(2)点D 是抛物线第二象限上的动点,过点D 作DE x ⊥轴于点E ,交线段AC 于点F ,连接CD ,若AEF △与CDF 相似(含全等),求点D 的坐标.10.如图,已知抛物线2()20y ax x c a =++≠,与x 轴交于点(1,0)A -和点(3,0)B ,与y 轴交于点C .(1)求该抛物线的函数表达式;(2)如图1,点P 是第一象限内抛物线上一动点,连接PC 、PB 、BC ,设点P 的横坐标为t .当t 为何值时,PBC △是以点C 为直角顶点的直角三角形;(3)如图2,过抛物线顶点E 作EF x ⊥轴于F ,若(,0)M m 是x 轴上一动点,N 是线段EF 上一点,若90MNC ∠=︒,请求出实数m 的取值范围.11.综合与探究如图,抛物线21382y x x =--与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为点D ,连接AC ,BC ,BC 与抛物线的对称轴交于点E .(1)求点A ,B ,C 的坐标.(2)若点P 是第四象限内抛物线上一动点,连接PB ,PC ,当35PBC ABC S S =时,求点P 的坐标.(3)若点Q 是对称轴右侧抛物线上的动点,试探究在射线ED 上是否存在一点H ,使以H ,Q ,E 为顶点的三角形与BOC 相似.若存在,直接写出点H 的坐标;若不存在,请说明理由.12.如图,已知抛物线2y x bx c =-++与x 轴交于A 、B 两点,与y 轴交于点C ,抛物线的对称轴交x 轴于点D .已知()3,0A ,()0,3C 连接AC ,BC .(1)求抛物线的函数解析式;(2)在抛物线的对称轴上找一点P ,使得以A D P 、、为顶点的三角形与OBC △相似,求出点P 的坐标;(3)若点M 是抛物线上的一个动点,且位于第一象限内,连接MC ,MA .设ACM △的面积为S ,试求S 的最大值.13.如图,直线1y x 42=-与x 轴、y 轴分别交于点A 、点B ,经过点A ,B 的抛物线218y x bx c =-++与x 轴另一个交点为C ,连接BC .平行于x 轴的动直线EF 从点B 开始,以每秒1个单位长度的速度向y 轴正方向平移,同时动点P 从点A 出发,在线段AO 上以每秒2个单位长度的速度向原点O 运动.(1)求抛物线的表达式;(2)设点P 运动的时间为t 秒,是否存在某一时刻,使APF 与ABC 相似?若存在,试求出t 值;若不存在,简述你的理由;(3)点D 在直线1y x 42=-上,横坐标为11,M 为x 轴上一动点,N 为抛物线上一动点,是否存在点M ,N ,使以A ,D ,M ,N 为顶点的四边形是平行四边形?若存在,请直接写出所有符合条件的点M 的坐标;若不存在,简述理由.14.已知:在平面直角坐标系中,点O 为坐标原点,直线=-3y x +与x 轴交于点B ,与y 轴交于点C ,抛物线2y x bx c =-++经过B 、C 两点,与x 轴的另一交点为点A .(1)如图1,求抛物线的解析式;(2)如图2,点D 为直线BC 上方抛物线上一动点,连接AC CD 、,设直线BC 交线段AD 于点E ,CDE 的面积为1S ACE ,的面积为2S ,当12S S 最大值时,求点D 的坐标; (3)如图3,在(2)的条件下,连接CD BD 、,将BCD △沿BC 翻折,得到BCF (点D 和点F 为对应点),直线BF 交y 轴于点P ,点S 为BC 中点,连接PS ,过点S 作SP 的垂线交x 轴于点R ,在对称轴TH 上有一点Q ,使得PQB △是以PB 为直角边的直角三角形,求直线RQ 的解析式.15.如图,在平面直角坐标系中,二次函数24y ax bx =++的图像与x 轴交于A 、B 两点,与y 轴交于点C ,点A 的坐标为()20-,,点B 的坐标为()80,.(1)求此二次函数的解析式;(2)动点D从点C5CB上运动,过点D作x轴的垂线,交二次函数图像于点E,交x轴于点F,连接CE和OD,若OCD与CDE的面积相等,求t的值.(3)点D在直线CB上运动,过点D作x轴的垂线,交二次函数图像于点E,交x轴于点F,是否存在点D,使得以B、E、F为顶点的三角形与ABC相似?若存在,求出D的坐标;若不存在,请说明理由.。
二次函数与相似三角形综合测试

测试 二次函数一、填空题(每空1分)1.抛物线y =-x 2+15有最______点,其坐标是______.2.抛物线y =x 2-4x -5的顶点坐标为____________.3.若函数y =x 2-mx +m -2的图像经过(3,6)点,则m=______.4.二次函数y =2x 2-6x +4 配方成y =a (x +h )2+k 的形式____________.5.抛物线y =-x 2+3x -2与y 轴交点的坐标______,与x 轴的交点坐标______.6.函数y =2x 2-8x +1,当x=_________时,y 有最________值等于__________.7.二次函数22212--=x x y 的图象在坐标平面内绕顶点旋转180°,再向左平移3个单位,向上平移5个单位后图象对应的二次函数解析式为____________.8. 若抛物线y =ax 2+bx +c (a ≠0)的图象与抛物线y =x 2-4x +3的图象关于y 轴对称,则函数y =ax 2+bx +c 的解析式为______.二、选择题(每小题2分)9.把二次函数253212++=x x y 的图象向右平移2个单位后,再向上平移3个单位,所得的函数图象顶点是( ) A .(-5,1) B .(1,-5) C .(-1,1) D .(-1,3)10.若点(2,5),(4,5)在抛物线y =ax 2+bx +c 上,则它的对称轴是( ) A .a b x -= B .x =1 C .x =2 D .x =311.已知函数4212--=x x y ,当函数值y 随x 的增大而减小时,x 的取值范围是( ) A .x <1 B .x >1 C .x >-2 D .-2<x <412.二次函数y =a (x +k )2+k ,当k 取不同的实数值时,图象顶点所在的直线是( )A .y =xB .x 轴C .y =-xD .y 轴13.图中有相同对称轴的两条抛物线,下列关系不正确的是( )A .h =mB .k >nC .k =nD .h >0,k >014.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列结论:1. abc >0;2. a +b +c =2;0-.3<+c b a ;4. b -2a<0;5.042<-ac b .其中正确的结论是( )A .1 2 3B .1 3 4C .2 3 4D .3 4 5三、解答题(每小题10分)15.把二次函数43212+-=x x y 配方成y =a (x -k )2+h 的形式,并求出它的图象的顶点坐标、对称轴方程,y <0时x 的取值范围,并画出图象.16.已知二次函数y =ax 2+bx +c (a ≠0)的图象顶点坐标为(-2,3),且过点(1,0),求这个二次函数解析式,并求此抛物线与x 轴的两个交点坐标?17.已知抛物线y =-x 2+bx +c ,当x=-1时有最小值-4,且图像在x 轴的两个交点之间的距离为4,求此函数解析式.(试用两种不同的方法)测试 相似三角形一、填空题(每空1分)1.相似三角形的对应角______,对应边的比等于______.2.相似三角形对应边上的中线之比等于_____,对应边上的高之比等于______,对应角的角平分线之比等于______.3.相似三角形的周长比等于______,相似三角形的面积比等于______.4.若两个相似多边形的对应边之比为5∶2,则它们的周长比是______,面积比______.5.同一个圆的内接正方形与其外切正方形的周长比是______,面积比是______.6.在比例尺1∶1000的地图上,1cm 2所表示的实际面积是______.二、选择题(每小题2分)7.已知相似三角形面积的比为9∶4,那么这两个三角形的周长之比为( )A .9∶4B .4∶9C .3∶2D .81∶168.如图所示,在平行四边形ABCD 中,E 为DC 边的中点,AE 交BD 于点Q ,若△DQE 的面积为9,则△AQB的面积为( )A .18B .27C .36D .459.如图所示,把△ABC 沿AB 平移到△A ′B ′C ′的位置,它们的重叠部分的面积是△ABC 面积的一半,若2=AB ,则此三角形移动的距离AA '是( ) A .12- B .22 C .1 D .21 10.如图,在平行四边形ABCD 中,AB =10,AD =6,E 是AD 的中点,在AB 上取一点F ,使△CBF ∽△CDE ,则BF 的长是( ) A .5 B .8.2 C .6.4 D .1.811.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC 相似的是( )三、解答题 (每小题8分)12.已知:如图,E 、M 是AB 边的三等分点,EF ∥MN ∥BC .求:△AEF 的面积∶四边形EMNF 的面积∶四边形MBCN 的面积.13.已知:如图,□ABCD 中,E 是BC 边上一点,且AE BD EC BE ,,21=交于F 点. (1)求△BEF 的周长与△AFD 的周长之比;(2)若△BEF 的面积S △BEF =6cm 2,求△AFD 的面积S △AFD .14.如图所示,在△APM 的边AP 上任取两点B ,C ,过B 作AM 的平行线交PM 于N ,过N 作MC 的平行线交AP 于D .求证:P A ∶PB =PC ∶PD .附加题.(15分)已知D 是BC 边延长线上的一点,BC =3CD ,DF 交AC 边于E 点,且AE =2EC .试求AF 与FB 的比.。
二次函数与相似三角形综合试题一
练习题(一)选择题1.梯形两底分别为m 、n ,过梯形的对角线的交点,引平行于底边的直线被两腰所截得的线段长为………………………………………………………………………( )(A )mnnm + (B )nm mn+2(C )nm mn+(D )mn nm 2+ 2.如图,在正三角形ABC 中,D ,E 分别在AC ,AB上,且ACAD =31,AE =BE ,则有………………………………………………………………………………………( ) (A )△AED ∽△BED (B )△AED ∽△CBD (C )△AED ∽△ABD (D )△BAD ∽△BCD3.P 是Rt △ABC 斜边BC 上异于B 、C 的一点,过点P 作直线截△ABC ,使截得的三角形与△ABC相似,满足这样条件的直线共有……………………………………( ) (A )1条 (B )2条 (C )3条 (D )4条4.如图,∠ABD =∠ACD ,图中相似三角形的对数是……………………………( )(A )2 (B )3 (C )4 (D )55.如图,ABCD 是正方形,E 是CD 的中点,P 是BC 边上的一点,下列条件中,不能推出△ABP 与△ECP 相似的是……………………………………………………( ) (A )∠APB =∠EPC (B )∠APE =90° (C )P 是BC 的中点 (D )BP ︰BC =2︰36.若二次函数y=mx2-3x+2m-m2的图象经过原点,则m 的值是( )A .1 B. 0 C. 2 D. 0或27.二次函数y= a (x+m)2-m (a ≠0) 无论m 为什么实数,图象的顶点必在 ( )A.直线y=-x 上B. 直线y=x 上C.y 轴上D.x 轴上8.下列各图中有可能是函数y=c ax+2,(0,0)ay a c x =≠>的图象是( )9.如图,已知正方形ABCD 中,对角线AC 、BD 交于O 点,AB=1 cm ,过B 作BG ∥AC ,过A 作AE ∥CG ,且∠ACG :∠G = 5:1,以下结论:①AE=3 cm ;②四边形AEGC 是菱形;③AEC BDC S S ∆∆=;④CE=21cm ;⑤△CFE 为等腰三角形,其中正确的有:A ①③⑤B ②③⑤C ②④⑤D ①②④10.如上 右图中有相同对称轴的两条抛物线,下列关系不正确的是( ) A .h=mB .k=nC .k >nD .h <0,k >0(二)填空题11.如图,梯形ABCD 中,A D ∥BC ,∠B=70°,∠C=40°,若AD=3,BC=10,则CD=________12.如上图,若双曲线xk y =与边长为5的等边三角形AOB 的边OA ,AB 分别相交于C 、D 两点,且OC=3 BD ,则K 值为_________13.如果kcb a dd b a c d c a b d c b a =++=++=++=++,则k 的值是___________14.如图,在△ABC 中,AB =AC =27,D 在AC 上,且BD =BC =18,DE ∥BC 交AB 于E ,则DE =_______.(三)解答题15.如图,在△ABC 中,AB =AC ,延长BC 至D ,使得CD =BC ,CE ⊥BD 交AD 于E ,连结BE 交AC 于F ,求证AF =FC .16.已知:关于x 的一元二次方程01)2()1(2=--+-x m x m (m 为实数) (1)若方程有两个不相等的实数根,求m 的取值范围;(2)在(1)的条件下,求证:无论m 取何值,抛物线1)2()1(2--+-=x m x m y 总过x 轴上的一个固定点;(3)若m 是整数,且关于x 的一元二次方程01)2()1(2=--+-x m x m 有两个不相等的整数根,把抛物线1)2()1(2--+-=x m x m y 向右平移3个单位长度,求平移后的解析式.。
初三数学(二次函数.相似三角形)测试卷

初三数学(二次函数.相似三角形)测试试题一.选择题(每小题3分,共24分)1.下列函数:①13+=x y ②132+=x y ③2323x x y -=④x mx y 22-= ⑤4)1(22-+=x a y ,其中二次函数的个数为( ) A. 1 B. 2 C. 3 D. 42. 如图,函数a ax y ax y +==与2在同一坐标系内的图象大致是( )3.下列四组立体图形中,不相似的一组是( )4.如图,小正方形的边长均为1,则下图中的三角形(阴影部分)与△ABC 相似的是( )5.如图,已知B ∠=∠=∠21则图中相似三角形共有( ) 对 对 对 对6.抛物线3)2(212+-=x y 的图象先向左平移3个单位,再向下平移4个单位,所得抛物线的关系式为( )A. 1)5(212--=x yB. 7)1(212++=x yC. 1)1(212-+=x yD. 7)5(212+-=x y7.如图,已知△ABC 中,AD ⊥BC 于点D,E 为BC 的中点,EF ⊥BC 于点E,交AB 于F,BD=6,DC=4,AB=8,则BF 的长为( )A.324 B. 8 C. 325 D. 320 8.二次函数c bx ax y ++=2的图象如图所示,则点),(bc ac A 在( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限 二.填空题(每小题4分,共20分)9.若m x m y )2(-=是二次函数(x 是自变量),且图象的开口向下,则m 的值为______ 10.小李存入银行人民币500元,年利率为x ,两年到期,本息和为y 元(不考虑利息税), 则y 与x 之间的函数关系式是_________,若年利率为6%,则两年到期的本息和是____ 11.已知点),(),(m b B m a A 和是抛物线3522-+=x x y 上的两个点,则______=+b a 12,如图,一个直立的油桶高米,在顶部的一个开口中将一根长为1米的木棒斜插入桶内,上端正好与桶面相平,抽出后看到棒上油浸到部分长为米,则桶内油面的高度为________.13.若抛物线4322+-=x x y 与轴y 交于点C,与直线23-=x y 相交于A,B 两点,则_______=∆ABC S三.解答题(每小题6分,共30分)14.如图,已知△ABC ∽△ADE.求证: △ABD ∽△ACE15. 如图,在正方形网格中,每个小正方形的边长都是1, 求证: △ABC ∽△EFD16. 如图,已知△ABC 中,∠ABC=2∠C,BD 平分∠ABC. 求证:CD AC BC AB ⋅=⋅17.已知抛物线的顶点是(-2,1),且经过点(1,6),求此抛物线的解析式.18.已知二次函数n m x m y +--=4)2(22的图象的对称轴是直线2=x ,且顶点在直线121+=x y 上,求这个二次函数的的表达式. 四.解答题(每小题7分,共21分)19.如图,在△ABC 中,D 是BC 的中点,且AD=AC,DE ⊥BC,交AB 于E,EC 与AD 相交于F (1)求证: △ABC ∽△FCD(2)若,10,5==∆BC S FCD 求DE 的长.20. 如图,已知△ABC 中,AF:FC=1:2,G 是BF 的中点.求BE:EC 的值.21.某商场以每件20元的价格购进一种商品,试销中发现,这种商品每天的销售量)(件m 与每件的销售价x m x 2140:)(-=之间满足关系式元 (1)写出这种商品每天的销售利润)()(元与每件的销售价元x y 之间的函数关系式 (2)如果商场要想每天获得最大的销售利润,每件商品的售价应定为多少元最合适最大利润是多少元22.已知抛物线n x x y ++-=52经过点A(1,0),与y 轴交于点B (1)求抛物线的解析式(2)若P 是y 轴上一点,且△PAB 是等腰三角形,求P 点的坐标五.解答题(每小题9分,共27分)23. 抛物线)3,(,1222m x y n x y 交于点与直线-=+= (1)求的值和n m(2)写出抛物线n x y +=22的顶点坐标和对称轴(3)抛物线n x y +=22与12-=x y 直线的图象是否还有其他交点?若有,请求出来;若没有,请说明理由.24. 如图,在Rt △ABC 中,∠C=900,AC=4,BC=3,E 为AB 上一动点(不与A,B 重合),F 是AC 上一动点(不与A,C 重合),当点E 自点B 沿BA 方向作匀速移动时,点F 自点A 沿AC 方向作匀速移动,移动速度均为1cm/s,设E,F 移动的时间为t s(1)写出△EAF 的面积S(cm 2)与时间t(s)之间的函数关系式并写出自变量的取值范围. (2)当t 为何值时, △EAF 为等腰三角形?初三数学(二次函数.相似三角形)测试答卷班级________姓名__________座号_____分数_______题号12345678答案,,三.解答题(每小题6分,共30分)14.15.16.17.18.四.解答题(每小题7分,共28分)19.20.21.22.五.解答题(每小题9分,共18分)23.24.。
中考数学专题复习《二次函数中的相似三角形问题》测试卷-附带答案

中考数学专题复习《二次函数中的相似三角形问题》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________1.如题 在平面直角坐标系xOy 中 抛物线22y ax bx =++与x 轴交于点()1,0A - 点()4,0B 与y 轴交于点C 连接AC BC .(1)求抛物线的解析式.(2)点D 为抛物线的对称轴上一动点 当ACD 周长最小时 求点D 的坐标.(3)点E 是OC 的中点 射线AE 交抛物线于点F P 是抛物线上一动点 过点P 作y 轴的平行线 交射线AF 与点G 是否存在点P 使得PFG △与AOE △相似?若存在 求出点P 的坐标 若不存在 请说明理由.2.如图 二次函数()220y ax bx a =+-≠的图象经过点()()2010A B -,,, 与y 轴交于点C 点P 为第四象限内抛物线上一点 连接BP AC 、 交于点Q .(1)求二次函数的表达式(2)连接BC 线段BC 的垂直平分线交x 轴于点M 求点M 的坐标 (3)探究:PQQB是否有最大值 如有请求出最大值 如没有请说明理由.3.如图 已知抛物线2y ax c =+过点(2,2)A -- 其顶点为D 过点A 作x 轴的平行线l 点12(,)(,)P p y Q q y 、是抛物线上位于点A 右侧和l 两侧的动点 直线l 始终平分∠P AQ .(1)若点(0,2)D 求抛物线的函数表达式 (2)在(1)的条件下 若1P = 求q 的值(3)在点P Q 、的运动过程中 试判断p q +的值是否变化 并说明理由.4.已知抛物线212y x bx c =++.经过()2,0A - ()0,4B - 与x 轴交于另一个点C 连接BC .(1)求抛物线的函数表达式(2)若点Q在抛物线上的对称轴上那么在抛物线上是否存在一点N使得A B Q N为顶点的四边形为平行四边形?若存在请求出N点的坐标∥交BC于点E过点D作(3)点D为直线BC下方抛物线上一动点过点D作DE AB∥轴交BC于点F求EF的最大值DF y(4)在抛物线上是否存在点P直线BP交x轴于点M使ABM与以A B C M中三点为顶点的三角形相似(不重合)?若存在请直接写出点P的坐标若不存在请说明理由.5.如图抛物线223=-++交x轴于A B两点交y轴于点C连接AC BC.y x x(1)求ABC 的面积(2)点M 为y 轴上一点 是否存在点M 使得MBC 与ABC 相似?若存在 请求出点M 的坐标 若不存在 请说明理由(3)点P 为抛物线上一点(点P 与点B 不重合) 且使得PAC △中有一个角是45︒ 请直接写出点P 的坐标.6.如图所示 已知抛物线21y ax bx =+-与x 轴交于()1,0A - ()1,0B 两点 与y 轴交于点C .(1)求此二次函数得解析式(2)过点A 作AP CB ∥交抛物线于点P 求四边形ACBP 的面积(3)在x 轴上方的抛物线上是否存在一点M 过M 作MG x ⊥轴于点G 使以A M G 三点为顶点的三角形与PCA 相似?若存在 请求出M 点的坐标 否则 请说明理由.7.如图1 平面直角坐标系xOy 中 抛物线2y ax bx c =++过点()1,0A - ()2,0B 和()0,2C 连接BC 点()(),02P m n m <<为抛物线上一动点 过点P 作PN x ⊥轴交直线BC 于点M 交x 轴于点N .(1)求抛物线和直线BC 的解析式(2)如图2 连接OM 当OCM 为等腰三角形时 求m 的值(3)当P 点在运动过程中 在y 轴上是否存在点Q 使得以O P Q 、、为顶点的三角形与以B C N 、、为顶点的三角形相似(其中点P 与点C 相对应) 若存在 直接写出点P 的坐标若不存在 请说明理由.8.抛物线2y x bx c =++与x 轴交于 ()1,0B (30)C ,-两点 与y 轴交于A 点.(1)求抛物线的表达式(2)如图1 连接AC 在y 轴的负半轴是否存在点Q 使得12OQC OAC ∠∠=?若存在 求Q 点的坐标 若不存在 请说明理由.(3)如图2 点P 是抛物线上的一个动点 且点P 在第三象限内. ∠连接PO 与直线AC 交于点D 求PDOD的最大值 ∠过点P 作y 轴的垂线交y 轴于点M 若ABO PAM △△ 求此时点P 的横坐标.9.如图 抛物线223(0)y ax ax a a =-->与x 轴交于A B 两点(点A 在点B 的左侧) 与y 轴交于点C 且OB OC =.(1)求抛物线的解析式(2)若P 是线段BC 上一动点(不与点B C 重合) 过点P 作垂直于x 轴的垂线交抛物线于点M 连接CM 当PCM △与ABC 相似时 求此时点P 的坐标.10.如图 已知直线24y x =-+分别交x 轴 y 轴于点A B 抛物线过A B 两点 点P 是线段AB 上一动点 过点P 作PC x ⊥轴于点C 交抛物线于点D .(1)若抛物线的解析式为2224y x x =-++ 设其顶点为M 其对称轴交AB 于点N . ∠求点M 和点N 的坐标∠在抛物线的对称轴上找一点Q 使AQ BQ -的值最大 请直接写出点Q 的坐标 ∠是否存在点P 使四边形MNPD 为菱形?并说明理由(2) 当点P 的横坐标为1时 是否存在这样的抛物线 使得以B P D 为顶点的三角形与AOB 相似?若存在 求出满足条件的抛物线的解析式 若不存在 请说明理由.11.如图 直线22y x =+与x 轴交于点A 与y 轴交于点B .把AOB 沿y 轴翻折 点A 落到点C 过点B 的抛物线2y x bx c =-++与直线BC 交于点(34)D -,.(1)求直线BD 和抛物线的解析式(2)在第一象限内的抛物线上 是否存在一点M 作MN 垂直于x 轴 垂足为点N 使得以M O N 为顶点的三角形与BOC 相似?若存在 求出点M 的坐标. 若不存在 请说明理由.12.抛物线223y x x =--+与x 轴交于A B 两点 与y 轴交于C 点.(1)直接写出A B C 三点的坐标(2)如图1 连接BC 点P 在抛物线上 且PAB BCO ∠=∠ 求P 点坐标.(3)如图2 点D 为抛物线顶点.点H 为AD 中点 过点H 作直线MN (异于直线AD )交抛物线于M N 两点 直线AM 与直线DN 交于点P .问点P 是否在一条定直线上?若是 求该直线的解析式 若不是 请说明理由.13.如图 在平面直角坐标系中 已知抛物线2y x bx c =++与x 轴交于点A B 两点 其中()0A 1, 与y 轴交于点()03C ,.(1)求抛物线解析式(2)如图 连接AC BC 、 过点B 作x 轴垂线 在该垂线上取点P 使得PBC 与ABC 相似(包括全等) 请求出点P 坐标.14.如图 在平面直角坐标系中 O 为坐标原点 抛物线26y ax ax a =--交x 轴负半轴于点A 交x 轴正半轴于点B 交y 轴正半轴于点C 且OB OC =.(1)如图1 求抛物线的解析式(2)如图2 点P 为第四象限的抛物线上一点 其横坐标为t 设OD d = 求d 于t 之间的函数关系(3)如图3 在(2)的条件下 过D 作DE AP ⊥ 过点A 作AF AB ⊥交ED 于F 延长PB 交DE 于点E 连接BF 并延长 连接PG 使EF PG = 若EFB PGB =∠∠ 求:点F 的坐标.15.如图 抛物线()222y x nx n =-+>与x 轴正半轴交于点A 点P 为线段OA 上一点 过P作PB x ⊥轴交抛物线()222y x nx n =-+>于点B 过B 作BC x ∥轴交抛物线()222y x nx n =-+>于点C 连接AC 交PB 于点D(1)如图1 若点A 的横坐标为92∠求抛物线的解析式:∠当45BCA ∠=︒时 求点P 的坐标:(2)若1AP = 点Q 为线段CD 上一点 点N 为x 轴上一点 且90PQN ∠=︒ 将AQP △沿直线PQ 翻折得到,A QP A Q ''所在的直线交x 轴于点M 且17PM MN = 求点Q 的纵坐标 参考答案: 1.(1)213222y x x =-++ (2)35,24D ⎛⎫ ⎪⎝⎭(3)存在 点P 的坐标为()1,32.(1)二次函数的表达式2y x x 2=--(2)M 的坐标302⎛⎫ ⎪⎝⎭,(3)PQQB 有最大值 最大值为133.(1)22y x =-+(2)3q =(3)p q +的值不变化 是定值44.(1)2142y x x =--(2)存在 53,2N ⎛⎫- ⎪⎝⎭(4)存在 ()8,205.(1)6(2)存在 点M 的坐标为30,2⎛⎫- ⎪⎝⎭(3)点P 坐标为(2,3) 57(,)246.(1)21y x =-(2)4(3)存在 ()2,3- 47,39⎛⎫⎪⎝⎭ ()4,157.(1)2y x =-+(2)1m =(3)P8.(1)223y x x =+-(2)(0,3--(3)∠912∠73- 9.(1)2=23y x x --(2)P 的坐标为5433⎛⎫- ⎪⎝⎭,10.(1)∠19,22M ⎛⎫ ⎪⎝⎭ 1,32N ⎛⎫ ⎪⎝⎭∠1,62Q ⎛⎫ ⎪⎝⎭ ∠不存在 (2)存在 2224y x x =-++或25342y x x =-++.11.(1)直线BD 的解析式为:22y x =-+ 抛物线解析式为:22y x x =-++.(2)存在 1(12)M , 2133133(M ++,.12.(1)()()()3,0,1,0,0,3A B C - (2)211,39⎛⎫ ⎪⎝⎭(3)点P 在一条定直线上 该直线的解析式为28y x =+13.(1)243y x x =-+(2)()39,14.(1)211322y x x =-++ (2)3d t =-(3)(29),F --15.(1)∠292y x x =-+ ∠7,02⎛⎫ ⎪⎝⎭(2)22+。
二次函数与相似三角形问题(含答案)

kx ( k
0) 与线段 BC 交于点 D (不与点 B, C 重合),则是否存在这样的直线 △ BAC 相似?若存在,求出该直线的函数表达式及点
以 B, O, D 为顶点的三角形与 在,请说明理由;
D 的坐标;若不存
A( 1,, 0) B (3, 0), C (0, 3)
试比较锐角
( 3) 若点 P 是位于该二次函数对称轴右边图象上不与顶点重合的任意一点, 的大小(不必证明) ,并写出此时点
O 、 C 、D 、B
2. 函数中因动点产生的相似三角形问题一般有三个解题途径 ① 求相似三角形的第三个顶点时,先要分析已知三角形的边 的特点,进而得出已知三角形是否为特 .和角 .
殊三角形。根据未知三角形中已知边与已知三角形的可能对应边分类讨论。 ②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来 推导边的大小。 ③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用 相似来列方程求解。
P, Q 分别是 AB 和 AD 上的动点,连接 PQ ,设 AP
( 3)在( 2)的条件下,如 在这样的
m 使得 △ APQ 与 △ ADB 相似,如存在,请求出
1
例题 2 :如图,已知抛物线 ( 1)求抛物线的对称轴及点 的结论;
y=ax +4ax+t ( a > 0 )交 x 轴于 A 、 B 两点,交 y 轴于点 C ,抛物线的对称轴 A 的坐标; P ,你能判断四边形 ABCP 是什么四边形?并证明你
2
交 x 轴于点 E ,点 B 的坐标为( -1 , 0 ) . ( 2)过点 C 作 x 轴的平行线交抛物线的对称轴于点 ( 3)连接 CA 与抛物线的对称轴交于点
(完整word版)二次函数与相似三角形综合题

O二次函数与相似三角形综合题黄陂区实验中学 邓静教学目标:1、会求二次函数解析式;2、根据条件寻找或构造相似三角形,在二次函数的综合题中利用其性质求出线段的长度,从而得出点的坐标。
教学重点:1、求二次函数解析式;2、相似三角形的判定与性质在二次函数综合题中的运用。
教学难点:根据条件构造相似三角形解决问题。
情感与态度:1、培养学生积极参与教学学习活动的兴趣,增强数学学习的好奇心和求知欲。
2、使学生感受在数学学习活动中获得成功的体验,锻炼学生克服困难的意志,建立自信心。
3、培养学生科学探索的精神。
教学过程:一、复习巩固如图,抛物线y=ax 2+b x -2与x 轴交于点A (-1,0),B (m ,0)两点,与y 轴交于C 点,且∠ACB=90°,求抛物线的解析式.分析:OC 2=OA·OB ∴4=1×m ,m=4 ∴B (4,0)设抛物线解析式为y=a(x+1)(x -4)代入C 点(0,-2) ∴抛物线解析式为213222y x x =--.二、新授例题、如图,直线y =-x+3与x 轴、y 轴分别相交于B 、C ,经过B 、C 两点的抛物线y=ax 2+bx+c与x 轴另一交点为A ,顶点为P ,且对称轴是直线x=2,(1)求抛物线解析式;(2)连结AC ,请问在x 轴上是否存在点Q ,使得以点P 、B 、Q 为顶点的三角形与△ACB 相似,若存在,请求出Q 点坐标;若不存在,说明理由.(3)D 点为第四象限的抛物线上一点,过点D 作DE ⊥x 轴,交CB 于E ,垂足于H ,过D 作DF ⊥CB ,垂足为F ,交x 轴于G ,试问是否存在这样的点D ,使得△DEF 的周长恰好被x 轴平分?若能,请求出D 点坐标;若不能,请说明理由.[解] (1)直线3y x =-+与x 轴相交于点B , ∴当0y =时,3x =,∴点B 的坐标为(30),. 又抛物线过x 轴上的A B ,两点,且对称轴为2x =,根据抛物线的对称性, ∴点A 的坐标为(10),. 3y x =-+过点C ,易知(03)C ,,3c ∴=. 又抛物线2y ax bx c =++过点(10)(30)A B ,,,, ∴(1)(3)y a x x =--,经过C 点(0,3)243y x x ∴=-+.(2)连结PB ,由2243(2)1y x x x =-+=--,得(21)P -,,设抛物线的对称轴交x 轴于点M ,在Rt PBM △中,1PM MB ==,45PBM PB ∴==,∠由点(30)(03)B C ,,,易得3OB OC ==,在等腰直角三角形OBC 中, 45ABC =∠,由勾股定理,得BC =假设在x 轴上存在点Q ,使得以点P B Q ,,为顶点的三角形与ABC △相似. ①当BQ PB BC AB=,45PBQ ABC ==∠∠时,PBQ ABC △∽△.2=,3BQ ∴=, 又3BO =,∴点Q 与点O 重合,1Q ∴的坐标是(00),. ②当QB PB AB BC=,45QBP ABC ==∠∠时,QBP ABC △∽△.即2QB =,23QB ∴=.x21P 273333OB OQ OB QB =∴=-=-=,, 2Q ∴的坐标是703⎛⎫ ⎪⎝⎭,. 180********PBx BAC PBx BAC =-=<∴≠,,∠∠∠∠.∴点Q 不可能在B 点右侧的x 轴上.综上所述,在x 轴上存在两点127(00)03Q Q ⎛⎫ ⎪⎝⎭,,,,能使得以点P B Q ,,为顶点的三角形与ABC △相似.(3)设D (a ,a 2-4a+3),则E (a ,-a+3)△DFE ∽△BOC∴DE :BC=L △DEF :L △BOC2∴L △DEF1+)×(-a 2+3a) ∴DH+DG=12DFE L ∆= 1)DH= 21)(43)a a -+- = 121)×(-a 2+3a) ∴243a a -+-=21(3)2a a -+ ∴a 1=2,a 2=3(舍)∴D (2,-1)应用变式:1、在此抛物线上是否存在P 点?使得∠1+∠2=45°,若存在,请求出P 点坐标;若不存在,请说明理由.分析:(1)延长CP 与x 轴交于E 点,∠1+∠2=45°=∠ABC=∠E+∠2∴∠1=∠E ,xx 又∵∠COA公共∴△OCA∽△OEC∴OC2=O A·OEOC2=9=1×OE∴OE=9∴E(9,0)∴直线解析式133y x=-+联立直线与抛物线∴ P的坐标为(113,169)(2)P点与A点重合,P(1,0),∴综上所述,P的坐标为(1116,39),(1,0).2、在上题抛物线中,P为抛物线上一点,PE⊥BC于E,且CE=3PE,求P点坐标.分析:连AC、PC,证△PEC∽△OAC,∠OCA=∠PCE,∴∠PCA=45°.延长CP交x轴于N,△ACB∽△ANC,AC2=A B·AN,∴N(6,0),1:32CN y x=-+,联立抛物线,得P(75,24).三、小结点的坐标是综合题的立足点(求解析式),又是综合题的制高点(求满足条件的点的坐标或存在性探求),求点的坐标一般历经下面两个关键步骤:(1)定位(2)计算四、作业练习1、如图,抛物线22y x x x=--交轴于A、B两点(A点在B点左侧),交y轴于C (0,-2),过A、C画直线,点M在y轴右侧的抛物线上,从M为圆心的圆与直线AC相切,切点为H,且ΔCHM∽ΔAOC,求M点坐标.。
二次函数与相似三角形综合题20160203
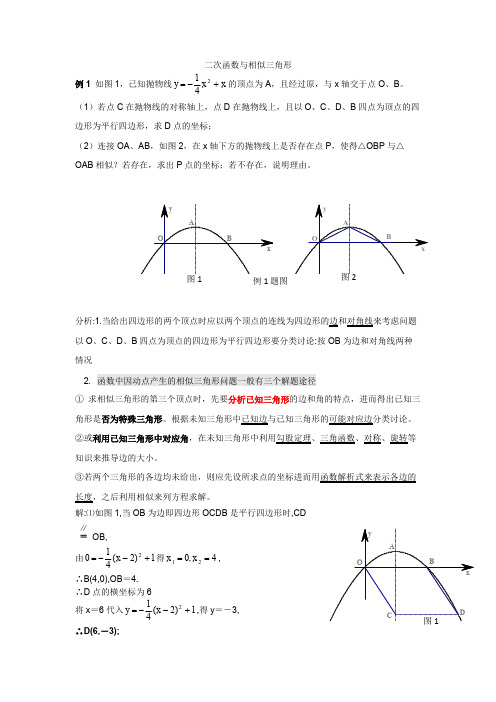
y A
O
B
x
y A
O
B x
图1
例 1 题图
图2
分析:1.当给出四边形的两个顶点时应以两个顶点的连线为四边形的边和对角线来考虑问题 以 O、C、D、B 四点为顶点的四边形为平行四边形要分类讨论:按 OB 为边和对角线两种
情况
2. 函数中因动点产生的相似三角形问题一般有三个解题途径 ① 求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三
AE=3﹣m,EM=﹣m+4,CF=m,PF=﹣m2+m+4﹣4=﹣m2+m.
若以 P、C、F 为顶点的三角形和△AEM 相似,分两种情况:①若△PFC∽△AEM,则
PF:AE=FC:EM,
即(﹣m2+m):(3﹣m0 且 m≠3,
∴m= .
∵△PFC∽△AEM,∴∠PCF=∠AME, ∵∠AME=∠CMF,∴∠PCF=∠CMF. 在直角△CMF 中,∵∠CMF+∠MCF=90°, ∴∠PCF+∠MCF=90°,即∠PCM=90°, ∴△PCM 为直角三角形; ②若△CFP∽△AEM,则 CF:AE=PF:EM, 即 m:(3﹣m)=(﹣m2+m):(﹣m+4), ∵m≠0 且 m≠3,
2 由 1 x 1 x2 x ,
24
y A
O
A'
B
E
x
得 x1 0, x 2 6
.∴P(6,-3) 过 P 作 PE⊥x 轴,在 Rt△BEP 中,BE=2,PE=3,
图2
P
∴PB= 13 ≠4.
∴PB≠OB,∴∠BOP≠∠BPO, ∴△PBO 与△BAO 不相似, 同理可说明在对称轴左边的抛物线上也不存在符合条件的 P 点. 所以在该抛物线上不存在点 P,使得△BOP 与△AOB 相似.
二次函数与相似三角形测试题

二次函数与相似三角形测试题一、选择题(本大题共10小题,每小题4分,满分40分)1.下列各组中得四条线段成比例的是( ). A .4cm 、2cm 、1cm 、3cm B .1cm 、2cm 、3cm 、5cm C .25cm 、35cm 、45cm 、55cm D .1cm 、2cm 、20cm 、40cm 2.给出下列四个命题,其中真命题有( ).(1)等腰三角形都是相似三角形 (2)直角三角形都是相似三角形(3)等腰直角三角形都是相似三角形 (4)等边三角形都是相似三角形A .1个B .2个C .3个D .4个 3、抛物线23(1)1y x =-+的顶点坐标是( )A 、(1,1)B 、(1,1)-C 、(1,1)--D 、(1,1)-4.如果点D 、E 分别在ΔABC 的边AB 、AC 上,下列条件中可以推出DE ∥BC 的是…( )(A) AD AB = 23 ,DE BC = 23 ; (B ) AD BD = 23 ,CE AE = 23 ;(C ) AB AD = 32 ,EC AE = 12 ; (D) AB AD =34,AEEC = 34.5、下列四个函数中,y 的值随着x 值的增大而减小的是( ) A 、2y x = B 、1(0)y x x=> C 、1y x =+ D 、2(0)y x x =>6、抛物线24y x mx =--与坐标轴的交点个数是( ) A 、1个 B 、2个 C 、3个 D 、0个7、若二次函数25y x bx =++配方后为2(2)y x k =-+,则,b k 分别为( ) A 、0,5 B 、0,1 C 、-4,5 D 、-4,18、已知点123(1,),(2,),(3,)y y y -在反比例函数21k y x--=的图象上,则下列结论正确的是( )A 、123y y y >>B 、132y y y >>C 、312y y y >>D 、231y y y >>9.在同一坐标系中一次函数y ax b =+和二次函数2y axbx =+的图象可能为( )10.在相似三角形中,已知其中一个三角形三边的长是4,6,8,另一个三角形的一边长是2,则另一个三角形的周长是 ( ) (A )4.5; (B ) 6; (C )9; (D ) 以上答案都有可能 二、填空题:(本大题共10题,每题4分,满分40分)11.两相似三角形面积比为1:3,则对应中线的比为 ___________ 12.如果线段c 是a 、b 的比例中项,且a = 2,b = 8,则c = . 13、若抛物线2(1)m m y m x -=-开口向下,则m =14.若43===f e d c b a , 则______3232=+-+-fd b ec a15.如图,点A 、B 是双曲线3y x=上的点,分别经过A 、B 两点向x 轴、y 轴作垂线段,若1S =阴影,则12S S += .16.已知二次函数2y ax bx c =++(0a ≠)的图象如图所示,有下列4个结论:①0abc >;②b a c <+;③420a b c ++>;④240b ac ->;其中正确的结第14题A14题论有_____________ (填序号)17. 如果先将抛物线()2234y x =-+向左平移3个单位,再向下平移1个单位,那么所得到的抛物线的表达式为__________18.如图,已知一次函数1y x =+的图象与反比例函数k y x=的图象在第一象限相交于点A ,与x 轴相交于点C AB x ,⊥轴于点B ,AOB △的面积为1,则AC 的长为 (保留根号).19.如图,L 1//L 2//L 3,AB=3,BD=5, FG :EG 的值是________20. 如图,双曲线()k y=k 0x≠上有一点A ,过点A 作AB ⊥x 轴于点B ,△AOB 的面积为2,则该双曲线的表达式为 。
二次函数与相似三角形综合题

二次函数取相似三角形概括题之阳早格格创做黄陂区真验中教邓静教教目标:1、会供二次函数剖析式;2、根据条件觅找或者构制相似三角形,正在二次函数的概括题中利用其本量供出线段的少度,进而得出面的坐标.教教沉面:1、供二次函数剖析式;2、相似三角形的判决取本量正在二次函数概括题中的使用.教教易面:根据条件构制相似三角形办理问题.情感取做风:1、培植教死主动介进教教教习活动的兴趣,坚韧数教教习的佳偶心战供知欲.2、使教死体验正在数教教习活动中赢得乐成的体验,锻炼教死克服艰易的毅力,修坐自自疑心.3、培植教死科教探索的粗神.教教历程:一、复习坚韧如图,扔物线y=ax2+bx-2取x轴接于面A(-1,0),B(m,0)二面,取y轴接于C面,且∠ACB=90°,O供扔物线的剖析式.分解:OC 2=OA·OB ∴4=1×m ,m=4 ∴B (4,0)设扔物线剖析式为y=a(x+1)(x -4)代进C 面(0,-2)∴扔物线剖析式为213222y x x =--.二、新授例题、如图,曲线y=-x+3取x 轴、y 轴分别相接于B 、C ,通过B 、C 二面的扔物线y=ax 2+bx+c 取x 轴另一接面为A ,顶面为P ,且对于称轴是曲线x=2,(1)供扔物线剖析式;(2)连结AC ,请问正在x 轴上是可存留面Q ,使得以面P 、B 、Q 为顶面的三角形取△ACB 相似,若存留,哀供出Q 面坐标;若没有存留,证明缘由.(3)D 面为第四象限的扔物线上一面,过面D 做DE ⊥x 轴,接CB 于E ,垂脚于H ,过D 做DF ⊥CB ,垂脚为F ,接x 轴于G ,试问是可存留那样的面D ,使得△DEF 的周少恰佳被x 轴仄分?若能,哀供出D 面坐标;若没有克没有及,请证明缘由.[解](1)曲线3y x =-+取x 轴相接于面B ,∴当0y =时,3x =,∴面B 的坐标为(30),. 又扔物线过x 轴上的A B ,二面,且对于称轴为2x =,ABCPO xy2x =根据扔物线的对于称性,∴面A 的坐标为(10),. 3y x =-+过面C ,易知(03)C ,, 3c ∴=.又扔物线2y ax bx c =++过面(10)(30)A B ,,,, ∴(1)(3)y a x x =--,通过C 面(0,3)243y x x ∴=-+.(2)连结PB ,由2243(2)1y x x x =-+=--,得(21)P -,, 设扔物线的对于称轴接x 轴于面M ,正在Rt PBM △中,1PM MB ==,45PBM PB ∴==,∠由面(30)(03)B C ,,,易得3OB OC ==,正在等腰曲角三角形OBC 中,45ABC =∠,由勾股定理,得BC =假设正在x 轴上存留面Q ,使得以面P B Q ,,为顶面的三角形取ABC △相似.①当BQ PB BCAB=,45PBQ ABC ==∠∠时,PBQ ABC △∽△.即2=,3BQ ∴=, 又3BO =,∴面Q 取面O 沉合,1Q ∴的坐标是(00),.②当QB PB ABBC=,45QBP ABC ==∠∠时,QBP ABC △∽△.21P即2232QB =,23QB ∴=.273333OB OQ OB QB =∴=-=-=,, 2Q ∴的坐标是703⎛⎫⎪⎝⎭,. 180********PBx BAC PBx BAC =-=<∴≠,,∠∠∠∠.∴面Q 没有成能正在B 面左侧的x 轴上.综上所述,正在x 轴上存留二面127(00)03Q Q ⎛⎫⎪⎝⎭,,,,能使得以面P B Q ,,为顶面的三角形取ABC △相似.(3)设D (a ,a 2-4a+3),则E (a ,-a+3)△DFE ∽△BOC∴DE :BC=L △DEF :L △BOC232632DFE∆+∴L △DEF 21)×(-a 2+3a)∴DH+DG=12DFE L ∆=(21)DH =2(21)(43)a a -+-=12(21)×(-a 2+3a)∴243a a -+-=21(3)2a a -+ ∴a 1=2,a 2=3(舍)∴D (2,-1)应用变式:1、正在此扔物线上是可存留P 面?使得∠1+∠2=45°,若存留,哀供出P 面坐标;若没有存留,请证明缘由.x分解:(1)延少CP 取x 轴接于E 面,∠1+∠2=45°=∠ABC=∠E+∠2∴∠1=∠E , 又∵∠COA 公同 ∴△OCA ∽△OEC ∴OC 2=OA ·OE OC 2=9=1×OE ∴OE=9 ∴E (9,0)∴ 曲线剖析式133y x =-+联坐曲线取扔物线∴ P 的坐标为(113,169)(2)P 面取A 面沉合,P (1,0),∴ 综上所述,P 的坐标为(1116,39),(1,0).2、正在上题扔物线中,P 为扔物线上一面,PE ⊥BC 于E ,且CE=3PE ,供P 面坐标.分解:连AC 、PC ,证△PEC ∽△OAC ,∠OCA=∠PCE ,∴∠PCA=45°.延少CP 接x 轴于N ,△ACB ∽△ANC ,AC 2=AB ·AN ,∴N (6,0),1:32CN y x =-+,联坐扔物线,得P (75,24).三、小结面的坐标是概括题的坐脚面(供剖析式),又是概括题的制下面(供谦脚条件的面的坐标或者存留性探供),供面的坐标普遍历经底下二个闭键步调:(1)定位(2)估计四、做业训练1、如图,扔物线22=--交轴于A、B二面(A面正在y x x xB面左侧),接y轴于C(0,-2),过A、C绘曲线,面M正在y轴左侧的扔物线上,从M为圆心的圆取曲线AC 相切,切面为H,且ΔCHM∽ΔAOC,供M面坐标.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PC 于 B 点,直线 QA 与直线 PC 及两坐标轴围成矩形 OABC .是否存在点 Q ,使得
△OPC 与 △PQB 相似?若存在,求出 Q 点的坐标;若不存在,说明理由.
(2)如果符合(2)中的 Q 点在 x 轴的上方,连结 OQ ,矩形 OABC 内的四个三角形
△O△P△C,△,, PQB OQP OQA 之间存在怎样的关系?为什么?
要使 △O∽C△P
QBP, BQ PB ,则有 3 n m
3
,即
OC CP
3
3
3
2 3
m2
53 3
m
m
3
3
3
解之得, m1 3 3, m2 3 ,当 m 3 时,即为 P 点, 当 m1 3 3 时, n 3 ,所以得 Q(3 3, 3) . 故存在两个 Q 点使得 △OCP 与 △PBQ 相似.
二次函数与相似三角形 例 1 如图 1,已知抛物线 y 1 x 2 x 的顶点为 A,且经过原,与 x 轴交于点 O、B。
4 (1)若点 C 在抛物线的对称轴上,点 D 在抛物线上,且以 O、C、D、B 四点为顶点的四 边形为平行四边形,求 D 点的坐标; (2)连接 OA、AB,如图 2,在 x 轴下方的抛物线上是否存在点 P,使得△OBP 与△ OAB 相似?若存在,求出 P 点的坐标;若不存在,说明理由。
例 2 (2013 凉山州压轴题)如图,抛物线 y=﹣x2+x+4 交 x 轴于 A、B 两点,与 y 轴交于点 C,以 OC、OA 为边作矩形 OADC 交抛物线于点 G. (1)抛物线的对称轴 l 在边 OA(不包括 O、A 两点)上平行移动,分别交 x 轴于点 E,交 CD 于点 F,交 AC 于点 M,交抛物线于点 P,若点 M 的横坐标为 m,请用含 m 的代数式表示 PM 的长; (2)在(1)的条件下,连结 PC,则在 CD 上方的抛物线部分是否存在这样的点 P,使得以 P、C、F 为顶点的三角形和△AEM 相似?若存在,求出此时 m 的值,并直接判断△PCM 的形 状;若不存在,请说明理由.
B,O, D 为顶点的三角形与 △BAC 相似.
在 y x2 2x 3 中,令 y 0 ,则由 x2 2x 3 0 ,解得 x1 1,x2 x 0 ,得 y 3 .C(0,3) . 设过点 O 的直线 l 交 BC 于点 D ,过点 D 作 DE ⊥ x 轴于点 E . Q 点 B 的坐标为 (3,0) ,点 C 的坐标为 (0,3) ,点 A 的坐标为 (1,0) .
角形是否为特殊三角形。根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等
知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的
长度,之后利用相似来列方程求解。
解:⑴如图 1,当 OB 为边即四边形 OCDB 是平行四边形时,CD
边形,此时 D 点的坐标为(-2,-3), 当 OB 为对角线即四边形 OCBD 是平行四边形时,D 点即为 A 点,此时 D 点的坐标为(2,1)
⑵如图 2,由抛物线的对称性可知:AO=AB,∠AOB=∠ABO. 若△BOP 与△AOB 相似,必须有∠POB=∠BOA=∠BPO
设 OP 交抛物线的对称轴于 A′点,显然 A′(2,-1) ∴直线 OP 的解析式为 y 1 x
Q 点的坐标为 (2 3,,2,) (3 3 3) .
(2)在 Rt△OCP 中,因为 tan COP CP 3 .所以 COP 30o . OC 3
当 Q 点的坐标为 (2 3, 2) 时, BPQ COP 30o. 所以 OPQ OCP B QAO 90o. 因此, △O△P△C,△,, PQB OPQ OAQ 都是直角三角形.
D
的坐标为
3 4
,9 4
.]
若是②,则有 BD BO gBA 3 4 2 2 . BC 3 2
而 OBC 45o, BE DE . 在 Rt△BDE 中,由勾股定理,得 BE 2 DE 2 2 BE 2 BD 2 (2 2)2 .
∥ = OB,
由0
1 (x 4
2) 2
1得 x1
0, x 2
4
,
∴B(4,0),OB=4.
∴D 点的横坐标为 6
将 x=6 代入 y 1 (x 2)2 1 ,得 y=-3, 4
∴D(6,-3);
y A
O
B x
C
D
图1
根据抛物线的对称性可知,在对称轴的左侧抛物线上存在点 D,使得四边形 ODCB 是平行四
2 9
2
.
BA
4
4
而 OBC 45o, BE DE .
在 Rt△BDE
中,由勾股定理,得
BE
2
DE
2
2
BE
2
BD
2
9
2 4
2 .
解得
BE
DE
9
(负值舍去).
4
OE
OB
BE
3 9
3
.
44
点
D
的坐标为
3 4
,9 4
.
将点 D 的坐标代入 y kx(k 0) 中,求得 k 3 .
∴点 P 的坐标为(m,﹣ m2+m+4),
4
7
∴PM=PE﹣ME=(﹣m2+m+4)﹣(﹣ m+4)=﹣m2+ m,
3
3
7
即 PM=﹣m2+ m(0<m<3);
3
(3)在(2)的条件下,连结 PC,在 CD 上方的抛物线部分存在这样的点 P,使得以
P、C、F 为顶点的三角形和△AEM 相似.理由如下:由题意,可得
AE=3﹣m,EM=﹣m+4,CF=m,PF=﹣m2+m+4﹣4=﹣m2+m.
若以 P、C、F 为顶点的三角形和△AEM 相似,分两种情况:①若△PFC∽△AEM,则
PF:AE=FC:EM,
即(﹣m2+m):(3﹣m)=m:(﹣ m+4),
∵m≠0 且 m≠3,
∴m= .
∵△PFC∽△AEM,∴∠PCF=∠AME, ∵∠AME=∠CMF,∴∠PCF=∠CMF. 在直角△CMF 中,∵∠CMF+∠MCF=90°, ∴∠PCF+∠MCF=90°,即∠PCM=90°, ∴△PCM 为直角三角形; ②若△CFP∽△AEM,则 CF:AE=PF:EM, 即 m:(3﹣m)=(﹣m2+m):(﹣m+4), ∵m≠0 且 m≠3,
∴m=1. ∵△CFP∽△AEM,∴∠CPF=∠AME, ∵∠AME=∠CMF,∴∠CPF=∠CMF. ∴CP=CM, ∴△PCM 为等腰三角形.
综上所述,存在这样的点 P 使△PFC 与△AEM 相似.此时 m 的值为 或 1,△PCM 为直角三
角形或等腰三角形.
点评:此题是二次函数的综合题,其中涉及到运用待定系数法求二次函数、一次函数的解 析式,矩形的性质,相似三角形的判定和性质,直角三角形、等腰三角形的判定,难度适 中.要注意的是当相似三角形的对应边和对应角不明确时,要分类讨论,以免漏解.
2.在平面直角坐标系 xOy 中,已知二次函数 y x2 2x 3 的图象与 x 轴交于 A,B 两点
(点 A 在点 B 的左边),与 y 轴交于点 C . (1)若直线 l : y kx(k 0) 与线段 BC 交于点 D (不与点 B,C 重合),则是否存在这样
的直线 l ,使得以 B,O, D 为顶点的三角形与 △BAC 相似?若存在,求出该直线的函数 表达式及点 D 的坐标;若不存在,请说明理由; A(1,0),,B(,3 0),C(0 3)
(2)若点 P 是位于该二次函数对称轴右边图象上不与顶点重x合的任意一点,试比较锐角
x
l
PCO 与 ACO 的大小l (不必证明),并写出此时点 P 的横坐标 xp 的取值范围.
C C
D
A
By
AOE
By
x 1
x 1
练习 3 图
(1)假设存在直线 l : y kx(k 0) 与线段 BC 交于点 D (不与点 B,C 重合),使得以
又在 Rt△OAQ 中,因为 tan QOA QA 3 .所以 QOA 30o . AO 3
即有 POQ QOA QPB COP 30o . 所以 △O∽P△C∽△∽PQ△B OQP OQA , 又因为 QP ⊥⊥OP, QA OA POQ AOQ 30o, 所以 △O≌Q△A OQP .
y
CP
B
Q
O
E
Ax
(1)存在.
设 Q 点的坐标为 (m,
n) ,则 n 2 m2 5
3 m,
3
3
要使 △O∽C△P
PBQ,
BQ
PB
3n
,则有
m
3
,即
CP OC
3
3
3
2 3
m2
53 3
m
m
3
3
3
解之得, m1 2 3, m2 2 .
当 m1 2 3 时, n 2 ,即为 Q 点,所以得 Q(2 3, 2)
