陕西省2017届高三数学下学期第十一次模考试题文
陕西省西安中学2017届高三下学期一模考试数学(文)试题Word版含答案
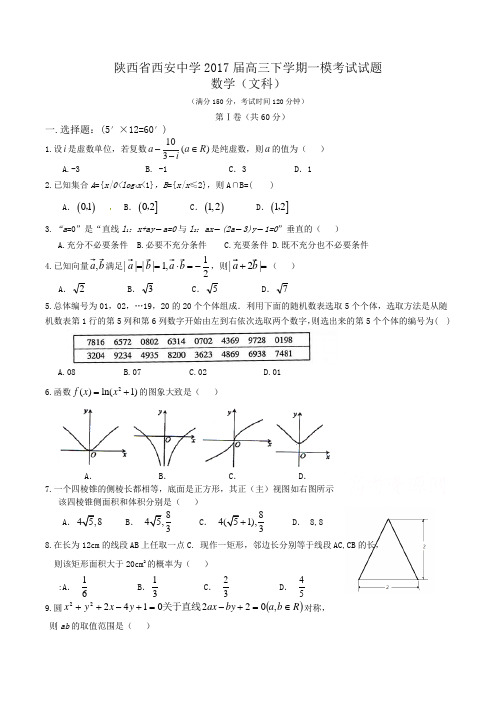
陕西省西安中学2017届高三下学期一模考试试题数学(文科)(满分150分,考试时间120分钟)第Ⅰ卷(共60分)一.选择题:(5′×12=60′)1.设i 是虚数单位,若复数10()3a a R i-∈-是纯虚数,则a 的值为( )A.-3B. -1C .3D .12.已知集合A ={x|0<log 4x <1},B ={x|x ≤2},则A∩B=( ) A .()01, B .(]02,C .()1,2D .(]12, 3.“a =0”是“直线l 1:x+ay -a=0与l 2:ax -(2a -3)y -1=0”垂直的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 4.已知向量,满足21,1||||-=⋅==,则=+|2|( )A .2B .3C .5D .75.总体编号为01,02,…19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )A.08B.07C.02D.01 6.函数)1ln()(2+=x x f 的图象大致是( )A .B .C .D .7.一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示 该四棱锥侧面积和体积分别是( )A .B . 83C . 81),3+ D . 8,8 8.在长为12cm 的线段AB 上任取一点C. 现作一矩形,邻边长分别等于线段AC,CB 的长, 则该矩形面积大于20cm 2的概率为( ):A .16 B .13 C . 23 D . 45 9.圆()R b a by ax y x y x ∈=+-=+-++,022014222关于直线对称,则ab 的取值范围是( )A.⎥⎦⎤ ⎝⎛∞-41,B. ⎥⎦⎤ ⎝⎛41,0C.⎪⎭⎫ ⎝⎛-0,41D. ⎪⎭⎫⎝⎛∞-41,10.x 为实数,[]x 表示不超过x 的最大整数,则函数()[]f x x x =-在R 上为 ( )A .奇函数B .偶函数C .增函数D . 周期函数 11.将函数()x x f y cos =的图像向左平移4π个单位后,再做关于x 轴的对称变换得到函数1cos 22-=x y 的图像,则()x f 可以是( )A.x cos 2-B. x sin 2-C. x cos 2D. x sin 212. 椭圆22:143x y C +=的左、右顶点分别为12,A A ,点P 在C 上且直线2PA 的斜率的 取值范围是[]2,1--,那么直线1PA 斜率的取值范围是( ) A .1324⎡⎤⎢⎥⎣⎦, B .3384⎡⎤⎢⎥⎣⎦, C .112⎡⎤⎢⎥⎣⎦, D .314⎡⎤⎢⎥⎣⎦,第Ⅱ卷(共90分)二.填空题:(5′×4=20′)13.定义运算a b ⊗为执行如图所示的程序框图输出的S 值,则552cos2tan 34ππ⎛⎫⎛⎫⊗ ⎪ ⎪⎝⎭⎝⎭的值为 14.已知不等式组⎪⎩⎪⎨⎧≥-≥-≤+0,1,1y y x y x 所表示的平面区域为D,若直线y=kx -3k与平面区域D 有公共点,则k 的取值范围为15.ABC ∆中,a,b,c 分别是角A 、B 、C 的对边,若C A B b c a sin cos 6sin ,222⋅==-且, 则b=16. 将数列{}13n -按“第n 组有n 个数”的规则分组如下:(1),(3,9),(27,81,243),…,则第10组中的第一个数是_____________三.解答题: (12′×5+10′=70′)17. 已知数列{}n x 的首项31=x ,通项()2,,n n x p qn n N p q *=+∈为常数,且541,,x x x 成等差数列,求: (Ⅰ)p,q 的值;(Ⅱ)数列{}n x 前n 项和n S 的公式.18. 若函数()()2sin sin cos 0f x ax ax ax a =->的图像与直线y=m (m 为常数)相切, 并且切点的横坐标依次成等差数列,且公差为2π. (Ⅰ)求m 的值;(Ⅱ)若点A ()00,y x 是y=f(x)图像的对称中心,且⎥⎦⎤⎢⎣⎡∈2,00πx ,求点A 的坐标.19. 甲乙两人进行两种游戏,两种游戏规则如下:游戏Ⅰ:口袋中有质地、大小完全相同的5个球, 编号分别为1,2,3,4,5,甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.游戏Ⅱ:口袋中有质地、大小完全相同的6个球,其中4个白球,2个红球,由裁判有放回的摸两次球,即第一次摸出记下颜色后放回再摸第二次,摸出两球同色算甲赢,摸出两球不同色算乙赢.(Ⅰ)求游戏Ⅰ中甲赢的概率;(Ⅱ)求游戏Ⅱ中乙赢的概率;并比较这两种游戏哪种游戏更公平?试说明理由.20. 18.如图:三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB =90°,AC =BC=121AA ,D 是侧棱AA 1的中点. (Ⅰ)证明:平面BDC 1⊥平面BDC ;(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比. 21. 设函数)1ln()(2++=x b x x f ,其中0≠b . (Ⅰ)若12b =-,求)(x f 在[]3,1的最小值;(Ⅱ)如果()f x 在定义域内既有极大值又有极小值,求实数b 的取值范围;请考生在第(22)、(23)、(24)三题中任选一题作答.注意:只能做所选定的题目,如果多做,则按所做的第一个题目计分. 22.选修4—1:几何证明选讲如图,已知PA 与圆O 相切于点A ,经过点O 的割线PBC 交圆O 于点B 、C ,∠APC 的平分线分别交AB 、AC 于点D 、E ,P(Ⅰ)证明:∠ADE =∠AED ; (Ⅱ)若AC=AP ,求PC PA的值.23.选修4-4:极坐标系与参数方程已知直线l的参数方程是2x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 是参数),圆C 的极坐标方程为ρ=2cos(θ+4).(Ⅰ)求圆心C 的直角坐标;(Ⅱ)由直线l 上的点向圆C 引切线,求切线长的最小值.24.选修4-5:不等式选讲设不等式112<-x 的解集为M , 且M b M a ∈∈,. (Ⅰ) 试比较1+ab 与b a +的大小;(Ⅱ) 设A max 表示数集A 中的最大数, 且⎭⎬⎫⎩⎨⎧+=b abb a ah 2,,2max , 求h 的范围.陕西省西安中学2017届高三下学期一模考试试题数学(文科)参考答案一、选择题:(5′×12=60′) (A 卷) CDABD ABCAD BB 二、填空题:(5′×4=20′) 13.4; 14.031≤≤-k ; 15.3; 16. 345; 三、解答题:(12′×5+10′=70′)17.解:(Ⅰ)由31=x 得2p+q=3,又∵45155442,52,42x x x q p x q p x =++=+=且∴q p q p 8252355+=++,解得p=1,q=1 ………..………………………….…..6分(Ⅱ)由(Ⅰ)得n x n n +=2∴()2122...3212 (2221)32++-=+++++++++=+n n n S n nn ……….……….12分 18.解:(Ⅰ) ∵()⎪⎭⎫ ⎝⎛+-=42sin 2221πax x f …………….………………………….……3分 ∴ 2221±=m ……………………………………………………………………..5分 (Ⅱ) ∵切点的横坐标依次成等差数列,且公差为2π, ∴a a T πππ===2222=⇒a ()⎪⎭⎫ ⎝⎛+-=44sin 2221πx x f ……………………………....7分 ∵ 点A ()00,y x 是y=f(x)图像的对称中心 ∴1644400ππππ-=⇒=+k x k x ….9分 ∵⎥⎦⎤⎢⎣⎡∈2,00πx ∴1671630ππ或=x ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛2116721163,或,ππA ……………………….12分 19.解:(Ⅰ)∵游戏Ⅰ中有放回地依次摸出两球基本事件有5*5=25种,其中甲赢包含(1,1)(1,3)(1,5)(3,3)(3,5)(5,5)(3,1)(5,1)(5,3)(2,2)(2,4)(4,4)(4,2)13种基本事件, ∴游戏Ⅰ中甲赢的概率为 P=2513…………………………..……………..5分 (Ⅱ)设4个白球为a,b,c,d, 2个红球为A,B ,则游戏Ⅱ中有放回地依次摸出两球基本事件有6*6=36种,其中乙赢包含(a,A ), (b,A ),(c,A )(d,A )(a,B )(b, B )(c, B )(d, B )(A,a )(A,b )(A,c )(A,d )(B,a )(B,b )(B,c )(B,d )16种基本事件, ∴游戏Ⅱ中乙赢的概率为P’=1583016= ………………………………...……………….10分 ∵21158212513-<- ∴游戏Ⅰ更公平 ………………………………....12分20.解:解:(1)证明:由题设可知1111,,A ACC BC C AC CC AC BC CC BC 平面⊥⇒=⊥⊥1111DC ACC A DC BC≠⊂∴⊥又平面…………………………………………2分DC DC CDC ADC DC A ⊥=∠∴=∠=∠1010119045即又 …………4分 BDC DC C BC DC 平面又⊥∴=1,111DC BDC BDC BDC ≠⊂⊥又平面,故平面平面…………………………6分(2)设棱锥1DACC B -的体积为/V ,21122113131,11/=⨯+⨯⨯=⋅=∴=DACC S BC V AC 设 ……………………………………9分又三棱柱的体积为V=1,故平面1BDC 分棱柱所得两部分的体积比为1:1 ……………12分 21.解:其中第一问6分,第二问6分,共12分.四、选考题(本题满分10分):请考生从第(22)、(23)、(24)三题中任选一题作答。
陕西省师范大学附属中学2017届高三下学期第十一次模考

物理第十一次模考答案一、选择题二、非选择题22.(5分) (1)D ;(2)C ,D ;(3) 3.1×102;(4)5×106 Pa 23.(10分)24.25.解:(1)设人经时间1t 下落到平板车上,车在这段时间内前进的距离为1x由运动学公式得:212121gt h h =- ① (2分)101t v x = ② (1分)代入数据由①②解得: 1x =6m (1分)所以人落在离车尾端的距离x =3.5m (2分)(2)设人落在车上后做匀加速运动的加速度为1a ,经过时间2t 人车速度相同为v 由牛顿第二定律得:1ma mg =μ ③(1分)v =2021at v t a -= ④ (1分)代入数据由③④解得:2t =1sv =2m/s (2分)在这段时间内的人相对车向后的位移为221222012121t a at t v x --=∆ =3m(2分)此后人车都减速运动直到静止,人相对车向前的位移为5.0222122=-=∆a v a v x m(2分)由于5.25.0321=-=∆-∆x x m 〈3.5m (1分)所以不会滑下(3)人车相对滑动产生的热量)(21x x mg Q ∆+∆=μ=455J (4分) 33.(1) BCE(2)解:(1)由玻意耳定律可知PLS =P 1(L +h )S 2分 活塞受力平衡 P 1 S =PS -mg 2分 联立方程可得S =mg (L +h )/Ph 2分 (2)由盖—吕萨克定律(L +h )S /T 0=L 0S /T 2分 解得 L 0=(L +h )T / T 0 34.(1) A DE(2) 解:①根据光的折射定律,分析光线OD 的折射情况,有23045==γ=o oi n sin sin sin sin (3分)由n θ1=sin 知θ=450 1分②由o oLOD 12045sin sin =得 4分 LDE OD 36== 2分。
陕西省西安市长安区高三数学第十一次质量检测试题 文

2017---2018学年度第十一次质量检测高三文科数学试题第Ⅰ卷(选择题 共60分)一.选择题(本题共12小题,每小题5分,共60分。
) 1. 设集合{}{}|2,|21,x A x x B y y =<==-则AB =( )A.(),3-∞B. (),2-∞C.[)2,3D.()1,2- 2.复数1cos sin z x i x =-,2sin cos z x i x =-,则=⋅21z z ( ) A .1 B .2 C .3 D .4 3.设命题P :,n N ∀∈()f n n ≤,则错误!未找到引用源。
是( )A. ,n N ∀∉()f n n >B. 0,n N ∃∈00()f n n >C. 0,n N ∃∈00()f n n ≤D. ,n N ∀∈()f n n > 4. 已知圆锥曲线的方程为2221x y -=,则该曲线的离心率为( )A.2B. 25. 宋元时期数学名著《算数启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的,a b 分别为5,2,则输出的n =( )A.2B.3C.4D.5 6. 设{}n a 是首项为1a ,公差为1-的等差数列,n S 为其前n 项和.若124,,S S S 成等比数列,则1a =( ) A.2 B.-2 C.12 D.12- 7. 矩形ABCD 中,2,1AB BC ==,O 为AB 的中点,在矩形ABCD 内随机取一点,则取到的点到O 的距离大于1的概率为( )A .8π B .18π- C .4π D .14π- 8. 如右图,在小正方形边长为1的网格中画出了某多面体的三视图,则该多面体的外接球表面积为( )A.27πB. 30πC. 32πD. 34π9.为了得到函数sin 3cos3y x x =+的图象,可以将函数y x =的图象( ) A.向右平移4π个单位 B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 10. 定义在R 上的函数()21x mf x -=-为偶函数,记2(1),(log 5),a f m b f =-=(2)c f m =,则( )A.a b c <<B.a c b <<C.c a b <<D.c b a <<11.抛物线2:4C y x =的焦点为F ,N 为准线上一点,M 为y 轴上一点,MNF ∠为直角,若线段MF 的中点E 在抛物线C 上,则MNF △的面积为( )D.12.已知函数,,,36,3)(2a x a x x x x x f ≤>⎩⎨⎧+++=函数x x f x g 2)()(-=恰有三个不同的零点,则实数a 的取值范围是( ).A. [)1,3-B. []3,1--C. [)3,3- D .[)1,1-第Ⅱ卷 (非选择题)二、填空题(本题共4小题,每小题5分,共20分。
陕西省2017届高三下学期第十一次模考数学(文)试题含答案

陕师大附中高三年级第十一次模考试题数学(文科)注意事项:1.本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 答案均写在答题纸上,满分150分,时间120分钟.2.学生领到试卷后,请检查条形码信息是否正确. 并按规定在答题纸上填写姓名、准考证号,及填涂对应的试卷类型信息.3.答卷必须用0.5mm 的黑色签字笔书写,字迹工整,笔迹清晰. 并且必须在题号所指示的答题区内作答,超出答题区域的书写无效.4.只交答题纸,不交试题卷.第 Ⅰ 卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分, 在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{||2}A x x =<,{13}B x x =<<,则AB 等于( ).A {21}x x -<<.B {12}x x << .C {23}x x <<.D {23}x x -<<2.设复数12z i =+,22z i =-,则12z z -=( ).A 4 .B 0 .C 2 .D 3.设数列{}n a 是等差数列,且26a =-,66a =,n S 是数列{}n a 的前n 项和,则( ).A 43S S < .B 43S S = .C 41S S > .D 41S S =4.若A B 、为对立事件,其概率分别为4()P A x=,1()P B y =,则x y +的最小值为( ).A 10 .B 9 .C 8 .D 65.P 是双曲线22219x y a -=上一点,双曲线的一条渐近线为320x y -=,12F F 、分别是双曲线的左、右焦点,若16PF =,则2PF =( ).A 2或10 .B 2 .C 10 .D 96.某几何体的三视图如右图所示,其中俯视图为扇形,则该几何体的体积为.A 23π.B 3π.C 29π.D 169π俯视图侧视图7.函数()f x 部分图象如图所示,则()f x 的解析式可能是( ) .A ()sin f x x x =+.B cos ()xf x x=.C 3()()()22f x x x x ππ=-- .D ()cos f x x x =8.函数()f x 在定义域R内可导,若()(2)f x f x =-,且(1)()0x f x '-<,若(0),a f =1()2b f = ,(3)c f =,则,,a b c 的大小关系是( ).A a b c >> .B b a c >> .C c b a >>.D a c b >>9.阅读程序框图,为使输出的数据为31,则①处应填的数字为( ).A 4.B 5 .C 6.D 710.如图,抛物线2:4W y x =与圆22:(1)25C x y -+=交于,A B两点,点P 为劣弧AB 上不同于,A B 的一个动点,与x 轴平行的直线PQ 交抛物线W 于点Q ,则PQC ∆的周长的取值范围是( ).A (10,14) .B (12,14) .C (10,12) .D (9,11)11.曲线3y x =上一点B 处的切线l 交x 轴于点A ,(OAB O ∆为原点)是以A 为顶点的等腰三角形,则切线l 的倾斜角为( ) .A 30o .B 45o.C 60o .D 120o12.在平行四边形ABCD 中,0AB BD ⋅=,且1AB =,2BD =BD 折起使平面ABD ⊥平面BCD ,则三棱锥A BDC -的外接球的表面积为( ).A 4π .B 8π .C 16π .D 2π第 Ⅱ 卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷中相应的横线上.)13.平面向量a 与b 的夹角为23π,且()1,0a =,1b =则2a b += . 14.从集合22{(,)4,,}x y x y x R y R +≤∈∈内任选一个元素(,)x y ,则满足2x y +≥的概率为 .15.设公比为q 的等比数列{}n a 的前n 项和为n S ,若2232S a =+,4432S a =+,则q = .16.若实数,x y 满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,目标函数2z ax y =+仅在点(1,0)处取得最小值,则实数a 的取值范围是 .三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)在ABC ∆中,角,,A B C 的对边分别是,,a b c ,若cos ,cos ,cosC c A b B a 成等差数列. (1)求B ;(2)若2a c +=,b =ABC ∆的面积.18.(本小题满分12分)在四棱锥P ABCD -中,PA ⊥平面ABCD ,ABC ∆是正三角形,AC 与BD 的交点为M ,又4PA AB ==,AD CD =,120CDA ∠=,点N 是CD 的中点. (1)求证:平面PMN ⊥平面PAB ; (2)求点M 到平面PBC 的距离.19.(本小题满分12分)为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:每名快递员完成一件货物投递可获得的劳务费情况如下: 甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.(1)根据表中数据写出甲公司员工A 在这10天投递的快递件数的平均数和众数;(2)为了解乙公司员工B 的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X (单位:元),求182X >的概率;(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.20.(本小题满分12分)定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的.如图,椭圆1C 与椭圆2C 是相似的两个椭圆,并且相交于上下两个顶点.椭圆22122:1(0)x y C a b a b+=>>的长轴长是4,椭圆 22222:1(0)y x C m n m n+=>>短轴长是1,点12,F F 分别是椭圆1C 的左焦点与右焦点.(1)求椭圆1C 与2C 的方程;(2)过1F 的直线交椭圆2C 于点,M N ,求2F MN ∆面积的最大值.21.(本小题满分12分)设函数()(1)()x f x ax e a R -=+∈.(1)当0a >时,求函数()f x 的单调递增区间;(2)对任意[0,)x ∈+∞,()1f x x ≤+恒成立,求实数a 的取值范围.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分. 并请考生务必将答题卡中对所选试题的题号进行涂写.22.(本小题满分10分)选修44-:坐标系与参数方程选讲.在直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为cos()13πρθ-=,,M N 分别为曲线C 与x 轴,y 轴的交点.(1)写出曲线C 的直角坐标方程,并求,M N 的极坐标; (2)设MN 的中点为P ,求直线OP 的极坐标方程.23.(本小题满分10分)选修45-:不等式选讲. 已知函数()2f x x x a =+-+.(1)当3a =时,解不等式1()2f x ≤; (2)若关于x 的不等式()f x a ≤解集为R ,求a 的取值范围.陕师大附中高三年级第十一次模考试题答案(文科)一、选择题(本大题共12小题,每小题5分,共60分)二、填空题(本大题共4小题,每小题5分,共20分)或三、解答题(本大题共6小题,共70分)17. (1)因为,,成等差数列.所以,由正弦定理得,即,而,所以,由,得(2)因为,所以,又,,所以,即,所以.18.(1)在正中,,在中,因为,易证,所以为的中点,因为点是的中点,所以.因为,所以,因为,所以,因为,所以,即,因为,所以,所以,又,所以.(2)设到的距离为,在中,,所以,在中,,所以,在中,,,,所以由即,解得.19.(1)甲公司员工投递快递件数的平均数为,众数为.(2)设为乙公司员工投递件数,则当时,元,当时,元,令,得,则得取值为44,42,42,42所以的概率为.(3)根据图中数据,可估算甲公司的员工该月收人为元,乙公司的员工该月收入元.20. (1)由已知,,.因为椭圆与椭圆的离心率相等,即,所以.所以椭圆的方程是,椭圆的方程是.(2)显然直线的斜率不为,故可设直线的方程为.联立得,即,所以设,,则,,所以又的高即为点到直线的距离所以的面积因为,当且仅当,即时等号成立.所以,即的面积的最大值为.21. (1).由,,令得:.所以当时,单调递增区间是.(2)令,则成立等价于.(i)若,当,则,,而,即成立.(ii)若时,则.当,由是减函数,,又,所以,在上是减函数,此时当,.(iii)当时,,.所以在有零点.在区间,设,所以在上是减函数,即在有唯一零点,且在上,.在为增函数,即在上所以,不合题意.综上可得,符合题意的的取值范围是.22. (1)由,得.曲线的直角坐标方程为.时,,所以;时,,所以.(2)点的直角坐标为,点的直角坐标为,所以点的直角坐标为,则点的极坐标为,所以直线的极坐标方程为,.23. (1)当时,,等价于,即或或即或或解得或或,故不等式的解集为:;(2)由的不等式解集为,得函数,因为(当且仅当取“”),所以,所以或解得.。
2017年陕西省西安市西工大高三第十一次适应性训练文科数学试题及答案

陕西省西安市西北工业大学附属中学2013年高三第十一次适应性训练数学(文)试题第Ⅰ卷 选择题(共50分)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的(本大题共10小题,每小题5分,共50分) 1.为虚数单位,复数1i计算的结果是( )A .1B .-1C .D .i -2.已知a R ∈,则“2a >”是“22a a >”成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件3.下列函数中,是奇函数且在区间(0,1)内单调递减的函数是( )A .12log y x = B .1y x= C .3y x = D .x y tan =4.已知约束条件222x y x y ≤⎧⎪≤⎨⎪+≥⎩,则目标函数 z = x + 2 y 的取值范围是( )A .[2 ,6]B . [2,5]C . [3,6]D . [3,5]5.已知函数1()||f x x x=+,则函数()y f x =的大致图像为( )6.若函数32()22f x x x x =+--的一个正数零点附近的函数值用二分法计32220x x x +--=) A .1.2 B .1.3 C .1.4 D .1.57.已知一个几何体的三视图如下图所示(单位:cm), 其中正视图是直角梯形,侧视图和俯视图都是矩 形,则这个几何体的体积是________cm 3. A .2 B . C. 23D.328.已知抛物线x y 82=的焦点与双曲线1222x y a-=的一个焦点重合,则该双曲线的离心率为( )A9.定义运算a b ⊗为执行如图所示的程序框图输出的s 值,则2cos 2tan 34ππ⎛⎫⎛⎫⊗ ⎪ ⎪⎝⎭⎝⎭的值为( ) A .4 B .3 C .2 D .―110.若函数2()log (2)a f x x ax =-+对于任意的1x 、2x ,当122ax x <≤时,恒有12()()f x f x >成立,则a 的取值范围是( )A .4B .(0,)4C .(1D .(1第Ⅱ卷 非选择题(共100分)二.填空题:把答案填在答题卡相应题号后的横线上(本大题共5小题,每小题5分,共25分)11.设向量,,a b c 满足0a b c ++=,且0,||3,||4,||a b a b c ⋅===则= .12.将全体正整数排成一个三角形数阵(右图):按此排列的规律,第10行从左向右的第3个数为 .13.若直线:1y kx =+被圆C :22230x y x +--=截得的弦最短,则k =_ .14.已知0,0,lg2lg8lg2x y x y >>+=,则113xy+的最小值是 .15.选做题(请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)A (不等式选讲)若关于x 的不等式|||1||2|a x x ++-…存在实数解,则实数a 的取值范围是 .B (几何证明选讲)如图,∠B =∠D ,AE BC ⊥,90ACD ∠= ,且AB =6,AC =4,AD =12,则BE = .C (极坐标系与参数方程)极坐标系下曲线θρsin 4=表示圆,则点)6,4(πA 到圆心的距离为 .三.解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6小题,共75分)16.(本小题满分12分)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为1的正方形,PA ⊥底面ABCD , PA =AB ,点M 在棱PD 上,PB ∥平面ACM . (Ⅰ)试确定点M 的位置,并说明理由;(Ⅱ)求四棱锥P -ABCD 的表面积. 17.(本小题满分12分)在ABC ∆中,角A ,B ,C 所对的边分别为c b a ,,,向量m =),sin sin ,sin (sin B A C B -+n=))sin(,sin (sin B C C B +-,且m ⊥n .(Ⅰ)求角C 的大小;(Ⅱ)若cos A =54,求sin B 的值.D18.(本小题满分12分)已知在等比数列}{n a 中,11=a ,且2a 是1a 和13-a 的等差中项. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)若数列}{n b 满足)(12*N n a n b n n ∈+-=,n S 是}{n b 的前n 项和,求使不等式2013n S >成立n 的最小值.19.(本小题满分12分)已知动点),(y x A 到点)0,2(F 和直线2-=x(Ⅰ)求动点A 的轨迹方程; (Ⅱ)记点)0,2(-K ,若AF AK 2=, 求△AFK 的面积.20.(本小题满分13分)某中学在校就餐的高一年级学生有440名,高二年级学生有460名,高三年级学生有500名;为了解学校食堂的服务质量情况,用分层抽样的方法从中抽取70名学生进行抽样调查,把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级:1级(很不满意);2级(不满意);3级(一般);4级(满意);5级(很满意),其统计结果如下表(服务满意度为x ,价格满意度为y ).(Ⅱ)求“服务满意度”为3时的5个“价格满意度”对应人数的方差; (Ⅲ)为提高食堂服务质量,现对样本进行研究,从3<x 且42<≤y 的学生中随机抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.(第19题图)21.(本小题满分14分)已知函数()()0≠++=x b xax x f ,其中R b a ∈,。
陕西省2017届高三数学下学期模拟试题七文

陕西省2017届高三数学下学期模拟试题(七)文一、选择题:本大题共12小题,每小题5分,共60分. 1.已知集合2{20},{55}A x x x B x x =->=<,则( )A .AB =∅B .A B R =C . B A ⊆D . A B ⊆2.已知复数z 满足21zi i=+-,则复数z 的共轭复数为( ) A .3i + B .3i - C .3i -- D .3i -+3.命题“(0,),ln 1x x x ∀∈+∞≠-”的否定是( )000.(0,),ln 1A x x x ∀∈+∞=- 000.(0,),ln 1B x x x ∃∉+∞=-000.(0,),ln 1C x x x ∃∈+∞=- 000.(0,),ln 1D x x x ∀∉+∞=-4.若一个底面是正三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( ).A π316 .B π319 .C π1219.D π345.已知数列{}n a 的前n 项和2(,)n S an bn a b R =+∈且23a =,611a =,则7S 等于( ).A 13 .B 35 .C 49 .D 636.执行如图所示的程序框图,若要使输入的x 值与输出的y 值相等,则这样的x 值的个数是( ).A 1.B 2.C 3.D 47.已知非零向量a b 、满足223a b =,且()(32)a b a b -⊥+,则a b 、的夹角 ( ).A π .B 2π .C 34π .D 4π 8.已知函数()2cos()3xf x πϕ=+的一个对称中心是(2,0),且(1)(3)f f >,要得到函数()f x 的图像,可将函数2cos3xy π=的图像( ).A 向左平移12个单位长度 .B 向左平移6π个单位长度.C 向右平移12个单位长度 .D 向右平移6π个单位长度1119.若双曲线 2221(0)x y a a-=>的一条渐近线与圆22(2)2x y +-=至多有一个交点,则双曲线的离心率的取值范围是( ).[2,)A +∞.[2,)B +∞ .(1,2]C .(1,2]D 10.已知数列{}n a 、{}n b 满足2log ,n n b a n N *=∈,其中{}n b 是等差数列,且920081,4a a ⋅=,则1232016b b b b ++++=( ).2016A -.2016B 2.log 2016C .1008D11.若实数,x y 满足0x y <<,且 1x y +=,则下列四个数中最大的是( ).A 12.B 22x y + .C 2xy .D x12.已知函数()(2)xf x x e ax a =---,若不等式()0f x >恰有两个正整数解,则a 的取值范围是( )31.[,0)4A e -1.[,0)2B e - 31.[,)42e C e - 31.[,2)4D e -二、填空题:本大题共4小题,每小题5分,共20分.13.设12,F F 为椭圆2222:1(0)x y C a b a b+=>>的焦点,过2F 在的直线交椭圆于,A B 两点,1AF AB ⊥且1AF AB =,则椭圆C 的离心率为______.14.若目标函数2z kx y =+在约束条件2122x y x y y x -≤⎧⎪+≥⎨⎪-≤⎩下仅在点(1,1)处取得最小值,则实数k 的取值范围______. 15.若函数1()||1x f x x +=+,x R ∈,则不等式2(2)(34)f x x f x -<-的解集是______.16.在ABC ∆中,,,A B C 的对边分别为,,a b c ,且满足:2a =,(2)(sin sin )()sin b A B c b C +-=-,则ABC ∆面积的最大值为______.三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤.17.(本小题满分12分)已知函数2()23sin cos 2cos 1()f x x x x x R =+-∈.(1)求函数()f x 的最小正周期及在区间[0,]2π上的最大值和最小值;(2)若06()5f x =,0[,]42x ππ∈,求0cos 2x 的值. 18.(本小题满分12分)在如图所示的几何体中,平面⊥ACE 平面ABCD ,四边形ABCD 为平行边形,90o ACB ∠=//EF BC ,2AC BC ==,1AE EC ==.(1)求证:⊥AE 平面BCEF ; (2)求三棱锥D ACF -的体积.19.(本小题满分12分)为了解某市的交通状况,现对其中的6条道路进行评估,得分分别为5,6,7,8,9,10.规定评估的平均得分与全市的总体交通状况等级如下表:(1)求本次评估的平均得分,并参照上表估计该市的总体交通状况等级;(2)用简单随机抽样方法从这6条道路中抽取2条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的绝对值不超过5.0的概率.20.(本小题满分12分)设直线0l 过抛物线2:2(0)C x py p =>的焦点且与抛物线分别相交于00,A B 两点,已知006A B =,直线0l 的倾斜角θ满足3sin θ=。
[精品]2017年陕西省高考数学试卷及解析答案word版(理科)(全国新课标ⅱ)
![[精品]2017年陕西省高考数学试卷及解析答案word版(理科)(全国新课标ⅱ)](https://img.taocdn.com/s3/m/dbc1bd3a58fb770bf78a55a8.png)
2017年陕西省高考数学试卷(理科)(全国新课标Ⅱ)一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)=()A.1+2i B.1﹣2i C.2+i D.2﹣i2.(5分)设集合A={1,2,4},B={x|x2﹣4x+m=0}.若A∩B={1},则B=()A.{1,﹣3}B.{1,0}C.{1,3}D.{1,5}3.(5分)我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()A.1盏 B.3盏 C.5盏 D.9盏4.(5分)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π5.(5分)设x,y满足约束条件,则z=2x+y的最小值是()A.﹣15 B.﹣9 C.1 D.96.(5分)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有()A.12种B.18种C.24种D.36种7.(5分)甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则()A.乙可以知道四人的成绩B.丁可以知道四人的成绩C.乙、丁可以知道对方的成绩D.乙、丁可以知道自己的成绩8.(5分)执行如图的程序框图,如果输入的a=﹣1,则输出的S=()A.2 B.3 C.4 D.59.(5分)若双曲线C:﹣=1(a>0,b>0)的一条渐近线被圆(x﹣2)2+y2=4所截得的弦长为2,则C的离心率为()A.2 B.C.D.10.(5分)已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,则异面直线AB1与BC1所成角的余弦值为()A.B.C.D.11.(5分)若x=﹣2是函数f(x)=(x2+ax﹣1)e x﹣1的极值点,则f(x)的极小值为()A.﹣1 B.﹣2e﹣3C.5e﹣3 D.112.(5分)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则•(+)的最小值是()A.﹣2 B.﹣ C.﹣ D.﹣1二、填空题:本题共4小题,每小题5分,共20分。
陕西省2017届高三下学期第十一次模考英语试题含答案

陕师大附中高三年级第十一次模考英语试题第一部分听力(共两节,满分30分)第一节(共5小题:每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间回答有关小题和阅读下一题。
每段对话仅读一遍。
1.How much will the man pay for the ticets?A.£7.5.B.£15.C.£50.2.Which is the right gate for the man’s flight?A. Gate 16.B. Gate 22.C. Gate 25.3.How does the man feel about going to school by bie?A. Happy.B. Tired.C. Worried.4.When can the woman get the computers?A. On Tuesday.B. On Wednesday.C.On Thursday.5.What does the woman thin of the shirt for the party?A.The sie is not large enough.B.The material is not good.C.The color is not suitable.第二节(共15小题:每小题1.5分,满分22.5分)听下面5 段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C、三个选项汇总选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每个小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6-7题。
听第6段材料,回答第6、7题。
6.What can we learn about Mr. Brown?A.He is in his office.B.He is at a meeting.C.He is out for a meal.7.What will the man probably do net?A.Call bac. Be again. C.Leave a message.听第7段材料,回答第8、9题。
完整word版,2017年陕西省西安市高考数学一模试卷(理科)--有答案

1 72017年陕西省西安市高考数学一模试卷(理科)、选择题:本大题共12小题,每小题5分,共60分•在每小题给出的四个选项中,只有一个是符合题目要求的.1•在复平面内,两共轭复数所对应的点( A .关于x 轴对称 B .关于y 轴对称直线x+2y - 5+ .匚=0被圆x 2+y 2 - 2x - 4y=0截得的弦长为( ) 1 B . 2 C . 4 D . 4 r.5 •将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个/ 由1名教师和2名学生组成,不同的安排方案共有( A . 12 种 B . 10 种 C . 9 种D . 8 种8•公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可 无限C .关于原点对称D .关于直线y=x 对称已知集合 M={ - 1, 0, 1},N={x|x=ab ,2. a,b € M ,且a ^b},则集合M 与集合N 的 勺关系是 M=N B . M n N=N C . M U N=N D . M n N=?3. 已知两个单位向量-1 ■1 B . C .空2的夹角为45°且满足珂丄(包-el ),则实数入的值为4. 小组 6.某几何体的三视图如图所示,且该几何体的体积是,则正视图中的x 的值是(C . 一D . 37.函数y=sin (2x+©)的图象沿x 轴向左平移* 个单位后,得到一个偶函数的图象,则©的一个可能的值为() 3K ~TC . 0D .A . 2B .逼近圆的面积,由此创立了割圆术,禾U用割圆术刘徽得到了圆周率精确到小数点后面两位值为(参考数据:|^=1. 732,sin 15*0.2588, sin7.5 見0.1305.9. 12 B. 24 C. 48 D. 96已知艮gin0l42casCI:il^,贝U tan2 a= )10.甲、乙两人约定晚6点到晚7点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率(B. C. D.11. F i、F2分别是双曲线=1 (a>0,b> 0)的左、右焦点,过点F1的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为(B. C. D.12.已知函数f (x)=aln (x+1)- x2在区间(0,1)内任取两个实数p,q,且q,>1恒成立,则实数a的取值范围为()A. [15,+x) B .( — X,15] C.( 12,30] D. (- 12,15]二、填空题:本大题共4小题,每小题5分,共20分).13.已知直线a、b和平面a B,下列命题中假命题的是(只填序号)①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/ a b// B,且a丄B,贝U a丄b;不等式值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.A. 12B. 24C. 48 D . 969.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题 5 分,共20 分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.A. 12B. 24C. 48 D . 969.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.A. 12B. 24C. 48 D . 969.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.A. 12B. 24C. 48 D . 969.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题 5 分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.A. 12B. 24C. 48 D . 969.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率( )A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为( )A. B. C. D.12. 已知函数f (x) =aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1 恒成立,则实数 a 的取值范围为( )A. [15, +x) B .( — x, 15] C.( 12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题 5 分,共20 分) .13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.A. 12B. 24C. 48 D . 969.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.A. 12B. 24C. 48 D . 969.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题 5 分,共20 分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.A. 12B. 24C. 48 D . 969.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题 5 分,共20 分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题 5 分,共20 分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题 5 分,共20 分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;值为( )参考数据:,sin15 °0.2588, sin7.5 見0.1305.9.已知则tan2a=()A. B. C. D.10.甲、乙两人约定晚6 点到晚7 点之间在某处见面,并约定甲若早到应等乙半小时,而乙还有其他安排,若乙早到则不需等待,则甲、乙两人能见面的概率()A . B. C. D.11. F i、F2分别是双曲线- =1 (a>0, b> 0)的左、右焦点,过点F i的直线I与双曲线的左右两支分别交于A、B两点,若△ ABF2是等边三角形,则该双曲线的离心率为()A. B. C. D.12. 已知函数f (x)=aln (x+1)- x2在区间(0, 1)内任取两个实数p, q,且q,不等式>1恒成立,则实数a的取值范围为()A. [15, +x)B .(— X, 15] C.(12, 30] D. (- 12, 15]二、填空题:本大题共4小题,每小题5分,共20分).13. 已知直线a、b和平面a B,下列命题中假命题的是(只填序号).①若a// b,则a平行于经过b的任何平面;②若a/ a b/ a 贝U a / b;③若a/a b//B,且a丄B,贝U a丄b;。
2017年高三11月调研考试理科参考答案

2017年高三11月调研考试理科数学参考答案一、选择题:(本大题共12个小题,每小题5分,满分60分.在每个小题给出的四个选二、填空题:(本大题共4小题,每小题5分,满分20分) 13. m = 14.6 15. 9416. 2017三、解答题:(本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤)17. 解:(Ⅰ)根据题意得:解得,所以 5分(Ⅱ) 令,则10分18.解:(Ⅰ)在中,因为,所以由正弦定理得:5分 (Ⅱ)在中,由余弦定理解得过点D 作在于E ,在直角中,.即梯形的高为12分2101340xx x x +⎧≥⎪-⎨⎪-+>⎩11x -≤<[1,1)M =-222()42(2)42(22)4x x x x x f x +=+=+⨯=+-12[,2)2x t =∈2()(2)4g t t =+-min min 19()()()24f xg t g ===19.解:(1)1q≠时,116()2nna-=⋅-4分(2)由题意知:116()2nna-=⋅-6分∴2116()4nna+=⋅∴2nb n=8分∴111111()2(2n2)4(n1)41ncn n n n===-⋅+⋅++10分∴123111(1)414nc c c cn++++=-<+12分20.解:(Ⅰ)∴∴6分(Ⅱ)由(Ⅰ)知,∴令∴∴或(舍去)(0,1) 1 ()-∴12分21.解:(Ⅰ)因为当=2x 时, 4.5y =,所以0.7 4.5a b +=①. 当=4x 时,8y =,所以1.48a b +=②.由①②解得5,1a b ==,所以当120x ≤≤时,5ln 1y x =+. 当20x >时,5ln 201=5(2ln 2ln5)116y =+++=.所以5ln 112016,20.x x y x +≤≤⎧=⎨>⎩,, 4分(Ⅱ) 设当日产量为x 吨时,每日的利润为()l x .则15ln ,120,2()()115,20.2x x x l x y c x x x ⎧-≤≤⎪⎪=-=⎨⎪->⎪⎩ 6分①若120x ≤≤,则5110'()22xl x x x-=-=.当110x <<时,'()0l x >,函数递增; 当1020x <<时,'()0l x <,函数递减.故10x =时,()l x 取得最大值. 即max ()(10)5ln105 6.5l x l ==-=. 10分 ②若20x >时,则1()=152l x x -单调递减,故()5l x <. 11分故当日产量为10吨时,每日的利润可以达到最大值,最大利润为6.5万元. 12分22.解:(Ⅰ)函数)(x f 的定义域为)0,(-∞, 当1a =时,2211()ln(1)'()1(1)1(1)x x x x f x x f x x x x x +--=-+∴=-=++++,, 所以当(1,0)x ∈-时,'()0,f x >函数在(1,0)-上单调递增; 当(0+)x ∈∞,时,'()0,f x <函数在(0+)∞,上单调递减;max ()(0)0f x f ∴==. 4分(Ⅱ)令1)()(+=x f x h ln(1)11xa x x=-+++, “若0a <,且对任意的1212,[0,2],()1()x x f x g x ∈+≥恒成立” 等价于“若0a <,且对任意的min max [0,2],()()x h x g x ∈≥恒成立”,22211'()(1)1(1)a ax a h x x x x --+=-=+++, 当0a <时,[0,2]x ∀∈有'()0,h x >所以函数()h x 在[0,2]上单调递增,min ()(0)1h x h ∴==. 6分 22'()2(2)mx mx mx g x xe mx e x mx e =+=+,若0m =,则2()g x x =,所以当[0,2]x ∈时,max ()(2)4g x g ==,不满足max ()1g x ≤;若0m ≠,令'()0g x =得1220,x x m==-, 7分 ① 当22m-≥,即10m -≤<时,'()0g x ≥,函数递增, 此时2max ()(2)4m g x g e ==,令241me≤得ln 2,1ln 2m m ≤-∴-≤≤-; 8分②当202m <-<,即1m <-时,在2[0,]m-上'()0g x ≥, 函数递增;在2(2]m -,上'()0g x <,函数递减, 此时max 2224()()g x g m m e=-=,令2241m e ≤得2,1m m m ≤-∴<-; 10分 ③当20m-<,即0m >时,'()0g x ≥,函数递增,此时2max ()(2)4m g x g e ==,241m e ≤不成立. 11分 综上所述,m 的取值范围是(,ln 2]-∞-. 12分。
2017届陕西省西安市高新一中高三下学期第十次大练习文科数学试题及答案 精品

2017届高三第十次大练习数学试题(文科)本试卷分第I 卷和第II 卷两部分,第I 卷、第II 卷共150分,考试时长120分钟,考生务必将答案答在答题卡上,在试卷上作答无效,考试结束后,将答题卡交回。
第一卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中选出符合题目要求的一项。
1.设全集U={1,2,3,4,5,6,7,8,},集合A={2,4,5,7},B={1,4,7,8},那么如图所示的阴影部分所表示的集合是( )A.{3,6}B.{4,7}C.{1,2,4,5,7,8} D{1,2,3,5,6,8}2.已知双曲线的标准方程为2212x y -=,则它的焦点坐标是( )A. (1,0)±B. (C.(0,D.(0,1)±3.一位同学种了甲、乙两种树苗各一株,分别观察了9次、10次得到树苗的高度数据的茎叶图如图(单位:厘米),则甲乙两种树苗高度的数据中位数和是( )A.44B.50C.52 D544. 若(1,2),(1,1),(2,1),a b c ka b c ==-=+与共线,则k 的值为( )A.2B.1C.0D.-15.曲线1xy xe =+在点(0,1)处的切线方程为( )A. x-y+1=0B.2x-y+1=0C.x-y-1=0D.x-2y+2=06.如图,正方体1111ABCD A BC D -的棱长为1,线段11B D 上有两个动点E ,F ,且12EF =,则下列结论中错误..的是( )A.AC BE ⊥B.EF ABCD 平面C.三棱锥A-BEF 的体积为定值D.AEF BEF ∆∆的面积与的面积相等7.23sin 2sin ,52cos παααπα=∈已知且(,),那么的值等于( ) A. 32- B.34- C.32 D. 348. 执行 如图的算法框图,如果输入p=5,则输出的S 等于( )A. 1516B. 3116C. 3132D. 63329.在[0,2]上任取两个数a,b 则函数2()f x x b =+无零点的概率为( )A. 18B. 14C. 34D. 7810. 已知函数()f x 是定义在实数集R 上的不恒为零的偶函数,且对任意实数x 都有(1)(1)()xf x x f x +=+,则5(())2f f 的值是( ) ( A.0 B.12C.1D.52第II 卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上。
陕西省西安市2017届高三下学期第二次模拟考试数学(文)试题有答案

西安市第八十三中学2016~2017学年度第二学期高三年级第二次模拟考试数学(文科)试题一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知全集U=R ,集合A={1,2,3,4,5},B={x∈R|x>2},下图中阴影部分所表示的集合为( )A .{1}B .{0,1}C .{1,2}D .{0,1,2}2.如果复数2-1+iz =,则( ) A .|z|=2 B .z 的实部为1 C .z 的虚部为﹣1 D .z 的共轭复数为1+i3.设命题:(,1),(2,1),//p a m m b m a b =+=+且;命题q :关于x 的函数(1)log (01)a y m x a a =->≠且是对数函数,则命题p 成立是命题q 成立的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不不要条件4.某几何体的三视图如图所示,则该几何体的体积为( )A .56π B .43π C .53π D .23π 差中项为54,则4S =5.等比数列}{n a 的前n 项和为n S ,已知2532a a a =,且4a 与72a 的等( )A .29B .30C .33D .366.在边长为4的正方形ABCD 内部任取一点M ,则满足0MA MB ⋅>的概率为( ) A .18π-B .8π C .14π-D .4π7.已知圆2220(0)M x y ay a +-=>:截直线0x y +=所得线段的长度是,则圆M 与圆22(1)(1)1N x y -+-=:的位置关系是( )A .内切B .相交C .外切D .相离8.阅读如图的程序框图,运行相应的程序,输出的结果为( )A .﹣2B .12C .﹣1D .29.函数2||2x y x e =-在的图象大致为( )A B CD10.已知函数3sin ,0()1,0x x x f x x x -<⎧=⎨+≥⎩,则下列结论正确的是( )A .()f x 有极值B .()f x 有零点C .()f x 是奇函数D .()f x 是增函数11.设O 为坐标原点, P 是以F 为焦点的抛物线22(0)y px p =>上任意一点,M 是线段PF 上的点,且|PM|=2|MF|,则直线OM 的斜率的最大值为( )A .B .23C D .1 12.如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切),已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( ) A .321122y x x x =-- B .3211+322y x x x =- C .314y x x =- D .3211+242y x x x =- 二、填空题 :(本题共4小题,每小题5分,共20分,请把答案填写在答题卡相应的位置上)13.sin(750)-︒= ;14.已知变量x ,y 满足约束任务5021010x y x y x +-≤⎧⎪-+≤⎨⎪-≥⎩,则z=x+2y 的最小值是 ;15.已知由一组样本数据确定的回归直线方程为 1.5+1y x =,且2x =,发现有两组数据(2.4,2.8)与(1.6,5.2)误差较大,去掉这两组数据后,重新求得回归直线的斜率为1,那么当x =4时,y 的估计值为 ; 16.如图所示将若干个点摆成三角形图案,每条边(色括两个端点)有n (n >1,n∈N*)个点,相应的图案中总的点数记为n a ,则233445201620179999...a a a a a a a a ++++= .三、解答题(本大题共70分.解答应写出文字说明、证明过程或演算步骤) 17.(12分)已知函数()sin()(0,||)2f x M x M πωϕϕ=+><的部分图象如图所示.(Ⅰ)求函数()f x 的解析式及单调递减区间;(Ⅱ)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若(2a﹣c )cosB=bcosC ,求()2Af 的取值范围.18.(12分)某微信群共有60人(不包括群主),春节期间,群主发60个随机红包(即每个人抢到的红包中的钱数是随机的,且每人只能抢一个).红包被一抢而空.据统计,60个红包中钱数(单位:元)分配如表:(Ⅰ)作出这些数据的频率分布(Ⅱ)估计红包中钱数的平均数及中位数;(Ⅲ)若该群中成员甲、乙二人都抢到4.5元红包,现系统将从抢到4元及以上红包的人中随机抽取2人给群中每个人拜年,求甲、乙二人至少有一人被选中的概率.19.(12分)如图,矩形ABCD 中,AD⊥平面ABE , AE=EB=BC=2,F 为CE 上的点,且BF⊥平面ACE . (Ⅰ)求证:AE⊥平面BCE ; (Ⅱ)求证;AE∥平面BFD ; (Ⅲ)求三棱锥C ﹣BGF 的体积.20.(12分)已知椭圆2222:1(0)x y E a b a b+=>>的短轴长为2,离心率为5,抛物线2:2(0)G y px p =>的焦点F 与椭圆E 的右焦点重合,若斜率为k 的直线l 过抛物线G 的焦点F 与椭圆E 相交于A ,B 两点,与抛物线G 相交于C ,D 两点.(Ⅰ)求椭圆E 及抛物线G 的方程; (Ⅱ)是否存在实数λ,使得1||||AB CD λ+为常数?若存在,求出λ的值,若不存在,请说明理由. 21.(12分)已知函数1()ln (0,)f x a x a a R x=+≠∈. (Ⅰ)若a=1,求函数()f x 的极值和单调区间;(Ⅱ)若在区间(0,e ]上至少存在一点0x 使得0()0f x <成立,求实数a 的取值范围.请考生在第22,23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号。
陕西省师范大学附属中学高三下学期第十一次模考——物

陕西省师范大学附属中学2017届高三下学期第十一次模考物理试题物理第十一次模考答案一、选择题题目14 15 16 17 18答案 D B C C二、非选择题22.(5分)(1)D;(2)C,D;(3)3.1×102;(4)5×106 Pa 23.(10分)24.25.解:(1)设人经时间下落到平板车上,车在这段时间内前进的距离为由运动学公式得:①(2分)②(1分)代入数据由①②解得:=6m (1分)所以人落在离车尾端的距离=3.5m (2分)(2)设人落在车上后做匀加速运动的加速度为,经过时间人车速度相同为由牛顿第二定律得:③(1分)= ④(1分)代入数据由③④解得:=1s =2m/s (2分)在这段时间内的人相对车向后的位移为221222012121t a at t v x --=∆ =3m(2分)此后人车都减速运动直到静止,人相对车向前的位移为m (2分)由于5.25.0321=-=∆-∆x x m3.5m (1分)所以不会滑下(3)人车相对滑动产生的热量=455J (4分) 33.(1) BCE (2)解:(1)由玻意耳定律可知PLS =P 1(L +h )S 2分 活塞受力平衡 P 1 S =PS -mg 2分 联立方程可得S =mg (L +h )/Ph 2分 (2)由盖—吕萨克定律(L +h )S /T 0=L 0S /T 2分 解得 L 0=(L +h )T / T 0 34.(1) A DE(2) 解:①根据光的折射定律,分析光线OD 的折射情况,有23045==γ=o oi n sin sin sin sin (3分)由知=450 1分②由得 4分 2分。
陕西省2017届高三下学期第十一次模考英语试题word版有答案AlMqUn

陕师大附中高三年级第十一次模考英语试题第一部分听力(共两节,满分30分)第一节(共5小题:每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一题。
每段对话仅读一遍。
1.How much will the man pay for the tickets?A.£7.5.B.£15.C.£50.2.Which is the righ t gate for the man’s flight?A. Gate 16.B. Gate 22.C. Gate 25.3.How does the man feel about going to school by bike?A. Happy.B. Tired.C. Worried.4.When can the woman get the computers?A. On Tuesday.B. On Wednesday.C.On Thursday.5.What does the woman think of the shirt for the party?A.The size is not large enough.B.The material is not good.C.The color is not suitable.第二节(共15小题:每小题1.5分,满分22.5分)听下面5 段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C、三个选项汇总选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每个小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6-7题。
听第6段材料,回答第6、7题。
6.What can we learn about Mr. Brown?A.He is in his office.B.He is at a meeting.C.He is out for a meal.7.What will the man probably do next?A.Call back.e again.C.Leave a message.听第7段材料,回答第8、9题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
陕西省2017届高三数学下学期第十一次模考试题 文注意事项:1.本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 答案均写在答题纸上,满分150分,时间120分钟.2.学生领到试卷后,请检查条形码信息是否正确. 并按规定在答题纸上填写姓名、准考证号,及填涂对应的试卷类型信息.3.答卷必须用0.5mm 的黑色签字笔书写,字迹工整,笔迹清晰. 并且必须在题号所指示的答题区内作答,超出答题区域的书写无效.4.只交答题纸,不交试题卷.第 Ⅰ 卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分, 在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{||2}A x x =<,{13}B x x =<<,则A B 等于( ).A {21}x x -<< .B {12}x x << .C {23}x x << .D {23}x x -<<2.设复数12z i =+,22z i =-,则12z z -=( ).A 4 .B 0 .C 2 .D 3.设数列{}n a 是等差数列,且26a =-,66a =,n S 是数列{}n a 的前n 项和,则( ) .A 43S S <.B 43S S = .C 41S S > .D 41S S = 4.若A B 、为对立事件,其概率分别为4()P A x =,1()P B y=,则x y +的最小值为( ).A 10 .B 9 .C 8 .D 65.P 是双曲线22219x y a -=上一点,双曲线的一条渐近线为320x y -=,12F F 、分别是双曲线的左、右焦点,若16PF =,则2PF =( ).A 2或10 .B 2 .C 10 .D 96.某几何体的三视图如右图所示,其中俯视图为扇形,则该几何体的体积为.A 23π.B 3π.C 29π.D 169π7.函数()f x 部分图象如图所示,则()f x 的解析式可能是( ).A ()sin f x x x =+.B cos ()xf x x =.C 3()()()22f x x x x ππ=--.D ()cos f x x x =俯视图侧视图8.函数()f x 在定义域R 内可导,若()(2)f x f x =-,且(1)()0x f x '-<,若(0),a f =1()b f =,(3)c f =,则,,a b c 的大小关系是( ).A a b c >> .B b a c >> .C c b a >> .D a c b >> 9.阅读程序框图,为使输出的数据为31,则①处应填的数字为( ).A 4 .B 5 .C 6.D 7 10.如图,抛物线2:4W y x =与圆22:(1)25C x y -+=交于,A B两点,点P 为劣弧AB 上不同于,A B 的一个动点,与x 轴平行的直线PQ 交抛物线W 于点Q ,则PQC ∆的周长的取值范围是( ).A (10,14) .B (12,14).C (10,12).D (9,11) 11.曲线3y x =上一点B 处的切线l 交x 轴于点A ,(OAB O ∆为原点)是以A 为 顶点的等腰三角形,则切线l 的倾斜角为( ) .A 30o .B 45o .C 60o .D 120o12.在平行四边形ABCD 中,0AB BD ⋅=,且1AB = ,BD = BD 折起使平面ABD ⊥平面BCD ,则三棱锥A BDC -的外接球的表面积为( ) .A 4π .B 8π .C 16π.D 2π第 Ⅱ 卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷中相应的横线上.)13.平面向量a 与b 的夹角为23π,且()1,0a = ,1b = 则2a b += .14.从集合22{(,)4,,}x y x y x R y R +≤∈∈内任选一个元素(,)x y ,则满足2x y +≥的概率为 .15.设公比为q 的等比数列{}n a 的前n 项和为n S ,若2232S a =+,4432S a =+,则q = .16.若实数,x y 满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,目标函数2z ax y =+仅在点(1,0)处取得最小值,则实数a 的取值范围是 .三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)在ABC ∆中,角,,A B C 的对边分别是,,a b c ,若cos ,cos ,cosC c A b B a 成等差数列. (1)求B ;(2)若2a c += ,b =ABC ∆的面积.18.(本小题满分12分)在四棱锥P ABCD -中,PA ⊥平面ABCD ,ABC ∆是正三角形,AC 与BD 的交点为M ,又4PA AB ==,AD CD =,120CDA ∠= ,点N 是CD 的中点. (1)求证:平面PMN ⊥平面PAB ; (2)求点M 到平面PBC 的距离.19.(本小题满分12分)为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.(1)根据表中数据写出甲公司员工A 在这10天投递的快递件数的平均数和众数;(2)为了解乙公司员工B 的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X (单位:元),求182X >的概率;(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.20.(本小题满分12分)定义:若两个椭圆的离心率相等,则称两个椭圆是“相似”的.如图,椭圆1C 与椭圆2C 是相似的两个椭圆,并且相交于上下两个顶点.椭圆22122:1(0)x y C a b a b+=>>的长轴长是4,椭圆22222:1(0)y x C m n m n+=>>短轴长是1,点12,F F 分别是椭圆1C 的左焦点与右焦点.(1)求椭圆1C 与2C 的方程; (2)过1F 的直线交椭圆2C 于点,M N ,求2F MN ∆面积的最大值.21.(本小题满分12分)设函数()(1)()x f x ax e a R -=+∈.(1)当0a >时,求函数()f x 的单调递增区间;(2)对任意[0,)x ∈+∞,()1f x x ≤+恒成立,求实数a 的取值范围.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分. 并请考生务必将答题卡中对所选试题的题号进行涂写.22.(本小题满分10分)选修44-:坐标系与参数方程选讲.在直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为cos()13πρθ-=,,M N 分别为曲线C 与x 轴,y 轴的交点.(1)写出曲线C 的直角坐标方程,并求,M N 的极坐标; (2)设MN 的中点为P ,求直线OP 的极坐标方程.23.(本小题满分10分)选修45-:不等式选讲.已知函数()2f x x x a =+-+. (1)当3a =时,解不等式1()2f x ≤; (2)若关于x 的不等式()f x a ≤解集为R ,求a 的取值范围.答案(文科)一、选择题(本大题共12小题,每小题5分,共60分)二、填空题(本大题共4小题,每小题5分,共20分)或三、解答题(本大题共6小题,共70分)17. (1)因为,,成等差数列.所以,由正弦定理得,即,而,所以,由,得(2)因为,所以,又,,所以,即,所以.18.(1)在正中,,在中,因为,易证,所以为的中点,因为点是的中点,所以.因为,所以,因为,所以,因为,所以,即,因为,所以,所以,又,所以.(2)设到的距离为,在中,,所以,在中,,所以,在中,,,,所以由即,解得.19.(1)甲公司员工投递快递件数的平均数为,众数为.(2)设为乙公司员工投递件数,则当时,元,当时,元,令,得,则得取值为44,42,42,42所以的概率为 .(3)根据图中数据,可估算甲公司的员工该月收人为元,乙公司的员工该月收入元.20. (1)由已知,,.因为椭圆与椭圆的离心率相等,即,所以.所以椭圆的方程是,椭圆的方程是.(2)显然直线的斜率不为,故可设直线的方程为.联立得,即,所以设,,则,,所以又的高即为点到直线的距离所以的面积因为,当且仅当,即时等号成立.所以,即的面积的最大值为.21. (1).由,,令得:.所以当时,单调递增区间是.(2)令,则成立等价于.(i)若,当,则,,而,即成立.(ii)若时,则.当,由是减函数,,又,所以,在上是减函数,此时当,.(iii)当时,,.所以在有零点.在区间,设,所以在上是减函数,即在有唯一零点,且在上,.在为增函数,即在上所以,不合题意.综上可得,符合题意的的取值范围是.22. (1)由,得.曲线的直角坐标方程为.时,,所以;时,,所以.(2)点的直角坐标为,点的直角坐标为,所以点的直角坐标为,则点的极坐标为,所以直线的极坐标方程为,.23. (1)当时,,等价于,即或或即或或解得或或,故不等式的解集为:;(2)由的不等式解集为,得函数,因为(当且仅当取“”),所以,所以或解得.。
