chap6-4双线性变换法
数字信号处理第六章6 双线性变换法

1)线性相位模拟滤波器
非线性相位数字滤波器
2)要求模拟滤波器的幅频响应为分段常数型,不 然会产生畸变 分段常数型模拟滤波器 经变换后仍为分段常数 型数字滤波器,但临界 频率点产生畸变
1 1 / T
2 tg
2012-10-11
1
1 1 c
数字信号处理
s1T
j
1T 2
e e
2 s1T 2
e e
s1T 2
s1T 2
e
s1 T 2
e
1 e 1 e
s1T s1T
1 z 1 z
1 1
z e
s1T
s
1 z 1 z
1 1
z
1 s 1 s
数字信号处理
2012-10-11
为使模拟滤波器某一频率与数字滤波器的任一
预畸变
给定数字滤波器的截止频率 1 ,则
1 c tg
1
2
按 1设计模拟滤 波器,经双线性 变换后,即可得 到 1 为截止频率 的数字滤波器
2012-10-11
数字信号处理
6、模拟滤波器的数字化方法
H (z) H a (s) 1 z Ha c 1 1 z
频率有对应关系,引入系数 c
c tg 1T 2
1 z 1 z
1 1
s c
z
c s cs
2012-10-11
数字信号处理
2、变换常数c的选择
1)低频处有较确切的对应关系:
1T 1T 1 c tg c 2 2
s1T
双线性变换法

第一步,将数字滤波器的频率指标{Wk}转换为模拟
滤波器的频率指标{wk} wk 2tan(Wk )
T2 第二步,由模拟滤波器的指标设计模拟滤波器的H(s) 第三步,利用双线性变换法,将H(s)转换H(z)。
H(z) H(s) s21z1 T 1z1
2、双线性变换法的设计方法
w 2 tan(W)
T2
设计模拟
双线性变换
Wp,Ws
wp,ws 滤波器 H(s)
H(z)
H(z) H(s) s21z1 T 1z1
例1: 利用BW型模拟低通滤波器和双线性变换法设计满
足指标Wp=p/3,Ap=3dB,N=1的数字低通滤波器,并与
脉冲响应不变法设计的DF比较。
解:设双线性变换中的参数为T
例2:利用BW模拟滤波器及双线性变换法设计一低通
DF,满足Wp=0.2p, Ws=0.6p, Ap2dB, As15dB
w p , w s Ap=0.3945dB As= 15.0000dB
例2:利用BW模拟滤波器及双线性变换法设计一低通
DF,满足Wp=0.2p, Ws=0.6p, Ap2dB, As15dB
[,]
[πT/,πT/]
w' p/T
w
p/T
Ww'T
W
模拟频率与数字 频率的关系为:
w 2 tan(W)
T2
W2arctan(wT)
2
1、双线性变换法的基本原理
s域到z域的映射关系
w
2
W
tan( )
T2
jw
j2 T
tanW( )
2
j2 T
sinW( )
2
6-4数字信号处理

2 1− z −1 s= ⋅ T 1+ z −1
第7页
2 1 − z −1 = Ha ⋅ T 1 + z −1
jω 频响: 频响 H ( e ) = H a ( jΩ )
ω 2 = H a j ⋅ tan 2 ω 2 Ω = ⋅ tan T
(4)将模拟滤波器 a(s),从s平面转换到 平面,得到数字低 将模拟滤波器H , 平面转换到 平面, 平面转换到z平面 将模拟滤波器 通滤波器系统函数H(z)。 。 通滤波器系统函数
X
第9页
参数采样间隔T的选取 参数采样间隔 的选取 脉冲响应不变法 避免频率混叠,要求所设计的模拟低通带限于± 避免频率混叠,要求所设计的模拟低通带限于±π/T 可选择T 可选择 满足 Ω s < 最高频率在ω=π 按照线性关系 Ω s = 那末一定满足 Ω s < 双线性变换法
通过标准变换关系将此横带变换到整个z由此建立s平面与z平面一一对应的单值关系消64用双线性变换法设计iir数字低通滤波器也因果稳定因果稳定从t经过0变化到t时则由经过0变化到实现了s平面上整个虚轴完全压缩到s平面上虚轴的t之间的转换
第1页
6.4 用双线性变换法设计 用双线性变换法设计IIR数字 数字 低通滤波器
X
当
经过0变化到 经过 变化到π/T时, 时 1 从 -π/T经过 变化到
则由-∞经过 变化到 则由 经过0变化到 经过
第3页
+∞,实现了 平面上整个虚轴完全压缩到 1平面上虚轴 ,实现了s平面上整个虚轴完全压缩到 平面上整个虚轴完全压缩到s 之间的转换。 的±π/T之间的转换。 之间的转换 将这一关系解析扩展至整个S平面, 将这一关系解析扩展至整个 平面,则得到 平面 S平面到 1平面的映射关系: 平面到S 平面的映射关系: 平面到
双线性变换法设计数字滤波器

双线性变换法在数字滤波器上应用冲击响应不变法是使数字滤波器在时域上模仿模拟滤波器的冲击响应,但是它的缺点是产生频响的混叠失真,这是因为从s平面到z平面不是一一映射关系。
为了克服这个缺点,可以采用双线性变换法。
既然冲击响应不变法是将一条横带变换到整个z平面上去,可以将s平面压缩变换到某一中介s1平面的一条横带里,再通过标准变换关系z=exp(s1*T)将此带变换到整个z平面上去,这样就使s平面与z平面之间建立一一对应的单值关系,消除了多值变换性。
为了将s平面的jΩ轴压缩到s1平面的jΩ1轴上的-pi/T到pi/T一段上,可以通过以下的正切变换来实现:Ω=c*tan(Ω1*T/2)这里c是任意常数。
这样当Ω1由-pi/T经0变化到pi/T时,Ω由-∞经过0变化到+∞,也映射到了整个jΩ轴。
将这个关系延拓到整个s平面和s1平面,则可以得到s=c*tanh(s1*T/2)=c*[1-exp(-s1*T)] /[1+exp(-s1*T)]再将s1平面通过标准变换关系映射到z平面,即令z=exp(s1*T),并且,通常取c=2/T,得到s=(2/T) * [1-z^(-1)] / [1+z^(-1)]同样对z求解,得到z=[1+((2/T)*s] / [1-((2/T)*s]这样的变换叫做双线性变换。
为了验证这种映射具有s平面的虚轴映射到z平面单位圆上的特性,考虑z=exp(j*ω),得s=(2/T) * [1-exp(-j*ω)] / [1+exp(-j*ω)]=(2/T) * j*[sin(ω/2)]/ cos(ω/2)]=(2/T) * j * tan(ω/2)=jΩ除了使s平面的虚轴映射到单位圆上之外,s平面的左半部分映射到单位圆的内部,s平面的右半部分映射到单位圆的外部。
观察式子z=[1+((2/T)*s] / [1-((2/T)*s],发现s的实部为负时,因子[1+((2/T)*s] / [1-((2/T)*s]的幅度小于1,相当于单位圆的内部。
双线性变换法设计数字低通滤波器

双线性变换法设计数字低通滤波器目录绪论...... (2)、用双线性法设计低通滤波器...... (2)2.1双线性变换法...... (2)2.1.1双线性变换法的基本原理......... 3 2.1.2 转换关系分析............... 4 2.2 巴特沃斯低通滤波器的原理...... 7 2.3 用双线法设计巴特沃斯数字低通滤波器的步骤. (8)序. ....................................................................... ....................................... 9 四、程序中命令介绍..................................................... 10五、运行结果及波形......................... 11六、结果分析................................... 13七.心得体会..................................... 14参考文献.......... MATLAB 程15一.绪论15数字滤波器是对数字信号实现滤波的线性时不变系统。
数字滤波实质上是一种运算过程,实现对信号的运算处理。
输入数字信号(数字序列)通过特定的运算转变为输出的数字序列,因此,数字滤波器本质上是一个完成特定运算的数字计算过程,也可以理解为是一台计算机。
描述离散系统输出与输入关系的卷积和差分方程只是给数字信号滤波器提供运算规则,使其按照这个规则完成对输入数据的处理。
时域离散系统的频域特性:Y (e j3) =X (e j 3) H (e j 3 ),j 3其中Y (e )、X (e ) 分别是数字滤波器的输出序列和输入序列的频域特性j 3(或称为频谱特性) , H (e ) 是数字滤波器的单位取样响应的频谱,又称为数字滤波器的频域响应。
数字信号处理,第十一讲双线性变换
p 2 fp / fs 0.25 rad
r 2 fr / fs 0.5 rad
p
2 T
tan( p
2
)
2 T
tan(
8
)
r
2 T
tan(r
2
)
2 T
tan( )
4
2 T
6.5 双线性变换法
(2)确定模拟低通滤波器H(s)
N 4
2
c p T tan( 8 ) rad / s
H(s)ຫໍສະໝຸດ 3c3c 2c2s 2cs2
s3
解: (1)确定数字域截止频率
c 2fcT 0.5
(2)确定预畸变的模拟滤波器的截止频率
c
2 T
tan(c
2
)
2 T
tan( 0.5
2
)
2 T
6.5 双线性变换法
(3)将Ωc代入三阶模拟巴特沃思滤波器H (s)
H (s)
3c
3c 2c2s 2cs2
s3
(2)利用
2 T
tan(
2
)计算出 p及r;
(3)得到模拟滤波器H (s);
(4)经H
(
z)
H
(s)
s 2 T
1 1
z1 z1
,就得到数字滤波器H
(z)。
6.5 双线性变换法
例1. 用双线性变换法设计一个三阶巴特沃思数字低通
滤波器,采样频率为 fs= 4 kHz,其3dB截止频率
为fc=1 kHz。 三阶模拟巴特沃思滤波器为
(3)用双线性变换将模拟滤波器H (s)转换为
数字滤波器H (z)。
H
数字信号处理-双线性变换法

(2)2 cosh1(s/c) 5.5338 0.50885
1
1 =
cosh1
1 101.51
cosh1(tan0.15 /tan.2)
=
3.016 = cosh1(1.0196/0.65) 1.0207
cosh1
3.0783
取 N=4,与脉冲不变法相同。
= 1 + 1+ 2 =1.9652+2.205=4.1702
这样模拟滤波器的设计指标为
通带截止频率p =0.65,通带最大衰减p ≤1dB; 阻带边缘频率s =1.019,阻带最小衰减பைடு நூலகம்s ≥15dB; 1 )求 N 、 c 10lg|H (jp)|2 ≥ 1 , lg|H (jp)|2 ≥ 0.1,
|H (j 2 tan(0.1))|2 ≥ 10-0.1 ; 10lg|H (js)|2 ≥ 15 , |H (j 2 tan(0.15))|2 ≥10-1.5。 lg|H (js)| 2 ≥ 1.5,
j j/2 j/2) (e e 2 2 j2 = 1 =j tan 2 T T j /2 j /2 +e ) 2 (e
2 + j = j tan 2 T
比较(6.4-8)等式两边,得到
(6.4-8)
=0
2 = tan 2 T
(6.4-9)
由(6.4-8)看到双线性变换法的映射关系使s平面的虚轴 映射为z平面的单位圆。 而(6.4-9)式频率正切变换关系 实现了频率压缩,使模拟域从~的变化,压缩为 数字域频率 从 ~ 变化。
函数H(z)。
与脉冲不变法一样,设计过程中除了的第一步求数字临 界频率{k}时,要用到取样间隔T或取样频率 fs 以外, 最后的结果与其它各步骤中T 或 f s的取值无关。所以为
双线性变换法

二、性能分析4
• 6.对于分段常数型AF滤波器,经双线性变换后, 仍得到幅频特性为分段常数的DF.但在各个分段 边缘的临界频率点产生畸变,这种频率的畸变, 可通过频率预畸变加以校正。
例1
• 一个线性相位的模拟滤波器经双线性变换后 得到非线性相位的数字滤波器,不再保持原 有的线性相位。如一个模拟微分器将不能通 过双线性变换成为数字微分器。
双线性变换法
• 冲激不变法(和阶跃响应):是使数字滤波器 在时域上模仿模拟滤波器,但它的缺点:产生 频率响应的混叠失真。这是由于从S平面->Z平 面是多值的映射关系所造成的。为了克服这一 缺点,我们采用双线性变换法
2
一、变换原理 1、定义
• 双线性变换法:是从频域出发,使DF的频率响 应与AF的频率响应相似的一种变换法。
(3)变换常数C的选择1
• 调节C,可使AF与DF在不同频率点处有对应的关 系。 • (a)使AF与DF在低频处有较确切的对应关系。
T 1T 1T 1T T tan( ) 2 2 2 2 1T 由 C tan( )C 2 2 2 C T
• 看出在低频处,AF的低频特性近似等于DF的低 频特性。
(3)变换常数C的选择2
(b)利用DF 的某一特定频率(例截止频率 c ) 与AF的某一特定频率 c 严格相对应。 cT 即: c C tan( ) 2 cT 2f c c c ctg ( ) c ctg 2 2 fs f c c cot( ) fs 看出:此方法优点:是在特定AF和特定DF 处, 频率响应是严格相等的, 它可以较准确地控制截止频率的位置。
) |在低频处
ze
s1T
(1)频率压缩
双线性变换法原理的解释

(3)
也就是说, 一次积分单元离散后是一个一阶差分方
程式 (2) 或系统函数式 (3) 描述的离散时间系统。 因
此, 一次积分运算可以用图 2 所示的离散系统实现
其数值计算。
113 连续时间一阶环节的离散实现
图 3 连续一阶环节离散化后的系统
可以求得该离散系统的系统函数为
H i (z ) =
Y X
(z ) (z )
=
1
KH 1 (z ) - pH 1 (z )
=
K
H
1 1 (z )
-
p
将式 (3) 代入得
H i (z ) = 2 T
K
11+
zz-
1 1
-
p
(4)
也就是说, 图 1 一阶连续时间系统离散化后所对应
的离散时间系统的系统函数由式 (4) 确定。 比较式
(1) 和式 (4) 可知, 若在式 (1) 中令
T 2
[x
(n
-
1) + x (n) ]
(2) 两边取单边 z 变换, 并考虑到 y (- 1) = x (- 1) = 0 有
Y (z ) =
z - 1Y (z ) +
T 2
[z-
1X
(z ) +
X
(z ) ]
整理得
H 1 (z ) =
Y X
(z ) (z )
=
T 2
1 + z- 1 1 - z- 1
现有信号与系统教材或数字信号处理教材在介 绍数字滤波器设计中的双线性变换法时, 或是直接 给出双线性变换公式, 或是从一阶微分方程的数值
求解引出变换公式。 第一种方法没有解释采用这一 双线性变换公式的依据是什么; 第二种方法部分地 回答了变换公式的由来, 但是在概念的解释上似乎 还欠透彻。根据笔者的教学体会, 本文对双线性变换 法的原理作了简单而系统的阐述, 以供参考。
chap6-4双线性变换法资料
s1T
e e e e 11 ee j1T
j1T
s1T
s1T
s1T
e 2 e 2 e 2 e 2
(2)数字化
• 将S1平面通过标准变换关系变换到z平面。
z es1T , 此时,s1 z 则可得到s平面 z平面的单值映射关系:
s
1 1
z 1 z 1
或z
1 1
s s
实际中,为了使模拟滤波器的某一频率与数字化滤波器
7所示。
由图6-7看出,在零频率附近,模拟角频率Ω与数字频率ω之 间的变换关系接近于线性关系;但当Ω进一步增加时,ω增长得 越来越慢,最后当Ω→∞时,ω终止在折叠频率ω=π处,因而双线 性变换就不会出现由于高频部分超过折叠频率而混淆到低频部分 去的现象, 从而消除了频率混叠现象。
=
2 T
tan
(2) 按Ω1、Ω2、Ω3和Ω4等指标设计模拟滤波器的系统函数Ha(s)。
(3)将
s
c
1 1
z z
1 1
代入Ha(s),得H(z)为
H
(z)
Ha
(s)
|s
c1 1
z z
1 1
Ha
c
1 1
z 1 z 1
其频率响应为
H (e j )
Ha (
j)
|
c
tan
2
Ha
jc
tan
2
上述这些步骤比用脉冲响应不变法设计滤波器要简便得多。
这样得到的模拟滤波器h经双线性变换后就映射到数字滤波器hz的原转折频率如果给出的是待设计的带通滤波器的模拟域转折频率通阻带截止频率f和采样频率1t则首先利用下式计算数字滤波器的转折频率通阻带截止频率与给定的模拟域转折频率f上述这些步骤比用脉冲响应不变法设计滤波器要简便得多
计算双线性变换的简便算法

计算双线性变换的简便算法
双线性变换是一种简单而有效的图像缩放技术,它在许多领域中都得到了应用,已被广泛用于图像处理,模拟技术,多媒体等。
它的基本原理就是,在将一幅图像的尺寸缩放时,维持图像中每一个像素点的相对位置不变,以保持图像整体的结构稳定。
双线性变换是采用四点插值方法来进行双线性插值,原图像上的所有像素点都
会被拆分成四个小一点,称为方块点(标杆点),每个标杆点背后的灰度值就是要插值的结果。
在做双线性变换插值时,将被放大的图像上的每一点像素都向它背后的四个标杆点中选取四个像素值,然后用它们的灰度值的加权平均值(居中插值)来得到新像素的颜色值。
由于此算法比较简便,效率也比较高,它比双三次插值计算速度更快,为了满
足多媒体应用的要求,双线性变换算法主要应用在视频处理,它可以精确缩放图像,从而更好地节省计算资源,帮助提高多媒体应用的性能和用户体验。
双线性变换算法是一种高效而可靠的图像处理和数据建模技术,可实现图像的
精准缩放处理,节省空间和计算资源,优化用户体验。
这种技术作为一种图像处理算法,目前已经得到广泛的应用,能有效满足移动互联网的多媒体要求,进一步拓展活跃用户流量,增强用户留存和提升营销成效。
6.3 双线性变换法

10
§6.5 设计IIR数字滤波器的频率变换法
又称为
•
“模拟域频率变换法 频率变换的两种基本方法 ” 法一:从归一化模拟低通原型出发,先在模拟域内经频率 变换成为所需类型的模拟滤波器;然后进行双线性变换, 由S域变换到Z域,而得到所需类型的数字滤波器。
又称为
“数字域频率变换法 ” 法二:先进行双线性变换,将模拟低通原型滤波器变换成 数字低通滤波器;然后在Z域内经数字频率变换为所需类 型的数字滤波器。
p 2 T 2 tg (
p
用脉冲响应不 ) tg0.125 0.4142136 变法怎么设计?
s
tg (
s
2
2
) tg0.275 1.1708496
T
② 确定巴特沃斯型数字低通滤波器的阶次。
N lg( k sp ) lg( sp ) 2.66
∴ 取滤波器阶次 N = 3
13
• 典型例题
例1:设计一个 3 阶巴特沃斯型数字高通滤波器 ,3dB数字截频为0.2π弧度,求该滤波器的系统 函数。
解:
① 3阶巴特沃斯型归一化模拟低通原型的系统函数为:
注意:这里是 模拟低通的, 应该是多少?
去归一化得到低通系统
函数: H aL ( s ) H aL ( p ) p
s c
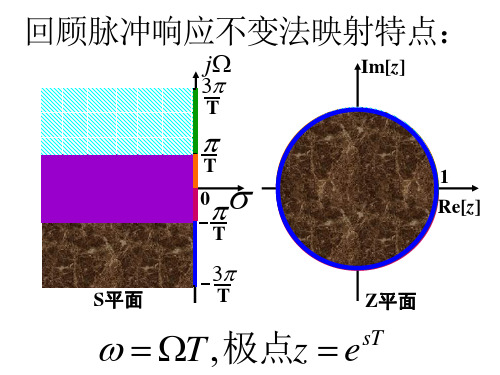
脉冲响应不变法的映射过程图示
2
2、双线性变换法的改进: 为避免频率的“混叠效应” ,分两步完成S平面到Z平面 的映射。
① 将S平面压缩到某一中介的S1平面的一条横带域 T , ; T ② 通过标准的变换将此横带域映射到整个Z平面上去。
双线性变换的映射过程图示
3
3、双线性变换法的基本思路: 从频率响应出发,直接使数字滤波器的频率响应 逼近模拟滤波器的频率响应 ,进而求得H(z)。
双线性变换法和窗函数法设计高通滤波器

目录摘要 (I)第一章数字滤波器设计的具体要求和目的 (1)第一节设计目的 (1)第二节设计要求 (1)第二章对数字信号处理的认识和了解 (2)第三章数字滤波器的设计原理 (3)第一节IIR数字滤波器的设计 (3)一IIR数字滤波器简介 (3)二双线性变换法设计IIR滤波器 (6)三方案的设计论证及选择 (7)第二节FIR滤波器的设计 (8)一FIR滤波器简介 (8)二窗函数法设计FIR滤波器 (10)第四章程序设计及调试 (12)第一节设计要求 (12)第二节双线性变换法设计巴特沃斯数字高通滤波器 (12)一模拟低通滤波 (12)二模拟到数字的转换 (13)三仿真结果与分析 (15)第三节凯泽窗法设计高通滤波器 (17)一程序设计 (17)二结果分析 (17)第五章心得体会 ......................................................... 错误!未定义书签。
参考文献 . (21)附录 (22)第一章 数字滤波器设计的具体要求和目的第一节 设计目的通过本课程设计,巩固数字信号处理的有关知识,熟悉各种数字滤波器的设计原理,设计方法。
学会分析有限字长效应带来的误差,合理设计数字滤波器的结构。
学会利用MATLAB 来进行滤波器的设计。
第二节 设计要求给定技术指标:通带截止频率KHz f c 3=,②通带最大衰减dB d p 3=阻带截止频率KHz f st 2= ,④阻带最小衰减dB d s 14=,抽样频率KHz F s 10=用双线性变换法设计一个巴特沃斯数字高通滤波器。
技术指标同上,用凯泽窗法设计一个FIR 数字高通滤波器。
设计时间为一周。
第二章对数字信号处理的认识和了解随着信息时代的到来,数字信号处理已经成为当今一门极其重要的学科和技术,并且在通信、语音、图像、自动控制等众多领域得到了广泛的应用。
在数字信号处理中,数字滤波器占有极其重要的地位,它具有精度高、可靠性好、灵活性大等特点。
脉冲响应不变法及双线性换法

概念讲解利用模拟滤波器理论设计数字滤波器,也就是使数字滤波器能模仿模拟滤波器的特性,这种模仿可从不同的角度出发。
脉冲响应不变法是从滤波器的脉冲响应出发,使数字滤波器的单位脉冲响应序列h(n) 模仿模拟滤波器的冲击响应ha (t), 使h(n)正好等于ha(t)的采样值,即h(n)=ha(nT)T为采样周期。
如以Ha (s)及H(z)分别表示ha(t)的拉氏变换及h(n)的z变换,即Ha(s)=L[ha(t)]H(z)=Z[h(n)]则根据采样序列z变换与模拟信号拉氏变换的关系,得:上式表明,采用脉冲响应不变法将模拟滤波器变换为数字滤波器时,它所完成的S平面到Z平面的变换,正是以前讨论的拉氏变换到Z变换的标准变换关系,即首先对H a(s)作周期延拓,然后再经过z=e st的映射关系映射到Z平面上。
z=e st的映射关系表明,S平面上每一条宽为2π/T的横带部分,都将重叠地映射到Z平面的整个全部平面上。
每一横带的左半部分映射到Z平面单位圆以内,每一横带的右半部分映射到Z平面单位圆以外,jΩ轴映射在单位圆上,但jΩ轴上的每一段2π/T都对应于绕单位圆一周,如下图所示:图脉冲响应不变法的映射关系应当指出,Z=e st的映射关系反映的是H a(s)的周期延拓与H(z)的关系,而不是H a(s)本身与H(z)的关系,因此,使用脉冲响应不变法时,从H a(s)到H(z)并没有一个由S平面到Z平面的简单代数映射关系,即没有一个s=f(z)的代数关系式。
另外,数字滤波器的频响也不是简单的重现模拟滤波器的频响,而是模拟滤波器频响的周期延拓,周期为Ω=2π/T=2πf s,即S正如第一章采样定理中所讨论的,如果模拟滤波器的频响带限于折叠频率ΩS/2以内,即Ha(jΩ)=0|Ω|≥π/T这时数字滤波器的频响才能不失真地重现模拟滤波器的频响(在折叠频率以内)|ω|<π但任何一个实际的模拟滤波器,其频响都不可能是真正带限的,因此不可避免地存在频谱的交叠,即混淆,这时,数字滤波器的频响将不同于原模拟滤波器的频响而带有一定的失真。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 H a ( s) 1 2( sT / 2) 2( sT / 2)2 ( sT / 2)3
最后,将双线性变换关系代入就得到数字滤波器的系统函数
H ( z ) H a ( s)
2 1 z 1 s T 1 z 1
c tan 2
上式表明,S平面上Ω与Z平面的ω成非线性的正切关系,如图67所示。
由图6-7看出,在零频率附近,模拟角频率Ω与数字频率ω之 间的变换关系接近于线性关系;但当 Ω 进一步增加时, ω增长得 越来越慢,最后当Ω→∞时,ω终止在折叠频率ω=π处,因而双线
性变换就不会出现由于高频部分超过折叠频率而混淆到低频部分
将双线性变换应用于模拟滤波器,有
H ( z ) H a ( s ) s 2 1 z
1
T 1 z 1
1 1 (2 / 0.828)[(1 z 1 ) /(1 z 1 )]
1 z 1 0.2920 1 0.4159z 1
1 z 1 由上题可知,T不参与设计,即双线性变换法中用 s , 1 1 z 1 2 1 z 2 设计得到的结 设计与用 s , tan tan 1 T 1 z T 2 2 果一致。
第二次变换: 数字化
图 6-6双线性变换的映射关系
• 双线性变换法的映射规则: (1)频率压缩:把整个S平面压缩变换到某一中 介的S1平面的一条横带里。
z (2)数字化:将S1平面通过标准变换关系 变换到z平面。
e
s1T
(1)频率压缩
• 把整个S平面压缩变换到某一中介的S1平面的一条横带 里。 2 宽度为 ,从 , 采用如下变换关系: T T T T t an( ) 2 1T tan 这样满足: 2 -π/T π/T , , 0,1 0 1 T 1T 又 s j j tan 2
如果给出的是待设计的带通滤波器的模拟域转折频率(通、
阻带截止频率)f1、f2、f3、f4和采样频率(1/T),则 首先,利用下式计算数字滤波器的转折频率(通、阻带截 止频率)ω1、ω2、ω3 和ω4。
2 fT
再利用式
c tan 2
对频率预畸变,得到预畸变后的模拟滤波器的转折频率Ω1、Ω2、 Ω3和Ω4。这样得到的模拟滤波器Ha(s)的转折频率Ω1、Ω2、Ω3和Ω4,
也是高通滤波器; 若为带通、带阻滤波器也是如此。 在IIR数字滤波器的设计中,当强调模仿滤波器的瞬态响应 时,采用冲激响应不变法较好; 而在其余情况下,大多采用双线 性变换法。
例 6-2 设计一个一阶数字低通滤波器,3 dB截止频率为ωc =0.25π,将双线性变换应用于模拟巴特沃思滤波器。
1 H a ( s) 1 ( s / c )
(1) 如果给出的是待设计的带通滤波器的数字域转折频率
(通、 阻带截止频率)ω1、ω2、ω3、ω4及采样频率(1/T),则直 接利用式
c tan 2
计算出相应的模拟滤波器的转折频率 Ω1、Ω2、Ω3和Ω4。这样得 到的模拟滤波器 Ha(s)的转折频率Ω1、Ω2、Ω3和Ω4,经双线性变 换后就映射到数字滤波器H(z)的原转折频率ω1、ω2、ω3和ω4。
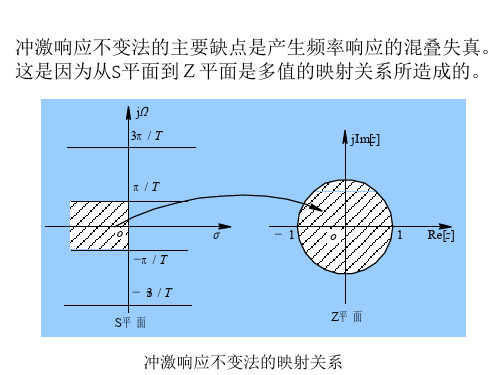
冲激响应不变法的主要缺点是产生频率响应的混叠失真。 这是因为从S平面到Z平面是多值的映射关系所造成的。
j 3 / T jIm[z]
/ T o - / T -3 / T S 平面 Z平面
-1
o
1
Re[z]
冲激响应不变法的映射关系
6.4 用双线性变换法设计IIR数字滤波器 一、 变换原理
这时S 平面与Z平面之间为单值映射关系,这种变换就称为双线性变换。
二、变换常数c的选择
调节c,可使AF的频率特性与DF的频率特性在不同频率 点处有对应的关系。也就是可以调节频带间的对应关 系。 • (a)使AF与DF在低频处有较确切的对应关系。在低 1 频处有 当1较小时有 1T 1T tan( ) 2 2 由于 1T 1T =c tan( )c 1 2 2 2 c T
z
cs ,得 cs
c j z c j
因此
2 c 2
| z |
c
2
2
由此看出,当σ<0时, |z|<1;当σ>0时,|z|>1。也就是说, S平面的左半平面映射到Z平面的单位圆内,S平面的右半平面
映射到Z平面的单位圆外,S平面的虚轴映射到 Z平面的单位圆
j
上述这些步骤比用脉冲响应不变法设计滤波器要简便得多。
需要特别强调的是,若模拟滤波器 Ha(s) 为低通滤波器,应 用
1 z 1 sc 1 z 1
变换得到的数字滤波器 H(z) 也是低通滤波器; 若
1 z 1 变换得到的数字滤波器H(z) sc 1 1 z
Ha(s)为高通滤波器,应用
但是双线性变换的这个特点是靠频率的严重非线性关系而 得到的。由于这种频率之间的非线性变换关系,就产生了新的
问题。首先,一个线性相位的模拟滤波器经双线性变换后得到
非线性相位的数字滤波器,不再保持原有的线性相位了;其次, 这种非线性关系要求模拟滤波器的幅频响应必须是分段常数型 的,即某一频率段的幅频响应近似等于某一常数(这正是一般 典型的低通、高通、带通、带阻型滤波器的响应特性),不然
经双线性变换后映射到数字滤波器 H(z)的转折频率ω1、ω2、 ω3、
ω4,并且能保证数字域频率 ω1、ω2、ω3 、ω4与给定的模拟域转折 频率f1、f2、f3、f4成线性关系。
(2) 按Ω1、Ω2、Ω3和Ω4等指标设计模拟滤波器的系统函数 Ha(s)。
1 z 1 (3)将 s c 1 代入Ha(s),得H(z)为 1 z
H a ( jΩ ) o o
c tan 2
Ω=ω/T
H (e j )
o
1 2
34
图 6-9 双线性变换时频率的预畸变
设计流程
• 1.根据要求,设定指标。 • 2.将各分段频率临界点预畸变。 • 3.将数字滤波器的性能指标转换为中间模拟滤 波器的性能指标。 • 4.根据设计要求,选定双线性变换常数C。 • 5.设计中间模拟滤波器的系统函数Ha(s). 1 z 1 • 6.将 S C 代入Ha(s)中,得到DF 的 1 1 z H(z).
标准变换关系 z=es1T将此横带变换到整个 Z 平面上去。这样就使 S
平面与Z平面建立了一一对应的单值关系, 消除了多值变换性, 也就消除了频谱混叠现象,映射关系如图6-6所示。
j
j 1
jIm[z]
/ T -1 o 1 o Re[z]
o - / T
1
S平面
S1 平面
Z平面
第一次变换: 频率压缩
所需要的数字频率上。
由图6-7看出,在零频率附近,模拟角频率Ω与数字频率ω之 间的变换关系接近于线性关系;但当 Ω 进一步增加时, ω增长得 越来越慢,最后当Ω→∞时,ω终止在折叠频率ω=π处,因而双线
性变换就不会出现由于高频部分超过折叠频率而混淆到低频部分
去的现象, 从而消除了频率混叠现象。
4 3 2 1
例6-3 用双线性变换法设计一个三阶巴特沃思数字低通滤波 器,采样频率为fs=4 kHz(即采样周期为T=250 μs),其3dB 截止频率为fc=1 kHz。 三阶模拟巴特沃思滤波器为
1 H a ( s) 1 2( s / c ) 2( s / c )2 ( s / c )3
解: 首先,确定数字域截止频率ωc=2πfcT=0.5π。 第二步,根据频率的非线性关系式,确定预畸变的模拟滤
波器的截止频率
2 c 2 0.5 c tan tan T 2 T 2
2 T
第三步,将Ωc代入三阶模拟巴特沃思滤波器Ha(s),得
双线性变换法是使数字滤波器的频率响应与模拟滤波器的频
率响应相似的一种变换方法。为了克服多值映射这一缺点,采用
非线性频率压缩方法,将整个频率轴上的频率范围压缩到 -π/T ~
π/T之间,再用z=esT转换到Z平面上。也就是说,第一步先将整个 S 平面压缩映射到 S1 平面的 -π/T ~ π/T 一条横带里;第二步再通过
上。 因此,稳定的模拟滤波器经双线性变换后所得的数字滤波
器也一定是稳定的。
四、 优缺点
双线性变换法与冲激响应不变法相比,其主要的优点是避
免了频率响应的混叠现象。这是因为 S平面与Z平面是单值的一
一对应关系。S平面整个jΩ轴单值地对应于 Z平面单位圆一周, 即频率轴是单值变换关系。这个关系下式所示,重写如下:
去的现象, 从而消除了频率混叠现象。
= 2 tan 2 T
-
o
图6-7 双线性变换法的频率变换关系
H a ( j Ω)
o
o
o
arg[ H a ( j Ω)] o o
H (e j )
o
arg[ H (e j )]
图 6-8 双线性变换法幅度和相位特性的非线性映射
变换所产生的数字滤波器幅频响应相对于原模拟滤波器的幅频
响应会有畸变,如图 6-8 所示。
对于分段常数的滤波器,双线性变换后,仍得到幅频特性 为分段常数的滤波器,但是各个分段边缘的临界频率点产生了
畸变, 这种频率的畸变,可以通过频率的预畸来加以校正。也
就是将临界模拟频率事先加以畸变, 然后经变换后正好映射到
解 数字低通滤波器的截止频率为ωc=0.25π,相应的巴特沃思 模拟滤波器的 3 dB截止频率是Ωc,就有
