第七章平面图形的认识二提高测试卷5
人教版七年级数学下册第七章 平面图形的认识 提高练习

第七章平面图形的认识(二) 提高练习班级:________姓名:___________学号:______得分:__________一、选择题:(每题3分,共30分)围成不同的三角形,则围成的三角形共有:( )A、1个B、2个C、3个D、4个6、若一个多边形每一个外角都与它的相邻的内角相等,则这个多边形的边数是:( )A 、6B 、5C 、4D 、3 7、下列叙述中,正确的有:( )①三角形的一个外角等于两个内角的和;②一个五边形最多有3个内角是直角;③任意一个三角形的三条高所在的直线相交于一点,且这点一定在三角形的内部;④ΔABC 中,若∠A=2∠B=3∠C ,则这个三角形ABC 为直角三角形. A 、0个B 、1个C 、2个D 、3个 8、如图,OP∥QR∥ST ,则下列各式中正确的是:( )A 、∠1+∠2+∠3=180°B 、∠1+∠2-∠3=90°C 、∠1-∠2+∠3=90°D 、∠2+∠3-∠1=180°9、如图是一块电脑主板的示意图,每一转角处都是直角,数据如图所示,则该主板的周长是:( )A 、88mmB 、96mmC 、80mmD 、84mm10、一幅三角板如图所示叠放在一起,则图中∠α的度数为: ( )A 、75°B 、60°C 、65°D 、55°二、填空题(每题2分,共20分)1、如图,面积为6cm 2的直角三角形ABC 沿BC 方向平移至三角形DEF 的位置,平移距离是BC 的2倍,则图中四边形ACED 的面积为_______ cm 2.2、如图,l 1∥l 2,AB ⊥l 2,垂足为O ,BC 交l 2于点E ,若∠ABC=140°,则∠1=_____°.第2题图l 1l 2A BOEC1ABC EF D123456aABCD第3题图第8题图第10题图4mm16mm24mm第9题图3、光线a 照射到平面镜CD 上,然后在平面镜AB 和CD 之间来回反射,这时光线的入射角等于反射角。
第7章平面图形的认识(二)综合提优测试及答案

第7章《平面图形的认识(二)》综合提优测试(时间:100分钟满分:100分)一、选择题(每题2分,共20分)1.下列命题中,不正确的是().A.如果两条直线都和第三条直线平行,那么这两条直线也互相平行B.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行C.两条直线被第三条直线所截,那么这两条直线平行D.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行2.图中有四条互相不平行的直线1l 、2l 、3l 、4l 所截出的七个角.关于这七个角的度数关系,下列说法正确的是().A.247∠=∠+∠B.316∠=∠+∠C.146180∠+∠+∠=︒D.235180∠+∠+∠=︒3.如图,//AB EF ,CD EF ⊥,若40ABC ∠=︒,则BCD ∠=().A.140︒B.130︒C.120︒D.110︒4.若多边形的边数增加1,则().A.其内角和增加180︒B.其内角和为360︒C.其内角和不变D.其外角和减少5.三角形的三条高所在直线的交点().A.一定在三角形的内部B.一定在三角形的外部C.一定在三角形的顶点D.都有可能6.若一个三角形的3个内角度数之比为5:3:1,则与之对应的3个外角的度数之比为().A.4:3:2B.2:3:4C.3:2:4D.3:1:57.如图,//AB CD ,CE 平分BCD ∠,36B ∠=︒,则DCE ∠等于().A.18︒B.36︒C.45︒D.54︒8.如图,六边形ABCDEF 的六个内角都相等,若1AB =,3BC CD ==,2DE =,则这个六边形的周长等于().A.15B.14C.17D.189.如图,若//AB CD ,则B ∠、C ∠、E ∠三者之间的关系是().A.180B C E ∠+∠+∠=︒B.180B E C ∠+∠-∠=︒C.180B C E ∠+∠-∠=︒D.180C E B ∠+∠-∠=︒10.如图,//AB CD ,AC BC ⊥,AC BC ≠,则图中与BAC ∠互余的角有().A.1个B.2个C.3个D.4个二、填空题(每题2分,共20分)11.如图所示,小华从点A 出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地点A 时,一共走的路程是.12.在ABC V 中,已知点D 、E 、F 分别是边BC 、AD 、CE 上的中点,且24ABC S cm =V ,则BEF S V 的值为.13.在ABC V 中,150A B ∠+∠=︒,2C A ∠=∠,则A ∠=,B ∠=.14.如图,直线//a b ,Rt ABC V 的直角顶点C 在直线b 上,120∠=︒,则2∠=.15.如果一个正多边形的每个外角都是30°,那么这个多边形的内角和为.16.如图,ABC V 中,AB AC =、12BC cm =,点D 在AC 上,4DC cm =.将线段DC 沿着CB 的方向平移7cm 得到线段EF ,点E 、F 分别落在边AB 、BC 上,则EBF V 的周长为cm .17.如图所示,A B C D E ∠+∠+∠+∠+∠=.18.教材在探索多边形的内角和为(2)180n -⨯︒时,都是将多边形转化为去探索的.从(3)n n >边形的一个顶点出发,画出条对角线,这些对角线把n 边形分成个三角形,分成的三角形内角的总和与多边形的内角和.19.如图,//AB CD ,26B ∠=︒,39D ∠=︒,求BED ∠的度数.解:过点E 作//EF AB ,126B ∴∠=∠=︒.()//AB CD Q (已知),//EF AB (所作),//EF CD ∴.()239D ∴∠=∠=︒.1265BED ∴∠=∠+∠=︒.20.在三角形纸片ABC 中,已知90ABC ∠=︒,6AB =,8BC =.过点A 作直线l 平行于BC ,折叠三角形纸片ABC ,使直角顶点B 落在直线l 上的T 处,折痕为MN .当点T 在直线l 上移动时,折痕的端点M 、N 也随之移动.若限定端点M 、N 分别在边AB 、BC 上移动,则线段AT 长度的最大值与最小值之和为.(计算结果不取近似值)三、解答题(共9题,共60分)21.如图,ABC V 的顶点都在方格纸的格点上.将ABC V 向左平移2格,再向上平移4格.请在图中画出平移后的三角形'''A B C ,再在图中画出三角形'''A B C 的高''C D .22.如图,直线AB 和直线CD 被直线GH 所截,交点分别为点E 、F ,AEF EFD ∠=∠.(1)AB 与CD 平行吗,为什么?(2)如果AEM NFD ∠=∠,那么EM 与FN 是否平行,为什么?23.如图,25B ∠=︒,45BCD ∠=︒,30CDE ∠=︒,10E ∠=︒,求证://AB EF .24.如图,在ABC V 中,CE AB ⊥,垂足为点E ,DF AB ⊥,垂足为点F ,//AC ED ,CE 是ACB ∠的角平分线.求证:EDF BDF ∠=∠.25.如图,从下列三个条件中:(1)//AD CB ;(2)//AB CD ;(3)A C ∠=∠.任选两个作为条件,另一个作为结论,编一道数学题,并说明理由.已知:结论:理由:26.如图,//AD BC ,96A ∠=︒,104D ∠=︒,BE 、CE 分别是ABC ∠和BCD ∠的角平分线,求BEC ∠的度数.27.如图,已知点D 为等腰直角ABC V 内一点,15CAD CBD ∠=∠=︒.E 为AD 延长线上的一点,且CE CA =.(1)求证:DE 平分BDC ∠;(2)若点M 在DE 上,且DC DM =,求证:ME BD =.28.小亮的父亲想用正三角形、正四边形和正六边形地板砖铺设一条小道地面,小亮根据所学的知识告诉父亲,为了能够做到无缝隙.不重叠地铺设.可按如图所示的规律拼图案.即从第二个图案开始,每个图案中正三角形的个数都比前一个图案中正三角形的个数多4个.请你帮助小明求第n 个图案中正只角形的个数有多少?(用含n 的代数式表示)29.平面内的两条直线有相交和平行两种位置关系.(1)AB 平行于CD ,如图(1),点P 在AB 、CD 外部时,由//AB CD ,有B BOD ∠=∠,又因为BOD ∠是POD V 的外角,故BOD BPD D ∠=∠+∠,得BPD B D ∠=∠-∠.如图(2),将点P 移到AB 、CD 内部,以上结论是否成立?若不成立,则BPD ∠、B ∠、D ∠之间有何数量关系?请证明你的结论;(2)在图(2)中,将直线AB 绕点B 逆时针方向旋转一定角度交直线CD 于点Q ,如图(3),则BPD ∠、B ∠、D ∠、BQD ∠之间有何数量关系?(不需证明)(3)根据(2)的结论求图(4)中A B C D E F ∠+∠+∠+∠+∠+∠的度数.参考答案1.C2.C3.B4.A5.D6.B7.A8.A9.B10.C11.150米12.1cm213.15°135°14.70°15.1800°16.13°17.180°18.三角形(3)n -(2)n -相等19.两直线平行,内错角相等平行于同一直线的两直线平行20.14-21.略22.(1)//AB CD 。
七年级数学第七章《平面图形的认识(二)》提优训练

七年级数学提优训练第七章《平面图形的认识(二)》一、选择题(每题2分,共20分)1.下列命题中,不正确的是( ).A.如果两条直线都和第三条直线平行,那么这两条直线也互相平行B.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行C.两条直线被第三条直线所截,那么这两条直线平行D.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行2.△ABC的高的交点一定在外部的是( ).A.锐角三角形B.钝角三角形C.直角三角形D.有一个角是60°的三角形3.现有两根木棒,它们的长分别是40 cm和50 cm,若要钉或一个三角形木架,则在下列四根木棒中应选取( ).A.10 cm的木棒B.40 cm的木棒C.90 cm的木棒D.100 cm的木棒4.已知等腰三角形的两边长分别为3 cm,4 cm,则它的周长为( ).A.10 cm B.11 cmC.10 cm或11 cm D.无法确定5.下列条件中,能判定△ABC为直角三角形的是( ).A.∠A=2∠B一3∠C B.∠A+∠B=2∠CC.∠A一∠B=30°D.∠A=12∠B=13∠C6.在四边形的4个内角中,钝角的个数最多为( ).A.1 B.2 C.3 D.47.如图,已知直线AB∥CD,∠C =115°,∠A=25°,∠E=( ).A.70°B.80°C.90°D.100°(第7题) (第10题)8.一个多边形的内角和等于它外角和的2倍,则这个多边形是( ).A.三角形B.四边形C.五边形D.六边形9.若△ABC的三边长分别为整数,周长为11,且有一边长为4,则这个三角形的最大边长为( ).A.7 B.6 C.5 D.410.在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4 cm2,则S△BEF的值为( ).A.2 cm2B.1 cm2C.0.5 cm2D.0.25 cm2二、填空题(每题3分,共24分)11.一个凸多边形的内角和与外角和相等,它是_________边形.12.如图,线段DE由线段AB平移而得,AB=4,EC=7-CD,则△DCE的周长为______cm.13.如图,直线a∥b,c∥d,∠1=115°,则∠2=________,∠3=__________.14.若一个多边形的每一个外角都是72°,则这个多边形是____边形,它的内角和为_____.15.根据下列各图所表示的已知角的度数,求出其中∠α的度数:(1)∠α=_________°;(2)∠α=_________°;(3)∠α=_________°.16.教材在探索多边形的内角和为(n-2)×180°时,都是将多边形转化为________去探索的.从n(n>3)边形的一个顶点出发,画出______条对角线,这些对角线把n边形分成_____个三角形,分成的三角形内角的总和与多边形的内角和___________.17.如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.解:过点E作EF∥AB,∠1=∠B=26°.( )∵AB∥CD(已知),EF∥AB(所作),∴EF∥CD.( )∴∠2=∠D=39°.∴∠BED=∠1+∠2=65°.18.中国象棋中的马颇有骑士风度,自古有“马踏八方”之说,如图(1),按中国象棋中“马”的行棋规则,图中的马下一步有A、B、C、D、E、F、G、H八种不同选择,它的走法就象一步从“日”字形长方形的对角线的一个端点到另一个端点,不能多也不能少.要将图(2)中的马走到指定的位置P处,即从(四,6)走到(六,4),现提供一种走法:(四,6)→(六,5)→(四,4)→(五,2)→(六,4)(1)下面是提供的另一走法,请你填上其中所缺的一步:(四,6)→(五,8)→(七,7)→__________→(六,4)(2)请你再给出另一种走法(只要与前面的两种走法不完全相同即可,步数不限),你的走法是:6___________________________________.三、解答题(第19、20题每题8分,第21~24题每题10分,共56分)19.如下图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的三角形A′B′C′,再在图中画出三角形A′B′C′的高C′D′.20.如图,直线AB和直线CD被直线GH所截,交点分别为点E、F,∠AEF=∠EFD.(1)AB与CD平行吗,为什么?(2)如果∠AEM=∠NFD,那么EM与FN是否平行,为什么?21.如图,从下列三个条件中:(1)AD∥CB;(2)AB∥CD;(3)∠A=∠C,任选两个作为条件,另一个作为结论,编一道数学题,并说明理由.已知:结论:理由:22.如图,AD∥BC,∠A=96°,∠D=104°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.23.如图,已知AB∥CD,BC∥AD,问∠B与∠D有怎样的大小关系,为什么?24.(1)如图(1),在△ABC中,∠ABC、∠ACB的平分线相交于点O.a)若∠A=60°,求∠BOC的度数.b)若∠A=n°,则∠BOC=_________.c)若∠BOC=3∠A,则∠A=__________.(2)如图(2),在△A′B′C′中的外角平分线相交于点O′,∠A′=40°,求∠B′O′C′的度数.(3)上面(1),(2)两题中的∠BOC与∠B′O′C′有怎样的数量关系?参考答案1.C 2.B 3.B 4.C 5.D 6.C 7.C 8.D 9.C 10.B 11.四12.11 13.65°65°14.五540°15.(1)70 (2)48 (3)5016.三角形(n一3) (n一2) 相等17.两直线平行,内错角相等平行于同一直线的两直线平行18.(1)(八,5) (2)略,答案不唯一19.略20.(1)AB∥CD,因为内错角相等.两直线平行(2)EM∥FN,因为内错角相等(∠ABF=∠EFN),两直线平行21.已知:AD∥CB,∠A=∠C,结论:AB∥CD.理由:∵AD∥CB,∴∠A=∠ABF.又∠A=∠C,∴∠ABF=∠C.∴AB∥CD.22.∵AD∥BC,∠A=96°,∴∠ABC=180°-∠A=180°-96°=84°.同理∠DCB=180°一∠D=180°一104°=76°.∵BE、CE分别是么ABC和么BCD的平分线,∴∠EBC=12∠ABC=12×84°=42°,∠ECB=12∠DCB=12×76°=38°.∴∠BEC=180°一42°一38°=100°.23.∠B=∠D.∵AB∥CD,∴∠B+∠C=180°.∵AD∥BC,∴∠C+∠D=180°.∴∠B=∠D.24.(1)a)∵∠A=60°,∴∠ABC+∠ACB=180°一∠A=120°.又BO、CO分别平分∠ABC、∠ACB,∴∠l=12∠ABC,∠2 =12∠ACB.∴∠1+∠2=12(∠ABC+∠ACB)=60°.∴∠BOC=180°一60°=120°.b) (90+12 n)°.c)36°(2) ∠B′O′C′=70°,(3) ∠BOC与∠B′O′C′=180°.。
2018-2019学年第7章《平面图形的认识(二)》提优卷(含答案)
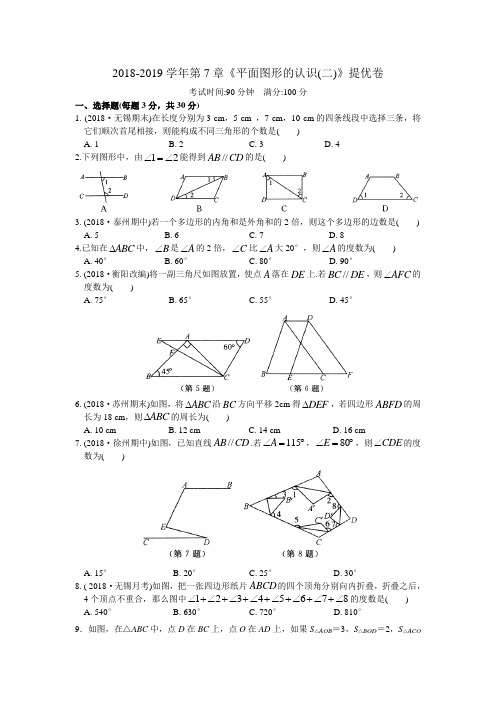
2018-2019学年第7章《平面图形的认识(二)》提优卷考试时间:90分钟 满分:100分一、选择题(每题3分,共30分)1. (2018·无锡期末)在长度分别为3 cm ,5 cm ,7 cm ,10 cm 的四条线段中选择三条,将它们顺次首尾相接,则能构成不同三角形的个数是( )A. 1B. 2C. 3D. 4 2.下列图形中,由12∠=∠能得到//AB CD 的是( )3. (2018·泰州期中)若一个多边形的内角和是外角和的2倍,则这个多边形的边数是( ) A. 5 B. 6 C. 7 D. 84.已知在ABC ∆中,B ∠是A ∠的2倍,C ∠比A ∠大20°,则A ∠的度数为( ) A. 40° B. 60° C. 80° D. 90°5. (2018·衡阳改编)将一副三角尺如图放置,使点A 落在DE 上.若//BC DE ,则AFC ∠的度数为( )A. 75°B. 65°C. 55°D. 45°6. (2018·苏州期末)如图,将ABC ∆沿BC 方向平移2cm 得DEF ∆,若四边形ABFD 的周长为18 cm ,则ABC ∆的周长为( )A. 10 cmB. 12 cmC. 14 cmD. 16 cm7. (2018·徐州期中)如图,已知直线//AB CD .若115A ∠=︒,80E ∠=︒,则CDE ∠的度数为( )A. 15°B. 20°C. 25°D. 30°8. ( 2018·无锡月考)如图,把一张四边形纸片ABCD 的四个顶角分别向内折叠,折叠之后,4个顶点不重合,那么图中12345678∠+∠+∠+∠+∠+∠+∠+∠的度数是( ) A. 540° B. 630° C. 720° D. 810°9.如图,在△ABC 中,点D 在BC 上,点O 在AD 上,如果S △AOB =3,S △BOD =2,S △ACO=1,那么S △COD 等于( )A .B .C .D .10.(2018•聊城)如图,将一张三角形纸片ABC 的一角折叠,使点A 落在△ABC 外的A '处,折痕为DE .如果∠A =α,∠CEA ′=β,∠BDA '=γ,那么下列式子中正确的是( ) A .γ=2α+βB .γ=α+2βC .γ=α+βD .γ=180°﹣α﹣β二、填空题(每题3分,共24分)11.(2018·扬州期末)十五边形的外角和等于 . 12.如图,由图可知x = ,y = .13.如图,已知直线//a b .若150∠=︒,230∠=︒,则3∠= .14.如图,已知AE 是正八边形ABCDEFGH 的一条对角线,则BAE ∠= .15.取一张长方形纸片,按如图所示的方法折叠一角,得到折痕EF ,若36DFE ∠=︒,则'D FA ∠的度数为 .16.如图,,,A B C 分别是线段111,,A B B C C A 的中点,若ABC ∆的面积是2,则111A B C ∆的面积是 .17.如图,在七边形ABCDEFG 中,,AB ED 的延长线相交于点O .若图中1,2,3,4∠∠∠∠的外角的度数和为220°,则BOD ∠的度数为 .18.如图,将长方形ABCD 分成15个大小相等的正方形,,,,E F G H 分别在边,,,AD AB BC CD 上,且是某个小正方形的顶点,若四边形EFGH 的面积为1,则长方形ABCD 的面积为 . 三、解答题(共76分)19.(9分)(2018·盐城期末)如图,在方格纸上,以格点为顶点的三角形叫做格点三角形,请按要求完成下列操作:(1)将ABC ∆先向右平移2个单位长度,再向上平移4个单位长度,画出平移后的111A B C ∆; (2)连接11,AA BB ,则线段11,AA BB 的位置关系为 ,数量关系为 ; (3)画出ABC ∆的边AB 上的中线CD 以及边BC 上的高AE .20. ( 9分)如图,已知//AB CD .(1)试判断FAB ∠与C ∠的大小关系,并说明理由; (2)若35C ∠=︒,AB 是FAD ∠的平分线. ①求FAD ∠的度数;②若110ADB ∠=︒,求BDE ∠的度数.21.(8分)(2018•重庆)如图,AB ∥CD ,△EFG 的顶点F ,G 分别落在直线AB ,CD 上,GE 交AB 于点H ,GE 平分∠FGD .若∠EFG =90°,∠E =35°,求∠EFB 的度数.22. (9分)小刚同学在进行多边形内角和的计算时,求得一个多边形的内角和为1 125°. (1)小芳同学看到他的计算结果后,马上就说小刚的计算肯定有误,你能知道小芳是如何判断的吗?(2)小刚重新检查后,发现自己真的少加了一个内角,请问:这个内角是多少度? (3)这个多边形有多少条边?23. ( 9分)在ABC ∆中,已知,CD CE 分别是ABC ∆的高和角平分线,BAC α∠=,B β∠=()αβ>.(1)如图①,若70,40αβ=︒=︒,求DCE ∠的度数; (2)试用含,αβ的代数式表示DCE ∠的度数;(直接写出结果)(3)如图②,将CE 改为ABC ∆的外角ACF ∠的平分线,且CE 交BA 的延长线于点E .若30αβ-=︒,求DCE ∠的度数.24.(9分)如图,已知//CB OA ,100C OAB ∠=∠=︒,且满足FOB AOB ∠=∠,OE 平分COF ∠.(1)求EOB ∠的度数;(2)如果平行移动AB ,那么:OBC OFC ∠∠的值是否随之变化?若变化,找出变化规律;若不变,求这个比值;(3)在平行移动过程中,是否存在某种情况,使OEC OBA ∠=∠?若存在,求此时OEC ∠的度数;若不存在,请说明理由.25. (10分)(2018·常州期末)如图①,直线l MN ⊥,垂足为O ,直线PQ 经过点O ,且30PON ∠=︒.点B 在直线l 上,位于点O 下方,1OB =.点C 在直线PQ 上运动.连接BC ,过点C 作AC BC ⊥,交直线MN 于点A ,连接AB (点,A C 与点O 都不重合).(1)小明经过画图、度量发现,在ABC ∆中,始终有一个角与PON ∠相等,这个角是 ;(2)当//BC MN 时,在图②中画出示意图.问://AC OB 吗?说明理由; (3)探索OCB ∠和OAB ∠之间的数量关系,并说明理由.26.(12分)某学习小组发现一个结论:已知直线a∥b,若直线c∥a,则c∥b.他们发现这个结论运用很广,请你利用这个结论解决以下问题:已知直线AB∥CD,点E在AB、CD之间,点P、Q分别在直线AB、CD上,连接PE、EQ.(1)如图1,运用上述结论,探究∠PEQ与∠APE+∠CQE之间的数量关系,并说明理由;(2)如图2,PF平分∠BPE,QF平分∠EQD,当∠PEQ=140°时,求出∠PFQ的度数;(3)如图3,若点E在CD的下方,PF平分∠BPE,QH平分∠EQD,QH的反向延长线交PF于点F.当∠PEQ=70°时,请求出∠PFQ的度数.参考答案一、1.B2.B3. B4. A5. A6. C7. A8. C9.D 10.A 二、 11. 360°12. 60° 50°13. 20° 14. 67.5° 15. 108° 16. 14 17. 40° 18. 53三、19.(1)如图所示(2) 11//AA BB 11AA BB =(3)如图所示20. (1)FAB C ∠=∠.因为//AB CD(2)①∵35FAB C ∠=∠=︒,AB 是FAD ∠的平分线, ∴270FAD FAB ∠=∠=︒.②∵110ADB ∠=︒,70FAD ∠=︒, ∴180ADB FAD ∠+∠=︒, ∴//CF BD ,∴35BDE C ∠=∠=︒. 21.∵∠EFG =90°,∠E =35°, ∴∠FGH =55°,∵GE 平分∠FGD ,AB ∥CD , ∴∠FHG =∠HGD =∠FGH =55°, ∵∠FHG 是△EFH 的外角, ∴∠EFB =55°﹣35°=20°.22. (1)因为多边形内角和度数一定是180°的整数倍,而1 125°不是. (2)设这个内角为x ︒(0180)x <<, 所以1125(2)180x n ︒+︒=-︒g ,所以458180xn +=+. 因为n 为正整数,且0180x <<, 所以135x =.故这个内角是135度. (3)由(2)得819n =+=所以这个多边形有9条边. 23. (1)15DCE ∠=︒(2)1()2DCE αβ∠=- (3)75DCE ∠=︒ 24. (1) 40EOB ∠=︒;(2):1:2OBC OFC ∠∠=(3)存在某种情况,使OEC OBA ∠=∠,此时60OEC ∠=︒. 25.(1) ABC ∠(2)//AC OB ,理由略(3)OCB ∠和OAB ∠之间的数量是相等或互补.26. (1)∠PEQ =∠APE +∠CQE , 理由如下:如图1,过点E 作EH ∥AB , ∴∠APE =∠PEH , ∵EH ∥AB ,AB ∥CD , ∴EH ∥CD , ∴∠CQE =∠QEH , ∵∠PEQ =∠PEH +∠QEH , ∴∠PEQ =∠APE +∠CQE ; (2)如图2,过点E 作EM ∥AB ,同理可得,∠PEQ =∠APE +∠CQE =140°, ∵∠BPE =180°﹣∠APE ,∠EQD =180°﹣∠CQE , ∴∠BPE +∠EQD =360°﹣(∠APE +∠CQE )=220°, ∵PF 平分∠BPE ,QF 平分∠EQD , ∴∠BPF =∠BPE ,∠DQF =∠EQD , ∴∠BPF +∠DQF =(∠BPE +∠EQD )=110°, 作NF ∥AB ,同理可得,∠PFQ =∠BPF +∠DQF =110°; (3)如图3,过点E 作EM ∥CD ,设∠QEM=α,∴∠DQE=180°﹣α,∵QH平分∠DQE,∴∠DQH=∠DQE=90°﹣α,∴∠FQD=180°﹣∠DQH=90°+α,∵EM∥CD,AB∥CD,∴AB∥EM,∴∠BPE=180°﹣∠PEM=180°﹣(70°+α)=110°﹣α,∵PF平分∠BPE,∴∠BPF=∠BPE=55°﹣α,作NF∥AB,同理可得,∠PFQ=∠BPF+∠DQF=145°.。
第7章平面图形的认识(二)单元测试卷(B卷提升篇)(苏科版)

第7章平面图形的认识(二)单元测试卷(B卷提升篇)【苏科版】考试时间:100分钟;满分:100分学校:___________姓名:___________班级:___________考号:___________题号一二三总分得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)评卷人得分一.选择题(共10小题,满分30分,每小题3分)1.(3分)(2019秋•海淀区校级期中)已知一个三角形的两条边长分别为3cm,6cm,则它的第三条边的长度可以是()A.3cm B.5cm C.9cm D.11cm2.(3分)(2019春•沂水县期中)如图,下列条件:①∠1=∠2,②∠2=∠3,③∠5+∠6=180°,④∠1+∠4=180°,⑤∠7=∠2+∠3中能判断直线a∥b的有()A.2个B.3个C.4个D.5个3.(3分)(2019秋•衢州期中)已知在△ABC中,∠A=∠B﹣∠C,则△ABC为()A.锐角三角形B.钝角三角形C.直角三角形D.以上都有可能4.(3分)(2019春•镇原县期中)如图,下列说法正确的是()A.图中没有同位角、内错角、同旁内角B.图中没有同位角和内错角,但是有一对同旁内角C.图中没有内错角和同旁内角,但有三对同位角D.图中没有同位角和内错角,但有三对同旁内角5.(3分)(2019秋•牡丹江期中)如图,△ABC的面积是1,AD是△ABC的中线,AF=FD,CE=EF,则△DEF的面积为()A.B.C.D.6.(3分)(2019秋•北流市期中)如图,七边形ABCDEFG中,AB,ED的延长线相交于点O,若图中∠1、∠2、∠3、∠4的外角和为240°,则∠BOD的度数为()A.40°B.45°C.50°D.60°7.(3分)(2019春•皇姑区校级期中)如图,若∠A=70°,∠B=40°,∠C=32°.则∠BDC=()A.102°B.110°C.142°D.148°8.(3分)(2019秋•泰兴市校级期中)如图,在△ABC中,AB=5,AC=3,BC=7,AI平分∠BAC,CI 平分∠ACB,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为()A.5B.8C.10D.79.(3分)(2019秋•东西湖区期中)如图1,∠DEF=20°,将长方形纸片ABCD沿直线EF折叠成图2,再沿折痕为BF折叠成图3,则∠CFE的度数为()A.100°B.120°C.140°D.160°10.(3分)(2019春•城关区校级期中)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为()A.60°和135°B.45°、60°、105°和135°C.30°和45°D.以上都有可能第Ⅱ卷(非选择题)评卷人得分二.填空题(共6小题,满分18分,每小题3分)11.(3分)(2019秋•温岭市校级期中)工人师傅盖房子时,常将房梁设计如图所示的图形,使其牢固不变形,这是利用性.12.(3分)(2019春•阜宁县期中)如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段是△ABC中AC边上的高.13.(3分)(2019春•武汉期中)如图,AB∥CD,∠B=48°,∠D=29°,则∠BED=°.14.(3分)(2019春•灵石县期中)将Rt△ABC沿边向右平移得到Rt△DEF,AB=8,BE=6,DG=3,则阴影部分的面积为.15.(3分)(2019秋•广州期中)过m边形的一个顶点有7条对角线,n边形没有对角线,过k边形一个顶点的对角线条数是边数的,则m﹣n+k=.16.(3分)(2019秋•芜湖期中)把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C =90°,∠A=45°,∠D=30°,则∠1+∠2=.评卷人得分三.解答题(共6小题,满分52分)17.(8分)(2019春•南京期中)如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格)(1)画出△ABC中BC边上的高AD;(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;(3)画一个△BCP(要求备顶点在格点上,P不与A点重合),使其而积等于△ABC的面积.并回答满足这样条件的点P共个.18.(8分)(2018春•相城区期中)将一副直角三角尺BAC和ADE如图放置,其中∠BAC=∠ADE=90°,∠BCA=30°,∠AED=45°,若∠AFD=75°,试判断AE与BC的位置关系,并说明理由.19.(8分)(2019秋•河北区期中)如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.20.(8分)(2019秋•东营期中)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,(1)求∠EDC的度数;(2)若∠BCD=40°,试求∠BED的度数.21.(10分)(2019春•成都期中)如图1,将三角板ABC与三角板ADE摆放在一起;如图2,其中∠ACB =30°,∠DAE=45°,∠BAC=∠D=90°.固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).(1)当α为度时,AD∥BC,并在图3中画出相应的图形;(2)在旋转过程中,试探究∠CAD与∠BAE之间的关系;(3)当△ADE旋转速度为5°/秒时,且它的一边与△ABC的某一边平行(不共线)时,直接写出时间t 的所有值.22.(10分)(2019春•兴化市期中)(Ⅰ)(1)问题引入如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=(用α表示);(2)拓展研究如图②,∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,试求∠BOC的度数(用α表示)(3)归纳猜想若BO、CO分别是△ABC的∠ABC、∠ACB的n等分线,它们交于点O,∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,则∠BOC=(用α表示).(Ⅱ)类比探索(1)特例思考如图③,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,求∠BOC的度数(用α表示).(2)一般猜想若BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=∠DBC,∠BCO =∠ECB,∠A=α,请猜想∠BOC=(用α表示).第7章平面图形的认识(二)单元测试卷(B卷提升篇)参考答案与试题解析一.选择题(共10小题,满分30分,每小题3分)1.(3分)(2019秋•海淀区校级期中)已知一个三角形的两条边长分别为3cm,6cm,则它的第三条边的长度可以是()A.3cm B.5cm C.9cm D.11cm【分析】根据三角形的三边关系:三角形第三边的长度应是大于两边的差而小于两边的和,这样就可求出第三边长的范围.【答案】解:设它的第三条边的长度为xcm,依题意有6﹣3<x<6+3,则3<x<9.故选:B.【点睛】本题考查了三角形的三边关系,已知三角形的两边,则第三边的范围是:大于已知的两边的差,而小于两边的和.2.(3分)(2019春•沂水县期中)如图,下列条件:①∠1=∠2,②∠2=∠3,③∠5+∠6=180°,④∠1+∠4=180°,⑤∠7=∠2+∠3中能判断直线a∥b的有()A.2个B.3个C.4个D.5个【分析】同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.依据平行线的判定方法即可得出结论.【答案】解:①由∠1=∠2,可得a∥b;②由∠2=∠3,不能得到a∥b;③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;④由∠1+∠4=180°,不能得到a∥b;⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;故能判断直线a∥b的有3个.故选:B.【点睛】本题主要考查了平行线的判定,掌握平行线的判定方法是解决问题的关键.3.(3分)(2019秋•衢州期中)已知在△ABC中,∠A=∠B﹣∠C,则△ABC为()A.锐角三角形B.钝角三角形C.直角三角形D.以上都有可能【分析】根据三角形的内角和是180°可得答案.【答案】解:∠A+∠B+∠C=180°①,又∠A=∠B﹣∠C②,把②代入①,得2∠B=180°,∠B=90°,故该三角形是直角三角形.故选:C.【点睛】本题考查了三角形的内角和是180°,熟练掌握三角形的内角和是解题的关键.4.(3分)(2019春•镇原县期中)如图,下列说法正确的是()A.图中没有同位角、内错角、同旁内角B.图中没有同位角和内错角,但是有一对同旁内角C.图中没有内错角和同旁内角,但有三对同位角D.图中没有同位角和内错角,但有三对同旁内角【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的两旁,则这样一对角叫做内错角.两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,则这样一对角叫做同旁内角.【答案】解:A.图中没有同位角、内错角,但有同旁内角,故本选项错误;B.图中没有同位角和内错角,但是有三对同旁内角,故本选项错误;C.图中没有同位角和内错角,但是有三对同旁内角,故本选项错误;D.图中没有同位角和内错角,但有三对同旁内角,故本选项正确;故选:D.【点睛】本题主要考查了三线八角,同位角的边构成“F“形,内错角的边构成“Z“形,同旁内角的边构成“U”形.5.(3分)(2019秋•牡丹江期中)如图,△ABC的面积是1,AD是△ABC的中线,AF=FD,CE=EF,则△DEF的面积为()A.B.C.D.【分析】根据三角形的中线把三角形分成面积相等的两个三角形依次求解即可.【答案】解:∵△ABC的面积是1,AD是△ABC的中线,∴S△ACD=S△ABC=,∵AF=FD,∴DF=AD,∴S△CDF=S△ACD=×=,∵CE=EF,∴S△DEF=S△CDF=×=,故选:D.【点睛】本题考查了三角形的面积,熟记三角形的中线把三角形分成面积相等的两个三角形是解题的关键.6.(3分)(2019秋•北流市期中)如图,七边形ABCDEFG中,AB,ED的延长线相交于点O,若图中∠1、∠2、∠3、∠4的外角和为240°,则∠BOD的度数为()A.40°B.45°C.50°D.60°【分析】由外角和内角的关系可求得∠1、∠2、∠3、∠4的和,由五边形内角和可求得五边形OAGFE 的内角和,则可求得∠BOD.【答案】解:∵∠1、∠2、∠3、∠4的外角的角度和为240°,∴∠1+∠2+∠3+∠4+240°=4×180°,∴∠1+∠2+∠3+∠4=480°,∵五边形OAGFE内角和=(5﹣2)×180°=540°,∴∠1+∠2+∠3+∠4+∠BOD=540°,∴∠BOD=540°﹣480°=60°,故选:D.【点睛】本题主要考查多边形的内角和,利用内角和外角的关系求得∠1、∠2、∠3、∠4的和是解题的关键.7.(3分)(2019春•皇姑区校级期中)如图,若∠A=70°,∠B=40°,∠C=32°.则∠BDC=()A.102°B.110°C.142°D.148°【分析】连接AD并延长,根据三角形的外角性质计算,得到答案.【答案】解:连接AD并延长,∠BDE=∠BAD+∠B,∠CDE=∠CAD+∠C,则∠BDC=∠BDE+∠CDE=∠BAD+∠B+∠CAD+∠C=∠BAC+∠B+∠C=142°,故选:C.【点睛】本题考查的是三角形的外角性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.8.(3分)(2019秋•泰兴市校级期中)如图,在△ABC中,AB=5,AC=3,BC=7,AI平分∠BAC,CI 平分∠ACB,将∠BAC平移,使其顶点与点I重合,则图中阴影部分的周长为()A.5B.8C.10D.7【分析】连接BI、由点I为△ABC的内心,得出BI平分∠ABC,则∠ABI=∠CBI,由平移得AB∥DI,则∠ABI=∠BID,推出∠CBI=∠BID,得出BD=DI,同理可得CE=EI,△DIE的周长=DE+DI+EI=DE+BD+CE=BC=5,即可得出结果.【答案】解:连接BI、如图所示:∵点I为△ABC的内心,∴BI平分∠ABC,∴∠ABI=∠CBI,由平移得:AB∥DI,∴∠ABI=∠BID,∴∠CBI=∠BID,∴BD=DI,同理可得:CE=EI,∴△DIE的周长=DE+DI+EI=DE+BD+CE=BC=7,即图中阴影部分的周长为7,故选:D.【点睛】本题考查了三角形内心的定义、平移的性质及角平分线的定义等知识,熟练掌握三角形的内心是角平分线的交点是解题的关键.9.(3分)(2019秋•东西湖区期中)如图1,∠DEF=20°,将长方形纸片ABCD沿直线EF折叠成图2,再沿折痕为BF折叠成图3,则∠CFE的度数为()A.100°B.120°C.140°D.160°【分析】根据两直线平行,同旁内角互补可得∠CFE=180°﹣∠DEF,然后得出图2中∠CFE度数;再根据两直线平行,内错角相等可得∠BFE=∠DEF,然后求出图2中∠BFC,再根据翻折的性质可得∠CFE+∠BFE=∠BFC,然后代入数据计算即可得解.【答案】解:∵矩形对边AD∥BC,∴CF∥DE,∴图1中,∠CFE=180°﹣∠DEF=180°﹣20°=160°,∵矩形对边AD∥BC,∴∠BFE=∠DEF=20°,∴图2中,∠BFC=160°﹣20°=140°,由翻折的性质得,图3中∠CFE+∠BFE=∠BFC,∴图3中,∠CFE+20°=140°,∴图3中,∠CFE=120°,故选:B.【点睛】本题考查了平行线的性质,翻折变换的性质,熟记各性质并准确识图,理清翻折前后重叠的角是解题的关键.10.(3分)(2019春•城关区校级期中)一副直角三角尺叠放如图1所示,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行,如图2,当∠BAD=15°时,BC∥DE,则∠BAD(0°<∠BAD<180°)其它所有可能符合条件的度数为()A.60°和135°B.45°、60°、105°和135°C.30°和45°D.以上都有可能【分析】根据题意画出图形,再由平行线的判定定理即可得出结论.【答案】解:如图,当AC∥DE时,∠BAD=∠DAE=45°;当BC∥AD时,∠DAB=∠B=60°;当BC∥AE时,∵∠EAB=∠B=60°,∴∠BAD=∠DAE+∠EAB=45°+60°=105°;当AB∥DE时,∵∠E=∠EAB=90°,∴∠BAD=∠DAE+∠EAB=45°+90°=135°.故选:B.【点睛】本题考查的是平行线的判定与性质,根据题意画出图形,利用平行线的性质及直角三角板的性质求解是解答此题的关键.二.填空题(共6小题,满分18分,每小题3分)11.(3分)(2019秋•温岭市校级期中)工人师傅盖房子时,常将房梁设计如图所示的图形,使其牢固不变形,这是利用三角形稳定性.【分析】根据三角形的稳定性即可得出结论.【答案】解:根据三角形稳定性;故答案为:三角形稳定.【点睛】本题考查了三角形的稳定性;熟记三角形的稳定性是关键.12.(3分)(2019春•阜宁县期中)如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段BE是△ABC中AC边上的高.【分析】根据过三角形的一个顶点向对边引垂线,顶点和垂足之间的线段叫做三角形的高线解答.【答案】解:∵BE⊥AC,∴△ABC中AC边上的高是BE.故答案为:BE【点睛】本题考查了三角形的角平分线、中线和高,是基础题,熟记概念是解题的关键.13.(3分)(2019春•武汉期中)如图,AB∥CD,∠B=48°,∠D=29°,则∠BED=77°.【分析】根据平行线的性质即可得到结论.【答案】解:过E作EF∥AB,∵AB∥CD,∴∠BEF=∠B=48°,∠DEF=∠D=29°,∴∠BED=∠BEF+∠DEF=48°+29°=77°,故答案为:77.【点睛】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.14.(3分)(2019春•灵石县期中)将Rt△ABC沿边向右平移得到Rt△DEF,AB=8,BE=6,DG=3,则阴影部分的面积为39.【分析】先利用平移的性质得到S△ABC=S△DEF,DE=AB=8,则EG=5,利用面积的和差得到阴影部分的面积=S梯形ABEG,然后利用梯形的面积公式计算即可.【答案】解:∵Rt△ABC沿边向右平移得到Rt△DEF,∴S△ABC=S△DEF,DE=AB=8,∴EG=DE﹣DG=8﹣3=5,∴阴影部分的面积=S梯形ABEG=(EG+AB)•BE=(5+8)×6=39.故答案为39.【点睛】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行(或共线)且相等.15.(3分)(2019秋•广州期中)过m边形的一个顶点有7条对角线,n边形没有对角线,过k边形一个顶点的对角线条数是边数的,则m﹣n+k=13.【分析】根据过n边形一个顶点有n﹣3条对角线进行解答即可.【答案】解:∵过10边形的一个顶点有7条对角线,∴m=10,∵三角形没有对角线,∴n=3,k﹣3=k,解得,k=6,∴m﹣n+k=13,故答案为:13.【点睛】本题考查的是多边形的对角线的求法,掌握过n边形一个顶点有n﹣3条对角线是解题的关键.16.(3分)(2019秋•芜湖期中)把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C =90°,∠A=45°,∠D=30°,则∠1+∠2=210°.【分析】根据三角形的内角和定理和三角形外角性质解答即可.【答案】解:如图:∵∠1=∠D+∠DOA,∠2=∠E+∠EPB,∵∠DOA=∠COP,∠EPB=∠CPO,∴∠1+∠2=∠D+∠E+∠COP+∠CPO=∠D+∠E+180°﹣∠C=30°+90°+180°﹣90°=210°,故答案为:210°.【点睛】此题考查三角形内角和,关键是根据三角形的内角和定理和三角形外角性质解答.三.解答题(共6小题,满分52分)17.(8分)(2019春•南京期中)如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格)(1)画出△ABC中BC边上的高AD;(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;(3)画一个△BCP(要求备顶点在格点上,P不与A点重合),使其而积等于△ABC的面积.并回答满足这样条件的点P共6个.【分析】(1)利用网格特点和正方形的性质画AD⊥BC于D;(2)利用网格特点和平移的性质画出A、B、C的对应点A1、B1、C1即可;(3)根据三角形面积公式,过A点作BC的平行线,找出此直线上的格点即可.【答案】解:(1)如图,AD为所作;(2)如图,△A1B1C1为所作;(3)过A点作BC的平行线,在此直线上的格点即为P点,如图,满足这样条件的点P共6个.故答案为6.【点睛】本题考查了作图﹣平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.18.(8分)(2018春•相城区期中)将一副直角三角尺BAC和ADE如图放置,其中∠BAC=∠ADE=90°,∠BCA=30°,∠AED=45°,若∠AFD=75°,试判断AE与BC的位置关系,并说明理由.【分析】根据三角形外角性质,可得∠EAF=30°,再根据∠C=30°,可得∠EAF=∠C,进而判定AE ∥BC.【答案】解:AE与BC平行.理由:∵∠AFD是△AEF的外角,∴∠EAF=∠AFD﹣∠E=75°﹣45°=30°,又∵∠C=30°,∴∠EAF=∠C,∴AE∥BC.【点睛】本题考查了平行线的判定与性质及三角形的外角的性质的运用,平行线的判定是由角的数量关系判断两直线的位置关系;平行线的性质是由平行关系来寻找角的数量关系.19.(8分)(2019秋•河北区期中)如图,AD是△ABC的BC边上的高,AE平分∠BAC,若∠B=42°,∠C=70°,求∠AEC和∠DAE的度数.【分析】由三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,有∠EAC=∠BAC,故∠EAD=∠EAC﹣∠DAC.【答案】解:∵∠B=42°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=68°,∵AE是角平分线,∴∠EAC=∠BAC=34°.∵AD是高,∠C=70°,∴∠DAC=90°﹣∠C=20°,∴∠DAE=∠EAC﹣∠DAC=34°﹣20°=14°,∠AEC=90°﹣14°=76°.【点睛】本题考查三角形的内角和定理及角平分线的性质,高线的性质,解答的关键是熟练掌握三角形的内角和定理.20.(8分)(2019秋•东营期中)如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,(1)求∠EDC的度数;(2)若∠BCD=40°,试求∠BED的度数.【分析】(1)由AB与CD平行,利用两直线平行内错角相等得到一对角相等,再由DE为角平分线,即可确定出∠EDC的度数;(2)过E作EF∥AB,则EF∥AB∥CD,利用两直线平行,内错角相等以及角平分线的定义求得∠BEF 的度数,根据平行线的性质求得∠FED的度数,则∠BED即可求解.【答案】解:(1)∵AB∥CD,∴∠ADC=∠BAD=70°,又∵DE平分∠ADC,∴∠EDC=∠ADC=35°;(2)过E作EF∥AB,则EF∥AB∥CD.∵AB∥CD,∴∠ABC=∠BCD=40°,又∵BE平分∠ABC,∴∠ABE=20°,∵EF∥AB,∴∠BEF=∠ABE=20°,∵EF∥CD,∴∠FED=∠EDC=35°,∴∠BED=20°+35°=55°.【点睛】本题考查了平行线的性质,两直线平行,内错角相等,以及角平分线的性质,正确作出辅助线是关键.21.(10分)(2019春•成都期中)如图1,将三角板ABC与三角板ADE摆放在一起;如图2,其中∠ACB=30°,∠DAE=45°,∠BAC=∠D=90°.固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).(1)当α为15度时,AD∥BC,并在图3中画出相应的图形;(2)在旋转过程中,试探究∠CAD与∠BAE之间的关系;(3)当△ADE旋转速度为5°/秒时,且它的一边与△ABC的某一边平行(不共线)时,直接写出时间t 的所有值.【分析】(1)通过画图,即可求解;(2)分①当α≤90°、α>90°时两种情况,画图计算即可;(3)分AD∥BC、DE∥AB、DE∥BC、AE∥BC四种情况,分别求解即可.【答案】解:(1)当α=15°时,AD∥BC,图形如下:故答案为15;(2)设:∠CAD=γ,∠BAE=β,①如上图,当α≤90°时,α+β=90°,α+γ=45°,故β﹣γ=45°;②当α>90°时,同理可得:γ﹣β=45°,故:|∠CAD﹣∠BAE|=45°;(3)①当AD∥BC时,α=15°,t=3;②当DE∥AB时,α=45°,t=9;③当DE∥BC时,α=105°,t=21;④当DE∥AC时,α=135°,t=27;⑤当AE∥BC时,α=150°,t=30;综上,t=3或9或21或27或30.【点睛】解答此题的关键是通过画图,确定旋转后△ADE的位置,还注意分类求解,避免遗漏.22.(10分)(2019春•兴化市期中)(Ⅰ)(1)问题引入如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC=90°+α(用α表示);(2)拓展研究如图②,∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,试求∠BOC的度数120°+α(用α表示)(3)归纳猜想若BO、CO分别是△ABC的∠ABC、∠ACB的n等分线,它们交于点O,∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,则∠BOC=(用α表示).(Ⅱ)类比探索(1)特例思考如图③,∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,求∠BOC的度数(用α表示).(2)一般猜想若BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=∠DBC,∠BCO =∠ECB,∠A=α,请猜想∠BOC=(用α表示).【分析】(Ⅰ)(1)根据点O是∠ABC和∠ACB平分线的交点,即可得到∠CBO=∠ABC,∠BCO=∠ACB,而∠A=α,再根据三角形内角和定理,即可得到∠BOC=90°+α;(2)根据∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,运用三角形内角和定理,即可得到∠BOC=120°+α;(3)根据∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,运用三角形内角和定理,即可得到∠BOC=;(Ⅱ)(1)根据∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,运用三角形内角和定理可得∠BOC=180°﹣(∠DBC+∠ECB),再根据平角的定义,即可得出∠BOC=180°﹣[360°﹣(∠ABC+∠ACB)],据此化简计算即可;(2)根据∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,运用三角形内角和定理可得∠BOC=180°﹣(∠DBC+∠ECB),再根据平角的定义,即可得出∠BOC=180°﹣[360°﹣(∠ABC+∠ACB)],据此化简计算即可.【答案】解:(Ⅰ)(1)如图①,∵点O是∠ABC和∠ACB平分线的交点,∴∠CBO=∠ABC,∠BCO=∠ACB,而∠A=α,∴∠BOC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣(180°﹣α)=180°﹣90°+α=90°+α,故答案为:90°+α;(2)如图②,∵∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,∴∠BOC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣(180°﹣α)=180°﹣60°+α=120°+α,故答案为:120°+α;(3)∵∠CBO=∠ABC,∠BCO=∠ACB,∠A=α,∴∠BOC=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=180°﹣(180°﹣α)=180°﹣×180°+α=,故答案为:;(Ⅱ)(1)如图③,∵∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,∴∠BOC=180°﹣(∠DBC+∠ECB)=180°﹣[360°﹣(∠ABC+∠ACB)]=180°﹣[360°﹣(180°﹣∠A)]=180°﹣(180°+α)=180°﹣60°﹣α=120°﹣α;(2)∵∠CBO=∠DBC,∠BCO=∠ECB,∠A=α,∴∠BOC=180°﹣(∠DBC+∠ECB)=180°﹣[360°﹣(∠ABC+∠ACB)]=180°﹣[360°﹣(180°﹣∠A)]=180°﹣(180°+α)=,故答案为:.【点睛】本题主要考查了三角形内角和定理,角平分线的定义以及三角形外角性质的运用,解题时注意:三角形内角和等于180°.根据角的和差关系进行计算是解决问题的关键.。
苏教版七年级数学第七章平面图形的认识(2)测试卷
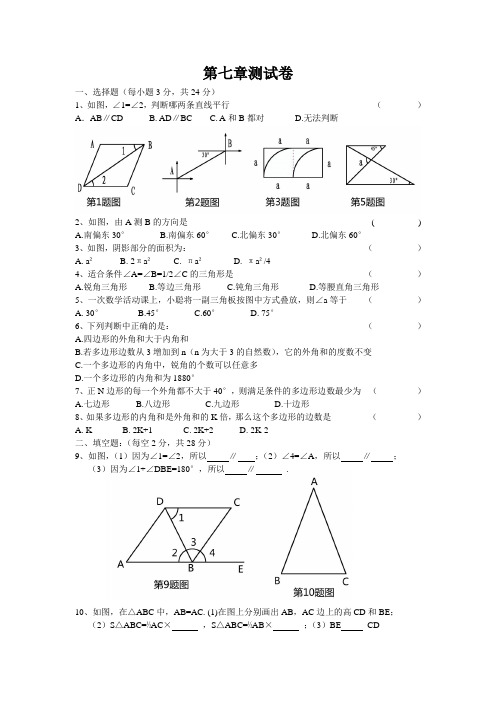
第七章测试卷一、选择题(每小题3分,共24分)1、如图,∠1=∠2,判断哪两条直线平行()A.AB∥CD B. AD∥BC C. A和B都对 D.无法判断2、如图,由A测B的方向是( )A.南偏东30°B.南偏东60°C.北偏东30°D.北偏东60°3、如图,阴影部分的面积为:()A. a²B. 2πa²C. πa²D. πa²/44、适合条件∠A=∠B=1/2∠C的三角形是()A.锐角三角形B.等边三角形C.钝角三角形D.等腰直角三角形5、一次数学活动课上,小聪将一副三角板按图中方式叠放,则∠a等于()A. 30°B.45°C.60°D. 75°6、下列判断中正确的是:()A.四边形的外角和大于内角和B.若多边形边数从3增加到n(n为大于3的自然数),它的外角和的度数不变C.一个多边形的内角中,锐角的个数可以任意多D.一个多边形的内角和为1880°7、正N边形的每一个外角都不大于40°,则满足条件的多边形边数最少为()A.七边形B.八边形C.九边形D.十边形8、如果多边形的内角和是外角和的K倍,那么这个多边形的边数是()A. KB. 2K+1C. 2K+2D. 2K-2二、填空题:(每空2分,共28分)9、如图,(1)因为∠1=∠2,所以∥;(2)∠4=∠A,所以∥;(3)因为∠1+∠DBE=180°,所以∥ .10、如图,在△ABC中,AB=AC. (1)在图上分别画出AB,AC边上的高CD和BE;(2)S△ABC=½AC×,S△ABC=½AB×;(3)BE CD11、八边形的内角和为度,正八边形的每个内角为度。
12、四边形ABCD中,若∠A+∠B=∠C+∠D,∠C=2∠D,则∠C=13、如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,…,照这样走下去,他第一次走到出发点A时,一共走了米。
第七章平面图形的认识二单元测试卷含答案

第七章平面图形的认识(二)单元测试卷(含答案)第七章平面图形的认识单元检测卷A(时间:90分钟,满分:120分)一、选择题(每题3分,共30分)1.下列语句中不是命题的是().A.锐角小于钝角B.作AC的垂直平分线C.对顶角不相等D.狗不是猫科动物2.下列命题中正确的是().A.任何数的平方都是正数B.相等的角是对顶角C.内错角相等D.直角都相等3.如图1,能使BF∥DG的条件是().A.∠1=∠3B.∠2=∠4C.∠2=∠3D.∠1=∠44.如图2,AE平分∠BAC,CE平分∠ACD,不能判定AB∥CD的条件是().A.∠1=∠2B.∠1+∠2=90°C.∠3+∠4=90°D.∠2+∠3=90°5.三角形的某一角的补角是120°,则此三角形的另两个角的和为().A.60°B.120°C.90°D.30°6.满足下列条件的△ABC中,不是直角三角形的是().A.∠A+∠B=∠CB.∠A:∠B:∠C=2:3:1C.∠A=2∠B=3∠CD.一个外角等于和它相邻的内角7.如图3,AB∥EF∥DC,EG∥BD,则图中与∠1相等的角(∠1除外)共有().A.6个B.5个C.4个D.2个8.一天,爸爸带小明到建筑工地玩,看见一个如图4所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于130°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是().A.50°B.65°C.90°D.130°9.如果三角形的一个外角等于与它相邻的内角的2倍,且等于与它不相邻的一个内角的2倍,那么这个三角形一定是().A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形10.已知α=80°,β的两边与α的两边分别垂直,则β等于().A.80°B.10°C.100°D.80°或100°二、填空题(每题3分,共27分)11.“同旁内角互补,两直线平行”的条件是____________,结论是_________________.12.在△ABC中,∠A+∠B=150°,∠C=2∠A,则∠A=_______,∠B=_______.13.如图5所示,AB∥CD,BC∥DE,则∠B+∠D=_如图6所示,在△ABC中,∠A=40°,BP、CP是△ABC的外角平分线,则∠P=________.15.如图7所示,直线a∥b,则∠A=_______.16.如图8所示,∠A+∠B+∠C+∠D+∠E=______.17.如果两条直线被第三条直线所截,一组同旁内角的度数比为3:2,差为36°,那么这两条直线的位置关系是___________,这是因为_____________.18.如图9,BC⊥ED于O,∠A=27°,∠D=20°,则∠B =________,∠ACB=_____如图10,给出下列论断:①AB∥CD;②AD∥BC;③∠A=∠C,以其中两个作为条件,另一个作为结论,用“如果…,那么…”的形式,写出一个你认为正确的命题是_____________________________________.三、解答题(共43分)20.(6分)指出下列命题的条件和结论.(1)一个锐角的补角大于这个角的余角;(2)不相等的两个角不是对顶角;(3)异号两数相加得零.21.(7分)已知实数a、b、c满足a=6-b,c2=ab-9,你能肯定a等于b吗?22.(7分)如图,∠1=∠B,∠A=35°,求∠2的度数.23.(7分)如图,∠BAP+∠APD=180°,∠1=∠2.求证:∠E=∠F.24.(8分)如图,已知AB∥CD,∠B=∠DCE,求证:CD 平分∠分)如图,△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.26.(10分)如图,D、E分别在BC、AC上,AD、BE交于F.求证:(1)∠AFB>∠C;(2)∠AFB=∠1+∠2+∠C. 27.(10分)如图,∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的关系,并证明你的猜想.参考答案一、1.B;提示:“作AC的垂直平分线”不失命题2.D;提示:“直角都相等”正确3.A;提示:∠1=∠2是同位角相等两直线平行4.A;提示:由∠1=∠2可推出大角相等,同旁内角相等两直线不一定平行5.B;提示:三角形的一个外角等于和它不相邻的两个内角和6.C;提示:由∠A=2∠B=3∠C不能推出直角三角形7.B;提示:根据同位角、内错角共5个8.A;提示:三角形的一个外角等于和它不相邻的两个内角和9.D;提示:等边三角形10.D;提示:相等或互补二、11.同旁内角互补;两直线平行12.15°,135°13.180°;提示:根据内错角和同位角相等14.70°;提示:根据外角及角平分线15.22°;提示:根据平行线及其三角形外角和16.180°;提示连结AC,转化为三角形的内角和17.平行;同旁内角互补,两直线平行18.43°,110°19.如果在四边形ABCD中,AB∥CD,AD∥BC,那么∠A=∠C.三、20.解:(1)条件:一个角是锐角;结论:这个角的补角大于这个角的余角.(2)条件:两个角不相等;结论:这两个角不是对顶角. (3)条件:两个数异号;结论:这两个数相加得零. 21.解:能肯定a=b.理由如下:将a=6-b代入c2=ab-9中得,c2=ab-9=(6-b)b-9=6b-b2-9=-(b-3)2.∵c2≥0,而-(b-3)2≤0,∴c=0,b-3=0,即c=0,b=3.∴a=6-b=6-3=3.∴a=b.22.解:∵∠1=∠B,∴AB∥CD(内错角相等,两直线平行).∴∠A+∠2=180°(两直线平行,同旁内角互补).∴∠2=180°-∠A=180°-35°=145°.23.证明:∵∠BAP+∠APD=180°(已知),∴AB∥CD(同旁内角互补,两直线平行).∴∠BAP=∠APC(两直线平行,内错角相等).又∵∠1=∠2(已知),∴∠FPA=∠内错角相等,两直线平行).∴∠E=∠F(两直线平行,内错角相等).24.证明:∵AB∥CD(已知),∴∠B=∠BCD(两直线平行,内错角相等).又∵∠B=∠DCE(已知),∴∠BCD=∠DCE(等量代换),即CD平分∠BCE.25.解:∵∠C+∠ABC+∠A=180°(三角形三个内角的和等于180°),而∠C=∠ABC=2∠A,∴2∠A+2∠A+∠A=180°.∴∠A=36°.∴∠C=72°.又∵BD⊥AC,∴∠DBC=90°-72°=18°.26.证明:(1)∵∠AFB是△AEF的一个外角,∴∠AFB>∠AEF(三角形的一个外角大于任何一个与它不相邻的内角).∵∠AEF是△BCE的一个外角,∴∠AEF>∠C(三角形的一个外角大于任何一个与它不相邻的内角).∴∠AFB>∠C(不等式的性质).(2)∵∠AFB=∠AEB+∠1,∠AEB=∠C+∠2(三角形的一个外角等于和它不相邻的两个内角的和),∴∠AFB=∠1+∠C+∠2(等量代换).27.解:猜想CD⊥AB.理由如下:∵∠3=∠B(已知),∴ED∥BC(同位角相等,两直线平行).∵FG⊥AB(已知),∴∠AGF=90°(垂直定义).∵∠AGF是△BFG的一个外角,∴∠AGF=∠B+∠2(三角形的一个外角等于和它不相邻的两个内角的和).∵∠ADC=∠1+∠3,而∠1=∠2,∠3=∠B,∴∠ADC=∠AGF=90°(等量代换).∴CD⊥AB(垂直定义).。
[数学]-第7章平面图形的认识(二)单元测试(能力提升卷,七下苏科)-【】2022-2023学年七年
![[数学]-第7章平面图形的认识(二)单元测试(能力提升卷,七下苏科)-【】2022-2023学年七年](https://img.taocdn.com/s3/m/1f807e43591b6bd97f192279168884868762b8e4.png)
【拔尖特训】2022-2023学年七年级数学下册尖子生培优必刷题【苏科版】第1章平面图形的认识(二)单元测试(能力提升卷,七下苏科)班级:___________________ 姓名:_________________ 得分:_______________注意事项:本试卷满分100分,试题共24题,其中选择8道、填空8道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.一、选择题(本大题共8小题,每小题2分,共16分)在每小题所给出的四个选项中,只有一项是符合题目要求的.1.(2022秋•山西期末)若一个三角形的两边长分别为7和9,则此三角形第三边的长可能为()A.1 B.7 C.16 D.172.(2022秋•城关区校级期末)若n边形的内角和比它的外角和的3倍少180°,则n是()A.5 B.7 C.8 D.93.(2022秋•临汾期末)如图,两条平行线a,b被第三条直线c所截.若∠2=56°,则∠1的度数为()A.120°B.112°C.124°D.56°4.(2022秋•硚口区期末)如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=70°,∠ACD=20°,∠ABE=25°,则∠BFC的大小是()A.90°B.95°C.105°D.115°5.(2022秋•重庆期末)如图,△ABC中,D在BC的延长线上,过D作DF⊥AB于F,交AC于E.已知∠A=33°,∠ECD=85°,则∠D=()A.52°B.43°C.33°D.38°6.(2022秋•蒲城县期末)如图,∠1=60°,下列推理正确的是()①若∠2=60°,则AB∥CD;②若∠5=60°,则AB∥CD;③若∠3=120°,则AB∥CD;④若∠4=120°,则AB∥CD.A.①②B.②④C.②③④D.②③7.(2022秋•大渡口区校级期末)如图,AB∥CD,∠ABE=125°,∠C=30°,则∠α=()A.70°B.75°C.80°D.85°8.(2022春•牡丹江期中)如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG ⊥EH于点G,且∠AFG=2∠D,则下列结论:①∠D=30°;②2∠D+∠EHC=90°;③FD平分∠HFB;④FH平分∠GFD.其中正确结论的个数是()A.1个B.2个C.3个D.4个二、填空题(本大题共8小题,每小题2分,共16分)请把答案直接填写在横线上9.(2022秋•凤凰县期末)如图,自行车的主框架采用了三角形结构,这样设计的依据是三角形具有.10.(2022秋•市北区校级期末)如图,将直角三角形的直角顶点放在直尺的一边上,若∠1=55°,∠2=60°,则∠3=°.11.(2023•惠阳区校级开学)已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=36cm2,则△DEC的面积为.12.(2022秋•广饶县校级期末)如图所示的是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到△DEF.若AB=10cm,BE=6cm,DH=4cm,则图中阴影部分面积为.13.(2022秋•朝阳区校级期末)一大门栏杆的平面示意图如图所示,BA垂直地面AE于点A,CD平行于地面AE,若∠BCD=135°,则∠ABC=度.14.(2022秋•天山区校级期末)如图,BE、CE分别为△ABC的内、外角平分线,BF、CF分别为△EBC 的内、外角平分线,若∠A=44°,则∠BFC=度.15.(2022秋•沙坪坝区校级期末)如图,直线GH分别与直线AB,CD相交于点G,H,且AB∥CD.点M在直线AB,CD之间,连接GM,HM,射线GH是∠AGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠BGM,∠M=∠N+∠HGN,则∠MHG的度数为.16.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图∠MON=40°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A 为端点作射线AD,交线段OB于点C(规定0°<∠OAC<60°).当△ABC为“灵动三角形”时,∠OAC的度数为.三、解答题(本大题共8小题,共68分.解答时应写出文字说明、证明过程或演算步骤)17.(2022秋•朝阳区校级期末)阅读下面的推理过程,将空白部分补充完整.已知:如图,在△ABC中,FG∥CD,∠1=∠3.求证:∠B+∠BDE=180°.证明:因为FG∥CD(已知),所以∠1=.又因为∠1=∠3(已知),所以∠2=(等量代换).所以BC∥(),所以∠B+∠BDE=180°().18.(2022秋•天山区校级期末)如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠ABD的度数.19.(2022秋•朝阳区校级期末)如图,淇淇从点A出发,前进10米后向右转20°,再前进10米后又向右转20°,这样一直下去,直到他第一次回到出发点A为止,他所走的路径构成了一个多边形.(1)求淇淇一共走了多少米?(2)求这个多边形的内角和.20.(2022秋•驿城区校级期末)如图,在△ABC中,CF⊥AB于F,ED∥CF,∠1=∠2.(1)求证:FG∥BC;(2)若∠A=60°,∠AGF=70°,求∠B及∠2的度数.21.(2022秋•江北区校级期末)在正方形网格中,小正方形的顶点称为“格点”,每个小正方形的边长均为1,△ABC的三个顶点均在“格点”处.(1)在给定方格纸中,点B与点B'对应,请画出平移后的△A'B'C';(2)线段AA'与线段CC'的关系是;(3)求平移过程中,线段BC扫过的面积.22.(2021秋•抚州期末)如图,已知直线AB∥CD,∠A=∠C=100°,点E,F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.(1)直线AD与BC有何位置关系?请说明理由;(2)求∠DBE的度数;(3)若平行移动AD,在平行移动AD的过程中是否存在∠BEC=∠ADB?若存在,求出∠BEC的度数;若不存在,请说明理由.23.(2022•南谯区校级开学)如图,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.(1)将图①中的三角板OMN沿BA方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)将图①中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图③,MN与CD相交于点E,求∠CEN的度数;(3)将图①中的三角尺COD绕点O按每秒15°的速度沿顺时针方向旋转一周,在旋转过程中,在第几秒时,MN恰好与CD平行;第几秒时,MN恰好与直线CD垂直.24.(2022春•顺德区校级期中)如图1,已知直线PQ∥MN,点A在直线PQ上,点C,D在直线MN 上,连接AC,AD,∠P AC=50°,∠ADC=30°,AE平分∠P AD,CE平分∠ACD,AE与CE相交于E.(1)求∠AEC的度数.(2)若将图1中的线段AD沿MN向右平移到A1D1,如图2所示位置,此时AE平分∠AA1D1,CE平分∠ACD1,A1E与CE相交于E,∠P AC=50°,∠A1D1C=30°,求∠A1EC的度数.(3)若将图1中的线段AD沿MN向左平移,若点A1的位置如图3,点D此时还在点C的右边,其他条件与(2)相同,请你在备用图图3上画出草图分析,并直接写出此时∠A1EC的度数.。
苏教版七年级数学 第七章平面图形的认识(二)提高测试卷及答案
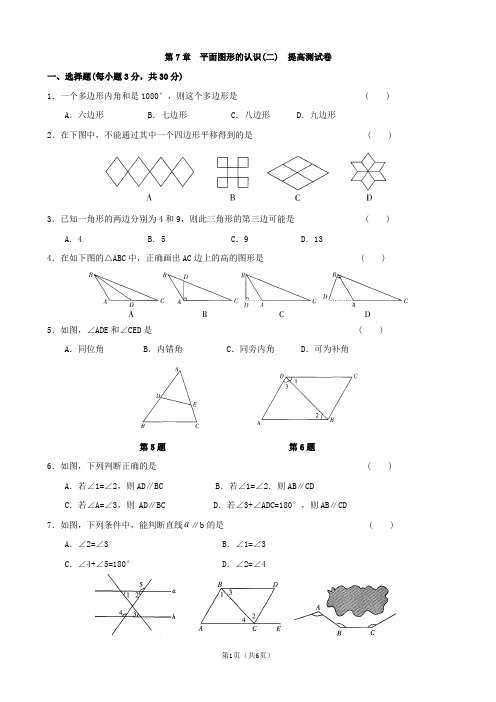
第7章平面图形的认识(二) 提高测试卷一、选择题(每小题3分,共30分)1.一个多边形内角和是1080°,则这个多边形是 ( ) A.六边形 B.七边形 C.八边形 D.九边形2.在下图中,不能通过其中一个四边形平移得到的是 ( )3.已知一角形的两边分别为4和9,则此三角形的第三边可能是 ( ) A.4 B.5 C.9 D.134.在如下图的△ABC中,正确画出AC边上的高的图形是 ( )5.如图,∠ADE和∠CED是 ( )A.同位角 B.内错角 C.同旁内角 D.可为补角第5题第6题6.如图,下列判断正确的是 ( ) A.若∠1=∠2,则AD∥BC B.若∠1=∠2.则AB∥CDC.若∠A=∠3,则 AD∥BC D.若∠3+∠ADC=180°,则AB∥CD7.如图,下列条件中,能判断直线a∥b的是 ( ) A.∠2=∠3 B.∠1=∠3C.∠4+∠5=180° D.∠2=∠4第7题第8题第10题8.如图,点E在AC延长线上,下列条件中能判断AB∥CD的是 ( )A.∠3=∠4 B.∠1=∠2C.∠D=∠DCE D.∠D+∠ACD=180°9.若∠1与∠2是内错角,且∠1=60°,则∠2是 ( )A.60° B.120° C.120°或60° D.不能确定10.如图,一条公路修到湖边时,需拐弯绕湖而过,若第一次拐角∠A=120°,第二次拐角∠B=150°.第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C为( )A.120° B.130° C.140° D.150°二、填空题(每小题3分,共24分)11.在△ABC中,∠A:∠B=2:1,∠C=60°,则∠A=_________.12.等腰三角形的两边长分别为4和9,则第三边长为__________.13.如图,直线a与直线c的夹角是∠α,直线b与直线c的夹角是∠β,把直线a“绕”点A按逆时针方向旋转,当∠α与∠β满足______时,直线a∥b,理由是_______.第13题第14题14.如图,∠1=120°,∠2=60°,∠3=100°,则当∠4=_________时,AB∥EF.15.如图,AB∥CD,CE平分∠ACD,∠A=110°,则∠ECD=__________.第15题第16题16.因修筑公路需要在某处开凿一条隧道,为了加快进度,决定在如图所示的A、B两处同时开工.如果在A地测得隧道方向为北偏东62°,那么在B地应按_______方向施工,就能保证隧道准确接通.17.如图,两平面镜α、β的夹角为θ,入射光线AO平行于β入射到α上,经两次反射后的出射光线O′R平行于α,则角θ等于_________度.第17题第18题18.如图,已知∠ABE=142°,∠C=72°,则∠A=________,∠ABC=________.三、解答题(共46分)19.(10分)一个多边形,它的内角和比外角和的4倍多180°,求这个多边形的边数及内角和度数.20.(10分)如图,AB∥CD,∠B=61°,∠D=35°.求∠1和∠4的度数.21.(5分)填写推理理由.已知:如图,D、E、F分别是BC、AB、AC上的点,DF∥AB,DE∥AC,∠FDE=70°,求∠A的度数.解:DE∥AB( )∴∠A+∠AED=180°( )DF∥AC( )∴∠AED+∠FDE=180°( )∴∠A=∠FDE=70°( ).22.(10分)我们知道,光线从空气射入水中会发生折射现象,光线从水中射人空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.由于折射率相同,因此有∠1=∠4,∠2=∠3.请你用所学知识来判断c与d是否平行?并说明理由.23.(11分)已知:如图,∠1=∠2,∠C=∠D,∠A与∠F相等吗?试说明理由.参考答案1.C 2.D 3.C 4.C 5.B 6.B 7.B 8.B 9.D 10.D11.80° 12.913.∠α=∠β同位角相等两直线平行14.100° 15.35°16.南偏西62°(或西偏南28°)17.6018.70° 38°19.解:设该多边形的边数为n,(n-2)·180°=360°×4+180°解这个方程得n=11(n-2)·180°=(9-2)×180°=1620°20.解:因为AB∥CD,所以∠1=∠B=61°所以∠BCD=119°,所以∠A=360°-61°-35°-119°=145°.21.已知两直线平行,同旁内角互补已知两直线平行,同旁内角互补等角的补角相等22.解:c∥d.如图,分别作出c、d所在的直线,可知∠2+∠5=∠1,∠3+∠6=∠4(对顶角相等),又∠1=∠4,∠2=∠3,可知∠5=∠6,故c∥d(内错角相等,两直线平行).23.解:∠A=∠F∠1=∠2(已知),∠2=∠AHC(对顶角相等)∴∠1=∠AHC(等量代换)∴BG∥CH(同位角相等,两直线平行)∴∠ABD=∠C(两直线平行,同位角相等) 又∠C=∠D(已知),∴∠ABD=∠D(等量代换)∴DF∥AC(内错角相等,两直线平行)∴∠A=∠F(两直线平行,内错角相等).。
第七章平面图形的认识二检测卷

第七章平面图形的认识(二)检测卷选择题(本大题共10小题,每小题3分,共30分。
在每小题列出的四个选项中只有一一、选择题项是符合题意的)1.(自编题)在具备下列条件的线段a,b,c中,一定能组成一个三角形的是()A、a+b>cB、a-b<cC、a:b:c=1:2:3D、a=b=2c2、(原创题)如果三角形的一个角的度数等于另两个角的度数之和,那么这个三角形一定是()(A)锐角三角形(B)直角三角形(C)钝角三角形(D)等腰三角形3、(原创题)一定在△ABC内部的线段是()A.锐角三角形的三条高、三条角平分线、三条中线B.钝角三角形的三条高、三条中线、一条角平分线C.任意三角形的一条中线、二条角平分线、三条高D.直角三角形的三条高、三条角平分线、三条中线4、(原创题)下列说法不正确的是()A、同旁内角相等,两直线平行B、内错角相等,两直线平行C、同位角相等,两直线平行D、若两个角的和是180°,则这两个角互补5、(自编题)如图,在△ABC中,D、E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有()A.4对B.5对C.6对D.7对6、(原创题)若等腰三角形的一边是7,另一边是4,则此等腰三角形的周长是()A.18B.15C.18或15D.无法确定7、(自编题)如图,△ABC经过平移到△GHI的位置,则有()A、点C和点H是对应点B、线段AC和GH对应C、∠A和∠G对应D、平移的距离是线段BI的长度8、(原创题)若一个多边形的每一个内角都是钝角,则这样的多边形边数最少是一个()边形。
A.5B.6C.7D.89、(原创题)如果三角形的一个外角不大于和它相邻的内角,那么这个三角形为()A.锐角或直角三角形B.钝角或锐角三角形C.直角三角形D.钝角或直角三角形10、(自编题)如图,直线a、b都与直线c相交,下列条件中,能说明a∥b的是()①∠1=∠2;②∠2=∠7;③∠2=∠8;④∠1+∠4=180°A、①②B、①②③C、①②④D、①②③④17、(自编题)木棒长的18、(原创题19、(原创题20、(自编题_______三、解答题(本题共50分)21、(原创题)(5分)将如图所示的方格纸中的图形向右平移4格,再向上平移3格,画出平移后的图形.22、(教材复习题第14题改编)(6分)一个零件的形状如图所示,按规定∠A应等于900,∠B,∠C应分别是210和320.检验工人量得∠BDC=1480.就断定这个零件不合格,这是为什么?23、(原创题)(10分)如图已知,△ABC中,∠B=40°,∠C=62°,AD是BC边上的高,AE是∠BAC的平分线。
七年级数学下册第7章平面图形的认识二单元综合测试5试题

卜人入州八九几市潮王学校第七章平面图形的认识〔二〕单元测试一、选择题(每一小题4分,一共32分)1.现有两根木棒,它们的长分别是20 cm和30 cm.假设要订一个三角架,那么以下四根木棒的长度应选()A.10 cmB.30 cmC.50 cmD.70 cm2.以下说法正确的选项是()A.三角形的角平分线,中线和高都在三角形的内部B.直角三角形的高只有一条C.钝角三角形的三条高都在三角形外D.三角形的高至少有一条在三角形内3.经过平移作图能得到图形的是()4.人们都知道“五角星☆〞的五个角相等,你知道每一个角是多少度吗答:()A.36°B.30°C.45°D.60°5.如图,AB∥CD,AC⊥BC,图中∠CAB互余的角有()A.1个B.2个C.3个D.4个6.△ABC中,∠A:∠B:∠C=1:2:3那么△ABC一定是()A.锐角三角形B.直角三角形C.钝角三角形D.选项A、B中的两种都有可能7.假设一个等腰三角形的两边长分别为2 cm和5 cm,那么它的周长是()A.9 cmB.12 cmC.9 cm或者12 cmD.以上答案都不对8.如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,那么∠A=()A.50°B.40°C.70°D.35°二、填空题(每一小题5分,一共25分)9.如图,H是△ABC三条高AD、BE、CF的交点,那么△ABC中BC边上的高是_________,△AHC中HC边上的高是______________,△ABH中AB边上的高是_________.10.等腰三角形的两边长分别是1 cm和2 cm,那么这个等腰三角形的周长为__________cm.11.如图,DAE是一条直线,DE∥BC,那么∠BAC=_________.第11题第12题12.如图,OP∥QR∥ST,假设∠2=110°,∠3=120°,那么∠1=__________.13.如图,在△ABC中,∠C=90°,延长AB到D,延长CB到F.设∠A=x+10°,∠CBA=x-10°,∠ABF=y,那么x=_______度,y=________度.三、解答题(14~18题每一小题7分,19题8分,一共43分)14.如图,一个角的两边是a和b,顶点在图纸的外面,请你在图纸内画一条和这个角的平分线平行的直线,并说明你的画法是正确的.15.如图,五边形ABCDE的内角都相等,且∠1=∠2,∠3=∠4,求x的值.16.如图,直线AB与直线CD被直线GH所截,交点分别为点E、F,∠AEF=∠EFD.(1)AB与CD平行吗为什么(2)假设ME是∠AEF的平分线,FN是∠EFD的平分线,那么能说明EM与FN平行吗假设能,请说明理由;假设不能,还应添加什么条件17.如图,在△ABC中,∠A:∠B:∠C=3:4:5,BD、CE分别是边AC、AB上的高,BD、CE相交于H,求∠BHC的度数.18.如图,D、E、F和A、B、C分别在两条直线上,BD∥CE,∠C=∠D.试说明∠A=∠F.19.(1)如图①,在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数;(2)如图②,△A′B′C′的外角平分线相交于点O′,∠A′=40°,求∠B′O′C′的度数;(3)上面(1)(2)两题中的∠BOC与∠B′O′C′有怎样的数量关系假设∠A=∠A′=n o,∠BOC与∠B′O′C′是否还具有这样的关系这个结论你是怎样得到的参考答案—、1.B2.D3.C4.A5.C6.B7.B8.B二、9.AD,AF,FH10.511.46°12.50°13.45°,145°三、14.过直线b与纸边的交点A作a的平行线c再作c与b所构成角的平分线.15.36°16.(1)平行,内错角相等,两直线平行;(2)平行,由∠AEF=2∠MEF,∠DFE=2∠NFE,那么∠MEF=∠NFE,得ME∥FN17.135°18.因为BD∥CE,所以∠D+∠DEC=180°,那么∠C+∠DEC=180°,得AC∥DF,所以∠A=∠F19.(1)110°(2)70°(3)互补。
(完整word版)第七章平面图形的认识(二)单元提优训练(含答案),推荐文档

第七章平面图形的认识(二)单元提优训练(时间:90分钟总分:100分)一、填空题(每题2分,共30分)1.如图,11 // |2.若/ 2= 2/ 1,则/ 1 = ___________ ,/ 2= _________-f//// r一711. ----------- h/ 1L L—/ ---------------- \C匚D僚1题){第2題)(第3駆)(»4«)2.小明不小心将形状是梯形的玻璃打碎成两部分(如图)•若量得上半部分的/ A = 123 ° , / D = 104°,则原梯形玻璃下半部分的/ B= ________ ,/ C= ________ .3•如图,用吸管吮吸易拉罐内的饮料时,吸管与易拉罐上部夹角/ 1 = 74°,那么吸管与易拉罐下部夹角/ 2= __________ .4. ______________________________________________________ 如图,AB // CD,/ A = 35。
,/ C= 78°,则/ M = ____________________________________________ .5. ______________________________________________________________ 如图,CD 平分/ ACB , DE // BC,/ AED = 80°,则/ EDC =________________________________ .6. 如图,AB // CD,/ BAE = 40 °,/ ECD = 62°, EF 平分/ AEC ,则/ AEF = ____________7. 若一个多边形的每个外角都是 ___ 72°,则这个多边形是边形,它的内角和为&如图,已知△ ABC的/ ABC和/ ACB的外角平分线交于点D,/ A = 40°,则/ D =9. 三角形两边的长分别为1和&若该三角形第三边长为偶数,则该三角形的周长为10. ______________ 如图,AB // CD,直线MN 与AB、CD 分别交于E、F, GE丄MN,/ 1= 130 °,则 /2的度数为.11. _________________________________________________________________________如图,等边三角形ABC沿边AB的方向平移到△ BDE的位置,则图中/ CBE = _______________ 连接CE后,线段CE与AD的关系是__________ .12. 如图,AB // CD,/ D = 80°,/ CAD :/ BAC = 3: 2,则/ CAD = _______________ .A .对顶角的平分线B .两条平行线被第三条直线所截,内错角的平分线C .两条平行线被第三条直线所截,D .两条平行线被第三条直线所截, 20.已知等腰三角形的一个底角是 A . 150°B . 120°21 .下列说法:①钝角三角形有两条高在三角形内部;②三角形的三条高最多有两条不在 三角形内部;③三角形的三条高的交点不在三角形内部,就在三角形外部;④钝角三角形 三个内角的平分线的交点一定不在三角形内部.其中正确的个数为( )〔第 1413. 65° 14. 如图,把△ ABC 平移到△ DEF 的位置,若 AB = 5 cm ,则 ,/ B = 30 °,那么/ F = _________ .如图,把厶ABC 沿RS 的方向平移到△ DEF 的位置, DE = 贝U AB //,BC =如果/ A = 80°,那么/ D = ____________ . 15. 如图,已知 DE // AB , / ACD = 75°,/ B = 25°, 二、选择题(每题 2分,共22分)16. 经过平移,图形上的每个点都沿同一方向移动 了一定距离,下列说法中正确的是 ( )A .不同的点移动的距离不同B .不同的点移动的距离相同C .不同的点移动的距离可能相同,也可能不同D .无法确定17. 已知在厶ABC 中有两个角的大小分别为A .直角三角形C 钝角三角形 则/ ACB 的度数为18 . 如图,AB // CD , 则 a 、3、 A .a+ 3= 180° — Y B .a+ 3= 180 ° + Y C .a+ 3+ Y =360 ° D.a+ 3+ Y= 270 °19 . 下列角平分线中互相垂直的是40° 和 70° B .等边三角形D .等腰三角形 丫三角之间的关系是 ,则这个三角形是同位角的平分线 同旁内角的平分线30°,则这个三角形的顶角等于( )C . 75 °D . 30 °【第13题)(第 123)R S D / ---------FA . 1个B . 2个C. 3个 D . 4个22 .下列给出的三条线段长度的相关条件能组成一个三角形的是()A . 4, 11, 71 1 C . 1 1 , 2, 3丄 2223. 下列叙述错误的是A . △ ABC 中,Z A +Z B<Z C ,此三角形不一定为钝角三角形B .三角形可分为锐角三角形、直角三角形和钝角三角形C .若三角形的一个外角小于与它相邻的一个内角,则这个三角形为钝角三角形D .直角三角形只有一条高在三角形内 24.等腰三角形的一边长等于 5,另一边长等于 9,它的周长是 A . 19 B . 14C . 2325. 如图,Z 1=Z 2, Z DAB =Z BCD .给出下列结论:① B = Z D :④/ D = Z DAC .其中,正确的结论有 ( A . 1个B . 2个C . 3个D . 4个29. (5 分)如图,AD // BC ,Z A = 96°,Z D = 104°, BE 、CE 分别是Z ABC 和Z BCD 的角平分线,求Z BEC 的度数.1 : 4: 611—? — ?()D . 19 或 23AB // DC :② AD // BC :③/(第閒题)Z 2-Z 3= 90°,Z 4 = 115 B . 65°(共48分)如图,Z A + Z B = 180° 26 .如图,Z 1 + 23= 90°, A . 45三、解答题 27 . ( 5 分)C . 60°/ D -Z C = 25° .如图,Z A = 70°,Z 1 = 写出推理过程.28. (5 分) 那么23的度数是 ()求/ C 、/ D 的度数.70°,Z 2 = 110°,你能判定图中哪些直线平行?30. (6 分)如图,AB // CD,/ 1:Z 2:/ 3 = 1 : 2: 3.(1)求/ 3的度数;⑵/ EBA与/ 2相等吗?为什么?31. (6分)如图,把一张长方形纸片ABCD沿EF折叠,ED'交BC于点G .已知/ EFG = 50°,试求/ DEG与/ BGD'的度数.32. (6分)如图,AD丄BC, EG丄BC ,垂足分别为D、G,/ E = / AFE .试说明AD是△ ABC的角平分线.33. (7分)如图,CE平分/ ACD , F为CA延长线上一点,FG // CE交AB于点G,/ ACD = 100°,/AGF = 20°,你能求出/ B的度数吗?若能,请写出求解过程;若不能,请说明理由.34. (8分)如图,O是厶ABC的3条角平分线的交点,OG丄BC,垂足为G .1⑴猜想/ BOC与90°+ - / BAC之间的数量关系,并说明理由;2⑵/ DOB与/ GOC相等吗?为什么?DG C参考答案、1. 60° 120° 2 .57° 76°3 .74° 4. 43° 5. 40° 6. 51°7 .五 540 ° 8. 70° 9. 17 10. 40°11. 60° CE / AD 且 CE =1 AD212. 60° 135c m 85° 14.DE EF 80 ° 1.80° 、16. B 17. D18.B 19 .D 20 . B 21. A 22. D 23 . A 24 . D 25 .C 26 . B、27./ C = 77.5O/ D = 102.5°28 . AC // DE ,AB // EF ,推理略29./ BEC = 100° 30.⑴/ 3 = 108° (2) / EBA = 180° -Z 1 -Z 2= 180° - 36° —72°= 72°,故/ EBA = / 2. 31 . / DEG = 100 °, / BGD' = 80° 32.因为 AD 丄 BC , EG 丄 BC ,所以 AD // EG ,从而/ E =/ CAD , / AFE =/ BAD .由/ E = / AFE 知,/ CAD = / BAD ,即AD 平分/ BAC ,所以AD 是厶ABC 的角平分线. 33 ./ B = 30° 34. (1)相等,理由略 (2)相等,理由略。
七年级数学下册 第七章 平面图形的认识二 测试卷 试题(共7页)

第七章平面(píngmiàn)图形的认识(二) 测试卷(60分钟,满分是100分)一、填空题(每一小题3分,一共18分)1.在△ABC中,∠A=∠B+∠C,那么∠A=_______度.2.如图,AB∥CD,∠B+58o,∠E=20o,那么∠D的度数为_______.3.如图,AB∥CD,∠BEF=85o,∠ABE+∠EFC+∠FCD=______o.4.假如等腰三角形的两边长分别为3和7,那么三角形的周长为______.5.在一个三角形内角中最多有______锐角,最多有______钝角.6.如图,五边形ABCDE是一块草地.小明从点S出发,沿着这个五边形的边步行一周,最后仍回到起点S处,小明在各拐弯处转过的角度之和是_____o.二、选择题(每一小题3分,一共18分)7.以下各组线段长为边,能组成三角形的是( )A.1cm,2cm,4cm B.8cm,6cm,4cmC.12cm,5cm,6cm D.2cm,3cm,6cm8.在以下(yǐxià)生活现象中,不是..平移现象的是( )A.站在运行的电梯上的人 B.左右推动的推拉窗帘C.小亮荡秋千的运动 D.坐在直线行驶的列车上的乘客9.一个多边形的每个内角都等于108。
,那么此多边形是( )A.五边形 B.六边形 C.七边形 D.八边形10.如图,△ABC为直角三角形,∠C=90o,假设沿图中虚线剪去∠C,那么∠1+∠2等于( )A.90oB.135oC.270oD.315o11.假如一个三角形的三条高都经过这个三角形的同一个顶点,那么这个三角形( )A.锐角三角形 B.直角三角形 C.钝角三角形 D.不存在12.假设(jiǎshè)∠A与∠B的两边分别平行,且∠A是∠B的2倍还少30o,那么∠B等于( )A.100o B.70o C.30o D.30o或者70o三、解答题(8小题,一共64分)13.(此题8分)如图,CD是∆ABC的高,点E、F、G分别在BC、AB、AC 上,且EF⊥AB,DG//BC.试判断∠1、∠2的数量关系,并说明理由.14.(此题8分)在四边形ABCD中,ABCD的外角之比是8:7:6:3,求四边形各内角的度数.15.(此题8分)在∆ABC中,∠A=∠B=∠C,试判断该三角形的形状.16.(此题8分)如图,AD是AABC的高,BE平分(píngfēn)∠ABC交AD于E,假设∠C=70o,∠BED=64o,求∠BAC的度数.17.(此题8分)如图,P是△ABC内任一点,试说明:∠BPC>∠A.18.(此题8分)如图,BD、CE相交于点A,∠D+∠E=120o,(1)假如∠B=47o,求∠C的度数;(2)假如∠B=62o,那么∠C又是多少?(3)你发现∠B、∠C、∠D、∠E之间存在着一个怎样的等量关系? 19.(此题8分)如图,把△ABC纸片沿DE折叠(zhédié),使点A落在四边形BCDE内部点A'的位置.聪明的同学,你能猜出么A'与∠1、∠2之间的数量关系吗?请找出来,并说明理由.20.(此题8分)在△ABC中,∠A=40o:(1)如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;(2)如图(2)假设BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;(3)如图(3)假设BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;(4)根据上述三问的结果,当∠A=n o时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).参考答案一、填空题1.∠A=90o2.∠D=38o3.265o4.175.3,16.360o二、选择题7.B 8.C 9.A 10.C 11.B 12.D 三、解答(jiědá)题13.∠1=∠214.60o、75o、90o、135o15.△ABC为直角三角形16.∠BAC=58o17.∠BPC>∠A.18. (1) ∠C=73o.(2) ∠C=58o.(3) ∠B+∠C=∠D+∠E.19.数量(shùliàng)关系:2∠A'=∠1+∠2 20. (1) ∠BOC=110o.(2) ∠BOC=70o.(3) ∠BOC= 20o.(4)当∠A=n o时,由(1)可以得出∠BOC=90o+12n o;由(2)得∠BOC=90o-1 2n o.由(3)得∠BOC=12n o内容总结。
苏科版七年级数学上册平面图形的认识(二)单元测试卷5

苏科版七年级数学上册平面图形的认识(二)单元测试卷5一、选择题(共10小题;共50分)1. 如图,下列说法错误的是A. 与是内错角B. 与是内错角C. 与是同旁内角D. 与是同位角2. 从六边形的一个顶点出发,可以画出条对角线,它们将六边形分成个三角形.则,的值分别为D.3. 如图,的度数为A. B. C. D.4. 已知三角形的两边长分别为和,则下列长度的四条线段中能作为第三边的是A.5. 如图,是一组按照某种规律摆放而成的图案,则图 5 中三角形的个数是A. B. C. D.6. 若一个多边形的内角和是其外角和的两倍,则它的边数是A. 四B. 五C. 六D. 七7. 当一辆长为米的豪华巴士在笔直的路面上朝前行驶米时,坐在豪华巴士正中间的客人A. 朝同一方向前进了米B. 朝同一方向前进了米C. 朝同一方向前进了米D. 朝同一方向前进了米8. 如图,直线,且分别与直线交于,两点,把一块含角的三角尺按如图所示的位置摆放,若,则的度数为A. B. C. D.9. 在下列图形中,由条件不能得到的是A. B.C. D.10. 如图,是同位角关系的是A. 和B. 和C. 和D. 不存在二、填空题(共6小题;共34分)11. 由三条线段所组成的图形叫做三角形.组成三角形的线段叫做;相邻两边的公共端点叫做;相邻两边所组成的角叫做,简称.12. 如图,边长为的正方形先向上平移,再向右平移,得到正方形,此时阴影部分的面积为.13. 如图,作平分线的反向延长线,以,,为内角可以分别作三个边长相等的正多边形.例如:若,则,图就是一个符合要求的图形.在所有符合要求的图形中,的度数是.(除外)14. 探究题:()如图,两条水平的直线被一条竖直的直线所截,同位角有对,内错角有对,同旁内角有对;()如图,三条水平的直线被一条竖直的直线所截,同位角有对,内错角有对,同旁内角有对;()根据以上探究的结果,(为大于的整数)条水平直线被一条竖直直线所截,同位角有对,内错角有对,同旁内角有对.(用含的式子表示)15. 两个相似三角形的面积之比为,小三角形的周长为,则另一个三角形的周长为.16. 如图,请填写一个条件,使结论成立.,.三、解答题(共8小题;共104分)17. 小刚想做一个三角形的零件,现手头上有,长的铁条,他想去商店里再买一根,到商店后发现商店里只有这样几种规格的铁条:,,,,.小刚应该买哪种铁条?18. 如图所示,和被哪些直线所截,得到了哪些同位角、内错角或同旁内角?19. 如图,填空:(1)若,则(,两直线平行).(2)因为,所以(,两直线平行).(3)因为,所以(,两直线平行).20. 如图所示,以为边的三角形有多少个?以为顶点的三角形有多少个?分别写出这些三角形.21. 如图,每个正方形的面积都为,试用皮克公式计算图中“喇叭”“小猫”“小狗”的面积各是多少?22. 如图,凸六边形的六个角都是,边长,,,,你能求出这个六边形的周长吗?23. 如图,已知,.点是射线上一动点(与点不重合),,分别平分和交射线于点,.(1)求的度数;(2)随着点的运动,与之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;(3)当时,求的度数.24. 将一副三角板拼成如图所示的图形,即,,,,与相交于点.若,写出图中与相等的角,并说明理由.答案第一部分1. B2. C3. C 【解析】,.4. B5. C【解析】第一个图案有三角形个,第二个图案有三角形个,第三个图案有三角形个,第四个图案有三角形个,第五个图案有三角形个.6. C 【解析】设这个多边形的边数为,根据题意,得,解得:.故这个多边形的边数为.7. B8. B 【解析】如图,,,又,.9. D 【解析】A.的对顶角与的对顶角是同旁内角,它们互补,所以能判定;B.的对顶角与是同旁内角,它们互补,所以能判定;C.的邻补角,所以能判定;D.由条件能得到,不能判定.10. B【解析】根据同位角的性质可得选项A中的和不是同位角;选项B中的和不是同位角;选项C中的和是同位角;选项D中的和不是同位角.第二部分11. 不在同一直线上的;首尾顺次相接;三角形的边;三角形的顶点;三角形的内角;,三角形的角.12.13. ,,【解析】设,所以以为内角的正多边形的边数为:,所以符合条件的的值为,,,,所以的值只能为,,.14. ,,,,,,,,15.【解析】两相似三角形面积比,相似比,它们的周长比,又小三角形周长,大三角形的周长.16. (或或)【解析】,(同位角相等,两直线平行).,(内错角相等,两直线平行).,(同旁内角互补,两直线平行).第三部分17. 或的铁条.18. (i)和可以被直线,或所截.(ii)当和被所截时,与是同位角,与是同旁内角;当和被所截时,和是内错角;当和被所截时,与是同旁内角,与是同位角.19. (1);;内错角相等.(2);;同位角相等.(3);同旁内角互补.20. 以为边的三角形有个,分别是,,,以为顶点的三角形有个,分别是,,.21. “喇叭”边界上有个格点,图内没有格点,面积为.“小猫”边界上有个格点,图内有个格点,面积为.“小狗”图案可以看做是由两个格点多边形组成,先分别求出每个格点多边形的面积,再求出总面积.躯干面积为,尾巴面积为,总面积为.22. 如图,分别作直线、、的延长线使它们交于点、、.因为六边形的六个角都是,所以六边形的每一个外角的度数都是.所以三角形、三角形、三角形、三角形都是等边三角形.所以,.所以,,.所以六边形的周长为.23. (1),,,平分,平分,,,.(2)不变.数量关系为:.,,,平分,,.(3),,当时,则有,,,.24. (对顶角相等),,理由如下:因为,(已知),所以(两直线平行,内错角相等),所以(三角形的一个外角等于与它不相邻的两个内角的和),因为,(已知),所以(两直线平行,内错角相等),因为(已知),所以,因为(已知),所以(三角形的一个外角等于与它不相邻的两个内角的和),所以(等量代换).。
第七章 平面图形的认识(二) 测试卷 2017.2.25

第七章平面图形的认识(二)知识点1.同位角:。
2.内错角:。
3.同旁内角:。
4.同位角相等,;内错角相等,;同旁内角互补,。
5.两直线平行,;两直线平行,;两直线平行,。
6.平行于同一条直线的两直线,垂直于同一条直线的两直线。
7.两条平行线的同位角(内错角)的平分线互相;两条平行线的同旁内角的平分线互相。
8.平移由两个方面所决定:平移的与平移的。
9.平移的两条性质:(1)平移不改变;(2)图形经过平移后,平行(或在同一直线上),并且相等。
10.三角形的定义:。
11.三角形的分类(1)按角分(2)按边分12.三角形有关性质(1)三角形的高、中线、角平分线都是。
每个三角形都有条高、中线、角平分线,并且他们都分别相交于。
(2)三角形任意两边之和;任意两边之差。
(3)的两个锐角互余。
(4)三角形的一个外角等于。
大于。
(5)三角形的内角和等于,n边形的内角和等于,,每一个内角等于,外角和等于。
第七章平面图形的认识(二)测试卷一、选择题(每小题2分,共40分)1.下列说法不正确的是( ) A.平面内两直线不平行就相交B.过一点只有一条直线与已知直线平行C.平行于同一直线的两直线平行D.同一平面内,垂直于同一直线的两直线平行2.a、b、c、d为三条直线,则下面推理不正确的是( ) A. a∥b,b∥c,∴a∥c B. a∥b,b∥d,∴a∥dC. a∥b,a∥c,∴b∥c D. a∥b,c∥d,∴a∥c3.三角形的三边的长度分别为2 cm,x cm,6 cm,则x的取值范围是( ) A.4≤x≤8 B.4<x<8 C.4≤x<8 D.4<x≤84.如图,若∠1与∠2互补,∠2与∠3互补,则( ) A.l3∥l4B.l2∥l5 C.l1∥l3D.l1∥l2第4题第5题第6题第7题第9题5.如果线段AB是线段CD经过平移得到的,如图所示,那么线段AC与BD的关系为( ) A.相交B.平行C.平行且相等D.相等6.如图,给出下面的推理,其中正确的是( )① ∠B=∠BEF,∴AB∥EF ② ∠B=∠CDE.∴AB∥CD③ ∠B +∠BEF=180°,∴AB∥EF ④ AB∥CD,CD∥EF,∴AB∥EFA.①②③B.①②④C.①③④D.②③④7.如图AB∥DE,∠B=150°,∠D=140°,则∠C的度数为( ) A.60°B.75°C.70°D.50°8.若一个正多边形的每一个外角都是30°,则这个正多边形的内角和等于( ) A.1440°B.1620°C.1800°D.1980°9.如图R t△ABC中∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°则∠A的度数为( ) A.35°B.45°C.55° D 65°10.已知等腰三角形的一边长为5,另一边长为8,则它的周长为( ) A.18 B.21 C.13 D.18或2111.∠1和∠2是直线l1,l2被第三条直线l3所截得的同旁内角,如果l1∥l2,则有( )A.∠1=∠2 B.∠1=∠2=90°C.12∠1+12∠2=90°D.∠1是钝角,∠2是锐角12.已知同一平面内的四条直线a、b、c、d下列命题不正确的是( ) A.若c⊥a,c⊥b,c⊥d,则a∥b∥d B.若a⊥b,c⊥a,d⊥c,则b⊥dC.若a∥b,a⊥c,d⊥b,则d∥c D.若a∥d,c∥b,a⊥b,则d∥c13.如图,下面推理正确的是( )A. ∠1=∠3.∴AD∥BCB. ∠A+∠1+∠2=180°.∴AD∥BCC. ∠A+∠3+∠4=180°,∴AB∥CDD. ∠2=∠4,∴AD∥BC 第13题14.如果一个三角形的三条高所在直线的交点在三角形外部,那么这个三角形是( ) A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形15.下列图形可由平移得到的是( )16.如图,已知AB∥DE,则∠B+∠C+∠E的度数是( ) A.180°B.270°C.360°D.不确定17.如图,已知∠1=70°,∠2=110°,∠3=95°,那么∠4= ( ) A.80°B.85°C.95°D.100°第16题第17题第18题第20题第26题18.如图,由已知条件推出的结论,正确的是( ) A.由∠1=∠5,可以推出AD∥CB B.由∠3=∠7,可以推出AB∥DCC.由∠2=∠6,可以推出AD∥BC D.由∠4=∠8,可以推出AD∥BC19.下列各角能成为某多边形的内角和的是( ) A.430°B.4343°C.4320°D.4360°20.如图AB∥CD,∠1=110°,∠ECD=70°,∠E的大小是( ) A.30°B.40°C.50°D.60°二、填空题(每空1分,共32分)21.在△ABC中,三条中线、角平分线、高线的交点一定在三角形内的是____________.22.已知等腰三角形的一个角为100°,则底角为____________度.23.已知三角形的两边长分别为3、4,且周长为整数,则这样的三角形共有_________个.24.在△ABC中,∠A-∠B=10°,∠B=12∠A,则∠A=____________.25.在四边形ABCD中,四角之比为1:2:3:4,则最小角为___________度.26.如图,已知直线a∥b,∠1=35°,则∠2的度数____________.第28题27.如果一个正多边形的内角和是900°,则这个多边形是_____________边形.28.已知∠PQR=138°,SQ⊥QR,PQ⊥QT,则∠TQR=__________,∠SQT=_________.29.在下列图案中可以用平移得到的是___________(填代号).30.n边形的内角和等于外角和,则n=__________,内角和=_________度.31.(1)如图(1),若∠1=80°,∠2=100°,则a∥b,根据_______________________.(2)如图(2),若c∥d,∠1=82°,则∠2=______________.根据___________________.第31题第33题32.把一个图形沿某一方向平移_________,得到一个新图形与原图形_________.新图形上的每一点是由原图形中的点移动后得到的,这样两个点是对应点,各组对应点的连线__________且____________.33.在(1)图中共有_________对同位角,_________对内错角,___________对同旁内角,在(2)图中共有_________对同旁内角.34.△ABC中,DE分别是AB,AC的中点,当BC=10 cm时,DE=______cm.35.如图,若AB∥CD,则α、β、γ之间的关系为_____________.第35题第37题第40题36.两根木棒的长分别为7 cm和19 cm,要选第三根木棒,将它钉成一个三角形,(首尾相接)则第三条木棒长应在____________的范围内.37.将一副三角板摆成如图所示,图中∠1=___________.38.△ABC中,∠A:∠B:∠C=1:1:2,则此三角形是__________三角形.39.正五边形的内角和为_________度,每个内角为_________度,每个外角为________度.40.已知,AD与BC相交于点O,AB∥CD,如果∠B=20°,∠D=40°,那么∠BOD=___三、画图题(每小题5分,共10分)41.(1)画△ABC的角平分线AD.(2)画DE∥AB交AC于E(3)画EC⊥BC于F(4)画△ADB的中线DG.42.重复画出下面的图案(至少画2个).四、计算与证明(共38分)43.(本题6分)如图,已知△ABC中,AD⊥BC于点D,AE为∠BAC的平分线,且∠B=36°,∠C=66°.求∠DAE的度数.44.(本题6分)如图,已知AE∥BD,∠1=3∠2,∠2=25°,求∠C的度数.45.(本题6分)已知AB∥CD,直线MN分别交AB,CD于E、F,∠MFD=50°,EG平分∠MEB,求∠MEG的度数.46.(本题8分)如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE内部点A'的位置.聪明的同学,你能猜出么A'与∠1、∠2之间的数量关系吗?请找出来,并说明理由.47.(本题12分)在△ABC中,∠A=40o:(1)如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;(2)如图(2)若BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;(3)如图(3)若BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;(4)根据上述三问的结果,当∠A=n o时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).参考答案1.B 2.D 3.B 4.C 5.C 6.B 7.C 8.C 9.C 10.D 11.C 12.D 13.D 14.C 15.A 16.C 17.B 18.C 19.C 20.B21.三角形的中线交点和三角形的角平分线交点.22.40 23.5 24.20°25.36 26.35°27.七28.48°42°29.③④⑤30.4 36031.(1)同旁内角互补,两直线平行(2)82°两直线平行,内错角相等32.一定距离形状相同、大小相等平行(或共线) 相等33.6 5 16 5 34.5 35.α+β-γ=180°36.大于2 cm且小于16 cm37.120°38.等腰直角39.540 108 7240.60 41~42.略43.解:在△ABC中 ∠B=36°∠C=66°∴∠BAC=180°-36°-66°=78°又 AE平分∠BAC∴∠EAC=39°在Rt△ADC中 ∠C=66°∠ADC=90°∴∠DAC=24°∴∠DAE=39°-24°=15°44.解∠1=3∠2=75°AE∥BD ∴∠EAB+∠ABD=180°∴∠CAB+∠ABC=180°-∠1+∠2=180°-75°+25°=130°∴∠C=180°-(∠CAB+∠ABC)=50°45.证明: AE平分∠BAD(已知)∴∠1=12∠BAD(角平分线定义)又 DE平分∠ADC∴∠2=12∠ADC∴∠1+∠2=12∠BAD+12∠ADC∠1+∠2=90°(已知)∴12(∠BAD+∠ADC)=90°(等量代换)∴∠B4D+∠ADC=180°.∴AB∥CD(同旁内角互补,两直线平行)又 AB⊥BC(已知) ∴DC⊥BC 46.证明: AB∥CD∴∠MEB=∠MFD又 ∠MFD=50°∴∠MEB=50°又 EG平分∠MEB∴∠MEG=12∠MEB=25°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章平面图形的认识
(5)
提高测试卷(5)
平面图形的认识((二)提高测试卷
(时间:90分钟,满分:120分)
选择题(
(每题3分,共30分)
一、选择题
1.下列语句中不是命题的是().
A.锐角小于钝角
B.作AC的垂直平分线
C.对顶角不相等
D.狗不是猫科动物
2.下列命题中正确的是().
A.任何数的平方都是正数
B.相等的角是对顶角
C.内错角相等
D.直角都相等
3.如图1,能使BF∥DG的条件是().
A.∠1=∠3
B.∠2=∠4
C.∠2=∠3
D.∠1=∠4
4.如图2,AE平分∠BAC,CE平分∠ACD,不能判定AB∥CD的条件是().
A.∠1=∠2
B.∠1+∠2=90°
C.∠3+∠4=90°
D.∠2+∠3=90°
5.三角形的某一角的补角是120°,则此三角形的另两个角的和为().
A.60°
B.120°
C.90°
D.30°
6.满足下列条件的△ABC中,不是直角三角形的是().
A.∠A+∠B=∠C
B.∠A:∠B:∠C=2:3:1
C.∠A=2∠B=3∠C
D.一个外角等于和它相邻的内角
7.如图3,AB∥EF∥DC,EG∥BD,则图中与∠1相等的角(∠1除外)共有().
A.6个
B.5个
C.4个
D.2个
8.一天,爸爸带小明到建筑工地玩,看见一个如图4所示的人字架,爸爸说:“小明,我
考考你,这个人字架的夹角∠1等于130°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是().
A.50°
B.65°
C.90°
D.130°
9.如果三角形的一个外角等于与它相邻的内角的2倍,且等于与它不相邻的一个内角的2
倍,那么这个三角形一定是().
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形
10.已知α=80°,β的两边与α的两边分别垂直,则β等于().
A.80°
B.10°
C.100°
D.80°或100°
(每题3分,共27分)
填空题(
二、填空题
11.“同旁内角互补,两直线平行”的条件是____________,结论是_________________.
12.在△ABC中,∠A+∠B=150°,∠C=2∠A,则∠A=_______,∠B=_______.
13.如图5所示,AB∥CD,BC∥DE,则∠B+∠D=____.
14.如图6所示,在△ABC中,∠A=40°,BP、CP是△ABC的外角平分线,则∠P=________.
15.如图7所示,直线a∥b,则∠A=_______.
16.如图8所示,∠A+∠B+∠C+∠D+∠E=______.
17.如果两条直线被第三条直线所截,一组同旁内角的度数比为3:2,差为36°,那么这
两条直线的位置关系是___________,这是因为_____________.
18.如图9,BC⊥ED于O,∠A=27°,∠D=20°,则∠B=________,∠ACB=________.
19.如图10,给出下列论断:①AB∥CD;②AD∥BC;③∠A=∠C,以其中两个作为条件,
另一个作为结论,用“如果…,那么…”的形式,写出一个你认为正确的命题是_____________________________________.
三、解答题
(共43分)
解答题(
20.(6分)指出下列命题的条件和结论.
(1)一个锐角的补角大于这个角的余角;(2)不相等的两个角不是对顶角;(3)异号两数相加得零.
21.(7分)已知实数a、b、c满足a=6-b,c2=ab-9,你能肯定a等于b吗?
22.(7分)如图,∠1=∠B,∠A=35°,求∠2的度数.
23.(7分)如图,∠BAP+∠APD=180°,∠1=∠2.求证:∠E=∠F.
24.(8分)如图,已知AB∥CD,∠B=∠DCE,求证:CD平分∠BCE.
25.(8分)如图,△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
26.(10分)如图,D、E分别在BC、AC上,AD、BE交于F.
求证:(1)∠AFB>∠C;(2)∠AFB=∠1+∠2+∠C.
27.(10分)如图,∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的关系,并证明你
的猜想.
参考答案
一、
1.B;提示:“作AC的垂直平分线”不失命题
2.D;提示:“直角都相等”正确
3.A;提示:∠1=∠2是同位角相等两直线平行
4.A;提示:由∠1=∠2可推出大角相等,同旁内角相等两直线不一定平行
5.B;提示:三角形的一个外角等于和它不相邻的两个内角和
6.C;提示:由∠A=2∠B=3∠C不能推出直角三角形
7.B;提示:根据同位角、内错角共5个
8.A;提示:三角形的一个外角等于和它不相邻的两个内角和
9.D;提示:等边三角形
10.D;提示:相等或互补
二、
11.同旁内角互补;两直线平行12.15°,135°
13.180°;提示:根据内错角和同位角相等
14.70°;提示:根据外角及角平分线
15.22°;提示:根据平行线及其三角形外角和
16.180°;提示连结AC,转化为三角形的内角和
17.平行;同旁内角互补,两直线平行18.43°,110°
19.如果在四边形ABCD中,AB∥CD,AD∥BC,那么∠A=∠C.
三、
20.解:(1)条件:一个角是锐角;结论:这个角的补角大于这个角的余角.
(2)条件:两个角不相等;结论:这两个角不是对顶角.
(3)条件:两个数异号;结论:这两个数相加得零.
21.解:能肯定a=b.理由如下:
将a=6-b代入c2=ab-9中得,
c2=ab-9=(6-b)b-9=6b-b2-9=-(b-3)2.
∵c2≥0,而-(b-3)2≤0,
∴c=0,b-3=0,即c=0,b=3.
∴a=6-b=6-3=3.∴a=b.
22.解:∵∠1=∠B,
∴AB∥CD(内错角相等,两直线平行).
∴∠A+∠2=180°(两直线平行,同旁内角互补).
∴∠2=180°-∠A=180°-35°=145°.
23.证明:∵∠BAP+∠APD=180°(已知),
∴AB∥CD(同旁内角互补,两直线平行).
∴∠BAP=∠APC(两直线平行,内错角相等).
又∵∠1=∠2(已知),
∴∠FPA=∠EAP.
∴AE∥PF(内错角相等,两直线平行).
∴∠E=∠F(两直线平行,内错角相等).
24.证明:∵AB∥CD(已知),
∴∠B=∠BCD(两直线平行,内错角相等).
又∵∠B=∠DCE(已知),
∴∠BCD=∠DCE(等量代换),即CD平分∠BCE.
25.解:∵∠C+∠ABC+∠A=180°(三角形三个内角的和等于180°),
而∠C=∠ABC=2∠A,
∴2∠A+2∠A+∠A=180°.
∴∠A=36°.∴∠C=72°.
又∵BD⊥AC,∴∠DBC=90°-72°=18°.
26.证明:(1)∵∠AFB是△AEF的一个外角,
∴∠AFB>∠AEF(三角形的一个外角大于任何一个与它不相邻的内角).
∵∠AEF是△BCE的一个外角,
∴∠AEF>∠C(三角形的一个外角大于任何一个与它不相邻的内角).
∴∠AFB>∠C(不等式的性质).
(2)∵∠AFB=∠AEB+∠1,∠AEB=∠C+∠2(三角形的一个外角等于和它不相邻的两个内角的和),
∴∠AFB=∠1+∠C+∠2(等量代换).
27.解:猜想CD⊥AB.理由如下:
∵∠3=∠B(已知),
∴ED∥BC(同位角相等,两直线平行).
∵FG⊥AB(已知),
∴∠AGF=90°(垂直定义).
∵∠AGF是△BFG的一个外角,
∴∠AGF=∠B+∠2(三角形的一个外角等于和它不相邻的两个内角的和).∵∠ADC=∠1+∠3,而∠1=∠2,∠3=∠B,
∴∠ADC=∠AGF=90°(等量代换).
∴CD⊥AB(垂直定义).。
