三角形中位线经典测试题

合集下载

三角形的中位线基础题30道选择题附详细答案

9.5 三角形的中位线基础题汇编（1）．．．2=．．．7+9.5 三角形的中位线基础题汇编（1）参考答案与试题解析一．选择题（共30小题）1．（2014•河北）如图，△ABC中，D，E分别是边AB，AC的中点．若DE=2，则BC=（）2．（2014•北海）如图△ABC中，D、E分别是边AB、AC的中点，已知DE=5，则BC的长为（）3．（2014•泸州）如图，等边△ABC中，点D、E分别为边AB、AC的中点，则∠DEC的度数为（）4．（2014•宜昌）如图，A，B两地被池塘隔开，小明通过下列方法测出了A、B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A、B间的距离．有关他这次探究活动的描述错误的是（）MN=MN=AB5．（2014•牡丹江一模）如图，⊙O的半径为5，弦AB=8，点C在弦AB上，且AC=6，过点C作CD⊥AB交OB 于点D，则CD的长为（）AB=4EO=1.5=47．（2013•怀化）如图，为测量池塘边A、B两点的距离，小明在池塘的一侧选取一点O，测得OA、OB的中点分别是点D、E，且DE=14米，则A、B间的距离是（）AB8．（2013•昆明）如图，在△ABC中，点D，E分别是AB，AC的中点，∠A=50°，∠ADE=60°，则∠C的度数为（）BC EF=则新三角形的周长为AC BC EF=（∴等边三角形的中位线长是：12．（2013•巴中）如图，在梯形ABCD中，AD∥BC，点E、F分别是AB、CD的中点且EF=6，则AD+BC的值是（）EF=．C D．×（14．（2013•德庆县二模）已知△ABC的三边长分别为3cm，4cm，5cm，D，E，F分别为△ABC各边的中点，则△DEF15．（2013•潮安县模拟）如图，△ABC中，已知AB=8，∠C=90°，∠A=30°，DE是中位线，则DE的长为（）DAB=4BC=216．（2013•南岗区三模）如图，在△ABC中，∠ACB=90°，AC=BC=4，M是CB中点，P、N分别在AC、AB上，若△APN的面积与△ANM的面积相等，则AP长为（）DPG=ANAP=AC=17．（2012•台州）如图，点D、E、F分别为△ABC三边的中点，若△DEF的周长为10，则△ABC的周长为（）18．（2012•聊城）如图，在△ABC中，点D、E分别是AB、AC的中点，则下列结论不正确的是（）D=BC=19．（2012•佛山）依次连接任意四边形各边的中点，得到一个特殊图形（可认为是一般四边形的性质），则这个图AC EF=AC EF=AC．cm ∴相似比是21．（2012•朝阳）如图，C、D分别为EA、EB的中点，∠E=30°，∠1=110°，则∠2的度数为（）BC AC EF=AB BC EF=23．（2012•邵阳）如图所示，在△ABC中，AB=AC，∠A＜90°，边BC、CA、AB的中点分别是D、E、F，则四边形AFDE是（）ABAC24．（2012•德城区三模）如图，在△ABC中，BC=6，M、N分别是AB、AC的中点，则MN等于（）DMN=25．（2012•黄埔区一模）如图，边长为4的等边△ABC中，DE为中位线，则四边形BCED的周长为（）AD=BD=AC BCAB=2AC=2BC=226．（2012•长宁区一模）如图，若DE是△ABC的中位线，△ABC的周长为1，则△ADE的周长为（）D．AD=，的周长为边长的．27．（2012•盐田区二模）如图，▱ABCD的对角线AC、BD相交于点O，E是BC边的中点，OE=1．那么AB=（）．29．（2011•黔南州）如图，△ABC中，AB=AC=6，BC=8，AE平分∠BAC交BC于点E，点D为AB的中点，连接DE，则△BDE的周长是（）+2BE=CE=AB=3AC=330．（2011•义乌市）如图，DE是△ABC的中位线，若BC的长为3cm，则DE的长是（）BC。

三角形中位线定理_练习题

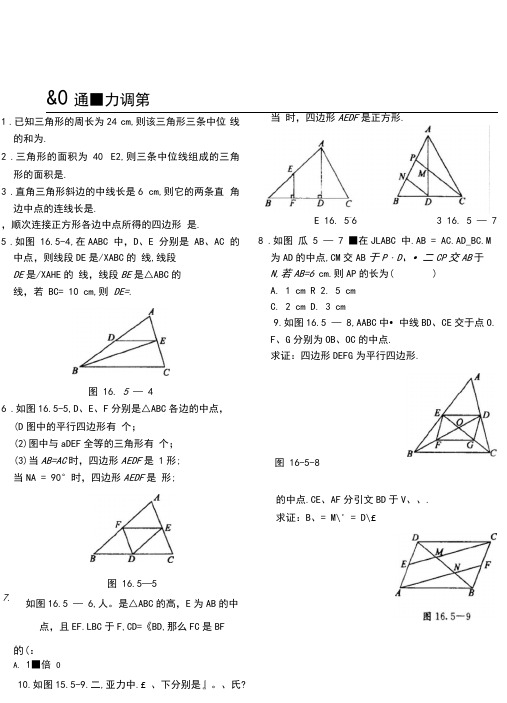
&0通■力调第1.已知三角形的周长为24 cm,则该三角形三条中位线的和为.2.三角形的面积为40 E2,则三条中位线组成的三角形的面积是.3.直角三角形斜边的中线长是6 cm,则它的两条直角边中点的连线长是.，顺次连接正方形各边中点所得的四边形是.5.如图 16.5-4,在AABC 中，D、E 分别是 AB、AC 的中点，则线段DE是/XABC的线,线段DE是/XAHE的线，线段BE是△ABC的线，若 BC= 10 cm,则DE=.图 16. 5— 46.如图16.5-5,D、E、F分别是△ABC各边的中点，(D图中的平行四边形有个；(2)图中与aDEF全等的三角形有个；(3)当AB=AC时，四边形AEDF是 1形;当NA = 90°时，四边形AEDF是形;当时，四边形AEDF是正方形.E 16. 5-6 3 16. 5 — 78.如图瓜 5 —7 ■在JLABC 中.AB = AC.AD_BC.M为AD的中点,CM交AB于P・D、•二CP交AB于N,若AB=6 cm.则AP的长为( )A. 1 cm R 2. 5 cmC. 2 cmD. 3 cm9.如图16.5 — 8,AABC中•中线BD、CE交于点O.F、G分别为OB、OC的中点.求证：四边形DEFG为平行四边形.图 16-5-8图 16.5—5如图16.5 — 6,人。

是△ABC的高，E为AB的中点，且EF.LBC于F,CD=《BD,那么FC是BF的(：A. 1■倍O10.如图15.5-9.二,亚力中.£、下分别是』。

、氏? 的中点.CE、AF分引文BD于V、、. 求证：B、= M\' = D\£7.三角形的中位线定理1.三角形中位线的定义:2.三角形中位线定理的证明：如图，在△ ABC^ , D E是AB和AC的中点，求证：DE// BC DE』BC. 2 方法一：方法二:3.归纳：(1)几何语言：(2)条中位线，对全等，个平行四边形(3)面积4.拓展：如图，在^ ABC+ , D是AB的中点，D日BQ 求证：DE=1 BCA【巩固练习】1.如图所示，□ ABCD的对角线AC BD相交于点Q AE=EB求证：O曰BCB2.如图所示，在^ ABC中，点D在BC上且CD=CA CF平分/ ACB AE=EB求证：EF=1 BD23.已知：如图，四边形ABC前，E、F、G H分别是AB BG CD DA的中点.求证：四边形EFGK平行四边形.4.如图所示，已知在DABC前，E, F分别是AD, BC的中点，求证：MN/ BC5.已知：△ ABC勺中线BD CE交于点Q F、G分别是OB OC勺中点.求证：四边形DEFG^平行四边形.6.已知：如图，E为DABCM DC边的延长线上的一点，且CE= DC连结AE分别交BC BD于点F、G,连结AC交BD于Q 连结OF求证：AB= 2OF.7.如图，在四边形ABC前，AD=BC点E, F, G分别是AB, CD AC的中点.求证：△EFG是等腰三角形。

(完整word版)三角形的中位线练习题含答案,推荐文档

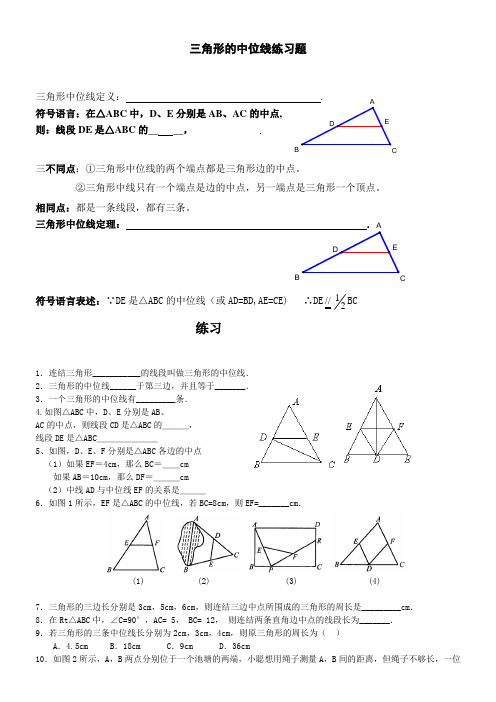
三角形的中位线练习题三角形中位线定义：.符号语言：在△ABC中，D、E分别是AB、AC的中点,则：线段DE是△ABC的__ __，三不同点：①三角形中位线的两个端点都是三角形边的中点。

②三角形中线只有一个端点是边的中点，另一端点是三角形一个顶点。

相同点：都是一条线段，都有三条。

三角形中位线定理： .符号语言表述：∵DE是△ABC的中位线（或AD=BD,AE=CE) ∴DE//21BC练习1．连结三角形___________的线段叫做三角形的中位线．2．三角形的中位线______于第三边，并且等于_______．3．一个三角形的中位线有_________条．4.如图△ABC中，D、E分别是AB、AC的中点，则线段CD是△ABC的＿＿＿，线段DE是△ABC＿＿＿＿＿＿＿5、如图，D、E、F分别是△ABC各边的中点（1）如果EF＝4cm，那么BC＝＿＿cm如果AB＝10cm，那么DF＝＿＿＿cm（2）中线AD与中位线EF的关系是＿＿＿6．如图1所示，EF是△ABC的中位线，若BC=8cm，则EF=_______cm．(1) (2) (3) (4)7．三角形的三边长分别是3cm，5cm，6cm，则连结三边中点所围成的三角形的周长是_________cm．8．在Rt△ABC中，∠C=90°，AC=•5，•BC=•12，•则连结两条直角边中点的线段长为_______．9．若三角形的三条中位线长分别为2cm，3cm，4cm，则原三角形的周长为（）A．4.5cm B．18cm C．9cm D．36cm10．如图2所示，A，B两点分别位于一个池塘的两端，小聪想用绳子测量A，B间的距离，但绳子不够长，一位EDBED同学帮他想了一个主意：先在地上取一个可以直接到达A ，B 的点C ，找到AC ，BC 的中点D ，E ，并且测出DE 的长为10m ，则A ，B 间的距离为（）A ．15mB ．25mC ．30mD ．20m11．已知△ABC 的周长为1，连结△ABC 的三边中点构成第二个三角形，•再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是（） A 、20081 B 、20091 C 、220081 D 、22009112．如图3所示，已知四边形ABCD ，R ，P 分别是DC ，BC 上的点，E ，F 分别是AP ，RP 的中点，当点P 在BC 上从点B 向点C 移动而点R 不动时，那么下列结论成立的是（） A ．线段EF 的长逐渐增大 B ．线段EF 的长逐渐减少 C ．线段EF 的长不变 D ．线段EF 的长不能确定13．如图4,在△ABC 中，E ，D ，F 分别是AB ，BC ，CA 的中点，AB=6，AC=4，则四边形AEDF•的周长是（） A ．10 B ．20 C ．30 D ．4014．如图所示，□ ABCD 的对角线AC ，BD 相交于点O ，AE=EB ，求证：OE ∥BC ．15.已知矩形ABCD 中，AB =4cm ，AD =10cm ，点P 在边BC 上移动，点E 、F 、G 、H 分别是AB 、AP 、DP 、DC 的中点.求证：EF +GH =5cm ；16．如图所示，在△ABC 中，点D 在BC 上且CD=CA ，CF 平分∠ACB ，AE=EB ，求证：EF=12BD ．17．如图所示，已知在□ABCD 中，E ，F 分别是AD ，BC 的中点，求证：MN ∥BC ．BG A E FH D C 图518．已知：如图，四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．19.如图，点E ，F ，G ，H 分别是CD ，BC ，AB ，DA 的中点。

三角形中位线专项训练(30道)(解析版)

三角形中位线专项训练(30道)(解析版)三角形中位线专项训练(30道)(解析版)1. 题目解析三角形中位线是指连接一个三角形的两个非邻边中点的线段。

在这个专项训练中，我们将解答30道关于三角形中位线的问题，并提供详细的解析，帮助你更好地理解和掌握相关概念和解题方法。

2. 题目设置2.1 第一类题目：中位线长度计算2.1.1 题目1：已知一个三角形的三边长度分别为a, b, c，求其中位线长度。

解析：根据中位线定义，连接三角形的两个非邻边中点可以得到一个平行四边形。

利用平行四边形的性质，可以计算出中位线长度为(c²+a²-0.5b²)/(2c)。

2.1.2 题目2：已知一个等边三角形的边长为a，求其中位线长度。

解析：等边三角形中位线长等于边长的一半，即中位线长度为a/2。

2.1.3 题目3：已知一个等腰三角形的底边长度为a，腰长为b，求其中位线长度。

解析：根据中位线定义，连接三角形的两个非邻边中点可以得到一个平行四边形。

利用平行四边形的性质，可以计算出中位线长度为(a²+b²)/(2a)。

2.2 第二类题目：中位线位置关系2.2.1 题目4：在一个等边三角形中，证明中位线与底边垂直且分割底边的比例为2:1。

解析：根据等边三角形的性质，中位线和底边垂直。

利用中位线定义和几何性质，可以证明中位线分割底边的比例为2:1。

2.2.2 题目5：已知在一个等腰三角形中，中位线长为x，底边长为y，求腰长。

解析：根据中位线定义，连接三角形的两个非邻边中点可以得到一个平行四边形。

利用平行四边形的性质，可以得到腰长为2x-y。

2.2.3 题目6：已知在一个一般三角形中，中位线等分了三角形的面积，证明这个三角形是等腰三角形。

解析：假设中位线等分了三角形的面积，利用三角形面积公式可以得到一个关于中位线和底边的方程。

通过求解这个方程，可以证明这个三角形是等腰三角形。

3. 题目变体上述题目只是针对三角形中位线的一部分问题进行了训练和解析。

三角形中位线经典测试题

三角形中位线经典测试题1、已知三角形ABC，其中AC与BD交于点O，BC边中点为E，OE=1，求AB的长。

2、已知三角形ABC，其中DE是BC边的中位线，DE=2cm，求BC的长。

3、已知三角形ABC，要测量A、B两点间的距离，取OA的中点C，OB的中点D，测得CD=30米，求AB的长。

4、顺次连结任意四边形各边中点所得到的四边形一定是平行四边形。

5、以三角形的三个顶点及三边中点为顶点的平行四边形共有4个。

6、已知四边形ABCD中，R、P分别是BC、CD上的点，E、F分别是AP、RP的中点，当点P在CD上从C向D移动而点R不动时，线段EF的长不变。

7、已知三角形三边长分别为6、8、10，则它的中位线构成的三角形的面积为24.8、已知△ABC中，AD=11/44AB，AE=AC，BC=16，求DE的长。

9、已知四边形ABCD中，M、N、P、Q分别为AB、BD、CD、AC的中点，证明四边形MNPQ是平行四边形。

10、已知四边形ABCD中，AD∥BC，BC=3AD，E、F分别是对角线AC、BD的中点，证明四边形ADEF是平行四边形。

11、已知四边形ABCD中，AB=CD，E、F分别为BC、AD的中点，BA、EF的延长线交于点M，CD、EF的延长线交于点N，证明∠AME=∠XXX。

12、已知△ABC中，P是中线AD的中点，连接BP并延长交AC于E，F为BE的中点，证明AF∥DE。

13、已知四边形ABCD中，M是OB的中点，连接AM并延长至P，使MP=AM，连接DP交AC于N，证明（1）MN∥AD；（2）S四边形MPNQ=S△XXX。

14、已知△ABC中，AD是外角平分线，CD⊥AD于D，E是BC的中点，证明（1）DE∥AB；（2）DE=1/2(AB+AC)。

15、已知等腰梯形ABCD中，AB∥CD，AB＞CD，AD=BC，对角线相交于点O，∠AOB=60°，且E、F、M分别是OD、OA、BC的中点，证明△EFM是等边三角形。

三角形中位线定理专练

三角形中位线定理专练1．如图，在△ ABC中，D是AB上一点，且AD=AC，AE⊥ CD，垂足是E，F 是CB的中点．求证：BD=2EF．2．如图所示，在四边形ABCD中，AD=BC，E，F，G分别是AB，CD，AC的中点．求证：△ EFG是等腰三角形．3．在△ ABC中，中线BE、CF交于点O，M、N分别是BO、CO中点，则四边形MNEF是什么特殊四边形？并说明理由．4．如图，BE，CF是△ ABC的角平分线，AN⊥ BE于N，AM⊥ CF于M，求证：MN∥ BC．5．如图，BM、CN分别平分△ABC的外角∠ ABD、∠ ACE，过A分别作BM、CN的垂线，垂足分别为M、N，交CB、BC的延长线于D、E，连结MN．求证：MN=（AB+BC+AC）6．如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．（1）求证：四边形ADEF是平行四边形；（2）求证：∠ DHF=∠ DEF．7．如图，在四边形ABCD中，对角线AC、BD交于点O，E、F分别是AB、CD 的中点，且AC=BD．求证：OM=ON．8．如图，M是△ ABC的边BC的中点，AN平分∠ BAC，BN⊥ AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3（1）求证：BN=DN；（2）求△ ABC的周长．三角形中位线定理专练参考答案与试题解析一．解答题（共8小题）1．（2014?山东模拟）如图，在△ABC中，D是AB上一点，且AD=AC，AE⊥CD，垂足是E，F是CB的中点．求证：BD=2EF．【考点】三角形中位线定理．菁优网版权所有【专题】常规题型．【分析】根据三角形的中位线定理，在三角形中准确应用，并且求证E为CD 的中点，再求证EF为△BCD的中位线．【解答】证明：在△ACD中，因为AD=AC 且AE⊥CD，所以根据等腰三角形中底边的垂线与底边的交点即中点，可以证明：E为CD的中点，又因为F是CB的中点，所以，EF∥BD，且EF为△BCD的中位线，因此EF=BD，即BD=2EF．【点评】此题主要是中位线定理在三角形中的应用，考查在三角形中位线为对应边长的的定理．2．（2015春?天津校级期中）如图所示，在四边形ABCD中，AD=BC，E，F，G分别是AB，CD，AC的中点．求证：△EFG是等腰三角形．【考点】三角形中位线定理；等腰三角形的判定．菁优网版权所有【专题】证明题．【分析】由于E，F，G分别是AB，CD，AC的中点，利用中位线定理，GF=AD，GE=BC，又因为AD=BC，所以GF=GE．【解答】证明：∵E，F，G分别是AB，CD，AC的中点．∴GF=AD，GE=BC．又∵AD=BC，∴GF=GE，即△EFG是等腰三角形．【点评】本题通过给出的中点，利用中位线定理，证得边相等，从而证明等腰三角形，是一道基础题．3．（2015秋?青岛校级月考）在△ABC中，中线BE、CF交于点O，M、N分别是BO、CO中点，则四边形MNEF是什么特殊四边形？并说明理由．【考点】三角形中位线定理；平行四边形的判定．菁优网版权所有【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，MN∥BC且MN=BC，从而得到EF∥MN且EF=MN，再根据一组对边平行且相等的四边形是平行四边形判断．【解答】解：四边形MNEF是平行四边形．理由如下：∵BE、CF是中线，∴E、F分别是AC、AB的中点，∴EF是△ABC的中位线，∴EF∥BC且EF=BC，∵M、N分别是BO、CO中点，∴MN是△OBC的中位线，∴MN∥BC且MN=BC，∴EF∥MN且EF=MN，∴四边形MNEF是平行四边形．【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半，平行四边形的判定，熟记定理并准确识图是解题的关键．4．（2015春?泗洪县校级期中）如图，BE，CF是△ABC的角平分线，AN⊥BE 于N，AM⊥CF于M，求证：MN∥BC．【考点】三角形中位线定理；等腰三角形的判定与性质．菁优网版权所有【专题】证明题．【分析】延长AN、AM分别交BC于点D、G，根据BE为∠ABC的角平分线，BE⊥AG可知∠BAN=∠BGN故△ABG为等腰三角形，所以BN也为等腰三角形的中线，即AM=GN．同理AM=DM，根据三角形中位线定理即可得出结论．【解答】证明：延长AN、AM分别交BC于点D、G．∵BE为∠ABC的角平分线，BE⊥AG，∴∠BAG=∠BGA，∴△ABG为等腰三角形，∴BN也为等腰三角形的中线，即AN=GN．同理AM=DM，∴MN为△ADG的中位线，∴MN∥BC．【点评】本题考查的是三角形中位线定理，熟知三角形的中位线平行于第三边，并且等于第三边的一半是解答此题的关键．5．（2015春?富顺县校级月考）如图，BM、CN分别平分△ABC的外角∠ABD、∠ACE，过A分别作BM、CN的垂线，垂足分别为M、N，交CB、BC的延长线于D、E，连结MN．求证：MN=（AB+BC+AC）【考点】三角形中位线定理；等腰三角形的判定与性质．菁优网版权所有【专题】证明题．【分析】首先通过△ABM≌△DBM，得到AB=DB，AM=DM，同理：AN=EN，AC=CE，再根据三角形的中位线定理即可得到结果．【解答】证明：∵AM⊥BM，∴∠AMB=∠DMB=90°，∵BM平分∠ABD，∴∠ABM=∠DBM，在△ABM与△DBM中，，∴△ABM≌△DBM（asa），∴AB=DB，AM=DM，同理：AN=EN，AC=CE，∴MN=DE=（DB+BC+CE）=（AB+BC+AC）．【点评】本题考查了三角形的中位线定理，全等三角形的判定与性质，证明三角形全等是解题的关键．6．（2014?宿迁）如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．（1）求证：四边形ADEF是平行四边形；（2）求证：∠DHF=∠DEF．【考点】三角形中位线定理；直角三角形斜边上的中线；平行四边形的判定．菁优网版权所有【专题】证明题；几何综合题．【分析】（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥AB，DE∥AC，再根据平行四边形的定义证明即可；（2）根据平行四边形的对角相等可得∠DEF=∠BAC，根据直角三角形斜边上的中线等于斜边的一半可得DH=AD，FH=AF，再根据等边对等角可得∠DAH=∠DHA，∠FAH=∠FHA，然后求出∠DHF=∠BAC，等量代换即可得到∠DHF=∠DEF．【解答】证明：（1）∵点D，E，F分别是AB，BC，CA的中点，∴DE、EF都是△ABC的中位线，∴EF∥AB，DE∥AC，∴四边形ADEF是平行四边形；（2）∵四边形ADEF是平行四边形，∴∠DEF=∠BA C，∵D，F分别是AB，CA的中点，AH是边BC上的高，∴DH=AD，FH=AF，∴∠DAH=∠DHA，∠FAH=∠FHA，∵∠DAH+∠FAH=∠BAC，∠DHA+∠FHA=∠DHF，∴∠DHF=∠BAC，∴∠DHF=∠DEF．【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半，等腰三角形的性质，直角三角形斜边上的中线等于斜边的一半的性质，平行四边形的判定与性质，熟记各性质并准确识图是解题的关键．7．（2014?丹阳市校级模拟）如图，在四边形ABCD中，对角线AC、BD交于点O，E、F分别是AB、CD的中点，且AC=BD．求证：OM=ON．【考点】三角形中位线定理；平行线的性质；等腰三角形的判定与性质．菁优网版权所有【专题】证明题．【分析】取AD的中点G，连接EG，FG，构造三角形的中位线，根据三角形的中位线定理进行证明即可．【解答】证明：取AD的中点G，连接EG，FG，∵G、F分别为AD、CD的中点，∴GF是△ACD的中位线，∴GF=AC，同理可得，GE=BD，∵AC=BD，∴GF=GE=AC=BD．∴∠GFN=∠GEM，又∵EG∥OM，FG∥ON，∴∠OMN=∠GEM=∠GFN=∠ONM，∴OM=ON．【点评】本题考查了三角形的中位线性质定理，解题的关键是构造三角形的中位线．运用三角形的中位线的数量关系和位置关系进行分析证明．8．（2013?永州）如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN 于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3（1）求证：BN=DN；（2）求△ABC的周长．【考点】三角形中位线定理；等腰三角形的判定与性质．菁优网版权所有【分析】（1）证明△ABN≌△ADN，即可得出结论；（2）先判断MN是△BDC的中位线，从而得出CD，由（1）可得AD=AB=10，从而计算周长即可．【解答】（1）证明：在△ABN和△ADN中，∵，∴△ABN≌△ADN（ASA），∴BN=DN．（2）解：∵△ABN≌△ADN，∴AD=AB=10，又∵点M是BC中点，∴MN是△BDC的中位线，∴CD=2MN=6，故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41．【点评】本题考查了三角形的中位线定理及等腰三角形的判定，注意培养自己的敏感性，一般出现高、角平分线重合的情况，都需要找到等腰三角形．。

三角形中位线典型题练习

三角形中位线典型题练习
———————————————————————————————— 作者：
———————————————————————————————— 日期：
三角形中位线典型题练习
一、周长及边长
1．如图1所示，EＦ是△ＡＢC的中位线，若BC=8cm,则ＥF＝_____＿_cｍ．
2.三角形的三边长分别是3cｍ，５cm,6cm,则连结三边中点所围成的三角形的周长是__＿____＿_ｃｍ.
2.已知：如图,DＥ是△ＡBC的中位线，AＦ是ＢC边上的中线，
求证:DＥ与AＦ互相平分
３．已知:如图,四边形AＢＣD中,Ｅ、F、G、H分别是AB、BC、CＤ、DA的中点.求证：四边形EＦＧH是平行四边形.
4.如图，点Ｅ，F,G,H分别是CD，ＢＣ,AＢ，DA的中点。
求证：四边形ＥFGH是平行四边形。
3．如图,△ABC中，AＤ= AB，AＥ= AＣ,BC＝16.求DE的长.
４．如图，Ｍ是△ABC的边BＣ的中点，AＮ平分∠BＡC,BN⊥ＡN于点Ｎ,延长BＮ交AC于点D,已知ＡB=10，BC=１5，MＮ=3
（1）求证：ＢN＝DN；ﻫ(2)求△ABC的周长.
三、线段的位置关系
1.如图所示,□ABCD的对角线ＡC，BD相交于点O，AE=ＥB，求证：OＥ∥BC.
３.已知：如图,在四边形ABCD中，AＤ＝ＢC，E、F分别是DC、AB边的中点，FE的延长线分别与AD、BＣ的延长线交于H、G点．
求证:∠AＨF=∠BＧＦ．
求证:四边形ABＣD是平行四边形.
六、巧取中点，妙构形(中点寻线，线无形）
1.如图，AD是△ABC的中线,Ｅ是ＡD的中点,F是ＢE延长线与ＡC的交点。
求证：AF= FC
２.在四边形ABCＤ中，AＣBＤ相交于Ｏ点，ＡC=BD，E、Ｆ分别是ＡB、CD的中点,连接EF分别交AC、BＤ于M、N，判断三角形ＭＯＮ的形状，并说明理由。

完整版三角形的中位线经典练习题及其答案

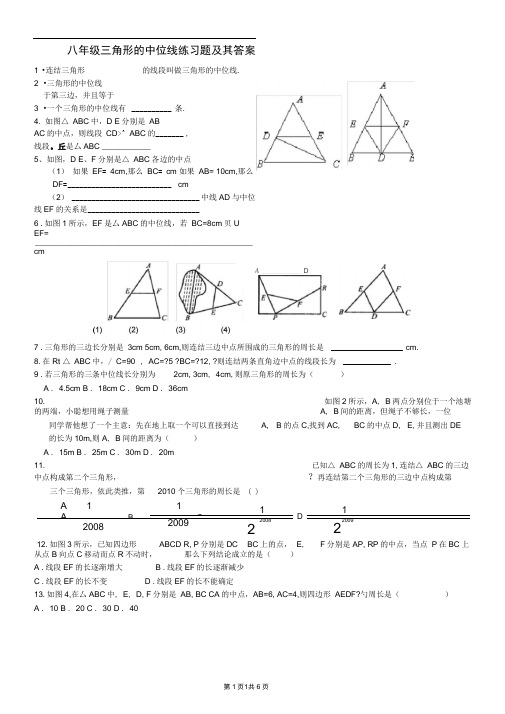
八年级三角形的中位线练习题及其答案1 •连结三角形2 •三角形的中位线于第三边，并且等于3 •一个三角形的中位线有__________ 条.4. 如图△ ABC中，D E分别是ABAC的中点，则线段CD>^ ABC的_______ ,线段。

丘是厶ABC ___________5、如图，D E、F分别是△ ABC各边的中点（1）如果EF= 4cm,那么BC= cm 如果AB= 10cm,那么DF= __________________________ cm（2） ________________________________ 中线AD与中位线EF的关系是____________________________6 .如图1所示，EF是厶ABC的中位线，若BC=8cm贝UEF=_________________________________________________cm7 .三角形的三边长分别是3cm 5cm, 6cm,则连结三边中点所围成的三角形的周长是 __________________ cm.8.在Rt △ ABC中，/ C=90°, AC=?5 ?BC=?12, ?则连结两条直角边中点的线段长为 ____________ .9 .若三角形的三条中位线长分别为2cm, 3cm, 4cm,则原三角形的周长为（）A . 4.5cmB . 18cmC . 9cmD . 36cm10. 如图2所示，A, B两点分别位于一个池塘的两端，小聪想用绳子测量A, B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A, B的点C,找到AC, BC的中点D, E,并且测出DE 的长为10m,则A, B间的距离为（）A . 15mB . 25mC . 30mD . 20m11. 已知△ ABC的周长为1,连结△ ABC的三边中点构成第二个三角形，？再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是( )A 1 1 1 1A、 B C D、2008 2009 20082 2009212.如图3所示，已知四边形ABCD R, P分别是DC BC上的点，E,F分别是AP, RP的中点，当点P在BC上从点B向点C移动而点R不动时，那么下列结论成立的是（）A .线段EF的长逐渐增大B .线段EF的长逐渐减少C .线段EF的长不变D .线段EF的长不能确定13.如图4,在厶ABC中, E, D, F分别是AB, BC CA的中点，AB=6, AC=4,则四边形AEDF?勺周长是（）A . 10B . 20C . 30D . 40A__________ D的线段叫做三角形的中位线.14. 如图所示，口ABCD的对角线AC, BD相交于点O, AE=EB求证：OE// BC.15. 已知矩形ABCD中，AB=4cm, AD=10cm，点P在边BC上移动，点E、F、G、H 分别是AB、AP、DP、DC的中点.求证：EF+GH=5cm；16 .如图所示，在△ ABC中，点D在BC上且CD=CA CF平分/ ACB AE=EB求证:EF=1BD.217.如图所示，已知在口ABCD中, E, F分别是AD, BC的中点，求证：MN/ BC.18.已知：如图，四边形ABCD中，E、F、G、H分别是AB、BC、arc CD、DA的中点.求证：四边形EFGH是平行四边形.19.如图，点E, F, G, H分别是CD, BC, AB , DA的中点。

三角形中位线专项训练(30道)(解析版)

专题9.7 三角形中位线专项训练（30道）【苏科版】1．（2021秋•淅川县期末）如图，四边形ABCD中，∠A＝90°，AB＝12，AD＝5，点M、N分别为线段BC、AB上的动点（含端点，但点M不与点B重合），点E、F分别为DM、MN的中点，则EF长度的可能为（）A．2B．5C．7D．9【分析】根据三角形的中位线定理得出EF=12DN，从而可知DN最大时，EF最大，因为N与B重合时DN最大，N与A重合时，DN最小，从而求得EF的最大值为6.5，最小值是2.5，可解答．【解答】解：连接DN，∵ED＝EM，MF＝FN，∴EF=12DN，∴DN最大时，EF最大，DN最小时，EF最小，∵N与B重合时DN最大，此时DN＝DB=√AD2+BD2=√52+122=13，∴EF的最大值为6.5．∵∠A＝90°，AD＝5，∴DN≥5，∴EF≥2.5，∴EF长度的可能为5；故选：B．2．（2021秋•渝中区校级期末）如图，在△ABC中，AB＝CB＝6，BD⊥AC于点D，F在BC上且BF＝2，连接AF，E为AF的中点，连接DE，则DE的长为（）A．1B．2C．3D．4【分析】根据等腰三角形的性质得到AD＝DC，根据三角形中位线定理解答即可．【解答】解：∵CB＝6，BF＝2，∴FC＝6﹣2＝4，∵BA＝BC，BD⊥AC，∴AD＝DC，∵AE＝EF，∴DE是△AFC的中位线，∴DE=12FC=12×4＝2，故选：B．3．（2021秋•龙岗区校级期末）如图，四边形ABCD中，E，F分别是边AB，CD的中点，则AD，BC和EF的关系是（）A．AD+BC＞2EF B．AD+BC≥2EF C．AD+BC＜2EF D．AD+BC≤2EF【分析】取AC的中点G，连接EF，EG，GF，根据三角形中位线定理求出EG=12BC，GF=12AD，再利用三角形三边关系：两边之和大于第三边，即可得出AD，BC和EF的关系．【解答】解：如图，取AC的中点G，连接EF，EG，GF，∵E，F分别是边AB，CD的中点，∴EG，GF分别是△ABC和△ACD的中位线，∴EG=12BC，GF=12AD，在△EGF中，由三角形三边关系得EG+GF＞EF，即12BC+12AD＞EF，∴AD +BC ＞2EF ，当AD ∥BC 时，点E 、F 、G 在同一条直线上，∴AD +BC ＝2EF ，所以四边形ABCD 中，E ，F 分别是边AB ，CD 的中点，则AD ，BC 和EF 的关系是AD +BC ≥2EF ．故选：B ．4．（2021秋•荆门期末）如图，△ABC 的周长为20，点D ，E 在边BC 上，∠ABC 的平分线垂直于AE ，垂足为N ，∠ACB 的平分线垂直于AD ，垂足为M ，若BC ＝8，则MN 的长度为（）A ．32B ．2C ．52 D ．3【分析】证明△BNA ≌△BNE ，得到BE ＝BA ，AN ＝NE ，同理得到CD ＝CA ，AM ＝MD ，求出DE ，根据三角形中位线定理计算即可．【解答】解：在△BNA 和△BNE 中，{∠NBA =∠NBE BN =BN ∠BNA =∠BNE，∴△BNA ≌△BNE （ASA ）∴BE ＝BA ，AN ＝NE ，同理，CD ＝CA ，AM ＝MD ，∴DE ＝BE +CD ﹣BC ＝BA +CA ﹣BC ＝20﹣8﹣8＝4，∵AN ＝NE ，AM ＝MD ，∴MN =12DE ＝2，故选：B ．5．（2021秋•宛城区期中）如图，在△ABC 中，∠A ＝90°，AC ＞AB ＞4，点D 、E 分别在边AB 、AC 上，BD ＝4，CE ＝3，取DE 、BC 的中点M 、N ，线段MN 的长为（）A ．2.5B ．3C ．4D ．5【分析】如图，作CH ∥AB ，连接DN ，延长DN 交CH 于H ，连接EH ，首先证明CH ＝BD ，∠ECH ＝90°，解直角三角形求出EH ，利用三角形中位线定理即可解决问题．【解答】解：作CH ∥AB ，连接DN 并延长交CH 于H ，连接EH ，∵BD ∥CH ，∴∠B ＝∠NCH ，∠ECH +∠A ＝180°，∵∠A ＝90°，∴∠ECH ＝∠A ＝90°，在△DNB 和△HNC 中，{∠B =∠NCH BN =CN ∠DNB =∠HNC，∴△DNB ≌△HNC （ASA ），∴CH ＝BD ＝4，DN ＝NH ，在Rt △CEH 中，CH ＝4，CE ＝3，∴EH =√CH 2+CE 2=√42+32=5，∵DM ＝ME ，DN ＝NH ，∴MN =12EH ＝2.5，故选：A ．6．（2021•丹东模拟）如图，在△ABC 中，CE 是中线，CD 是角平分线，AF ⊥CD 交CD延长线于点F ，AC ＝7，BC ＝4，则EF 的长为（）A ．1.5B ．2C ．2.5D ．3【分析】延长AF 、BC 交于点G ，证明△ACF ≌△GCF ，根据全等三角形的性质得到CG ＝AC ＝7，AF ＝FG ，求出BG ，根据三角形中位线定理解答即可．【解答】解：延长AF 、BC 交于点G ，∵CD 是△ABC 的角平分线，∴∠ACF ＝∠BCF ，在△ACF 和△GCF 中，{∠ACF =∠GCF CF =CF ∠AFC =∠GFC =90°，∴△ACF ≌△GCF （ASA ），∴CG ＝AC ＝7，AF ＝FG ，∴BG ＝CG ﹣CB ＝3，∵AE ＝EB ，AF ＝FG ，∴EF =12BG ＝1.5，故选：A ．7．（2021•碑林区校级模拟）如图，AD 为△ABC 的角平分线，BE ⊥AD 于E ，F 为BC 中点，连接EF ，若∠BAC ＝80°，∠EBD ＝20°，则∠EFD ＝（）A ．26°B ．28°C ．30°D ．32°【分析】延长BE 交AC 于G ，证△ABE ≌△AGE （ASA ），得BE ＝GE ，再由三角形中位线定理得EF ∥GC ，则∠EFD ＝∠C ，然后求出∠ABC ＝∠ABE +∠EBD ＝70°，即可解决问题．【解答】解：延长BE 交AC 于G ，如图所示：∵AD 平分∠BAC ，∠BAC ＝80°，∴∠BAE ＝∠GAE =12∠BAC ＝40°，∵BE ⊥AD ，∴∠BEA ＝∠GEA ＝90°，∵AE ＝AE ，∴△ABE ≌△AGE （ASA ），∴BE ＝GE ，∵F 为BC 的中点，∴EF 是△BCG 的中位线，∴EF ∥GC ，∴∠EFD ＝∠C ，∵∠BEA ＝90°，∴∠ABE ＝90°﹣∠BAE ＝90°﹣40°＝50°，∴∠ABC ＝∠ABE +∠EBD ＝50°+20°＝70°，∴∠EFD ＝∠C ＝180°﹣∠BAC ﹣∠ABC ＝180°﹣80°﹣70°＝30°，故选：C ．8．（2021秋•广饶县期末）如图，AD 是△ABC 的中线，E 是AD 的中点，F 是BE 延长线与AC 的交点，若AC ＝4，则AF ＝（）A ．85 B ．43 C ．1 D ．23 【分析】取EF 的中点H ，连接DH ，根据三角形中位线定理得到DH =12FC ，DH ∥AC ，证明△AEF ≌△DEH ，根据全等三角形的性质得到AF ＝DH ，计算即可．【解答】解：取EF 的中点H ，连接DH ， ∵BD ＝DC ，BH ＝HF ，∴DH =12FC ，DH ∥AC ，∴∠HDE ＝∠F AE ，在△AEF 和△DEH 中，{∠AEF =∠DEH AE =DE ∠EAF =∠EDH，∴△AEF ≌△DEH （ASA ）， ∴AF ＝DH ，∴AF =12FC ， ∵AC ＝4，∴AF =43，故选：B ．9．（2021春•平邑县期末）如图，在△ABC 中，AB ＝8，AC ＝6，AD 、AE 分别是其角平分线和中线，过点C 作CG ⊥AD 于F ，交AB 于G ，连接EF ，则线段EF 的长为（）A ．1B ．2C ．32D ．12【分析】证明△AFG ≌△AFC ，得到GF ＝FC ，根据三角形中位线定理计算即可．【解答】解：∵AD 是∠BAC 的角平分线，∴∠GAF ＝∠CAF ，∵CG ⊥AD ，∴∠AFG ＝∠AFC ＝90°，在△AFG 和△AFC 中，{∠AFG =∠AFC AF =AF ∠FAG =∠FAC，∴△AFG≌△AFC（ASA），∴GF＝FC，AG＝AC＝6，∴GB＝AB﹣AG＝2，∵GF＝FC，BE＝EC，∴EF=12GB＝1，故选：A．10．（2021春•宽城县期末）如图，E，F是四边形ABCD两边AB，CD的中点，G，H是对角线AC，BD的中点，若EH＝6，则以下结论不正确的是（）A．BC＝12B．GF＝6C．AD＝12D．EH∥GF【分析】先判定EH为△ABD的中位线，GF为△ADC的中位线，然后根据三角形中位线性质对各选项进行判断．【解答】解：∵点E为AB的中点，点H为BD的中点，∴EH为△ABD的中位线，∴EH=12AD，EH∥AD，∵点F为CD的中点，点G为AC的中点，∴GF为△ADC的中位线，∴GF=12AD，GF∥AD，∴GF＝EH＝6，AD＝2EH＝12，EH∥GF，所以A选项符合题意，B选项、C选项和D 选项不符合题意．故选：A．二．填空题（共10小题）11．（2021秋•莱阳市期末）如图，D、E分别为△ABC的边AB、AC的中点．连接DE，过点B作BF平分∠ABC，交DE于点F．若EF＝4，AD＝7，则BC的长为22．【分析】根据三角形中位线定理得到DE ∥BC ，DE =12BC ，BD ＝AD ＝7，根据平行线的性质、角平分线的定义得到∠DBF ＝∠FBC ，根据等腰三角形的判定定理得到DF ＝BD ＝7，计算即可．【解答】解：∵D 、E 分别为△ABC 的边AB 、AC 的中点，∴DE ∥BC ，DE =12BC ，BD ＝AD ＝7，∴∠DFB ＝∠FBC ，∵BF 平分∠ABC ，∴∠DFB ＝∠DBF ，∴∠DBF ＝∠FBC ，∴DF ＝BD ＝7，∴DE ＝DF +EF ＝11，∴BC ＝2DE ＝22，故答案为：22．12．（2021秋•让胡路区校级期末）如图，△ABC 的周长为64，E 、F 、G 分别为AB 、AC 、BC 的中点，A ′、B ′、C ′分别为EF 、EG 、GF 的中点，△A ′B ′C ′的周长为 16 ．如果△ABC 、△EFG 、△A ′B ′C ′分别为第1个、第2个、第3个三角形，按照上述方法继续作三角形，那么第n 个三角形的周长是 27﹣n ．【分析】根据E 、F 、G 分别为AB 、AC 、BC 的中点，可以判断EF 、FG 、EG 为三角形中位线，利用中位线定理求出EF 、FG 、EG 与BC 、AB 、CA 的长度关系即可求得△EFG 的周长是△ABC 周长的一半，△A ′B ′C ′的周长是△EFG 的周长的一半，以此类推，可以求得第n 个三角形的周长．【解答】解：∵如图，△ABC 的周长为64，E 、F 、G 分别为AB 、AC 、BC 的中点， ∴EF 、FG 、EG 为三角形中位线，∴EF =12BC ，EG =12AC ，FG =12AB ，∴EF +FG +EG =12（BC +AC +AB ），即△EFG 的周长是△ABC 周长的一半．同理，△A ′B ′C ′的周长是△EFG 的周长的一半，即△A ′B ′C ′的周长为14×64＝16．以此类推，第n 个小三角形的周长是第一个三角形周长的64×（12）n ﹣1＝27﹣n故答案是：27﹣n ．13．（2021春•安徽月考）如图，在四边形ABCD 中，AD ＝BC ，∠DAB ＝50°，∠CBA ＝70°，P 、M 、N 分别是AB 、AC 、BD 的中点，若BC ＝6，则△PMN 的周长是 9 ．【分析】根据三角形中位线定理得到PM ∥BC ，PM =12BC ＝3，PN ∥AD ，PN =12AD ＝3，根据等边三角形的判定和性质定理解答即可．【解答】解：∵P 、M 分别是AB 、AC 的中点，∴PM ∥BC ，PM =12BC ＝3，∴∠APM ＝∠CBA ＝70°，同理可得：PN ∥AD ，PN =12AD ＝3，∴∠BPN ＝∠DAB ＝50°，∴PM ＝PN ＝3，∠MPN ＝180°﹣50°﹣70°＝60°，∴△PMN 为等边三角形，∴△PMN 的周长为9，故答案为：9．14．（2021秋•长春期中）如图所示，在△ABC 中，BC ＞AC ，点D 在BC 上，DC ＝AC ＝10，且AD BD =32，作∠ACB 的平分线CF 交AD 于点F ，CF ＝8，E 是AB 的中点，连接EF ，则EF 的长为 4 ．【分析】根据等腰三角形的性质得到F 为AD 的中点，CF ⊥AD ，根据勾股定理得到DF =√CD 2−CF 2=6，根据三角形的中位线定理即可得到结论．【解答】解：∵DC ＝AC ＝10，∠ACB 的平分线CF 交AD 于F ，∴F 为AD 的中点，CF ⊥AD ，∴∠CFD ＝90°，∵DC ＝10，CF ＝8，∴DF =√CD 2−CF 2=6，∴AD ＝2DF ＝12，∵AD BD =32，∴BD ＝8，∵点E 是AB 的中点， ∴EF 为△ABD 的中位线，∴EF =12BD ＝4，故答案为：4．15．（2021•商丘四模）如图，四边形ABCD 中，点E 、F 分别为AD 、BC 的中点，延长FE交CD 延长线于点G ，交BA 延长线于点H ，若∠BHF 与∠CGF 互余，AB ＝4，CD ＝6，则EF 的长为 √13 ．【分析】根据三角形的中位线定理和勾股定理解答即可．【解答】解：连接BD ，取BD 的中点M ，连接EM ，FM ，∵E 、F 分别为AD 、BC 的中点，M 为BD 的中点，∴EM ，MF 分别为△ADB 、△BCD 的中位线，∴EM ∥AB ，MF ∥DC ，EM =12AB ＝2，MF =12DC ＝3，∵MF ∥DC ，∴∠FGC ＝∠EFM ，∵EM ∥AB ，∴∠FEM ＝∠FHB ，∵∠BHF 与∠CGF 互余，∴∠CGF +∠BHF ＝∠EFM +∠FEM ＝90°，∴∠EMF ＝180°﹣∠EFM ﹣∠FEM ＝90°，∴△EMF 是直角三角形，∴EF=√EM2+FM2=√22+32=√13，故答案为：√13．16．（2021•香坊区校级开学）如图，在△ABC中，E是AB的中点，D是AC上一点，连接DE，BH⊥AC于H，若2∠ADE＝90°﹣∠HBC，AD：BC＝4：3，CD＝2，则BC的长为6．【分析】如图，延长AC至N，使CN＝BC，连接BN，由等腰三角形的性质可得∠ADE ＝∠N，可证DE∥BN，由三角形中位线定理可得AD＝DN，即可求解．【解答】解：如图，延长AC至N，使CN＝BC，连接BN，∵2∠ADE＝90°﹣∠HBC，∠BCA＝90°﹣∠HBC，∴∠BCA＝2∠ADE，∵CN＝BC，∴∠N＝∠CBN，∴∠BCA＝∠N+∠CBN＝2∠N，∴∠ADE＝∠N，∴DE∥BN，又∵E是AB的中点，∴DE是△ABN的中位线，∴AD＝DN，∵AD：BC＝4：3，∴设AD＝DN＝4x，BC＝CN＝3x，∴CD＝DN﹣CN＝x＝2，∴BC＝6，故答案为6．17．（2021春•牡丹区期末）如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB＝13，AC＝8，则DF的长为 2.5．【分析】延长CF交AB于点G，判断出AF垂直平分CG，得到AC＝AG，根据三角形中位线定理解答．【解答】解：延长CF交AB于点G，∵AE平分∠BAC，∴∠GAF＝∠CAF，∴AF垂直平分CG，∴AC＝AG，GF＝CF，又∵点D是BC中点，∴DF是△CBG的中位线，∴DF=12BG=12（AB﹣AG）=12（AB﹣AC）＝2.5，故答案为：2.5．18．（2021春•洛阳期末）如图，D是△ABC的边BC的中点，AE平分∠BAC，BE⊥AE于点E，且AB＝10cm，DE＝2cm，则AC的长为6cm．【分析】延长AC 、BE 交于点F ，证明△AEB ≌△AEF ，根据全等三角形的性质得到AF ＝AB ＝10cm ，BE ＝EF ，根据三角形中位线定理计算即可．【解答】解：延长AC 、BE 交于点F ，∵AE 平分∠BAC ，∴∠BAE ＝∠CAE ，在△AEB 和△AEF 中，{∠BAE =∠FAE AE =AE ∠AEB =∠AEF =90°，∴△AEB ≌△AEF （ASA ），∴AF ＝AB ＝10（cm ），BE ＝EF ，∵BD ＝DC ，DE ＝2cm ，∴CF ＝2DE ＝4（cm ），∴AC ＝AF ﹣CF ＝6（cm ），故答案为：6．19．（2021春•盐湖区校级期末）如图，在四边形ABCD 中，AB ＝CD ，M 、N 、P 分别是AD 、BC 、BD 的中点，若∠MPN ＝130°，则∠NMP 的度数为 25° ．【分析】根据中位线定理和已知，易证明△PMN 是等腰三角形，根据等腰三角形的性质和三角形内角和定理即可求出∠PMN 的度数．【解答】解：在四边形ABCD 中，M 、N 、P 分别是AD 、BC 、BD 的中点，∴PN ，PM 分别是△CDB 与△DAB 的中位线，∴PM =12AB ，PN =12DC ，PM ∥AB ，PN ∥DC ，∵AB ＝CD ， ∴PM ＝PN ，∴△PMN 是等腰三角形，∵∠MPN＝130°，∴∠PMN=180°−130°2=25°．故答案为：25°．20．（2021春•虹口区校级期末）如图，在△ABC中，BM、CN平分∠ABC和∠ACB的外角，AM⊥BM于M，AN⊥CN于N，AB＝10，BC＝13，AC＝6，则MN＝ 4.5．【分析】延长AM交BC于点G，根据BM为∠ABC的平分线，AM⊥BM得出∠BAM＝∠G，故△ABG为等腰三角形，所以AM＝GM．同理AN＝DN，根据三角形中位线定理即可求得MN．【解答】解：延长AM交BC于点G，延长AN交BC延长线于点D，∵BM为∠ABC的平分线，∴∠CBM＝∠ABM，∵BM⊥AG，∴∠ABM+∠BAM＝90°，∠MGB+∠CBM＝90°，∴∠BAM＝∠MGB，∴△ABG为等腰三角形，∴AM＝GM．BG＝AB＝10，同理AN＝DN，CD＝AC＝6，∴MN为△ADG的中位线，∴MN=12DG=12（BC﹣BG+CD）=12（BC﹣AB+AC）=12（13﹣10+6）＝4.5．故答案为：4.5．三．解答题（共10小题）21．（2019春•岐山县期末）△ABC的中线BD，CE相交于O，F，G分别是BO，CO的中点，求证：EF∥DG，且EF＝DG．【分析】连接DE，FG，由BD与CE为中位线，利用中位线定理得到ED与BC平行，FG与BC平行，且都等于BC的一半，等量代换得到ED与FG平行且相等，进而得到四边形EFGD为平行四边形，利用平行四边形的性质即可得证．【解答】证明：连接DE，FG，∵BD，CE是△ABC的中线，∴D，E是AB，AC的中点，∴DE∥BC，DE=12BC，同理：FG∥BC，FG=12BC，∴DE∥FG，DE＝FG，∴四边形DEFG是平行四边形，∴EF∥DG，EF＝DG．22．（2021秋•桓台县期末）如图，在四边形ABCD中，E，F分别是AD，BC的中点．（1）若AB＝6，CD＝8，∠ABD＝30°，∠BDC＝120°，求EF的长；（2）若∠BDC﹣∠ABD＝90°，求证：AB2+CD2＝4EF2．【分析】（1）取BD的中点P，利用三角形中位线定理可以求得EP、FP的长度，然后利用勾股定理来求EF的长度；（2）如图，取BD的中点P，连接EP、FP．用三角形中位线定理可以求得EP、FP的长度，然后利用勾股定理即可得到结论．【解答】（1）解：如图，取BD的中点P，连接EP、FP．∵E，F分别是AD、BC的中点，AB＝6，CD＝8，∴PE ∥AB ，且PE =12AB ＝3，PF ∥CD 且PF =12CD ＝4．又∵∠ABD ＝30°，∠BDC ＝120°，∴∠EPD ＝∠ABD ＝30°，∠DPF ＝180°﹣∠BDC ＝60°，∴∠EPF ＝∠EPD +∠DPF ＝90°，在直角△EPF 中，由勾股定理得到：EF =√EP 2+PF 2=√32+42=5，即EF ＝5；（2）证明：如图，取BD 的中点P ，连接EP 、FP ．∵E ，F 分别是AD 、BC 的中点，∴PE ∥AB ，且PE =12AB ，PF ∥CD 且PF =12CD ．∴∠EPD ＝∠ABD ，∠BPF ＝∠BDC ，∴∠DPF ＝180°﹣∠BPF ＝180°﹣∠BDC ，∵∠BDC ﹣∠ABD ＝90°，∴∠BDC ＝90°+∠ABD ，∴∠EPF ＝∠EPD +∠DPF ＝∠ABD +180°﹣∠BDC ＝∠ABD +180°﹣（90°+∠ABD ）＝90°，∴PE 2+PF 2＝（12AB ）2+（12CD ）2＝EF 2，∴AB 2+CD 2＝4EF 2．23．（2021秋•莱州市期末）已知：如图，在四边形ABCD 中，对角线AC 、BD 相交于点O ，且AC ＝BD ，E 、F 分别是AB 、CD 的中点，EF 分别交BD 、AC 于点G 、H ．求证：OG ＝OH ．【分析】取BC 边的中点M ，连接EM ，FM ，则根据三角形的中位线定理，即可证得△EMF 是等腰三角形，根据等边对等角，即可证得∠MEF ＝∠MFE ，然后根据平行线的性质证得∠OGH ＝∠OHG ，根据等角对等边即可证得．【解答】解：取BC边的中点M，连接EM，FM，∵M、F分别是BC、CD的中点，∴MF∥BD，MF=12BD，同理：ME∥AC，ME=12AC，∵AC＝BD∴ME＝MF∴∠MEF＝∠MFE，∵MF∥BD，∴∠MFE＝∠OGH，同理，∠MEF＝∠OHG，∴∠OGH＝∠OHG∴OG＝OH．24．（2021春•抚州期末）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AE平分∠CAB，CE⊥AE于点E，延长CE交AB于点D．（1）求证：CE＝DE；（2）若点F为BC的中点，求EF的长．【分析】（1）根据ASA证明△AEC和△AED全等，进而利用全等三角形的性质解答即可；（2）根据勾股定理得出AB，进而利用三角形中位线定理解答即可．【解答】（1）证明：∵AE平分∠CAB，∴∠CAE＝∠BAE，∵CE⊥AE，∴∠AEC ＝∠AED ＝90°，在△AEC 和△AED 中，{∠CAE =∠DAE AE =AE ∠AEC =∠AED，∴△AEC ≌△AED （ASA ），∴CE ＝DE ；（2）在Rt △ABC 中，∵AC ＝6，BC ＝8，∴AB =√AC 2+BC 2=√62+82=10，∵△AEC ≌△AED ，∴AD ＝AC ＝6，∴BD ＝AB ﹣AD ＝4，∵点E 为CD 中点，点F 为BC 中点，∴EF =12BD =2．25．（2021春•秦都区期末）如图，在△ABC 中，AB ＝AC ，点D 、E 分别是边AB 、AC 上的点，连接BE 、DE ，∠ADE ＝∠AED ，点F 、G 、H 分别为BE 、DE 、BC 的中点．求证：FG ＝FH ．【分析】根据等腰三角形的判定定理得到AD ＝AE ，根据线段的和差得到BD ＝CE ，根据三角形的中位线定理即可得到结论．【解答】证明：∵∠ADE ＝∠AED ，∴AD ＝AE ，∵AB ＝AC ，∴AB ﹣AD ＝AC ﹣AE ，即BD ＝CE ，∵点F 、G 、H 分别为BE 、DE 、BC 的中点，∴FG 是△EDB 的中位线，FH 是△BCE 的中位线，∴FG =12BD ，FH =12CE ，∴FG ＝FH ．26．（2021春•泰兴市月考）如图，在四边形ABCD 中，AB ＝CD ，E 、F 分别是BC 、AD的中点，连接EF并延长，分别与BA，CD的延长线交于点M、N，证明：∠BME＝∠CNE．【分析】连接BD，取BD的中点H，连接HE，HF，根据三角形的中位线的性质得到FH∥BM，FH=12AB，EH∥CN，EH=12CD，根据平行线的性质得到∠BME＝∠HFE，∠CNE＝∠HEF，根据等腰三角形的性质得到∠HFE＝∠HEF，等量代换即可得到结论．【解答】证明：连接BD，取BD的中点H，连接HE，HF，∵E、F分别是BC、AD的中点，∴FH∥BM，FH=12AB，EH∥CN，EH=12CD，∴∠BME＝∠HFE，∠CNE＝∠HEF，∵AB＝CD，∴FH＝EH，∴∠HFE＝∠HEF，∴∠BME＝∠CNE．27．（2021春•沈北新区期末）如图，AD是△ABC的中线，E是AD的中点，F是BE延长线与AC的交点，求证：AF=12CF．【分析】过D 作DG ∥AC ，可证明△AEF ≌△DEG ，可得AF ＝DG ，由三角形中位线定理可得DG =12CF ，可证得结论．【解答】证明：如图，过D 作DG ∥AC ，则∠EAF ＝∠EDG ，∵AD 是△ABC 的中线，∴D 为BC 中点， ∴G 为BF 中点，∴DG =12CF ，∵E 为AD 中点，∴AE ＝DE ，在△AEF 和△DEG 中，{∠EAF =∠EDG AE =DE ∠AEF =∠DEG，∴△AEF ≌△DEG （ASA ）， ∴DG ＝AF ，∴AF =12CF ．28．（2021春•莆田期末）如图，已知四边形ABCD 的对角线AC 与BD 相交于点O ，且AC＝BD ，M 、N 分别是AB 、CD 的中点，MN 分别交BD 、AC 于点E 、F ．你能说出OE 与OF 的大小关系并加以证明吗？【分析】此题要构造三角形的中位线，根据三角形的中位线定理进行证明．【解答】解：相等．理由如下：取AD 的中点G ，连接MG ，NG ，∵G 、N 分别为AD 、CD 的中点， ∴GN 是△ACD 的中位线，∴GN =12AC ，同理可得，GM=12BD，∵AC＝BD，∴GN＝GM=12AC=12BD．∴∠GMN＝∠GNM，又∵MG∥OE，NG∥OF，∴∠OEF＝∠GMN＝∠GNM＝∠OFE，∴OE＝OF．29．（2021春•城固县期末）如图，在四边形ABCD中，对角线AC＝BD，E，F为AB、CD 的中点，连接EF交BD、AC于P、Q，取BC中点G，连EG、FG，求证：OP＝OQ．【分析】根据三角形中位线定理得到EG=12AC，EG∥AC，FG=12BD，FG∥BD，根据平行线的性质、等腰三角形的性质和判定定理证明结论．【解答】证明：∵E，G为AB、BC中点，∴EG=12AC，EG∥AC，∴∠FEG＝∠OQP，同理，FG=12BD，FG∥BD，∴∠EFG＝∠OPQ，∵AC＝BD，∴EG＝FG，∴∠FEG＝∠EFG，∴∠OPQ＝∠OQP，∴OP＝OQ．30．（2021春•三水区期末）如图，在△ABC中，AB＝AC，点D，E分别是边AB，AC的中点，连接DE、BE，点F，G，H分别为BE，DE，BC的中点．（1）求证：FG＝FH；（2）若∠A＝90°，求证：FG⊥FH；（3）若∠A＝80°，求∠GFH的度数．【分析】（1）由中点性质及AB＝AC，得到BD＝EC，再由中位线性质证明FG∥BD，GF=12BD，FH∥EC，FH=12EC，从而得到FG＝FH；（2）由（1）FG∥BD，FH∥EC，再由∠A＝90°，可证FG⊥FH；（3）由（1）FG∥BD，∠A＝80°，可求得∠FKC，再由FH∥EC，可求得∠GFH的度数．【解答】（1）证明：∵AB＝AC，点D，E分别是边AB，AC的中点∴BD＝EC∵点F，G，H分别为BE，DE，BC的中点∴FG∥BD，GF=12 BDFH∥EC，FH=12 EC∴FG＝FH；（2）证明：由（1）FG∥BD又∵∠A＝90°∴FG⊥AC∵FH∥EC∴FG⊥FH；（3）解：延长FG交AC于点K，∵FG∥BD，∠A＝80°∴∠FKC＝∠A＝80°∵FH∥EC∴∠GFH＝180°﹣∠FKC＝100°。

(完整版)三角形的中位线经典练习题及其答案

八年级三角形的中位线练习题及其答案1．连结三角形___________的线段叫做三角形的中位线． 2．三角形的中位线______于第三边，并且等于_______． 3．一个三角形的中位线有_________条． 4。

如图△ABC 中,D 、E 分别是AB 、AC 的中点，则线段CD 是△ABC 的＿＿＿，线段DE 是△ABC ＿＿＿＿＿＿＿5、如图，D 、E 、F 分别是△ABC 各边的中点（1）如果EF ＝4cm ，那么BC ＝＿＿cm 如果AB ＝10cm ，那么DF ＝＿＿＿cm（2）中线AD 与中位线EF 的关系是＿＿＿6．如图1所示，EF 是△ABC 的中位线,若BC=8cm ，则EF=_______cm ．(1） (2） (3) (4）7．三角形的三边长分别是3cm ，5cm ，6cm ，则连结三边中点所围成的三角形的周长是_________cm ． 8．在Rt △ABC 中，∠C=90°，AC=•5，•BC=•12,•则连结两条直角边中点的线段长为_______． 9．若三角形的三条中位线长分别为2cm ，3cm,4cm,则原三角形的周长为（） A ．4。

5cm B ．18cm C ．9cm D ．36cm10．如图2所示,A ，B 两点分别位于一个池塘的两端,小聪想用绳子测量A ，B 间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A ，B 的点C ，找到AC ，BC 的中点D,E ，并且测出DE 的长为10m ，则A ，B 间的距离为（）A ．15mB ．25mC ．30mD ．20m11．已知△ABC 的周长为1,连结△ABC 的三边中点构成第二个三角形，•再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是( ） A 、20081 B 、20091 C 、220081 D 、22009112．如图3所示，已知四边形ABCD ，R ，P 分别是DC ，BC 上的点,E ，F 分别是AP ，RP 的中点，当点P 在BC上从点B 向点C 移动而点R 不动时, 那么下列结论成立的是（） A ．线段EF 的长逐渐增大 B ．线段EF 的长逐渐减少 C ．线段EF 的长不变 D ．线段EF 的长不能确定13．如图4，在△ABC 中，E ，D ，F 分别是AB ，BC ，CA 的中点，AB=6,AC=4，则四边形AEDF•的周长是（） A ．10 B ．20 C ．30 D ．4014．如图所示，□ ABCD 的对角线AC ，BD 相交于点O ，AE=EB ，求证：OE ∥BC ．15.已知矩形ABCD 中,AB =4cm ，AD =10cm ，点P 在边BC 上移动，点E 、F 、G 、H 分别是AB 、AP 、DP 、DC 的中点。

三角形的中位线习题归类(绝对经典,绝对震撼)

三角形的中位线习题归类一、直接应用1．如图1所示，EF 是△ABC 的中位线，若BC=8cm ，则EF=_______cm ．2．三角形的三边长分别是3cm ，5cm ，6cm ，则连结三边中点所围成的三角形的周长是_________cm ．3．在Rt △ABC 中，∠C=90°，AC=•5，•BC=•12，•则连结两条直角边中点的线段长为_______．4．若三角形的三条中位线长分别为2cm ，3cm ，4cm ，则原三角形的周长为_______．5．如图2所示，A ，B 两点分别位于一个池塘的两端，小聪想用绳子测量A ，B 间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A ，B 的点C ，找到AC ，BC 的中点D ，E ，并且测出DE的长为10m ，则A ，B 间的距离为_______．6.已知△ABC 的周长为1，连结△ABC 的三边中点构成第二个三角形， •再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是（）A 、20081B 、20091C 、220081D 、220091 7．如图4,在△ABC 中，E ，D ，F 分别是AB ，BC ，CA 的中点，AB=6， AC=4，则四边形AEDF•的周长是（）A ．10B ．20C ．30D ．408.如图所示，□ ABCD 的对角线AC ，BD相交于点O ，AE=EB ，求证：OE ∥BC ．9.如图所示，在△ABC 中，点D 在BC 上且CD=CA ，CF 平分∠ACB ，AE=EB ，求证：EF=12BD ．10.如图所示，已知在□ABCD 中，E ，F 分别是AD ，BC 的中点，求证：MN ∥BC ．11.已知：如图，E 为□ABCD 中DC 边的延长线上的一点，且CE ＝DC ，连结AE 分别交BC 、BD 于点F 、G ，连结AC交BD 于O ，连结OF ．求证：AB ＝2OF ．12.如图，△ABC 中，AD=41AB ，AE=41AC ，BC=16.求DE 的长.(角平分线的垂线必有等腰三角形)13.如图，在△ABC 中，已知AB=6，AC=10，AD 平分∠BAC ，BD ⊥AD 于点D ，E•为BC 中点．求DE 的长．14.如图，AD 是△ABC 的外角平分线，CD ⊥AD 于D ，E 是BC 的中点.求证：（1）DE ∥AB ；（2）DE=21（AB+AC ）如图17，BE 、CF 是△ABC 的角平分线，AN ⊥BE 于N ，AM ⊥CF 于M . 求证：MN ∥BC .B G A E F H D C二、中点寻线，线组形（多个中点）1.如图，在四边形ABCD 中，点E 是线段AD 上的任意一点，G F H ，，分别是BE BC CE ，，的中点．证明四边形EGFH 是平行四边形；2.如图，在四边形ABCD 中，AD=BC ，点E ，F ，G 分别是AB ，CD ，AC 的中点。

中位线(三角形)例题

6、已知D、E分别是AC、BC的中点，S△OBE=4, 求：S△ODE=_______ S△ABC=_________
A D O B E C
7、已知：BD平分∠ABC，BD⊥AD，AB=8， BC=12，E是AC的中点， 1 求DE的长；求证： DE 2 ( BC AB )
A
E
D B C
8、如图，在四边形ABCD中，AB＞CD，E、F分别是对角线BD、AC的中点.求证：EF＞
.
9、已知D、E、F分别是△ABC的三边的中点，依次取第二个三角形三边的中点，第三个三角形三边的中点……，若△ABC的周长为a，面积为S。求：①第二个三角形DEF的周长；②第三个三角形GHI的周长；③第2014个三角形的周长。
F C
E
①顺次连接任意四边形的中点得到的四边形是？ ②顺次连接矩形四边的中点得到的四边形是？ ③顺次连接菱形四边中点得到的四边形是？ ④顺次连接正方形四边中点得到的四边形是？ ①当ABCD满足_______时， D D1 A1B1C1D1是矩形； C2 A D 2 ②当ABCD满足_______时， C1 A1 A1B1C1D1是菱形； B2 A2 ③当ABCD满足_______时， B C B1 A1B1C1D1是正方形； ④若ABCD的面积为S，则A1B1C1D1的面积是_____； A2B2C2D2的面积是_____；AnBnCnDn的面积是 _______。
A A A A A A
A F B E
G D
C
4、已知，G是重心，过G作EF平行于BC,求： AF:FC=？EG:GF=？S△BGC:S△ABC=？
A
D
E G F
B
C
5、已知：D、E分别是AB、AC的中点， S△DOE=3，求S△ABC=_____； S△OBC=_____A ；S△ADE=____。

三角形中位线定理38道

三角形中位线定理精选题38道一．选择题（共15小题）1．如图，△ABC中，AB＝4，AC＝3，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为（）A．B．1C．D．72．如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为P A，PB的中点，对下列各值：①线段MN的长；②△P AB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是（）A．②③B．②⑤C．①③④D．④⑤3．如图，四边形ABCD中，∠A＝90°，AB＝，AD＝3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为（）A．3B．4C．4.5D．54．如图，在矩形ABCD中，P、R分别是BC和DC上的点，E、F分别是AP和RP的中点，当点P在BC上从点B向点C移动，而点R不动时，下列结论正确的是（）A．线段EF的长逐渐增长B．线段EF的长逐渐减小C．线段EF的长始终不变D．线段EF的长与点P的位置有关5．如图，△ABC的周长为19，点D，E在边BC上，∠ABC的平分线垂直于AE，垂足为N，∠ACB的平分线垂直于AD，垂足为M，若BC＝7，则MN的长度为（）A．B．2C．D．36．如图，△ABC的面积是12，点D、E、F、G分别是BC、AD、BE、CE的中点，则△AFG 的面积是（）A．4.5B．5C．5.5D．67．如图，△ABC中，已知AB＝8，∠C＝90°，∠A＝30°，DE是中位线，则DE的长为（）A．4B．3C．D．28．如图，在△ABC中，BD、CE是角平分线，AM⊥BD于点M，AN⊥CE于点N．△ABC 的周长为30，BC＝12．则MN的长是（）A．15B．9C．6D．39．如图，在四边形ABCD中，已知AB＝CD，M、N、P分别是AD、BC、BD的中点∠ABD ＝20°，∠BDC＝70°，则∠NMP的度数为（）A．50°B．25°C．15°D．20°10．如图，在△ABC中，延长BC至D，使得CD＝BC，过AC中点E作EF∥CD（点F 位于点E右侧），且EF＝2CD，连接DF．若AB＝8，则DF的长为（）A．3B．4C．2D．311．如图，DE是△ABC的中位线，过点C作CF∥BD交DE的延长线于点F，则下列结论正确的是（）A．EF＝CF B．EF＝DE C．CF＜BD D．EF＞DE12．如图，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，点D在BC上，以AC为对角线的所有平行四边形ADCE中，DE的最小值是（）A．10B．8C．6D．513．如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（）A．7B．9C．10D．1114．如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB＝10，BC ＝15，MN＝3，则AC的长是（）A．12B．14C．16D．1815．如图，D，E分别是△ABC的边AB，AC上的中点，如果△ADE的周长是6，则△ABC 的周长是（）A．6B．12C．18D．24二．填空题（共13小题）16．如图，∠MAN＝90°，点C在边AM上，AC＝4，点B为边AN上一动点，连接BC，△A′BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE 并延长交A′B所在直线于点F，连接A′E．当△A′EF为直角三角形时，AB的长为．17．如图，正方形ABCD和正方形EFCG的边长分别为3和1，点F，G分别在边BC，CD 上，P为AE的中点，连接PG，则PG的长为．18．如图，在Rt△ABC中，∠ACB＝90°，点D，E，F分别为AB，AC，BC的中点．若CD＝5，则EF的长为．19．如图，已知AB＝10，P是线段AB上的动点，分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB，连接CD，设CD的中点为G，当点P从点A运动到点B时，则点G移动路径的长是．20．如图，∠ACB＝90°，D为AB中点，连接DC并延长到点E，使CE＝CD，过点B 作BF∥DE交AE的延长线于点F．若BF＝10，则AB的长为．21．如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝6，BC＝8，则EF的长为．22．如图所示，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为．23．如图，△ABC的周长为26，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC＝10，则PQ的长．24．在四边形ABCD中，对角线AC⊥BD且AC＝6、BD＝8，E、F分别是边AB、CD的中点，则EF＝．25．如图，在△ABC中，∠ACB＝90°，M、N分别是AB、AC的中点，延长BC至点D，使CD＝BD，连接DM、DN、MN．若AB＝6，则DN＝．26．如图，在四边形ABDC中，E、F、G、H分别为AB、BC、CD、DA的中点，并且E、F、G、H四点不共线．当AC＝6，BD＝8时，四边形EFGH的周长是．27．如图，在Rt△ABC中，∠ACB＝90°，BC＝3，AC＝4，点M为边AC的中点，点N 为边BC上任意一点，若点C关于直线MN的对称点C′恰好落在△ABC的中位线上，则CN的长为．28．如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD ＝BC，∠FPE＝100°，则∠PFE的度数是．三．解答题（共10小题）29．如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF ＝BC，连接CD和EF．（1）求证：DE＝CF；（2）求EF的长．30．如图，在△ABC中，点D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．（1）求证：四边形ADEF是平行四边形；（2）求证：∠DHF＝∠DEF．31．如图，在四边形ABCD中，∠ABC＝90°，AC＝AD，M，N分别为AC，CD的中点，连接BM，MN，BN．（1）求证：BM＝MN；（2）∠BAD＝60°，AC平分∠BAD，AC＝2，求BN的长．32．如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB＝10，AC＝6，求DF的长．33．如图，在四边形ABCD中，AC⊥BD，BD＝12，AC＝16，E，F分别为AB，CD的中点，求EF的长．34．在△ABC中，E是AC边上一点，线段BE垂直∠BAC的平分线于D点，点M为BC边的中点，连接DM．（1）求证：DM＝CE；（2）若AD＝6，BD＝8，DM＝2，求AC的长．35．如图，在四边形ABCD中，AB＝DC，E、F分别是AD、BC的中点，G、H分别是对角线BD、AC的中点．（1）求证：四边形EGFH是菱形；（2）若AB＝，则当∠ABC+∠DCB＝90°时，求四边形EGFH的面积．36．如图，E、F、G、H分别为四边形ABCD四边之中点．（1）求证：四边形EFGH为平行四边形；（2）当AC、BD满足时，四边形EFGH为菱形．当AC、BD满足时，四边形EFGH为矩形．当AC、BD满足时，四边形EFGH为正方形．37．如图，在△ABC中，AE平分∠BAC，BE⊥AE于点E，点F是BC的中点．（1）如图1，BE的延长线与AC边相交于点D，求证：EF＝（AC﹣AB）；（2）如图2，写出线段AB、AC、EF的数量关系，并证明你的结论．38．已知：△ABC中，AB＝10．（1）如图①，若点D、E分别是AC、BC边的中点，求DE的长；（2）如图②，若点A1，A2把AC边三等分，过A1，A2作AB边的平行线，分别交BC 边于点B1，B2，求A1B1+A2B2的值；（3）如图③，若点A1，A2，…，A10把AC边十一等分，过各点作AB边的平行线，分别交BC边于点B1，B2，…B10．根据你所发现的规律，直接写出A1B1+A2B2+…+A10B10的结果．。

初二数学三角形中位线练习题(含答案)

初二数学三角形中位线练习题一．选择题（共5小题）1．如图，为了测量池塘边A、B两地之间的距离，在线段AB的同侧取一点C，连结CA并延长至点D，连结CB并延长至点E，使得A、B分别是CD、CE的中点，若18DE m=，则线段AB的长度是()A．9m B．12m C．8m D．10m2．已知三角形的周长是16，它的三条中位线围成的三角形的周长是()A．16B．12C．8D．43．如图，在四边形ABCD中，点P是边CD上的动点，点Q是边BC上的定点，连接AP，PQ，E，F分别是AP，PQ的中点，连接EF．点P在由C到D运动过程中，线段EF的长度() A．保持不变B．逐渐变小C．先变大，再变小D．逐渐变大4．如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD BC=，∠的度数是()∠=︒，则EFPEPF136A．68︒B．34︒C．22︒D．44︒5．如图，D是ABC⊥，E、F、G、H分别是边AB、BD、CD、AC的中点．若∆内一点，BD CDCD=，则四边形EFGH的周长是()BD=，6AD=，810A．24B．20C．12D．10第3题图第4题图第5题图二．填空题（共5小题）6．某直角三角形的两条边长分别是10和24，则连接两条直角边中点的线段的长是．7．如图，在Rt ABCABC∠=︒，点D、E、F分别是AB、AC，∆中，90BE=，则DF=．BC边上的中点，连结BE，DF，已知58．如图，在四边形ABCD中，220∠+∠=︒，E、F分别是AC、ADC BCDBD 的中点，P 是AB 边上的中点，则EPF ∠= ︒．9．如图，在四边形ABCD 中，//AB CD ，E ，F 分别是AC ，BD 的中点，已知12AB =，6CD =，则EF = ．10．如图，在ABC ∆中，8AB =，6AC =，AM 平分BAC ∠，CM AM ⊥于点M ，N 为BC 的中点，连结MN ，则MN 的长为．第8题图第9题图第10题图三．解答题（共3小题）11．如图所示，在ABC ∆中，点D 在BC 上且CD CA =，CF 平分ACB ∠，AE EB =，求证：12EF BD =．12．如图：D 、E 是ABC ∆边AB ，AC 的中点，O 是ABC ∆内一动点，F 、G 是OB ，OC 的中点．判断四边形DEGF 的形状，并证明．13．已知：如图，在四边形ABCD 中，对角线AC 、BD 相交于O ，且AC BD =，E 、F 分别是AB 、CD 的中点，E 、F 分别交BD 、AC 于点G 、H ．求证：OG OH =．答案与解析一．选择题（共5小题）1．如图，为了测量池塘边A 、B 两地之间的距离，在线段AB 的同侧取一点C ，连结CA 并延长至点D ，连结CB 并延长至点E ，使得A 、B 分别是CD 、CE 的中点，若18DE m =，则线段AB 的长度是( )A ．9mB ．12mC ．8mD ．10m【分析】根据三角形的中位线定理解答即可．【解答】解：A 、B 分别是CD 、CE 的中点， ∴AB 是△CDE 的中位线，192AB DE m ∴==，故选：A ．2．已知三角形的周长是16，它的三条中位线围成的三角形的周长是( ) A ．16 B ．12 C ．8 D ．4【分析】由中位线定义可得新三角形的各边长为原三角形各边长的一半，即可得出其周长等于原三角形周长的一半．【解答】解：三角形的周长是16，∴它的三条中位线围成的三角形的周长是11682⨯=．故选：C ．3．如图，在四边形ABCD 中，点P 是边CD 上的动点，点Q 是边BC 上的定点，连接AP ，PQ ，E ，F 分别是AP ，PQ 的中点，连接EF ．点P 在由C 到D 运动过程中，线段EF 的长度( )A ．保持不变B ．逐渐变小C ．先变大，再变小D ．逐渐变大【分析】连接AQ ，根据三角形中位线定理解答即可．【解答】解：如图所示，连接AQ ，点Q 是边BC 上的定点， AQ ∴的大小不变，E ，F 分别是AP ，PQ 的中点， ∴EF 是△APQ 的中位线， 12EF AQ ∴=， ∴线段EF 的长度保持不变，故选：A ．4．如图，在四边形ABCD 中，P 是对角线BD 的中点，E 、F 分别是AB 、CD 的中点，AD BC =，136EPF ∠=︒，则EFP ∠的度数是( )A ．68︒B ．34︒C ．22︒D ．44︒【分析】根据三角形中位线定理得到12PE AD =，12PF BC =，根据等腰三角形的性质、三角形内角和定理计算即可．【解答】解：P 是BD 的中点，E 是AB 的中点， ∴EP 是△BCD 的中位线， 12PE AD ∴=，同理，12PF BC =， AD BC =， PE PF ∴=，1(180)222EFP EPF ∴∠=⨯︒-∠=︒，故选：C ． 5．如图，D 是ABC ∆内一点，BD CD ⊥，E 、F 、G 、H 分别是边AB 、BD 、CD 、AC 的中点．若10AD =，8BD =，6CD =，则四边形EFGH 的周长是( )A ．24B ．20C ．12D ．10【分析】利用勾股定理列式求出BC 的长，再根据三角形的中位线平行于第三边并且等于第三边的一半求出12EH FG BC ==，12EF GH AD ==，然后代入数据进行计算即可得解．【解答】解：BD CD ⊥，8BD =，6CD =，22228610BC BD CD ∴=+=+，E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点，12EH FG BC ∴==，12EF GH AD ==，∴四边形EFGH 的周长EH GH FG EF AD BC =+++=+，又10AD =，∴四边形EFGH 的周长101020=+=，故选：B ．二．填空题（共5小题）6．某直角三角形的两条边长分别是10和24，则连接两条直角边中点的线段的长是 13或12 ．【分析】根据勾股定理求出AB ，根据三角形中位线定理计算，得到答案．【解答】解：分两种情况讨论：①当24是直角边时，由勾股定理得，斜边2222241026AB AC BC =+=+=，M 、N 分别为CA 、CB 的中点， ∴MN 是△ABC 的中位线，1132MN AB ∴==，②当24是斜边时，1122MN AB ==，故答案为：13或12．7．如图，在Rt ABC ∆中，90ABC ∠=︒，点D 、E 、F 分别是AB 、AC ，BC 边上的中点，连结BE ，DF ，已知5BE =，则DF = 5 ．【分析】已知BE 是Rt ABC ∆斜边AC 的中线，那么12BE AC =；DF 是ABC ∆的中位线，则12DF AC =，则5DF BE ==．【解答】解：ABC ∆是直角三角形，BE 是斜边的中线， 12BE AC ∴=，又DF 是ABC ∆的中位线，12DF AC ∴=， 5DF BE ∴==．故答案为5．8．如图，在四边形ABCD 中，220ADC BCD ∠+∠=︒，E 、F 分别是AC 、BD 的中点，P 是AB 边上的中点，则EPF ∠= 40 ︒．【分析】依据四边形内角和即可得到140BAD ABC ∠+∠=︒，再根据三角形中位线定理即可得到BPF BAD ∠=∠，APE ABC ∠=∠，进而得出140APE BPF ∠+∠=︒，即可得到EPF ∠的度数．【解答】解：四边形ABCD 中，220ADC BCD ∠+∠=︒， 360220140BAD ABC ∴∠+∠=︒-︒=︒，E 、F 分别是AC 、BD 的中点，P 是AB 边上的中点， PE ∴是ABC ∆的中位线，PF 是ABD ∆的中位线， //PE BC ∴，//PF AD ，BPF BAD ∴∠=∠，APE ABC ∠=∠，140APE BPF BAD ABC ∴∠+∠=∠+∠=︒， 18014040EPF ∴∠=︒-︒=︒，故答案为：40．9．如图，在四边形ABCD 中，//AB CD ，E ，F 分别是AC ，BD 的中点，已知12AB =，6CD =，则EF = 3 ．【分析】连接CF 并延长交AB 于G ，证明FDC FBG ∆≅∆，根据全等三角形的性质得到6BG DC ==，CF FG =，求出AG ，根据三角形中位线定理计算，得到答案．【解答】解：连接CF 并延长交AB 于G ， //AB CD ，FDC FBG ∴∠=∠，在FDC ∆和FBG ∆中， FDC FBG FD FBDFC BFG ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()FDC FBG ASA ∴∆≅∆ 6BG DC ∴==，CF FG =， 1266AG AB BG ∴=-=-=， CE EA =，CF FG =， ∴EF 是△ACG 的中位线， 132EF AG ∴==，故答案为：3． 10．如图，在ABC ∆中，8AB =，6AC =，AM 平分BAC ∠，CM AM ⊥于点M ，N 为BC 的中点，连结MN ，则MN 的长为 1 ．【分析】延长CM 交AB 于H ，证明AMH AMC ∆≅∆，根据全等三角形的性质得到6AH AC ==，CM MH =，根据三角形中位线定理解答．【解答】解：延长CM 交AB 于H ，在AMH ∆和AMC ∆中， 90MAH MAC AM AMAMH AMC ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩， ()AMH AMC ASA ∴∆≅∆6AH AC ∴==，CM MH =， 2BH AB AH ∴=-=， CM MH =，CN BN =， ∴MN 是△BCH 的中位线， 112MN BH ∴==，故答案为：1．三．解答题（共3小题）11．如图所示，在ABC ∆中，点D 在BC 上且CD CA =，CF 平分ACB ∠，AE EB =，求证：12EF BD =．【分析】首先根据等腰三角形的性质可得F 是AD 中点，再根据三角形的中位线定理可得12EF BD =．【解答】证明：CD CA =，CF 平分ACB ∠， F ∴是AD 中点， AE EB =， E ∴是AB 中点，EF ∴是ABD ∆的中位线， 12EF BD ∴=． 12．如图：D 、E 是ABC ∆边AB ，AC 的中点，O 是ABC ∆内一动点，F 、G 是OB ，OC 的中点．判断四边形DEGF 的形状，并证明．【分析】根据三角形中位线定理得到12DE BC =，//DE BC ，12FGT BC =，//FG BC ，得到DE FG =，//DE FG ，根据平行四边形的判定定理证明结论．【解答】解：四边形DEGF 是平行四边形，理由：D 、E 是ABC ∆边AB ，AC 的中点， ∴DE 是△ABC 的中位线，12DE BC ∴=，//DE BC ， F 、G 是OB ，OC 的中点， ∴FG 是△BCO 的中位线，12FG BC ∴=，//FG BC ，DE FG ∴=，//DE FG∴四边形DEGF 是平行四边形．13．已知：如图，在四边形ABCD中，对角线AC、BD相交于O，且AC BD=，E、F分别是AB、CD的中点，E、F分别交BD、AC于点G、H．求证：OG OH=．【分析】取BC边的中点M，连接EM，FM，则根据三角形的中位线定理，即可证得EMF∆是等腰三角形，根据等边对等角，即可证得MEF MFE∠=∠，然后根据平行线的性质证得OGH OHG∠=∠，根据等角对等边即可证得．【解答】解：取BC边的中点M，连接EM，FM，M、F分别是BC、CD的中点，∴MF是△BCD的中位线，//MF BD ∴，12MF BD=，同理：//ME AC，12ME AC=，AC BD=ME MF∴=MEF MFE∴∠=∠，//MF BD，MFE OGH∴∠=∠，同理，MEF OHG∠=∠，OGH OHG∴∠=∠OG OH∴=．。

三角形的中位线专题练习题含答案

三角形的中位线专题练习题1．如图，为测量池塘边A，B两点间的距离，小明在池塘的一侧选取一点O，测得OA，OB 的中点分别是点D，E，且DE＝14米，则A，B间的距离是()A．18米B．24米C．28米D．30米2．如图，在△ABC中，点D，E分别是AB，AC的中点，∠A＝50°，∠ADE＝60°，则∠C 的度数为()A．50°B．60°C．70°D．80°3．如图，在Rt△ABC中，∠A＝30°，BC＝1，点D，E分别是直角边BC，AC的中点，则DE的长为()A．1 B．2 C. 3 D．1＋ 34．如图，点D，E，F分别是△ABC各边的中点，连接DE，EF，DF.若△ABC的周长为10，则△DEF的周长为____．5．如图，▱ABCD的对角线AC，BD相交于点O，点E是CD的中点，△ABD的周长为16 cm，则△DOE的周长是____cm.6．如图，在△ABC中，D，E，F分别是BC，AC，AB的中点．(1)若DE＝10 cm，则AB＝____cm；(2)中线AD与中位线EF有什么特殊关系？证明你的猜想．7．我们把依次连接任意一个四边形各边中点得到的四边形叫做中点四边形．如图，在四边形ABCD中，E，F，G，H分别是边AB，BC，CD，DA的中点，依次连接各边中点得到中点四边形EFGH.(1)这个中点四边形EFGH的形状是___________；(2)请证明你的结论．8．如图，四边形ABCD中，点P是对角线BD的中点，点E，F分别是AB，CD的中点，AD＝BC，∠PEF＝30°，则∠PFE的度数是()A．15°B．20°C．25°D．30°9．如图，在四边形ABCD中，R，P分别是BC，CD上的点，E，F分别是AP，RP的中点，当点P在CD上从C向D移动而点R不动时，那么下列结论成立的是()A．线段EF的长逐渐增大B．线段EF的长逐渐减小C．线段EF的长不变D．线段EF的长与点P的位置有关10．如图，EF是△ABC的中位线，BD平分∠ABC交EF于点D，若DE＝2，则EB＝____．11．如图，△ABC 的周长是1，连接△ABC 三边的中点构成第2个三角形，再连接第2个三角形三边中点构成第3个三角形，依此类推，第2017个三角形的周长为________．12．如图，E ，F ，G ，H 分别是AB ，BC ，CD ，DA 的中点．求证：四边形EFGH 是平行四边形．13．如图，M 是△ABC 的边BC 的中点，AN 平分∠BAC ，BN ⊥AN 于点N ，延长BN 交AC 于点D ，已知AB ＝10，BC ＝15，MN ＝3.(1)求证：BN ＝DN ；(2)求△ABC 的周长．14．如图，在▱ABCD 中，AE ＝BF ，AF ，BE 相交于点G ，CE ，DF 相交于点H.求证：GH ∥BC且GH ＝12BC.15．如图，在▱ABCD中，E是CD的中点，F是AE的中点，FC与BE相交于点G.求证：GF ＝GC.方法技能：1．三角形有三条中位线，每条中位线都与第三边有相应的位置关系和数量关系，位置关系可证明两直线平行，数量关系可证明线段相等或倍分关系．2．三角形的三条中位线将原三角形分为四个全等的小三角形，每个小三角形的周长都等于原三角形周长的一半．3．当题目中有中点时，特别是有两个中点且都在一个三角形中，可直接利用三角形中位线定理．易错提示：对三角形中位线的意义理解不透彻而出错答案：1. C2. C3. A4. 55. 86. (1) 20(2) 解：AD与EF互相平分．证明：∵D，E，F分别为BC，AC，AB的中点，∴DE∥AB，DE＝12AB，AF＝12AB，∴DE＝AF，∴四边形AFDE是平行四边形，∴AD与EF互相平分7. (1) 平行四边形(2) 解：连接AC，由三角形中位线性质得，EF∥AC且EF＝12AC，GH∥AC且GH＝12AC，∴EF綊GH，∴四边形EFGH是平行四边形8. D9. C10. 211.1 2201612. 解：连接BD，∵E，H分别是AB，AD的中点，∴EH是△ABD的中位线，∴EH＝12BD，EH∥BD，同理可证FG＝12BD，FG∥BD，∴EH綊FG，∴四边形EFGH是平行四边形13. 解：(1)∵AN平分∠BAD，∴∠1＝∠2，∵BN⊥AN，∴∠ANB＝∠AND＝90°，又∵AN＝AN，∴△ABN≌△ADN(ASA)，∴BN＝DN(2)∵△ABN≌△ADN，∴AD＝AB＝10，∵DN＝BN，点M是BC的中点，∴MN是△BDC的中位线，∴CD＝2MN＝6，∴△ABC的周长＝AB＋BC＋CD＋AD＝10＋15＋6＋10＝4114. 解：连接EF，证四边形ABEF，EFCD分别为平行四边形，从而得G是BE的中点，H是EC的中点，∴GH是△EBC的中位线，∴GH∥BC且GH＝12BC15. 解：取BE的中点H，连接FH，CH，∵F是AE的中点，H是BE的中点，∴FH是△ABE的中位线，∴FH∥AB且FH＝12AB.在▱ABCD中，AB∥DC，AB＝DC，∴FH∥EC，又∵点E是DC的中点，∴EC＝12DC＝12AB，∴FH＝EC，∴四边形EFHC是平行四边形，∴GF＝GC。

中考数学总复习《三角形中位线定理》练习题(含答案)

三角形中位线定理一、选择题1.如图，四边形ABCD 中，E F ，分别是边AB CD ，的中点，则AD BC ，和EF 的关系是（）A ．2AD BC EF +>B ．2AD BC EF +≥C ．2AD BC EF +< D ．2AD BC EF +≤二、填空题2.如图，△ABC 的周长为64，E 、F 、G 分别为AB 、AC 、BC 的中点，A ′、B ′、C ′分别为EF 、EG 、GF 的中点，△A ′B ′C ′的周长为_________．如果△ABC 、△EFG 、△A ′B ′C ′分别为第1个、第2个、第3个三角形，按照上述方法继续作三角形，那么第n 个三角形的周长是__________________．3.已知如图，四边形ABCD 中，90ABC ADC ∠=∠=︒，E F 、分别是AC BD 、的中点，如果2612AC BF ==，，则EF = ．4.如图，ABC ∆中，AD 是BAC ∠的平分线，CE AD ⊥于E ，M 为BC 的中点，14cm AB =，10cm AC =，则ME 的长为．A BD F ECFEDCB A5.已知：如图，△ABC 中，D 是BC 边的中点，AE 平分∠BAC ，BE ⊥AE 于E 点，若AB ＝5，AC ＝7，则ED= ．三、解答题6.已知：△ABC 的中线BD 、CE 交于点O ，F 、G 分别是OB 、OC 的中点．求证：四边形DEFG 是平行四边形．7.已知：如图，AD BC ⊥于D 点，2B C ∠=∠，CE EB =，求证：2AB DE =．8.已知：如图，E 为□ABCD 中DC 边的延长线上的一点，且CE ＝DC ，连结AE 分别交BC 、BD 于点F 、G ，连结AC 交BD 于O ，连结OF ．求证：AB ＝2OF ．M ED CBAE D C BA9.已知：如图，四边形ABCD 中，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点．求证：四边形EFGH 是平行四边形．10.已知：如图，在四边形ABCD 中，AD ＝BC ，E 、F 分别是DC 、AB 边的中点，FE的延长线分别与AD 、BC 的延长线交于H 、G 点．求证：∠AHF ＝∠BGF ．11.已知：如图，在□ABCD 中，E 是CD 的中点，F 是AE 的中点，FC 与BE 交于G ．求证：GF ＝GC ．12.如图在△ABC 中，D 、E 分别为AB 、AC 上的点，且BD ＝CE ，M 、N 分别是BE 、CD 的中点．过MN 的直线交AB 于P ，交AC 于Q ，线段AP 、AQ 相等吗?为什么?HGF EDC BA三角形中位线定理答案解析一、选择题1.B ；连结BD ，取BD 的中点P ，连结FP EP ，，由三角形的中位线可知选B二、填空题2.16；11642n -⎛⎫⨯ ⎪⎝⎭3.54.2；延长CE 交AB 于点N ．利用中位线的性质和直角三角形斜边中线可得()14102cm 2-=．5.1；延长BE 交AC 于点G ，故2GC ED =，1ED =三、解答题6.∵12ED BC ED BC =∥，，12FG BC FG BC =∥，，∴ED FG ED FG =，∥ 7.取AB 边中点F ，连接EF ，DF ，∵DF BF B FDB =∠=∠，， ∴2FDB C ∠=∠，∴AC EF ∥，∴ACE FEB ∠=∠，∴2FDB FEB ∠=∠,故2DE DF AB DE ==，【解析】利用斜边中线与三角形中位线8.∵ABF CEF ≌△△，BF CF =，12OF AB =9.连接BD ，通过中位线就能证明四边形EFGH 是平行四边形10.∵取AC 中点P ，连接EP FP 、，故1122EP AD PF BC AD BC EP FP ====，，，，EP AH ∥，∴∠AHF =PEF ∠，PF BH ∥，PFH BGF ∠=∠∴∠AHF ＝∠BGFC E FPD B AE NM D C B A11.∵取BE 中点P ，连接FP ，12PF AB PF AB =∥，，故四边形EFPC 为平行四边形，故GF ＝GC12.取BC 中点F ，连接MF NF 、，得到NF AB MF AC ∥，∥又12MF EC =、12NF BD =，∴APN FNP FMQ AQP ∠=∠∠=∠，，AP AQ = PHGF ED CB A。

三角形中位线习题

三角形中位线练习题（一）计算2．已知△ABC中，AB∶BC∶CA=3∶2∶4，AB=9厘米，D，E，F分别是AB，BC，AC的中点，求△DEF的周长．3．已知△ABC中，D，E，F分别是AB，BC，AC的中点，△ABC的周长与△DEF的周长的和等于18厘米，求△DEF的周长．4．已知△ABC中，D，E分别是AB，AC的中点，F为BC上5．已知△ABC中，D为AB的中点，E为AC上一点，AE=2CE，CD，BE交于O点，OE=2厘米，求BO的长．6．已知梯形ABCD中，AD∥BC，AD＜BC，E，F分别是AB，DB的中点，EF交DC于G，EF∶FG=1∶2，AD=7厘米，求BC的长．7．已知△ABC中，D为BC上的一点，E，F，H，G分别是AC，CD，DB，AB的中点，EF ＋AD=6厘米，求GH的长．8．已知△ABC中，AD⊥BC于D，E，F，G分别是AB，BD，9．已知四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点，HF=EG，AC=4厘米，BD=2厘米，求四边形ABCD的面积．10．已知梯形ABCD中，AB∥CD，AD=BC，AC平分∠DAB，AC⊥BC，AB=8厘米，M，N分别是AC，BD的中点，求MN的长．11．已知梯形ABCD中，AD∥BC，AD＜BC，AB=DC=12厘米，E，F分别是AB，DB的中点，延长EF交DC于G，EF=4厘米，FG=10厘米，求梯形ABCD的底角．12．已知△ABC中，BD，CE分别是∠ABC，∠ACB的平分线，AH⊥BD于H，AF⊥CE于F．若AB=14厘米，AC=9厘米，BC=18厘米，求FH的长．（二）证明13．已知：如图4-108，从△ABC的顶点A向∠B，∠C的平分线引垂线，垂足分别是D，E．求证：DE∥BC．14．已知：在四边形ABCD中，AB=CD，AD＜BC，E，F，P分别是BD，AC，BC的中点．求证：∠PEF=∠PFE．15．已知：在△ABC中，AH⊥BC于H，D，E，F分别是BC，AC，AB的中点．求证：△DEF≌△HFE．16．已知：在△ABC中，AB＞AC，AD⊥BC于D，E，F，G分别是AB，BC，AC的中点．求证：∠BFE=∠EGD．17．已知：在△ABC中，AB＞AC，D，E，F分别是BC，AB，AC的中点，EG∥AD交FD的延长线于G．求证：AB=GF．18．已知：△ABC中，AB＞AC，CD平分∠ACB，AD⊥DC，F为AC的中点，延长FD交AB 于E点．求证：19．已知：△ABC中，E为AC上一点，AE=2CE，D为AB的中20．已知：在△ABC中，中线BE，CF交于O点，G，H分别是OB，OC的中点．求证：FG∥EH．21．已知：如图4-109，E，F分别是AB，AC的中点，延长EF交∠ACD的平分线于G 点．求证：AG⊥CG．22．证明：四边形两组对边中点连线互相平分．23．已知：在矩形ABCD中，AC，BD相交于O点，E，F分别是OA，OD的中点．求证：四边形EBCF是等腰梯形．24．求证：等腰梯形的上、下底中点的连线与两腰中点连线互相垂直．25．已知：在四边形ABCD中，AB=DC，E，F分别是AD，BC的中点，GH⊥EF与AB，DC 分别交于G，H，O为垂足．求证：∠AGH=∠DHG．26．已知：四边形ABCD中，AC=BD，AC，BD交于O点，E，F分别是AB，CD的中点，连结EF分别与BD，AC交于G，H．求证：△OGH是等腰三角形．27．已知：如图4-110，P为矩形ABCD内的一点，四边形BCPQ是平行四边形，A′，B′，C′，D′分别是AP，PB，BQ，QA的中点．求证：A′C′=B′D′．28．已知：在四边形ABCD中，CD≥AB，E，F分别是AC，29．已知：在四边形ABCD中，AD≥BC，E，F分别是AB，30．已知：△ABC中，D，E，F分别是AB，BC，AC的中点，H为BE上任一点，作DG∥FH交CB的延长线于G．求证：GB=HE．31．已知：在△ABC中，∠A=90°，D，E分别是AB，AC上任意一点，M，N，P，Q分别是DE，BE，BC，CD的中点．求证：MP=NQ．32．已知：如图4-111，△ACN，△ABM为等边三角形，D，E，F分别是BM，BC，CN的中点．求证：DE=EF．33．已知：如图4-112，△ABC中，F为BC的中点，D，E为△ABC外的两点，∠D=90°，AD=DB，∠E=90°，AE=EC．求证：DF=EF．34．已知：在四边形ABCD中，G，H分别是AB，AD的中点，连结CG，CH与BD分别交于E，F两点，且BE=EF=FD．求证：四边形ABCD是平行四边形．若HF=3厘米，求CH的长．35．已知：在△ABC中，D，E分别是AB，AC上的点，且BD=CE，F，G分别是BE，CD 的中点，直线FG与AB，AC分别交于M，N．求证：AM=AN．若∠AMN=62°，求∠A的度数．36．已知：梯形ABCD中，AD∥BC，AD＜BC，AB=DC，AC，BD交于O点，∠BOC=60°，E，F，G分别是AO，BO，DC的中点．求证：△EFG是等边三角形．37．如图4-113，已知在直角三角形ABC中，∠BAC=90°，D，E，F分别是BC，CA，AB 的中点，AD，EF交于O点．（1）求证：AD=EF；（2）若∠DOF=2∠AOF，求证：△ABD是等边三角形．。

专题11 三角形中位线定理(原卷版)

专题11 三角形中位线定理【考点归纳】（1）三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．（2）几何语言：【好题必练】一、选择题1．（2020秋•罗湖区期末）如图，已知△ABC中，AB＝AC，AD是∠BAC的平分线，AE是∠BAC的外角平分线，ED∥AB交AC于点G，下列结论：①AD⊥BC；②AE∥BC；③AE＝AG；④AD2+AE2＝4AG2．其中正确结论的个数是（）A．1B．2C．3D．42．（2020秋•安丘市期末）如图，面积为2的等边三角形ABC中，D，E，F分别是AB，BC，CA的中点，则△DEF的面积是（）A．1B．C．D．3．（2020秋•长春期末）如图，在边长为4的等边三角形ABC中，DE为△ABC的中位线，则四边形BCED 的面积为（）A．2B．3C．4D．64．（2020秋•长春期末）△ABC中，AB＝7，BC＝6，AC＝5，点D、E、F分别是三边的中点，则△DEF 的周长为（）A．4.5B．9C．10D．125．（2020秋•绿园区期末）如图，为测量位于一水塘旁的两点A，B间的距离，在地面上确定点O，分别取OA，OB的中点C，D，量得CD＝10m，则A，B之间的距离是（）A．5m B．10m C．20m D．40m6．（2020秋•内江期末）如图，在四边形ABCD中，P是对角线BD的中点，点E、F分别是AB、CD的中点，AD＝BC，∠EPF＝140°，则∠EFP的度数是（）A．50°B．40°C．30°D．20°二、填空题7．（2020春•兴化市期中）如图，D、E分别是△ABC的边AB、AC的中点．若BC＝6，则DE的长为．8．（2020春•姜堰区期中）已知以三角形各边中点为顶点的三角形的周长为6cm，则原三角形的周长为cm．9．（2020春•建湖县期中）如图，AB∥CD，AB＝7，CD＝3，M、N分别是AC和BD的中点，则MN的长度．10．（2020春•常熟市期中）如图，在△ABC中，BC＝14，D、E分别是AB、AC的中点，F是DE延长线上一点，连接AF、CF，若DF＝12，∠AFC＝90°，则AC＝．11．（2020•凤山县一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，D，E，F分别为AB，AC，AD的中点．若BC＝2，则EF的长度为．三、解答题12．（2020•房山区二模）如图，在△ABC中，BD平分∠ABC交AC于点D，DE∥AB交BC于点E，F是BD中点．求证：EF平分∠BED．13．如图，四边形ABCD中，AB＝AD，对角线BD平分∠ABC，E，F分别是BD，CD的中点．求证：AD∥EF．14．如图，在△ABC中，D为BC的中点，E为AC的中点，AB＝6，求DE的长．15．如图，在△Rt△ABC中，∠ACB＝90°，DE、DF是△ABC的中位线，连接EF、CD，求证：CD＝EF．16．如图，点D，E，F分别为△ABC三边的中点，若△DEF的周长为10，求△ABC的周长。

三角形中位线的性质经典练习题

基础知识3 三角形的中位线1.三角形的中位线：连结三角形的线段叫做三角形的中位线，一个三角形有______条中位线.2.三角形中位线的性质：三角形的中位线于第三边，并且等于．【题型1】三角形中位线的应用1.如图，△ABC中，D、E分别是AB、AC的中点，则线段CD是△ABC的＿＿＿，线段DE 是△ABC＿＿＿＿.2.如图，D、E、F分别是△ABC各边的中点；如果EF＝4cm，那么BC＝＿＿cm；如果AB＝10cm，那么DF＝＿＿＿cm；中线AD与中位线EF的关系是＿＿＿.3．三角形的三边长分别是3cm，5cm，6cm，则连结三边中点所围成的三角形的周长是____ _cm．4.若三角形的三条中位线长分别为2cm，3cm，4cm，则原三角形的周长为 .5.已知△ABC的周长为1，连结△ABC的三边中点构成第二个三角形，•再连结第二个三角形的三边中点构成第三个三角形，依此类推，第2010个三角形的周长是 .6.在Rt△ABC中，∠C=90°，AC=5，•BC=12，•则连结两条直角边中点的线段长为_______．7.如图，A，B两点分别位于一个池塘的两端，小朱想用绳子测量A，B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A，B的点C，找到AC，BC的中点D，E，并且测出DE的长为10m，则A，B间的距离为 .8.如图,在△ABC中，E，D，F分别是AB，BC，CA的中点，AB=6，AC=4，则四边形AEDF•的周长是 .9.如图,□ABCD的对角线AC，BD相交于点O，AE=EB. 求证：OE∥BC．第1题第8题第7题第2题10.如图，在△ABC中，中线BE，CD交于点O，F，G分别是OB，OC的中点．求证：四边形DFGE是平行四边形．11.如图，四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点．求证：四边形EFGH是平行四边形．12.如图，E为□ABCD中DC边的延长线上的一点，且CE＝DC，连结AE分别交BC、BD于点F、G，连结AC交BD于O，连结OF．求证：AB＝2OF．。

三角形中位线经典测试题

三角形的中位线基础题30道选择题附详细答案

三角形中位线定理_练习题

(完整word版)三角形的中位线练习题含答案,推荐文档

三角形中位线专项训练(30道)(解析版)

三角形中位线经典测试题

三角形中位线定理专练

三角形中位线典型题练习

完整版三角形的中位线经典练习题及其答案

三角形中位线专项训练(30道)(解析版)

(完整版)三角形的中位线经典练习题及其答案

三角形的中位线习题归类(绝对经典,绝对震撼)

中位线(三角形)例题

三角形中位线定理38道

初二数学三角形中位线练习题(含答案)

三角形的中位线 专题练习题 含答案

中考数学总复习《三角形中位线定理》练习题(含答案)

三角形中位线习题

专题11 三角形中位线定理(原卷版)

三角形中位线的性质经典练习题

三角形的中位线专题练习题含答案