新浙教版等腰三角形的性质定理(课堂PPT)
合集下载
浙教版数学八年级上册2.3等腰三角形的性质定理(共16张PPT)

直角三角形
四边形及特 殊四边形
……
1、必做题:课本P58页 作业题A, B组; 2、选做题:作业本拓展提高
证角等,找等腰,巧转化
综合—提高
如图,在△ ABC中,AD平分∠BAC,AD的垂 直平分线EF交BC的延长线于点F,连结AF,求 证: ∠CAF= ∠B.
感悟—展望
通过本节课的学习,请你畅所欲言, 谈谈自己学习到了哪些知识?有何收获 与体会?
感悟—展望 边
两边相等
角
两个底角 相等
整体
轴对称图形
感悟—展望 知识
能力
经验
1、等腰三角 形的两个底 角相等
2、等边三角 形的各个内角 都等于60 °
1、进行有关 角度的计算 (分类讨论 思想)
2、进行简单 的推理论证
1.证角等, 找全等,巧 构造
2.证角等, 找等腰,巧 转化
感悟—展望
全等三角形
定义 性质 判定
解决相关问题
等腰三角形
定义 性质 判定 解决相关问题
2.3 等腰三角形的性质定理(1)
回顾—思考
全等三角形
定义 性质 判定
解决相关问题
等腰三角形
定义 性质 判定 解决相关问题
回顾—思考
A
1、有两边相等的三角形叫做
顶
角
腰
腰
等腰三角形;
2、等腰三角形是 轴对称 图形,
底角 底角
B 顶角平分线所在的直线 是它的对称轴。 底边
C
发现—验证
如图在等腰三角形ABC中,AB=AC, AD平分∠BAC,交BC于D.
现将△ABC沿着AD所在的直线 对折,你发现∠B与∠C存在怎样
A
的数量关系?
等腰三角形课件(浙教版)

4、能运用等腰三角形的性质进行简单 的论证和计算。
5、养成仔细视察认真分析的良好学习习惯。
2024/9/18
三、等腰三角形的性质:
A
B
C
2024/9/18
1、性质定理:
等腰三角形的两个底角相等
(简写成“等边对等角”)
。
A
几何语言:
因为:AB=AC(已知)
B
2024/9/18
所以:B=C C
2、证明:已知:△ ABC中, AB=AC 求证: B= C
等腰三角形
A
B
2024/9/18
C
一、复习引入:
有两条边相等 的三角形
1、什么是等腰三角形?
2、用尺规作一个等腰三角形,测量它 的两底角,它们相等吗?
A
B
C
2024/9/18
二、教学目标:
1、掌握等腰三角形的性质定理及推论。
2、理解定理的证明及所用数学方法。 3、了解等腰三角形和等边三角形的 从属关系,能说出等边三角形的有关性质。
证明:作A的平分线AD。 A
在△ABC中
AB=AC(已知)
12
1=2(已作)
AD=AD(公共边)
△ ABD= △ ACD(SAS) B
D
C
∴ B= C(全等三角 2024/9/18 形的对应角相等)。
练习1:
还有其它辅助线作法吗? 讨论一下,看谁能想出更 好的办法?
2024/9/18
作高:
作△ABC的高AD:
2024/9/18
六、作业:P72 第3、5题
2024/9/18
(2)推论2
2024/9/18
五、达标检测:
1、判断:
(1)在等腰三角形中,有一个角是84度,则这个 角必定是顶角( × );
5、养成仔细视察认真分析的良好学习习惯。
2024/9/18
三、等腰三角形的性质:
A
B
C
2024/9/18
1、性质定理:
等腰三角形的两个底角相等
(简写成“等边对等角”)
。
A
几何语言:
因为:AB=AC(已知)
B
2024/9/18
所以:B=C C
2、证明:已知:△ ABC中, AB=AC 求证: B= C
等腰三角形
A
B
2024/9/18
C
一、复习引入:
有两条边相等 的三角形
1、什么是等腰三角形?
2、用尺规作一个等腰三角形,测量它 的两底角,它们相等吗?
A
B
C
2024/9/18
二、教学目标:
1、掌握等腰三角形的性质定理及推论。
2、理解定理的证明及所用数学方法。 3、了解等腰三角形和等边三角形的 从属关系,能说出等边三角形的有关性质。
证明:作A的平分线AD。 A
在△ABC中
AB=AC(已知)
12
1=2(已作)
AD=AD(公共边)
△ ABD= △ ACD(SAS) B
D
C
∴ B= C(全等三角 2024/9/18 形的对应角相等)。
练习1:
还有其它辅助线作法吗? 讨论一下,看谁能想出更 好的办法?
2024/9/18
作高:
作△ABC的高AD:
2024/9/18
六、作业:P72 第3、5题
2024/9/18
(2)推论2
2024/9/18
五、达标检测:
1、判断:
(1)在等腰三角形中,有一个角是84度,则这个 角必定是顶角( × );
新浙教版八年级数学上册《等腰三角形的性质定理》精品课件
A 12
DC
1、“手和脑在一块干是创造教育的开始,手脑双全是创造教育的目的。” 2、一切真理要由学生自己获得,或由他们重新发现,至少由他们重建。 3、反思自我时展示了勇气,自我反思是一切思想的源泉。 4、好的教师是让学生发现真理,而不只是传授知识。 5、数学教学要“淡化形式,注重实质.
6、“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞”。2021年11月2021/11/82021/11/82021/11/811/8/2021 7、“教师必须懂得什么该讲,什么该留着不讲,不该讲的东西就好比是学生思维的器,马上使学生在思维中出现问题。”“观察 是思考和识记之母。”2021/11/82021/11/8November 8, 2021 8、普通的教师告诉学生做什么,称职的教师向学生解释怎么做,出色的教师示范给学生,最优秀的教师激励学生。 2021/11/82021/11/82021/11/82021/11/8
D
C A
D C
3、等边三角形的定义。 三边都相等的三角形是等边三角形
4、等边三角形是特殊的等腰三角形,除具有等腰 三角形的性质外,还具有特殊的性质吗?
等边三角形的各角都都等于60°
2.3 等腰三角形的性质定 理
执教:刘化雷
如果已知AB=AC,∠BAD=∠CAD(AD是顶角 平分线). 那么有什么结论?
AD⊥BC(AD是底边上的高), ∠BAD=∠CAD(AD是顶角平分线)
等腰三角形的性质2:
BD C
等腰三角形的顶角平分线、底边上的中线 和底边上的高互相重合.
简称“等腰三角形三线合一”
不是等腰三角形有没有这个特征呢?
等腰三角形“三线合一”的性质
用符号语言表示为:
在△ABC中 (1)∵AB=AC,AD⊥BC, ∴∠1___=∠_2__,_B__D_=_C_D__; (2)∵AB=AC,AD是中线, ∴(3∠)1_∵=A∠B_=2 A,C_A,_D_A_⊥D是_B_C角__平;分线,B ∴_A_D__⊥_B_C__,B__D__=_C_D__。
浙教版八年级数学上册课件:2.4 等腰三角形的性质定理 (共16张PPT)

教学课件
数学 八年级上册 浙教版
第2章 特殊三角形
2.4 等腰三角形的性质定理
复习回顾:
等腰三角形的性等. (在同一个三角形中,等边对等角) 3、等腰三角形三线合一 顶角平分线、底边上的中线 和底边上的高
等腰三角形的判定方法:
1、有两边相等的三角形是等腰三角形。(定义)
解: ∵ ∠ DAC= ∠ C+ ∠ ABC (三角形外角和的性质) 又 ∵ ∠ C=30 ° ∠ DAC= 60 ° ∴ ∠ ABC= ∠ DAC -∠ ACB=60 °- 30 ° =30 °∴ ∠ ABC= ∠ C ∴ AB=AC(在同一个三角形中, 等角对等边) 即AC的长就是河宽。
30
O
60
形.
“在同一个三角形中,等角对等边。” 辨一辨: “在同一个三角形中, 等边对等角。” 性质 判定
在同一个三角形中, 等角对等边
问:如图,下列推理正确吗? A
1 2
C
1
D
B
D ∵∠1=∠2 ∴ BD=DC (等角对等边)
C
A
2
B
∵∠1=∠2 ∴ DC=BC (等角对等边)
错,因为都不是在同一个三角形中。
60°
A
C
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形(三个角都相等的三角形是等边三角 形).
第二种情况:顶角是60°; 已知:如图,在△ABC中,AB=AC,∠A=60°. 求证:△ABC是等边三角形. 证明:∵AB=AC,∠A=60°(已知), ∴∠C=∠B=60°(在同一个三角形 中,等角对等边) ∴∠A=∠B=∠C =60°, ∴△ABC是等边三角形(三个角都相 等的三角形是等边三角形). B C A
数学 八年级上册 浙教版
第2章 特殊三角形
2.4 等腰三角形的性质定理
复习回顾:
等腰三角形的性等. (在同一个三角形中,等边对等角) 3、等腰三角形三线合一 顶角平分线、底边上的中线 和底边上的高
等腰三角形的判定方法:
1、有两边相等的三角形是等腰三角形。(定义)
解: ∵ ∠ DAC= ∠ C+ ∠ ABC (三角形外角和的性质) 又 ∵ ∠ C=30 ° ∠ DAC= 60 ° ∴ ∠ ABC= ∠ DAC -∠ ACB=60 °- 30 ° =30 °∴ ∠ ABC= ∠ C ∴ AB=AC(在同一个三角形中, 等角对等边) 即AC的长就是河宽。
30
O
60
形.
“在同一个三角形中,等角对等边。” 辨一辨: “在同一个三角形中, 等边对等角。” 性质 判定
在同一个三角形中, 等角对等边
问:如图,下列推理正确吗? A
1 2
C
1
D
B
D ∵∠1=∠2 ∴ BD=DC (等角对等边)
C
A
2
B
∵∠1=∠2 ∴ DC=BC (等角对等边)
错,因为都不是在同一个三角形中。
60°
A
C
∴∠A=∠B =∠C=60°.
∴△ABC是等边三角形(三个角都相等的三角形是等边三角 形).
第二种情况:顶角是60°; 已知:如图,在△ABC中,AB=AC,∠A=60°. 求证:△ABC是等边三角形. 证明:∵AB=AC,∠A=60°(已知), ∴∠C=∠B=60°(在同一个三角形 中,等角对等边) ∴∠A=∠B=∠C =60°, ∴△ABC是等边三角形(三个角都相 等的三角形是等边三角形). B C A
【浙教版】最新八年级上:2.3《等腰三角形的性质定理》ppt课件(第1课时)

⒊等腰三角形一个角为110°,它的 另外两个角为_3_5_°__,3_5.°
1.填空题:
(1)如图,在△ ABC中,AB=AC,外角∠ ACD=100, 则∠ B=____度
(2)如图,在等腰三角形ABC中,AB=AC,D为
BC的中点,则点D到AB,AC的距离相等.
请说明理由.
A
A
E
F
100 °
B
•
14、抱最大的希望,作最大的努力。2021年4月30日 星期五 2021/4/302021/4/302021/4/30
•
15、一个人炫耀什么,说明他内心缺 少什么 。。2021年4月 2021/4/302021/4/302021/4/304/30/2021
•
16、业余生活要有意义,不要越轨。2021/4/302021/4/30Apr il 30, 2021
•
11、人总是珍惜为得到。2021/4/302021/4/302021/4/30Apr-2130-Apr-21
•
12、人乱于心,不宽余请。2021/4/302021/4/302021/4/30Fri day, April 30, 2021
•
13、生气是拿别人做错的事来惩罚自 己。2021/4/302021/4/302021/4/302021/4/304/30/2021
等边三角形的各个内角都等于60°.
思考:
等腰三角形的底角可以是直 角或钝角吗?为什么?
(不能,因为等腰三角形两底角相等,若底角 是直角或钝角,则三角形的内角和大于180°.)
试一试
1.等腰三角形一个底角为75°,它
的另外两个角为7__5_°__,_3_0.°
⒉等腰三角形一个角为70°,它的
浙教版八年级数学上册课件:2.3 等腰三角形的性质定理(一) (共11张PPT)

初中数学
【解析】 (1)AF=BD.证明如下: ∵△ ABC 是等边三角形, ∴BC=AC,∠BCA=60°. 同理,CD=CF,∠DCF=60°. ∴∠BCA-∠DCA=∠DCF-∠DCA, 即∠BCD=∠ACF. 在△ BCD 和△ ACF 中,∵B∠CB=CADC=,∠ACF,
CD=CF, ∴△ BCD≌△ACF(SAS).∴BD=AF. (2)仍成立. 证明过程同(1)类似,证得△ BCD≌△ACF(SAS),则 BD=AF.
初中数学
(3)①AF+BF′=AB.证明如下: 由(1)知,△ BCD≌△ACF(SAS),则 BD=AF.
同理,△ BCF′≌△ACD(SAS),则 BF′=AD.
∴AF+BF′=BD+AD=AB. ②不成立,新的结论是 AF=AB+BF′.证明如下: 由(2)知,△ BCD≌△ACF(SAS),则 BD=AF.
AB=AC,
∴△ ABD≌△ACE(AAS). ∴BD=CE.
图 2-3-1
初中数学
反思
本题也可以证明△ ABE≌△ACD,得出 BE=CD,进一步 可得 BD=CE.
初中数学
【例 2】 (2015·丹东)如图 2-3-2,在△ ABC 中,AB=AC,
∠ABC=75°,E 为 BC 延长线上一点,∠ABC 与
同,猜想 AF 与 BD 在(1)中的结论是否仍成立.
初中数学
深入探究: (3)①如图 2-3-3③,当动点 D 在等边三角形 ABC 的边 BA 上运动时(点 D 与点 B 不重合),连
结 DC,以 DC 为边在 DC 上方、下方分别作等边三角形 DCF 和等边三角形 DCF′,连结 AF,BF′,探究 AF,BF′与 AB 的数量关系,并证明你探究的结论. ②如图 2-3-3④,当动点 D 在等边三角形 ABC 的边 BA 的延长线上运动时,其他作法与图③ 相同,①中的结论是否仍成立?若不成立,是否有新的结论?并证明你提出的结论.
【解析】 (1)AF=BD.证明如下: ∵△ ABC 是等边三角形, ∴BC=AC,∠BCA=60°. 同理,CD=CF,∠DCF=60°. ∴∠BCA-∠DCA=∠DCF-∠DCA, 即∠BCD=∠ACF. 在△ BCD 和△ ACF 中,∵B∠CB=CADC=,∠ACF,
CD=CF, ∴△ BCD≌△ACF(SAS).∴BD=AF. (2)仍成立. 证明过程同(1)类似,证得△ BCD≌△ACF(SAS),则 BD=AF.
初中数学
(3)①AF+BF′=AB.证明如下: 由(1)知,△ BCD≌△ACF(SAS),则 BD=AF.
同理,△ BCF′≌△ACD(SAS),则 BF′=AD.
∴AF+BF′=BD+AD=AB. ②不成立,新的结论是 AF=AB+BF′.证明如下: 由(2)知,△ BCD≌△ACF(SAS),则 BD=AF.
AB=AC,
∴△ ABD≌△ACE(AAS). ∴BD=CE.
图 2-3-1
初中数学
反思
本题也可以证明△ ABE≌△ACD,得出 BE=CD,进一步 可得 BD=CE.
初中数学
【例 2】 (2015·丹东)如图 2-3-2,在△ ABC 中,AB=AC,
∠ABC=75°,E 为 BC 延长线上一点,∠ABC 与
同,猜想 AF 与 BD 在(1)中的结论是否仍成立.
初中数学
深入探究: (3)①如图 2-3-3③,当动点 D 在等边三角形 ABC 的边 BA 上运动时(点 D 与点 B 不重合),连
结 DC,以 DC 为边在 DC 上方、下方分别作等边三角形 DCF 和等边三角形 DCF′,连结 AF,BF′,探究 AF,BF′与 AB 的数量关系,并证明你探究的结论. ②如图 2-3-3④,当动点 D 在等边三角形 ABC 的边 BA 的延长线上运动时,其他作法与图③ 相同,①中的结论是否仍成立?若不成立,是否有新的结论?并证明你提出的结论.
等腰三角形性质1课件(浙教版)
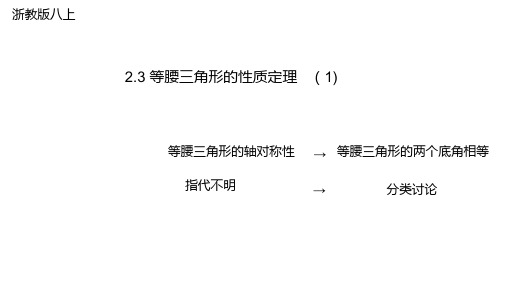
= (已知)
∠ = ∠(已证)
∴ △ABD≌△ACE(ASA)
∴ BD=CE(全等三角形的对应边相等)
C
归纳总结:
1.等腰三角形的性质定理1
定理:等腰三角形的两个底角相等,也就是说,在同一个三角形
中,等边对等角.
2.等边三角形的性质
定理:等边三角形的各个内角都等于600.
说明:等边三角形的特殊性质主要指:三个内角都相等,三条边都
E
B
D
C
4. 求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.
法1:
求证:BD=CE
A
证明:∵ AB=AC(已知)
∴ ∠ABC=∠ACB(等腰三角形的两个底角相等)
E
∵ BD,CE分别是∠ABC和∠ACB的平分线
∴ ∠CBD=
1
1
∠ABC, ∠BCE= ∠ACB
证明一:作顶角的平分线A D.
证明二:作底边上的中线AD
B
D
C
证明三:作底边上的高AD.(待以后证明)
方法一:作顶角的平分线
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
证明:作顶角的平分线AD,则∠1=∠2
在△BAD和△CAD中
B
.
= ( 已知 )
൞ ∠ = ∠ ( 已作 )
2
2
∴ ∠CBD=∠BCE
B
∠ = ∠(已证)
在△BCE和△CBD中
൞ = (公共边)
∠ = ∠(已证)
∴ △BCE≌△CBD(ASA)
∴ BD=CE(全等三角形的对应边相等)
D
∠ = ∠(已证)
∴ △ABD≌△ACE(ASA)
∴ BD=CE(全等三角形的对应边相等)
C
归纳总结:
1.等腰三角形的性质定理1
定理:等腰三角形的两个底角相等,也就是说,在同一个三角形
中,等边对等角.
2.等边三角形的性质
定理:等边三角形的各个内角都等于600.
说明:等边三角形的特殊性质主要指:三个内角都相等,三条边都
E
B
D
C
4. 求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.
法1:
求证:BD=CE
A
证明:∵ AB=AC(已知)
∴ ∠ABC=∠ACB(等腰三角形的两个底角相等)
E
∵ BD,CE分别是∠ABC和∠ACB的平分线
∴ ∠CBD=
1
1
∠ABC, ∠BCE= ∠ACB
证明一:作顶角的平分线A D.
证明二:作底边上的中线AD
B
D
C
证明三:作底边上的高AD.(待以后证明)
方法一:作顶角的平分线
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
证明:作顶角的平分线AD,则∠1=∠2
在△BAD和△CAD中
B
.
= ( 已知 )
൞ ∠ = ∠ ( 已作 )
2
2
∴ ∠CBD=∠BCE
B
∠ = ∠(已证)
在△BCE和△CBD中
൞ = (公共边)
∠ = ∠(已证)
∴ △BCE≌△CBD(ASA)
∴ BD=CE(全等三角形的对应边相等)
D
八年级数学浙教版上册课件:2.3 等腰三角形的性质定理 (共15张PPT)

CB
C
等腰三角形 两腰上的中线
_相__等__
等腰三角形 两底角的平分线
相等吗?
若∠A=40度,则∠BOC=?
D E
B
C
等腰三角形 两腰上的高线呢 ?
在△ABC中,若AD=AE,∠1--- 两边相等
②从角看---------- 两个底角相等
2.3等腰三角形的 性质定理
回顾旧知
(1)有__两__边__相__等__的三角形 叫做等腰三角形
A
(2) 底边和腰相等的等腰三角形
是____等__边____三角形?
腰
顶 角
腰
(3)从图形的对称性来说, 等腰三角形是___轴__对__称___图形,
它的对称轴是
B 底角 底角 C
_顶__角__平__分__线__所__在__的__直___线__。___
底边
探究新知 “等腰三角形的两个底角相等”
已知:在△ABC中,AB=AC 求证: ∠ C =∠ B A
B
C
已知:如图,∆ABC中, AB=AC 求证:∠C=∠B
证明:作底边BC上的中线AD
则BD=CD 在∆ABD 和 ∆ACD中
∵ AB=AC (已知)
B
AD=AD (公共边)
BD=CD
A DC
∴∆∴A∠BBD=≌∠C∆AC(D 全等三角形(SSS)
A
∴∠1 = ∠A ∠ 2= ∠C
(?)
∵AB=AC
∴ ∠ ABC= ∠C (?)
1 3 B
F 2
设∠A=x,则∠1=x
∴∠2=∠1+ ∠A=2x
∠C=∠ABC=2x ∠3=2 x-x=x
C ∵∠3+ ∠ 2+∠C =180° ∴x+2x+2x=180°
《等腰三角形的性质定理》PPT课件 (公开课获奖)2022年浙教版 (4)

运用已学的知识 ,根据以下问题中的条件 ,分别列出
方程:
1、一件衣服按 8 折销售的售价为72元,这件衣服的原价是多
少元? 设这件衣服的原价为x元,可列出方程
_0__.8_x____7_2_;
2、物体在水下 ,水深每增加米承受的压力就会增加1个大气压.
当 "蛟龙〞号下潜至||3500米时 ,它承受的压力约为340个
明各投进多少个
2x 12 14
设第|一次射击的成绩为x个 , 可列方程为3
0.8x72
观察你所列的方程 ,这些方
340 1 x500 10.33
程之间有什么共同的特点
★方程两边都是整式;
?
2x 12 14 3
★方程中只含有一个未知数; ★未知数的指数是一次 .
方程的两边都是整式,只含 有一个未知数,并且未知数 的指数是一次,这样的方程 叫做 一元一次方程 。
宋元时期 ,中|国数学家创立了 "天元术〞 ,用天元 表示未知数进而建立方程.这种方法的代表作是数学 家李冶写的<测圆海镜>书中所说的 "立天元一〞相当 于现在的 "设未知数x〞.
清代数学家李善兰翻译外国数学著作时 ,开始将 equation一词译为 "方程〞 ,至||今一直这样沿用.
在小学我们已经学过,方程是指含有未知数的等式.
BD
C
〔3〕∵AB =AC ,AD是角平分线 ,
∴____⊥____ ,____ =____.
试一试
1、 ,如图 ,在△ABC中 ,AB =AC ,
(1)假设AD是BC边上的中线 ,那么∠AD9C0
=______;
4cm °
(2)假设AD⊥BC ,BD =2cm ,那么BC 2、=等_腰__△__D_E__F.中DE =DF,DM是EF边的中
《等腰三角形的性质定理》PPT课件 (公开课获奖)2022年浙教版 (5)

13、某人到瓷砖商店去购置一种多边形形状的瓷砖,用
来铺设无缝地板.他购置的瓷砖形状不可以是〔 C 〕
〔A〕正三角形 〔B〕正四边形 〔C〕正八边形 〔D〕正六边形
14、平行四边形一边长为12cm,那么它的两条
对角线的长度可能是〔 C 〕.
〔A〕8cm和14cm 〔B〕10cm和14cm 〔C〕18cm和20cm 〔D〕10cm和34cm
4、如图,在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交 AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是
(B )
5、已知
ABCD中,E,F是对角线AC上的两
点,且AE=CF,
求证:四边形BEDF是平行四边形.
6.已知
ABCD中,E,F分别是AD,BC
的中点.
求证:MN∥BC,且MN= 1 BC
B
c
2.:线段a、b,∠1.求作一个平行四边形ABCD, 使AB=a,BC=b, ∠B= ∠1.
a
b
1
3、如图,在 ▱ABCD中,两条对角线相交于点O, E、F、G、H分别是AO、BO、CO、DO的中点, 以图中的点为顶点,尽可能多地画出平行四边形。
A
D
E
H
F
O
G
C B
探索提高
我们知道,三角形的三条中线交于一点.这一点 叫做三角形的重心.
O点作直线EF分别交BC、AD于E、F.
(1)求证:BE=DF.
(2)若AC、EF
ABCD分成的四部分的面积相等,指
出E点的位置,并说明理由.
【例2】
ABCD的周长为30cm,AE⊥BC于E
点,AF⊥CD于F点,且AE∶AF=2∶3,∠C=120°,求S
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图,在△ABC中,AB=AC,∠ACD=100°,
则∠A= 200 。
2.已知:如图,在△ABC中,AB=AC, P为BC的中点,D、E分别为AB、AC上 的点,且AD=AE.求证:PD=PE
8
完成书中作业题1、2、3、4、5
9
10
1.作业本、课本作业题A组. (B组选做) 2.课外探究题:
1
在等腰三角形ABC中,AB=AC,AD平分∠BAC,交BC于D.
(1)若将△ABD作关于直线AD折叠,所得的像是什么?
所得的像是△ACD
(2)找出图中的全等三角形以及所有 相等的角.
A
△ABD≌△ACD
相等的角: ∠B=∠C,∠BAD=∠CAD, ∠ADB=∠ADC.
B
C
D
2
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C
启发:1、求证图形中的两个角相等,
A
前面用的较多的是什么方法?
2、为使要证明相等的两个角∠B和∠C位
于能证明全等的两个三角形中,你会怎
么添辅助线? 3、△ABD和△ACD具备那些边角对应的 相等的条件?它们全等吗?
BDC
可以说成 “在同一个三角形中,等边对等角”
3
你能举反例说明不在同一个 三角形中不具备等边对等角 的反例吗?
⒊等腰三角形一个角为110°,它的 另外两个角为_3_5_°__,3_5°
12
变式练习3:等腰三角形一个角为110°,A 它的另外两个角为_3_5_°__,3_5°
B C
6Hale Waihona Puke 例2:求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD,CE是 A
△ABC的两条角平分线。 求证:BD=CE.
ED
B
C
归纳:等腰三角形两腰上的中线、高
线、两底角的平分线相等
7
反例:如图, AC=CD,但 ∠ABC≠∠DBC
AD
B
C
4
例1、求等边三角形ABC三个内角的度数.
A
B
C
“等腰三角形的两个底角相等”的推论:
推论:等边三角形的各个内角都 等于60°
5
变式练习1:已知:在△ABC中,AB = AC, ∠AB = 80°, 求∠AB 和 ∠C的度数。
变式练习2:已知:等腰三角形的一个 内角为 80 °, 求另两个角的度数.
等腰三角形的性质在生产、生活中有着 广泛应用。以小组为单位, 对此进行研究, 写成研究报告,于下周一上交评比。
11
试一试
1.等腰三角形一个底角为75°,它
的另外两个角为_7_5_°__,_3_0°
⒉等腰三角形一个角为70°,它的
另外两个角为_7_0_°__,_4_0_°__或__5_5_°__,5_5_°
