Logistic映射是一维离散混沌系统

基于Simulink可视化混沌模型的研究

基于Simulink可视化混沌模型的研究
混沌模型是目前非线性科学研究的重点之一，其表现出的随机性、确定性和极度敏感性使其在信息加密、通信技术、生态学、金融、天气预报等领域得到了广泛应用。

本文基于Simulink平台，探讨了几种常用的混沌模型，并进行了可视化仿真研究。

首先，本文介绍了三个经典的混沌模型：Logistic映射、Henon映射和Lorenz系统，分别介绍了其数学表达式和特征。

Logistic映射是一维非线性映射，其具有周期倍增的特征，可以用来生成随机数序列；Henon映射是二维非线性映射，其表现出的奇特轨迹使其被广泛应用于图像加密、压缩等领域；Lorenz系统是三维非线性动力学系统，其奇妙的漩涡结构与天气系统之间的联系被广泛研究。

接着，本文用Simulink实现了以上三个混沌模型，并进行了仿真分析。

通过对Logistic映射的仿真结果分析，可以看出当初始值接近3.57时，其混沌性质最为明显，即使微小的改变也能导致结果的不可预测性。

通过对Henon映射的仿真结果分析，可以看出其二维奇特的轨迹，进一步证实了其在图像加密、压缩等领域的应用价值。

通过对Lorenz系统的仿真结果分析，可以看出其漩涡结构的特征，说明其在天气预报、气候学等领域的重要性。

最后，通过对以上仿真结果的分析，证明了Simulink平台在混沌模型的研究中的优越性，其可视化的特点使得模型的仿真分析更加生动、直观。

在未来的研究中，可以通过优化模型参数，进一步探讨混沌模型的特性，应用于更多的领域。

4种混沌映射的特点

4种混沌映射的特点
混沌映射是一种重要的非线性动力学系统，具有复杂的动力学特性，已经被广泛应用于许多领域。

本文介绍了四种常见的混沌映射及其特点。

1. Logistic映射
Logistic映射是一种广泛应用于混沌理论研究中的典型非线性动力学系统。

它的特点是简单易行，具有双稳态和混沌行为，是研究混沌现象的经典示例。

2. Henon映射
Henon映射是一种双参数混沌映射，它的特点是具有分形结构、非周期性、高度敏感依赖于初值和参数，并且在参数空间中形成了复杂的混沌吸引子。

3. Lorenz映射
Lorenz映射是一种具有吸引子的三维非线性动力学系统，它的特点是具有强的混沌行为和灵敏的初始条件依赖性，常被用于模拟大气和海洋中的流体运动。

4. Ikeda映射
Ikeda映射是一种典型的非线性动力学系统，它的特点是具有高度敏感的初值和参数、分形结构和复杂的混沌吸引子，常被用于研究光学系统中的非线性动力学现象。

以上是四种典型的混沌映射及其特点。

混沌映射在科学研究、信息加密、密码学、图像处理等领域有着广泛的应用价值，未来将会有
更多的研究和应用。

逻辑斯谛(Logistic)映射

§4 从倍周期分定走向混沌4-1 逻辑斯谛（Logistic ）映射我们将以一个非常简单的数学模型来加以说明从倍周期分定走向混沌现象。

该模型称为有限环境中无世代交替昆虫生息繁衍模型。

若昆虫不加以条件控制，每年增加λ倍，我们将一年作为一代，把第几代的虫日记为，则有：i N o i i i N N N 11++==λλ (4-1)i N ,1>λ增长很快，发生“虫口爆炸”，但虫口太多则会由于争夺有限食物和生存空间，以及由于接触传染导致疾病曼延，使虫口数目减少，它正比于，假定虫口环境允许的最大虫口为，并令2i N o N oii N N x =，则该模型由一个迭代方程表示： 21i i i N N N λλ−=+即为：)1(1i i i x x x −=+λ （4-2）其中：]4,0[],1,0[∈∈λi x 。

（4-2）式就是有名的逻辑斯谛映射。

4-2 倍周期分歧走向混沌借助于对这一非线性迭代方程进行迭代计算，我们可以清楚地看到非线性系统通过倍周期分岔进入混沌状态的途径。

（一）迭代过程迭代过程可以用图解来表示。

图4-1中的水平轴表示，竖直轴表示，抛物线表示（4-2）式右端的迭代函数。

45º线表示n x 1+n x n n x x =+1的关系。

由水平轴上的初始点作竖直线，找到与抛物线的交点，A 的纵坐标就是。

由点)0,(0x R ),(10x x A 1x),(10x x A 作水平直线，求它与45º线的交点，经B 点再作竖直线，求得与抛物线的交点，这样就得到了。

仿此做法可得到所迭代点。

),(11x x B ),(21x x 2x 从任何初始值出发迭代时，一般有个暂态过程。

但我们关心的不是暂态过程，而是这所趋向的终态集。

终态集的情况与控制参数λ有很大关系。

增加λ值就意味着增加系统的非线性的程度。

改变λ值，不仅仅改变了终态的量，而且也改变了终态的质。

它所影响的不仅仅是终态所包含的定态的个数和大小，而且也影响到终态究竟会不会达到稳定。

logistic混沌加密原理

logistic混沌加密原理Logistic混沌加密原理是一种基于混沌理论的加密算法，它利用混沌系统的不可预测性和复杂性来保护数据的安全性。

Logistic混沌加密原理的基本思想是通过对明文进行混沌变换，使其变得随机和不可预测，从而达到加密的目的。

Logistic混沌加密原理的核心是Logistic映射函数，它是一种非线性的动态系统，可以产生复杂的混沌序列。

Logistic映射函数的公式为：Xn+1 = r * Xn * (1 - Xn)其中，Xn表示第n次迭代的结果，r是一个常数，通常取值在3.57到4之间。

通过不断迭代，Logistic映射函数可以产生一个随机的、不可预测的序列，这个序列被称为Logistic混沌序列。

Logistic混沌加密原理的加密过程如下：1. 初始化：选择一个初始值X0和一个密钥K，将X0作为明文的一部分，K作为加密密钥。

2. 生成密钥流：使用Logistic映射函数生成一个随机的、不可预测的密钥流，将其与明文进行异或运算，得到密文。

3. 解密：使用相同的初始值X0和密钥K，使用Logistic映射函数生成相同的密钥流，将其与密文进行异或运算，得到明文。

Logistic混沌加密原理具有以下优点：1. 安全性高：Logistic混沌序列具有随机性和不可预测性，使得攻击者无法破解密文。

2. 速度快：Logistic混沌加密算法的加密和解密速度都很快，适用于实时加密和解密。

3. 灵活性强：Logistic混沌加密算法可以根据需要选择不同的参数，以适应不同的加密需求。

4. 实现简单：Logistic混沌加密算法的实现非常简单，只需要进行一些基本的数学运算即可。

总之，Logistic混沌加密原理是一种非常有效的加密算法，它利用混沌系统的不可预测性和复杂性来保护数据的安全性。

在实际应用中，Logistic混沌加密算法可以用于保护敏感数据的安全，例如网络通信、金融交易等领域。

logistic映射混沌加密算法

logistic映射混沌加密算法混沌理论是一种非线性动力学系统的研究方法，其核心思想是通过微小的初始条件差异引起系统的巨大变化，表现出复杂、随机且不可预测的行为。

混沌理论在信息安全领域具有重要的应用，其中logistic映射混沌加密算法是一种常用的加密方法。

logistic映射是一种简单而有效的动力学系统，其公式为Xn+1 = r*Xn*(1-Xn)，其中Xn表示第n个时间点的状态值，r为控制参数，通常取值在0到4之间。

通过迭代计算，logistic映射可以产生一系列的状态值，这些值呈现出混沌的特性。

logistic映射混沌加密算法的基本思想是将待加密的数据与logistic映射的状态值进行异或运算，以增加数据的随机性和不可预测性。

具体加密过程如下：1. 初始化：设置初始状态X0和控制参数r的值，选择合适的初始状态和控制参数是保证加密效果的关键。

2. 生成密钥流：通过迭代计算logistic映射的状态值，得到一系列的随机数作为密钥流。

密钥流的长度取决于需要加密的数据长度。

3. 加密：将待加密的数据与密钥流进行异或运算，生成密文。

异或运算的特点是相同位上的数字相同则结果为0，不同则结果为1，这样可以实现简单而高效的加密过程。

4. 解密：使用相同的初始状态和控制参数，再次生成密钥流，将密文与密钥流进行异或运算，得到原始数据。

logistic映射混沌加密算法具有以下特点：1. 高度随机性：由于logistic映射本身的混沌性质，生成的密钥流具有高度随机性，使得加密后的数据无法被破解。

2. 非线性变换：logistic映射混沌加密算法采用非线性的异或运算，使得加密后的数据与原始数据之间的关系变得非常复杂，增加了破解的难度。

3. 实时性：logistic映射混沌加密算法具有较高的加密速度，适用于对大量数据进行实时加密和解密的场景。

4. 简单性：logistic映射混沌加密算法的实现较为简单，只需要进行简单的数学运算，不需要复杂的计算和存储。

混沌系统分类

混沌系统分类混沌系统是指那些看似无序、无规律、复杂且难以被完全预测的系统。

混沌系统在自然界和人工系统中都有广泛的应用，如气象学、生物学、经济学、物理学等领域。

根据混沌系统的特征和行为，可以将其分为以下几类：1. 离散映射混沌系统离散映射混沌系统是指在离散时间步中，系统状态通过一个离散映射进行更新。

这类系统中最著名的是Logistic映射，其表达式为：x_n+1 = r*x_n*(1-x_n)，其中x_n为系统在第n个时间步的状态，r 为常数。

这个映射可以产生极其复杂的行为，如周期倍增、途中混沌、周期混沌等。

2. 连续系统混沌系统连续系统混沌系统是指系统的状态是连续的，并且通过微分方程系统进行更新。

这类系统中最著名的是Lorenz系统，它可用下列方程组描述：dx/dt = σ(y-x), dy/dt = x(ρ-z)-y, dz/dt = xy-βz，其中x、y、z分别表示系统的三个状态，σ、ρ、β为参数。

该系统表现出极其复杂的行为，如奇异吸引子、周期倍增等。

3. 分数阶混沌系统分数阶混沌系统是指系统的微分方程中含有分数阶导数，这类系统的行为更加复杂。

比如，分数阶Lorenz系统的方程为：_C^0D_t^αx(t) = σ(y-x), _C^0D_t^αy(t) = x(ρ-z)-y, _C^0D_t^αz(t) = xy-βz，其中_C^0D_t^α表示Caputo分数阶导数，α为分数阶指数。

该系统表现出的行为更加丰富，如多重奇异吸引子、混沌吸引子等。

4. 拓扑混沌系统拓扑混沌系统是指系统的结构可以用拓扑学的方法来描述，比如网络拓扑结构。

这类系统中最著名的是Chua电路，它可用下列方程描述：C(dVc/dt) = g(Vb-Vc) - I_1, L(di/dt) = Vc-Va, C(dVb/dt) = g(Vc-Vb) + g(Va-Vb), L(di_1/dt) = Vb-Va-Ri_1，其中Va、Vb、Vc、i、i_1为电路的状态变量，C、L、R、g分别表示电容、电感、电阻和非线性电感。

Logistic映射的混沌行为

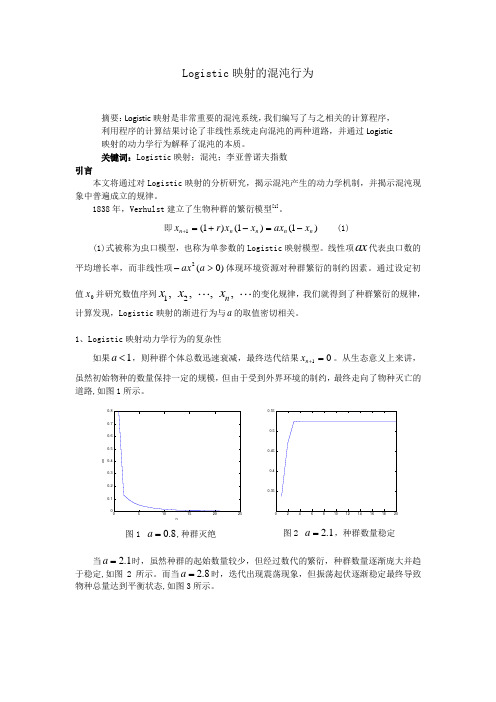
Logistic 映射的混沌行为摘要：Logistic 映射是非常重要的混沌系统，我们编写了与之相关的计算程序，利用程序的计算结果讨论了非线性系统走向混沌的两种道路，并通过Logistic映射的动力学行为解释了混沌的本质。

关键词：Logistic 映射；混沌；李亚普诺夫指数引言本文将通过对Logistic 映射的分析研究，揭示混沌产生的动力学机制，并揭示混沌现象中普遍成立的规律。

1838年，Verhulst 建立了生物种群的繁衍模型[1]。

即)1()1()1(1n n n n n x ax x x r x -=-+=+ (1)(1)式被称为虫口模型，也称为单参数的Logistic 映射模型。

线性项ax 代表虫口数的平均增长率，而非线性项)0(2>-a ax 体现环境资源对种群繁衍的制约因素。

通过设定初值0x 并研究数值序列12,,,,n x x x 的变化规律，我们就得到了种群繁衍的规律，计算发现，Logistic 映射的渐进行为与a 的取值密切相关。

1、Logistic 映射动力学行为的复杂性如果1<a ，则种群个体总数迅速衰减，最终迭代结果01=+n x 。

从生态意义上来讲，虽然初始物种的数量保持一定的规模，但由于受到外界环境的制约，最终走向了物种灭亡的道路,如图1所示。

n x n当1.2=a 时，虽然种群的起始数量较少，但经过数代的繁衍，种群数量逐渐庞大并趋于稳定,如图2所示。

而当8.2=a 时，迭代出现震荡现象，但振荡起伏逐渐稳定最终导致物种总量达到平衡状态,如图3所示。

图1 ,种群灭绝 8.0=a 图2 ，种群数量稳定 1.2=a图3 8.2=a ，种群数量稳定图4 ，种群数量出现周期二行为当3>a 时，Logistic 映射开始出现周期振荡现象，当1.3=a 时，迭代结果在两个值之间交替出现，意味着物种繁衍出现了大小年情况，此时，Logistic 映射进入周期二轨道, 如图4所示。

circle混沌映射公式

circle混沌映射公式摘要：1.混沌映射公式的背景与意义2.混沌映射公式的定义与表达3.混沌映射公式的应用与实例4.混沌映射公式的局限性与未来发展正文：【1.混沌映射公式的背景与意义】混沌映射公式，又称为Logistic 映射，是一种描述混沌现象的数学公式。

混沌现象，即系统的演化过程中呈现出极度复杂的变化，是一种介于确定性与随机性之间的状态。

混沌映射公式以其简单易懂的表达形式，展示了混沌现象的丰富内涵，从而在数学、物理、生物等多个领域引起了广泛关注。

【2.混沌映射公式的定义与表达】混沌映射公式的定义为一个迭代函数，通常用符号f(x) 表示。

其表达式为：f(x) = λ * (1 - x^2)其中，λ为参数，x 为迭代变量。

通过对参数λ的调整，可以实现对混沌现象的控制。

当λ=0 时，映射公式变为洛伦兹系统，呈现周期性变化；而当λ≠0 时，系统表现出混沌现象，即无规则且极度复杂的变化。

【3.混沌映射公式的应用与实例】混沌映射公式在多个领域具有广泛的应用，例如：(1) 在气象学中，混沌映射公式可以用于描述大气环流的演变，从而预测天气变化；(2) 在生态学中，混沌映射公式可以用于描述种群数量的变化，从而揭示生态系统的动态规律；(3) 在经济学中，混沌映射公式可以用于描述经济系统的演化，从而预测市场变化。

【4.混沌映射公式的局限性与未来发展】尽管混沌映射公式在描述混沌现象方面具有较高的准确性，但它仍然存在一定的局限性。

例如，在实际应用中，映射公式的参数λ选取较为主观，不同的参数选取可能导致系统表现出不同的混沌现象。

因此，如何客观地选取参数λ，提高混沌映射公式的预测准确性，是未来研究的一个重要方向。

Logistic映射及其混沌序列特性分析_曹书豪 (1)

１）当μ ∈ （０，１）时，系统稳定于ｘ＝０；２）当μ∈［１，３］时，系统有两个稳定点ｘ＝０或ｘ＝１－１；
μ ３）当μ ∈ （３，３．４４９）时，系统存在两个周期
点ｘ
＝１＋μ±
槡（μ＋１）（μ－３）；
２μ
４）当μ∈（３．４４９，３．５４４）时，系统存在４个周
期点；
［３］范九伦，张雪锋．分段Ｌｏｇｉｓｔｉｃ混沌映射及其性能分析［Ｊ］．电子学报，２００９，３７（４）：７２０－７２５．
［４］邱跃洪，何晨，诸鸿文．一种无限折叠混沌映射及其量化序列［Ｊ］．上海交通大学学报，２００２，３６（１２）：
经过多次分岔后，当参数μ ＞３．５７０时，系统进入混沌状态．
２Ｌｏｇｉｓｔｉｃ映射混沌序列
分岔图能从总体上反映系统的倍周期运动过程．根据倍周期分岔定理，以参数μ 为横坐标、迭代函数值为纵坐标，由（１）式可得到处于不同参数区间的Ｌｏｇｉｓｔｉｃ映射分岔图．
第２期
曹书豪，等：Ｌｏｇｉｓｔｉｃ映射及其混沌序列特性分析
１３５
在给定参数 μ 以及系统初值ｘ０的情况下，通过对（１）式的迭代计算可以获得任意长度的
Ｌｏｇｉｓｔｉｃ序列．当参数μ 取不同值时，Ｌｏｇｉｓｔｉｃ映射经过多次迭代以后会出现以下情况：
Ｎ
Ｎ
∑ ∑ ａｋ
＝
１ｎ
ｉ＝１ｘｉｃｏｓπＮｉｊ，ｂｋ
＝
ｎ１ｉ＝１ｘｉｓｉｎπＮｉｊ．然后，

典型的混沌系统

典型的混沌系统 (1)1.1 一维混沌系统 (1)§1.1.1 Logistic 映射 (1)§1.1.2 Chebyshev 映射 (2)§1.1.3 Logistic 映射与Chebyshev 映射 (3)§1.1.4 概率密度函数PDF 的作用 (3)1.2二维混沌系统(≠超混沌系统) (3)§1.2.1 Henon 映射 (4)典型的混沌系统混沌现象是在非线性动力系统中表现的确定性、类随机的过程，这种过程既非周期又不收敛，并且对于初始值具有敏感的依赖性。

按照动力学系统的性质，混沌可以分成四种类型：➢ 时间混沌；➢ 空间混沌；➢ 时空混沌；➢ 功能混沌；1.1 一维混沌系统一个一维离散时间非线性动力学系统定义如下：)(1k k x x τ=+其中，x k ∈V ， k=0,1,2,3…，我们称之为状态。

而τ: V →V 是一个映射，将当前状态xk 映射到下一个状态xk+1。

如果我们从一个初始值x0 开始，反复应用 τ ，就得到一个序列{ xk ; k=0,1,2,3…..}。

这一序列称为该离散时间动力系统的一条轨迹。

原始的虫口模型方程是（37文）：k k ax x =+1体现了两代虫子的数量关系。

将此方程推导一下，可以得到如下方程：0x a x k k =可以得到第n 代虫子和第0代虫子的数量关系。

但是，从中不能表现自然的虫子变换关系，因为虫子的增长变化不是恒定的（考虑到很多负面影响，如虫子太多时，由于食物有限和生存空间有限，还由于疾病等多种原因，使得虫口数量减少），所以这个线性模型完全不能反映虫口的变化规律。

§1.1.1 Logistic 映射一类非常简单却被广泛研究的动力系统是logistic 映射，它起源于虫口模型。

其定义有多种形式。

1．形式一)1(1k k k x x x -=+μ其中，混沌域为(0,1)，0 ≤ μ ≤ 4 称为分枝参数，x k ∈(0,1)。

基于混沌系统的加密算法研究与实现

基于混沌系统的加密算法研究与实现加密技术在当今互联网时代已成为不可缺少的一部分，保障了个人信息的安全性。

随着网络安全的不断提升，传统加密算法已经逐渐暴露出安全性不足的问题，为此，人们提出了基于混沌系统的加密算法，以应对日益复杂的网络安全环境。

一、混沌系统简介混沌系统是一种复杂的动力学系统，其演化过程具有随机性、敏感性和不可预测性的特征。

混沌系统的数学模型主要包括Lorenz方程、Henon映射等。

在物理、天文、生物学、经济学等领域，混沌理论已经成为一种重要的工具。

二、基于混沌系统的加密算法基于混沌系统的加密算法主要分为两种方式，一种是混沌加密，另一种是加密混沌。

1.混沌加密混沌加密是将混沌理论应用于加密算法中，通过混沌系统产生的随机数序列来改变明文的内容，从而实现安全的加密算法。

其中，主要包括Arnold映射、Logistic映射、Henon映射等。

Arnold映射是一种离散的二维混沌映射，其具有高度的敏感性和随机性。

在Arnold映射算法中，通过使用Arnold映射的逆映射来加密明文，并通过Arnold映射的正向映射来解密密文，从而使得加密过程具有高度的安全性。

Arnold映射加密算法可以广泛应用于网络传输、电子商务等领域。

Logistic映射是一种典型的一维混沌映射，其演化过程具有高度的不可预测性。

在Logistic映射加密算法中，通过Logistic映射产生的随机数序列来改变原始明文，从而得到加密后的密文。

与Arnold映射加密算法不同，Logistic映射加密算法采用的是一维映射，因此在实际应用中的安全性相对较低。

Henon映射是一种强混沌映射，具有高度的随机性和敏感性。

在Henon映射加密算法中，通过使用Henon映射来改变明文的内容，从而得到加密后的密文。

Henon映射加密算法在网络通信、数码加密、数字水印等领域均有广泛的应用。

2.加密混沌加密混沌是将加密算法应用于混沌系统中，通过混沌系统的演化过程来产生随机数序列，从而实现安全的加密算法。

逻辑斯谛（Logistic）映射

逻辑斯谛（Logistic）映射§4 从倍周期分定⾛向混沌4-1 逻辑斯谛（Logistic ）映射我们将以⼀个⾮常简单的数学模型来加以说明从倍周期分定⾛向混沌现象。

该模型称为有限环境中⽆世代交替昆⾍⽣息繁衍模型。

若昆⾍不加以条件控制，每年增加λ倍，我们将⼀年作为⼀代，把第⼏代的⾍⽇记为，则有：i N o i i i N N N 11++==λλ (4-1)i N ,1>λ增长很快，发⽣“⾍⼝爆炸”，但⾍⼝太多则会由于争夺有限⾷物和⽣存空间，以及由于接触传染导致疾病曼延，使⾍⼝数⽬减少，它正⽐于，假定⾍⼝环境允许的最⼤⾍⼝为，并令2i N o N oii N N x =，则该模型由⼀个迭代⽅程表⽰： 21i i i N N N λλ?=+即为：)1(1i i i x x x ?=+λ（4-2）其中：]4,0[],1,0[∈∈λi x 。

（4-2）式就是有名的逻辑斯谛映射。

4-2 倍周期分歧⾛向混沌借助于对这⼀⾮线性迭代⽅程进⾏迭代计算，我们可以清楚地看到⾮线性系统通过倍周期分岔进⼊混沌状态的途径。

（⼀）迭代过程迭代过程可以⽤图解来表⽰。

图4-1中的⽔平轴表⽰，竖直轴表⽰，抛物线表⽰（4-2）式右端的迭代函数。

45o线表⽰n x 1+n x n n x x =+1的关系。

由⽔平轴上的初始点作竖直线，找到与抛物线的交点，A 的纵坐标就是。

由点)0,(0x R ),(10x x A 1x),(10x x A 作⽔平直线，求它与45o线的交点，经B 点再作竖直线，求得与抛物线的交点，这样就得到了。

仿此做法可得到所迭代点。

),(11x x B ),(21x x 2x 从任何初始值出发迭代时，⼀般有个暂态过程。

但我们关⼼的不是暂态过程，⽽是这所趋向的终态集。

终态集的情况与控制参数λ有很⼤关系。

增加λ值就意味着增加系统的⾮线性的程度。

改变λ值，不仅仅改变了终态的量，⽽且也改变了终态的质。

它所影响的不仅仅是终态所包含的定态的个数和⼤⼩，⽽且也影响到终态究竟会不会达到稳定。

logistic-tent 混沌映射原理

logistic-tent 混沌映射原理logistic-tent混沌映射原理混沌理论是一种描述复杂系统行为的数学工具，它揭示了系统的非线性特性和灵敏依赖于初始条件的性质。

在混沌理论中，logistic-tent混沌映射是一种常见的混沌映射模型，它具有简单的结构和复杂的动力学行为，被广泛应用于各个领域。

logistic-tent混沌映射模型由比萨诺大学的数学家May等人于1976年提出，其形式为：Xn+1 = r * Xn * (1 - Xn)其中，Xn表示第n次迭代后的状态，r为控制参数，取值范围为0到1之间。

通过不同的初始条件和参数设置，logistic-tent混沌映射可以呈现出丰富的动力学行为，包括周期轨道、混沌轨道和分岔现象等。

logistic-tent混沌映射模型的动力学行为丰富多样，其中最为常见的是周期轨道。

当参数r取值在0到1之间时，系统的状态会收敛到一个周期轨道上，该轨道周期为2的n次幂。

通过改变参数r 的值，我们可以观察到周期轨道的数量和长度发生变化，系统呈现出不同的稳定性和周期性。

logistic-tent混沌映射模型还可以呈现出混沌轨道。

当参数r取值在1到3之间时，系统的状态表现出非周期性的、混沌的行为。

这意味着系统的状态在长时间内呈现出无规律的变化，对初始条件的微小改变也会导致系统演化出完全不同的轨道。

混沌轨道的出现使得logistic-tent混沌映射模型具有了灵敏依赖于初始条件的特性，这也是混沌系统的一个重要特征。

logistic-tent混沌映射模型还可以呈现出分岔现象。

当参数r取值在3到4之间时，系统的状态会发生分岔现象，即系统从一个稳定的轨道突然分裂出多个周期轨道。

随着参数r的增大，分岔现象会越来越频繁，最终系统进入混沌状态。

logistic-tent混沌映射模型的应用广泛，特别是在密码学、通信和图像处理等领域。

在密码学中，混沌序列可以用于生成随机密钥，提高密码系统的安全性。

Logistic映射产生的混沌序列

Logistic映射产生的混沌序列作者：刘臣等来源：《卷宗》2014年第06期摘要：混沌理论是一门专门研究奇异函数、奇异图形的数学理论，是一门研究自然界有序、无序规律的学科。

混沌学被很多学者认为是二十世纪继相对论、量子力学之后，物理学发生的第三次大革命。

混沌学中的混沌是貌似无序的有序，紊乱中的规律。

混沌学的面世，标志着人类历史上又一次重大科学的进步，因为人们可以从更接近实际的角度去认识这个既无序又有序的世界。

混沌序列的产生有多种方法，常用的是Logistic映射和Chebyshev映射，本文采用的是Logistic映射的满映射。

关键字：混沌；logistic映射；序列1963年美国气象学家E.N.Lorenz提出了著名的“蝴蝶效应”，“蝴蝶效应”大意为：一只南美洲亚马逊河流域热带雨林中的蝴蝶，不经意间扇动几下翅膀，两周后可能就会在美国德克萨斯州引起一场龙卷风。

其原因在于：蝴蝶翅膀的运动，会导致其身边的空气系统发生变化，并会产生微弱的气流，而微弱气流的产生又会引起四周空气或其他系统产生相应的变化，由此引起一系列的连锁反映，最终可能会导致其他系统的极大变化。

这是他在研究大气时发现，当选取一定量的参数时，一个由确定三阶常微分方程组描述的大气对流模型变得不可预测。

经过长期反复的数值实验和理论思考， Lorenz从同一系统出现的一系列非周期无规则行为中发现了混沌运动，这为后来的混沌研究奠定了基础。

一般地，当一个接近实际而没有内在随机性的模型，仍然具有貌似随机的行为，我们就可以说这个真实物理系统是混沌的。

混沌系统具有三个关键要素：一是对初始条件的敏感依赖性，即蝴蝶效应；二是奇异吸引子，这里是非线性事件的发生点，它通过诱发系统的活力，使其变为非预设模式，从而产生了不可预测性；三是分形，它具有二个普通特征：自始至终都是不规则的以及在不同的尺度上，不规则程度却是一个常量，这同时也表明了有序和无序的统一。

混沌系统经常是自反馈系统，出来的东西回去之后，经过变换再出来，循环往复，任何初始值的微小变动都会按指数放大，因此会导致系统内在长期的不可预测性。

logistic映射混沌加密算法

logistic映射混沌加密算法Logistic映射混沌加密算法混沌加密算法是一种基于混沌理论的加密方法，它利用混沌系统的随机性和不可预测性来加密数据，使得加密后的数据具有高度的随机性和安全性。

其中，Logistic映射是混沌加密算法中的一种常用的混沌系统。

Logistic映射是由比利时数学家Robert May于1976年提出的，它是一种简单但非常有效的混沌系统。

Logistic映射的表达式为：Xn+1 = r * Xn * (1 - Xn)其中，Xn为当前时刻的状态变量，Xn+1为下一时刻的状态变量，r 为控制参数，用于调节系统的混沌程度。

在Logistic映射中，控制参数r的取值范围为[0,4]，当r小于3时，系统的状态趋于稳定，当r在3到4之间变化时，系统表现出混沌行为。

Logistic映射混沌加密算法的基本思想是将明文数据映射到Logistic映射的状态空间中，并根据映射结果进行加密。

具体的加密过程可以分为以下几个步骤：1. 初始化：选择一个适当的初始状态X0，确定控制参数r的值。

2. 映射阶段：将明文数据按照一定的规则映射到Logistic映射的状态空间中。

这个映射规则可以根据具体需求进行设计，常见的规则有根据明文数据的大小来选择映射的初始状态和控制参数的值。

3. 加密阶段：根据映射结果进行异或运算，将明文数据进行加密。

具体的加密算法可以根据需要进行设计，常见的算法有按位异或、模运算等。

4. 解密阶段：使用相同的初始状态和控制参数，将加密后的数据进行解密。

解密的过程与加密的过程相反，即先进行异或运算，然后根据映射结果进行反向映射，得到明文数据。

Logistic映射混沌加密算法具有以下特点：1. 高度随机性：Logistic映射具有高度的随机性和不可预测性，使得加密后的数据具有高度的随机性，难以破解。

2. 灵活性：通过调节控制参数r的值，可以控制系统的混沌程度，从而实现不同级别的加密需求。

Logistic混沌映射

Logistic混沌映射引言如果一个系统的演变过程对初始的状态十分敏感，就把这个系统称为是混沌系统。

在1972年12月29日，美国麻省理工教授、混沌学开创人之一E.N.洛仑兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文，提出一个貌似荒谬的论断：在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风，并由此提出了天气的不可准确预报性。

至此以后，人们对于混沌学研究的兴趣十分浓厚，今天，伴随着计算机等技术的飞速进步，混沌学已发展成为一门影响深远、发展迅速的前沿科学。

混沌来自于非线性动力系统，而动力系统又描述的是任意随时间变化的过程，这个过程是确定性的、类似随机的、非周期的、具有收敛性的，并且对于初始值有极敏感的依赖性。

而这些特性正符合序列密码的要求。

1989年Robert Matthews 在Logistic映射的变形基础上给出了用于加密的伪随机数序列生成函数，其后混沌密码学及混沌密码分析等便相继发展起来。

混沌流密码系统的设计主要采用以下几种混沌映射：一维Logistic映射、二维He’non映射、三维Lorenz映射、逐段线性混沌映射、逐段非线性混沌映射等，在本文中，我们主要探讨一维Logistic映射的一些特性。

Logistic映射分析一维Logistic映射从数学形式上来看是一个非常简单的混沌映射，早在20世纪50年代，有好几位生态学家就利用过这个简单的差分方程，来描述种群的变化。

此系统具有极其复杂的动力学行为，在保密通信领域的应用十分广泛，其数学表达公式如下：Xn+1=Xn×μ×(1-Xn) μ∈[0,4] X∈[0,1]其中μ∈[0,4]被称为Logistic参数。

研究表明，当X∈[0,1] 时，Logistic 映射工作处于混沌状态，也就是说，有初始条件X0在Logistic映射作用下产生的序列是非周期的、不收敛的，而在此范围之外，生成的序列必将收敛于某一个特定的值。

Logistic混沌映射

Logistic混沌映射引言如果一个系统的演变过程对初始的状态十分敏感，就把这个系统称为是混沌系统。

在1972年12月29日，美国麻省理工教授、混沌学开创人之一E.N.洛仑兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文，提出一个貌似荒谬的论断：在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风，并由此提出了天气的不可准确预报性。

至此以后，人们对于混沌学研究的兴趣十分浓厚，今天，伴随着计算机等技术的飞速进步，混沌学已发展成为一门影响深远、发展迅速的前沿科学。

混沌来自于非线性动力系统，而动力系统又描述的是任意随时间变化的过程，这个过程是确定性的、类似随机的、非周期的、具有收敛性的，并且对于初始值有极敏感的依赖性。

而这些特性正符合序列密码的要求。

1989年Robert Matthews 在Logistic映射的变形基础上给出了用于加密的伪随机数序列生成函数，其后混沌密码学及混沌密码分析等便相继发展起来。

混沌流密码系统的设计主要采用以下几种混沌映射：一维Logistic映射、二维He’non映射、三维Lorenz映射、逐段线性混沌映射、逐段非线性混沌映射等，在本文中，我们主要探讨一维Logistic映射的一些特性。

Logistic映射分析一维Logistic映射从数学形式上来看是一个非常简单的混沌映射，早在20世纪50年代，有好几位生态学家就利用过这个简单的差分方程，来描述种群的变化。

此系统具有极其复杂的动力学行为，在保密通信领域的应用十分广泛，其数学表达公式如下：Xn+1=Xn×μ×(1-Xn) μ∈[0,4] X∈[0,1]其中μ∈[0,4]被称为Logistic参数。

研究表明，当X∈[0,1] 时，Logistic 映射工作处于混沌状态，也就是说，有初始条件X0在Logistic映射作用下产生的序列是非周期的、不收敛的，而在此范围之外，生成的序列必将收敛于某一个特定的值。

复合混沌加密算法在电力系统信息安全中的应用

了时间的检验。
【关键词】算法；电力；信息安全
对于复合混沌加密算法而言，是一种较新的算法，但这种方法相较于其他的方法又有很多的优势。一般的算法在刚刚开发出来的时候，总是存在很多的漏洞，复合混沌加密算法却不是这样，复合混沌加密算法具有准确，详细，简单的优势，而且在实际的应用中，也展现出了优良的特点，在现阶段的研究中，正在不断的深化，专家对于复合混沌加密算法的前景也是比较看好的。对于复合混沌加密算法来说，任何一个优势都能够有效的帮助电力系统信息安全的发展。本文就复合混沌加密算法在电力系统信息安全中的应用进行
电力科技
复合混沌加密算法在电力系统信息安全中的应用
．
周
科
朱
睿
（重庆市电力公司信通分公司。重庆４０００１４）
【摘
要】随着社会不断的发展，电力系统也得到了相应的大
幅度提高，与此同时，新的问题也随之而来，那就是电力系统的信息安全问题。对于电力系统而言，时刻牵扯着百姓的生活与工作，同时也牵扯着国家的发展与社会的安定，因此，良好的保护电力系统的沌加密算法是一种较好的方法，主要原因在于这种方法经过
分析低频信号时，时间窗又自动变宽。复合混沌加密算法在电力系统信息安全中的应用中，小波分析理论是不可或缺的一个重要组成部分，主要原因在于它提供了连续的可调的时间频率窗。对于复合混沌加密算法来说，准确和详细是两个非常明显的优势。而小波分析理论恰好的帮助其提供了这两个优势。首先是准确，在小波分析理论中，连续的时间频率窗对于复合混沌加密算法的准确性提供了可能，经过科研人员的不断探索和研究，终于在准确性方面有所建树。其次，小波分析理论的可调的时间频率窗为复合混沌加密算法的详细创造了条件，在科研人员的积极研究中，对复合混沌加密算法的详细创造了可能。这只是两个方面而已，对于小波分析理论而言，最重要的就是提供了连续的可调的时间频率窗，两个重要的方面结合到了一起，对复合混沌加密算法产生非常大的积极影响，使得详细和准确有增添了较大的积极影响。对于在电力系统信息安全中的应用而言，可以说是 “ 如虎添翼 ” 。在现阶段的研究中，还在不断的深化，希望能够获得更大的突破。３小波复合混沌加密算法小波复合混沌加密系统基于Ｌｏｇｉｓｔｉｃ与Ｃｕｂｉｃ二级映射机制，采用位置置乱与数值变换相结合的数据加密思想，引入以密文相关系数为阈值函数的自适应加密机制，在小波变换空间对明文数据的小波系数进行二级混沌加密，输出混沌序列具有很高的复杂度和很强的伪随机性，从而保证了算法的安全性和抗攻击能力。由此可见，对于现阶段的复合混沌加密算法来说，主要是引入了两种映射的机制，再加上小波分析理论的重要指导作用，从而能够在电力系统信息安全中良好的应用。就现阶段的发展而言，复合混沌加密算法已经取得了良好的成绩，但由于社会发展的步伐不断的加快，复合混沌加密算法还需要不断的进行深化和研究，只有这样才能更好的发展，从而更好的在电力系统信息安全中应用，改善居民的生活与工作，促进国家的发展和社会的进步。４对复合混沌加密算法在电力系统信息安全中的应用建议