高考文科数学全国1卷.pdf
(23)2022年高考真题——文科数学(全国乙卷) 答案(1)

所以 ;
【小问2详解】
,则 ,
当 时, ,所以当 时, , 单调递增;
当 时, , 单调递减;
所以 ,此时函数无零点,不合题意;
当 时, ,在 上, , 单调递增;
在 上, , 单调递减;
又 ,当x趋近正无穷大时, 趋近于正无穷大,
所以 仅在 有唯一零点,符合题意;
当 时, ,所以 单调递增,又 ,
【分析】根据古典概型计算即可
【详解】从5名同学中随机选3名的方法数为
甲、乙都入选的方法数为 ,所以甲、乙都入选的概率
故答案为:
15.过四点 中的三点的一个圆的方程为____________.
【答案】 或 或 或 ;
【解析】
【分析】设圆的方程为 ,根据所选点的坐标,得到方程组,解得即可;
【详解】解:依题意设圆的方程为 ,
(2)求该林区这种树木的根部横截面积与材积量的样本相关系数(精确到0.01);
(3)现测量了该林区所有这种树木的根部横截面积,并得到所有这种树木的根部横截面积总和为 .已知树木的材积量与其根部横截面积近似成正比.利用以上数据给出该林区这种树木的总材积量的估计值.
附:相关系数 .
【答案】(1) ;
(2)
在区间 上 ,即 单调递减,
又 , , ,
所以 在区间 上的最小值为 ,最大值为 .
故选:D
12.已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O的球面上,则当该四棱锥的体积最大时,其高为()
A. B. C. D.
【答案】C
【解析】
【分析】先证明当四棱锥 顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为 ,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积最大时其高的值.
2020年高考文科数学全国卷1附答案解析版

1| 2
PF1 ||
PF2 | 中计算即可.
由已知,不妨设 F1 2,0,F2 2,0,
则a
1,c
2 ,因为| OP | 1
1| 2
F
1F2
|,
所以点 P 在以 F1F2为直径的圆上, 即 △F1F2P 是以 P 为直角顶点的直角三角形,
【解析】根据已知条件求得q 的值,再由a 6 a 7 a 8 q a5 1a 2 a3 可求得结果. 设等比数列an的公比为q ,则 a 1 a2 a3 a1 1 q q 2 1 , a2 a3 a4 a1q a1q 2 a1q3 a1q 1 q q 2 q 2 , 因此, a6 a7 a8 a1 q5 a1 q6 a1 q7 a1 q5 1 q q 2 q5 32 .
数学试卷 第 6 页(共 6 页)
2020年普通高等学校招生全国统一考试·全国I卷
文科数学答案解析
一、选择题 1.【答案】D 【解析】首先解一元二次不等式求得集合 A,之后利用交集中元素的特征求得 A 由 x2 3x 4<0 解得1<x<4,
所以 A x | 1<x<4, 又因为 B 4,1,3,5,所以 A B 1,3,
xi,yi i 1,2,,20得到下面的散点图:
由此散点图,在10℃ 至 40℃之间,下面四个回归方程类型中最适宜作为发芽率 y 和
温度 x 的回归方程类型的是
()
A. y a bx
B. y a bx2
C. y a bex
D. y a b ln x
6.已知圆 x2 y2 6x 0 ,过点1,2的直线被该圆所截得的弦的长度的最小值为
数学试卷 第 4 页(共 6 页)
毕业学校
姓名
考生号
2019年高考全国1卷文科数学及答案

绝密★启用前2019年普通高等学校招生全国统一考试文科数学本试卷共23题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设3i12i z -=+,则||z =A .2B .3C .2D .12.已知集合{1,2,3,4,5,6,7}U =,{2,3,4,5}A =,{2,3,6,7}B =,则U B A = A .{1,6} B .{1,7} C .{6,7} D .{16,7},3.已知0.20.32log 0.2,2,0.2a b c ===,则A .a b c <<B .a c b <<C .c a b <<D .b c a <<之比是512-4.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度(512-≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是512-.若某人满足上述两个黄金分割比例,且腿长为105cm ,头顶至脖子下端的长度为26 cm ,则其身高可能是 A .165 cm B .175 cm C .185 cm D .190 cm5.函数f (x )=2sin cos x xx x++在[—π,π]的图像大致为 A .B .C .D .6.某学校为了解1 000名新生的身体素质,将这些学生编号为1,2,…,1 000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是 A .8号学生 B .200号学生 C .616号学生 D .815号学生 7.tan255°=A .-2-3B .-2+3C .2-3D .2+38.已知非零向量a ,b 满足a =2b ,且(a –b )⊥b ,则a 与b 的夹角为 A .π6B .π3C .2π3D .5π69.如图是求112122++的程序框图,图中空白框中应填入A .A =12A + B .A =12A +C .A =112A+D .A =112A+10.双曲线C :22221(0,0)x y a b a b-=>>的一条渐近线的倾斜角为130°,则C 的离心率为A .2sin40°B .2cos40°C .1sin50︒D .1cos50︒11.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a sin A -b sin B =4c sin C ,cos A =-14,则b c=A .6B .5C .4D .312.已知椭圆C 的焦点为12(1,0),(1,0)F F -,过F 2的直线与C 交于A ,B 两点.若22||2||AF F B =,1||||AB BF =,则C 的方程为A .2212x y +=B .22132x y +=C .22143x y +=D .22154x y +=二、填空题:本题共4小题,每小题5分,共20分。
2019年高考文科数学全国1卷(附答案)
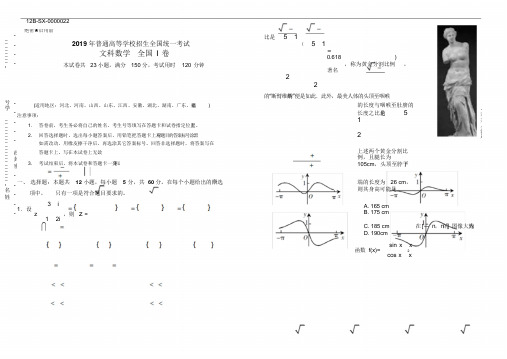
12B-SX-0000022_ _ _ _ _ _ _ _ :----绝密★启用前2019年普通高等学校招生全国统一考试文科数学全国I 卷本试卷共23 小题,满分150 分,考试用时120 分钟比是 5 1( 5 1≈0.618 ),称为黄金分割比例,著名22的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉号学_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ :名姓-----线封密-----(适用地区:河北、河南、山西、山东、江西、安徽、湖北、湖南、广东、福建)注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
3 i1.设z ,则z =1 2i的长度与咽喉至肚脐的长度之比也是 512上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是A. 165 cmB. 175 cmC. 185 cmD. 190cmsin x x函数f(x)= 2cos x x.若某人满足在[—π,π的]图像大致为班_ _ _ _ _ _ _ 年_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ __ _ _ _ _ _ _ _ _ :校学----线封密---------A.2 B. 3 C. 2 D.12.已知集合U 1,2,3,4,5,6,7 ,A 2,3,4,5 ,B 2,3,6,7 ,则B e AUA.1,6 B.1,7 C.6,7 D.1,6,73.已知0.2 0.3a log 0.2,b 2 ,c0.2 ,则2A.a b c B.a c bC.c a b D.b c a4.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之A. B.C. D.6.某学校为了解1 000 名新生的身体素质,将这些学生编号为1,2,⋯,1 000,从这些新生中用系统抽样方法等距抽取100 名学生进行体质测验.若46 号学生被抽到,则下面4名学生中被抽到的是A .8 号学生B.200 号学生C.616 号学生D.815 号学生7.tan255 =°A .-2- 3 B.-2+ 3 C.2- 3 D.2+ 3- 1 - - 2 -12B-SX-00000228.已知非零向量 a ,b 满足 a =2 b ,且(a –b )b ,则 a 与 b 的夹角为A . π 6B . π 3C .2 π3 D .5 π 619. 如图是求2 2 1 12的程序框图,图中空白框中应填入222x y 3222x y 5 4x21yB .1D .A .C .2112 2x y4 3二、填空题:本题共4小题,每小题5分,共20分。
2023年全国乙卷文科高考数学试题+答案解析

绝密★启用前2023年普通高等学校招生全国统一考试(全国乙卷∙文科)数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.2+i 2+2i 3 =()A.1B.2C.5D.5【答案】C【解析】∵2+i 2+2i 3=2-2i -1=1-2i ,∴|2+i 2+2i 3|=1-2i =12+(-2)2=5,选C 。
2.设全集U ={0,1,2,4,6,8},集合M ={0,4,6},N ={0,1,6},则M ⋃C U N =()A.{0,2,4,6,8} B.{0,1,4,6,8}C.{1,2,4,6,8}D.U【答案】A【解析】∵N ={2,4,8},∴M ⋃C U N ={0,2,4,6,8},选A.3.如图,网格纸上绘制的一个零件的三视图,网格小正方形的边长为1,则该零件的表面积为()A.24B.26C.28D.30【答案】D【解析】如图所示,在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2, AA 1=3,点H ,I ,J ,K 为所在棱上靠近点B 1,C 1,D 1,A 1的三等分点,O ,L ,M ,N 为所在棱的中点,则三视图所对应的几何体为长方体ABCD -A 1B 1C 1D 1去掉长方体ONIC 1-LMHB 1之后所得的几何体,该几何体表面积为:2×(2×2)+4×(2×3)-2×(1×1)=30,选D 。
4.在△BC 中,内角A,B,C 的对边分别是a,b,c,若acosB -bcosA =c,且C =π5,则∠B =()A.π10B.π5C.3π10D.2π5【答案】C【解析】∵sinAcosB -sinBcosA =sinC,即sinAcosB -sinBcosA =sin (A +B )=sinAcosBsinBcosA,∴sinBcosA =0,∵B ∈(0,π),∴sinB >0,∴cosA =0,A =π2,∴B =π-A -C =3π10,选C 。
2019高考新课标全国1卷文科数学试题及答案

2019高考新课标全国1卷文科数学试题及答案2019年普通高等学校招生全国统一考试真题文科数学本试卷共5页,满分150分。
考生注意:1.答卷前,务必将准考证号、姓名填写在答题卡上,并核对条形码上的信息是否正确。
2.选择题用铅笔将答案标号涂黑,非选择题需写在答题卡上。
3.考试结束后,将试题卷和答题卡交回。
一、选择题(共12小题,每小题5分,共60分)1.已知集合A={x|x0},则B={x|x<3/2},故选C。
2.要评估农作物亩产量的稳定程度,应该考虑其数据的离散程度,即标准差,故选B。
3.i(1+i)2=i(1+2i-i2)=i(1+2i+1)=2i,为纯虚数,故选A。
4.由于黑色部分和白色部分关于正方形中心对称,且黑色部分占整个圆的面积为1/2,故选A。
5.双曲线的对称轴为x=1,故焦点左侧的点P不在双曲线上,面积为0,故选A。
6.由于正方体A、B的对角线垂直于MNQ平面,故不与该平面平行,故选D。
7.根据约束条件,可得x≥y+1,即z=x+y≥y+2,故最大值为2,故选C。
8.函数y=sin2x的图像为一条上下振荡的曲线,故选B。
frac{16}{3}$,求AB的长度。
19.(12分)已知函数$f(x)=\frac{1}{2}\sin2x-\sin x+1$,$g(x)=\frac{1}{2}\cos2x+\cos x$。
1)证明$f(x)$在$(0,\pi)$内单调递减;2)若$f(x)=g(x)$,求$x$的取值。
20.(12分)已知函数$f(x)=\frac{1}{x^2-2x+2}$,$g(x)=\frac{x^2}{x^2+1}$。
1)求$f(x)$和$g(x)$的定义域;2)证明:对于任意$x\in(0,1]$,都有$f(x)\geq g(x)$。
21.(12分)如图,在$\triangle ABC$中,$AB=AC$,$D$为$BC$中点,$E$为$AD$的中点,$F$为$\triangle ADE$的重心。
2022年全国乙卷数学(文科)高考真题文档版(含答案)

2022年普通高等学校招生全国统一考试(全国乙卷)文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号框涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号框。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.集合{2,4,6,8,10},{16}M N x x ==-<<,则M N = ()A .{2,4}B .{2,4,6}C .{2,4,6,8}D .{2,4,6,8,10}2.设(12i)2i a b ++=,其中,a b 为实数,则()A .1,1a b ==-B .1,1a b ==C .1,1a b =-=D .1,1a b =-=-3.已知向量(2,1)(2,4)==-,a b ,则||-=a b ()A .2B .3C .4D .54.分别统计了甲、乙两位同学16周的各周课外体育运动时长(单位:h ),得如下茎叶图:则下列结论中错误的是()A .甲同学周课外体育运动时长的样本中位数为7.4B .乙同学周课外体育运动时长的样本平均数大于8C .甲同学周课外体育运动时长大于8的概率的估计值大于0.4D .乙同学周课外体育运动时长大于8的概率的估计值大于0.65.若x ,y 满足约束条件则2z x y =-的最大值是()A .2-B .4C .8D .126.设F 为抛物线2:4C y x =的焦点,点A 在C 上,点(3,0)B ,若||||AF BF =,则||AB =()A .2B .C .3D .7.执行右边的程序框图,输出的n =()A .3B .4C .5D .68.右图是下列四个函数中的某个函数在区间[3,3]-的大致图像,则该函数是()A .3231x x y x -+=+B .321x x y x -=+C .22cos 1x x y x =+D .22sin 1xy x =+9.在正方体1111ABCD A B C D -中,,E F 分别为,AB BC 的中点,则()A .平面1B EF ⊥平面1BDD B .平面1B EF ⊥平面1A BDC .平面1B EF ∥平面1A ACD .平面1B EF ∥平面11A C D10.已知等比数列{}n a 的前3项和为168,5242a a -=,则6a =()A .14B .12C .6D .311.函数()()cos 1sin 1f x x x x =+++在区间[]0,2π的最小值、最大值分别为()A .ππ22-,B .3ππ22-,C .ππ222-+,D .3ππ222-+,12.已知球O 的半径为1,四棱锥的顶点为O ,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为()A .13B .12C .3D .2二、填空题:本题共4小题,每小题5分,共20分。
2019年全国统一高考数学试卷(文科)(全国一卷)

2019年全国统一高考数学试卷(文科)(全国一卷)2019年全国统一高考数学试卷(文科)选择题部分共12小题,每小题5分,共60分。
1.设 $z=\frac{2}{3-i}$,则 $z=$(A)1+2i(B)3(C)2(D)1.2.已知集合 $U=\{1,2,3,4,5,6,7\}$,$A=\{2,3,4,5\}$,$B=\{2,3,6,7\}$,则$B\cap \overline{A}=$(A)$\{1,6\}$(B)$\{1,7\}$(C)$\{6,7\}$(D)$\{1,6,7\}$。
3.已知 $a=\log_2 0.2$,$b=2$,$c=0.2$,则(A)$a<b<c$(B)$a<c<b$(C)$c<a<b$(D)$b<c<a$。
4.古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是$\frac{5-\sqrt{5}}{2}\approx 0.618$,称为黄金分割比例。
若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至咽喉的长度与咽喉至肚脐的长度之比也是$\frac{5-\sqrt{5}}{2}$,且头顶至脖子下端的长度为26cm,则其身高可能是(A)165cm(B)175cm(C)185cm(D)190cm。
5.函数 $f(x)=\frac{\sin x+x}{\cos x+x^2}$ 在 $[-\pi,\pi]$ 的图像大致为(A)(图略)(B)(图略)(C)(图略)(D)(图略)。
6.某学校为了解1000名新生的身体素质,将这些学生编号为1,2,…,1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验。
若46号学生被抽到,则下面4名学生中被抽到的是(A)8号学生(B)200号学生(C)616号学生(D)815号学生。
7.$\tan 255^\circ =$(A)$-2-\sqrt{3}$(B)$-2+\sqrt{3}$(C)$2-\sqrt{3}$(D)$2+\sqrt{3}$。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学海无涯 20.(XXXX 课标全国Ⅰ,文 20)(本小题满分 12 分)已知函数 f(x)=ex(ax+b)-x2-4x,曲 线 y=f(x)在点(0,f(0))处的切线方程为 y=4x+4. (1)求 a,b 的值; (2)讨论 f(x)的单调性,并求 f(x)的极大值.
10.(XXXX 课标全国Ⅰ,文 10)已知锐角△ABC 的内角 A,B,C 的对边分别为 a,b,c,23cos2A
+cos 2A=0,a=7,c=6,则 b=( ).
A.10
B.9
C.8
D.5
学海无涯
11.(XXXX 课标全国Ⅰ,文 11)某几何体的三视图如图所示,则该几何体的体积为( ).
A.16+8π
16.(XXXX 课标全国Ⅰ,文 16)设当 x=θ 时,函数 f(x)=sin x-2cos x 取得最大值,则
cos θ=______.
三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(XXXX 课标全国Ⅰ,文 17)(本小题满分 12 分)已知等差数列{an}的前 n 项和 Sn 满足
S3=0,S5=-5. (1)求{an}的通项公式;
(2)求数列
1 a a 2n−1 2n+1
的前
n
项和.
学海无涯
18.(XXXX 课标全国Ⅰ,文 18)(本小题满分 12 分)为了比较两种治疗失眠症的药(分别称为 A 药,B 药)的疗效,随机地选取 20 位患者服用 A 药,20 位患者服用 B 药,这 40 位患者在 服用一段时间后,记录他们日平均增加的睡眠时间(单位:h).试验的观测结果如下: 服用 A 药的 20 位患者日平均增加的睡眠时间: 0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5 2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4 服用 B 药的 20 位患者日平均增加的睡眠时间: 3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4 1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5 (1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好? (2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
下列命题中为真命题的是( ).
A.p∧q
B. p∧q
C.p∧ q
D. p∧ q
6.(XXXX 课标全国Ⅰ,文 6)设首项为 1,公比为 2 的等比数列{an}的前 n 项和为 3
Sn,则( ).
A.Sn=2an-1
B.Sn=3an-2
C.Sn=4-3an
D.Sn=3-
2an
7.(XXXX 课标全国Ⅰ,文 7)执行下面的程序框图,如果输入的 t∈[-1,3],则
值为 2 的概率是( ).
1
1
1
1
A. 2
B. 3
C. 4
D. 6
4.(XXXX
课标全国Ⅰ,文
4)已知双曲线
C:
x2 a2
−
y2 b2
=1(a>0,b>0)的离心率为
5 ,则 2
C 的渐近线方程为( ).
1x A.y= 4
1x B.y= 3
1x C.y= 2
D.y=±x
5.(XXXX 课标全国Ⅰ,文 5)已知命题 p:∀x∈R,2x<3x;命题 q:∃x∈R,x3=1-x2,则
A.{1,4}
B.{2,3}
C.{9,16}
D.{1,2}
2.(XXXX 课标全国Ⅰ,文 2) 1+ 2i =( ). (1− i)2
−1− 1 i A. 2
−1+ 1 i B. 2
1+ 1 i C. 2
1− 1 i D. 2
3.(XXXX 课标全国Ⅰ,文 3)从 1,2,3,4 中任取 2 个不同的数,则取出的 2 个数之差的绝对
学海无涯
XXXX 年普通高等学校夏季招生全国统一考试数学文史类
(全国卷 I 新课标)
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.(XXXX 课标全国Ⅰ,文 1)已知集合 A={1,2,3,4},B={x|x=n2,n∈A},则 A∩B=( ).
14.(XXXX
课标全国Ⅰ,文
14)设
x,y
满足约束条件
1 −1
x
3, x− y
0,
则
z=2x-y
的最大值
为______.
15.(XXXX 课标全国Ⅰ,文 15)已知 H 是球 O 的直径 AB 上一点,AH∶HB=1∶2,AB⊥平面
α,H 为垂足,α 截球 O 所得截面的面积为 π,则球 O 的表面积为______.
输出的 s 属于( ).
A.[-3,4]
B.[-5,2]
C.[-4,3]
D.[-2,5]
8.(XXXX 课标全国Ⅰ,文 8)O 为坐标原点,F 为抛物线 C:y2= 4 2x 的焦点,P
为 C 上一点,若|PF|= 4 2 ,则△POF 的面积为( ).
A.2
B. 2 2
C. 2 3
D.4
9.(XXXX 课标全国Ⅰ,文 9)函数 f(x)=(1-cos x)sin x 在[-π,π]的图像大致为( ).
B.8+8π C.16+16π D.8+16π
12.(XXXX
课标全国Ⅰ,文
12)已知函数
f(x)=
−
x2
+
2
x,
x
0,
若
ln(x +1), x 0.
|f(x)|≥ax,则 a 的取值范围是( ).
A.(-∞,0]
B.(-∞,1]
C.[-2,1]
D.[-2,0]
第Ⅱ卷
二、填空题:本大题共 4 小题,每小题 5 分. 13.(XXXX 课标全国Ⅰ,文 13)已知两个单位向量 a,b 的夹角为 60°,c=ta+(1-t)b.若 b·c=0,则 t=______.
21.(XXXX 课标全国Ⅰ,文 21)(本小题满分 12 分)已知圆 M:(x+1)2+y2=1,圆 N:(x-1)2 +y2=9,动圆 P 与圆 M 外切并且与圆 N 内切,圆心 P 的轨迹为曲线 C. (1)求 C 的方程; (2)l 是与圆 P,圆 M 都相切的一条直线,l 与曲线 C 交于 A,B 两点,当圆 P 的半径最长时, 求|AB|.
