(完整版)向心力练习题
专题6-2 向心力(练)(原卷版)

专题6.2 向心力(练)一、单选题1.如图所示,一圆盘可绕过圆盘的中心O 且垂直于盘面的竖直轴转动,在圆盘上放一小木块A ,它随圆盘一起运动——做匀速圆周运动,则关于木块A 的受力,下列说法中正确的是( )A .木块A 受重力、支持力和向心力B .木块A 受重力、支持力和静摩擦力,摩擦力的方向与木块运动方向相反C .木块A 受重力、支持力和静摩擦力,摩擦力的方向指向圆心D .木块A 受重力、支持力和静摩擦力,摩擦力的方向与木块运动方向相同 2.如图所示,质量为m 的鹰,以速率v 在水平面内做半径为R 的匀速圆周运动,空气对鹰作用力的大小等于( )A .B .m 2v R C .D .mg3.如图所示,在“神舟十一号”沿曲线从M 点到N 点的飞行过程中,速度逐渐增大。
在此过程中“神舟十一号”所受合力F 的方向可能是( )A .B .C .D . 4.两根长度不同的细线下面分别悬挂着小球,细线上端固定在同一点,若两个小球以相同的角速度,绕共同的竖直轴在水平面内做匀速圆周运动,则两个小球在运动过程中的相对位置关系示意图正确的是( )A.B.C.D.5.如图所示,轻杆的一端拴一小球,另一端与竖直杆铰接。
当竖直杆以角速度ω匀速转动时,轻杆与竖直杆之间的张角为θ。
下列图像中能正确表示角速度ω与张角θ关系的是()A.B.C.D.6.辽宁舰质量为7m=⨯,如图是辽宁舰在海上转弯时的照片,假设整个过程中辽宁610kg舰做匀速圆周运动的速度大小为20m/s,圆周运动的半径为1000m,下列说法正确的是()A.在A点时水对舰的作用力指向圆心B.在A点时水对舰的作用力大小约为8F=⨯6.010NC.在A点时水对舰的作用力大小约为7F=⨯2.410ND.在A点时水对舰的作用力大小为07.如图所示,质量相等的小球A、B分别固定在轻杆的中点及端点,当轻杆在光滑的水平F与轻杆的AB段对B球的拉力面上绕O点匀速转动时,轻杆的OA段对A球的拉力大小T1F之比为()大小T2A.1:1B.2:1C.3:2D.2:38.向心力演示器如图所示。
向心力典型例题(附答案解析详解)

1、如图所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为()A. B. C. D.2、下面关于向心力的叙述中,正确的是()A.向心力的方向始终沿着半径指向圆心,所以是一个变力B.做匀速圆周运动的物体,除了受到别的物体对它的作用外,还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力D.向心力只改变物体速度的方向,不改变物体速度的大小3、关于向心力的说法,正确的是()A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变5、如图所示,质量为m的木块,从半径为r的竖直圆轨道上的A点滑向B点,由于摩擦力的作用,木块的速率保持不变,则在这个过程中A.木块的加速度为零B.木块所受的合外力为零C.木块所受合外力大小不变,方向始终指向圆心D.木块所受合外力的大小和方向均不变6、甲、乙两名溜冰运动员,M 甲=80 kg,M乙=40 kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图所示,两个相距0.9 m,弹簧秤的示数为9.2 N,下列判断正确的是()A.两人的线速度相同,约为40 m/sB.两人的角速度相同,为6 rad/sC.两人的运动半径相同,都是0.45 mD.两人的运动半径不同,甲为0.3 m,乙为0.6 m7、如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,下列说法正确的是()A.物体所受弹力增大,摩擦力也增大B.物体所受弹力增大,摩擦力减小C.物体所受弹力减小,摩擦力也减小D.物体所受弹力增大,摩擦力不变8、用细绳拴住一球,在水平面上做匀速圆周运动,下列说法中正确的是()A.当转速不变时,绳短易断B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D.当周期不变时,绳长易断9、如图,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变A.因为速率不变,所以木块加速度为零C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变,方向时刻指向球心解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,故选项A、B不正确.在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C错. 答案:D10、如图所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球,两球用轻细线连接.若M>m,则()A.当两球离轴距离相等时,两球相对杆不动B.当两球离轴距离之比等于质量之比时,两球相对杆都不动C.若转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动D.若两球相对杆滑动,一定向同一方向,不会相向滑动解析:由牛顿第三定律可知M、m间的作用力相等,即F M=F m,F M=Mω2r M,F m=mω2rm,所以若M、m不动,则r M∶r m=m∶M,所以A、B不对,C 对(不动的条件与ω无关).若相向滑动,无力提供向心力,D对. 答案:CD 11、一物体以4m/s的线速度做匀速圆周运动,转动周期为2s,则物体在运动过程的任一时刻,速度变化率的大小为()A.2m/s2B.4m/s2C.0D.4πm/s2ω=2π/T=2π/2=πv=ω*r 所以r=4/πa=v∧2/r=16/(4/π)=4π12、在水平路面上安全转弯的汽车,向心力是()A.重力和支持力的合力B.重力、支持力和牵引力的合力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、如图所示,半径为R的半球形碗内,有一个具有一定质量的物体A,A与碗壁间的动摩擦因数为μ,当碗绕竖直轴OO′匀速转动时,物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度.分析:物体A随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O,故此向心力不是重力而是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡.解析:物体A做匀速圆周运动,向心力:F n=mω2R而摩擦力与重力平衡,则有μF n=mg 即F n=mg/μ由以上两式可得:mω2R= mg/μ即碗匀速转动的角速度为:ω=.2、汽车沿半径为R的水平圆跑道行驶,路面作用于车的摩擦力的最大值是车重的1/10,要使汽车不致冲出圆跑道,车速最大不能超过多少?解析:跑道对汽车的摩擦力提供向心力,1/10mg=mv2/r,所以要使汽车不致冲出圆跑道,车速最大值为v=. 答案:车速最大不能超过3、一质量m=2 kg的小球从光滑斜面上高h=3.5 m处由静止滑下,斜面的底端连着一个半径R=1 m的光滑圆环(如图所示),则小球滑至圆环顶点时对环的压力为_____________,小球至少应从多高处静止滑下才能通过圆环最高点,hmin=_________(g=10 m/s2).匀速圆周运动典型问题剖析匀速圆周运动问题是学习的难点,也是高考的热点,同时它又容易和很多知识综合在一起,形成能力性很强的题目,如除力学部分外,电学中“粒子在磁场中的运动”涉及的很多问题仍然要用到匀速圆周运动的知识,对匀速圆周运动的学习可重点从两个方面掌握其特点,首先是匀速圆周运动的运动学规律,其次是其动力学规律,现就各部分涉及的典型问题作点滴说明。
人教版必修二6.2向心力练习(word版含答案)

人教版必修二6.2向心力一、单项选择题(共1小题;共4分)1. 一种玩具的结构如图所示,竖直放置的光滑铁环的半径为R=20cm,环上有一穿孔的小球m,仅能沿环做无摩擦的滑动,如果圆环绕着过环心的竖直轴以10rad/s的角速度旋转(取g= 10m/s2),则相对环静止时小球与环心O的连线与O1O2的夹角θ是A. 30∘B. 45∘C. 60∘D. 75∘二、填空题(共5小题;共16分)2. (多选题)关于向心力,下列说法正确的是(A)向心力是一种效果力(B)向心力是一种具有某种性质的力(C)因为向心力总是指向圆心,且大小不变,故向心力是一个恒力(D)因向心力指向圆心,且与线速度方向垂直,所以它不能改变线速度的大小3. 物体做圆周运动时一定会受到向心力的作用。
这个向心力不断改变物体的运动,并始终沿着半径指向。
4. 做匀速圆周运动物体受到的合外力充当向心力,向心力的方向总是指向,向心力不能改变线速度的大小,只能改变线速度的。
5. 能够作为向心力的力可以是:重力(万有引力)、弹力、及。
6. 向心力大小的计算公式:。
三、解答题(共3小题;共39分)7. 自主活动:用一根细绳拴住一个小球或一串钥匙,抡动细绳使小球或钥匙做圆周运动,感受手对绳子的拉力,并说明为什么?8. 物体做曲线运动的条件:(1)动力学角度:物体所受合力的方向与它的速度方向时,物体做曲线运动。
(2)运动学角度:物体的加速度方向与速度方向时,物体做曲线运动。
9. 如图所示,旋转木马被水平钢杆拴住绕转台的中心轴做匀速圆周运动。
若相对的两个木马间的杆长为6m,木马质量为30kg,骑木马的小孩质量为40kg,当木马旋转的速度为6m/s时,试问:(1)此时木马和小孩受到的向心力分别是由哪个物体提供的? (2)此时小孩受到的向心力是多大?答案第一部分1. C【解析】小球转动的半径为Rsinθ,小球所受的合力垂直指向转轴,根据平行四边形定则:F合= mgtanθ=mRsinθω2,解得:θ=60∘,故C正确,ABD错误。
向心力典型例题(附答案详解)

1、如图所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为()A. B. C. D.2、下面关于向心力的叙述中,正确的是()A.向心力的方向始终沿着半径指向圆心,所以是一个变力B.做匀速圆周运动的物体,除了受到别的物体对它的作用外,还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力D.向心力只改变物体速度的方向,不改变物体速度的大小3、关于向心力的说法,正确的是()A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变5、如图所示,质量为m的木块,从半径为r的竖直圆轨道上的A点滑向B点,由于摩擦力的作用,木块的速率保持不变,则在这个过程中A.木块的加速度为零B.木块所受的合外力为零C.木块所受合外力大小不变,方向始终指向圆心D.木块所受合外力的大小和方向均不变6、甲、乙两名溜冰运动员,M甲=80 kg,M乙=40 kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图所示,两个相距0.9 m,弹簧秤的示数为9.2 N,下列判断正确的是()A.两人的线速度相同,约为40 m/sB.两人的角速度相同,为6 rad/sC.两人的运动半径相同,都是0.45 mD.两人的运动半径不同,甲为0.3 m,乙为0.6 m7、如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,下列说法正确的是()A.物体所受弹力增大,摩擦力也增大B.物体所受弹力增大,摩擦力减小C.物体所受弹力减小,摩擦力也减小D.物体所受弹力增大,摩擦力不变8、用细绳拴住一球,在水平面上做匀速圆周运动,下列说法中正确的是()A.当转速不变时,绳短易断B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D.当周期不变时,绳长易断9、如图,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变A.因为速率不变,所以木块加速度为零C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变,方向时刻指向球心解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,故选项A、B不正确.在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C错. 答案:D10、如图所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球,两球用轻细线连接.若M>m,则()A.当两球离轴距离相等时,两球相对杆不动B.当两球离轴距离之比等于质量之比时,两球相对杆都不动C.若转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动D.若两球相对杆滑动,一定向同一方向,不会相向滑动解析:由牛顿第三定律可知M、m间的作用力相等,即F M=F m,F M=Mω2r M,F m=mω2rm,所以若M、m不动,则r M∶r m=m∶M,所以A、B不对,C对(不动的条件与ω无关).若相向滑动,无力提供向心力,D对. 答案:CD 11、一物体以4m/s的线速度做匀速圆周运动,转动周期为2s,则物体在运动过程的任一时刻,速度变化率的大小为()A.2m/s2B.4m/s2C.0D.4π m/s2ω=2π/T=2π/2=πv=ω*r所以r=4/πa=v∧2/r=16/(4/π)=4π12、在水平路面上安全转弯的汽车,向心力是()A.重力和支持力的合力B.重力、支持力和牵引力的合力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、如图所示,半径为R的半球形碗内,有一个具有一定质量的物体A,A与碗壁间的动摩擦因数为μ,当碗绕竖直轴OO′匀速转动时,物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度.分析:物体A随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O,故此向心力不是重力而是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡.解析:物体A做匀速圆周运动,向心力:F n=mω2R而摩擦力与重力平衡,则有μF n=mg 即F n=mg/μ由以上两式可得:mω2R= mg/μ即碗匀速转动的角速度为:ω=.2、汽车沿半径为R的水平圆跑道行驶,路面作用于车的摩擦力的最大值是车重的1/10,要使汽车不致冲出圆跑道,车速最大不能超过多少?解析:跑道对汽车的摩擦力提供向心力,1/10mg=mv2/r,所以要使汽车不致冲出圆跑道,车速最大值为v=. 答案:车速最大不能超过3、一质量m=2 kg的小球从光滑斜面上高h=3.5 m处由静止滑下,斜面的底端连着一个半径R=1 m的光滑圆环(如图所示),则小球滑至圆环顶点时对环的压力为_____________,小球至少应从多高处静止滑下才能通过圆环最高点,hmin=_________(g=10 m/s2).匀速圆周运动典型问题剖析匀速圆周运动问题是学习的难点,也是高考的热点,同时它又容易和很多知识综合在一起,形成能力性很强的题目,如除力学部分外,电学中“粒子在磁场中的运动”涉及的很多问题仍然要用到匀速圆周运动的知识,对匀速圆周运动的学习可重点从两个方面掌握其特点,首先是匀速圆周运动的运动学规律,其次是其动力学规律,现就各部分涉及的典型问题作点滴说明。
向心力典型例题(附答案详解)

1、如下图,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,那么圆筒转动的角速度ω至少为〔〕A. B. C. D.2、下面关于向心力的表达中,正确的选项是〔〕A.向心力的方向始终沿着半径指向圆心,所以是一个变力B.做匀速圆周运动的物体,除了受到别的物体对它的作用外,还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力D.向心力只改变物体速度的方向,不改变物体速度的大小3、关于向心力的说法,正确的选项是〔〕A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变5、如下图,质量为m的木块,从半径为r的竖直圆轨道上的A点滑向B点,由于摩擦力的作用,木块的速率保持不变,那么在这个过程中C.木块所受合外力大小不变,方向始终指向圆心D.木块所受合外力的大小和方向均不变6、甲、乙两名溜冰运发动,M 甲=80 kg,M乙=40 kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如下图,两个相距0.9 m,弹簧秤的示数为9.2 N,以下判断正确的选项是〔〕A.两人的线速度一样,约为40 m/sB.两人的角速度一样,为6 rad/sC.两人的运动半径一样,都是0.45 mD.两人的运动半径不同,甲为0.3 m,乙为0.6 m7、如下图,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.假设圆筒和物体以更大的角速度做匀速转动,以下说法正确的选项是〔〕A.物体所受弹力增大,摩擦力也增大B.物体所受弹力增大,摩擦力减小C.物体所受弹力减小,摩擦力也减小D.物体所受弹力增大,摩擦力不变8、用细绳拴住一球,在水平面上做匀速圆周运动,以下说法中正确的选项是〔〕A.当转速不变时,绳短易断B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D.当周期不变时,绳长易断9、如图,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变A.因为速率不变,所以木块加速度为零C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变,方向时刻指向球心解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,应选项A、B不正确.在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C错. 答案:D10、如下图,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球,两球用轻细线连接.假设M>m,那么〔〕A.当两球离轴距离相等时,两球相对杆不动B.当两球离轴距离之比等于质量之比时,两球相对杆都不动C.假设转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动D.假设两球相对杆滑动,一定向同一方向,不会相向滑动解析:由牛顿第三定律可知M、m间的作用力相等,即F M=F m,F M=Mω2r M,F m=mω2rm,所以假设M、m不动,那么r M∶r m=m∶M,所以A、B不对,C 对〔不动的条件与ω无关〕.假设相向滑动,无力提供向心力,D对. 答案:CD11、一物体以4m/s的线速度做匀速圆周运动,转动周期为2s,那么物体在运动过程的任一时刻,速度变化率的大小为〔〕A.2m/s2B.4m/s2C.0D.4π m/s2ω=2π/T=2π/2=πv=ω*r所以r=4/πa=v∧2/r=16/(4/π)=4π12、在水平路面上平安转弯的汽车,向心力是〔〕C 汽车与路面间的静摩擦力D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、如下图,半径为R的半球形碗内,有一个具有一定质量的物体A,A与碗壁间的动摩擦因数为μ,当碗绕竖直轴OO′匀速转动时,物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度.分析:物体A随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O,故此向心力不是重力而是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡.解析:物体A做匀速圆周运动,向心力:F n=mω2R而摩擦力与重力平衡,那么有μF n=mg 即F n=mg/μ由以上两式可得:mω2R=mg/μ即碗匀速转动的角速度为:ω=. 2、汽车沿半径为R的水平圆跑道行驶,路面作用于车的摩擦力的最大值是车重的1/10,要使汽车不致冲出圆跑道,车速最大不能超过多少?解析:跑道对汽车的摩擦力提供向心力,1/10mg=mv2/r,所以要使汽车不致冲出圆跑道,车速最大值为v=. 答案:车速最大不能超过3、一质量m=2 kg的小球从光滑斜面上高h=3.5 m处由静止滑下,斜面的底端连着一个半径R=1 m的光滑圆环〔如下图〕,那么小球滑至圆环顶点时对环的压力为_____________,小球至少应从多高处静止滑下才能通过圆环最高点,hmin=_________(g=10 m/s2).匀速圆周运动典型问题剖析匀速圆周运动问题是学习的难点,也是高考的热点,同时它又容易和很多知识综合在一起,形成能力性很强的题目,如除力学局部外,电学中“粒子在磁场中的运动〞涉及的很多问题仍然要用到匀速圆周运动的知识,对匀速圆周运动的学习可重点从两个方面掌握其特点,首先是匀速圆周运动的运动学规律,其次是其动力学规律,现就各局部涉及的典型问题作点滴说明。
向心力典型例题

向心力典型例题(附答案详解)一、选择题【共12道小题】1、如图所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为()A. B. C. D.解析:要使a不下滑,则a受筒的最大静摩擦力作用,此力与重力平衡,筒壁给a的支持力提供向心力,则N=mrω2,而fm=mg=μN,所以mg=μmrω2,故 . 所以A、B、C均错误,D正确.4、在光滑水平面上相距20 cm的两点钉上A、B两个钉子,一根长1 m的细绳一端系小球,另一端拴在A钉上,如图所示.已知小球质量为0.4 kg,小球开始以2 m/s的速度做水平匀速圆周运动,若绳所能承受的最大拉力为4 N,则从开始运动到绳拉断历时为()A.2.4π sB.1.4π sC.1.2π sD.0.9π s解析:当绳子拉力为4 N时,由F=可得r=0.4 m.小球每转半个周期,其半径就减小0.2 m,由分析知,小球分别以半径为1 m,0.8 m和0.6 m各转过半个圆周后绳子就被拉断了,所以时间为t==1.2π s. 答案:C6、甲、乙两名溜冰运动员,M甲=80 kg,M乙=40 kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图所示,两个相距0.9 m,弹簧秤的示数为9.2 N,下列判断正确的是()A.两人的线速度相同,约为40 m/sB.两人的角速度相同,为6 rad/sC.两人的运动半径相同,都是0.45 mD.两人的运动半径不同,甲为0.3 m,乙为0.6 m解析:甲、乙两人绕共同的圆心做圆周运动,他们间的拉力互为向心力,他们的角速度相同,半径之和为两人的距离.设甲、乙两人所需向心力为F 向,角速度为ω,半径分别为r 甲、r 乙.则F 向=M 甲ω2r 甲=M 乙ω2r 乙=9.2 N ① r 甲+r 乙=0.9 m ②由①②两式可解得只有D 正确 答案:D7、如图所示,在匀速转动的圆筒壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,下列说确的是( )A.物体所受弹力增大,摩擦力也增大B.物体所受弹力增大,摩擦力减小C.物体所受弹力减小,摩擦力也减小D.物体所受弹力增大,摩擦力不变 析:物体在竖直方向上受重力G 与摩擦力F ,是一对平衡力,在向心力方向上受弹力F N .根据向心力公式,可知F N =mω2r ,当ω增大时,F N 增大,选D.8、用细绳拴住一球,在水平面上做匀速圆周运动,下列说法中正确的是( )A.当转速不变时,绳短易断B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D.当周期不变时,绳长易断析:由公式a=ω2R=知,当角速度(转速)不变时绳长易断,故A 、B 错误.周期不变时,绳长易断,故D 正确.由,当线速度不变时绳短易断,C 错9、如图,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变A.因为速率不变,所以木块加速度为零C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变,方向时刻指向球心解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,故选项A、B不正确.在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C错. 答案:D10、如图所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M 的两球,两球用轻细线连接.若M>m,则()A.当两球离轴距离相等时,两球相对杆不动B.当两球离轴距离之比等于质量之比时,两球相对杆都不动C.若转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动D.若两球相对杆滑动,一定向同一方向,不会相向滑动解析:由牛顿第三定律可知M、m间的作用力相等,即F M=F m,F M=Mω2r M,F m=mω2rm,所以若M、m不动,则r M∶r m=m∶M,所以A、B不对,C对(不动的条件与ω无关).若相向滑动,无力提供向心力,D对. 答案:CD 11、一物体以4m/s的线速度做匀速圆周运动,转动周期为2s,则物体在运动过程的任一时刻,速度变化率的大小为()A.2m/s2B.4m/s2C.0D.4π m/s2ω=2π/T=2π/2=πv=ω*r所以r=4/πa=v∧2/r=16/(4/π)=4π12、在水平路面上安全转弯的汽车,向心力是()A.重力和支持力的合力B.重力、支持力和牵引力的合力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、如图所示,半径为R的半球形碗,有一个具有一定质量的物体A,A与碗壁间的动摩擦因数为μ,当碗绕竖直轴OO′匀速转动时,物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度.分析:物体A随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O,故此向心力不是重力而是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡.解析:物体A做匀速圆周运动,向心力:F n=mω2R而摩擦力与重力平衡,则有μF n=mg 即F n=mg/μ由以上两式可得:mω2R= mg/μ即碗匀速转动的角速度为:ω=.2、汽车沿半径为R的水平圆跑道行驶,路面作用于车的摩擦力的最大值是车重的1/10,要使汽车不致冲出圆跑道,车速最大不能超过多少?解析:跑道对汽车的摩擦力提供向心力,1/10mg=mv2/r,所以要使汽车不致冲出圆跑道,车速最大值为v=. 答案:车速最大不能超过3、一质量m=2 kg 的小球从光滑斜面上高h=3.5 m 处由静止滑下,斜面的底端连着一个半径R=1 m 的光滑圆环(如图所示),则小球滑至圆环顶点时对环的压力为_____________,小球至少应从多高处静止滑下才能通过圆环最高点,hmin=_________(g=10 m/s2).解析:①设小球滑至圆环顶点时速度为v 1,则mgh=mg·2R+ 1/2mv 12 F n +mg= mv 12/R 得:F n =40 N②小球刚好通过最高点时速度为v 2,则mg= mv 22/R 又mgh′=mg2R+1/2 mv 22/R 得h′=2.5R 答案:40 N;2.5R匀速圆周运动典型问题剖析1. 基本概念、公式的理解和运用[例2] 在绕竖直轴匀速转动的圆环上有A 、B 两点,如图1所示,过A 、B 的半径与竖直轴的夹角分别为30°和60°,则A 、B 两点的线速度之比为 ;向心加速度之比为 。
高一物理向心力典型例题(含标准答案)

向心力典型例题(附答案详解)一、选择题【共12道小题】1、如图所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为()A.B.C.D.解析:要使a不下滑,则a受筒的最大静摩擦力作用,此力与重力平衡,筒壁给a的支持力提供向心力,则N=mrω2,而fm=mg=μN,所以mg=μmrω2,故. 所以A、B、C均错误,D 正确.2、下面关于向心力的叙述中,正确的是()A.向心力的方向始终沿着半径指向圆心,所以是一个变力B.做匀速圆周运动的物体,除了受到别的物体对它的作用外,还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力D.向心力只改变物体速度的方向,不改变物体速度的大小解析:向心力是按力的作用效果来命名的,它可以是物体受力的合力,也可以是某一个力的分力,因此,在进行受力分析时,不能再分析向心力.向心力时刻指向圆心与速度方向垂直,所以向心力只改变速度的方向,不改变速度的大小,即向心力不做功. 答案:ACD3、关于向心力的说法,正确的是()A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变解析:向心力并不是物体受到的一个特殊力,它是由其他力沿半径方向的合力或某一个力沿半径方向的分力提供的.因为向心力始终与速度方向垂直,所以向心力不会改变速度的大小,只改变速度的方向.当质点做匀速圆周运动时,向心力的大小保持不变. 答案:BCD4、在光滑水平面上相距20 cm的两点钉上A、B两个钉子,一根长1 m的细绳一端系小球,另一端拴在A钉上,如图所示.已知小球质量为0.4 kg,小球开始以2 m/s的速度做水平匀速圆周运动,若绳所能承受的最大拉力为4 N,则从开始运动到绳拉断历时为()A.2.4π sB.1.4π sC.1.2π sD.0.9π s解析:当绳子拉力为4 N时,由F=可得r=0.4 m.小球每转半个周期,其半径就减小0.2 m,由分析知,小球分别以半径为1 m,0.8 m和0.6 m各转过半个圆周后绳子就被拉断了,所以时间为t==1.2π s. 答案:C5、如图所示,质量为m的木块,从半径为r的竖直圆轨道上的A点滑向B 点,由于摩擦力的作用,木块的速率保持不变,则在这个过程中A.木块的加速度为零B.木块所受的合外力为零C.木块所受合外力大小不变,方向始终指向圆心D.木块所受合外力的大小和方向均不变解析:木块做匀速圆周运动,所以木块所受合外力提供向心力. 答案:C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用6、甲、乙两名溜冰运动员,M 甲=80 kg,M乙=40 kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图所示,两个相距0.9 m,弹簧秤的示数为9.2 N,下列判断正确的是()A.两人的线速度相同,约为40 m/sB.两人的角速度相同,为6 rad/sC.两人的运动半径相同,都是0.45 mD.两人的运动半径不同,甲为0.3 m,乙为0.6 m解析:甲、乙两人绕共同的圆心做圆周运动,他们间的拉力互为向心力,他们的角速度相同,半径之和为两人的距离.设甲、乙两人所需向心力为F向,角速度为ω,半径分别为r甲、r乙.则F向=M甲ω2r甲=M乙ω2r乙=9.2 N ①r甲+r乙=0.9 m ②由①②两式可解得只有D正确答案:D7、如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,下列说法正确的是()A.物体所受弹力增大,摩擦力也增大B.物体所受弹力增大,摩擦力减小C.物体所受弹力减小,摩擦力也减小D.物体所受弹力增大,摩擦力不变析:物体在竖直方向上受重力G与摩擦力F,是一对平衡力,在向心力方向上受弹力F N.根据向心力公式,可知F N=mω2r,当ω增大时,F N增大,选D.8、用细绳拴住一球,在水平面上做匀速圆周运动,下列说法中正确的是()A.当转速不变时,绳短易断B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D.当周期不变时,绳长易断析:由公式a=ω2R=知,当角速度(转速)不变时绳长易断,故A、B错误.周期不变时,绳长易断,故D正确.由,当线速度不变时绳短易断,C错9、如图,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变A.因为速率不变,所以木块加速度为零C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变,方向时刻指向球心解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,故选项A、B不正确.在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C错. 答案:D10、如图所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球,两球用轻细线连接.若M>m,则()A.当两球离轴距离相等时,两球相对杆不动B.当两球离轴距离之比等于质量之比时,两球相对杆都不动C.若转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动D.若两球相对杆滑动,一定向同一方向,不会相向滑动解析:由牛顿第三定律可知M、m间的作用力相等,即F M=F m,F M=Mω2r M,F m=mω2rm,所以若M、m不动,则r M∶r m=m∶M,所以A、B不对,C对(不动的条件与ω无关).若相向滑动,无力提供向心力,D对. 答案:CD 11、一物体以4m/s的线速度做匀速圆周运动,转动周期为2s,则物体在运动过程的任一时刻,速度变化率的大小为()A.2m/s2B.4m/s2C.0D.4π m/s2ω=2π/T=2π/2=πv=ω*r所以r=4/πa=v∧2/r=16/(4/π)=4π12、在水平路面上安全转弯的汽车,向心力是()A.重力和支持力的合力B.重力、支持力和牵引力的合力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、如图所示,半径为R的半球形碗内,有一个具有一定质量的物体A,A与碗壁间的动摩擦因数为μ,当碗绕竖直轴OO′匀速转动时,物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度.分析:物体A随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O,故此向心力不是重力而是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡.解析:物体A做匀速圆周运动,向心力:F n=mω2R而摩擦力与重力平衡,则有μF n=mg 即F n=mg/μ由以上两式可得:mω2R= mg/μ即碗匀速转动的角速度为:ω=.2、汽车沿半径为R的水平圆跑道行驶,路面作用于车的摩擦力的最大值是车重的1/10,要使汽车不致冲出圆跑道,车速最大不能超过多少?解析:跑道对汽车的摩擦力提供向心力,1/10mg=mv2/r,所以要使汽车不致冲出圆跑道,车速最大值为v=. 答案:车速最大不能超过3、一质量m=2 kg的小球从光滑斜面上高h=3.5 m处由静止滑下,斜面的底端连着一个半径R=1 m的光滑圆环(如图所示),则小球滑至圆环顶点时对环的压力为_____________,小球至少应从多高处静止滑下才能通过圆环最高点,hmin=_________(g=10 m/s2).解析:①设小球滑至圆环顶点时速度为v1,则mgh=mg·2R+ 1/2mv12F n+mg= mv12/R 得:F n=40 N②小球刚好通过最高点时速度为v2,则mg= mv22/R又mgh′=mg2R+1/2 mv22/R得h′=2.5R答案:40 N;2.5R匀速圆周运动典型问题剖析匀速圆周运动问题是学习的难点,也是高考的热点,同时它又容易和很多知识综合在一起,形成能力性很强的题目,如除力学部分外,电学中“粒子在磁场中的运动”涉及的很多问题仍然要用到匀速圆周运动的知识,对匀速圆周运动的学习可重点从两个方面掌握其特点,首先是匀速圆周运动的运动学规律,其次是其动力学规律,现就各部分涉及的典型问题作点滴说明。
(完整版)向心力练习题
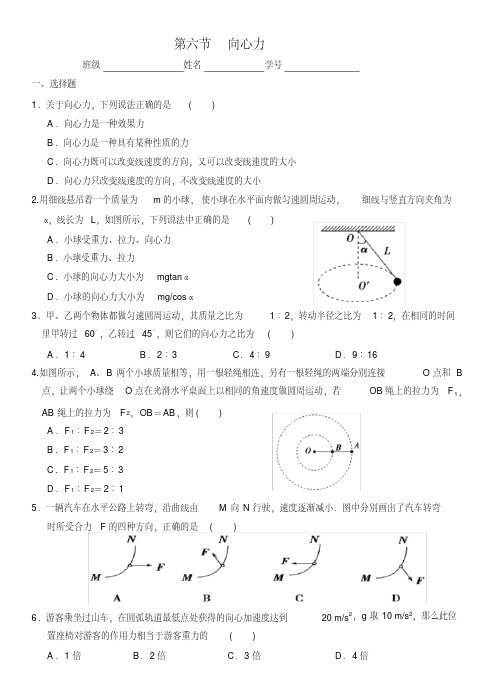
第六节向心力班级姓名学号一、选择题1.关于向心力,下列说法正确的是()A.向心力是一种效果力B.向心力是一种具有某种性质的力C.向心力既可以改变线速度的方向,又可以改变线速度的大小D.向心力只改变线速度的方向,不改变线速度的大小2.用细线悬吊着一个质量为m的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向夹角为α,线长为L,如图所示,下列说法中正确的是()A.小球受重力、拉力、向心力B.小球受重力、拉力C.小球的向心力大小为mgtanαD.小球的向心力大小为mg/cosα3.甲、乙两个物体都做匀速圆周运动,其质量之比为1∶2,转动半径之比为1∶2,在相同的时间里甲转过60°,乙转过45°,则它们的向心力之比为()A.1∶4 B.2∶3 C.4∶9 D.9∶164.如图所示,A、B两个小球质量相等,用一根轻绳相连,另有一根轻绳的两端分别连接O点和B点,让两个小球绕O点在光滑水平桌面上以相同的角速度做圆周运动,若OB绳上的拉力为F1,AB绳上的拉力为F2,OB=AB,则()A.F1∶F2=2∶3B.F1∶F2=3∶2C.F1∶F2=5∶3D.F1∶F2=2∶15.一辆汽车在水平公路上转弯,沿曲线由M向N行驶,速度逐渐减小.图中分别画出了汽车转弯时所受合力F的四种方向,正确的是()6.游客乘坐过山车,在圆弧轨道最低点处获得的向心加速度达到20 m/s2,g取10 m/s2,那么此位置座椅对游客的作用力相当于游客重力的()A.1倍B.2倍C.3倍D.4倍7.我们经常在电视中看到男、女花样滑冰运动员手拉手在冰面上旋转并表演各种优美动作.现有甲、乙两名花样滑冰运动员,M甲=80 kg,M乙=40 kg,他们面对面拉着弹簧测力计各自以他们连线上某一点为圆心做匀速圆周运动,若两人相距0.9 m,弹簧测力计的示数为600 N,则() A.两人的线速度相同,为0.4 m/sB.两人的角速度相同,为 5.0 rad/sC.两人的运动半径相同,都是0.45 mD.两人的运动半径不同,甲的半径是0.3 m、乙的半径是0.6 m8.如右图所示,质量不计的轻质弹性杆P插入桌面上的小孔中,杆的另一端套有一个质量为m的小球,今使小球在水平面内做半径为R的匀速圆周运动,且角速度为ω,则杆的上端受到球对其作用力的大小为()A.mω2RB.m g2-ω4R2C.m g2+ω4R2D.不能确定9.如图所示某物体沿14光滑圆弧轨道由最高点滑到最低点的过程中,物体的速率逐渐增大,则()A.物体的合外力为零B.物体的合力大小不变,方向始终指向圆心OC.物体的合外力就是向心力D.物体的合力方向始终与其运动方向不垂直(最低点除外)10.质量分别为M和m的两个小球,分别用长2l和l的轻绳拴在同一转轴上,当转轴稳定转动时,拴M和m的悬线与竖直方向夹角分别为α和β,如图所示,则()A.cosα=cosβ2B.cosα=2cosβC.tanα=tanβ2D.tanα=tanβ11.如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆角速度为ω1时,小球旋转平面在A处;当杆角速度为ω2时,小球旋转平面在B处,设球对杆的压力为F N,则有()A.F N1>F N2B.F N1=F N2C.ω1<ω2D.ω1>ω212.如图所示,在水平转台上放一个质量M=2 kg的木块,它与转台间最大静摩擦力F max=6.0 N,绳的一端系挂木块,通过转台的中心孔O(孔光滑),另一端悬挂一个质量m=1.0 kg的物体,当转台以角速度ω=5 rad/s匀速转动时,木块相对转台静止,则木块到O点的距离可以是(g取10 m/s2,M、m均视为质点)()A.0.04 m B.0.08 m C.0.16 m D.0.32 m13.如图所示,质量为m的滑块与轨道间的动摩擦因数为μ,当滑块从A滑到B的过程中,受到的摩擦力的最大值为Fμ,则()A.Fμ=μmg B.Fμ<μmgC.Fμ>μmg D.无法确定Fμ的值二、计算题15.甲乙两球都做匀速圆周运动,甲球的质量是乙球的3倍,甲球在半径为25 cm的圆周上运动,乙球在半径为16 cm的圆周上运动,在 1 min内,甲球转30转,乙球转75转,求甲球所受向心力与乙球所受向心力之比?16.汽车起重机用5米长的钢绳吊着1吨的重物以2米/秒的速度水平匀速行驶,如果汽车突然停车,则在一瞬间钢绳受的拉力比匀速行驶时增加了多少?17.有一种叫“飞椅”的游乐项目,示意图如图所示.长为L的钢绳一端系着座椅,另一端固定在半径为r的水平转盘边缘.转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ.不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.18.如图所示,小球沿光滑的水平面冲上一光滑的半圆形轨道,轨道半径为R,小球在轨道的最高点对轨道压力等于小球的重力,求:(1)小球离开最高点时的速度大小;(2)小球离开轨道落到地面上,小球的水平位移是多少?(3)小球落地时速度为多大?19.如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角为2θ,当圆锥和球一起以角速度ω匀速转动时,球压紧锥面.此时绳的张力是多少?若要小球离开锥面,则小球的角速度至少为多少?。
(完整版)向心力典型例题(附答案详解).docx

1、如图所示,半径为r 的圆筒,绕竖直中心轴OO′转动,小物块 a 靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使 a 不下滑,则圆筒转动的角速度ω至少为()A. B. C. D.2、下面关于向心力的叙述中,正确的是()A.向心力的方向始终沿着半径指向圆心,所以是一个变力B.做匀速圆周运动的物体,除了受到别的物体对它的作用外,还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力D.向心力只改变物体速度的方向,不改变物体速度的大小3、关于向心力的说法,正确的是()A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变5、如图所示,质量为 m 的木块,从半径为 r 的竖直圆轨道上的 A 点滑向 B 点,由于摩擦力的作用,木块的速率保持不变,则在这个过程中A.木块的加速度为零B.木块所受的合外力为零C.木块所受合外力大小不变,方向始终指向圆心D.木块所受合外力的大小和方向均不变6=80 kg,M=40 kg,面对面拉着弹簧秤做、甲、乙两名溜冰运动员, M 甲乙圆周运动的溜冰表演,如图所示,两个相距 0.9 m,弹簧秤的示数为 9.2 N,下列判断正确的是()A.两人的线速度相同,约为 40 m/sB.两人的角速度相同,为 6 rad/sC.两人的运动半径相同,都是0.45 mD.两人的运动半径不同,甲为 0.3 m,乙为 0.6 m7、如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,下列说法正确的是()A.物体所受弹力增大,摩擦力也增大B.物体所受弹力增大,摩擦力减小C.物体所受弹力减小,摩擦力也减小D.物体所受弹力增大,摩擦力不变8、用细绳拴住一球,在水平面上做匀速圆周运动,下列说法中正确的是()A.当转速不变时,绳短易断B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D.当周期不变时,绳长易断9、如图,质量为 m 的木块从半径为 R 的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变A.因为速率不变,所以木块加速度为零 C.木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变 ,方向时刻指向球心解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,故选项 A、B 不正确 .在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C 错. 答案:D10、如图所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m 和 M 的两球,两球用轻细线连接 .若 M>m,则()A.当两球离轴距离相等时,两球相对杆不动B.当两球离轴距离之比等于质量之比时,两球相对杆都不动C.若转速为ω时,两球相对杆都不动,那么转速为 2ω时两球也不动D.若两球相对杆滑动,一定向同一方向,不会相向滑动解析:由牛顿第三定律可知 M、m 间的作用力相等,即 F M =F m,F M=Mω2r M,F m=mω2rm,所以若 M、m 不动,则 r M∶r m=m∶M ,所以 A 、B 不对, C 对(不动的条件与ω无关).若相向滑动,无力提供向心力, D 对. 答案:CD 11、一物体以 4m/s 的线速度做匀速圆周运动,转动周期为 2s,则物体在运动过程的任一时刻,速度变化率的大小为()22C.02A.2m/sB.4m/s D.4 π m/s ω =2π/T=2 π/2= πv= ω *r所以r=4/πa=v ∧2/r=16/(4/π)=4 π12、在水平路面上安全转弯的汽车,向心力是()A.重力和支持力的合力B.重力、支持力和牵引力的合力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1、如图所示,半径为 R 的半球形碗内,有一个具有一定质量的物体 A,A 与碗壁间的动摩擦因数为μ,当碗绕竖直轴 OO′匀速转动时,物体 A 刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度 .分析:物体A 随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω物.体A 做匀速圆周运动所需的向心力方向指向球心O,故此向心力不是重力而是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡 .解析:物体 A 做匀速圆周运动,向心力: Fω2Rn=m而摩擦力与重力平衡,则有μF即 F n=mg/μn=mg由以上两式可得: mω2μ即碗匀速转动的角速度为:ω=R= mg/.2、汽车沿半径为 R 的水平圆跑道行驶,路面作用于车的摩擦力的最大值是车重的1/10,要使汽车不致冲出圆跑道,车速最大不能超过多少 ?解析:跑道对汽车的摩擦力提供向心力,1/10mg=mv2/r,所以要使汽车不致冲出圆跑道,车速最大值为 v=. 答案:车速最大不能超过3、一质量 m=2 kg 的小球从光滑斜面上高 h=3.5 m处由静止滑下,斜面的底端连着一个半径 R=1 m 的光滑圆环(如图所示),则小球滑至圆环顶点时对环的压力为,小球至少应从多高处静止滑下才能通过圆环最高点, hmin=_________(g=10 m/s2).匀速圆周运动典型问题剖析匀速圆周运动问题是学习的难点,也是高考的热点,同时它又容易和很多知识综合在一起,形成能力性很强的题目,如除力学部分外,电学中“粒子在磁场中的运动”涉及的很多问题仍然要用到匀速圆周运动的知识,对匀速圆周运动的学习可重点从两个方面掌握其特点,首先是匀速圆周运动的运动学规律,其次是其动力学规律,现就各部分涉及的典型问题作点滴说明。
向心力典型例题(附答案详解)

4、在光滑水平面上相距 20 cm的两点钉上 A、B 两个钉子,一根 长1 m 的细绳一端系小球, 另一端拴在 A 钉上,如图所示 .已知小 球质量为0.4 kg,小球开始以2 m/s 的速度做水平匀速圆周运动, 若绳所能承受的最大拉力为 4 N,则从开始运动到绳拉断历时为( )
A.2.4 π s
B.1.4 π s
A.两人的线速度相同,约为 40 m/s B.两人的角速度相同,为 6 rad/s
C.两人的运动半径相同,都是 0.45 m
D.两人的运动半径不同,甲为 0.3 m,乙为0.6 m
解析:甲、乙两人绕共同的圆心做圆周运动,他们间的拉力互为向心力,他 们的角速度相同,半径之和为两人的距离 .
设甲、乙两人所需向心力为 F 向,角速度为 ω,半径分别为 r 甲、r 乙.则
于皮带不打滑,所以 A、B 两点的线速度大小相等,即 vA vB 。
(1)根据
v知 C
r
B
A rB 1 (2)根据 v r 知 vC vC rC rB 1
B rA 2
vB vA rA rA 2
(3)根据 a v 知 aC
aB
vC C vB B
11 1 22 4
点评: 共轴转动的物体上各点的角速度相同,不打滑的皮带传动的两轮
(一)运动学特征及应用
匀速圆周运动的加速度、线速度的大小不变,而方向都是时刻变化的,
因此匀速圆周运动是典型的变加速曲线运动。为了描述其运动的特殊性,又
引入周期( T)、频率(f )、角速度( )等物理量,涉及的物理量及公式较
多。因此,熟练理解、掌握这些概念、公式,并加以灵活选择运用,是我们
学习的重点。
冲出圆跑道,车速最大值为 v= . 答案:车速最大不能超过 3、一质量 m=2 kg 的小球从光滑斜面上高 h=3.5 m 处由静止滑下,斜面的底 端连着一个半径 R=1 m 的光滑圆环(如图所示),则小球滑至圆环顶点时对 环的压力为 ____________,_ 小球至少应从多高处静止滑下才能通 过圆环最高点, hmin=_________(g=10 m/s2).
《向心力》习题

《向心力》习题一、单选题(本大题共9小题,共36。
0分)1、如图所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为( )A. B.C. D.2、如图所示,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动。
系A的吊绳较短,系B的吊绳较长,若天车运动到P处突然静止,则两吊绳所受拉力F A、F B的大小关系是( )A.F A>F B>mgB.F A<F B<mgC.F A=F B=mgD.F A=F B>mg3、如图所示,一根不可伸长的轻绳一端拴着一个小球,另一端固定在竖直杆上,当竖直杆以角速度ω转动时,小球跟着杆一起做匀速圆周运动,此时绳与竖直方向的夹角为θ,下列关于ω与θ关系的图象正确的是( )A. B.C. D.4、关于向心力,下列说法中正确的是( )A.物体由于做圆周运动而产生一个向心力B.向心力不改变做匀速圆周运动物体的速度大小C.做匀速圆周运动的物体的向心力是个恒力D.做一般曲线运动的物体的合力即为向心力5、如图所示,用细绳拴一小球在光滑桌面上绕一铁钉(系一绳套)做匀速圆周运动,关于小球的受力,下列说法正确的是( )A.重力、支持力B.重力、支持力、绳子拉力C.重力、支持力、绳子拉力和向心力D.重力、支持力、向心力6、图所示是上海锦江乐园新建的“摩天转轮”,它的直径达98 m,世界排名第五。
游人乘坐时,转轮始终不停地做匀速转动,每转一周用时25 min,每个厢轿共有6个座位。
试判断下列说法中正确的是()A.每时每刻,每个人受到的合力都不等于零B.每个乘客都在做加速度为零的匀速运动C.乘客在乘坐过程中对座位的压力始终不变D.乘客在乘坐过程中的速度始终保持不变7、如图所示,一个随水平圆盘转动的小物块,当圆盘加速转动时,小物块相对于圆盘保持静止,关于小物块的受力,下列说法正确的是( )A.支持力增大B.向心力变大C.摩擦力方向指向圆心D.合力指向圆心8、质量相等的A。
(完整版)向心力典型例题(附答案详解)

向心力典型例题一、选择题【共12道小题】1、如图6-7-7所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为()图6-7-7A. B. C. D.您的答案:参考答案与解析:解析:要使a不下滑,则a受筒的最大静摩擦力作用,此力与重力平衡,筒壁给a的支持力提供向心力,则N=mrω2,而f m=mg=μN,所以mg=μmrω2,故.所以A、B、C均错误,D正确.答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用2、下面关于向心力的叙述中,正确的是()A.向心力的方向始终沿着半径指向圆心,所以是一个变力B.做匀速圆周运动的物体,除了受到别的物体对它的作用外,还一定受到一个向心力的作用C.向心力可以是重力、弹力、摩擦力中的某个力,也可以是这些力中某几个力的合力,或者是某一个力的分力D.向心力只改变物体速度的方向,不改变物体速度的大小您的答案:参考答案与解析:解析:向心力是按力的作用效果来命名的,它可以是物体受力的合力,也可以是某一个力的分力,因此,在进行受力分析时,不能再分析向心力.向心力时刻指向圆心与速度方向垂直,所以向心力只改变速度的方向,不改变速度的大小,即向心力不做功.答案:ACD主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用3、关于向心力的说法,正确的是()A.物体由于做圆周运动而产生了一个向心力B.向心力不改变圆周运动物体速度的大小C.做匀速圆周运动的物体其向心力即为其所受的合外力D.做匀速圆周运动的物体其向心力大小不变您的答案:参考答案与解析:解析:向心力并不是物体受到的一个特殊力,它是由其他力沿半径方向的合力或某一个力沿半径方向的分力提供的.因为向心力始终与速度方向垂直,所以向心力不会改变速度的大小,只改变速度的方向.当质点做匀速圆周运动时,向心力的大小保持不变.答案:BCD主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用4、在光滑水平面上相距20 cm的两点钉上A、B两个钉子,一根长1 m的细绳一端系小球,另一端拴在A钉上,如图6-7-8所示.已知小球质量为0.4 kg,小球开始以2 m/s的速度做水平匀速圆周运动,若绳所能承受的最大拉力为4 N,则从开始运动到绳拉断历时为()图6-7-8A.2.4π sB.1.4π sC.1.2π sD.0.9π s您的答案:参考答案与解析:解析:当绳子拉力为4 N时,由F=可得r=0.4 m.小球每转半个周期,其半径就减小0.2 m,由分析知,小球分别以半径为1 m,0.8 m和0.6 m各转过半个圆周后绳子就被拉断了,所以时间为t==1.2π s.答案:C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用5、如图6-7-9所示,质量为m的木块,从半径为r的竖直圆轨道上的A点滑向B点,由于摩擦力的作用,木块的速率保持不变,则在这个过程中()图6-7-9A.木块的加速度为零B.木块所受的合外力为零C.木块所受合外力大小不变,方向始终指向圆心D.木块所受合外力的大小和方向均不变您的答案:参考答案与解析:解析:木块做匀速圆周运动,所以木块所受合外力提供向心力.答案:C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用6、甲、乙两名溜冰运动员,M甲=80 kg,M乙=40 kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图6-7-9所示,两个相距0.9 m,弹簧秤的示数为9.2 N,下列判断正确的是()图6-7-9A.两人的线速度相同,约为40 m/sB.两人的角速度相同,为6 rad/sC.两人的运动半径相同,都是0.45 mD.两人的运动半径不同,甲为0.3 m,乙为0.6 m您的答案:参考答案与解析:解析:甲、乙两人绕共同的圆心做圆周运动,他们间的拉力互为向心力,他们的角速度相同,半径之和为两人的距离.设甲、乙两人所需向心力为F向,角速度为ω,半径分别为r甲、r乙.则F向=M甲ω2r甲=M乙ω2r乙=9.2 N ①r甲+r乙=0.9 m ②由①②两式可解得只有D正确答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用7、如图6-7-6所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动.若圆筒和物体以更大的角速度做匀速转动,下列说法正确的是()图6-7-6A.物体所受弹力增大,摩擦力也增大B.物体所受弹力增大,摩擦力减小C.物体所受弹力减小,摩擦力也减小D.物体所受弹力增大,摩擦力不变您的答案:参考答案与解析:解析:物体在竖直方向上受重力G与摩擦力F,是一对平衡力,在向心力方向上受弹力F N.根据向心力公式,可知F N=mω2r,当ω增大时,F N增大,所以应选D.答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用8、用细绳拴住一球,在水平面上做匀速圆周运动,下列说法中正确的是()A.当转速不变时,绳短易断B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D.当周期不变时,绳长易断您的答案:参考答案与解析:解析:由公式a=ω2R=知,当角速度(转速)不变时绳长易断,故A、B 错误.周期不变时,绳长易断,故D正确.由,当线速度不变时绳短易断,C错.答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用9、如图6-7-9,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变()图6-7-9A.因为速率不变,所以木块的加速度为零B.木块下滑的过程中所受的合外力越来越大C.木块下滑过程中的摩擦力大小不变D.木块下滑过程中的加速度大小不变,方向时刻指向球心您的答案:参考答案与解析:解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,故选项A、B不正确.在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C错.答案:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用10、如图6-7-10所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m和M的两球,两球用轻细线连接.若M>m,则()图6-7-10A.当两球离轴距离相等时,两球相对杆不动B.当两球离轴距离之比等于质量之比时,两球相对杆都不动C.若转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动D.若两球相对杆滑动,一定向同一方向,不会相向滑动您的答案:参考答案与解析:解析:由牛顿第三定律可知M、m间的作用力相等,即F M=F m,F M=Mω2r M,F m=mω2r m,所以若M、m不动,则r M∶r m=m∶M,所以A、B不对,C对(不动的条件与ω无关).若相向滑动,无力提供向心力,D对.答案:CD主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用11、一物体以4m/s的线速度做匀速圆周运动,转动周期为2s,则物体在运动过程的任一时刻,速度变化率的大小为()A.2m/s2B.4m/s2C.0D.4π m/s2您的答案:参考答案与解析:D主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用12、在水平路面上安全转弯的汽车,向心力是()A.重力和支持力的合力B.重力、支持力和牵引力的合力C.汽车与路面间的静摩擦力D.汽车与路面间的滑动摩擦力您的答案:参考答案与解析:C主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用二、非选择题【共3道小题】1、如图6-7-5所示,半径为R的半球形碗内,有一个具有一定质量的物体A,A与碗壁间的动摩擦因数为μ,当碗绕竖直轴OO′匀速转动时,物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度.图6-7-5错题收藏参考答案与解析:思路分析:物体A随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O,故此向心力不是重力而是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡.解析:物体A做匀速圆周运动,向心力:F n=mω2R而摩擦力与重力平衡,则有μF n=mg即F n=由以上两式可得:mω2R=即碗匀速转动的角速度为:ω=.答案:主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用2、汽车沿半径为R的水平圆跑道行驶,路面作用于车的摩擦力的最大值是车重的十分之一,要使汽车不致冲出圆跑道,车速最大不能超过多少?错题收藏参考答案与解析:解析:跑道对汽车的摩擦力提供向心力,,所以要使汽车不致冲出圆跑道,车速最大值为v=.答案:车速最大不能超过主要考察知识点:匀速圆周运动、变速圆周运动、离心现象及其应用。
(完整版)高一物理__向心力_习题、答案(可编辑修改word版)

向心力习题1.在匀速圆周运动中,下列物理量不变的是()A.向心加速度B.线速度C.向心力D.角速度2.下列关于做匀速圆周运动的物体所受的向心力的说法中,正确的是 ( )A.物体除其他的力外还要受到—个向心力的作用B.物体所受的合外力提供向心力C.向心力是一个恒力D.向心力的大小—直在变化3.下列关于向心力的说法中正确的是()A.物体受到向心力的作用才可能做圆周运动B.向心力是指向圆心方向的合力,是根据力的作用效果来命名的,但受力分析时应该画出C.向心力可以是重力、弹力、摩擦力等各种力的合力,也可以是其中某一种力或某几种力的合力D.向心力只改变物体运动的方向,不改变物体运动的快慢4.如图所示的圆锥摆中,摆球A 在水平面上作匀速圆周运动,关于A 的受力情况,下列说法中正确的是()A.摆球 A 受重力、拉力和向心力的作用;B.摆球 A 受拉力和向心力的作用;C.摆球 A 受拉力和重力的作用;D.摆球 A 受重力和向心力的作用。
(第 4 题)(第 5 题)5.如图所示,在匀速转动的圆筒内壁上紧靠着一个物体一起运动,物体所受向心力是 ( )A.重力B.弹力C.静摩擦力D.滑动摩擦力6.如图所示,一圆盘可绕通过圆盘中心O 且垂直于盘面的竖直轴转动,在圆盘上放置一小木块A,它随圆盘一起做匀速圆周运动。
则关于木块A 的受力,下列说法正确的是()A.木块A 受重力、支持力和向心力(第 6 题)B.木块A 受重力、支持力和静摩擦力,静摩擦力的方向指向圆心C.木块A 受重力、支持力和静摩擦力,静摩擦力的方向与木块运动方向相反D.木块A 受重力、支持力和静摩擦力,静摩擦力的方向与木块运动方向相同7.甲、乙两个物体都做匀速圆周运动,其质量之比为1∶2,转动半径之比为1∶2,在相同时间里甲转过60°角,乙转过45°角。
则它们的向心力之比为()A.1∶4B.2∶3C.4∶9D.9∶168.如图所示,长为L 的悬线固定在O 点,在O 点正下方L处有一钉子C,把悬2线另一端的小球m 拉到跟悬点在同一水平面上无初速度释放,小球到悬点正下方时悬线碰到钉子,则小球的()A.线速度突然增大B.角速度突然增大C.向心加速度突然增大D.悬线拉力突然增大D.当ω增大时,P 球将向外运动(第8 题)10.如图所示,质量为m 的滑块与轨道间的动摩擦因数为μ,当滑块从A 滑到B 的过程中,受到的摩擦力的最大值为Fμ,则()A.Fμ=μmg B.Fμ<μmgC.Fμ>μmg D.无法确定Fμ的值(第10 题)13.一个质量为M 的物体在水平转盘上,距离转轴的距离为r,当转盘的转速为n 时,物体相对于转盘静止,如果转盘的转速增大时,物体仍然相对于转盘静止,则下列说法中正确的是 ( )A.物体受到的弹力增大B.物体受到的静摩擦力增大C.物体受到的合外力不变D.物体对转盘的压力减小14.如图所示,质量为m 的滑块从半径为R 的光滑固定圆弧形轨道的a 点滑到b 点,下列说法中正确的是()A.它所受的合外力的大小是恒定的B.向心力大小逐渐增大C.向心力逐渐减小D.向心加速度逐渐增大(第 4 题)15.一木块放于水平转盘上,与转轴的距离为r,若木块与盘面间的最大静摩擦力是木块重力的μ倍,则转盘转动的角速度最大是。
向心力练习题

向心力练习题姓名班级学号一、选择题1、对做圆周运动的物体所受的向心力说法正确的是()A.因向心力总是沿半径指向圆心,且大小不变,故向心力是一个恒力B.向心力和向心加速度的方向都是不变的C.向心力是物体所受的合外力D.因向心力指向圆心,且与线速度方向垂直,所以它不能改变线速度的大小2.如图所示,一只老鹰在水平面内盘旋做匀速圆周运动,则关于老鹰受力的说法正确的是()A.老鹰受重力、空气对它的作用力和向心力的作用B.老鹰受重力和空气对它的作用力C.老鹰受重力和向心力的作用D.老鹰受空气对它的作用力和向心力的作用3、如图所示,一辆轿车正在水平路面上转弯,下列说法正确的是()A.水平路面对轿车弹力的方向斜向上B.轿车受到的静摩擦力提供转弯的向心力C.轿车受到的向心力是重力、支持力和牵引力的合力D.轿车所受的合力方向一定与运动路线的切线方向垂直4、平冰面上,狗拉着雪橇,雪橇做匀速圆周运动,O点为圆心(如图所示).能正确地表示雪橇受到的拉力F及摩擦力Ff的图是()5、种杂技表演叫“飞车走壁”,由杂技演员驾驶摩托车沿圆台形表演台的侧壁高速行驶,做匀速圆周运动,如图所示.图中虚线表示摩托车的行驶轨迹,轨迹离地面的高度为h.下列说法中正确的是()A.h越大,摩托车对侧壁的压力将越大B.h越大,摩托车做圆周运动的向心力将越大C.h越大,摩托车做圆周运动的周期将越大D.h越大,摩托车做圆周运动的线速度将越大6、所示,物块质量为m,一直随转筒一起以角速度ω绕竖直轴做匀速圆周运动,以下描述正确的是()A.物块所需向心力由圆筒对物块的摩擦力提供B.若角速度ω增大,物块所受摩擦力增大C.若角速度ω增大,物块所受弹力增大D.若角速度ω减小,物块所受摩擦力减小7、所示,在粗糙水平板上放一个物体,使水平板和物体一起在竖直平面内沿逆时针方向做匀速圆周运动,ab为水平直径,cd为竖直直径,在运动过程中木板始终保持水平,物块相对木板始终静止,则:()A.物块始终受到三个力作用B.只有在a、b、c、d四点,物块受到合外力才指向圆心C.从a到b,物体所受的摩擦力先增大后减小D.从b到a,物块处于超重状态8、所示,光滑水平面上有原长为L的轻弹簧,它一端固定在光滑的转轴O上,另一端系一小球.当小球在该平面上做半径为2L的匀速圆周运动时,速率为v;当小球在该平面上做半径为3L的匀速圆周运动时,速率为v′.弹簧总处于弹性限度内.则v:v′等于()A.:B.2:3C.1:3D.1:9、量为m的小物块沿半径为R的圆弧轨道下滑,滑到最低点时的速度是v,若小物块与轨道的动摩擦因数是μ,则当小物块滑到最低点时受到的摩擦力是()A.μB.μm()D.μm(g--g))C.μm(g+10、和B用细线连接,可以在光滑的水平杆上无摩擦地滑动,已知它们的质量之比m1∶m2=3∶1,当这一装置绕着竖直轴做匀速转动且A、B 两球与水平杆达到相对静止时(如图所示),则A、B两球做匀速圆周运动的()A.线速度大小相等B.角速度相等C.向心力的大小之比为F1∶F2=3∶1D.半径之比为r1∶r2=1∶311、如图所示,一个内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在图中所示的水平面内做匀速圆周运动,则()A.球A的线速度必定大于球B的线速度B.球A的角速度必定小于球B 的角速度C.球A的运动周期必定小于球B的运动周期D.球A对筒壁的压力必定大于球B对筒壁的压力12、示,一个圆形框架以竖直的直径为转轴匀速转动。
向心力典型例题

向心力典型例题(附答案详解)一、选择题【共12道小题】1、如图所示,半径为r的圆筒,绕竖直中心轴OO′转动,小物块a靠在圆筒的内壁上,它与圆筒的动摩擦因数为μ,现要使a不下滑,则圆筒转动的角速度ω至少为( )A、B、 C. D.解析:要使a不下滑,则a受筒的最大静摩擦力作用,此力与重力平衡,筒壁给a的支持力提供向心力, 则N=mrω2,而fm=mg=μN,所以mg=μmrω2,故、所以A、B、C均错误,D正确、4、在光滑水平面上相距20 cm的两点钉上A、B两个钉子,一根长1 m的细绳一端系小球,另一端拴在A钉上,如图所示、已知小球质量为0、4kg,小球开始以2 m/s的速度做水平匀速圆周运动,若绳所能承受的最大拉力为4N,则从开始运动到绳拉断历时为( )A.2.4πs B.1、4π s C、1、2π s D、0、9π s解析:当绳子拉力为4N时,由F=可得r=0、4 m、小球每转半个周期,其半径就减小0.2 m,由分析知,小球分别以半径为1m,0、8 m与0.6 m各转过半个圆周后绳子就被拉断了,所以时间为t==1.2πs.答案:C6、甲、乙两名溜冰运动员,M 甲=80 kg,M 乙=40 kg,面对面拉着弹簧秤做圆周运动的溜冰表演,如图所示,两个相距0、9 m,弹簧秤的示数为9、2 N,下列判断正确的就是( )A 、两人的线速度相同,约为40 m /sB 、两人的角速度相同,为6 rad/sC 、两人的运动半径相同,都就是0.45 mD 、两人的运动半径不同,甲为0、3 m,乙为0、6 m 解析:甲、乙两人绕共同的圆心做圆周运动,她们间的拉力互为向心力,她们的角速度相同,半径之与为两人的距离、设甲、乙两人所需向心力为F 向,角速度为ω,半径分别为r 甲、r 乙、则F 向=M 甲ω2r 甲=M 乙ω2r 乙=9.2 N ① r甲+r 乙=0、9 m ②由①②两式可解得只有D 正确 答案:D7、如图所示,在匀速转动的圆筒内壁上有一物体随圆筒一起转动而未滑动、若圆筒与物体以更大的角速度做匀速转动,下列说法正确的就是( )A.物体所受弹力增大,摩擦力也增大 B 、物体所受弹力增大,摩擦力减小C 、物体所受弹力减小,摩擦力也减小D 、物体所受弹力增大,摩擦力不变析:物体在竖直方向上受重力G 与摩擦力F,就是一对平衡力,在向心力方向上受弹力F N、根据向心力公式,可知F N=mω2r,当ω增大时,F N增大,选D、8、用细绳拴住一球,在水平面上做匀速圆周运动,下列说法中正确的就是()A、当转速不变时,绳短易断 B.当角速度不变时,绳短易断C.当线速度不变时,绳长易断D、当周期不变时,绳长易断析:由公式a=ω2R=知,当角速度(转速)不变时绳长易断,故A、B错误、周期不变时,绳长易断,故D正确、由,当线速度不变时绳短易断,C错9、如图,质量为m的木块从半径为R的半球形的碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使得木块的速率不变A、因为速率不变,所以木块加速度为零C、木块下滑过程中的摩擦力大小不变B.木块下滑的过程中所受的合外力越来越大D.木块下滑过程中的加速度大小不变,方向时刻指向球心解析:木块做匀速圆周运动,所受合外力大小恒定,方向时刻指向圆心,故选项A、B不正确、在木块滑动过程中,小球对碗壁的压力不同,故摩擦力大小改变,C 错、答案:Dﻫ10、如图所示,在光滑的以角速度ω旋转的细杆上穿有质量分别为m与M的两球,两球用轻细线连接、若M>m,则( )A、当两球离轴距离相等时,两球相对杆不动B、当两球离轴距离之比等于质量之比时,两球相对杆都不动C.若转速为ω时,两球相对杆都不动,那么转速为2ω时两球也不动D、若两球相对杆滑动,一定向同一方向,不会相向滑动解析:由牛顿第三定律可知M、m间的作用力相等,即FM=Fm,F M=Mω2r M,F m=mω2rm,所以若M、m不动,则rM∶rm=m∶M,所以A、B不对,C对(不动的条件与ω无关).若相向滑动,无力提供向心力,D对、答案:CD11、一物体以4m/s的线速度做匀速圆周运动,转动周期为2s,则物体在运动过程的任一时刻,速度变化率的大小为( )A、2m/s2B、4m/s2C、0D、4π m/s2ω=2π/T=2π/2=πv=ω*r所以r=4/πa=v∧2/r=16/(4/π)=4π12、在水平路面上安全转弯的汽车,向心力就是( )A、重力与支持力的合力B、重力、支持力与牵引力的合力C 汽车与路面间的静摩擦力 D.汽车与路面间的滑动摩擦力二、非选择题【共3道小题】1ﻫ、如图所示,半径为R的半球形碗内,有一个具有一定质量的物体A,A与碗壁间的动摩擦因数为μ,当碗绕竖直轴OO′匀速转动时,物体A刚好能紧贴在碗口附近随碗一起匀速转动而不发生相对滑动,求碗转动的角速度、分析:物体A随碗一起转动而不发生相对滑动,物体做匀速圆周运动的角速度ω就等于碗转动的角速度ω.物体A做匀速圆周运动所需的向心力方向指向球心O,故此向心力不就是重力而就是由碗壁对物体的弹力提供,此时物体所受的摩擦力与重力平衡、解析:物体A做匀速圆周运动,向心力:F n=mω2R而摩擦力与重力平衡,则有μFn=mg 即F n=mg/μ由以上两式可得:mω2R= mg/μ即碗匀速转动的角速度为:ω=、2、汽车沿半径为R的水平圆跑道行驶,路面作用于车的摩擦力的最大值就是车重的1/10,要使汽车不致冲出圆跑道,车速最大不能超过多少?解析:跑道对汽车的摩擦力提供向心力,1/10mg=mv2/r,所以要使汽车不致冲出圆跑道,车速最大值为v=、答案:车速最大不能超过ﻫ3、一质量m=2 kg的小球从光滑斜面上高h=3、5m处由静止滑下,斜面的底端连着一个半径R=1 m的光滑圆环(如图所示),则小球滑至圆环顶点时对环的压力为_____________,小球至少应从多高处静止滑下才能通过圆环最高点,hmin=_________(g=10 m/s2)、解析:①设小球滑至圆环顶点时速度为v1,则mgh=mg·2R+1/2mv12Fn+mg=mv12/R得:F n=40 N ②小球刚好通过最高点时速度为v2,则mg= mv22/R又mgh′=mg2R+1/2 mv 22/R 得h′=2.5R 答案:40 N;2.5R ﻫ匀速圆周运动典型问题剖析1. 基本概念、公式的理解与运用[例2] 在绕竖直轴匀速转动的圆环上有A 、B 两点,如图1所示,过A 、B的半径与竖直轴的夹角分别为30°与60°,则A、B 两点的线速度之比为 ;向心加速度之比为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六节向心力
班级姓名学号
一、选择题
1.关于向心力,下列说法正确的是()
A.向心力是一种效果力
B.向心力是一种具有某种性质的力
C.向心力既可以改变线速度的方向,又可以改变线速度的大小
D.向心力只改变线速度的方向,不改变线速度的大小
2.用细线悬吊着一个质量为m的小球,使小球在水平面内做匀速圆周运动,细线与竖直方向夹角为
α,线长为L,如图所示,下列说法中正确的是()
A.小球受重力、拉力、向心力
B.小球受重力、拉力
C.小球的向心力大小为mgtanα
D.小球的向心力大小为mg/cosα
3.甲、乙两个物体都做匀速圆周运动,其质量之比为1∶2,转动半径之比为1∶2,在相同的时间里甲转过60°,乙转过45°,则它们的向心力之比为()
A.1∶4 B.2∶3 C.4∶9 D.9∶16
4.如图所示,A、B两个小球质量相等,用一根轻绳相连,另有一根轻绳的两端分别连接O点和B
点,让两个小球绕O点在光滑水平桌面上以相同的角速度做圆周运动,若OB绳上的拉力为F1,AB绳上的拉力为F2,OB=AB,则()
A.F1∶F2=2∶3
B.F1∶F2=3∶2
C.F1∶F2=5∶3
D.F1∶F2=2∶1
5.一辆汽车在水平公路上转弯,沿曲线由M向N行驶,速度逐渐减小.图中分别画出了汽车转弯时所受合力F的四种方向,正确的是()
6.游客乘坐过山车,在圆弧轨道最低点处获得的向心加速度达到20 m/s2,g取10 m/s2,那么此位置座椅对游客的作用力相当于游客重力的()
A.1倍B.2倍C.3倍D.4倍
7.我们经常在电视中看到男、女花样滑冰运动员手拉手在冰面上旋转并表演各种优美动作.现有甲、乙两名花样滑冰运动员,M甲=80 kg,M乙=40 kg,他们面对面拉着弹簧测力计各自以他们连线上某一点为圆心做匀速圆周运动,若两人相距0.9 m,弹簧测力计的示数为600 N,则() A.两人的线速度相同,为0.4 m/s
B.两人的角速度相同,为 5.0 rad/s
C.两人的运动半径相同,都是0.45 m
D.两人的运动半径不同,甲的半径是0.3 m、乙的半径是0.6 m
8.如右图所示,质量不计的轻质弹性杆P插入桌面上的小孔中,杆的另一端套有一个质量为m
的小球,今使小球在水平面内做半径为R的匀速圆周运动,且角速度为ω,则杆的上端受到球对其作用力的大小为()
A.mω2R
B.m g2-ω4R2
C.m g2+ω4R2
D.不能确定
9.如图所示某物体沿1
4
光滑圆弧轨道由最高点滑到最低点的过程中,物体的速率逐渐增大,则()
A.物体的合外力为零
B.物体的合力大小不变,方向始终指向圆心O
C.物体的合外力就是向心力
D.物体的合力方向始终与其运动方向不垂直(最低点除外)
10.质量分别为M和m的两个小球,分别用长2l和l的轻绳拴在同一转轴上,当转轴稳定转动时,
拴M和m的悬线与竖直方向夹角分别为α和β,如图所示,则()
A.cosα=cosβ2
B.cosα=2cosβ
C.tanα=tanβ2
D.tanα=tanβ
11.如图所示,光滑杆偏离竖直方向的夹角为θ,杆以O为支点绕竖直线旋转,质量为m的小球套在杆上可沿杆滑动.当杆角速度为ω1时,小球旋转平面在A处;当杆角速度为ω2时,小球旋转平面在B处,设球对杆的压力为F N,则有()
A.F N1>F N2
B.F N1=F N2
C.ω1<ω2
D.ω1>ω2
12.如图所示,在水平转台上放一个质量M=2 kg的木块,它与转台间最大
静摩擦力F max=6.0 N,绳的一端系挂木块,通过转台的中心孔O(孔光滑),
另一端悬挂一个质量m=1.0 kg的物体,当转台以角速度ω=5 rad/s匀速
转动时,木块相对转台静止,则木块到O点的距离可以是(g取10 m/s2,
M、m均视为质点)()
A.0.04 m B.0.08 m C.0.16 m D.0.32 m
13.如图所示,质量为m的滑块与轨道间的动摩擦因数为μ,当滑块从A滑到B的过程中,受到的摩擦力的最大值为Fμ,则()
A.Fμ=μmg B.Fμ<μmg
C.Fμ>μmg D.无法确定Fμ的值
二、计算题
15.甲乙两球都做匀速圆周运动,甲球的质量是乙球的3倍,甲球在半径为25 cm的圆周上运动,乙球在半径为16 cm的圆周上运动,在 1 min内,甲球转30转,乙球转75转,求甲球所受向心力与乙球所受向心力之比?
16.汽车起重机用5米长的钢绳吊着1吨的重物以2米/秒的速度水平匀速行驶,如果汽车突然停车,则在一瞬间钢绳受的拉力比匀速行驶时增加了多少?
17.有一种叫“飞椅”的游乐项目,示意图如图所示.长为L的钢绳一端系着座椅,另一端固定在
半径为r的水平转盘边缘.转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时,钢绳与转轴在同一竖直平面内,与竖直方向的夹角为θ.不计钢绳的重力,求转盘转动的角速度ω与夹角θ的关系.
18.如图所示,小球沿光滑的水平面冲上一光滑的半圆形轨道,轨道半径为R,小球在轨道的最高点对轨道压力等于小球的重力,求:
(1)小球离开最高点时的速度大小;
(2)小球离开轨道落到地面上,小球的水平位移是多少?
(3)小球落地时速度为多大?
19.如图所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角为2θ,当圆锥和
球一起以角速度ω匀速转动时,球压紧锥面.此时绳的张力是多少?若要小球离开锥面,则小球的角速度至少为多少?。
