材料力学剪切.
材料力学-剪切

剪切
一、剪切强度计算及挤压强度计算
1.单剪
设两块钢板有 n 个铆钉联接,钢板两端受拉力 P 作用 (见图3-1)。
P t1
t2 P
P
P
钢板联接图 图3-1
(1)绘铆钉受力图:
t1 P/n
Q P n
P/n
t2
Pc= P/n
|d|
|d|
铆钉受力图 图3-2
(2)剪切强度条件为:
Q P 3 1
2 20 12106
104MPa
II-II截面
3P
3 200103
II II
b2
5
3d t2
5
200 3 20 12106
71.4MPa
(2)盖板:
P/5
II
P/2
盖板轴力图
II II-II截面
II-II截面内力比I-I截面大,而截面积比I-I截面小,故只 需校核II-II截面。
II II
P nAC 2
P nt2d
C1
PC 1 AC 1
P nAC 1
P 2nt1d
比较: C2 C1
C2
200 103 5 12 20106
167MPa
C2
(四)绘主板和盖板的轴力图并进行强度校核。
(1)主板:
P
I
3P
II
5
主板轴力图
I-I截面
I
II
II
b2
P
2d t2
200
200 103
Q P 3 1
AQ 2nAQ
如需求铆钉的个数,则
n
P
2AQ
3
2
挤压强度条件:
材料力学:第三章 剪切

F 挤压面上应力分布也是复杂的
F
实用计算中,名义挤压应力公式
bs
Fbs Abs
Fbs
Fbs
Abs d
——挤压面的计算面积
挤压强度条件:
bs
Fbs Abs
bs
挤压强度条件同样可解三类问题 bs 常由实验方法确定
例: 已知: =2 mm,b =15 mm,d =4 mm,[ =100 MPa, [] bs =300 MPa,[ ]=160 MPa。 试求:[F]
第三章 剪 切
一. 剪切的概念和实例 二. 剪切的实用计算 三. 挤压的实用计算
一. 剪切的概念和实例 工程实际中用到各种各样的连接,如: 铆钉
销轴
平键 榫连接
(剪切)受力特点: 作用在构件两侧面上的外力合力大小相 等、方向相反且作用线相距很近。
变形特点: 构件沿两力作用线之间的某一截面产生相 对错动或错动趋势。
F F
剪切面上的内力 Fs (用截面法求)
实用计算中假设切应力在剪切
F
m m
面(m-m截面)上是均匀分布的 F
名义切应力计算公式:
F
m
m
FS
FS m
m
F
Fs
A
剪切强度条件:
Fs
A
——名义许用切应力
由实验方法确定
剪切强度条件同样可解三类问题
三. 挤压的实用计算
挤压力不是内力,而是外力
解: 1、剪切强度
4F πd 2
[
]
F πd 2[ ] 1.257 kN
4
2、挤压强度
bs
F
d
[ ]bs
F d[ ]bs 2.40KN
3、钢板拉伸强度 F
材料力学 第三章 剪切

根据平衡条件可得
F0 =F =70kN
钢板危险截面拉伸应力为
0
F0 A0
=
70103 N 252106 m2
277.78MPa>275MPa
277.78 275 100% 1.01% 故螺栓满足强度条件
275
明德行远 交通天下
材料力学
例题3-2 某接头部分销钉如图所示,F=110 kN,试求销钉的切应力和挤压应力。
明德行远 交通天下
材料力学
单面剪切
双面剪切
明德行远 交通天下
复杂双面剪切
材料力学
二、剪切的工程实例
铆钉或高强螺栓连接
销轴连接
明德行远 交通天下
铆钉连接
榫连接
材料力学
§3-2 剪切的实用计算
一、连接处破坏三种形式 ①剪切破坏
以铆钉为例:
沿铆钉的剪切面剪断,如沿m–
m面剪断 。
②挤压破坏
铆钉与钢板在相互接触面上因
明德行远 交通天下
材料力学
解:先分析螺栓的剪切面积和挤压面积
剪切面积为 挤压面积为
A
d2
3.14 30 mm2
=
706.5mm2
4
4
Abs dh=3018mm2 540mm2
根据平衡条件可得
挤压力为
FS=F =70kN
FbS =F =70kN
明德行远 交通天下
材料力学
螺栓截面切应力为
FS A
材料力学
第三章 剪切
明德行远 交通天下
材料力学
主要内容
• §3-1 剪切的概念和工程实例 • §3-2 剪切的实用计算 • §3-3 挤压的实用计算
明德行远 交通天下
材料力学第二章剪切

64kN
m P
L
b
d
材料力学
2 剪切面与挤压面的判定
AQ bl
h Abs 2 l
h
L
AQ
b
材料力学
3 切应力和挤压应力的强度条件
FQ [ ]
Lb
[
L1
]
FQ
b
64 16 80
10 3 (
m
)
50mm
2 Pbs Lh
[ bs ]
[
L2
]
2 Pbs
h[ bs ]
2 64 10 240
F
F
F
b
τ FS AS
n πd2
4F nπd 2
[τ]
4
(b) 图7−6
材料力学
➢对于对接方式,每个铆钉有两个剪切面.
每个铆钉每个剪切面上的剪力为
FS
F 2n
F
F
剪切强度条件为
(a)
F
F
F
b
FS AS
2n
d2
4F
n d 2
(b)
4
材料力学
2. 铆钉与钢板孔壁之间的挤压实用计算
➢ 对于搭接构件,挤压强度条件为
材料力学
键: 连接轴和轴上的传动件(如齿轮、皮带轮等),使轴
和传动件不发生相对转动,以传递扭矩。
材料力学
键连接的传动系统
材料力学
分析轮、轴、平键结构中键的剪切面与挤压面
(1)、 取轴和键为研究对象进行受力分析 F
M F d 0
M
2
(2)、单独取键为研究对象受力分析
键的左侧上半部分受到轮给键的约束反力的作用,合力大小F;
T
材料力学课件第三章剪切

剪切现象
生活中的剪切现象
如剪刀剪纸、锯子锯木头等,都 是典型的剪切现连接处, 由于受到垂直于连接面的力而发 生相对错动。
剪切应力与应变
剪切应力
在剪切过程中,作用在物体上的剪切力与物体截面面积的比值称 为剪切应力。
剪切应变
04
剪切破坏与预防措施
剪切破坏类型
01
02
03
04
脆性剪切
材料在无明显屈服的情况下突 然发生剪切断裂,多发生在脆 性材料中。
韧性剪切
材料在发生屈服后逐渐发生剪 切断裂,多发生在韧性材料中 。
疲劳剪切
材料在循环应力作用下发生的 剪切断裂,多发生在高强度材 料中。
热剪切
由于温度变化引起的剪切断裂 ,多发生在高温环境下。
车辆工程中的剪切问题
航空航天器在高速飞行时,会受到气 动力的剪切效应,影响其稳定性。
车辆在行驶过程中,车体结构会受到 风力、路面等载荷的剪切作用,影响 车辆的安全性和舒适性。
船舶结构中的剪切变形
船舶在航行过程中,会受到波浪、水 流等载荷的剪切作用,影响其结构安 全。
THANK YOU
感谢聆听
患。
05
剪切在实际工程中的应用
建筑结构中的剪切问题
80%
桥梁结构的剪切变形
桥梁在受到车辆等载荷作用时, 会发生剪切变形,影响结构的稳 定性。
100%
高层建筑的剪切力传递
高层建筑中的剪切力对建筑物的 稳定性和安全性具有重要影响。
80%
地震作用下的剪切效应
地震时,建筑结构会受到地震波 的剪切作用,可能导致结构破坏 。
03
剪切与弯曲的关系
弯曲与剪切的相互作用
材料力学剪切

P
n
P
面剪断;
三、破坏形式分析:
连接处可能发生的三种破坏形式: 1 、剪切破坏
P
2 、挤压破坏
铆钉与钢板在相互接触面上因挤
而使连接松动,发生破坏。 3 、拉伸破坏 钢板在受铆钉孔削弱的截面处, 应力增大,易在连接处拉断。
剪切和挤压的实用计算方法: 1、连接件的受力和变形较复杂;
2、受加工工艺的影响;
挤压面积:
FS P 40 10 7 0.952 MPa AS a b 12 35
Abs c b
Fbs P 40 bs 10 7 7.4MPa Abs c b 4.5 12
思考题1: 在平板和受拉螺栓之间垫上一个垫圈,如 图所示,可以提高( )。 A.螺栓的拉伸强度 C.螺栓的挤压强度 正确答案:D B.螺栓的剪切强度 D.平板的挤压强度
b
d
As
d 2
4
;
FS 4 F 2 AS d
F 1 1.257 KN
F 2 2.4KN
铆钉的挤压面积及挤压应力:
Abs d
Fbs F bs bs Abs d
例1——例8-12 解:2、板的轴力为: F
2 F
FN F
F
δ
F
b
d
可能的破坏形式分析:
F
δ 1 2 F 1
F
1、铆钉沿1-1截面被剪断; 2、铆钉被挤压发生显 著塑性变形;
3、板在铆钉孔处沿2-2 截面被拉断; 4、板在铆钉孔处沿3-3 截面被剪断; 3 3
F
2
例1——例8-12 解:1、铆钉的剪切力和挤 压力为:
F
δ
材料力学——第二章剪切

不等,而外力作用线通过钉群截 F1
F2
F
面 形心,
则每一铆钉的受力与该铆钉的横 截面面积成正比。
(3) 各铆钉材料相同、直径相等,外力偶作用面垂直于铆钉轴线
各铆钉受力大小与该铆钉横截面形心至钉群截面形心的距离 成正比, 而力的方向与该铆钉至钉群截面形心的连线相 垂直。
T
FQ
1. 铆钉的剪切实用计算
(2)假设:
切应力在剪切面上均匀分布;
(3)名义切应力 A:剪切面面积,不一定是横截面面积,但与外截荷平行;
剪切强度条件:
可解决三类问题: 1、强度校核; 2、选择截面尺寸; 3、确定许可载荷;
名义许用切应力
在假定的前提下进行 实物或模型实验,确 定许用应力。
例1 图示冲床的最大冲压力为400KN,冲头的直径 d=34mm,试求此冲床所能冲剪钢板的最大厚度 t。
h L b
综上,键满足强度要求。
m P
d
例2 齿轮与轴由平键(b=16mm,h=10mm,)连接,它传递的扭
矩m=1600Nm,轴的直径d=50mm,键的许用剪应力为[]= 80M Pa ,许用挤压应力为[bs]= 240M Pa,试设计键的长度。
键的受力分析 m
h
L b
m P
d
2 剪切面与挤压面的判定
连接件,通常发生与轴向拉压不同的变形,但也是杆件的 基本变形之一; 实用计算:
按构件的破坏可能性,采用既反映受力的基本特征,又 简化计算的假设,计算其名义应力,然后根据直接试验 的结果,确定许用应力,进行强度计算。
§2-2 剪切的实用计算
FS=F
剪力 与剪切面平行的内力
剪切变形的实用计算
(1)实际: 从有限元计算结果看剪切面上 应力的分布情况十分复杂,工 程中采用近似计算。
材料力学-第三章-剪切实用计算(上交)

FQ A
材料力学
剪切实用计算
剪切强度条件:
FQ A
[ ]
名义许用剪应力
可解决三类问题: 1、选择截面尺寸; 2、确定最大许可载荷, 3、强度校核。
材料力学
在假定的前提下进行 实物或模型实验,确 定许用应力。
[例3.1 ] 图示装置常用来确定胶接处的抗剪强度,如已知 破坏时的荷载为10kN,试求胶接处的极限剪(切)应力。 F F
F / 2n [ j ] 1 A d 2 4
2F n 3 . 98 2 d [ j ]
FQ
(2)铆钉的挤压计算
jy
Fb F /n [ A jy t1 d
]
jy
]
F n t1 d [
材料力学
3 . 72
jy
剪切实用计算
因此取 n=4. I F/n F/n F/n F F/n
R
R0
t
1 t R0 10 为薄壁圆筒
材料力学
材料力学
(1)
C D A B C D
A B
横截面上存在剪应力
材料力学
纯剪切的概念
(2)其他变形现象:圆周线之间的距离保持不变,仍为圆形, 绕轴线产生相对转动。 横截面上不存在正应力,且横截面上的剪应力的 方向是沿着圆周的切线方向,并设沿壁厚方向是 均匀分布的。 T
h d F d
剪切面
h
解
FN 4 F A d 2 F Q F AQ dh
当 , 分别达到 [] , [] 时, 材料的利用最合理
材料力学
F 4F 0 .6 2 得 d : h 2 .4 dh d
材料力学2-3剪切

1、剪切的概念 2、剪切的假定计算 3、挤压的概念 4、挤压的假定计算 5、连接板的计算
1、剪切的概念
(1)受力特点 ) 作用于构件某一截面( 作用于构件某一截面(剪 切面)两侧的力,大小相等、 切面)两侧的力,大小相等、 方向相反且相距很近。 方向相反且相距很近。 (2)变形特点 ) 构件的两部分沿剪切面 发生相对错动。 发生相对错动。
解:(1)铆钉剪切强度 :( ) 各铆钉受到剪力: 各铆钉受到剪力: Q=P/4=17.5kN 各铆钉受剪面积: 各铆钉受剪面积: A= πd2/4=254mm2 τ=Q/ A =68.8MPa<[τ] ∴铆钉剪切强度符合要求。 铆钉剪切强度符合要求。 (2)铆钉或板的挤压强度 ) 挤压力P 挤压力 jy=P/4=17.5kN,挤压计算面积 bs= td=180mm2, ,挤压计算面积A σbs= Pjy /Abs=97.2MPa<[σbs], , ∴铆钉挤压强度符合要求
d
t
(2)挤压强度计算 )
σ bs
P = ≤ [σ bs ] Abs
• 材料的许用挤压应力[σbs]可由有关规范中查到。 材料的许用挤压应力[σ 可由有关规范中查到。 • 对于钢材,一般可取[σbs]=(1.7—2.0)[σ] 对于钢材,一般可取[σ ]=(1.7 2.0)[σ]
例题1 铆钉和板用同一种材料制成,已知t=8mm, 例题 、铆钉和板用同一种材料制成,已知 , [τ]=30MPa,[σbs]=100MPa, P=15kN,试选择直径 。 , ,试选择直径d。 解:取铆钉中段研究 铆钉中段研究 • • • • • • • • • ①剪切强度计算 剪力: 剪力:Q=P/2=7.5kN τ= Q/A =Q/(πd2/4)≤[τ] → d ≥ 17.8mm ②挤压强度计算 挤压力:P=15kN,Abs=2td, 挤压力: , σbs= P /Abs≤[σbs] → d ≥ 9.4mm ∴ d ≥ 17.8mm。若取标准件,查手册,d=20mm。 。若取标准件,查手册, 。
材料力学第2章13节剪切

t
FS A
tb
tb为剪切强
度极限 。
t Fs F
A lb
bs
Fbs Abs
F cb
例1 齿轮与轴由平键(b=16mm,h=10mm,) 连接,它传递的扭矩m=1600N·m,轴的直径
d=50mm,键的许用切应力为[t]= 80MPa ,许用 挤压应力为[bs]= 240MPa,试设计键的长度。
或圆钉的直径平面面积dd(即图b中画阴影线的面
积)除挤压力F,则所得应力大致上与实际最大应 力接近。
剪切破坏的利用
在工程实际中,有时也会遇到与前面问题 相反的情况,就是剪切破坏的利用。例如车床 传动轴上的保险销(图a),当载荷增加到某一数 值时,保险销即被剪断,从而保护车床的重要 部件。又如冲床冲模时使工件发生剪切破坏而 得到所需要的形状(图b),也是利用剪切破坏的 实例。对这类问题所要求的破坏条件为:
188103 99104
19106 Pa
19MPa
[bs ] 200MPa
故挤压强度也是足够的。
例4 一铆接头如图所示,受力P=110kN,已知
钢板厚度为 t=1cm,宽度 b=8.5cm ,许用应力
为[ ]= 160MPa ;铆钉的直径d=1.6cm,许用剪
应力为[t ]= 140MPa ,许用挤压应力为[bs]=
4
4
销轴的工作切应力为
t
FS A
94 103 63.6 104
14.8106 Pa
14.8 MPa
[t ] 90
MPa
符合强度条件, 所以销轴的剪切强度是足够的。
(2) 校核挤压强度
d1=110 mm, d2=75 mm
销轴的挤压面是圆柱面, 用通过圆柱直径的平面面积作 为挤压面的计算面积。
材料力学课件:剪切应力
铆钉连接
剪切面
F
F
m m
F
F
§ 4 . 2 剪切
双剪切
§ 4 . 2 剪切
剪切面在哪?
§ 4 . 2 剪切
连接件的破坏形式一般有两种:
1、剪切破坏
构件两部分
F
沿剪切面发生滑
移、错动
F
F
m
m
F
2、挤压破坏 在接触区的局
部范围内,产生显 著塑性变形
挤压破坏实例
Fbs Fbs
剪切与挤压破坏都是复杂的情况,这里仅介绍工程上的实用计算方法
挤压面积的计算 (1)挤压面积为平面按实际面积计算。 (2)挤压面积为非平面按投影面积计算。
§ 4 . 2 剪切
4.2.2 挤压的实用计算
P
P
Fbs
挤压力
Fs
• 假设挤压应力在挤压面积上均匀分布
bs
=
Fbs Abs
t 板的厚度
Fbs
§ 4 . 2 剪切
4.2.3 板的抗拉强度
F
由于截面急剧变化引起应力局部增大现象-应力集 中
d=20mm,铆钉的[ ]=100 MPa, 铆钉的[bs]=300 MPa, 钢板的
[ ]=160 MPa ,试求许用载荷 F
解:1.按剪切强度条件求 F
F t
tF
假定每个铆钉受力相同,每个铆钉
剪切面上的剪力为Fs=F/3
F
d F
b
Fs F /3 [] A d2 /4
F3
F
F 3d2[] 3 100103 20103 2 94.2kN
bs
Fbs A
F /3 td
[bs ]
F3
材料力学第三章剪切

σ jy
Pjy A jy
pbL / 2 td
pbL 2td
2.0 0.06 0.15 2 0.012 0.015
50(MPa)
21
例3 如图所示为铆接接头,板厚t=2mm,板宽b=15mm, 板端部长a=8mm,铆钉直径d=4mm,拉力P=1.25kN,材料 的许用剪切应力[τ]=100MPa,许用挤压应力[σjy] =300MPa, 拉伸许用应力[σ]=160MPa。试校核此接头的 强度。
t
t
P
P
P
P
d
(a)
(b)
22 P
P
b
P
P
22
a
(c)
22
1、接头强度分析 2、铆钉的剪切与挤压强度计算
QP
τ Q 1.25 10 3 99.5N / mm 2 99.5MPa [τ]
A 42
4 Pjy P ; Ajy d t
σ jy
Pjy A jy
1.25103 42
4
概 述(续)
简单典型 —— 1个螺栓、2个被联接的构件
Q Q
先研究螺栓的受力情况
5
概 述(续)
Q
Q
螺栓受力特点
1、 横截面 mn, pq 上 有作用力 Q —— 象剪刀一样,试图把螺栓从该截面处剪开称Q为剪力
(Shear force),引起切应力( Shear stress) 2、杆段①、②、③ 受到被联接构件的挤压(Bearing)引起挤
P
P
P
P
2
2
t
t
P
2t2
Q
Q
剪切力

材料力学的定义很清楚:“剪切”是在一对(1)相距很近、(2)大小相同、(3)指向相反的横向外力(即垂直于作用面的力)作用下,材料的横截面沿该外力作用方向发生的相对错动变形现象。
能够使材料产生剪切变形的力称为剪力或剪切力。
发生剪切变形的截面称为剪切面。
判断是否“剪切”的关键是材料的横截面是否发生相对错动。
因此,菜刀切菜不是剪切现象(因蔬菜的横截面没有发生相对错动),而用剪刀剪指甲则是(指甲的横截面发生相对错动。
注:用指甲剪剪指甲不是一种剪切现象,虽然它同样能把指甲剪下来。
为什么?)。
至于“剪切力”的来源,当然是压力造成的。
也可以说,剪切力是一种特殊形式的压力。
流变学是针对物体的流动和变形所展开的研究科目。
涂料配方中颜料的选择,流变性能是一项极其重要的指标。
简单的说,颜料添加入涂料基料中将不可避免的改变涂料的流变特性。
反映流变性能最常用的指标就是涂料体系的粘度。
当涂料体系流动的时候,通过粘度,我们很容易了解到流体发生的变化。
如果是在任意小的外力下都可以流动的流体,同时所加的剪切应力的大小(单位面积上流体所受的力)和流体的速度梯度(D)(也被称之为剪切速率,即流体受力以后两层流体间的速度随位置的变化率)成正比,我们称之为牛顿流体。
从本质上讲,黏度是流体抗拒流动的一种性质,是流体分子间相互吸引而产生的阻碍分子间相对运动能力的量度,即流体流动的内部阻力。
而牛顿流体中切应力和速度梯度D的比值是固定不变的。
此项比值被称为液体黏度系数,简称黏度。
然而有另一种流体,背离了上述的比例关系,被称为非牛顿流体。
非牛顿流体分为塑性流体,触变性流体,假塑性流体,膨胀性流体等不同类型。
当一种流体受到外力作用时,并不立即开始流动。
只有在所加外力大到某一程度时才开始流动。
流体开始流动所需的最小切应力被称为屈服值。
此类流体被称为属于非牛顿流体的塑性流体。
黏度已不能独立于所受切应力之外而保持不变。
而是随着剪切速率的变化呈现复杂的变化。
材料力学7(剪切)

挤压计算中螺栓、铆钉、销钉等圆柱形连接件,其接 触面为半圆柱面,则挤压面面积应为实际接触面在垂直于 挤压方向的投影面积(直径平面面积)。
五、轴向压缩与剪切变形比较
例题图示某起重机吊具,它由销钉将吊钩的上端与吊板联结而成, 起吊重物为F。己知:F=40kN.销钉直径d=22mm,吊钩厚度t =20mm,销钉许用切应力[]=60MPa,[jy]=120MPa。试校核销 钉的强度。
解:(1)校核剪切强度 销钉受力如图,两个受剪面m和n,为“双剪” 每个受剪面积: A
d 2
4
受剪面上剪力:FQ=F/2
剪切强度条件:
4F 2 40 103 2 A 2d 3.14 22 2 52.6 MPa [ ] 60MPa FQ
(2)校核挤压强度 销钉与吊钩及吊板均有接触,故在销轴的上、下两侧 面上都有挤压应力且大小相等。 挤压力Fjy=F 挤压计算面积Ajy=
1 d 2 FQ F A 5 4 FQ A
4F 4 200 10 d 19mm 5 5 3.14 140
3
(2)按挤压强度条件设计d
1 F jy F 5
பைடு நூலகம்
A jy t1d
jy
F jy A jy
F
jy
200 10 15.6mm 5 8 320
3
d
5t1 jy
所以:取d=19mm
剪切问题
二、单项选择题(每小题1分)
1.图示铆钉联接件,受F力作用,各铆钉的材料和直径均 相同,那么受力最大的铆钉是( C ) D
A. (1)铆钉 B. (2)铆钉 C. (3)铆钉 D. (4)铆钉
材料力学剪切第1节 剪切的概念
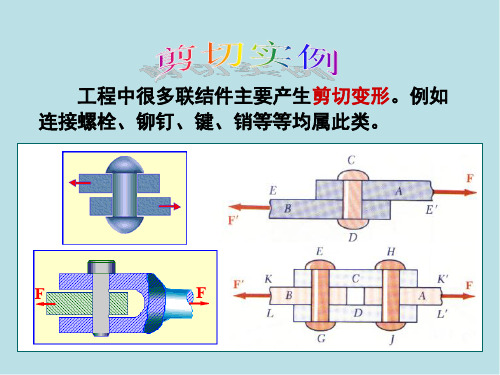
• 剪切的受力特点:构件受一对大小相等、方向相 反、作用线相距很近(差一个几何平面)的平行 力系作用。
• 剪切的变形特点:两外力作用线间截面发生错动, 由矩形变为平行四边形。
注意
为了正确求得剪 力,就必须正确地确 定剪切面和剪切面的 个数。(合力)F m Nhomakorabean
F
(合力)
销钉有两个剪切面
焊缝有两个剪切面
工程中很多联结件主要产生剪切变形。例如 连接螺栓、铆钉、键、销等等均属此类。
F
F
• 剪切变形:构件在一对大小相等、方向相反、作用 线相隔很近的外力(或外力的合力)作用下,截面 沿着力的方向发生相对错动的变形,称剪切变形。
• 剪切面:在变形过程中,产生相对错动的截面(如 mn)称为剪切面。它位于方向相反的两个外力之 间,且与外力的作用线平行。
材料力学 材料的剪切力

110106 110MPa [ ]
3.板和铆钉的挤压强度
bs
Fbs Abs
F
2d
50103 2 0.017 0.01
147106 147MPa [ bs ]
结论:强度足够。
12
§3-2 纯剪切 切应力互等定理 剪切胡克定律
一、纯剪切
单元体截面上只有切应力而无正应力作用, 这种应力状态叫做纯剪切应力状态。
料相同,试校核其强度。
解:1.板的拉伸强度
FN F A (b 2d )
50 103
(0.15 2 0.017) 0.01
43.1106 43.1MPa [ ]
11
§3-1 连接件的强度计算
d
b
a
2.铆钉的剪切强度
Fs A
4F 2πd 2
2F πd 2
2 50103 π 0.0172
3.挤压的实用计算
F
Fbs
假设应力在挤压面上是均
匀分布的
F
得实用挤压应力公式
bs
Fbs Abs
*注意挤压面面积的计算
Fbs
Abs d
挤压强度条件: bs
Fbs Abs
bs
bs 常由实验方法确定
7
§3-1 连接件的强度计算
切应力强度条件: Fs
A
挤压强度条件:
bs
Fbs Abs
G E
2(1 )
表明3个常数只有2个是独立的
17
小结
1. 剪切变形的特点 2. 剪切实用计算 3. 挤压实用计算 4. 纯剪切的概念 5. 切应力应力应满足
bs 2
F dh
2
4F
d 2
d 8h
材料力学 第3章剪切和扭转

( L ) R
剪切胡克定律:当切应力不超过材料的剪切比例极限 时(τ ≤τp),剪应力与剪应变成正比关系。
G
(3-8)
式中:G是材料的一个弹性常数,称为切变模量(剪切弹性
模量),因 无量纲,故G的量纲与 相同,不同材料的G值可通
过实验确定,钢材的G值约为80GPa。 剪切弹性模量、弹性模量和泊松比是表明材料弹性性质的三 个常数。对各向同性材料,这三个弹性常数之间存在下列关系 (推导详见后面章节):
2 D 2 d 2
d O D
d ( D d ) ( ) D 32
4 4
D
4
32
(1 ) 0.1D (1 )
4 4 4
(3-16)
④ 应力分布
(实心截面)
(空心截面)
工程上采用空心截面构件:提高强度,节约材料,重量轻, 结构轻便,应用广泛。
⑤ 确定最大剪应力: 由
G1G d tg dx dx
d dx
距圆心为 任一点处的与到圆心的距离成正比。
d —— 扭转角沿长度方向变化率。 dx
2. 物理关系: 胡克定律:
G
dx dx
代入上式得: G G d G d
W ' M e M e 2 n
60 s M e 2n
PKW M e N m 9550 nr min
(3-5)
二、 功率、转速与外力偶矩间的关系
P m 9.55 (kN m) n m 7.024 P (kN m) n
其中:P — 功率,千瓦(kW)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
25
Fbs Fbs
*注意挤压面面积的计算
Fbs bs 挤压强度条件: bs Abs
Abs d
bs 常由实验方法确定
7
连接件的强度计算
Fs 切应力强度条件: A
Fbs bs 挤压强度条件: bs Abs
塑性材料: 0.5 0.7
一、纯剪切
单元体截面上只有切应力而无正应力作用, 这种应力状态叫做纯剪切应力状态。
19
纯剪切 切应力互等定理 剪切胡克定律 二.切应力互等定理
20
纯剪切 切应力互等定理 剪切胡克定律
21
纯剪切 切应力互等定理 剪切胡克定律 三.剪切胡克定律
G
其中,比例常数G 称为切变模量。常用单位GPa
d
3.铆钉的剪切强度
Fs 4F 2F 2 2 A 2 πd πd 2 50103 2 π 0.017 110106 110MP a [ ]
b
a
4.板和铆钉的挤压强度 Fbs F 50103 bs Abs 2d 2 0.017 0.01
50 103 (0.15 2 0.017) 0.01 43.1 106 43.1MP a [ ]
11
2.板的剪切强度
Fs F 50103 A 4a 4 0.08 0.01 15.7 106 15.7MPa [ ]
连接件的强度计算
为充分利用材 料,切应力和挤压 应力应满足
bs 2
F 4F 2 2 dh d
d
8h
10
连接件的强度计算
d
例题 图示接头,受轴向力F 作
b
a
用。已知F=50kN,b=150mm, δ=10mm,d=17mm,a=80mm, [σ]=160MPa,[τ]=120MPa, [σbs]=320MPa,铆钉和板的材 料相同,试校核其强度。 解:1.板的拉伸强度 FN F A (b 2d )
14
例 拉杆头部尺寸如图所示,已知[τ] =100MPa,许用
挤压应力[σbs]=200MPa。校核拉杆头部的强度。
15
P 40 103 63.7MPa [ ] dh 20 10
P 40 10 3
bs
2 (D d 2 ) 4
(402 20 2 ) 4
42.4 MPa [ ]
16
连接件的强度计算
4.其它连接件的实用计算方法 焊缝剪切计算
h l
45
有效剪切面
L
17
连接件的强度计算
4.其它连接件的实用计算方法 胶粘缝的计算 F 不同的粘接方式
F
F
F
F
[ ]
F
[ ] [ ]
18
[ ]
纯剪切 切应力互等定理 剪切胡克定律
F
m m
F
假设切应力在剪切面(m-m 截面)上是均匀分布的 得切应力计算公式:
Fs A
F
m
FS m
m FS m
F
常由实验方法确定
Fs 切应力强度条件: A
6
连接件的强度计算
3.挤压的实用计算
F F
假设应力在挤压面上是均 匀分布的
Fbs 得实用挤压应力公式 bs A bs
22
纯剪切 切应力互等定理 剪切胡克定律
对各向同性材料可以证明,弹性常数E、G、 μ存在关系
E G 2(1 )
表明3个常数只有2个是独立的
23
小
1. 2. 3. 4. 5.
结
剪切变形的特点 剪切实用计算 挤压实用计算 纯剪切的概念 切应力互等定理
6.
剪切胡克定理
24
作业 3—3、 6、 8、 10、
147 106 147MP a [ bs ]
结论:强度足够。
12
例 图示受拉力P作用下的螺栓,已知材料的剪切许 用应力[τ]是拉伸许用应力[σ]的0.6倍。求螺栓直径d 和螺栓头高度h的合理比值。
13
P 解: [ ] dh
P [ ] 2 d 4
(1)
( 2)
(1) d [ ] 得: 4 2.4 ( 2) h [ ]
剪
切
1
连接件的强度计算
1.剪切的工程实例
2
连接件的强度计算
3
连接件的强度计算
铆钉连接 螺栓连接
销轴连接
4
连接件的强度计算
平键连接
焊接连接
榫连接
5
连接件的强度计算
2.剪切的实用计算
F F
剪切受力特点:作用在构件两侧 面上的外力合力大小相等、方向 相反且作用线很近。 变形特点:位于两力之间的截面 发生相对错动。
bs 1.5 2.5
脆性材料:
0.8 1.0 bs 0.9 1.5
8
连接件的强度计算
Fs F A lb
Fbs F bs Abs cb
9
连接件的强度计算
Fs 4 F 2 A d Fbs F bs Abs dh
