材料力学剪切与扭转PPT课件
合集下载
材料力学课件第3-4章

L M x( x) d x
0 GIP (x)
28
3.5 圆轴扭转时的变形与刚度条件
二. 刚度条件
对等直轴:
d
dx
Mx GIP
单位长度的扭转角
等直圆轴扭转
max
M x max GIP
180
[ ](o /m)
对阶梯轴: 需分段校核。
max
M x max GIP
180
[ ](ο /m)
2. 给出功率, 转速
(kw)
Me = 9549
P n
(N. m)
(r/min)
5
3.2 外力偶矩的计算 扭矩和扭矩图 二.横截面上的内力
截面法求内力: 截,取,代,平
Mx 称为截面上的扭矩
Mx 0 Mx Me 0 即 Mx Me
按右手螺旋法:
指离截面为正,
M x 指向截面为负。
6
3.2 外力偶矩的计算 扭矩和扭矩图
10
3.3 薄壁圆筒的扭转 纯剪切
一. 薄壁筒扭转实验
nm
t
实验观察 分析变形
x
r
nm l
mn没变 x = 0
x = 0
Me
nm
γ
Me
φ
x
r没变 = 0
= 0
nm
Me
nm
Mx
x
n m Mx
11
3.3 薄壁圆筒的扭转 纯剪切
Me Mx
nm
Mx
n m Mx
由于轴为薄壁,所以认
为 沿t 均布.即 =C
max
M x max Wp
31.5 103 m
M x max d 3
16
材料力学第四版课件 第三章 扭转

2
例1:图示空心圆轴外径D=100mm,内径 图示空心圆轴外径D=100mm,内径 d=80mm, M1=6kN·m, M2=4kN·m, 材料的切变 =6kN· 模量 G=80GPa. (1) 试画轴的扭矩图; 试画轴的扭矩图; (2) 求轴的最大切应力,并指出其位置. 求轴的最大切应力,并指出其位置.
平面假设:圆轴扭转后各横截面仍保持为平面, 平面假设:圆轴扭转后各横截面仍保持为平面, 各横截面如同刚性平面仅绕轴线作相对转动。 各横截面如同刚性平面仅绕轴线作相对转动。
横截面上无σ 1)横截面上无σ 2)横截面上只有τ
F O1 a d dφ d1 dx O2
dd1 ρdφ γ ρ ≈ tanγ ρ = = ad dx
4
πd
3 0
(
)
16T ∴d0 ≥ 3 = 76.3mm 4 π (1−α )[τ ]
取 d0 = 76.3mm、 、 (3)比较空心轴与实心轴的重量 比较空心轴与实心轴的重量 积之比: 二者重量之比等于横截面 积之比:
π (d − di ) 4 = 0.395 β= 2 4 πd
2 0 2
可见空心轴比实心轴的重量轻 可见空心轴比实心轴的重量轻
任一点处的切应变 切应变与到 距圆心为 ρ 任一点处的切应变与到 成正比。 圆心的距离ρ成正比。
2. 物理方面
dφ γρ = ρ dx
dφ τ ρ = Gρ dx
3. 静力学方面
dφ 2 T = ∫ ρτ ρ dA = G ∫ ρ dA dx A A
Ip = ∫ ρ dA 称为极惯性矩
2 A
ρ
dA
MB
1
MC
MA
2 2
A
3
MD
例1:图示空心圆轴外径D=100mm,内径 图示空心圆轴外径D=100mm,内径 d=80mm, M1=6kN·m, M2=4kN·m, 材料的切变 =6kN· 模量 G=80GPa. (1) 试画轴的扭矩图; 试画轴的扭矩图; (2) 求轴的最大切应力,并指出其位置. 求轴的最大切应力,并指出其位置.
平面假设:圆轴扭转后各横截面仍保持为平面, 平面假设:圆轴扭转后各横截面仍保持为平面, 各横截面如同刚性平面仅绕轴线作相对转动。 各横截面如同刚性平面仅绕轴线作相对转动。
横截面上无σ 1)横截面上无σ 2)横截面上只有τ
F O1 a d dφ d1 dx O2
dd1 ρdφ γ ρ ≈ tanγ ρ = = ad dx
4
πd
3 0
(
)
16T ∴d0 ≥ 3 = 76.3mm 4 π (1−α )[τ ]
取 d0 = 76.3mm、 、 (3)比较空心轴与实心轴的重量 比较空心轴与实心轴的重量 积之比: 二者重量之比等于横截面 积之比:
π (d − di ) 4 = 0.395 β= 2 4 πd
2 0 2
可见空心轴比实心轴的重量轻 可见空心轴比实心轴的重量轻
任一点处的切应变 切应变与到 距圆心为 ρ 任一点处的切应变与到 成正比。 圆心的距离ρ成正比。
2. 物理方面
dφ γρ = ρ dx
dφ τ ρ = Gρ dx
3. 静力学方面
dφ 2 T = ∫ ρτ ρ dA = G ∫ ρ dA dx A A
Ip = ∫ ρ dA 称为极惯性矩
2 A
ρ
dA
MB
1
MC
MA
2 2
A
3
MD
材料力学-扭转1ppt课件

横截面上 —
max
T IP
max
IP
T
max
T WP
Ip—截面的极惯性矩,单位:m4 , mm 4
WP
Ip
max
WP —抗扭截面模量,单位:m3, mm3.
整个圆轴上——等直杆:
max
Tm a x WP
三、公式的使用条件: 1、等直的圆轴, 2、弹性范围内工作。
30
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
d
dx
d / dx-扭转角变化率
二)物理关系:
弹性范围内 max P
G → G
G
d
dx
方向垂直于半径。
28
三)静力关系:
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dxp
29
二、圆轴中τmax的确定
结论:
横截面上 0, 0 0 0
根据对称性可知剪应力沿圆周均匀分布;
t D, 可认为剪应力沿壁厚均匀分布,
且方向垂直于其半径方向。
t
D
20
3、剪应力的计算公式:
T
AdA.r0
2 0
r0
2td
r02t2
d
T
2r0 2t
薄壁圆筒横截面上的剪应力计算式
21
二、关于剪应力的若干重要性质
例题: 1、一传动轴作200r/min的匀速转动,轴上装有五个轮子。 主动轮2输入的功率为60kW,从动轮1、3、4、5依次输出的 功率为18kW、12kW、22kW和8kW。试作出该轴的扭矩图。
材料力学第3章扭转

试问:纵向截面里的切应力是由什么内力平衡的?
§3.8 薄壁杆件的自由扭转
薄壁杆件:杆件的壁厚远小于截面的其它尺寸。 开口薄壁杆件:杆件的截面中线是不封闭的折线或曲
线,例如:工字钢、槽钢等。 闭口薄壁杆件:杆件的截面中线是封闭的折线或曲线,
例如:封闭的异型钢管。
一、开口薄壁杆的自由扭转
= Tl
GI t
变形特点:截面发生绕杆轴线的相对转动 本章主要研究圆截面等直杆的扭转
§3.2 外力偶矩的计算 扭矩和扭矩图
功率: P(kW) 角速度:ω 外力偶矩:Me
P = Meω
转速:n(r/min)
2n/ 60
Me
1000 P=9549
P n
(N
m)
内力偶矩:扭矩 T 求法:截面法
符号规则: 右手螺旋法则 与外法线同向“ + ” 与外法线反向“-”
max
T max
It
It
1 3
hi
3 i
二、闭口薄壁杆的自由扭转
max
T
2 min
TlS
4G 2
其中:ω截面为中线所围的面积
S 截面为中线的长度
闭口薄壁杆的应力分布:
例: 截面为圆环形的开口和闭口薄壁杆件如图所 示,设两杆具有相同平均半径 r 和壁厚δ,试 比较两者的扭转强度和刚度。
开=3 r 闭 开=3( r )2 闭
8FD3n Gd 4
C
ห้องสมุดไป่ตู้
Gd 4 8D3n
F C
§3.7 矩形截面杆扭转的概念
1) 翘曲
变形后杆的横截面不再保持为平面的现象。
2) 自由扭转和约束扭转
自由扭转:翘曲不受限制的扭转。 各截面翘曲程度相同,纵向纤维无伸缩, 所以,无正应力,仅有切应力。
材料力学课件:扭转

B
D
C
12 3
A P
Page4
§3-6 热应力与预应力
扭转
§4-1 引言 §4-2 圆轴扭转应力
Page5
§3-6 热应力与预应力
lT=ll T
B
C
A A’
变形不受限制(静定结构),杆内未引起应力
Page6
B lT=ll T
CB
C
A’
A
A
变形受到限制(静不定结构),杆内引起应力
热应力:因温度的变化在杆件内部引起的应力 预应力:由于实际尺寸的误差在杆件内部引起的应力
各
截面的扭矩。
Page20
扭矩图:外扭力矩随杆轴线变化的情况。
M 3ml
m
x
A
B
C
D
l
l/2 l/2
T1 ( x)
x
T ml
x
2ml
例:(m:单位长度的扭力偶矩)
AB段: T1 x mx
BC段: T2 ml CD段: T3 2ml
Page21
思考:
M
M’
M’
M
(1)
M’
(2)
M’
(3)
FN3
FN1
FN2
Page9
3
1
2
3
1
2
协调方程:
l3+ l1/cos()=
l3
FN3
FN1
FN2
Page10
➢ 装配应力在工程结构中的应用
1 23
P
在准确加工、装配的情况下,2杆 的应力最大。
如果能使3根杆同时达到许用应力, 将对结构更有利。
FN1 [1 ]A FN 2 [ 2 ]A FN 3 [ 3 ]A
材料力学-第4章 扭转 ppt课件

dA
T
O
dA
23
材料力学-第4章 扭转
圆轴扭转横截面上的应力
A dA T
代入:
G
G
d dx
得到:
G d 2dA T dx A
记: IP -2dA称为圆截面的极惯性矩
A
则:圆轴扭转角的变化率 d T
dx GIP
圆截面切应力
采用右手螺旋法则,如果用四指表示扭矩的转向, 拇指的指向与截面的外法线n的方向相同时,该扭矩为 正;反之,规定扭矩为负
正扭矩
负扭矩
——保证了无论从哪一段计算,扭矩的大小和符号 都相同
12
材料力学-第4章 扭转
扭力偶矩计算与扭矩
讨论:如图受扭圆轴,m-m截面上扭矩为多少?
Me
m
2M e
m m
T Me
17
材料力学-第4章 扭转
圆轴扭转横截面上的应力
几何变形:
1. 横截面绕圆轴的轴线转动
?
主要
2. 圆轴中段的横截面缩小 几何变形特征
有剪切应变 rz 次要
3. 圆轴的长度略有增长
有轴向应变 z 次要
– 变形后,横截面仍保持为平面,其形状和大小均不
改变,半径仍为直线
– 变形后,相邻横截面的间距保持不变,相邻横截面 绕圆轴轴线转动一定的角度
外力偶矩的计算
• 工程中的传动轴,通常给出传动轴所传递的功率和转 速,而不直接给出外力偶矩的数值
• 设外力偶矩为Me,传动轴的功率为P,角速度为w,则
有(理论力学)
Me
P
w
外力偶矩Me 单位:N·m (牛顿·米) 功率为P 单位:J (焦耳)
材料力学扭转教学课件PPT

200 kW。试做轴力图。
(a)
P2
P3
P1
n
P4
B
C
D
A
例题3-2图
m P2 2
m P3 3
P1
m1
m n
4 P4
B
C
D
A
m2
m3
m1
m4
(b)
B
C
A
D
解:1.计算外力偶矩
m1
m2
9.55 P1 15.9kN .m
m3
n
9.55
P2
n
4.78kN
.m
m4
9.55 P4 n
6.37kN .m
2.由计算简图用截面法计算各段轴内的扭矩,然后画扭矩图
§3.1 扭转的概念和实例
➢ 扭转变形 ——作用在垂直于杆件轴线的平面内 的力偶矩,使得杆件的任意两个 横截面都发生了绕轴线的相对转 动。
➢ 扭转变形杆件的内力 ——扭矩(T )
➢ 轴 ——主要承受扭矩的构件
m A'
g
A
m B j B'
扭转的受力特征 :在杆件的两端作用两个大小相等、
转向相反、且作用平面垂直于杆件轴线的力偶。
dA
O r
dA
dA
O
A
G 2
dj
dx
dA
G
dj
dx
A
2dA
T
GI p
dj
dx
令 Ip A 2dA
dj
dx
T GI p
代入物理关系式
G
dj
dx
得:
T
Ip
T
Ip
—横截面上距圆心为处任一点剪应力计算公式。
(a)
P2
P3
P1
n
P4
B
C
D
A
例题3-2图
m P2 2
m P3 3
P1
m1
m n
4 P4
B
C
D
A
m2
m3
m1
m4
(b)
B
C
A
D
解:1.计算外力偶矩
m1
m2
9.55 P1 15.9kN .m
m3
n
9.55
P2
n
4.78kN
.m
m4
9.55 P4 n
6.37kN .m
2.由计算简图用截面法计算各段轴内的扭矩,然后画扭矩图
§3.1 扭转的概念和实例
➢ 扭转变形 ——作用在垂直于杆件轴线的平面内 的力偶矩,使得杆件的任意两个 横截面都发生了绕轴线的相对转 动。
➢ 扭转变形杆件的内力 ——扭矩(T )
➢ 轴 ——主要承受扭矩的构件
m A'
g
A
m B j B'
扭转的受力特征 :在杆件的两端作用两个大小相等、
转向相反、且作用平面垂直于杆件轴线的力偶。
dA
O r
dA
dA
O
A
G 2
dj
dx
dA
G
dj
dx
A
2dA
T
GI p
dj
dx
令 Ip A 2dA
dj
dx
T GI p
代入物理关系式
G
dj
dx
得:
T
Ip
T
Ip
—横截面上距圆心为处任一点剪应力计算公式。
材料力学 剪切和扭转.

§3–2 连接接头的强度计算
(合力) P 1、连接处破坏三种形式: ①剪切破坏
n
n
P (合力) 剪切面 n
沿铆钉的剪切面剪断,如
沿n– n面剪断 。 ②挤压破坏 铆钉与钢板在相互接触面 上因挤压而使溃压连接松动,
FS n
P
发生破坏。
③拉伸破坏
钢板在受铆钉孔削弱的截面处,应力增大,易在连接处拉断。
2、剪切的实用计算
此杆安全。
[例6]木榫接头如图所示,宽b=20cm,材料[]=1MPa, [bs]=10MPa。受拉力P=40kN作用,试设计尺寸a 、h 。 F F
a
h
剪切面
Fbs
挤压面
F
解: 剪切面面积:As
ab bh
Abs 挤压面面积:
a
h
剪切面
Fbs
挤压面
F
取接头右边,受力如图。
Fs Fbs F
P=40KN,试求接头的剪应力和挤压应力。 h P a 解::受力分析如图∶ P
FS Fbs P 挤压面和挤压力为:
P :剪应力和挤压应力
剪切面和剪力为∶
P b
c
As
Abs
P P
FS P 40 107 0.952MPa AS bh 12 35
Pbs P 40 bs 107 7.4MPa Abs cb 4.5 12
度条件。
P
t
d
t
P
多铆钉连接件,为计算方便,各铆钉受力可视作相同。
上板受力图
F/4 F/4 F/4
F/4
3F/4
F
F
上板轴力图
铆钉受力图
F/4
材料力学剪切和扭转

F
A
许用剪应力
上式称为剪切强度条件 其中,F 为剪切力——剪切面上内力旳合力
A 为剪切面面积
受剪切螺栓剪切面面积旳计算:
d 2
A 4
受剪切单键剪切面面积计算:
取单键下半部分进行分析
假设单键长宽高分别为 l b h
则受剪切单键剪切面面积:
剪切面
A bl
剪切力
d
l h b
合力 外力
螺栓和单键剪应力及强度计算:
P/2
积单倍
结论:不论用中间段还是左右段分析,成果是一样旳。
例2-1 图示拉杆,用四个直径相同旳铆钉连接,校核铆钉和拉 杆旳剪切强度。假设拉杆与铆钉旳材料相同,已知P=80KN, b=80mm,t=10mm,d=16mm,[τ]=100MPa,[σ]=160MPa。
构件受力和变形分析:
假设下板具有足够
例3-2 已知A轮输入功率为65kW,B、C、D轮输出功率分别为 15、30、20kW,轴旳转速为300r/min,画出该轴扭矩图。
TB
TC
TA
TD
B
C
955N·m
A
477.5N·m
Tn
637N·m
计算外力偶矩
D
TA
9550
NA n
1592N
•m
TB
TC
9550
NB n
477.5N
•
m
TD
9550
ND n
挤压面为上半个圆周面
键连接
上半部分挤压面
l
h 2
下半部分挤压面
2、挤压应力及强度计算
在挤压面上,单位面积上所具有旳挤压力称为挤
压应力。
bs
材料力学课件第三章 扭转

工程上采用空心截面构件:提高强度,节约材料,重量轻, 结构轻便,应用广泛。
3.4 圆轴扭转时横截面上的应力
3.4.2 最大扭转切应力和强度条件
第三章 扭转
1. 最大扭转切应力:
由
T
Ip
知:当
R , max
max
TR Ip
T Ip R
T Wp
(令 Wp I p R )
max
T Wp
Wp — 扭转截面系数,单位:mm3或m3。
对于实心圆截面: 对于空心圆截面:
Wp
d3
16
Wp
(D4
16
d4)
D3(1 4 )
16
3.4 圆轴扭转时横截面上的应力
2、强度条件
强度条件:
max
Tm a x Wp
[ ]
第三章 扭转
许用切应力 u
n
τ s---- 扭转屈服极限 ——塑性材料 τ b---- 扭转强度极限 ——脆性材料 τ u---- 扭转极限应力 ——τs和τb的统称
MB
MC
MA
MD
B
C
解:计算外力偶矩
A
D
MA
9549 PA n
1592N m
MB
MC
9549 PB n
477.5N m
MD
9549 PD n
637N m
3.2 外力偶矩的计算 扭矩和扭矩图
第三章 扭转
3.2.2 扭矩和扭矩图
1 扭矩:构件受扭时,横截面上的内力偶矩,记作“T”。
2 截面法求扭矩
剪应力在互相垂直的面上同时存在,数值相等,其方向都垂直于这 两个面的交线,且都指向或者都背离该交线。
第六章 材料力学剪切与扭转

土木工程力学
第六章
• • • • 6.1 6.2 6.3 6.4
剪切与扭转
剪切和挤压的实用计算 扭矩的概念 圆轴扭转的应力及强度计算 圆轴扭转时的变形及刚度计算
6.1 剪切和挤压的实用计算
6.1.1
剪切和挤压的概念
1、连接件 在构件连接处起连接作用的部件,称为连接件。例如: 螺栓、铆钉等。连接件虽小,起着传递载荷的作用。 螺栓 P
F /2 F /2 2 d A 4
d
2F
11.97(mm)
选取d=1 2mm。 3)校核销钉的挤压强度为
jy
F 150( MPa) jy Ajy
故选取d= 1 2mm,可以同时满足挤压和剪切强度的要求。
Fs 4 F 2 A d Fbs F bs Abs dh
6.2.3 扭矩和扭矩图
1. 扭矩:构件受扭时,横截面上的内力偶矩,记作“T”。
2. 截面法求扭矩
M
x
0
Me Me
T Me 0 T Me
3. 扭矩的符号规定:
Me
T
x
“T”的转向与截面外法线方向满足右手螺旋规则为正,
反之为负。
右手螺旋法则
右手拇指指向外法线方向为 正(+),反之为 负(-)
P4 25 M 4 9550 9550 1194 ( N .m) n 200
2) 计算各截面上的扭矩(分段应用截面法) 各截面上的扭矩假设为正值。
• • • •
• • •
①沿截面I—I截开,取左侧为研究对象[图 6.11(b)],则根据平衡条件∑m=0,有 T1+M2=0 T1=–M2=–9 5 5N· m ②沿截面Ⅱ一Ⅱ截开,取左侧为研究对象[图 6.11(c)],则根据平衡条件∑m=0,有 T2+M2一M1=0 T2=M1一M2=3 8 2 0—9 5 5=2 8 6 5N· m ③沿截面Ⅲ一Ⅲ截开,取右侧为研究对象[图 6.11(d)],则根据平衡条件∑m=0,有
第六章
• • • • 6.1 6.2 6.3 6.4
剪切与扭转
剪切和挤压的实用计算 扭矩的概念 圆轴扭转的应力及强度计算 圆轴扭转时的变形及刚度计算
6.1 剪切和挤压的实用计算
6.1.1
剪切和挤压的概念
1、连接件 在构件连接处起连接作用的部件,称为连接件。例如: 螺栓、铆钉等。连接件虽小,起着传递载荷的作用。 螺栓 P
F /2 F /2 2 d A 4
d
2F
11.97(mm)
选取d=1 2mm。 3)校核销钉的挤压强度为
jy
F 150( MPa) jy Ajy
故选取d= 1 2mm,可以同时满足挤压和剪切强度的要求。
Fs 4 F 2 A d Fbs F bs Abs dh
6.2.3 扭矩和扭矩图
1. 扭矩:构件受扭时,横截面上的内力偶矩,记作“T”。
2. 截面法求扭矩
M
x
0
Me Me
T Me 0 T Me
3. 扭矩的符号规定:
Me
T
x
“T”的转向与截面外法线方向满足右手螺旋规则为正,
反之为负。
右手螺旋法则
右手拇指指向外法线方向为 正(+),反之为 负(-)
P4 25 M 4 9550 9550 1194 ( N .m) n 200
2) 计算各截面上的扭矩(分段应用截面法) 各截面上的扭矩假设为正值。
• • • •
• • •
①沿截面I—I截开,取左侧为研究对象[图 6.11(b)],则根据平衡条件∑m=0,有 T1+M2=0 T1=–M2=–9 5 5N· m ②沿截面Ⅱ一Ⅱ截开,取左侧为研究对象[图 6.11(c)],则根据平衡条件∑m=0,有 T2+M2一M1=0 T2=M1一M2=3 8 2 0—9 5 5=2 8 6 5N· m ③沿截面Ⅲ一Ⅲ截开,取右侧为研究对象[图 6.11(d)],则根据平衡条件∑m=0,有
材料力学课件(路桥)第4章扭转

计算过程中需要考虑材料的弹性模量、泊松比、剪切模量等参数,以及 结构的几何尺寸和边界条件。
强度条件的工程意义
满足强度条件是保证路桥工程安全性和 稳定性的基础。
通过满足强度条件,可以防止桥梁结构 在承受外力矩和扭矩时发生破坏或过度
变形。
在路桥工程的设计、施工和运营过程中 ,需要定期进行检测和维护,以确保结
扭矩的量纲
扭矩的量纲是力和长度(L)的乘积,表示为ML^2。
量纲是描述物理量本质属性的方式,通过量纲可以判断物理量的性质和相互关系 。
03
扭转的应力分析
切应力与剪切应变的关系
切应力与剪切应变的关系是线 性的,即剪切应变与切应力成 正比。
在剪切弹性范围内,切应力与 剪切应变之间的关系可以用剪 切弹性模量来描述。
扭转过程中,杆件上各点的角位移和 剪切变形程度不同,导致杆件横截面 绕其自身轴线发生转动。
扭转的物理现象
01
杆件在扭转时,横截面上的正应 力分布不均匀,呈现出剪切变形 的特点。
02
杆件上各点的剪切变形程度与该 点到轴线的距离成正比,导致横 截面上的切向力分布不均匀。
扭转的分类
根据杆件上所受外力矩的方向, 扭转可分为左旋和右旋两种类型
构的强度和稳定性。
05
扭转的刚度条件
刚度条件的定义
刚度条件是指在材料力学中,杆件在受到扭矩作用时,其横 截面上的剪切应力和剪切变形之间的关系。
刚度条件是材料力学中一个重要的基本概念,它描述了杆件 在扭矩作用下抵抗变形的能力。
刚度条件的计算方法
根据材料力学的基本理论,刚度条件可以通过杆件的剪切 弹性模量和剪切应变来计算。
材料力学课件(路桥)第4章 扭转
目录 CONTENTS
强度条件的工程意义
满足强度条件是保证路桥工程安全性和 稳定性的基础。
通过满足强度条件,可以防止桥梁结构 在承受外力矩和扭矩时发生破坏或过度
变形。
在路桥工程的设计、施工和运营过程中 ,需要定期进行检测和维护,以确保结
扭矩的量纲
扭矩的量纲是力和长度(L)的乘积,表示为ML^2。
量纲是描述物理量本质属性的方式,通过量纲可以判断物理量的性质和相互关系 。
03
扭转的应力分析
切应力与剪切应变的关系
切应力与剪切应变的关系是线 性的,即剪切应变与切应力成 正比。
在剪切弹性范围内,切应力与 剪切应变之间的关系可以用剪 切弹性模量来描述。
扭转过程中,杆件上各点的角位移和 剪切变形程度不同,导致杆件横截面 绕其自身轴线发生转动。
扭转的物理现象
01
杆件在扭转时,横截面上的正应 力分布不均匀,呈现出剪切变形 的特点。
02
杆件上各点的剪切变形程度与该 点到轴线的距离成正比,导致横 截面上的切向力分布不均匀。
扭转的分类
根据杆件上所受外力矩的方向, 扭转可分为左旋和右旋两种类型
构的强度和稳定性。
05
扭转的刚度条件
刚度条件的定义
刚度条件是指在材料力学中,杆件在受到扭矩作用时,其横 截面上的剪切应力和剪切变形之间的关系。
刚度条件是材料力学中一个重要的基本概念,它描述了杆件 在扭矩作用下抵抗变形的能力。
刚度条件的计算方法
根据材料力学的基本理论,刚度条件可以通过杆件的剪切 弹性模量和剪切应变来计算。
材料力学课件(路桥)第4章 扭转
目录 CONTENTS
材料力学(第五版)扭转切应力 PPT课件
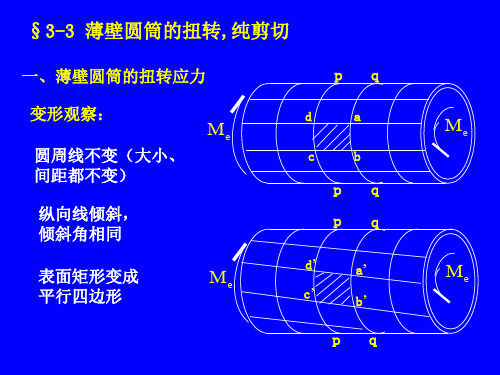
得:
pq
da
Me
cb
pq
pq
d’ a’
Me
c’
b’
pq
切应力互等定理
切应力互等定理
d
a
d
a
c
b
c
b
在相互垂直的两个截面上,切应力 必然成对出现,且大小相等,方向为共 同指向或共同背离两个截面的交线。
二、剪切胡克定律
d
a
Me
c
b
d’
γ
a’
pq
da
Me
cb
pq pq
T3 158.7 N m
Wp1
d13 16
703 109 16
67.34 106 m3
Wp 2
d32 16
503 109 16
24.54 106 m3
Wp3
d33 16
353 109 16
8.418106 m3
(max )E
D4 d 4 32
D
I p
πD4
1 α4 32
d
O
式中: d
D
D
圆轴扭转最大切应力
max
|R
TR IP
令:
Wp
IP R
抗扭截面系数
圆轴扭转最大切应力为:
max
T Wp
实心圆轴的抗扭截面系数为:
D3 Wp 16
空心圆轴的抗扭截面系数为:
Wp
A1
4
d12
A2
4
pq
da
Me
cb
pq
pq
d’ a’
Me
c’
b’
pq
切应力互等定理
切应力互等定理
d
a
d
a
c
b
c
b
在相互垂直的两个截面上,切应力 必然成对出现,且大小相等,方向为共 同指向或共同背离两个截面的交线。
二、剪切胡克定律
d
a
Me
c
b
d’
γ
a’
pq
da
Me
cb
pq pq
T3 158.7 N m
Wp1
d13 16
703 109 16
67.34 106 m3
Wp 2
d32 16
503 109 16
24.54 106 m3
Wp3
d33 16
353 109 16
8.418106 m3
(max )E
D4 d 4 32
D
I p
πD4
1 α4 32
d
O
式中: d
D
D
圆轴扭转最大切应力
max
|R
TR IP
令:
Wp
IP R
抗扭截面系数
圆轴扭转最大切应力为:
max
T Wp
实心圆轴的抗扭截面系数为:
D3 Wp 16
空心圆轴的抗扭截面系数为:
Wp
A1
4
d12
A2
4
《材料力学》课件3-2薄壁圆筒的扭转

切应力计算
根据材料力学的基本原理,切应力的大小可以通过扭矩和横截面 面积的比值计算得到。
变形量计算
通过测量薄壁圆筒在扭转变形前后的长度变化,可以计算出其变 形量。
弹性模量
在一定条件下,切应力和变形量之间的关系可以用弹性模量来描 述。
薄壁圆筒的变形特性
变形方向
薄壁圆筒的扭转变形是沿着圆筒轴线的方向进行的。
04
根据实验结果,讨论薄壁圆筒在纯扭状态 下横截面上的应力分布规律。
实验结论与讨论
01
实验结果表明,薄壁圆筒在纯扭 状态下横截面上的应力分布符合 剪切应力与剪切应变线性关系;
02
与理论公式对比,实验结果与理 论公式基本一致,验证了理论公
式的正确性;
在实验过程中,应采取措施减小 误差,提高实验精度;
薄壁圆筒的扭转原理
当薄壁圆筒受到一对大小相等、 方向相反的力偶作用时,圆筒
就会发生扭转。
薄壁圆筒的剪切模量是衡量 其抗扭能力的物理量,剪切 模量越大,抗扭能力越强。
薄壁圆筒的弯曲应力与轴向应 力在剪切模量中得到体现,弯 曲应力与轴向应力的比值决定
了圆筒的形状变化。
薄壁圆筒的扭转应用
薄壁圆筒广泛应用于机械、化工、建筑等工程领域,如管道、压力容器、塔器等。
计算时应根据实际情况选择合适的 公式进行计算。
薄壁圆筒的应力特性
01
薄壁圆筒的应力特性主要表现为剪切应力和弯曲应力的共同作 用。
02
在扭转载荷作用下,圆筒的外侧受到较大的剪切应力和弯曲应
力,而内侧受到较小的剪切应力和弯曲应力。
圆筒的应力特性与圆筒的材料属性、几何形状以及扭转载荷的
03
大小有关。
03
《材料力学》课件3-2薄壁圆 筒的扭转
材料力学课件第3章扭转

扭转外力及变 形特点:
杆件受到大小相等,方向相反且作用平 面垂直于杆件轴线的力偶作用, 杆件的横截 面绕轴线产生相对转动。
受扭转变形杆件通常为轴类零件,其横 截面大都是圆形的。所以本章主要介绍圆轴 扭转。
第3章-扭 转
圆轴扭转的内力
3-2 圆轴扭转的内力
1.外力偶矩 直接计算
3-2 圆轴扭转的内力
dx
也发生在垂直于
半径的平面内。
3-3 圆轴扭转横截面上的切应力
2.物理关系
根据剪切胡克定律
G
距圆心为
处的切应力:
G
G
d
dx
垂直于半径
横截面上任意点的切应力 与该点到圆心的距离 成正比。
3-3 圆轴扭转横截面上的切应力
3.静力学关系
T A dA
T A dA
令
Wt
Ip R
抗扭截面系数
在圆截面边缘上,有最 大切应力
3-3 圆轴扭转横截面上的切应力
I
与
p
Wt
的计算
实心轴
T
Ip
max
T Wt
Wt I p / R 1 D3
16
3-3 圆轴扭转横截面上的切应力
空心轴
则
令
Wt I p /(D / 2)
3-3 圆轴扭转横截面上的切应力
实心轴与空心轴 I p 与 Wt 对比
m1=1000Nm,m2=600Nm,m3=200Nm,m4=200Nm,G=79GPa,试求:
(1)各段轴内的最大切应力 (2)若将外力偶m1和m2的位置互换一下,问轴的直径可否减小
3-4 圆轴扭转的强度条件和强度计算
4.强度条件及应用
B
C
杆件受到大小相等,方向相反且作用平 面垂直于杆件轴线的力偶作用, 杆件的横截 面绕轴线产生相对转动。
受扭转变形杆件通常为轴类零件,其横 截面大都是圆形的。所以本章主要介绍圆轴 扭转。
第3章-扭 转
圆轴扭转的内力
3-2 圆轴扭转的内力
1.外力偶矩 直接计算
3-2 圆轴扭转的内力
dx
也发生在垂直于
半径的平面内。
3-3 圆轴扭转横截面上的切应力
2.物理关系
根据剪切胡克定律
G
距圆心为
处的切应力:
G
G
d
dx
垂直于半径
横截面上任意点的切应力 与该点到圆心的距离 成正比。
3-3 圆轴扭转横截面上的切应力
3.静力学关系
T A dA
T A dA
令
Wt
Ip R
抗扭截面系数
在圆截面边缘上,有最 大切应力
3-3 圆轴扭转横截面上的切应力
I
与
p
Wt
的计算
实心轴
T
Ip
max
T Wt
Wt I p / R 1 D3
16
3-3 圆轴扭转横截面上的切应力
空心轴
则
令
Wt I p /(D / 2)
3-3 圆轴扭转横截面上的切应力
实心轴与空心轴 I p 与 Wt 对比
m1=1000Nm,m2=600Nm,m3=200Nm,m4=200Nm,G=79GPa,试求:
(1)各段轴内的最大切应力 (2)若将外力偶m1和m2的位置互换一下,问轴的直径可否减小
3-4 圆轴扭转的强度条件和强度计算
4.强度条件及应用
B
C
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
解:受力分析如图
Fs
Fbs
P 4
P 123
P
P
d
P/4 123
切应力和挤压应力的强度条件
A F Q sP d 2 3 .1 4 1 1 0 1 .6 2 1 0 7 1 3 6 .8 M P a b s F A b b s s 4 P td 4 1 1 1 0 1 .6 1 0 7 1 7 1 .9 M P a b s
dx z
在物体上取一微小六面体,称之为单元 体。
x
X 0
dz
y
(dx
dz)
' y
(dx
dz)
0
y
y
' y
x’ y’
x Y 0
x (dydz)'x (dydz) 0 x 'x
y
dx
x’
x
dy
切应力互等定理:二个相互垂直的截面上, 切应力成对出现。大小相等方向相反,都垂 直于两平面的交线。
y’
dz
(合力) P
n
FS n
n
P (合力)
③剪切面: 构件将发生相互的错动面,如n– n 。
④剪切面上的内力: 内力 — 剪力FS ,其作用线与剪切面平行。
剪切面
n P
3、连接处破坏的形式
(1)剪切破坏 沿铆钉的剪切面剪断,如沿1-1面剪断。
P
n
n
P
1
1
(2)挤压破坏
c
d
铆钉和钢板在相互接触面上因挤压而使接触的 局部区域内产生显著塑性变形,或发生破坏。如ab
,cd接触面。
a
b
(3)拉伸破坏 钢板因铆钉连接,在铆钉孔处截面受到削弱,应力增大,易在连接处被拉断。
二、剪切的实用计算
实用计算方法:根据构件的破坏可能性,采用能反映受力基本特征,并简化计算的假设,计 算其名义应力,然后根据直接试验的结果,确定其相应的许用应力,以进行强度计算。 适用:构件体积不大,真实应力相当复杂情况,如连接件等。
钢板的2--2和3--3面为危险面
2 4 t(b 3 P 2 d ) 4 (8 3 .5 1 2 1 1 .6 ) 0 17 0 1.7 5 M 5 P a
3t(bP d)1 (8 1 .5 1 1 .6 )0 17 01.5 4 M 9P a 综上,接头安全。 123
P
P
P
t t
三、挤压的实用计算
挤压:构件局部面积的承压现象。 挤压力:在接触面上的压力,记Fbs 。
1、挤压力―Fbs :接触面上的合力。
假设:挤压应力在有效挤压面上均匀分布。
2、挤压面积:接触面在垂直Fbs方向上的投影面的面积。
挤压面积 Abs dt
3、挤压强度条件(准则): 工作挤压应力不得超过材料的许用挤压应力。
P
P
可拆卸。
P P
铆钉
无间隙
特点:可传递一般力,不可拆卸。如桥梁桁架结点处用它连接。
m m
齿轮 键
轴 特点:传递扭矩。
2、受力特点和变形特点:
以铆钉为例:
(合力) P
n
①受力特点: 构件受两组大小相等、方向相反、作用线相距
很近(差一个几何平面)的平行力系作用。
n
P (合力)
②变形特点: 构件沿两组平行力系的交界面发生相对错动。
P
P
切应力和挤压应力
b
AQ
A jy
F s P 40 1070.952M Pa
A Q bh 1235
P
P
bsF A b bsscP b4.5 4 0121077.4M Pa
[例] 齿轮与轴由平键(b×h×L=20 ×12 ×100)连接,它传递的扭矩m=2KNm,轴的直径 d=70mm,键的许用剪应力为[]= 60M Pa ,许用挤压应力为[jy]= 100M Pa,试校核键的强度。
d
P/4 123
第十四章 扭转
§14-1 概述 §14-2 外力偶矩、扭矩和扭矩图 §14-3 圆轴扭转时的应力与强度条件 §14-4 圆轴扭转时的变形与刚度条件
概述
轴:工程中以扭转为主要变形的构件。如:机器中的传动轴、 石油钻机中的钻杆等。
实用计算假设:假设切应力在整个剪切面上均匀分布,等于剪切面上的平均应力。
(合力) P
n
FS
n
1、剪切面--A : 错动面。 剪力—FS: 剪切面上的内力。
n
P (合力)
剪切面 n P
2、名义切应力--:
FS A
3、剪切强度条件(准则):
FS
A
其中: jx
n
工作应力不得超过材料的许用应力。
[例] 一铆接头如图所示,受力P=110kN,已知钢板厚度为 t=1cm,宽度 b=8.5cm ,许用应力为 [ ]= 160M Pa ;铆钉的直径d=1.6cm,许用切应力为[]= 140M Pa ,许用挤压应力为[jy]= 320M Pa,试校核铆接头的强度。(假定每个铆钉受力相等。)
t
b
t
P
第十三章 剪切
§13-1 剪切的概念 §13-2 剪切和挤压的实用计算 §13-3 切应力互等定理和剪切胡克定理
剪应力的产生
连接件的剪切 一、连接件的受力特点和变形特点:
1、连接件
在构件连接处起连接作用的部件,称为连接件。例如:螺栓、铆钉、键等。连接件虽 小,却起着传递载荷的作用。
螺栓
特点:可传递一般 力,
z
MZ 0
x (dydz)dxy (dxdz)dy0
x y
当单元体上同时存在切应力和正应力时,切应力 互等定理是否成立?为什么?
剪应变 剪切胡克定律
1. 剪应变
直角的改变量
A
C
A
C
B
D
B
D
F
F 剪切面
2.剪切虎克定律
A C
c
B
D
D
且 单位:Mpa、Gpa.
实验证明:当切应力不超过
பைடு நூலகம்
材料的比例极限
应力 与剪应变
bs
Fbs Abs
bs
四、应用
1 、 校 核 强 度 : [] ; b s [b s ]
2、 设 计 尺 寸 : A Q[F s]; A bs[F b bs s]
3 、 设 计 外 载 : F s A Q [] ; F b s A b s [b s ]
y 切应力互等定律
dy
解:键的受力分析如图
m
h 2
P2m2257kN d 0.07
P m
b d
h
P
L
剪应力和挤压应力的强度校核
QPjy P
QP5 71302.6 8M Pa
A Q bL2 0100
jyA P jjy yLh P25 1 7 0 1 6 30 0 9.3 5 M P ja y
Q
h L b
m d
综上,键满足强度要求。
即
时,剪
成正比。p
G
其中G是材料的剪切弹性模量。
G E
2(1 )
[例] 木榫接头如图所示,a = b =12cm,h=35cm,c=4.5cm, P=40KN,试求接头的切应力和挤压应力。
hh
解: 受力分析如图∶
P
a
c
P
剪切面和剪力为∶
AQbh; Fs P
挤压面和挤压力为: Abs cb; Fbs P
