圆锥曲线的焦半径公式(2020年整理).pptx

合集下载

圆锥曲线焦半径公式及其应用(解析版)

圆锥曲线焦半径公式及其应用一、坐标形式的焦半径公式1.椭圆的坐标形式的焦半径公式（1）设点),(00y x P 是椭圆)0(12222>>=+b a b y a x 上任意一点，21,F F 是其左右焦点，则=1PF 0ex a +，=2PF 0ex a -，记忆方式：长加短减（2）设点),(00y x P 是椭圆)0(12222>>=+b a b x a y 上任意一点，21,F F 是其下上焦点，则=1PF 0ey a +，=2PF 0ey a -，记忆方式：长加短减2.双曲线的坐标形式的焦半径公式（1）设点),(00y x P 是双曲线)0,0(12222>>=-b a by a x 上任意一点，21,F F 是其左、右焦点，则①当点P 在右支上时，=1PF a ex +0，=2PF a ex -0，②当点P 在左支上时，=1PF a ex --0，=2PF a ex +-0，记忆方式：长加短减（2）设点),(00y x P 是双曲线)0,0(12222>>=-b a bx a y 上任意一点，21,F F 是其下、上焦点，则①当点P 在上支上时，=1PF a ey +0，=2PF a ey -0，②当点P 在下支上时，=1PF a ey --0，=2PF a ey +-0，记忆方式：长加短减（3）若弦AB 过左焦点，则=AB a x x e 2)(21-+-；若弦AB 过右焦点，则=AB ax x e 2)(21-+3.抛物线的坐标形式的焦半径公式（1）设),(00y x P 是抛物线)0(22>=p px y 上任意一点，F 为其焦点，则=PF 20p x +（2）设),(00y x P 是抛物线)0(22>-=p px y 上任意一点，F 为其焦点，则=PF 20p x +-（3）设),(00y x P 是抛物线)0(22>=p py x 上任意一点，F 为其焦点，则=PF 20p y +（4）设),(00y x P 是抛物线)0(22>-=p py x 上任意一点，F 为其焦点，则=PF 20p y +-例1.（2021年新高考Ⅰ卷）已知21,F F 是椭圆C ：14922=+y x 的两个焦点，点M 在C 上，则21MF MF ⋅的最大值为（）A.13B.12C.9D.6解法1：（基本不等式）由题意知621=+MF MF ，所以21MF MF ⋅9)2(221=+≤MF MF 当且仅当321==MF MF 时等号成立，所以21MF MF ⋅的最大值为9，故选C 解法2：（焦半径公式）设点),(00y x M ，则由题意知355,2,3=====a c e c b a ，所以9959)353)(353(200021≤-=-+=⋅x x x MF MF ，当且仅当00=x 时等号成立所以21MF MF ⋅的最大值为9，故选C例2.（2019年全国Ⅲ卷理）设21,F F 为椭圆C ：1203622=+y x 的两个焦点，M 为C 上一点且在第一象限，若21F MF ∆为等腰三角形，则点M 的坐标为解析：设点),(00y x M ，则由题意知211F F MF =，所以⇒=+c ex a 203832600=⇒=+x x 所以点M 的坐标为)15,3(例3.点),(00y x P 为双曲线C ：132422=-y x 的右支上一点，若点P 到右焦点的距离等于02x ，则=0x 解析：由题意知3,6,24,2====e c b a ，222300002=⇒=-=-=x x x a ex PF 例4.双曲线116922=-y x 的两个焦点为21,F F ，点P 在双曲线上，若21PF PF ⊥，则点P 到x轴的距离为解法1：51651645tan 0221=⇒⨯===∆P P F PF y y b S ，即点P 到x 轴的距离为516解法2：设点),(00y x P ，不妨设点P 在右支上，则由21PF PF ⊥得2212221F F PF PF =+25269100)335()335(202020=⇒=-++⇒x x x ，所以25256)14(322020=-=x y 5160=⇒y 即点P 到x 轴的距离为516例5.（2011年辽宁卷）已知F 是抛物线x y =2的焦点，B A ,是该抛物线上两点，3=+BF AF ，则线段AB 的中点到y 轴的距离为A.43 B.1C.45 D.47解析：设点),(),,(2211y x B y x A ，线段AB 的中点),(00y x M ，则25341412121=+⇒=+++=+x x x x BF AF ，从而452210=+=x x x ，故选C 例8.（2013年全国Ⅱ卷）设抛物线C ：)0(22>=p px y 的焦点为F ，点M 在C 上，5=MF ，若以MF 为直径的圆过点)2,0(，则C 的方程为（）A.x y 42=或x y 82= B.x y 22=或x y 82=C.x y 42=或xy 162= D.x y 22=或xy 162=解法1：设点),(00y x M ，则255200p x p x MF -=⇒=+=，即),25(0y pM -，MF 的中点为)2,25(0y B ，以MF 为直径的圆过点)2,0(，所以MF AB 21=，所以4425)22(425020=⇒=-+y y ，又点M 在抛物线上，所以2)25(216=⇒-=p p p 或8所以抛物线的方程是x y 42=或x y 162=，故选C解法2：设点),(00y x M ，因为以焦半径为直径的圆与y 轴相切，所以MF 的中点的纵坐标为2，所以40=y ，所以p p x 82160==，所以2528=⇒=+=p pp MF 或8所以抛物线的方程是x y 42=或x y 162=，故选C 注：以抛物线的焦半径为直径的圆与y 轴相切二、角度形式的焦半径公式1.椭圆的角度形式的焦半径公式（1）设过椭圆)0(12222>>=+b a b y a x 的焦点F 的弦AB 的倾斜角为θ，则=AF θcos 2c a b -；=BF θcos 2c a b +；焦点弦长=AB θ2222cos 2c a ab -；（2）设过椭圆)0(12222>>=+b a b x a y 的焦点F 的弦AB 的倾斜角为θ，则=AF θsin 2c a b -；=BF θsin 2c a b +；焦点弦长=AB θ2222sin 2c a ab -；2.双曲线的角度形式的焦半径公式设过双曲线)0,0(12222>>=-b a by a x 右焦点)0,(c F 的弦AB 的倾斜角为α，渐近线xa b y ±=的倾斜角为θ，则（1）当θπαθ-<<时，焦点弦AB 在右支上，=AF θcos 2c a b -；=BF θcos 2c a b +；=AB α2222cos 2c a ab -，弦AB 在双曲线一支上时，焦点弦最短为通径（2）当θα<≤0或παθπ<<-焦点弦AB 在两支上，=AF a c b -θcos 2；=BF ac b +θcos 2；=AB 2222cos 2a c ab -α，弦AB 交双曲线两支上时，焦点弦最短为实轴长a23.抛物线的角度形式的焦半径公式（1）设过焦点F 且倾斜角为θ的直线交抛物线)0(22>=p px y 于B A ,两点，则=AF θcos 1-p ；=BF θcos 1+p；=AB θ2sin 2p （2）设过焦点F 且倾斜角为θ的直线交抛物线)0(22>=p py x 于B A ,两点，则=AF θsin 1-p ；=BF θsin 1+p ；=AB θ2cos 2p例1.如图，设过椭圆13422=+y x 的右焦点F 的直线l 交椭圆于B A ,两点，线段AB 的垂直平分线交x 轴于点M ，则=ABMF 解法1：（设线韦达定理）略解法2：（点差法）略解法3：（角度形式的焦半径公式）设AB 的倾斜角为θ，则θθcos 23cos 2-=-=c a b AF ，θθcos 23cos 2+=+=c a b BF 所以θθθ2cos 412cos 23cos 23-=++-=+=BF AF AB θθθθ2cos 43cos 2cos 2cos -=-=+-==BF AF BFAF AF NF MF ，所以=AB MF 41例2.如图，过椭圆13422=+y x 的左焦点F 任作一直线交椭圆于B A ,两点，若=+BF AF BF AF λ，则=λ解析：设AB 的倾斜角为θ，则θθcos 23cos 2-=-=c a b AF ，θθcos 23cos 2+=+=c a b BF 所以=λ3411=+BF AF例2.已知椭圆12322=+y x 的左右焦点分别为21,F F ，过1F 的直线交椭圆于D B ,两点，过2F 的直线交椭圆于C A ,两点，且BD AC ⊥，则四边形ABCD 的面积的最小值为解析：设直线AC 的倾斜角为θ，则θθθ222222cos 334cos 3232cos 2-=-⨯⨯=-=c a ab AC θθ202sin 334)90(cos 334-=+-=BD 所以)sin 3)(cos 3(242122θθ--=⋅=BD AC S ABCD 2596)2sin 3cos 3(24222=-+-≥θθ，所以四边形ABCD 的面积的最小值为2596例3.过双曲线)0,0(12222>>=-b a by a x 的一个焦点F 作平行于渐近线的两直线，与双曲线分别交于B A ,两点，若a AB 2=，双曲线的离心率为e ，则[]=e 解析：设θ=∠AFO ，则a b a c a c b a c b AF 2cos 222=+⋅=+=θ所以222sin b a AF a ==θ，又c b=θsin ，所以c b b a =22⇒=-⇒=⇒232234)1(2e e c a b 例4.已知双曲线191622=-y x 的左焦点弦交双曲线左支于B A ,两点，且772=AB ，求直线AB 的方程解析：设AB 的倾斜角为θ，则77216cos 25942cos 222222=-⨯⨯=-=θθa c ab AB 53cos ±=⇒θ所以34tan ±=θ，所以直线AB ：)5(34+±=x y 即02034=+-y x 或02034=++y x例5.已知F 为抛物线C ：x y 42=的焦点，过F 作两条互相垂直的直线21,l l ，直线1l 与C 交于B A ,两点，直线2l 与C 交于E D ,两点，则DE AB +的最小值为解析：设AB 的倾斜角为θ，则θθ22sin 4sin 2==p AB ，所以θθ202cos 4)90(sin 2=+=p DE 所以16)11(4)cos )(sin cos 1sin 1(4)cos 1sin 1(42222222=+⨯≥++=+=+θθθθθθDE AB 当且仅当4πθ=时等号成立，所以16)(min =+DE AB 三、焦半径定比模型（1）设AB 为焦点在x 轴上的圆锥曲线的过焦点F 的弦，AB 的倾斜角为θ，斜率为k ，且FB AF λ=，则=θcos e 11+-λλ；=e 21k+11+-λλ（2）设AB 为焦点在y 轴上的圆锥曲线的过焦点F 的弦，AB 的倾斜角为θ，斜率为k ，且FB AF λ=，则11sin +-=λλθe ；=e 211k +11+-λλ例1.（2010年辽宁理科）设椭圆C ：)0(12222>>=+b a by a x 的左焦点为F ，过点F 的直线与椭圆C 相交于B A ,两点，直线l 的倾斜角为060，FB AF 2=，则椭圆的离心率为解析：32121260cos 0=⇒+-=e e 例2.（2010年全国Ⅰ卷）已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C 于D ，FD BF 2=，则C 的离心率为解析：设BD 的倾斜角为θ，则311212cos =+-=θe ，又e a c ==θcos ，所以33312=⇒=e e 例3.（2010年全国Ⅱ卷）已知椭圆)0(12222>>=+b a by a x 的离心率为23，过右焦点F 且斜率为)0(>k k 的直线与C 相交于B A ,两点，若FB AF 3=，则=k （）A.1B.2C.3D.2解析：33cos 211313cos 2311cos =⇒=+-=⇒+-=θθλλθe ，所以2tan ==θk例4.（2014年全国Ⅱ卷理）设21,F F 分别是椭圆)0(12222>>=+b a b y a x 的左右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N ，若直线MN 在y 轴上的截距为2，且N F MN 15=，则椭圆C 的方程为解析：由题意知a b ab MF 44222=⇒==--------------------------------------①由N F MF N F MN 11145=⇒=，所以531414cos =+-=θe ，又2422cos 121-=-==a c a c MF F F θ，所以532=-⋅a c a c -------------------------------------------------------------------------②联立①②得72,7==b a ，所以椭圆的方程为1284922=+y x。

巧用圆锥曲线的焦半径

巧用圆锥曲线的焦半径圆锥曲线的焦半径为：二次曲线上任意一点Q 到焦点的距离．圆锥曲线的焦半径概念，是圆锥曲线中的一个重要的概念．许多圆锥曲线的求解问题，往往都牵涉到它，且运用圆锥曲线的焦半径分析问题可给解题带来生机．因此，掌握它是非常重要的．椭圆焦半径： R 左 = a + x e , R 右 = a - x e ,右支双曲线焦半径：R 左 = x e + a ，R 右 = x e - a ( x > 0) ，左支双曲线焦半径：R 左 = - (x e + a )，R 右 = - (x e - a ) ( x < 0) ,抛物线焦半径：R 抛 = x +2P ．对于这些结论我们无须花气力去记，只要掌握相应的准线方程及标准方程的两种定义，可直接推得．如对双曲线而言：当P(x 0 , y 0)是双曲线b 2x 2 - a 2y 2 = a 2b 2 (a > 0, b > 0) 右支上的一点，F 1, F 2是其左右焦点．则有左准线方程为 ca x 2-=．由双曲线的第二定义得，左焦半径为 a ex ca x e PF +=+=0201)(||; 由 |PF 1|- |PF 2| =2a ，得 |PF 2| = |PF 2| - 2a = ex 0 - a ．( |PF 2|亦可由第二定义求得)．例1 已知F 1，F 2是椭圆E 的左、右焦点，抛物线C 以F 1为顶点，F 2为焦点，设P 为椭圆与抛物线的一个交点，如果椭圆E 的离心率e 满足 |PF 1| = e | PF 2 |，则e 的值为 ( )22)( 33)( 32)( 22)(--D C B A解法1 设F 1(- c, 0 )，F 2(c , 0)，P(x 0 , y 0)，于是，抛物线的方程为 y 2 = 2 (4 c )(x + c ) , 抛物线的准线 l ：x =- 3 c ，椭圆的准线 m ：ca x 2-=，设点P 到两条准线的距离分别为d 1 , d 2．于是，由抛物线定义，得 d 1 = | PF 2 | , ……………………① 又由椭圆的定义得 |PF 1| = ed 2，而 |PF 1| = e | PF 2 |，………………………………②由①②得 d 2 = | PF 2 |, 故 d 1 = d 2，从而两条准线重合．∴ 3331322=⇒=⇒-=-e e c a c ．故选 (C)．解法2 由椭圆定义得 |PF 1| + | PF 2 | = 2a ，又 |PF 1| = e | PF 2 |，∴ | PF 2 | (1+ e ) = 2a ，………①又由抛物线定义得 | PF 2 | = x 0 + 3c , 即 x 0 = | PF 2 | - 3c ，……………………………② 由椭圆定义得 | PF 2 | = a - ex 0 , ………………………………………③由②③ 得 | PF 2 | = a - e | PF 2 | + 3ec ，即 | PF 2 | (1+ e ) = a + 3ec ， ………………… ④ 由①④得 2a = a + 3ec ，解得 33=e ，故选 (C)．点评结合椭圆、抛物线的定义，并充分运用焦半径是解答本题的基本思想．例2 设椭圆E ：b 2x 2 + a 2y 2 = a 2b 2 (a> b> 0)，的左、右焦点分别为 F 1, F 2，右顶点为A, 如果点M 为椭圆E 上的任意一点，且 |MF 1|·|MF 2| 的最小值为243a ．(1) 求椭圆的离心率e ；(2) 设双曲线Q ：是以椭圆E 的焦点为顶点，顶点为焦点，且在第一象限内任取Q 上一点P ，试问是否存在常数λ(λ> 0)，使得∠PAF 1 =λ∠PF 1A 成立？试证明你的结论．分析对于(1)可利用焦半径公式直接求解．而 (2) 是一探索型的命题，解题应注重探索．由于在解析几何中对角的问题的求解，往往要主动联想到斜率．而∠PF 1A 显然是一锐角，又易知∠PAF 1是(0, 120o ) 内的角，且90o 是斜率不存在的角．于是，抓住90o 这一特殊角试探，可得解法1，若注重斜率的研究，考查所两角差的正切，可得解法2；若转变角的角度来观察，将∠PF 1A 变为∠PNF 1，使∠PAF 1变成△PNA 的外角，可得解法3；若考查角平分线的性质可得解法4；若从图像与所求式的特点分析得知，所求的λ必须是大于1的正数，从常规看来可以猜想到它可能是二倍角或三倍角的关系．由此先探索一下二倍角的情形，考查角平分线定理，可得解法5；若是考查∠PF 1A 与∠PAF 1的图形位置，直接解三角形PAF 1，可得到解法6．(1) 解设M(x 0, y 0), 由椭圆的焦半径定义得|MF 1| = a + ex 0，|MF 2| = a - ex 0，|MF 1|·|MF 2| = (a + ex 0)(a - ex 0) = a 2- e 2x 02,∵ |MF 1|·|MF 2| 的最小值为243a , 且 |x 0|≤a ，∴ a 2- e 2x 02 ≥a 2- e 2a 2 =243a ，解得 21=e ． (2) 解法1 由题意得双曲线的离心率e = 2, 且双曲线的实半轴长为c ,半焦距为2c , 故设双曲线Q 的方程为132222=-c y c x ，假设存在适合题意的常数λ(λ> 0)，① 考虑特殊情形的λ值．当PA ⊥x 轴时，点P 的横坐标为2c ，从而点P 的纵坐标为y = 3c ，而 |AF 1| = 3c , ∴ △PAF 1是等腰直角三角形，即 ∠PAF 1 =2π , ∠PF 1A =4π, 从而可得 λ= 2． ② PA 不与x 轴垂直时，则要证∠PAF 1 = 2∠PF 1A 成立即可．由于点P(x 1, y 1)在第一象限内，故PF 1 , PA 的斜率均存在，从而，有A PF c x y k PF 111tan 1∠=+=, 111tan 2PAF cx y k PA ∠-=-=，且有 ))((31121c x c x y -+=,………… ※ 又∵21211121)()(2122tan 11y c x y c x kk A PF PF PF -++=-=∠，将※代入得PA k cx y y c x y c x A PF -=--=-++=∠2)()(22tan 112121111, 由此可得 tan2∠PF 1A = tan ∠PA F 1， ∵ P 在第一象限，A(2c , 0), ∴ )32,2()2,0(1πππ⋃∈∠PAF ,又∵ ∠PF 1A 为锐角，于是，由正切函数的单调性得 2∠PF 1A =∠PA F 1．综合上述得，当λ= 2时，双曲线在第一象限内所有点均有∠PAF 1 = 2∠PF 1A 成立．解法2 由题意得双曲线的离心率e = 2, 且双曲线的实半轴长为c , 半焦距为2c , 故设双曲线Q 的方程为132222=-c y c x ，由于点P(x 1, y 1)在第一象限内，故PF 1 , PA 的斜率均存在．且∠PF 1A 为锐角．又∵ ))((31121c x c x y -+=, …………………………………………………… ※ 设∠PF 1A =β，则 ,tan 111cx y k PF +==β 设∠PAF 1=λβ, λβ≠90o 时, 则 tan(λβ)cx y k PA 211--=-=, 而 tan(λβ-β)βλββλβtan )tan(1tan )tan(+-=))(2(1211111111c x y c x y cx y c x y +--++---=212121112)2(y c cx x c x y -----= ))((3))(2()2(111111c x c x c x c x c x y -+-+---=)()2)(()2(111111c x y x c c x c x y +=-+--=．∴ tan(λβ-β) = tan β．∵ ∠PF 1A =β为锐角，又 ∠P A F 1 =λβ∈)32,0(π, ∴ tan(λβ-β) = tan β > 0, 故λβ-β是锐角，由正切函数的单调性得 λ= 2．显然，当λβ= 90o 时亦成立．故存在λ= 2，使得双曲线在第一象限内所有点均有2∠PF 1A =∠PA F 1成立．解法3 由上述①，得λ= 2，设P ′是射线PA 上的一点, 其横坐标为x 0 ( x 0 > c )，在x 轴上取一点N (2 x 0 +c , 0)，使△P ′F 1N 为等腰三角形，∴∠P ′F 1N =∠P ′NF 1．故当∠P ′AF 1 = 2∠P ′F 1A 时，有∠P ′AF 1 = 2∠P ′NA ，从而∠AP ′N =∠P ′NA, 则 |AN| = |AP ′|，又 A(2c ,0)，于是 |AN| = |AP ′| = 2x 0-c ．过P ′作P ′H 垂直于准线l 于H ，如图9-5．则 |P ′H| = x 0-c 21．故22||||00c x cx H P A P --='' = 2 = e ．故点P ′是双曲线上的点，且与P 重合．由x 0 > c 的任意性得，当λ= 2时，双曲线在第一象限内所有点均有2∠PF 1A =∠PAF 1成立．解法4 由题意得，设点P(x 1 , y 1)，∵ 点P 是双曲线在第一象限内的点，又A(2c , 0)是一焦点，∴ |AP| = 2x 1- c ，|AF 1| = 3c ，设AD 为∠F 1AP 的平分线， ……… ※由角平分线性质及定比分点公式，得 222)32(23123111111cc x x c x c cx c x c x cc x D =+++-=-+-+-=，由此可得，点D 在双曲线的右准线上，从而可得准线是AF 1故△AF 1D 为等腰三角形，且∠PF 1A =∠DAF 1，又由※得∠PAF 1 = 2∠PAD =2∠DAF 1， ∴ ∠PA F 1 = 2∠PF 1A ，故λ＝2．解法5 由题意得，设点P(x 1 , y 1)，因为点P 又A(2c , 0)是一焦点，于是，有|AP| = 2x 1- c ，|AF 1| = 3c ，| PF 1| 2 = (x 1 + c )2 + y 12 = x 12 + 2 x 1c+ c 2 + 3 x 12- 3 c 2 = 4 x 12 + 2 x 1c - 2 c 2,在△APF 1中有 21212121212122432)2(2249cos c c x x c c x c c x x c F -+⨯⨯---++=∠)2(2))(2(26)(611111c x cx c x c x c c x c -+=+-+=，)2(32)224()2(9cos 12121212c x c c c x x c x c A -⨯⨯-+--+=∠c x x c c x c c x c --=-⨯⨯--=111122)2(32)2(6，于是，有 2()2(211c x cx -+)2- 1 =c x x c --1122, 即 2(co s ∠F 1)2- 1 = cos 2∠F 1 = cos ∠A,∵ ∠A 、∠F 1是△APF 1中的内角，且∠F 1是锐角，故有 2∠F 1 =∠A, 即 ∠PA F 1 = 2∠PNF 1，所以λ= 2时，能使得双曲线在第一象限内所有点均有 ∠PA F 1 = 2∠PF 1A ．解法6 设点P(x 1 , y 1)是双曲线第一象限的点．∵ A(2c , 0)，F 1(- c , 0)，连AP ，F 1P ，如图 9-5．由双曲线的焦半径定义得 |AP| = 2x 1- c ,又设点N 是点F 1关于直线x = x 1的对称点，则有 |PF 1| = |PN|, 且N (2x 1+ c , 0)，从而 ∠PF 1N =∠PNF 1．又 |AN| = 2x 1 + c - 2c = 2x 1- c = |AP| , ∠APN =∠PNF 1．由此可得 ∠F 1AP = 2∠PNF 1 ，即 ∠F 1AP = 2∠PNF 1 = 2∠PF 1N ，所以 λ= 2．故存在λ= 2，使得双曲线在第一象限内所有点均有2∠PF 1A =∠PA F 1成立．例3 已知抛物线 y 2 = 2P x 的焦点弦AB 被焦点分成长度为m 、n 的两段，求证：Pn m 211=+．证明设A 、B 在该抛物线的准线上的射影为C 、D ，连AD 交x 轴与E ，如图9-6．由抛物线的焦半径的定义得 |AC| = |AF| = m , |BD| = |BF| = n ,由相似三角形性质知 ||||||||AB AF BD EF =，∴ n m mn EF +=||，同理 nm mnEH +=||，故 |EF| = |EH|, 即 E 与O 重合．故A 、O 、D 三点共线．同理B 、O 、C 三点共线． ∴ |EF| + |EH| = P =n m mn+2, 故 Pn m 211=+．图9-6 点评本题有一个特殊的几何模型，即直角梯形ABCD ．由此还可发现许多有用的结论：①∠CFD = 90o ;②∠CAB 的平分线与∠DBA 的平分线交于一点N ，则NA 、NB 为抛物线的切线，且∠ANB= 90o ； ③在准线上任取一点向抛物线引两条切线，则两切线互相垂直； ④若M 为AB 中点，则N M 被抛物线平分； ⑤若A(x 1 , y 1), B(x 2, y 2)，则 |AB| =||2121y y P-，当AB ⊥x 轴时, |AB| = 2 P; ⑥以AB 为直径的圆与抛物线的准线相切； ⑦NF ⊥AB; y 1y 2 = - P 2; …．。

圆锥曲线的统一定义焦半径公式PPT课件

a2 cx a x c2 y2
思考1. x c2 y2 a ex , 即为 MF2 a ex ;
若另一种移法可得： MF1 a ex . 这是焦半径公式
思考2.
x c2 y2 c
a2 x
. a
这是椭圆的第二定义.
c
若另一种移法可得：
xB2 3

y B,由2 1

得F1 A 5 F2 B x,A 2 5(xB
xA2 3

yA2
1
2) yA 5yB
,联立方程组可得 xA . 0
x 分析2:（数形结合）如果右准线与轴的交点为 ,C可以证
明A、B、C三点共线，由定义可以知道到A 左右准线距离相
等，所以 x。A 0
微课小结回归课本、高于课本······
一个背景二种结论
一次探究
二类思想
椭圆标准方程的推导圆锥曲线的统一定义、焦半径公式点坐标
数形结合、消元引参、
移项、两边平方得
x c2 y2 4a2 4a x c2 y2 x c2 y2
a2 cx a x c2 y2
方程形式
两边再平方，得 a4 2a2cx c2 x2 a2 x2 2a2cx a2c2 a2 y2
整理得 a2 c2 x2 a2 y2 a2 a2 c2
x c2
x a2
y2

c. a
c
1.圆锥曲线的统一定义 2.圆锥曲线的焦半径公式
材料1.
设
F1
,F2分
别
为
椭
圆x2 3

巧用圆锥曲线的焦半径

巧用圆锥曲线的焦半径圆锥曲线的焦半径为：二次曲线上任意一点Q 到焦点的距离．圆锥曲线的焦半径概念，是圆锥曲线中的一个重要的概念．许多圆锥曲线的求解问题，往往都牵涉到它，且运用圆锥曲线的焦半径分析问题可给解题带来生机．因此，掌握它是非常重要的．椭圆焦半径： R 左 = a + x e , R 右 = a - x e ,右支双曲线焦半径：R 左 = x e + a ，R 右 = x e - a ( x > 0) ，左支双曲线焦半径：R 左 = - (x e + a )，R 右 = - (x e - a ) ( x < 0) ,抛物线焦半径：R 抛 = x +2P ．对于这些结论我们无须花气力去记，只要掌握相应的准线方程及标准方程的两种定义，可直接推得．如对双曲线而言：当P(x 0 , y 0)是双曲线b 2x 2 - a 2y 2 = a 2b 2 (a > 0, b > 0) 右支上的一点，F 1, F 2是其左右焦点．则有左准线方程为 ca x 2-=．由双曲线的第二定义得，左焦半径为 a ex ca x e PF +=+=0201)(||; 由 |PF 1|- |PF 2| =2a ，得 |PF 2| = |PF 2| - 2a = ex 0 - a ．( |PF 2|亦可由第二定义求得)．例1 已知F 1，F 2是椭圆E 的左、右焦点，抛物线C 以F 1为顶点，F 2为焦点，设P 为椭圆与抛物线的一个交点，如果椭圆E 的离心率e 满足 |PF 1| = e | PF 2 |，则e 的值为 ( )22)( 33)( 32)( 22)(--D C B A解法1 设F 1(- c, 0 )，F 2(c , 0)，P(x 0 , y 0)，于是，抛物线的方程为 y 2 = 2 (4 c )(x + c ) , 抛物线的准线 l ：x =- 3 c ，椭圆的准线 m ：ca x 2-=，设点P 到两条准线的距离分别为d 1 , d 2．于是，由抛物线定义，得 d 1 = | PF 2 | , ……………………① 又由椭圆的定义得 |PF 1| = ed 2，而 |PF 1| = e | PF 2 |，………………………………②由①②得 d 2 = | PF 2 |, 故 d 1 = d 2，从而两条准线重合．∴ 3331322=⇒=⇒-=-e e c a c ．故选 (C)．解法2 由椭圆定义得 |PF 1| + | PF 2 | = 2a ，又 |PF 1| = e | PF 2 |，∴ | PF 2 | (1+ e ) = 2a ，………①又由抛物线定义得 | PF 2 | = x 0 + 3c , 即 x 0 = | PF 2 | - 3c ，……………………………②由椭圆定义得 | PF 2 | = a - ex 0 , ………………………………………③由②③ 得 | PF 2 | = a - e | PF 2 | + 3ec ，即 | PF 2 | (1+ e ) = a + 3ec ， ………………… ④由①④得 2a = a + 3ec ，解得 33=e ，故选 (C)．点评结合椭圆、抛物线的定义，并充分运用焦半径是解答本题的基本思想．例2 设椭圆E ：b 2x 2 + a 2y 2 = a 2b 2 (a> b> 0)，的左、右焦点分别为 F 1, F 2，右顶点为A, 如果点M 为椭圆E 上的任意一点，且 |MF 1|·|MF 2| 的最小值为243a ．(1) 求椭圆的离心率e ；(2) 设双曲线Q ：是以椭圆E 的焦点为顶点，顶点为焦点，且在第一象限内任取Q 上一点P ，试问是否存在常数λ(λ> 0)，使得∠PAF 1 =λ∠PF 1A 成立？试证明你的结论．分析对于(1)可利用焦半径公式直接求解．而 (2) 是一探索型的命题，解题应注重探索．由于在解析几何中对角的问题的求解，往往要主动联想到斜率．而∠PF 1A 显然是一锐角，又易知∠PAF 1是(0, 120o ) 内的角，且90o 是斜率不存在的角．于是，抓住90o 这一特殊角试探，可得解法1，若注重斜率的研究，考查所两角差的正切，可得解法2；若转变角的角度来观察，将∠PF 1A 变为∠PNF 1，使∠PAF 1变成△PNA 的外角，可得解法3；若考查角平分线的性质可得解法4；若从图像与所求式的特点分析得知，所求的λ必须是大于1的正数，从常规看来可以猜想到它可能是二倍角或三倍角的关系．由此先探索一下二倍角的情形，考查角平分线定理，可得解法5；若是考查∠PF 1A 与∠PAF 1的图形位置，直接解三角形PAF 1，可得到解法6．(1) 解设M(x 0, y 0), 由椭圆的焦半径定义得|MF 1| = a + ex 0，|MF 2| = a - ex 0，|MF 1|·|MF 2| = (a + ex 0)(a - ex 0) = a 2- e 2x 02,∵ |MF 1|·|MF 2| 的最小值为243a , 且 |x 0|≤a ，∴ a 2- e 2x 02 ≥a 2- e 2a 2 =243a ，解得 21=e ． (2) 解法1 由题意得双曲线的离心率e = 2, 且双曲线的实半轴长为c ,半焦距为2c ,故设双曲线Q 的方程为 132222=-c y c x ，假设存在适合题意的常数λ(λ> 0)，① 考虑特殊情形的λ值．当PA ⊥x 轴时，点P 的横坐标为2c ，从而点P 的纵坐标为y = 3c ，而 |AF 1| = 3c ,∴ △PAF 1是等腰直角三角形，即 ∠PAF 1 =2π , ∠PF 1A =4π, 从而可得 λ= 2． ② PA 不与x 轴垂直时，则要证∠PAF 1 = 2∠PF 1A 成立即可．由于点P(x 1, y 1)在第一象限内，故PF 1 , PA 的斜率均存在，从而，有A PF c x y k PF 111tan 1∠=+=, 111tan 2PAF cx y k PA ∠-=-=，且有 ))((31121c x c x y -+=,………… ※ 又∵21211121)()(2122tan 11y c x y c x k k A PF PF PF -++=-=∠，将※代入得PA k cx y y c x y c x A PF -=--=-++=∠2)()(22tan 112121111, 由此可得 tan2∠PF 1A = tan ∠PA F 1， ∵ P 在第一象限，A(2c , 0), ∴ )32,2()2,0(1πππ⋃∈∠PAF ,又∵ ∠PF 1A 为锐角，于是，由正切函数的单调性得 2∠PF 1A =∠PA F 1．综合上述得，当λ= 2时，双曲线在第一象限内所有点均有∠PAF 1 = 2∠PF 1A 成立．解法2 由题意得双曲线的离心率e = 2, 且双曲线的实半轴长为c , 半焦距为2c ,故设双曲线Q 的方程为 132222=-c y c x ，由于点P(x 1, y 1)在第一象限内，故PF 1 , PA 的斜率均存在．且∠PF 1A 为锐角．又∵ ))((31121c x c x y -+=, …………………………………………………… ※设∠PF 1A =β，则 ,tan 111cx y k PF +==β 设∠PAF 1=λβ, λβ≠90o 时, 则 tan(λβ)c x y k PA 211--=-=, 而 tan(λβ-β)βλββλβtan )tan(1tan )tan(+-=))(2(1211111111cx y c x y c x y c x y +--++---=212121112)2(y c cx x c x y -----= ))((3))(2()2(111111c x c x c x c x c x y -+-+---=)()2)(()2(111111c x y x c c x c x y +=-+--=． ∴ tan(λβ-β) = tan β．∵ ∠PF 1A =β为锐角，又 ∠P A F 1 =λβ∈)32,0(π, ∴ tan(λβ-β) = tan β > 0, 故λβ-β是锐角，由正切函数的单调性得 λ= 2．显然，当λβ= 90o 时亦成立．故存在λ= 2，使得双曲线在第一象限内所有点均有2∠PF 1A =∠PA F 1成立．解法3 由上述①，得λ= 2，设P ′是射线PA 上的一点, 其横坐标为x 0 ( x 0 > c )，在x 轴上取一点N (2 x 0 +c , 0)，使△P ′F 1N 为等腰三角形，∴∠P ′F 1N =∠P ′NF 1．故当∠P ′AF 1 = 2∠P ′F 1A 时，有∠P ′AF 1 = 2∠P ′NA ，从而∠AP ′N =∠P ′NA, 则 |AN| = |AP ′|，又 A(2c ,0)，于是 |AN| = |AP ′| = 2x 0-c ．过P ′作P ′H 垂直于准线l 于H ，如图9-5．则 |P ′H| = x 0-c 21．故 22||||00c x c x H P A P --='' = 2 = e ．故点P ′是双曲线上的点，且与P 重合．由x 0 > c 的任意性得，当λ= 2时，双曲线在第一象限内所有点均有2∠PF 1A =∠PAF 1成立．解法4 由题意得，设点P(x 1 , y 1)，∵ 点P 是双曲线在第一象限内的点，又A(2c , 0)是一焦点，∴ |AP| = 2x 1- c ，|AF 1| = 3c ，设AD 为∠F 1AP 的平分线， ……… ※由角平分线性质及定比分点公式，得 222)32(23123111111c c x x c x c cx c x c x c c x D =+++-=-+-+-=，由此可得，点D 在双曲线的右准线上，从而可得准线是AF 1故△AF 1D 为等腰三角形，且∠PF 1A =∠DAF 1，又由※得∠PAF 1 = 2∠PAD =2∠DAF 1， ∴ ∠PA F 1 = 2∠PF 1A ，故λ＝2．解法5 由题意得，设点P(x 1 , y 1)，因为点P 又A(2c , 0)是一焦点，于是，有|AP| = 2x 1- c ，|AF 1| = 3c ，| PF 1| 2 = (x 1 + c )2 + y 12 = x 12 + 2 x 1c+ c 2 + 3 x 12- 3 c 2 = 4 x 12 + 2 x 1c - 2 c 2, 在△APF 1中有 21212121212122432)2(2249cos c c x x c c x c c x x c F -+⨯⨯---++=∠)2(2))(2(26)(611111c x c x c x c x c c x c -+=+-+=， )2(32)224()2(9cos 12121212c x c c c x x c x c A -⨯⨯-+--+=∠c x x c c x c c x c --=-⨯⨯--=111122)2(32)2(6，于是，有 2()2(211c x c x -+)2- 1 =c x x c --1122, 即 2(co s ∠F 1)2- 1 = cos 2∠F 1 = cos ∠A, ∵ ∠A 、∠F 1是△APF 1中的内角，且∠F 1是锐角，故有 2∠F 1 =∠A, 即 ∠PA F 1 = 2∠PNF 1，所以λ= 2时，能使得双曲线在第一象限内所有点均有 ∠PA F 1 = 2∠PF 1A ．解法6 设点P(x 1 , y 1)是双曲线第一象限的点．∵ A(2c , 0)，F 1(- c , 0)，连AP ，F 1P ，如图 9-5．由双曲线的焦半径定义得 |AP| = 2x 1- c ,又设点N 是点F 1关于直线x = x 1的对称点，则有 |PF 1| = |PN|, 且N (2x 1+ c , 0)，从而 ∠PF 1N =∠PNF 1．又 |AN| = 2x 1 + c - 2c = 2x 1- c = |AP| , ∠APN =∠PNF 1．由此可得 ∠F 1AP = 2∠PNF 1 ，即 ∠F 1AP = 2∠PNF 1 = 2∠PF 1N ，所以 λ= 2．故存在λ= 2，使得双曲线在第一象限内所有点均有2∠PF 1A =∠PA F 1成立．点评对于(1)，利用焦半径公式求解是解题的常规方法；对于(2)，方法1、先由特殊情形探求出λ的值，然后再证明它对一般的情形也成立，这种方法是解决有关探索性问题的常用方法；方法2巧用了斜率与正切函数的性质直接求得λ；方法6与方法3、思维独到，都是通过变换角，把∠PF 1N 变为∠PNF 1，利用三角形的内角外角的关系，发现到|AN| = |AP|，从而也就发现了相应的解法．且解法3与解法6是不同，解法6事先不知道λ的值是2，它具有探索性．而解法3是先知道λ的值，后推证P 点在双曲线上，它是具有目的的推证．解法4，具有猜想性，是我们分析问题时常用的一种思想方法；解法5，注重对两角所在的三角形的探索，坚定不移地解三角形PAF 1，抓住了问题的本质特征分析，这种方法也是使问题获得巧解的常用一种思想方法．例3 已知抛物线 y 2 = 2P x 的焦点弦AB 被焦点分成长度为m 、n 的两段，求证：P n m 211=+．证明设A 、B 在该抛物线的准线上的射影为C 、D ，连AD 交x 轴与E ，如图9-6．由抛物线的焦半径的定义得 |AC| = |AF| = m , |BD| = |BF| = n ,由相似三角形性质知 ||||||||AB AF BD EF =，∴ nm mn EF +=||，同理 n m mn EH +=||，故 |EF| = |EH|, 即 E 与O 重合．故A 、O 、D 三点共线．同理B 、O 、C 三点共线．∴ |EF| + |EH| = P =n m mn +2, 故 Pn m 211=+．图9-6 点评本题有一个特殊的几何模型，即直角梯形ABCD ．由此还可发现许多有用的结论：①∠CFD = 90o ;②∠CAB 的平分线与∠DBA 的平分线交于一点N ，则NA 、NB 为抛物线的切线，且∠ANB= 90o ； ③在准线上任取一点向抛物线引两条切线，则两切线互相垂直；④若M 为AB 中点，则N M 被抛物线平分；⑤若A(x 1 , y 1), B(x 2, y 2)，则 |AB| =||2121y y P-，当AB ⊥x 轴时, |AB| = 2 P; ⑥以AB 为直径的圆与抛物线的准线相切；⑦NF ⊥AB; y 1y 2 = - P 2; …．。

圆锥曲线的焦半径公式推导

圆锥曲线的焦半径公式推导如下：圆锥曲线的焦半径公式是解决与圆锥曲线相关问题的重要工具。

对于椭圆来说，如果焦点在x轴上，且设点A(x_1, y_1)在椭圆上，那么点A到左焦点F_1的焦半径为a + ex_1，到右焦点F_2的焦半径为a - ex_1。

推导过程可以基于椭圆的标准方程和定义来进行：1. 椭圆的标准方程：对于中心在原点，半长轴为a，半短轴为b的椭圆，其标准方程通常写作：x²/(a²) + y²/(b²) = 1 (其中a > b > 0)2. 离心率：离心率e是描述椭圆形状的一个参数，定义为c/a，其中c是椭圆的焦距。

3. 焦半径的定义：对于椭圆上的任意一点P(x, y)，到焦点的距离称为焦半径。

4. 使用相似三角形：根据圆锥曲线的第二定义，从椭圆的一个焦点出发到椭圆上一点的射线，与从另一焦点出发到同一点的射线以及与主轴的夹角θ之间存在关系。

通过构建相似三角形，可以得到焦半径的计算公式。

5. 坐标式：当焦点在x轴上时，若已知椭圆上一点的横坐标x_1，则到左焦点F_1的焦半径长度可以用a + ex_1来计算，到右焦点F_2的焦半径长度用a - ex_1来计算。

这里的e是椭圆的离心率。

6. 倾斜角式：利用焦半径与主轴正方向的夹角θ，可以得到更为通用的焦半径表达式，尤其适用于焦点不在坐标轴上的情况。

在这种情况下，焦半径的长度与夹角θ有关，表达式为r = b²/(a±ccosθ)，这里±的选择取决于焦点的位置。

综上所述，圆锥曲线的焦半径公式有多种表达形式，可以根据具体问题的需要选择合适的公式进行计算。

这些公式不仅在理论研究中有着重要作用，在解题和实际应用中也极其重要。

圆锥曲线的焦半径公式

圆锥曲线的焦半径公式之袁州冬雪创作
圆锥曲线上任意一点到核心的间隔叫做圆锥曲线关于该点的焦半径.操纵圆锥曲线的第二定义很容易)为椭圆 + =1(a>b>0)上任意一点，F 、F 分别为椭圆的左、右核心，则 =a+e x , =a-e x .
(2)若P(x ,y )为椭圆 + =1(a>b>0)上任意一点，F 、F 分别为椭圆的上、下核心，则 =a+e y , =a-e y .
(4)若P(x ,y )为抛物线x =-2py(p>0)上任意一点，则 = -y +
不克不及，请说明来由.(答案：点P不存在)
(1)若P(x ,y )为双曲线 - =1(a>0，b>0)上任意一点，F 、F 分别为双曲线的左、右核心，则
①当点P在双曲线的左支上时， =-e x -a, =-e x +a.
②当点P在双曲线的右支上时， =e x +a, = e x -a.
(2)若P(x ,y )为双曲线 - =1(a>0，b>0)上任意一点，F 、F 分别为双曲线的上、下核心，则
①当点P在双曲线的下支上时， =-e y -a, = -ey +a.
②当点P在双曲线的上支上时， =ey +a, = ey -a.
(1)若P(x ,y )为抛物线y =2px(p>0)上任意一点，则 = x +
(2)若P(x ,y )为抛物线y =-2px(p>0)上任意一点，则 = -x +
(3)若P(x ,y )为抛物线x =2py(p>0)上任意一点，则 = y +

圆锥曲线综合1：焦半径与焦点弦的三角形式

圆锥曲线综合1：焦半径与焦点弦的三角形式圆锥曲线焦半径和焦点弦的三角形式及其性质(以焦点在x 轴上的曲线为例)设圆锥曲线的焦点弦AB 所在直线的倾斜角为θ，斜率为k ，离心率为e ，焦准距为p (抛物线只需令e=1)性质1：焦半径AF=|cos ||cos 1|2θθc a b e ep -=-，BF=|cos ||cos 1|2θθc a b e ep +=+抛物线：AF=|cos 1|θ-p ，BF=|cos 1|θ-p 性质2：焦点弦AB=|cos 2||cos 12|222222θθc a ab e ep -=-，抛物线：AB=|sin 2|2θp 性质3：222BF 1AF 1b a ep ==+；抛物线：p2BF 1AF 1=+性质4：若→→=FB AF λ，则有|11|12+-+=λλk e ，|11||cos |+-=λλθe 典型例题例1：过椭圆1222=+y x 的左焦点作倾斜角为60°的直互，直线和椭圆交于A 、B 两点，则AB=____例2：已知F 为抛物线C ：x y 42=的焦点，过F 作两条互相垂直的直线l 1和l 2，直线l 1与C 交于A 、B 两点，直线l 2与D 、E 交于两点，则AB+DE 的最小值为_______例3：已知双曲线C ：)0,0(12222>>=-b a by a x 的右焦点为F ，过F 且斜率为3的直线交C 于A 、B 两点，若→→=FB 4AF ，则C 的离心率为______.例4：已知F 是抛物线C ：x y 42=的焦点，过F 且斜率为1的直线交C 于A 、B 两点，设FA>FB ，则FA 与FB 的比值等于___________例5:已知椭圆C 的焦点为F 1(-1,0),F 2(1，0)，过F 2的直线与C 交于A 、B 两点，若AF 2=2F 2B ，AB=BF 1，则C 的方程为________例6设圆的圆心为A ，直线l 过点B(1,0)且与x 轴不重合，l 交圆于C 、D 两点，过B 作AC 的平行线交AD 于点E.(1)证明EA+EB 为定值，并写出点E 的轨迹方程；(2)设点E 的轨迹为曲线C 1，直线l 交C 1于M 、N 两点，过B 且与l 垂直的直线与圆A 交于P 、Q 两点，求四边形MPNQ 面积的取值范围.练习题1.设F 1、F 2分别是C:)0(12222>>=+b a by a x 的左右焦点，M 是C 上一点且MF 2与x 轴垂直，直线MF 1与C 的另一个交点为N(1)若直线MN 的斜率为43，求C 的离心率(2)若直线MN 在y 轴上的截距为2，且MN=5F 1N ，求a 、b2.中心在原点O 的椭圆的右焦点为F(3,0),右准线l 的方程为：x =12(1)求椭圆的方程；(2)在椭圆上任取三个不同点P 1、P 2、P 3，使得∠P 1FP 2=∠P 2FP 3=∠P 3FP 1，证明:321FP 1FP 1FP 1=+为定值，并求此定值.。

圆锥曲线的焦半径公式及其应用

技法点拨圆锥曲线的焦半径公式及其应用■郭海先摘要：利用圆锥曲线的焦半径公式以及圆锥曲线的第二定义解答圆锥曲线类问题，能起到事半功倍之效果。

关键词：椭圆焦半径公式；双曲线的焦半径公式；抛物线的焦半径公式圆锥曲线上任意一点到焦点的距离叫作圆锥曲线关于该点的焦半径。

利用圆锥曲线的第二定义很容易得到圆锥曲线的焦半径公式。

一、椭圆的焦半径公式椭圆上的任意一点到焦点F 的长，称为此曲线上该点的焦半径。

根据椭圆的定义，很容易推导出椭圆的焦半径公式。

在涉及焦半径或焦点弦的一些问题时，用焦半径公式解题可以简化运算过程。

1.若P （x 0，y 0）为椭圆x 2a 2+y 2b2=1（a>b >0）上任意一点，F 1、F 2分别为椭圆的左、右焦点，则||PF 1=a+ex 0，||PF 2=a-e x 0.2.若P （x 0，y 0）为椭圆y 2a 2+x 2b2=1（a>b >0）上任意一点，F 2、F 1分别为椭圆的上、下焦点，则||PF 1=a+e y 0，||PF 2=a-e y 0.例1．椭圆x 225+y 29=1上三个不同的点A （x 1，y 1）、B （4，95）、C（x 2，y 2）到焦点F （4，0）的距离成等差数列，求x 1+x 2的值.解：在已知椭圆中，右准线方程为x =254，设A 、B 、C 到右准线的距离为d 1、d 2、d 3，则d 1=254-x 1、d 2=254-4、d 3=254-x 2.∵|AF |=d 1·e ，|BF |=d 2·e ，|CF |=d 3·e ，而|AF|、|BF|、|CF|成等差数列.∴2d 2=d 1+d 3，即2（254-4）=2×254-（x 1+x 2），x 1+x 2=8.评析：涉及椭圆上点到焦点的距离问题，一般采用焦半径公式求解，即利用焦半径公式可求出A 、B 、C 三点到焦点的距离，再利用等差数列的性质即可求出x 1+x 2的值。

圆锥曲线焦半径公式及其应用(学生版)

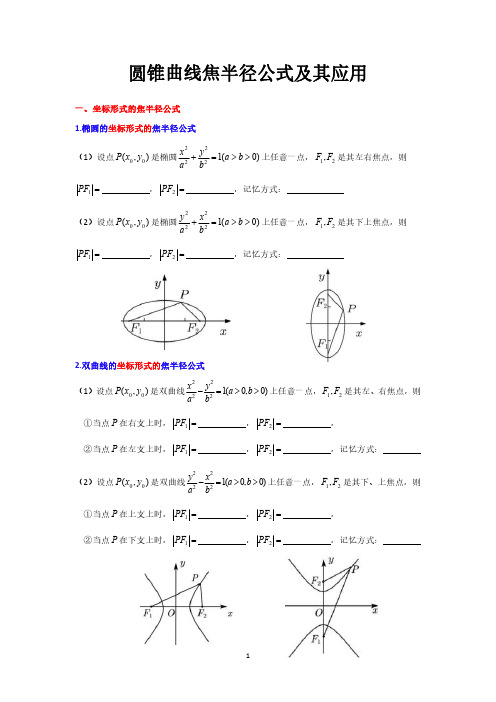
圆锥曲线焦半径公式及其应用一、坐标形式的焦半径公式1.椭圆的坐标形式的焦半径公式（1）设点),(00y x P 是椭圆)0(12222>>=+b a b y a x 上任意一点，21,F F 是其左右焦点，则=1PF ，=2PF ，记忆方式：（2）设点),(00y x P 是椭圆)0(12222>>=+b a b x a y 上任意一点，21,F F 是其下上焦点，则=1PF ，=2PF ，记忆方式：2.双曲线的坐标形式的焦半径公式（1）设点),(00y x P 是双曲线)0,0(12222>>=-b a by a x 上任意一点，21,F F 是其左、右焦点，则①当点P 在右支上时，=1PF ，=2PF ，②当点P 在左支上时，=1PF ，=2PF ，记忆方式：（2）设点),(00y x P 是双曲线)0,0(12222>>=-b a bx a y 上任意一点，21,F F 是其下、上焦点，则①当点P 在上支上时，=1PF ，=2PF ，②当点P 在下支上时，=1PF ，=2PF ，记忆方式：（3）若弦AB 过左焦点，则=AB ；若弦AB 过右焦点，则=AB 3.抛物线的坐标形式的焦半径公式（1）设),(00y x P 是抛物线)0(22>=p px y 上任意一点，F 为其焦点，则=PF （2）设),(00y x P 是抛物线)0(22>-=p px y 上任意一点，F 为其焦点，则=PF （3）设),(00y x P 是抛物线)0(22>=p py x 上任意一点，F 为其焦点，则=PF （4）设),(00y x P 是抛物线)0(22>-=p py x 上任意一点，F 为其焦点，则=PF 例1.（2021年新高考Ⅰ卷）已知21,F F 是椭圆C ：14922=+y x 的两个焦点，点M 在C 上，则21MF MF ⋅的最大值为（）A.13B.12C.9D.6例2.（2019年全国Ⅲ卷理）设21,F F 为椭圆C ：1203622=+y x 的两个焦点，M 为C 上一点且在第一象限，若21F MF ∆为等腰三角形，则点M 的坐标为例3.点),(00y x P 为双曲线C ：132422=-y x 的右支上一点，若点P 到右焦点的距离等于02x ，则=0x例4.双曲线116922=-y x 的两个焦点为21,F F ，点P 在双曲线上，若21PF PF ⊥，则点P 到x轴的距离为例5.（2011年辽宁卷）已知F 是抛物线x y =2的焦点，B A ,是该抛物线上两点，3=+BF AF ，则线段AB 的中点到y 轴的距离为A.43 B.1C.45 D.47例8.（2013年全国Ⅱ卷）设抛物线C ：)0(22>=p px y 的焦点为F ，点M 在C 上，5=MF ，若以MF 为直径的圆过点)2,0(，则C 的方程为（）A.x y 42=或x y 82= B.x y 22=或x y 82=C.x y 42=或xy 162= D.x y 22=或xy 162=注：以抛物线的焦半径为直径的圆与y 轴相切二、角度形式的焦半径公式1.椭圆的角度形式的焦半径公式（1）设过椭圆)0(12222>>=+b a b y a x 的焦点F 的弦AB 的倾斜角为θ，则=AF ；=BF ；焦点弦长=AB ；（2）设过椭圆)0(12222>>=+b a bx a y 的焦点F 的弦AB 的倾斜角为θ，则=AF ；=BF ；焦点弦长=AB ；2.双曲线的角度形式的焦半径公式设过双曲线)0,0(12222>>=-b a by a x 右焦点)0,(c F 的弦AB 的倾斜角为α，渐近线xa b y ±=的倾斜角为θ，则（1）当θπαθ-<<时，焦点弦AB 在右支上，=AF ；=BF ；=AB ，弦AB 在双曲线一支上时，焦点弦最短为（2）当θα<≤0或παθπ<<-焦点弦AB 在两支上，=AF ；=BF ；=AB ，弦AB 交双曲线两支上时，焦点弦最短为3.抛物线的角度形式的焦半径公式（1）设过焦点F 且倾斜角为θ的直线交抛物线)0(22>=p px y 于B A ,两点，则=AF ；=BF ；=AB （2）设过焦点F 且倾斜角为θ的直线交抛物线)0(22>=p py x 于B A ,两点，则=AF ；=BF ；=AB 例1.如图，设过椭圆13422=+y x 的右焦点F 的直线l 交椭圆于B A ,两点，线段AB 的垂直平分线交x 轴于点M ，则=ABMF例2.如图，过椭圆13422=+y x 的左焦点F 任作一直线交椭圆于B A ,两点，若=+BF AF BF AF λ，则=λ例2.已知椭圆12322=+y x 的左右焦点分别为21,F F ，过1F 的直线交椭圆于D B ,两点，过2F 的直线交椭圆于C A ,两点，且BD AC ⊥，则四边形ABCD 的面积的最小值为例3.过双曲线)0,0(12222>>=-b a by a x 的一个焦点F 作平行于渐近线的两直线，与双曲线分别交于B A ,两点，若a AB 2=，双曲线的离心率为e ，则[]=e 例4.已知双曲线191622=-y x 的左焦点弦交双曲线左支于B A ,两点，且772=AB ，求直线AB 的方程例5.已知F 为抛物线C ：x y 42=的焦点，过F 作两条互相垂直的直线21,l l ，直线1l 与C 交于B A ,两点，直线2l 与C 交于E D ,两点，则DE AB +的最小值为三、焦半径定比模型（1）设AB 为焦点在x 轴上的圆锥曲线的过焦点F 的弦，AB 的倾斜角为θ，斜率为k ，且FB AF λ=，则=θcos e ；=e （2）设AB 为焦点在y 轴上的圆锥曲线的过焦点F 的弦，AB 的倾斜角为θ，斜率为k ，且FB AF λ=，则=θsin e ；=e 例1.（2010年辽宁理科）设椭圆C ：)0(12222>>=+b a by a x 的左焦点为F ，过点F 的直线与椭圆C 相交于B A ,两点，直线l 的倾斜角为060，FB AF 2=，则椭圆的离心率为例2.（2010年全国Ⅰ卷）已知F 是椭圆C 的一个焦点，B 是短轴的一个端点，线段BF 的延长线交C 于D ，FD BF 2=，则C 的离心率为例3.（2010年全国Ⅱ卷）已知椭圆)0(12222>>=+b a by a x 的离心率为23，过右焦点F 且斜率为)0(>k k 的直线与C 相交于B A ,两点，若FB AF 3=，则=k （）A.1B.2C.3D.2例4.（2014年全国Ⅱ卷理）设21,F F 分别是椭圆)0(12222>>=+b a b y a x 的左右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N ，若直线MN 在y 轴上的截距为2，且N F MN 15=，则椭圆C 的方程为。

圆锥曲线焦半径

设A 11(,)x y椭圆的焦点弦的两个焦半径倒数之和为常数（焦准距倒数的2倍）11112||||ep AF BF +=22a b =椭圆中（A 点靠下，过2F 类似）21||cos b AF a c θ=+，21||cos b BF a c θ=-，θ为焦点弦的倾斜角.椭圆焦半径公式：2111||[()]a AF e x ex a c =--=+；2211||()a AF e x a ex c=-=- 双曲线的焦点弦同支（异支）的两个焦半径倒数之和（之差的绝对值）为常数（焦准距倒数的2倍）AB 同支11112||||ep AF BF +=22a b = AB 异支11112||||||ep AF BF -=22a b= 双曲线中（A 点靠下，过2F 类似）同左支21||cos b AF a c θ=-，21||cos b BF a c θ=+， θ为焦点弦的倾斜角；异支（B 点在右支）21|||cos |b AF c a θ=+,21|||cos |b BF c a θ=- 双曲线焦半径公式：11||||AF a ex =+，21||||AF a ex =-A 在左支：2111||()a AF e x a ex c =--=--；2211||()a AF e x a ex c=-=-。

A 在右支：2111||[()]a AF e x ex a c =--=+；2211||()a AF e x ex a c=-=-抛物线的焦点弦（A 点靠下）的两个焦半径倒数之和为常数（焦准距倒数的2倍） 111122||||ep p AF BF +==||1cos p AF θ=- ，||1cos p BF θ=+ 抛物线焦半径公式：1||2p AF x =+。

圆锥曲线的焦半径巧用print

圆锥曲线的焦半径巧用圆锥曲线的焦半径为：二次曲线上任意一点Q 到焦点的距离．圆锥曲线的焦半径概念，是圆锥曲线中的一个重要的概念．许多圆锥曲线的求解问题，往往都牵涉到它，且运用圆锥曲线的焦半径分析问题可给解题带来生机．因此，掌握它是非常重要的．椭圆焦半径： R 左 = a + x e , R 右 = a - x e ,右支双曲线焦半径：R 左 = x e + a ，R 右 = x e - a ( x > 0) ，左支双曲线焦半径：R 左 = - (x e + a )，R 右 = - (x e - a ) ( x < 0) ,抛物线焦半径：R 抛 = x +2P ．对于这些结论我们无须花气力去记，只要掌握相应的准线方程及标准方程的两种定义，可直接推得．如对双曲线而言：当P(x 0 , y 0)是双曲线b 2x 2 - a 2y 2 = a 2b 2 (a > 0, b > 0) 右支上的一点，F 1, F 2是其左右焦点．则有左准线方程为 ca x 2-=．由双曲线的第二定义得，左焦半径为 a ex ca x e PF +=+=0201)(||; 由 |PF 1|- |PF 2| =2a ，得 |PF 2| = |PF 2| - 2a = ex 0 - a ．( |PF 2|亦可由第二定义求得)．例1 已知F 1，F 2是椭圆E 的左、右焦点，抛物线C 以F 1为顶点，F 2为焦点，设P 为椭圆与抛物线的一个交点，如果椭圆E 的离心率e 满足 |PF 1| = e | PF 2 |，则e 的值为 ( )22)( 33)( 32)( 22)(--D C B A解法1 设F 1(- c, 0 )，F 2(c , 0)，P(x 0 , y 0)，于是，抛物线的方程为 y 2= 2 (4 c )(x + c ) , 抛物线的准线 l ：x =- 3 c ，椭圆的准线 m ：c a x 2-=，设点P 到两条准线的距离分别为d 1 , d 2．于是，由抛物线定义，得 d 1 = | PF 2 | , ……………………① 又由椭圆的定义得 |PF 1| = ed 2，而 |PF 1| = e | PF 2 |，………………………………②由①②得 d 2 = | PF 2 |, 故 d 1 = d 2，从而两条准线重合．∴ 3331322=⇒=⇒-=-e e c a c ．故选 (C)．解法2 由椭圆定义得 |PF 1| + | PF 2 | = 2a ，又 |PF 1| = e | PF 2 |，∴ | PF 2 | (1+ e ) = 2a ，………① 又由抛物线定义得 | PF 2 | = x 0 + 3c , 即 x 0 = | PF 2 | - 3c ，……………………………②由椭圆定义得 | PF 2 | = a - ex 0 , ………………………………………③由②③ 得 | PF 2 | = a - e | PF 2 | + 3ec ，即 | PF 2 | (1+ e ) = a + 3ec ， ………………… ④由①④得 2a = a + 3ec ，解得 33=e ，故选 (C)．点评结合椭圆、抛物线的定义，并充分运用焦半径是解答本题的基本思想．例2 设椭圆E ：b 2x 2 + a 2y 2 = a 2b 2 (a> b> 0)，的左、右焦点分别为 F 1, F 2，右顶点为A, 如果点M 为椭圆E 上的任意一点，且 |MF 1|·|MF 2| 的最小值为243a ．(1) 求椭圆的离心率e ；(2) 设双曲线Q ：是以椭圆E 的焦点为顶点，顶点为焦点，且在第一象限内任取Q 上一点P ，试问是否存在常数λ(λ> 0)，使得∠PAF 1 =λ∠PF 1A 成立？试证明你的结论．分析对于(1)可利用焦半径公式直接求解．而 (2) 是一探索型的命题，解题应注重探索．由于在解析几何中对角的问题的求解，往往要主动联想到斜率．而∠PF 1A 显然是一锐角，又易知∠PAF 1是(0, 120o ) 内的角，且90o 是斜率不存在的角．于是，抓住90o 这一特殊角试探，可得解法1，若注重斜率的研究，考查所两角差的正切，可得解法2；若转变角的角度来观察，将∠PF 1A 变为∠PNF 1，使∠PAF 1变成△PNA 的外角，可得解法3；若考查角平分线的性质可得解法4；若从图像与所求式的特点分析得知，所求的λ必须是大于1的正数，从常规看来可以猜想到它可能是二倍角或三倍角的关系．由此先探索一下二倍角的情形，考查角平分线定理，可得解法5；若是考查∠PF 1A 与∠PAF 1的图形位置，直接解三角形PAF 1，可得到解法6．(1) 解设M(x 0, y 0), 由椭圆的焦半径定义得|MF 1| = a + ex 0，|MF 2| = a - ex 0，|MF 1|·|MF 2| = (a + ex 0)(a - ex 0) = a 2- e 2x 02,∵ |MF 1|·|MF 2| 的最小值为243a , 且 |x 0|≤a ，∴ a 2- e 2x 02 ≥a 2- e 2a 2 =243a ，解得 21=e ．(2) 解法1 由题意得双曲线的离心率e = 2, 且双曲线的实半轴长为c ,半焦距为2c ,故设双曲线Q 的方程为 132222=-c y c x ，假设存在适合题意的常数λ(λ> 0)，① 考虑特殊情形的λ值．当PA ⊥x 轴时，点P 的横坐标为2c ，从而点P 的纵坐标为y = 3c ，而 |AF 1| = 3c ,∴ △PAF 1是等腰直角三角形，即 ∠PAF 1 =2π, ∠PF 1A =4π, 从而可得 λ= 2．② PA 不与x 轴垂直时，则要证∠PAF 1 = 2∠PF 1A 成立即可．由于点P(x 1, y 1)在第一象限内，故PF 1 , PA 的斜率均存在，从而，有A PF c x y k PF 111tan 1∠=+=, 111tan 2PAF cx y k PA ∠-=-=，且有 ))((31121c x c x y -+=,………… ※ 又∵21211121)()(2122tan 11y c x y c x k k A PF PF PF -++=-=∠，将※代入得PA k c x y y c x y c x A PF -=--=-++=∠2)()(22tan 112121111, 由此可得 tan2∠PF 1A = tan ∠PA F 1，∵ P 在第一象限，A(2c , 0), ∴ )32,2()2,0(1πππ⋃∈∠PAF ,又∵ ∠PF 1A 为锐角，于是，由正切函数的单调性得 2∠PF 1A =∠PA F 1．综合上述得，当λ= 2时，双曲线在第一象限内所有点均有∠PAF 1 = 2∠PF 1A 成立．解法2 由题意得双曲线的离心率e = 2, 且双曲线的实半轴长为c , 半焦距为2c ,故设双曲线Q 的方程为 132222=-c y c x ，由于点P(x 1, y 1)在第一象限内，故PF 1 , PA 的斜率均存在．且∠PF 1A 为锐角．又∵ ))((31121c x c x y -+=, …………………………………………………… ※设∠PF 1A =β，则 ,tan 111c x y k PF +==β设∠PAF 1=λβ, λβ≠90o 时, 则 tan(λβ)c x y k PA 211--=-=,而 tan(λβ-β)βλββλβtan )tan(1tan )tan(+-=))(2(1211111111cx y c x y c x y c x y +--++---=212121112)2(y c cx x c x y -----= ))((3))(2()2(111111c x c x c x c x c x y -+-+---=)()2)(()2(111111c x y x c c x c x y +=-+--=．∴ tan(λβ-β) = tan β．∵ ∠PF 1A =β为锐角，又 ∠P A F 1 =λβ∈)32,0(π, ∴ tan(λβ-β) = tan β > 0, 故λβ-β是锐角，由正切函数的单调性得 λ= 2．显然，当λβ= 90o 时亦成立．故存在λ= 2，使得双曲线在第一象限内所有点均有2∠PF 1A =∠PA F 1成立．解法3 由上述①，得λ= 2，设P ′是射线PA 上的一点, 其横坐标为x 0 ( x 0 > c )，在x 轴上取一点N (2 x 0 +c , 0)，使△P ′F 1N 为等腰三角形，∴∠P ′F 1N =∠P ′NF 1．故当∠P ′AF 1 = 2∠P ′F 1A 时，有∠P ′AF 1 = 2∠P ′NA ，从而∠AP ′N =∠P ′NA, 则 |AN| = |AP ′|，又 A(2c ,0)，于是 |AN| = |AP ′| = 2x 0-c ．过P ′作P ′H 垂直于准线l 于H ，如图9-5．则 |P ′H| = x 0-c 21．故 22||||00c x c x H P A P --='' = 2 = e ．故点P ′是双曲线上的点，且与P 重合．由x 0 > c 的任意性得，当λ= 2时，双曲线在第一象限内所有点均有2∠PF 1A =∠PAF 1成立．解法4 由题意得，设点P(x 1 , y 1)，∵ 点P 是双曲线在第一象限内的点，又A(2c , 0)是一焦点，∴ |AP| = 2x 1- c ，|AF 1| = 3c ，设AD 为∠F 1AP 的平分线， ……… ※由角平分线性质及定比分点公式，得 222)32(23123111111c c x x c x c cx c x c x c c x D =+++-=-+-+-=，由此可得，点D 在双曲线的右准线上，从而可得准线是AF 1故△AF 1D 为等腰三角形，且∠PF 1A =∠DAF 1，又由※得∠PAF 1 = 2∠PAD =2∠DAF 1， ∴ ∠PA F 1 = 2∠PF 1A ，故λ＝2．解法5 由题意得，设点P(x 1 , y 1)，因为点P 又A(2c , 0)是一焦点，于是，有|AP| = 2x 1- c ，|AF 1| = 3c ，| PF 1| 2 = (x 1 + c )2 + y 12 = x 12 + 2 x 1c+ c 2 + 3 x 12- 3 c 2 = 4 x 12 + 2 x 1c - 2 c 2, 在△APF 1中有 21212121212122432)2(2249cos c c x x c c x c c x x c F -+⨯⨯---++=∠)2(2))(2(26)(611111c x c x c x c x c c x c -+=+-+=， )2(32)224()2(9cos 12121212c x c c c x x c x c A -⨯⨯-+--+=∠cx x c c x c c x c --=-⨯⨯--=111122)2(32)2(6，于是，有 2()2(211c x c x -+)2- 1 =cx x c --1122, 即 2(co s ∠F 1)2- 1 = cos 2∠F 1 = cos ∠A, ∵ ∠A 、∠F 1是△APF 1中的内角，且∠F 1是锐角，故有 2∠F 1 =∠A, 即 ∠PA F 1 = 2∠PNF 1，所以λ= 2时，能使得双曲线在第一象限内所有点均有 ∠PA F 1 = 2∠PF 1A ．解法6 设点P(x 1 , y 1)是双曲线第一象限的点．∵ A(2c , 0)，F 1(- c , 0)，连AP ，F 1P ，如图 9-5．由双曲线的焦半径定义得 |AP| = 2x 1- c ,又设点N 是点F 1关于直线x = x 1的对称点，则有 |PF 1| = |PN|, 且N (2x 1+ c , 0)，从而 ∠PF 1N =∠PNF 1．又 |AN| = 2x 1 + c - 2c = 2x 1- c = |AP| , ∠APN =∠PNF 1．由此可得 ∠F 1AP = 2∠PNF 1 ，即 ∠F 1AP = 2∠PNF 1 = 2∠PF 1N ，所以 λ= 2．故存在λ= 2，使得双曲线在第一象限内所有点均有2∠PF 1A =∠PA F 1成立．点评对于(1)，利用焦半径公式求解是解题的常规方法；对于(2)，方法1、先由特殊情形探求出λ的值，然后再证明它对一般的情形也成立，这种方法是解决有关探索性问题的常用方法；方法2巧用了斜率与正切函数的性质直接求得λ；方法6与方法3、思维独到，都是通过变换角，把∠PF 1N 变为∠PNF 1，利用三角形的内角外角的关系，发现到|AN| = |AP|，从而也就发现了相应的解法．且解法3与解法6是不同，解法6事先不知道λ的值是2，它具有探索性．而解法3是先知道λ的值，后推证P 点在双曲线上，它是具有目的的推证．解法4，具有猜想性，是我们分析问题时常用的一种思想方法；解法5，注重对两角所在的三角形的探索，坚定不移地解三角形PAF 1，抓住了问题的本质特征分析，这种方法也是使问题获得巧解的常用一种思想方法．例3 已知抛物线 y 2 = 2P x 的焦点弦AB 被焦点分成长度为m 、n 的两段，求证：P n m 211=+．证明设A 、B 在该抛物线的准线上的射影为C 、D ，连AD 交x 轴与E ，如图9-6．由抛物线的焦半径的定义得 |AC| = |AF| = m , |BD| = |BF| = n ,由相似三角形性质知 ||||||||AB AF BD EF =，∴ n m mn EF +=||，同理 n m mnEH +=||，故 |EF| = |EH|, 即 E 与O 重合．故A 、O 、D 三点共线．同理B 、O 、C 三点共线． ∴ |EF| + |EH| = P =n m mn+2, 故 P n m 211=+．图9-6点评本题有一个特殊的几何模型，即直角梯形ABCD ．由此还可发现许多有用的结论：①∠CFD = 90o ;②∠CAB 的平分线与∠DBA 的平分线交于一点N ，则NA 、NB 为抛物线的切线，且∠ANB= 90o ； ③在准线上任取一点向抛物线引两条切线，则两切线互相垂直；④若M 为AB 中点，则N M 被抛物线平分；⑤若A(x 1 , y 1), B(x 2, y 2)，则 |AB| =||2121y y P -，当AB ⊥x 轴时, |AB| = 2 P;⑥以AB 为直径的圆与抛物线的准线相切；⑦NF ⊥AB; y 1y 2 = - P 2; …．。

初中数学-圆锥曲线焦半径体系-公式与证明-

规定半通径p =b 2a圆锥曲线焦半径体系1.椭圆的焦点弦：若过焦点的直线与椭圆相交于两点A 和B ，∠AF1F 2为α，则称线段AB 为焦点弦。

AF 1 =b 2a −c cos α=p 1−e cos αBF 1 =b 2a +c cos α=p 1+e cos α1AF 1 +1BF 1=2p ①如图，当焦点弦过左焦点时，焦点弦的长度AB =2ab 2a 2−c 2cos 2α=2p 1−e 2cos 2α；当焦点弦过右焦点时，焦点弦的长度AB =2ab 2a 2−c 2cos 2α=2p 1−e 2cos 2α．② 过椭圆焦点的所有弦中通径(垂直于焦点的弦)最短，通径为AB =2b 2a．③4a 体:过椭圆x 2a 2+y 2b2=1a >b >0 的左焦点F 1的弦AB 与右焦点F 2围成的三角形△ABF 2的周长是4a ；证明：(1)AF 1 +AF 2 =2a ;BF 1 +BF 2 =2a ，故AB +AF 2 +BF 2 =4a ；(2)设AF 1 =m ;BF 1 =n ;AF 2 =2a -m ;BF 2 =2a -n ;由余弦定理得m 2+2c 2-2a -m 2=2m ⋅2c cos α；整理得AF 1 =b 2a -c cosα=p 1−e cos α同理：n 2+2c 2-2a -n 2=2n ⋅2c cos 180°-α ；整理得BF 1 =b2a +c cos α=p 1+e cos α两式相加得，则过焦点的弦长：AB =m +n =2ab2a 2-c 2cos 2α=2p 1−e 2cos 2α2.双曲线的焦点弦问题：双曲线x 2a 2-y 2b2=1(a >0，b >0)的两个焦点为F 1、F 2，弦AB 过左焦点F 1(A 、B 都在左支上)，AB =l ，则△ABF 2的周长为4a +2l (如下图左)AF 1 =b 2a −c cos α=p 1−e cos αBF 1 =b 2a +c cos α=p 1+e cos α1AF 1 +1BF 1=2p 焦半径公式：当AB 交双曲线于一支时，与椭圆公式一样。