2013年广州市二模文科数学试题及答案(纯WORD)
2013广东高考文科数学试题及答案(完美版)

2013广东高考文科数学试卷及答案一、 选择题:本大题共10小题,每小题5分,满分50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 设集合{}{}22|20,,|20,S x x x x R T x x x x R =+=∈=-=∈,则ST =( )A. {}0B. {}0,2C. {}2,0-D. {}2,0,2-【答案】A ;【解析】由题意知{}0,2S =-,{}0,2T =,故{}0ST =;2. 函数()lg 11x y x +=-的定义域是( )A. ()1,-+∞B. [)1,-+∞C. ()()1,11,-+∞D. [)()1,11,-+∞【答案】C ; 【解析】由题意知1010x x +>⎧⎨-≠⎩,解得1x >-且1x ≠,所以定义域为()()1,11,-+∞;3. 若()34i x yi i +=+,,x y R ∈,则复数x yi +的模是( )A. 2B. 3C. 4D. 5 【答案】D ;【解析】因为()34i x yi i +=+,所以34xi y i -=+,根据两个复数相等的条件得:3y -=即3y =-,4x =,所以x yi +43i =-,x yi +的模5==;4. 已知51sin 25πα⎛⎫+=⎪⎝⎭,那么cos α=( ) A. 25-B. 15-C. 15D. 25【答案】C ; 【解析】51sin sin()cos ()cos()cos 22225ππππααααα⎛⎫⎡⎤+=+=-+=-==⎪⎢⎥⎝⎭⎣⎦;5. 执行如图1所示的程序框图,若输入n 的值为3,则输出s 的值是( )A. 1B. 2C. 4D. 7 【答案】D ;【解析】1i =时,1(11)1s =+-=;2i =时,1(21)2s =+-=;3i =时,2(31)4s =+-=;4i =时,4(41)7s =+-=;图1 图26. 某三棱锥的三视图如图2所示,则该三棱锥的体积是( )A.16 B. 13 C. 23D. 1 【答案】B ;【解析】由三视图可看出该三棱锥的底面为直角边为1的等腰直角三角形,高为2, 所以该三棱锥的体积111112323V =⋅⋅⋅⋅=; 7. 垂直于直线1y x =+且与圆221x y +=相切于第Ⅰ象限的直线方程是( )A. 20x y +-=B. 10x y ++=C. 10x y +-=D. 20x y ++= 【答案】A ;【解析】设所求直线为l ,因为l 垂直直线1y x =+,故l 的斜率为1-,设直线l 的方程为y x b =-+,化为一般式为0x y b +-=;因为l 与圆相切221x y +=相切,所以圆心(0,0)到直线l 的距离12b -==,所以2b =±,又因为相切与第一象限,所以0b >,故2b =,所以l 的方程为20x y +-=;8. 设l 为直线,,αβ是两个不同的平面,下列命题中正确的是( )A. 若//,//l l αβ,则//αβB. 若,l l αβ⊥⊥,则//αβC. 若,//l l αβ⊥,则αβ//D. 若,l αβα⊥//,则l β⊥ 【答案】B ;【解析】若α与β相交,且l 平行于交线,则也符合A ,显然A 错;若,//l l αβ⊥,则αβ⊥,故C 错;,l αβα⊥//,若l 平行交线,则//l β,故D 错; 9. 已知中心在原点的椭圆C 的右焦点为()1,0F ,离心率等于12,则C 的方程是( ) A. 22134x y += B. 2214x = C. 22142x y += D. 22143x y +=【答案】D ;【解析】由焦点可知()1,0F 可知椭圆焦点在x 轴上,由题意知11,2c c a ==,所以2,a b ===,故椭圆标准方程为22143x y +=; 10. 设a 是已知的平面向量且0a ≠,关于向量a 的分解,有如下四个命题:① 给定向量b ,总存在向量c ,使a b c =+;② 给定向量b 和c ,总存在实数λ和μ,使a b c λμ=+;③ 给定单位向量b 和正数μ,总存在单位向量c 和实数λ,使a b c λμ=+; ④ 给定正数λ和μ,总存在单位向量b 和单位向量c ,使a b c λμ=+.上述命题中的向量b ,c 和a 在同一平面内且两两不共线,则真命题的个数是( )A. 1B. 2C. 3D. 4【答案】D ;【解析】因为单位向量(模为1的向量,方向不确定)和一个不为零的实数可以表示任何一个向量,由题意可知A,B,C,D 均正确;二、 填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(一)必做题(11~13题)11. 设数列{}n a 是首项为1,公比为2-的等比数列,则1234a a a a +++=____________; 【答案】15;【解析】由题意知11a =,22a =-,34a =,48a =-,所以;1234a a a a +++124815=+++=;12. 若曲线2ln y ax x =-在点()1,a 处的切线平行于x 轴,则a =_____________;【答案】12; 【解析】因为2ln y ax x =-,所以12y ax x'=-,因为曲线2ln y ax x =-在点()1,a 处的切线平行于x 轴,所以1210x y a ='=-=,所以12a =;13. 已知变量,x y 满足约束条件30111x y x y -+≥⎧⎪-≤≤⎨⎪≥⎩,则z x y =+的最大值是_____________;【答案】5;【解析】作出可行域可得直角梯形的四个顶点分别为(1,1),(1,2),(1,1),(1,4)--,代入可知z 的最大值为145z =+=;(二)选做题(14~15题,考生只能从中选做一题)14. (坐标系与参数方程选做题)已知曲线C 的极坐标方程为2cos ρθ=,以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为___________________;【答案】22(1)1x y -+=;【解析】因为曲线C 的极坐标方程为2cos ρθ=;所以2cos 2cos1cos2x ρθθθ===+① ,sin 2sin cos sin 2y ρθθθθ===②;①可变形得:cos 21x θ=-③,②可变形得:sin 2y θ=;由22sin 2cos 21θθ+=得:22(1)1x y -+=;15. (几何证明选讲选做题)如图3,在矩形ABCD 中,3AB =,3BC =,BE AC ⊥,垂足为E ,则ED =___________; 【答案】212; 【解析】因为在矩形ABCD 中,3AB =,3BC =,BE AC ⊥,所以030BCA ∠=,所以03cos3032CE CB =⋅=;在CDE 中,因为060ECD ∠=,由余弦定理得: ()22222033331212cos603232224DE CE CD CE CD ⎛⎫=+-⋅⋅⋅=+-⨯⨯⨯=⎪ ⎪⎝⎭,所以212CD =;三、 解答题:本大题共6小题,满分80分. 解答须写出文字说明和演算步骤.16. (本小题满分12分)已知函数(),12f x x x R π⎛⎫=-∈ ⎪⎝⎭.(1) 求3f π⎛⎫⎪⎝⎭的值; (2) 若3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,求6f πθ⎛⎫- ⎪⎝⎭.【答案与解析】(1)133124f ππππ⎛⎫⎛⎫=-===⎪ ⎪⎝⎭⎝⎭;(2)因为3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,所以4sin 5θ==-;cos cos sin sin 6612333f ππππππθθθθθ⎛⎫⎛⎫⎛⎫⎫-=--=-=+ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎭314525210=⨯-⨯=⎭;17. (本小题满分12分)从一批苹果中,随机抽取50个,其重量(单位:克)的频数分布表如下:(1) 根据频数分布表计算苹果的重量在[)90,95的频率;(2) 用分层抽样的方法从重量在[)80,85和[)95,100的苹果中共抽取4个,其中重量在[)80,85的有几个?(3) 在(2)中抽出的4个苹果中,任取2个,求重量在[)80,85和[)95,100中各有一个的概率;【答案与解析】(1)重量在[)90,95的频率200.450==; (2)若采用分层抽样的方法从重量在[)80,85和[)95,100的苹果中共抽取4个,则重量在[)80,85的个数541515=⨯=+;(3)设在[)80,85中抽取的一个苹果为x ,在[)95,100中抽取的三个苹果分别为,,a b c ,从抽出的4个苹果中,任取2个共有(,),(,),(,),(,),(,),(,)x a x b x c a b a c b c 6种情况,其中符合“重量在[)80,85和[)95,100中各有一个”的情况共有(,),(,),(,)x a x b x c 种;设“抽出的4个苹果中,任取2个,求重量在[)80,85和[)95,100中各有一个”为事件A ,则事件A 的概率31()62P A ==; 18. (本小题满分14分)如图4,在边长为1的等边三角形ABC 中,,D E 分别是,AB AC 上的点,AD AE =,F 是BC 的中点,AF 与DE 交于点G . 将ABF ∆沿AF 折起,得到如图5所示的三棱锥A BCF -,其中22BC =. (1) 证明:DE BCF //平面; (2) 证明:CF ABF ⊥平面; (3) 当23AD =时,求三棱锥F DEG -的体积F DEG V -.图4 图5(1)证明:在图4中,因为ABC 是等边三角形,且AD AE =,所以AD AEAB AC=,//DE BC ;在图5中,因为//DG BF ,//GE FC ,所以平面DGE //平面BCF ,所以DE BCF //平面;(2)证明:在图4中,因为因为ABC 是等边三角形,且F 是BC 的中点,所以AF BC ⊥; 在图5中,因为在BFC 中,1,22BF FC BC ===,所以222BF FC BC +=,BF CF ⊥,又因为AF CF ⊥,所以CF ABF ⊥平面;(3)因为,AF CF AF BF ⊥⊥,所以AF ⊥平面BCF ,又因为平面DGE //平面BCF ,所以AF ⊥平面DGE;所以11111113323233F DEG DGEV SFG DG GE FG -=⋅⋅=⋅⋅⋅⋅=⋅⋅⋅=; 19. (本小题满分14分)设各项均为正数的数列{}n a 的前n 项和为n S ,满足2*1441,n n S a n n N +=--∈,且2514,,a a a 构成等比数列;(1)证明:2a =(2) 求数列{}n a 的通项公式; (3) 证明:对一切正整数n ,有1223111112n n a a a a a a ++++<. (1)证明:因为2*1441,n n S a n n N +=--∈,令1n =,则212441S a =--,即22145a a =+,所以2a =(2)当2n ≥时,()()221144441411n n n n n a S S a n a n -+⎡⎤=-=------⎣⎦2214n n a a +=--,所以221(2)n n a a +=+,因为{}n a 各项均为正数,所以12n n a a +=+;因为2514,,a a a 构成等比数列,所以22145a a a ⋅=,即2222(24)(6)aa a +=+,解得23a =,因为2a =11a =, 212a a =+ ,符合12n n a a +=+,所以12n n a a +=+对1n =也符合,所以数列{}n a 是一个以11a =为首项,2d =为公差的等差数列,1(1)221n a n n =+-⋅=-;(3)因为111111()(21)(21)22121n n a a n n n n +==-+--+,所以12231111111111111()()()21323522121n n a a a a a a n n ++++=-+-+⋅⋅⋅+--+ 111111111112133521212121212n n n n n ⎛⎫⎛⎫=-+-+⋅⋅⋅-=-=< ⎪ ⎪-+++⎝⎭⎝⎭; 所以对一切正整数n ,有1223111112n n a a a a a a ++++<. 20. (本小题满分14分)已知抛物线C 的顶点为原点,其焦点()()0,0F c c >到直线:20l x y --=的距离为2. 设P 为直线l 上的点,过点P 作抛物线C 的两条切线,PA PB ,其中,A B 为切点.(1) 求抛物线C 的方程;(2) 当点()00,P x y 为直线l上的定点时,求直线AB 的方程; (3) 当点P 在直线l上移动时,求AF BF ⋅的最小值. 【答案与解析】(1)因为抛物线焦点()()0,0F c c >到直线:20l x y --=的距离为2所以d ==,又因为0c >,所以解得1c =,抛物线的焦点坐标为(0,1),所以抛物线C 的方程为24x y =;(2)因为抛物线的方程为24x y =,即214y x =,所以12y x '=,设过()00,P x y 点的切线l '与抛物线的切点坐标为21(,)4m m ,所以直线l '的斜率2001142y m k m x m-==-,解得10m x =20m x=-A 点坐标为2111(,)4m m ,B 点坐标为2221(,)4m m ==0=>,所以12m m ≠;221212012111144()42AB m m k m m x m m -==+=-;所以直线AB 的方程为210111()42y m x x m -=-,代入整理得:012y x =; (3)A 点坐标为2111(,)4m m ,B 点坐标为2221(,)4m m ,F 点坐标为()0,1,因为0020x y --=;所以100m x x ==,200m x x ==,1202m m x +=,12048m m x =-;因此AF BF ⋅=()2222222212121212121211111111()1()2144164164m m m m m m m m m m m m ⎛⎫⎛⎫⎡⎤=++=+++=++-+ ⎪⎪⎣⎦⎝⎭⎝⎭()22220000001139(48)22(48)12692()16422x x x x x x ⎡⎤=-+--+=-+=-+⎣⎦,所以当032x =时,AF BF ⋅取最小值92;21. 设函数()()32f x x kx x k R =-+∈.(1) 当1k =时,求函数()f x 的单调区间;(2) 当0k <时,求函数在[,]k k -上的最小值m 和最大值M . 【答案与解析】(1) 因为()32f x x kx x =-+,所以2()321f x x kx '=-+;当1k =时,2212()3213()033f x x x x =-+=-+>,所以()f x 在R 上单调递增;(2) 因为2()321f x x kx '=-+,22(2)4314(3)k k ∆=--⨯⨯=-;① 当0∆≤时,即0k ≤<时,()0f x '≥,()f x 在R 上单调递增,此时无最小值和最大值;② 当0∆>时,即k <令()0f x '=,解得x ==或x ==;令()0f x '>,解得x <或3k x >;令()0f x '<,解得33k k x +<<;因为0k <=<-23kk >=>作()f x的最值表如下:。
2013年广东省广州市天河区中考二模数学试题及答案
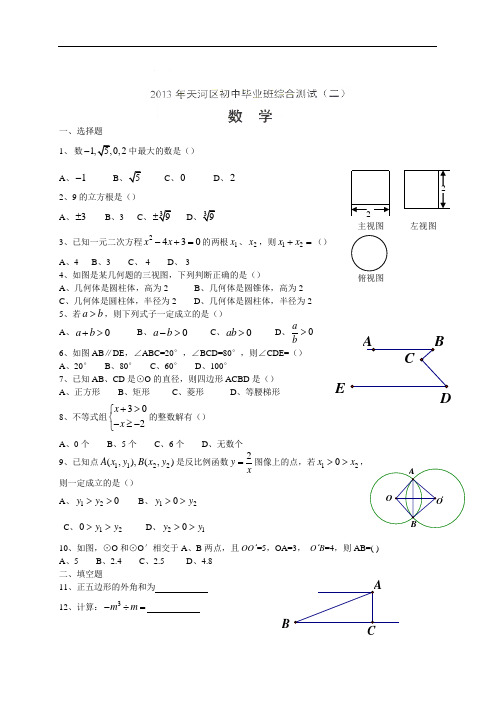
一、选择题1、 数1,5,0,2-中最大的数是()A 、1-B 、5C 、0D 、2 2、9的立方根是()A 、3±B 、3C 、39±D 、393、已知一元二次方程2430x x -+=的两根1x 、2x ,则12x x +=()A 、4B 、3C 、-4D 、-3 4、如图是某几何题的三视图,下列判断正确的是() A 、几何体是圆柱体,高为2 B 、几何体是圆锥体,高为2 C 、几何体是圆柱体,半径为2 D 、几何体是圆柱体,半径为2 5、若a b >,则下列式子一定成立的是()A 、0a b +>B 、0a b ->C 、0ab >D 、0a b> 6、如图AB ∥DE ,∠ABC=20°,∠BCD=80°,则∠CDE=() A 、20° B 、80° C 、60° D 、100°7、已知AB 、CD 是⊙O 的直径,则四边形ACBD 是() A 、正方形 B 、矩形 C 、菱形 D 、等腰梯形8、不等式组302x x +>⎧⎨-≥-⎩的整数解有()A 、0个B 、5个C 、6个D 、无数个 9、已知点1122(,),(,)A x y B x y 是反比例函数2y x=图像上的点,若120x x >>, 则一定成立的是()A 、120y y >>B 、120y y >>C 、120y y >>D 、210y y >>10、如图,⊙O 和⊙O ′相交于A 、B 两点,且OO ’=5,OA=3, O ’B =4,则AB=( )A 、5B 、2.4C 、2.5D 、4.8 二、填空题11、正五边形的外角和为 12、计算:3m m -÷=A CBBDECA22 主视图左视图俯视图 OBOA‘13、分解因式:2233x y -=14、如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC=1200米,从飞机上看地面控制点B 的俯角20α=︒,则飞机A 到控制点B 的距离约为 。
2013广州二模数学试题(文科试题含答案)

数学(文科)试题A 第 1 页 共 16 页试卷类型:B2013年广州市普通高中毕业班综合测试(二)数学(文科)2013.4本试卷共4页,21小题, 满分150分.考试用时120分钟注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号。
用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式Sh V 31=,其中S 是锥体的底面积,h 是锥体的高.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.命题“x ∃∈R ,2450x x ++≤”的否定是A .x ∃∈R ,2450x x ++>B .x ∃∈R ,2450x x ++≤ C .x ∀∈R ,2450x x ++> D .x ∀∈R ,2450x x ++≤2.如果函数()()ln 2f x x a =-+的定义域为(),1-∞,则实数a 的值为A .2-B .1-C .1D .23.对于任意向量a 、b 、c ,下列命题中正确的是A .= a b a bB .+=+a b a bC .()()= a b c a b cD .2= a a a4.若直线()1y k x =+与圆()2211x y ++=相交于A 、B 两点,则AB 的值为A .2B .1C .12D .与k 有关的数值数学(文科)试题A 第 2 页 共 16 页5.若1i -(i 是虚数单位)是关于x 的方程220x px q ++=(p q ∈R 、)的一个解,则p q += A .3- B .1- C .1 D .36.执行如图1所示的程序框图,输出的S 值为A .225B .196C .169D .144(注:框图中的赋值符号“=”也可以写成 “←”或“﹕=”)7.若函数cos y x ω=()*ω∈N 的一个对称中心是06π⎛⎫⎪⎝⎭,,则ω的最小值为 A .2 B .3 C .6 D .98.一个圆锥的正(主)视图及其尺寸如图2所示.若一个平行于 圆锥底面的平面将此圆锥截成体积之比为1﹕7的上、下两 部分,则截面的面积为A .14π B .π C .94π D .4π9.已知01a <<,01x y <<≤,且log log 1a a x y = ,那么xy 的取值范围是 A .(20a ⎤⎦, B .(]0a , C .10a ⎛⎤ ⎥⎝⎦,D .210a ⎛⎤ ⎥⎝⎦,10.某校高三(1)班50个学生选择选修模块课程,他们在A 、B 、C 三个模块中进行选择,且至少需要选择1个模块,具体模块选择的情况如下表:模块 模块选择的学生人数模块 模块选择的学生人数A 28 A 与B 11 B 26 A 与C 12 C26B 与C13则三个模块都选择的学生人数是A .7B .6C .5D .4图1 S S i =+ 0,1S i ==结束 开始 否 是 输出S 27?i > 2i i =+ 46图2数学(文科)试题A 第 3 页 共 16 页二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题)11.如图3,一个等腰直角三角形的直角边长为2,分别以三个顶点为圆心,1为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P ,则点P 落在区域M 内的概率为 . 12.已知α为锐角,且3c o s 45απ⎛⎫+= ⎪⎝⎭,则 sin α= . 13.数列}{n a 的项是由1或2构成,且首项为1,在第k 个1和第1k +个1之间有21k -个2,即数列}{n a 为:1,2,1,2,2,2,1,2,2,2,2,2,1,…,记数列}{n a 的前n 项和为n S ,则20S = ;2013S = . (二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)在△ABC 中,D 是边AC 的中点,点E 在线段BD 上,且满足13BE BD =,延长AE 交BC 于点F , 则BFFC的值为 . 15.(坐标系与参数方程选做题)在极坐标系中,已知点1,2A π⎛⎫ ⎪⎝⎭,点P 是曲线2sin 4cos ρθθ=上任一点,设点P 到直线 cos 10ρθ+=的距离为d ,则PA d +的最小值为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:(1)用上述样本数据估计高三(1)班学生视力的平均值;(2)已知其余五个班学生视力的平均值分别为4.3、4.4、4.5、4.6、4.8.若从这六个班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于...0.2的概率.视力数据 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0 5.1 5.2 5.3 人数2 2 2 1 1图3M数学(文科)试题A 第 4 页 共 16 页某单位有A 、B 、C 三个工作点,需要建立一个公共无线网络发射点O ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为80AB =m ,70BC =m ,50CA =m .假定A 、B 、C 、O 四点在同一平面上. (1)求BAC ∠的大小;(2)求点O 到直线BC 的距离. 18.(本小题满分14分)如图4, 在三棱锥P ABC -中,90PAB PAC ACB ∠=∠=∠=.(1)求证:平面PBC ⊥平面PAC ;(2)若1PA =,=2AB ,当三棱锥P ABC -的体积最大时, 求BC 的长.PABC图4数学(文科)试题A 第 5 页 共 16 页在等差数列{}n a 中,125a a +=,37a =,记数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n S .(1)求数列{}n a 的通项公式;(2)是否存在正整数m 、n ,且1m n <<,使得1S 、m S 、n S 成等比数列?若存在,求出所有符合条件的m 、n 的值;若不存在,请说明理由.数学(文科)试题A 第 6 页 共 16 页已知函数2()2ln f x x a x =-()0a a ∈≠R 且.(1)若()f x 在定义域上为增函数,求实数a 的取值范围; (2)求函数()f x 在区间[1,2]上的最小值.数学(文科)试题A 第 7 页 共 16 页经过点()0,1F 且与直线1y =-相切的动圆的圆心轨迹为M .点A 、D 在轨迹M 上,且关于y 轴对称,过线段AD (两端点除外)上的任意一点作直线l ,使直线l 与轨迹M 在点D 处的切线平行,设直线l 与轨迹M 交于点B 、C . (1)求轨迹M 的方程;(2)证明:BAD CAD ∠=∠; (3)若点D 到直线AB 的距离等于22AD ,且△ABC 的面积为20,求直线BC 的方程.数学(文科)试题A 第 8 页 共 16 页2013年广州市普通高中毕业班综合测试(二)数学(文科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力对照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分.题号 1 23 4 56 7 8 9 10答案 C D D A C B B C A B二、填空题:本大题查基本知识和基本运算,体现选择性.共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.第13题第一个空2分,第二个空3分.11.14π-12.210 13.36;3981 14.1415.2三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题主要考查随机抽样、平均数、古典概型等基础知识,考查数据处理能力,本小题满分12分) 解:(1)高三文科(1)班抽取的8名学生视力的平均值为4.42 4.62 4.82 4.95.14.78⨯+⨯+⨯++=.据此估计高三文科(1)班学生视力的平均值约为4.7.………………………………………………3分 (2)因为高三文科六个班学生视力的平均值分别为4.3、4.4、4.5、4.6、4.7、4.8,所以任意抽取两个文科班学生视力的平均值数对有()4.34.4,,()4.34.5,,()4.34.6,,()4.34.7,,()4.34.8,,()4.44.5,,()4.44.6,,()4.44.7,,()4.44.8,,()4.54.6,,()4.54.7,,()4.54.8,, ()4.64.7,,()4.64.8,,()4.74.8,,共15种情形.…………………………………………………7分 其中抽取的两个班学生视力的平均值之差的绝对值不小于0.2的有()4.34.5,,()4.34.6,,()4.34.7,,()4.34.8,,()4.44.6,,()4.44.7,,()4.44.8,,()4.54.7,,()4.54.8,,()4.64.8,,共10种. ……………………10分 所以抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率为102=153. ………………12分数学(文科)试题A 第 9 页 共 16 页17.(本小题主要考查解三角形等基础知识,考查正弦定理与余弦定理的应用,本小题满分12分) 解:(1)在△ABC 中,因为80AB =m ,70BC =m ,50CA =m ,由余弦定理得222cos 2AB AC BC BAC AB AC+-∠=⨯⨯ ………………………………………………………2分2228050701280502+-==⨯⨯. ……………………………………………………3分因为BAC ∠为△ABC 的内角,所以3BAC π∠=.……………………………………………………4分 (2)方法1:因为发射点O 到A 、B 、C 三个工作点的距离相等,所以点O 为△ABC 外接圆的圆心.……………………………………………………………………5分 设外接圆的半径为R ,在△ABC 中,由正弦定理得2sin BCR A=, ……………………………………………………………7分 因为70BC =,由(1)知3A π=,所以3sin 2A =. 所以7014032332R ==,即7033R =.…………………8分 过点O 作边BC 的垂线,垂足为D ,…………………………9分在△OBD 中,7033OB R ==,703522BC BD ===, 所以2222703353OD OB BD ⎛⎫=-=- ⎪ ⎪⎝⎭………………………………………………………11分 3533=. 所以点O 到直线BC 的距离为3533m .……………………………………………………………12分 方法2:因为发射点O 到A 、B 、C 三个工作点的距离相等, 所以点O 为△ABC 外接圆的圆心.……………………5分 连结OB ,OC ,过点O 作边BC 的垂线,垂足为D , …………………6分 由(1)知3BAC π∠=, 所以3BOC 2π∠=. ABCODABCOD数学(文科)试题A 第 10 页 共 16 页所以3BOD π∠=.…………………………………………………………………………………………9分 在Rt △BOD 中,703522BC BD ===, 所以35353tan tan 603BD OD BOD ===∠ .…………………………………………………………11分 所以点O 到直线BC 的距离为3533m .……………………………………………………………12分18.(本小题主要考查空间直线与平面的位置关系和几何体的体积计算等基础知识,考查空间想象能力等,本小题满分14分)(1)证明:因为90PAB PAC ∠=∠=,所以PA AB ⊥,PA AC ⊥.………………………………1分因为AB AC A = ,所以PA ⊥平面ABC .…………………………………………………………2分 因为BC ⊂平面ABC ,所以BC PA ⊥.………………………………………………………………3分因为90ACB ∠=,所以BC CA ⊥.……………………………………………………………………4分因为PA CA A = ,所以BC ⊥平面PAC .…………………………………………………………5分 因为BC ⊂平面PBC ,所以平面PBC ⊥平面PAC .………………………………………………6分 (2)方法1:由已知及(1)所证可知,PA ⊥平面ABC ,BC CA ⊥, 所以PA 是三棱锥P ABC -的高.……………………………7分 因为1PA =,=2AB ,设BC x =()02x <<,……………8分 所以2222224AC AB BC x x =-=-=-.…………9分因为13P ABC ABC V S PA -=⨯△ 2146x x =-………………………………………………………………………………10分()22146x x =- ()224162x x +-≤⨯…………………………………………………………………………11分 13=.…………………………………………………………………………………………12分 当且仅当224x x =-,即2x =时等号成立.………………………………………………………13分所以当三棱锥P ABC -的体积最大时,2=BC .…………………………………………………14分PABC数学(文科)试题A 第 11 页 共 16 页方法2:由已知及(1)所证可知,PA ⊥平面ABC ,所以PA 是三棱锥P ABC -的高.………………………………………………………………………7分因为90ACB ∠=,设ABC θ∠=02πθ⎛⎫<<⎪⎝⎭,……………………………………………………8分 则cos 2cos BC AB θθ==,sin 2sin AC AB θθ==.……………………………………………9分所以112cos 2sin sin 222ABC S BC AC θθθ=⨯⨯=⨯⨯=△.………………………………………10分 所以13P ABC ABC V S PA -=⨯△1sin 23θ=. ………………………………………………………………………………11分因为02πθ<<,所以当4πθ=,P ABC V -有最大值13. …………………………………………………………………12分 此时2cos24BC π==.………………………………………………………………………………13分所以当三棱锥P ABC -的体积最大时,2=BC .…………………………………………………14分19.(本小题主要考查等差数列、裂项法求和等基础知识,考查运算求解能力和推理论证能力等,本小题满分14分)解:(1)设等差数列{}n a 的公差为d ,因为1235,7.a a a +=⎧⎨=⎩即1125,27.a d a d +=⎧⎨+=⎩………………………………………………………………………2分 解得11,3.a d =⎧⎨=⎩………………………………………………………………………………………………3分 所以()()1113132n a a n d n n =+-=+-=-.所以数列{}n a 的通项公式为32n a n =-*()n ∈N . …………………………………………………4分(2)因为()()111111323133231n n a a n n n n +⎛⎫==- ⎪-+-+⎝⎭, ……………………………………………5分 所以数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和数学(文科)试题A 第 12 页 共 16 页1223341111111n n n n n S a a a a a a a a a a -+=+++++1111111111111113434737103353233231n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+- ⎪ ⎪ ⎪⎪ ⎪---+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ 11133131nn n ⎛⎫=-= ⎪++⎝⎭.……………………………………………………………………………7分 假设存在正整数m 、n ,且1m n <<,使得1S 、m S 、n S 成等比数列,则21m n S S S =.……………………………………………………………………………………………8分即2131431m n m n ⎛⎫=⨯ ⎪++⎝⎭.………………………………………………………………………………9分 所以224361m n m m =-++.因为0n >,所以23610m m -++>. 即23610m m --<. 因为1m >,所以231133m <<+<. 因为*m ∈N ,所以2m =.……………………………………………………………………………12分此时22416361m n m m ==-++.…………………………………………………………………………13分 所以存在满足题意的正整数m 、n ,且只有一组解,即2m =,16n =. ………………………14分 20.(本小题主要考查函数的单调性和最值等基础知识,考查数形结合思想、分类讨论思想和运算求解能力等,本小题满分14分)解:(1)因为函数2()2ln f x x a x =-,所以函数()f x 的定义域为(0,)+∞.……………………………………………………………………1分 且2()2af x x x'=-.………………………………………………………………………………………2分 若()f x 在定义域上是增函数,数学(文科)试题A 第 13 页 共 16 页则2()20af x x x'=-≥在(0,)+∞上恒成立.…………………………………………………………3分 即2a x ≤在(0,)+∞上恒成立,所以0a ≤. …………………………………………………………4分 由已知0a ≠,所以实数a 的取值范围为(),0-∞.……………………………………………………………………5分 (2)①若0a <,由(1)知,函数2()2ln f x x a x =-在区间[1,2]上为增函数.所以函数()f x 在区间[1,2]上的最小值为(1)1f =.…………………………………………………6分②若0a >,由于()()2222()x a x ax a f x x x+--'==, 所以函数()f x 在区间()0,a 上为减函数,在区间(),a +∞上为增函数.………………………7分(ⅰ)若1a ≤,即01a <≤时,()[1,2],a ⊂+∞,函数2()2ln f x x a x =-在区间[1,2]上为增函数,所以函数()f x 在[1,2]的最小值为(1)1f =.…………………………………………………………9分 (ⅱ)若12a <≤,即14a <≤时,函数2()2ln f x x a x =-在区间()1,a 为减函数,在(),2a 上为增函数,所以函数()f x 在区间[1,2]上的最小值为()ln f a a a a =-.……………………………………11分(ⅲ)若2a >,即4a >时,()[1,2]0,a ⊂,函数()f x 在区间[1,2]上为减函数,所以函数()f x 在[1,2]的最小值为(2)42ln 2f a =-. ……………………………………………13分 综上所述,当1a ≤且0a ≠时,函数()f x 在区间[1,2]上的最小值为(1)1f =. 当14a <≤时,函数()f x 在区间[1,2]的最小值为()ln fa a a a =-.当4a >时,函数()f x 在区间[1,2]上的最小值为(2)42ln 2f a =-.………………14分数学(文科)试题A 第 14 页 共 16 页21.(本小题主要考查动点的轨迹和直线与圆锥曲线的位置关系、导数的几何意义等基础知识,考查运算求解能力和推理论证能力等,本小题满分14分)解:(1)方法1:设动圆圆心为(),x y ,依题意得,()2211x y y +-=+.…………………………1分整理,得24x y =.所以轨迹M 的方程为24x y =.…………………………………………………2分 方法2:设动圆圆心为P ,依题意得点P 到定点()0,1F 的距离和点P 到定直线1y =-的距离相等, 根据抛物线的定义可知,动点P 的轨迹是抛物线.……………………………………………………1分 且其中定点()0,1F 为焦点,定直线1y =-为准线.所以动圆圆心P 的轨迹M 的方程为24x y =.………………………………………………………2分 (2)由(1)得24x y =,即214y x =,则12y x '=. 设点2001,4D x x ⎛⎫⎪⎝⎭,由导数的几何意义知,直线l 的斜率为012BC k x =.…………………………3分由题意知点2001,4A x x ⎛⎫- ⎪⎝⎭.设点2111,4C x x ⎛⎫ ⎪⎝⎭,2221,4B x x ⎛⎫⎪⎝⎭,则2212120121114442BCx x x x k x x x -+===-,即1202x x x +=.………………………………………………4分因为2210101011444ACx x x x k x x --==+,2220202011444AB x x x x k x x --==+.……………………………5分 由于()120102020444AC ABx x x x x x x k k +---+=+==,即AC AB k k =-.………………………6分所以BAD CAD ∠=∠.…………………………………………………………………………………7分 (3)方法1:由点D 到AB 的距离等于22AD ,可知BAD ∠45= .………………………………8分 不妨设点C 在AD 上方(如图),即21x x <,直线AB 的方程为:()20014y x x x -=-+. 由()20021,44.y x x x x y ⎧-=-+⎪⎨⎪=⎩A B CDOxylE数学(文科)试题A 第 15 页 共 16 页解得点B 的坐标为()20014,44x x ⎛⎫-- ⎪⎝⎭.……………………………………………………………10分 所以()()00024222AB x x x =---=-.由(2)知CAD BAD ∠=∠45=,同理可得0222AC x =+.………………………………11分 所以△ABC 的面积2000122222244202S x x x =⨯-⨯+=-=, 解得03x =±.……………………………………………………………………………………………12分 当03x =时,点B 的坐标为11,4⎛⎫- ⎪⎝⎭,32BC k =, 直线BC 的方程为()13142y x -=+,即6470x y -+=.…………………………………………13分 当03x =-时,点B 的坐标为497,4⎛⎫- ⎪⎝⎭,32BC k =-, 直线BC 的方程为()493742y x -=-+,即6470x y +-=. ……………………………………14分 方法2:由点D 到AB 的距离等于22AD ,可知BAD ∠45= .…………………………………8分 由(2)知CAD BAD ∠=∠45= ,所以CAB ∠90=,即AC AB ⊥.由(2)知104AC x x k -=,204AB x x k -=. 所以1020144AC ABx x x xk k --=⨯=-.即()()102016x x x x --=-. ① 由(2)知1202x x x +=. ②不妨设点C 在AD 上方(如图),即21x x <,由①、②解得10204,4.x x x x =+⎧⎨=-⎩…………………………10分因为()2222202001122244AB x x x x x ⎛⎫=++-=- ⎪⎝⎭,同理0222AC x =+. ………………………………………………………………………………11分 以下同方法1.数学(文科)试题A 第 16 页共 16 页。
2013年广州二模文综(含答案)

试卷类型:B 2013年广州市普通高中毕业班综合测试(二)文科综合2013.4 本试卷共11页,41小题,满分300分。
考试用时150分钟。
注意事项:1. 答卷前,考生务必用2B铅笔在“考生号”处填涂考生号。
用黑色字迹的钢笔或签字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上c3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
—、选择题:本题包括35小题,每小题4分,共140分。
在每小题列出的四个选项中,只有一项是符合题目要求的。
1. 因纽特人告别冬季、迎接春天到来的“春节”在A. 12月25日B.1月1日C. 3月最后一个周末D.6月第一个周末读“某河流年径流变化示意图”,完成2〜3题。
2. 该河流位于A.乞力马扎罗山B.塔里木盆地C.苔原地区D.赤道地区3. 该流域的地理环境是A.有极昼极夜B.沙漠遍布C.垂直地带性明显D.人口稠密读“我国距今2300万年前植被带分布示意图”,完成4~5题。
4. 中部自然带的主要成因是受A.副热带高气压带影响B.副极地低气压带影响C.赤道低气压带影响D.季风环流影响5. 自然带分布的格局反映了A.经度地带性规律B.纬度地带性规律C.垂直地带性规律D.非地带性规律读“我国15〜64岁年龄段人口变化图”,完成6〜7题。
6. 2015年后,我国人口变化的特点是A.少儿人口比重上升B.总人口数量不断减少C.老年人口比重下降D.劳动力数量不断减少7. 影响图中人口变化的最主要因素是A.出生率B.医疗卫生C. 死亡率D.自然环境读“世界某农作物产区分布示意图”,完成8〜9题。
广州市高考二模数学试题及答案(文科)

广州市2013届普通高中毕业班综合测试(二)数学(文科)本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1. 答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号。
用黑色字迹的钢笔或签 字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写 在答题卡上。
用2B 铅笔将试卷类型(B)填涂在答题卡相应位置上。
2. 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑; 如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区 域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使 用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、 错涂、多涂的,答案无效。
5. 考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
,其中S 是锥体的底面积,h 是锥体的高. 一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只 有一项是符合题目要求的.1. 命题“054,2≤++∈∃x x R x ”的否定是A 054,2>++∈∃x x R xB 054,2≤++∈∃x x R xC 054,2>++∈∀x x R xD 054,2≤++∈∀x x R x2. 如果函数f(x)=ln(-2x+ a)的定义域为(-∞,1),则实数a 的值为A. -2B. -1C. 1D. 2 3. 对于任意向量a 、B 、C ,下列命题中正确的是A. |a.b| = |a| |b|B. |a+b|=|a|+丨b 丨C. (a.b)c =a (b-c)D. a.a =|a|24. 直线y=kx +1与圆(x+1)2+y 2=0相交于A ,B 两点,则|AB|的值为A.2B.1C. 21D.与k 有关的数值 5. 若1-i(i 是虚数单位)是关于x 的方程x 2+2px +q=0(p 、q ∈R)的一个解,则p+q= A. -3 B. -1 C. 1 D. 3 6. 执行如图l 所示的程序框图,输出的S 值为A. 225B. 196C. 169D. 144(注:框图中的赋值符号“=”也可以写成“←”或“:=”)7.若函数*)(cos N x y ∈=ωω的一个对称中心是(6π,0),则ω的最小值为 A. 2 B. 3 C. 6 D. 98. 一个圆锥的正(主)视图及其尺寸如图2所示.若一个平 行于圆锥底面的平面将此圆锥截成体积之比为l:7的上、下两部分,则截面的面积为A.π41 B. π C π49 B π4 9. 已知0<a<1,0<x ≤y < 1,且log a x.log a y=1,那么xy 的取值范围为A. (0,a 2]B. (0,a]C. ]1,0(a D. ]1,0(2a10.某校高三(1)班50个学生选择选修模块课程,他们在A 、B 、C 三个模块中进行选择,R 至少需要选择l 个模块,具体模块选择的情况如下表:则三个模块都选择的学生人数是A. 7B. 6C. 5D. 4二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.(—)必做题(11~13题) 11.如图3,一个等腰直角三角形的直角边长为2,分别以三个顶点为 圆心,l 为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部分).若在此三角形内随机取一点P,则点P 落在区 域M 内的概率为 . 12.已知a 为锐角,且53)4cos(=+πa ,则sina= _ . 13. 数列{a n }的项是由l 或2构成,且首项为1,在第k 个l 和第k+ 1个l 之间有2k-1 个2,即数列{a n } 为:1, 2,1, 2,2,2,1,2,2,2,2,2, 1, …,记数列 {a n }的前n 项和为S n ,则S 20=________; S 2013 =_____(二)选做题(14~15题,考生只能从中选做一题)14.(几何证明选讲选做题)在ΔBC 中,D 是边AC 的中点,点E 在线段BD 上,且满足BE =31BD,延长A E 交 BC 于点F ,则FC BF 的值为_______.15.(坐标系与参数方程选做题)在极坐标系中,已知点A(1, 2π),点P 是曲线ρsin 2θ=4cos θ上任意一点,设点P 到直 线ρcos θ + 1 = 0的距离为d ,则丨PA 丨+ d 的最小值为_______.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16. (本小题满分12分)某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中 以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三(1)班抽取的8名学生的视力数据与人数见下表:(1) 用上述样本数据估计高三(1)班学生视力的平均值;(2)已知其余五个班学生视力的平均值分别为4.3、4.4,4.5、4.6、4.8.若从这六个 班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.17. (本小题满分12分)某单位有A 、B 、C 三个工作点,需要建立一个公共无线网络发射点0,使得发射点到 三个工作点的距离相等.已知这三个工作点之间的距离分别为AB=80m, BC=10M , CA=50m.假定A 、B 、C 、O 四点在同一平面上.(1) 求BAC ∠的大小;(2)求点O 到直线BC 的距离18(本小题满分14分)如图4,在三棱锥P-ABC 中,PAB ∠=PAC ∠=ACB ∠=900.(1) 求证:平面PBC 丄平面PAC(2)已知PA=1,AB=2,当三棱锥P-ABC 的体积 最大时,求BC 的长.19. (本小题满分14分)在等差数列{a n }中,a 1 +a 2 =5, a 3 =7,记数列}1{1+n n a a 的前n 项和为S n . (1) 求数列{a n }的通项公式;(2)是否存在正整数m 、n,且1<m <n ,使得S 1、S nt S n 成等比数列?若存在,求出所有符合条件的m,n 值;若不存在,请说明理由20.(本小题满分14分)已知函数f(x)=x 2 -2alnx ()0≠∈a R a 且).(1) 若f(x)在定义域上为增函数,求实数a 的取值范围;(2) 求函数f (x)在区间[1,2]上的最小值.21. (本小题满分14分)经过点F (0,1)且与直线y = -1相切的动圆的圆心轨迹为M 点A 、D 在轨迹M 上, 且关于y 轴对称,过线段AD (两端点除外)上的任意一点作直线l ,使直线l 与轨迹M 在点D 处的切线平行,设直线l 与轨迹M 交于点B 、 C.(1) 求轨迹M 的方程;(2) 证明:CAD BAD ∠=∠;(3) 若点D 到直线AB 的距离等于||22AD ,且ΔABC 的面积为20,求直线BC 的方程.。
广州二模纯word试题及答案

2013年广州二模化学试题7.下列实验能达到实验目的的是A.用乙醇萃取碘水中的碘B.用饱和NaHCO3溶液除去CO2中的HClC.用Ba(NO3)2溶液鉴别SO32-和SO42-D.用淀粉KI溶液鉴别FeCl3溶液和溴水8.下列说法正确的是A.溴乙烷和甲醇都能发生消去反应B.乙烯和苯都能与酸性KMnO4溶液发生反应C.糖类和蛋白质都是人体需要的营养物质D.纤维素和油脂的水解产物都是葡萄糖9.设n A为阿伏加德罗常数的数值,下列说法正确的是A.常温下,18gH2O中含有2n A个氢原子B.标准状况下,22.4L苯含有n A个苯分子C.1mol Na与足量水反应转移2n A个电子D.0.1 mol·L-1CH3COOH溶液中含有0.1n A个CH3COO-10.下列物质的制取,实验操作正确的是A.将CuCl2溶液置于蒸发皿中加热蒸干,可制取无水CuCl2固体B.将NH4HCO3饱和溶液置于蒸发皿中加热蒸干,可制取NH4HCO3固体C.向FeCl3饱和溶液缓慢滴入过量氨水加热,可制取Fe(OH)3胶体D.向电石中缓慢滴入饱和食盐水,可制取C2H211.下列离子方程式正确的是A.铝溶于NaOH溶液:Al +2OH-=AlO2-+H2↑B.铜溶于稀硝酸:3Cu+ 8H+ +2NO3-=3Cu2++2NO↑ + 4H2OC.碳酸镁中滴加稀盐酸:CO32-+2H+ =CO2↑ + H2OD.稀硫酸中滴加氢氧化钡溶液:H+ + OH=H2O12.短周期元素甲、乙、丙、丁、戊的原子序数依次增大,甲是周期表中原子半径最小的元素,乙形成的气态氢化物的水溶液呈碱性,乙与丁同族,丙、丁、戊同周期,丙单质可制成半导体材料,戊的最高化合价为+7,则A.原子半径:乙>丁>丙B.非金属性:丙>丁>戊C.甲与戊形成的化合物是共价化合物D.乙、丙、丁最高价氧化物对应的水化物均是强酸22.HA为酸性略强于醋酸的一元弱酸,则下列叙述正确的是A.0.1 mol·L-1 HA 中c(H+) = c(OH-) + c(A-)B.0.1 mol·L-1 HA 与0.1 mol·L-1NaOH 混合至溶液呈中性:C.0.1 mol·L-1 NaA 中c(Na+) > c(OH-)>c(A-)> c(H+)D.0.1 mol·L-1 HA中加入少量NaA固体,HA的电离常数减小23.下列实验现象预测正确的是A.实验I:电流表A指针偏转,碳棒上有红色固体析出B.实验II:电流表A指针偏转,铁极上有无色气体产生C.实验III:碳棒上有无色气体产生,铁极上有黄绿色气体产生D.实验IV:粗铜溶解,精铜上有红色固体析出30.(16分)钯(Pd)催化偶联反应是近年有机合成的研究热点之一。
2013年广州市普通高中毕业班综合测2答案

值. ……………………………………………10分
若 p q 是真命题,则 p 是真命题且 q 是真命题,即 p 是假命题且 q 是真命
题.……………11分
所以
0
a≤
2 1,或a 1 , 2
……………………………………………………12分
0 a≤1.
解
得
0 a≤ 2 1
或
1 a≤1. ………………………………………………………………………13分 2
不同的线段.…………………………5 分
其中长度为 1 的线段有 8 条,长度为 2 的线段有 4 条,长度为 2 的线段有 6 条,长度
为 5 的线段有 8 条,长度为 2 2 的线段有 2 条. 所以 所有可能的取值为1, 2,2, 5,2 2 .………7 分
且 P 1 8 2 , P 2 4 1 , P 2 6 3 ,
由
余
弦
定
理
15. 2
得
AB2 AC2 BC2 cos BAC
………………………………………………………2 分
2 AB AC
802 502 702 1 .………………………3 分 280 50 2
因为 BAC 为△ ABC 的内角,所以 BAC .……………………4 分 3
(2)方法 1:因为发射点 O 到 A 、 B 、 C 三个工作点的距离相等, 所以点 O 为△ ABC 外接圆的圆心.…………………… 5 分 设外接圆的半径为 R , 在△ ABC 中,由正弦定理得 BC 2R , …………………………………7 分 sin A
半轴,建立空间直角坐标系 D xyz 如图.…………………5 分
D
H B x
E y
2013届广州市高三年级调研测试数学(文科)试题及参考答案详解
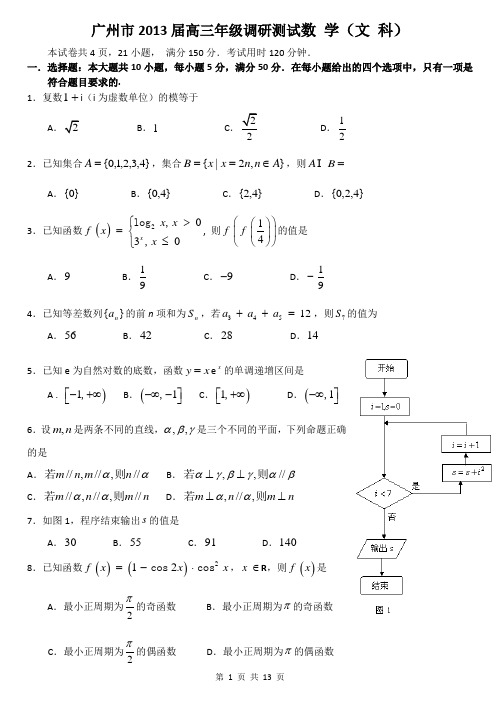
广州市2013届高三年级调研测试数 学(文 科)本试卷共4页,21小题, 满分150分.考试用时120分钟.一.选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数1+i (i 为虚数单位)的模等于AB .1 CD .122.已知集合}4,3,2,1,0{=A ,集合},2|{A n n x x B ∈==,则=B AA .}0{B .}4,0{C .}4,2{D .}4,2,0{ 3.已知函数()2030x x x fx x log ,,⎧>=⎨≤⎩, 则14f f ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭的值是A .9B .19 C .9- D .19- 4.已知等差数列}{n a 的前n 项和为n S ,若34512a a a ++=,则7S 的值为A .56B .42C .28D .145.已知e 为自然对数的底数,函数y x =e x的单调递增区间是A . )1,⎡-+∞⎣B .(1,⎤-∞-⎦C .)1,⎡+∞⎣D .(1,⎤-∞⎦ 6.设n m ,是两条不同的直线,γβα,,是三个不同的平面,下列命题正确的是A .αα//,//,//n m n m 则若B .βαγβγα//,,则若⊥⊥C .n m n m //,//,//则若ααD .n m n m ⊥⊥则若,//,αα 7.如图1,程序结束输出s 的值是A .30B .55C .91D .140 8.已知函数()()212fx x x cos cos =-⋅,x ∈R ,则()f x 是A .最小正周期为2π的奇函数 B .最小正周期为π的奇函数 C .最小正周期为2π的偶函数 D .最小正周期为π的偶函数图29.在区间15,⎡⎤⎣⎦和24,⎡⎤⎣⎦分别取一个数,记为a b ,, 则方程22221x y a b +=表示焦点在x轴上且离心率小于2的椭圆的概率为 A .12 B .1532C .1732D .3132 10.在R 上定义运算).1(:y x y x -=⊗⊗若对任意2x >,不等式()2x a x a -⊗≤+都成立,则实数a 的取值范围是A. 17,⎡⎤-⎣⎦B. (3,⎤-∞⎦C. (7,⎤-∞⎦D. ()17,,⎤⎡-∞-+∞⎦⎣二.填空题: 本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题) 11.已知()fx 是奇函数, ()()4g x f x =+, ()12g =, 则()1f -的值是 .12.已知向量a ,b 都是单位向量,且 a b 12=,则2-a b 的值为 . 13.设x x f cos )(1=,定义)(1x f n +为)(x f n 的导数,即)(' )(1x f x f n n =+,n ∈N *,若ABC ∆的内角A 满足1220130f A f A f A ()()()+++= ,则sin A 的值是 . (二)选做题(14~15题,考生只能从中选做一题)14.(几何证明选讲选做题)如图2,已知AB 是⊙O 的一条弦,点P 为AB 上一点,PC OP ⊥,PC 交⊙O 于C ,若4AP =,2PB =,则PC 的长是 . 15.(坐标系与参数方程选讲选做题)已知圆C 的参数方程为2x y cos ,sin ,θθ⎧=⎨=+⎩(θ为参数), 以原点为极点,x 轴的正半轴为极轴建立极坐标系,直线l 的极坐标方程为1sin cos ρθρθ+=, 则直线l 截圆C 所得的弦长是 .侧视D CBAP 图5图4图3625x 0611y 11988967乙甲三.解答题: 本大题共6小题,满分80分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分) 已知函数2f x x x ()sin sin π⎛⎫=-+⎪⎝⎭. (1)求函数)(x f y =的单调递增区间;(2)若43f ()πα-=,求)42(πα+f 的值. 17.(本小题满分12分)某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图3,其中甲班学生的平均分是85,乙班学生成绩的中位数是83. (1)求x 和y 的值;(2)计算甲班7位学生成绩的方差2s ;(3)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.参考公式:方差()()()2222121n s x x x x x x n ⎡⎤=-+-+⋅⋅⋅+-⎢⎥⎣⎦, 其中12nx x x x n+++= .18.(本小题满分14分)已知四棱锥P ABCD -的正视图是一个底边长为4、腰长为3的等腰三角形,图4、图5 分别是四棱锥P ABCD -的侧视图和俯视图. (1)求证:AD PC ⊥;(2)求四棱锥P ABCD -的侧面PAB 的面积.19.(本小题满分14分)已知数列}{n a 的前n 项和为n S ,数列}1{+n S 是公比为2的等比数列,2a 是1a 和3a 的等比中项. (1)求数列}{n a 的通项公式; (2)求数列{}n na 的前n 项和n T .20.(本小题满分14分) 已知()fx 是二次函数,不等式()0f x <的解集是()05,,且()f x 在点()()11f ,处的切线与直线610x y ++=平行. (1)求()fx 的解析式;(2)是否存在t ∈N *,使得方程()370fx x+=在区间()1t t ,+内有两个不等的实数根?若存在,求出t 的值;若不存在,说明理由.21.(本小题满分14分)已知椭圆()22122:10x y C a b a b+=>>的右焦点与抛物线22:4C y x =的焦点F 重合,椭圆1C 与抛物线2C 在第一象限的交点为P ,53PF =. (1) 求椭圆1C 的方程;(2) 若过点()1,0A -的直线与椭圆1C 相交于M 、N 两点,求使FM FN FR +=成立的动点R 的轨迹方程;(2) 若点R 满足条件(2),点T 是圆()2211x y -+=上的动点,求RT 的最大值.2013届广州市高三年级调研测试数学(文科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题主要考查基本知识和基本运算.共10小题,每小题5分,满分50分.二、填空题:本大题主要考查基本知识和基本运算.本大题共5小题,考生作答4小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题.11.2 12.13. 1 14. 15.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)(本小题主要考查三角函数性质、同角三角函数的基本关系、二倍角公式等知识, 考查化归与转化的数学思想方法和运算求解能力) (1) 解:2f x x x ()sin sin π⎛⎫=-+⎪⎝⎭x x cos sin =+ …………… 1分22x x sin cos ⎛⎫=+ ⎪ ⎪⎝⎭4x sin π⎛⎫=+ ⎪⎝⎭. …………… 3分由22242k x k ,πππππ-+≤+≤+ …………… 4分解得32244k x k k ,ππππ-+≤≤+∈Z . …………… 5分∴)(x f y =的单调递增区间是32244k k k [,],ππππ-++∈Z . ………… 6分 (2)解:由(1)可知)4sin(2 )(π+=x x f ,∴43f ()sin παα-==,得13sin α=. …………… 8分∴)42(πα+f =22sin πα⎛⎫+ ⎪⎝⎭ …………… 9分2cos α= …………… 10分()212sin α=- …………… 11分9=…………… 12分 17.(本小题满分12分)(本小题主要考查茎叶图、样本均值、样本方差、概率等知识, 考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识) (1)解:∵甲班学生的平均分是85,∴92968080857978857x +++++++=. …………… 1分∴5x =. …………… 2分∵乙班学生成绩的中位数是83,∴3y =. …………… 3分 (2)解:甲班7位学生成绩的方差为2s ()()()22222221675007117⎡⎤=-+-+-++++⎢⎥⎣⎦40=. …… 5分 (3)解:甲班成绩在90分以上的学生有两名,分别记为,A B , …………… 6分 乙班成绩在90分以上的学生有三名,分别记为,,C D E . …………… 7分 从这五名学生任意抽取两名学生共有10种情况:()()(),,,,,,A B A C A D ()()()()()()(),,,,,,,,,,,,,A E B C B D B E C D C E D E . …………… 9分 其中甲班至少有一名学生共有7种情况:()()(),,,,,,A B A C A D()()()(),,,,,,,A E B C B D B E . ……………11分FE D CBAP记“从成绩在90分以上的学生中随机抽取两名学生,甲班至少有一名学生”为事件M ,则()710P M =. 答:从成绩在90分以上的学生中随机抽取两名学生,甲校至少有一名学生的概率为710. ……………12分18.(本小题满分14分)(本小题主要考查空间线面位置关系、三视图、几何体的侧面积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力)(1)证明:依题意,可知点P 在平面ABCD 上的正射影是线段CD 的中点E ,连接PE , 则PE ⊥平面ABCD . …………… 2分 ∵AD ⊂平面ABCD ,∴AD PE ⊥. …………… 3分 ∵AD CD ⊥,CD PE E CD ,=⊂ 平面PCD ,PE ⊂平面PCD , ∴AD ⊥平面PCD . …………… 5分 ∵PC ⊂平面PCD ,∴AD PC ⊥. …………… 6分 (2)解:依题意,在等腰三角形PCD 中,3PC PD ==,2DE EC ==, 在R t △PED中,PE ==,…………… 7分过E 作EF AB ⊥,垂足为F ,连接PF ,∵PE ⊥平面ABCD ,AB ⊂平面ABCD ,∴AB PE ⊥. …………… 8分∵EF ⊂平面PEF ,PE ⊂平面PEF ,EF PE E = ,∴AB ⊥平面PEF . …………… 9分 ∵PF ⊂平面PEF ,∴AB PF ⊥. …………… 10分 依题意得2EF AD ==. …………… 11分 在R t △PEF 中,3PF ==, …………… 12分∴△PAB 的面积为162S AB PF == . ∴四棱锥P ABCD -的侧面PAB 的面积为6. …………… 14分 19.(本小题满分14分)(本小题主要考查数列、数列求和等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识) (1)解:∵}1{+n S 是公比为2的等比数列,∴11112)1(2)1(1--⋅+=⋅+=+n n n a S S . …………… 1分 ∴12)1(11-⋅+=-n n a S .从而11122+=-=a S S a ,221233+=-=a S S a . …………… 3分 ∵2a 是1a 和3a 的等比中项∴)22()1(1121+⋅=+a a a ,解得=1a 1或11-=a . …………… 4分 当11-=a 时,11+S 0=,}1{+n S 不是等比数列, …………… 5分 ∴=1a 1.∴12-=n n S . …………… 6分 当2n ≥时,112--=-=n n n n S S a . …………… 7分 ∵11=a 符合12-=n n a ,∴12-=n n a . …………… 8分(2)解:∵12n n na n -=,∴1211122322n n T n -=⨯+⨯+⨯++. ① …………… 9分21231222322nn T n =⨯+⨯+⨯++.② …………… 10分 ①-②得2112222n n n T n --=++++- …………… 11分12212nn n -=-- …………… 12分 =()121nn -- . …………… 13分∴()121nn T n =-+ . …………… 14分20.(本小题满分14分)(本小题主要考查二次函数、函数的性质、方程的根等知识, 考查函数与方程、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和应用意识) (1)解法1:∵()f x 是二次函数,不等式()0f x <的解集是()05,,∴可设()()5fx ax x =-,0a >. …………… 1分∴25f x ax a /()=-. …………… 2分∵函数()fx 在点()()11f ,处的切线与直线610x y ++=平行,∴()16f /=-. …………… 3分 ∴256a a -=-,解得2a =. …………… 4分 ∴()()225210fx x x x x =-=-. …………… 5分解法2:设()2fx ax bx c =++, ∵不等式()0fx <的解集是()05,,∴方程20ax bx c ++=的两根为05,.∴02550c a b ,=+=. ① …………… 2分 ∵2f x ax b /()=+. 又函数()fx 在点()()11f ,处的切线与直线610x y ++=平行,∴()16f /=-.∴26a b +=-. ② …………… 3分由①②,解得2a =,10b =-. …………… 4分 ∴()2210fx x x =-. …………… 5分(2)解:由(1)知,方程()370fx x+=等价于方程32210370x x -+=.…………… 6分设()h x=3221037x x -+,则()()26202310hx x x x x /=-=-. …………… 7分当1003x ,⎛⎫∈ ⎪⎝⎭时,()0h x /<,函数()h x 在1003,⎛⎫ ⎪⎝⎭上单调递减; ……… 8分 当103x ,⎛⎫∈+∞⎪⎝⎭时,()0h x />,函数()h x 在103,⎛⎫+∞ ⎪⎝⎭上单调递增. … 9分 ∵()()1013100450327h h h ,,⎛⎫=>=-<=>⎪⎝⎭, …………… 12分∴方程()0h x=在区间1033,⎛⎫ ⎪⎝⎭,1043,⎛⎫⎪⎝⎭内分别有唯一实数根,在区间()03,,()4,+∞内没有实数根. …………… 13分∴存在唯一的自然数3t =,使得方程()370fx x+=在区间()1t t ,+内有且只有两个不等的实数根. …………… 14分21.(本小题满分14分)(本小题主要考查求曲线的轨迹方程、直线、椭圆、抛物线等知识, 考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力、运算求解能力和创新意识) (1)解法1:抛物线22:4C y x =的焦点F 的坐标为()1,0,准线为1x =-, 设点P 的坐标为()00,x y ,依据抛物线的定义,由53PF =,得01x +53=, 解得023x =. …………… 1分∵ 点P 在抛物线2C 上,且在第一象限,∴ 2002443y x ==⨯,解得03y =.∴点P 的坐标为2,33⎛ ⎝⎭. …………… 2分∵点P 在椭圆22122:1x y C a b+=上, ∴2248193a b +=. …………… 3分又1c =,且22221a b c b =+=+, …………… 4分 解得224,3a b ==.∴椭圆1C 的方程为22143x y +=. …………… 5分 解法2: 抛物线22:4C y x =的焦点F 的坐标为()1,0,设点P 的坐标为()00x y ,,0000x y ,>>. ∵53PF =,∴()22002519x y -+=. ① …………… 1分 ∵点P 在抛物线22:4C y x =上,∴2004y x =. ②解①②得023x =,03y =.∴点P 的坐标为2,33⎛ ⎝⎭. …………… 2分∵点P 在椭圆22122:1x y C a b+=上, ∴2248193a b +=. …………… 3分 又1c =,且22221a b c b =+=+, …………… 4分解得224,3a b ==. ∴椭圆1C 的方程为22143x y +=. …………… 5分 (2)解法1:设点M ()11,x y 、()22,N x y 、(),R x y ,则()()()11221,,1,,1,FM x y FN x y FR x y =-=-=- .∴()12122,FM FN x x y y +=+-+ .∵ FM FN FR += ,∴121221,x x x y y y +-=-+=. ① …………… 6分∵M 、N 在椭圆1C 上, ∴222211221, 1.4343x y x y +=+= 上面两式相减得()()()()12121212043x x x x y y y y +-+-+=.②把①式代入②式得()()()12121043x x x y y y +--+=.当12x x ≠时,得()1212314x y y x x y+-=--. ③ …………… 7分 设FR 的中点为Q ,则Q 的坐标为1,22x y +⎛⎫⎪⎝⎭. ∵M 、N 、Q 、A 四点共线, ∴MN AQ k k =, 即121221312y y y y x x x x -==+-++. ④ …………… 8分 把④式代入③式,得()3134x y x y+=-+, 化简得()2243430y x x +++=. …………… 9分 当12x x =时,可得点R 的坐标为()3,0-,经检验,点()3,0R -在曲线()2243430y x x +++=上.∴动点R 的轨迹方程为()2243430y x x +++=. …………… 10分 解法2:当直线MN 的斜率存在时,设直线MN 的方程为()1y k x =+, 由()221143y k x x y ,,⎧=+⎪⎨+=⎪⎩消去y ,得()22223484120k x k x k +++-=. 设点M ()11,x y 、()22,N x y 、(),R x y ,则2122834k x x k+=-+, ()()()1212122611234k y y k x k x k x x k +=+++=++=+.…6分 ∵()()()11221,,1,,1,FM x y FN x y FR x y =-=-=- .∴()12122,FM FN x x y y +=+-+ .∵ FM FN FR += ,∴121221,x x x y y y +-=-+=. ∴21228134k x x x k+=+=-+, ① 2634k y k=+. ② …………… 7分 ①÷②得()314x k y +=-, ③ …………… 8分 把③代入②化简得()2243430y x x +++=. (*) …………… 9分 当直线MN 的斜率不存在时,设直线MN 的方程为1x =-,依题意, 可得点R 的坐标为()3,0-,经检验,点()3,0R -在曲线()2243430y x x +++=上.∴动点R 的轨迹方程为()2243430y x x +++=. …………… 10分(3)解: 由(2)知点R ()x y ,的坐标满足()2243430y x x +++=, 即()224343y x x =-++, 由20y ≥,得()23430x x -++≥,解得31x -≤≤-. …………… 11分 ∵圆()2211x y -+=的圆心为()10F ,,半径1r =,∴RF ==12=…………… 12分 ∴当3x =-时,4RFmax =, …………… 13分 此时,415RTmax =+=. …………… 14分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广州市2013届普通高中毕业班综合测试(二)
数学(文科)
本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:
1. 答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号。
用黑色字迹的钢笔或签 字笔将自己所在的市、县/区、学校以及自己的姓名和考生号、试室号、座位号填写 在答题卡上。
用2B 铅笔将试卷类型(B)填涂在答题卡相应位置上。
2. 选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑; 如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区 域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使 用铅笔和涂改液。
不按以上要求作答的答案无效。
4. 作答选做题时,请先用2B 铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、 错涂、多涂的,答案无效。
5. 考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只 有一项是符合题目要求的.
1. 命题“054,2≤++∈∃x x R x ”的否定是
A 054,2>++∈∃x x R x
B 054,2≤++∈∃x x R x
C 054,2>++∈∀x x R x
D 054,2≤++∈∀x x R x
2. 如果函数f(x)=ln(-2x+ a)的定义域为(-∞,1),则实数a 的值为
A. -2
B. -1
C. 1
D. 2
3. 对于任意向量a 、B 、C ,下列命题中正确的是
A. |a.b| = |a| |b|
B. |a+b|=|a|+丨b 丨
C. (a.b)c =a (b-c)
D. a.a =|a|2
4. 直线y=kx +1与圆(x+1)2+y2=0相交于A,B两点,则|AB|的值为
5. 若1-i(i是虚数单位)是关于x的方程x2+2px +q=0(p、q∈R)的一个解,则p+q=
A. -3
B. -1
C. 1
D. 3
6. 执行如图l所示的程序框图,输出的S值为
A. 225
B. 196
C. 169
D. 144
(注:框图中的赋值符号“=”也可以写成“←”或“:=”)
A. 2
B. 3
C. 6
D. 9
8. 一个圆锥的正(主)视图及其尺寸如图2所示.若一个平行于圆锥底面的平面将此圆锥截成体积之比为l:7的上、下两部分,则截面的面积为
9. 已知0<a<1,0<x≤y < 1,且log a x.log a y=1,那么xy的取值范围为
10.某校高三(1)班50个学生选择选修模块课程,他们在A、B、C三个模块中进行选
则三个模块都选择的学生人数是
A. 7
B. 6
C. 5
D. 4
二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分.
(—)必做题(11~13题)
11.如图3,一个等腰直角三角形的直角边长为2,分别以三个顶点为圆
心,l为半径在三角形内作圆弧,三段圆弧与斜边围成区域M (图中白色部
分).若在此三角形内随机取一点P,则点P落在区域M内的概率为.
13. 数列{a n}的项是由l或2构成,且首项为1,在第k个l和第k+ 1个l之间有2k-1 个2,即数列{a n} 为:1, 2,1, 2,2,2,1,2,2,2,2,2, 1, …,记数列{a n}的前n项和为S n,则S20=________; S2013 =_____
(二)选做题(14~15题,考生只能从中选做一题)
14.(几何证明选讲选做题)
15.(坐标系与参数方程选做题)
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16. (本小题满分12分)
某校高三学生体检后,为了解高三学生的视力情况,该校从高三六个班的300名学生中以班为单位(每班学生50人),每班按随机抽样抽取了8名学生的视力数据.其中高三
(1)班抽取的8名学生的视力数据与人数见下表:
(1) 用上述样本数据估计高三(1)班学生视力的平均值;
(2)已知其余五个班学生视力的平均值分别为4.3、4.4, 4.5、4.6、4.8.若从这六个 班中任意抽取两个班学生视力的平均值作比较,求抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率.
17. (本小题满分12分)
某单位有A 、B 、C 三个工作点,需要建立一个公共无线网络发射点0,使得发射点到 三个工作点的距离相等.已知这三个工作点之间的距离分别为AB=80m, BC=10M , CA=50m.假定A 、B 、C 、O 四点在同一平面上.
(1) 求BAC ∠的大小;
18(本小题满分14分)
如图4,在三棱锥P-ABC 中,PAB ∠=PAC ∠=ACB ∠=900.
(1) 求证:平面PBC 丄平面PAC
(2)已知PA=1,AB=2,当三棱锥P-ABC 的体积 最大时,求
BC 的长.
19. (本小题满分14分)
(1) 求数列{a n }的通项公式;
(2)是否存在正整数m 、n,且1<m <n ,使得S 1、S nt S n 成等比数列?若存在,求出所有符合条件的m,n 值;若不存在,请说明理由
20.(本小题满分14分)
已知函数f(x)=x 2 -2alnx ()0≠∈a R a 且).
(1) 若f(x)在定义域上为增函数,求实数a 的取值范围;
(2) 求函数f (x)在区间[1,2]上的最小值.
21. (本小题满分14分)
经过点F (0,1)且与直线y = -1相切的动圆的圆心轨迹为M 点A 、D 在轨迹M 上, 且关于y 轴对称,过线段AD (两端点除外)上的任意一点作直线l ,使直线l 与轨迹M 在点D 处的切线平行,设直线l 与轨迹M 交于点B 、 C.
(1) 求轨迹M 的方程;
(2) 证明:CAD BAD ∠=∠;
程.。
