江西省南昌二中2014届高三第十一次模拟考试数学(文)试题

合集下载

江西省南昌市2014届高三二模考试数学(文科)试卷 word版

江西省南昌市2014届高三二模考试数学（文科）试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至4页，共150分．考生注意：1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上，考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致．2.第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．第Ⅱ卷用0.5毫米的黑色墨水签字笔在答题卡上作答．若在试题卷上作答，答案无效．3.考试结束，监考员将试题卷、答题卡一并收回．第Ⅰ卷一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．复数12i+在复平面内对应的点位于 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．已知全集{}2,1,0,1,2,3U =--，{}1,0,1,3M =-，{}2,0,2,3N =-，则(∁U M )N 为 A ． {}1,1- B ．{}2- C ．{}2,2- D ．{}2,0,2- 3．下列说法正确的是A ．命题“存在x ∈R ，220130x x ++>”的否定是“任意x ∈R ，220130x x ++<” B ．两个三角形全等是这两个三角形面积相等的必要条件C ．函数1()f x x=在其定义域上是减函数 D ．给定命题p q 、，若“p 且q ”是真命题，则p ⌝是假命题4．已知函数x x f ωcos )(=)0,(>∈ωR x 的最小正周期为π，为了得到函数()=x g)4sin(πω+x 的图象，只要将()x f y =的图象A ．向左平移8π个单位长度 B ．向右平移8π个单位长度 C ．向左平移4π个单位长度 D ．向右平移4π个单位长度5．一几何体的三视图如图，该几何体的顶点都在球O的球面上，球O 的表面积是A ．2πB ．4πC ．8πD ．16π6．方程22(20x y x +-=表示的曲线是A ．一个圆和一条直线B ．一个圆和一条射线C ．一个圆D ．一条直线7．已知函数()y f x =是周期为2的周期函数，且当[1,1]x ∈-时，||()21x f x =-，则函数()()|lg |F x f x x =-的零点个数是A ．9B ．10C ．11D ．128．已知函数()y f x =对任意的x ∈R 满足2'()2()ln 20x xf x f x ->（其中'()f x 是函数()f x 的导函数），则下列不等式成立的是2正(主)视图左(侧)视图俯视图A ．2(2)(1)f f -<-B ．2(1)(2)f f >C ．4(2)(0)f f ->D ．2(0)(1)f f >9．如图：正方体1111ABCD A BC D -的棱长为1，,E F 分别是棱11,A B CD 的中点，点M 是EF 的动点，FM x =，过点M 、直线AB 的平面将正方体分成上下两部分，记下面那部分的体积为()V x ，则函数()V x 的大致图像是10．过双曲线22221x y a b-=(0,0)a b >>的左焦点(,0)(0)F c c ->，作圆2224a x y +=的切线，切点为E ，延长FE 交双曲线右支于点P ，若2O P O E O F =-，则双曲线的离心率为 AB．5C ．2D文科数学第Ⅱ卷注意事项：第Ⅱ卷共2页，须用黑色墨水签字笔在答题卡上书写作答，若在试题上作答，答案无效．二、填空题：本大题共5小题，每小题5分，共25分11．若不等式2222x x a ++>-对于一切实数x 均成立，则实数a 的取值范围是______． 12．已知角α(0)πα-<<的终边与单位圆交点的横坐标是13，则cos()2πα+的值是___． 13．如果执行如图的程序框图，那么输出的值是__________．14AB C D13333235,37911,413151719,52123252729,=+=++=+++=++++，若类似上面各式方法将3m 分拆得到的等式右边最后一个数是109，则正整数m 等于____．15．如图放置的边长为1的正方形PABC 沿x 轴滚动,点B 恰好经过原点.设顶点(),P x y 的轨迹方程是()y f x =，则对函数()y f x =有下列判断：①函数()y f x =是偶函数；②对任意的x ∈R ，都有(2)(2)f x f x +=-；③函数()y f x =在区间[2,3]上单调递减；④函数()y f x =在区间[4,6]上是减函数.其中判断正确的序号是 .三、解答题：本大题共6个题，共75分．解答应写出文字说明、证明过程或演算步骤． 16. （本小题满分12分）某公司生产产品A ，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于80小于90为二等品，小于80为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利30元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工人乙生产的这种产品各100件进行检测，检测结果统计如下：们生产产品A 为一等品、二等品、三等品的概率．（1）计算甲生产一件产品A ，给工厂带来盈利不小于30元的概率；（2）若甲一天能生产20件产品A ，乙一天能生产15件产品A ，估计甲乙两人一天生产的35件产品A 中三等品的件数. 17．（本小题满分12分）已知公比不为1的等比数列{}na 的首项112a =，前n 项和为n S ，且445566,,a S a S a S +++成等差数列．（1）求等比数列{}n a 的通项公式；（2）对n +∈N ，在n a 与1n a +之间插入3n个数，使这32n+个数成等差数列，记插入的这3n个数的和为n b ，求数列{}n b 的前n 项和n T ． 18．（本小题满分12分）如图，已知正方形ABCD 的边长为6,点,E F 分别在边,AB AD 上,4AE AF ==,现将△AEF 沿线段EF 折起到△'A EF 位置，使得'A C =（1）求五棱锥'A BCDFE -的体积；（2）在线段'A C 上是否存在一点M ,使得//BM 平面'A EF ？若存在，求'A M ；若不存在，说明理由． 19．（本小题满分12分）如图已知ABC △中，1,2,120AB AC BAC ==∠=︒，点M 是边BC 上的动点，动点N 满足30MAN ∠=︒（点,,A M N 按逆时针方向排列）．（1）若2AN AC =，求BN 的长；（2）若3AM AN ⋅=，求△ABN 面积的最大值．ABCD F A 'ABCN20．（本小题满分13分）已知椭圆:C 22221(0)x y a b a b+=>>的左焦点为F ,左、右顶点分别为,A B ,过点F 且倾斜角为4π的直线l 交椭圆于,C D 两点,椭圆C AC AD BC BD ⋅-⋅=．（1）求椭圆C 的方程；（2）若12,P P 是椭圆上不同两点，12,P P x ⊥轴，圆R 过点12,P P ，且椭圆上任意一点都不在圆R 内，则称圆R 为该椭圆的内切圆．问椭圆C 是否存在过点F 的内切圆？若存在，求出点R 的坐标；若不存在，说明理由．21．（本小题满分14分）已知函数()sin cos f x x ax bx x =--(,)a b ∈∈R R . （1）若0b =，讨论函数()f x 在区间(0,)π上的单调性；（2）若2a b =且23a ≥，对任意的0x >，试比较()f x 与0的大小．参考答案二、填空题：本大题共4小题，每小题5分，共20分．11. (1,3) 12 13．32- 14． 10 15．①②④三、解答题：本大题共6个题，共75分．16．解：（1）甲生产一件产品A ，给工厂带来盈利不小于30元的概率为：11911010P =-=……………………………………………………………………………6分（2）估计甲一天生产的20件产品A 中有120210⨯=件三等品，………………………8分估计乙一天生产的15件产品A 中有215310⨯=件三等品，……………………………10分所以估计甲乙两人一天生产的35件产品A 中共有5件三等品.………………………12分17．解：（1）因为445566,,a S a S a S +++成等差数列，所以55446655a S a S a S a S +--=+--，………………………………………………2分即654230a a a -+=，所以22310q q -+=，因为1q ≠，所以12q =，……………4分所以等比数列{}n a 的通项公式为12n na =；………………………………………………6分（2）1333()242n nn n n a a b ++=⋅=，………………………………………………………9分133()39322[()1]344212n n n T +-==--．………………………………………………………12分18．解（1）连接AC ，设AC EF H ⋂=，由ABCD 是正方形，4AE AF ==，得H 是EF 的中点，且,EF AH EF CH ⊥⊥，从而有',A H EF CH EF ⊥⊥，所以EF ⊥平面'A HC ，从而平面'A HC ⊥平面ABCD ，…………………………… 2分过点'A 作'A O 垂直HC 且与HC 相交于点O ，则'A O ⊥平面ABCD ………………3分因为正方形ABCD 的边长为6，4AE AF ==，得到：'A H CH ==所以1cos '2A HC ∠==，所以'cos ''HO A H A HC A O =⋅∠==所以五棱锥'A BCDFE -的体积211(644)323v =⨯-⨯⨯=；………………6分（2）线段'A C 上存在点M ，使得'//A M 平面'A EF，'2A M =．……………7分证明：'A M =1'4A C =，14HO HC =，所以//'OM A H ，所以//OM 平面'A EF ，……………………………………………9分又//BD EF ，所以//BD 平面'A EF ，…………………………………………………10分所以平面//MBD 平面'A EF ， …………………………………………………………11分由BM 在平面MBD 内，所以//BM 平面'A EF .……………………………………12分 19．解：（1）由2AN AC =，得点N 在射线AC 上， 4AN =，2116214cos12021BN =+-⨯⨯⨯︒=，即BN =5分（2）设B A M x ∠=，则120CAM x ∠=︒-，因为ABC △的面积等于△ABM 与△ACM面积的和，所以111sin sin(120)sin120222AB AM x AC AM x AB AC ⋅⋅⋅+⋅⋅⋅︒-=⋅⋅⋅︒，得：AM =，………………………………………………………7分又30,3MAN AM AN ∠=︒⋅=,所以cos303AM AN ⋅⋅︒=,即4sin AN x x =+，所以△ABN的面积1(4sin )sin(30)2S x x x =⋅+⋅+︒225sin cos 2x x x x =+即5sin 22)44444S x x x φ=-+=-+ ………………………10分 ABCD F A 'O H（其中：sin φφφ==为锐角），所以当290x φ-=︒时，△ABN12分 20．解：（12,a b c =，所以椭圆方程可化为：222214x y b b+=，直线l的方程为y x =，………………2分由方程组222214x y b b y x ⎧+=⎪⎨⎪=+⎩，得：2224()4x x b +=,即22580x b ++=,…4分设1122(,),(,)C x y D x y，则125x x +=-，………………………………………5分又1122112212(,)(,)(,)(,)2()AC AD BC BD x a y x a y x a y x a y a x x ⋅-⋅=+⋅+--⋅-=+，所以4()b ⋅=，所以1b =，椭圆方程是2214x y +=；………………7分（2）由椭圆的对称性，可以设12(,),(,)P m n P m n -，点R 在x 轴上，设点(,0)R t ，则圆R 的方程为2222:()()x t y m t n -+=-+，由内切圆定义知道，椭圆上的点到点R 距离的最小值是1||PR ，设点(,)M x y 是椭圆C 上任意一点，则222223||()214MR x t y x tx t =-+=-++,…9分当x m =时，2||MR 最小，所以24332t tm -=-=①……………………………………10分又圆R 过点F，所以222()()t m t n =-+②……………………………………11分点1P 在椭圆上，所以2214m n =-③ ……………………………………………………12分由①②③解得：t =t =又t =时，2m =<-，不合，综上：椭圆C 存在符合条件的内切圆，点R的坐标是(．……………………13分 21.解：（1）0b =时，()sin f x x ax =-，则'()cos f x x a =-，……………………2分当1a ≥时，'()0f x <，所以函数()f x 在区间(0,)π上单调递减；…………………3分当1a ≤-时，'()0f x >，所以函数()f x 在区间(0,)π上单调递增；……………… 4分当11a -<<时，存在(0,)φπ∈，使得cos a φ=，即()0f φ=，(0,)x φ∈时，'()0f x >，函数()f x 在区间(0,)φ上单调递增， ……………………5分 (,)x φπ∈时，'()0f x <，函数()f x 在区间(,)φπ上单调递减. ……………………6分（2）2a b =时，()sin (2cos )2af x x x x =-+，猜测()0f x <恒成立，……………7分证明：()0f x <等价于sin 2cos 2x ax x <+，记sin ()2cos 2x ag x x x =-+，则 222cos 1111'()3()(2cos )22cos 323x a a g x x x +=-=---+++，……………………………10分当123a ≥，即23a ≥时，'()0g x ≤，()g x 在区间(0,)+∞上单调递减，……………12分所以当0x >时，()(0)0g x g <=，即()0f x <恒成立；……………………………14分。

江西省南昌市第二中学2014-2015学年高二上学期第一次考试(月考)数学(文)试题 Word版含答案(人教A版)

高二上学期第一次考试数学（文）试题命题人：余毛毛审题人：曹开文一、选择题（本大题共10小题，每小题5分，共50分） 1. 直线x +y ﹣1=0的倾斜角为（）.A ．B ．C ．D ．2. 直线l 1的斜率为2，l 1∥l 2，直线l 2过点(－1,1)且与y 轴交于点P ，则P 点坐标为( ) A ．(3,0) B ．(－3,0) C ．(0，－3) D ．(0,3) 3．过点且倾斜角为60°的直线方程为（）A ．B ．C ．D ．4．已知直线ax+2y+2=0与3x ﹣y ﹣2=0平行，则系数a=（）. A.﹣3B.﹣6C.D.5．若直线210ax y ++=与直线20x y +-=互相垂直，那么a 的值等于( )A ．1B ．13-C ．23- D ．2-6．圆心在y 轴上，半径为1，且过点（1，2）的圆的方程为（） A ．x 2+(y ﹣2)2=1 B ．x 2+(y +2)2=1 C ．(x ﹣1)2+(y ﹣3)2=1 D ．x 2+(y ﹣3)2=17．直线x -y =2被圆22(4)4x y -+=所截得的弦长为（） A ．2 B ．22 C ．42 D ．48．圆222430x x y y ++-+=与直线0x y b ++=相切,正实数b 的值为 ( )A.12B ．1C ．221-D ．3 9．圆x 2+y 2=1和圆x 2+y 2﹣6y +5=0的位置关系是（）. A. 外切 B. 内切 C. 外离 D. 内含10．已知实数x 、y 满足x 2+y 2=4，则22-+y x xy的最小值为( )A ．222-B ．222-C ．222+D ．222--二、填空题（本大题共5小题，每小题5分，共25分） 11．平行线0943=-+y x 和620x my ++=的距离是_______12．已知圆22:230M x y mx +--=(0)m <的半径为2，则其圆心坐标为。

江西省南昌一中、南昌十中2014届高三上学期联考数学(文)试题(附答案)

南昌一中、南昌十中2014届高三两校上学期联考数学（文）试题一、选择题（5×10=50分）1. 若数列｛a n ｝的前n 项和为S n ＝kq n －k (k ≠0)，则这个数列的特征是( ) (A )等比数列(B )等差数列(C )等比或等差数列 (D )非等差数列2. 已知1sin ,(,)322ππθθ=∈-，则3sin()sin()2πθπθ--的值为(A )922 (B )922-(C )91 (D )91-3. 数2()f x x =在点()2,(2)f 处的切线方程为（）(A )4y = (B )44y x =+ (C )42y x =+ (D )44y x =- 4. 设n S 是等差数列{}n a 的前n 项和，若65911a a =，则119SS ＝( ) (A )1 (B )－1 (C )2D.125.若变量,x y 满足约束条件30101x y x y y +-≤⎧⎪-+≥⎨⎪≥⎩，则24z x y =+-的最大值为(A )5 (B )4- (C )1- (D )1 6. 在∆A B C 中，a ，B ，c 分别是角A ，B ，C 的对边，若，B=A ． 45°或135°(B )45° (C )135°(D ) 以上答案都不对7. 已知等比数列{}n a 的前三项依次为1a -，1a +，4a +，则n a =（）(A )342n ⎛⎫⋅ ⎪⎝⎭ (B )1342n -⎛⎫⋅ ⎪⎝⎭(C )243n ⎛⎫⋅ ⎪⎝⎭ (D )1243n -⎛⎫⋅ ⎪⎝⎭8. 设b a 、是正实数，以下不等式恒成立的序号为（） ①b a ab ab +>2，② b b a a -->，③ 22234b ab b a ->+，④ 22>+abab (A ) ②③ (B ) ①④ (C) ②④ (D ) ①③9. 若曲线1122(,)y x a a --=在点处的切线与两坐标轴围成的三角形的面积为9，则a =(A )16(B )8 (C )32 (D )6410. 已知向量()()ABC ∆︒︒=︒︒=则,45sin ,30cos ,120sin ,120cos 的形状为(A )直角三角形(B )等腰三角形 (C )钝角三角形 (D )锐角三角形二、填空题（5×5=25分）11. 在等比数列{}n a 中，n S 为其前n 项和，已知5423a S =+，6523a S =+，则此数列的公比q 为.12. 若数列{}n a 满足11a =，*12()nn n a n a a -=∈+N ，则它的通项n a =．（1）求A 的大小；（2）若sin sin 1B C +=，试判断ABC ∆的形状．17. （12分）在ABC ∆中，已知BC BA AC AB ⋅=⋅3．（1）求证：tanB=3tanA（2）若cos C =求A 的值．18．（12分）已知,)sin ,cos sin (),cos 32,cos sin (x x x x x x ωωωωωω+-=--=设函数f (x )=)(R x ∈+⋅λ的图像关于对称,其中λ，ω为常数,且ω∈)1,21(（1）求函数f (x )的最小正周期T ；（2）函数过)0,4(π求函数在⎥⎦⎤⎢⎣⎡53,0π上取值范围。

江西省南昌市教研室命制2014届高三数学交流卷试题(二) 文

南昌市教研室命制2014届高三交流卷（二）数学（文）试题第I 卷（选择题共60分）一、选择题:本大题共12个小题，每小题5分，共60分.每小题给出的四个选项中只有一项是符合题目要求的.1．已知全集R U =，集合{}21x A x =>，{}2340B x x x =-->，则A B ⋂=（）A ．{}0x x >B ．{}10x x x <->或 C ．{}4x x > D ．{}14x x -≤≤2．已知复数 231ii --（i 是虚数单位），它的实部和虚部的和是（）A ．4B ．6C ．2D ．3 3．下列命题中是假命题的是（）A ．,)1()(,342是幂函数使+-⋅-=∈∃m m x m x f m R ),0(+∞且在上递减 B ．有零点函数a x x x f a -+=>∀ln ln )(,02 C ．βαβαβαsin cos )cos(,,+=+∈∃使R ; D ．,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数4．已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩，则目标函数y x z-=的最小值为（）A ．5B ．2-C ．6D ．7 5． “1a =”是“函数ax x f -=)(在区间[2,)+∞上为增函数”的（） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6．设振幅、相位、初相为方程sin()(0)y A x b A ωϕ=++>的基本量，则方程3sin(21)+4y x =- 的基本量之和为（） A ．4 B ．23x + C ．8D ．21x +7．已知正四面体的俯视图如图所示，其中四边形ABCD 是边长为2的正方形，则这个正四面体的主视图的面积为（） A ．22 B ．2 C ．23 D ．38．F1，F2是双曲线2222:1(,0)x y C a b b a b -=>>的左、右焦点，过左焦点F1的直线l 与双曲线C 的左、右两支分别交于A ，B 两点，若22||:||:||3:4:5AB BF AF =，则双曲线的离心率是（）A ．3B ．15C ．2D ．139．设函数()12+-=ax x x f 在区间⎪⎭⎫⎝⎛321，上有零点，则实数a 的取值范围为（） A. ()∞+，2 B. [)∞+，2 C. ⎪⎭⎫⎢⎣⎡252， D. ⎪⎭⎫⎢⎣⎡3102， 10．已知()f x 是R 上的偶函数，当0x ≥时，12()22xf x x =-，又a 是函数2()ln(1)g x x x =+-的正零点，则(2)f -，()f a ，(1.5)f 的大小关系是（） A ．(1.5)()(2)f f a f <<-B ．(2)(1.5)()f f f a -<<C ．()(1.5)(2)f a f f <<-D ．(1.5)(2)()f f f a <-<第Ⅱ卷（非选择题共90分）二、填空题：本大题共4个小题，每小题4分，共16分.11．右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中有一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率是____________．12．如图，已知||1,||3OA OB ==，OA 与OB 的夹角为56π，点C 是AOB ∆的外接圆上优孤AB 上的一个动点，则OA OC ⋅的最大值为 .13．右图是一个算法的程序框图，最后输出的W =________.14. n n .13S =++=，210S =++++=，321S =++++++=，那么5S =.15.若对于2||||,2≥-+-∈∀a x a x R x 恒成立，则实数a 的取值范围三、解答题:本大题共6小题，共74分. 16． (本题满分12分)已知θ为向量a 与b 的夹角，||2=a ，||1=b ，关于x 的一元二次方程2x -||a x 0+⋅=a b 有实根.（Ⅰ）求θ的取值范围；（Ⅱ）在（Ⅰ）的条件下，求函数2()sin cos f θθθθ=的最值.17．已知正方形ABCD 的边长为2，E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点．（1）从C 、D 、E 、F 、G 、H 这六个点中，随机选取两个点，记这两个点之间的距离的平方为m ，求概率P （m ≤ 4）．（2）在正方形ABCD 内部随机取一点P ，求满足｜PE ｜＜2的概率．已知数列{}n a 的前n 项和为n S ，且满足22n n S aa a =-- （a 是常数且0a >,2a ≠）, 21n n n S b a =+．（1）求数列{}n a 的通项公式；（2）若数列{}n b 为等比数列，求{}n b 的通项公式；（3）在（2）的条件下，记31323log log log n n c b b b =+++()n N +∈，是否存在正整数m ，使111113n m c c c +++≥都成立？若存在，求出m 的值；若不存在，请说明理由．19．（本小题满分12分）如图，在斜三棱柱ABC-A1B1C1中，O 是AC 的中点，A1O ⊥平面ABC ，∠BCA=90°，AA1=AC=BC. （I ）求证： AC1⊥平面A1BC;（II ）若AA1=2，求三棱锥C-A1AB 的高的大小．如图，设F 是椭圆C :22221(0)x y a b a b +=>>的左焦点，MN 为椭圆的长轴，P 为椭圆C 上一点，且||[2,6]PF ∈．（Ⅰ）求椭圆C 的方程；（Ⅱ）设点(8,0)Q -，①求证：对于任意的割线QAB ，恒有AFM BFN ∠=∠；②求三角形ABF ∆面积的最大值．21.（本小题满分14分）设函数2()ln ()2af x x x a =+--，a R ∈.（1）若函数()f x 在1[, 2]2上单调递增，求实数a 的取值范围；（2）求函数)(x f 的极值点.（3）设x m =为函数()f x 的极小值点，()f x 的图象与x 轴交于1212(,0),(,0)()A x B x x x <两点,且120x x m<<<，AB 中点为0(,0)C x ，比较)('x f 与0的大小.答案第I 卷（选择题共60分）一、选择题:本大题共12个小题，每小题5分，共60分.每小题给出的四个选项中只有一项是符合题目要求的.1．已知全集R U =，集合{}21x A x =>，{}2340B x x x =-->，则A B ⋂=（）A ．{}0x x >B ．{}10x x x <->或 C ．{}4x x > D ．{}14x x -≤≤2．已知复数 231ii --（i 是虚数单位），它的实部和虚部的和是（）A ．4B ．6C ．2D ．3 3．下列命题中是假命题的是（） A ．,)1()(,342是幂函数使+-⋅-=∈∃m m xm x f m R ),0(+∞且在上递减B ．有零点函数a x x x f a -+=>∀ln ln )(,02C ．βαβαβαsin cos )cos(,,+=+∈∃使R ;D ．,()sin(2)f x x ϕϕ∀∈=+R 函数都不是偶函数4．已知实数y x ,满足1218y y x x y ≥⎧⎪≤-⎨⎪+≤⎩，则目标函数y x z -=的最小值为（）A ．5B ．2-C ．6D ．7 5． “1a =”是“函数ax x f -=)(在区间[2,)+∞上为增函数”的（） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件6．设振幅、相位、初相为方程sin()(0)y A x b A ωϕ=++>的基本量，则方程3sin(21)+4y x =- 的基本量之和为（） A ．4 B ．23x + C ．8D ．21x +7．已知正四面体的俯视图如图所示，其中四边形ABCD 是边长为2的正方形，则这个正四面体的主视图的面积为（） A ．22 B ．2 C ．23 D ．38．F1，F2是双曲线2222:1(,0)x y C a b b a b -=>>的左、右焦点，过左焦点F1的直线l 与双曲线C 的左、右两支分别交于A ，B 两点，若22||:||:||3:4:5AB BF AF =，则双曲线的离心率是（）A 3B 15C ．2D 139．设函数()12+-=ax x x f 在区间⎪⎭⎫⎝⎛321，上有零点，则实数a 的取值范围为（） A. ()∞+，2 B. [)∞+，2 C. ⎪⎭⎫⎢⎣⎡252， D. ⎪⎭⎫⎢⎣⎡3102， 10．已知()f x 是R 上的偶函数，当0x ≥时，12()22xf x x =-，又a 是函数2()ln(1)g x x x =+-的正零点，则(2)f -， ()f a ，(1.5)f 的大小关系是（） A ．(1.5)()(2)f f a f <<-B ．(2)(1.5)()f f f a -<<C ．()(1.5)(2)f a f f <<-D ．(1.5)(2)()f f f a <-<第Ⅱ卷（非选择题共90分）二、填空题：本大题共4个小题，每小题4分，共16分.11．右边茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中有一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率是____________．答案：11012．如图，已知||1,||3OA OB ==，OA 与OB 的夹角为56π，点C 是AOB ∆的外接圆上优孤AB 上的一个动点，则OA OC ⋅的最大值为 . 17213．右图是一个算法的程序框图，最后输出的W =_____22___.14. n n . 11233S ⎡⎡⎡=++=⎣⎣⎣，24567810S ⎡⎡⎡⎤⎡=++++=⎣⎣⎣⎦⎣，3910111213141521S ⎡⎡⎡⎡⎡⎤⎡⎡⎤=++++++=⎣⎣⎣⎣⎣⎦⎣⎣⎦，那么5S =.5515.若对于2||||,2≥-+-∈∀a x a x R x 恒成立，则实数a 的取值范围 ),2[]1,(+∞--∞三、解答题:本大题共6小题，共74分.⋅CBAO17．已知正方形ABCD 的边长为2，E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 的中点．（1）从C 、D 、E 、F 、G 、H 这六个点中，随机选取两个点，记这两个点之间的距离的平方为m ，求概率P （m ≤ 4）．（2）在正方形ABCD 内部随机取一点P ，求满足｜PE ｜＜2的概率．解：（1）P=1115………………………6分(2)这是一个几何概型．所有点P 构成的平面区域是正方形ABCD 的内部，其面积是224⨯=．满足2<PE 的点P 构成的平面区域是以E 为圆心，2为半径的圆的内部与正方形ABCD 内部的公共部分，它可以看作是由一个以E 为圆心、2为半径、圆心角为3π的扇形的内部与两个直角边分别为1和3的直角三角形内部构成.其面积是3323121223212+=⨯⨯⨯+⨯⨯ππ．所以满足2<PE 的概率为.4364332+=+ππ…………………………12分18． (本题满分12分)已知数列{}n a 的前n 项和为n S ，且满足22n n S aa a =-- （a 是常数且0a >,2a ≠）, 21n n n S b a =+．（1）求数列{}n a 的通项公式；（2）若数列{}n b 为等比数列，求{}n b 的通项公式；（3）在（2）的条件下，记31323log log log n n c b b b =+++()n N +∈，是否存在正整数m ，使111113n m c c c +++≥都成立？若存在，求出m 的值；若不存在，请说明理由．解：(1)由22n n S aa a =--得：(2)2n n aS a a =--∴111(2)2aS a a a ==--，1a a =当n ≥2时，11(2)(2)2222n n n n n a a a a a a a a a a a a a --=---=----- 1(2)n n n a a aa aa --=-，∴12n n a aa -=∴数列{}n a 是首项为a ，公比为2a的等比数列 ∴1()2()22n nn a a a a -== (2)解：([1()]22()22212n nn a aa a a S a a --==--44()2(23)()12223221()2(2)22()(2)()22nnn n n naaa a a a a ab a a aa a a a -+--=⨯+==⨯+----若数列{}n b 为等比数列，则230a -=，23a =，此时，3nn b =(3)证：12313233123(1)log log log log log 32nn n n n n c b b b b b b ++++=+++===∴12112()(1)1n c n n n n ==-++121111111112[(1)()()]2(1)22311n c c c n n n +++=-+-++-=-++由121113n mc c c +++≥∀n ∈N*都成立得：12(1)13m n -+≥即661m n -+≤∀n ∈N*都成立 ∵m 是正整数，∴m 的值为1、2、3．19．（本小题满分12分）如图，在斜三棱柱ABC-A1B1C1中，O 是AC 的中点，A1O ⊥平面ABC ，∠BCA=90°，AA1=AC=BC. （I ）求证： AC1⊥平面A1BC;（II ）若AA1=2，求三棱锥C-A1AB 的高的大小．解：（Ⅰ）因为A1O ⊥平面ABC ，所以A1O ⊥BC ．又BC ⊥AC ，所以BC ⊥平面A1ACC1，所以AC1⊥BC ． …2分因为AA1＝AC ，所以四边形A1ACC1是菱形，所以AC1⊥A1C ．所以AC1⊥平面A1BC ． …6分（Ⅱ）设三棱锥C-A1AB 的高为h ．由（Ⅰ）可知，三棱锥A-A1BC 的高为 12AC1＝3．因为VC-A1AB ＝VA-A1BC ，即1 3S △A1ABh ＝ 13S △A1BC ·3．在△A1AB 中，AB ＝A1B ＝22，AA1＝2，所以S △A1AB ＝7． …10分在△A1BC 中，BC ＝A1C ＝2，∠BCA1＝90︒，所以S △A1BC ＝ 12BC ·A1C ＝2．所以h ＝2217．…12分20．(本题满分13分)如图，设F 是椭圆C :22221(0)x y a b a b +=>>的左焦点，MN 且||[2,6]PF ∈．（Ⅰ）求椭圆C 的方程；（Ⅱ）设点(8,0)Q -，①求证：对于任意的割线QAB ，恒有AFM BFN ∠=∠；②求三角形ABF ∆面积的最大值．解：（Ⅰ）2211612x y +=；（Ⅱ）①易知直线AB 斜率存在．当AB 的斜率为0时，显然0AFM BFN ∠=∠=，满足题意，当AB 的斜率不为0时，设ABl : 8(0)x my m =-≠，11(,)A x y ，22(,)A x y ，由 22228(34)48144011612x my m y my x y =-⎧⎪⇒+-+=⎨+=⎪⎩．∴222222248412(34)24(4)04m m m m ∆=-⨯+=->⇒>， 1224834m y y m +=+，12214434y y m =+．则121222AF BF y y k k x x +=+++1212211212(6)(6)66(6)(6)y y y my y my my my my my -+-=+=----12121226()(6)(6)my y y y my my -+=--，又1212221444826()2603434mmy y y y m m m -+=⋅-⋅=++，∴0AF BF k k +=，从而AFM BFN ∠=∠．综合可知：对于任意的割线QAB ，恒有AFMBFN ∠=∠．②由①，211||||2ABF QBF QAFS S S QF y y ∆∆∆=-=⋅-=，272163(4)16m ==≤=-+，当且仅当=，即3m =±（此时适合于0>∆的条件）时取等号．∴ 三角形ABF ∆面积的最大值是33．(0)t t =>，则27272163163t t t t ==≤=++．21.（本小题满分14分）设函数2()ln ()2af x x x a =+--，a R ∈.（1）若函数()f x 在1[, 2]2上单调递增，求实数a 的取值范围；（2）求函数)(x f 的极值点.（3）设x m =为函数()f x 的极小值点，()f x 的图象与x 轴交于1212(,0),(,0)()A x B x x x <两点,且120x x m<<<，AB 中点为0(,0)C x ，比较)('x f 与0的大小.解：（1） 21221()2()x ax f x x a x x -+'=+-=依题意得，在区间1[, 2]2上不等式22210x ax -+≥恒成立.又因为0x >，所以12(2)a x x ≤+.所以2a ≤a ≤所以实数a的取值范围是(,-∞.（2）2221()x ax f x x -+'=，令2()221h x x ax =-+①显然，当0a ≤时，在(0,)+∞上()0h x >恒成立，这时()0f x '>，此时，函数()f x 没有极值点； …………………………………6分 ②当0a >时，（ⅰ）当0∆≤，即0a <时，在(0,)+∞上()0h x ≥恒成立，这时()0f x '≥，此时，函数()f x 没有极值点；（ⅱ）当0∆>，即a >易知，当22a a x +<<时，()0h x <，这时()0f x '<；当02a x -<<或2a x >时，()0h x >，这时()0f x '>；所以，当a >x 是函数()f x的极大值点；x =是函数()f x 的极小值点.综上，当a ≤()f x 没有极值点；当a >x =是函数()f x 的极大值点；x =是函数()f x 的极小值点. ………9分（3）由已知得2211122222()ln ()02()ln ()02a f x x x a a f x x x a ⎧=+--=⎪⎪⎨⎪=+--=⎪⎩两式相减，得：()112122ln ()2x x x x x a x +-+-……①由'1()2()f x x a x =+-，得'0001()2()f x x a x =+-…………② 得①代入②，得'001201212()2()(2)f x x a x x a x x x =+-=++-+=221222*********(1)211ln ln ()()1x x x x x x x x x x x x x x ⎡⎤-⎢⎥⎢⎥-=-+--⎢⎥+⎢⎥⎣⎦令12(0,1),x t x =∈且2222(1)()ln (01),()0,1(1)t t t t t t t t t ϕϕ--'=-<<=-<++()t ϕ∴在(0,1)上递减，()(1)0t ϕϕ∴>= 120,()0x x f x '<∴<。

2014年江西省南昌市高三文科数学第二次模拟考试试卷及答案

2014年江西省南昌市高三文科数学第二次模拟考试试卷及
答案
绝密★启用前
2014年江西省南昌市高三第二次模拟考试
文科数学
本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至4页，共150分．
考生注意：
1.答题前，考生务必将自己的准考证号、姓名填写在答题卡上，考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致．
2.第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．第Ⅱ卷用0.5毫米的黑色墨水签字笔在答题卡上作答．若在试题卷上作答，答案无效．
3.考试结束，监考员将试题卷、答题卡一并收回．
第Ⅰ卷
一．选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1．复数在复平面内对应的点位于
A．第一象限B．第二象限C．第三象限D．第四象限
2．已知全集，，，则(∁U)为
3．下列说法正确的是
A．命题“存在，”的否定是“任意，”
B．两个三角形全等是这两个三角形面积相等的必要条件
C．函数在其定义域上是减函数
D．给定命题，若“且”是真命题，则是假命题
1/ 2
4．已知函数的最小正周期为，为了得到函数的图象，只要将的图象
A．向左平移个单位长度B．向右平移个单位长度
C．向左平移个单位长度D．向右平移个单位长度
5．一几何体的三视图如图，该几何体的顶点都在球的球面上，
球的表面积是
2014年江西省南昌市高三文科数学第二次模拟考试试卷及答案阅读版
(可调整文字大小)
2/ 2。

2014南昌二模文科数学答案及评分标准

高三数学(文科)答案第1页（共4页）2014年南昌市高三年级二模数学(文科)参考答案及评分标准二、填空题：本大题共4小题，每小题5分，共20分．11. (1,3) 12．3 13．32- 14． 10 15．①②④ 三、解答题：本大题共6个题，共75分．16．解：（1）甲生产一件产品A ，给工厂带来盈利不小于30元的概率为：11911010P =-=……………………………………………………………………………6分（2）估计甲一天生产的20件产品A 中有120210⨯=件三等品，………………………8分估计乙一天生产的15件产品A 中有215310⨯=件三等品，……………………………10分所以估计甲乙两人一天生产的35件产品A 中共有5件三等品.………………………12分 17．解：（1）因为445566,,a S a S a S +++成等差数列，所以55446655a S a S a S a S +--=+--，………………………………………………2分即654230a a a -+=，所以22310q q -+=，因为1q ≠，所以12q =，……………4分所以等比数列{}n a 的通项公式为12n n a =；………………………………………………6分（2）1333()242n nn n n a a b ++=⋅=，………………………………………………………9分 133()39322[()1]344212n n n T +-==--．………………………………………………………12分18．解（1）连接AC ，设AC EF H ⋂=，由ABCD 是正方形，4AE AF ==，得H 是EF 的中点，且,EF AH EF CH ⊥⊥，从而有',A H EF CH EF ⊥⊥，所以EF ⊥平面'A HC ，从而平面'A HC ⊥平面ABCD ，…… 2分过点'A 作'A O 垂直HC 且与HC 相交于点O ，则'A O ⊥平面ABCD ………………3分因为正方形ABCD 的边长为6，4AE AF ==，ABCD F A 'OH高三数学(文科)答案第2页（共4页）得到：'A H CH ==1cos '2A HC ∠==，所以'cos ''HO A H A HC A O =⋅∠==所以五棱锥'A BCDFE -的体积211(644)323v =⨯-⨯⨯=；………………6分（2）线段'A C 上存在点M ，使得'//A M 平面'A EF，'A M =7分证明：'A M =1'4A C =，14HO HC =，所以//'OM A H ，所以//OM 平面'A EF ，……………………………………………9分又//BD EF ，所以//BD 平面'A EF ，…………………………………………………10分所以平面//MBD 平面'A EF ， …………………………………………………………11分由BM 在平面MBD 内，所以//BM 平面'A EF .……………………………………12分19．解：（1）由2AN AC =，得点N 在射线AC 上， 4AN =，2116214cos12021BN =+-⨯⨯⨯︒=，即BN =5分（2）设BAM x ∠=，则120CAM x ∠=︒-，因为ABC △的面积等于△ABM 与△ACM 面积的和，所以111sin sin(120)sin120222AB AM x AC AM x AB AC ⋅⋅⋅+⋅⋅⋅︒-=⋅⋅⋅︒，得：AM =，………………………………………………………7分又30,3MAN AM AN ∠=︒⋅=,所以cos303AM AN ⋅⋅︒=,即4sin AN x x =+，所以△ABN的面积1(4sin )sin(30)2S x x x =⋅+⋅+︒225sin cos 2x x x x +即5sin 22)4S x x x φ==-+ ………………………10分（其中：sin φφφ==为锐角），所以当290x φ-=︒时，△ABN的面积最大，最大值是4．………………12分 20．解：（1，所以2,a b c ==，高三数学(文科)答案第3页（共4页）所以椭圆方程可化为：222214x y b b+=，直线l的方程为y x =，………………2分由方程组222214x y b by x ⎧+=⎪⎨⎪=+⎩，得：2224()4x x b ++=,即22580x b ++=,…4分设1122(,),(,)C x y D x y，则125x x +=-，………………………………………5分又1122112212(,)(,)(,)(,)2()AC AD BC BD x a y x a y x a y x a y a x x ⋅-⋅=+⋅+--⋅-=+，所以4()b ⋅=1b =，椭圆方程是2214x y +=；………………7分（2）由椭圆的对称性，可以设12(,),(,)P m n P m n -，点E 在x 轴上，设点(,0)E t ，则圆E 的方程为2222:()()x t y m t n -+=-+，由内切圆定义知道，椭圆上的点到点E 距离的最小值是1||PE ，设点(,)M x y 是椭圆C 上任意一点，则222223||()214ME x t y x tx t =-+=-++,…9分当x m =时，2||ME 最小，所以24332t tm -=-=①……………………………………10分又圆E 过点F，所以222()()t m t n =-+②……………………………………11分点1P 在椭圆上，所以2214m n =-③ ……………………………………………………12分由①②③解得：t =或t =t =2m =<-，不合，综上：椭圆C 存在符合条件的内切圆，点E的坐标是(2-．……………………13分 21.解：（1）0b =时，()sin f x x ax =-，则'()cos f x x a =-，……………………2分当1a ≥时，'()0f x <，所以函数()f x 在区间(0,)π上单调递减；…………………3分当1a ≤-时，'()0f x >，所以函数()f x 在区间(0,)π上单调递增；……………… 4分当11a -<<时，存在(0,)φπ∈，使得cos a φ=，即()0f φ=，(0,)x φ∈时，'()0f x >，函数()f x 在区间(0,)φ上单调递增， ……………………5分 (,)x φπ∈时，'()0f x <，函数()f x 在区间(,)φπ上单调递减. ……………………6分（2）2a b =时，()sin (2cos )2af x x x x =-+，猜测()0f x <恒成立，……………7分证明：()0f x <等价于sin 2cos 2x a x x <+，记sin ()2cos 2x ag x x x =-+，则222cos 1111'()3()(2cos )22cos 323x a a g x x x +=-=---+++，……………………………10分高三数学(文科)答案第4页（共4页）当123a ≥，即23a ≥时，'()0g x ≤，()g x 在区间(0,)+∞上单调递减，……………12分所以当0x >时，()(0)0g x g <=，即()0f x <恒成立；……………………………14分。

2014年江西省南昌市高考数学二模试卷(文科)

2014年江西省南昌市高考数学二模试卷（文科）学校:___________姓名：___________班级：___________考号：___________一、选择题(本大题共10小题，共50.0分)1.已知复数，则z在复平面上对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】解：===，则此复数在复平面上对应的点为（，），在第四象限，故选D．由题意，可对复数代数式分子与分母都乘以2-i，再进行计算求出此复数对应的点得坐标，即可得到答案．本题考查复数代数形式的乘除运算和复数的几何意义，解题的关键是分子分母都乘以分母的共轭复数，复数的四则运算是复数考查的重要内容，要熟练掌握．2.已知全集U={-2，-1，0，1，2，3}，M{-1，0，1，3}，N{-2，0，2，3}，则（∁U M）∩N为（）A.{-1，1}B.{-2}C.{-2，2}D.{-2，0，2}【答案】C【解析】解：∵U={-2，-1，0，1，2，3}，M{-1，0，1，3}，∴∁U M={-2，2}，又N={-2，0，2，3}，∴（∁U M）∩N={-2，2}，故选C．依题意，可求得∁U M={-2，2}，从而可求得（∁U M）∩N．本题考查交、并、补集的混合运算，属于基础题．3.下列说法正确的是（）A.命题“存在x∈R，x2+x+2013＞0”的否定是“任意x∈R，x2+x+2013＜0”B.两个三角形全等是这两个三角形面积相等的必要条件C.函数f（x）=在其定义域上是减函数D.给定命题p、q，若“p且q”是真命题，则￢p是假命题【答案】D【解析】解：对于A，命题“存在x∈R，x2+x+2013＞0”的否定是“任意x∈R，x2+x+2013≥0”，∴A错误；对于B，两个三角形面积相等，不能得出这两个三角形全等，∴必要条件不成立，∴B错误；对于C，函数f（x）=在其定义域的两个区间（-∞，0）和（0，+∞）上分别是减函数，∴C错误；对于D，给定命题p、q，若“p且q”是真命题，∴p、q都是真命题，∴￢p是假命题，∴D正确．故选：D．A中，写出命题p的否定￢p，判定A错误；B中，由两三角形面积相等，不能推出两三角形全等，判定B错误；C中，函数f（x）在其定义域的两个区间上分别是减函数，判定C错误；D中，由“p且q”是真命题，得出p、q都是真命题，从而得￢p是假命题，判定D正确．本题通过命题真假的判定，考查了命题的否定、充分与必要条件，函数的单调以及复合命题的真假性问题，是综合性题目．4.已知函数f（x）=cosωx（x∈R，ω＞0）的最小正周期为π，为了得到函数g（x）=sin（ωx+）的图象，只要将y=f（x）的图象（）A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【答案】B【解析】解：∵函数f（x）=cosωx（x∈R，ω＞0）的最小正周期为π，∴由得ω=2，∴函数f（x）=cos2x，g（x）=sin（2x+）∴要得到函数g（x）=sin（2x+）的图象，由于sin（2x+）=cos（2x+-）=cos（2x-），得到函数g（x）=cos（2x-）即可，∴需要把函数f（x）=cos2x图象向右平移个单位长度，故选B．根据最小正周期为π，可以求出ω的值，然后再利用图象平移求解．本题考查了余弦型函数的性质、诱导公式及图象变换，关键是用诱导公式把两个函数的名称化成一致的．5.一几何体的三视图如图，该几何体的顶点都在球O的球面上，球O的表面积是（）A.2πB.4πC.8πD.16π【答案】C【解析】解：由三视图知：几何体为三棱锥，且三棱锥的一条侧棱与底面垂直，高为2，底面为等腰直角三角形，如图：SA⊥平面ABC，SA=2，AC的中点为D，在等腰直角三角形SAC中，取O为SC的中点，∴OS=OC=OA=OB，∴O为三棱锥外接球的球心，R=，∴外接球的表面积S=4π×=8π．故选：C．几何体为三棱锥，且三棱锥的一条侧棱与底面垂直，底面为等腰直角三角形，取O为SC的中点，可证OS=OC=OA=OB，由此求得外接球的半径，代入球的表面积公式计算．本题考查了由三视图求几何体的外接球的表面积，判断几何体的特征性质及数据所对应的几何量是关键．6.方程（x2+y2-2x）=0表示的曲线是（）A.一个圆和一条直线B.一个圆和一条射线C.一个圆D.一条直线【答案】D【解析】解：由题意，（x2+y2-2x）=0可化为x+y-3=0或x2+y2-2x=0（x+y-3≥0）∵x+y-3=0在x2+y2-2x=0的上方，∴x2+y2-2x=0（x+y-3≥0）不成立，∴x+y-3=0，∴方程（x2+y2-2x）=0表示的曲线是一条直线．故选：D．将方程等价变形，即可得出结论．本题考查轨迹方程，考查学生分析解决问题的能力，属于基础题．7.已知函数y=f（x）是周期为2的周期函数，且当x∈[-1，1]时，f（x）=2|x|-1，则函数F（x）=f（x）-|lgx|的零点个数是（）A.9B.10C.11D.12【答案】B【解析】解：∵函数F（x）=f（x）-|lgx|的零点，即为函数y1=|lgx|，y2=f（x）的图象的交点，又∵函数y=f（x）是周期为2的周期函数，且当x∈[-1，1]时，f（x）=2|x|-1，在同一坐标系中画出两个函数y1=|lgx|，y2=f（x）的图象，如下图所示：由图可知：两个函数y1=|lgx|，y2=f（x）的图象共有10个交点，故函数F（x）=f（x）-|lgx|有10个零点，故选：B．在坐标系中画出两个函数y1=|lgx|，y2=f（x）的图象，分析两个图象交点的个数，进而可得函数F（x）=f（x）-|lgx|的零点个数．本题考查了函数零点、对应方程的根和函数图象之间的关系，通过转化和作图求出函数零点的个数．8.已知函数y=f（x）对任意的x∈R满足2x f′（x）-2x f（x）ln2＞0（其中f′（x）是函数f（x）的导函数），则下列不等式成立的是（）A.2f（-2）＜f（-1）B.2f（1）＞f（2）C.4f（-2）＞f（0）D.2f（0）＞f（1）【答案】A【解析】解：构造函数g（x）=，则g′（x）=′，∵x∈R满足2x f′（x）-2x f（x）ln2＞0，∴g′（x）＞0，即函数g（x）在R上单调递增，则g（-2）＜g（-1），g（1）＜g（2），g（-2）＜g（0），g（0）＜g（1），即＜，＜，＜，＜，即2f（-2）＜f（-1），2f（1）＜f（2），4f（-2）＜f（0），2f（0）＜f（1），故A正确．故选：A．根据条件构造函数g（x）=，求函数的导数，利用函数的单调性和导数之间的关系即可得到结论．本题主要考查函数单调性的应用，利用条件构造函数是解决本题的关键，综合性较强，有一点的难度．9.如图：正方体ABCD-A1B1C1D1的棱长为1，E，F分别是棱A1B1，CD的中点，点M是EF的动点，FM=x，过点M、直线AB的平面将正方体分成上下两部分，记下面那部分的体积为V（x），则函数V（x）的大致图象是（）A. B. C.D.【答案】C【解析】解：如图：（1）当＜＜时，过点M、直线AB作平面交CC1，DD1于点P、Q，则四边形ABPQ为矩形，此时，截面下面那部分是三棱矩ADQ-BCP，∵FM=CM1=x，如图：B1C=，△BB1M1∽△PM1C，由相似比得，，，∴CP=，∴三棱矩ADQ-BCP的体积V（x）=S△BCP•AB==；（2）当＜＜时，过点M、直线AB作平面交B1C1，A1D1于点P、Q，则四边形ABPQ为矩形，此时，截面下面那部分是四棱矩ADQA1-BCPB1，∵FM=x，由相似比知C1P=，∴四棱矩ADQA1-BCPB1的体积V（x）==．＜∴V（X）=．＜＜由解析式，知V（x）的图象为C．故选：C．本题关键是理解，体积V（x）的变化是随变x的变化而怎样变化的，可以找列出V关于x的关系式，利用相似比就可以找到它们的关系，从而得到答案，当然此题也可以从体积的变化快慢来理解得到答案．本题考查空间相象能力，函数思想，关键是要求理解变量与变量之间的关系．属于较难题．10.过双曲线=1（a＞0，b＞0）的左焦点F（-c，0）（c＞0），作圆x2+y2=的切线，切点为E，延长FE交双曲线右支于点P，若=2-，则双曲线的离心率为（）A. B. C. D.【答案】C【解析】解：设右焦点为F′，则∵=2-，∴+=2，∴E是PF的中点，∴PF′=2OE=a，∴PF=3a，∵OE⊥PF，∴PF′⊥PF，∴（3a）2+a2=4c2，∴e==，故选：C．设右焦点为F′，由=2-，可得E是PF的中点，利用O为FF'的中点，可得OE为△PFF'的中位线，从而可求PF′、PF，再由勾股定理得出关于a，c的关系式，最后即可求得离心率．本题主要考查双曲线的标准方程，以及双曲线的简单性质的应用，考查抛物线的定义，考查运算求解能力，考查数形结合思想、化归与转化思想，属于中档题．二、填空题(本大题共5小题，共25.0分)11.若不等式x2+2x+2＞|a-2|对于一切实数x均成立，则实数a的取值范围是______ ．【答案】（1，3）【解析】解：∵函数y=x2+2x+2的最小值为1，∴不等式x2+2x+2＞|a-2|对于一切实数x均成立，则|a-2|＜1，∴1＜a＜3，∴实数a的取值范围是（1，3）．故答案为：（1，3）．构造函数y=x2+2x+2，由二次函数的性质，可以求出函数的最小值，根据不等式x2+2x+2＞|a-2|对于一切实数x均成立，可得|a-2|＜1，即可得到a的取值范围，进而得到答案．本题考查的知识点函数恒成立问题，其中根据二次函数的性质得到函数y=x2+2x+2的最小值是解答本题的关键．12.已知角α（-π＜α＜0）的终边与单位圆交点的横坐标是，则cos（+α）的值是______ ．【答案】【解析】解：角α（-π＜α＜0）的终边与单位圆交点的横坐标是，则角α（-π＜α＜0）的终边与单位圆交点的纵坐标是-，∴cosα=，sinα=-，则cos（+α）=-sinα=，故答案为：．由题意可得角α的终边与单位圆交点的纵坐标是-，由此求得cosα和sinα的值，再根据cos（+α）=-sinα，计算求得结果．本题主要考查任意角的三角函数的定义，诱导公式，属于中档题．13.如果执行如图的程序框图，那么输出的值是______ ．【答案】-【解析】解：由程序框图知：算法的功能是求S=cos+cos+cosπ+…+cos的值，∵跳出循环的n值为2014，∴输出S=cos+cos+cosπ+…+cos，又cos+cos+cos+cos+cos+cos=0，∴输出S=cos+cos+cosπ+cos=--1=-．故答案为：-．的功能是求S=cos+cos+cosπ+…+cos的值，根据条件判断跳出循环的n值，利用余弦函数的周期性求输出S的值．本题考查了循环结构的程序框图，根据框图的流程判断算法的功能是关键．14.观察下列等式23=3+5，33=7+9+11，43=13+15+17+19，53=21+23+25+27+29，…，若类似上面各式方法将m3分拆得到的等式右边最后一个数是109，则正整数m等于______ ．【答案】10【解析】解：由题意可得第n行的左边是m3，右边是m个连续奇数的和，设第n行的最后一个数为a n，则有a2-a1=11-5=6=2×（1+2）=1×2+4，a3-a2=19-11=8=2×（2+2）=2×2+4，a4-a3=29-19=10=2×（3+2）=3×2+4，…a n-a n-1=2（n-1+2）=（n-1）×2+4，以上（n-1）个式子相加可得a n-a1=n2+3n-4故a n=n2+3n+1，即n2+3n+1=109解得n=9．∴m=n+1=9+1=10故答案为：10．可得规律：第n行的左边是m3，右边是m个连续奇数的和，设第n行的最后一个数为a n，累加可得a n，本题考查类比推理，涉及累加法求数列的通项公式，属基础题．15.如图放置的边长为1的正方形PABC沿x轴滚动，点B恰好经过原点．设顶点P（x，y）的轨迹方程是y=f（x），则对函数y=f（x）有下列判断：①函数y=f（x）是偶函数；②对任意的x∈R，都有f（x+2）=f（x-2）；③函数y=f（x）在区间[2，3]上单调递减；④函数y=f（x）在区间[4，6]上是减函数．其中判断正确的序号是______ ．【答案】①②④【解析】解：当-2≤x≤-1，P的轨迹是以A为圆心，半径为1的圆，当-1≤x≤1时，P的轨迹是以B为圆心，半径为的圆，当1≤x≤2时，P的轨迹是以C为圆心，半径为1的圆，当3≤x≤4时，P的轨迹是以A为圆心，半径为1的圆，∴函数的周期是4．因此最终构成图象如下：①根据图象的对称性可知函数y=f（x）是偶函数，∴①正确．②由图象即分析可知函数的周期是4．∴②正确．③函数y=f（x）在区间[2，3]上单调递增，∴③错误．④函数y=f（x）在区间[4，6]上是减函数，由函数的图象即可判断是真命题、∴④正确．故答案为：①②④．根据正方形的运动，得到点P的轨迹方程，然后根据函数的图象和性质分别进行判断即可．本题考查的知识点是函数图象的变化，其中根据已知画出正方形转动过程中的一个周期内的图象，利用数形结合的思想对本题进行分析是解答本题的关键．三、解答题(本大题共6小题，共75.0分)16.某公司生产产品A，产品质量按测试指标分为：指标大于或等于90为一等品，大于或等于80小于90为二等品，小于80为三等品，生产一件一等品可盈利50元，生产一件二等品可盈利30元，生产一件三等品亏损10元．现随机抽查熟练工人甲和新工他们生产产品A为一等品、二等品、三等品的概率．（1）计算甲生产一件产品A，给工厂带来盈利不小于30元的概率；（2）若甲一天能生产20件产品A，乙一天能生产15件产品A，估计甲乙两人一天生产的35件产品A中三等品的件数．【答案】解：（1）甲生产一件产品A，三等品的件数为3+7=10，此时给工厂带来盈利小于30元的概率为，则给工厂带来盈利不小于30元的概率为P=1-=．（2）估计甲一天生产的20件产品A中有20×=2件三等品，估计乙一天生产的15件产品A中有15×=3件三等品，所以估计甲乙两人一天生产的35件产品A中共有5件三等品．【解析】（1）根据古典概型的概率公式进行求解即可．（2）根据条件求出甲乙两人一天内生产的三等品的件数即可得到结论．本题主要考查统计与概率的应用，比较基础．17.已知公比不为1的等比数列{a n}的首项a1=，前n项和为S n，且a4+S4，a5+S5，a6+S6成等差数列．（1）求等比数列{a n}的通项公式；（2）对n∈N+，在a n与a n+1之间插入3n个数，使这3n+2个数成等差数列，记插入的这3n个数的和为b n，求数列{b n}的前n项和T n．【答案】解：（1）∵a4+S4，a5+S5，a6+S6成等差数列，∴2（a5+S5）=（a4+S4）+（a6+S6）…（2分）即2a6-3a5+a4=0，∴2q2-3q+1=0，∵q≠1，∴，…（4分）所以等比数列{a n}的通项公式为；…（6分）（2），…（9分）∴数列{b n}为等比数列，∴．…（12分）【解析】（1）根据a4+S4，a5+S5，a6+S6成等差数列，列出方程，求出公比，得到通项公式；（2）由等差数列的性质求出，利用等比数列的前n项和公式求出数列{b n}的前n项和T n．本题主要考查了等比数列的通项公式及求和公式及性质的应用，属于一道中档题．18.如图，已知正方形ABCD的边长为6，点E，F分别在边AB，AD上，AE=AF=4，现将△AEF沿线段EF折起到△A′EF位置，使得A′C=2．（1）求五棱锥A′-BCDFE的体积；（2）在线段A′C上是否存在一点M，使得BM∥平面A′EF？若存在，求A′M；若不存在，说明理由．【答案】解：（1）连接AC，设AC∩EF=H，由ABCD是正方形，AE=AF=4，得H是EF的中点，且EF⊥AH，EF⊥CH，从而有A′H⊥EF，CH⊥EF，∴EF⊥平面A′HC，从而平面A′HC⊥平面ABCD，…（2分）过点A′作A′O垂直HC且与HC相交于点O，则A′O⊥平面ABCD．…（4分）∵正方形ABCD的边长为6，AE=AF=4，得到：A′H=2，CH=4，∴cos∠A′HC==，∴HO=A′H•cos∠A′HC=，A′O=，∴五棱锥A′-BCDFE的体积V=×（62-×4×4）×=；…（6分）（2）线段A′C上存在一点M，使得BM∥平面A′EF，A′M=．…（7分）证明：∵A′M==A′C，HO=HC，∴OM∥A′H，∴OM∥平面A′EF，…（9分）又BD∥EF，∴BD∥平面A′EF，…（10分）∴平面MBD∥平面A′EF，…（11分）由BM在平面MBD内，∴BM∥平面A′EF．…（12分）【解析】（1）连接AC，设AC∩EF=H，由已知条件推导出平面A′HC⊥平面ABCD，过点A′作A′O垂直HC且与HC相交于点O，则A′O⊥平面ABCD，由此能求出五棱锥A′-BCDFE的体积．（2）线段A′C上存在一点M，使得BM∥平面A′EF，A′M=．证明平面MBD∥平面A′EF，即可得出结论．本题考查五棱锥的体积的求法，考查线面平行，考查学生分析解决问题的能力，难度中等．19.如图已知△ABC中，AB=1，AC=2，∠BAC=120°，点M是边BC上的动点，动点N满足∠MAN=30°（点A，M，N按逆时针方向排列）．（1）若=2，求BN的长；（2）若•=3，求△ABN面积的最大值．【答案】解：（1）由=2，得点N在射线AC上，AN=4，BN2=1+16-2×1×4×cos120°=21，即BN=；（2）设∠BAM=x，则∠CAM=120°-x，∵△ABC的面积等于△ABM与△ACM面积的和，∴°=°，得：AM=，又∠MAN=30°，=3，∴AM•AN•cos30°=3，即，∴△ABN的面积S=°=，即S==+．（其中：sinφ=，cosφ=（其中φ为锐角），∴当2x-φ=90°时，△ABN的面积最大，最大值是．【解析】（1）由=2，得点N在射线AC上，AN=4，再利用余弦定理即可得出；（2）设∠BAM=x，则∠CAM=120°-x，由于△ABC的面积等于△ABM与△ACM面积的和，可得AM=，已知∠MAN=30°，=3，利用数量积可得：，可得△ABN的面积S=°，再利用倍角公式、两角和差的正弦公式及其单调性即可得出．本题综合考查了余弦定理、两角和差的正弦余弦公式、倍角公式、三角形的面积公式、三角函数的单调性等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．20.已知椭圆C：+=1（a＞b＞0）的左焦点为F，左、右顶点分别为A，B，过点F 且倾斜角为的直线l交椭圆于C，D两点，椭圆C的离心率为，•-•=-．（1）求椭圆C的方程；（2）若P1，P2是椭圆上不同两点，P1，P2⊥x轴，圆R过点P1，P2，且椭圆上任意一点都不在圆R内，则称圆R为该椭圆的内切圆．问椭圆C是否存在过点F的内切圆？若存在，求出点R的坐标；若不存在，说明理由．【答案】解：（1）因为离心率为，所以a=2b，c=，所以椭圆方程可化为：，直线l的方程为y=x+，…（2分）由方程组，得：，即，…（4分）设C（x1，y1），D（x2，y2），则，…（5分）又=（x1+a，y1）•（x2+a，y2）-（x1-a，y1）•（x2-a，y2）=2a（x1+x2），∴4b•（-）=-，解得b=1，∴椭圆方程是．…（7分）（2）由椭圆的对称性，可以设P1（m，n），P2（m，-n），点R在x轴上，设点R（t，0），则圆R的方程为：（x-t）2+y2=（m-t）2+n2，由内切圆定义知道，椭圆上的点到点R距离的最小值是|P1R|，设点M（x，y）是椭圆C上任意一点，则|MR|2=（x-t）2+y2=，…（9分）当x=m时，|MR|2最小，∴m=-=，①…（10分）又圆R过点F，所以（-）2=（m-t）2+n2，②…（11分）点P1在椭圆上，∴，③…（12分）由①②③解得：t=-或t=-，又t=-时，m=＜，不合题意，综上：椭圆C存在符合条件的内切圆，点R的坐标是（-，）．…（13分）【解析】（1）由离心率为，得a=2b，c=，直线l的方程为y=x+，由方程组，得，由此利用已知条件能求出椭圆方程．（2）由椭圆的对称性，设P1（m，n），P2（m，-n），点R在x轴上，设点R（t，0），圆R的方程为：（x-t）2+y2=（m-t）2+n2，由此利用内切圆定义结合已知条件能求出椭圆C存在符合条件的内切圆，点R的坐标是（-，）．本题考查椭圆方程的求法，考查椭圆的内切圆是否存在的判断与求法，解题时要认真审题，注意函数与方程思想的合理运用．21.已知函数f（x）=sinx-ax-bxcosx（a∈R，b∈R）．（1）若b=0，讨论函数f（x）在区（0，π）上的单调性；（2）若a=2b且a≥，对任意的x＞0，试比较f（x）与0的大小．【答案】解：（1）b=0时，f（x）=sinx-ax，则f′（x）=cosx-a，当a≥1时，f′（x）＜0，所以函数f（x）在区间（0，π）上单调递减；当a≤-1时，f′（x）＞0，所以函数f（x）在区间（0，π）上单调递增；当-1＜a＜1时，存在θ∈（0，π），使得cosθ=a，即f（θ）=0，①x∈（0，θ）时，f′（x）＞0，函数f（x）在区间（0，θ）上单调递增，②x∈（θ，π）时，f′（x）＜0，函数f（x）在区间（θ，π）上单调递减．（2）a=2b时，f（x）=sinx-x（2+cosx），猜测f（x）＜0恒成立，证明：f（x）＜0等价于＜，令g（x）=，则g（x）==-+，当，即a≥时，g′（x）≤0，g（x）在区间（0，+∞）上单调递减，所以当x＞0时，g（x）＜g（0）=0，即f（x）＜0恒成立．【解析】（1）问中，分a≥1，a≤-1，-1＜a＜1进行讨论；（2）中引进新函数g（x），将问题转化为求新函数的单调性问题．本题属于利用导数求函数的单调性问题，解题过程中用到了分类讨论思想，转化思想．。

2014江西省南昌市高三交流卷数学文试题及答案

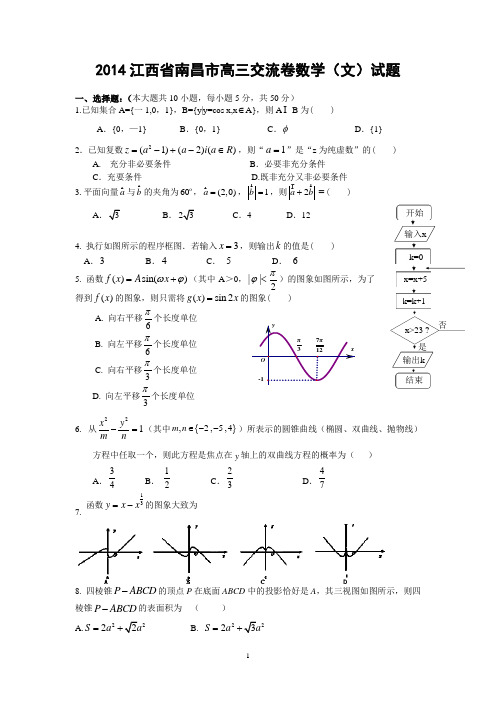
2014江西省南昌市高三交流卷数学（文）试题一、选择题：（本大题共10小题，每小题5分，共50分）1.已知集合A={一1,0，1}，B={y|y=cos x,x ∈A}，则A B 为( ) A ．{0，—1}B ．{0，1}C ．φD ．{1}2．已知复数2(1)(2)()z a a i a R =-+-∈，则“1a =”是“z 为纯虚数”的( ) A. 充分非必要条件 B ．必要非充分条件C ．充要条件 D.既非充分又非必要条件 3.平面向量a 与b 的夹角为60，(2,0)a =，1b =，则2a b +=( )A ．3B ．23C ．4D ．124. 执行如图所示的程序框图．若输入3x =，则输出k 的值是( ) A ．3 B ．4 C ． 5 D ． 65. 函数()sin()f x A x ωϕ=+（其中A ＞0，2||πϕ<）的图象如图所示，为了得到()f x 的图象，则只需将()sin 2g x x =的图象( )A. 向右平移6π个长度单位B. 向左平移6π个长度单位C. 向右平移3π个长度单位D. 向左平移3π个长度单位6. 从221x y m n-=（其中{},2,5,4m n ∈--）所表示的圆锥曲线（椭圆、双曲线、抛物线）方程中任取一个，则此方程是焦点在y 轴上的双曲线方程的概率为（）A ．34B ．12C ．23D ．477.函数13y x x =-的图象大致为8. 四棱锥P ABCD -的顶点P 在底面ABCD 中的投影恰好是A ，其三视图如图所示，则四棱锥P ABCD -的表面积为（）A.2222S a a =+ B. 2223S a a =+yx7π12π3O -1是结束输出k 否x>23 ?k=k+1x=x+5k=0输入x 开始C. 2242S a a =+D. 2233S a a =+9.已知抛物线22(0)y p xp =>的焦点F与椭圆22221(0)x y a b a b+=>>的一个焦点重合，它们在第一象限内的交点为T ，且T F 与x 轴垂直，则椭圆的离心率为（）A ．212- Ｂ．21- Ｃ．13- Ｄ．213-10.如图，点P 从点O 出发，分别按逆时针方向沿周长均为12的正三角形、正方形运动一周，,O P 两点连线的距离y 与点P 走过的路程x 的函数关系分别记为(),()y f x y g x ==，定义函数()()()()()()()f x f x g x h x g x f x g x ⎧⎪=⎨>⎪⎩，≤，，．对于函数()y h x =，下列结论正确的个数是（）① (4)10h = ； ②函数()h x 的图象关于直线6x =对称； ③函数()h x 值域为013⎡⎤⎣⎦，；④函数()h x 增区间为05（，）．第10题图 A ．1 B ．2 C ．3 D ．4二、填空题（本大题共5小题，每小题5分，共25分. ）11．已知数列1,,9a 是等比数列，数列121,,,9b b 是等差数列，则12a b b +的值为 .12．某校高三第一次模考中，对总分450分（含450分）以上的成绩进行统计，其频率分布直方图如图所示，若650～700分数段的人数为90，则500～550分数段的人数为_________人.13. 若关于x ，y 的不等式组10,10,10x y x ax y +-≥⎧⎪-≤⎨⎪-+≥⎩（a 为常数）所表示的平面区域的面积等于2，则a 的值为 .14. 在直角三角形ABC 中，90ACB ∠=︒，2AC BC ==，点P 是斜边AB 上的一个三等分点，则CP CB CP CA ⋅+⋅= ．15. 给出下列四个命题：①ABC ∆中，A B >是sin sin A B >成立的充要条件； ②当01x x >≠且时，有1ln 2ln x x+≥； ③已知n S 是等差数列{}n a 的前n 项和，若75S S >，则93S S >； ④若函数)23(-=x f y 为R 上的奇函数，则函数)(x f y =的图象一定关于点)0,23(F 成OPPO700650600**********.0010.0020.0030.0050.009分数频率组距中心对称.⑤函数)(cos sin cos )(23R x x x x x f ∈-+=有最大值为2，有最小值为0。

江西省南昌二中2014届高三最后一次模拟考试数学文试题 Word版含答案

江西省南昌二中2014届高三最后一次模拟考试数学文试题3.{}n a 为等差数列,n S 为前n 项和,566778,,S S S S S S <=>,则下列错误的是（）.0A d < 7.0B a = 95.C S S > 67.n D S S S 和均为的最大值；4.下列命题： ①经过三点可以确定一个平面；②复数2iZ =在复平面上对应的点在第四象限； ③已知平面//;a a αβααββ⊥⊥，，若平面且平面平面，则平面 ④若回归直线方程的斜率的估计值是1.23,样本的中心点为(4,5)，则回归直线的方程是：ˆ 1.230.08;yx =+ 以上命题中错误的命题个数是（） .0A .1B .2C .3D5.已知函数()()()2,(),f x x a x b a b =--+<若,()αβαβ<是方程()0f x =的两个根，则实数,,,a b αβ之间的大小关系是（）.;.;.;.A a b B a b C b a D a b αβαβαβαβ<<<<<<<<<<<<6.在ABC ∆中，90,C P ∠=为三角形内一点且PAB PBC PCA S S S ∆∆∆==,则222PA PB PC +=( ).2AC .5D7. ,a b 是方程220mx nx +-=的两个不等的实数根，且点(,)M m n 在圆22:1C x y +=上，那么过点2(,)A a a 和2(,)B b b 的直线与圆C 的位置关系（） .A 相离 .B 相切 .C 相交 .D 随,m n 的变化而变化8.两位工人加工同一种零件共100个,甲加工了40个,其中35个是合格品,乙加工了60个, 其中有50个合格,令A 事件为”从100个产品中任意取一个,取出的是合格品”,B 事件为” 从100个产品中任意取一个,取到甲生产的产品”,则P (A|B)等于( ) A.25B.35C.78D.579. 执行如图的程序框图，如果输入的N 的值是6，那么输出的p 的值是A ．15B ．120 D ．720 10. 如图，正方形ABCD 的顶点，顶点CD 、位于第一象限，直线:(02)l x t t =≤≤将正方形ABCD 分成两部分，记位于直线l 左侧阴影部分的面积为()f t ，则函数()s f t =的图象大致是（）一、填空题 11.)(x f '是函数()1x f x x =-的导数，则(2)(2)f f '的值是 .12. 设双曲线的渐近线为：x y 23±=，则其离心率为 .15,,0,,3,5,4ABC ABC AB a AC b a b S a b a b θ∆∆==⋅<===13.已知中，则与的夹角为 14.如图，正方体的底面与正四面体的底面在同一平面α上，且AB ∥CD ，正方体的六个面所在的平面与直线CE ，EF 相交的平面个数分别记为m ，n ，那么m ＋n ＝15.在实数范围内，不等式||x －2|－1|≤1的解集为________．三、解答题16. （本小题满分12分）已知函数)50)(3π6πsin(2)(≤≤+=x x x f ，点A 、B 分别是函数y f x =（）图像上的最高点和最低点．（I ）求点A 、B 的坐标以及OB OA ⋅的值；（II ）设点A 、B 分别在角α、β的终边上，求)2tan(βα-的值．17. （本小题满分12分）某迷宫有三个通道，进入迷宫的每个人都要经过一扇智能门。

江西省南昌市第二中学2014届高三上学期第三次考试数学(文)试题 Word版含答案

江西省南昌市第二中学2013-2014学年高三上学期第三次考试数学（文）试卷一、选择题（本题10小题，每小题5分，共50分） 1. 已知A ＝{－1，0，1}，B ＝{y|y=sinx,x ∈A},则A ∩B ＝（） A. {0} B. {1} C. {0，1} D. {0，－1}2. 已知θ∈（π，32π），cos θ＝－45,则tan(4π－θ)＝（） A. 7B. 17C. －17D. －73. 已知等差数列{a n }的前n 项的和为S n ，若65911a a =，则119SS =( ) A. 1 B. －1C. 2D.124. 已知直线ax －by －2＝0与曲线y ＝x 3在点P(1，1)处的切线互相垂直，则ab ＝( ) A.13B.23C. －23D. －135. 已知数列{a n }中，a 1＝0，a n+1，则a 2013＝( )A. 0B.D.6. 函数f (x )＝2sin(2x －3π)的图象的一条对称轴方程是( ) A. x ＝12πB. x ＝6π C. x ＝512πD. x ＝3π7. 在△ABC 中，若a sinA+bsinB<csinC ，则△ABC 的形状是( )三角形. A. 锐角 B. 直角 C. 钝角 D. 等边8. 等差数列{a n }的前n 项和是S n ，若22012OB a OA a OC =+，且A ，B ，C 三点共线（O 为该直线外一点），则S 2013＝( ) A.20132B. 2013C. 22013D. 2-20139. 已知O 在△ABC 的内部，满足：40OA OB OC ++=，，则△ABC 的面积与△AOC 的面积之比为( ) A. 3:2B. 2:3C. 5:4D. 4:510. 已知||2||0a b =≠ ，且关于x 的函数3211()||32f x x a x a bx =++⋅在R 上有极值，则a 与b 的夹角θ范围是( )A. (0，6π) B. （6π，π] C. [3π，π] D. (3π，23π]二、填空题（本题5小题，每小题5分，共25份）11. 已知：(1,2),(4,2)a b =-=，且2a a b -与的夹角为θ，则cos θ＝___________. 12. 在△ABC 中，若（a +b －c ）(a +b +c )＝ab ，则角C ＝______________. 13. 已知θ∈（0，2π）且sin 2θ+cos2θ＝14，则tan θ＝___________.14. 数列{a n }中，前n 项和为S n 且S n ＝n －5a n －85，则a n ＝__________. 15. 有限数列A ＝（a 1，a 2，a 3……a n ），S n 为其前n 项和，定义：123ns s s s n+++为A 的“四维光军和”。

2014年江西省南昌十中高考数学模拟试卷(文科)

2014年江西省南昌十中高考数学模拟试卷（文科）学校:___________姓名：___________班级：___________考号：___________一、选择题(本大题共10小题，共50.0分)1.若z==x+yi，x，y∈R，则集合{x，2x，y}子集个数是（）A.8B.7C.6D.92.已知函数f（x）=2x2-bx（b∈R），则下列结论正确的是（）A.∀b∈R，f（x）在（0，+∞）上是增函数B.∀b∈R，f（x）在（0，+∞）上是减函数C.∃b∈R，f（x）为奇函数D.∃b∈R，f（x）为偶函数3.函数y=2的图象大致是（）A. B. C. D.4.函数f（x）=2x-4+lnx的零点一定位于下列哪个区间（）A.（1，2）B.（2，3）C.（3，4）D.（4，5）5.已知一个空间几何体的三视图如图所示，且这个空间几何体的所有顶点都在一个球面上，则这个球的体积是（）A. B. C. D.6.函数f（x）=cosx在区间[a，b]上是增函数，且f（a）=-1，f（b）=1，则sin=（）A.±B.C.±1D.-7.为了从甲乙两人中选一人参加数学竞赛，老师将二人最近6次数学测试的分数进行统计，甲乙两人的平均成绩分别是甲、，则下列说法正确的是（）乙A.甲＞乙，乙比甲成绩稳定，应选乙参加比赛B.甲＞乙，甲比乙成绩稳定，应选甲参加比赛C.甲＜乙，甲比乙成绩稳定，应选甲参加比赛D.甲＜乙，乙比甲成绩稳定，应选乙参加比赛8.一个样本容量为10的样本数据，它们组成一个公差不为0的等差数列{a n}，若a3=8，且a1，a3，a7成等比数列，则此样本的平均数和中位数分别是（）A.13，12B.13，13C.12，13D.13，149.若直线2ax-by+2=0（a＞0，b＞0）被圆x2+y2+2x-4y+1=0截得的弦长为4，则+的最小值为（）A. B.6 C.12 D.1610.已知函数f（x）=x2-2ax+5，若f（x）在区间（-∞，2]上是减函数，且对任意的x1，x2∈[1，a+1]，总有|f（x1）-f（x2）|≤4，则实数a的取值范围是（）A.[2，3]B.[1，2]C.[-1，3]D.[2，+∞）二、填空题(本大题共5小题，共25.0分)11.设m，n是两条不同的直线，α，β，γ是三个不同的平面，给出下列命题：①若m⊂β，α⊥β，则m⊥α；②若m∥α，m⊥β，则α⊥β；③若α⊥β，α⊥γ，则β⊥γ；④若α∩γ=m，β∩γ=n，m∥n，则α∥β；⑤若α∥β，P∈α，PQ∥β，则PQ⊂α．上面命题中，真命题的序号是______ （写出所有真命题的序号）．12.（文）已知向量=（-3，-4），=（0，1），点C对应的向量=+λ，且C点在函数y=cos x的图象上，则实数λ= ______ ．13.设函数f（x）=f（a）+f（-1）=3，则实数a= ______ ．＜，若14.已知A，B，P是双曲线-=1（a＞0，b＞0）上不同的三个点，且A，B的连线经过坐标原点，若直线PA、PB的斜率的乘积k PA•k PB=，则该双曲线的离心率为______ ．15.已知函数f（x）=|x-1|+|x-a|．如果∀x∈R，f（x）≥2，求a的取值范围为______ ．三、解答题(本大题共6小题，共75.0分)16.已知函数f（x）=sin2ωx+sinωxsin（ωx+）+2cos2ωx，x∈R（ω＞0），在y轴右侧的第一个最高点的横坐标为．若将函数f（x）的图象向右平移个单位后，再将得到的图象上各点横坐标伸长到原来的2倍，纵坐标不变，得到函数y=g（x）的图象．（1）求函数g（x）的最大值及单调递减区间．（2）（文）在△ABC中，a，b，c分别是角A，B，C的对边，a=，b+c=3且f（A）=2，求角A的值．17.（文）在等比数列{a n}中，a1＞0，n∈N*，且a5-a4=8，又a2、a8的等比中项为16．（1）求数列{a n}的通项公式；（2）设b n=log4a n，数列{b n}的前n项和为S n，求和++…+．18.某班同学利用寒假进行社会实践活动，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念的称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：（1）补全频率分布直方图并求n、a、p的值；（2）从年龄段在[40，50）的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动，其中选取2人作为领队，求选取的2名领队中恰有1人年龄在[40，45）岁的概率．19.如图所示，在正三棱柱ABC-A1B1C1中，底面边长和侧棱长都是2，D是侧棱CC1上任意一点，E是A1B1的中点．（Ⅰ）求证：A1B1∥平面ABD；（Ⅱ）求证：AB⊥CE；（Ⅲ）求三棱锥C-ABE的体积．20.已知椭圆C1：=1（a＞b＞0）的左、右焦点分别为F1、F2，其中F2也是抛物线C2：y2=4x的焦点，M是C1与C2在第一象限的交点，且（I）求椭圆C1的方程；（Ⅱ）已知菱形ABCD的顶点A、C在椭圆C1上，顶点B、D在直线7x-7y+1=0上，求直线AC的方程．21.对于函数f（x），若在定义域内存在实数x，使得f（-x）=-f（x），则称f（x）为“局部奇函数”．（1）已知二次函数f（x）=ax2+4x-a（a∈R），试判断f（x）是否为“局部奇函数”？并说明理由；（2）若f（x）=2x+m是定义在区间[-1，1]上的“局部奇函数”，求实数m的取值范围；（3）（文）若f（x）=e x-ex-2m为定义域R上的“局部奇函数”，求证：若x＞1，则e x ＞x2-2mx+1．。

2014年高考江西文科数学试题及答案（word解析版）

2014年⾼考江西⽂科数学试题及答案（word解析版）2014年普通⾼等学校招⽣全国统⼀考试（江西卷）数学（⽂科）第Ⅰ卷（选择题共40分）⼀、选择题：本⼤题共8⼩题，每⼩题5分，共40分，在每⼩题给出的四个选项中，只有⼀项符合题⽬要求．（1）【2014年江西，⽂1，5分】若复数z 满⾜(1i)2i z +=（i 为虚数单位），则||z =（）（A ）1 （B ）2 （C （D 【答案】C【解析】解法⼀：∵若复数z 满⾜(1i)2i z +=，∴()()()21i 2i 1i 1i 1i 1i i z -===+++-，∴z ==，故选C ．解法⼆：设i z a b =+，则()()i 1i 2i a b ++=，()()i 2i a b a b -++=，0a b -=，2a b +=，解得1a =，1b =，1i z =+，1i z =+C ．【点评】本题主要考查两个复数代数形式的乘除法，虚数单位i 的幂运算性质，求复数的模，属于基础题．（2）【2014年江西，⽂2，5分】设全集为R ，集合2{|90},{|15}A x x B x x =-<=-<≤，则()R A C B = （）（A ）(3,0)- （B ）(3,1)-- （C ）(]3,1-- （D ）(3,3)- 【答案】C【解析】{|33},{|15}A x x B x x =-<<=-<≤，所以{}()31R A C B x x =-<<- ，故选C ．【点评】本题主要考查集合的表⽰⽅法、集合的补集，两个集合的交集的定义和求法，属于基础题．（3）【2014年江西，⽂3，5分】掷两颗均匀的骰⼦，则点数之和为5的概率等于（）（A ）118 （B ）19（C ）16 （D ）112【答案】B【解析】点数之和为5的基本事件有：()1,4，()4,1，()2,3，()3,2，所以概率为41369=，故选B ．【点评】本题是⼀个古典概率模型问题，解题的关键是理解事件“抛掷两颗骰⼦，所得两颗骰⼦的点数之和为5”，由列举法计算出事件所包含的基本事件数，判断出概率模型，理解求解公式nN是本题的重点，正确求出事件“抛掷两颗骰⼦，所得两颗骰⼦的点数之和为5”所包含的基本事件数是本题的难点．（4）【2014年江西，⽂4，5分】已知函数2,0()()2,0x x a x f x a R x -??≥=∈?，若[(1)]1f f -=，则a =（）（A ）14 （B ）12（C ）1 （D ）2【答案】A【解析】(1)2f -=，(2)4f a =，所以[(1)]41f f a -==，解得14a =，故选A ．【点评】本题主要考查了求函数值的问题，关键是分清需要代⼊到那⼀个解析式中，属于基础题．（5）【2014年江西，⽂5，5分】在ABC ?中，内⾓,,A B C 所对应的边分别为,,a b c ，若32a b =，则2222sin sin sin B AA -的值为（）（A ）19- （B ）13（C ）1 （D ）72【答案】D【解析】222222222sin sin 2372121sin 22B A b a b A a a --==-=-= ? ?????，故选D ．【点评】本题主要考查正弦定理的应⽤，⽐较基础．（6）【2014年江西，⽂6，5分】下列叙述中正确的是（）（A ）若,,a b c R ∈，则2"0"ax bx c ++≥的充分条件是2"40"b ac -≤（B ）若,,a b c R ∈，则22""ab cb >的充要条件是""a c >（C ）命题“对任意x R ∈，有20x ≥”的否定是“存在x R ∈，有20x ≥” （D ）l 是⼀条直线，,αβ是两个不同的平⾯，若,l lαβ⊥⊥，则//αβ【答案】D 【解析】（1）对于选项A ：若,,a b c R ∈，当2"0"ax bx c ++≥对于任意的x 恒成⽴时，则有：①当0a =时，0b =，0c ≥，此时240b ac -≤成⽴；②当0a >时，240b ac -≤．∴2"0"ax bx c ++≥是2"40"b ac -≤充分不必要条件，2"40"b ac -≤是2"0"ax bx c ++≥必要不充分条件．故A 不正确．（2）对于选项B ：当22""ab cb >时，20b ≠，且a c >，∴22""ab cb >是""a c >的充分条件．反之，当a c >时，若0b =，则22ab cb =，不等式22ab cb >不成⽴．∴""a c >是22""ab cb >的必要不充分条件．故B 不正确．（3）对于选项C ：结论要否定，注意考虑到全称量词“任意”，命题“对任意x R ∈，有20x ≥”的否定应该是“存在x R ∈，有20x <”．故选项C 不正确．（4）对于选项D ：命题“l 是⼀条直线，,αβ是两个不同的平⾯，若,l l αβ⊥⊥，则//αβ．”是两个平⾯平⾏的⼀个判定定理，故选D ．【点评】本题考查独⽴性检验的应⽤，考查学⽣的计算能⼒，属于中档题．（7）【2014年江西，⽂7，5分】某⼈研究中学⽣的性别与成绩、视⼒、智商、阅读量这4个变量之间的关系，随机抽查52名中学⽣，得到统计数据如表1⾄表4，则与性别有关联的可能性最⼤的变量是（）（A ）成绩（B ）视⼒（C ）智商（D ）阅读量【答案】D【解析】表1：()225262210140.00916362032X ??-?=≈；表2：()22524201216 1.76916362032X ??-?=≈；表3：()2252824812 1.316362032X ??-?=≈；表4：()22521430616223.4816362032X ??-?=≈，∴阅读量与性别有关联的可能性最⼤，故选D ．【点评】本题考查独⽴性检验的应⽤，考查学⽣的计算能⼒，属于中档题．（8）【2014年江西，⽂8，5分】阅读如下程序框图，运⾏相应的程序，则程序运⾏后输出的结果为（）（A ）7 （B ）9 （C ）10 （D ）11 【答案】B【解析】由程序框图知：135i 0lg lg lg lg 357i 2S =++++++ 的值，∵1371lg lg lg lg 13599S =+++=>- ，⽽1391lg lg lg lg 1351111S =+++=<- ，∴跳出循环的i 值为9，∴输出i 9=，故选B ．【点评】本题考查了循环结构的程序框图，根据框图的流程判断算法的功能是解题的关键．（9）【2014年江西，⽂9，5分】过双曲线22221x y C a b-=：的右顶点作x 轴的垂线与C 的⼀条渐近线相交于A ．若以C 的右焦点为圆⼼、半径为4的圆经过A 、O 两点（O 为坐标原点），则双曲线C 的⽅程为（）（A ）221412x y -= （B ）22179x y -= （C ）22188x y -= （D ）221124x y -=【答案】A 【解析】以C 的右焦点为圆⼼、半径为4的圆经过坐标原点O ，则4c =．且4CA =．设右顶点为(),0B a ，(),C a b ，ABC ? 为Rt ?222BA BC AC ∴+=，()22416a b ∴-+=，⼜22216a b c +== ．得1680a -=，2a =，24a =，212b =，所以双曲线⽅程221412x y-=，故选A ．【点评】本题考查双曲线的⽅程与性质，考查学⽣的计算能⼒，属于基础题．（10）【2014年江西，⽂10，5分】在同⼀直⾓坐标系中，函数22ay ax x =-+与()2322y a x ax x a a =-++∈R 的图像不可能的是（）（A ）（B ）（C ）（D ）【答案】B【解析】当0a =时，函数22ay ax x =-+的图象是第⼆，四象限的⾓平分线，⽽函数2322y a x ax x a =-++的图象是第⼀，三象限的⾓平分线，故D 符合要求；当0a ≠时，函数22ay ax x =-+图象的对称轴⽅程为直线12x a =，由2322y a x ax x a =-++可得：22341y a x ax '=-+，令0y '=，则113x a =，21x a =，即113x a =和21x a =为函数2322y a x ax x a =-++的两个极值点，对称轴12x a =介于113x a =和21x a=两个极值点之间，故A 、C 符合要求，B 不符合，故选B ．【点评】本题考查的知识点是函数的图象，其中熟练掌握⼆次函数的图象和性质，三次函数的极值点等知识点是解答的关键．⼆、填空题：本⼤题共5⼩题，每⼩题5分，共25分．（11）【2014年江西，⽂11，5分】若曲线ln y x x =上点P 处的切线平⾏于直线210x y -+=，则点P 的坐标是．【答案】(),e e【解析】11ln ln 1y x x x x=?+?=+，切线斜率2k =，则0ln 12x +=，0ln 1x =，0x e ∴= ()0f x e∴=，所以(),P e e ．【点评】本题主要考查导数的⼏何意义，以及直线平⾏的性质，要求熟练掌握导数的⼏何意义．（12）【2014年江西，⽂12，5分】已知单位向量12,e e 的夹⾓为α，且1cos 3α=，若向量1232a e e =- ，则||a =．【答案】3【解析】()()()222221212123232129412cos 9a a e e e e e e α==-=+-?=+-=，解得3a =．【点评】本题主要考查两个向量的数量积的定义，求向量的模的⽅法，属于基础题．（13）【2014年江西，⽂13，5分】在等差数列{}n a 中，17a =，公差为d ，前n 项和为n S ，当且仅当8n =时n S取最⼤值，则d 的取值范围．【答案】71,8?--【解析】因为170a =>，当且仅当8n =时n S 取最⼤值，可知0d <且同时满⾜890,0a a ><，所以，89770780a d a d =+>??=+18d -<<-．【点评】本题主要考查等差数列的前n 项和公式，解不等式⽅程组，属于中档题．（14）【2014年江西，⽂14，5分】设椭圆()2222:10x y C a b a b+=>>的左右焦点为12F F ，，作2F 作x 轴的垂线与C交于A B ，两点，1F B 与y 轴交于点D ，若1AD F B ⊥，则椭圆C 的离⼼率等于．【解析】因为AB 为椭圆的通径，所以22b AB a=，则由椭圆的定义可知：212b AF a a =-，⼜因为1AD F B ⊥，则1AF AB =，即2222b b a a a =-，得2223b a =，⼜离⼼率ce a =，结合222a b c =+，得到：e =．【点评】本题主要考查椭圆离⼼率的求解，根据条件求出对应点的坐标，利⽤直线垂直于斜率之间的关系是解决本题的关键，运算量较⼤．为了⽅便，可以先确定⼀个参数的值．（15）【2014年江西，⽂15，5分】,x y R ∈，若112x y x y ++-+-≤，则x y +的取值范围为．【答案】[]0,2【解析】 11x x +-≥，11y y +-≥，要使112x x y y +-++-≤，只能112x x y y +-++-=，11x x +-=，11y y +-=，∴01x ≤≤，01y ≤≤，∴02x y ≤+≤．【点评】本题主要考查绝对值的意义，绝对值不等式的解法，属于中档题．三、解答题：本⼤题共6题，共75分．解答应写出⽂字说明，演算步骤或证明过程．（16）【2014年江西，⽂16，12分】已知函数()()()22cos cos 2f x a x x θ=++为奇函数，且04f π??=，其中a ∈R ，()0,θπ∈．（1）求,a θ的值；（2）若245f α??=- ，,2παπ??∈，求sin 3πα?+的值．解：（1）()()1cos 1sin 042f a a ππθθ=++=-+= ? ?Q ()0θπ∈，,∴sin 0θ≠,∴10,1a a +=∴=- ………2分 Q 函数()()()22cos cos 2f x a x x θ=++为奇函数()()02cos cos 0f a θθ∴=+==……………4分 2πθ∴=． ……………5分（2）有（1）得()()2112cos cos 2cos 2sin 2sin 422f x x x x x x π??=-++=-=- ?g……………7分 Q 12sin 425f αα??=-=- ∴4s i n 5α=………8分 Q 2πθπ??∈，，3cos 5α∴=- ……………10分413sin sin cos cos sin 333525πππααα??∴+=+=?-=……………12分【点评】本题主要考查了同⾓三⾓函数关系，三⾓函数恒等变换的应⽤，函数奇偶性问题．综合运⽤了所学知识解决问题的能⼒．（17）【2014年江西，⽂17，12分】已知数列{}n a 的前n 项和232n n nS -=，*n N ∈．（1）求数列{}n a 的通项公式；（2）证明：对任意1n >，都有*m N ∈，使得1a ，n a ，m a 成等⽐数列．解：（1）当1n =时111a S ==，当2n ≥时，()22131133222n n n n n n n a S S n ---+-=-=-=-检验，当1n =时11a =，32n a n ∴=-．（2）使1a ，n a ，m a 成等⽐数列．则21n m a a a =，()23232n m ∴--=，即满⾜()2233229126m n n n =-+=-+，所以2342m n n =-+，所以对任意1n >，都有m N *∈，使得1n m a a a ，，成等⽐数列．【点评】本题考查了递推式的意义、等差数列与等⽐数列的通项公式、⼆次函数的单调性等基础知识与基本技能⽅法，考查了恒成⽴问题的等价转化⽅法，考查了反证法，考查了推理能⼒和计算能⼒，属于难题．（18）【2014年江西，⽂18，12分】已知函数22()(44f x x ax a =++，其中0a <．（1）当4a =-时，求()f x 的单调递增区间；（2）若()f x 在区间[1,4]上的最⼩值为8，求a 的值．解：（1）当4a =-时，()()()2422f x x x =--()f x 的定义域为[)0,+∞，()(2'242x f x x-=-252x x --，令()'0f x >得20,25x x ≤<>，所以当4a =-时，()f x 的单调递增区间为()20,2+5??∞和，．（2）()()2f x x a =+，()(2'221022x a x a x a f x x a +++=+=令()'0f x =，得12,210a a x x =-=-，0a ">，"所以，在区间,,,102a a --+∞ ? ?0上，()'0f x >， )(x f 的单调递增；在区间,102a a ??--上，()'0f x <，)(x f 的单调递减；⼜易知()()220f x x a =+，且02a f ??-=．①当12a-≤时，即20a -≤<时，)(x f 在区间]4,1[上的最⼩值为()1f ，由()21448f a a =++=，得2a =-±，均不符合题意．②当142a<-≤时，即82a -≤<-时，)(x f 在区间]4,1[上的最⼩值为02a f ??-= ，不符合题意．③当42a->时，即8a <-时，)(x f 在区间]4,1[上的最⼩值可能为1x =或4x =处取到，⽽()18f ≠，()242(6416)8f a a =++=，得10a =-或6a =-（舍去），当10a =-时，()f x 在区间[1,4]上单调递减，()f x 在区间[1,4]上的最⼩值()48f =符合题意．综上，10a =-．【点评】本题考查的是导数知识，重点是利⽤导数判断函数的单调性，难点是分类讨论．对学⽣的能⼒要求较⾼，属于难题．（19）【2014年江西，⽂19，12分】如图，三棱柱111ABC A B C -中，111,AA BC A B BB ⊥⊥．（1）求证：111AC CC ⊥；（2）若2,AB AC BC ==1AA 为何值时，三棱柱111ABC A B C -体积最⼤，并求此最⼤值．解：（1）三棱柱111ABC A B C -中，1AA BC ⊥，1BB BC ∴⊥，⼜11BB A B ⊥且1BC A B C = ，11BB BCA ∴⊥⾯，11BB CC ∥11CC BCA ∴⊥⾯，⼜11AC BCA ∴?⾯， 11AC CC ⊥．（4分）（2）设1AA x =，在Rt △11Rt A BB ?中，AB同理，1A 1ABC ?中1cos BAC ∠=222211112A B AC BC A B AC +-=1sin BAC ∠=（6分）所以11111sin BA C 2A BCS A B A C =∠= △（7分）从⽽三棱柱111ABC A B C -的体积11A BCV S l S AA =?=?=△8分），因10分）故当x1AA 时，体积V【点评】本题考查空间直线与平⾯垂直的判定与应⽤，⼏何体的体积的最值的求法，考查转化思想以及空间想象能⼒．（20）【2014年江西，⽂20，13分】如图，已知抛物线2:4C x y =，过点(0,2)M 任作⼀直线与C 相交于,A B 两点，过点B 作y 轴的平⾏线与直线AO 相交于点D （O 为坐标原点）．（1）证明：动点D 在定直线上；（2）作C 的任意⼀条切线l （不含x 轴）与直线2y =相交于点1N ，与（1）中的定直线相交于点2N ，证明：2221||||MN MN -为定值，并求此定值解：（1）根据题意可设AB ⽅程为2y kx =+，代⼊2=4x y ，得()242x kx =+，即2480x k x --=，设()11,A x y ，()22,B x y ，则有：128x x =-，（2分）直线AO 的⽅程为11y y x x =；BD 的⽅程为2x x =，解得交点D 的坐标为2121x x y x y x =??=（4分），注意到128x x =-及211=4x y ，则有1121211824y x x y y x y -===-，（5分）因此D 点在定直线y=-2上（2x ≠）（6分）．（2）依据题设，切线l 的斜率存在且不等于0，设切线l 的⽅程为()0y ax b a =+≠，代⼊2=4x y 得2=4+x ax b （）,即2440x ax b --=，由0?=得216160a b +=，化简整理得2b a =-（8分）故切线l 的可写为2y ax a =-．令2y =、2y =-得12,N N 坐标为12(,2)N a a +，22(,2)N a a-+-（11分）则222222122()4()8MN MN a a a a-=-+-+=，即2221MN MN -为定值8．（13分）【点评】本题考查抛物线的⽅程与性质、直线与圆锥曲线的位置关系等基础知识，考查抽象概括能⼒、推理论证能⼒、运算求解能⼒，考查特殊与⼀般思想、数形结合思想、函数与⽅程思想，属于难题．（21）【2014年江西，⽂21，14分】将连续正整数1,2,,(*)n n N ∈从⼩到⼤排列构成⼀个数123n ，()F n 为这个数的位数（如12n =时，此数为123456789101112，共有15个数字，(12)15f =），现从这个数中随机取⼀个数字，()p n 为恰好取到0的概率．（1）求(100)p ；（2）当2014n ≤时，求()F n 的表达式．（3）令()g n 为这个数字0的个数，()f n 为这个数中数字9的个数，()()()h n f n g n =-，{|()1,100,*}S n h n n n N ==≤∈，求当n S ∈时()p n 的最⼤值．解：（1）当100n =时，这个数中总共有192个数字，其中数字0的个数为11，所以恰好取到0的概率为()11100192p =．（2分）（2）当19n ≤≤时，这个数有1位数组成，()9F n =，当1099n ≤≤时，这个数有9个1位数组成，9n -个两位数组成，则()29F n n =-，当100999n ≤≤时，这个数有9个1位数组成，90个两位数组成，99n -个三位数组成，()3108F n n =-，当10002014n ≤≤时，这个数有9个1位数组成，90个两位数组成，900个三位数组成，999n -个四位数组成，()41107F n n =-，所以,1929,1099()3108,10099941107,10002014n n n n F n n n n n ≤≤??-≤≤?=?-≤≤??-≤≤?（5分）（3）当n b =（+19N b b ≤≤∈，），()0g n =；当()1019,09,,n k b k b k N b N +=+≤≤≤≤∈∈时，()g n k =；100n =时()11g n =，即,0,19,(),n 10,19,09,,11,n 100n g n k k b k b k N b N +?≤≤?==+≤≤≤≤∈∈??=?（8分）同理有,0,18,,n 10,19,09,,()80,8998,20,n 99,100n k k b k b k N b N f n n n +≤≤??=+≤≤≤≤∈∈?=?-≤≤??=?（10分）由()()()1h n f n g n =-=h ，可知9,19,29,49,59,69,79,89,90n =，所以当n 100≤时，}{9,19,29,39,49,59,69,79,89,90S =（11分）当9n =时，()90p =，当90n =，()()()901909019g p F ==，当()10918,n k k k N +=+≤≤∈时， ()()()29209g n k k p n F n n k ===-+（13分）由209ky k =+关于k 单调递增，故当109n k =+（18k ≤≤，k N +∈）时，()p n 的最⼤值为()889169p =，⼜8116919<，所以最⼤植为119．（14分）【点评】本题为信息题，也是本卷的压轴题，考查学⽣认识问题、分析问题、解决问题的能⼒，本题的命题新颖，对学⽣能⼒要求较⾼，难度较⼤，解决本题的关键⾸先在于审清题意，搞清楚()F n 、()p n 的含义，这样就可以解决前两问，同时为第三问做好铺垫，第三问在前两问的基础上再加以深⼊，考查学⽣综合分析问题的能⼒．本题由易到难，层层深⼊，是⼀道难得的好题．。

江西省南昌市教研室命制2014届高三数学交流卷试题(一)文

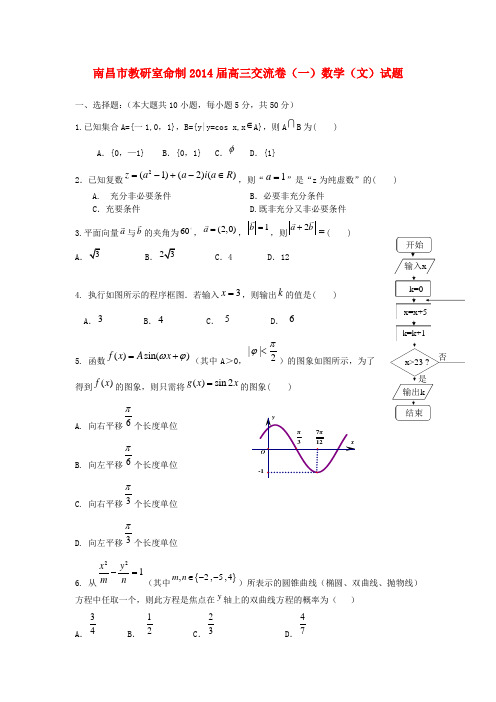
南昌市教研室命制2014届高三交流卷（一）数学（文）试题一、选择题：（本大题共10小题，每小题5分，共50分） 1.已知集合A={一1,0，1}，B={y|y=cos x,x ∈A}，则A B 为( )A ．{0，—1}B ．{0，1}C ．φD ．{1}2．已知复数2(1)(2)()z a a i a R =-+-∈，则“1a =”是“z 为纯虚数”的( ) A. 充分非必要条件 B ．必要非充分条件C ．充要条件 D.既非充分又非必要条件 3.平面向量a 与b 的夹角为60，(2,0)a =，1b =，则2a b+=( )AB． C ．4 D ．124. 执行如图所示的程序框图．若输入3x =，则输出k 的值是( ) A ．3 B ．4 C ． 5 D ． 65. 函数()sin()f x A x ωϕ=+（其中A ＞0，2||πϕ<）的图象如图所示，为了得到()f x 的图象，则只需将()sin 2g x x =的图象( )A. 向右平移6π个长度单位B. 向左平移6π个长度单位 C. 向右平移3π个长度单位 D. 向左平移3π个长度单位6. 从221x y m n -=（其中{},2,5,4m n ∈--）所表示的圆锥曲线（椭圆、双曲线、抛物线）方程中任取一个，则此方程是焦点在y 轴上的双曲线方程的概率为（）A ．34B ． 12 C ．23D ．47是结束输出k 否x>23 ?k=k+1x=x+5k=0输入x 开始7. 函数13y x x =-的图象大致为8. 四棱锥P ABCD -的顶点P 在底面ABCD 中的投影恰好是A ，其三视图如图所示，则四棱锥P ABCD -的表面积为（）A.2222S a a =+ B. 2223S a a =C. 2242S a a =+ D. 2233S a a =9.已知抛物线22(0)y p xp =>的焦点F 与椭圆22221(0)x y a b a b +=>>的一个焦点重合，它们在第一象限内的交点为T ，且T F 与x 轴垂直，则椭圆的离心率为（）A ．212- 21- Ｃ．13- Ｄ．213-10.如图，点P 从点O 出发，分别按逆时针方向沿周长均为12的正三角形、正方形运动一周，,O P 两点连线的距离y 与点P 走过的路程x 的函数关系分别记为(),()y f x y g x ==，定义函数()()()()()()()f x f x g x h x g x f x g x ⎧⎪=⎨>⎪⎩，≤，，．对于函数()y h x =，下列结论正确的个数是（）① (4)10h = ； ②函数()h x 的图象关于直线6x =对称； ③函数()h x 值域为013⎡⎣，； ④函数()h x 增区间为05（，）．第10题图 A ．1 B ．2 C ．3 D ．4二、填空题（本大题共5小题，每小题5分，共25分. ）OPPO11．已知数列1,,9a 是等比数列，数列121,,,9b b 是等差数列，则12ab b +的值为 .12．某校高三第一次模考中，对总分450分（含450分）以上的成绩进行统计，其频率分布直方图如图所示，若650～700分数段的人数为90，则500～550分数段的人数为_________人.13. 若关于x ，y 的不等式组10,10,10x y x ax y +-≥⎧⎪-≤⎨⎪-+≥⎩（a 为常数）所表示的平面区域的面积等于2，则a 的值为 .14. 在直角三角形ABC 中，90ACB ∠=︒，2AC BC ==，点P 是斜边AB 上的一个三等分点，则CP CB CP CA ⋅+⋅= ． 15. 给出下列四个命题：①ABC ∆中，A B >是sin sin A B >成立的充要条件；②当01x x >≠且时，有1ln 2ln x x +≥；③已知n S 是等差数列{}n a 的前n 项和，若75S S >，则93S S >；④若函数)23(-=x f y 为R 上的奇函数，则函数)(x f y =的图象一定关于点)0,23(F 成中心对称.⑤函数)(cos sin cos )(23R x x x x x f ∈-+=有最大值为2，有最小值为0。

2014南昌二中高考数学第十一次模拟试卷(带答案文科)

2014南昌二中高考数学第十一次模拟试卷（带答案文科）一、选择题（题型注释）1．设集合{}1,0,2A =-，集合{}2B x x A x A =-∈-∉且，则B =（） A ．{}1B ．{}2-C ．{}1,2--D ．{}1,0-2．复数122ii -+的计算结果是（） A ．35i - B ．i - C ．iD ．35i3．若双曲线2214x y m -=，则m= AB ．3 CD ．4．设等差数列{n a }的前n 项和为S n ，若a 1=1，a 2+a 3=11，则S 6一S 3=A ．27B ．39C ．45D ．635．某几何体的三视图如题（6）所示，其侧视图是一个边长为1的等边三角形，俯视图是两个正三角形拼成的菱形，则这个几何体的体积为（）A ．1B ．12 C ．14D ．18 6．若直线cos sin 10x y θθ+-=与圆221(1)(sin )16x y θ-+-=相切，且θ为锐角，则这条直线的斜率是( )A．． CD7．若下面框图所给的程序运行结果为20S =,那么判断框中应填入的关于k 的条件是（）A ．9?k =B ．8?k ≥C ．8?k <D ．8?k >8．已知ABC ∆中，D BC 是边的中点，过点D 的直线分别交直线AB 、AC 于点E 、F ，若AE AB λ=，AF AC μ=，其中0,0λμ>>，则λμ的最小值是（）A ．1B ．12C ．13D ．149．设y x .满足不等式组⎪⎩⎪⎨⎧≤≥+≥+-2004x y x y x ，若y ax Z +=的最大值为62+a ，最小值为22-a ，则实数a 的取值范围是( ) A.()1,1-B.[]1,1-C.[)1,2-D.[]1,2-10．已知 21()sin(),'()42f x x x f x π=++为 ()f x 的导函数，则 '()y f x =的图象大致是（）二、填空题（题型注释）11．若3sin()45πα+=，则sin 2α= . 12．直线32y x =与椭圆22221(0)+=>>x y a b a b相交于A 、B 两点，过点A 作x 轴的垂线，垂足恰好是椭圆的一个焦点，则椭圆的离心率是．13．在已知平面区域(){,0x y y Ω=≤≤，直线:2l y mx m =+和曲线:C y =有两个不同的交点，直线l 与曲线C 围成的平面区域为M ，向区域Ω内随机投一点A ，点A 落在区域M 内的概率为()P M ，若2(),12P M ππ-⎡⎤∈⎢⎥⎣⎦，则实数m 的取值范围是 . 14．函数()1f x x x a =++-，若不等式()6f x ≥的解集为(][),24,-∞-+∞，则实数a 的值为 .15．空间中任意放置的棱长为2的正四面体ABCD .下列命题正确的是_________.（写出所有正确的命题的编号）①正四面体ABCD 的主视图面积可能是2； ②正四面体ABCD 的主视图面积可能是3； ③正四面体ABCD 的主视图面积可能是2； ⑤正四面体ABCD 的主视图面积可能是22 ⑥正四面体ABCD 的主视图面积可能是4.三、解答题（题型注释）16．已知函数()2cossin 222x x x f x ⎫=-⎪⎭．（1）设ππ22θ⎡⎤∈-⎢⎥⎣⎦，，且()1f θ=，求θ的值；（2）在△ABC 中，AB=1，()1f C =，且△ABC ，求sinA+sinB 的值．17．已知数列{}n a 的前n 项和为n S 满足：332n n S a n =+-．（1）求证：数列{1}n a -是等比数列；（2）令31323log (1)log (1)log (1)n n c a a a =-+-++-，对任意*n ∈N ，是否存在正整数m ，使121113n mc c c +++≥都成立？若存在，求出m 的值；若不存在，请说明理由．18．如图，在四棱锥P －ABCD 中，PD⊥平面ABCD ，四边形ABCD 是菱形，AC ＝6，BD ＝8，E 是PB 上任意一点，△AEC 面积的最小值是3．（1）求证： AC⊥DE；（2）求四棱锥P －ABCD 的体积．19．一个均匀的正四面体面上分别涂有1,2,3,4四个数字，现随机投掷两次，正四面体面朝下的数字分别为b c ，．(1)记22(3)(3)z b c ＝－＋－，求4z ＝的概率；(2)若方程20x bx c －－＝至少有一根{}1,2,3,4a ∈，就称该方程为“漂亮方程”，求方程为“漂亮方程”的概率．20．已知椭圆:C 22221(0)x y a b a b +=>>的左焦点为F ,左、右顶点分别为,A B ,过点F 且倾斜角为4π的直线l 交椭圆于,C D 两点,椭圆C,AC AD BC BD ⋅-⋅=．（1）求椭圆C 的方程；（2）若12,P P 是椭圆上不同两点，12PP x ⊥轴，圆E 过点12,P P ，且椭圆上任意一点都不在圆E 内，则称圆E 为该椭圆的内切圆．问椭圆C 是否存在过点F 的内切圆？若存在，求出点E 的坐标；若不存在，说明理由．21．已知函数()()24ln 1f x ax x =--，a ∈R ．（1）当1a =时，求()f x的单调区间；（2）已知点()1,1P 和函数()f x 图象上动点()(),M m f m ，对任意[]2,1m e ∈+，直线PM 倾斜角都是钝角，求a 的取值范围．南昌二中2014届高三第十一次模拟考试试题数学(文)参考答案1．A 2．（B ） 3．B 4．B 5．C 6．A 7．（D ） 8．A 【解析】试题分析：由已知得：11112222AD AB AC AE AF λμ=+=+，因为D 、E 、F 三点共线，所以11122λμ+=，由重要不等式得：111112,12222λμλμλμλμ+≥⋅=∴≥.EDAB CF考点：向量的运算.9．B 10．A【解析】因为，2211()sin()cos 424f x x x x x π=++=+，所以，1'()sin 2f x x x =-为奇函数，其图象关于原点对称．可排除,B D ；由于6x π=时，1'()(1)0626f ππ=-<，即'()y f x =的图象位于x 轴下方，故选A ．考点：函数的奇偶性、单调性，导数的计算． 11．725- 12．1213．]1,0[ 14．3当光线平行于底面BCD ，沿CD方向时，主视图为图中△ABE ，则其面积为122⨯⨯=，①正确；将正四面体放入正方体中，如上右图，光线垂直于正方体正对我们的面时，主视图是正方形，2=，并且此时主视图面积最大，故③正确，④⑤不正确.考点：1.几何体的三视图；2.几何图形的面积.16．（1）ππ26θ=-或，（2）1【解析】试题分析：（1）研究三角函数性质，首先将三角函数化为基本三角函数形式，即：2()2sin cos222x x xf x=-=cos)sinx x+-=π2cos6x⎛⎫++⎪⎝⎭．再由()1fθ=得π1cos62θ⎛⎫+=⎪⎝⎭于是ππ2π()63k kθ+=±∈Z，因为()0f x'<，所以ππ26θ=-或．（2）解三角形，基本方法利用正余弦定理进行边角转化. 因为△ABC的面积，所以1πsin26ab=，于是ab=.因为(0π)C∈，，由（1）知π6C=．由余弦定理得2222π12cos66a b ab a b=+-=+-，所以227a b+=．可得2ab=⎧⎪⎨=⎪⎩，或2.ab⎧=⎪⎨=⎪⎩由正弦定理得sin sin sin112A B Ca b===,所以()1sin sin12A B a b+=+=+．【解】（1）2()2sin cos222x x xf x=-cos)sinx x+-=π2cos6x⎛⎫++⎪⎝⎭．由π2cos16θ⎛⎫+=+⎪⎝⎭，得π1cos62θ⎛⎫+=⎪⎝⎭，于是ππ2π()63k kθ+=±∈Z，因为ππ22θ⎡⎤∈-⎢⎥⎣⎦，，所以ππ26θ=-或．（2）因为(0π)C∈，，由（1）知π6C=．因为△ABC1πsin26ab=，于是ab=. ①在△ABC中，设内角A、B的对边分别是a，b.由余弦定理得2222π12cos66a b ab a b=+-=+-，所以227a b+=．②由①②可得2ab=⎧⎪⎨=⎪⎩，2.ab⎧=⎪⎨=⎪⎩于是2a b+=+．由正弦定理得sin sin sin112A B Ca b===，所以()1sin sin 12A B a b +=+=+．考点：三角函数性质，正余弦定理17．（1）详见解析；（2）m 的值为1，2，3．【解析】试题分析：（1）首先由题设找到n a 与1n a -间的关系，然后证明111n n a a ---是一个常数.（2）首先求得31323(1)log (1)log (1)log (1)122n n n n c a a a n +=-+-++-=+++=，由此得12112()(1)1n c n n n n ==-++，用裂项法可求得和121111111112[(1)()()]2(1)22311n c c c n n n +++=-+-++-=-++.由121113n mc c c +++≥对任意*n ∈N 都成立，得12(1)13m n -≥+，即16(1)1m n ≤-+对任意*n ∈N 都成立，所以 m 小于等于16(1)1n -+的最小值. （1）当1n =时，111322S a a ==-，解得14a =， 1分当2n ≥时，由332n n S a n =+-得11342n n S a n --=+-， 2分两式相减，得1133122n n n n S S a a ---=-+，即132n n a a -=-（2n ≥）， 3分则113(1)n n a a --=-，故数列{1}n a -是以113a -=为首项，公比为3的等比数列． 4分（2）由（1）知13n n a -=， 31323(1)log (1)log (1)log (1)122n n n n c a a a n +=-+-++-=+++=， 6分所以12112()(1)1n c n n n n ==-++， 7分则121111111112[(1)()()]2(1)22311n c c c n n n +++=-+-++-=-++， 8分由121113n mc c c +++≥对任意*n ∈N 都成立，得12(1)13m n -≥+， 10分即16(1)1m n ≤-+对任意*n ∈N 都成立，又*m ∈N ，所以m 的值为1，2，3． .12分考点：1、等比数列；2、裂项法求和；3、不等关系.18．（1）详见解析，（2【解析】试题分析：（1）证明线线垂直，一般利用线面垂直性质与判定定理进行转化. 因为四边形ABCD 是菱形，所以AC ⊥BD ．又因为PD ⊥平面ABCD ，所以PD ⊥AC ．因而AC ⊥平面PDB ，从而AC ⊥DE ．（2）设AC 与BD 相交于点F ．连EF ．由（1），知AC ⊥平面PDB ，所以AC ⊥EF ．所以S △ACE ＝12AC ·EF ，因此△ACE 面积最小时，EF 最小，则EF ⊥PB ．由△PDB ∽△FEB，解得PD ，因为PD ⊥平面ABCD ，所以VP —ABCD ＝13S □ABCD ·PD ＝13×24＝．（1）证明：连接BD ，设AC 与BD 相交于点F ．因为四边形ABCD 是菱形，所以AC ⊥BD ．又因为PD ⊥平面ABCD ，AC ⊂平面ABCD ，所以PD ⊥AC ．而AC ∩BD ＝F ，所以AC ⊥平面PDB ．E 为PB 上任意一点，DE ⊂平面PBD ，所以AC ⊥DE ．（2）连EF ．由（1），知AC ⊥平面PDB ，EF ⊂平面PBD ，所以AC ⊥EF ． S △ACE ＝12AC ·EF ，在△ACE 面积最小时，EF 最小，则EF ⊥PB ．S △ACE ＝3，12×6×EF ＝3，解得EF ＝1．由△PDB ∽△FEB ，得PD PB EF FB=．由于EF ＝1，FB ＝4，PB =，所以PB ＝4PD 4PD =．解得PDVP —ABCD ＝13S □ABCD ·PD ＝13×24．考点：线面垂直性质与判定定理，四棱锥体积 19．(1) 1(4)8P z =＝；(2)316P =．【解析】试题分析：（1）由于要将均匀的面上分别涂有1、2、3、4四个数字的正四面体随机投掷两次，故基本事件共有4×4=16个，然后求出4z ＝时，基本事件的个数，代入古典概型公式即可得到结果；（2）分类讨论方程根分别为1，2，3，5时，基本事件的个数，然后代入古典概型公式即可得到结果．(1)因为是投掷两次，因此基本事件()b c ，共有16个，当4z ＝时，()b c ，的所有取值为(1,3)，(3,1)，所以21(4)168P z =＝＝． (2)①若方程一根为1x ＝，则10b c －－＝，即1b c ＋＝，不成立． ②若方程一根为2x ＝，则420b c －－＝，即24b c +=，所以12b c =⎧⎨=⎩．③若方程一根为3x ＝，则930b c －－＝，即39b c ＋＝，所以23b c =⎧⎨=⎩． ④若方程一根为4x ＝，则1640b c －－＝，即416b c ＋＝，所以34b c =⎧⎨=⎩．综合①②③④知，()b c ，的所有可能取值为(1,2)，(2,3)， (3, 4)，所以，“漂亮方程”共有3个，方程为“漂亮方程”的概率为316P =．考点：1．创新能力；2．古典概型．20．（1）2214x y +=；（2）存在E (【解析】试题分析：（1）由离心率为，倾斜角为4π的直线l交椭圆于,C D两点，AC AD BC BD⋅-⋅=.通过联立直线方程与椭圆的方程，可求得,a b的值.即可得结论.（2）依题意可得符合要求的圆E，即为过点F,12,P P的三角形的外接圆.所以圆心在x轴上.根据题意写出圆E的方程.由于圆的存在必须要符合，椭圆上的点到点E距离的最小值是1||PE，结合图形可得圆心E在线段12PP上，半径最小.又由于点F已知，即可求得结论. 试题解析：（1，所以2,a b c==，所以椭圆方程可化为：222214x yb b+=，直线l的方程为y x=+， 2分由方程组222214x yb by x⎧+=⎪⎨⎪=+⎩，得：2224()4x x b++=,即22580x b++=, 4分设1122(,),(,)C x yD x y，则12x x+=， 5分又1122112212(,)(,)(,)(,)2()AC AD BC BD x a y x a y x a y x a y a x x ⋅-⋅=+⋅+--⋅-=+，所以4()b⋅=1b=，椭圆方程是2214xy+=； 7分（2）由椭圆的对称性，可以设12(,),(,)P m n P m n-，点E在x轴上，设点(,0)E t，则圆E的方程为2222:()()x t y m t n-+=-+，由内切圆定义知道，椭圆上的点到点E距离的最小值是1||PE，设点(,)M x y是椭圆C上任意一点，则222223||()214ME x t y x tx t=-+=-++, 9分当x m=时，2||ME最小，所以24332t tm-=-=① 10分又圆E过点F，所以222()()t m t n-=-+② 11分点1P在椭圆上，所以2214mn=-③ 12分由①②③解得：t=t=，又t=时，2m=<-，不合，综上：椭圆C存在符合条件的内切圆，点E的坐标是(． 13分考点：1.待定系数求椭圆方程.2.函数的最值.3.方程的思想解决解决解几问题.3.归纳化归的思想.4.运算能力.21．（1）单调递增区间为()2,+∞，单调递减区间为()1,2；（2）14a<【解析】试题分析：（1）先求导，再令导数等于0，解导数大于0得函数的增区间，解导数小于0得函数的减区间。

江西省南昌市2014届高三数学(文)交流卷(九)

江西省南昌市2014届高三数学（文）交流卷（九）一、选择题（本题共10个小题，每题5分，共50分，每小题给出的四个选项中，只有一个是符合要求的）1若纯虚.数z 满足2(2i)4(1i)z b -=-+（其中是虚数单位，b 是实数），则b =（）A ．2-B ．2C ．-4D ．42．设集合33{|0},{|||},""""122x P x Q x x m P m Q x =≤=-≤∈∈-那么是的（） A ．充分不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件 3．如图是函数y ＝sin(ωx ＋φ)(ω>0，0<φ<π)的图像的一部分，A ，B 是图像上的一个最高点和一个最低点，O 为坐标原点，则OA ·OB 的值为 A.12πB.19π2＋1C.19π2－1 D.13π2－1 4．设各项为正的等比数列}{n a 的公比1≠q ，且653,,a a a 成等差数列，则6453a a a a ++的值为 A ．215+ B.215- C.21 D.2 5．若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为( ) A.163π B.193π C.1912π D.43π 6.已知奇函数)0,()(-∞在x f 上是单调减函数，且0)2(=f ，则不等式0)1()1(>--x f x 的解集为:A ．}13|{-<<-x x B.}3111|{<<<<-x x x 或C ．}3103|{<<<<-x x x 或 D.}213|{><<-x x x 或7.已知1tan()42πα+=，且02πα-<<，则22sin sin 2cos()4ααπα+=-（）A.8．抛物线y 2＝2px (p ＞0)的焦点为F ，其准线经过双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左顶点，点M 为这两条曲线的一个交点，且|MF |＝2p ，则双曲线的离心率为( )． A.102 B ．2 C. 5 D.529. 在R 上定义运算⊗：x ⊗y ＝x (1－y )，若不等式(x －a )⊗(x ＋a )＜1对任意实数x 成立，则( ).A ．－1＜a ＜1B ．0＜a ＜2C ．－12＜a ＜32D ．－32＜a ＜1210. 设函数f (x )＝1x，g (x )＝－x 2＋bx .若y ＝f (x )的图象与y ＝g (x )的图象有且仅有两个不同的公共点A (x 1，y 1)，B (x 2，y 2)，则下列判断正确的是( )A.x 1＋x 2>0，y 1＋y 2>0B.x 1＋x 2>0，y 1＋y 2<0C.x 1＋x 2<0，y 1＋y 2>0D.x 1＋x 2<0，y 1＋y 2<0二、填空题（本题共5个小题，每小题5分，共25分）11．已知向量a =(2,1),b =(x ,y ). 若x ∈{-1,0,1,2}，y ∈{-1,0,1}，求向量a ∥b 的概率为 .12．如图，正三角形ABC 的中线AF 与中位线DE相交于点G ，已知△A ′ED 是△AED 绕DE 旋转过程中的一个图形，现给出下列四个命题：①动点A ′在平面ABC 上的射影在线段AF 上； ②恒有平面A ′GF ⊥平面BCED ；③三棱锥A ′－FED 的体积有最大值；④直线A ′E 与BD 不可能垂直．其中正确的命题的序号是________．13．运行如右图所示的程序框图，若输出的y 值的范围是[0, 10]，则输入的x 的值的范围是．14. 已知函数⎩⎨⎧≤+>+=0),3(20,2log )(2x x f x x x f ，则=-)5(f 15.已知数列{a n }中，a 1＝1，且P (a n ，a n ＋1)(n ∈N *)在直线x －y ＋1＝0上，若函数f (n )＝1n ＋a 1＋1n ＋a 2＋1n ＋a 3＋…＋1n ＋a n (n ∈N *，且n ≥2)，函数f (n )的最小值是________．四、解答题（本题共6个小题，共75分，解答应写出文字说明、证明过程或演算步骤）.16．（本题满分12分）已知(cos sin )m x x x ωωω=+，()cos sin ,2sin n x x x ωωω=-，其中ω＞0．设函数f (x )＝m n ⋅，且函数f (x )的周期为π．(Ⅰ) 求ω的值；(Ⅱ)在△ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，且a ，b ，c 成等差数列，当f (B )＝1时，判断△ABC 的形状．17．(本小题满分12分)有一个3×4×5的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成60个1×1×1的小正方体，从这些小正方体中随机地任取1个.（1）求小正方体各面没有涂色的概率.（2）求小正方体有2面或3面涂色的概率.18.（本小题满分12分）如图，已知正三棱柱ABC —A 1B 1C 1中，D 是BC 的中点，AA 1=AB=1.（1）求证：平面AB 1D ⊥平面B 1BCC 1；（2）求证：A 1C//平面AB 1D ；.19．（本小题满分12分）数列{a n }中，a 1＝1，当n ≥2时，其前n 项和S n 满足S 2n ＝a n (S n －1)．(1)求证：数列⎩⎨⎧⎭⎬⎫1S n 是等差数列；(2)设b n ＝log 2S n S n ＋2，数列{b n }的前n 项和为T n ，求满足T n ≥6的最小正整数n .20．（本小题满分13分）已知中心在原点的椭圆C ：x 2a 2＋y 2b 2＝1的一个焦点为F 1(0, 3)，M (x,4)(x ＞0)为椭圆C 上一点，△MOF 1的面积为32.(1)求椭圆C 的方程；(2)是否存在平行于OM 的直线l ，使得直线l 与椭圆C 相交于A ，B 两点，且以线段AB 为直径的圆恰好经过原点？若存在，求出直线l 的方程；若不存在，说明理由．答案17．(本题满分12分)(1)60个1×1×1的小正方体中，没有涂上颜色的有6个，61(0)6010P ξ===； (2) ）由（1）可知P =(2)P ξ=+(3)P ξ=2460=886015+=. 18.（本小题满分12分）解法一：证明：（1）因为B 1B ⊥平面ABC ，AD ⊂平面ABC ，所以AD ⊥B 1B （1分）因为D 为正△ABC 中BC 的中点，所以AD ⊥BD （2分）又B 1B ∩BC=B ，所以AD ⊥平面B 1BCC 1 （3分）又AD ⊂平面AB 1D ，故平面AB 1D ⊥平面B 1BCC 1 （4分）（2）连接A 1B ，交AB 1于E ，连DE （5分）因为点E 为矩形A 1ABB 1对角线的交点，所以E 为AB 1的中点（6分）又D 为BC 的中点，所以DE 为△A 1BC 的中位线，所以DE//A 1C （7分）又DE ⊂平面AB 1D ，所以A 1C//平面AB 1D （8分）解法二：解：建立如图所示的直角坐标系，依题意有：111(((0,,0),(0,,1),221(0,,0),(0,0,0)(2)2A A B B C D --分（1）证明：由13(,0,0),(0,1,0),(0,0,1)AD BC BB ===，得110,,,0,AD BC AD BC AD BB AD BB ⎧⋅=⊥⎧⎪⎨⎨⊥⋅=⎩⎪⎩所以又BC ∩⊥BB 1=B ，所以AD ⊥平面B 1BCC 1. （4分）又AD ⊂平面AB 1D ，所以平面AB 1D ⊥B 1BCC 1 （5分）（2）证明：连接A 1B ，交AB 1于E ，连DE ，因为点E 为正方形A 1ABB 1对角线的交点，所以E 为AB 1的中点，即11(,).42E - （6分） 11131131(,,),(,,1),4222,DE A C A C ED ==-=由得所以A C//ED.(7分)又DE ⊂平面AB 1D ，所以A 1C//平面AB 1D （8分）19. (1)证明：∵2n S ＝a n (S n －1)，∴2n S ＝(S n －S n －1)(S n －1)(n ≥2)．∴S n S n －1＝S n －1－S n ，即1S n －1S n －1＝1. ∴⎩⎨⎧⎭⎬⎫1S n 是以1为首项，1为公差的等差数列． (2)解：由(1)知S n ＝1n ，∴b n ＝log 2n ＋2n. ∴T n ＝log 2(31×42×53×64×…×n ＋2n )＝log 2(n ＋1)(n ＋2)2≥6.∴(n ＋1)(n ＋2)≥128.∵n ∈N *，∴n ≥10.∴满足T n ≥6的最小正整数为10.20. 解：(1)因为椭圆C 的一个焦点为F 1(0,3)，所以b 2＝a 2＋9.则椭圆C 的方程为x 2a 2＋y 2a 2＋9＝1. 因为x ＞0，所以S △MOF 1＝12×3×x ＝32，解得x ＝1. 故点M 的坐标为(1,4)．因为M (1,4)在椭圆上，所以1a 2＋16a 2＋9＝1，得a 4－8a 2－9＝0，解得a 2＝9或a 2＝－1(不合题意，舍去)，则b 2＝9＋9＝18，所以椭圆C 的方程为x 29＋y 218＝1. (2)假设存在符合题意的直线l 与椭圆C 相交于A (x 1，y 1)，B (x 2，y 2)两点，其方程为y ＝4x ＋m (因为直线OM 的斜率k ＝4)．由⎩⎪⎨⎪⎧y ＝4x ＋m ，x 29＋y 218＝1，消去y 化简得18x 2＋8mx ＋m 2－18＝0. 进而得到x 1＋x 2＝－8m 18，x 1x 2＝m 2－1818. 因为直线l 与椭圆C 相交于A ，B 两点，所以Δ＝(8m )2－4×18×(m 2－18)＞0，化简得m 2＜162，解得－92＜m ＜9 2.因为以线段AB 为直径的圆恰好经过原点，所以·＝0，所以x 1x 2＋y 1y 2＝0.又y 1y 2＝(4x 1＋m )(4x 2＋m )＝16x 1x 2＋4m (x 1＋x 2)＋m 2，x 1x 2＋y 1y 2＝17x 1x 2＋4m (x 1＋x 2)＋m 2＝17(m 2－18)18－32m 218＋m 2＝0. 解得m ＝±102.由于±102∈(－92，92)，所以符合题意的直线l 存在，且所求的直线l 的方程为y ＝4x ＋102或y ＝4x －102.21.【解析】（1）因为()22ln (0)a f x x a x x x =+->，所以()()222222222()1x a x a a a x ax a f x x x x x+---'=--==． ①若0=a ，()x x f =，()x f 在()+∞,0上单调递增．②若0>a ，当()0,2x a ∈时，()0f x '<， ()x f 在()a 2,0上单调递减；当()2,x a ∈+∞时，()0f x '>，()x f 在()+∞,2a 上单调递增．③若0<a ，当()0,x a ∈-时，()0f x '<， ()x f 在()a -,0上单调递减；当(),x a ∈-+∞时，()0f x '>，()x f 在()+∞-,a 上单调递增．综上：①当0=a 时，()x f 在()+∞,0上单调递增．②当0>a 时，()x f 在()a 2,0上单调递减，()x f 在()+∞,2a 上单调递增． ③当0<a 时，()x f 在()a -,0上单调递减，()x f 在()+∞-,a 上单调递增．（2）当1a =时，()()0ln 2>-+=x x xx x f ．由（1）知，若1a =，当()0,2x ∈时，()0f x '<，()x f 单调递减，当()2,x ∈+∞时，()0f x '>，()x f 单调递增，所以()()2ln 32min -==f x f ．因为对任意的12,[1,e]x x ∈，都有12()()f x g x ≥成立，问题等价于对于任意[]1,e x ∈，()()min f x g x ≥恒成立，即23ln 224ln 2x bx --+-≥对于任意[]1,e x ∈恒成立，即12b x x+≥对于任意[]1,e x ∈恒成立，因为函数x x y 1+=的导数21'10y x =-≥在[]1,e 上恒成立，所以函数x x y 1+=在[]1,e 上单调递增，所以max 11e e x x ⎛⎫+=+ ⎪⎝⎭，所以12e e b +≥，所以e 122eb +≥．。

江西省南昌市第二中学2013-2014学年高三上学期第一次月考文数试卷

江西省南昌市第二中学2013-2014学年高三上学期第一次月考文数试卷一、选择题（60125=⨯分）1. 已知集合{}{})2lg(.1x y R x B x y R x A -=∈=-=∈=则=⋂B A[)2,1.A (]2,1.B []2,1.C)2,1.(D2.已知命题;32,:xxR x P <∈∀命题231,:x x R x q -=∈∃则下列命题中为真命题的是：q p A ∧. q p B ∧⌝. q p C ⌝∧. q p D ⌝∧⌝. 3.若集合{}.0142=++∈=x ax R x A 中只有一个元素，则=a 016.==a a A 或 04.==a a B 或 02.==a a C 或 42.==a a D 或 4.已知角α的终边过点0),3,(≠--a a a P ，则=αsin101010103.或A 10103.B 10101010.-或C 1010310103.-或D 5.已知,51)25sin(=+απ那么=αcos562.-A 562.B 51.C 51.-D6.对数函数a x x f -=ln )(在[]1,1-区间上恒有意义，则a 的取值范围是: []1,1.-A (][)+∞⋃-∞-,11,.B ),1()1,.(+∞⋃--∞C ),0()0,.(+∞⋃-∞D7.对于函数,12log 212)(33++++=xx x b ax x f 若,2)1(=-f 则=)1(f2.A 23.B 23.-C 5.D8.已知函数),2(,ln )1(21)(2>-+-=a x a ax x x f 则)(x f 的单调增区),1()1,.(+∞--∞a A 和 ),1()1,0.(+∞-a B 和 ),1()1,0.(+∞-和a C ),1()1,.(+∞--∞和a D9.设函数3ln )(,2)(2-+=-+=x x x g x e x f x，若实数b a ,满足0)(,0)(==b g a f ，则)(0)(.b f a g A << )()(.a g o b f B <<)()(0.b f a g C <<)(0)(.a g b f D <<10. 对实数a 和b ，定义运算“⊗”：a ⊗b ＝⎩⎪⎨⎪⎧a ，a －b ≤1，b ，a －b >1.设函数f (x )＝(x 2－2)⊗(x －x 2)，x ∈R ，若函数y ＝f (x )－c 的图象与x 轴恰有两个公共点，则实数c 的取值范围是( )A ．(－∞，－2]∪⎝⎛⎭⎫－1，32B ．(－∞，－2]∪⎝⎛⎭⎫－1，－34 C.⎝⎛⎭⎫－1，14∪⎝⎛⎭⎫14，＋∞ D.⎝⎛⎭⎫－1，－34∪⎣⎡⎭⎫14，＋∞ 二、填空题（2054=⨯分）11.函数x ax xx f ln 1)(+-=的导函数是)(x f '，则=')1(f 12.已知集合{}1,2,43,12322≥+=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡∈+-==m x x B x x x y y A 若B A ⊆，则实数m 的取值范围是：13.设9log ,6log ,3log 842===c b a ，则c b a ,,的大小关系是：14.已知函数⎩⎨⎧>+≤+-=0),1ln(0,2)(2x x x x x x f 若ax x f ≥)(，则a 的取值范围是：15.若函数158148)(234++---=x x x x x f ，则)(x f 的最大值是：三、解答题16.（满分12分）已知,552sin -=α且0tan <α （1）求αtan 的值；（2）求)23sin()2cos()2cos()sin(2αππααππα+---++的值；17. （满分12分）已知集合{}⎭⎬⎫⎩⎨⎧≤<-∈=≤+<∈=221,510x R x B ax R x A （1）B A ,能否相等？若能，求出实数a 的值，若不能，试说明理由？（2）若命题,:A x p ∈命题B x q ∈:且p 是q 的充分不必要条件，求实数a 的取值范围；18. （满分12分）已知函数b a a b y xx ,(,22++=是常数0>a 且1≠a ）在区间⎥⎦⎤⎢⎣⎡-0,23上有25,3m in m ax ==y y （1）求b a ,的值；（2）若*∈N a 当10>y 时，求x 的取值范围；19. （满分12分）已知函数1()ln 1()af x x ax a R x-=-+-∈ （1）当a=1时，求曲线在点（3，(3)f ）处的切线方程（2）求函数()f x 的单调递增区间20. （满分13分）设函数21()ln .2f x x ax bx =-- （1）已知()f x 在点(1,(1))P f 处的切线方程是21y x =-，求实数,a b 的值；（2）若方程2(),(0)f x xλλ=>有唯一实数解，求实数λ的值。

江西省南昌二中高三第十一次模拟考试语文试题 Word版含答案.pdf

江西省南昌二中2014届高三第十一次模拟考试语文试题一、（分，每小题3分）词语中A．房檩（lǐn）呵欠（hē）入场券（juàn）恬不知耻（tián ） B．体己（tǐ）岑寂（cén）花骨朵（gū）重湖叠（yǎn） C．八佾(yì) 鲑珍（guì）白炽灯（chì）冯虚御风（píng） D．蕈菌（xùn）脖颈（gěng）文绉绉（zhōu）掌而谈（zhǐ） 2.下列词语中没有错别字的一项是 A．咨嗟坐阵胶合板头晕目眩 B．闪烁驯熟大拇指前合后揠 C．訾詈戟吊角楼凤冠霞帔 D．班驳屠戮综合征匿迹销声 3．上级已经下达了命令，虽然时间紧，任务重，我们也必须为之。

勉力勉力勉励勉励下列各句中，加点的成语使用恰当的一句是 A在责任和使命面前，我们看到的、听到的，是委员和代表正在身体力行，他们用最朴素的语言，为人民更好的生活呐喊、呼吁。

说实话，从里我们不仅没有捕捉到近期复出的信号，相反还感到十分诡异。

于是心中立即产生了这样的念头：刘翔是否会自己的运动生涯呢？二、（9分，每小题3分）阅读下面的文章，完成—8题9．下面对“清醒梦”和《盗梦空间》中的梦境相同点表述正确的一项是 A．《盗梦空间》的梦境就是清醒梦，在自己或他人的梦境中穿越游走，以旁观者的身份观赏梦境的幕布缓缓开启。

B．清醒梦中控制自身梦境的过程与电影描述的场景完全相同，只不过，现实中的“清醒梦”情形没那么华丽。

C．研究表明，要做清醒梦已是轻而易举的事，人们可以像影片中人那样在梦境里按计划完成任务，利用梦境的功能。

D．两种梦境中梦主自己能控制故事情节的发展，将表层意识中一直念念不忘的愿望在梦中实现，引导梦中的行为。

三、（9分，每小题3分）阅读下面的文言文，完成-11题。

/无不同提衡者/权重于物/则坠负担者前/重于后则倾不平/故也 B.人之生也/无不同提衡者/权重于物则坠/负担者前重于后/则倾不平/故也 C.人之生也/无不同/提衡者权重于物则坠/负担者前重于后则倾/不平故也 D.人之生也/无不同/提衡者权重/于物则坠负担者/前重于后则倾/不平故也 12.把文言文阅读材料中画横线的句子翻译成现代汉语。

江西省南昌市名校2014届高考数学模拟卷(5)及答案

江西省南昌市名校2014届高考数学模拟卷（五）命题人：南昌二中审题人：南昌二中一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知i是虚数单位，a∈R．若复数2i2iaa+-为实数，则a ＝A．14B．1C．0 D．2±2.（理）下列函数中，在其定义域上不是奇函数的是A．ln(y x=B．11()212xy x=+-C．123312331ln1x xyx x++=-+D．ln(sec tan)y x x=+（文）以下有关命题的说法错误的是A．命题“若2320,1x x x-+==则”的逆否命题为“若21,320x x x≠-+≠则”B．“cosα=”是“52,6k k zπαπ=+∈”的必要不充分条件C．对于命题22:,10,:,10 p x R x x p x R x x ∃∈++<⌝∀∈++≥使得则则D．若qp∧为假命题，则p、q均为假命题3．（理）已知数列{}na的通项公式2(62)2014na n nλ=-++，若6a或7a为数列{}na的最小项，则实数λ的取值范围A．(3 , 4) B．[ 2 , 5 ] C．[ 3 , 4 ] D．[59 , 22]（文）函数f(x)＝sin x cos xcos 2x的最小正周期和振幅分别是A．πB．πC．2π，1 D．π，4．（理）32sin cos siny x x x=+-的最大值A．2827B．3227C．43D．4027（文）下图是某公司10个销售店某月销售某产品数量(单位：台)的茎叶图，则数据落在区间[22,30)内的概率为A. ．0.2 B．0.4 C．0.5 D．0.65．（理）7(354)x y z+-展开式的项数为A．21 B．28 C．36 D．45（文）现有10个数，它们能构成一个以1为首项，3-为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是A．15B．110C．35D．7106．（理）由曲线28y x=与直线28y x=-围成的封闭图形的面积A．24 B．36 C．42 D．48（文）已知a，b，c∈R，函数f(x)＝ax2＋bx＋c.若f(0)＝f(4-)<f(1)，则A．a>0,4a-b＝0 B．a<0,4a-b＝0 C．a>0,2a-b＝0 D．a<0,2a-b＝07．如程序框图所示，已知集合A＝{x|框图中输出的x值}，集合B＝{y|框图中输出的y值}，全集U＝Z，Z为整数集．当x＝－1时()UC A B＝A．{－3，－1,5} B．{－3，－1,5,7}C．{－3，－1,7} D．{－3，－1,7,9}8.一个由三个正方体组成几何体的三视图如图所示，则该几何体的体积为A．9+ B. 11C. 9.125 D．10+9．（理）椭圆2211625x y+=上的点到圆22(6)1x y++=上的点的距离的最大值D（文）如图，F1、F2是椭圆C1：24x ＋y2＝1与双曲线C2的公共焦点，A 、B 分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是C.3210如图中的阴影部分由底为1，高为1的等腰三角形及高为2和3的两矩形所构成．设函数()y S a =是图中阴影部分介于平行线y a =及x 轴之间的那一部分的面积，则函数()y S a =的图象大致为二、填空题(本大题共5小题,每小题5分共25分.把答案填在答题卷中的横线上.)11．（理）在ABC ∆中，C ∠为钝角，设B A P B A N B A M cos cos ,sin sin ),sin(+=+=+=, 则P N M ,,的大小关系（文）曲线y=323++x x 在1=x 处的切线方程为．12．（理）已知点)3,3(A ， O 为坐标原点，点P （x ，y ）的坐标x ， y 满足⎪⎪⎩≥0y 则向量OP 在向量A O 方向上的投影的取值范围是（文）已知数列}{n a 的通项公式2014)26(2++-=n n a n λ，若6a 或7a 为数列}{n a 的最小项，则实数λ的取值范围13. （理）若函数,3,2,1)),(()(),()(,1)(112===+=+k x f f x f x f x f xx x f k k 又记：,则=)1(2014f（文）设0≤α≤π，不等式x2－(2sin α)x ＋α2cos 21≥0对x ∈R 恒成立，则a 的取值范围为________．14．（理）若P ，Q 为21x y -=上在y 轴两侧的点，则过P,Q 的切线与x 轴围成的三角形的面积的最小值（文）直线82+=x y 的任意点P ,圆x2＋y2－2x －4y ＝0上的任意点为Q ,线段PQ 的长度最小值等于________．15.（理科）选做题：本大题共2小题，任选一题作答. 若做两题，则按所做的第(1)题给分，共5分．(1)(坐标系与参数方程选做题)在直角坐标系xoy 中，直线l 的参数方程为3214x ty t =-⎧⎨=--⎩（t 为参数），若以直角坐标系xoy 的O 点为极点，ox 为极轴，且长度单位相同，建立极坐标系，得曲线C 的极坐标方程为222(cos sin )16ρθθ-=．若直线l 与曲线C 交于,A B 两点，则AB = （2）（不等式选做题）若关于x 的不等式12a x x ≥++-存在实数解，则实数a 的取值范围是 .（文科）已知正四棱锥O －ABCD 的体积为322，底面边长为3，则以O 为球心，OA 为半径的球的表面积为________． .三、解答题（本大题共6小题共75分．解答应写出文字说明、证明过程或演算步骤） 16. （本小题12分）（理）在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ，且222b ac a c bc ==-+．（1）求sin b Bc 的值；（2）试判断△ABC 的形状，并说明理由．（文）已知数列{}n a 满足：11a =，14n n a a n ++=,n S 是数列{}n a 的前n 项和.（1）求数列{}n a 的通项公式；（2）设数列111n S +⎧⎫⎨⎬-⎩⎭的前n 项和为n K ,证明：对于任意的n ∈N*，都有34n K <17（理）已知数列{}n a 满足：11=a ，n a a n n 41=++,n S 是数列{}n a 的前n 项和;数列{}n b 前n 项的积为n T ，且(1)2n n n T -=。

数学_2014年江西省高考数学模拟试卷(文科)(含答案)

2014年江西省高考数学模拟试卷（文科）一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 集合A ={x|−2<x <2}，B ={x|−1≤x +2<3}，那么A ∪B =( )A {x|−2<x <3}B {x|−3≤x <2}C {x|−3≤x <1}D {x|−2<x ≤1} 2. 复数(1+2i)2（其中i 为虚数单位）的虚部为（） A 4i B −4i C 4 D −43. 函数y =√x +2⋅lg(2−x)的定义域为（） A (−2, 0) B (0, 2) C (−2, 2) D [−2, 2)4. “α是第二象限角”是“sinαtanα<0”的（）A 充分不必要条件B 必要不充分C 充分条件D 既不充分也不必要5. 设e 1→，e 2→为单位向量，其中a→=2e 1→+e 2→，b→=e 2→，且a →在b →上的投影为2，则e 1→与e 2→的夹角为（）A π6B π4C π3D π26. 如图是一个空间几何体的三视图，则该几何体的表面积是（）A 12+πB 16+πC 12+2πD 16+2π7. 已知定义域在R 上的函数f(x)图象关于直线x =−2对称且当x ≥−2时，f(x)=3x −4，若函数f(x)在区间(k −1, k)上有零点，则符合条件的k 的值是（） A −8 B −7 C −6 D −58. 阅读如图的程序框图，若运行相应的程序，则输出的S 的值为（）A 64B 66C 98D 2589. 如图，正方体ABCD −A 1B 1C 1D 1的棱长为1，点E 在线段BB 1和线段B 1A 1上移动，∠EAB =θ，θ∈(0, π2)．过直线AE ，AD 的平面ADFE 将正方体分成两部分，记棱BC 所在部分的体积为V(θ)，则函数V =V(θ)，θ∈(0, π2)的大致图象是（）A B C D10. 已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)，F 1，F 2为左右焦点，点P(2, √3)在椭圆C 上，△F 1PF 2的重心为G ，内心为I ，且有IG →=λF 1F 2→（λ为实数），则椭圆方程为（） Ax 28+y 26=1 Bx 216+y 24=1 Cx 29+5y 227=1 Dx 210+y 25=1二、填空题：本大题共5小题，每小题5分，满分25分）11. 命题：“存在正实数x ，y ，使5x +5y =5x+y 成立”的否定形式为________．12. 若不等式组{x +y −1≤0，x −y +1≥0，y ≥0表示的平面区域内的点都不在圆x 2+(y −12)2=r 2(r >0)外，则r 的最小值为________．13. 定义|abcd |=ad −bc ，则|2468|+|10121416|+...+|2010201220142016|=________．14. 已知0<a ≤π2，设函数f(x)=2x −12x +1−cos(x +π2)+1(x ∈[−a, a]的最大值为P ，最小值为Q ，则P +Q 的值为________．15. 已知x ∈R ，则不等式|x +3|−|2x −1|<4的解集为________．三、解答题：本大题共6小题，满分75分，解答时应写出文字说明、证明过程或演算步骤。